Содержание
- Использование интерполяции
- Способ 1: интерполяция для табличных данных
- Способ 2: интерполяция графика с помощью его настроек
- Способ 3: интерполяция графика с помощью функции
- Вопросы и ответы
Бывает ситуация, когда в массиве известных значений нужно найти промежуточные результаты. В математике это называется интерполяцией. В Excel данный метод можно применять как для табличных данных, так и для построения графиков. Разберем каждый из этих способов.
Использование интерполяции
Главное условие, при котором можно применять интерполяцию – это то, что искомое значение должно быть внутри массива данных, а не выходить за его предел. Например, если мы имеем набор аргументов 15, 21 и 29, то при нахождении функции для аргумента 25 мы можем использовать интерполяцию. А для поиска соответствующего значения для аргумента 30 – уже нет. В этом и является главное отличие этой процедуры от экстраполяции.
Способ 1: интерполяция для табличных данных
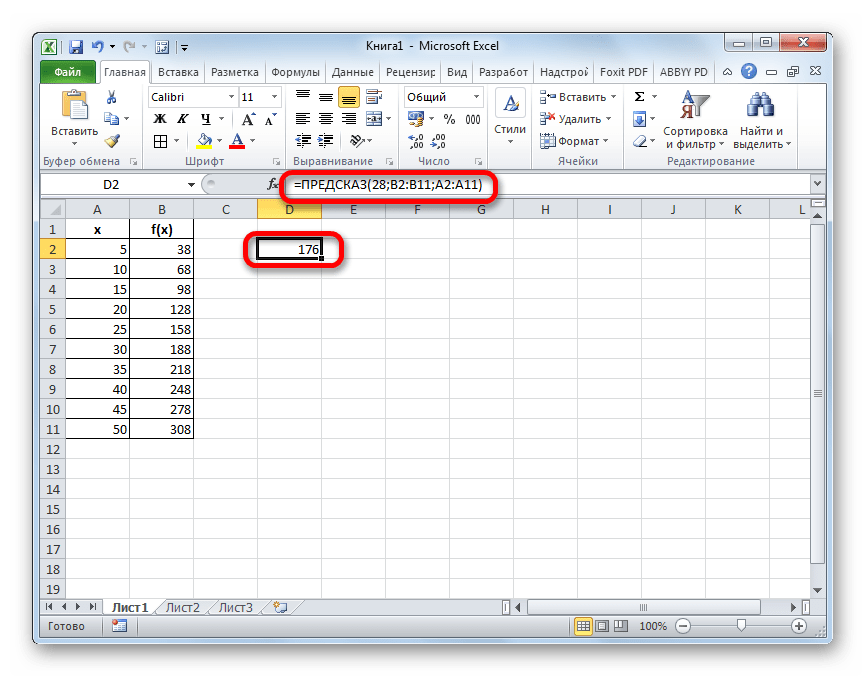
Прежде всего, рассмотрим применения интерполяции для данных, которые расположены в таблице. Для примера возьмем массив аргументов и соответствующих им значений функции, соотношение которых можно описать линейным уравнением. Эти данные размещены в таблице ниже. Нам нужно найти соответствующую функцию для аргумента 28. Сделать это проще всего с помощью оператора ПРЕДСКАЗ.
- Выделяем любую пустую ячейку на листе, куда пользователь планирует выводить результат от проведенных действий. Далее следует щелкнуть по кнопке «Вставить функцию», которая размещена слева от строки формул.
- Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK».
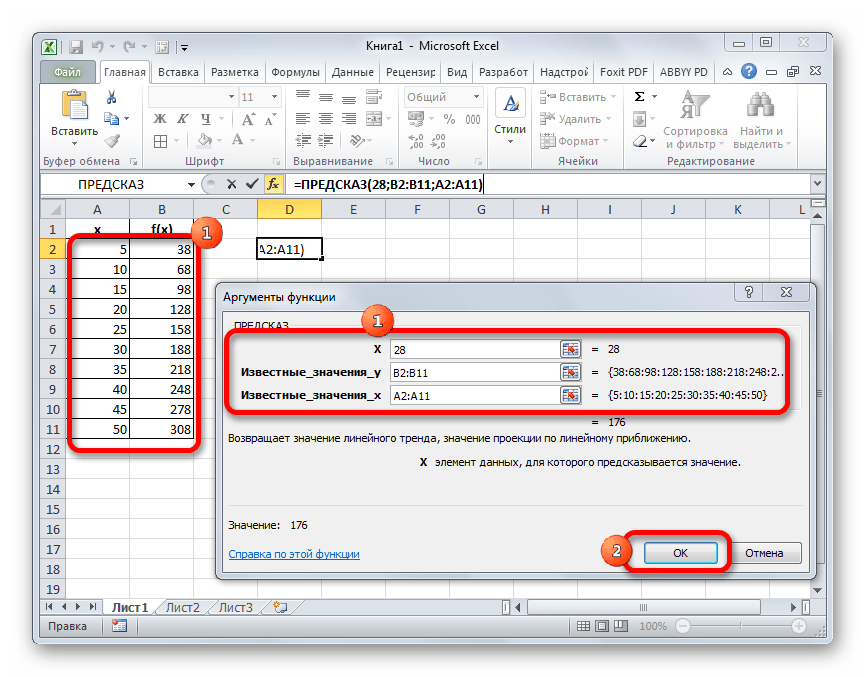
- Запускается окно аргументов функции ПРЕДСКАЗ. В нем имеется три поля:
- X;
- Известные значения y;
- Известные значения x.
В первое поле нам просто нужно вручную с клавиатуры вбить значения аргумента, функцию которого следует отыскать. В нашем случае это 28.
В поле «Известные значения y» нужно указать координаты диапазона таблицы, в котором содержатся значения функции. Это можно сделать вручную, но гораздо проще и удобнее установить курсор в поле и выделить соответствующую область на листе.
Аналогичным образом устанавливаем в поле «Известные значения x» координаты диапазона с аргументами.
После того, как все нужные данные введены, жмем на кнопку «OK».
- Искомое значение функции будет отображено в той ячейке, которую мы выделили ещё в первом шаге данного способа. В результате получилось число 176. Именно оно и будет итогом проведения процедуры интерполяции.
Урок: Мастер функций в Экселе
Способ 2: интерполяция графика с помощью его настроек
Процедуру интерполяции можно применять и при построении графиков функции. Актуальна она в том случае, если в таблице, на основе которой построен график, к одному из аргументов не указано соответствующее значение функции, как на изображении ниже.
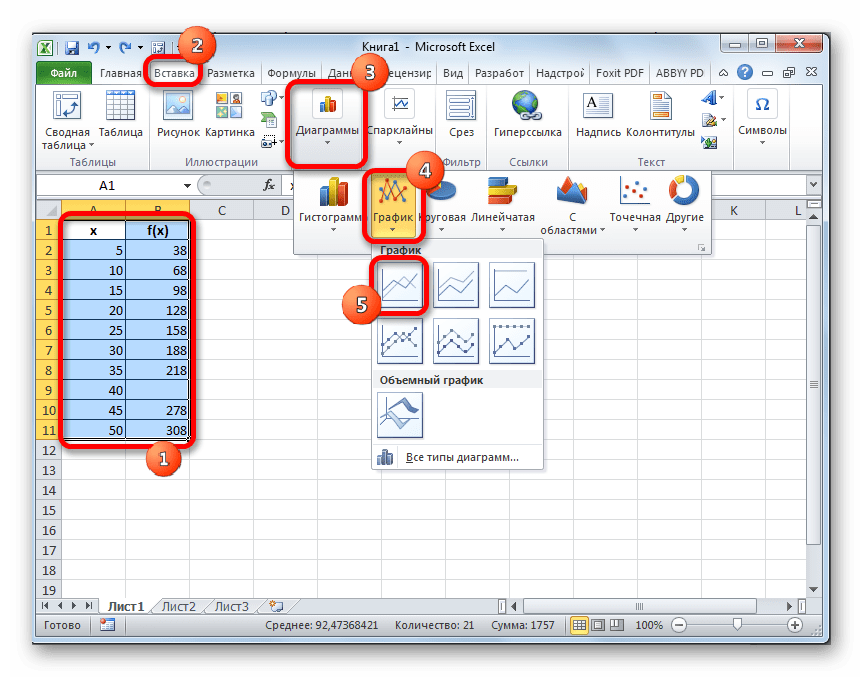
- Выполняем построение графика обычным методом. То есть, находясь во вкладке «Вставка», выделяем табличный диапазон, на основе которого будет проводиться построение. Щелкаем по значку «График», размещенному в блоке инструментов «Диаграммы». Из появившегося списка графиков выбираем тот, который считаем более уместным в данной ситуации.
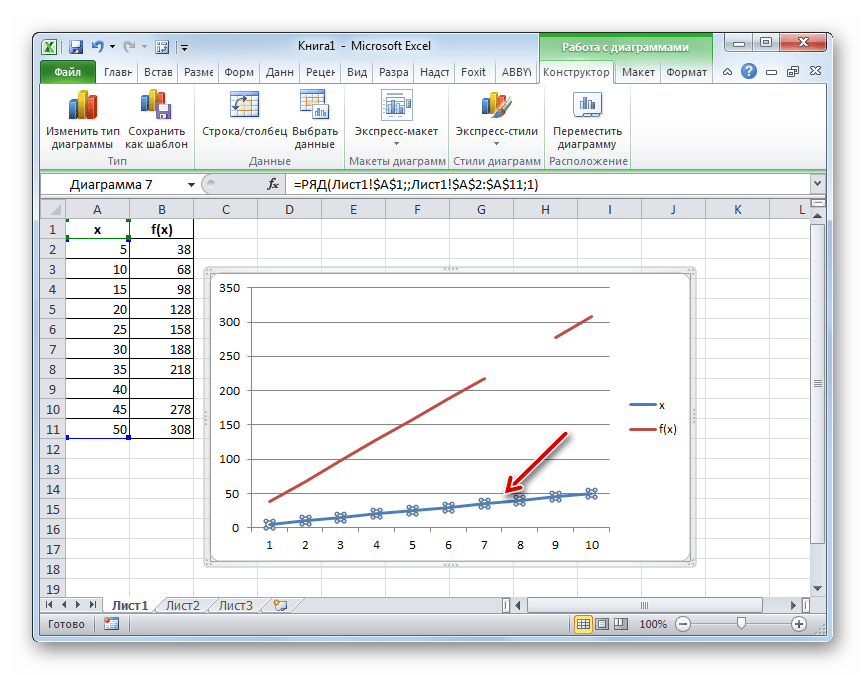
- Как видим, график построен, но не совсем в таком виде, как нам нужно. Во-первых, он разорван, так как для одного аргумента не нашлась соответствующая функция. Во вторых, на нем присутствует дополнительная линия X, которая в данном случае не нужна, а также на горизонтальной оси указаны просто пункты по порядку, а не значения аргумента. Попробуем исправить все это.
Для начала выделяем сплошную синюю линию, которую нужно удалить и жмем на кнопку Delete на клавиатуре.
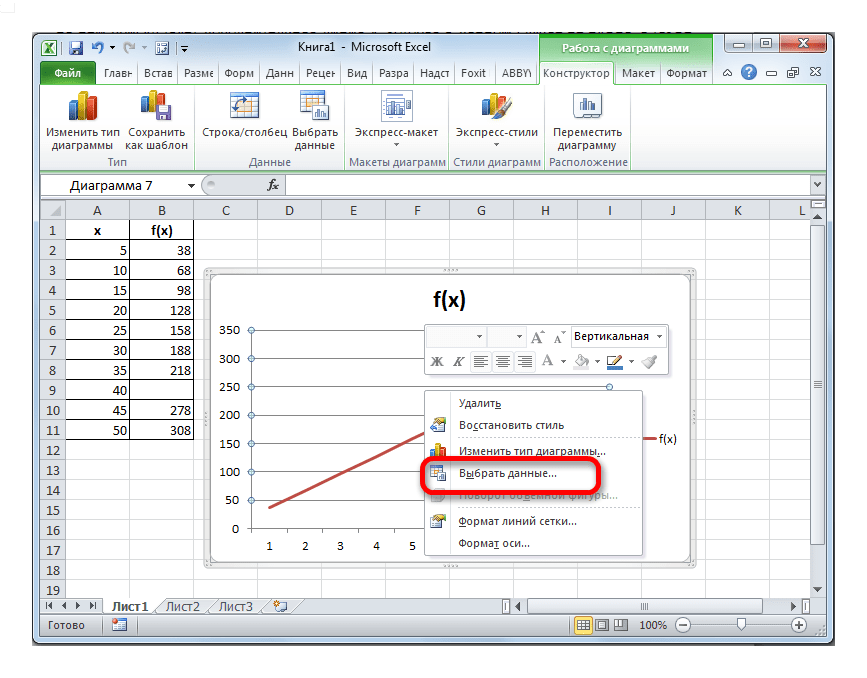
- Выделяем всю плоскость, на которой размещен график. В появившемся контекстном меню щелкаем по кнопке «Выбрать данные…».
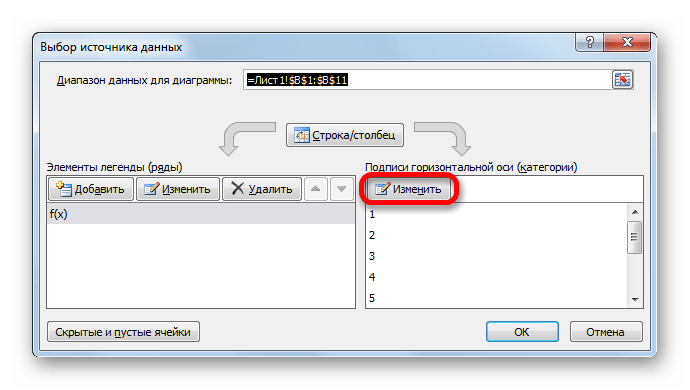
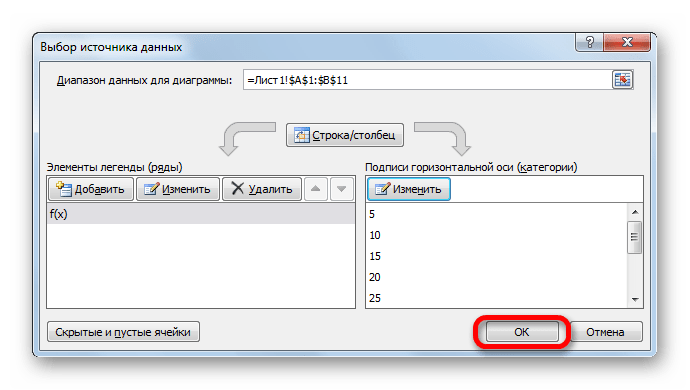
- Запускается окно выбора источника данных. В правом блоке «Подписи горизонтальной оси» жмем на кнопку «Изменить».
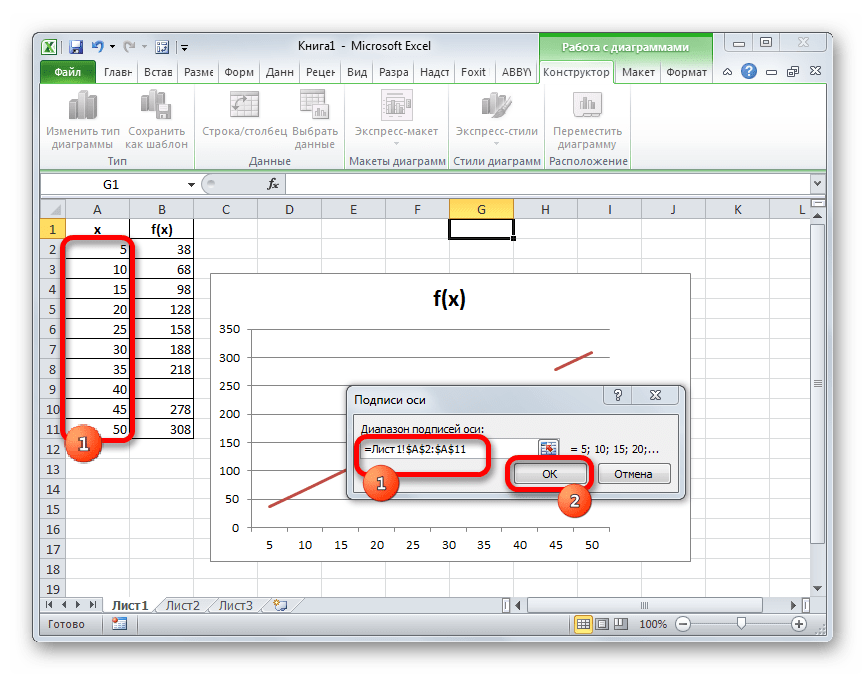
- Открывается небольшое окошко, где нужно указать координаты диапазона, значения из которого будут отображаться на шкале горизонтальной оси. Устанавливаем курсор в поле «Диапазон подписей осей» и просто выделяем соответствующую область на листе, в которой содержаться аргументы функции. Жмем на кнопку «OK».
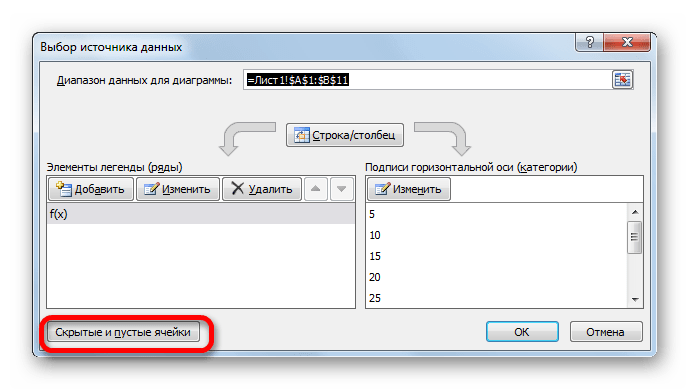
- Теперь нам осталось выполнить основную задачу: с помощью интерполяции устранить разрыв. Вернувшись в окно выбора диапазона данных жмем на кнопку «Скрытые и пустые ячейки», расположенную в нижнем левом углу.
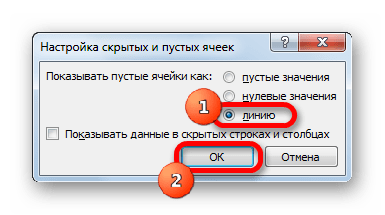
- Открывается окно настройки скрытых и пустых ячеек. В параметре «Показывать пустые ячейки» выставляем переключатель в позицию «Линию». Жмем на кнопку «OK».
- После возвращения в окно выбора источника подтверждаем все сделанные изменения, щелкнув по кнопке «OK».
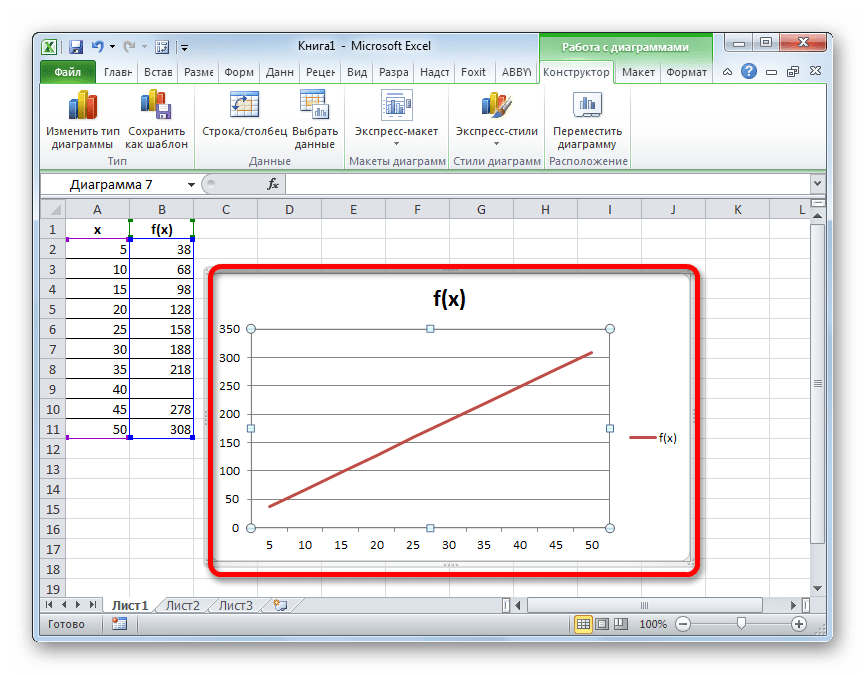
Как видим, график скорректирован, а разрыв с помощью интерполяции удален.
Урок: Как построить график в Excel
Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.
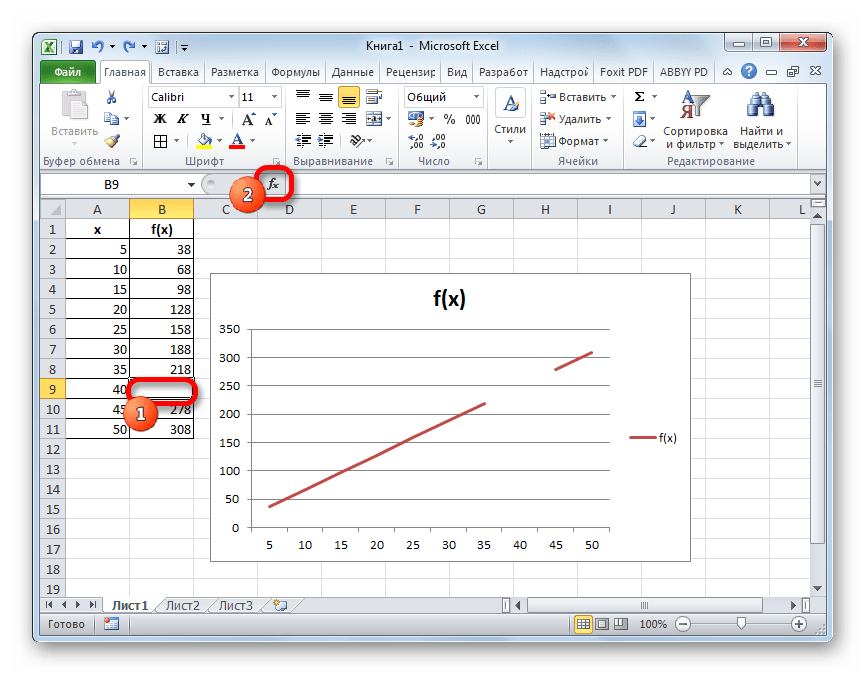
- После того, как график построен и отредактирован, так как вам нужно, включая правильную расстановку подписи шкалы, остается только ликвидировать разрыв. Выделяем пустую ячейку в таблице, из которой подтягиваются данные. Жмем на уже знакомый нам значок «Вставить функцию».
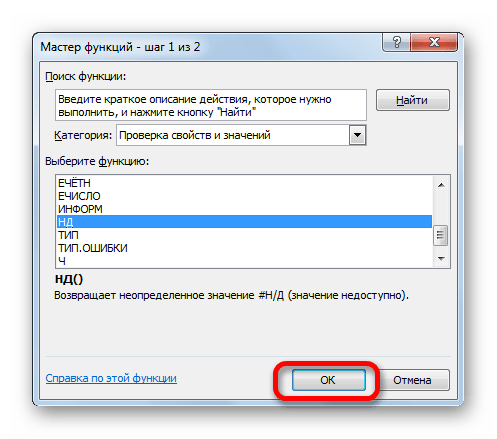
- Открывается Мастер функций. В категории «Проверка свойств и значений» или «Полный алфавитный перечень» находим и выделяем запись «НД». Жмем на кнопку «OK».
- У данной функции нет аргумента, о чем и сообщает появившееся информационное окошко. Чтобы закрыть его просто жмем на кнопку «OK».
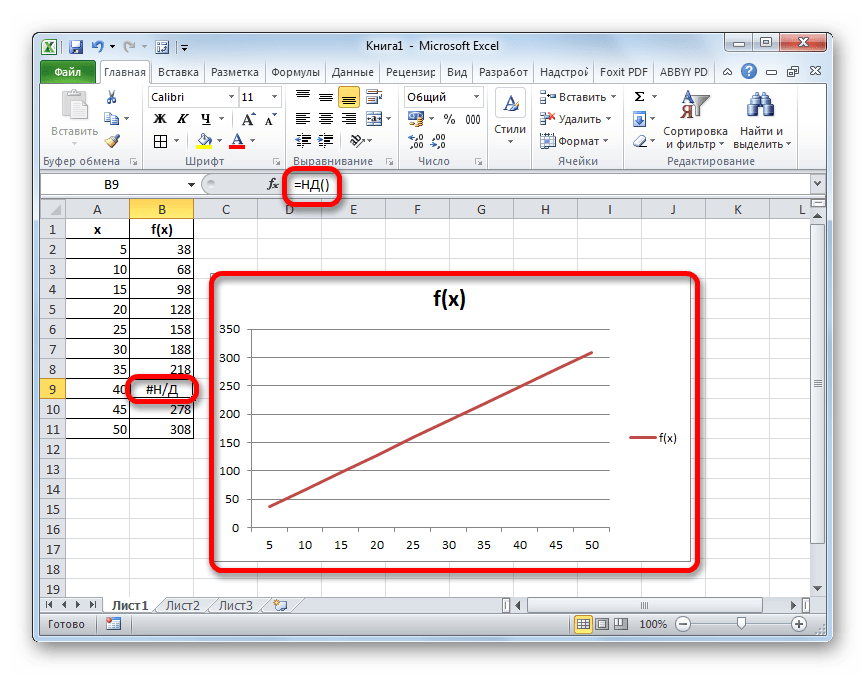
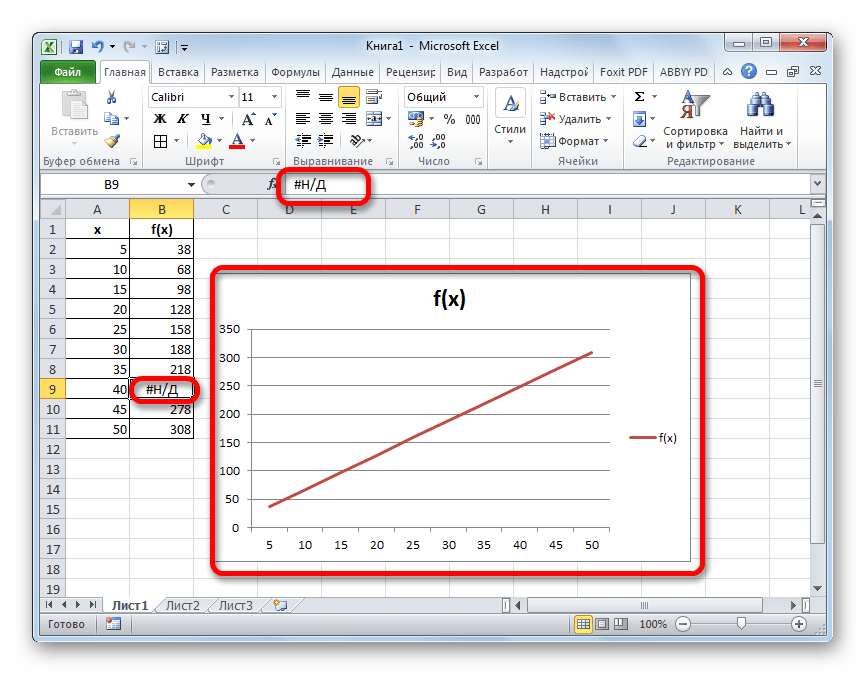
- После этого действия в выбранной ячейке появилось значение ошибки «#Н/Д», но зато, как можно наблюдать, обрыв графика был автоматически устранен.
Можно сделать даже проще, не запуская Мастер функций, а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д» без кавычек. Но это уже зависит от того, как какому пользователю удобнее.
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию ПРЕДСКАЗ, так и графика. В последнем случае это осуществимо с помощью настроек графика или применения функции НД, вызывающей ошибку «#Н/Д». Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.
Еще статьи по данной теме:
Помогла ли Вам статья?
Linear interpolation is used for fitting curves using linear polynomials. Linear Interpolation is a method that constructs new data points from a given set of data points. Linear interpolation is useful when looking for a value between two data points. It can be considered as “filling in the gaps” in a table of data. The strategy for linear interpolation is to use a straight line to connect the known data points on either side of the unknown point. It finds the unknown values in the table. The formula of linear interpolation is given by,
Linear Interpolation Formula
Where,
- x1 and y1 are the first coordinates, and
- x2 and y2 are the second coordinates
- x is the point to perform the interpolation
- y is the interpolated value
Linear Interpolation in Excel
We’ll be looking at two ways to calculate the Linear Interpolation in Excel.
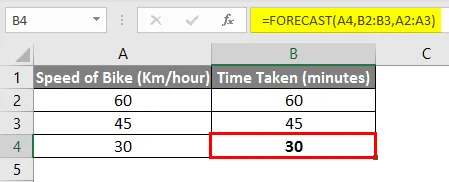
Case 1: When we have 2 pairs of values for the x and y coordinates. For Example:
We want to check the value of 2.3 and hence we have to use interpolation. We are using linear interpolation because the values of x and y are changing linearly. We’ll be using the FORECAST formula,
=FORECAST(x, known_y’s, known_x’s)
Note: In Excel 2016, the FORECAST function was replaced with FORECAST.LINEAR. The syntax and usage of the two functions are the same.
Step 1: Add the FORECAST.LINEAR formula to the cell where you want to add the interpolated value.
Step 2: Fill the formula with the desired values. First, the value of x will go, then add the y-axis values and finally add x-axis values in the formula and click Enter. You’ll get the desired result.
Here the interpolated value of 2.3 is 5.6
Case 2: When we have more than 2 pairs of values for the x and y coordinates.
For Example, We have the data of rainfall (in cm) received in some parts of India for consecutive 7 days. We want to predict rainfall at 1.5 days.
First, we need to check x1, x2, y1, and y2. To perform this we will be using VLOOKUP, INDEX, and MATCH
VLOOKUP: It is used when you need to find things in a table or a range by row.
Syntax:
=VLOOKUP (lookup_value, table_array, col_index_num, [range_lookup])
range_lookup: It is an optional parameter. We can enter 1/True, which looks for an approximate match while 0/False, which looks for an exact match.
INDEX: It is used when you need a value or reference to a value from within a table or range.
Syntax:
= INDEX(array, row_num, [column_num])
Where array and row_num are required values and column_num is optional.
MATCH: This function searches for a specified item in a range of cells, and then returns the relative position of that item in the range.
Syntax:
= MATCH(lookup_value, lookup_array, [match_type])
Where lookup_value and lookup_array are required values and match_type is optional.
We will be calculating all the other values using the formulas above.
Step 1: Calculating x1 using VLOOKUP. Enter the formula and values as shown below.
Step 2: Press Enter and you’ll get the desired value (as shown below).
Step 3: Calculating y1 using VLOOKUP. Enter the formula and values as shown below. The only change we need to do here is the change in col_index_num to 2 because we want the values from column C.
Step 4: Press Enter and you’ll get the desired value (as shown below).
To calculate the values of x2 and y2, we’ll be using INDEX and MATCH functions.
Step 5: Calculate x2 using INDEX and MATCH functions. Enter the formula and values as shown below.
Step 6: Press Enter and you’ll get the desired value (as shown below).
Step 7: Calculate y2 using INDEX and MATCH functions. Enter the formula =INDEX($C$2:$C$8, MATCH(F6,$C$2:$C$8)+1) and values as shown below. The only change here is of Column C and the value of y1.
Step 8: Press Enter and you’ll get the desired value (as shown below).
Now, we’ll be using the above-mentioned formula to calculate the y value.
Step 9: Put all the calculated values in the formula in the desired cell. (as shown below)
Step 10: Press Enter and you’ll get the desired results.
17 авг. 2022 г.
читать 2 мин
Интерполяция — это процесс оценки неизвестного значения функции между двумя известными значениями.
Имея два известных значения (x 1 , y 1 ) и (x 2 , y 2 ), мы можем оценить значение y для некоторой точки x, используя следующую формулу:
у = у 1 + (хх 1 )(у 2 -у 1 )/(х 2 -х 1 )
В этом руководстве объясняется, как использовать линейную интерполяцию для поиска неизвестного значения y на основе значения x в Excel.
Пример: линейная интерполяция в Excel
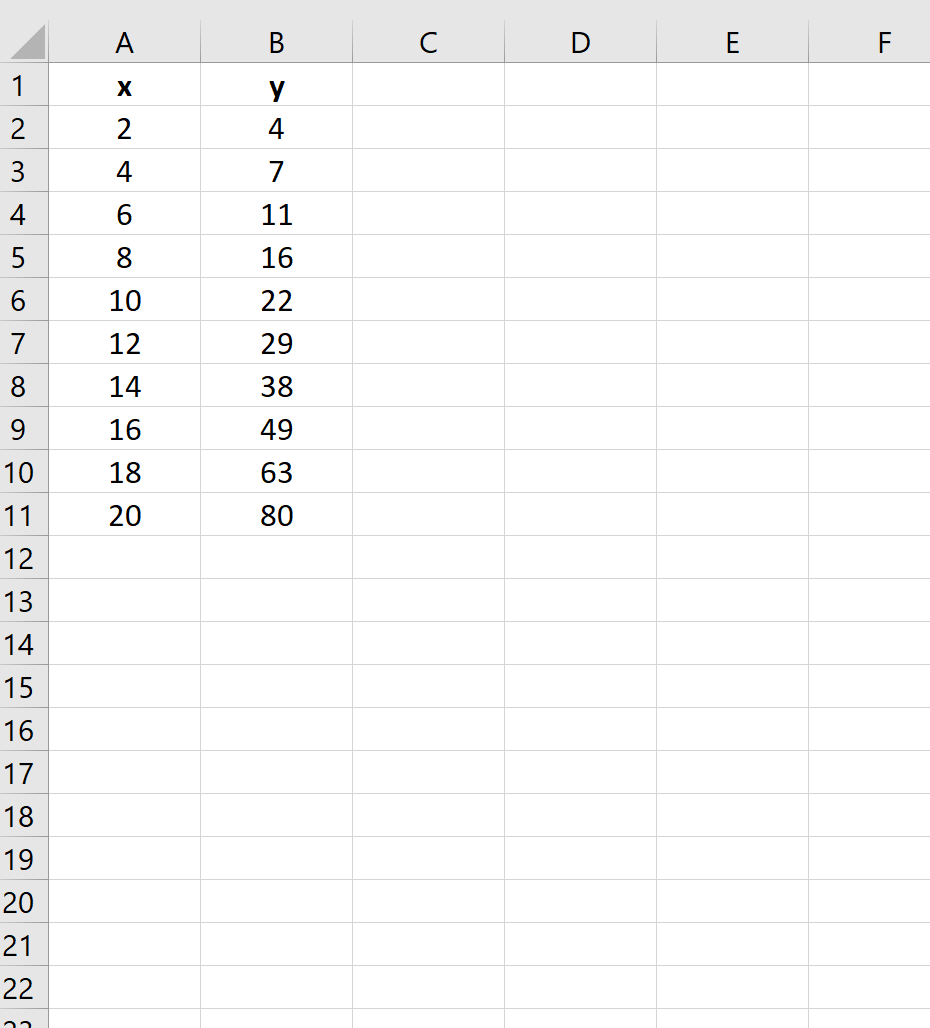
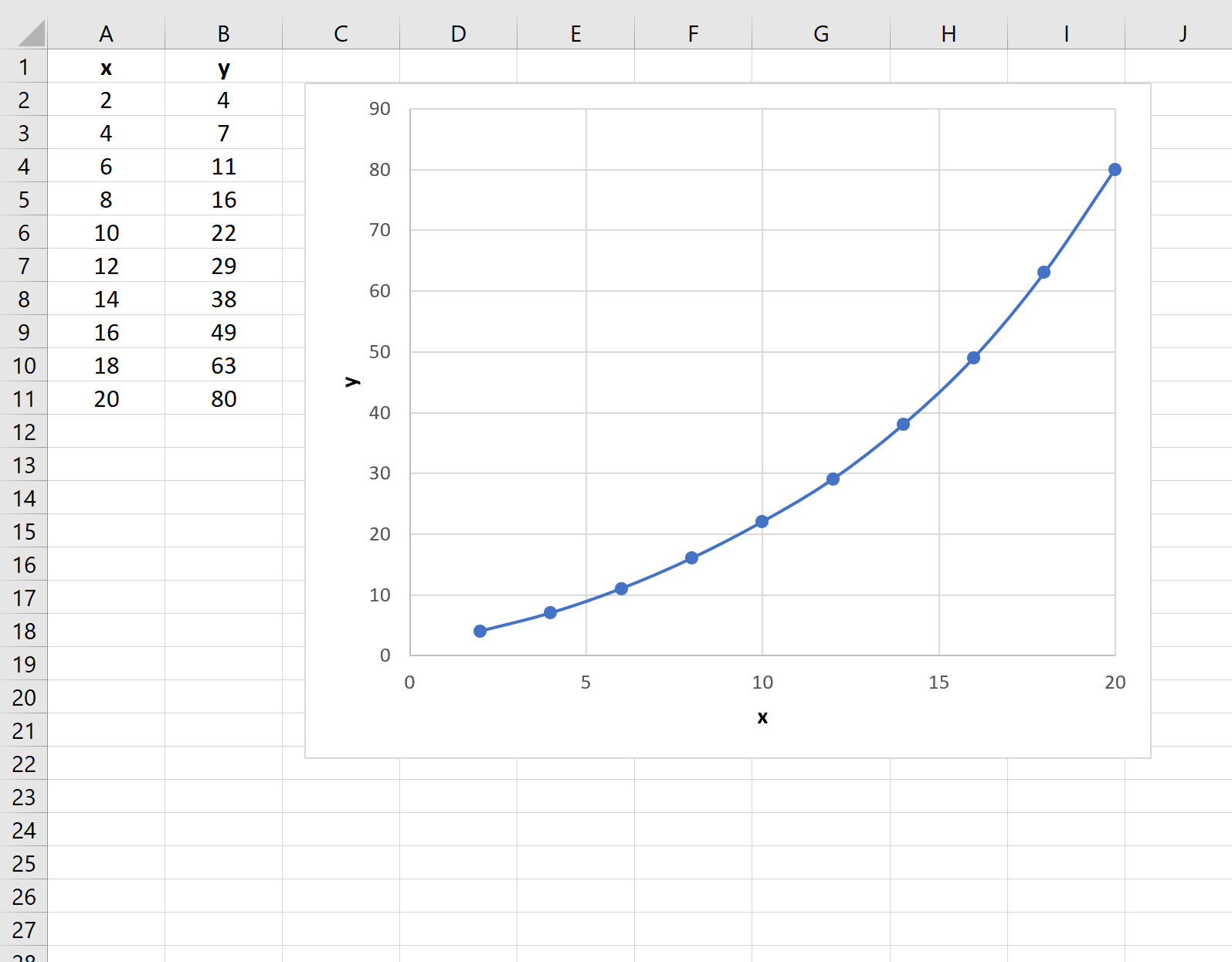
Предположим, у нас есть следующий набор данных в Excel:
Если мы создадим быстрый график данных, вот как это будет выглядеть:
Теперь предположим, что мы хотим найти значение y, связанное с новым значением x, равным 13.Мы видим, что мы измерили значения y для значений x 12 и 14, но не для значения x 13.
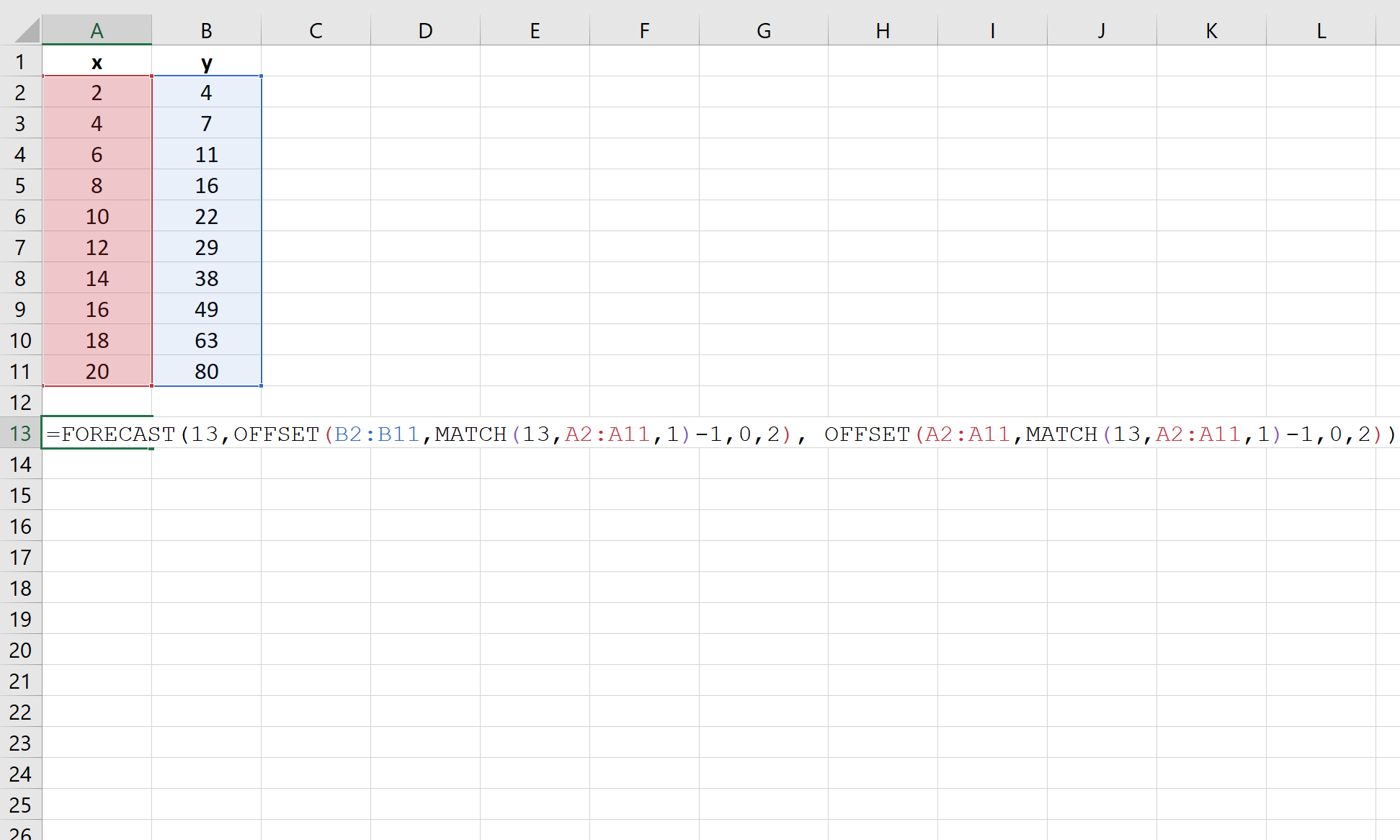
Мы можем использовать следующую формулу для выполнения линейной интерполяции в Excel, чтобы найти расчетное значение y:
= FORECAST (NewX, OFFSET (KnownY, MATCH (NewX,KnownX,1)-1,0,2), OFFSET (KnownX, MATCH (NewX,KnownX,1)-1,0,2))
Вот как использовать эту функцию для оценки значений y, связанных со значением x, равным 13:
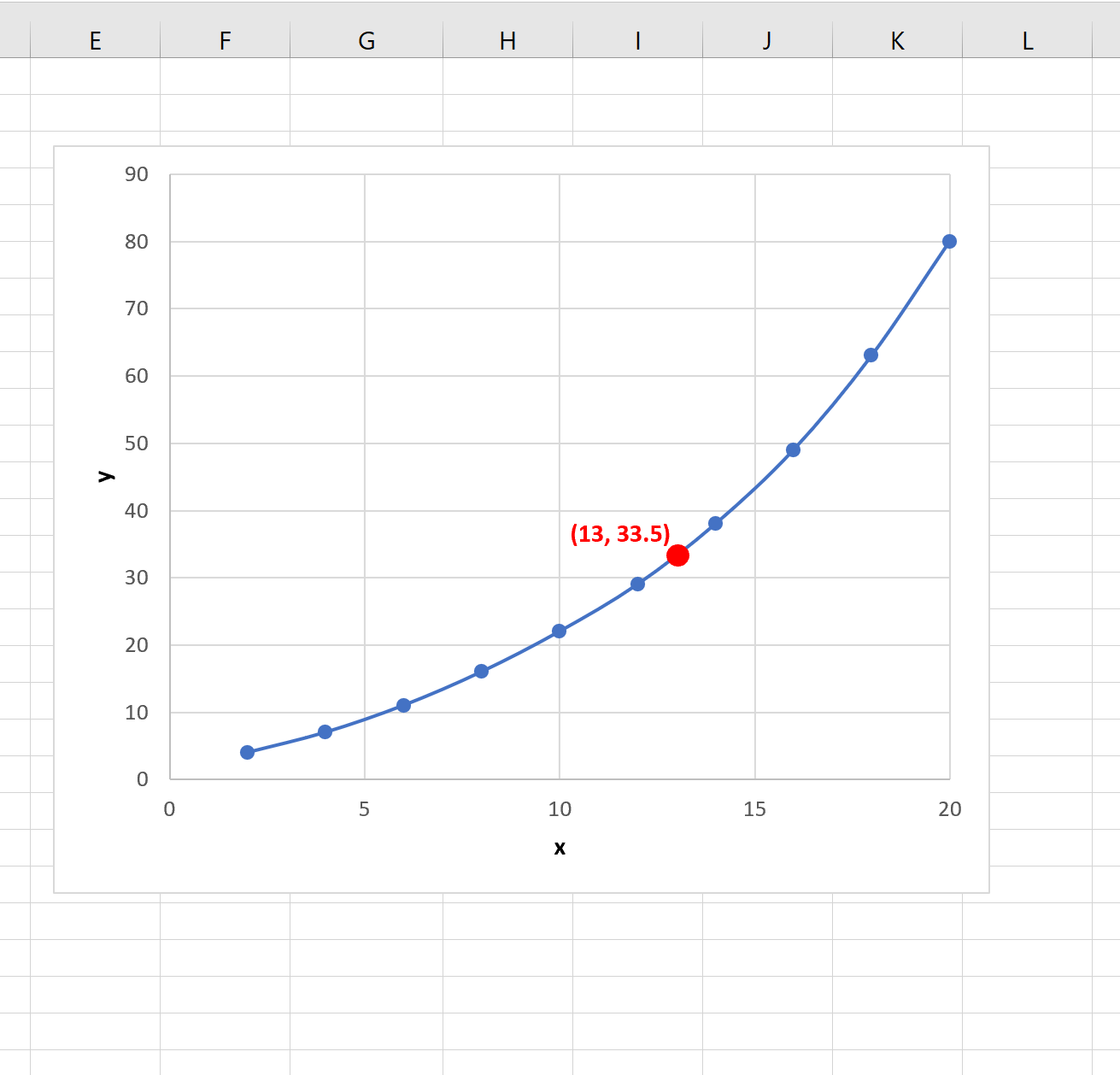
Расчетное значение y оказывается равным 33,5 .
Если мы добавим точку (13, 33,5) к нашему графику, она, похоже, будет хорошо соответствовать функции:
Мы можем использовать эту формулу для оценки значения y любого значения x, просто заменив NewX в формуле любым новым значением x.
Обратите внимание, что для того, чтобы эта функция работала, новое значение x должно находиться в диапазоне существующих значений x.
Вы можете найти больше учебников по Excel здесь .
- Что такое интерполяция?
Линейная интерполяция Excel (Содержание)
- Что такое интерполяция?
- Интерполяция с функцией прогноза в Excel
- Примеры линейной интерполяции в Excel
Что такое интерполяция?
В мире математики интерполяция — это метод создания новых точек данных с помощью известных точек данных. Интерполяция оценивает значение на основе существующих доступных значений данных, которые являются связанными.
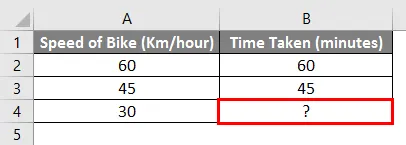
Например: если мы едем на велосипеде со скоростью 60 км / час и достигаем определенного пункта назначения за 1 час, а если мы едем со скоростью 45 км / час и достигаем определенного пункта назначения за 45 минут. Так сколько же потребуется времени, чтобы добраться до пункта назначения, если мы едем со скоростью 30 км / час.
Используя простую математику, мы можем вычислить недостающие значения в приведенном выше примере. Нам нужно вставить следующую формулу в ячейку B4.
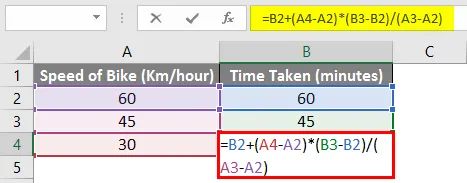
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
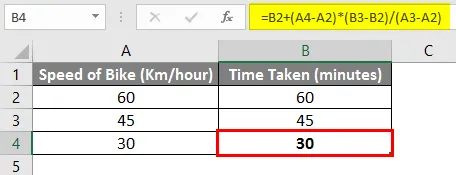
Таким образом, исходя из приведенной выше формулы, мы можем сказать, что для достижения цели требуется 30 минут, если мы едем со скоростью 30 км / час.
Давайте попробуем разбить вышеприведенную формулу и понять формулу в деталях.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
В приведенном выше примере последний раздел формулы, который выделен красным цветом, вычисляет, сколько времени занимает изменение, когда скорость велосипеда изменяется на 1. В нашем примере, время, необходимое, изменяется на 1 минуту, когда скорость велосипеда изменяется на 1 км. /час.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Во втором разделе (синим цветом выше) вычисляется, насколько далеко наша скорость велосипеда от первой заданной скорости велосипеда, а затем умножает ее на значение, рассчитанное выше. Исходя из нашего примера, это 30 (ячейка A4) минус 60 (ячейка A2), результат которого затем умножается на 1 (что равно -30).
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Наконец, первый раздел формулы (коричневым цветом выше); мы добавляем первое значение скорости велосипеда. В нашем примере это дает конечный результат 60 + (-30) * (1) = 30 минут. В школе мы использовали следующую формулу для расчета недостающего значения Y.
Y = Y1 + (X-X1) * (Y2-Y1) / (X2 — X1)
Это пример того, как вычислить пропущенные значения с помощью ручной формулы, чтобы понять интерполяцию.
В Excel есть встроенная функция, которая выполняет вычисления, аналогичные описанным выше, и она известна как функция ПРОГНОЗ. Теперь мы подробно изучим эту функцию.
Интерполяция с функцией прогноза в Excel
Прогноз — это функция рабочего листа, доступная в MS Excel, которая использует линейную регрессию для определения пропущенного значения. Прогноз, как следует из его названия, используется для прогнозирования будущего значения точки данных, но также может использоваться для интерполяции значения. По сути, он используется для расчета будущего значения на основе существующих значений конкретного набора данных.
Синтаксис функции прогноза
Аргументы функции прогноза:
- x — это точка данных, для которой мы хотим знать результирующее значение.
- Known_y’s — диапазон ячеек, содержащих значения Y.
- Known_x’s — диапазон ячеек, содержащих значения X.
Теперь, рассмотрев тот же пример, приведенный выше, попробуем использовать функцию Forecast.
В нашем примере
x — ячейка B4 (так как мы хотим узнать время, затрачиваемое при скорости в 30 км / час).
Known_y’s — от ячейки B2 до ячейки B3 (время, необходимое для известной скорости велосипеда).
Known_x’s — от ячейки A2 к ячейке A3 (скорость велосипеда, указанная нами, для которой мы знаем время, затраченное).
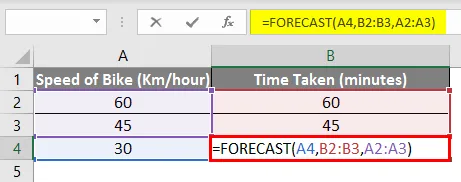
Итак, окончательная формула в ячейке B4 будет такой:
= ПРОГНОЗ (А4, В2: В3, А2: А3)
И, как вы можете видеть, конечный результат такой же, то есть 30 минут .
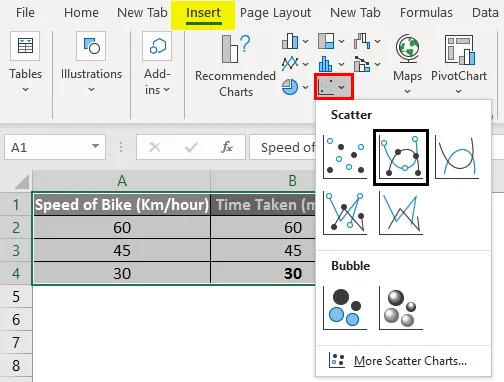
Для создания диаграммы перейдите в меню «Вставка», нажмите «Разброс», а затем выберите «Разброс с гладкими линиями и маркерами».
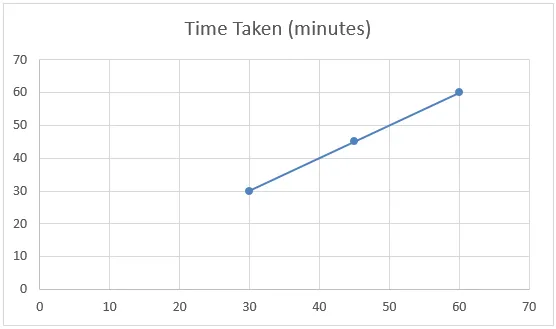
Если мы посмотрим на диаграмму ниже приведенного выше примера, мы можем сказать, что набор данных имеет линейную зависимость и известен как линейная интерполяция.
Примеры линейной интерполяции в Excel
Давайте разберемся с линейной интерполяцией в Excel на нескольких примерах.
Вы можете скачать этот шаблон Excel с линейной интерполяцией здесь — Шаблон Excel с линейной интерполяцией
Пример № 1
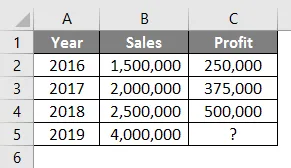
Предположим, у вас есть данные о продажах и прибыли за предыдущие годы, и вы хотите узнать прибыль за текущий год, если достигнете определенного уровня продаж.
Посмотрите на таблицу ниже. У вас есть данные о продажах с 2016 по 2018 год, и вы хотите знать, какой должна быть прибыль, если ваши продажи составляют рупии. 40 000 000 в 2019 году.
Таким образом, с помощью функции прогнозирования мы можем интерполировать прибыль 2019 года, когда продажи составляют рупии. 4000000
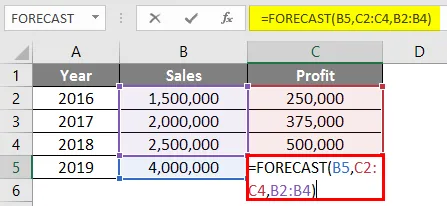
Формула в ячейке C5 будет выглядеть следующим образом:
= ПРОГНОЗ (B5, C2: C4, B2: B4)
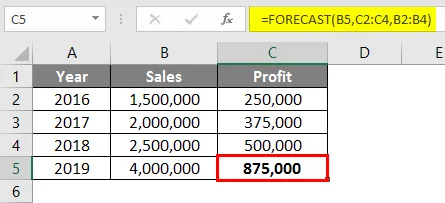
После использования формулы прогноза ответ показан ниже.
Результат для функции Прогноз будет Rs. 875 000 на основе данных о продажах и прибыли, доступных с 2016 по 2018 год.
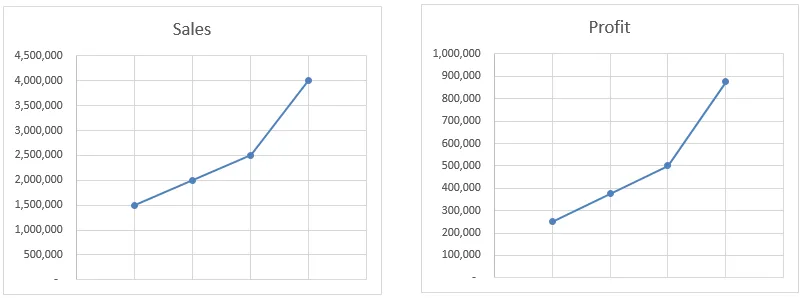
В этом примере функция Forecast интерполирует значение на основе всех доступных данных, а не только начальной и конечной точки. Как видно из графиков, прибыль движется точно так же, как и продажи. Даже если мы вычислим значение вручную, оно все равно даст нам тот же результат.
Пример № 2
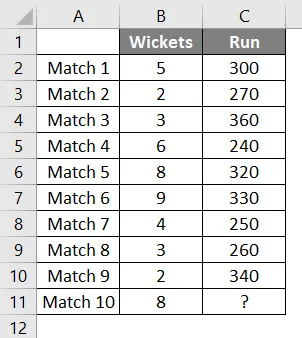
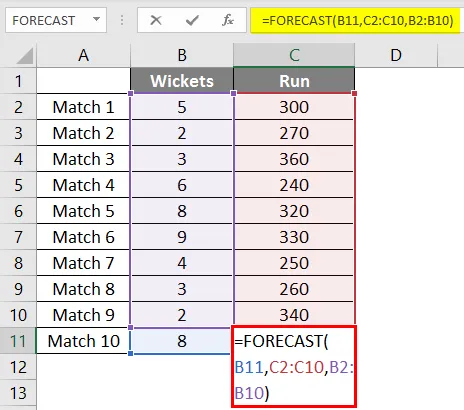
У нас есть данные о последних 9 матчах команды по крикету, в которой пропали калитки и забиты команды.
Мы хотим выяснить, сколько пробежек принесет команда, если выпадет 8 калиток.
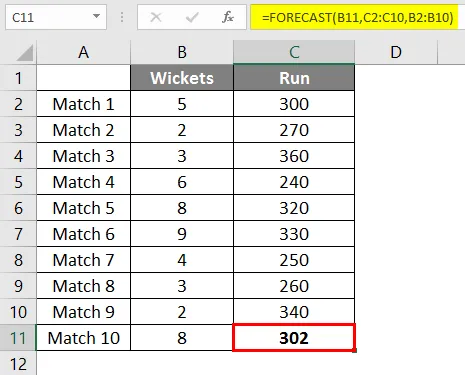
Поэтому мы снова будем использовать ту же функцию прогноза, что и выше.
После применения формулы мы получаем результат 302 пробежек, если у нас выпало 8 калиток на основе линейной регрессии последних 9 матчей, сыгранных командой.
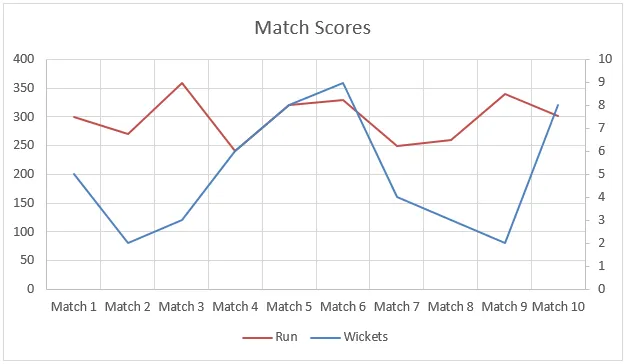
В этом примере данные не были линейными, и вы можете увидеть это на графике ниже. Но все же функция Forecast помогла нам интерполировать прогоны с помощью данных предыдущих матчей.
Что нужно помнить о линейной интерполяции в Excel
- Функция прогнозирования используется для прогнозирования / оценки значения на основе существующих доступных значений, но также может помочь в интерполяции отсутствующего значения.
- В случае, если данные не являются линейными, функция «Прогноз» не даст вам точного значения, основанного на линейной интерполяции, но даст вам ближайшее значение.
- Если x в функции Forecast является текстовым или не числовым, функция Forecast возвращает ошибку #VALUE.
- Если Known_x и Known_y не содержат каких-либо данных или содержат другой набор точек данных, функция Forecast выдаст ошибку # N / A.
- Если дисперсия Known_x равна нулю, тогда функция Forecast выдает ошибку # DIV / O.
Рекомендуемые статьи
Это руководство по линейной интерполяции в Excel. Здесь мы обсуждаем, как использовать линейную интерполяцию в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи —
- Линейная регрессия в Excel
- Поиск текста в Excel
- Текстовая формула в Excel
- Marimekko Chart Excel
- Интерполировать в Excel
- Линейное программирование в Excel
Линейная интерполяция в Excel означает прогнозирование или угадывание следующего значения любой определенной переменной, заданной на основе текущих данных. Здесь мы создаем прямую линию, которая соединяет два значения и оценивает будущую стоимость. В Excel мы используем функцию ПРОГНОЗ и функцию ПРОСМОТРА для выполнения линейной интерполяции.
Интерполяция — это математический или статистический инструмент, предсказывающий значения между двумя точками на кривой или линии. Этот инструмент используется в статистике и во многих других областях, таких как бизнес, наука и т. д., везде, где есть возможность прогнозировать значения между двумя точками данных.
Оглавление
- Линейная интерполяция Excel
- Как сделать линейную интерполяцию в Excel?
- Пример №1
- Пример #2
- То, что нужно запомнить
- Рекомендуемые статьи
- Как сделать линейную интерполяцию в Excel?
Как сделать линейную интерполяцию в Excel?
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон линейной интерполяции Excel здесь — Шаблон линейной интерполяции Excel
Пример №1
Выполнение интерполяции, чтобы узнать температуру погоды в разных часовых поясах
Во-первых, запишите показатели температуры в регионе Бангалор за каждый час, и данные будут следующими:
Данные показывают, что у нас есть данные о температуре в регионе Бангалор на определенную дату. У нас есть часовые пояса на весь день в колонке времени. В столбце часа мы указываем часы с начала дня, например, 00:00 — это 0 часов, 1:00 — 1 час и так далее.
Мы выполним интерполяцию. Интерполяция. Интерполяция — это математическая процедура, применяемая для получения значения между двумя точками, имеющими заданное значение. Он аппроксимирует значение данной функции в заданном наборе дискретных точек. Его можно применять при оценке различных концепций стоимости, математики, статистики. Читать далее по данным, чтобы вытащить значение температуры для нужного часового пояса, которое может быть любым временем, а не только точным часом.
Мы должны использовать несколько формул в Excel, таких как ПРОГНОЗExcel Как ПРОГНОЗФункция ПРОГНОЗ в Excel используется для расчета или прогнозирования будущего значения на основе существующих значений и статистического значения прогноза. Если мы знаем прошлые данные, мы можем использовать функцию для прогнозирования будущего значения. Подробнее, OFFSET и MATCH. Давайте кратко рассмотрим эти формулы, прежде чем двигаться дальше.
ПРОГНОЗ() — Эта функция Excel для прогнозированияФункция Forecast ExcelФункция FORECAST в Excel используется для расчета или прогнозирования будущего значения на основе существующих значений и статистического значения прогноза. Если мы знаем прошлые данные, мы можем использовать функцию для прогнозирования будущего значения. Читать далее вычисляет или прогнозирует будущее значение на основе существующих значений и линейного тренда.
- Икс – Это значение, для которого мы хотим спрогнозировать.
- Известные_ys – Это зависимое значение от данных и обязательное поле для заполнения.
- Известные_xs – Это независимое значение от данных и обязательное поле для обслуживания.
СООТВЕТСТВОВАТЬ() — Эта функция Match excel Функция Match Excel Функция ПОИСКПОЗ ищет определенное значение и возвращает его относительное положение в заданном диапазоне ячеек. Результатом является первая позиция, найденная для данного значения. Будучи поисковой и справочной функцией, она работает как для точного, так и для приблизительного совпадения. Например, если диапазон A11:A15 состоит из чисел 2, 9, 8, 14, 32, формула «ПОИСКПОЗ(8,A11:A15,0)» возвращает 3. Это связано с тем, что число 8 находится на третьем месте. позиция. read more вернет относительную позицию искомого значения в строке, столбце или таблице, которая соответствует указанному значению в указанном порядке.
- Искомое_значение – Это значение, которое необходимо сопоставить с lookup_array.
- Lookup_array – это диапазон для поиска
[match_type] – Это может быть 1,0,-1. Значение по умолчанию — 1. Для функции 1 — ПОИСКПОЗ вы найдете наибольшее значение, меньшее или равное значению look_up. Значение должно быть в порядке возрастания. Для 0 — функция ПОИСКПОЗ находит первое значение, точно равное искомому_значению, и его не нужно сортировать. Для -1 — Match найдет наименьшее значение, большее или равноеGreater Than Or Equal«Больше или равно» — это сравнение или логический оператор, который помогает сравнить две ячейки данных одного и того же типа данных. быть отсортированы в порядке убывания.
КОМПЕНСИРОВАТЬ() — Эта функция смещенияФункция смещенияФункция смещения в Excel возвращает значение ячейки или диапазона (соседних ячеек), которое представляет собой определенное количество строк и столбцов от контрольной точки. read more вернет ячейку или диапазон ячеек, которые содержат указанное количество строк и столбцов. Ячейка или диапазон ячеек будет зависеть от высоты и ширины строк и столбцов, которые мы указываем.
- Ссылка – Это начальная точка, откуда будут подсчитываться строки и столбцы. Строки и столбцы. Ячейка – это пересечение строк и столбцов. Строки и столбцы составляют программное обеспечение, которое называется Excel. Область рабочего листа Excel разделена на строки и столбцы, и в любой момент времени, если мы хотим сослаться на определенное место этой области, нам нужно сослаться на ячейку. Будет сделано больше.
- Ряды – Количество строк для смещения ниже начальной опорной ячейки.
- Столбцы – Количество столбцов для смещения справа от начальной опорной ячейки.
- [height] – Высота в строках из возвращенной ссылки. Это необязательно.
- [width] – Ширина в столбцах из возвращенной ссылки. Это необязательно.
Мы вкратце рассмотрели формулы, которые будем использовать для выполнения интерполяции. Теперь давайте выполним интерполяцию следующим образом:
Введите в ячейку формулу, которая нам нужна, чтобы увидеть температуру для разных часовых поясов. Это говорит о том, что мы должны выбрать ячейку, которую необходимо спрогнозировать, и функция OFFSET и MATCH используется для определения known_ys и known_xs.
ПРОГНОЗ($F$5 – Выберите ячейку с часовым поясом для прогноза.
СМЕЩ($C$3:$C$26,ПОИСКПОЗ($F$5,$B$3:$B$26,1)-1,0,2) – Это используется для выбора known_ys в качестве ссылки на временный столбец, поскольку это зависимые значения. Функция match используется для генерации позиции значения, которое нам нужно для прогноза и расчета количества строк. Столбцы должны быть равны 0, потому что мы хотим, чтобы зависимое значение в том же выбранном столбце и высота были равны 2, поскольку нам нужно выполнить прогноз на основе двух последних значений.
СМЕЩ($B$3:$B$26, ПОИСКПОЗ($F$5,$B$3:$B$26,1)-1,0,2) – Это используется для выбора known_xs в качестве эталонного столбца часов, потому что это независимые значения, а остальные такие же, как мы сделали для подсчета строк.
Теперь укажите часовой пояс в ячейке, который мы рассматривали для прогнозирования. Здесь введено значение 19,5, что соответствует 19:30, и мы получим температуру 30, которая прогнозируется на основе значений температуры, предоставляемых на почасовой основе.
Точно так же эта формула может отображать временные значения для разных часовых поясов.
Пример #2
Выполнение линейной интерполяции, чтобы узнать продажи организации в 2018 году
Предположим, что мы получили данные о продажах организации в 2018 году, как показано ниже. У нас есть данные в пересчете на дни и их продажи нарастающим итогом. За первые 25 дней года мы получили 7 844 единицы, за 50 дней года — 16 094 единицы и т. д.
Мы можем использовать ту же формулу, что и при интерполяции, для прогнозирования стоимости продаж в разные дни, которые мы не упомянули в рассмотренных нами данных. Здесь продажи идут по прямой линии (линейно), как мы взяли кумулятивно.
Если мы хотим увидеть количество продаж, достигнутое за 215 дней, мы можем получить прогнозируемое количество продаж за 215 дней, как показано ниже, с учетом данных о продажах.
Точно так же мы можем определить количество продаж в этом году, прогнозируя между заданными точками.
То, что нужно запомнить
- Это наименее точный метод, но он быстрый и точный, если табличные значения расположены близко друг к другу.
- Его также можно использовать для оценки значений географических точек данных, осадков, уровней шума и т. д.
- Он очень прост в использовании и не очень точен для нелинейных функций.
- Помимо линейной интерполяции Excel, у нас также есть различные методы, такие как полиномиальная интерполяция, сплайн-интерполяция и т. д.
Рекомендуемые статьи
Эта статья представляет собой руководство по линейной интерполяции в Excel. Здесь мы увидим, как выполнять интерполяцию и линейную интерполяцию в Excel, несколько примеров и загружаемый шаблон Excel. Вы можете узнать больше об Excel из следующих статей: –
- Формула относительного изменения
- Полный список функций Excel
- Формула прогноза в Excel
- Формула стандартного нормального распределения
Интерполяция – это процесс оценки точек данных в существующем наборе данных. Вот как интерполировать в Excel
Если вы увлекаетесь математикой и вам нужно найти неизвестные точки данных из выборки известных точек данных, интерполяция в Excel – это отличный выбор
Excel – это надежный калькулятор с визуализацией данных. Таким образом, для различных математических и статистических анализов он всегда пригодится. Хотя прямой функции для интерполяции не существует, вы можете использовать различные функции для оценки новых точек данных из заданной таблицы данных значений X и Y
Читайте далее, чтобы узнать популярные и простые методы интерполяции данных в Excel
1. Использование математического уравнения
Одним из основных подходов интерполяции данных в Microsoft Excel является применение математической формулы линейной интерполяции. Этот метод можно использовать при получении линейной линии тренда для графика
Y= Y1 + (X-X1)⨯(Y2-Y1)/(X2-X1)
Например, вы хотите узнать значение Y, когда X равно 15, из этой таблицы. Вот как:
- Создайте таблицу значений X1, X2, Y1 и Y2, проанализировав таблицу.
- Вы должны выбрать точки данных на шаг выше и ниже искомого нового значения X.
- Теперь примените следующую формулу в любой ячейке, чтобы найти интерполированное значение Y, соответствующее значению X 15.
=G5+(K4-E5)*(H5-G5)/(F5-E5)
Этот процесс довольно прост и выполняется вручную. Для больших наборов данных вам придется потратить много времени на интерполяцию точек данных
Скачать: Интерполировать в электронной таблице Excel (бесплатно)
Похожие: Как сделать диаграмму рассеяния в Excel и представить свои данные
2. Использование метода подгонки кривых
Подгонка кривых – это еще один быстрый, но ручной метод интерполяции в Excel. Просто создайте диаграмму рассеяния и создайте уравнение графика.Excel использует линейную регрессию для составления уравнения. Вам нужно применить это уравнение для подгонки кривой, чтобы найти значение Y:
Y= Slope * X + Y-intercept
Чтобы найти значение Y из заданного значения X, которое равно 15, можно попробовать выполнить следующие действия:
- Выберите таблицу и вставьте диаграмму рассеяния.
- Щелкните правой кнопкой мыши на линии тренда и выберите Форматировать линию тренда.
- Установите флажки напротив Отображать значение R-квадрат на графике и Отображать уравнение на графике.
- Также выберите Линейная линия тренда.
- Когда график рассеяния покажет уравнение, подставьте в него значение X, чтобы найти значение Y.
- Следующая формула позволяет найти значение Y.
=0. 9889*K4+3. 5333
Метод подгонки кривых подходит только для небольших наборов данных. Этот процесс не поддается простой автоматизации, и вы можете полагаться только на макросы Microsoft Excel для автоматизации на основе горячих клавиш
Вы можете использовать функции SLOPE и INTERCEPT в Excel для линейной интерполяции значения Y. Вы можете легко применить эти функции, поскольку для их работы требуются только значения известных X и Y. Ниже приведены синтаксисы, которые необходимо использовать:
=SLOPE(known_y's, known_x's)
=INTERCEPT(known_y's, known_x's)
Вот как можно интерполировать точки данных с помощью этого метода:
- Переименуйте две ячейки в Slope и Intercept.
- Примените функцию SLOPE под заголовком Slope и выберите соответствующие данные из таблицы.
- Аналогично, примените функцию INTERCEPT и введите значение перехвата.
- Теперь примените формулу Y= Slope * X + Y-intercept , чтобы найти значение Y.
- Вы можете создать формулу Excel для приведенного выше уравнения, в которой вы можете просто изменить значение X, чтобы найти другие неизвестные точки данных.
Интерполяцию можно выполнить быстрее, если создать ячейки для значения X, наклона и перехвата. Однако этот процесс может не дать точных данных для нелинейной интерполяции
4. Использование функции Excel: FORECAST
Это популярная функция Excel для прогнозирования производительности путем анализа набора реальных точек данных. Вы найдете FORECAST и FORECAST.LINEAR в Excel 2016 и более поздних редакциях. Для получения надежных результатов целесообразно использовать FORECAST.LINEAR
Функция использует три аргумента для получения прогнозируемой точки данных. Этими аргументами являются заданное значение X, известные значения Y и значения Xs из таблицы. Посмотрите на синтаксис ниже:
=FORECAST.LINEAR(x, known_y's, known_x's)
Вы можете быстро определить значение Y, выполнив следующие действия:
- Ячейка, в которую вы хотите ввести значение Y, должна иметь знак равенства ( = ).
- Теперь введите Прогноз и выберите функцию FORECAST.LINEAR из выпадающего меню формул.
- Щелкните на значении X и поставьте запятую.
- Затем выделите диапазон ячеек с известным значением Ys и поставьте запятую.
- Выберите известный диапазон ячеек Xs и закройте формулу круглой скобкой.
- Нажмите Enter , чтобы получить интерполированное значение Y.
- Вы можете продолжать изменять значение X в пределах диапазона данной таблицы, чтобы получить значения Y.
- Формула FORECAST этого учебника выглядит следующим образом:
=FORECAST.LINEAR(K4,C2:C10,B2:B10)
Функция FORECAST.LINEAR обеспечивает высокоточное прогнозирование данных для линейных и слегка нелинейных точек данных. Она использует первое и последнее значения для заданного значения X и учитывает весь набор данных
Поэтому эту функцию можно использовать для критически важной аналитики данных, например, для прогнозирования веб-трафика, моделирования финансовых данных и расчета эффективности бизнеса
5. Функция GROWTH для нелинейной интерполяции
Когда у вас есть таблица реальных данных в экспоненциальной форме, FORECAST.LINEAR не даст точных интерполированных точек данных. В Excel есть еще одна отличная функция для прогнозирования данных – это СКОРОСТЬ. Как и другие функции, упомянутые выше, эта формула также проста в применении
Помимо привычных аргументов, таких как известный диапазон ячеек Xs, известные значения Ys и заданное значение X, GROWTH использует дополнительное логическое значение. Обычно для этой логической константы нужно ввести единицу. Вот как выглядит синтаксис:
=GROWTH(known_y s, known_x s , new_x s , const )
Чтобы интерполировать данные в Excel с помощью функции GROWTH, вы можете выполнить следующие действия:
- Вставьте функцию СРЗНАЧ в любую ячейку, где требуется интерполированное значение для Y.
- Введите диапазон ячеек для известных значений Y, за которым следует запятая.
- Повторите описанный выше шаг, чтобы ввести диапазон ячеек для известных значений X.
- Теперь введите значение заданного X и поставьте запятую.
- Введите 1 в качестве последнего аргумента и закройте формулу.
- Нажмите Enter для создания значения интерполированного Y.
- Вы можете использовать ссылки на ячейки вместо фактических значений, чтобы получить больше значений, просто изменив заданные данные.
- Окончательная формула будет выглядеть следующим образом:
.
=GROWTH(B2:B12,A2:A12,E2,1)
По сравнению с функцией FORECAST, GROWTH генерирует более надежные и точные интерполированные точки данных для экспоненциальных наборов данных, которые в основном являются нелинейными. Как и FORECAST, функцию GROWTH можно автоматизировать, не прилагая особых усилий
Интерполяция данных и прогнозирование – это просто
Теперь вы можете эффективно интерполировать данные для своих предстоящих задач с работы или учебы
Такое быстрое понимание данных поможет вам в различных аспектах, например, сократить несколько повторяющихся этапов исследования данных или оценить объем задач, прежде чем браться за новые проекты
Interpolation is forecasting using existing data to predict future patterns and values. Being able to forecast helps every business leader make the right decisions when it comes to cutting costs, investing in growth and establishing marketing strategies. Use the Excel interpolate function to get accurate data calculations. Keep in mind that forecasting business numbers are often like forecasting the weather; many things can change and business leaders need to be nimble to deal with unexpected rainy days.
Excel Interpolate Function
Launch Excel and open a worksheet you wish to extract interpolated data from. If you are building a worksheet, then create the columns with values that will correspond to an x-axis and a y-axis. For example, if you want to forecast the target revenues, you can interpolate this data as long as you have some basic data points. Column A is the time-frame set at monthly dates. Your revenue goals are in Column B. Column C will be what records the interpolated forecasted data. Enter the data you have which might be two rows of existing units sold and revenues and a target revenue goal in row 12. This suggests a 12-month period to forecast your production.
Once you have the data and goals typed into the spreadsheet, click on the first data row in Column C and type INTERPOLATE into the function bar and select fx in the front of the bar. A box pops up called Function Arguments. In our example, the x-axis is represented by the date column. The financial goal is represented on the y-axis with the target being the units needed to achieve this. You enter the range information by selecting it in the worksheet by choosing the top of the range, clicking and holding the mouse and scrolling to the end of the range in the column. Use Tab to toggle from the function arguments fields.
Select the range of 12 data points for the X Function Argument field. Select the range of 12 revenue goals for the Y Function Argument field. It’s okay if there is missing data. In the Target field, enter the first data point in Column A and then select the Method of interpolation. You can go forward or backward if you are recreating data. Once all information is entered, click OK. Copy the formula to the rest of Column C. The missing data fields from Column B are now forecast in Column C.
Linear or Nonlinear Interpolation
Many business leaders are interested in the Excel «forward» function to calculate a present or future value factor. This uses linear data estimations. This helps forecast revenues or even production costs when scaling up. It uses the difference between two values to determine other values. The idea with «step value» is that there is a linear growth of values. As long as this linear component is true, the margin of error in step value interpolation is minimal and insignificant. In Microsoft Excel, use the Forecast function to accomplish interpolation values.
Nonlinear interpolation is also useful to business owners when the information in the first column, x-axis data is inconsistent with data point movement. The nonlinear interpolation method is beneficial when looking at annual sales cycles and helps with inventory control.
Back to Algebra Basics
Microsoft Excel makes forecasting must easier for everyone, especially those of us who have forgotten most of our high school algebra basis. Interpolation is taking the difference at different points to create a line or curve on a graph. For business owners, this is ideally the growth curve. Excel uses the following equation to determine these graph points:
y = y1 + (x -x1) [(y2-y1)/(x2 -x1)]
If the y-axis is time and the x-axis represents dollars, this equation is calculating the change in dollars over specific periods of time. We are seeking y, which is the period of time we are forecasting a specific dollar value for. This gives you one point; Excel moves this through multiple points, seeking data points potential for y3, y4, y5, etc…. Excel makes more dynamic data forecasting easier to process.