Linear interpolation is used for fitting curves using linear polynomials. Linear Interpolation is a method that constructs new data points from a given set of data points. Linear interpolation is useful when looking for a value between two data points. It can be considered as “filling in the gaps” in a table of data. The strategy for linear interpolation is to use a straight line to connect the known data points on either side of the unknown point. It finds the unknown values in the table. The formula of linear interpolation is given by,
Linear Interpolation Formula
Where,
- x1 and y1 are the first coordinates, and
- x2 and y2 are the second coordinates
- x is the point to perform the interpolation
- y is the interpolated value
Linear Interpolation in Excel
We’ll be looking at two ways to calculate the Linear Interpolation in Excel.
Case 1: When we have 2 pairs of values for the x and y coordinates. For Example:
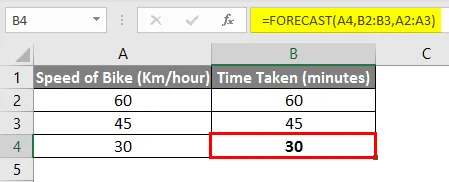
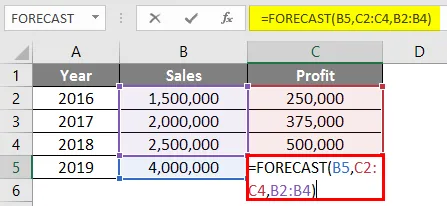
We want to check the value of 2.3 and hence we have to use interpolation. We are using linear interpolation because the values of x and y are changing linearly. We’ll be using the FORECAST formula,
=FORECAST(x, known_y’s, known_x’s)
Note: In Excel 2016, the FORECAST function was replaced with FORECAST.LINEAR. The syntax and usage of the two functions are the same.
Step 1: Add the FORECAST.LINEAR formula to the cell where you want to add the interpolated value.
Step 2: Fill the formula with the desired values. First, the value of x will go, then add the y-axis values and finally add x-axis values in the formula and click Enter. You’ll get the desired result.
Here the interpolated value of 2.3 is 5.6
Case 2: When we have more than 2 pairs of values for the x and y coordinates.
For Example, We have the data of rainfall (in cm) received in some parts of India for consecutive 7 days. We want to predict rainfall at 1.5 days.
First, we need to check x1, x2, y1, and y2. To perform this we will be using VLOOKUP, INDEX, and MATCH
VLOOKUP: It is used when you need to find things in a table or a range by row.
Syntax:
=VLOOKUP (lookup_value, table_array, col_index_num, [range_lookup])
range_lookup: It is an optional parameter. We can enter 1/True, which looks for an approximate match while 0/False, which looks for an exact match.
INDEX: It is used when you need a value or reference to a value from within a table or range.
Syntax:
= INDEX(array, row_num, [column_num])
Where array and row_num are required values and column_num is optional.
MATCH: This function searches for a specified item in a range of cells, and then returns the relative position of that item in the range.
Syntax:
= MATCH(lookup_value, lookup_array, [match_type])
Where lookup_value and lookup_array are required values and match_type is optional.
We will be calculating all the other values using the formulas above.
Step 1: Calculating x1 using VLOOKUP. Enter the formula and values as shown below.
Step 2: Press Enter and you’ll get the desired value (as shown below).
Step 3: Calculating y1 using VLOOKUP. Enter the formula and values as shown below. The only change we need to do here is the change in col_index_num to 2 because we want the values from column C.
Step 4: Press Enter and you’ll get the desired value (as shown below).
To calculate the values of x2 and y2, we’ll be using INDEX and MATCH functions.
Step 5: Calculate x2 using INDEX and MATCH functions. Enter the formula and values as shown below.
Step 6: Press Enter and you’ll get the desired value (as shown below).
Step 7: Calculate y2 using INDEX and MATCH functions. Enter the formula =INDEX($C$2:$C$8, MATCH(F6,$C$2:$C$8)+1) and values as shown below. The only change here is of Column C and the value of y1.
Step 8: Press Enter and you’ll get the desired value (as shown below).
Now, we’ll be using the above-mentioned formula to calculate the y value.
Step 9: Put all the calculated values in the formula in the desired cell. (as shown below)
Step 10: Press Enter and you’ll get the desired results.
Содержание
- Использование интерполяции
- Способ 1: интерполяция для табличных данных
- Способ 2: интерполяция графика с помощью его настроек
- Способ 3: интерполяция графика с помощью функции
- Вопросы и ответы
Бывает ситуация, когда в массиве известных значений нужно найти промежуточные результаты. В математике это называется интерполяцией. В Excel данный метод можно применять как для табличных данных, так и для построения графиков. Разберем каждый из этих способов.
Использование интерполяции
Главное условие, при котором можно применять интерполяцию – это то, что искомое значение должно быть внутри массива данных, а не выходить за его предел. Например, если мы имеем набор аргументов 15, 21 и 29, то при нахождении функции для аргумента 25 мы можем использовать интерполяцию. А для поиска соответствующего значения для аргумента 30 – уже нет. В этом и является главное отличие этой процедуры от экстраполяции.
Способ 1: интерполяция для табличных данных
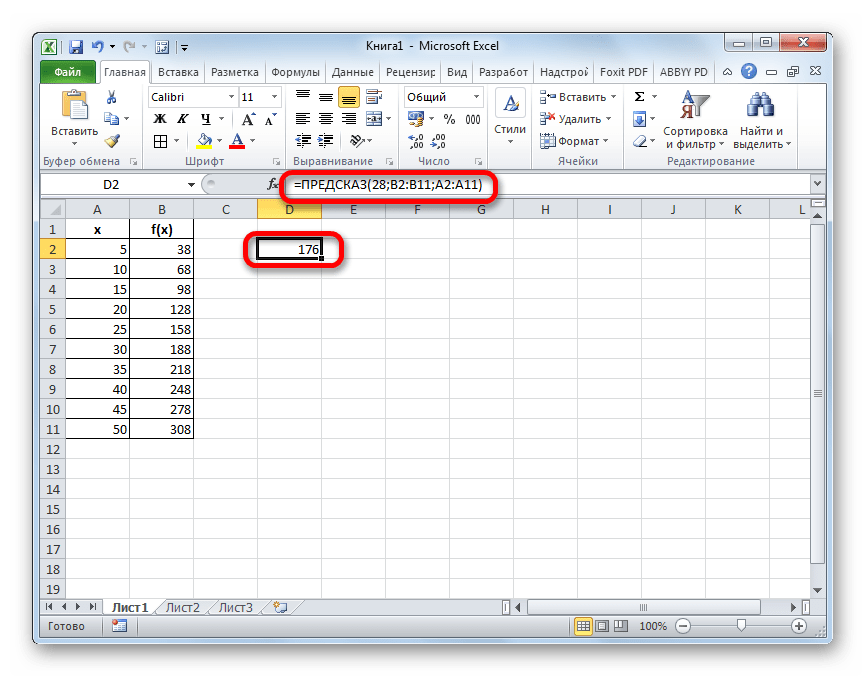
Прежде всего, рассмотрим применения интерполяции для данных, которые расположены в таблице. Для примера возьмем массив аргументов и соответствующих им значений функции, соотношение которых можно описать линейным уравнением. Эти данные размещены в таблице ниже. Нам нужно найти соответствующую функцию для аргумента 28. Сделать это проще всего с помощью оператора ПРЕДСКАЗ.
- Выделяем любую пустую ячейку на листе, куда пользователь планирует выводить результат от проведенных действий. Далее следует щелкнуть по кнопке «Вставить функцию», которая размещена слева от строки формул.
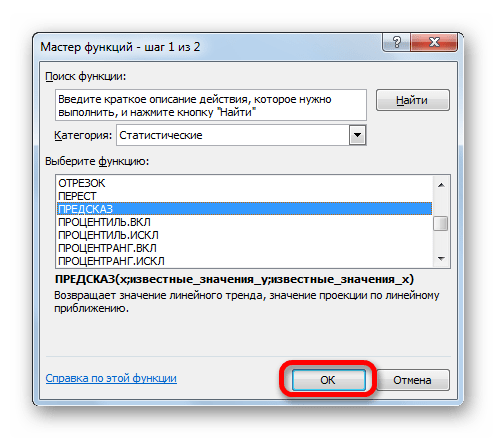
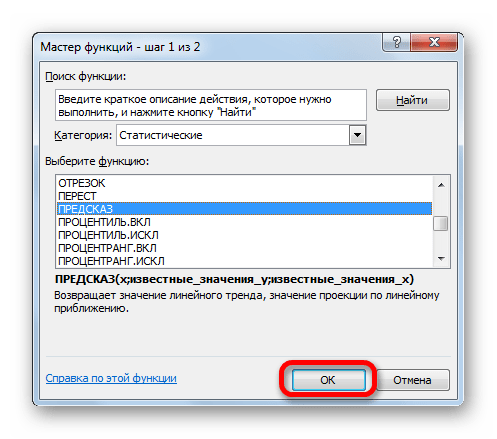
- Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK».
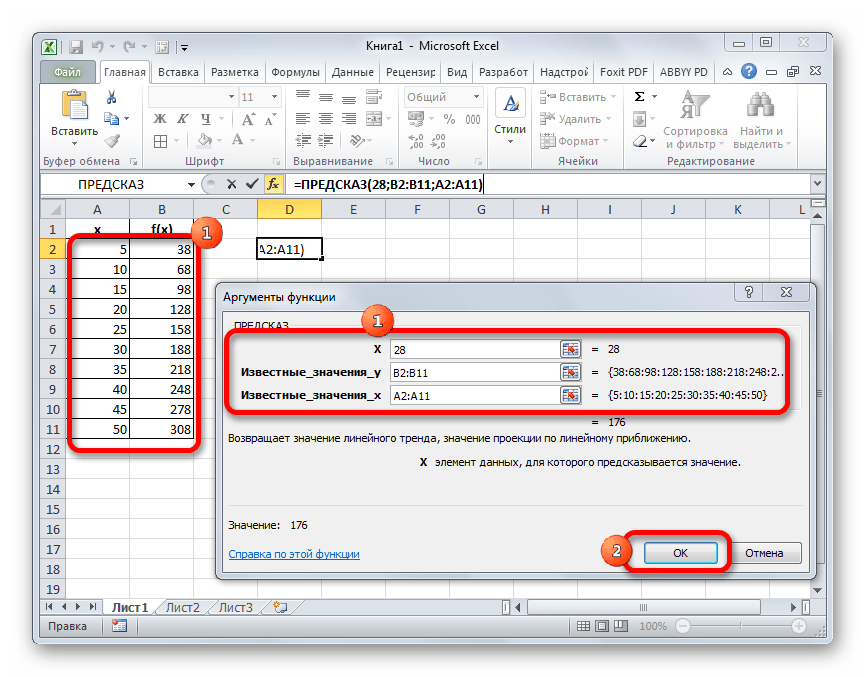
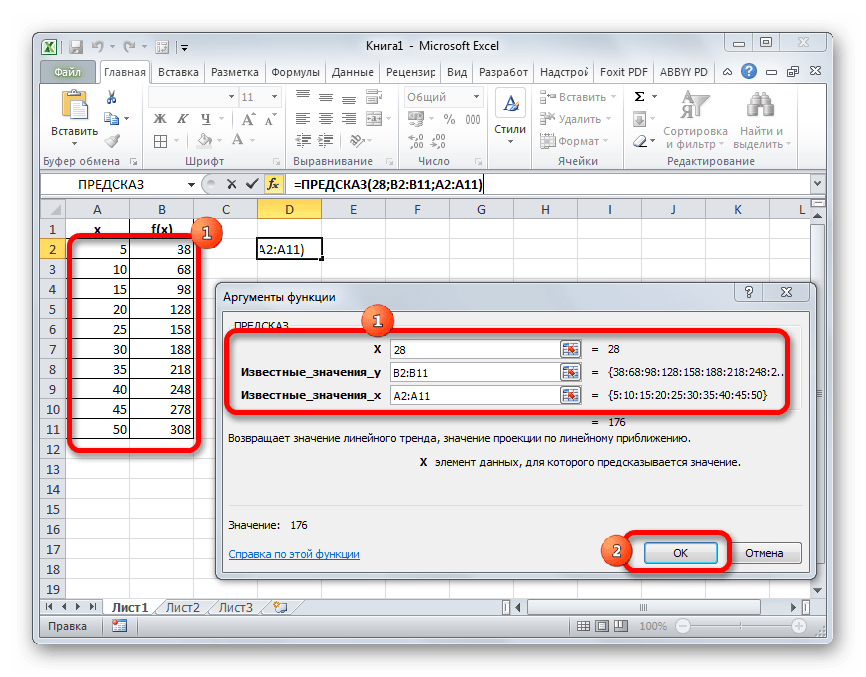
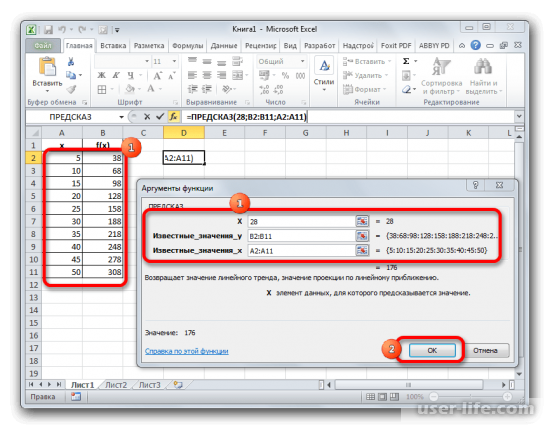
- Запускается окно аргументов функции ПРЕДСКАЗ. В нем имеется три поля:
- X;
- Известные значения y;
- Известные значения x.
В первое поле нам просто нужно вручную с клавиатуры вбить значения аргумента, функцию которого следует отыскать. В нашем случае это 28.
В поле «Известные значения y» нужно указать координаты диапазона таблицы, в котором содержатся значения функции. Это можно сделать вручную, но гораздо проще и удобнее установить курсор в поле и выделить соответствующую область на листе.
Аналогичным образом устанавливаем в поле «Известные значения x» координаты диапазона с аргументами.
После того, как все нужные данные введены, жмем на кнопку «OK».
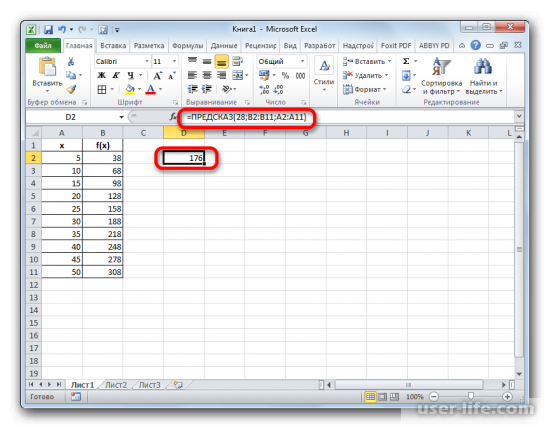
- Искомое значение функции будет отображено в той ячейке, которую мы выделили ещё в первом шаге данного способа. В результате получилось число 176. Именно оно и будет итогом проведения процедуры интерполяции.
Урок: Мастер функций в Экселе
Способ 2: интерполяция графика с помощью его настроек
Процедуру интерполяции можно применять и при построении графиков функции. Актуальна она в том случае, если в таблице, на основе которой построен график, к одному из аргументов не указано соответствующее значение функции, как на изображении ниже.
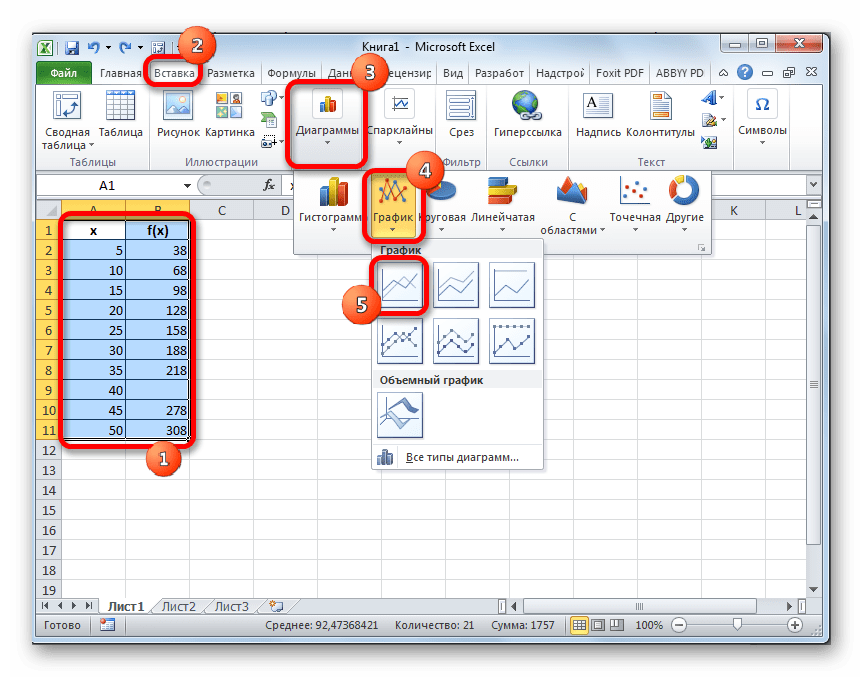
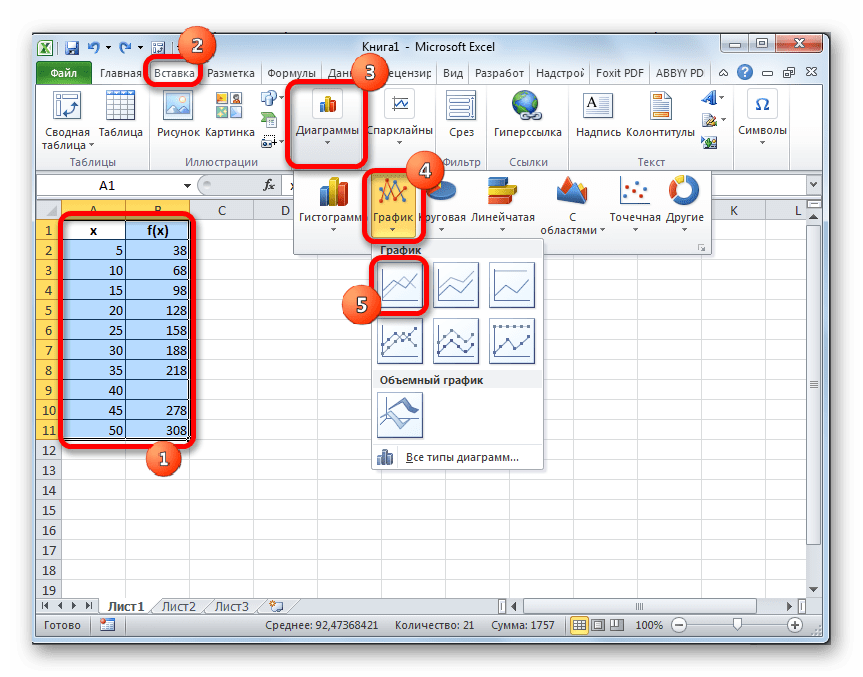
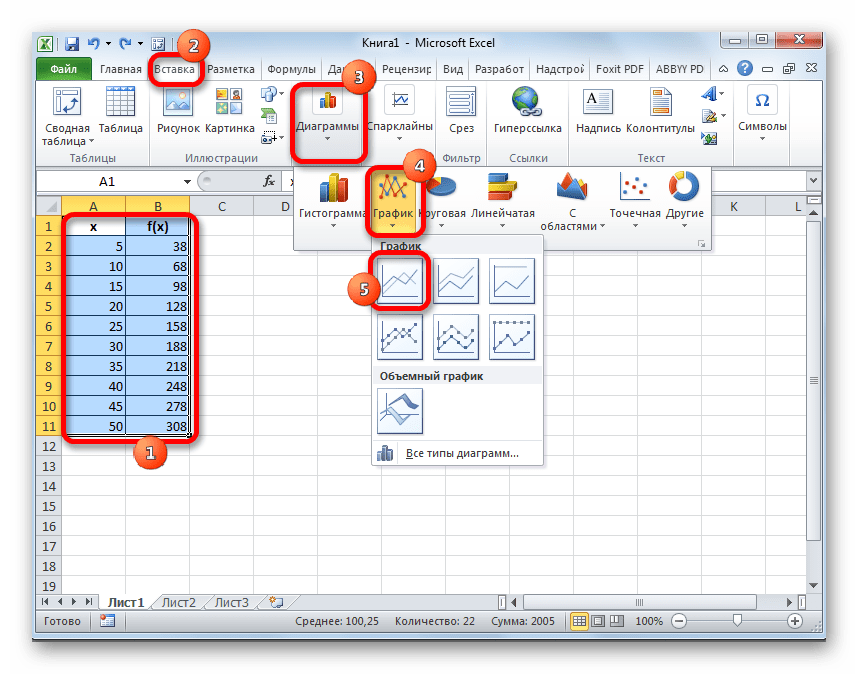
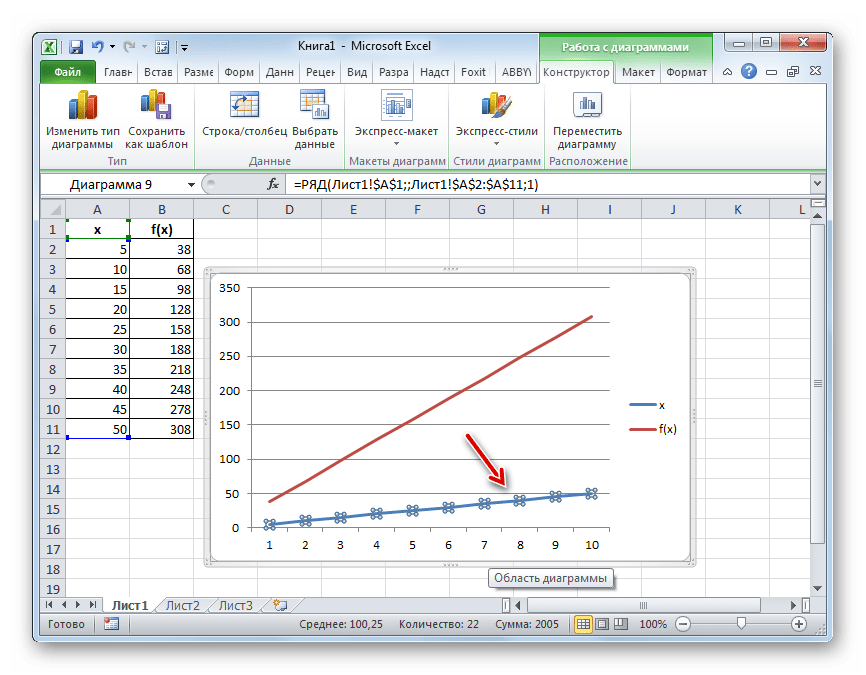
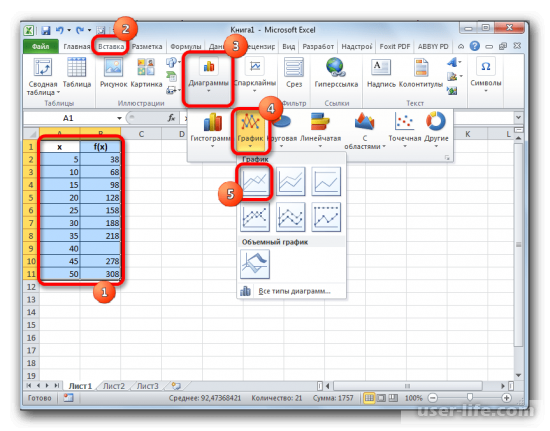
- Выполняем построение графика обычным методом. То есть, находясь во вкладке «Вставка», выделяем табличный диапазон, на основе которого будет проводиться построение. Щелкаем по значку «График», размещенному в блоке инструментов «Диаграммы». Из появившегося списка графиков выбираем тот, который считаем более уместным в данной ситуации.
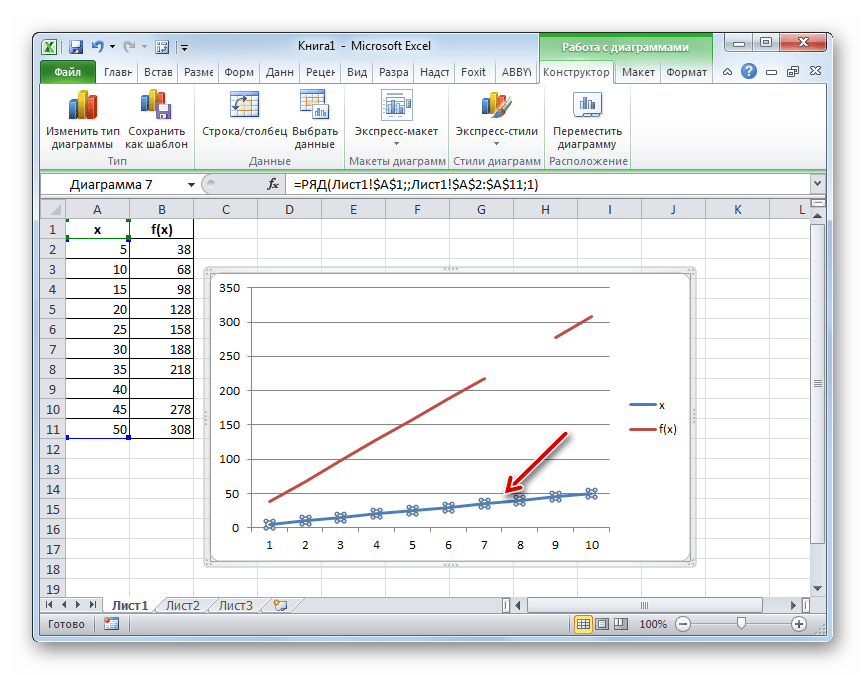
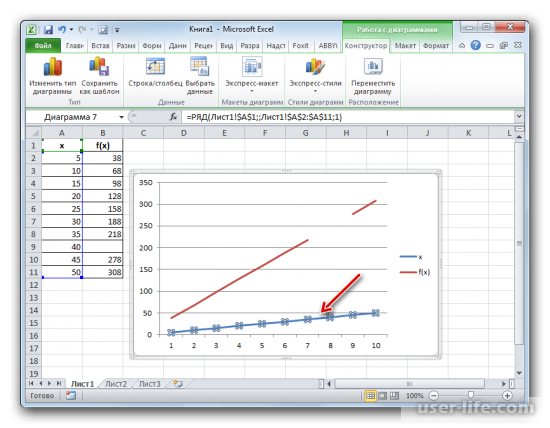
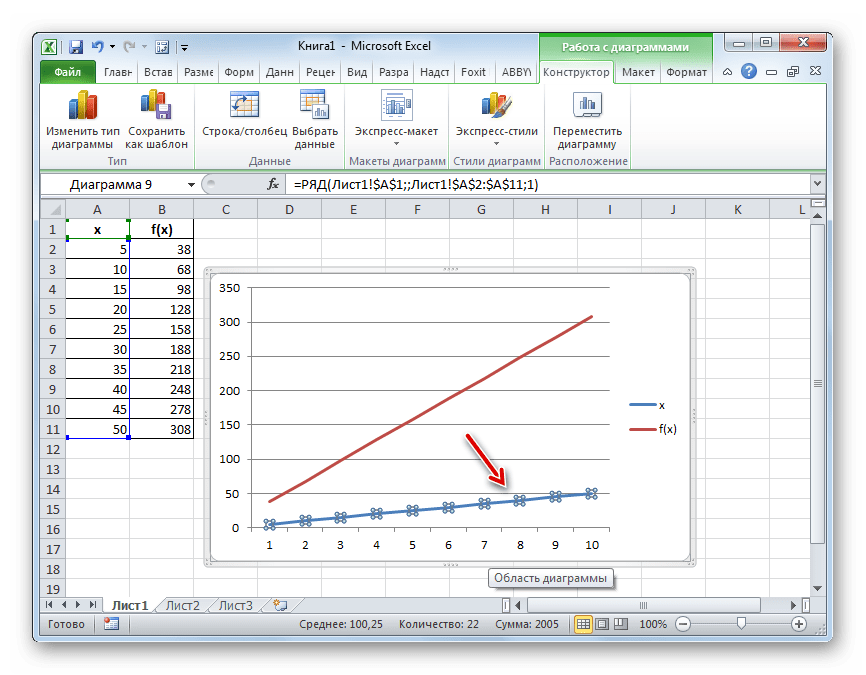
- Как видим, график построен, но не совсем в таком виде, как нам нужно. Во-первых, он разорван, так как для одного аргумента не нашлась соответствующая функция. Во вторых, на нем присутствует дополнительная линия X, которая в данном случае не нужна, а также на горизонтальной оси указаны просто пункты по порядку, а не значения аргумента. Попробуем исправить все это.
Для начала выделяем сплошную синюю линию, которую нужно удалить и жмем на кнопку Delete на клавиатуре.
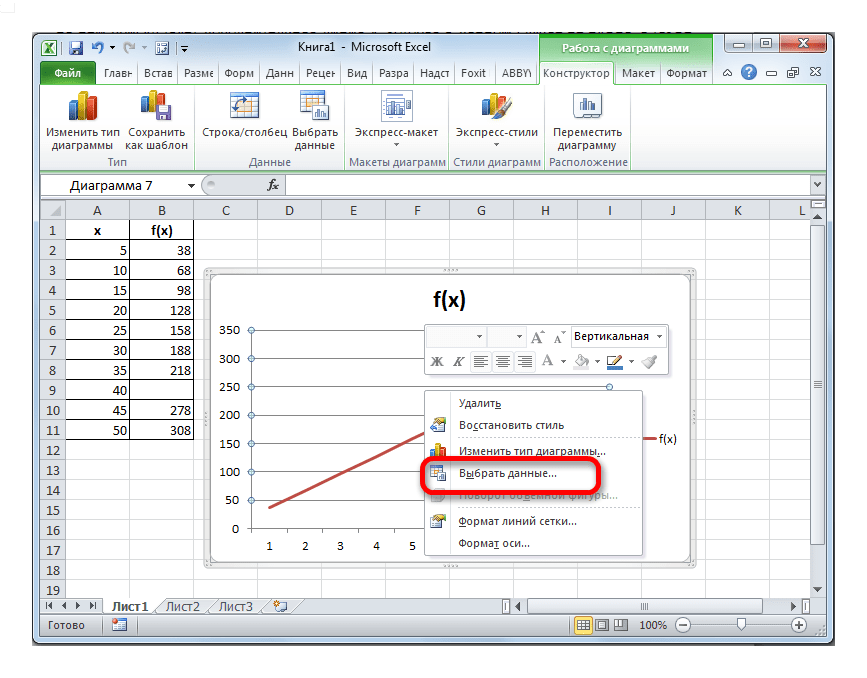
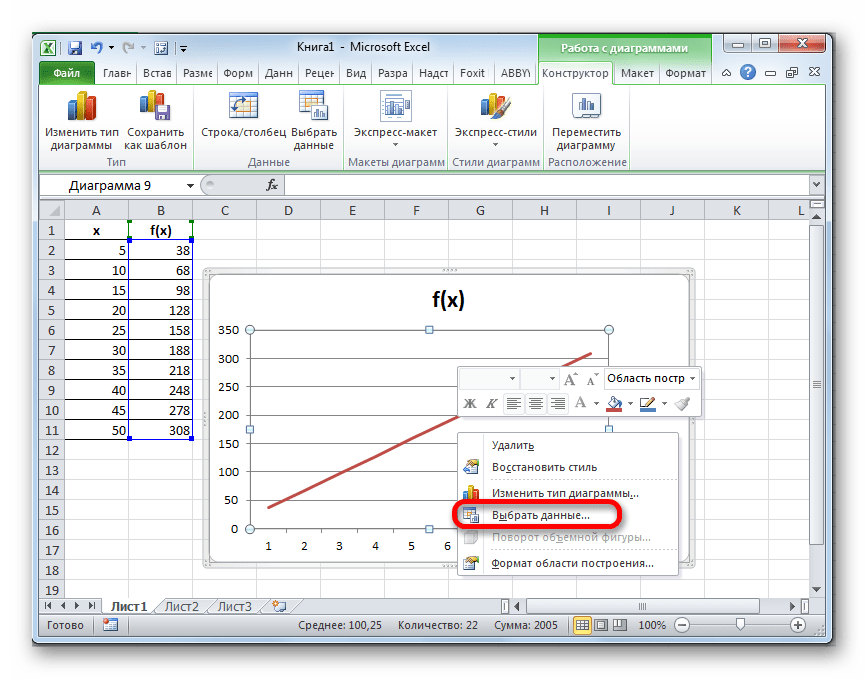
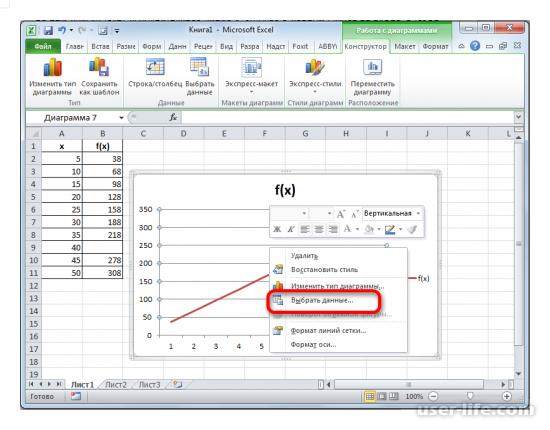
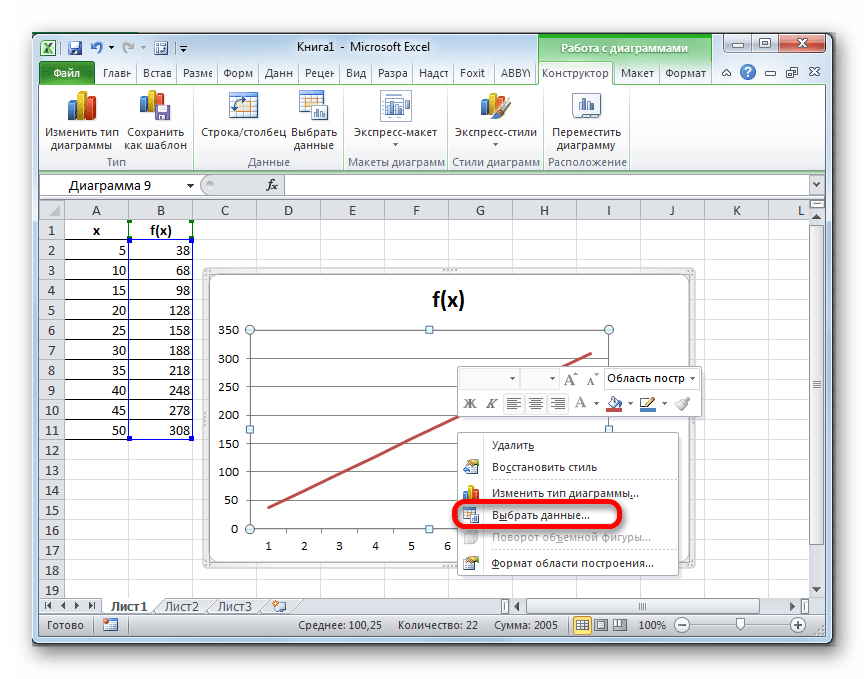
- Выделяем всю плоскость, на которой размещен график. В появившемся контекстном меню щелкаем по кнопке «Выбрать данные…».
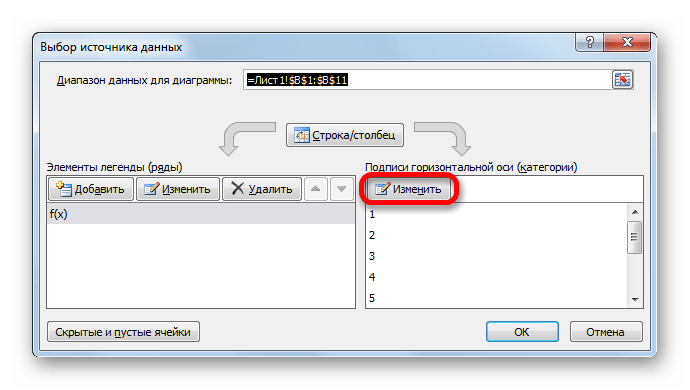
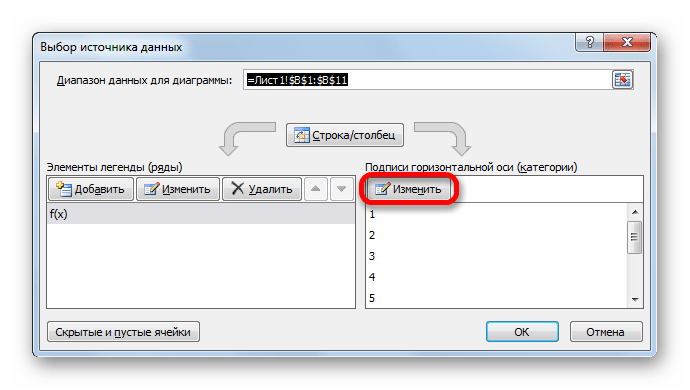
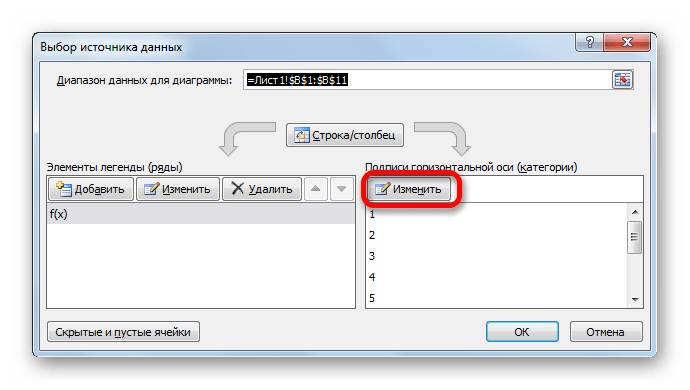
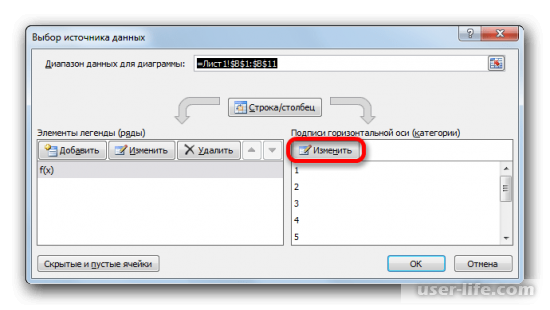
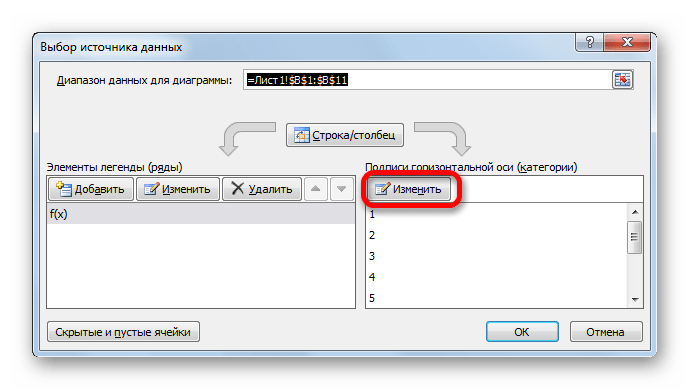
- Запускается окно выбора источника данных. В правом блоке «Подписи горизонтальной оси» жмем на кнопку «Изменить».
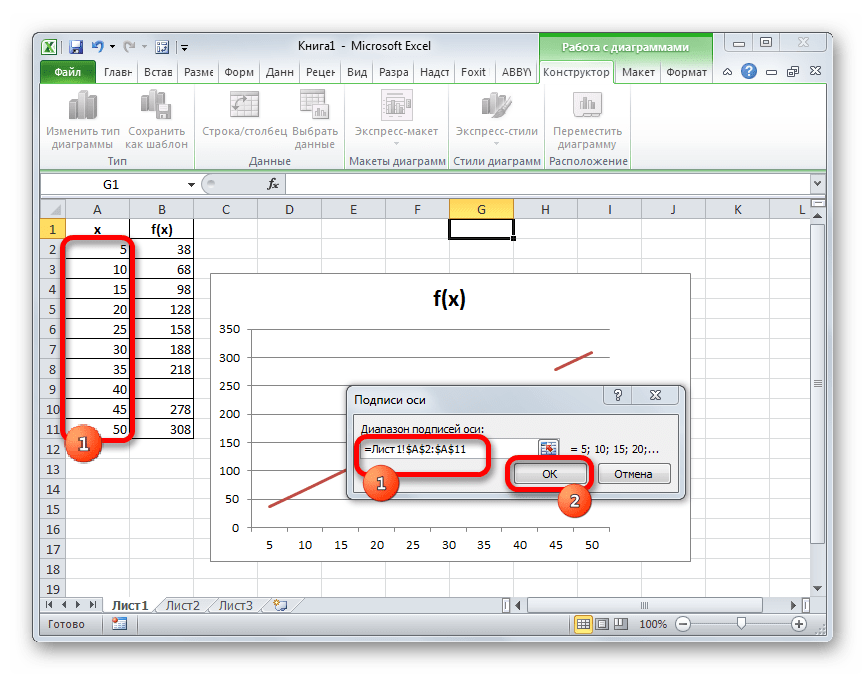
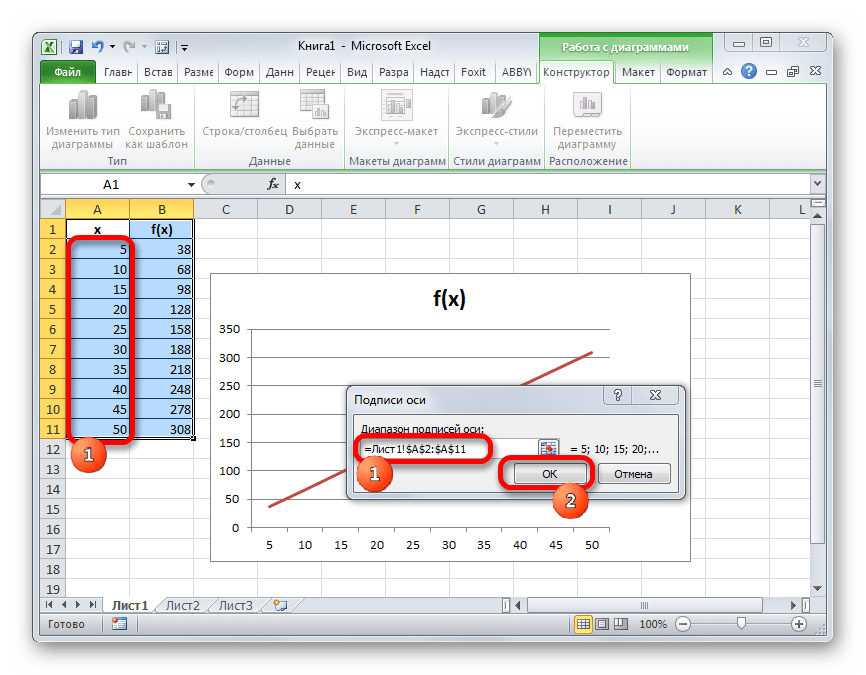
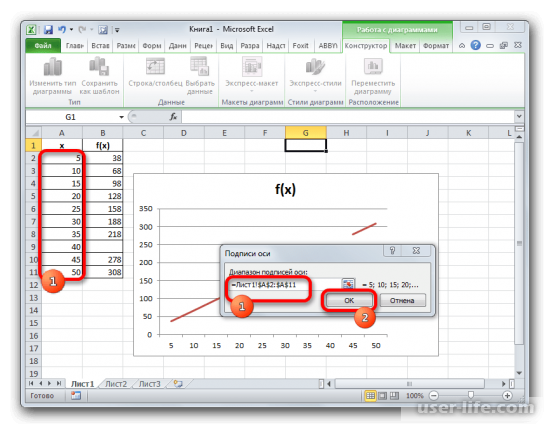
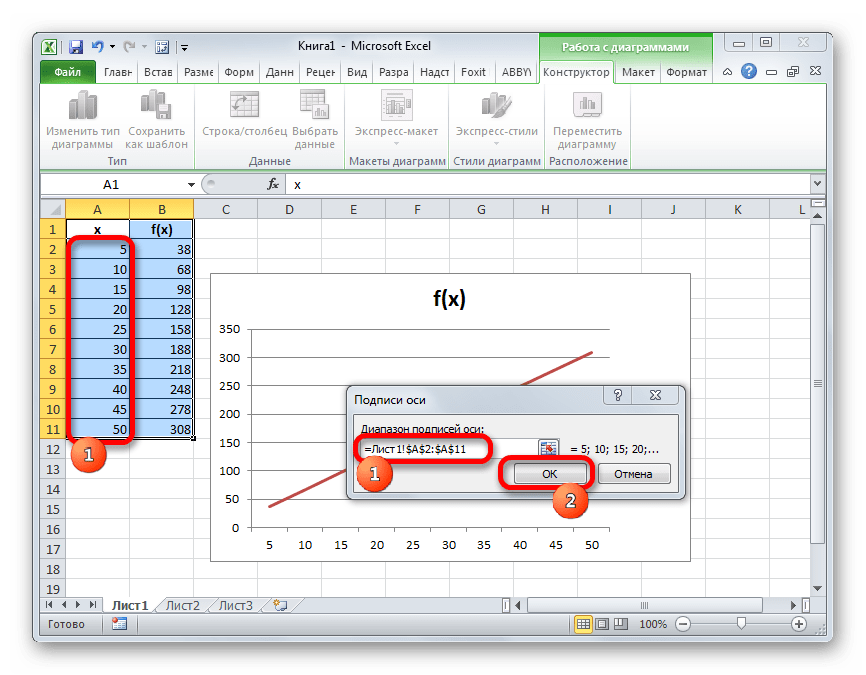
- Открывается небольшое окошко, где нужно указать координаты диапазона, значения из которого будут отображаться на шкале горизонтальной оси. Устанавливаем курсор в поле «Диапазон подписей осей» и просто выделяем соответствующую область на листе, в которой содержаться аргументы функции. Жмем на кнопку «OK».
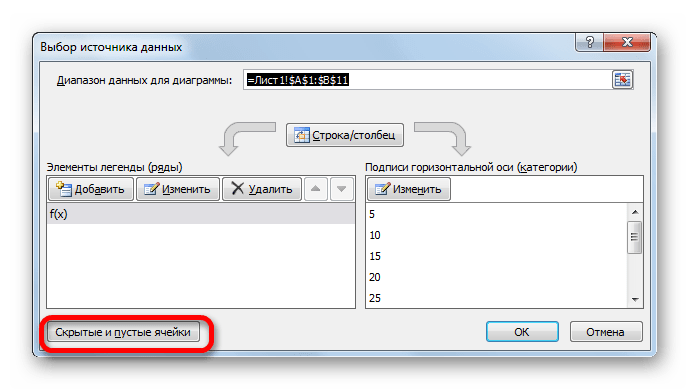
- Теперь нам осталось выполнить основную задачу: с помощью интерполяции устранить разрыв. Вернувшись в окно выбора диапазона данных жмем на кнопку «Скрытые и пустые ячейки», расположенную в нижнем левом углу.
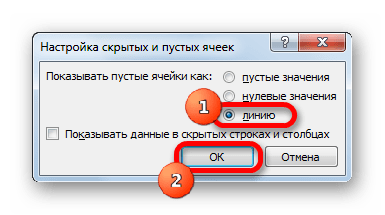
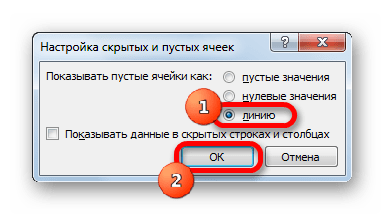
- Открывается окно настройки скрытых и пустых ячеек. В параметре «Показывать пустые ячейки» выставляем переключатель в позицию «Линию». Жмем на кнопку «OK».
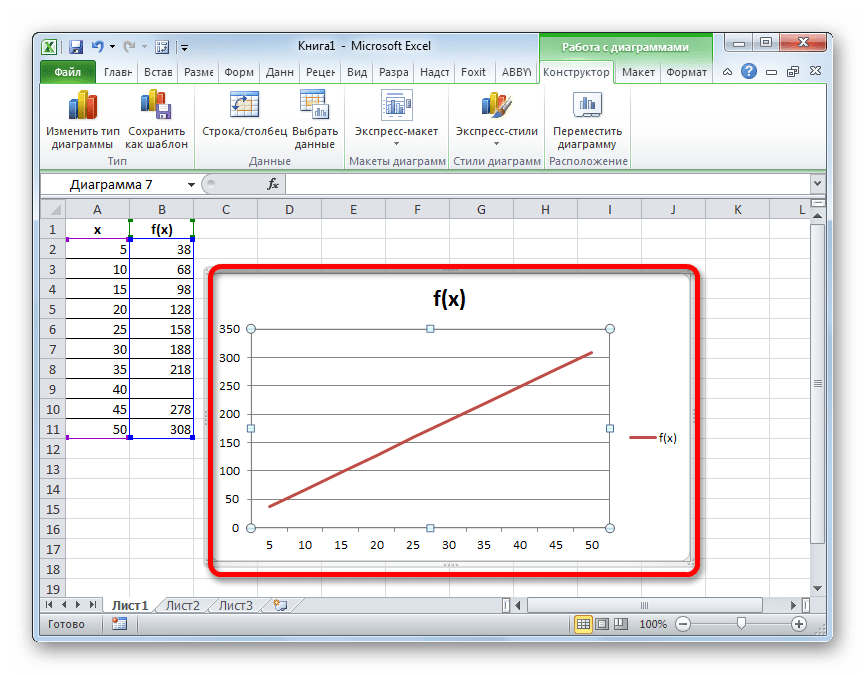
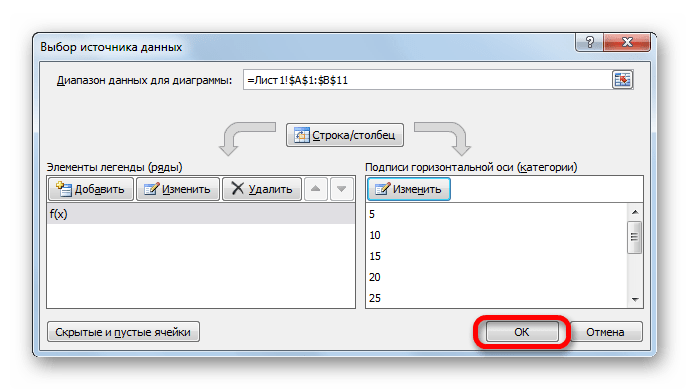
- После возвращения в окно выбора источника подтверждаем все сделанные изменения, щелкнув по кнопке «OK».
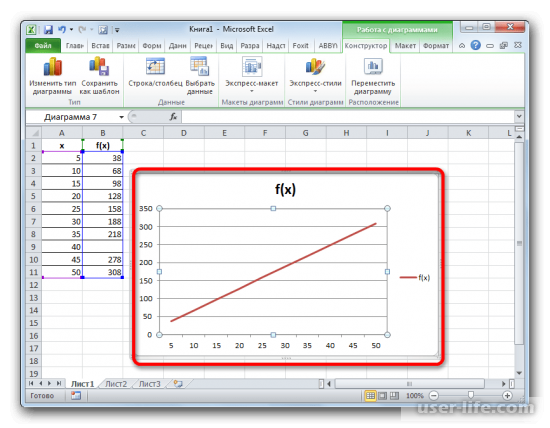
Как видим, график скорректирован, а разрыв с помощью интерполяции удален.
Урок: Как построить график в Excel
Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.
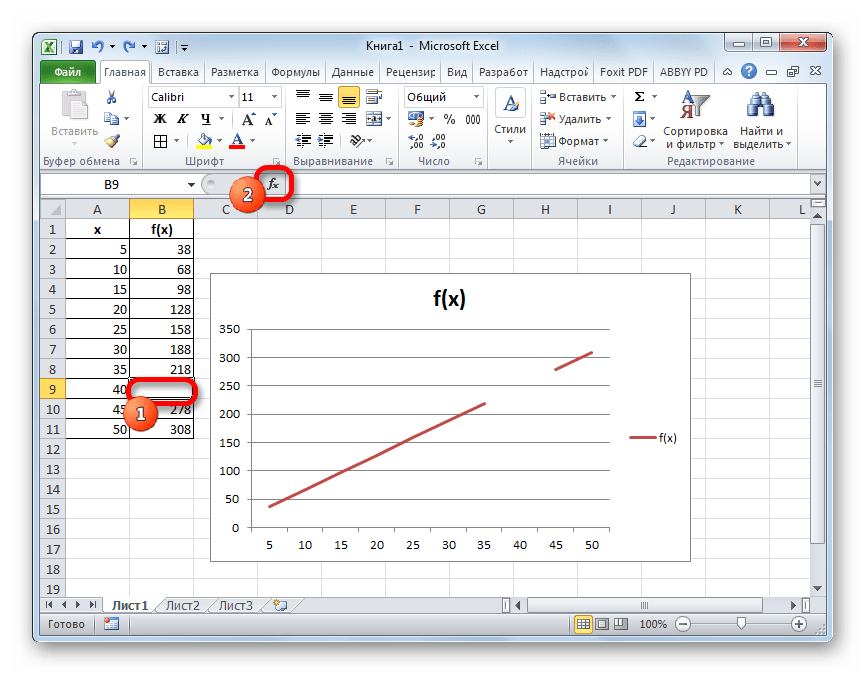
- После того, как график построен и отредактирован, так как вам нужно, включая правильную расстановку подписи шкалы, остается только ликвидировать разрыв. Выделяем пустую ячейку в таблице, из которой подтягиваются данные. Жмем на уже знакомый нам значок «Вставить функцию».
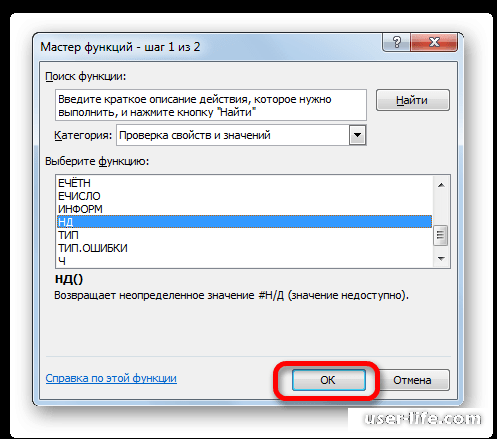
- Открывается Мастер функций. В категории «Проверка свойств и значений» или «Полный алфавитный перечень» находим и выделяем запись «НД». Жмем на кнопку «OK».
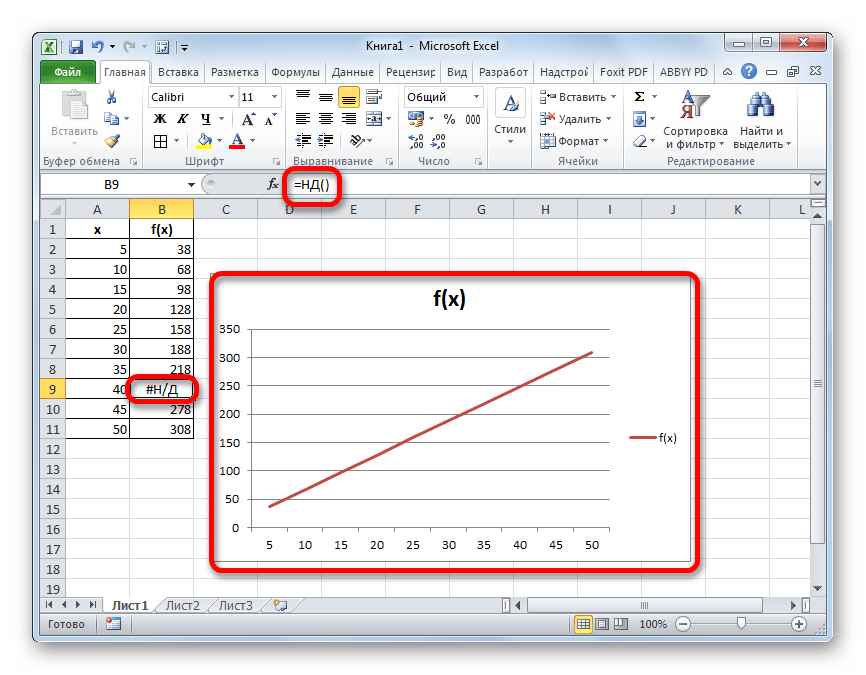
- У данной функции нет аргумента, о чем и сообщает появившееся информационное окошко. Чтобы закрыть его просто жмем на кнопку «OK».
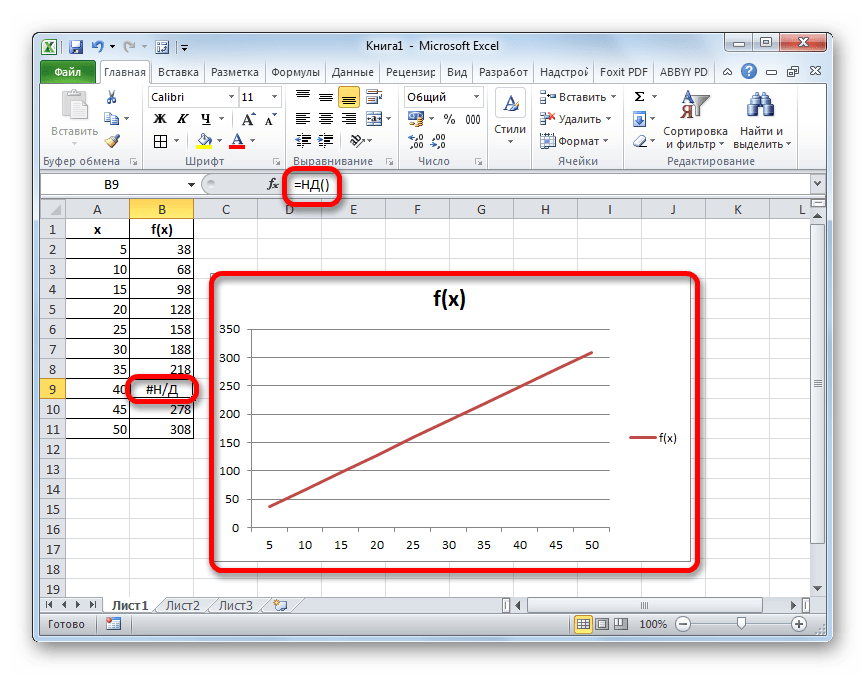
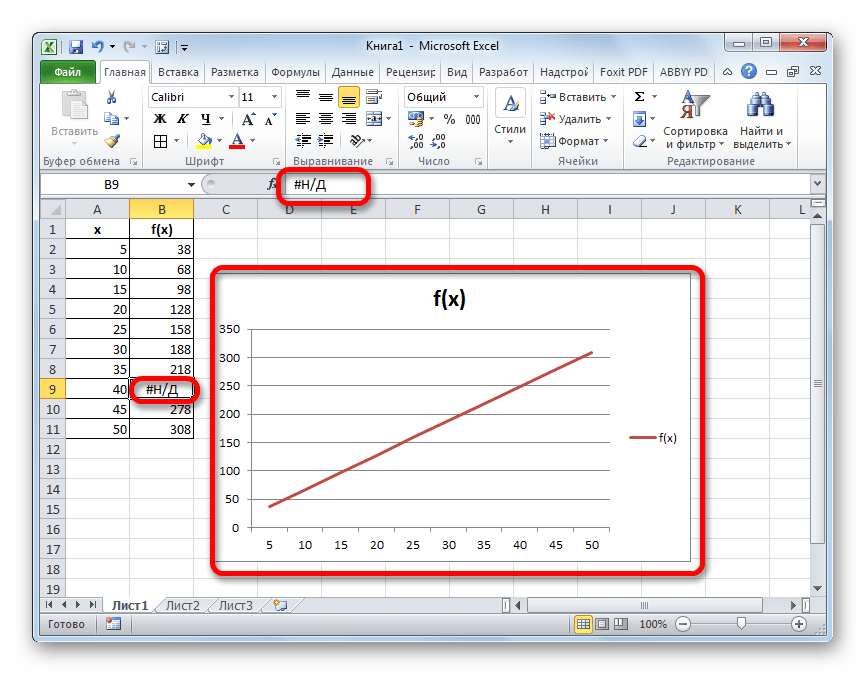
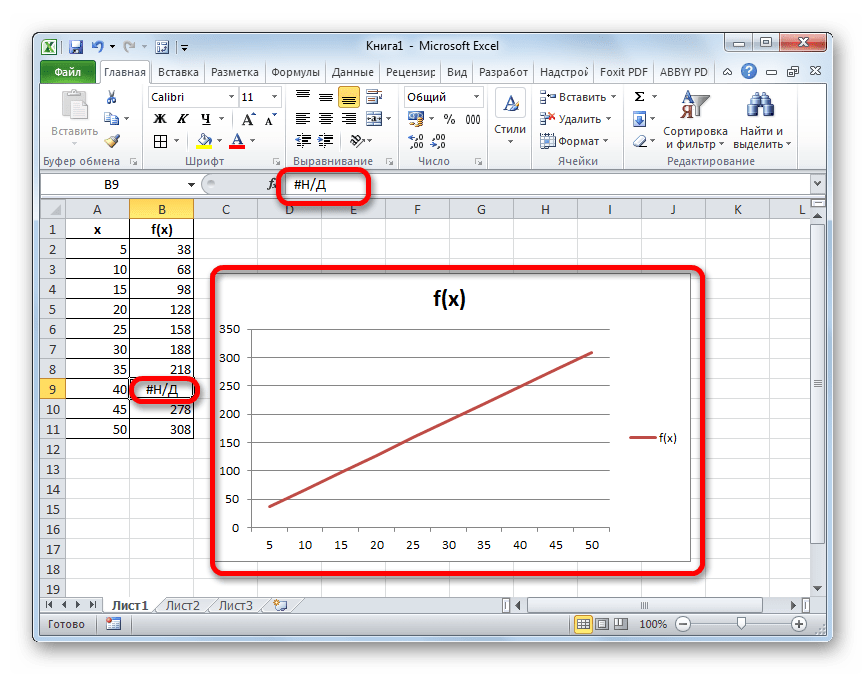
- После этого действия в выбранной ячейке появилось значение ошибки «#Н/Д», но зато, как можно наблюдать, обрыв графика был автоматически устранен.
Можно сделать даже проще, не запуская Мастер функций, а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д» без кавычек. Но это уже зависит от того, как какому пользователю удобнее.
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию ПРЕДСКАЗ, так и графика. В последнем случае это осуществимо с помощью настроек графика или применения функции НД, вызывающей ошибку «#Н/Д». Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.
Еще статьи по данной теме:
Помогла ли Вам статья?
17 авг. 2022 г.
читать 2 мин
Интерполяция — это процесс оценки неизвестного значения функции между двумя известными значениями.
Имея два известных значения (x 1 , y 1 ) и (x 2 , y 2 ), мы можем оценить значение y для некоторой точки x, используя следующую формулу:
у = у 1 + (хх 1 )(у 2 -у 1 )/(х 2 -х 1 )
В этом руководстве объясняется, как использовать линейную интерполяцию для поиска неизвестного значения y на основе значения x в Excel.
Пример: линейная интерполяция в Excel
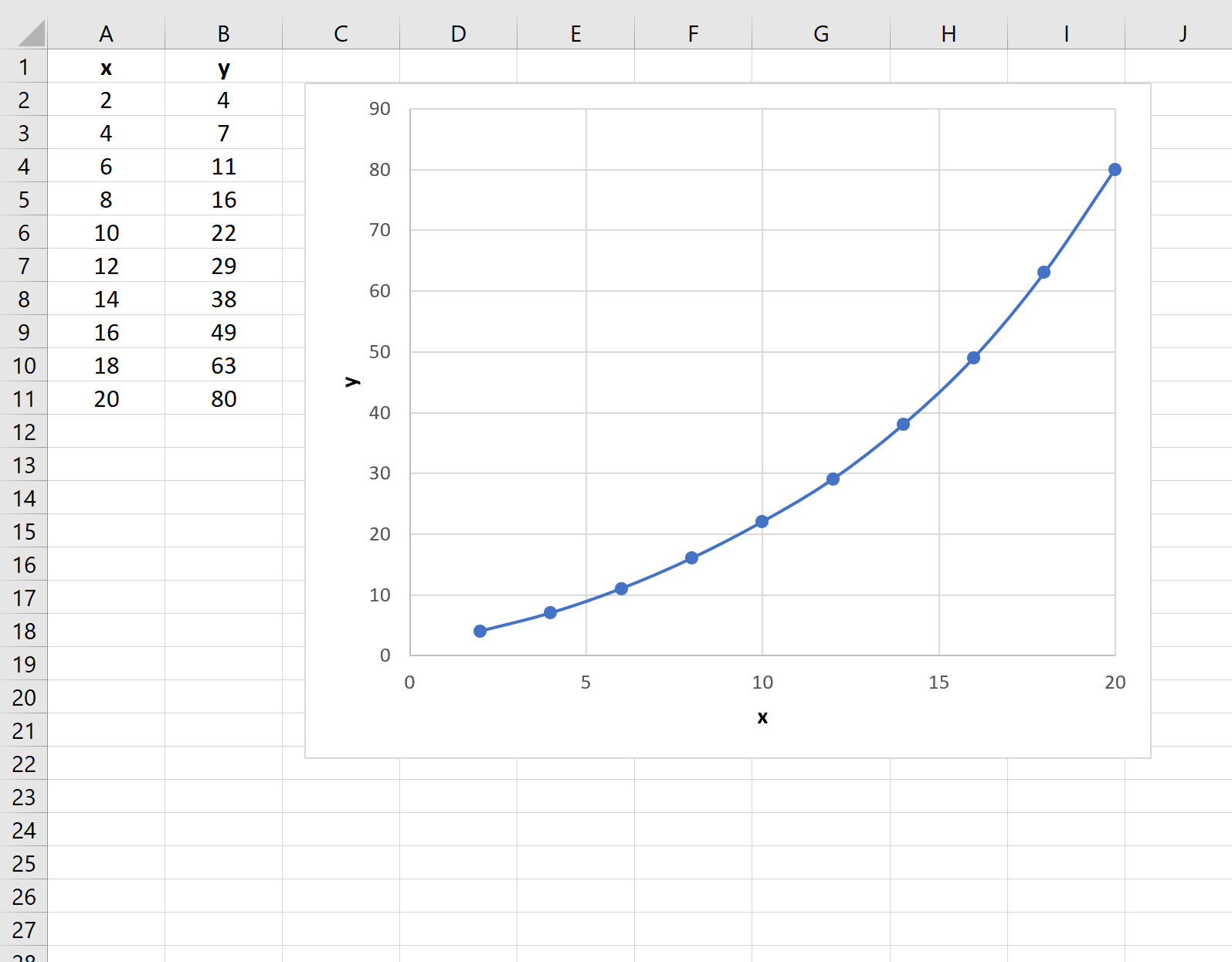
Предположим, у нас есть следующий набор данных в Excel:
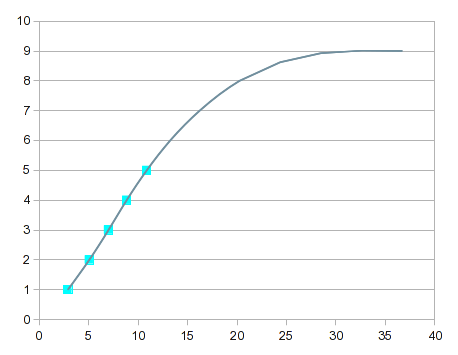
Если мы создадим быстрый график данных, вот как это будет выглядеть:
Теперь предположим, что мы хотим найти значение y, связанное с новым значением x, равным 13.Мы видим, что мы измерили значения y для значений x 12 и 14, но не для значения x 13.
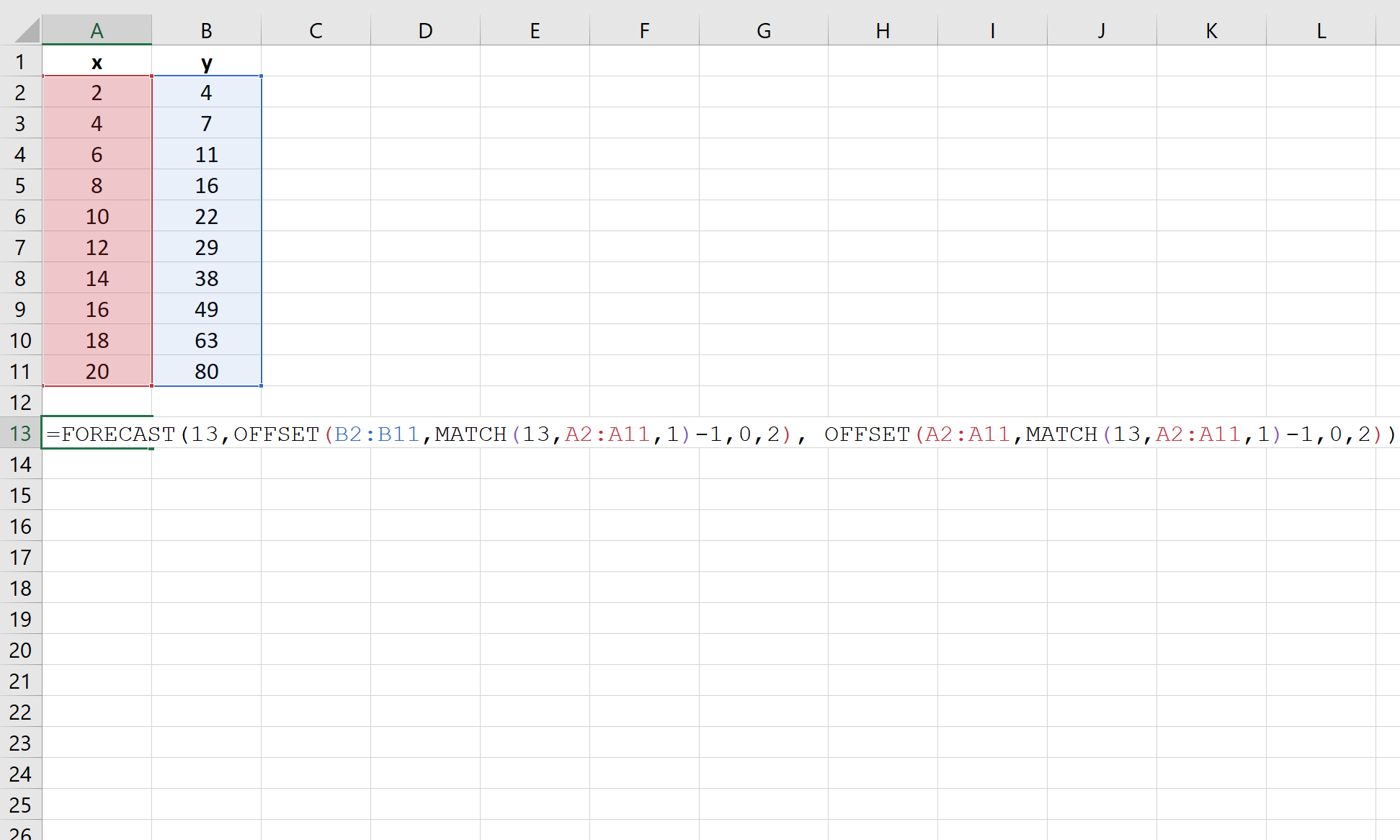
Мы можем использовать следующую формулу для выполнения линейной интерполяции в Excel, чтобы найти расчетное значение y:
= FORECAST (NewX, OFFSET (KnownY, MATCH (NewX,KnownX,1)-1,0,2), OFFSET (KnownX, MATCH (NewX,KnownX,1)-1,0,2))
Вот как использовать эту функцию для оценки значений y, связанных со значением x, равным 13:
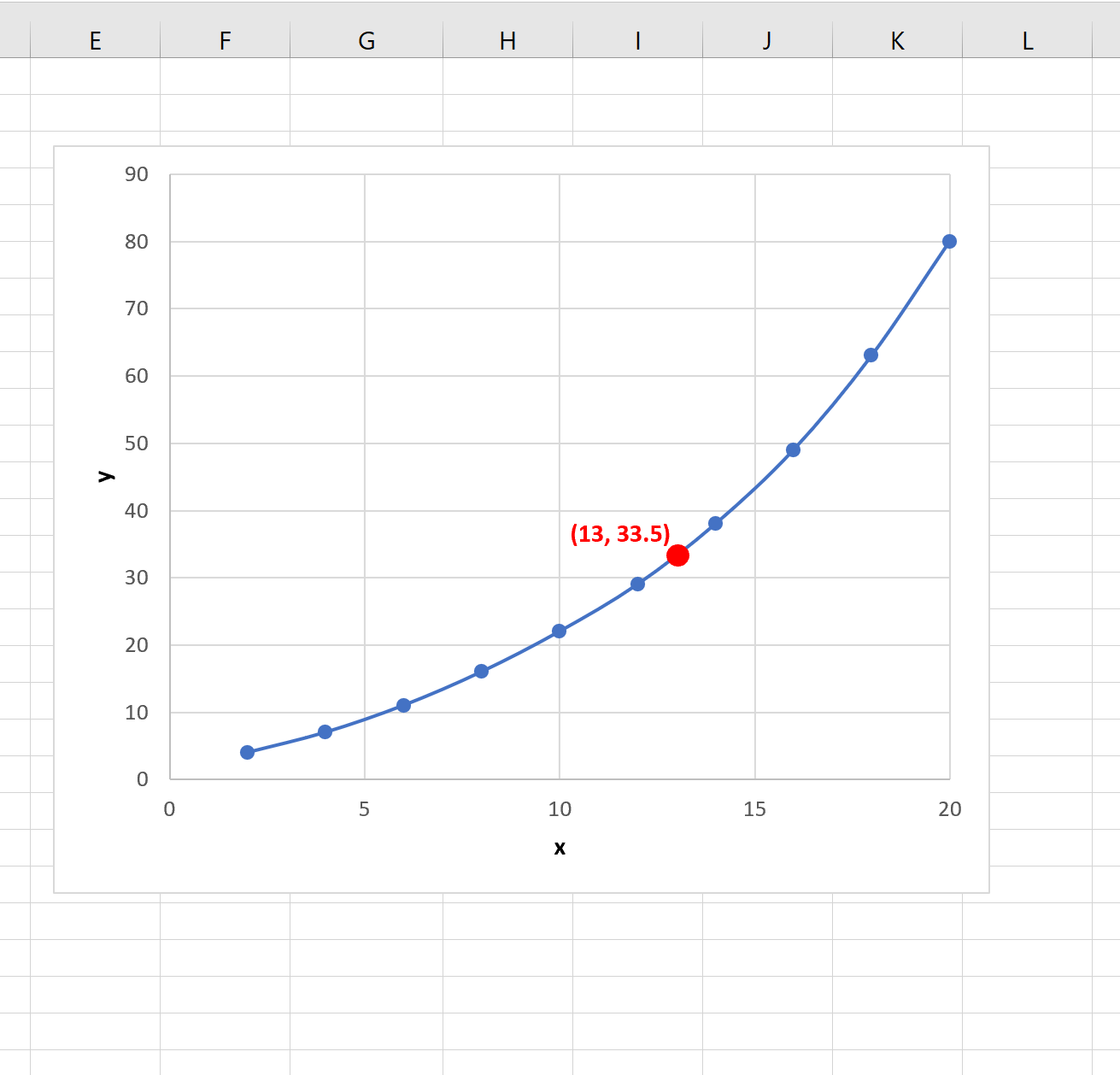
Расчетное значение y оказывается равным 33,5 .
Если мы добавим точку (13, 33,5) к нашему графику, она, похоже, будет хорошо соответствовать функции:
Мы можем использовать эту формулу для оценки значения y любого значения x, просто заменив NewX в формуле любым новым значением x.
Обратите внимание, что для того, чтобы эта функция работала, новое значение x должно находиться в диапазоне существующих значений x.
Вы можете найти больше учебников по Excel здесь .
- Что такое интерполяция?
Линейная интерполяция Excel (Содержание)
- Что такое интерполяция?
- Интерполяция с функцией прогноза в Excel
- Примеры линейной интерполяции в Excel
Что такое интерполяция?
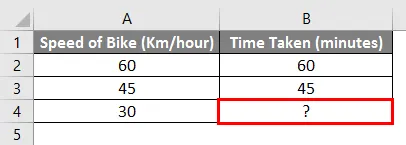
В мире математики интерполяция — это метод создания новых точек данных с помощью известных точек данных. Интерполяция оценивает значение на основе существующих доступных значений данных, которые являются связанными.
Например: если мы едем на велосипеде со скоростью 60 км / час и достигаем определенного пункта назначения за 1 час, а если мы едем со скоростью 45 км / час и достигаем определенного пункта назначения за 45 минут. Так сколько же потребуется времени, чтобы добраться до пункта назначения, если мы едем со скоростью 30 км / час.
Используя простую математику, мы можем вычислить недостающие значения в приведенном выше примере. Нам нужно вставить следующую формулу в ячейку B4.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Таким образом, исходя из приведенной выше формулы, мы можем сказать, что для достижения цели требуется 30 минут, если мы едем со скоростью 30 км / час.
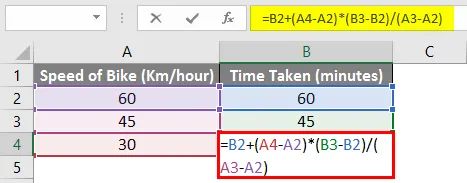
Давайте попробуем разбить вышеприведенную формулу и понять формулу в деталях.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
В приведенном выше примере последний раздел формулы, который выделен красным цветом, вычисляет, сколько времени занимает изменение, когда скорость велосипеда изменяется на 1. В нашем примере, время, необходимое, изменяется на 1 минуту, когда скорость велосипеда изменяется на 1 км. /час.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Во втором разделе (синим цветом выше) вычисляется, насколько далеко наша скорость велосипеда от первой заданной скорости велосипеда, а затем умножает ее на значение, рассчитанное выше. Исходя из нашего примера, это 30 (ячейка A4) минус 60 (ячейка A2), результат которого затем умножается на 1 (что равно -30).
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
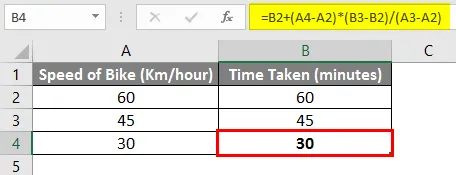
Наконец, первый раздел формулы (коричневым цветом выше); мы добавляем первое значение скорости велосипеда. В нашем примере это дает конечный результат 60 + (-30) * (1) = 30 минут. В школе мы использовали следующую формулу для расчета недостающего значения Y.
Y = Y1 + (X-X1) * (Y2-Y1) / (X2 — X1)
Это пример того, как вычислить пропущенные значения с помощью ручной формулы, чтобы понять интерполяцию.
В Excel есть встроенная функция, которая выполняет вычисления, аналогичные описанным выше, и она известна как функция ПРОГНОЗ. Теперь мы подробно изучим эту функцию.
Интерполяция с функцией прогноза в Excel
Прогноз — это функция рабочего листа, доступная в MS Excel, которая использует линейную регрессию для определения пропущенного значения. Прогноз, как следует из его названия, используется для прогнозирования будущего значения точки данных, но также может использоваться для интерполяции значения. По сути, он используется для расчета будущего значения на основе существующих значений конкретного набора данных.
Синтаксис функции прогноза
Аргументы функции прогноза:
- x — это точка данных, для которой мы хотим знать результирующее значение.
- Known_y’s — диапазон ячеек, содержащих значения Y.
- Known_x’s — диапазон ячеек, содержащих значения X.
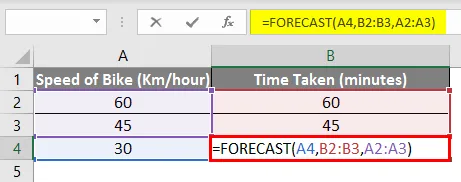
Теперь, рассмотрев тот же пример, приведенный выше, попробуем использовать функцию Forecast.
В нашем примере
x — ячейка B4 (так как мы хотим узнать время, затрачиваемое при скорости в 30 км / час).
Known_y’s — от ячейки B2 до ячейки B3 (время, необходимое для известной скорости велосипеда).
Known_x’s — от ячейки A2 к ячейке A3 (скорость велосипеда, указанная нами, для которой мы знаем время, затраченное).
Итак, окончательная формула в ячейке B4 будет такой:
= ПРОГНОЗ (А4, В2: В3, А2: А3)
И, как вы можете видеть, конечный результат такой же, то есть 30 минут .
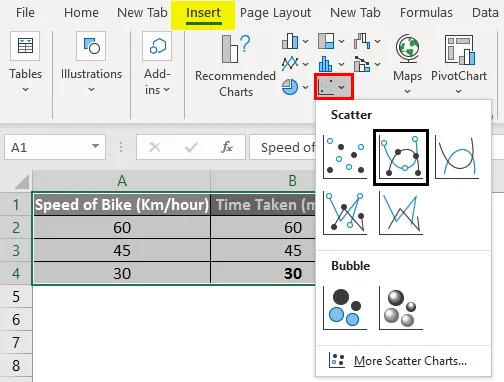
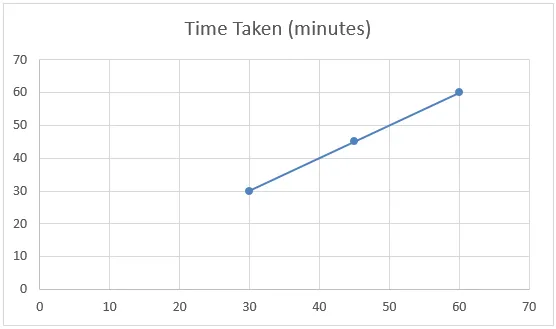
Для создания диаграммы перейдите в меню «Вставка», нажмите «Разброс», а затем выберите «Разброс с гладкими линиями и маркерами».
Если мы посмотрим на диаграмму ниже приведенного выше примера, мы можем сказать, что набор данных имеет линейную зависимость и известен как линейная интерполяция.
Примеры линейной интерполяции в Excel
Давайте разберемся с линейной интерполяцией в Excel на нескольких примерах.
Вы можете скачать этот шаблон Excel с линейной интерполяцией здесь — Шаблон Excel с линейной интерполяцией
Пример № 1
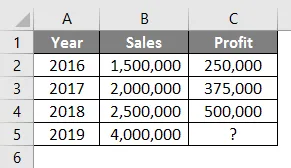
Предположим, у вас есть данные о продажах и прибыли за предыдущие годы, и вы хотите узнать прибыль за текущий год, если достигнете определенного уровня продаж.
Посмотрите на таблицу ниже. У вас есть данные о продажах с 2016 по 2018 год, и вы хотите знать, какой должна быть прибыль, если ваши продажи составляют рупии. 40 000 000 в 2019 году.
Таким образом, с помощью функции прогнозирования мы можем интерполировать прибыль 2019 года, когда продажи составляют рупии. 4000000
Формула в ячейке C5 будет выглядеть следующим образом:
= ПРОГНОЗ (B5, C2: C4, B2: B4)
После использования формулы прогноза ответ показан ниже.
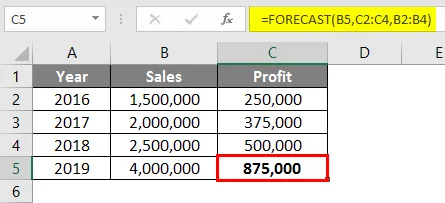
Результат для функции Прогноз будет Rs. 875 000 на основе данных о продажах и прибыли, доступных с 2016 по 2018 год.
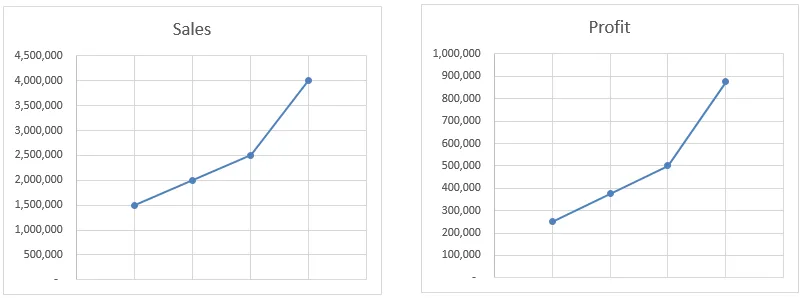
В этом примере функция Forecast интерполирует значение на основе всех доступных данных, а не только начальной и конечной точки. Как видно из графиков, прибыль движется точно так же, как и продажи. Даже если мы вычислим значение вручную, оно все равно даст нам тот же результат.
Пример № 2
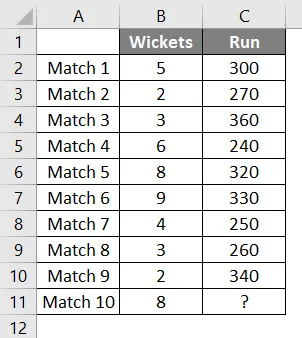
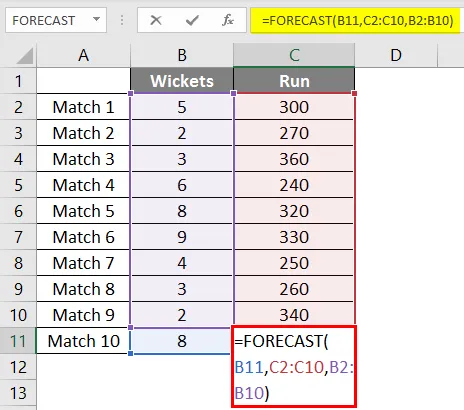
У нас есть данные о последних 9 матчах команды по крикету, в которой пропали калитки и забиты команды.
Мы хотим выяснить, сколько пробежек принесет команда, если выпадет 8 калиток.
Поэтому мы снова будем использовать ту же функцию прогноза, что и выше.
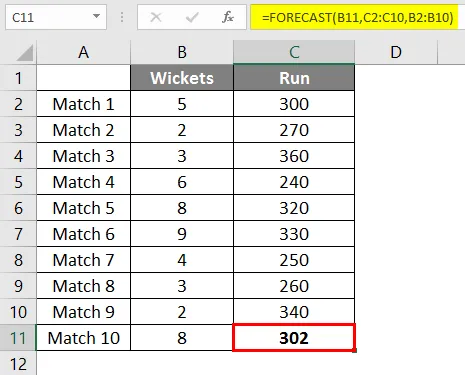
После применения формулы мы получаем результат 302 пробежек, если у нас выпало 8 калиток на основе линейной регрессии последних 9 матчей, сыгранных командой.
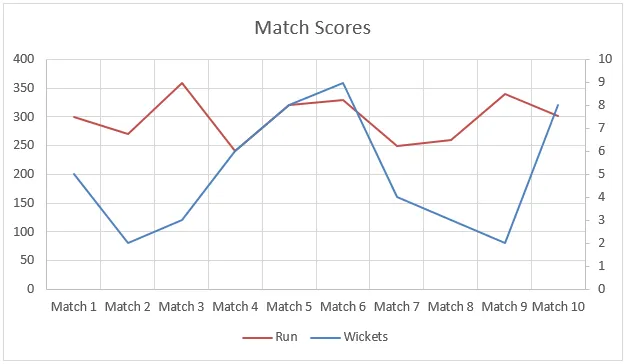
В этом примере данные не были линейными, и вы можете увидеть это на графике ниже. Но все же функция Forecast помогла нам интерполировать прогоны с помощью данных предыдущих матчей.
Что нужно помнить о линейной интерполяции в Excel
- Функция прогнозирования используется для прогнозирования / оценки значения на основе существующих доступных значений, но также может помочь в интерполяции отсутствующего значения.
- В случае, если данные не являются линейными, функция «Прогноз» не даст вам точного значения, основанного на линейной интерполяции, но даст вам ближайшее значение.
- Если x в функции Forecast является текстовым или не числовым, функция Forecast возвращает ошибку #VALUE.
- Если Known_x и Known_y не содержат каких-либо данных или содержат другой набор точек данных, функция Forecast выдаст ошибку # N / A.
- Если дисперсия Known_x равна нулю, тогда функция Forecast выдает ошибку # DIV / O.
Рекомендуемые статьи
Это руководство по линейной интерполяции в Excel. Здесь мы обсуждаем, как использовать линейную интерполяцию в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи —
- Линейная регрессия в Excel
- Поиск текста в Excel
- Текстовая формула в Excel
- Marimekko Chart Excel
- Интерполировать в Excel
- Линейное программирование в Excel
Линейная интерполяция в Excel означает прогнозирование или угадывание следующего значения любой определенной переменной, заданной на основе текущих данных. Здесь мы создаем прямую линию, которая соединяет два значения и оценивает будущую стоимость. В Excel мы используем функцию ПРОГНОЗ и функцию ПРОСМОТРА для выполнения линейной интерполяции.
Интерполяция — это математический или статистический инструмент, предсказывающий значения между двумя точками на кривой или линии. Этот инструмент используется в статистике и во многих других областях, таких как бизнес, наука и т. д., везде, где есть возможность прогнозировать значения между двумя точками данных.
Оглавление
- Линейная интерполяция Excel
- Как сделать линейную интерполяцию в Excel?
- Пример №1
- Пример #2
- То, что нужно запомнить
- Рекомендуемые статьи
- Как сделать линейную интерполяцию в Excel?
Как сделать линейную интерполяцию в Excel?
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон линейной интерполяции Excel здесь — Шаблон линейной интерполяции Excel
Пример №1
Выполнение интерполяции, чтобы узнать температуру погоды в разных часовых поясах
Во-первых, запишите показатели температуры в регионе Бангалор за каждый час, и данные будут следующими:
Данные показывают, что у нас есть данные о температуре в регионе Бангалор на определенную дату. У нас есть часовые пояса на весь день в колонке времени. В столбце часа мы указываем часы с начала дня, например, 00:00 — это 0 часов, 1:00 — 1 час и так далее.
Мы выполним интерполяцию. Интерполяция. Интерполяция — это математическая процедура, применяемая для получения значения между двумя точками, имеющими заданное значение. Он аппроксимирует значение данной функции в заданном наборе дискретных точек. Его можно применять при оценке различных концепций стоимости, математики, статистики. Читать далее по данным, чтобы вытащить значение температуры для нужного часового пояса, которое может быть любым временем, а не только точным часом.
Мы должны использовать несколько формул в Excel, таких как ПРОГНОЗExcel Как ПРОГНОЗФункция ПРОГНОЗ в Excel используется для расчета или прогнозирования будущего значения на основе существующих значений и статистического значения прогноза. Если мы знаем прошлые данные, мы можем использовать функцию для прогнозирования будущего значения. Подробнее, OFFSET и MATCH. Давайте кратко рассмотрим эти формулы, прежде чем двигаться дальше.
ПРОГНОЗ() — Эта функция Excel для прогнозированияФункция Forecast ExcelФункция FORECAST в Excel используется для расчета или прогнозирования будущего значения на основе существующих значений и статистического значения прогноза. Если мы знаем прошлые данные, мы можем использовать функцию для прогнозирования будущего значения. Читать далее вычисляет или прогнозирует будущее значение на основе существующих значений и линейного тренда.
- Икс – Это значение, для которого мы хотим спрогнозировать.
- Известные_ys – Это зависимое значение от данных и обязательное поле для заполнения.
- Известные_xs – Это независимое значение от данных и обязательное поле для обслуживания.
СООТВЕТСТВОВАТЬ() — Эта функция Match excel Функция Match Excel Функция ПОИСКПОЗ ищет определенное значение и возвращает его относительное положение в заданном диапазоне ячеек. Результатом является первая позиция, найденная для данного значения. Будучи поисковой и справочной функцией, она работает как для точного, так и для приблизительного совпадения. Например, если диапазон A11:A15 состоит из чисел 2, 9, 8, 14, 32, формула «ПОИСКПОЗ(8,A11:A15,0)» возвращает 3. Это связано с тем, что число 8 находится на третьем месте. позиция. read more вернет относительную позицию искомого значения в строке, столбце или таблице, которая соответствует указанному значению в указанном порядке.
- Искомое_значение – Это значение, которое необходимо сопоставить с lookup_array.
- Lookup_array – это диапазон для поиска
[match_type] – Это может быть 1,0,-1. Значение по умолчанию — 1. Для функции 1 — ПОИСКПОЗ вы найдете наибольшее значение, меньшее или равное значению look_up. Значение должно быть в порядке возрастания. Для 0 — функция ПОИСКПОЗ находит первое значение, точно равное искомому_значению, и его не нужно сортировать. Для -1 — Match найдет наименьшее значение, большее или равноеGreater Than Or Equal«Больше или равно» — это сравнение или логический оператор, который помогает сравнить две ячейки данных одного и того же типа данных. быть отсортированы в порядке убывания.
КОМПЕНСИРОВАТЬ() — Эта функция смещенияФункция смещенияФункция смещения в Excel возвращает значение ячейки или диапазона (соседних ячеек), которое представляет собой определенное количество строк и столбцов от контрольной точки. read more вернет ячейку или диапазон ячеек, которые содержат указанное количество строк и столбцов. Ячейка или диапазон ячеек будет зависеть от высоты и ширины строк и столбцов, которые мы указываем.
- Ссылка – Это начальная точка, откуда будут подсчитываться строки и столбцы. Строки и столбцы. Ячейка – это пересечение строк и столбцов. Строки и столбцы составляют программное обеспечение, которое называется Excel. Область рабочего листа Excel разделена на строки и столбцы, и в любой момент времени, если мы хотим сослаться на определенное место этой области, нам нужно сослаться на ячейку. Будет сделано больше.
- Ряды – Количество строк для смещения ниже начальной опорной ячейки.
- Столбцы – Количество столбцов для смещения справа от начальной опорной ячейки.
- [height] – Высота в строках из возвращенной ссылки. Это необязательно.
- [width] – Ширина в столбцах из возвращенной ссылки. Это необязательно.
Мы вкратце рассмотрели формулы, которые будем использовать для выполнения интерполяции. Теперь давайте выполним интерполяцию следующим образом:
Введите в ячейку формулу, которая нам нужна, чтобы увидеть температуру для разных часовых поясов. Это говорит о том, что мы должны выбрать ячейку, которую необходимо спрогнозировать, и функция OFFSET и MATCH используется для определения known_ys и known_xs.
ПРОГНОЗ($F$5 – Выберите ячейку с часовым поясом для прогноза.
СМЕЩ($C$3:$C$26,ПОИСКПОЗ($F$5,$B$3:$B$26,1)-1,0,2) – Это используется для выбора known_ys в качестве ссылки на временный столбец, поскольку это зависимые значения. Функция match используется для генерации позиции значения, которое нам нужно для прогноза и расчета количества строк. Столбцы должны быть равны 0, потому что мы хотим, чтобы зависимое значение в том же выбранном столбце и высота были равны 2, поскольку нам нужно выполнить прогноз на основе двух последних значений.
СМЕЩ($B$3:$B$26, ПОИСКПОЗ($F$5,$B$3:$B$26,1)-1,0,2) – Это используется для выбора known_xs в качестве эталонного столбца часов, потому что это независимые значения, а остальные такие же, как мы сделали для подсчета строк.
Теперь укажите часовой пояс в ячейке, который мы рассматривали для прогнозирования. Здесь введено значение 19,5, что соответствует 19:30, и мы получим температуру 30, которая прогнозируется на основе значений температуры, предоставляемых на почасовой основе.
Точно так же эта формула может отображать временные значения для разных часовых поясов.
Пример #2
Выполнение линейной интерполяции, чтобы узнать продажи организации в 2018 году
Предположим, что мы получили данные о продажах организации в 2018 году, как показано ниже. У нас есть данные в пересчете на дни и их продажи нарастающим итогом. За первые 25 дней года мы получили 7 844 единицы, за 50 дней года — 16 094 единицы и т. д.
Мы можем использовать ту же формулу, что и при интерполяции, для прогнозирования стоимости продаж в разные дни, которые мы не упомянули в рассмотренных нами данных. Здесь продажи идут по прямой линии (линейно), как мы взяли кумулятивно.
Если мы хотим увидеть количество продаж, достигнутое за 215 дней, мы можем получить прогнозируемое количество продаж за 215 дней, как показано ниже, с учетом данных о продажах.
Точно так же мы можем определить количество продаж в этом году, прогнозируя между заданными точками.
То, что нужно запомнить
- Это наименее точный метод, но он быстрый и точный, если табличные значения расположены близко друг к другу.
- Его также можно использовать для оценки значений географических точек данных, осадков, уровней шума и т. д.
- Он очень прост в использовании и не очень точен для нелинейных функций.
- Помимо линейной интерполяции Excel, у нас также есть различные методы, такие как полиномиальная интерполяция, сплайн-интерполяция и т. д.
Рекомендуемые статьи
Эта статья представляет собой руководство по линейной интерполяции в Excel. Здесь мы увидим, как выполнять интерполяцию и линейную интерполяцию в Excel, несколько примеров и загружаемый шаблон Excel. Вы можете узнать больше об Excel из следующих статей: –
- Формула относительного изменения
- Полный список функций Excel
- Формула прогноза в Excel
- Формула стандартного нормального распределения
Interpolation is the process of estimating data points within an existing data set. Here’s how to interpolate in Excel.
If you’re into mathematics and need to discover unknown data points from a survey sample of known data points, interpolating with Excel is an effortless choice.
Excel is a robust calculator with data visualization. Thus, for various mathematical and statistical analyses, you’ll always find it useful. Though there is no straightforward function for interpolation, you can use various functions to estimate new data points from a given data table of X and Y values.
Read on to know the popular and easy data interpolation methods in Excel.
1. Using a Mathematical Equation
One of the basic approaches of data interpolation in Microsoft Excel is to apply the mathematical formula of linear interpolation. You can use this method if getting a linear trendline for a chart.
Y= Y1 + (X-X1)⨯(Y2-Y1)/(X2-X1)
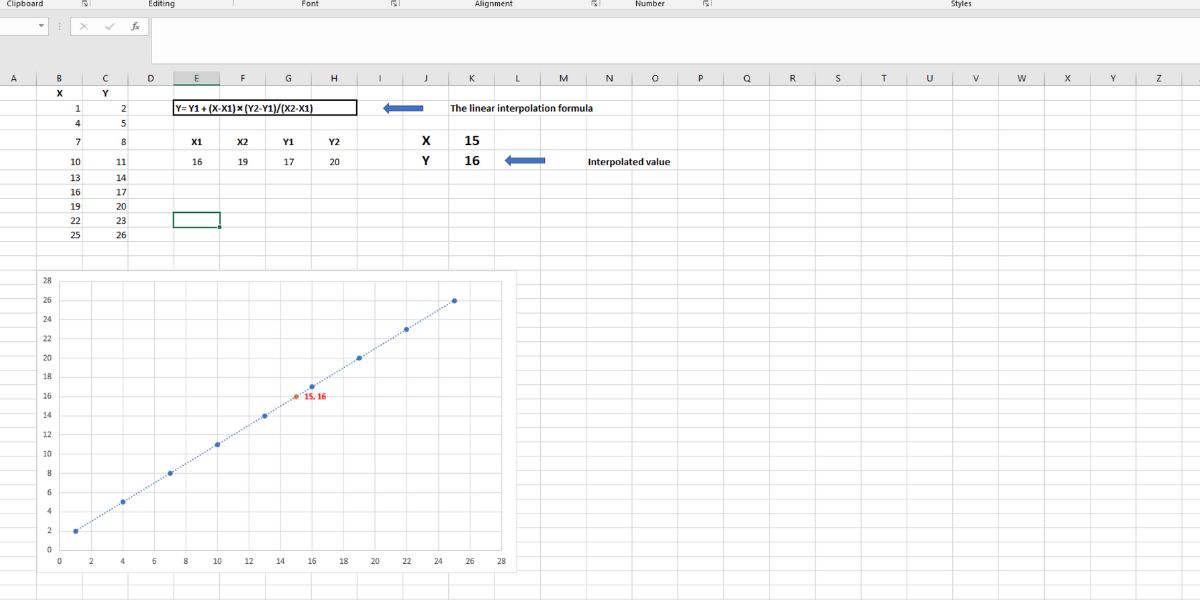
For example, you want to find out the value of Y when X is 15 from this table. Here is how:
- Create a table of X1, X2, Y1, and Y2 values by analyzing the table.
- You have to choose the data points one step above and below the new X-value that you’re looking for.
- Now, apply the following formula in any cell to find the interpolated value of Y that corresponds to the X-value 15.
=G5+(K4-E5)*(H5-G5)/(F5-E5)
The process is pretty simple and manual. For larger data sets, you’ll have to invest a lot of time in interpolating the data points.
Download: Interpolate in Excel Spreadsheet (Free)
2. Using the Curve Fitting Method
Curve fitting is another quick yet manual method to interpolate with Excel. Just create a scatter plot and generate the graph equation. Excel utilizes linear regression to populate the equation. You need to apply this curve fit equation to find the value of Y:
Y= Slope * X + Y-intercept
To discover the value of Y from a given value of X, which is 15, you can try these steps:
- Select the table and insert a scatter chart.
- Right-click on the trendline and then select Format Trendline.
- Check the boxes beside Display R-squared value on chart and Display Equation on chart.
- Also, choose the Linear trendline.
- Once the scatter graph reveals the equation, fit the value of X into it to find the value of Y.
- The following formula reveals the value of Y.
=0.9889*K4+3.5333
The curve fitting method is only suitable for small data sets. There is no easy automation for this process, and you can only rely on the Microsoft Excel macros for hot-key-based automation.
3. Using Excel Functions: Slope and Intercept
You can utilize the SLOPE and INTERCEPT functions in Excel for linear interpolation of the Y value. You can easily apply these functions since they only require the values of known Xs and Ys. The following are the syntaxes that you’ll need to use:
=SLOPE(known_y's, known_x's)
=INTERCEPT(known_y's, known_x's)
Here is how you can interpolate data points via this method:
- Rename two cells with Slope and Intercept.
- Apply the SLOPE function beneath the Slope header and choose the relevant data from the table.
- Similarly, apply the INTERCEPT function and populate the value of intercept.
- Now, apply the Y= Slope * X + Y-intercept formula to discover the value of Y.
- You can create an Excel formula for the above equation, where you can simply change the X’s value to find out other unknown data points.
You can interpolate faster if you make cells for the X-value, Slope, and Intercept. However, this process may not fetch accurate data for non-linear interpolation.
4. Using Excel Function: FORECAST
It’s a popular Excel function for predicting performance by analyzing a set of real-world data points. You’ll find FORECAST and FORECAST.LINEAR in Excel 2016 and later editions. It’s good to use FORECAST.LINEAR for reliable results.
The function utilizes three arguments to produce a predicted data point. These arguments are a given value for X, known values of Y, and values of Xs from a table. Check out the syntax below:
=FORECAST.LINEAR(x, known_y's, known_x's)
You can quickly determine the value of Y by following these steps:
- The cell where you want to populate the value for Y should have an equal (=) sign.
- Now, type Forecast and select FORECAST.LINEAR function from the formula drop-down menu.
- Click on the X’s value and put a comma.
- Then select the known Ys’ value cell range followed by a comma.
- Select the known Xs’ cell range and close the formula with a parenthesis.
- Press Enter to retrieve the interpolated value of Y.
- You can keep on changing the value of X within the range of the given table to fetch Y-values.
- The FORECAST formula of this tutorial is as follows:
=FORECAST.LINEAR(K4,C2:C10,B2:B10)
The FORECAST.LINEAR functions offer highly accurate data prediction for linear and slightly nonlinear data points. It utilizes the first and last values for a given X-value and takes into account the entire data set.
Therefore, you’ll see the utilization of this function for mission-critical data analytics like forecasting web traffic, modeling financial data, and calculating business performance.
5. GROWTH Function for Nonlinear Interpolation
When you’ve got a table of real-world data in exponential form, FORECAST.LINEAR won’t yield accurate interpolated data points. Excel has another excellent function for you to predict data, and that’s GROWTH. Like other functions mentioned above, this formula is also easy-to-apply.
Apart from the familiar arguments like known Xs’ cell range, known Ys’ values, and the given value of X, GROWTH utilizes an additional logical value. Usually, you need to enter one for this logical constant. Here is how the syntax looks:
=GROWTH(known_y’s,[known_x’s],[new_x’s],[const])
To interpolate data in Excel by using the GROWTH function, you may follow these steps:
- Insert the GROWTH function in any cell where you want the interpolated value for Y.
- Enter the cell range for known Y-values followed by a comma.
- Repeat the above step to input the cell range for known X-values.
- Now, enter the value of given X and put a comma.
- Enter 1 as the last argument and close the formula.
- Hit Enter to generate the value of interpolated Y.
- You can use cell references instead of actual values to discover more values by simply changing the given data.
- The final formula will look like the following:
=GROWTH(B2:B12,A2:A12,E2,1)
When compared to the FORECAST function, GROWTH generates more reliable and accurate interpolated data points for exponential data sets that are mostly nonlinear. Similar to FORECAST, you can also automate the GROWTH function without applying much effort.
Data Interpolation and Forecasting Made Easy
You can now efficiently interpolate data for your upcoming tasks from work or school.
Such quick data insights help you in various ways, like cutting a few repetitive steps of data research or estimating your task load before taking up any more projects.
Бывает ситуация, когда в массиве известных значений нужно найти промежуточные результаты. В математике это называется интерполяцией. В Excel данный метод можно применять как для табличных данных, так и для построения графиков. Разберем каждый из этих способов.
Использование интерполяции
Главное условие, при котором можно применять интерполяцию – это то, что искомое значение должно быть внутри массива данных, а не выходить за его предел. Например, если мы имеем набор аргументов 15, 21 и 29, то при нахождении функции для аргумента 25 мы можем использовать интерполяцию. А для поиска соответствующего значения для аргумента 30 – уже нет. В этом и является главное отличие этой процедуры от экстраполяции.
Способ 1: интерполяция для табличных данных
Прежде всего, рассмотрим применения интерполяции для данных, которые расположены в таблице. Для примера возьмем массив аргументов и соответствующих им значений функции, соотношение которых можно описать линейным уравнением. Эти данные размещены в таблице ниже. Нам нужно найти соответствующую функцию для аргумента
28. Сделать это проще всего с помощью оператора ПРЕДСКАЗ.
- Выделяем любую пустую ячейку на листе, куда пользователь планирует выводить результат от проведенных действий. Далее следует щелкнуть по кнопке «Вставить функцию», которая размещена слева от строки формул.
- Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень»
ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK». - Запускается окно аргументов функции ПРЕДСКАЗ. В нем имеется три поля:
- X;
- Известные значения y;
- Известные значения x.
В первое поле нам просто нужно вручную с клавиатуры вбить значения аргумента, функцию которого следует отыскать. В нашем случае это 28.
В поле «Известные значения y» нужно указать координаты диапазона таблицы, в котором содержатся значения функции. Это можно сделать вручную, но гораздо проще и удобнее установить курсор в поле и выделить соответствующую область на листе.
Аналогичным образом устанавливаем в поле
«Известные значения x» координаты диапазона с аргументами.После того, как все нужные данные введены, жмем на кнопку «OK».
- Искомое значение функции будет отображено в той ячейке, которую мы выделили ещё в первом шаге данного способа. В результате получилось число 176. Именно оно и будет итогом проведения процедуры интерполяции.
Урок: Мастер функций в Экселе
Способ 2: интерполяция графика с помощью его настроек
Процедуру интерполяции можно применять и при построении графиков функции. Актуальна она в том случае, если в таблице, на основе которой построен график, к одному из аргументов не указано соответствующее значение функции, как на изображении ниже.
- Выполняем построение графика обычным методом. То есть, находясь во вкладке «Вставка», выделяем табличный диапазон, на основе которого будет проводиться построение. Щелкаем по значку «График», размещенному в блоке инструментов «Диаграммы». Из появившегося списка графиков выбираем тот, который считаем более уместным в данной ситуации.
- Как видим, график построен, но не совсем в таком виде, как нам нужно. Во-первых, он разорван, так как для одного аргумента не нашлась соответствующая функция. Во вторых, на нем присутствует дополнительная линия X, которая в данном случае не нужна, а также на горизонтальной оси указаны просто пункты по порядку, а не значения аргумента. Попробуем исправить все это.
Для начала выделяем сплошную синюю линию, которую нужно удалить и жмем на кнопку Delete на клавиатуре.
- Выделяем всю плоскость, на которой размещен график. В появившемся контекстном меню щелкаем по кнопке «Выбрать данные…».
- Запускается окно выбора источника данных. В правом блоке «Подписи горизонтальной оси» жмем на кнопку «Изменить».
- Открывается небольшое окошко, где нужно указать координаты диапазона, значения из которого будут отображаться на шкале горизонтальной оси. Устанавливаем курсор в поле
«Диапазон подписей осей» и просто выделяем соответствующую область на листе, в которой содержаться аргументы функции. Жмем на кнопку «OK». - Теперь нам осталось выполнить основную задачу: с помощью интерполяции устранить разрыв. Вернувшись в окно выбора диапазона данных жмем на кнопку «Скрытые и пустые ячейки», расположенную в нижнем левом углу.
- Открывается окно настройки скрытых и пустых ячеек. В параметре «Показывать пустые ячейки» выставляем переключатель в позицию «Линию». Жмем на кнопку «OK».
- После возвращения в окно выбора источника подтверждаем все сделанные изменения, щелкнув по кнопке «OK».
Как видим, график скорректирован, а разрыв с помощью интерполяции удален.
Урок: Как построить график в Excel
Способ 3: интерполяция графика с помощью функции
Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.
- После того, как график построен и отредактирован, так как вам нужно, включая правильную расстановку подписи шкалы, остается только ликвидировать разрыв. Выделяем пустую ячейку в таблице, из которой подтягиваются данные. Жмем на уже знакомый нам значок
«Вставить функцию». - Открывается Мастер функций. В категории «Проверка свойств и значений» или «Полный алфавитный перечень» находим и выделяем запись «НД». Жмем на кнопку «OK».
- У данной функции нет аргумента, о чем и сообщает появившееся информационное окошко. Чтобы закрыть его просто жмем на кнопку «OK».
- После этого действия в выбранной ячейке появилось значение ошибки «#Н/Д», но зато, как можно наблюдать, обрыв графика был автоматически устранен.
Можно сделать даже проще, не запуская Мастер функций, а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д» без кавычек. Но это уже зависит от того, как какому пользователю удобнее.
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию
ПРЕДСКАЗ, так и графика. В последнем случае это осуществимо с помощью настроек графика или применения функции НД, вызывающей ошибку «#Н/Д». Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.
Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТ
Метод вычисления значения шага интерполяции в Excel
-
22.05.2020
- Чтение занимает 2 мин
-
- Применяется к:
- Microsoft Office Excel 2007, Excel 2010, Excel 2013, Excel 2016
В этой статье
Примечание
Office 365 ProPlus переименован в Майкрософт 365 корпоративные приложения. Для получения дополнительной информации об этом изменении прочитайте этот блог.
Аннотация
Приведенная ниже формула Microsoft Excel выполняет линейную интерполяцию, вычисляя значение шага интерполяции:
= (End-Start)/(строка (конец) — строка (начало))
где End — это адрес ячейки с большим номером, а Start — адрес ячейки меньшего числа.
Интерполяция это метод, используемый для определения текущего или будущего коэффициента стоимости, когда точный фактор не отображается в текущей или будущей таблице значений. В интерполяции предполагается, что изменение между двумя значениями является линейным и то, что поле ошибки не является существенным.
Дополнительная информация
Чтобы создать пример линейной формулы интерполяции, выполните указанные ниже действия.
-
Введите на листе следующие значения:
A1: 9 B1: =(A7-A1)/(ROW(A7)-ROW(A1)) A2: =A1+$B$1 A3: A4: A5: A6: A7: 11 -
Выберите ячейки A2: A6. В меню Правка выберите команду заполнить, а затем нажмите кнопку вниз. Формула заполнена, а в ячейках A2 отображаются следующие значения: A6:
A2: 9.33333 A3: 9.66667 A4: 10. A5: 10.33333 A6: 10.66667
Примечание
Необходимо ввести ссылку на значение шага в ячейке B1 в виде абсолютной ссылки (со знаками доллара).
Интерполяция промежуточных значений для произвольных данных в Excel
читая ваши комментарии и изменения к вопросу, есть несколько вещей, которые вы хотите сделать, которые на самом деле не рассматриваются в моем предыдущем ответе. Этот ответ будет иметь дело с этими элементами, и я включил пошаговое пошаговое руководство о том, как вы выполните весь процесс интерполяции.
Недостоверные Сведения
вы описываете процесс, который сгенерировал данные, как снятие показаний за интервал времени, а числа округляются. Тот уравнение так же хорошо, как и данные. В вашем фактическом анализе вы должны использовать самые точные доступные числа (возможно, вы просто сохраняли свой пример простым, показывая округленные времена).
Однако, данные, которые вы показываете, точно не соответствуют виду кривой, которую вы обычно видите для физического процесса. Теоретические кривые, как правило, гладкие, когда есть только одна движущая переменная и нет шума. Если вы используете очень точное оборудование и для того чтобы вызвать чтение на preset интервал и обеспечить точное измерение, вы можете принимать результаты как точные. Однако, если вы вручную приурочиваете чтение и вручную принимаете чтение, то X значения могут быть неточными, порой даже если показания, сами по себе, являются точными. Сдвиг персонажа X значения немного так или иначе введут виды небольших неровностей, которые вы видите на кривой ваших данных (если пример не является просто числами, которые вы составили для целей образец.)
если это так, вы можете воспользоваться регрессией для оценки наилучшего соответствия.
используя Y как X
в вашей задаче вы хотите определить значения для Y (целочисленные значения от 1 до 37 в данном примере), и поиска соответствующего значения x. Это было достаточно легко сделать в вашей Y=2^X проблема, потому что это простое уравнение можно легко обратить к X=log(Y)/log(2), и вы можете сразу рассчитать любое значение вы хотите. Если уравнение не что-то простое, часто нет практического способа инвертировать его. «Злоупотребленный» регрессионный подход в моем предыдущем ответе дает вам уравнение высокого порядка, но это «однонаправленное», часто непрактичное решение для обратного уравнения.
самый простой подход-просто обратить X и Y С самого начала. Это дает уравнение можно использовать с целочисленными значениями введут (анализ дает coeficients уравнения, как описано в предыдущем ответ.)
это никогда не повредит, чтобы увидеть, если простая кривая будет работать. Вот обратные данные, и вы можете видеть, что нет полезной подгонки:
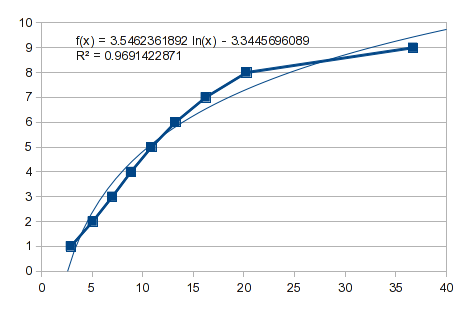
Итак, попробуйте полиномиальную подгонку. Однако это случай, как я описал в предыдущем ответе. Значения от 1 до 8 подходят хорошо, но 9 дает ему несварение. Многочлен 3-го порядка дает вам bump:
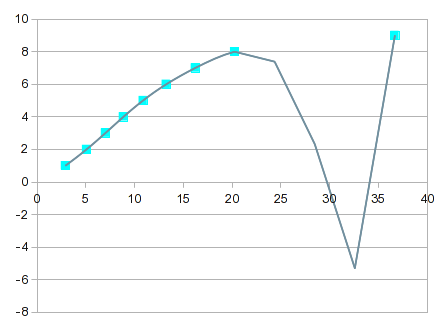
это становится все более «интересным» по мере увеличения порядка уравнения. По 7-м порядка, вы получите это:
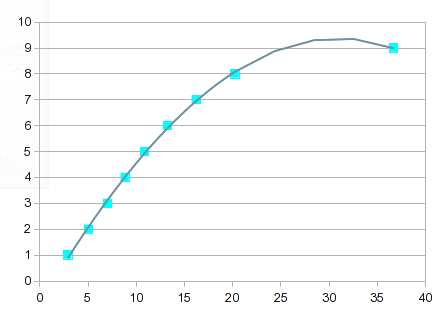
он проходит почти точно через каждую точку, но кривая между 8 и 9 не полезно. Одним из решений было бы обойтись линейной интерполяцией между 8 и 9. В этом случае, однако, вы можете получить лучшие значения включение сплайнов для верхнего конца. Опция сплайны обеспечивает хорошую посадку и кривую, которая имеет больше смысла между 8 и 9:
к сожалению, сплайновые уравнения немного запутаны и уравнения не представлены. Тем не менее, вы можете сделать линейную интерполяцию на промежуточных значениях, предоставляемых анализом, которая должна получить Вас очень близко к числам, которые соответствуют разумным кривая.
экстраполяция и интерполяция
в этом примере, Ваш первый Y значение 2.9. Вы хотите создать значения для 1 и 2, которые находятся вне диапазона данных. Это требует экстраполяции, а не интерполяции, что является совершенно иным требованием.
-
если уравнение известно, как ваш
Y=2^Xпример, вы можете рассчитать любое значение, которое вы хотите. -
если известно, что процесс генерации данных следует простой кривой, и вы уверены в подгонке, вы можете проецировать значения за пределы диапазона данных и даже получить значимый доверительный интервал для диапазона, в котором могут быть значения (на основе того, сколько вариаций между данными и кривой внутри диапазона данных).
-
если вы принудительно подгоняете уравнение высокого порядка к данным, проекции вне диапазона данных обычно бессмысленны.
-
если вы используете сплайны, нет оснований для проецирования за пределы диапазона данных.
какие бы проекции вы ни делали за пределами диапазона ваших данных, они хороши только как уравнение, которое вы используете, и если вы не используете точное уравнение, чем дальше вы получаете от своих данных, тем более неточным оно будет.
глядя на кривую журнала на первом графике, вы можете видеть, что она будет проецировать совсем другое значение чем вы и ожидали.
для полиномиальных уравнений коэффициент нулевой мощности является константой, и это значение, которое будет получено для X стоимостью 0. Это простой способ посмотреть, куда пойдет кривая в этом направлении.
обратите внимание, что в 4-м или 5-м порядке точки с 1 по 8 довольно точны. Но как только вы выходите за пределы диапазона, уравнения могут вести себя очень иначе.
экстраполяция с использованием ограниченных данных
один из способов улучшить ситуацию-подогнать только точки На этом конце и включить столько последовательных точек, сколько следует за формой кривой на этом конце. Точка 9-это явно. Перед этим на кривой есть несколько перегибов, один из которых находится вокруг точки 5 или 6, поэтому точки выше этого следуют другой кривой. Используя только точки от 1 до 5, вы приближаетесь к идеальной подгонке с полиномом 3-го порядка. Это уравнение будет нулевой точки 0.12095 (сравните таблицу выше), а для X стоимостью 1,0.3493.
что произойдет, если просто подогнать прямую к первым пяти точкам:
что проектов с нулевой точки -0.5138 и X на 1,-0.0071.
этот диапазон возможных результатов указывает на уровень неопределенности за пределами диапазона ваших данные. Нет правильного ответа. И это было на» хорошем » конце твоей кривой. The Y значение X на 9 is 36.7. Ты хочешь пойти в 37. Сплайны предполагают, что кривая асимптотична при 9. Проецирование прямой линии в необработанных данных приведет к значению чуть больше, чем 9 (то же самое с полиномом 4-го порядка). Полином 3-го порядка предлагает значение меньше 9 (как сделать 5 и 6 заказов). Многочлен 7-го порядка предлагает значение существенно выше 9. Таким образом, все, что находится за пределами диапазона данных, является предположением или чем-то другим.
собираем все вместе
Итак, давайте шаг через то, что фактическое решение будет выглядеть. Мы предположим, что вы уже пытались найти точное уравнение и протестировали общие кривые с помощью линии тренда. Следующим шагом будет попробовать регрессию, потому что это дает вам формулу для кривой, и вы можете подключить целочисленные значения.
I нет готового доступа к Excel 2013 или инструментарию анализа. Для иллюстрации я буду использовать LibreOffice Calc. Он не идентичен, но достаточно близок, чтобы вы могли следить за ним в Excel. В LO Calc это фактически бесплатное расширение, которое необходимо загрузить. Я использую CorelPolyGUI, которую можно скачать здесь. Насколько я помню, инструментарий анализа не включал сплайны. Если это все еще так, и вы хотите сделать это в Excel, я наткнулся это бесплатное дополнение (который я не проверял). Альтернативой будет использование Lo Calc, который будет работать в Windows и является бесплатным.
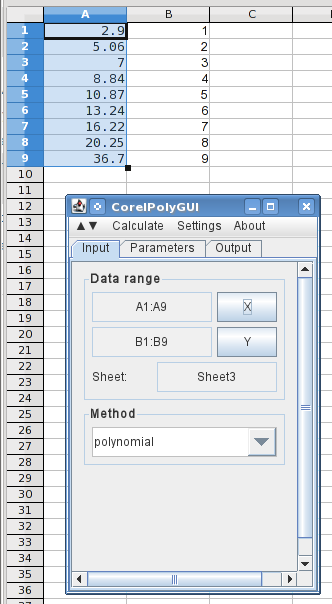
здесь я ввел значения X и Y (реверсированные) в Столбцах A и B и открыл диалоговое окно анализа. Выделение значений X и нажатие кнопки X загружает диапазоны данных, и я выбрал полином.
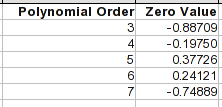
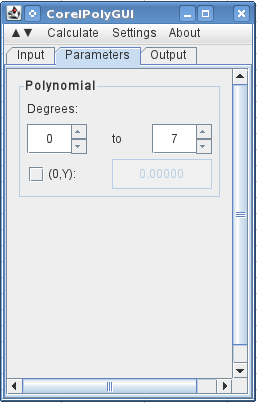
на следующей вкладке я указываю, что хочу использовать 0 to 7 Градусы (многочлен 7-го порядка со всеми порядками).
чтобы указать вывод, я выбираю C1 и нажимаю столбцы, и он регистрирует столбцы, необходимые для вывода. Я выбираю, что я хочу, чтобы он выводил исходные данные, вычисленные результаты, и я выбрал добавьте три промежуточные точки между каждой исходной точкой данных. И я говорю, что хочу график результатов на новом графике. Затем перейдите в меню calculate и нажмите calculate.
и вот оно. Если вы посмотрите на вычисленные значения, вы можете заметить проблему. Это станет очевидным на следующем этапе.
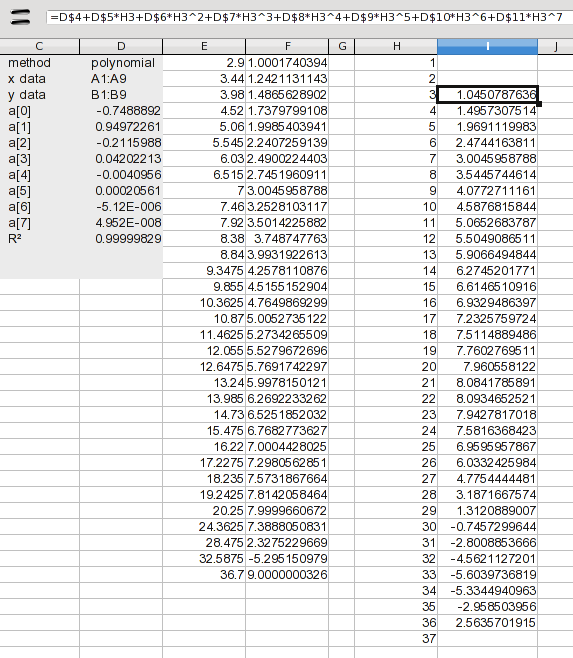
вот, я добавил 1 через 37 значения. На данный момент мы хотим иметь дело только с интерполяцией, поэтому я добавил формулу для вычисления только значений 3 через 36. Формула просто расширяет коэффициенты, перечисленные в результатах (значения a (n)). Формула в I2:
=D+D*h4+D*h4^2+D*h4^3+D*h4^4+D*h4^5+D*h4^6+D*h4^7
это просто каждый коэффициент, умноженный на соответствующую мощность значения X. Перетащите это вниз, и у вас есть результаты. Ну не совсем; Вы должны смотреть на него, чтобы увидеть, если он проходит здравомыслие испытание. Мы знали, что между 8 и 9, но это оказывается половина значений, которые вы хотите. Мы могли бы использовать значения из 3 через 20, но нет смысла объединять так много значений из другого метода. Так что давайте просто использовать сплайны для всего этого.
снова откройте диалоговое окно анализ и измените метод на «сплайны» на вкладке ввод (здесь не показано). Дайте ему новое выведите наружу ряд и скажите, что он высчитал. Это все, что для этого нужно.
у нас есть новые результаты в работе. Разделение диапазона данных на это множество сегментов делает каждый сегмент коротким, поэтому линейная интерполяция должна быть довольно хорошей (лучше, чем использовать ее на исходных данных).
процесс подгонки кривой или интерполяции включает в себя создание точек данных; используя свое собственное суждение о том, что кривая «должна» (или не должна) выглядеть (регрессия предполагает, что даже исходные данные неточны).
проверка правильности этих данных показывает, что даже сплайны создают соединительную кривую с выпуклостью; одно значение немного превышает 9, который скорее артефакт, нежели отражение процесса вы были измерения. В этом случае кривая асимптотика при 9 более вероятно, поэтому я произвольно назначил высокую точку a значение, что волос меньше!—24 — > глядя на него. Предположение не в том, что моя ценность точна, только в том, что это улучшение. Для этой иллюстрации я создал новый столбец со значениями, которые будут использоваться.
я добавил столбец с вашими номерами 1 через 37. Из предыдущего обсуждения у нас нет надежной основы для проектирования значений для 1 и 2, поэтому я оставил их пустыми. Для 37, я пошел с асимптотическим предположением и сделал это 9. Значения для 3 через 36 найдены линейной интерполяцией (и это формула, которую вы могли бы адаптировать к другим данным). Формула в Q3:
=TREND(OFFSET($M,MATCH(P3,M:M)-1,2,2),OFFSET($M,MATCH(P3,M:M)-1,0,2),P3)
функция TREND просто интерполирует, когда диапазон равен двум точкам. Синтаксис команды:
TREND(Y_range, X_range, X_value)
функция смещения используется для каждого диапазона. В каждом случае функция MATCH используется для поиска первой строки диапазона, содержащего целевое значение. The -1 значения, потому что это смещения, а не местоположения; совпадение в первой строке является смещением 0 из исходной строки. И обратите внимание, что Y столбец смещен на 2, в данном случае, потому что я добавил дополнительный столбец для ручной настройки значения. Параметры смещения выбирают столбец, содержащий значения Y или X, и выбирают высоту диапазона 2, которая дает вам значения ниже и выше цели.
в результат:
мастер анализа делает тяжелую работу, и независимо от того, используете ли вы полиномиальную регрессию или сплайны, для генерации результата требуется всего одна формула.
Линейная интерполяция формула пример расчета. Применение интерполяции в Microsoft Excel
Это глава из книги Билла Джелена .
Задача: некоторые инженерные проблемы проектирования требуют использования таблиц для вычисления значений параметров. Поскольку таблицы являются дискретными, дизайнер использует линейную интерполяцию для получения промежуточного значения параметра. Таблица (рис. 1) включает высоту над землей (управляющий параметр) и скорость ветра (рассчитываемый параметр). Например, если надо найти скорость ветра, соответствующую высоте 47 метров, то следует применить формулу: 130 + (180 – 130) * 7 / (50 – 40) = 165 м/сек.
Скачать заметку в формате или , примеры в формате
Как быть, если существует два управляющих параметра? Можно ли выполнить вычисления с помощью одной формулы? В таблице (рис. 2) показаны значения давления ветра для различных высот и величин пролета конструкций. Требуется вычислить давление ветра на высоте 25 метров и величине пролета 300 метров.
Решение: проблему решаем путем расширения метода, используемого для случая с одним управляющим параметром. Выполните следующие действия.
Начните с таблицы, изображенной на рис. 2. Добавьте исходные ячейки для высоты и пролета в J1 и J2 соответственно (рис. 3).
Рис. 3. Формулы в ячейках J3:J17 объясняют работу мегаформулы
Для удобства использования формул определите имена (рис. 4).
Проследите за работой формулы последовательно переходя от ячейки J3 к ячейке J17.
Путем обратной последовательной подстановки соберите мегаформулу. Скопируйте текст формулы из ячейки J17 в J19. Замените в формуле ссылку на J15 на значение в ячейке J15: J7+(J8-J7)*J11/J13. И так далее. Получится формула, состоящая из 984 символов, которую невозможно воспринять в таком виде. Вы можете посмотреть на нее в приложенном Excel-файле. Не уверен, что такого рода мегаформулы полезны в использовании.
Резюме: линейная интерполяция используется для получения промежуточного значения параметра, если табличные значения заданы только для границ диапазонов; предложен метод расчета по двум управляющим параметрам.
Существуют случаи, когда требуется узнать результаты вычисления функции за пределами известной области. Особенно актуален данный вопрос для процедуры прогнозирования. В Экселе есть несколько способов, с помощью которых можно совершить данную операцию. Давайте рассмотрим их на конкретных примерах.
Способ 2: экстраполяция для графика
Выполнить процедуру экстраполяции для графика можно путем построения линии тренда.
- Прежде всего, строим сам график. Для этого курсором при зажатой левой кнопке мыши выделяем всю область таблицы, включая аргументы и соответствующие значения функции. Затем, переместившись во вкладку «Вставка»
, кликаем по кнопке «График»
. Этот значок расположен в блоке «Диаграммы»
на ленте инструментов. Появляется перечень доступных вариантов графиков. Выбираем наиболее подходящий из них на свое усмотрение. - После того, как график построен, удаляем из него дополнительную линию аргумента, выделив её и нажав на кнопку Delete
на клавиатуре компьютера. - Далее нам нужно поменять деления горизонтальной шкалы, так как в ней отображаются не значения аргументов, как нам того нужно. Для этого, кликаем правой кнопкой мыши по диаграмме и в появившемся списке останавливаемся на значении «Выбрать данные»
. - В запустившемся окне выбора источника данных кликаем по кнопке «Изменить»
в блоке редактирования подписи горизонтальной оси. - Открывается окно установки подписи оси. Ставим курсор в поле данного окна, а затем выделяем все данные столбца «X»
без его наименования. Затем жмем на кнопку «OK»
. - После возврата к окну выбора источника данных повторяем ту же процедуру, то есть, жмем на кнопку «OK»
. - Теперь наш график подготовлен и можно, непосредственно, приступать к построению линии тренда. Кликаем по графику, после чего на ленте активируе
Excel интерполяция по таблице
Бывает ситуация, когда в массиве известных значений нужно найти промежуточные результаты. В математике это называется интерполяцией. В Excel данный метод можно применять как для табличных данных, так и для построения графиков. Разберем каждый из этих способов.
Использование интерполяции
Главное условие, при котором можно применять интерполяцию – это то, что искомое значение должно быть внутри массива данных, а не выходить за его предел. Например, если мы имеем набор аргументов 15, 21 и 29, то при нахождении функции для аргумента 25 мы можем использовать интерполяцию. А для поиска соответствующего значения для аргумента 30 – уже нет. В этом и является главное отличие этой процедуры от экстраполяции.
Способ 1: интерполяция для табличных данных
Прежде всего, рассмотрим применения интерполяции для данных, которые расположены в таблице. Для примера возьмем массив аргументов и соответствующих им значений функции, соотношение которых можно описать линейным уравнением. Эти данные размещены в таблице ниже. Нам нужно найти соответствующую функцию для аргумента 28. Сделать это проще всего с помощью оператора ПРЕДСКАЗ.
-
Выделяем любую пустую ячейку на листе, куда пользователь планирует выводить результат от проведенных действий. Далее следует щелкнуть по кнопке «Вставить функцию», которая размещена слева от строки формул.
Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK».
В первое поле нам просто нужно вручную с клавиатуры вбить значения аргумента, функцию которого следует отыскать. В нашем случае это 28.
В поле «Известные значения y» нужно указать координаты диапазона таблицы, в котором содержатся значения функции. Это можно сделать вручную, но гораздо проще и удобнее установить курсор в поле и выделить соответствующую область на листе.
Аналогичным образом устанавливаем в поле «Известные значения x» координаты диапазона с аргументами.
После того, как все нужные данные введены, жмем на кнопку «OK».
Способ 2: интерполяция графика с помощью его настроек
Процедуру интерполяции можно применять и при построении графиков функции. Актуальна она в том случае, если в таблице, на основе которой построен график, к одному из аргументов не указано соответствующее значение функции, как на изображении ниже.
-
Выполняем построение графика обычным методом. То есть, находясь во вкладке «Вставка», выделяем табличный диапазон, на основе которого будет проводиться построение. Щелкаем по значку «График», размещенному в блоке инструментов «Диаграммы». Из появившегося списка графиков выбираем тот, который считаем более уместным в данной ситуации.
Как видим, график построен, но не совсем в таком виде, как нам нужно. Во-первых, он разорван, так как для одного аргумента не нашлась соответствующая функция. Во вторых, на нем присутствует дополнительная линия X, которая в данном случае не нужна, а также на горизонтальной оси указаны просто пункты по порядку, а не значения аргумента. Попробуем исправить все это.
Для начала выделяем сплошную синюю линию, которую нужно удалить и жмем на кнопку Delete на клавиатуре.
Выделяем всю плоскость, на которой размещен график. В появившемся контекстном меню щелкаем по кнопке «Выбрать данные…».
Запускается окно выбора источника данных. В правом блоке «Подписи горизонтальной оси» жмем на кнопку «Изменить».
Открывается небольшое окошко, где нужно указать координаты диапазона, значения из которого будут отображаться на шкале горизонтальной оси. Устанавливаем курсор в поле «Диапазон подписей осей» и просто выделяем соответствующую область на листе, в которой содержаться аргументы функции. Жмем на кнопку «OK».
Теперь нам осталось выполнить основную задачу: с помощью интерполяции устранить разрыв. Вернувшись в окно выбора диапазона данных жмем на кнопку «Скрытые и пустые ячейки», расположенную в нижнем левом углу.
Открывается окно настройки скрытых и пустых ячеек. В параметре «Показывать пустые ячейки» выставляем переключатель в позицию «Линию». Жмем на кнопку «OK».
Как видим, график скорректирован, а разрыв с помощью интерполяции удален.
Способ 3: интерполяция графика с помощью функции
Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.
-
После того, как график построен и отредактирован, так как вам нужно, включая правильную расстановку подписи шкалы, остается только ликвидировать разрыв. Выделяем пустую ячейку в таблице, из которой подтягиваются данные. Жмем на уже знакомый нам значок «Вставить функцию».
Открывается Мастер функций. В категории «Проверка свойств и значений» или «Полный алфавитный перечень» находим и выделяем запись «НД». Жмем на кнопку «OK».
У данной функции нет аргумента, о чем и сообщает появившееся информационное окошко. Чтобы закрыть его просто жмем на кнопку «OK».
Можно сделать даже проще, не запуская Мастер функций, а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д» без кавычек. Но это уже зависит от того, как какому пользователю удобнее.
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию ПРЕДСКАЗ, так и графика. В последнем случае это осуществимо с помощью настроек графика или применения функции НД, вызывающей ошибку «#Н/Д». Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.
Отблагодарите автора, поделитесь статьей в социальных сетях.
размещено: 03 Октября 2011
В архиве находится два файла.
1) Лист Excel с примером таблицы для интерполирования. Вводить значения надо в поля, выделенные желтым. При использовании данного файла можно менять значения таблицы и размер таблицы с последующим сохранением и повторным использованием.
2) Надстройка для Excel *.xla с функцией пользователя Interpol(X_n, Y_n, arX, arY, arZ, X, Y)
X_n, Y_n — кол-во строк и столбцов таблицы
arX — столбец аргументов таблицы
arY — строка аргументов таблицы
arZ — двумерным массив значений в таблице
X — аргумент «по столбцу»
Y — аргумент «по строке»
Если не совсем понятно расписал значения аргументов функции Interpol — см. первый файл из архива.
Для работы обоих файлов надо не отключать макросы.
При работе с различными данными среди значений нужно найти промежуточное число, для этого есть такое определение как интерполяция. Рассмотрим как это сделать в программе Excel для значений в таблицах и в графиках.
В отличии от экстраполяции, в интерполяции число, которое нужно найти, должно быть в пределах рабочих данных. Как пример, если есть числа 10, 15, 25, то для определения числа 11 или 16, можно использовать интерполяцию, если же значение например 26, то нет.
Метод первый. Использование интерполяции для значений в таблице
Часто интерполяция используется при работе с табличными значениями. Рассмотрим таблицу с аргументами и функции, которая относится к ним. Проведем интерполяцию соответственно к аргументу 28 с помощью функции ПРЕДСКАЗ.
Нужно выбрать ячейку без значения, в которой в конечном итоге мы получим результат. Далее кликнуть в строке формул слева на кнопку «Вставка функции».
В окне мастера функций нужно выбрать категорию «Математические» и в списке функций выбрать ПРЕДСКАЗ, а после этого подтвердить действие.
Откроется окно, в котором нужно задать параметры выбранной нами функции. В поле с названием «Х» нужно ввести искомое число (28). В поле где надо ввести известные значения у вводим диапазон ячеек, где введены значения в таблице. Аналогично делается и для поля значений аргументов Х. После произведенных манипуляций — подтверждаем действие.
Число, которое нужно было определить, будет показано в ячейке, которая была выбрана для показа результата.
Метод второй. Интерполяция с помощью настроек графика
Определение с помощью графика функции, если одно из значений не относится к значению функции f(x).
Чтобы сделать график, надо перейти в раздел «Вставка», и выбрать кнопку «Диаграммы» и кликнуть на пункт «График», в котором уже пользователю надо выбрать наиболее оптимальный для него вариант, предварительно выделив таблицу, а точнее табличные значения, на основе которых и будет построен график.
Результатом будет выданный в листе график, но он пока что не оптимизирован. Видно что для одного значения не была найдена функция и есть ненужная линия и не указаны значения аргументов. Для начала кликаем на цельную синюю линию и удаляем её.
Далее нужно выделить область где находится график.А потом нажать в списке на «Выбрать данные».
Появится новое окно, в нем в правой стороне кликаем на «Изменить».
После этого надо задать диапазон подписи оси, выделив нужные данные в таблице и подтвердить действие.
Возвращаемся в окно выбора источника данных и устраняем неточность, используя интерполяцию. Кликаем на «Скрытые и пустые ячейки».
В новом окне нужно произвести настройки. Под надписью «Показ пустых ячеек», кликаем на кружок возле наименования «Линия» и подтверждаем действие. И после проведенных манипуляций не забываем подтвердить действие в окне «Выбор источника данных».
Результатом будет показ правильного графика с проведенной интерполяцией.
Метод третий. Интерполяция графика с использованием функции НД
Действия важно проводить в корректном графике, как его сделать правильным, выше уже было показано. Теперь проведем интерполяцию для устранения разрыва. Для начала нажимаем в таблице на ту ячейку, в которой генерируются данные и в строке ввода формул нажимаем на значок «Fx».
В окне мастера функций выбираем категорию проверки свойств и значений. В списке нужно кликнуть на «НД» и подтвердить действие.
Если у функции нету числа аргумента, то об этом программой будет сообщено. Просто движемся далее.
После таких манипуляций в ячейке генерируемых данных появится надпись ошибки #НД. Но особенность данного метода есть то, что разрыв в графике исчезнет. Также если в этой же ячейке просто ввести #Н/Д, то результат будет аналогичный.
Было рассмотрено три вариации для того чтобы провести интерполяцию в Excel. Выбирайте тот, который наиболее подходит и наиболее оптимальный для выполнения конкретной цели.
Экстраполяция в Excel
Существуют случаи, когда требуется узнать результаты вычисления функции за пределами известной области. Особенно актуален данный вопрос для процедуры прогнозирования. В Экселе есть несколько способов, с помощью которых можно совершить данную операцию. Давайте рассмотрим их на конкретных примерах.
Использование экстраполяции
В отличие от интерполяции, задачей которой является нахождения значения функции между двумя известными аргументами, экстраполяция подразумевает поиск решения за пределами известной области. Именно поэтому данный метод столь востребован для прогнозирования.
В Экселе можно применять экстраполяцию, как для табличных значений, так и для графиков.
Способ 1: экстраполяция для табличных данных
Прежде всего, применим метод экстраполяции к содержимому табличного диапазона. Для примера возьмем таблицу, в которой имеется ряд аргументов (X) от 5 до 50 и ряд соответствующих им значений функции (f(x)). Нам нужно найти значение функции для аргумента 55, который находится за пределом указанного массива данных. Для этих целей используем функцию ПРЕДСКАЗ.
- Выделяем ячейку, в которой будет отображаться результат проведенных вычислений. Кликаем по значку «Вставить функцию», который размещен у строки формул.
- Запускается окно Мастера функций. Выполняем переход в категорию «Статистические» или «Полный алфавитный перечень». В открывшемся списке производим поиск наименования «ПРЕДСКАЗ». Найдя его, выделяем, а затем щелкаем по кнопке «OK» в нижней части окна.
- Мы перемещаемся к окну аргументов вышеуказанной функции. Она имеет всего три аргумента и соответствующее количество полей для их внесения.
В поле «X» следует указать значение аргумента, функцию от которого нам следует вычислить. Можно просто вбить с клавиатуры нужное число, а можно указать координаты ячейки, если аргумент записан на листе. Второй вариант даже предпочтительнее. Если мы произведем внесение именно таким способом, то для того, чтобы просмотреть значение функции для другого аргумента нам не придется менять формулу, а достаточно будет изменить вводную в соответствующей ячейке. Для того, чтобы указать координаты этой ячейки, если был выбран все-таки второй вариант, достаточно установить курсор в соответствующее поле и выделить эту ячейку. Её адрес тут же отобразится в окне аргументов.
В поле «Известные значения y» следует указать весь имеющийся у нас диапазон значений функции. Он отображается в колонке «f(x)». Следовательно, устанавливаем курсор в соответствующее поле и выделяем всю эту колонку без её наименования.
В поле «Известные значения x» следует указать все значения аргумента, которым соответствуют внесенные нами выше значения функции. Эти данные находятся в столбце «x». Точно так же, как и в предыдущий раз выделяем нужную нам колонку, предварительно установив курсор в поле окна аргументов.
После того, как все данные внесены, жмем на кнопку «OK».
- После этих действий результат вычисления путем экстраполяции будет выведен в ячейку, которая была выделена в первом пункте данной инструкции перед запуском Мастера функций. В данном случае значение функции для аргумента 55 равно 338.
- Если все-таки был выбран вариант с добавлением ссылки на ячейку, в которой содержится искомый аргумент, то мы легко сможем его поменять и просмотреть значение функции для любого другого числа. Например, искомое значение для аргумента 85 буде равно 518.
Урок: Мастер функций в Excel
Способ 2: экстраполяция для графика
Выполнить процедуру экстраполяции для графика можно путем построения линии тренда.
- Прежде всего, строим сам график. Для этого курсором при зажатой левой кнопке мыши выделяем всю область таблицы, включая аргументы и соответствующие значения функции. Затем, переместившись во вкладку «Вставка», кликаем по кнопке «График». Этот значок расположен в блоке «Диаграммы» на ленте инструментов. Появляется перечень доступных вариантов графиков. Выбираем наиболее подходящий из них на свое усмотрение.
- После того, как график построен, удаляем из него дополнительную линию аргумента, выделив её и нажав на кнопку Delete на клавиатуре компьютера.
- Далее нам нужно поменять деления горизонтальной шкалы, так как в ней отображаются не значения аргументов, как нам того нужно. Для этого, кликаем правой кнопкой мыши по диаграмме и в появившемся списке останавливаемся на значении «Выбрать данные».
- В запустившемся окне выбора источника данных кликаем по кнопке «Изменить» в блоке редактирования подписи горизонтальной оси.
- Открывается окно установки подписи оси. Ставим курсор в поле данного окна, а затем выделяем все данные столбца «X» без его наименования. Затем жмем на кнопку «OK».
- После возврата к окну выбора источника данных повторяем ту же процедуру, то есть, жмем на кнопку «OK».
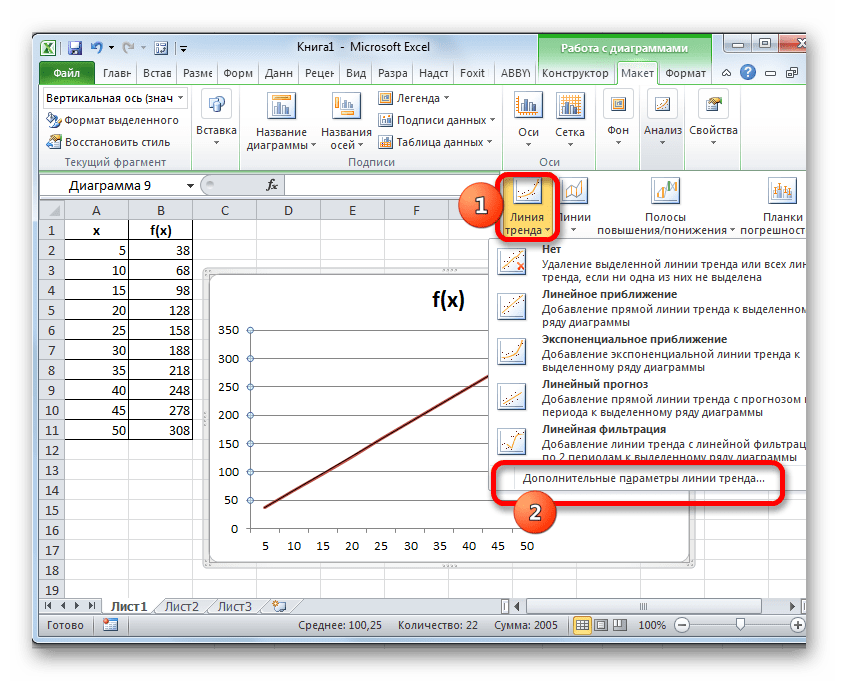
- Теперь наш график подготовлен и можно, непосредственно, приступать к построению линии тренда. Кликаем по графику, после чего на ленте активируется дополнительный набор вкладок – «Работа с диаграммами». Перемещаемся во вкладку «Макет» и жмем на кнопку «Линия тренда» в блоке «Анализ». Кликаем по пункту «Линейное приближение» или «Экспоненциальное приближение».
- Линия тренда добавлена, но она полностью находится под линией самого графика, так как мы не указали значение аргумента, к которому она должна стремиться. Чтобы это сделать опять последовательно кликаем по кнопке «Линия тренда», но теперь выбираем пункт «Дополнительные параметры линии тренда».
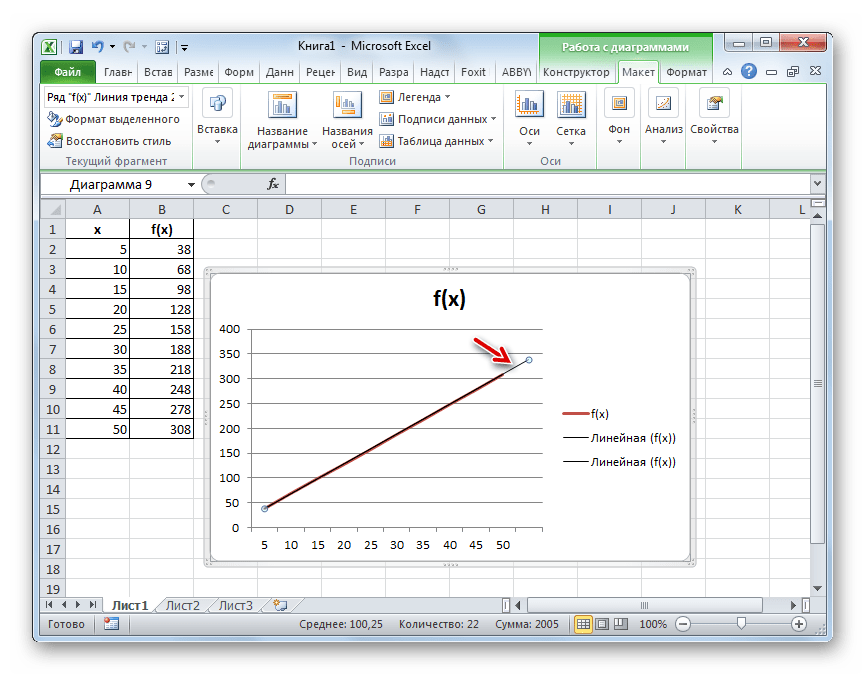
- Запускается окно формата линии тренда. В разделе «Параметры линии тренда» есть блок настроек «Прогноз». Как и в предыдущем способе, давайте для экстраполяции возьмем аргумент 55. Как видим, пока что график имеет длину до аргумента 50 включительно. Получается, нам нужно будет его продлить ещё на 5 единиц. На горизонтальной оси видно, что 5 единиц равно одному делению. Значит это один период. В поле «Вперед на» вписываем значение «1». Жмем на кнопку «Закрыть» в нижнем правом углу окна.
- Как видим, график был продлен на указанную длину с помощью линии тренда.
Урок: Как построить линию тренда в Excel
Итак, мы рассмотрели простейшие примеры экстраполяции для таблиц и для графиков. В первом случае используется функция ПРЕДСКАЗ, а во втором – линия тренда. Но на основе этих примеров можно решать и гораздо более сложные задачи прогнозирования.
Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТ
Интерполировать с помощью Excel — Excel вне сети
Интерполяция — это процесс оценки точек данных в существующем наборе данных. Поскольку это блог об Excel, очевидно, что мы хотим ответить на следующий вопрос: можем ли мы выполнять интерполяцию с помощью Excel. Это частый вопрос. Фактически, это был следующий вопрос от читателя, который впервые заставил меня заглянуть в эту тему:
«У меня вопрос по Excel — есть ли способ интерполировать значение из таблицы? У меня есть X и Y, которых нет в таблице, но есть коррелированные данные, поэтому я хочу вычислить интерполированное значение ».
В качестве простого примера, если пройти 1 милю в понедельник нужно 15 минут, а во вторник — 1 час, чтобы пройти 4 мили, мы могли бы разумно оценить, что пройти 2 мили потребуется 30 минут.
Не следует путать с экстраполяцией, которая оценивает значения вне набора данных. Оценка того, что пройти 8 миль займет 2 часа, будет экстраполяцией, поскольку оценка выходит за рамки известных значений.
Excel — отличный инструмент для интерполяции, так как в конечном итоге это большой визуальный калькулятор.
Загрузите файл с примером.
Я рекомендую вам загрузить файлы, поддерживающие эту публикацию, так как вы сможете работать вместе с примерами. Это лучший способ учиться. Вы сможете увидеть решения в действии, а файл будет полезен для использования в будущем. Файлы поддержки доступны БЕСПЛАТНО подписчикам информационных бюллетеней.
Нажмите ниже, чтобы подписаться и получить доступ к зоне для подписчиков. Вы также получите:
- Мои любимые советы и рекомендации прямо на ваш почтовый ящик
- Эксклюзивный контент (доступен только подписчикам)
- БЕСПЛАТНЫЕ инструменты и загрузки
Если вы уже являетесь подписчиком, щелкните здесь, чтобы войти в систему в области загрузок подписчика.
Имя файла для этого сообщения: 0020 Интерполировать с помощью Excel.xlsx
Опции для интерполяции в Excel
Что касается ответа на вопрос, есть несколько сценариев, которые приведут к различным решениям.
Во-первых, мы могли использовать простую математику. Это сработало бы, если бы результаты были абсолютно линейными (т.е. значения X и Y перемещались синхронно друг с другом). Но в противном случае мы можем получить немного искаженный результат.
В качестве альтернативы мы могли бы использовать функцию ПРОГНОЗ в Excel (или ПРОГНОЗ.ЛИНЕЙНЫЙ в Excel 2016 и последующих версиях). Судя по названию, функция ПРОГНОЗ выглядит странным выбором. Казалось бы, это функция специально для экстраполяции; однако это также один из лучших вариантов линейной интерполяции в Excel. FORECAST использует все значения в наборе данных для оценки результата; поэтому он отлично подходит для линейных отношений, даже если они не полностью коррелированы.
Тогда еще одна мысль, а что, если отношения X и Y вообще не линейны? Как мы могли интерполировать значение, когда данные экспоненциальны?
Давайте посмотрим на все эти сценарии.
Интерполяция с использованием простой математики
Простая математика хорошо работает, когда есть только две пары чисел или когда отношения между X и Y совершенно линейны.
Вот базовый пример (посмотрите вкладку Пример 1 в вспомогательном файле загрузки):
Формула в ячейке E4:
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
Кому-то это может показаться немного сложным, так что вот краткий обзор формулы.
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
В последнем разделе (выделенном зеленым цветом выше) вычисляется, насколько значение Y перемещается, когда значение X перемещается на 1. В нашем примере Y перемещается на 1,67 для каждого 1 из X.
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
Вторая секция (выделенная зеленым цветом выше) вычисляет, как далеко интерполированный X отстоит от первого X, затем умножается на значение, вычисленное выше. В нашем примере результат равен 17.5 (ячейка E2) минус 10 (ячейка A2), результат которого затем умножается на 1,67. Все это равно 12,5.
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
Наконец, мы переходим к первой части формулы (выделенной зеленым цветом выше), которая добавляет первое значение Y. В нашем примере это дает окончательный результат 77,5 (65 + 12,5). Для тех, кто помнит математику в средней школе, формула будет следующей:
Вот результат, наложенный на график.
Даже если вы не помните линейную интерполяцию в школе, хорошая новость заключается в том, что Excel предоставил нам более простой вариант — функцию ПРОГНОЗ.
Загрузить электронную книгу «100 макросов Excel»
- Содержит 100 макросов Excel VBA
- Изучите VBA, следуя примерам кодов
- Применяйте к своим макросам, автоматизируйте Excel, экономьте время.
Загрузите электронную книгу сегодня!
Нажмите кнопку ниже, чтобы подписаться, вы получите доступ к зоне для подписчиков, в которой вы можете скачать электронную книгу.
Интерполяция с использованием функции ПРОГНОЗ
В версии Excel 2016 года было добавлено множество новых статистических функций.Чтобы освободить место для этих новых функций, FORECAST был заменен функцией FORECAST.LINEAR. Хотя ПРОГНОЗ все еще остается на данный момент с целью обратной совместимости с Excel 2013 и ранее.
Поскольку FORECAST и FORECAST.LINEAR фактически одно и то же, мы будем использовать эти термины как синонимы.
Интерполяция при идеальной линейности
Теперь давайте воспользуемся ПРОГНОЗОМ для интерполяции результата.
Используя те же числа из приведенного выше примера, формула в ячейке E6:
= ПРОГНОЗ (E2, B2: B3, A2: A3)
Функция ПРОГНОЗ имеет следующий синтаксис:
= ПРОГНОЗ (x, известные_y, известные_x)
Три аргумента функции:
- x — точка данных, для которой мы хотим предсказать значение
- known_y’s — диапазон ячеек или массив значений, содержащий известные значения Y
- known_x’s — диапазон ячеек или массив значений, содержащий известные значения X
При использовании функции ПРОГНОЗ результат ячейки E6 также равен 77.5 (как и в математическом подходе).
Для полноты картины файл примера также содержит использование функции FORECAST.LINEAR. Как и следовало ожидать, результат идентичен устаревшей функции FORECAST.
Интерполяция при приблизительно линейном приближении
Но … что, если наши данные не совсем линейны? Посмотрите на диаграмму ниже, данные явно имеют линейную зависимость, но она не идеальна. Посмотрите на вкладку Example 2 во вспомогательном файле.
В этих обстоятельствах функция ПРОГНОЗ даже более полезна, поскольку она не просто интерполирует между первым и последним значениями.Вот данные, используемые в диаграмме.
Функция ПРОГНОЗ в ячейке E4 интерполирует значение Y на основе значения X, равного 17,5.
= ПРОГНОЗ (E2, B2: B11, A2: A11)
В этом сценарии FORECAST оценивает значение на основе всех доступных точек данных, а не только начала и конца. Результат функции ПРОГНОЗ в ячейке E4 равен 77,3 (округлено до 1 десятичного знака), что в большинстве случаев будет более точным, чем простая линейная интерполяция, применяемая в математическом подходе.
Помните, что для оценки значений используется интерполяция. 77.3 может быть неточным результатом, но это разумная оценка, основанная на имеющейся у нас информации.
И снова FORECAST.LINEAR вычисляет тот же результат.
Интерполяция при нелинейных данных
Но вот более сложный вопрос: что, если данные вообще не линейны? Тогда что?
Посмотрите на вкладку Example 3 во вспомогательном файле. Вот наш новый сценарий графика:
Если бы мы использовали простой линейный подход, это дало бы нам значение 77.5, который, как вы можете видеть ниже, довольно далеко от кривой. Использование функции ПРОГНОЗ даст результат 70,8, что лучше, но также далеко от кривой.
Есть еще два варианта для получения более точной оценки (1) интерполяция экспоненциальных данных с использованием функции РОСТА (2) вычисление внутренней линейной интерполяции
Интерполировать экспоненциальные данные
Функция РОСТ похожа на ПРОГНОЗ, но может применяться к данным с экспоненциальным ростом.
Результат функции РОСТ в ячейке E10 равен 70,4. Еще раз, это ближе к линии, но все же немного далеко.
Формула в ячейке E10:
= РОСТ (B2: B11, A2: A11, E2)
Функция РОСТ имеет следующий синтаксис:
= РОСТ (известные_y, [известные_x], [новые_x], [const])
Четыре аргумента в функции РОСТ (только имейте в виду, что аргументы не в том же порядке, что и функция ПРОГНОЗ).
- known_y’s — диапазон ячеек или массив значений, содержащий известные значения Y
- [известные_x] — диапазон ячеек или массив значений, содержащий известные значения X
- [new_x’s] — точка данных, для которой мы хотим спрогнозировать значение
- [Const] — мера истина / ложь, указывающая, как должна вычисляться формула. В нашем сценарии мы можем оставить этот последний аргумент.
Квадратные скобки указывают, какие аргументы являются необязательными для функции для вычисления результата.Нам нужны known_y, , known_x, и new_x, , но мы проигнорировали аргумент const .
Хотя результат 70,4 является более близким приближением, мы не должны слепо использовать функцию РОСТ. Проверьте свои интерполяции, чтобы убедиться, что они разумны.
Внутренняя линейная интерполяция
Разумным вариантом может быть найти результат выше и ниже нового значения X, а затем применить линейную интерполяцию между этими двумя точками.Это было бы довольно близко.
В нашем примере значения по обе стороны от X, равного 17,5:
- X: 16 и 18
- Y: 66,3 и 68
Используя эти значения, теперь мы можем выполнить стандартную линейную интерполяцию.
Быстрый одноразовый метод
Если бы это было разовое действие, мы могли бы сделать это быстро, включив в формулу только основные ячейки.
= ПРОГНОЗ (E2, B6: B7, A6: A7)
Однако, как только мы изменим интерполированное значение, FORECAST может вычислить неточный результат.Итак, перейдем к рассмотрению гибкого метода.
Гибкий подход
Для создания гибкого подхода мы будем использовать функции ИНДЕКС, ПОИСКПОЗ и ПРОГНОЗ вместе. Это может показаться сложным, но не волнуйтесь, мы рассмотрим это медленно. В конечном итоге мы пытаемся достичь того же результата, что и описанный выше одноразовый метод, но автоматически регулируем диапазоны в зависимости от интерполируемого значения.
ПРИМЕЧАНИЕ. Для того, чтобы этот метод работал, необходимо, чтобы диапазон известных X был указан в порядке возрастания.
Функция ПОИСКПОЗ
Во-первых, мы используем функцию ПОИСКПОЗ, чтобы получить позицию значения ниже 17,5.
= ПОИСКПОЗ (E2; A2: A11,1)
Эта формула говорит, что найдите значение в ячейке E2 из диапазона ячеек A2-A11. 1 в конце формулы сообщает функции ПОИСКПОЗ, что мы хотим использовать приблизительное совпадение (т. Е. Ближайшее значение ниже значения поиска). 16 — ближайшее значение ниже 17,5. Поскольку 16 — это 5-й элемент в ячейках A2-A11, ПОИСКПОЗ возвращает значение 5.
Функция ИНДЕКС
Определив на предыдущем этапе, что пятая позиция содержит значение ниже, мы можем использовать функцию ИНДЕКС, чтобы определить ссылку на ячейку для этого значения.
ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1))
Это вернет ссылку на ячейку A6.
Чтобы найти указанное выше значение, мы можем использовать ту же функцию, но добавить 1 к функции ПОИСКПОЗ.
ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1) +1 )
Приведенная выше формула вернет ссылку на ячейку A7.
Динамический диапазон
Теперь все становится интереснее. Мы можем объединить эти функции с двоеточием (:) посередине, чтобы создать диапазон для двух значений X.
ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1) +1)
Первая функция ИНДЕКС возвращает ссылку на ячейку A6 (результат выделенного зеленым цветом раздела). Вторая функция ИНДЕКС возвращает ссылку на ячейку A7 (результат выделенного фиолетовым цветом раздела).Они разделены двоеточием (:) (выделены красным) для создания диапазона — A6: A7
Мы можем сделать то же самое, чтобы создать диапазон для двух значений Y. Единственная разница в том, что функции ИНДЕКС будут смотреть на ячейки B2-B11.
ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1) +1)
Используя ячейки B2-B11 в функции ИНДЕКС, вычисляется диапазон B6: B7.
ИНДЕКС МАТЧИ И ПРОГНОЗ
Теперь у нас есть два диапазона; значения X A6: A7 и значения Y B6: B7.Давайте объединим все это в функции ПРОГНОЗ.
= ПРОГНОЗ (E2; ИНДЕКС (B2: B11; ПОИСКПОЗ (E2; A2: A11,1)): ИНДЕКС (B2: B11; ПОИСКПОЗ (E2; A2: A11,1) +1), ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1) +1))
Это довольно большая формула, верно. Но, надеюсь, мне удалось объяснить это так, что это не слишком страшно.
Результат внутренней линейной интерполяции с использованием функции ПРОГНОЗ составляет 67,6 (с точностью до 1 десятичного знака, как показано в ячейке E14). Взгляните на график еще раз; вы увидите, что 67.6 — разумная оценка, основанная на имеющихся данных.
ПРЕДУПРЕЖДЕНИЕ. В конечном счете, это все еще вычисление линейной интерполяции, основанное на двух значениях по обе стороны от значения X. Расстояние между значениями выше и ниже будет напрямую влиять на точность интерполяции.
Заключение
Изначально то, что казалось простым вопросом, привело нас к множеству потенциальных решений для трех различных сценариев. Ключевым моментом является то, что вам необходимо знать свои данные, чтобы выбрать метод, обеспечивающий наиболее точные результаты.
В процессе мы рассмотрели функции FORECAST и FORECAST.LINEAR и увидели, что они полезны как для интерполяции, так и для экстраполяции.
Кроме того, в этом посте мы использовали ИНДЕКС и ПОИСКПОЗ для создания динамических диапазонов, что является очень мощным методом для сложных формул в Excel.
Не забудьте:
Если вы нашли этот пост полезным или у вас есть лучший подход, оставьте, пожалуйста, комментарий ниже.
Вам нужна помощь в адаптации этого к вашим потребностям?
Я полагаю, что примеры в этом посте не совсем соответствуют вашей ситуации.Все мы используем Excel по-разному, поэтому невозможно написать сообщение, которое удовлетворит потребности всех. Потратив время на то, чтобы понять методы и принципы, изложенные в этом посте (и в других местах на этом сайте), вы сможете адаптировать их к своим потребностям.
Но если вы все еще боретесь, вам следует:
- Прочтите другие блоги или посмотрите видео на YouTube по той же теме. Вы получите гораздо больше пользы, открыв свои собственные решения.
- Спросите «Excel Ninja» в своем офисе.Удивительно, что знают другие люди.
- Задайте вопрос на форуме, например в Mr Excel, или в сообществе ответов Microsoft. Помните, что люди на этих форумах обычно посвящают свое время бесплатно. Так что постарайтесь сформулировать свой вопрос, сделайте его ясным и кратким. Составьте список всего, что вы пробовали, и предоставьте скриншоты, фрагменты кода и примеры рабочих книг.
- Используйте Excel Rescue, мой партнер-консультант. Они помогают, предлагая решения небольших проблем с Excel.
Что дальше?
Не уходите, об Excel Off The Grid можно узнать еще много. Ознакомьтесь с последними сообщениями:
.
Линейная интерполяция в Excel | EngineerExcel
До сих пор в сообщениях о поиске табличных данных в Excel я сосредоточился на том, как извлечь известные значения x и y из таблицы. Но что, если данные в таблице слишком «грубые» и вам нужна более высокая точность? Что ж, также возможно выполнить линейную интерполяцию в Excel, которая позволяет вам оценить значение y для любого значения x, которое не указано явно в данных.
Чтобы выполнить линейную интерполяцию в Excel, мы будем использовать приведенное ниже уравнение, где x — независимая переменная, а y — значение, которое мы хотим найти:
Этот метод предполагает, что изменение y для данного изменения x является линейным.
В большинстве случаев это дает достаточно точные результаты. Однако, если вам нужна еще большая точность, вы можете рассмотреть более продвинутый метод, такой как кубические сплайны.
Как показано в приведенном выше уравнении, нам нужно найти значения x1, y1, x2 и y2. Чтобы найти их, мы воспользуемся функциями ПОИСКПОЗ и ИНДЕКС.
Я писал здесь о синтаксисе этих функций, поэтому, если вам нужно что-то напомнить, обязательно ознакомьтесь с этим. Но в основном MATCH возвращает местоположение значения (n) в столбце или строке данных.ИНДЕКС возвращает фактическое значение в позиции n -й строки или столбца данных.
Используя эти функции вместе, мы можем извлечь значения x1, y1, x2 и y2, которые нам нужны для интерполяции.
Давайте посмотрим, как выполнить этот анализ на реальных данных.
В таблице ниже представлена зависимость плотности воздуха от температуры с шагом 20 градусов Цельсия. Если мы хотим получить данные при любых температурах, кроме тех, что указаны в первом столбце, нам придется интерполировать.
Если мы хотим оценить плотность при 53 градусах Цельсия, нам понадобится Excel, чтобы найти в таблице значения x1 = 40, y1 = 1,127, x2 = 60 и y2 = 1,067. Затем мы можем использовать эти значения в приведенном выше уравнении.
Найдите значение x1 по следующей формуле:
В этом примере я дал ячейке C2 имя «x», создав именованную ячейку. Формула возвращает 40, что является максимальной температурой, которая меньше 53, нашего значения x.
Далее мы можем получить y1 по следующей формуле:
Это
.
Линейная интерполяция с помощью Excel — Dagra Data Digitizer
Как работает реализация Excel
Простую реализацию легче всего понять, проанализировав снаружи и работая внутри. Вот полное уравнение:
= ПРОГНОЗ ( NewX , OFFSET ( KnownY , MATCH ( NewX , KnownX , 1)) - 1,0,2), OFFSET ( KnownX , MATCH ( NewX , KnownX , 1) -1,0,2))
Вкратце уравнение состоит из 3 частей:
- функция ПРОГНОЗ для вычисления линейной интерполяции,
- два вызова функции ПОИСКПОЗ, чтобы найти ближайшее табличное значение x, но меньше нового значения x, и
- два вызова функции OFFSET для ссылки на табулированные значения x и значения y чуть выше и чуть ниже нового значения x.
Более подробно, функция ПРОГНОЗ выполняет фактическую интерполяцию, используя уравнение линейной интерполяции, показанное выше. Его синтаксис: FORECAST ( NewX , known_y_pair , known_x_pair ).
Первый параметр, NewX — это просто значение для интерполяции. Следующие два параметра, известная_y_ пара и известная_x_ пара , являются значениями по обе стороны от NewX . То есть {x1, x2} и {y1, y2} на диаграмме выше.
Функция ПОИСКПОЗ используется для нахождения табличного значения x чуть ниже NewX . Его синтаксис: MATCH ( lookup_value , lookup_table , match_type ). MATCH возвращает относительное положение элемента в отсортированном массиве. Итак, lookup_value — это значение для интерполяции, lookup_table — это массив из KnownX значений, а match_type — это 1, чтобы найти наибольшее значение в массиве, которое меньше или равно NewX .
Функция ПОИСКПОЗ возвращает индекс, но для функции ПРОГНОЗ требуется два диапазона ячеек: один для пары известных_x_ и один для пары известных_y_. Таким образом, функция OFFSET используется дважды для создания этих диапазонов. Его синтаксис — OFFSET ( ссылка , row_offset , column_offset , row_count , column_count ). Он берет начальную точку, ссылку , и создает ссылку на ячейку с заданным смещением и размером.Чтобы получить диапазон known_y_pair , ссылка устанавливается в таблицу KnownY значений; для диапазона known_x_pair , ссылка устанавливается в массив KnownX значений. Если табличные значения расположены вертикально, row_offset является результатом функции MATCH меньше 1, а row_count равно 2; column_offset равно 0, а column_count равно 1. Это дает нам ссылку на массив ячеек на 2 ячейки в высоту и 1 ячейку в ширину.Если табличные значения расположены горизонтально, строка и столбец переключаются в функции OFFSET.
.
Метод расчета значения шага интерполяции в Excel — Office
- 22.05.2020
- 2 минуты на чтение
-
- Применимо к:
- Microsoft Office Excel 2007, Excel 2010, Excel 2013, Excel 2016
В этой статье
Примечание
Office 365 ProPlus переименовывается в Microsoft 365 Apps for Enterprise .Дополнительные сведения об этом изменении см. В этом сообщении в блоге.
Сводка
Следующая формула Microsoft Excel выполняет линейную интерполяцию путем вычисления значения шага интерполяции:
= (конец-начало) / (ROW (конец) -ROW (начало))
, где конец — это адрес ячейки большего числа, а начало — адрес ячейки меньшего числа.
Интерполяция — это метод, используемый для определения фактора текущей или будущей стоимости, когда точный коэффициент не появляется ни в таблице текущей, ни в будущей таблице значений.Интерполяция предполагает, что изменение между двумя значениями является линейным, а допустимая погрешность незначительна.
Дополнительная информация
Чтобы создать пример формулы линейной интерполяции, выполните следующие действия:
-
Введите следующие значения на листе:
A1: 9 B1: = (A7-A1) / (ROW (A7) -ROW (A1)) A2: = A1 + $ B $ 1 A3: A4: A5: A6: A7: 11 -
Выберите ячейки A2: A6. В меню «Правка» наведите указатель на «Заливка» и нажмите «Вниз».Формула заполняется, и в ячейках A2 отображаются следующие значения: A6:
A2: 9.33333 A3: 9.66667 A4: 10. A5: 10.33333 A6: 10.66667
Примечание
Вы должны ввести ссылку на значение шага в ячейку B1 как абсолютную ссылку (со знаками доллара).
.