Простая линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между объясняющей переменной x и переменной отклика y.
В этом руководстве объясняется, как выполнить простую линейную регрессию в Excel.
Пример: простая линейная регрессия в Excel
Предположим, нас интересует взаимосвязь между количеством часов, которое студент тратит на подготовку к экзамену, и полученной им экзаменационной оценкой.
Чтобы исследовать эту взаимосвязь, мы можем выполнить простую линейную регрессию, используя часы обучения в качестве независимой переменной и экзаменационный балл в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы провести простую линейную регрессию.
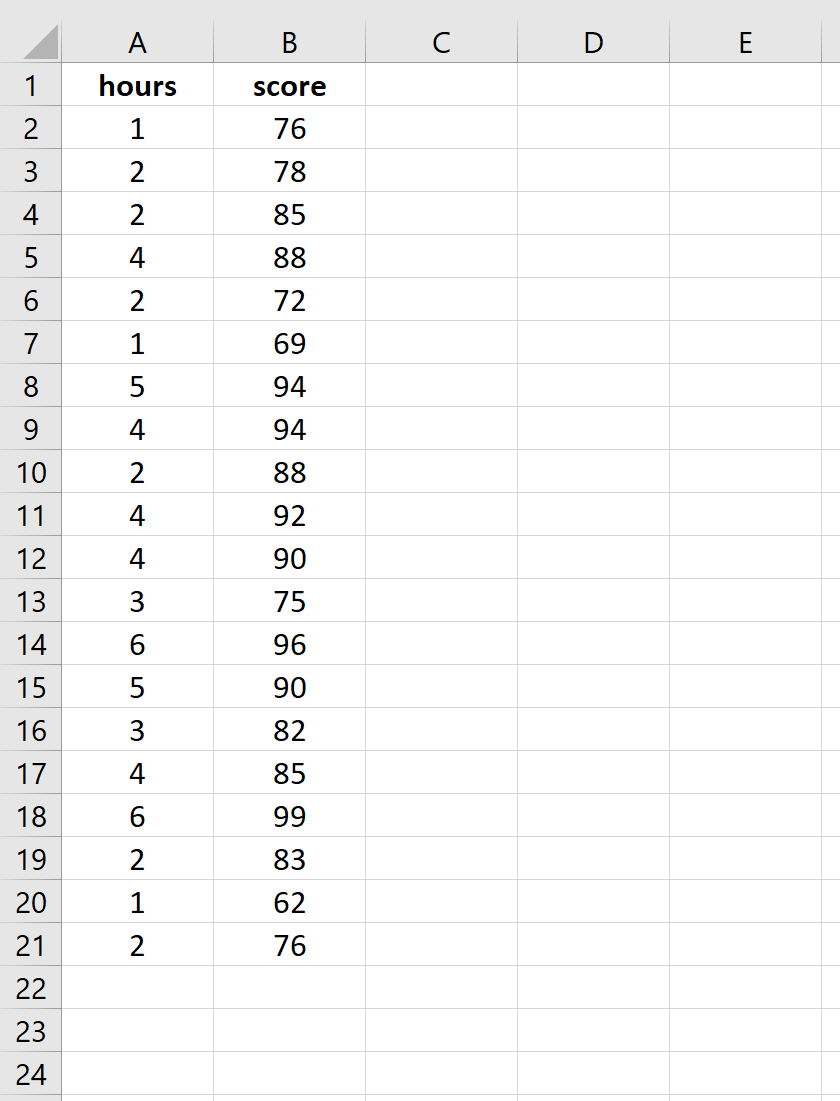
Шаг 1: Введите данные.
Введите следующие данные о количестве часов обучения и экзаменационном балле, полученном для 20 студентов:
Шаг 2: Визуализируйте данные.
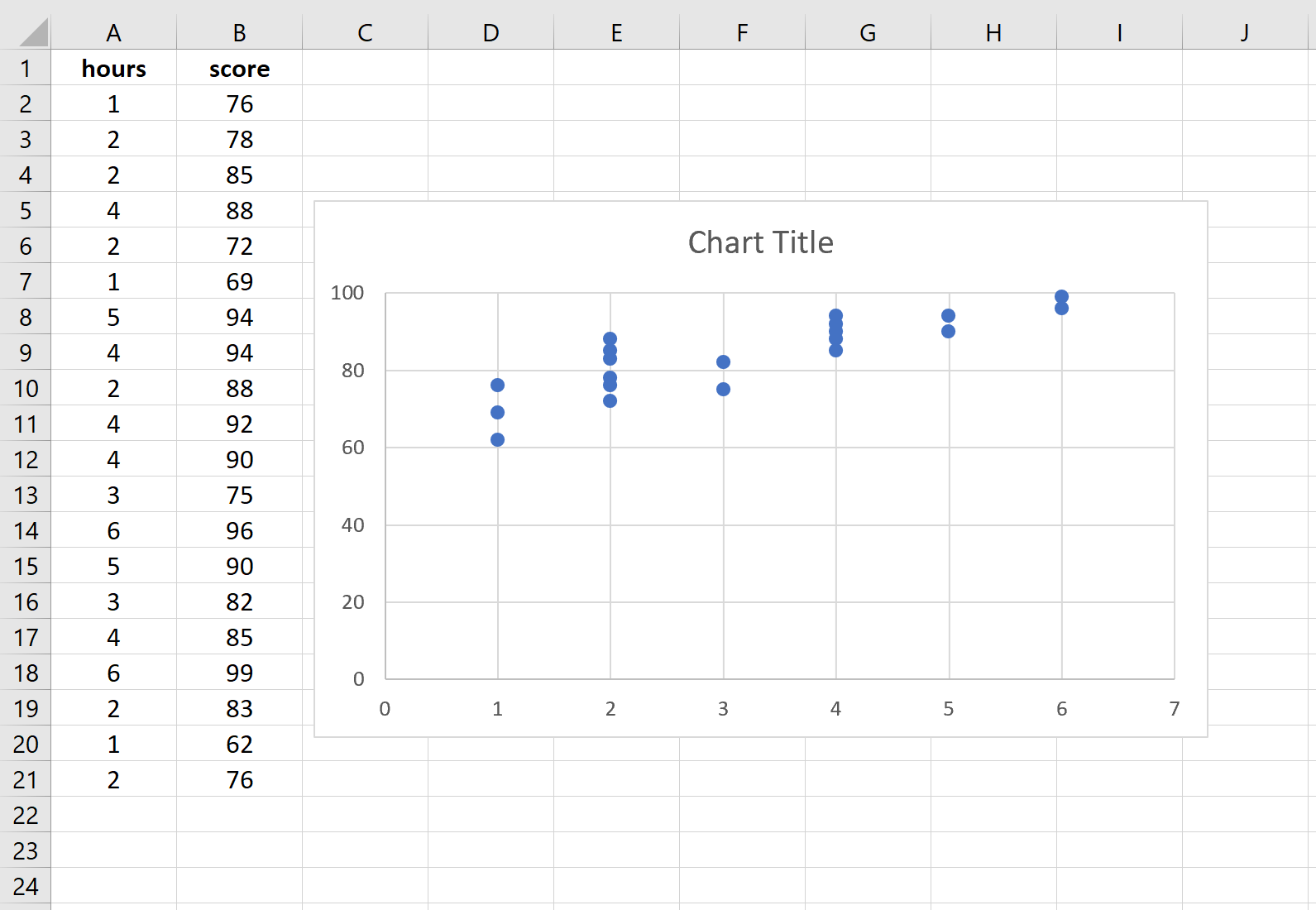
Прежде чем мы выполним простую линейную регрессию, полезно создать диаграмму рассеяния данных, чтобы убедиться, что действительно существует линейная зависимость между отработанными часами и экзаменационным баллом.
Выделите данные в столбцах A и B. В верхней ленте Excel перейдите на вкладку « Вставка ». В группе « Диаграммы » нажмите « Вставить разброс» (X, Y) и выберите первый вариант под названием « Разброс ». Это автоматически создаст следующую диаграмму рассеяния:
Количество часов обучения показано на оси x, а баллы за экзамены показаны на оси y. Мы видим, что между двумя переменными существует линейная зависимость: большее количество часов обучения связано с более высокими баллами на экзаменах.
Чтобы количественно оценить взаимосвязь между этими двумя переменными, мы можем выполнить простую линейную регрессию.
Шаг 3: Выполните простую линейную регрессию.
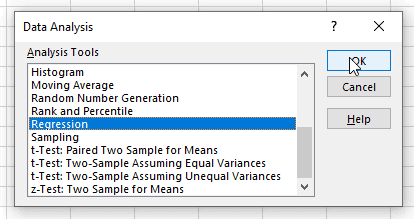
В верхней ленте Excel перейдите на вкладку « Данные » и нажмите « Анализ данных».Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа .
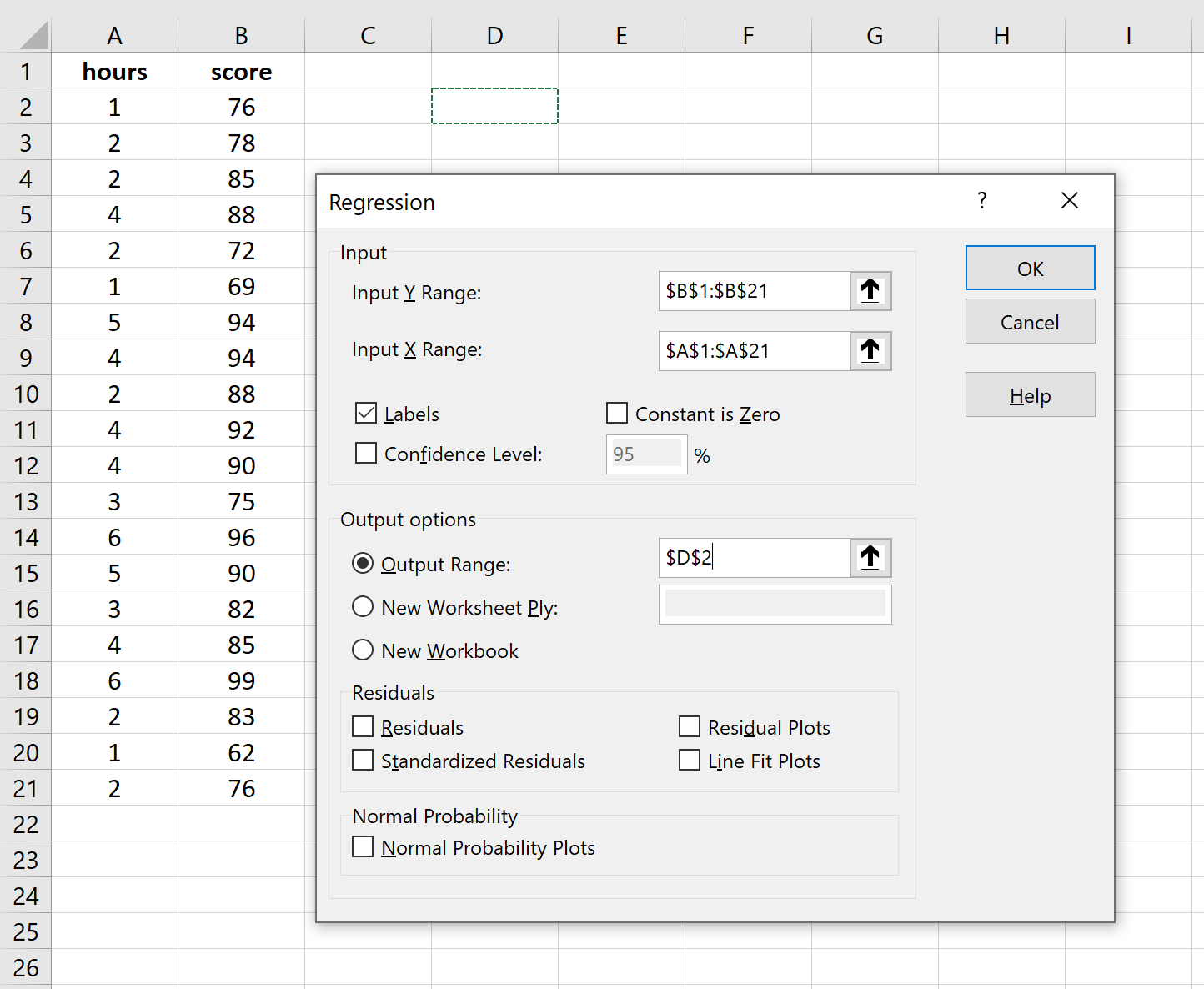
Как только вы нажмете « Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
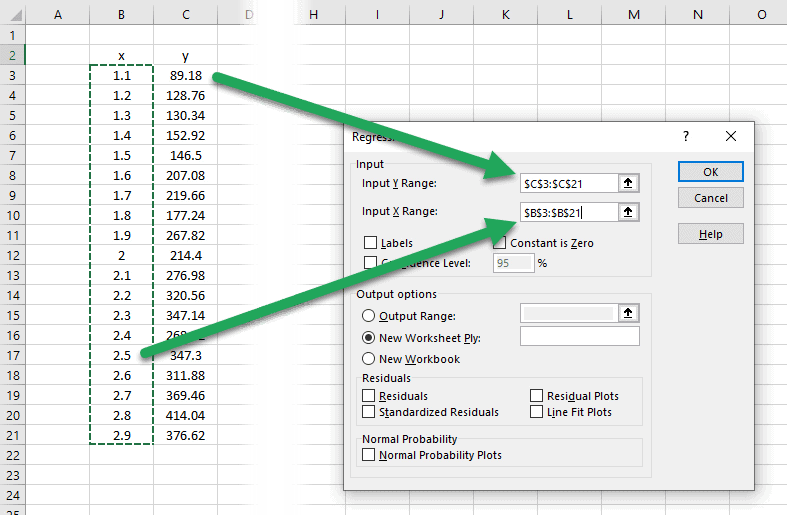
Для Input Y Range заполните массив значений для переменной ответа. Для Input X Range заполните массив значений для независимой переменной.
Установите флажок рядом с Метки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны.
В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии.
Затем нажмите ОК .
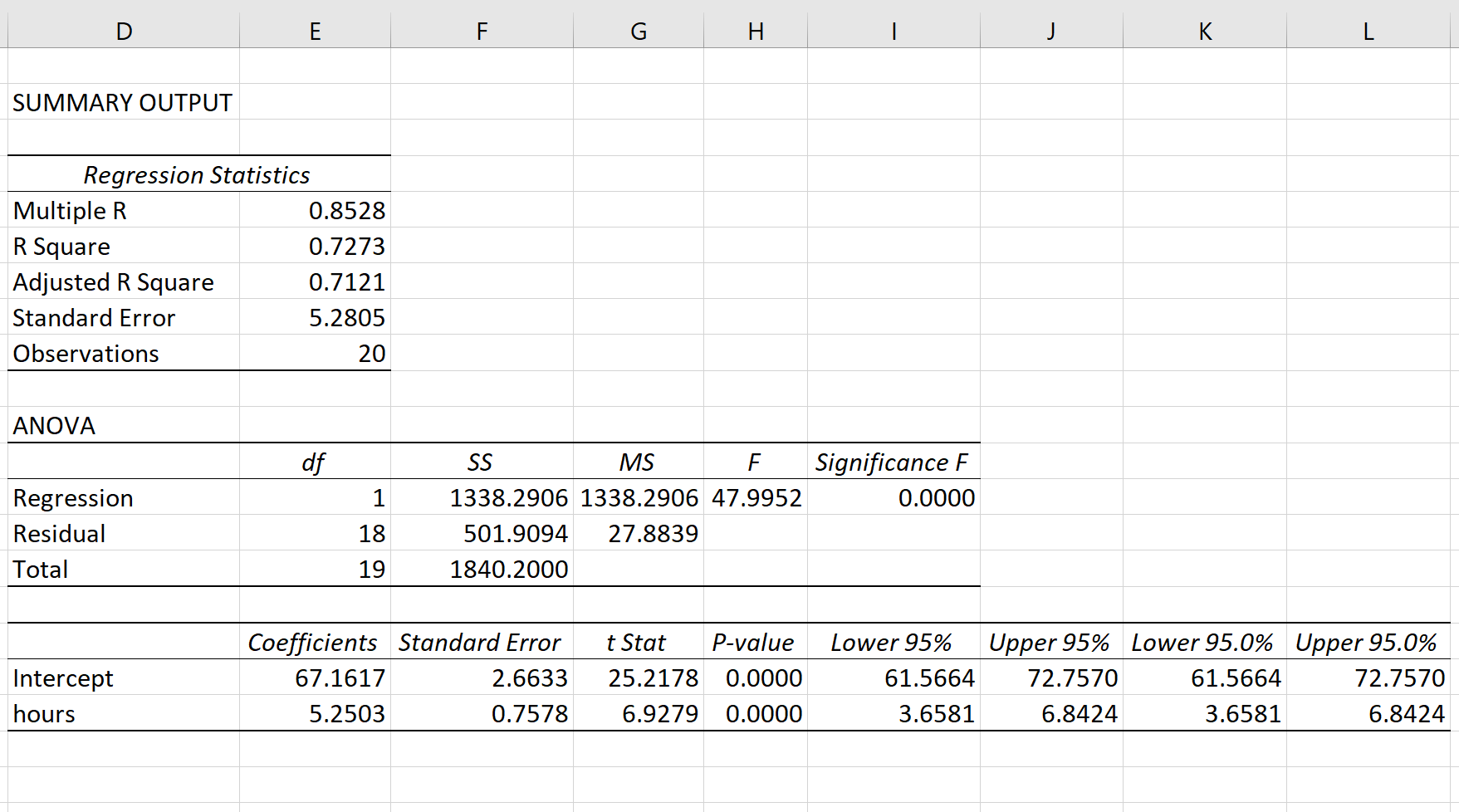
Автоматически появится следующий вывод:
Шаг 4: Интерпретируйте вывод.
Вот как интерпретировать наиболее релевантные числа в выводе:
R-квадрат: 0,7273.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющей переменной. В этом примере 72,73 % различий в баллах за экзамены можно объяснить количеством часов обучения.
Стандартная ошибка: 5.2805.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,2805 единиц.
Ф: 47,9952.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель статистически значимой. Другими словами, он говорит нам, имеет ли независимая переменная статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на наличие статистически значимой связи между отработанными часами и полученными экзаменационными баллами.
Коэффициенты: коэффициенты дают нам числа, необходимые для написания оценочного уравнения регрессии. В этом примере оцененное уравнение регрессии:
экзаменационный балл = 67,16 + 5,2503*(часов)
Мы интерпретируем коэффициент для часов как означающий, что за каждый дополнительный час обучения ожидается увеличение экзаменационного балла в среднем на 5,2503.Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится без часов, составляет 67,16 .
Мы можем использовать это оценочное уравнение регрессии для расчета ожидаемого экзаменационного балла для учащегося на основе количества часов, которые он изучает.
Например, ожидается, что студент, который занимается три часа, получит на экзамене 82,91 балла:
экзаменационный балл = 67,16 + 5,2503*(3) = 82,91
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как создать остаточный график в Excel
Как построить интервал прогнозирования в Excel
Как создать график QQ в Excel
Linear regression is a statistical tool in Excel used as a predictive analysis model to check the relationship between two sets of data or variables. We can estimate the relationship between two or more variables using this analysis. For example, we can see two variables: dependent and independent variables.
- The dependent variable is the factor we are trying to estimate.
- The independent variable is the factor that influences the dependent variable.
So, using Excel linear regression, we can see how the dependent variable goes through changes when the independent variable changes and helps us to decide which variable has a real impact mathematically.
Table of contents
- Excel Linear Regression
- How to Add Linear Regression Data Analysis Tool in Excel?
- Examples
- Things to Remember
- Recommended Articles
You are free to use this image on your website, templates, etc, Please provide us with an attribution linkArticle Link to be Hyperlinked
For eg:
Source: Linear Regression in Excel (wallstreetmojo.com)
How to Add Linear Regression Data Analysis Tool in Excel?
Linear Regression in excel is available under analysis toolpakExcel’s data analysis toolpak can be used by users to perform data analysis and other important calculations. It can be manually enabled from the addins section of the files tab by clicking on manage addins, and then checking analysis toolpak.read more, a hidden tool in Excel. We can find this under the “Data” tab.
You can download this Linear Regression Excel Template here – Linear Regression Excel Template
This tool is not visible until the user enables this. To enable this, follow the below steps.
- We must first go to the FILES >>Options.
- Then, click on “Add-ins” under “Excel Options.”
- Select “Excel Add-ins” under the “Manage” dropdown list in Excel and click on “Go.”
- Check the box “Analysis ToolPak” in the “Add-Ins.”
- Now, we should see the ” Data Analysis” option under the “Data” tab.
With this option, we can conduct many “Data Analysis” options. Let us see some of the examples now.
Examples
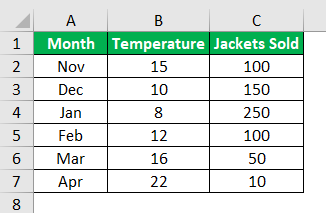
As we told you, linear regression Excel consists of two things: dependent and independent variables. For this example, we will use the below data of winter season jacket sold data with temperature in each month.
We have each month’s average temperature and jacket sold data. Here, we need to know which independent and dependent variables are.
Here “Temperature” is the independent variable because one cannot control the temperature, so this is the independent variable.
“Jackets Sold” is the dependent variable because the temperature increases and decreases in jacket sales.
Now, we will do the Excel linear regression analysis for this data.
- Step 1: We must click on the “Data” tab and “Data Analysis.”
- Step 2: Once we click on “Data Analysis,” we will see the below window. Scroll down and select “Regression” in excel.
- Step 3: Select the “Regression” option and click on “OK” to open the window below.
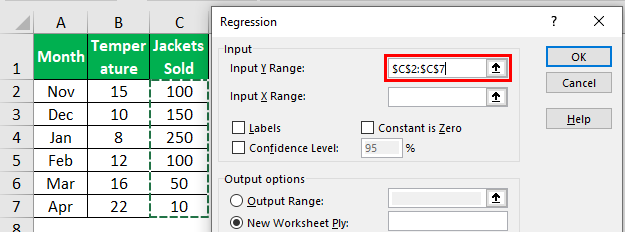
- Step 4: Here, the “Input Y Range” is the dependent variable, so in this case, our dependent variable is “Jackets Sold” data.
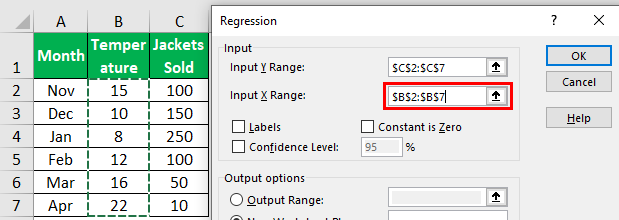
- Step 5: The “Input X Range” is the independent variable, so in this case, our independent variable is “Temperature” data.
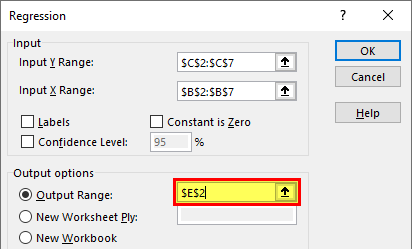
- Step 6: Select the output range as one of the cells.
- Step 7: To get the difference between the predicted and actual values, check the “Residuals” box.
- Step 8: Click on the “OK.” We will have the below analysis.
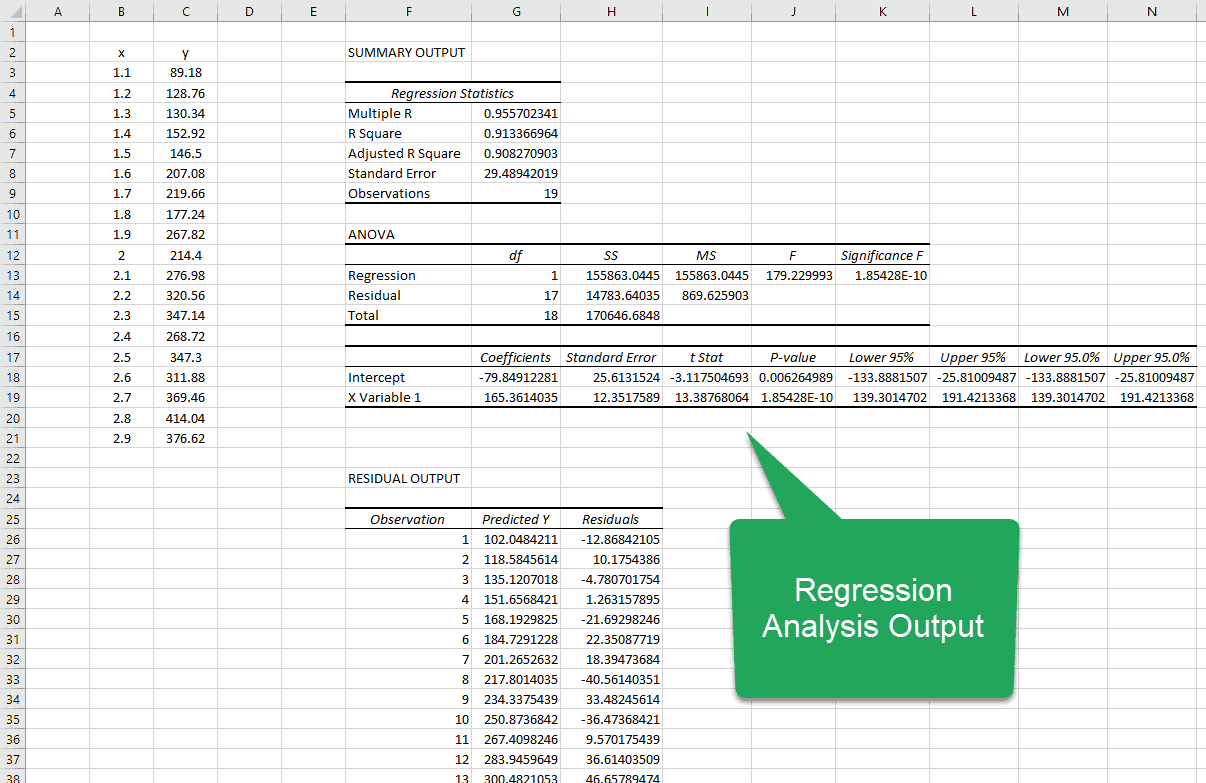
The first part of the analysis is “Regression Statistics.”
Multiple R: This calculation refers to the correlation coefficient, which measures the strength of a linear relationshipA linear relationship describes the relation between two distinct variables — x and y — in the form of a straight line on a graph. When presenting a linear relationship through an equation, the value of y is derived through the value of x, reflecting their correlation.read more between two variables. The Correlation Coefficient is the value between -1 and 1.
- 1 Indicates a strong positive relationship.
- -1 indicates a strong negative relationship.
- 0 indicates no relationship.
R Square: It is the coefficient of determinationCoefficient of determination, also known as R Squared determines the extent of the variance of the dependent variable which can be explained by the independent variable. Therefore, the higher the coefficient, the better the regression equation is, as it implies that the independent variable is chosen wisely.read more used to indicate the goodness of fit.
Adjusted R Square: This is the adjusted value for R SquareAdjusted R Squared refers to the statistical tool which helps the investors in measuring the extent of the variance of the variable which is dependent that can be explained with the independent variable and it considers the impact of only those independent variables which have an impact on the variation of the dependent variable.read more based on the number of independent variables in the data set.
Things to Remember
- We can also use the LINEST function in excelThe built-in LINEST Function in Excel calculates statistics for a line by the least-squares regression method & returns an array that defines the line proving to be well-suited for the given data. read more.
- We need to have a strong knowledge of statistics to interpret the data.
- If the data analysis is not visible under the “Data” tab, we need to enable this option under the “Add-ins” option.
Recommended Articles
This article is a guide to Linear Regression in Excel. We discuss linear regression data analysis in Excel, examples, and a downloadable Excel template. You may also look at these useful functions in Excel: –
- Formula of Coefficient of Determination
- Non-Linear Regression in Excel
- Regression vs. ANOVA
- Formula of Multiple Regression
With many things we try to do in Excel, there are usually multiple paths to the same outcome. Some paths are better than others depending on the situation. The same holds true for linear regression in Excel. There are four ways you can perform this analysis (without VBA). They are:
- Chart Trendlines
- LINEST function
- “Old School” regression using the Solver
- Linear regression with the Analysis Toolpak Add-In
Each of these linear regression methods has an appropriate time and place. Let’s take a look at each one individually.
Simple Linear Regression with Excel Charts
When you need to get a quick and dirty linear equation fit to a set of data, the best way is to simply create an XY-chart (or “Scatter Chart”) and throw in a quick trendline. Add the equation to the trendline and you have everything you need. You can go from raw data to having the slope and intercept of a best-fit line in 6 clicks (in Excel 2016).
Let’s say we have the data set below, and we want to quickly determine the slope and y-intercept of a best-fit line through it.
We’d follow these 6 steps (in Excel 2016):
- Select x- and y- data
- Open Insert Tab
- Select Scatter Chart
- Right-Click Data Series
- Select Add Trendline
- Check Display Equation on Chart
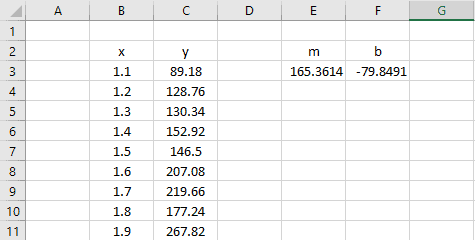
Now we know that the data set shown above has a slope of 165.4 and a y-intercept of -79.85.
Easy, right?
Linear Regression with the LINEST function
The chart trendline method is a quick way to perform a very simple linear regression and fit a curve to a series of data, but it has two significant downfalls.
The first is that the equation displayed on the chart cannot be used anywhere else. It’s essentially “dumb” text.
If you want to use that equation anywhere in your spreadsheet, you have to manually enter it. However, if you change the data set used to obtain the equation, that equation you manually entered will not update, leaving your spreadsheet with an erroneous equation.
The second issue is that sometimes the number of significant digits displayed in the formula on the chart is very limited. In fact, sometimes, you’ll only be able to see one or two significant digits. And that will lead to inaccuracy in the predicted values of y.
What we need for these situations is a function that can perform the same kind of simple linear regression done by the charting utility and output the coefficients to cells where we can use them in an equation. Of course, it also needs to return values with more significant digits.
The LINEST function does this perfectly. Given two sets of data, x and y, it will return the slope (m) and intercept (b) values that complete the equation
y = mx + b
The syntax of the function is as follows:
LINEST(known_y’s, [known_x’s], [const], [stats])
Where:
Known_y’s is the y-data you are attempting to fit
Known_x’s is the x-data you are attempting to fit
Const is a logical value specifying whether the intercept is forced to zero (FALSE) or not (TRUE)
Stats is a logical value that specifies whether regression statistics are returned
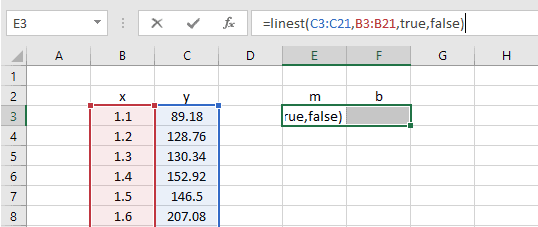
LINEST is an array function, so we need to enter it as an array formula, providing two cells to which it can return the values of m and b.
Let’s take a look at how LINEST could be used to determine the equation of a best-fit line for the data above.
Since LINEST will return two values, I start by selecting two adjacent cells on the worksheet.
Next, I enter the formula in the formula bar, rather than in the cell.
Finally, because it’s an array formula, I press CTRL+SHIFT+ENTER to calculate the cells.
The results are…
…exactly the same as those provided by the trendline method.
This was obviously more work than using a trendline, but the real advantage here is that the slope and y-intercept values have been output to a cell. That means we can use them dynamically in a calculation somewhere else in the spreadsheet.
Linear Regression Using Solver
This method is more complex than both of the previous methods. Fortunately, it will probably be unnecessary to ever use this method for simple linear regression. I’ve included it here because it provides some understanding into the way that the previous linear regression methods work. It will also introduce you to the possibilities for more complicated curve fitting using Excel.
- Enter “guess-values” for the slope and intercept of the equation
- Calculate new y-values based on those guess values
- Calculate the error between the calculated y-values and the y-data
- Use the Solver to find values of the slope and intercept that minimize the total error
Let’s start again with the x- and y- data we had before.
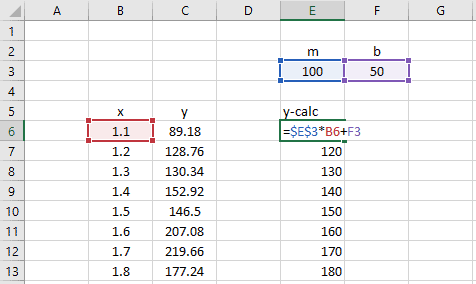
Next, enter some guess values for m and b into some cells on the worksheet.
Now create a new column of calculated y-values based on the m and b guess values and the known x-data.
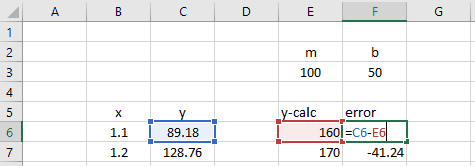
Next, create an error column, calculating the difference between the y-data and calculated y-values.
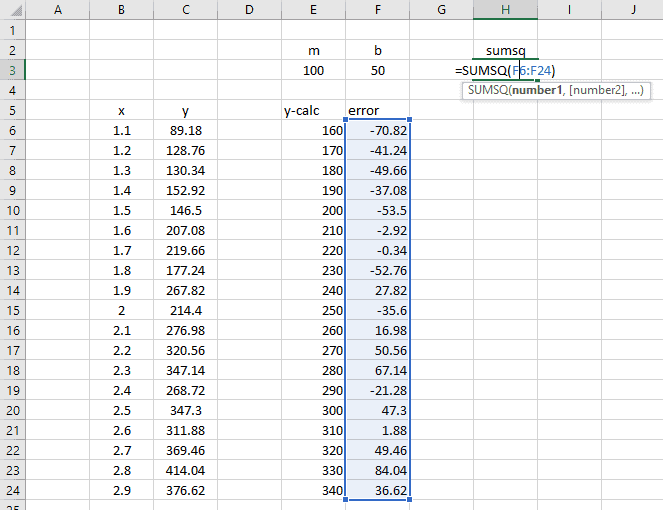
Finally, create a new formula, calculating the sum of squares of the error column.
We will use the Solver to minimize this value – the sum of the squared errors. The reason why we use “sum of squares” instead of just “sum” is because we do not want an error of -100 in one cell to cancel out an error of 100 in another cell. We want each value in the error column to be driven to its minimum absolute value.
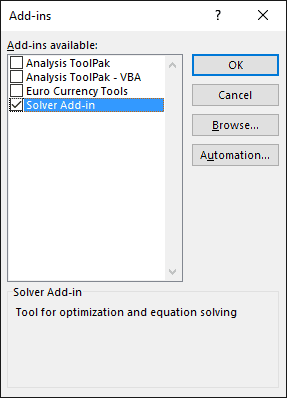
Now, let’s open up the Solver. If you have never used the Solver Add-In before, you must first enable it. Follow the steps here to enable the Solver.
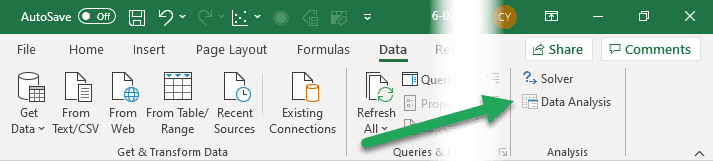
After the Add-In has been loaded, you can open the Solver from the Data tab. You’ll find it way over on the right side of the ribbon:
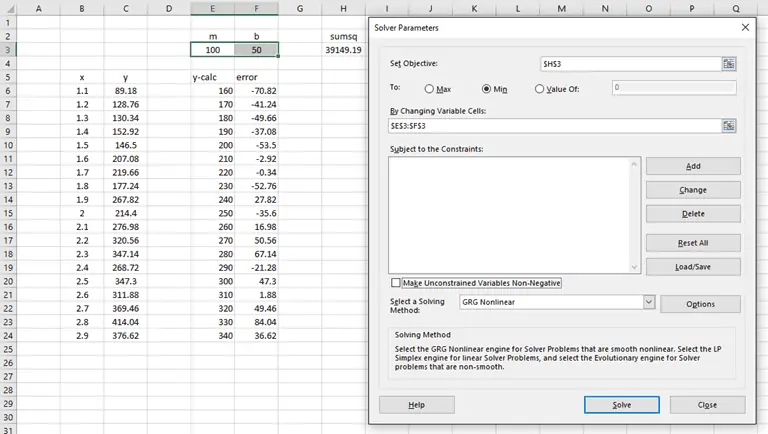
With the Solver open, the setup for this is pretty straightforward.
- We want to minimize the objective, cell H3, or the sum of the squared errors.
- To do so, we will change variable cells E3 and F3, the slope and y-intercept of our linear equation.
- As a last step, uncheck the option to “Make Unconstrained Variables Non-Negative”.
When properly set up, the solver dialog should look like this:
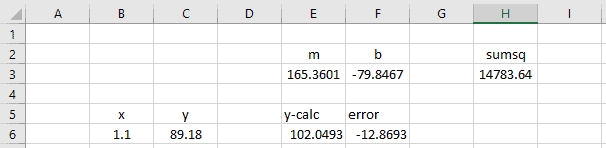
When we click “Solve”, the Solver does its thing and finds that the values m = 165.36 and b = -79.85 define the best-fit line through the data. Exactly what was predicted by the chart trendline and LINEST.
Of course, this is totally expected. After all, we have just done “manually” what the Trendline tool and LINEST do automatically.
In the case of a simple linear regression like we have here, Solver is probably complete overkill. However, this is just the start. We can use this same concept to do more complex multiple linear regression or non-linear regression analysis in Excel. Using Solver, you can fit whatever kind of equation you can dream up to any set of data. But that’s a topic for a completely different post.
Regression Analysis in Excel with the Analysis Toolpak Add-In
The final method for performing linear regression in Excel is to use the Analysis Toolpak add-in. This add-in enables Excel to perform difficult statistical analysis, but it is not enabled by default in Excel installations.
Install the Analysis Toolpak Add-In
To enable the Analysis Toolpak, follow these steps:
- Open the File tab, then select Options in the lower left corner
- Click Add-Ins in the lower left of the Excel Options window
- In the Manage drop-down, select “Excel Add-Ins”
- Click Go
- Select Analysis Toolpak
- Click OK
The Analysis Toolpak will be available in the Data tab in the Analysis group (on the far right of the ribbon and next to Solver). It is labelled as “Data Analysis”.
Simple Linear Regression Analysis with the Analysis Toolpak
Open the Analsis Toolpak Add-In from the ribbon and scroll down until you see Regression. Select it and click OK.
When the regression window opens, you’ll be greeted by tons of options. We’ll cover those in a minute, but let’s just keep it simple for now.
First, place the cursor in the box for “Input Y Range”, and select the y-values or dependent variables.
Repeat this for the “Input X Range”.
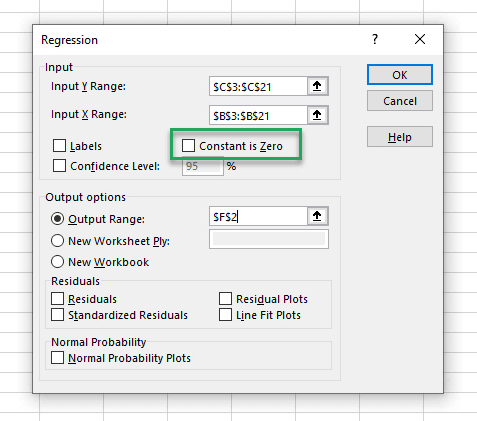
We can choose to set the intercept, or constant, to zero. If this box is unchecked, the constant will be calculated similarly to our previous regression analyses.
Next, select where the output data should be stored. The regression tool generates a large table of statistics, so you may want to store them on a new worksheet. Or you can specify a specific output range cell on the current worksheet. This cell will become the upper right cell in the output table. In the example below, I chose cell F2.
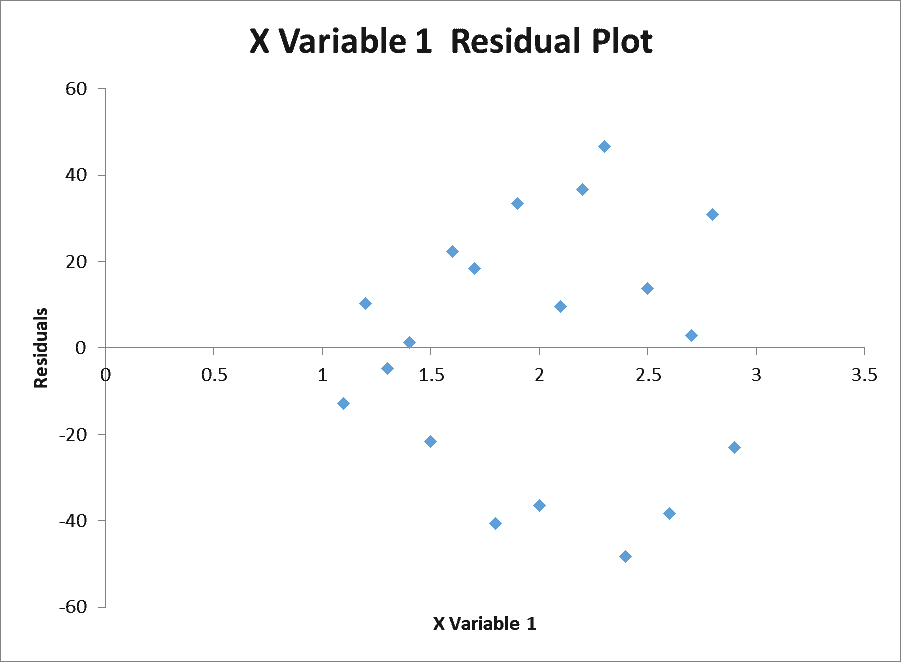
Finally, the regression tool provides several options for examining the residuals. Residuals are the difference between the observed y-values and the predicted y-values. Generally, the residuals should be randomly distributed with no obvious trends, such as increasing or decreasing in value as the x-values increase.
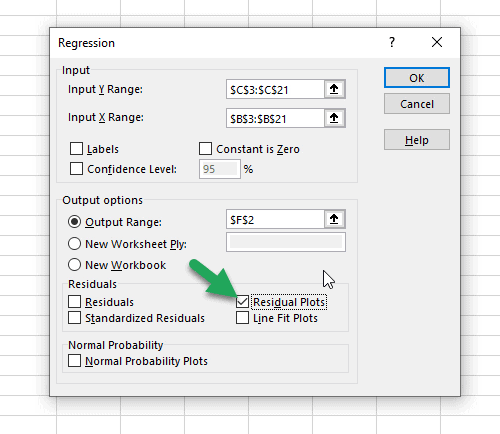
To examine for this easily, we can choose to create a residual plot with the regression analysis by checking the box next to “Residual Plots”.
Finally, with everything set up, all that is left to do is click the OK button to generate the report.
This is what it should look like:
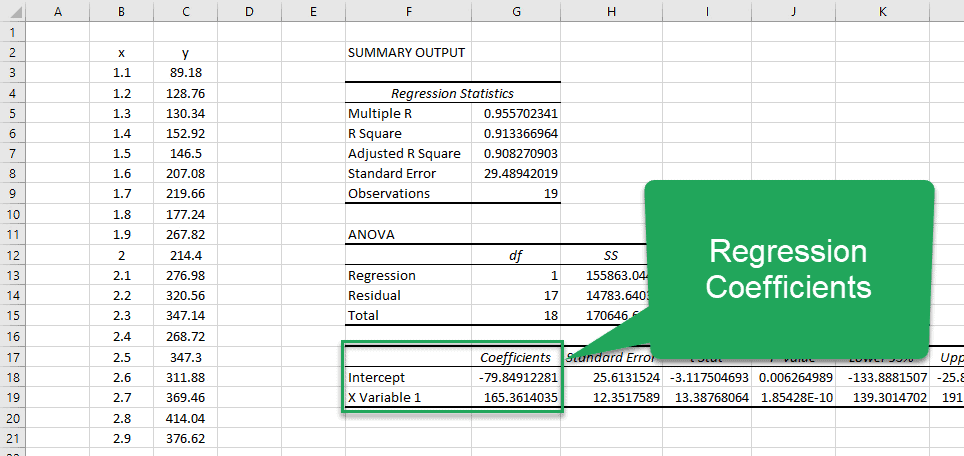
If you are looking for the coefficients that describe the best-fit line, you’ll have to go all the way down into the third table in the report. Here, you’ll see two rows:
- Intercept
- X Variable 1
The column in this table labeled “Coefficients” contains the values of the intercept and slope (X Variable 1). You can see that they match the values we obtained using the other methods. (Which is always nice to see!)
The plot of residuals is random, and there are no trends in the residuals:
The regression tool generates a lot of other data as well, so let’s look at some of the more important details:
Linear Regression Statistics
The first table in the report contains the Regression Statistics. These statistics are important because they tell us how well the line that results from the linear regression analysis fits the observed data.
Multiple R: This is the Pearson correlation coefficient that describes the correlation between the predicted values of Y and the observed values of Y. A value of 1 means that there is a perfect correlation between the two, and a value of 0 means that there is no correlation at all. In this analysis the value is 0.96, so there is a very strong correlation between the predicted and observed y-values.
R-Square: This is the coefficient of determination and it explains how much of the variation in the dependent variable can be explained by the equation. In this case, the R-Squared value is 0.91, so 91% of the variation is captured by the equation. That means the other 9% of the variation is not explained by the equation. It may be due to randomness or measurement error, for example.
Adjusted R-Square: This term is used for multiple linear regression and is useful in determining if a new term added to the model has helped to improve the prediction capability of the model or not. If an added term improves the model, this value increases. If an added term does not improve the model, this value decreases.
Standard Error: This is an estimate of how far the observed values are from the line that results from the regression analysis.
Observations: This is simply the number of observed data points.
Regression Coefficients
This is the third table in the report that contains a row for each of the coefficients and several columns:
- Coefficients
- Standard Error
- t Stat
- P-value
- Lower 95%
- Upper 95%
Coefficients: These are the coefficients on the variables that describe the line of best fit. In this example, we would assemble the coefficients into the equation:
Standard Error: This value tells us how much the observed values deviate from the best-fit line.
t Stat: This is the value you would use in a t-test.
P-value: This is the P-value used for the hypothesis test. If the P-value is low, we reject the null hypothesis.
Lower 95%: This is the lower bound of the 95% confidence interval.
Upper 95%: This is the upper bound of the 95% confidence interval.
Residual Output
The final table in the report lists the predicted value of y and the residual, or error between the predicted and observed value, for each value of x.
Regression Analysis Options
Performing a basic linear regression analysis with the Analysis Toolpak is straightforward, but there are many options to really expand its capability.
Labels: By selecting this option, the regression tool will use the cell value in the top row of the x-values as a label for the x-values.
Confidence Level: It’s possible to set a different confidence level in this field. The default is 95%.
Residuals: Choosing this option will add the residuals to the output table.
Standardized Residuals: When this option is selected, standardized residuals will be written to the worksheet.
Line Fit Plots: This will create a plot that includes the original observations and the predicted y-values. It is like adding a trendline to a plot.
Normal Probability Plot: This will plot the data against a normal distribution, which helps to determine whether the data is normally distributed.
How to do Linear Regression in Excel: Full Guide (2023)
Linear regression is an easy way of evaluating the relationship between two variables.
Previously, performing linear regression in Excel was nothing less than a complex task. But with advanced Excel data analysis tools, it is now only a matter of a few clicks.
The guide below will not only teach you how to perform linear regression in Excel but also how you may analyze a linear regression graph in Excel.
So, without further ado, let’s dive right in 👇
Download our free sample workbook here as you continue reading.
Linear regression equation
Simple linear regression draws the relationship between a dependent and an independent variable.
👉 The dependent variable is the variable that needs to be predicted (or whose value is to be found).
👉 The independent variable explains (or causes) the change in the dependent variable.
Simply put, the dependent variable depends upon the independent variable. And as the independent variable changes, the dependent variable changes too.
Mathematically, the linear relationship between these two variables is explained as follows:
Y= a + bx
Where,
Y = dependent variable
a = regression intercept term
b = regression slope coefficient
x = independent variable
“a” and “b” are also called regression coefficients. And Excel returns the predicted values of these regression coefficients too.
How to do linear regression through a graph
Imagine a company that sells sweaters in a cold region. And the sale of sweaters is directly linked to the temperatures in that region.
The colder it is (low temperatures 🥶), the higher the sales of sweaters 🧣 go. This means sales (the dependent variable) depend upon the temperature (the independent variable).
Now, to predict the company’s sales for the future, you must analyze the sales trend in the past. This can be done by drawing a trendline.
Drawing this trendline between a dependent variable Y (the sales) and an independent variable X (the temperature) is called running linear regression.
So let’s do it!

The image above contains the historical data for both variables (temperatures and sales) for a few months.
To explain the relationship between these variables, we need to make a scatter plot.
To plot the above data in a scatter plot in Excel:
- Select the data.
- Go to the Insert Tab > Charts Group

- Click on the scatterplot part icon.
- Choose a scatter plot type from the drop-down menu.

Excel plots the data in a scatter plot.

Note that each dot in the scatter plot above is formed at the intersection of Variable X and Y.
For example, the first dot is plotted at the point where Y = 625 and X = 2.
Next, we must draw a trend line out of this scatter plot. To do so:
- Click anywhere on the chart to select it.
- Click on the “+” icon on the top right of the chart.

- Hover your cursor over the option “Trendline”📈
A drop-down menu appears.

- Select More Options. This will take you to the Format Trendline Pane.
- Choose the linear trendline option to draw a trendline between the scatter points.

And there you go! Excel draws a linear trendline on the scatterplot.

The above image shows a downward regression line which represents a negative trend. But why is that?
To understand that, you must know how to analyze the results of a linear regression graph. And don’t worry – it’s only a section ahead.
Adding the equation and R-squared
We also want Excel to show the equation and R-squared for this graph. For that:
- Scroll down the Task pane.
- Check the option for “Equation” and “R-squared” on the graph.

And Excel will display the following regression statistics on the graph:
Equation: y= -19.622x + 612.77
R-squared= 0.7456

What are these? And what do they tell? We will discuss this shortly.
Pro Tip!
How to quickly interpret the relationship between two variables? By checking the sign of the x variable 💡
A positive sign means a positive relationship. And a negative sign means a negative relationship between the two variables.
Since our equation shows a “-19.622x”, the relation between our variables is negative.
Formatting the trendline
Do you also find the trendline a little overshadowed? Not to worry – You can always format it in Excel.
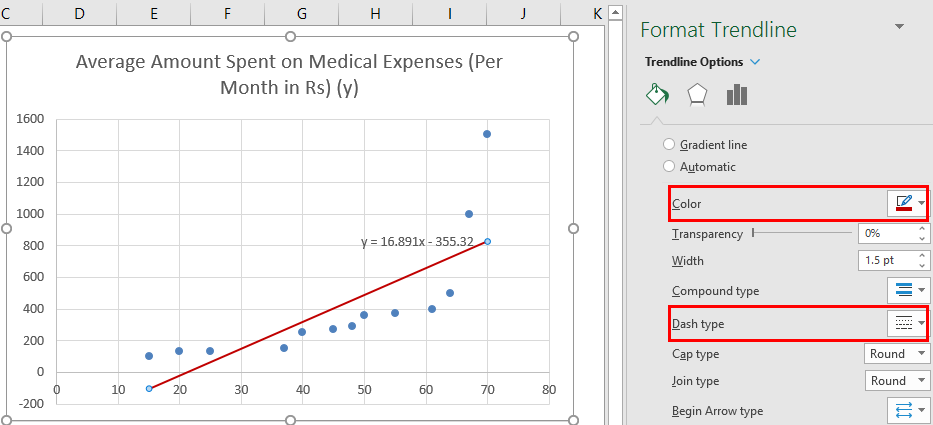
For example, to change the color of the trendline:
- Select the trendline and right-click on it to launch the context menu.
- Go to Format Trendline.
- Under the Format Trendline pane, select “Fill & Line”.
- To change the color of the trendline, choose a color as shown below.

Guess we will go with red for now 🚩 What do you think about it?

Trendline Style
Not only the color, but you can also change the style of the trendline.
Say, we want to change our dotted trendline to a solid one. To do so:
- Select the trendline and right-click on it to launch the context menu.
- Click on Format Trendline to launch the Format Trendline Pane.
- Go to “Dash type” from the fill & line menu.
- Select a solid line type.

This will change the style of the trendline from a dotted line to a perfectly solid line.

Chart Title
To enhance the readability of the graph, you may add graph titles and axes titles to it as follows:
- Select the graph.
- Go to Chart Elements > Chart Title > above chart.

- Type in a Graph/Chart title as desired.

Axis titles
How about adding the Axis titles too?
To add a vertical title (for the Y-axis) to your chart:
- Click Chart Elements > Axis Titles > Primary Vertical.

- Type in a suitable title for the subject axis.
We have set the title for the Y-axis to “Sale of Sweaters”.

To add a horizontal Axis Title (for the X-axis):
- Go to Chart elements > Axis Titles > Primary Horizontal.

- Type in a suitable title for the subject axis.
We have set the title for the X-axis to “Avg. Temperature”

And that’s it. We’ve successfully run linear regression in Excel 🥳
How to analyze the linear regression graph
Good job with running linear regression in Excel.
Now is the time that we analyze the linear regression trendline formed above.
A linear trendline in Excel can take the following three shapes:
Positive trendline (upward facing)
If your trendline is upward facing (it elevates as it goes from left to right), it denotes a positive trend.
This means that there exists a positive relationship between both variables. An increase in the independent variable causes the dependent variable to increase.
This is how your graph will look with a positive trendline to it.

Negative trendline (downward sloping)
If your trendline is downward sloping (it slopes down as it goes from left to right), it denotes a negative trend.
A negative trendline means a negative relationship between both variables.
When there is a negative relationship between two variables, an increase in the independent variable causes the dependent variable to decrease.
This is how your graph will look with a negative trendline to it.

Jog down your memory lane to remember the trendline type in our example above. It was also a downward-sloping (negative) trendline.
That’s because there exists a negative relationship between sales and temperature. As the temperature falls, sales increase.
No trend
The two variables can also be independent of each other. In this case, movement in both variables is random with no relation to each other.
As there exists no relationship between them (neither positive nor negative), there is no particular slope for the trendline between them (neither upward facing nor downward sloping).
Such a trendline might look like this.

The trendline above is not exactly horizontal but very close to that. This is because there is no relation between the variables.
The slope of the graph
What if we want to know the percentage of change in Y caused by a change in X?
For example, for every 1% decrease in temperature, sales increase by what percentage?
The slope of the graph is an answer to this. Remember the linear regression equation?
Y = a + bx
In the above equation, the slope is represented by “b”. And the linear regression equation for our example turned out as follows:
Y= 612.77 – 19.622x
Here, the value for b is -19.622 and so is our slope. This means that a 1% change in the X variable (the temperature) causes a -19.622% change in the Y variable (the sales).
Also, as the sign with the value for b is a minus sign, this means that a 1% decrease in Variable X (temperature) causes a 19.622% increase in Variable Y (Sales).

Pro Tip!
An easy way to remember the slope is to remember Rise over Run. Rise means vertical axis. Run means horizontal axis. So the slope defines the change in variable Y caused by a change in variable X.
R-Squared
Another important output of our scatterplot is the R-squared value 👀
It tells us how much variation of the dependent variable comes from the change in the independent variable.

The R-squared for our example is 0.7456.
This tells that only 74.56% variation of Variable Y can be explained by Variable X.
Another statistical measure relevant to the linear regression model is the p value. However, it is totally opposite to the concept of R-squared.
That’s it – Now what?
The above guide explains how to perform a linear regression analysis in Excel. And then, how to analyze the linear regression trendline and other relevant statistics.
👉 In addition to that, it also explains how you may format a trendline in Excel in different ways.
Performing linear regression in Excel through a scatter plot is super smart. But this is only one feature of Excel.
And there are many more smart functions in Excel. Like the VLOOKUP, SUMF, and IF functions.
Want to learn them already? Enroll in my 30-minute free email course that teaches you these and many more functions of Excel.
Other resources
Linear regression can be challenging to understand. But once you get a hold of it, you can run it for any possible dataset with sheer ease.
In addition to linear regression, Excel offers other forecasting functions too. Like the data analysis tools in Excel and the Excel FORECAST function.
Kasper Langmann2023-02-23T14:55:48+00:00
Page load link
What Is Linear Regression?
Linear regression is a type of data analysis that considers the linear relationship between a dependent variable and one or more independent variables. It is typically used to visually show the strength of the relationship or correlation between various factors and the dispersion of results – all for the purpose of explaining the behavior of the dependent variable. The goal of a linear regression model is to estimate the magnitude of a relationship between variables and whether or not it is statistically significant.
Say we wanted to test the strength of the relationship between the amount of ice cream eaten and obesity. We would take the independent variable, the amount of ice cream, and relate it to the dependent variable, obesity, to see if there was a relationship. Given a regression is a graphical display of this relationship, the lower the variability in the data, the stronger the relationship and the tighter the fit to the regression line.
In finance, linear regression is used to determine relationships between asset prices and economic data across a range of applications. For instance, it is used to determine the factor weights in the Fama-French Model and is the basis for determining the Beta of a stock in the capital asset pricing model (CAPM).
Here, we look at how to use data imported into Microsoft Excel to perform a linear regression and how to interpret the results.
Key Takeaways
- Linear regression models the relationship between a dependent and independent variable(s).
- Also known as ordinary least squares (OLS), a linear regression essentially estimates a line of best fit among all variables in the model.
- Regression analysis can be considered robust if the variables are independent, there is no heteroscedasticity, and the error terms of variables are not correlated.
- Modeling linear regression in Excel is easier with the Data Analysis ToolPak.
- Regression output can be interpreted for both the size and strength of a correlation among one or more variables on the dependent variable.
Important Considerations
There are a few critical assumptions about your data set that must be true to proceed with a regression analysis. Otherwise, the results will be interpreted incorrectly or they will exhibit bias:
- The variables must be truly independent (using a Chi-square test).
- The data must not have different error variances (this is called heteroskedasticity (also spelled heteroscedasticity)).
- The error terms of each variable must be uncorrelated. If not, it means the variables are serially correlated.
If those three points sound complicated, they can be. But the effect of one of those considerations not being true is a biased estimate. Essentially, you would misstate the relationship you are measuring.
Outputting a Regression in Excel
The first step in running regression analysis in Excel is to double-check that the free Excel plugin Data Analysis ToolPak is installed. This plugin makes calculating a range of statistics very easy. It is not required to chart a linear regression line, but it makes creating statistics tables simpler. To verify if installed, select «Data» from the toolbar. If «Data Analysis» is an option, the feature is installed and ready to use. If not installed, you can request this option by clicking on the Office button and selecting «Excel options».
Using the Data Analysis ToolPak, creating a regression output is just a few clicks.
The independent variable in Excel goes in the X range.
Given the S&P 500 returns, say we want to know if we can estimate the strength and relationship of Visa (V) stock returns. The Visa (V) stock returns data populates column 1 as the dependent variable. S&P 500 returns data populates column 2 as the independent variable.
- Select «Data» from the toolbar. The «Data» menu displays.
- Select «Data Analysis». The Data Analysis — Analysis Tools dialog box displays.
- From the menu, select «Regression» and click «OK».
- In the Regression dialog box, click the «Input Y Range» box and select the dependent variable data (Visa (V) stock returns).
- Click the «Input X Range» box and select the independent variable data (S&P 500 returns).
- Click «OK» to run the results.
[Note: If the table seems small, right-click the image and open in new tab for higher resolution.]
Interpret the Results
Using that data (the same from our R-squared article), we get the following table:
The R2 value, also known as the coefficient of determination, measures the proportion of variation in the dependent variable explained by the independent variable or how well the regression model fits the data. The R2 value ranges from 0 to 1, and a higher value indicates a better fit. The p-value, or probability value, also ranges from 0 to 1 and indicates if the test is significant. In contrast to the R2 value, a smaller p-value is favorable as it indicates a correlation between the dependent and independent variables.
Interpreting the Results
The bottom line here is that changes in Visa stock seem to be highly correlated with the S&P 500.
- In the regression output above, we can see that for every 1-point change in Visa, there is a corresponding 1.36-point change in the S&P 500.
- We can also see that the p-value is very small (0.000036), which also corresponds to a very large T-test. This indicates that this finding is highly statistically significant, so the odds that this result was caused by chance are exceedingly low.
- From the R-squared, we can see that the V price alone can explain more than 62% of the observed fluctuations in the S&P 500 index.
However, an analyst at this point may heed a bit of caution for the following reasons:
- With only one variable in the model, it is unclear whether V affects the S&P 500 prices, if the S&P 500 affects V prices, or if some unobserved third variable affects both prices.
- Visa is a component of the S&P 500, so there could be a co-correlation between the variables here.
- There are only 20 observations, which may not be enough to make a good inference.
- The data is a time series, so there could also be autocorrelation.
- The time period under study may not be representative of other time periods.
Charting a Regression in Excel
We can chart a regression in Excel by highlighting the data and charting it as a scatter plot. To add a regression line, choose «Add Chart Element» from the «Chart Design» menu. In the dialog box, select «Trendline» and then «Linear Trendline». To add the R2 value, select «More Trendline Options» from the «Trendline menu. Lastly, select «Display R-squared value on chart». The visual result sums up the strength of the relationship, albeit at the expense of not providing as much detail as the table above.
How Do You Interpret a Linear Regression?
The output of a regression model will produce various numerical results. The coefficients (or betas) tell you the association between an independent variable and the dependent variable, holding everything else constant. If the coefficient is, say, +0.12, it tells you that every 1-point change in that variable corresponds with a 0.12 change in the dependent variable in the same direction. If it were instead -3.00, it would mean a 1-point change in the explanatory variable results in a 3x change in the dependent variable, in the opposite direction.
How Do You Know If a Regression Is Significant?
In addition to producing beta coefficients, a regression output will also indicate tests of statistical significance based on the standard error of each coefficient (such as the p-value and confidence intervals). Often, analysts use a p-value of 0.05 or less to indicate significance; if the p-value is greater, then you cannot rule out chance or randomness for the resultant beta coefficient. Other tests of significance in a regression model can be t-tests for each variable, as well as an F-statistic or chi-square for the joint significance of all variables in the model together.
How Do You Interpret the R-Squared of a Linear Regression?
R2 (R-squared) is a statistical measure of the goodness of fit of a linear regression model (from 0.00 to 1.00), also known as the coefficient of determination. In general, the higher the R2, the better the model’s fit. The R-squared can also be interpreted as how much of the variation in the dependent variable is explained by the independent (explanatory) variables in the model. Thus, an R-square of 0.50 suggests that half of all of the variation observed in the dependent variable can be explained by the dependent variable(s).
Linear Regression in Excel (Table of Contents)
- Introduction to Linear Regression in Excel
- Methods for Using Linear Regression in Excel
Introduction to Linear Regression in Excel
Linear regression is a statistical technique/method used to study the relationship between two continuous quantitative variables. In this technique, independent variables are used to predict the value of a dependent variable. If there is only one independent variable, then it is a simple linear regression, and if a number of independent variables are more than one, then it is multiple linear regression. Linear Regression models have a relationship between dependent and independent variables by fitting a linear equation to the observed data. Linear refers to the fact that we use a line to fit our data. The dependent variables used in regression analysis are also called the response or predicted variables, and independent variables are also called explanatory variables or predictors.
A linear regression line has an equation of the kind: Y= a + bX;
Where:
- X is the explanatory variable,
- Y is the dependent variable,
- b is the slope of the line,
- a is the y-intercept (i.e. the value of y when x=0).
The least-squares method is generally used in linear regression that calculates the best fit line for observed data by minimizing the sum of squares of deviation of data points from the line.
Methods for Using Linear Regression in Excel
This example teaches you the methods to perform Linear Regression Analysis in Excel. Let’s look at a few methods.
You can download this Linear Regression Excel Template here – Linear Regression Excel Template
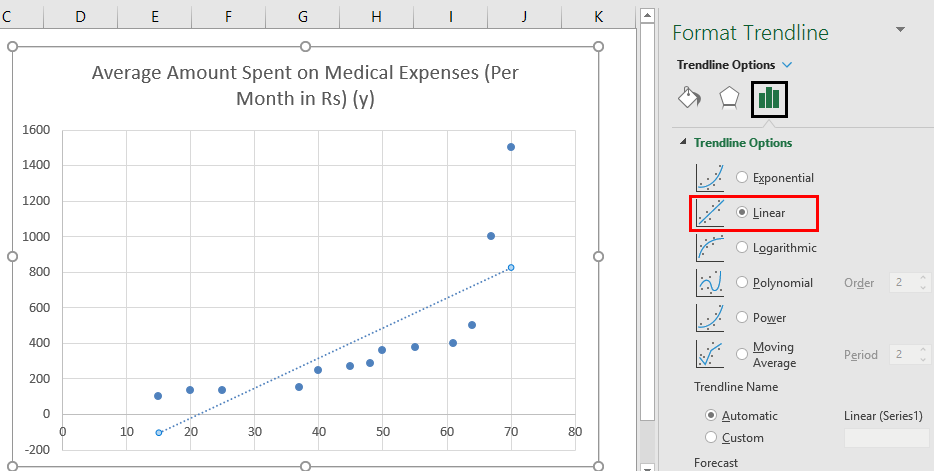
Method #1 – Scatter Chart with a Trendline
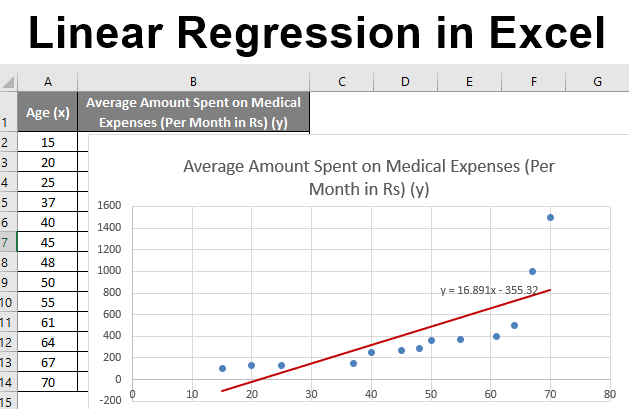
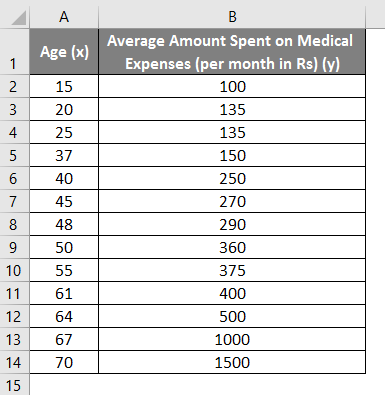
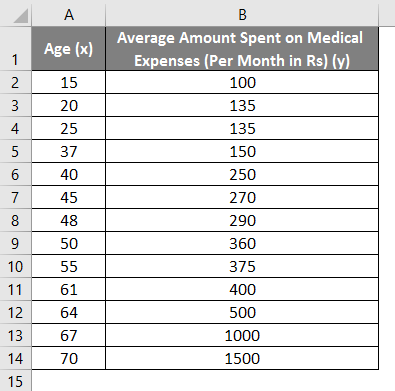
Let us say we have a dataset of some individuals with their age, bio-mass index (BMI), and the amount spent by them on medical expenses in a month. Now with an insight into the individuals’ characteristics like age and BMI, we wish to find how these variables affect the medical expenses, and hence use these to carry out regression and estimate/predict the average medical expenses for some specific individuals. Let us first see how only age affects medical expenses. Let us see the dataset:
Amount on medical expenses= b*age + a
- Select the two columns of the dataset (x and y), including headers.
- Click on ‘Insert’ and expand the dropdown for ‘Scatter Chart’ and select ‘Scatter’ thumbnail (first one)
- Now a scatter plot will appear, and we would draw the regression line on this. To do this, right-click on any data point and select ‘Add Trendline.’
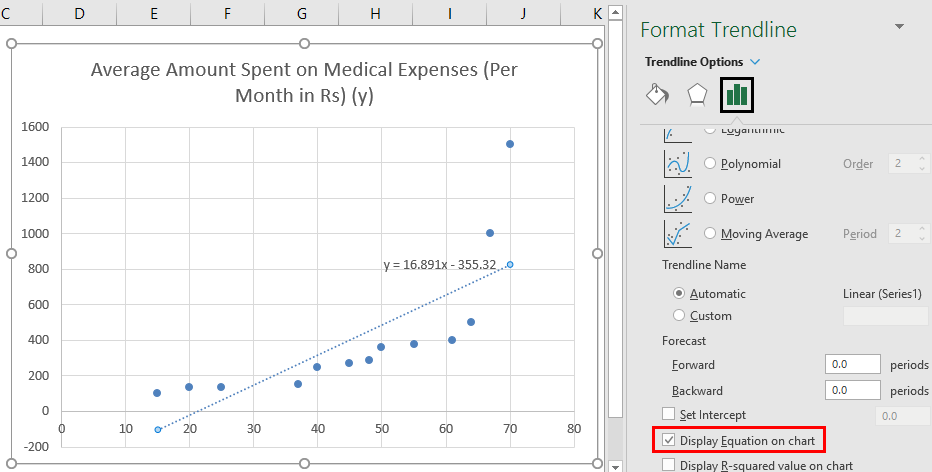
- Now in the ‘Format Trendline’ pane on the right, select ‘Linear Trendline’ and ‘Display Equation on Chart’.
- Select ‘Display Equation on Chart’.
We can improvise the chart as per our requirements, like adding axes titles, changing the scale, color and line type.
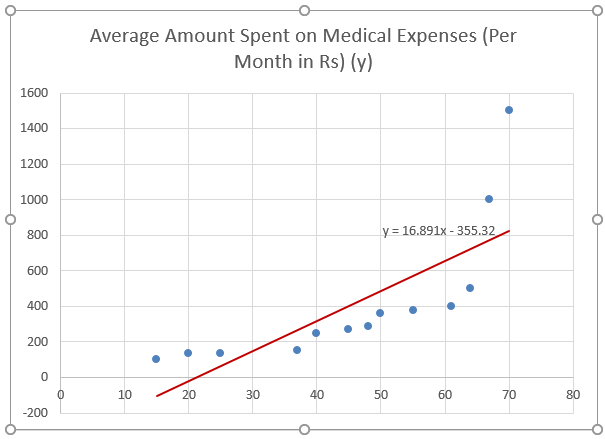
After Improvising the chart, this is the output we get.
Note: In this type of regression graph, the dependent variable should always be on the y-axis and independent on the x-axis. If the graph gets plotted in reverse order, then either switch the axes in a chart or swap the columns in the dataset.
Method #2 – Analysis ToolPak Add-In Method
Analysis ToolPak is sometimes not enabled by default, and we need to do it manually. To do so:
- Click on the ‘File’ menu.
After that, click on ‘Options’.
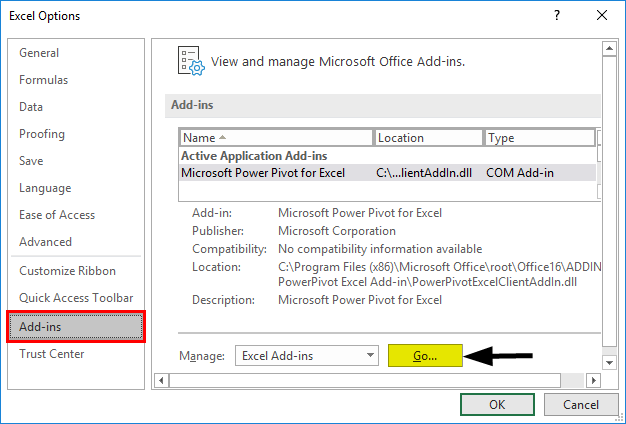
- Select ‘Excel Add-Ins’ in the ‘Manage’ box, and click on ‘Go.’
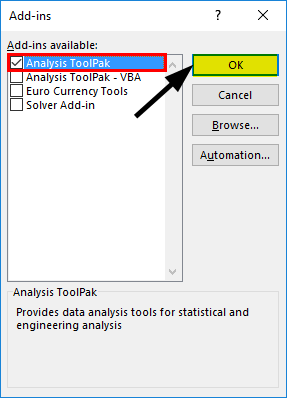
- Select ‘Analysis ToolPak’ -> ‘OK’
This will add ‘Data Analysis’ tools to the ‘Data’ tab. Now we run the regression analysis:
- Click on ‘Data Analysis’ in the ‘Data’ tab
- Select ‘Regression’ -> ‘OK’
- A regression dialog box will appear. Select the Input Y range and Input X range (medical expenses and age, respectively). In the case of multiple linear regression, we can select more columns of independent variables (like if we wish to see the impact of BMI as well on medical expenses).
- Check the ‘Labels’ box to include headers.
- Choose the desired ‘output’ option.
- Select the ‘residuals’ checkbox and click ‘OK.
Now our regression analysis output will be created in a new worksheet, stating the Regression Statistics, ANOVA, residuals and coefficients.
Output Interpretation:
- Regression Statistics tells how well the regression equation fits the data:
- Multiple R is the correlation coefficient that measures the strength of a linear relationship between two variables. It lies between -1 and 1, and its absolute value depicts the relationship strength with a large value indicating a stronger relationship, a low value indicating negative and zero value indicating no relationship.
- R Square is the Coefficient of Determination used as an indicator of goodness of fit. It lies between 0 and 1, with a value close to 1 indicating that the model is a good fit. In this case, 0.57=57% of y-values are explained by the x-values.
- Adjusted R Square is R Square adjusted for a number of predictors in the case of multiple linear regression.
- Standard Error depicts the precision of regression analysis.
- Observations depict the number of model observations.
- Anova tells the level of variability within the regression model.
This is generally not used for simple linear regression. However, the ‘Significance F values’ indicate how reliable our results are, with a value greater than 0.05 suggesting to choose another predictor.
- Coefficients are the most important part used to build regression equation.
So, our regression equation would be: y= 16.891 x – 355.32. This is the same as that done by method 1 (scatter chart with a trendline).
Now, if we wish to predict average medical expenses when age is 72:
So y= 16.891 * 72 -355.32 = 860.832
So this way, we can predict values of y for any other values of x.
- Residuals indicate the difference between actual and predicted values.
The last method for regression is not so commonly used and requires statistical functions like slope (), intercept (), correl (), etc., to carry out regression analysis.
Things to Remember About Linear Regression in Excel
- Regression analysis is generally used to see if there is a statistically significant relationship between two sets of variables.
- It is used to predict the value of the dependent variable based on the values of one or more independent variables.
- Whenever we wish to fit a linear regression model to a group of data, then the range of data should be carefully observed. If we use a regression equation to predict any value outside this range (extrapolation), it may lead to wrong results.
Recommended Articles
This is a guide to Linear Regression in Excel. Here we discuss how to do Linear Regression in Excel along with practical examples and a downloadable excel template. You can also go through our other suggested articles –
- Excel Regression Analysis
- Linear Programming in Excel
- Linear Interpolation in Excel
- Statistics in Excel
In this article, I will show you how to perform a simple linear regression test in Microsoft Excel.
Not only will I show you how to perform the linear regression, but I’ll show you how to analyse the outputs of the regression test.
My example data
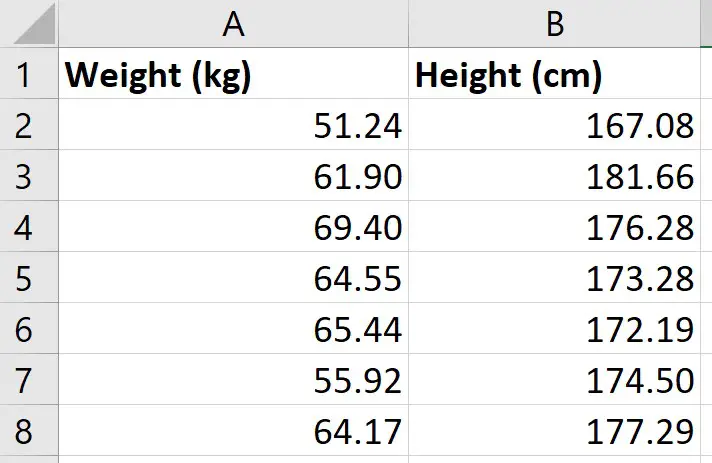
For this example, I just have two variables of data:
- Weight (kg)
- Height (cm)
I have these measures for 49 different participants; each row represents a different participant.
So, for the first participant, I can see that they had a weight of 51.24 kg and a height of 167.08 cm.
What I want to do is to perform a simple linear regression to see how well the measures of height in my sample can predict the measures of weight.
Installing the Analysis ToolPak
There are a few ways you can perform a linear regression in Excel, but perhaps the easiest method is to use the Analysis ToolPak. This is an add-on created by Microsoft to provide data analysis tools for statistical analyses.
Here are the intrustions for installing the Analysis Toolpak:
- Go to File>Options
- Then click on Add-ins
- At the bottom, you want to manage the Excel add-ins and click the Go button
- Then, ensure you tick the Analysis ToolPak add-in, and click OK
Now, when you click on the Data ribbon, you should see a Data Analysis button in a sub-section called Analyze

We are now ready to perform the linear regression in Excel.
Performing the linear regression in Excel
To perform the linear regression, click on the Data Analysis button.
Then, select Regression from the list.
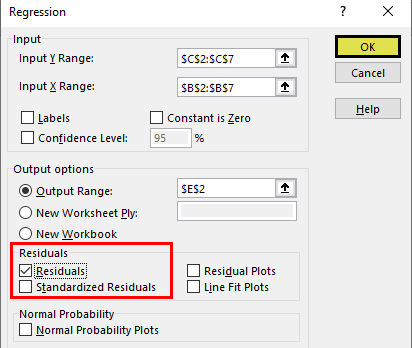
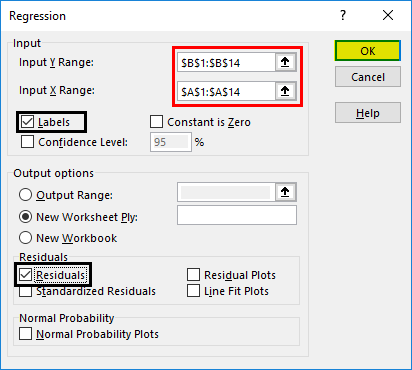
You must then enter the following:
- Input Y Range – this is the data for the Y variable, otherwise known as the dependent variable. The Y variable is the one that you want to predict in the regression model. For me, this will be the weight data
- Input X Range – this is the data for the X variable, otherwise known as the independent variable. For me, this will be the height data
If you have highlighted the labels of the columns when selecting the data, then tick the Labels options. If you didn’t have any labels when you selected your data, then you should not tick this option.
The next option called Constant is Zero is used if you want the regression line to start at 0, otherwise known as the origin. Doing so would mean there is no Y intercept in the model. Generally, for linear regression, this option is not selected, so I will leave it unchecked for this example.
It is also possible to specify the confidence level for the test. By default, the results will return the 95% confidence intervals without having to change any options. However, if you want to use a different confidence level than 95%, then you need to select this option and enter the desired value here.
Output options
For the Output Options, you can specify where you want the regression results to be placed.
- Output Range – you can highlight where you want the results to be placed in that worksheet
- New Worksheet Ply – lets you place the results in a new worksheet
- New Workbook – lets you save the results in an entirely separate workbook
For my example, I’m going to select the second option and have the results placed in a new worksheet.
Residuals
The final set of options concerns the residuals in the analysis.
- Residuals – will return the list of predicted dependent values, based on the regression line, as well as the residual values for each point
- Standardized Residuals – will return the standardized residuals; these values can be useful when identifying potential outliers
- Residual Plots – will create a scatter graph where the residuals are plotted on the Y axis and the X variable is plotted on the X axis
- Line Fit Plots – will create another scatter graph where the Y and X variables are plotted, but it will also add the predicted Y values onto the graph
Finally, the Normal Probability Plots option plots another scatter plot, which is used to determine whether the Y variable data fits a normal distribution.
Interpretation of the linear regression results
Depending on the options selected in the set-up window, you will have quite a lot of information in the results sheet.
I’ll now break down the output and go through each in more detail.
- Summary Output table
- ANOVA table
- Coefficients table
- Residual Output table
- Residual plot
- Standardized Residuals
- Line Fits plot
- Normal Probability plot
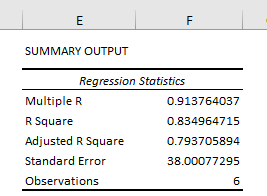
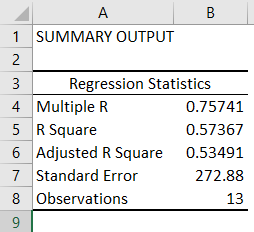
Summary Output table
In the first table called Summary Output, there are some regression statistics from the test.
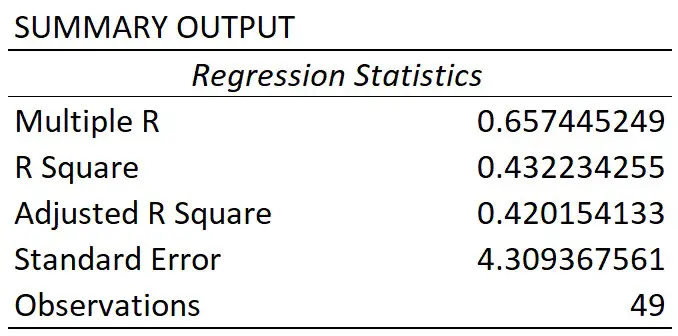
Multiple R
This is the absolute value of the correlation coefficient between the two variables of interest. Briefly, it is a value that tells you how strong the linear relationship is.
A value of 0.65 in this case indicates a fairly strong linear correlation between height and weight measures.
If you’re interested to learn more about correlation, then I suggest you refer to the What is Pearson Correlation post.
R square
You may sometimes see the R square being referred to as the coefficient of determination.
To get this value, you simple square the multiple R value.
The R square value tells you how much variance the dependent variable can be accounted for by the values of the independent variable. Researchers often multiple this value by 100 to get a percentage value.
So, for my example, I can say that 43% of the variance in weight can be accounted for by the height measures. The other 57% of the variance is therefore caused by other factors, such as measurements errors.
Adjusted R square
The adjusted R square takes into account the number of independent variables in the regression analysis, and corrects for bias.
Usually, this value is only relevant when you are performing multiple linear regression, where there are more than 1 independent variables in the model.
Standard error
The standard error of the regression is the average distance that the observed values fall from the regression line.
What’s useful about the standard error is that it is in the same units as the dependent variable. So, here my standard error is 4.31 kg, when rounded. This means, on average, my observed values were 4.31 kg from the regression line.
The smaller the standard error, the more precise the linear regression model is.
Observations
Finally, we have the number of observations. This is just the number of subjects in the test.
So, for my example, I had 49 participants.
ANOVA table
The main thing you will be concerned with when looking at this table is the value under the Significance F header; this is in fact the P value for the regression model.
To be able to interpret this, we need our hypotheses:
- Null hypothesis – there is no linear relationship between the height and weight measures
- Alternative hypothesis – there is a linear relationship between the height and weight measures
If my alpha was 0.05, this means I will reject the null and accept the alternative hypothesis if P≤0.05. The opposite will be true if P>0.05; in this case, I would fail to reject the null hypothesis.
As you can see, the P value (Significance F) for the model was considerably lower than my alpha value of 0.05. So, I can conclude that the linear regression model is significant.
Coefficients table
Let me now move on to the final table of results regarding the coefficients.

The first row displays the results for the intercept, this is the point where the line of best fit (regression line) crosses the Y axis when the value of X is zero.
The second row displays the results for the slope.
For a simple linear regression model, the most basic version of the equation is Y = m.X + b.

Using the information reported from the results, we can then say:
Y = 0.800264.X – 79.599
So, in this example, if we knew a participants height (in cm), we can predict their weight (in kg) by using this equation. For example, if a participant measured 175 cm, the model estimates their height to be 60.45 kg.
Looking back at the coefficient results table, we can see there are other columns which tells us the standard error, as well as the lower and upper 95% confidence intervals, or a different confidence interval if a different confidence level was entered. And these values are for the intercept and slope values.
You will also notice each also has a T-statistic. This value is used to compute the P value.
Again, to interpret this P value we need our hypotheses:
- Null hypothesis – the intercept or slope is 0
- Alternative hypothesis – the slope of the line is not 0
As you can see, both values are less than my alpha of 0.05. However, we usually ignore the P value for the intercept.
For the slope, this means that height is a significant variable that impacts weight in this case.
Residual options
So, that’s an overview of the regression model results, let me know cover the other outputs from the regression test.
Residual Output
If you selected to have the Residuals option during the regression set-up, you will have a table titled Residual Output.

For each observation from your data that was entered into the regression test, you will get a predicted value of Y based on the regression model.
For example, if you look at the first observation in my original data, you see this participant had a height of 167.08 cm. If I put this into the regression equation, along with the slope and intercept values, I get the predicted weight value of 54.10999 kg.
This is what the Predicted column represents; Excel does this for each of the observations.
Using the predicted values, Excel can then calculate the residuals.
A residual is simply the distance between the actual data point and the line of best fit.
For my first participant they had a height of 167.08 cm and a weight of 51.24 kg. As calculated above, the predicted weight value based on the model was 54.10999 kg. The residual for this point therefore is the difference between the actual weight value (51.24 kg), and the predicted weight value (54.10999 kg), which comes out at around -2.867 kg.
Excel then repeats this process for the rest of the observations.
Residual Plot
If you also selected the Residual Plots option in the Regression set-up window, you will also get a graph returned.
Here is my Residual Plot.
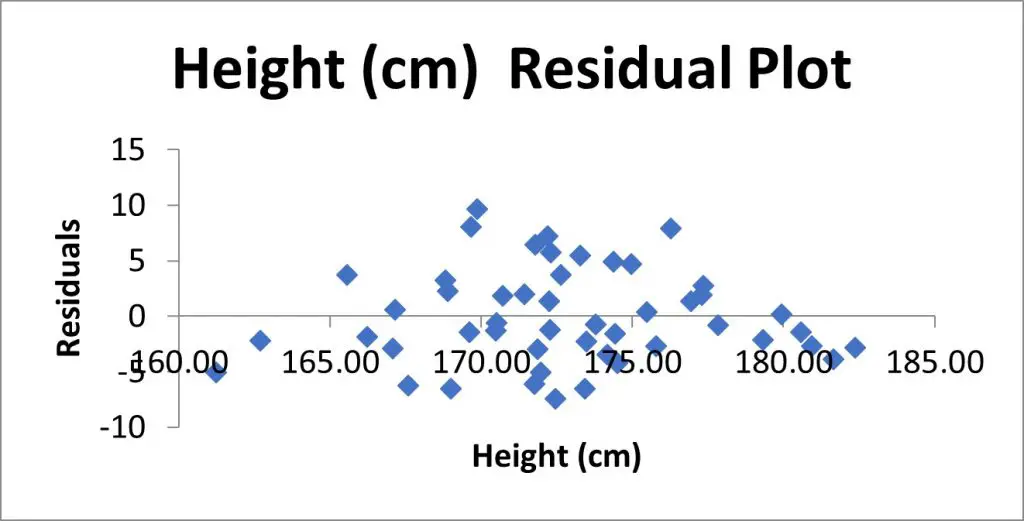
This is a scatter plot of the residuals on the Y axis and the values of the independent variable on the X axis.
Residual plots are useful to look at when investigating homogeneity of variance, which is an assumption of the linear regression test.
What you are looking for here is a random pattern to the graph; there should be roughly half the number of data points above 0 and below 0, and there vertical spread of the data points should be roughly constant the further along the X axis you go.
Standardized Residuals
If you selected the Standardized Residuals option in the regression options, you will also see a column called Standard Residuals in the residuals table.
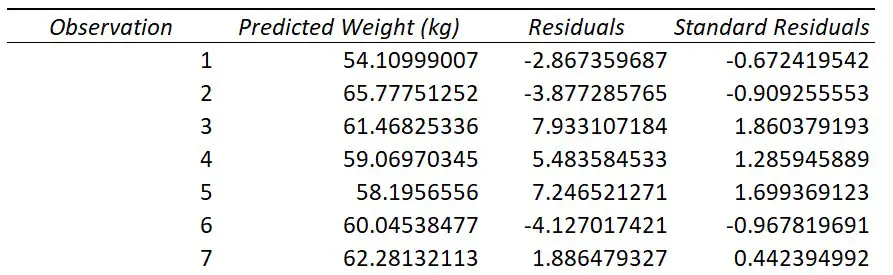
The standardized residual is the residual divided by an estimate of its standard deviation. You can think of them as Z scores.
These values are useful to look at when trying to identify potential outliers in your sample.
Generally, any standardized residuals with a value greater than 3 or -3 is a sign that it may be an outlier.
Line Fits Plot
If you selected to have the Line Fit Plots option, you will also see a scatter plot containing the data that was entered into the regression test.
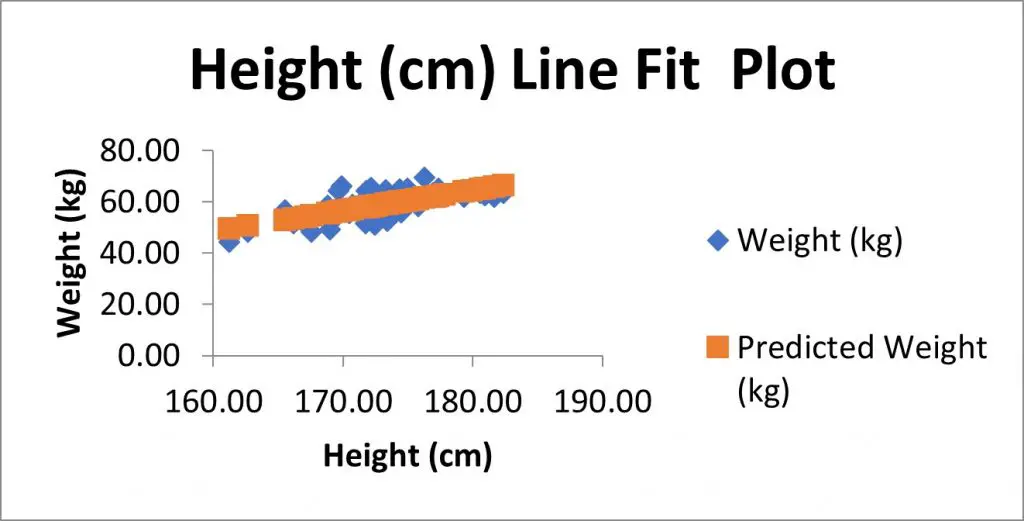
In my example, I have the height measures on the X axis and the weight measures on the Y axis.
There is also another set of data, as shown in orange here, which are in fact the predicted Y value based on the model. These are the Predicted values from the residuals table.
If instead of showing the Predicted values on the graph, but you instead wanted to plot the line of best fit (which will pass through the predicted values), then you could remove the predicted values from the graph.
To do this:
- Right-click on on the graph, and go to Select Data
- Highlight the predicted Y variable in the legend entry, select remove, and click Okay
- Select the graph, then go to Add Chart Element>Trendline, and select the Linear option
- If you also want to show the equation of the line, then double-click on the line
- Then, in the Format Trendline options that have opened to the right, scroll down and select Display Equation on Chart
Normal Probability plot
Finally, if you selected the Normal Probability plots option in the regression setup window, you will also see a table called Probability Output and a graph, called the Normal Probability Plot, which is a scatter plot of this data in the graph.
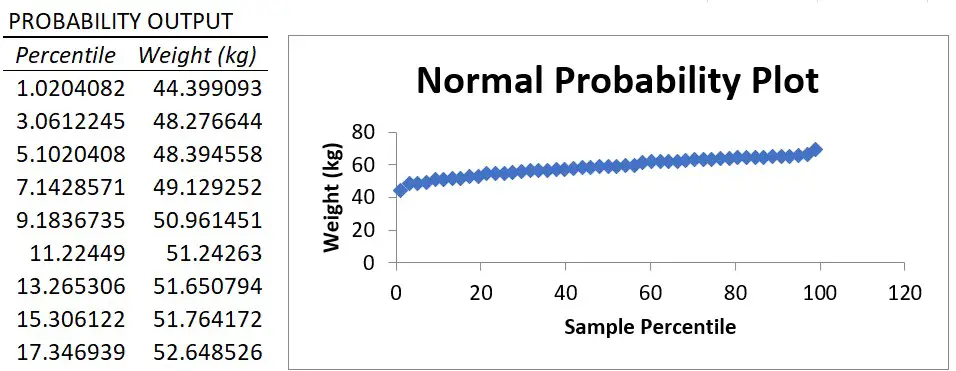
The X axis plots the percentile value ranging from 0 to 100 and the Y axis plots the Y variable data.
The normal probability plot is used to determine whether the data fits a normal distribution.
Essentially, what you are looking for is a straight line of data. And, as you can see, there is a nice straight line of data for my example, which suggests the weight data are normally distributed.
However, it’s worth noting that the Y variable does not actually have to be normally distributed when fitting a linear regression model. I’ll go into a bit more detail about the assumptions of linear regression in a future tutorial.
Wrapping up
You now know how to perform a simple linear regression test in Microsoft Excel, and how to interpret the output of results.
Microsoft Excel version used: 365 ProPlus
In this tutorial, you’ll learn how to perform Linear Regression in Excel. Linear regression is an approach to linear modeling the relationship between a dependent and an independent variable. Simple linear regression uses an independent variable to predict the outcome of the dependent variable.
The equation for linear regression is given by: y = a + bx, where x is the independent variable, y is the dependent variable and the coefficients are given by:
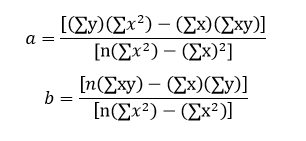
Our aim is to find coefficients a which is the intercept and b which is the slope to obtain the equation of the straight line which best fits our data by the least square method. There are two ways in Excel in which we can find the linear regression line which is discussed below for the following data set:
Calculate Linear Regression in Excel Using Its Formula
First, we need to calculate the parameters in the formula for coefficients a and b. The parameters are Σx, Σy, Σxy and Σx2 . To calculate Σx follow these steps:
- Select the cell where you want to calculate and display the summation of x.
- Type =SUM(, select the cells containing the numbers and complete the formula with ).
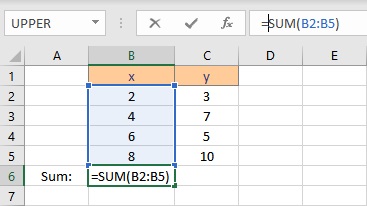
- Press the Enter key to display the result.
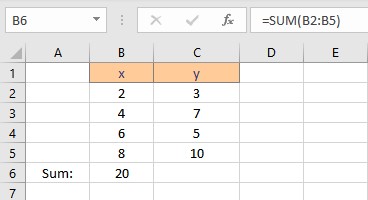
To calculate Σy follow these steps:
- Select the cell where you want to calculate and display the summation of y.
- Type =SUM(, select the cells containing the numbers and complete the formula with ).
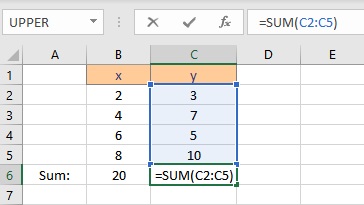
- Press the Enter key to display the result.
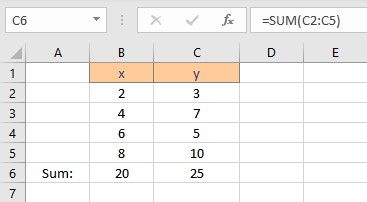
To calculate Σxy follow these steps:
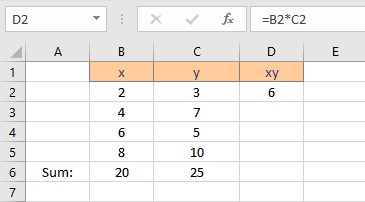
- Select the cell where you want to calculate and display the product of a pair of x and y values.
- Type =B2*C2, as the first x and y values are in cells B2 and C2 respectively.
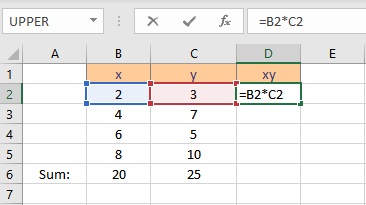
- Press the Enter key to display the result.
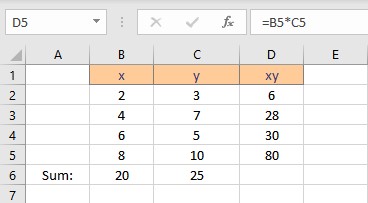
- Copy the formula for the calculation of product xy for the entire list by dragging down the fill handle.
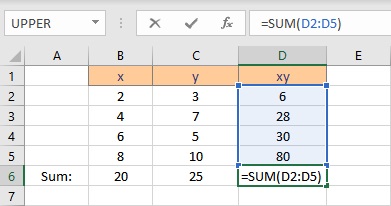
- Select the cell where you want to calculate and display the summation of xy.
- Type =SUM(, select the cells containing the numbers and complete the formula with ).
- Press the Enter key to display the result.
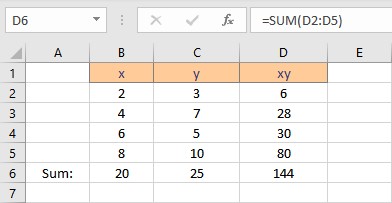
To calculate Σx2 follow these steps:
- Select the cell where you want to calculate and display the square of the first x value.
- Type =B2^2, as the first x value, is in cell B2. The caret operator raises the number to the power written next to it.
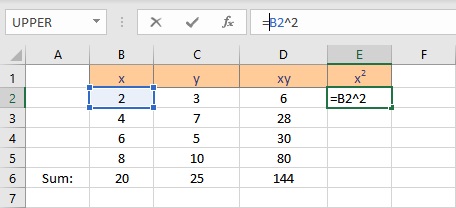
- Press the Enter key to display the result.
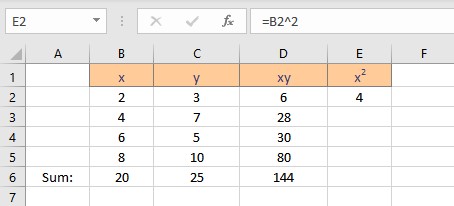
- Copy the formula for the calculation of squares of x for the entire list by dragging down the fill handle.
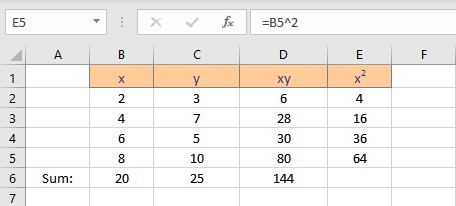
- Select the cell where you want to calculate and display the summation of x2.
- Type =SUM(, select the cells containing the numbers and complete the formula with ).
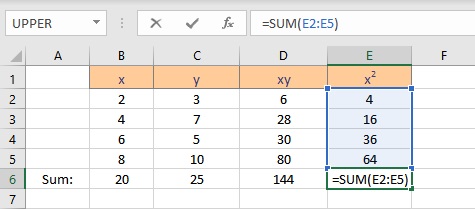
- Press the Enter key to display the result.
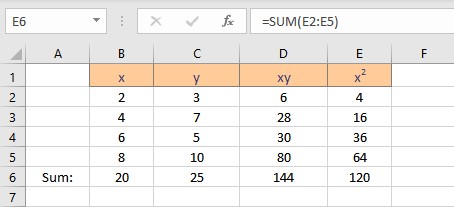
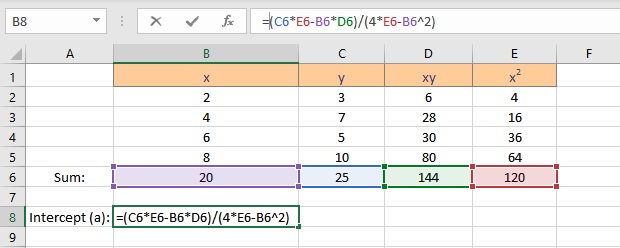
We now have the parameters essential for the calculation of coefficients intercept a and slope b. Follow the steps to calculate the intercept a:
- Select the cell where you want to display the value of the intercept.
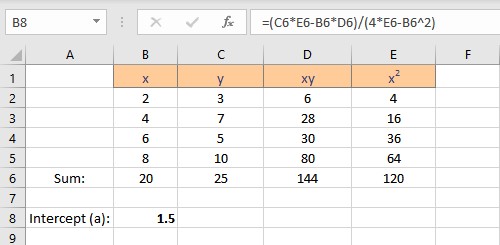
- Type =(C6*E6-B6*D6)/(4*E6-B6^2), where C6 contains the value of Σy, E6 contains the value of Σx2, B6 contains the value of Σx, D6 contains the value of Σxy and 4 is the number of data points in the data set.
- Press the Enter key to display the result.
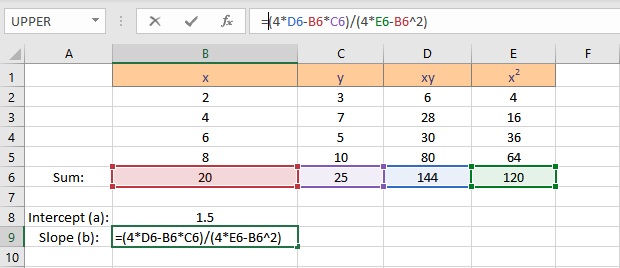
Follow the steps to calculate the slope b:
- Select the cell where you want to display the value of the slope.
- Type =(4*D6-B6*C6)/(4*E6-B6^2), where C6 contains the value of Σy, E6 contains the value of Σx2, B6 contains the value of Σx, D6 contains the value of Σxy and 4 is the number of data points in the data set.
- Press the Enter key to display the result.
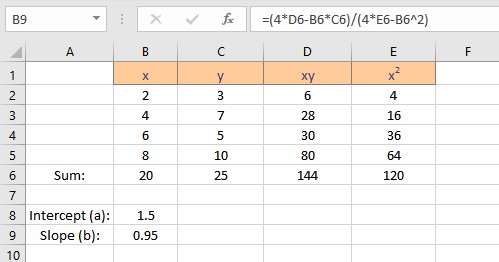
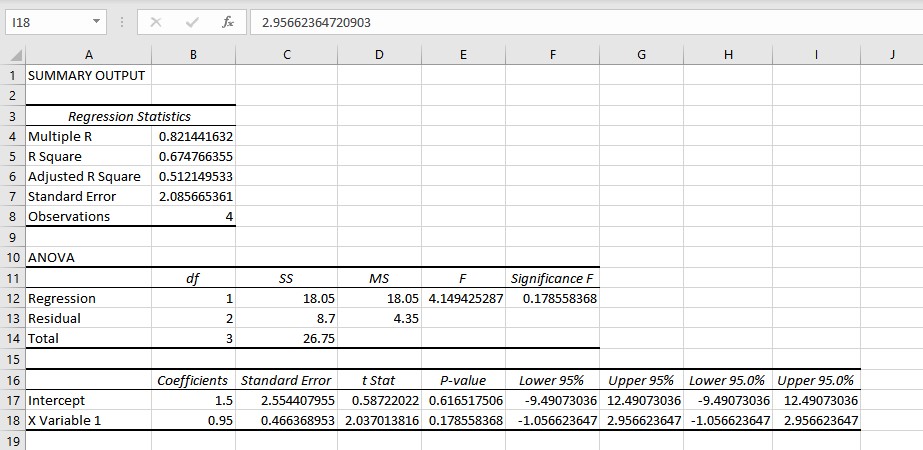
We have the values for the slope and intercept, the equation for the linear regression can be written as y = 1.5 + 0.95x. This equation can now be used to predict values of y for different values of x.
Linear Regression in Excel Using Data Analysis
To use the Data Analysis feature, you need to enable Analysis Toolpak in Excel. Follow these steps to manually enable the feature:
- Click on the File option present at the top left corner of the Excel window.
- From the menu that appears, click on Options to launch the Excel Options dialog box.
- Select the Add-ins option at the left side of the Excel Options dialog box.
- Select Excel Add-ins in the Manage box, and click Go.
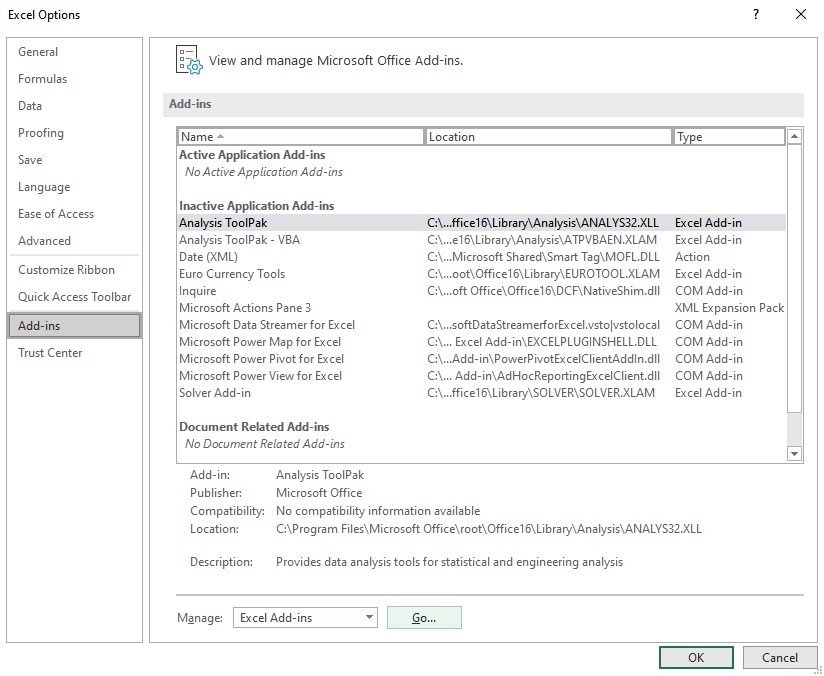
- In the Add-ins dialog box, check the Analysis Toolpak checkbox, and then click OK.
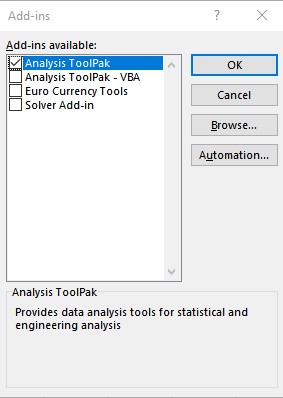
- The Data Analysis option now appears in the Analysis group on the Data tab.

Follow these steps to perform linear regression using Data Analysis:
- Click on Data Analysis present in the Analysis group on the Data tab.
- From the Data Analysis dialog box that appears, select Regression under the Analysis Tools and click on OK.
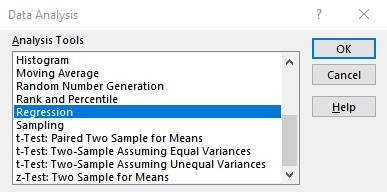
- Enter the cell ranges containing y values in the Input Y Range: text box and x values in the Input X Range: text box in the Regression dialog box and click OK.
- The results are displayed in a new worksheet. You can copy the intercept and slope coefficients to obtain an equation for the linear regression: y = 1.5 + 0.95x.
Conclusion
In this tutorial, we learned how to perform linear regression both using the formulas and Excel Add-ins.
References
- Load the Analysis ToolPak in Excel – Office Support (microsoft.com)