Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
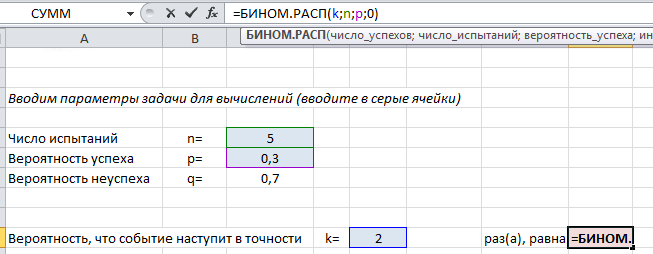
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>right)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>right)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)=\ = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>=\=left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1right)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Плоские алгебраические кривые в EXCEL
history 16 апреля 2015 г.
-
Группы статей
- Диаграммы и графики
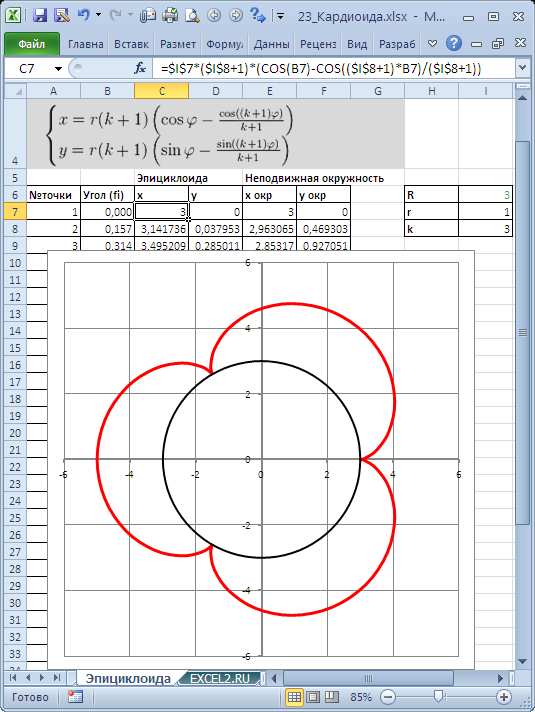
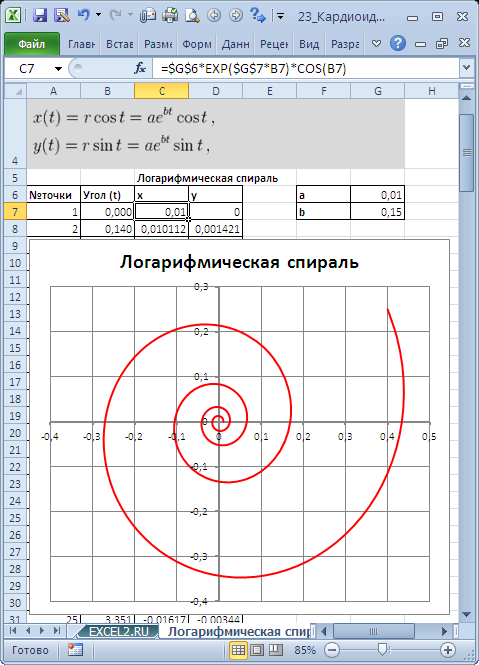
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
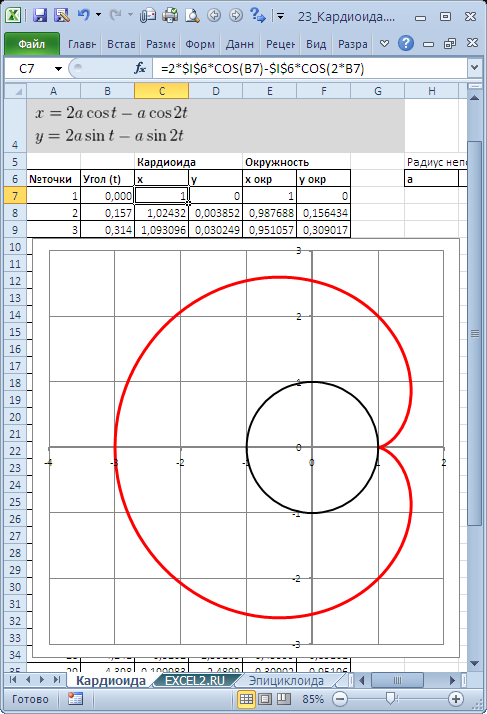
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Практическая работа «Красивые графики функций»
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )
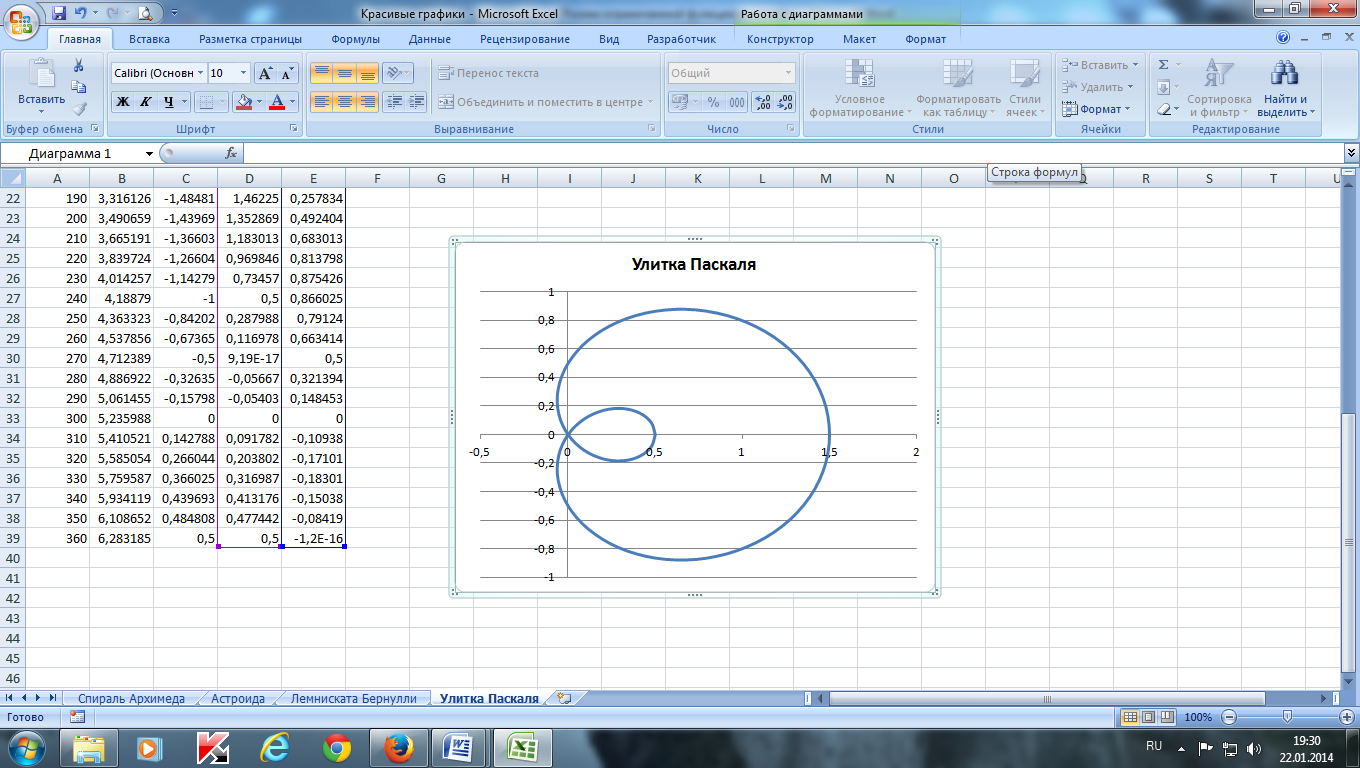
П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
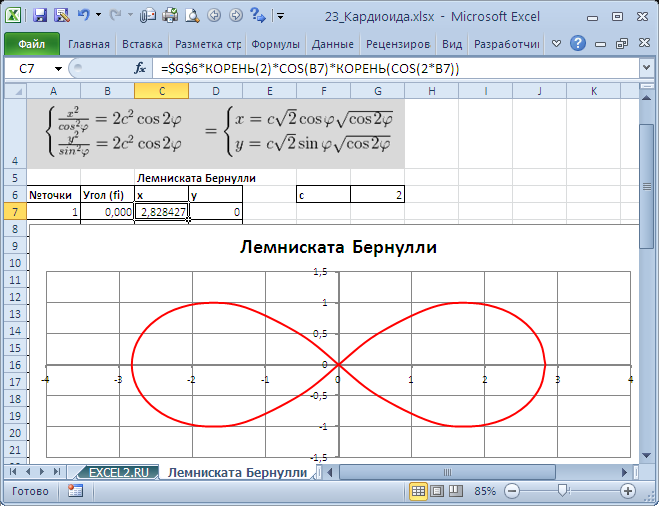
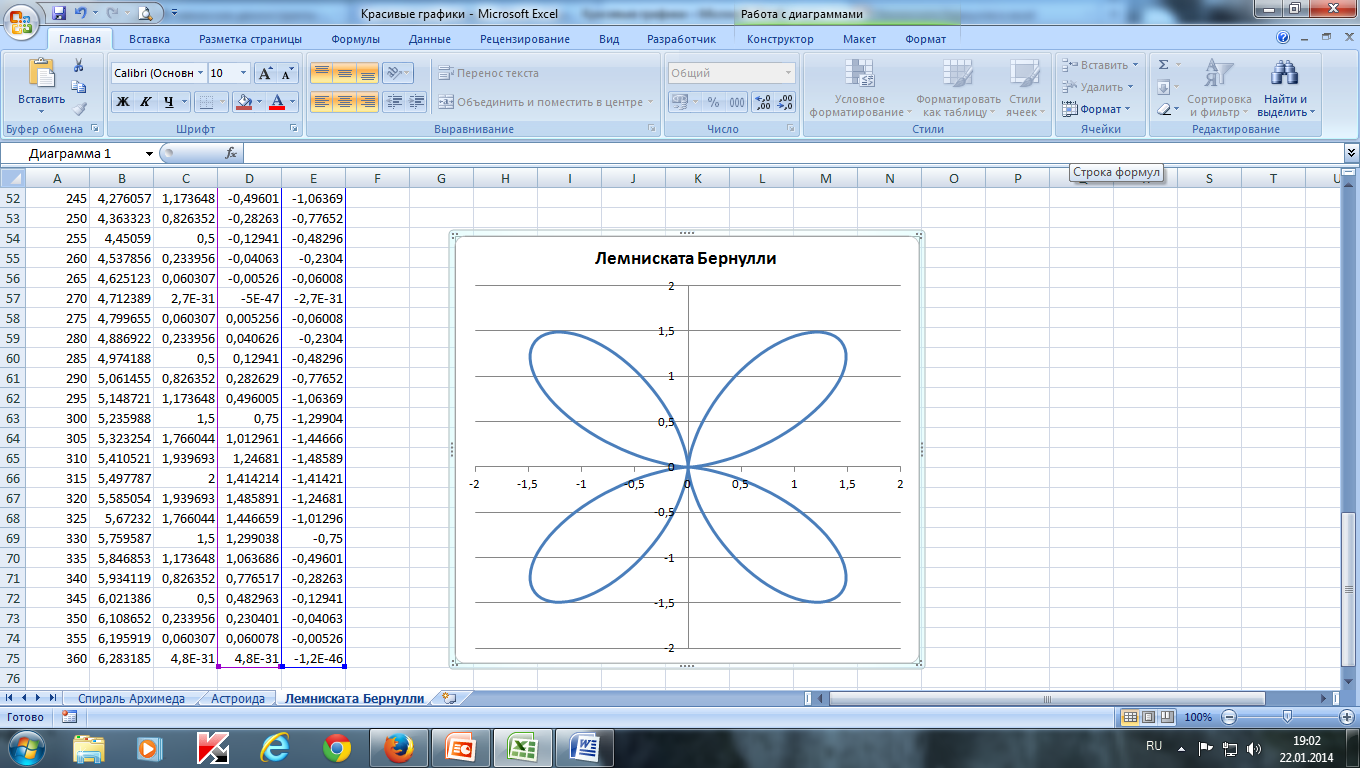
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
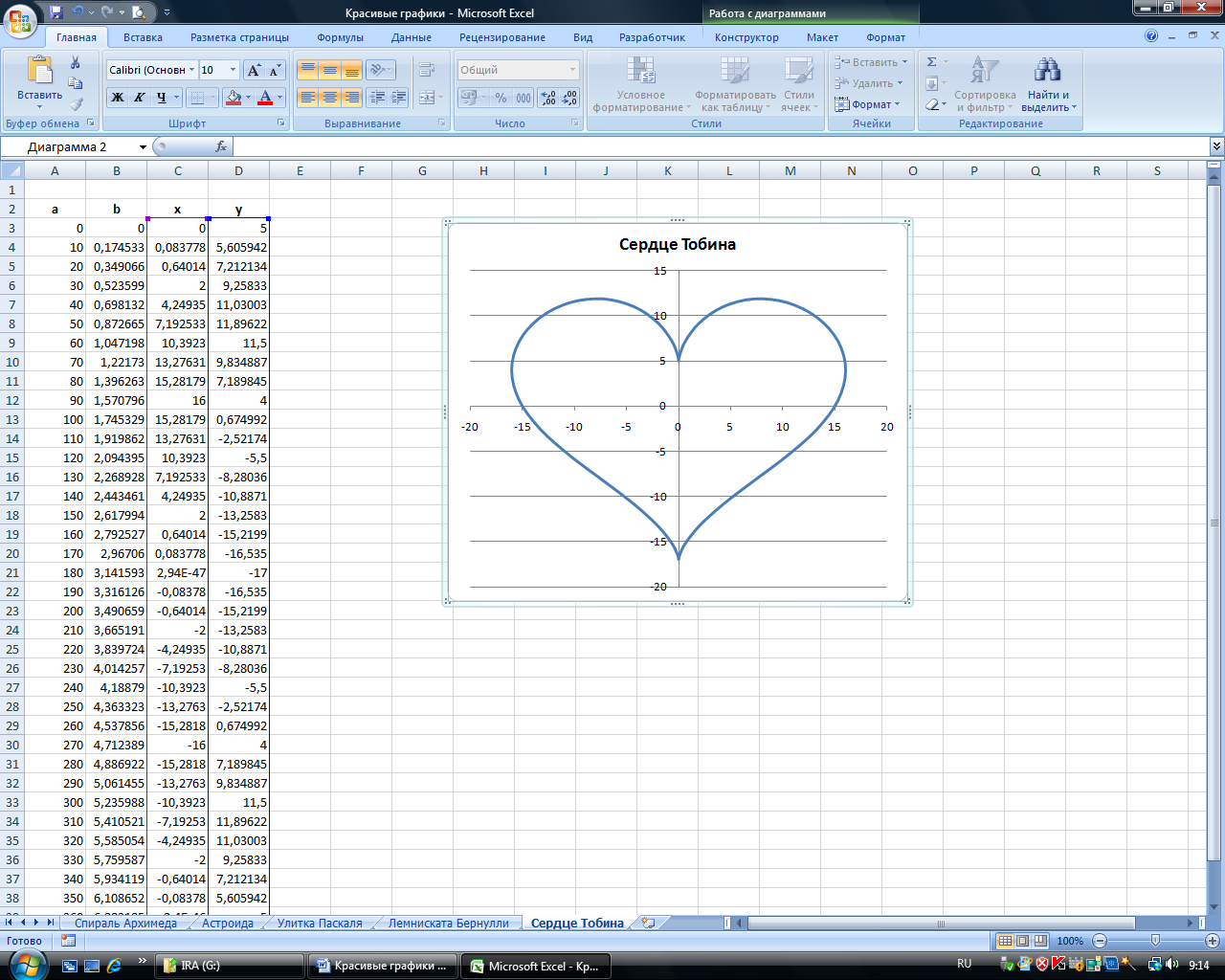
П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
источники:
http://excel2.ru/articles/ploskie-algebraicheskie-krivye-v-ms-excel
http://pedsovet.su/excel/48255_krasivye_grafiki_v_excel
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см.
файл примера
):
х=2*а*cos(t)-а*cos(2*t)
y=2*а*sin(t)-а*sin(2*t)
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье
Эллипс и окружность в MS EXCEL
построены окружность и эллипс.
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.
Плоские алгебраические кривые в EXCEL
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
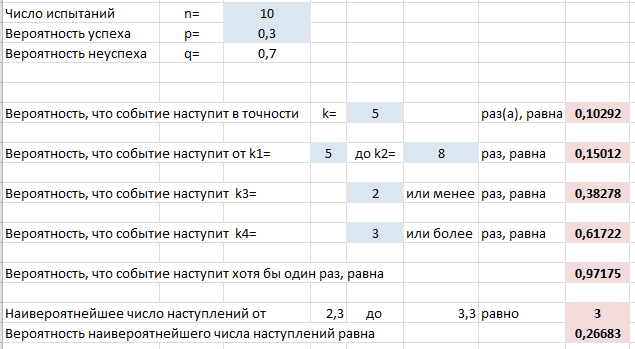
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_^6 cdot 0,75^6 cdot 0,25^1+C_^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:
Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_(k)=C_^k cdot 0,5^kcdot 0,5^=C_^k cdot 0,5^$$ Приступим к вычислениям:
$$1. P_(2)=C_^2 cdot 0,5^ = fraccdot 0,5^ approx 0,044.$$ $$2. P_(4)+P_(5)=C_^4 cdot 0,5^ + C_^5 cdot 0,5^=left( frac + frac right)cdot 0,5^ approx 0,451.$$ $$3. P_(0)+P_(1)+P_(2)=C_^0 cdot 0,5^ + C_^1 cdot 0,5^+ C_^2 cdot 0,5^=left( 1+10+ frac right)cdot 0,5^ approx 0,055.$$ $$4. P_(7)+P_(8)+P_(9)+P_(10)=\ = C_^7 cdot 0,5^ + C_^8 cdot 0,5^+ C_^9 cdot 0,5^+ C_^10 cdot 0,5^ =\=left(frac+ frac + 10 +1right)cdot 0,5^ approx 0,172.$$ $$5. P_(ge 1)=1-P_(0)=1-C_^0 cdot 0,5^ = 1- 0,5^ approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:
Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.
Изучение распределения Бернулли средствами Excel
Цель данной работы – изучить задачу теории вероятностей о повторении однородных независимых испытаний. Для небольшого числа испытаний n < 30 эта задача была разрешена Бернулли, при большем числе испытаний используются предельные формулы Пуассона и Лапласа. При использовании компьютера область применения исходной формулы Бернулли может быть расширена до n = 200, поэтому представляется возможность оценить точность предельных формул Пуассона – Лапласа. На практическом занятия осваиваются также приемы работы с электронной таблицей Excel – как организовать вычисления по формулам Бернулли, Пуассона, Лапласа; как строятся графики зависимостей и как эти графики форматируются к стандартному виду; как работать с большими таблицами и по заданному аргументу находить в таблице значение функции; и многое другое.
Изучение распределения Бернулли средствами Excel
Распределение Бернулли зависит от двух параметров n и p (q = 1 – p). На рабочем листе Exсel предлагается построить графики распределения при различных значениях параметра p (0 < p < 1) и при различных значениях другого параметра n (n = 10, 20, 30, 50). Эти графики позволят заметить характерные особенности распределения Бернулли. Кроме этого, полезно убедиться, что характеристики распределения правильно воспроизводятся известными формулами: M(m) = np, D(m) = npq. Далее полезно также убедиться в справедливости правила «3-х сигм»: M(m) – 3×sm< m < M(m) + 3×sm , где ; значения m, выходящие за пределы указанного интервала, маловероятны (их вероятность меньше 0,01).
Ниже приведен фрагмент рабочего листа таблицы Excel.
| A | B | C | D | E | F | G | H | I | J |
| Распределение Бернулли | |||||||||
| Pn(m)=n!/m!/(n-m)!*p^m*q^(n-m) | |||||||||
| Pn(m)=Pn(m-1)*(n-m+1)/m*p/q | Pn(0)=q^n | ||||||||
| n = | n = | n = | n = | n = | |||||
| p = | 0,1 | p = | 0,3 | p = | 0,5 | p = | 0,7 | p = | 0,9 |
| q = | 0,9 | q = | 0,7 | q = | 0,5 | q = | 0,3 | q = | 0,1 |
| M = | M = | M = | M = | M = | |||||
| D = | 0,9 | D = | 2,1 | D = | 2,5 | D = | 2,1 | D = | 0,9 |
| M-3Sm= | -1,84605 | M-3Sm= | -1,34741 | M-3Sm= | 0,256584 | M-3Sm= | 2,652587 | M-3Sm= | 6,15395 |
| M+3Sm= | 3,84605 | M+3Sm= | 7,347413 | M+3Sm= | 9,743416 | M+3Sm= | 11,34741 | M+3Sm= | 11,84605 |
| m | р=0,1 | m | р=0,3 | m | р=0,5 | m | р=0,7 | m | р=0,9 |
| 0,34868 | 0,02825 | 0,00098 | 5,9E-06 | 1E-10 | |||||
| 0,38742 | 0,12106 | 0,00977 | 0,00014 | 9E-09 | |||||
| 0,19371 | 0,23347 | 0,04395 | 0,00145 | 3,64E-07 | |||||
| 0,05740 | 0,26683 | 0,11719 | 0,00900 | 8,75E-06 | |||||
| 0,01116 | 0,20012 | 0,20508 | 0,03676 | 0,00014 | |||||
| 0,00149 | 0,10292 | 0,24609 | 0,10292 | 0,00149 | |||||
| 0,00014 | 0,03676 | 0,20508 | 0,20012 | 0,01116 | |||||
| 8,75E-06 | 0,00900 | 0,11719 | 0,26683 | 0,05740 | |||||
| 3,65E-07 | 0,00145 | 0,04395 | 0,23347 | 0,19371 | |||||
| 9E-09 | 0,00014 | 0,00977 | 0,12106 | 0,38742 | |||||
| 1E-10 | 5,9E-06 | 0,00098 | 0,02825 | 0,34868 |
Рассмотрим внимательно первый блок (столбцы A, B таблицы Excel).
В строках 5 и 6 задаем значения параметров n = 10, p = 0,1. В следующих строках вычисляем q = 1 – p, M = S m Pn(m), D = S m 2 Pn(m) – M^2, M-3Sm = M – 3*КОРЕНЬ(D), M+3Sm = M + 3*КОРЕНЬ(D). Последние 4 формулы можно набрать позже, когда будет заполнен диапазон B14:B24, содержащий значения Pn(m). Отметим полезный прием: в столбце А записываем текст и сдвигаем его вправо, а в столбце В – вычисляем числовое значение и сдвигаем его влево. Получается понятный комментарий к выполненным действиям. Лист Excel, помимо всего прочего, является отчетным документом, поэтому не стоит экономить на комментариях и заголовках. Из информации в строках 8 – 11 первого блока, видно, что, действительно, M = np = 10´0,1 = 1; D = npq = 10´0,1´0,9 = 0,9; и что все вероятные значения m не превзойдут 4.
Значения Pn(m) удобно вычислять по реккурентной формуле (эта формула приведена в строке 3 рабочего листа). Начальное значение Pn(0) = q n вычисляем в ячейке В14. При наборе реккурентной формулы в ячейке В15 следует зафиксировать (знаками $) неизменяемые значения n, p, q. Далее формула копируется ниже до ячейки В24.
Заполнив первый блок, копируем его несколько раз вправо и в новых блоках заменяем значение параметра p на p = 0,3; p = 0,5; p = 0,7; p = 0,9. Все автоматически пересчитывается. В блоках серым фоном выделены значения Pn(m), которые признаны значимыми по правилу «3-х сигм».
Теперь строим графики. Выделяем значения m вместе с заголовком в ячейке А13, далее при нажатой клавише Ctrl выделяем мышкой значения Pn(m) для p = 0,1; 0,3; 0,5; 0,7; 0,9. Выделять диапазоны надо вместе с заголовками в строке 13, тогда эти заголовки автоматически будут отображены в легенде (пояснениях к каждой линии на графике). Вызываем Мастер диаграмм, выбираем тип диаграммы – точечная, легенда – внизу, линии сетки – основные, заголовок: “Распределение Бернулли при разных p (n=10)”. В результате получаем следующий график, который почти не требует дополнительного форматирования:
Из этого графика видно, как меняется асимметрия распределения при увеличении параметра p: при p = 0,5 распределение симметричное, при p < 0,5 – распределение скошено влево (положительная асимметрия), а при p > 0,5 – скошено вправо (отрицательная асимметрия).
Как уже указывалось выше, заголовки из строки 13 автоматически переносятся в легенду диаграммы. Но тогда хотелось бы, чтобы они автоматически корректировались при изменении параметра p. Поэтому в качестве заголовка в ячейке В13 набрана формула =»р=»&ТЕКСТ(B9;»0,0″). Функция ТЕКСТ(Число;Формат) переводит в символьную форму значение p из ячейки В9; в тексте заголовка это число будет округлено до одного знака после запятой. Остальные заголовки в строке 13 корректируются автоматически при копировании.
Теперь переходим к изучению зависимости распределения Бернулли от второго параметра n. Скопируем все 5 готовых блоков вправо, начиная со столбца K, и заменим в новых блоках значения параметров: n = 10, 20, 30, 40, 50 и p = 0,1 (для всех новых блоков). Естественно, новые таблицы надо продлить вниз до строки 64 (они теперь будут иметь разную длину). Ненужную информацию можно скрыть с помощью условного форматирования. Так, таблица для n = 10 фактически обрывается на строке 24, поэтому можно сделать так, чтобы дальнейшие значения m и нулевые значения Pn(m) выводились серым цветом на белом фоне (тогда они почти не будут видны). Условный формат для колонки m задаем по условию:
Обратите внимание, что в ссылке на ячейку L8 зафиксирован только номер строки. Для колонки Pn(m) с заголовком n=10 условие будет более простое: значение равно 0 . При копировании отформатированного блока, копируются также все условные форматы.
Наконец, надо заменить заголовки в строке 13 на формулы =»n=»&ТЕКСТ(L8;»0″).
| K | L | M | N | O | P | Q | R | S | T |
| n = | n = | n = | n = | n = | |||||
| p = | 0,1 | p = | 0,1 | p = | 0,1 | p = | 0,1 | p = | 0,1 |
| q = | 0,9 | q = | 0,9 | q = | 0,9 | q = | 0,9 | q = | 0,9 |
| M = | M = | M = | M = | M = | |||||
| D = | 0,9 | D = | 1,8 | D = | 2,7 | D = | 3,6 | D = | 4,5 |
| M-3Sm= | -1,84605 | M-3Sm= | -2,02492 | M-3Sm= | -1,9295 | M-3Sm= | -1,6921 | M-3Sm= | -1,36396 |
| M+3Sm= | 3,84605 | M+3Sm= | 6,024922 | M+3Sm= | 7,929503 | M+3Sm= | 9,6921 | M+3Sm= | 11,36396 |
| m | n=10 | m | n=20 | m | n=30 | m | n=40 | m | n=50 |
| 0,348678 | 0,121577 | 0,042391 | 0,014781 | 0,005154 | |||||
| 0,387420 | 0,270170 | 0,141304 | 0,065693 | 0,028632 | |||||
| 0,193710 | 0,285180 | 0,227656 | 0,142334 | 0,077943 | |||||
| 0,057396 | 0,190120 | 0,236088 | 0,200323 | 0,138565 | |||||
| 0,01116 | 0,089779 | 0,177066 | 0,205887 | 0,180905 | |||||
| 0,001488 | 0,031921 | 0,102305 | 0,164710 | 0,184925 | |||||
| 0,000138 | 0,008867 | 0,047363 | 0,106756 | 0,154104 | |||||
| 8,75E-06 | 0,00197 | 0,018043 | 0,057614 | 0,107628 | |||||
| 3,65E-07 | 0,000356 | 0,005764 | 0,026407 | 0,064278 | |||||
| 9E-09 | 5,27E-05 | 0,001565 | 0,010432 | 0,033329 | |||||
| 1E-10 | 6,44E-06 | 0,000365 | 0,003593 | 0,015183 | |||||
| 6,51E-07 | 7,38E-05 | 0,001089 | 0,006135 | ||||||
| 5,42E-08 | 1,3E-05 | 0,000292 | 0,002215 | ||||||
| 3,71E-09 | 2E-06 | 7E-05 | 0,000719 | ||||||
| 2,06E-10 | 2,69E-07 | 1,5E-05 | 0,000211 | ||||||
| 9,15E-12 | 3,19E-08 | 2,89E-06 | 5,63E-05 | ||||||
| 3,18E-13 | 3,33E-09 | 5,01E-07 | 1,37E-05 | ||||||
| 8,31E-15 | 3,04E-10 | 7,86E-08 | 3,04E-06 | ||||||
| 1,54E-16 | 2,44E-11 | 1,12E-08 | 6,2E-07 | ||||||
| 1,8E-18 | 1,71E-12 | 1,44E-09 | 1,16E-07 | ||||||
| 1E-20 | 1,05E-13 | 1,68E-10 | 2E-08 |
Интересно, что хотя таблицы продолжаются до строки 64, фактически (согласно правилу «3-х сигм») их можно было оборвать на строке 25 (это отразится только на значениях M и D в строках 8, 9). Все готово для построения нового графика, из которого будет видно, как с увеличением n распределение Бернулли приближается к некой стандартной форме – к распределению Лапласа, или к, так называемому, нормальному закону распределения Гаусса.
Считается, что при n ³ 30 распределение уже практически нормальное. Этот вопрос еще будет обсуждаться ниже при изучении распределения Лапласа. Там же рассмотрим применение кумуляты.


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Был в сети 07.04.2023 09:00

Куликовский Максим Юрьевич
преподаватель
10 546
2 245
13.12.2018 08:46
Просмотр содержимого документа
«Практическая работа в MS Excel «Графики»»
Практическая работа «Красивые графики функций»
-
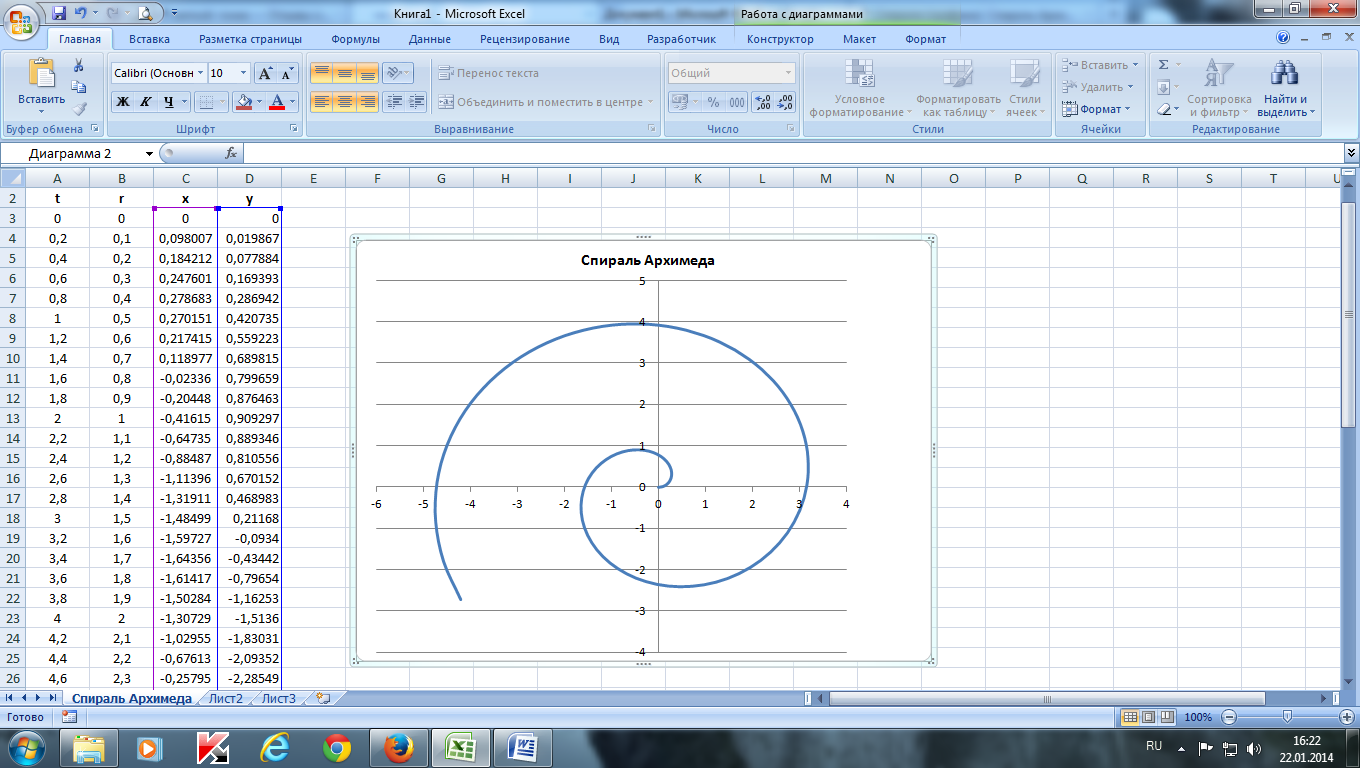
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5*t
— в столбце С – значения х = r*cos(t)
— в столбце D – значения y = r*sin(t)
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми)
-
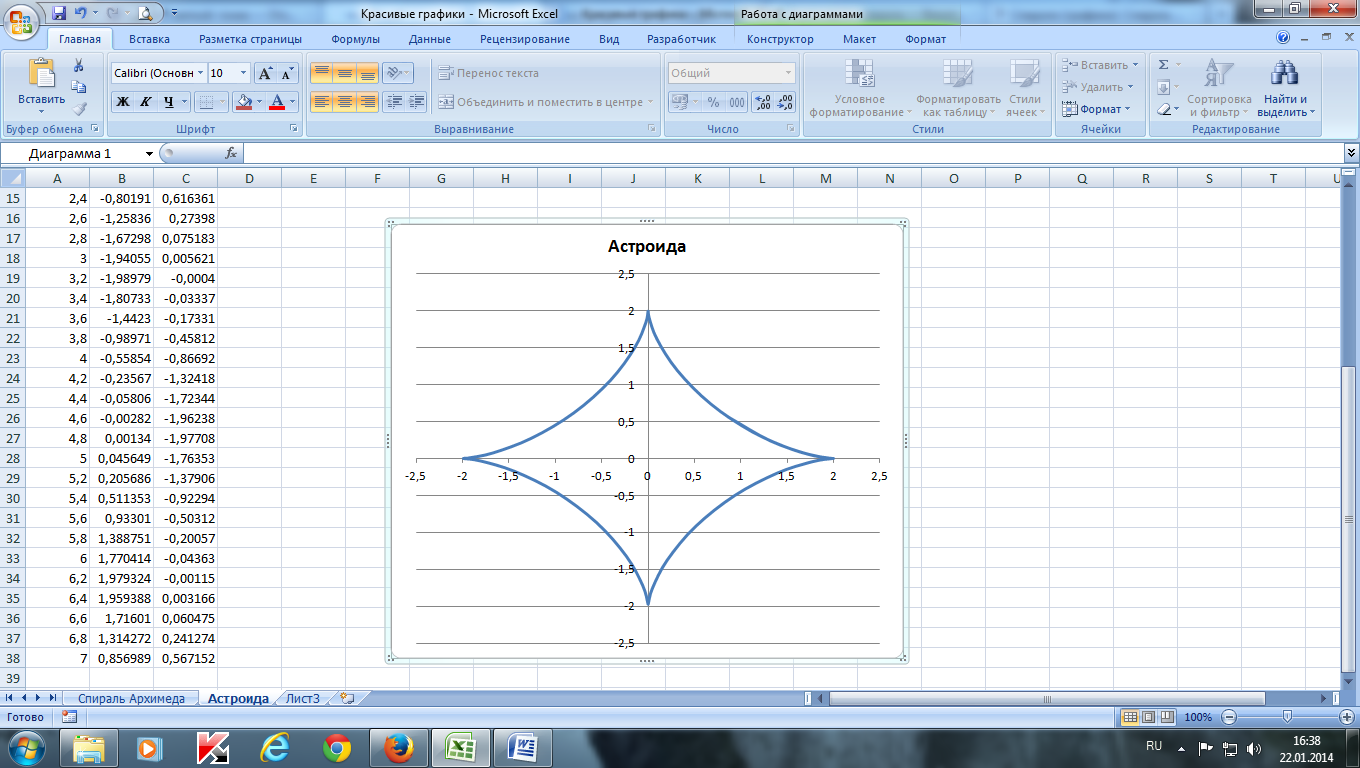
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*(cos (t))3
— в столбце С – значения y = 2*(sin (t))3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми)
-
Построить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения p = cos(t)–0,5
— в столбце D – значения x = p*cos(t)
— в столбце Е – значения у = p*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми) -
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения r = 2*sin(2*t)2
— в столбце D – значения x = r*cos(t)
— в столбце E – значения y = r*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
-
Построить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения x = 16*(sin(t))3
— в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми)
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
ТРЕНИНГИ
Быстрый старт
Расширенный Excel
Мастер Формул
Прогнозирование
Визуализация
Макросы на VBA
КНИГИ
Готовые решения
Мастер Формул
Скульптор данных
ВИДЕОУРОКИ
Бизнес-анализ
Выпадающие списки
Даты и время
Диаграммы
Диапазоны
Дубликаты
Защита данных
Интернет, email
Книги, листы
Макросы
Сводные таблицы
Текст
Форматирование
Функции
Всякое
Коротко
Подробно
Версии
Вопрос-Ответ
Скачать
Купить
ПРОЕКТЫ
ОНЛАЙН-КУРСЫ
ФОРУМ
Excel
Работа
PLEX
© Николай Павлов, Planetaexcel, 2006-2022
info@planetaexcel.ru
Использование любых материалов сайта допускается строго с указанием прямой ссылки на источник, упоминанием названия сайта, имени автора и неизменности исходного текста и иллюстраций.
Техническая поддержка сайта
|
ООО «Планета Эксел» ИНН 7735603520 ОГРН 1147746834949 |
ИП Павлов Николай Владимирович ИНН 633015842586 ОГРНИП 310633031600071 |