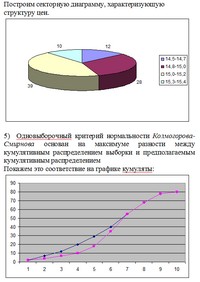
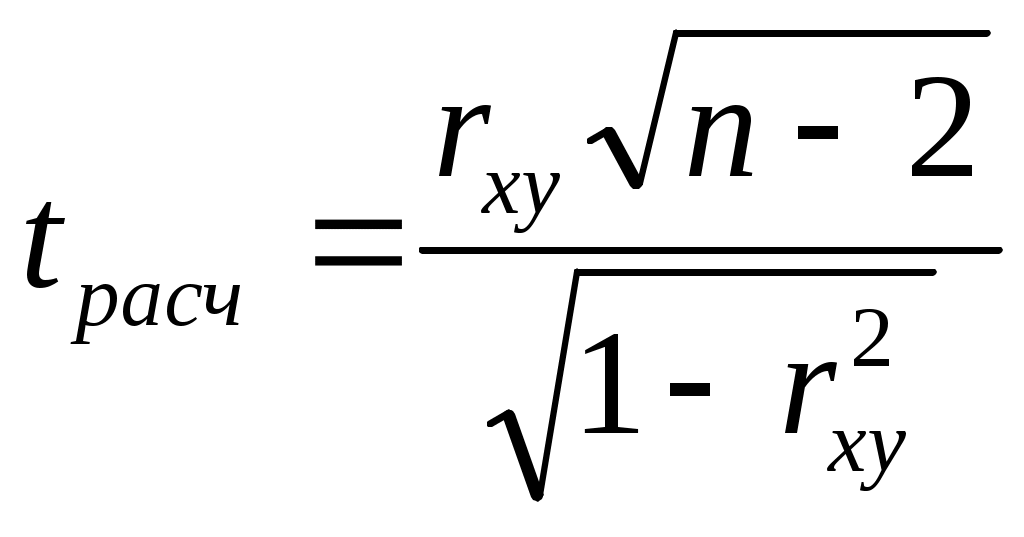Лабораторные работы по статистике в excel готовые

Лабораторные по статистике для студентов

Ниже представлены лабораторные работы по статистике (с использованием пакета MS Excel и без него), содержание работы можно посмотреть по ссылке, полное решение доступно для скачивания в формате pdf.

Внизу страницы вы найдете полезные ссылки на другие решенные задачи по статистике и материалы для самостоятельного решения лабораторных практикумов с помощью Эксель.

Готовые лабораторные работы по статистике

• Лабораторная работа по статистике
  Объем 31 страница.
  
  Показать содержание ЛР

  Задача 1. Организация статистического наблюдения. Сводка и группировка.
  1.1. Определение необходимого и достаточного числа наблюдений.
  1.2. Сводка и группировка результатов выборочного наблюдения.

  Задача 2. Средние величины в статистике
  2.1. Вычисление степенных средних
  2.2. Вычисление структурных средних
  2.3. Дисперсия $sigma^2$, средняя $mu$ и предельная $Delta$ ошибки выборочной средней $S$

  Задача 3. Дисперсионный анализ. Общая, внутригрупповая и межгрупповая дисперсии

  Задача 4. Корреляционный анализ

  Задача 5. Показатели динамических рядов

  Задача 6. Индексы количественных и качественных показателей. Индексы средних взвешенных показателей

• Лабораторная по статистике с расчетами в Excel, Расчетный файл Excel
  Объем 22 страницы.
  
  Показать содержание ЛР

  Часть А. Задание по теме «Сводка и группировка статистических материалов»
  1) Постройте группировку предприятий по величине первого факторного показателя, указанного в вышеприведенной таблице.
  2) Подсчитайте по каждой группе среднее значение результативного показателя.
  Проанализируйте полученную группировку.

  Часть В. Задание по теме «Средние величины и показатели вариации»
  По результативному показателю определите:
  1) Модальное значение;
  2) Медианное значение;
  3) Квартили;
  4) Децили.
  Расчеты следует выполнить по исходным (несгруппированным) данным. Сделайте экономические выводы по рассчитанным показателям.

  Часть С. Задание по теме «Статистическое изучение взаимосвязей финансово-экономических показателей»
  1) Построить корреляционные поля результативного показателя с каждым из факторных показателей. Сделать экономические выводы. Выбрать факторный признак, оказывающий наибольшее влияние на результативную переменную.
  2) Рассчитать коэффициенты корреляции Фехнера и Спирмена, взяв в качестве факторного признака, признак, оказывающий наибольшее влияние на результативную переменную.
  3) Рассчитать парный коэффициент корреляции между результативным и факторным (выбранном в пункте 1) признаками. Сделать выводы.
  4) Построить линейное регрессионное уравнение зависимости результативного показателя от факторного показателя, выбранного в пункте 1.
  5) По полученному уравнению регрессии определить теоретическое корреляционное отношение. Сделать выводы.

  Часть D. Задание по теме: «Ряды динамики»
  Рассчитайте по своему динамическому ряду за период 2007-13 гг.:
  1) Средний уровень динамического ряда;
  2) Показатели динамического ряда:
  — абсолютные приросты (цепные, базисные (по отношению к 2005 г.)), средний абсолютный прирост;
  — темпы роста и прироста (цепные, базисные (по отношению к 2005 г.)), средние темпы роста и прироста.
  3) проведите аналитическое выравнивание динамического ряда по прямой;
  4) сделайте прогноз анализируемого показателя на 2014 г. и на 2015 г. тремя методами (по полученному в пункте 3 регрессионному уравнению; по среднему абсолютному приросту; по среднему темпу роста).

  Часть E. Задание по теме: «Статистические индексы»
  Рассчитайте по своим исходным данным:
  1) Индивидуальные и общие индексы: цен, физического объема продаж, объемов торгов в рублевом выражении;
  2) Абсолютное изменение объемов торгов в рублевом выражении: общее, за счет изменения цен, за счет изменения физического объема продаж;
  3) Средневзвешенную цену акций за указанные периоды;
  4) Абсолютное и относительное изменение средней цены акций за указанный период: общее, за счет изменения индивидуальных цен на акции; за счет изменения физического объема продаж акций.

• Лабораторная работа «Основные методы определения рыночной стоимости ВВП»
  Объем 24 страницы.
  
  Текст задания

  Цель лабораторной работы: закрепить знания студентов по определению рыночной стоимости ВВП, навыки в построении основных счетов СНС, статистических методах анализа структуры рыночной стоимости ВВП, оценки ее динамики;
  Изучение основных макроэкономических статистических показателей (понятие, взаимосвязь);
  Построение счетов «Производства», «Образования доходов», «Товаров и услуг» за несколько лет (минимум два года 2008 -2009), анализ изменения структуры ВВП, динамики структуры ВВП;
  Сделать выводы о выявленных тенденциях по результатам лабораторной работы

• Лабораторная работа на исследование выборки
  Объем 7 страниц.
  
  Текст задания

  Имеются следующие данные о распределении турфирм города по размеру затрат на рекламу:
  Затраты на рекламу, у.е. Число турфирм
  6 – 8 3
  8 – 10 9
  10 – 12 5
  12 – 14 4

  Задание:
  1. Постройте график вариационного ряда (гистограмму и полигон).
  2. Вычислите:
  – среднее значение варьирующего признака;
  – моду и медиану;
  – показатели вариации: размах, среднее линейное, среднее квадратическое отклонение, дисперсию, коэффициент вариации;
  – коэффициент асимметрии.
  3. Сделайте письменный вывод по каждому показателю, рассчитанному в п.2.

Отзывы студентов

• Огромное спасибо за оперативную и качественную работу! Задачи по статистике выполнены на самом высоком уровне. Дальнейшего процветания компании!

  Евгений
• Все отлично, сдала! Спасибо за подробное решение задачи по предмету статистика рынка товаров и услуг.

  Ольга

• Заказывала контрольную по статистике, поставили пятерку. Сделали все качественно и оперативно, очень хороший сервис. Спасибо!

  Гульнара

• Заказывала контрольную работу по статистике. Отвечали очень оперативно и работу выполнили в срок и качественно. Спасибо сайту и исполнителю Андрею! Буду рекомендовать.

  Наталья

• «Добрый вечер! Заказала домашнюю работу на данном сайте по статистике. Советовали друзья. Я приятно была удивлена: выполнено все в срок, приемлемые цены и ни одного замечания от преподавателя. Советую воспользоваться услугами сайта!
  Благодарю Исполнителей за проделанную работу!»

  Анастасия

Все отзывы о МатБюро

Решаете сами? Может пригодиться

• Эконометрика и статистика в Gretl, SPSS, Eviews, Statistica
• Более 50 бесплатных задач по статистике
• Лучшие учебники для изучения статистики
• Готовые контрольные по статистике
• «Нахождение числовых характеристик выборки стандартными средствами ЭТ MS Excel»: пример выполненной лабораторной, 10 страниц, формат pdf.
• «Статистический анализ средствами MS Excel»: лабораторный практикум, 51 страница, формат pdf.
• «Обработка экспериментальных данных в MS Excel»: методические указания, 32 страницы, формат pdf.

Задание

Для
случайной выборки объемом n=50
с несовпадающими числами выполнить
следующую последовательность действий:

1.Вывести
на лист Excel
исходные статистические данные.

2. Построить
вариационный ряд.

3. Вычислить
статистические характеристики.

4. Построить
интервальный статистический ряд.

5.Построить
гистограмму частот.

6. Составить
статистическую функцию распределения
статистического ряда.

7.
Составить и постоить статистическую
функцию распределения группированного
статистического ряда.

В качестве примера
рассмотрим следующую выборку

Порядок выполнения работы

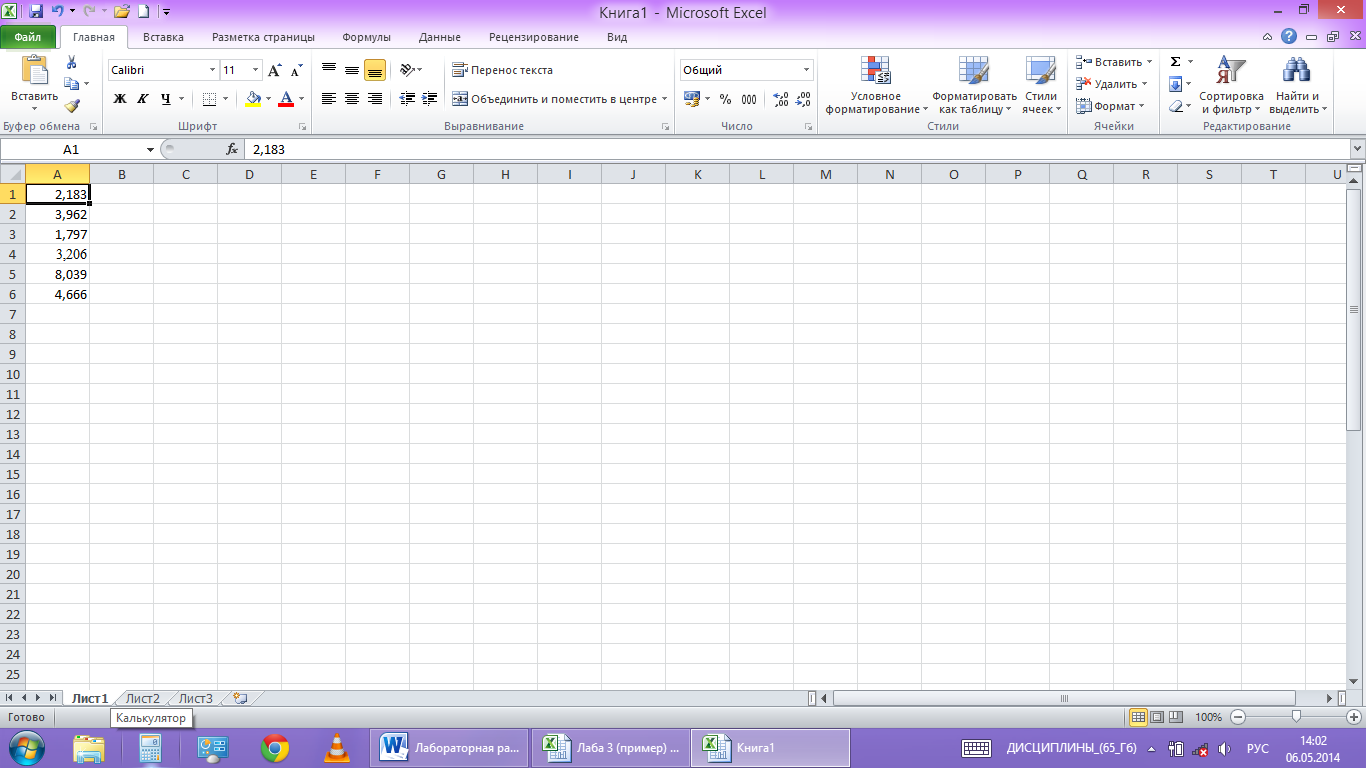
1.Ввод исходных статистических данных.

Вводим данные в
первый столбец таблицы (рис.1).

рис.1

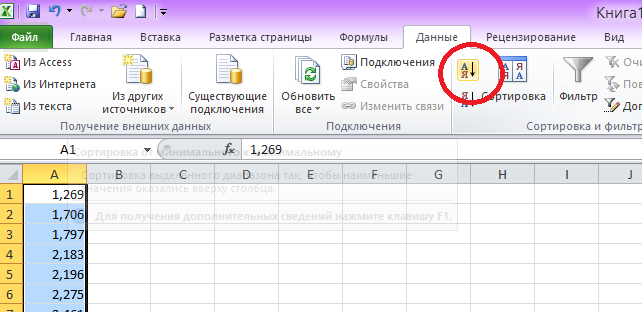
2. Построение вариационного ряда.

Производим
сортировку данных в порядке возрастания.
Для этого:

а) выделяем первый
столбец;

б)
на ленте
во вкладке «Данные» выбираем «Сортировка
и фильтр» (рис.2)

рис. 2

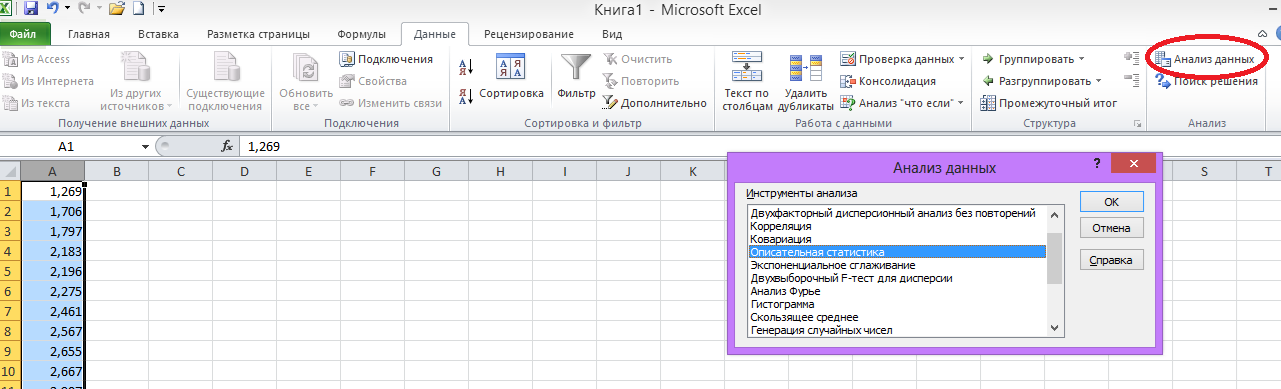
3. Вычисление статистических характеристик.

На ленте
во вкладке «Данные» выбираем «Анализ
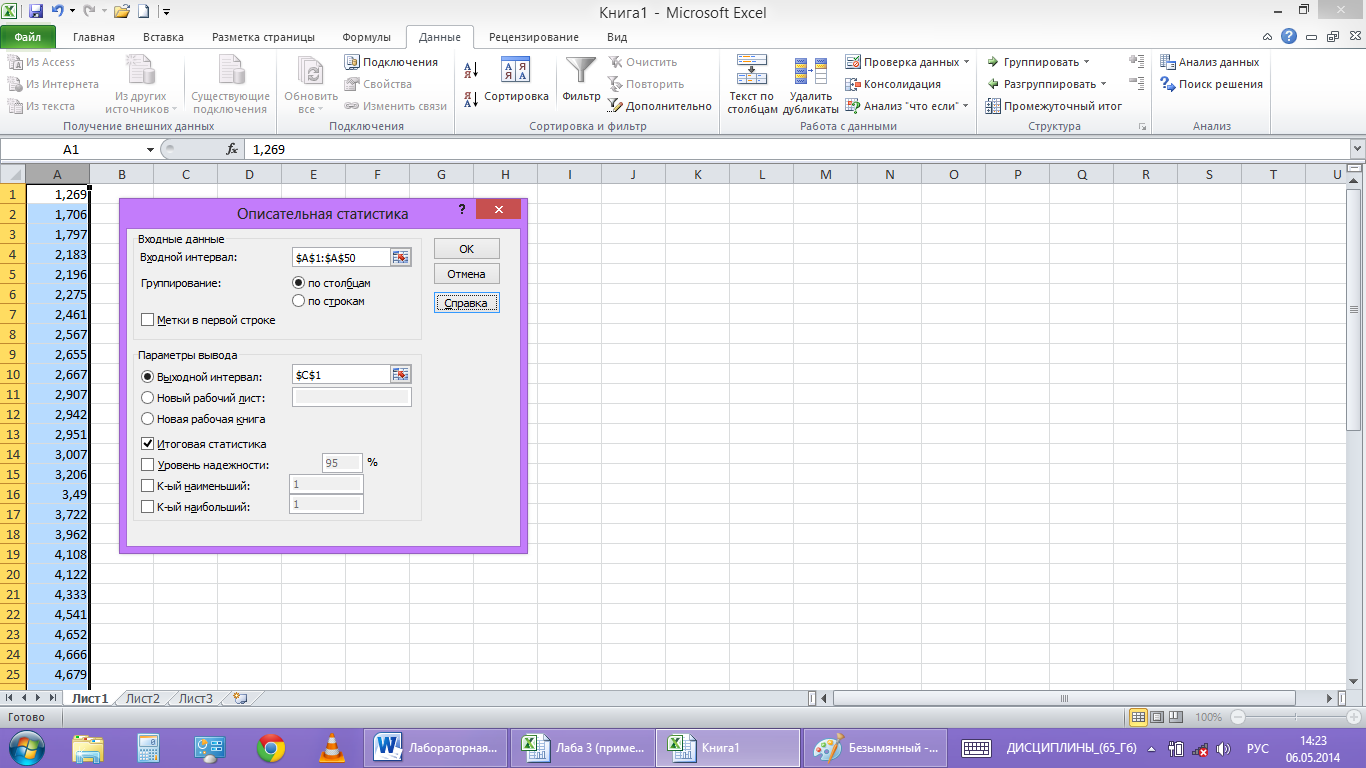
данных» меню «Описательная статистика»
нажимаем ОК.

рис. 3

В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
а в пункте «Выходной интервал» обозначим
первую ячейку для записи результаов
$C$1.
Ставим флажок напротив пункта «Итоговая
статистика» и нажимаем ОК.(рис.4)

рис. 4

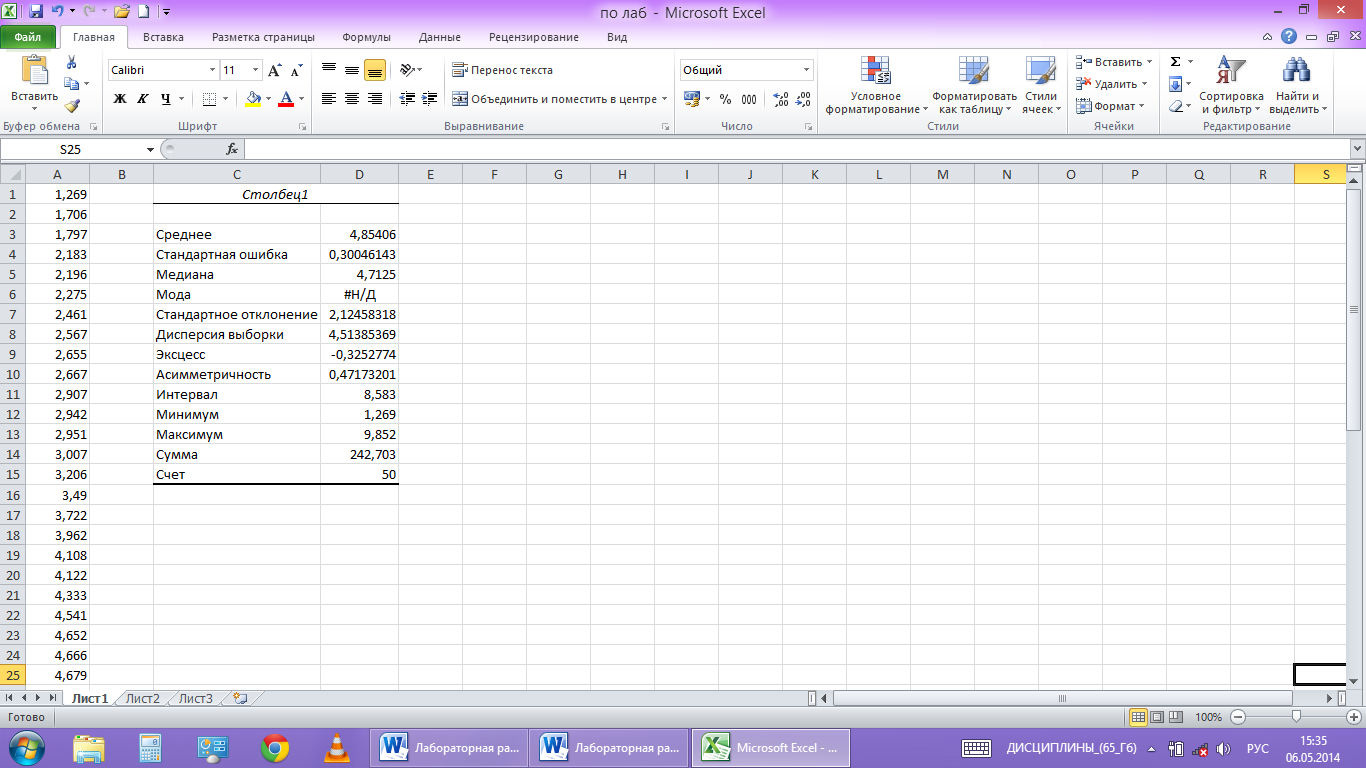
На
рабочем листе появляется таблица с
вычисленными значениями числовых
характеристик выборки (рис.5)

рис. 5

Здесь
«Среднее»означает математическое
ожидание выборки, а «Стандартная ошибка»
— погрешность ее значения. «Дисперсия
выборки» означает исправленную выборочную
дисперсию, а «Стандартное отклонение»
— исправленное среднее квадратичное
отклонение. Положительное значение
«Асимметричности» означает, что «длинная
часть» кривой лежит правее моды.
Отрицательное значение «Эксцесса»
означает, что кривая имеет более низкую
и «плоскую» вершину, чем нормальная
кривая. «Интервал» равен разности
Xmax−Xmin.
«Сумма»
дает результат суммирования всех
элементов выборки. «Счет» задает общее
число элементов выборки.

4. Построение интервального статистического ряда.

Длину интервала
группировки определяем по формуле

Необходимые данные
имеем в таблице: Xmax
– в ячейке D13,
Xmin–
в ячейке D12,
число элементов выборки n
— в ячейке D15.

В ячейку С16 вводим
слово «Интервал», в ячейку D16
вводим формулу

в ячейке D16
появится значение числа h.
В ячейку C17
вводим букву h.
В ячейку D17
вводим формулу

В ячейке
D17
получаем округленное до одного знака
после запятой значение интерала h.

Проведем формирование
интервалов. Для этого от Xmin
отступим влево примерно на h/2
и получим начальную точку отсчета.
Последовательно прибавляя к ней целое
число отрезков h,
получим все граничные точки интервалов.

В ячейку
F1
вводим формулу

В этой
ячейке появляется значение начальной
точки отсчета. В ячейку F2
вводим формулу

В этой
ячейке появляется значение второй
граничной точки первого интервала.
Возвращаемся в ячейку F2,
ставим курсор в правый нижний угол рамки
и двигаем его вниз, не отпуская левую
кнопку мыши. В результате такой процедуры
(протяжка) столбец F
заполнят граничные точки интервалов.
Самый нижний интервал должен включать
Xmax
(рис.6).

Проведем подсчет
числа вариант, попавших в каждый интервал,
определим относительные частоты и
серединные точки этих интервалов.

Для
этого на ленте во вкладке «Данные»
выбираем «Анализ данных» меню
«Гистограмма». (рис.
7)

рис. 6	рис. 7

В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
в пункт «Интервал карманов» — диапазон
ячеек с границами интервалов $F$1:$F$9.
Отметим точкой пункт «Выходной интервал»
и введем в него адрес первой ячейки для
записи результатов $Н$1. Появится таблица
из двух столбцов с обозначениями «Карман»
и «Частота» (рис.8).

Определим
относительные частоты р_i^*,
значения серединных точек интервалов

и высоты
прямоугольников

Для этого

1. в ячейку
   J1
   введем заголовок «Относительная
   частота»;

2. В ячейку
   J3
   введем формулу

и
протягиваем её вниз до ячейки J10.
В результате к таблице из двух столбцов
добавится третий столбец (рис.8). В этой
таблице частота появления случайной
величины в каждом интервале записана
в одной строке с концом интервала;

1. в ячейку
   K1
   введем заголовок столбца Х*;

2. в ячейку
   К3 введем формулу

Протягиваем
эту формулу до ячейки К10. В результате
в четвертом столбце таблицы (рис.8)
появятся значения серединных точек
интервалов;

1. в ячейку
   L1
   введем заголовок столбца У_i;

2. в ячейку
   L3
   введем формулу

Протягиваем
её вниз до ячейки L10.

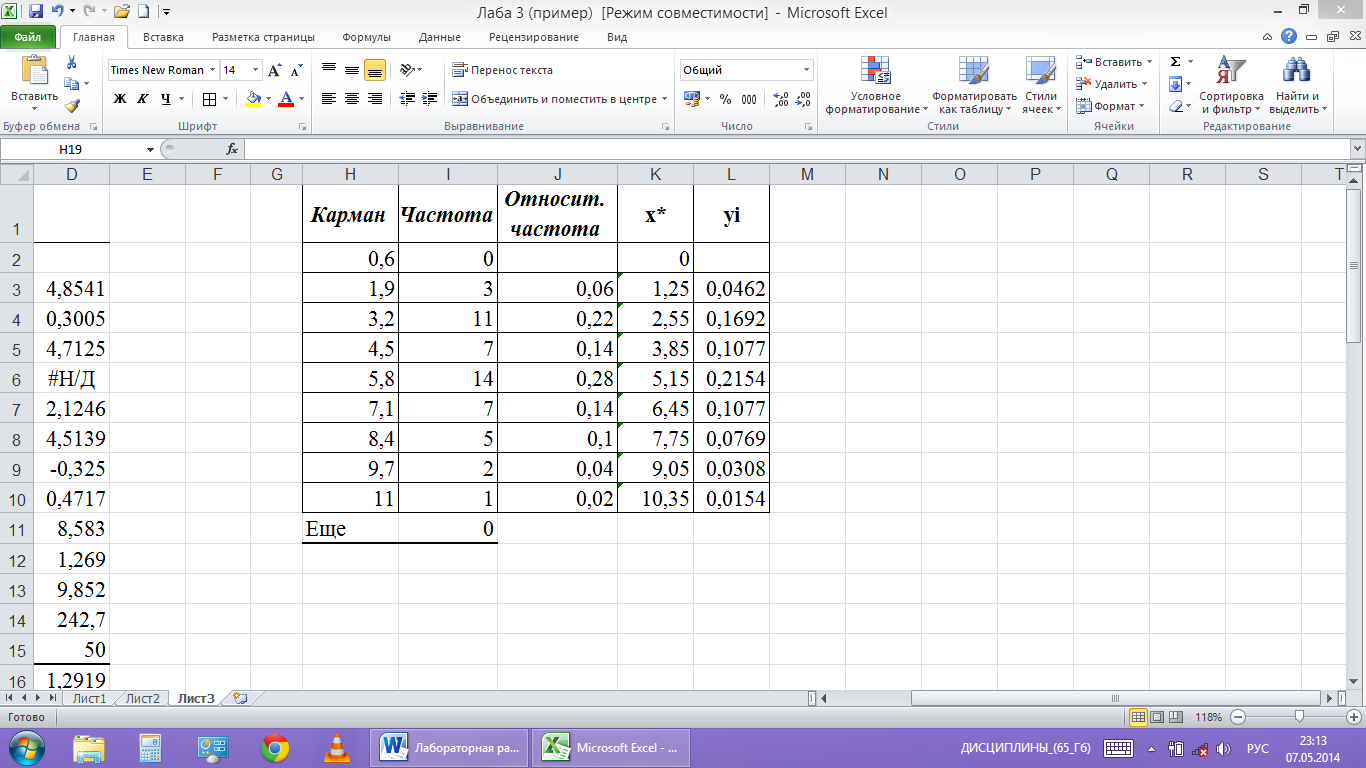
В
результате в пятом столбце таблицы
(рис.8) появятся значения У_i.

рис.8

Соседние файлы в папке Лаб.работы

• #
• #
• #
• #

ЛАБОРАТОРНАЯ РАБОТА

«Статистические функции MS Excel 2013. Построение рядов данных»

Цели работы:

1. научиться применять статистические функции для обработки данных; закрепить навыки форматирования таблицы;

2. воспитывать в себе аккуратность и внимательность при выполнении работ с электронными таблицами;

3. развивать логическое мышление, необходимое для работы с большими массивами информации

Задание:

1. изучите п.1 «Учебный материал»;

2. выполните задания, приведенные в п.2;

3. ответьте на контрольные вопросы (п.3).

1. Учебный материал

1. 1. Функции категории Статистические

Статистические функции позволяют выполнять статистический анализ диапазонов данных: нахождение минимального и максимального значения среди исходных чисел, выполнение элементарного подсчёта числовых значений, подсчёт числовых значений в соответствии с определённым условием и т.д. Статистические функции входят в категорию Статистические Мастера функций (рис.1).

Рис.1. Окно Мастера функций с выбранное категорией функций Статистические

Рассмотрим ряд статистических функций, встречающихся в простейших вычислениях.

1. Нахождение минимального значения (среди числовых значений) в списке аргументов с помощью функции МИН. Формат записи функции:

МИН (число1; число2;…)

Количество допустимых аргументов, среди которых находится минимальное значение, равно 255.

Пример. Найти наименьшее значение цены на книгу «Гарри Поттер и дары смерти» среди магазинов города. Пусть в ячейках B3:B7 внесены значения цены (рис.2). Установите курсор в ячейку В9, вызовите Мастер функций и из категории Статистические выберите функцию МИН. Укажите исходные значения и нажмите OK.

1. Нахождение максимального значения (среди числовых значений) в списке аргументов с помощью функции МАКС. Формат записи функции:

МАКС (число1; число2;…)

Количество допустимых аргументов, среди которых находится максимальное значение, равно 255.

Пример. Найти максимальное значение цены на книгу «Гарри Поттер и дары смерти» среди магазинов города. Пусть в ячейках B3:B7 внесены значения цены (рис.3). Установите курсор в ячейку В9, вызовите Мастер функций и из категории Статистические выберите функцию МАКС. Укажите исходные значения и нажмите OK.

Рис. 2. Нахождение минимального значения среди аргументов

Рис. 3. Нахождение максимального значения среди аргументов

1. Нахождение среднего арифметического значения с помощью функции СРЗНАЧ. Формат записи функции:

СРЗНАЧ(число1; число2;…)

Количество допустимых аргументов, среди которых находится среднее значение, равно 255.

Пример. Найти среднее значение цены на книгу «Гарри Поттер и дары смерти» в магазинах города. Пусть в ячейках B3:B7 внесены значения цены (рис. 4). Установите курсор в ячейку В9, вызовите Мастер функций и из категории Статистические выберите функцию СРЗНАЧ. Укажите исходные данные и нажмите OK.

Рис. 4. Нахождение среднего значения среди аргументов

1. Подсчет количества значений в списке аргументов осуществляется с помощью функции СЧЕТ. Формат записи функции:

СЧЕТ(число1; число2;…)

Количество допустимых аргументов, среди которых находится среднее значение, равно 255.

Пример. Найти количество студентов, получающих стипендию. Пусть в ячейках B3:B7 внесены сведения о стипендии студентов группы (рис.5). Установите курсор в ячейку В9, вызовите Мастер функций и из категории Статистические выберите функцию СЧЕТ. Укажите исходные данные и нажмите OK. В ячейке В9 будет найдено искомое значение.

Рис. 5. Нахождение количества числовых значений среди аргументов

1. Нахождение количества значений, удовлетворяющих заданному условию, выполняется с помощью функции СЧЕТЕСЛИ. Формат записи функции:

СЧЕТЕСЛИ(диапазон; критерий),

где диапазон – диапазон, в котором подсчитывается количество непустых ячеек;

критерий – проверяемое условие в заданном интервале (в форме числа, выражения, текста).

Примеры записи функции:

1. =СЧЕТЕСЛИ(А1:А9; 85) – подсчитывает, сколько раз число 85 встречается в интервале А1:А9;

2. =СЧЕТЕСЛИ(А1:А9; “>85”) – подсчитывает, сколько раз в интервале А1:А9 встречаются числа, большие 85;

3. =СЧЕТЕСЛИ(А1:А9; “высший”) – подсчитывает, сколько раз в интервале А1:А9 встречается слово «высший»;

4. =СЧЕТЕСЛИ(А1:А9; “в*”) – подсчитывает, сколько раз в интервале А1:А9 встречаются слова, начинающиеся на букву «в».

Обратите внимание на то, что если в качестве критерия указываются не числовые значения, а текст или символы, то они заключаются в кавычки.

1. Определение ранга (номера позиции) числа в списке других чисел (т.е. порядкового номера относительно других чисел списка) выполняется с помощью функции РАНГ. РВ. Формат записи функции:

РАНГ.РВ(число; ссылка; порядок),

где число – число, для которого определяется ранг (порядковый номер);

ссылка – массив или ссылка на список чисел, с которым сравнивается число;

порядок – число (0 либо отличное от 0), определяющее способ ранжирования (в порядке убывания или возрастания).

Пример. Используем функцию РАНГ.РВ, которая присвоит номер места каждой марке автомобиля в зависимости от определенного параметра. Пусть в ячейки В3:В8 занесены значения расхода топлива на 100 км пробега (рис.6). Наилучшим будем считать автомобиль, имеющий минимальный расход. В ячейку С3 занесем формулу

=РАНГ.РВ(B3;$B$3:$B$8;1)

и скопируем ее в оставшиеся ячейки С4:С8. Аргументы в этой формуле означают следующее: В3 – адрес ячейки, которой присваиваем в ячейке С3 номер искомого места; $B$3:$B$8 – блок ячеек, в который занесены все известные значения расхода топлива и среди которых мы выясняем ранг. Здесь используем абсолютную адресацию ($) для того, чтобы при копировании формулы из ячейки С3 адрес участвующих в вычислении ячеек В3:В8 не изменялся. Последний аргумент функции 1 указывает на то, что сравнение результатов происходит в порядке возрастания, т.е. наилучшим результатом считаем наименьший. Если поставим 0, то лучшим результатом будет наибольший, как, например, в случае с объемом двигателя (рис.7).

Рис. 22. Нахождение ранга числа в порядке возрастания значений

Рис.7. Нахождение ранга числа в порядке убывания значений

1. 1. Построение рядов данных

Для ввода в смежные ячейки повторяющейся с определенной закономерностью информации (текст, даты, числа), т.е. построения рядов данных, существует несколько способов.

1. Использование маркера заполнения и перетаскивания ячеек.

Пусть необходимо построить ряд чисел от 1 до 5,5 с шагом 0,5, т.е. получить арифметическую прогрессию. Для этого:

• в окне открытого листа введите данные в первую ячейку диапазона (рис.8);

• наведите курсор мыши на правый нижний угол ячейки (там располагается маркер заполнения) и, когда курсор станет тонким черным крестом, при нажатой левой кнопке мыши протащите маркер заполнения вниз по столбцу;

• в конце нужного диапазона отпустите левую кнопку мыши. Оцените результат.

В данном случае в новые ячейки заносятся соответствующие значения, а также форматы исходной ячейки.

Рис.8. Использование маркера заполнения для получения арифметической прогрессии

Если после ввода первых двух значений потянуть за маркер заполнения при нажатой клавише <Ctrl>, то будет реализован принцип автозаполнения, а не получение арифметической прогрессии, и во всех ячейках получится чередование чисел 1 и 1,5 (рис.9).

Рис.9. Использование маркера заполнения для автозаполнения ячеек

1. Использование команды Прогрессия.

• Занесите в ячейку А1 число 1;

• выберите команду Прогрессия…, находящуюся в группе Редактирование вкладки Главная (рис.10), которая позволяет заполнить ряд соответствующим образом;

Рис.10. Команда Прогрессия для заполнения рядов данных

• в появившемся диалоговом окне установите параметры, как показано на рис.11.

Рис.11. Диалоговое окно для построения рядов данных

• нажмите ОК. Оцените результат.

3) Использование формул.

• Занесите в ячейку А1 число 1;

• по условию задачи, каждое следующее число отличается от предыдущего на 0,5, поэтому для построения ряда чисел воспользуемся формулой: =А1+0,5, которую внесем в ячейку А2 и с помощью маркера скопируем по столбцу вниз (рис.12).

Рис.12. Построение ряда чисел с использованием формулы

4) Использование параметров автозаполнения.

• Введите данные в первую ячейку диапазона;

• наведите курсор мыши на правый нижний угол ячейки и, когда курсор станет тонким черным крестом, при нажатой правой кнопке мыши протащите маркер заполнения, верх или вниз по столбцу либо вправо или влево по строке;

• в конце нужного диапазона отпустите правую кнопку мыши;

• в контекстном меню выберите соответствующий пункт:

• «Копировать ячейки» – будут копироваться и значения, и форматы исходной ячейки;

• «Заполнить только форматы» – будет копироваться только формат исходной ячейки;

• «Заполнить только значения» – будет копироваться только значение исходной ячейки.

1. Задание к лабораторной работе

Для выполнения лабораторной работы введите исходные данные в соответствии с выданным номером задания. Отформатируйте таблицу по приведенным ниже параметрам.

1. 1. Заголовок таблицы Применение статистических функций сделайте жирным шрифтом, размер шрифта – 12 пт. Для центрирования заголовка таблицы необходимо выделить ячейки A1:G2 и нажать на кнопку Объединить и поместить в центре , расположенную в группе Выравнивание вкладки Главная. Затем, не убирая курсора с объединенных ячеек, в контекстном меню выберите команду Формат ячеек и в открывшемся диалоговом окне выберите: вкладка Выравнивание→область Выравнивание→по горизонтали – по центру; по вертикали — по центру;

   2. Заголовки столбцов таблицы (№ п/п; ФИО студента; Рост (см); Вес (кг)… и т.д. в зависимости от варианта задания) – по центру, полужирным шрифтом, размер шрифта – 10 пт). Возможность отображать текст внутри ячейки таблицы в несколько строк добивается следующим образом:

1. 1. выделить ячейки A3:G3, формат которых требуется изменить;

   2. в контекстном меню выберите команду Формат ячеек и в открывшемся диалоговом окне выберите: вкладка Выравнивание→область Выравнивание→по горизонтали – по центру; по вертикали — по центру;

   3. в области Отображение установить флажок переносить по словам.

1. 1. Ячейки А4:А13 заполните значениями от 1 до 10 одним из способов, описанных в п.1.2 «Построение рядов данных».

   2. К тексту ячеек B15:B22 примените начертание курсив и сделайте перенос по словам.

   3. Выделите ячейки A1:G13 таблицы. С помощью кнопки Границы→Все границы группы Шрифт измените границы таблицы.

   4. Символ, соответствующий степени 2 числа, можно вставить с помощью команды Символ группы Символы вкладки Вставка. Другой способ указания символа степени: написать степень числа, выделить его, нажать кнопку группы Шрифт и в появившемся диалоговом окне во вкладке Шрифт в области Видоизменение установить флажок надстрочный.

Задание 1

Задание. Для данной группы студентов определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.13. На вашем рабочем листе цвет ячеек изменять не обязательно):

1. минимальное значение роста, веса и бега на 100 м;

2. максимальное значение роста, веса и бега на 100 м;

3. среднее значение роста, веса и бега на 100 м;

4. количество студентов, имеющих рост < 180 см;

5. количество студентов, имеющих рост > 185 см;

6. количество студентов, имеющих вес < 80 кг;

7. количество студентов, имеющих вес > 85 кг;

8. количество студентов, участвовавших в соревновании;

9. ранг студентов (порядковый номер относительно друг друга) в беге на 100 м.

Рис.13. Исходные данные для выполнения лабораторной работы

Задание 2

Задание. Для данной группы продуктов определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.14. На вашем рабочем листе цвет ячеек изменять не обязательно):

1. минимальное значение цен в магазинах;

2. максимальное значение цен в магазинах;

3. среднее значение цен в магазинах;

4. количество продуктов, название которых начинается на букву «м»;

5. количество продуктов, название которых начинается на букву «к»;

6. количество продуктов дороже 25 руб.;

7. количество продуктов дешевле 25 руб.;

8. количество продуктов, ассортимент которых обновлялся;

9. ранг продуктов магазина «Рублик» (порядковый номер относительно стоимости друг друга).

Рис.14. Исходные данные для выполнения лабораторной работы

Задание 3

Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.15. На вашем рабочем листе цвет ячеек изменять не обязательно):

1. минимальное значение цен в парикмахерских;

2. максимальное значение цен в парикмахерских;

3. среднее значение цен на услуги парикмахерских;

4. количество услуг со стоимостью < 200 руб.;

5. количество услуг со стоимостью ≥200 руб.;

6. среднее значение стоимости стрижек в парикмахерской «Люкс»;

7. средняя стоимость других услуг (отличных от стрижек) парикмахерской «Люкс»;

8. количество скидок;

9. ранг стоимости услуг парикмахерской «Аванта» (порядковый номер стоимости относительно друг друга).

Рис.15. Исходные данные для выполнения лабораторной работы

Задание 4

Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.16. На вашем рабочем листе цвет ячеек изменять не обязательно):

1. минимальное значение цен на услуги компаний сотовой связи;

2. максимальное значение цен на услуги компаний сотовой связи;

3. среднее значение цен на услуги компаний сотовой связи;

4. количество услуг со стоимостью < 2 руб.;

5. количество услуг со стоимостью ≥2 руб.;

6. среднее значение стоимости звонков оператора «МТС»;

7. средняя стоимость других услуг (отличных от звонков) оператора «МТС»;

8. количество скидок именинникам;

9. ранг стоимости услуг оператора «МТС» (порядковый номер стоимости относительно друг друга).

Рис.16. Исходные данные для выполнения лабораторной работы

Задание 5

Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.17. На вашем рабочем листе цвет ячеек изменять не обязательно):

1. минимальное значение населения, площади территории страны, количества городов-миллионеров;

2. максимальное значение населения, площади территории страны, количества городов-миллионеров;

3. среднее значение населения, площади территории страны, количества городов-миллионеров;

4. количество стран с населением < 100 млн. чел.;

5. количество стран с населением ≥ 100 млн. чел.;

6. количество стран площадью территории >5 млн. км²;

7. количество стран площадью территории <1 млн. км²;

8. количество стран, берега которых омываются океанами;

9. ранг стран по площади территории (порядковый номер страны относительно значений площадей).

Рис.17. Исходные данные для выполнения лабораторной работы

Задание 6

Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.18. На вашем рабочем листе цвет ячеек изменять не обязательно):

1. минимальное значение населения, площади территории страны, количества городов-миллионеров;

2. максимальное значение населения, площади территории страны, количества городов-миллионеров;

3. среднее значение населения, площади территории страны, количества городов-миллионеров;

4. количество стран с населением < 100 млн. чел.;

5. количество стран с населением ≥ 100 млн. чел.;

6. количество стран площадью территории >10 млн. км²;

7. количество стран площадью территории <1 млн. км²;

8. количество стран с океанами;

9. ранг стран по населению (порядковый номер страны относительно значений количества человек).

Рис.18. Исходные данные для выполнения лабораторной работы

Задание 7

Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.19. На вашем рабочем листе цвет ячеек изменять не обязательно):

1. минимальное значение длины реки, площади бассейна реки и количества крупных городов, где эти реки протекают;

2. максимальное значение длины реки, площади бассейна реки и количества крупных городов;

3. среднее значение длины рек, площади бассейна и количества крупных городов;

4. количество рек длиной < 5000 км;

5. количество рек длиной ≥ 5000 км;

6. количество рек с площадью бассейна >1000 тыс. км²;

7. количество рек с площадью бассейна ≤ 1000 тыс. км²;

8. количество стран с указанными реками;

9. ранг рек по длине (порядковый номер реки относительно значений длины).

Рис.19. Исходные данные для выполнения лабораторной работы

1. Контрольные вопросы

1. Назовите известные вам функции из категорий Статистические и их аргументы.

2. Сколько аргументов могут иметь функции МИН и МАКС?

3. Каковы отличия функций СЧЕТ и СЧЕТЕСЛИ. Назовите аргументы этих функций.

4. С какой целью в функции РАНГ.РВ используется абсолютная адресация ячеек?

5. Самостоятельно выясните назначение и работу функций НАИМЕНЬШИЙ, НАИБОЛЬШИЙ, ТЕНДЕНЦИЯ категории Статистические, используя справку по каждой из них. Приведите примеры.

---

Подборка по базе: 5 вар Практическая работа №3. (1).docx, Практическая работа по теме Урал по географии 9 класс.docx, Итоговая контрольная работа рус6.docx, Практическая работа 2.docx, Самостоятельная работа к теме 3.6.4.docx, Самостоятельная работа к теме 3.6.3.docx, Практическая работа 3 по литературе.docx, (Информационные сист) Понятие новой информационной технологии.do, Практическая работа №1.docx, Самостоятельная работа 3. 6. 2 ФХД.docx

---

Лабораторная работа №25. Технологии статистических расчетов в MS EXCEL.

Цель: научиться использовать возможности MS Excel для проведения статистических расчетов.

Задачи:

1. Расчет коэффициента корреляции Пирсона и t-статистики Стьюдента.
2. Построение модели регрессии различными способами.
3. Выбор наиболее точной модели связи между двумя величинами.

1. Параметрический корреляционный анализ.

Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками. Обычно связь между выборками носит не функциональный, а вероятност­ный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей разли­чают корреляцию и регрессию.

Корреляционный анализ состоит в определении степени связи между двумя слу­чайными величинами Xи Y. В качестве меры такой связи используется коэффи­циент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (x_i, y_i) из совместной генеральной совокупности Xи Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от измерения (способа шкалирования) величин Xи Y.

Для оценки степени взаимосвязи величин Xи Y, измеренных в количественных шкалах, используется коэффи­циент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки Xи Y распределены по нормальному закону.

1. Линейный коэффициент корреляции — параметр, который характеризует степень линей­ной взаимосвязи между двумя выборками, рассчитывается по формуле:

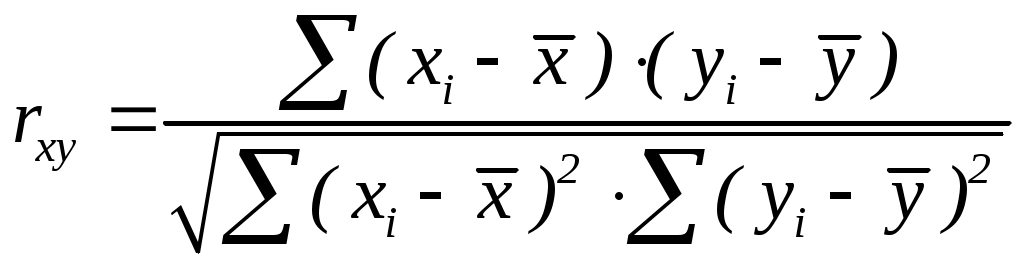
где х_i — значения, принимаемые в выборке X,

y_i — значения, принимаемые в выборке Y;

— средняя по X, — средняя по Y.
Коэффициент корреляции изменяется от -1 до 1. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно, произошла ошибка в вычислениях. При значении 0 линейной зависимости между двумя вы­борками нет.

Знак коэффициента корреляции очень важен для интерпре­тации полученной связи. Если знак ко­эффициента линейной корреляции — плюс, то связь между кор­релирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина дру­гого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно уве­личивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости.

Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе гово­ря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой пере­менной. Такая зависимость носит название обратно пропорцио­нальной зависимости.

Теснота связи и величина коэффициента корреляции.

Коэффициент корреляции rxy	Теснота связи
+ 0,91-1,0	Очень сильная
+ 0,81-0,9	Весьма сильная
+ 0,65-0,8	Сильная
+ 0,45-0,64	Умеренная
+ 0,25-0,44	Слабая
До + 0,25	Очень слабая
«+» — прямая зависимость «-» — обратная зависимость

2. t-статистика Стьюдента.

Для того чтобы оценить наличие связи между двумя переменными, также можно использовать t-статистику Стьюдента, которая оценивает отношение величины линейного коэффициента корреляции к среднему квадратическому отклонению и рассчитывается по формуле

Полученную величину t_расч сравнивают с табличным значением t-критерия Стьюдента с n-2 степенями свободы. Если t_расч > t_табл, то практически невероятно, что найденное значение обусловлено только случайными совпадениями величин X и Y d в выборке из генеральной совокупности, т.е. существует зависимость между X и Y. И наоборот, если t_расч < t_табл , то величины X и Y независимы.

3. Регрессионный анализ.

Цель регрессионного анализа – определить количественные связи между зависимыми случайными величинами. Одна из этих величин полагается зависимой и называется откликом, другие – независимые, называются факторами. Для установления степени зависимости между откликом и факторами используются вычисляемые величины ковариации и коэффициент корреляции. Если коэффициент корреляции по абсолютной величине близок к единице, то для построения зависимости используется линейная модель. Для других случаев используются более сложные нелинейные модели.

Уравнение линейной регрессии имеет вид:

Y=a₁X₁ + a₂X₂ + …+ a_kX_k, где а₁, а₂… а_{k –} параметры, подлежащие определению методом наименьших квадратов (МНК). В среде MS Excel для этого используется встроенная функция ЛИНЕЙН и инструмент Регрессия из Пакета анализа.
Задание 1. Исследование связей между двумя исследуемыми признаками.

Условие задачи: По 20 туристическим фирмам были установлены затраты на рекламную кампанию и количество туристов, воспользовавшихся после ее проведения услугами каждой фирмы. Определить коэффициент корреляции между исследуемыми признаками.

Ход выполнения:

1. Откройте новую книгу MS Excel и создайте таблицу согласно рис. 1:

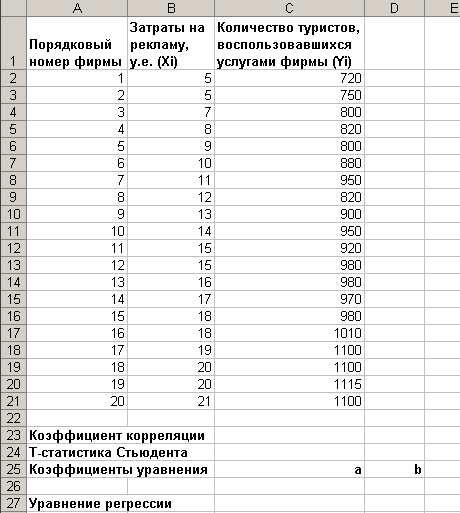
Рис.1.

1. Рассчитайте в ячейке С23 коэффициент корреляции, используя функцию КОРРЕЛ из категории Статистические. Синтаксис функции:

КОРРЕЛ (массив1 ; массив 2):

где массив1 – ссылка на диапазон ячеек первой выборки (X);

массив2 – ссылка на диапазон ячеек второй выборки (Y).

В нашей задаче формула будет иметь вид: =КОРРЕЛ(B2:B21;C2:C21)

1. Сделайте вывод о тесноте связи между затратами на рекламу и количеством привлеченных туристов.

1. Оцените значимость коэффициента корреляции. С этой целью рассматриваются две гипотезы. Основная Н₀: _xy=0 и альтернативная Н₁: _xy≠0. Для проверки гипотезы Н₀ рассчитайте t-статистику Стьюдента по формуле, указанной выше в ячейке С24. В нашем случае число степеней свободы ν = n-2=20-2 = 18 и формула будет следующей: =C23*КОРЕНЬ(20-2)/КОРЕНЬ(1-(C23*C23))
2. Сравните полученное значение с критическим значением t_ν,α распределения Стьюдента. (При ν =18 и доверительной вероятности α = 0,05, t_{ν,α,табл} = 1,734). Сделайте вывод о наличии связи между исследуемыми величинами.

Задание 2. Построение регрессионной модели.

1-й способ. Функция ЛИНЕЙН.

1. В первом способе для получения коэффициентов а и b линейного уравнения регрессии Y=а*X+b, описывающего зависимость количества привлеченных туристов от затрат на рекламу воспользуемся статистической функцией ЛИНЕЙН. Для этого выделите две ячейки C26:D26 и выполните вставку функции ЛИНЕЙН с аргументами согласно рис.2. Здесь Известные_значения_y – диапазон значений Количество туристов, Известные_значения_x – диапазон значений Затраты на рекламу. Нажмите комбинацию клавиш SHIFT+CTRL+ENTER.

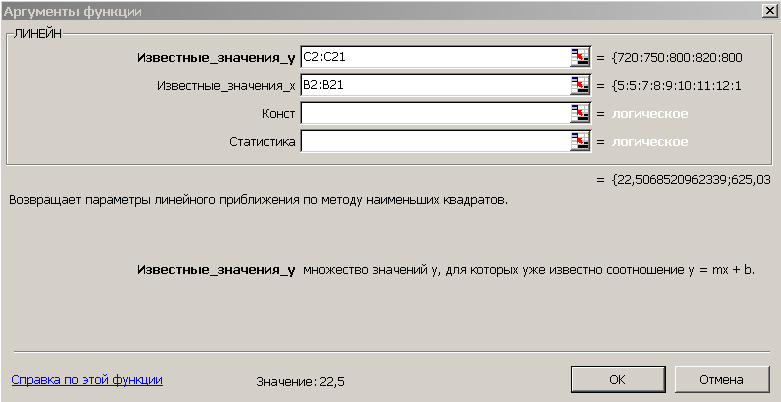
Рис. 2. Аргументы функции ЛИНЕЙН.

1. В ячейку D27 введите уравнение Y= a*X+b (вместо a и b подставьте полученные коэффициенты линейной регрессии).

2-й способ (графический). Построение линии тренда.

1. Для получения уравнения регрессии построим корреляционное поле переменных X (затраты на рекламу) и Y (количество туристов).
2. Выделите диапазон ячеек В2:С21, запустите мастера диаграмм и выберите тип диаграммы – Точечная. Задайте для диаграммы имя – Корреляционное поле, ось Х – Затраты на рекламу, ось Y – Количество туристов. На последнем шаге мастера укажите место расположения – отдельный лист.
3. Добавьте линию тренда на точечный график. Для этого необходимо выделить диаграмму и выполнить команду меню Диаграмма /Добавить линию тренда, либо выполнить данную команду из контекстного меню, щелкнув по любой точке графика. Линия тренда – графическое представление направления изменения ряда данных
4. Выберите тип тренда Линейный, который используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением: y = ax +b, где a — угол наклона и b — координата пересечения оси абсцисс.
5. На вкладке Параметры установите флажки Показать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации . Щелкните по кнопке ОК. — это число от 0 до 1, которое отражает близость линии тренда к фактическим данным. Линия тренда наиболее соответствует действительности, когда значение близко к 1.
6. Сравните уравнение регрессии, полученное графическим методом (рис. 3), с уравнением, рассчитанным с помощью функции ЛИНЕЙН.

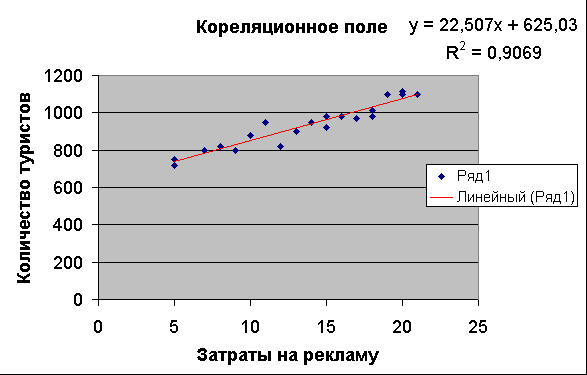
Рис.3.

3-й способ. Инструмент анализа Регрессия.

1. Сначала убедитесь, что был активизирован Пакет анализа, т.е. в меню Сервис есть команда Анализ данных. Если нет, то выполните команду Сервис/Надстройки. В диалоговом окне Надстройки установите флажок Пакет анализа и щелкните по кнопке ОК.
2. Далее выполните команду Сервис/Анализ данных. Выберите инструмент анализа Регрессия из списка Инструменты анализа. Щелкните по кнопке ОК.
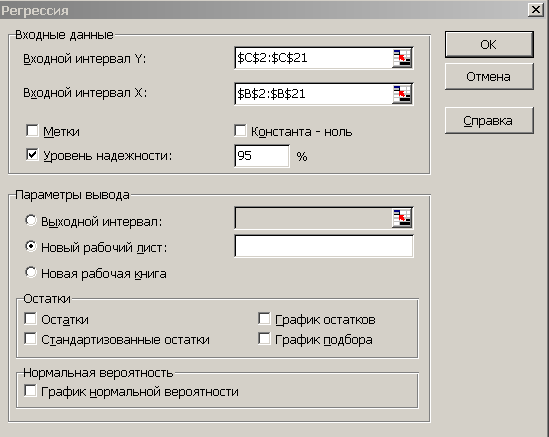
3. На экране появится диалоговое окно Регрессия (рис.4).
   • в текстовом поле ВХОДНОЙ ИНТЕРВАЛ Y введите диапазон со значениями зависимой переменной $C$2:$C$21.
   • в текстовом поле ВХОДНОЙ ИНТЕРВАЛ Х введите диапазон со значениями независимых переменных $В$2:$В$21.
   • Убедитесь, что в поле Уровень надежности введено 95 % и переключатель Параметры вывода установлен в положении Новый рабочий лист.
   • Щелкните по кнопке ОК.

Рис. 4 Диалоговое окно инструмента анализа Регрессия.

1. В результате на новом листе будет отображены результаты использования инструмента Регрессия (рис.5).

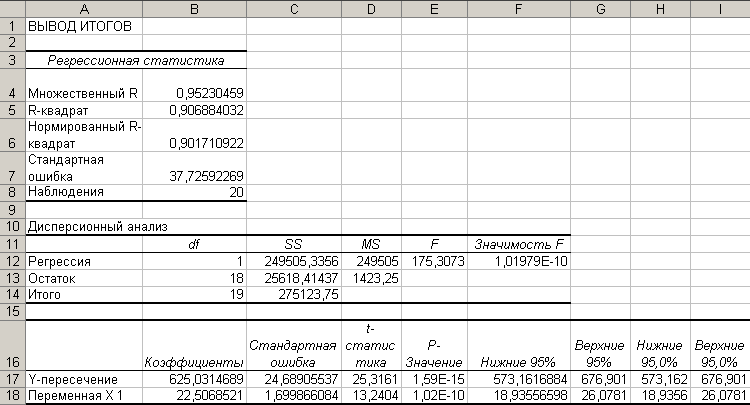
Рис. 5. Вывод итогов инструмента Регрессия.

1. Среди полученных результатов после применения инструмента Регрессия есть столбец «Коэффициенты», содержащий значение b в строке «Y-пересечение», а – в строке «Переменная Х1».
2. Сравните полученные результаты с ранее рассчитанными коэффициентами a и b.
3. Обратите также внимание на следующие показатели:

Столбец df — число степеней свободы (используется при проверке адекватности модели по статистическим таблицам):

Столбец SS (сумма квадратов):

Столбец MS — вспомогательные величины:

Столбец F — критерий Фишера. Используется для проверки адекватности модели: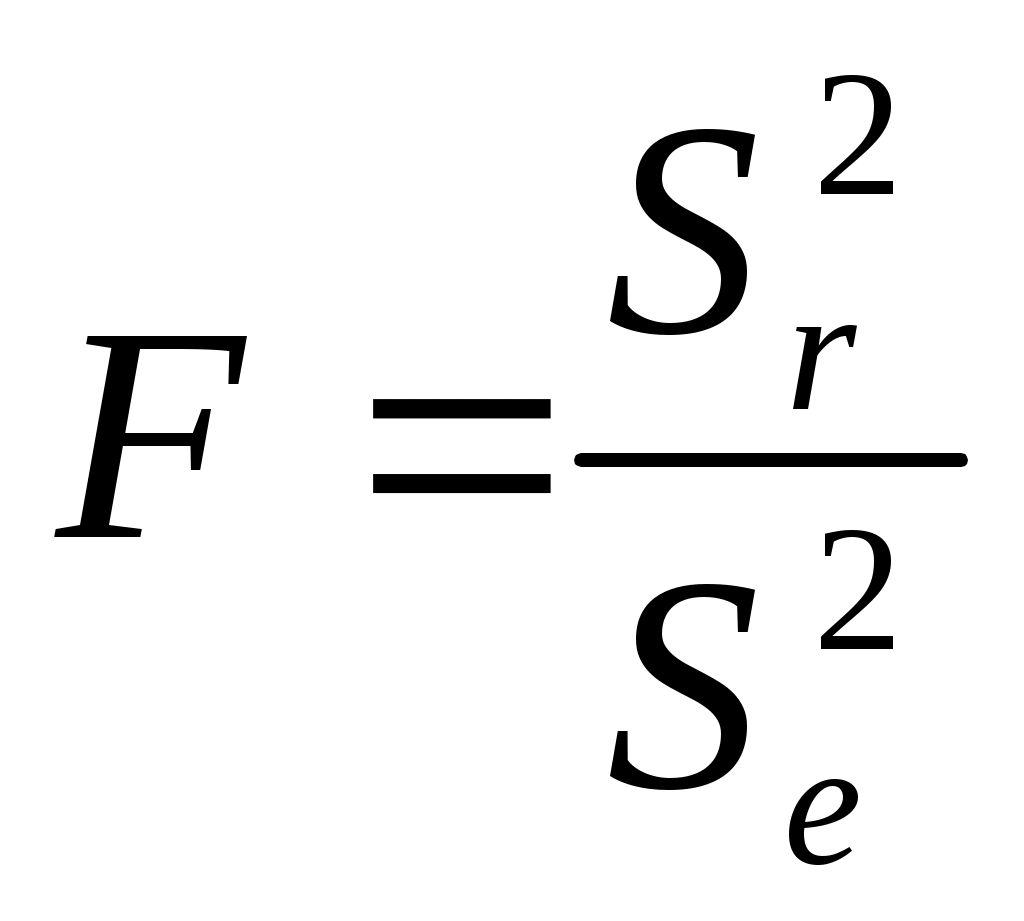
.

Столбец Значимость F — оценка адекватности построенной модели. Находится по значениям F, и с помощью функции FРАСП. Если Значимость F меньше 0,05, то модель может считаться адекватной с вероятностью 0,95.

Стандартная ошибка, t-статистика — это вспомогательные величины, используемые для проверки значимости коэффициентов модели.

Р — величина — оценка значимости коэффициентов модели. Если Р — величина меньше 0,05, то с вероятностью 0,95 можно считать, что соответствующий коэффициент модели значим (т.е. его нельзя считать равным нулю и Y значимо зависит от соответствующего Х).

Нижние и верхние 95 — доверительные интервалы для коэффициентов модели.
Задание 3. Выбор наиболее точной модели связи.

Условие задачи. Исследуется зависимость дозы облучения от толщины слоя защитного материала. Имеются результаты 10 экспериментов (см. рис.6).

Имеются основания предполагать, что зависимость дозы (функция) от толщины
слоя материала (аргумент) может выражаться одним из следующих уравнений:

• Y=A₀ + A₁*X (линейная модель);
• Y=A₀* (степенная модель);
• Y=A₀+A₁/X (гиперболическая модель).

Выберите наиболее точную модель и определите ее коэффициенты.

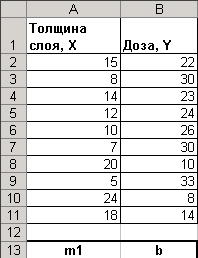
Рис.6 Исходные данные.

1. Создайте на новом листе таблицу согласно рис. 6.
2. Постройте на этом же листе точечную диаграмму зависимости Y=f(X).
3. Нанесите на нее линейный и степенной тренды с уравнениями и величиной
   достоверности аппроксимации ( ).
4. Для построения гиперболической модели преобразуйте модель в линейную, получив в ячейках С2:С11 величину 1/Х. А в ячейку С1 введите заглавие: «Величина U=1/X».
5. Используя функцию ЛИНЕЙН, получите в ячейках А14:В14 коэффициенты уравнения m1 и b (т.е. уравнение Y= b+m1*U).
6. В ячейку A16 введите заголовок «Гиперболическая модель». В ячейку A17 введите уравнение Y= b+m*x (вместо b и m укажите конкретные числа).
7. Для построенной гиперболической модели найдите величину достоверности
   аппроксимации. Для этого найдите сначала среднее значение c помощью функции СРЗНАЧ в ячейке D2. В ячейку D1 введите заглавие «Ср. знач. Y».
8. В столбце E2:E11 получите модельные значения путем подстановки значений U из блока ячеек С2:С11 в построенную модель. Для этого в ячейку E2 введите формулу =$B$14+$A$14*C2. Скопируйте формулу вниз в смежные ячейки. В ячейку E1 введите заголовок: «Модельные значения Y».
9. Найдите сумму квадратов , скорректированную на среднее: . Для этого в столбце F2:F11 получите разность . В ячейку F1 введите заголовок: «Yi—Ycp.».
10. В столбце G2:G11 получите квадраты разностей, а в ячейку G1 введите заголовок: «( ».
11. В ячейке Н2 получите итоговую сумму, а в ячейку Н1 введите заголовок: «SSy».
12. Аналогичным образом найдите сумму квадратов прогнозируемых (модельных) значений, скорректированную на среднее . Для этого используйте столбцы I, J, K.
13. Найдите величину достоверности аппроксимации: в ячейке L2.
14. По значениям коэффициентов достоверности аппроксимации выберите наиболее точную модель, которая соответствует максимальному коэффициенту достоверности.
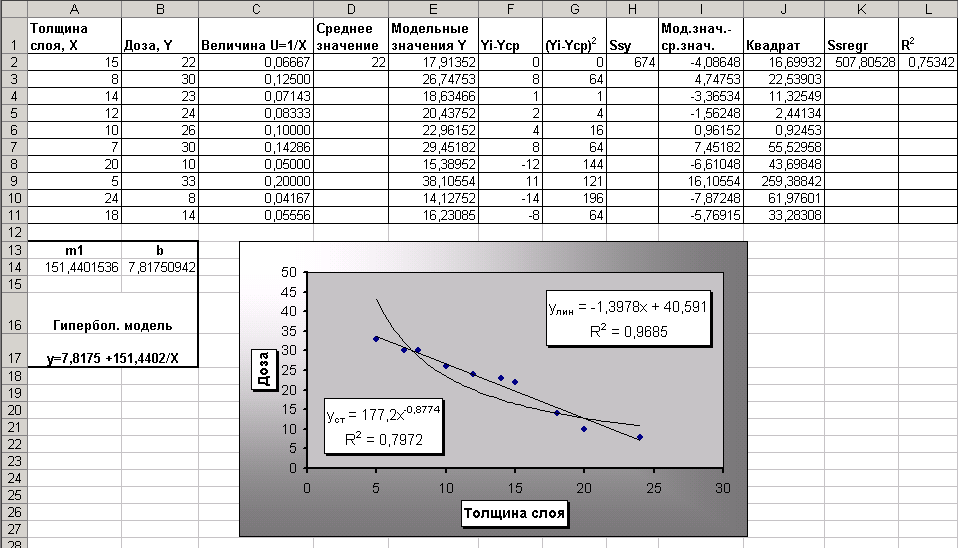
15. Копия экрана Задания 3. приведена на рис. 7.

Рис. 7. Расчеты гиперболической модели.

1. Проверьте правильность вычислений, воспользовавшись инструментом анализа Регрессия.

Задания для самостоятельной работы.

1. Имеются данные по двум экономическим показателям X и Y. Необходимо:

• Вычислить коэффициент корреляции.
• Построить корреляционное поле.
• Построить регрессионную модель (с использованием функции ЛИНЕЙН).

Цена (X)	997	987	1002	1012	1011	1017	978	997	1010	989
Спрос (Y)	120	140	115	100	100	90	150	130	95	155

2. Установить, зависит ли количество посетителей музея и посетителей парка от числа ясных дней за определенный период. Для этого:

• Вычислить коэффициенты корреляции.
• Построить корреляционное поле.
• Построить регрессионную модель (графическим способом и с помощью инструмента Регрессия).

Число ясных дней (Х)	8	14	20	25	20	15
Количество посетителей музея (Y)	495	503	380	305	348	465
Количество посетителей парка (Y)	132	348	643	865	743	541