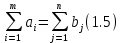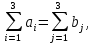Лабораторная работа транспортная задача в excel

Транспортная
задача –
это задача о минимизации транспортных
расходов, связанных с обеспечением
пунктов потребления определенным
количеством однородной продукции,
производимой в нескольких пунктах
производства [1, 3, 7]. В общем виде задача
может быть сформулирована следующим
образом.

Однородный
продукт, сосредоточенный в

пунктах производства, необходимо
распределить между

пунктами потребления. Стоимость перевозки
единицы продукции известна для всех
маршрутов. Необходимо составить такой
план перевозок, при котором запросы
всех пунктов потребления были бы
удовлетворены за счет имеющихся продуктов
в пунктах производства и общие транспортные
расходы по доставке продуктов были бы
минимальными.

Примем
следующие обозначения: i
– номер пункта производства, j
–номер пункта потребления,
–
количество продукта, имеющееся в i-ом
пункте производства,

– количество продукта, необходимое для
j-го
пункта потребления,

– стоимость перевозки единицы продукта
из i-го
пункта производства в j-й
пункт потребления,

– количество груза, планируемого к
перевозке из i-го
пункта производства в j-й
пункт потребления, i=1,2,…,m;
j=1,2,…,n.
Математическая модель транспортной
задачи будет выглядеть следующим
образом:

Условия
задачи удобно записывать в виде таблицы,
которая называется матрицей
планирования:

с11 с12 … с1n . . . сm1 сm2 … сmn	a1 … am
b1 b2 … bn

Рассмотрим решение
транспортной задачи в табличном
процессоре MS
Excel.
Так как транспортная задача является
частным случаем задачи линейного
программирования, то эту задачу можно
решать так, как описано выше. Однако
благодаря свойствам задачи, ее можно
записать в более компактной форме.

Рассмотрим
транспортную задачу, матрица планирования
которой имеет вид:

Bj Ai	B1	B2	B3	B4	B5
A1	14	25	18	19	23	33
A2	2	17	16	24	2	25
A3	29	3	7	15	22	25
A4	5	20	17	23	10	17
	33	11	11	11	34	bj ai

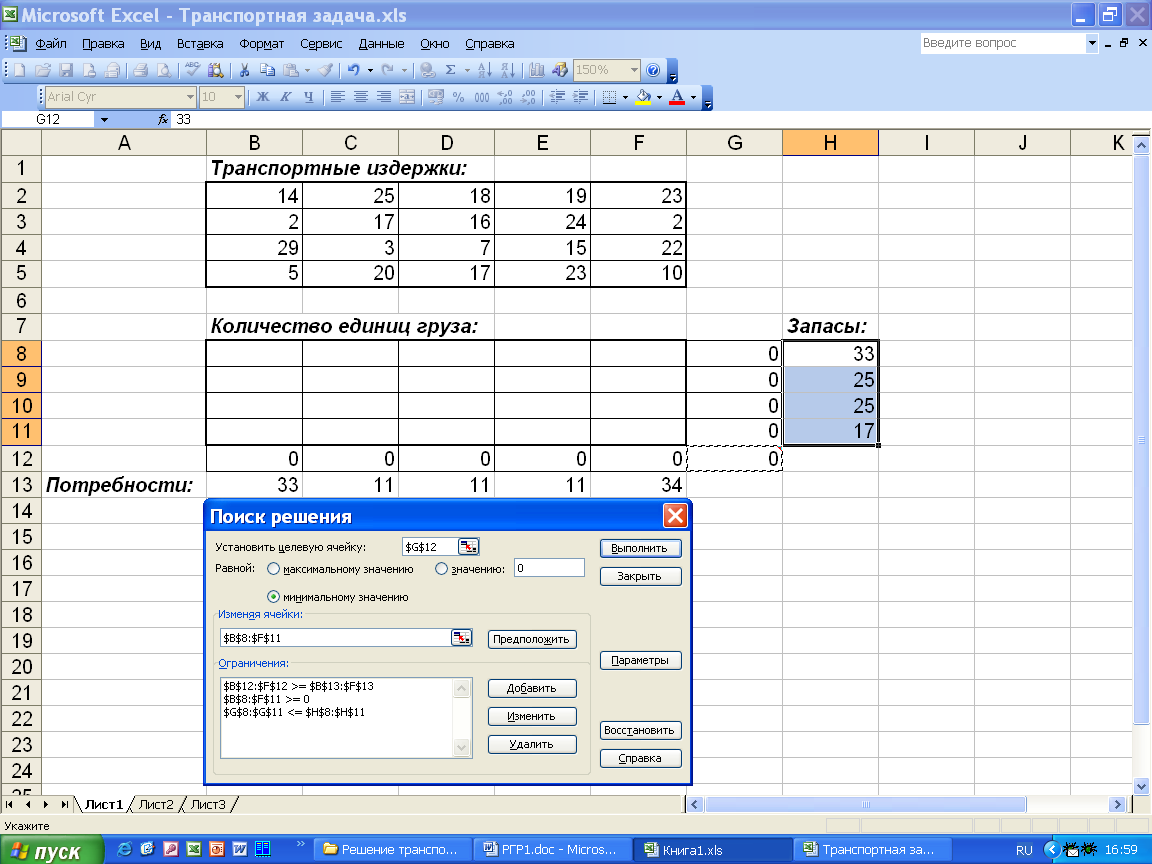
Для решения
транспортной задачи введем данные, как
показано на рис.6.

Рис.6.
Исходные данные транспортной задачи.

В
ячейки
B2
: F5
введем стоимость перевозок. Ячейки B8
: F11
отведены под значения объемов перевозок,
пока не­известные. В ячейки H8
: H11
введены объемы производства, а в ячейки
B13
: F13
— потребности (спрос) в продукции в
пунктах потребления.

В
ячейку G12
вводится целевая функция

=
СУММПРОИЗВ (B2
: F5;
B8
: F11)
.

В
ячейки B12
: F12
вводятся формулы

=
СУММ (B8
: B11),

=
СУММ (C8
: C11),

=
СУММ (D8
: D11),

=
СУММ (E8
: E11),

=
СУММ (F8
: F11),

определяющие объем
продукции, ввозимой в пункты потребления.
В ячейки

G8
: G11
введены формулы

= СУММ (B8
: F8),

= СУММ (B9
: F9),

= СУММ (B10
: F10),

= СУММ (B11
: F11),

характеризующие
объем продукции, вывозимой из пунктов
производства.

Далее выбираем
команду Сервис,
Поиск решения и
заполняем
открывшееся диалоговое окно Поиск
решения, как
показано на рис.7.

Рис.7.
Диалоговое окно Поиск
решения
для транспортной задачи.

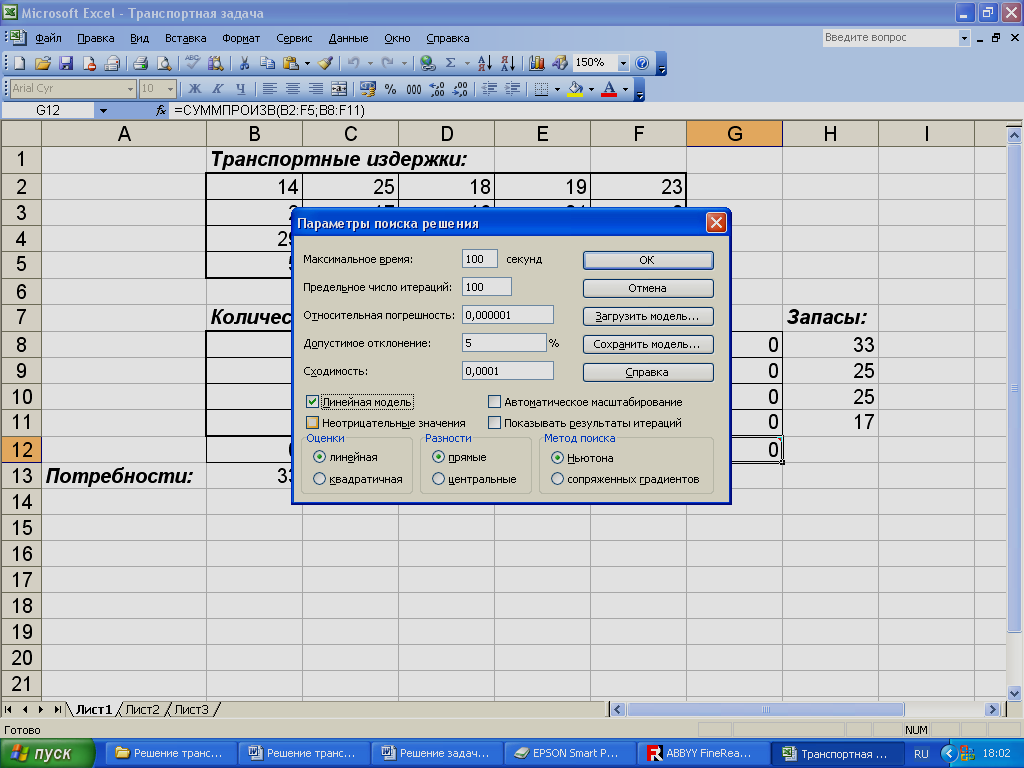
В диалоговом окне
Параметры
поиска решения установить
флажок Линейная
модель (рис.8).

Рис.8.
Диалоговое окно Параметры
поиска решений.

После нажатия
кнопки Выполнить
получаем
оптимальный план поставок продук­ции
и соответствующие ему транспортные
расходы (рис. 9).

Рис.9.
Оптимальное решение транспортной
задачи.

Соседние файлы в папке 5_Практикум

• #
• #

Цель работы: изучение технологии решения транспортных задач линейного программирования с использованием инструмента поиска оптимальных решений табличного процессора MS Excel.

Постановка задачи. Рассматривается логистическая задача минимизации затрат на доставку товаров от нескольких производителей, источников (заводов, складов) к нескольким потребителям (складам, магазинам). Поставка товара от конкретного производителя конкретному потребителю обычно может быть выполнена несколькими маршрутами с разной стоимостью перевозки по ним. Поэтому возможно определение оптимального маршрута и, соответственно, минимальной стоимости доставки единицы товара от конкретного производителя до потребителя. Особенностью задачи является однородность груза: потребителю не важно, с какого склада и каким маршрутом привёзен заказанный товар. Стоимость доставки любой партии условно принимается пропорциональной стоимости доставки единицы товара (вид транспорта, снижение/повышение стоимости доставок малых/крупных партий не учитывается). Подобные задачи решаются на уровне территориально распределённых транспортных, логистических и торговых компаний, подобным образом может осуществляться маршрутизация информации в сетях связи.

Исходные данные

1. Число поставщиков N и общее количество потребителей M. Для определённости принимается N = 5 и M = 3, что отражается в размерности последующих таблиц

2. Стоимости доставки единицы товара от каждого поставщика до каждого потребителя сведены в матрицу стоимостей перевозок С с элементами , где i = 1. M — номер потребителя; j = 1. N — номер поставщика.

Таблица 2.5.1

Таблица стоимостей перевозок

Стоимость перевозки единицы товара от поставщика к потребителю	Поставщики
1	2	3	4	5
Потребители	А
Б
В

3. Каждый поставщик характеризуется наличием ресурса, где i = 1. N — номер поставщика.

4. Каждый потребитель характеризуется величиной потребности в ресурсе , где j = 1. M — номер потребителя

Описание решения

Предполагается, что транспортная задача сбалансированная, то есть запросы потребителей равны располагаемым ресурсам поставщиков:

. (2.5.1)

Требуется определить такие элементы матрицы перевозок (i = 1. M — номер потребителя; j = 1. N — номер поставщика), чтобы все потребности потребителей были обеспечены, все ресурсы поставщиков были потрачены, а общая стоимость затрат на перевозки W (целевая функция) была минимальной.

Таблица 2.5.2

Таблица объёмов перевозок

Объем перевозки товара от поставщика к потребителю	Поставщики
1	2	3	4	5	Потребность
Потребители	А
Б
В
Объём располагаемого ресурса

Целевая функция имеет вид

. (2.5.2)

Особенностью численного решения данной задачи является неотрицательность всех элементов матрицы объёмов перевозок: у программного пакета появляется «соблазн» уменьшения целевой функции за счёт выполнения некоторых перевозок в обратных направлениях, что математически соответствует получению прибыли от таких перевозок. Поэтому при решении транспортной задачи обязательным является ограничение на положительность объёмов перевозок

. (2.5.3)

Для сбалансированной задачи ограничениями при поиске целевой функции будут являться использование всех имеющихся ресурсов каждого поставщика (2.5.4) и обеспечение потребностей каждого покупателя (2.5.5):

для j = 1. M; (2.5.4)

для i = 1. N. (2.5.5)

Возможны два варианта несбалансированной задачи.

1. Суммарные потребности поставщиков превосходят общие потребности потребителей, т.е.

. (2.5.6)

Тогда все потребности потребителей должны быть выполнены, а некоторая часть ресурсов поставщиков окажется неизрасходованной, что приведёт к изменению знака в условии (2.5.4) с равенства на неравенство

2. Потребности потребителей превосходят имеющиеся ресурсы поставщиков, т.е.

. (2.5.7)

Тогда запросы потребителей будут обеспечены не полностью, что приведёт к изменению знака в условии (2.5.5) с равенства на неравенство.

В настоящей лабораторной работе транспортная задача будет решаться с помощью надстройки Поиск решения табличного процессора MS Excel.

Порядок решения задачи

1. Подготовка шаблона для решения задачи

По образцу фрагмента рабочего листа MS Excel, изображённого на рис.2.5.1, введите на новом листе матрицы объёмов и стоимостей перевозок. Транспортная задача пока не решена, поэтому матрица объёмов перевозок пока пуста. В рассчитываемые ячейки введите формулы, приведённые в табл.2.5.3

	A	B	C	D	E	F	G	H	I
1	Таблица стоимостей перевозок
2			Оптовые базы
3	1	2	3	4	5
4	Магазины	А	10	8	6	5	4
5	Б	6	5	4	3	6
6	В	3	4	5	5	9
7
8	Таблица объёмов перевозок
9			Оптовые базы
10	1	2	3	4	5	Всего	Потребность
11	Магазины	А	250
12	Б	350
13	В	200
14	Всего
15	Мощность	120	200	190	210	80
16
17	Целевая функция

Рис. 2.5.1 Шаблон MS Excel для решения транспортной задачи

Таблица 2.5.3

Формулы Excel для решения транспортной задачи

Ячейка	Формула	Описание
1	2	3
H11	=CУММ (С11: G11)	Расчёт объёмов перевозок ресурса от всех оптовых баз (поставщиков) в каждый магазин (потребитель)
H12	=CУММ (С12: G12)
H13	=CУММ (С13: G13)
С14	=СУММ (C11: C13)	Расчёт объёмов перевозок ресурса от каждой оптовой базы (поставщика) всем магазинам (потребителям)
D14	=СУММ (D11: D13)
E14	=СУММ (E11: E13)
F14	=СУММ (F11: F13)
G14	=СУММ (G11: G13)
C17	=СУММПРОИЗВ (C4: G6; C11: G13)	Расчёт значения целевой функции — суммарной стоимости перевозок

2. Настройка сервиса Поиск решения

Откройте окно Поиск решения, выполнив команду Сервис Поиск решения. Укажите в качестве целевой — ячейку С17, установите переключатель целевой ячейки в положение «минимальное значение». Введите в качестве изменяемых ячеек диапазон С11: G13.

Нажатием кнопки Добавить (условие) в окне Поиск решения последовательно введите ограничения поиска решения (2.5.3) — (2.5.5):

Таблица 2.5.4

Ограничения решения задачи для окна Поиск решения

Ссылка на ячейку	Знак	Ограничение
$C$11: $G$13	>=	0
$C$14: $G$14	=	$C$15: $G$15
$H$11: $H$13	=	$I$11: $I$13

Получившееся окно Поиска решения изображено на рис. 2.5.2.

Рис. 2.5.2 Настройки окна Поиск решения для сбалансированной транспортной задачи

После нажатия кнопки Выполнить в диалоговом окне Поиск решения откроется окно Результаты поиска решения с текстом «Решение найдено». Сохраните найденное решение и нажмите кнопку ОК. Результатом решения задачи оптимизации является таблица перевозок, соответствующая суммарной стоимости перевозок (целевой функции), равной 3330.

3. Решение несбалансированной транспортной задачи: запросы потребителей превосходят возможности отправителей

Решаемая в п.1 — 2 задача является сбалансированной, т.е. потребности получателей равны возможностям отправителей. В этом можно убедиться, введя функции =СУММ (I11: I13) и =СУММ (С15: G15) в ячейки I14 и С16 соответственно. Увеличьте потребность магазина Б до 550. При этом суммарная потребность всех магазинов будет равна 1000, а пропускная способность всех оптовых баз — 800. Естественно, что суммарный объём перевозок в этом случае не превысит 800, так как пропускная способность и потребителей, и поставщиков не может быть превышена исходя из требований здравого смысла. Для решения задачи в третьем ограничении (см. рис.2.5.2 или последнюю строку табл.2.5.4) знак равенства замените на знак <=. После окончания процесса решения задачи суммарная стоимость перевозок (целевая функция) принимает значение 2990, т.е. уменьшится по сравнению со сбалансированной задачей. Однако магазины А и Б не обеспечивают свои потребности, так как возможности оптовых баз ограничены. Снижение общей стоимости перевозок при неизменном их объёме (800) стало возможным за счёт преобладания самых дешёвых маршрутов доставки: так, поставки в магазин Б увеличены с 350 до 520 единиц, а в магазин А — снижены с 250 до 80 единиц, так как в магазин Б доставлять товар в целом дешевле, чем в магазин А.

4. Решение несбалансированной транспортной задачи: предложение поставщиков превосходит потребности потребителей

Подобное соотношение на практике встречается чаще, чем в случае, рассмотренном в п.3. Восстановите потребность магазина Б до исходного значения 350, а пропускную способность (мощность) оптовой базы 5 увеличьте с 80 до 180 единиц. При этом суммарная потребность всех магазинов будет равна 800, а пропускная способность всех оптовых баз — 900. Суммарный объём перевозок в этом случае также не превысит 800 исходя из требований здравого смысла. Для решения задачи в третьем ограничении (см. рис.2.5.2 или последнюю строку табл.2.5.4) восстановите знак равенства, а во втором ограничении (см. рис.2.5.2 или последнюю строку табл.2.5.4) замените равенство на знак <=. После окончания процесса решения задачи суммарная стоимость перевозок (целевая функция) примет значение 3030, т.е. также уменьшится по сравнению со сбалансированной задачей. Однако на оптовой базе 2 образуется резерв пропускной способности 100 единиц, так как все потребности потребителей (магазинов) уже исполнены. Снижение общей стоимости перевозок при неизменном их объёме (800) также стало возможным за счёт выбора самых дешёвых маршрутов доставки.

5. Задача для самостоятельного решения

Имеется пять морских портов-отправителей грузов и четыре морских порта-получателя, между которыми необходимо оптимизировать перевозки. Таблица стоимостей перевозок, а также пропускные способности портов отправления и назначения по вариантам приведены в табл.2.5.5 и 2.5.6 Вариант задания выберите в соответствии с номером компьютера: первый вариант — для нечётных номеров, второй — для чётных.

Таблица 2.5.5

Исходные данные для самостоятельного решения транспортной задачи (вариант 1)

Исходные данные	Порт-отправитель	Пропускная способность получателя
1	2	3	4
Порт — получатель	А	20	12	30	23	140
В	47	14	38	18	160
С	18	49	15	28	240
D	23	34	22	30	180
E	34	45	28	22	160
Пропускная способность отправителя	200	350	180	150

Таблица 2.5.6

Исходные данные для самостоятельного решения транспортной задачи (вариант 2)

Исходные данные	Порт-отправитель	Пропускная способность получателя
1	2	3	4
Порт — получатель	А	40	24	60	46	70
В	94	28	76	36	80
С	38	98	29	56	120
D	46	68	90	60	90
E	68	90	60	44	80
Пропускная способность отправителя	100	175	90	75

5.1 Проверьте задачу на сбалансированность и решите её. Результаты решения сохраните на отдельном листе.

5.2 Решите несбалансированную задачу, аналогичную п.3. Для этого измените пропускную способность двух любых портов отправления на 20 единиц. Результаты решения сохраните на отдельном листе.

5.3 Решите несбалансированную задачу, аналогичную п.4. Для этого измените пропускную способность трёх любых портов назначения на 30 единиц. Результаты решения сохраните на отдельном листе.

Покажите полученную рабочую книгу MS Excel преподавателю.

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.

Транспортная задача: описание

С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.

Транспортные задачи бывают двух типов:

• Закрытая – совокупное предложение продавца равняется общему спросу.
• Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).

Подготовительный этап: включение функции “Поиск решения”

Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:

1. Открываем меню “Файл”.
2. В перечне слева выбираем пункт “Параметры”.
3. В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
4. В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
5. В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.

Пример задачи и ее решение

Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.

Условия задачи

Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.

Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).

Алгоритм решения

Итак, приступи к решению нашей задачи:

1. Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
2. Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
3. В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
4. На экране отобразится окно, в котором нужно заполнить аргументы:
   • в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
   • в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
   • по готовности жмем OK.
5. Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
6. На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
7. Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
8. В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
9. Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
10. Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
11. В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
12. С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
13. Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
14. Перед нами появится окно с параметрами функции:
    • в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
    • для параметра “До” выбираем вариант – “Минимум”.
    • в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
    • нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
15. Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
    • становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
    • затем выбираем знак “равно”.
    • в качестве значения для параметра “Ограничение” указываем координаты  аналогичного столбца в исходной таблице.
    • щелкаем OK по готовности.
16. Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
17. Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
    • больше или равно нулю;
    • целое число.
18. В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
19. В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
20. Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Заключение

Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.

---

Подборка по базе: Практическая работа № 1.doc, практическая работа.docx, Самостоятельная работа 2.docx, практическая работа.docx, Практическая работа 1 Организация оплаты труда персонала.doc, Практическая работа.docx, Контрольная работа_Деловая этика.doc, самостоятельная работа 1.docx, ср работа газа.docx, Практическая работа № 2.doc

---

ЛАБОРАТОРНАЯ РАБОТА №2

Использование MS Excel для решения транспортной задачи

ТИТУЛЬНИК!!!!

1. Цели и задачи лабораторной работы

Цель работы – овладение навыками работы различных пакетов прикладных программ для решения задач нелинейного программирования.

Задачи – составить математическую модель задачи определенного варианта и найти ее решение с использованием пакета MS Excel.

1. Решение транспортной задачи с помощью функции «Поиск решения»

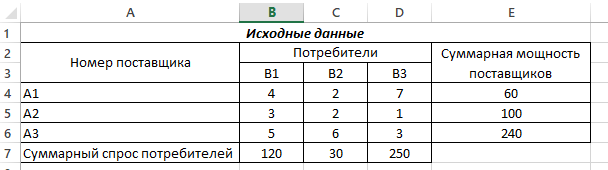
Задание: Рассматривается следующая транспортная задача.

Номер потребителя Номер поставщика	1	2	3	Суммарная мощность поставщиков
1	4	2	7	60
2	3	2	1	100
3	5	6	3	240
Суммарный спрос потребителей	120	30	250

В 5-м столбце указаны мощности поставщиков, в 5-й строке — спрос потребителей. Остальные числа таблицы — это стоимость перевозки единицы груза от соответствующего поставщика к соответствующему потребителю. Таким образом, стоимость перевозки единицы груза от 3-го поставщика ко 2-му потребителю равна 1 ден.ед. Необходимо составить оптимальный план поставок при котором затраты будут минимальными.
Решение
Транспортная задача относится к специальным задачам линейного программирования. Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из i пунктов от- правления A₁, A₂, … Aᵢ, в j пунктов назначения B₁, B₂, … Bⱼ.

При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через cᵢⱼ тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через aᵢ– запасы груза в i-м пункте отправления, через bⱼ– потребности в грузе в j-м пункте назначения, а через xᵢⱼ количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка транспортной задачи состоит в определении минимального значения функции:

(1.1)

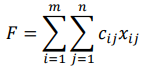
при условиях:

(1.2)

(1.3)
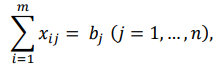
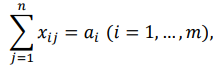
(1.4)
Функция (1.1) называется целевой функцией задачи. Поскольку переменные xᵢⱼ удовлетворяют системам линейных уравнений (1.2) и (1.3) и условию неотрицательности (1.4), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки. План X*=(x*ᵢⱼ)(i=1,2…m; j=1,2…n), при котором функция (1.1) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.

Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, то есть выполняется равенство (1.5), то модель такой транспортной задачи будет закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.

В таком случае, решение транспортной задачи при помощи MS Excel будет иметь следующий алгоритм:

1. Занесем исходные данные в MS Excel (Рис. 1).

Рис. 1 – Исходные данные транспортной задачи в MS Excel

Проверяем – открытая модель или закрытая. Для этого необходимо проверить выполняется ли уравнение:

где ai — объем производства на i-м филиале (i = 1, 2, 3); bj — объем потребления j-м потребителем (j = 1, 2, 3).

В нашем случае модель закрытая (120 + 30 + 250 = 60 + 100 + 240 = 400).

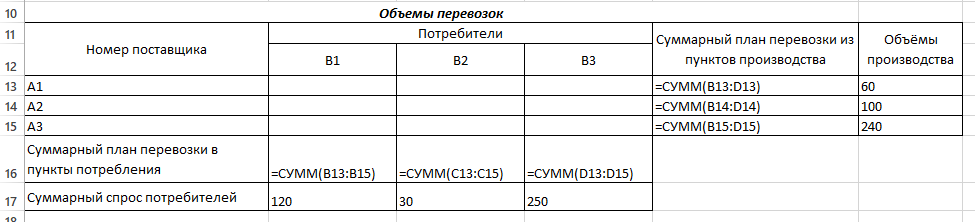
1. Обозначим X_ij – количество товара, перевозимое от i-го поставщика j-му потребителю (i = 1, 2, 3; j = 1, 2, 3). Выделим под переменные X_ij ячейки B13:D15 (Рис. 2).

Рис. 2 – Подготовка к решению транспортной задачи

1. В ячейках B16:D16 будем рассчитывать сумму поставок каждому потребителю. Для этого воспользуемся функцией СУММ. Аналогично в ячейках E13:E15 рассчитаем суммарные поставки каждого поставщика.
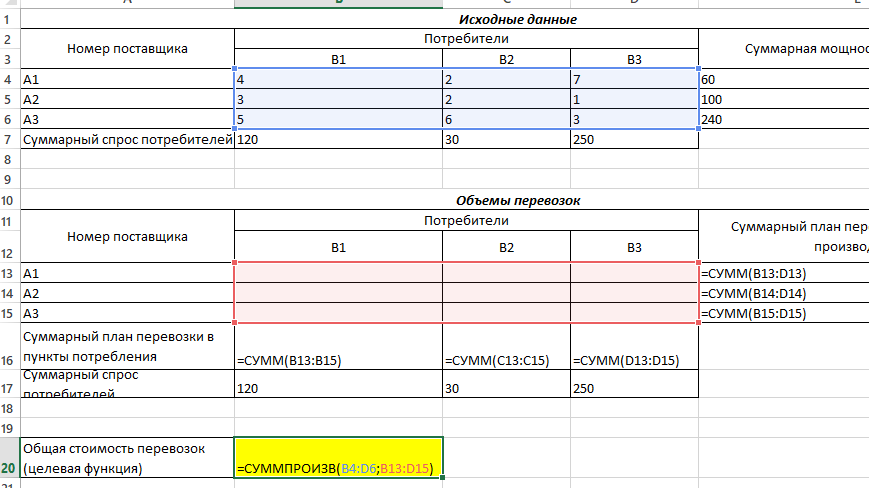
2. В ячейку B20 запишем целевую функцию – суммарные затраты на осуществление всех поставок.

+5 →min

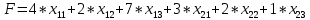
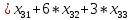
1. Эта функция вычисляется как сумма произведения величин поставок X_ij на соответствующую им стоимость. Для этого воспользуемся функцией СУММПРОИЗВ (Рис. 3).

Рис. 3 – Целевая функция транспортной задачи

1. Выделим ячейку с формулой целевой функции. Запустим надстройку «Поиск решения». В диалоговом окне в поле ввода «Установить целевую» ячейку уже содержится $В$20. Установим переключатель «Равной минимальному значению». В поле ввода «Изменяя ячейки» нужно указать величины поставок X_ij, т.е. выбрать ячейки B13:D15 (Рис. 4).

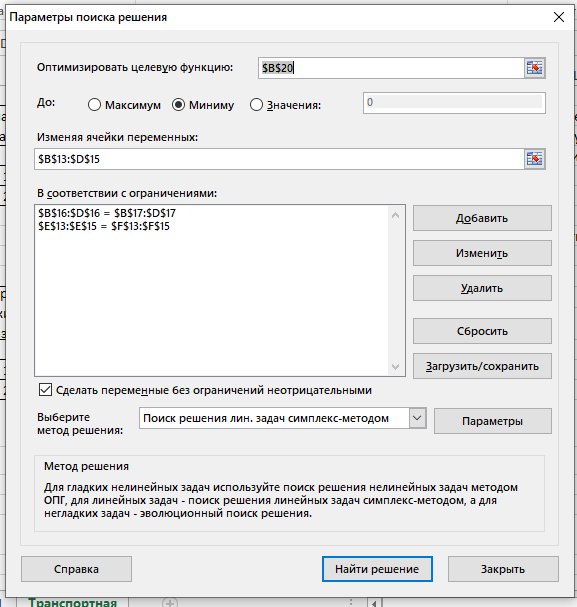
Рис. 4 – Окно «Поиск решения»

1. Щелкаем кнопку «Добавить». И в появившееся диалоговое окно «Добавление ограничения» пропишем необходимые ограничения по суммарным спросу и мощности.
2. Нажимаем кнопку «Выполнить». И получим необходимые значения (Рис. 5).

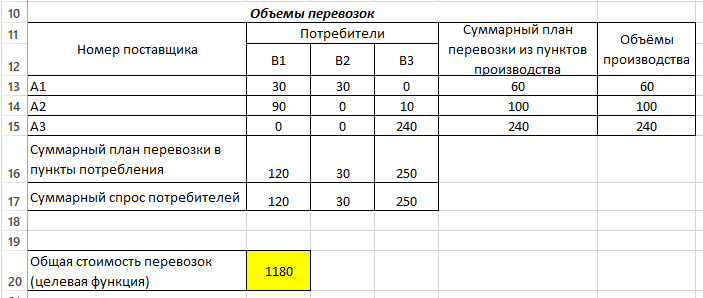
Рис. 5 – Результаты решения задачи
В ячейке В20 указано 1180 ден.ед. Это минимальные затраты на перевозку. В ячейках B13:D15 указаны значения для рассчитанного оптимального плана поставок:

1-й поставщик должен доставить 30 единиц груза 1-му потребителю и 30 единиц груза 2-му потребителю.

2-й поставщик должен доставить 90 единиц груза 1-му потребителю и 10 единиц груза 3-му потребителю.

3-й поставщик должен доставить 240 единиц груза 3-му потребителю.

Список литературы

1. Лесин В.В., Лисовец Ю.П. Основы методов оптимизации: Учебное пособие. – Спб.: Издательство «Лань», 2011. – 352 с. – ISBN 978-5-8114-1217-4 http://e.lanbook.com/view/book/1552/>
2. Дьяконов В.П. MATLAB 7.*/R2006/R2007: Самоучитель. – М.: ДМК Пресс., 2009. – 768 с. – ISBN 978-5-94074-424-5

http://e.lanbook.com/view/book/1178/>

1. Сдвижков О.А. Дискретная математика и математические методы экономики с применением VBA Excel. – М.: ДМК Пресс, 2012. – 212 с. – ISBN 978-5-94074-655-3 http://e.lanbook.com/view/book/4151/>