Задание
Для
случайной выборки объемом n=50
с несовпадающими числами выполнить
следующую последовательность действий:
1.Вывести
на лист Excel
исходные статистические данные.
2. Построить
вариационный ряд.
3. Вычислить
статистические характеристики.
4. Построить
интервальный статистический ряд.
5.Построить
гистограмму частот.
6. Составить
статистическую функцию распределения
статистического ряда.
7.
Составить и постоить статистическую
функцию распределения группированного
статистического ряда.
В качестве примера
рассмотрим следующую выборку
Порядок выполнения работы
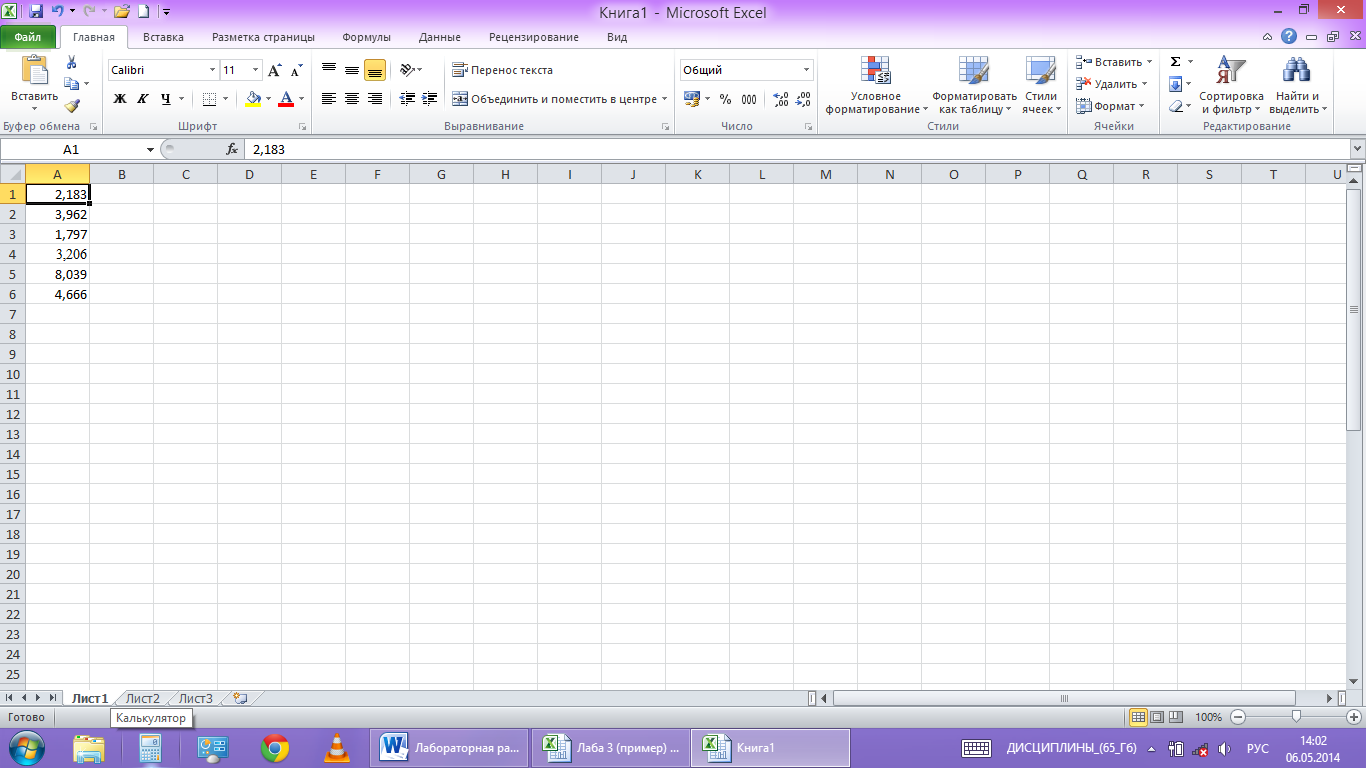
1.Ввод исходных статистических данных.
Вводим данные в
первый столбец таблицы (рис.1).
рис.1
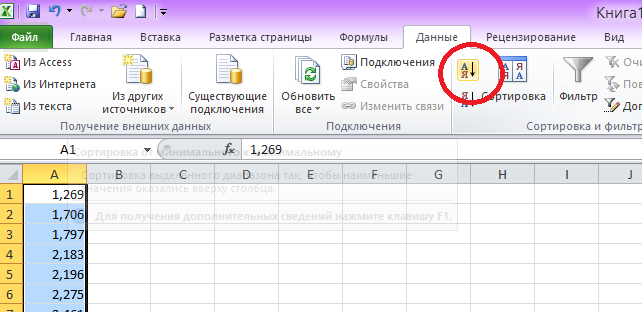
2. Построение вариационного ряда.
Производим
сортировку данных в порядке возрастания.
Для этого:
а) выделяем первый
столбец;
б)
на ленте
во вкладке «Данные» выбираем «Сортировка
и фильтр» (рис.2)
рис. 2
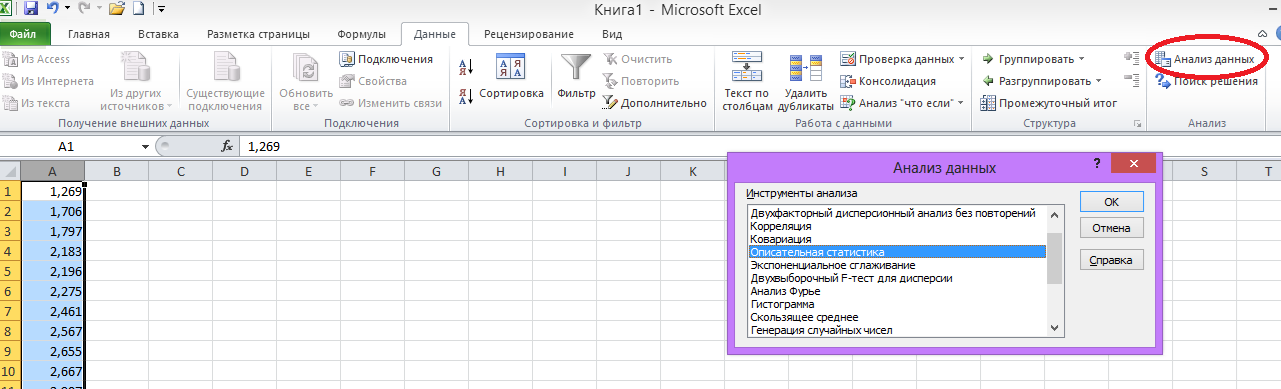
3. Вычисление статистических характеристик.
На ленте
во вкладке «Данные» выбираем «Анализ
данных» меню «Описательная статистика»
нажимаем ОК.
рис. 3
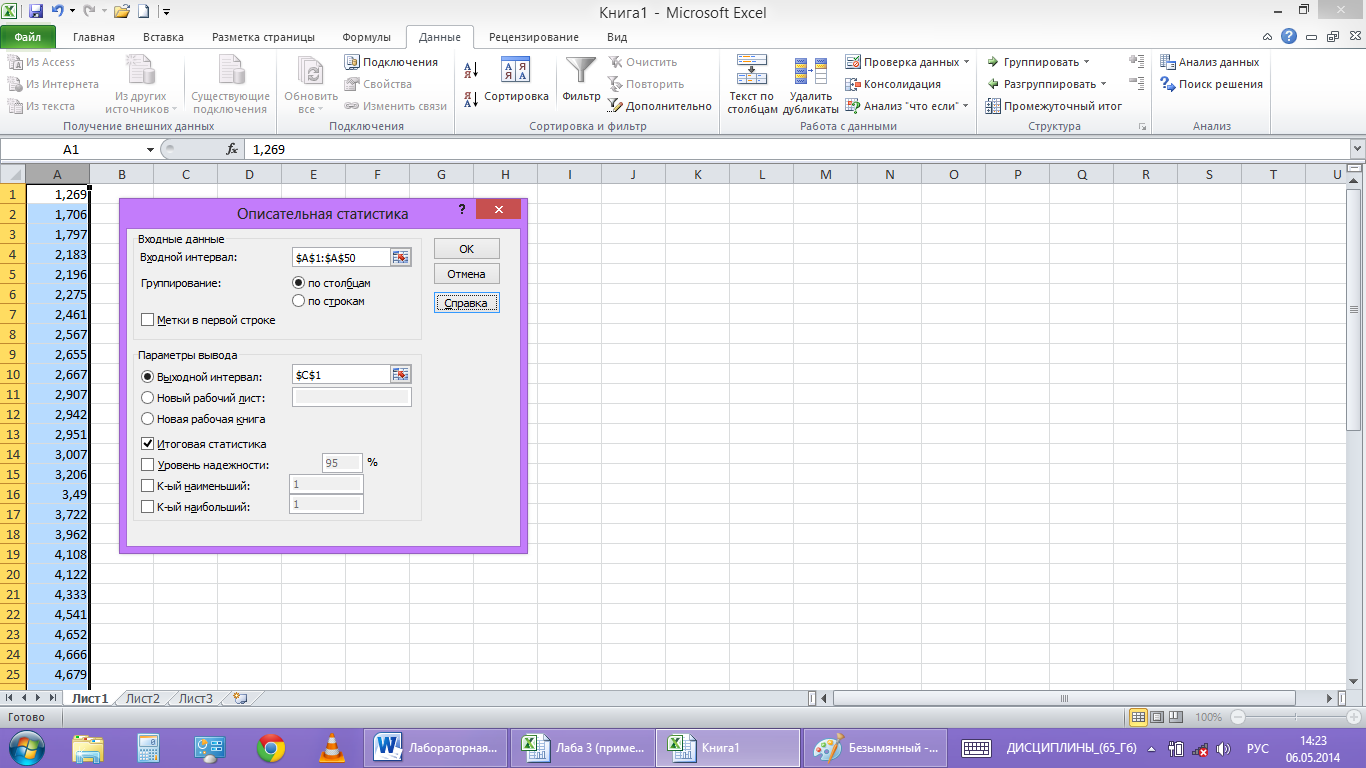
В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
а в пункте «Выходной интервал» обозначим
первую ячейку для записи результаов
$C$1.
Ставим флажок напротив пункта «Итоговая
статистика» и нажимаем ОК.(рис.4)
рис. 4
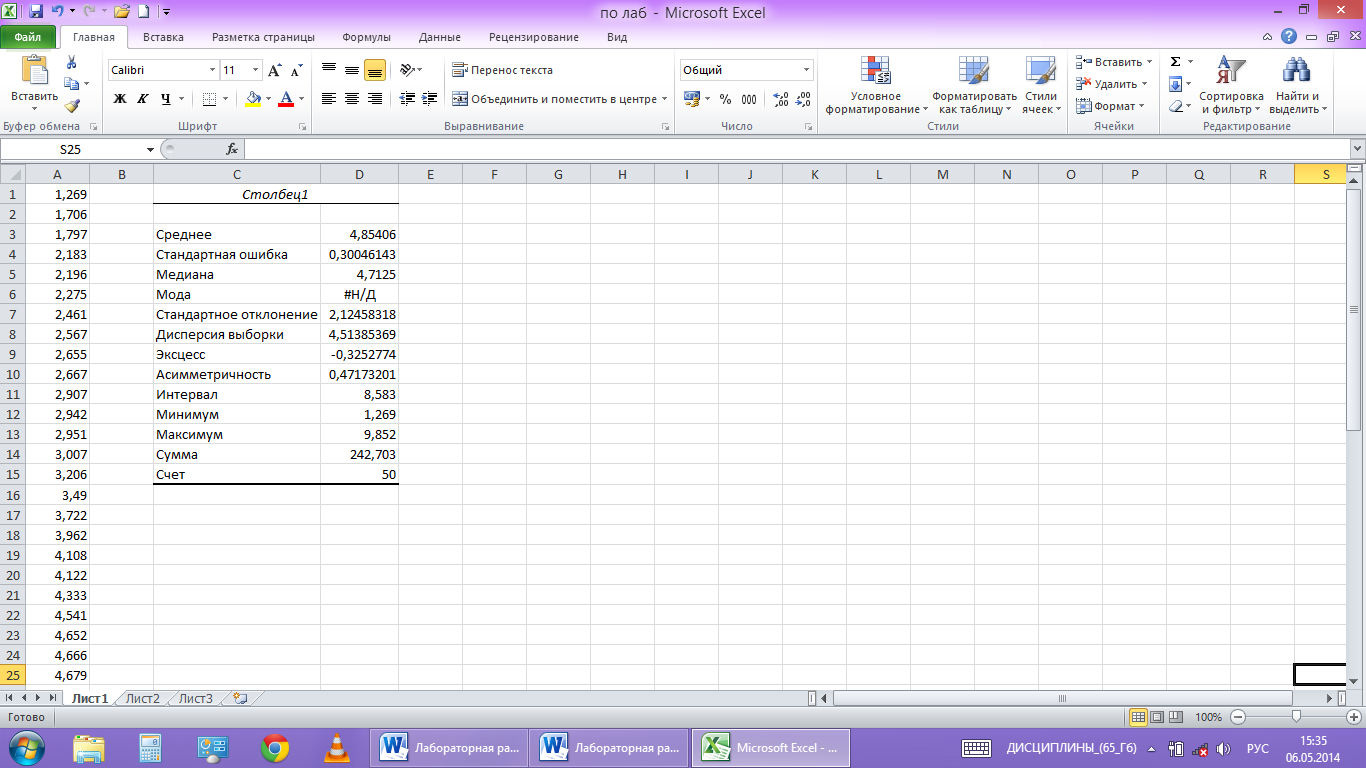
На
рабочем листе появляется таблица с
вычисленными значениями числовых
характеристик выборки (рис.5)
рис. 5
Здесь
«Среднее»означает математическое
ожидание выборки, а «Стандартная ошибка»
— погрешность ее значения. «Дисперсия
выборки» означает исправленную выборочную
дисперсию, а «Стандартное отклонение»
— исправленное среднее квадратичное
отклонение. Положительное значение
«Асимметричности» означает, что «длинная
часть» кривой лежит правее моды.
Отрицательное значение «Эксцесса»
означает, что кривая имеет более низкую
и «плоскую» вершину, чем нормальная
кривая. «Интервал» равен разности
Xmax−Xmin.
«Сумма»
дает результат суммирования всех
элементов выборки. «Счет» задает общее
число элементов выборки.
4. Построение интервального статистического ряда.
Длину интервала
группировки определяем по формуле
Необходимые данные
имеем в таблице: Xmax
– в ячейке D13,
Xmin–
в ячейке D12,
число элементов выборки n
— в ячейке D15.
В ячейку С16 вводим
слово «Интервал», в ячейку D16
вводим формулу
в ячейке D16
появится значение числа h.
В ячейку C17
вводим букву h.
В ячейку D17
вводим формулу
В ячейке
D17
получаем округленное до одного знака
после запятой значение интерала h.
Проведем формирование
интервалов. Для этого от Xmin
отступим влево примерно на h/2
и получим начальную точку отсчета.
Последовательно прибавляя к ней целое
число отрезков h,
получим все граничные точки интервалов.
В ячейку
F1
вводим формулу
В этой
ячейке появляется значение начальной
точки отсчета. В ячейку F2
вводим формулу
В этой
ячейке появляется значение второй
граничной точки первого интервала.
Возвращаемся в ячейку F2,
ставим курсор в правый нижний угол рамки
и двигаем его вниз, не отпуская левую
кнопку мыши. В результате такой процедуры
(протяжка) столбец F
заполнят граничные точки интервалов.
Самый нижний интервал должен включать
Xmax
(рис.6).
Проведем подсчет
числа вариант, попавших в каждый интервал,
определим относительные частоты и
серединные точки этих интервалов.
Для
этого на ленте во вкладке «Данные»
выбираем «Анализ данных» меню
«Гистограмма». (рис.
7)
|
|
|
|
рис. 6 |
рис. 7 |
В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
в пункт «Интервал карманов» — диапазон
ячеек с границами интервалов $F$1:$F$9.
Отметим точкой пункт «Выходной интервал»
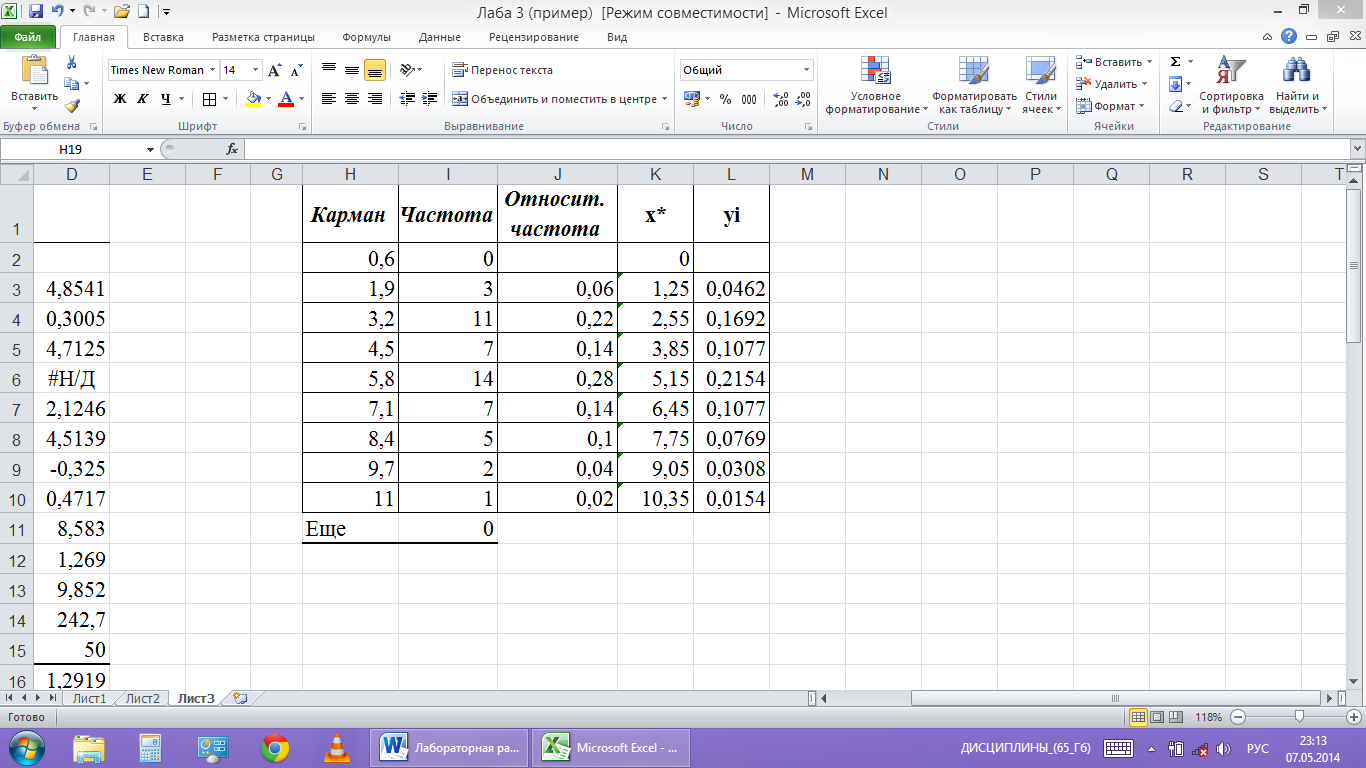
и введем в него адрес первой ячейки для
записи результатов $Н$1. Появится таблица
из двух столбцов с обозначениями «Карман»
и «Частота» (рис.8).
Определим
относительные частоты рi*,
значения серединных точек интервалов
и высоты
прямоугольников
Для этого
-
в ячейку
J1
введем заголовок «Относительная
частота»; -
В ячейку
J3
введем формулу
и
протягиваем её вниз до ячейки J10.
В результате к таблице из двух столбцов
добавится третий столбец (рис.8). В этой
таблице частота появления случайной
величины в каждом интервале записана
в одной строке с концом интервала;
-
в ячейку
K1
введем заголовок столбца Х*; -
в ячейку
К3 введем формулу
Протягиваем
эту формулу до ячейки К10. В результате
в четвертом столбце таблицы (рис.8)
появятся значения серединных точек
интервалов;
-
в ячейку
L1
введем заголовок столбца Уi; -
в ячейку
L3
введем формулу
Протягиваем
её вниз до ячейки L10.
В
результате в пятом столбце таблицы
(рис.8) появятся значения Уi.
рис.8
Соседние файлы в папке Лаб.работы
- #
- #
- #
- #
Лабораторная
работа
Тема:
Статистическая обработка данных MS Excel
Цель
работы:
· Получить
практические навыки отбора информации в электронной таблицы MS Excel по
заданным критериям.
· Закрепить
навыки редактирования и печати таблиц.
Используемые
программные средства: текстовый редактор MS Word,
табличный процессор MS Excel.
Оборудование: ПК,
принтер.
Литература: конспект
лекций.
Время на
выполнение:
2 часа
Порядок
выполнения работы:
1. В своей
папке создайте документ MS Excel и
назовите его «Создание простого документа»
2. Создайте
таблицу по предложенному образцу:
|
№ |
Планета |
Масса |
Диаметр |
Средняя |
Ускорение |
Расстояние |
Среднее |
Средняя |
|
1 |
Меркурий |
3,33022*1023 |
2440 |
5440 |
3,7 |
82 |
58 |
48 |
|
2 |
Венера |
4,8685*1024 |
6052 |
5240 |
8,8 |
38 |
108 |
35 |
|
3 |
Марс |
0,64185*1024 |
3394 |
3950 |
3,8 |
56 |
228 |
24,1 |
|
4 |
Земля |
5,9736*1024 |
6371 |
5518 |
9,81 |
0 |
152,1 |
30 |
|
5 |
Нептун |
|||||||
|
6 |
Плутон |
|||||||
|
7 |
Юпитер |
1,8986*1027 |
||||||
|
8 |
Сатурн |
|||||||
|
9 |
Уран |
3. Выполните
отбор планет в таблице по группам:
·
1
гр. – диаметр > 2 тыс. км, но меньше 7 тыс. км
·
2
гр. – от 7 тыс. км до 49 тыс. км
·
3
гр. – от 50 тыс. км и больше
4. Каждую
группу планет скопируйте на Лист 2 в виде отдельной таблицы.
5. Выполните
форматирование таблиц и их подготовку к печати.
6. Сохраните
созданный документ в своей папке.
Отчет
о работе должен содержать:
1. Название
лабораторной работы
2. Цель
работы
3. Используемые
программные средства
4. Содержание
заданий.
Лабораторная работа
Статистические функции Excel
Цель работы: Освоение приемов работы с функциями массивов (табличными функциями). Изучение элементарных статистических функций Excel
- Формулы массивов (табличные формулы)
Массивом называют блок ячеек электронной таблицы, который используется для создания формул, возвращающих некоторое множество результатов или оперирующих множеством значений, а не отдельными значениями.
Формулы массивов (иногда их называют табличными формулами), используют несколько множеств значений (массивов аргументов), и возвращают одно или несколько значений. Такие формулы позволяют обращаться с блоками, как с обычной ячейкой.
Рассмотрим работу с использованием массивов на следующем примере. Требуется определить прибыль для каждого года деятельности отеля, представленного в таблице 1.
Таблица 1.
Пример использования функций массива
|
A |
B |
C |
D |
|
|
1 |
Год |
Приход |
Расход |
Прибыль |
|
2 |
2005 |
200 |
150 |
{B2:B5-C2:C5} |
|
3 |
2006 |
360 |
230 |
{B2:B5-C2:C5} |
|
4 |
2007 |
410 |
250 |
{B2:B5-C2:C5} |
|
5 |
2008 |
200 |
180 |
{B2:B5-C2:C5} |
Выделим блок D2:D5. Начнем ввод формулы – наберем знак =. Выделим блок B2:B5, наберем знак минус -, выделим блок С2:С5. Ввод формул массива заканчивается комбинацией клавиш Ctrl+Shift+Enter. После нажатия такой комбинации во всех ячейках блока D2:D5 появится формула {B2:B5-C2:C5}.
- Основные правила работы с формулами массива:
- перед вводом формулы нужно выделить ячейку или диапазон для результатов, если формула возвращает несколько значений, то диапазон результатов должен быть того же размера, что и диапазон исходных данных;
- фигурные скобки, отмечающие формулу массива, вводятся при завершении ввода формулы клавишами Ctrl+Shift+Enter, если фигурные скобки ввести вручную, такой ввод будет воспринят Excel как текст.
- для редактирования формулы массива необходимо выделить блок, активировать строку формул, внести изменения и завершить редактированием клавишами Ctrl+Shift+Enter;
- блок ячеек может указываться присвоенным ему именем (клавиша F3 и выбор имени в диалоге «Вставка имени»;
- массив исходных данных и массив результатов могут быть многомерными, т.е. включать несколько строк и столбцов.
- Функции Excel, используемые для статистического анализа
Статистический анализ данных необходим для оценки деятельности фирмы и прогноза ее работы на какой-то срок. Такой анализ основывается на сборе информации, определении по представленным массивам данных оценок, статистических показателей и тенденций развития фирмы.
В категорию статистических функций Excel входит около 80 функций, кроме того, значительное число функций статистического анализа входят в надстройку «Пакет анализа».
Для выполнения задания потребуются статистические функции, полное описание которых приведено ниже.
- МАКС(число1;число2; …) — возвращает наибольшее значение из набора значений.
- Число1, число2,…— от 1 до 30 чисел, среди которых требуется найти наибольшее.
- Можно задавать аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел. Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, вызывают значения ошибок.
- Если аргумент является массивом или ссылкой, то в нем учитываются только числа. Пустые ячейки, логические значения или текст в массиве или ссылке игнорируются. Если логические значения или текст не должны игнорироваться, следует использовать функцию МАКСА. Если аргументы не содержат чисел, то функция МАКС возвращает 0 (ноль);
- МИН(число1;число2; …) — возвращает наименьшее значение из набора значений, в остальном полностью аналогична функции ^ МАКС;
- СРЗНАЧ(число1; число2; …) — возвращает среднее (арифметическое) своих аргументов.
- Число1, число2, … — это от 1 до 30 аргументов, для которых вычисляется среднее.
- Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.
- Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются;
ТЕНДЕНЦИЯ (известные_значения_y; известные_значения_x; новые значения_x; конст) — возвращает значения в соответствии с линейным трендом, т.е. аппроксимирует прямой линией (по методу наименьших квадратов) массивы ”известные_значения_y” и “известные_значения_x”. Возвращает значения y, в соответствии с этой прямой для заданного массива новые_значения_x.
- Известные_значения_y — множество значений y, которые уже известны для соотношения y = mx + b.
- Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная. - Известные_значения_x — необязательное множество значений x, которые уже известны для соотношения y = mx + b.
- Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные_значения_y и известные_значения_x могут иметь любую форму, при условии, что они имеют одинаковую размерность.
- Если используется более одной переменной, то известные_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец).
Если известные_значения_x опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_y. - Новые_значения_x — новые значения x, для которых ТЕНДЕНЦИЯ возвращает соответствующие значения y. Новые_значения_x должны содержать столбец (или строку) для каждой независимой переменной, как иизвестные_значения_x. Таким образом, если известные_значения_y — это один столбец, то известные_значения_x и новые_значения_x должны иметь такое же количество столбцов. Если известные_значения_y — это одна строка, то известные_значения_x и новые_значения_x должны иметь такое же количество строк.
- Если новые_значения_x опущены, то предполагается, что они совпадают с известные_значения_x.
- Если опущены оба массива известные_значения_x и новые_значения_x, то предполагается, что это массив {1;2;3;…} такого же размера, что и известные_значения_y.
- Конст — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
- Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.
- Если конст имеет значение ЛОЖЬ, то b полагается равным 0, и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
РОСТ(известные_значения_y;известные_значения_x;новые_значения_x; конст) — возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих x- и y-значений, т.е. функция рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных.
- Известные_значения_y — это множество значений y, которые уже известны в соотношении y = b*mx. Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная. Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
- Известные_значения_x — это необязательное множество значений x, которые уже известны для соотношения y=b*mx. Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_xинтерпретируется как отдельная переменная. Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные_значения_y иизвестные_значения_x могут иметь любую форму, при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец). Если известные_значения_x опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_y.
- Новые_значения_x — это новые значения x, для которых РОСТ возвращает соответствующие значения y. Новые_значения_x должны содержать столбец (или строку) для каждой независимой переменной, как иизвестные_значения_x. Таким образом, если известные_значения_y — это один столбец, то известные_значения_x и новые_значения_x должны иметь такое же количество столбцов. Если известные_значения_y — это одна строка, то известные_значения_x и новые_значения_x должны иметь такое же количество строк. Если аргумент новые_значения_x опущен, то предполагается, что он совпадает с аргументом известные_значения_x. Если оба аргумента известные_значения_x и новые_значения_x опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_y.
- Конст — это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 1. Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если конст имеет значение ЛОЖЬ, то b полагается равным 1, а значения m подбираются так, чтобы y = mx.
ПРЕДСКАЗ(x, известные_значения_y, известные_значения_x) – вычисляет или предсказывает будущее значение по существующим значениям. Предсказываемое значение — это значение y, соответствующее заданному значению x. Значения x и y известны; новое значение предсказывается с использованием линейной регрессии. Эту функцию можно использовать для прогнозирования будущих продаж, потребностей в оборудовании или тенденций потребления.
- Функция ПРЕДСКАЗ имеет аргументы, указанные ниже.
- x — обязательный аргумент. Точка данных, для которой предсказывается значение.
- Известные_значения_y — обязательный аргумент. Зависимый массив или интервал данных.
- Известные_значения_x — обязательный аргумент. Независимый массив или интервал данных.
- Если x не является числом, функция ПРЕДСКАЗ возвращает значение ошибки #ЗНАЧ!.
- Если аргументы «известные_значения_y» и «известные_значения_x» пусты или количество точек данных в этих аргументах не совпадает, функция ПРЕДСКАЗ возвращает значение ошибки #Н/Д.
- Если дисперсия аргумента «известные_значения_x» равна 0, функция ПРЕДСКАЗ возвращает значение ошибки #ДЕЛ/0!.
- Замечания
- 1) Формулы, которые возвращают массивы, должны быть введены как формулы массива.
2) При вводе константы массива для аргумента, такого как известные_значения_x, следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк.
- Задание
Для приведенных в таблице 2 данных о реализации гостиничных услуг сетью отелей «Европа» вычислить:
- минимальные, максимальные и среднее показатели по каждому кварталу;
- средние показатели по каждому отелю;
- вычислить средний доход по всей сети отелей за отчетный период;
- дать оценку работы каждого отеля: «хорошо», если доход отеля превышает средний по сети, и «плохо», если доход меньше среднего по сети;
- построить линейную и экспоненциальную модель деятельности сети отелей и дать прогноз для двух следующих кварталов;
- оценить относительные отклонения для среднего значения и «Тенденции», для среднего значения и «Роста».
^ Таблица 2.
Исходные данные
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Отель |
1 кв. |
2 кв. |
3 кв. |
4 кв. |
Среднее по |
Оценка |
|
отелю |
|||||||
|
2 |
Швеция |
1500 |
2000 |
6000 |
8000 |
||
|
3 |
Дания |
1400 |
5000 |
4100 |
5000 |
||
|
4 |
Норвегия |
3600 |
3600 |
3000 |
4500 |
||
|
5 |
Финляндия |
1100 |
1045 |
9100 |
7800 |
||
|
6 |
Германия |
3850 |
3650 |
7800 |
11000 |
||
|
7 |
Польша |
6800 |
7250 |
8122 |
9450 |
||
|
8 |
Чехия |
6590 |
7050 |
6400 |
6440 |
||
|
9 |
Словакия |
930 |
3970 |
4512 |
4600 |
||
|
10 |
Венгрия |
8912 |
7490 |
3570 |
8000 |
||
|
11 |
Болгария |
3590 |
3800 |
5464 |
5954 |
||
|
12 |
Мин |
||||||
|
13 |
Мах |
||||||
|
14 |
Среднее |
||||||
|
15 |
1 |
2 |
3 |
4 |
|||
|
16 |
Тенденция по среднему |
||||||
|
17 |
Рост по среднему |
||||||
|
18 |
Погрешность |
||||||
|
тенденции |
|||||||
|
19 |
Погрешность |
||||||
|
роста |
|||||||
|
20 |
Лучший отель по сети |
||||||
|
Доход |
- Технология выполнения
- Минимальные, максимальные и средние значения по кварталам и средние значения по турам подсчитываются с помощью Мастера функций.
- Для оценки работы отеля используется среднее значение дохода по сети и функция ЕСЛИ().
- Функция Тенденция показывает динамику изменения данных и позволяет получить прогноз на будущее. При этом изменение данных описывается линейным уравнением. Для определения Тенденции:
- Выделить новый диапазон ячеек для размещения результатов (B16:E16);
- В строке формул вставить функцию Тенденция и в Мастере функций в поле аргумента известные_значения_y указать диапазон средних по кварталу значений.
- Известные_значения_x можно не устанавливать, т.к. это 1, 2, 3, 4 кварталы.
- Выйти из Мастера функций – Ok.
- Установить курсор в строке формул, нажать комбинацию клавиш Ctrl+Shift+Enter, в выделенном новом массиве появятся результаты.
- Функция Тенденция показывает линейную модель изменения показателей, экспоненциальная модель строится функцией Рост.
- Самостоятельно вычислите функцию Рост для средних по кварталам, подобно тому, как вычислялась функция Тенденция.
- Вычислить прогноз развития событий на ближайшие два квартала, используя функцию Тенденция:
- Справа от ячейки со значением Тенденция для 4-го квартала выделить две свободные ячейки.
- Вставить функцию Тенденция и в Мастере функций указать:
- в поле известные_значения_y вычисленные ранее значения Тенденция за четыре квартала (диапазон B16:E16);
- в поле новые_значения_x – диапазон F15:G15 – кварталы 5 и 6, для которых выполняется прогноз.
- Завершить работу Мастера – Ok, завершить ввод функции массива Ctrl+Shift+Enter, в выделенных ячейках появятся предсказанные по линейной модели значения для 5 и 6 кварталов.
- Таким же образом рассчитать прогноз по экспоненциальной модели с помощью функции Рост.
- Оценить относительные отклонения в процентах для среднего значения и Тенденции, для среднего значения и Роста (для каждого из четырех кварталов) по формуле:
Относительное отклонение=(yфакт — yмодели)/yмодели,
где yфакт — среднее значение;
yмодели – значение, определенное с помощью Тенденции или Роста.
Пример расчета показателей работы отелей по первому кварталу приведен в таблице 3.
Таблица 3.
Пример расчета показателей работы отелей по первому кварталу
|
A |
B |
|
|
13 |
Мин |
=МИН(В3:В12) |
|
14 |
Мах |
=МАКС(В3:В12) |
|
15 |
Среднее |
=СРЗНАЧ(В3:В12) |
|
17 |
Тенденция по среднему |
=ТЕНДЕНЦИЯ(В15:Е15) |
|
18 |
Рост по среднему |
=РОСТ(В15:Е15) |
|
19 |
Погрешность |
=(В15-В17)/В17 |
|
тенденции |
||
|
20 |
Погрешность |
=(В15-В18)/В18 |
|
роста |
||
|
21 |
Лучший отель по сети |
=ИНДЕКС($А$3:В12;ПОИСКПОЗ(МАКС(В3:В12);В3:В12;0);1) |
|
22 |
Доход |
=ИНДЕКС($А$3:В12;ПОИСКПОЗ(МАКС(В3:В12);В3:В12;0);2) |
Результаты расчетов приведены в таблице 4.
Таблица 4.
Результаты расчетов
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Отель |
1 кв. |
2 кв. |
3 кв. |
4 кв. |
Среднее по |
Оценка |
|
отелю |
|||||||
|
2 |
Швеция |
1500 |
2000 |
6000 |
8000 |
4375 |
Плохо |
|
3 |
Дания |
1400 |
5000 |
4100 |
5000 |
3875 |
Плохо |
|
4 |
Норвегия |
3600 |
3600 |
3000 |
4500 |
3675 |
Плохо |
|
5 |
Финляндия |
1100 |
1045 |
9100 |
7800 |
4761,25 |
Плохо |
|
6 |
Германия |
3850 |
3650 |
7800 |
11000 |
6575 |
Хорошо |
|
7 |
Польша |
6800 |
7250 |
8122 |
9450 |
7905,5 |
Хорошо |
|
8 |
Чехия |
6590 |
7050 |
6400 |
6440 |
6620 |
Хорошо |
|
9 |
Словакия |
930 |
3970 |
4512 |
4600 |
3503 |
Плохо |
|
10 |
Венгрия |
8912 |
7490 |
3570 |
8000 |
6993 |
Хорошо |
|
11 |
Болгария |
3590 |
3800 |
5464 |
5954 |
4702 |
Плохо |
|
12 |
Мин |
930 |
1045 |
3000 |
4500 |
||
|
13 |
Мах |
8912 |
7490 |
9100 |
11000 |
||
|
14 |
Среднее |
3827 |
4486 |
5807 |
7074 |
5298 |
|
|
15 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
16 |
Тенденция по среднему |
3639 |
4745 |
5852 |
6958 |
8064 |
9170 |
|
17 |
Рост по среднему |
3760 |
4639 |
5724 |
7063 |
8714 |
10752 |
|
18 |
Погрешность |
5,17% |
-5,48% |
-0,77% |
1,67% |
||
|
тенденции |
|||||||
|
19 |
Погрешность |
1,79% |
-3,32% |
1,44% |
0,17% |
||
|
роста |
|||||||
|
20 |
Лучший отель по сети |
Венгрия |
Венгрия |
Финляндия |
Германия |
||
|
21 |
Доход |
8912 |
7490 |
9100 |
11000 |
Дополнительные задания
- Выполнить условное форматирование Столбца Оценка – выделить красным цветом отели, доход которых меньше среднего.
- Определить лучший отель по сети за квартал и его доход.
- Дополнить таблицу строкой Предсказание для 5 и 6 кварталов.
- Построить диаграмму – график изменения доходов по кварталам и тенденцию изменения доходов по кварталам, включая прогноз на два следующие квартала, а также рост изменения доходов по кварталам.
Пример для отеля «Венгрия» представлен на диаграмме 1.
Диаграмма 1.
- Добавить на график линию тренда.
- Проще всего построить график функции тренда непосредственно сразу после внесения имеющихся данных в массив. Для этого на листе с таблицей данных выделите не менее двух ячеек диапазона, для которого будет построен график, и сразу после этого вставьте диаграмму. Вы можете воспользоваться такими видами диаграмм, как график, точечная, гистограмма, пузырьковая, биржевая. Остальные виды диаграмм не поддерживают функцию построения тренда.
- В меню «Диаграмма» выберите пункт «Добавить линию тренда». В открывшемся окне на вкладке «Тип» выберите необходимый тип линии тренда, что в математическом эквиваленте также означает и способ аппроксимации данных. При использовании описываемого метода вам придется делать это «на глаз», т.к. никаких математических вычислений для построения графика вы не проводили.
- Поэтому просто прикиньте, какому типу функции более всего соответствует график имеющихся данных: линейной, логарифмической, экспоненциальной, степенной или иной. Если же вы сомневаетесь в выборе типа аппроксимации, можете построить несколько линий, а для большей точности прогноза на вкладке «Параметры» этого же окна отметить флажком пункт «поместить на диаграмму величину достоверности аппроксимации (R^2)».
- Сравнивая значения R^2 для разных линий, вы сможете выбрать тот тип графика, который характеризует ваши данные наиболее точно, а, следовательно, строит наиболее достоверный прогноз. Чем ближе значение R^2 к единице, тем точнее вы выбрали тип линии. Здесь же, на вкладке «Параметры», вам необходимо указать период, на который делается прогноз.
- Такой способ построения тренда является весьма приблизительным, поэтому лучше все-таки произвести хотя бы самую примитивную статистическую обработку имеющихся данных. Это позволит построить прогноз более точно.
- Если вы предполагаете, что имеющиеся данные описываются линейным уравнением, просто выделите их курсором и произведите автозаполнение на необходимое число периодов, или количество ячеек. В данном случае нет необходимости находить значение R^2, т.к. вы заранее подогнали прогноз к уравнению прямой.
- Если же вы считаете, что известные значения переменной лучше всего могут быть описаны с помощью экспоненциального уравнения, также выделите исходный диапазон и произведите автозаполнение необходимого количества ячеек, удерживая правую клавишу мыши. При помощи автозаполнения вы не сможете построить других типов линий, кроме двух указанных.
Рабочее окно для построения линии тренда представлено на рисунке 1.
Рисунок 1.