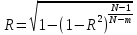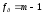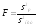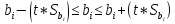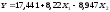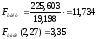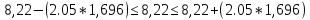Министерство
образования и науки Российской Федерации
Федеральное
агентство по образованию
Саратовский
государственный технический университет
Балаковский
институт техники, технологии и управления
Методическое
указание к выполнению лабораторной
работы
по дисциплине
“Идентификация и диагностика систем
управления”
для студентов
специальности 220201
очной и заочной
форм обучения
Одобрено
редакционно-издательским
советом
Балаковского
института техники,
технологии
и управления
Балаково 2010
Цель работы:
Освоение регрессионного анализа в
пакете EXCEL.
ОСНОВНЫЕ ПОНЯТИЯ
Задачами
регрессионного анализа являются:
установление формы зависимости между
переменными, оценка функций регрессии,
оценка неизвестных значений зависимой
переменной (прогноз).
Односторонняя
зависимость случайной зависимой
переменной Y
от одной или нескольких независимых
переменных Х
называется объясняющей
регрессией.
Такая
зависимость может возникать тогда,
когда при каждом фиксированном значении
X,
соответствующее значение Y
подвержено случайному разбросу под
воздействием неконтролируемых факторов.
Такая зависимость Y(X)
называется регрессионной.
Она может
быть представлена в виде модельного
уравнения регрессии:
(1)
где
— случайная переменная характеризующая
отклонение функции регрессии.
Линейный
регрессионный анализ
— это анализ, для которого функция f(X)
линейна относительно оцениваемых
факторов. Уравнение линейной регрессии
имеет вид:
(2)
Регрессионный
анализ включает в себя две основные
компоненты:
1. оценка вектора
коэффициентов с помощью метода наименьших
квадратов:

2. дисперсионный
анализ.
Предпосылки
регрессионный анализ:
-
чтобы количество
экспериментальных данных было больше
либо равно 30 на один вход; -
распределение
выходной величины должно быть нормальным; -
в процессе
эксперимента дисперсия выходной
величины Y
не меняется:
;
-
переменная X
изменяется с пренебрежительно малыми
ошибками, то есть является детерменированой; -
выходные переменные
Y1,
Y2,
… Yn
стохастически независимы между собой:
;
-
дискретность
проведения экспериментов во времени
берется
таким образом, чтобы последовательно
взятые значения Y1,
Y2,
… Yn
были стохастически независимы, то есть
больше времени затухания автокорреляционной
функции; -
учет динамики в
регрессионном анализе производится в
виде транспортного запаздывания,
которое определяется как время нахождения
максимума взаимно корреляционной
функции X
и Y.
На основании этих
предпосылок получают уравнение
регрессионной модели методом наименьших
квадратов.
Задача дисперсионного
анализа заключается в определении той
части экспериментальных данных, которая
описывается регрессионной моделью
(определяется коэффициент детерминации
R2
),
а также определение адекватности
регрессионной модели. Для этого
используется основное уравнение
дисперсионного анализа, которое имеет
вид:
(3)
где

сумма квадратичных отклонений
характеризует разброс значений выходной
величины Y
вокруг его среднего значения;
— остаточная
сумма отклонений используется в качестве
критерия МНК;
сумма
обусловленная регрессией.
Коэффициент
детерминации R2
определяется
соотношением суммы обусловленной
регрессией и остаточной
суммы отклонений:
(4)
Коэффициент
детерминации изменяется от 0 до 1:
При
коэффициент детерминации
а при
коэффициент детерминации

Чем ближе коэффициент детерминации к
1, тем точнее регрессионная модель.
При малых объемах
выборки используется коэффициент
множественной корреляции:
,
(5)
где N
– количество выборки; m
– количество входов.
Для оценки
адекватности регрессионной модели
используется критерий Фишера, который
определяется отношением дисперсии
обусловленной регрессией и остаточной
дисперсией:

(6)
Дисперсия,
обусловленная регрессией — среднее
значение квадратов отклонения
обусловленных регрессией определяется
выражением:
(7)
где fр
— число
степеней свободы суммы обусловленной
регрессией:

(8)
где m
– число
коэффициентов уравнения регрессии.
Остаточная дисперсия
определяется выражением:
(9)
где fост
— число
степеней свободы остаточной суммы:

(10)
где N
— число
экспериментов.
Для определения
адекватности регрессионной модели
сравнивают F-отношение,
рассчитанное по выражению (6), со значением
критерия Фишера выбранного из таблиц
для принятого уровня значимости
и числа степеней свободы сравниваемых
дисперсий


Если

то при соответствующем уровне значимости
регрессионная модель не адекватна.
Если

то при соответствующем уровне значимости
регрессионная модель адекватна.
Результаты
дисперсионного анализа сводятся в
таблицу 1.
Таблица
1.
Дисперсионный
анализ
|
SS |
f |
MS |
F |
P— |
F |
|
|
регрессия |
|
|
|
|
||
|
остатки |
|
|
|
|||
|
Итого |
|
|
Интерпретация
результатов:
SS
— сумма квадратов; f
— число
степеней свободы; MS
— средний квадрат отклонений (дисперсия);
F—
расчетное значение отношения Фишера;
P—уровень
значимости для вычисленного значения
F;
Fкрит
— табличное значение отношения Фишера.
Если регрессионная
модель адекватна, определяют значимость
коэффициентов регрессии. Для проверки
значимости анализируется отношение
коэффициента регрессии и его
среднеквадратичного отклонения. Это
отношение является распределением
Стьюдента, то есть для определения
значимости используем t
– критерий:
(11)
где

,

значение коэффициента и его
среднеквадратичное отклонение.
Для определения
значимости коэффициента сравнивают
расчетное и табличное значение t
– критерия. Табличное значение t
– критерия определяется степенью
свободы

значением заданной вероятности Р
: tтаб.
(
Р).
Если tрас.>tтаб.,
то коэффициент bi
является
значимым.
Доверительный
интервал определяется по формуле:
.
(12)
Если коэффициент
регрессии незначим, то соответствующий
ему входной фактор несущественно влияет
на выходную величину и его можно исключить
из регрессионной модели.
ПОРЯДОК ВЫПОЛНЕНИЯ
РАБОТЫ
-
Исходные данные
взять в таблицах(2,3) согласно варианту
(по номеру студента в журнале). -
Ввести исходные
данные в таблицу в пакете Excel. -
Подготовить два
столбца для ввода расчетных значений
Y
и остатков. -
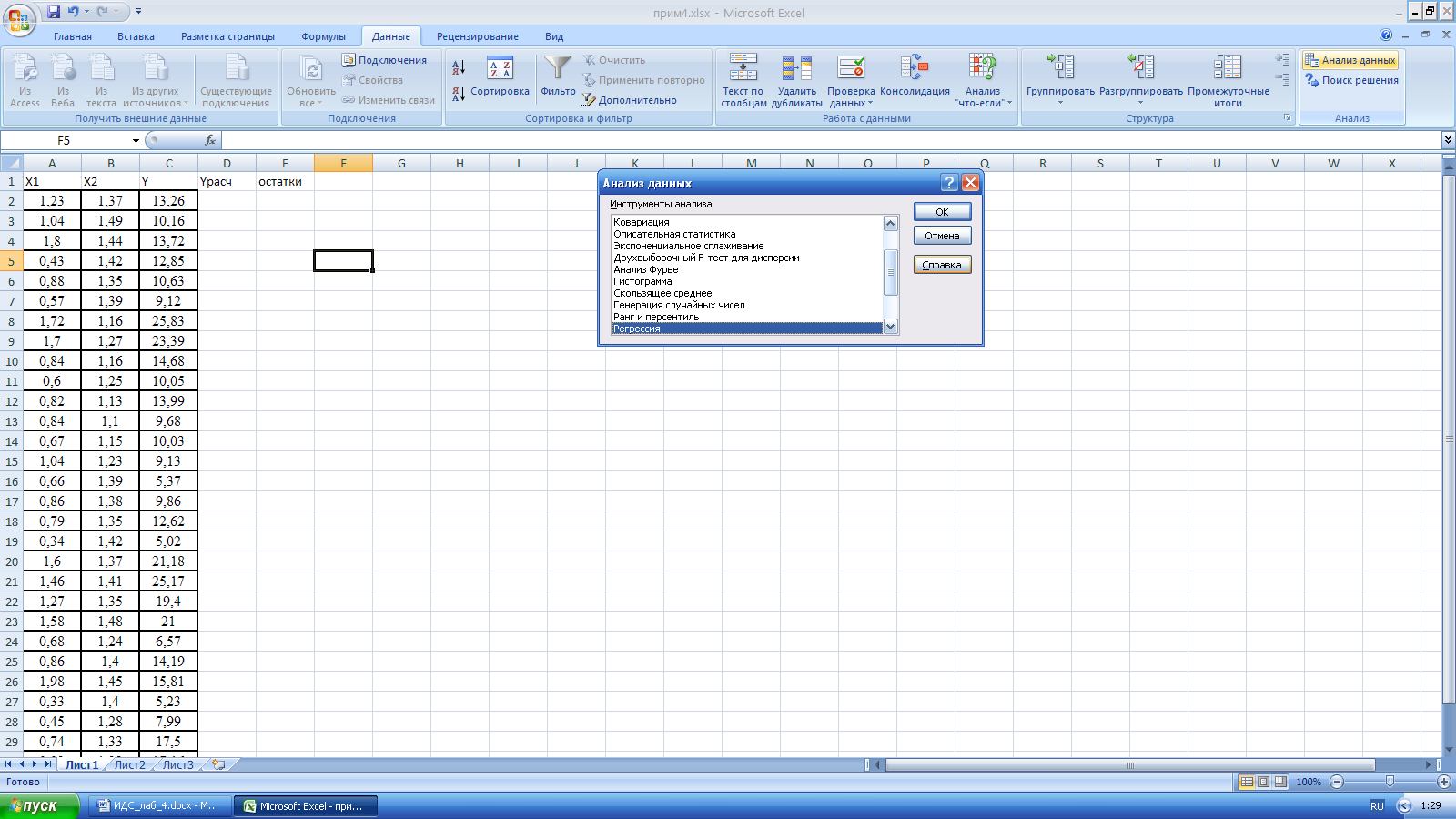
Вызвать программу
«Регрессия»: Данные/ Анализ данных/
Регрессия. Диалоговое окно «Анализ
данных» представлено на рисунке 1.
Рис. 1. Диалоговое окно «Анализ данных».
-
Ввести в диалоговое
окно «Регрессия» адреса исходных
данных:
-
входной интервал
Y,
входной интервал X
(3 столбца), -
установить уровень
надежности 95%, -
в опции «Выходной
интервал, указать левую верхнюю ячейку
места вывода данных регрессионного
анализа (первую ячейку на 2-странице
рабочего листа), -
включить опции
«Остатки» и «График остатков», -
нажать кнопку ОК
для запуска регрессионного анализа.
Диалоговое окно «Регрессия» представлено
на рисунке 2.
Рис. 2. Диалоговое окно
«Регрессия».
-
Excel выведет четыре
таблицы и два графика зависимости
остатков от переменных Х1
и Х2. -
Построить графики
для Yэксп,
Yрасч
и график ошибки прогноза (остатка). -
По полученным
графикам оценить правильность модели
по входам Х1,
Х2. -
Рассчитать
коэффициент множественной корреляции,
расчетные значения t-критериев,
доверительные интервалы коэффициентов
регрессии по выражениям (5,11,12). -
Сделать выводы
по результатам регрессионного анализа. -
Подготовить отчет
по работе.
ПРИМЕР ВЫПОЛНЕНИЯ
РАБОТЫ
Результаты
регрессионного анализа представлены
на рисунке 3.
Графики зависимости
остатков от переменных Х1
и Х2 представлены
на рисунке 4.
Графики расчетной
и экспериментальной выходной величины,
и график ошибки прогноза представлены
на рисунке 5.
Рис. 3. Пример регрессионного анализа в
пакете EXCEL
Рис.4 . Графики остатков переменных Х1,
Х2
Рис. 5. Графики Yэксп,
Yрасч и
ошибки прогноза (остатки).
По результатам
регрессионного анализа можно сказать:
-
Уравнение регрессии
полученное с помощью Excel,
имеет вид:
-
Коэффициент
детерминации:
Вариация результата
на 46,5% объясняется вариацией факторов.
-
Коэффициент
множественной корреляции:
-
Проверка на
адекватность модели. Анализ выполняется
при сравнении фактического и табличного
значения F-критерия
Фишера.
Фактическое
значение F-критерия Фишера
превышает табличное
— модель адекватна.
-
Проверка значимости
коэффициента b0.
Расчетное значение
t-критерия
для коэффициента
b0:
Табличное значение
t-критерия
tтаб.
(29, 0.975)=2.05
-
Доверительный
интервал коэффициента b0:
-
Проверка значимости
коэффициента b1.
Расчетное значение
t-критерия
для коэффициента
b1:
tрас.>tтаб.,
коэффициент b1
является значимым
-
Доверительный
интервал
коэффициента
b1:
-
Проверка значимости
для коэффициентаb2.
Расчетное значение
t-критерия
для коэффициента
b2:
tрас.<tтаб.,
коэффициент b2
является не значимым, значит фактор X
2 незначительно влияет на выходную
величину Y,
и его можно исключить из уравнения
регрессии.
-
На основании
анализа значимости коэффициентов
уравнение регрессии примет вид:
Соседние файлы в папке LR-3
- #
- #
17.02.201457.34 Кб36Копия Xl0000004.xls
- #
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Подборка по базе: Исхаков А.А. Практическая работа 3 Управление персоналом.docx, Исхаков А.А. Практическая работа 3 Документационное обеспечение , Практическая работа № 5.docx, Контрольная работа в 5 классе по разделу Русские традиции.docx, Воспитательная работа _Программа по половому воспитанию школы на, Практическая работа.pdf, моя аттестационная работа за 2015 год.docx, Контрольная работа материаловедение.docx, Практическая работа 1.doc, Практическая работа 1.docx
Лабораторная работа №1
Прогнозирование в среде EXCEL.
метод корреляционно-регрессионного анализа.
Задание 1. Прогнозирование с помощью функций регрессии Excel
Простое скользящее среднее является быстрым, но довольно неточным способом выявления общих тенденций временного ряда. Передвинуть границу оценки будущего по временной оси можно с помощью одной из функций регрессии Excel.
Каждый из методов регрессии оценивает взаимосвязь фактических данных наблюдений и других параметров, которые зачастую являются показателями того, когда были сделаны эти наблюдения. Это могут быть как числовые значения каждого результата наблюдения во временном ряду, так и дата наблюдения.
Составление линейных прогнозов: функция ТЕНДЕНЦИЯ
Использование функции рабочего листа ТЕНДЕНЦИЯ — это самый простой способ вычисления регрессионного анализа. Предположим, результаты ваших наблюдений внесены в ячейки А1:А10, а дни месяца расположены в ячейках В1:В10. Выделите ячейки С1:С10 и введите следующую формулу, используя формулу массива:
ТЕНДЕНЦИЯ (А1 :А10;В1 :В10)
Замечание
Для ввода формулы массива нажмите комбинацию клавиш <Ctrl+Shift+Enter>.
Упоминалось, что регрессивный анализ позволяет производить перспективную оценку более удаленного будущего. Применяя данные рабочего листа. введите в ячейку В11 число 11, а в ячейку С11 — следующее:
=ТЕНДЕНЦИЯ(А1:А10;В1:В10;В11)
Первый аргумент — А1:А10— определяет данные наблюдений базовой линии (известные-значения-у); второй аргумент — В1:В10 — определяет временные моменты, в которые эти данные были получены (известные-значения-х). Значение 11 в ячейке В11 является новым значением- х и определяет время, которое связывается с перспективной оценкой.
Введя в ячейку В11 большее значение, вы сможете прогнозировать данные более позднего временного момента, чем непосредственно следующего за текущим. Число 24, введенное в ячейку В11, будет определять двадцать четвертый месяц, т.е. декабрь 2009 года. Выполняя вычисления с помощью функции тенденция, получаем результат 23,8, который и будет отражать прогнозируемый объем продаж в декабре 2009 года, полученный на основе фактических результатов наблюдений за период с января по октябрь 2008 года.
Кроме того, существует возможность одновременного прогнозирования данных для нескольких новых временных моментов. Например, введите числа 11-24 в ячейки В11-В24 а затем выделите ячейки С11:С24 и введите с помощью формулы массива следующее: {=ТЕНДЕНЦИЯ(А1:А10;В1:В10;В11:В24)}.
Рис. 1. Функция ТЕНДЕНЦИЯ прогнозирует базовую линию результатов наблюдений на основе некоторых переменных. Для ввода формулы массива нажмите комбинацию клавиш .
Excel вернет в ячейки С11:С24 прогноз на временные моменты с 11 по 24. Данный прогноз будет базироваться на связи между данными наблюдений базовой линии диапазона А1:А10 и временными моментами базовой линии с 1 по 10, указанными в ячейках В1:В10.
Составление нелинейного прогноза: функция РОСТ
Функция ТЕНДЕНЦИЯ вычисляет прогнозы, основанные на линейной связи между результатом наблюдения и временем, когда это наблюдение было зафиксировано. Однако, если линия резко изгибается в одном из направлений, то это означает, что взаимосвязь показателей носит нелинейный характер. Существует большое количество типов данных, которые изменяются во времени нелинейным cпoсобом. Некоторыми примерами таких данных являются объем продаж новой продукции, прирост населения, выплаты по основному кредиту и коэффициент удельной прибыли. В случае нелинейной взаимосвязи функция Excel РОСТ поможет вам получить более точную картину направления развития вашего бизнеса, чем функция ТЕНДЕНЦИЯ.
Задание 2. Анализ ситуации: продажи новой компьютерной программы
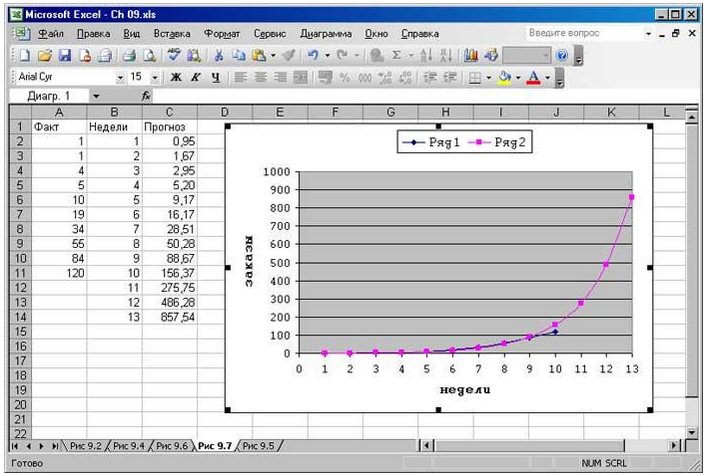
Представим, что менеджер по закупкам отдела «Soft-почтой» недавно разослал клиентам каталог, рекламирующий новую программу, получившую очень высокую оценку экспертов. Менеджер считает, что следует заранее заказать дополнительное количество экземпляров, чтобы не оказаться в ситуации, когда CD c программой закончатся раньше, чем перестанут приходить заявки на нее, менеджер начал отслеживать ежедневные заказы на программный продукт и регистрировать объемы продаж.
Рис. 2. Функция РОСТ очень удобна при прогнозировании нелинейных базовых линий
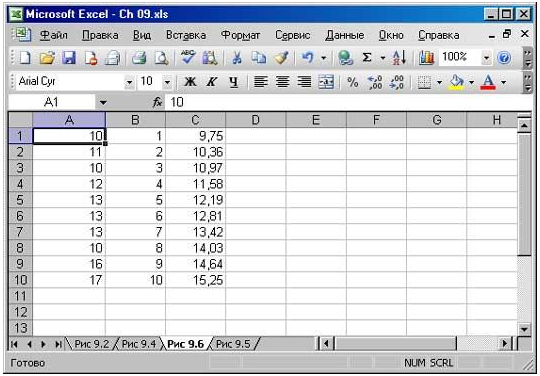
Поскольку линия имеющихся наличии товаров резко изгибается вверх, менеджер принимает решение составить прогноз с использованием функции РОСТ. Как и при использовании функции ТЕНДЕНЦИЯ, пользователь в данном случае может генерировать прогнозы, просто подставляя новые значения-х. Чтобы прогнозировать результаты 11—13 недель, следует ввести эти числа в ячейки В12:В14, а затем с помощью формулы массива в диапазон ячеек С2:С14 ввести следующее: {=РОСТ(B2:B11;A2:A11;A2:A14)}.
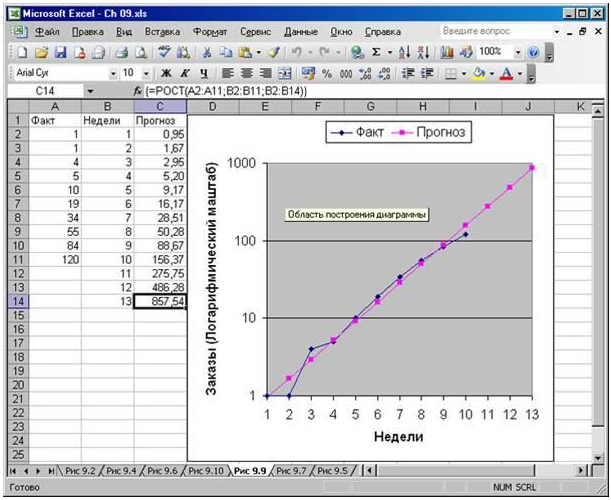
В случаях, когда вы имеете дело с очень резким ростом, удобнее оперировать не самими данными наблюдений, а логарифмами этих показателей. Например, экспоненциальный рост можно представить в виде прямой, используя логарифмическую шкалу для вертикальной оси графика. Постройте линейный график с логарифмической зависимостью экспоненциального роста заказов по отделу «Soft-почтой».
Сравним использование функции РОСТ и ТЕНДЕНЦИЯ применив их к анализу следующих значений.
В ячейках С2:С14 используется следующая формула:
ЕХР(ТЕНДЕНЦИЯ(LN(B2:B11);А2:All;А2:А14))
Рис. 3. Логарифмическая зависимость экспоненциального роста заказов в книжной торговле зачастую более удобна для интерпретации, чем стандартный линейный график
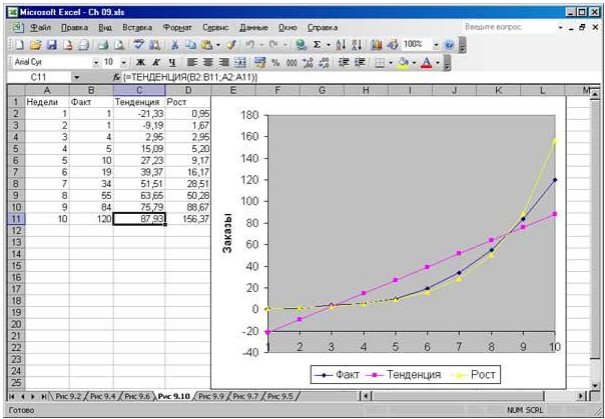
Рис. 4. Линия тренда, построенная с помощью функции РОСТ, дает на основе нелинейной базовой линии намного более точный прогноз, чем линия тренда, построенная с помощью функции ТЕНДЕНЦИЯ
Задание 3. Регрессивный анализ с помощью диаграмм
Во многих случаях диаграммы Excel бывают очень полезны при создании прогнозов. Иногда возникает необходимость провести регрессивный анализ непосредственно на графике, без введения в рабочий лист значений для прогноза. Это можно сделать с помощью графической линии тренда методом, во многом сходным с методом получения прогноза с применением скользящего среднего на основе графика. Постройте диаграмму на основе данных объема продаж: 593,581,395,625,711,536,565,418,231,243,338,433,714,516,563,656,744,468,594,505,520,685,569,701
Кликнув мышью на диаграмме, вы получите возможность ее редактировать. Кликните правой кнопкой мыши на ряде нужных данных для его выбора. После этого выполните следующие действия.
1. Выберите из контекстного меню команду Добавить линию тренда.
2. Выберите тип линии тренда Линейная.
3. Щелкните на вкладке Параметры.
4. В поле В перед на «ведите количество желаемых периодов, на протяжении которых линия тренда будет прокладываться вперед.
5. При желании можете установить флажок показывать уравнение на диаграмме. В результате уравнение для прогноза разместится на графике в виде текста Excel может расположить уравнение таким образом, что оно перекроет некоторые данные графика или линии тренда (либо (частично) само уравнение), этом случае выделите уравнение, щелкнув на нем мышью, а затем перетащит его в другое, более удобное место.
6. Кликните на кнопке ОК.
Рис. 5 С помощью линий тренда можно создавать прогнозы, основанные на регрессии, непосредственно на диаграмме
Задание 4. Прогнозирование с использованием функции экспоненциального сглаживания
Сглаживание — это способ, обеспечивающий быстрое реагирование вашего прогноза на все события, происходящие в течение периода протяженности базовой для и. Методы, основанные на регрессии, такие как функции ТЕНДЕНЦИЯ и РОСТ, применяют ко всем точкам прогноза одну и ту же формулу. По этой причине достижение быстрой реакции на сдвиги в уровне базовой линии значительно затрудняется сглаживание представляет собой простой способ обойти данную проблему.
Разработка перспективных оценок с применением метода сглаживания
Основная идея применения метода сглаживания состоит в том, что каждый новый прогноз, получается, посредством перемещения предыдущего прогноза в направлении, которое дало бы лучшие результаты по сравнению со старым прогнозом. Базовое уравнение имеет следующий вид:
- t— временной период (например, 1-й месяц, 2-й месяц и т.д.);
- F[t] — это прогноз, сделанный в момент времени t; F[t+l] отражает прогноз во временной период, следующий непосредственно за моментом времени t;
- а — константа сглаживания;
- e[t] — погрешность, т.е. различие между прогнозом, сделанным в момент времени t, ифактическими результатами наблюдений в момент времени t.
Таким образом, константа сглаживания является самокорректирующейся величиной. Сделайте сглаживающий прогноз на основании данных (10,4,5,5,7,8,6,20,19,20) используя формулу =B4+0,8*(A4-A8). Дайте графическое представление полученным результатам (график).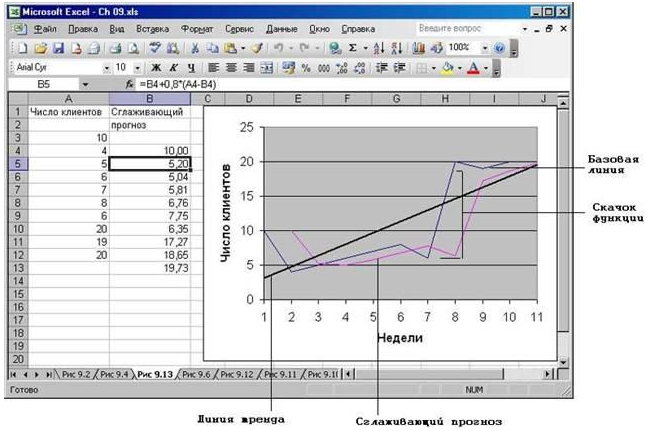
Рис. 6. При прогнозе с использованием линейной линии тренда пропускается скачок функции базовой линии, тогда как при прогнозе с применением сглаживания он отслеживается
Рис. 7. В диалоговом окне Экспоненциальное сглаживание необходимо ввести фактор затухания, а не константу сглаживания
Задание 5. Индивидуальное задание.
1.Выберите любой социально-экон6омический процесс (например, объем продаж товара, количество клиентов социальной службы, план производства изделий и т.д.).
2.Для выбранного вами процесса подберите совокупность исходных данных (не менее 50 значений).
3.Выполните расчет прогноза с применением метода скользящего среднего (см. задания 1-4).
4.Оформите отчет по лабораторной работе.
Отчет по лабораторной работе должен включать:
- Исходные данные и задание.
- Расчётные формулы для проведения необходимых расчетов исходя из задания лабораторной работы.
- Графическое представление полученных результатов расчета (при необходимости).
- Результаты расчёта показателей, оформленные в виде таблиц.
- Основные выводы. Выводы, сделанные в ходе проведенных расчетов должны быть четко и полно аргументированы.
5.Ответьте на вопросы к защите лабораторной работы:
- Какой процесс вы прогнозировали?
- При помощи какого метода вы прогнозировали процесс? Его особенности.
- Какие выводы можно сделать выводы?


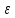

 ;
; ;
; берется
берется