Элементы
теории вероятностей
Цели
задания:
-
Повторение
основных приемов создания и форматирования
таблиц средствами MS
Excel. -
Изучение
новых математических функций, входящих
в MS
Excel. -
Решение
задач по теме «Элементы теории
вероятностей. Классическое определение
вероятности».
Подготовка
к заданию:
-
Повторить
тему «Элементы
теории вероятностей»
по электронному конспекту, расположенному
на сервере по адресу «F:Методические
материалы Информационные технологии
Математика и информатика для юристов». -
Познакомиться
с помощью справочной системы MS Excel с
математическими функциями ФАКТР
и ЧИСЛОКОМБ.
Состав
задания:
-
Решить
задачи по теории вероятностей и оформить
их решение средствами MS Excel
в виде таблиц в соответствии с
предложенными ниже образцами. Для
вычисления числа вариантов по формулам
комбинаторики использовать соответствующие
математические функции MS
Excel.
Задачи:
-
Назовём
игральной костью кубик из однородного
материала с гранями, занумерованными
цифрами от 1 до 6. Бросаются 2 игральных
кости. Какова вероятность того, что
сумма очков, выпавших на 2 костях,
окажется равной 8?
-
Юная
студентка юрфака наивно верит, что
если она соберет 20 разных крышек от
«Pepsi» и отошлет их по указанному адресу,
то добрые дяди и тети предоставят ей
путевку в «DisneyLand».
Какова вероятность того, что удастся
собрать 20 разных крышек, купив 20
бутылок?
-
В
соревнованиях по стрельбе на огневом
рубеже размещаются 8 стрелков. Какова
вероятность того, что два определенных
участника окажутся рядом?
-
Колода
карт содержит 36 различных карт (9 карт
пиковой масти, 9 треф, 9 бубен и 9 червей).
Сдача карт одному игроку состоит из 6
карт, порядок которых не важен. Какова
вероятность того, что:
-
в
сдаче все карты будут трефовой масти? -
в
сдаче все карты будут одной масти? -
в
сдаче будет 4 туза? -
в
сдаче будет точно 2 дамы?
-
В
урне 5 белых и 7 черных шаров. Из урны
одновременно вынимают два шара. Какова
вероятность, что оба шара белые?
Образцы
решения и оформления задач:
Задача
1.
Из урны, в которой находятся 8 синих,
3 красных,
6 чёрных
и 7 белых
шаров, наудачу вынимается один. Какова
вероятность того, что вынутый шар
окажется а)
белым;
б) зеленым?
Решение.
Это испытание имеет 24 равновозможных
исхода. Каждый исход означает выбор
одного шара. Пусть событие А означает
выбор
белого шара,
а событие В – выбор
зеленого шара.
Число исходов, благоприятных событию
А , равно 7, а исходов, благоприятных
событию В, нет (оно является невозможным).
Оформление
этой задачи в среде MS
Excel
приведено ниже.
Задача
2.
На зачёте по Истории студенту предлагается
ответить на 2 вопроса из 36. Студент
подготовил ответы на 19 вопросов. Какова
вероятность, что на зачёте ему предложат
два вопроса, на которые он подготовил
ответ?
Решение.
Рассмотрим
испытание, состоящее в выборе двух из
36 вопросов. Исходом испытания является
пара вопросов. Поскольку порядок выбора
вопросов несущественен,
то число всех n
исходов
равно числу
сочетаний из 36 по 2.
Для определения числа сочетаний
воспользуемся функцией ЧИСЛОКОМБ(36;2).
Пусть
событие А состоит в том, что студенту
достаются два подготовленных вопроса.
Число исходов, благоприятных этому
событию определяется как число сочетаний
из 19 по 2. Применим вышеуказанную функцию
ЧИСЛОКОМБ(19;2).
Оформление
решения задачи в среде MS
Excel
приведено ниже
Задача
3.
Десять
различных книг расставлены наудачу на
одной полке. Найти вероятность того,
что три определенные книги окажутся
поставлены рядом.
Решение.
Условимся,
что три определенные книги как бы
находятся в одной упаковке. Тогда число
возможных способов расположения книг
на полке равно числу
перестановок из 8
элементов (одна упаковка плюс остальные
7 книг), т. е. Р8=8!.
Внутри упаковки три книги можно
переставить Р3=3!
способами. По правилу умножения m(A)=
Р8
х Р3.
Число возможных вариантов расстановки
10 книг n=Р10=10!.
Для вычисления факториалов чисел
воспользуемся функцией ФАКТР.
Оформление
решения задачи в среде MS
Excel
приведено ниже
Соседние файлы в папке MS Excel
- #
- #
- #
Распределение вероятностей – одно из центральных понятий теории
вероятности и математической статистики. Определение распределения вероятности
равносильно заданию вероятностей всех СВ, описывающих некоторое случайное
событие. Распределение вероятностей некоторой СВ, возможные значения которой x1, x2, … xn образуют
выборку, задается указанием этих значений и соответствующих им вероятностей p1, p2,… pn. (pn должны быть
положительны и в сумме давать единицу).
В данной лабораторной работе будут рассмотрены и построены с помощью MS Excel наиболее
распространенные распределения вероятности: биномиальное и нормальное.
1 Биномиальное распределение
Представляет собой распределение вероятностей числа наступлений
некоторого события («удачи») в n повторных
независимых испытаниях, если при каждом испытании вероятность наступления этого
события равна p. При этом
распределении разброс вариант (есть или нет события) является следствием
влияния ряда независимых и случайных факторов.
Примером практического использования биномиального распределения
может являться контроль качества партии фармакологического препарата. Здесь
требуется подсчитать число изделий (упаковок), не соответствующих требованиям.
Все причины, влияющие на качество препарата, принимаются одинаково вероятными и
не зависящими друг от друга. Сплошная проверка качества в этой ситуации не
возможна, поскольку изделие, прошедшее испытание, не подлежит дальнейшему
использованию. Поэтому для контроля из партии наудачу выбирают определенное
количество образцов изделий (n). Эти образцы всестороннее
проверяют и регистрируют число бракованных изделий (k). Теоретически число
бракованных изделий может быть любым, от 0 до n.
В Excel функция БИНОМРАСП
применяется для вычисления вероятности в задачах с фиксированным числом тестов
или испытаний, когда результатом любого испытания может быть только успех или
неудача.
Функция использует следующие
параметры:
БИНОМРАСП (число_успехов;
число_испытаний; вероятностъ_успеха; интегральная), где
число_успехов — это количество успешных
испытаний;
число_испытаний — это число независимых
испытаний (число успехов и число испытаний должны быть целыми числами);
вероятность_ успеха — это вероятность успеха
каждого испытания;
интегральный — это логическое значение,
определяющее форму функции.
Если данный параметр имеет
значение ИСТИНА (=1), то считается интегральная функция распределения
(вероятность того, что число успешных испытаний не менее значения число_
успехов);
если этот параметр имеет
значение ЛОЖЬ (=0), то вычисляется значение функции плотности
распределения (вероятность того, что число успешных испытаний в точности равно
значению аргумента число_ успехов).
Пример 1. Какова вероятность того,
что трое из четырех новорожденных будут мальчиками?
Решение:
1. Устанавливаем табличный курсор в свободную
ячейку, например в А1. Здесь должно оказаться значение искомой
вероятности.
2. Для получения значения вероятности
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка
функции (fx).
3. В появившемся диалоговом окне Мастер
функций — шаг 1 из 2 слева в поле Категория указаны виды функций.
Выбираем Статистическая. Справа в поле Функция выбираем функцию БИНОМРАСП
и нажимаем на кнопку ОК.
Появляется диалоговое окно
функции. В поле Число_s вводим с клавиатуры
количество успешных испытаний (3). В поле Испытания вводим с клавиатуры
общее количество испытаний (4). В рабочее поле Вероятность_s
вводим с клавиатуры вероятность успеха в отдельном испытании (0,5). В поле Интегральный
вводим с клавиатуры вид функции распределения — интегральная или весовая (0).
Нажимаем на кнопку ОК.
В ячейке А1 появляется
искомое значение вероятности р = 0,25. Ровно 3 мальчика из 4
новорожденных могут появиться с вероятностью 0,25.
Если изменить формулировку
условия задачи и выяснить вероятность того, что появится не более трех
мальчиков, то в этом случае в рабочее поле Интегральный вводим 1 (вид
функции распределения интегральный). Вероятность этого события будет равна
0,9375.
Задания для самостоятельной работы
1. Какова вероятность того, что восемь из десяти студентов,
сдающих зачет, получат «незачет». (0,04)
2.
Нормальное распределение
Нормальное распределение — это совокупность объектов, в которой крайние значения
некоторого признака — наименьшее и наибольшее — появляются редко; чем ближе значение признака к математическому ожиданию,
тем чаще оно встречается. Например, распределение студентов по их весу приближается
к нормальному распределению. Это распределение имеет очень широкий круг приложений в
статистике, включая проверку гипотез.
Диаграмма нормального
распределения симметрична относительно точки а (математического
ожидания). Медиана нормального распределения равна тоже а. При этом в
точке а функция f(x) достигает своего максимума, который равен
.
В Excel для вычисления значений
нормального распределения используются функция НОРМРАСП, которая
вычисляет значения вероятности нормальной функции распределения для указанного
среднего и стандартного отклонения.
Функция имеет параметры:
НОРМРАСП (х; среднее;
стандартное_откл; интегральная), где:
х — значения выборки, для
которых строится распределение;
среднее — среднее арифметическое
выборки;
стандартное_откл — стандартное отклонение
распределения;
интегральный — логическое значение,
определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то
функция НОРМРАСП возвращает интегральную функцию распределения; если это
аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности
распределения.
Если среднее = 0 и
стандартное_откл = 1, то функция НОРМРАСП возвращает стандартное
нормальное распределение.
Пример 2. Построить график
нормальной функции распределения f(x) при x, меняющемся от 19,8 до 28,8
с шагом 0,5, a=24,3 и
=1,5.
Решение
1. В ячейку А1 вводим символ
случайной величины х, а в ячейку B1 — символ функции
плотности вероятности — f(x).
2. Вводим в диапазон А2:А21
значения х от 19,8 до 28,8 с шагом 0,5. Для этого воспользуемся
маркером автозаполнения: в ячейку А2 вводим левую границу диапазона (19,8), в
ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:А3. Затем за правый
нижний угол протягиваем мышью до ячейки А21 (при нажатой левой кнопке мыши).
3. Устанавливаем табличный курсор в ячейку В2 и
для получения значения вероятности воспользуемся специальной функцией —
нажимаем на панели инструментов кнопку Вставка функции (fx). В появившемся диалоговом
окне Мастер функций — шаг 1 из 2 слева в поле Категория указаны виды
функций. Выбираем Статистическая. Справа в поле Функция выбираем
функцию НОРМРАСП. Нажимаем на кнопку ОК.
4. Появляется диалоговое
окно НОРМРАСП. В рабочее поле X вводим адрес ячейки А2
щелчком мыши на этой ячейке. В рабочее поле Среднее вводим с клавиатуры
значение математического ожидания (24,3). В рабочее поле Стандартное_откл
вводим с клавиатуры значение среднеквадратического отклонения (1,5). В рабочее
поле Интегральная вводим с клавиатуры вид функции распределения (0).
Нажимаем на кнопку ОК.
5. В ячейке В2 появляется
вероятность р = 0,002955. Указателем мыши за правый нижний угол табличного
курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В21
копируем функцию НОРМРАСП в диапазон В3:В21.
6. По полученным данным строим искомую диаграмму
нормальной функции распределения. Щелчком указателя мыши на кнопке на панели
инструментов вызываем Мастер диаграмм. В появившемся диалоговом окне
выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки
Далее указываем диапазон данных — В1:В21 (с помощью мыши). Проверяем,
положение переключателя Ряды в: столбцах. Выбираем закладку Ряд и с
помощью мыши вводим диапазон подписей оси X: А2:А21. Нажав на кнопку Далее,
вводим названия осей Х и У и нажимаем на кнопку Готово.
Рис. 1 График нормальной функции распределения
Получен приближенный график
нормальной функции плотности распределения (см. рис.1).
Задания для самостоятельной работы
1. Построить график нормальной
функции плотности распределения f(x) при x, меняющемся от 20 до 40 с
шагом 1 при
= 3.
3. Генерация случайных величин
Еще одним аспектом
использования законов распределения вероятностей является генерация случайных величин. Бывают ситуации, когда необходимо
получить последовательность случайных чисел. Это, в частности, требуется для
моделирования объектов, имеющих случайную природу, по известному распределению
вероятностей.
Процедура генерации
случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из
одного или нескольких распределений.
В MS Excel для генерации СВ используются функции из категории Математические:
СЛЧИС () – выводит на экран равномерно
распределенные случайные числа больше или равные 0 и меньшие 1;
СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экран
случайное число, лежащее между произвольными заданными
значениями.
В случае использования
процедуры Генерация случайных чисел из пакета Анализа необходимо
заполнить следующие поля:
— число переменных
вводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то все
столбцы в выходном диапазоне будут заполнены;
— число случайных чисел
вводится число случайных значений, которое необходимо вывести для
каждой переменной, если число случайных чисел не будет введено, то все строки выходного диапазона будут заполнены;
— в поле распределение необходимо выбрать тип распределения,
которое следует использовать для генерации случайных переменных:
1. равномерное — характеризуется
верxней и нижней границами. Переменные извлекаются с одной и
той же вероятностью для всех значений интервала.
2. нормальное
— характеризуется средним значением и стандартным отклонением. Обычно для
этого распределения используют среднее значение
0 и стандартное отклонение 1.
3. биномиальное
— характеризуется вероятностью успеха (величина р) для некоторого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биномиальной случайной
переменной;
4. дискретное
— характеризуется значением СВ и соответствующим ему интервалом вероятности, диапазон должен состоять из двух столбцов: левого,
содержащего значения, и правого, содержащего
вероятности, связанные со значением в данной строке. Сумма вероятностей должна быть
равна 1;
5. распределения Бернулли, Пуассона
и Модельное.
— в поле случайное рассеивание
вводится произвольное значение, для которого необходимо
генерировать случайные числа. Впоследствии можно снова использовать это
значение для получения тех же самых случайных чисел.
— выходной диапазон
вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и
на экран будет выведено сообщение в случае
возможного наложения выходного диапазона на исходные
данные.
Рассмотрим пример.
Пример 3. Повар столовой может готовить 4 различных первых блюда (уха, щи, борщ, грибной суп). Необходимо составить меню на месяц, так чтобы
первые блюда чередовались в случайном порядке.
Решение
1.
Пронумеруем первые
блюда по порядку: 1 — уха, 2 — щи, 3 — борщ, 4 — грибной суп. Введем числа 1-4 в диапазон А2:А5 рабочей таблицы.
2.
Укажем желаемую вероятность появления
каждого первого блюда. Пусть все блюда будут
равновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.
3.
В меню Сервис
выбираем пункт Анализ данных и далее указываем строку Генерация
случайных чисел. В появившемся диалоговом окне указываем Число
переменных — 1, Число случайных чисел — 30 (количество
дней в месяце). В поле Распределение указываем Дискретное (только натуральные числа). В поле Входной
интервал значений и вероятностей
вводим (мышью) диапазон, содержащий номера супов и их
вероятности. – А2:В5.
4.
Указываем выходной
диапазон и нажимаем ОК. В столбце С появляются случайные числа: 1, 2, 3,
4.
Задание для
самостоятельной работы
1. Сформировать
выборку из 10 случайных чисел, лежащих в диапазоне от 0 до 1.
2. Сформировать
выборку из 20 случайных чисел, лежащих в диапазоне от 5 до 20.
3. Пусть
спортсмену необходимо составить график тренировок на 10 дней, так чтобы
дистанция, пробегаемая каждый день, случайным образом менялась от 5 до 10 км.
4. Составить
расписание внеклассных мероприятий на неделю для случайного проведения:
семинаров, интеллектуальных игр, КВН и спец. курса.
5. Составить
расписание на месяц для случайной демонстрации на телевидении одного из четырех
рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1
должна быть в два раза выше, чем остальных рекламных роликов.
Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
- ДИСП;
- ГИПЕРГЕОМ.РАСП;
- СРЗНАЧ и другие.
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
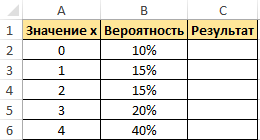
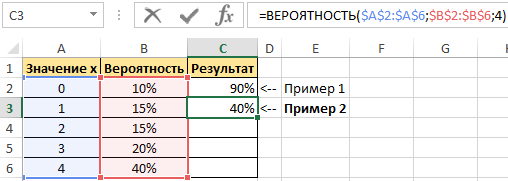
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
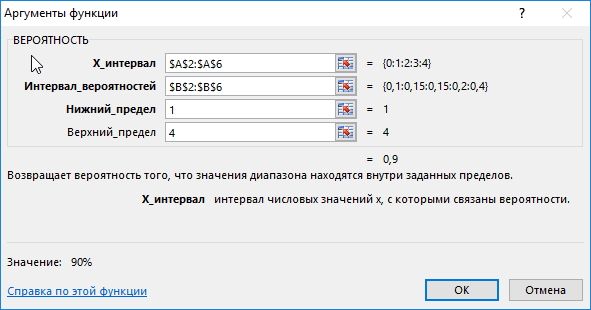
Для этого введем функцию со следующими аргументами:
тут:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
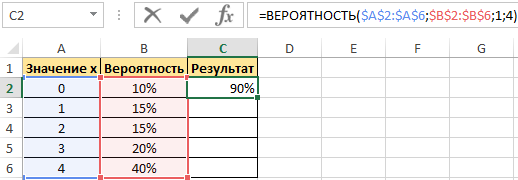
В результате выполненных вычислений получим:
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
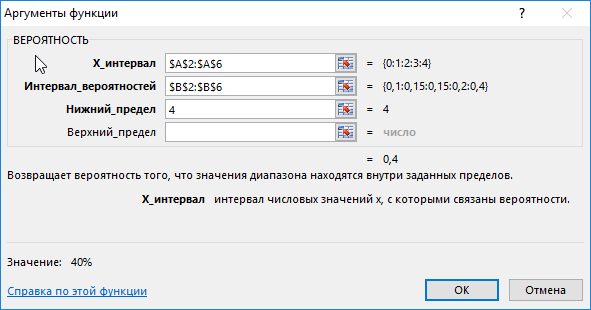
Введем в ячейку С3 введем функцию с такими аргументами:
тут:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Получим:
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Введем формулу:
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Скачать примеры функции ВЕРОЯТНОСТЬ в Excel
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Цели и задачи:
Образовательные: закрепить такие
понятия теории вероятности как: среднее
арифметическое, размах, мода и медиана рядов
чисел; систематизировать знания по пройденной
теме, формировать умение учащихся применять
знания к решению практических задач, контроль,
оценка и проверка знаний учащихся, закрепить
знание способов ввода данных в ячейки и порядок
создания формул с использованием встроенных
функций в табличном процессоре MS Excel. Показать
важность межпредметных связей
Развивающие: развитие
познавательной активности, творческих
способностей учащихся, умения сопоставлять,
анализировать, развить навыки ввода данных в
ячейки с использованием автозаполнения и
вычисления итоговых значений с помощью
статистических функций табличного процессора MS
Excel;
Воспитательные: способствовать
воспитанию у учащихся аккуратности, усидчивости,
навыков учебного труда, интереса к предмету.
Ход урока
-
Организационный момент.
-
Актуализация опорных знаний. Опрос.
- Как определить среднее арифметическое ряда?
- Что называется модой ряда?
- Как определить размах ряда?
- Что называется медианой ряда?
- Что такое адрес ячейки и из чего он состоит?
- Чем абсолютный адрес отличается от
относительного? - Что такое автозаполнение и как им пользоваться?
- Что такое функция Excel?
-
Решить задачу:
- Администрация школы решила проверить
математическую подготовку учащихся 8 класса. С
этой целью был составлен тест, содержащий 9
заданий. Работу выполняли 40 учащихся школы. При
проверке каждой работы учитель отмечал число
верно выполненных заданий. В результате был
составлен такой ряд чисел:
- Определить сколько заданий в среднем выполнил
каждый ученик верно? - Найти разницу в числе верно выполненных заданий
между учащимися. - Чему равна мода и медиана данного ряда?
-
Закрепление материала
6,5,4,0,4,5,7,9,1,6,8,7,9,5,8,6,7,2,5,7,6,3,4,4,5,6,8,6.7,7,4,3.5,9,6,7,8,6,9,8.
Задача разбирается вместе с учителем
для постановки проблемной ситуации, в разрешении
которой помогает использование электронных
таблиц.
Чтобы ответить на вопросы задачи
необходимо упорядочить ряд данных, а при
нахождении статистических характеристик ряда
нам помогут на доске записанные статистические
функции Excel, которые используются для нахождения
среднего арифметического, размаха, моды и
медианы рядов чисел:
=МЕДИАНА(аргументы) – медиана
ряда;
=СРЗНАЧ(аргументы) – среднее
арифметическое ряда;
=МОДА(аргументы) – мода ряда;
=МАКС(аргументы)-МИН(аргументы)
– размах ряда.
Учащиеся получают листки с задачами,
рассаживаются за компьютеры и решают их с
помощью Excel. Для решения задач необходим файл
(Приложение1)
Задачи для закрепления
- Найдите среднее арифметическое, размах, моду и
медиану рядов чисел; - За четверть Люда получила по алгебре пять двоек,
четыре четверки и две пятерки. Ее мама считает,
что за четверть Люде надо ставить двойку, папа
считает, что надо ставить тройку, а сама Люда
считает, что надо ставить четверку. Попробуйте
привести аргументы в пользу каждой точки зрения
(какие статистические характеристики вычисляет
каждый член семьи?). Какую бы оценку вы поставили
Люде? - В таблице представлены результаты опроса 100
человек. - Света, Люда и Женя договорились в течение трех
дней по-очереди поливать в классе цветы. Сколько
у них есть способов установить порядок
дежурства? - 8 детей делят пирожки. Все пирожки имеют разную
начинку. Один из них с морковью. Сколько
существует способов разделить пирожки (каждому
по штуке) так, чтобы пирожок с морковью не
достался ребенку, который не любит такую начинку?
| Количество опрошенных | Зарплата |
| 10 | 500 |
| 30 | 1000 |
| 50 | 1500 |
| 10 | 3000 |
а) сколько денег, в среднем, получает один
человек из этой группы (найдите среднее
арифметическое ряда данных)?
б) сколько денег получает ежемесячно
“средний” человек из этой группы (найдите
медиану этих данных)?
в) какой заработок наиболее распространен у
членов этой группы (найдите моду этих данных)?
-
Подведение итогов (выставление оценок)
Приложение