4
ЛАБОРАТОРНАЯ РАБОТА
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ В EXCEL
1.1 Корреляционный анализ в MS Excel
Корреляционный анализ состоит в
определении степени связи между двумя
случайными величинами X и Y. В качестве
меры такой связи используется коэффициент
корреляции. Коэффициент корреляции
оценивается по выборке объема п связанных
пар наблюдений (xi, yi) из
совместной генеральной совокупности
X и Y. Для оценки степени взаимосвязи
величин X и Y, измеренных в количественных
шкалах, используется коэффициент
линейной корреляции (коэффициент
Пирсона), предполагающий, что выборки
X и Y распределены по нормальному закону.
Коэффициент корреляции изменяется от
-1 (строгая обратная линейная зависимость)
до 1 (строгая прямая пропорциональная
зависимость). При значении 0 линейной
зависимости между двумя выборками
нет.
Общая классификация корреляционных
связей (по Ивантер Э.В., Коросову А.В.,
1992):
-
сильная,
или тесная
при коэффициенте корреляции r0,70;
-
средняя при
0,50r
0,69;
-
умеренная при
0,30r
0,49;
-
слабая при
0,20r
0,29;
-
очень слабая при r
0,19.
Существует несколько типов
коэффициентов корреляции, что зависит
от переменных Х и Y,
которые могут быть измерены в разных
шкалах. Именно этот факт и определяет
выбор соответствующего коэффициента
корреляции (см. табл. 13):
В MS Excel для вычисления парных коэффициентов
линейной корреляции используется
специальная функция КОРРЕЛ (массив1;
массив2),
|
№ испытуемых |
X |
Y |
|
1 |
19 |
17 |
|
2 |
32 |
7 |
|
3 |
33 |
17 |
|
4 |
44 |
28 |
|
5 |
28 |
27 |
|
6 |
35 |
31 |
|
7 |
39 |
20 |
|
8 |
39 |
17 |
|
9 |
44 |
35 |
|
10 |
44 |
43 |
где массив1 – ссылка на диапазон
ячеек первой выборки (X);
массив2 – ссылка на диапазон ячеек
второй выборки (Y).
Пример 1: 10 школьникам были даны
тесты на наглядно-образное и вербальное
мышление. Измерялось среднее время
решения заданий теста в секундах.
Исследователя интересует вопрос:
существует ли взаимосвязь между
временем решения этих задач? Переменная
X — обозначает среднее время решения
наглядно-образных, а переменная Y—
среднее время решения вербальных
заданий тестов.
Р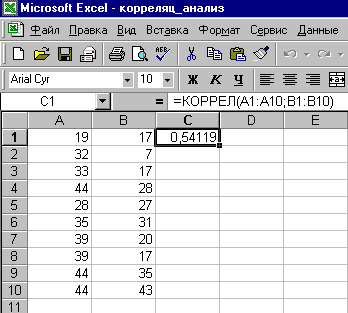
Для выявления степени взаимосвязи,
прежде всего, необходимо ввести данные
в таблицу MS Excel (см. табл., рис. 1). Затем
вычисляется значение коэффициента
корреляции. Для этого курсор установите
в ячейку C1. На панели инструментов
нажмите кнопку Вставка функции (fx).
В появившемся диалоговом окне Мастер
функций выберите категорию
Статистические и функцию КОРРЕЛ,
после чего нажмите кнопку ОК. Указателем
мыши введите диапазон данных выборки
Х в поле массив1 (А1:А10). В поле массив2
введите диапазон данных выборки У
(В1:В10). Нажмите кнопку ОК. В ячейке С1
появится значение коэффициента
корреляции — 0,54119. Далее необходимо
посмотреть на абсолютное число
коэффициента корреляции и определить
тип связи (тесная, слабая, средняя и
т.д.)
Рис. 1. Результаты вычисления коэффициента
корреляции
Таким образом, связь между
временем решения наглядно-образных и
вербальных заданий теста не доказана.
Задание 1. Имеются данные по 20
сельскохозяйственным хозяйствам. Найти
коэффициент корреляции между
величинами урожайности зерновых культур
и качеством земли и оценить его значимость.
Данные приведены в таблице.
Таблица 2. Зависимость урожайности
зерновых культур от качества земли
|
Номер |
Качество |
Урожайность, |
|
1 |
32 |
19,5 |
|
2 |
33 |
19 |
|
3 |
35 |
20,5 |
|
4 |
37 |
21 |
|
5 |
38 |
20,8 |
|
6 |
39 |
21,4 |
|
7 |
40 |
23 |
|
8 |
41 |
23,3 |
|
9 |
42 |
24 |
|
10 |
44 |
24,5 |
|
11 |
45 |
24,2 |
|
12 |
46 |
25 |
|
13 |
47 |
27 |
|
14 |
49 |
26,8 |
|
15 |
50 |
27,2 |
|
16 |
52 |
28 |
|
17 |
54 |
30 |
|
18 |
55 |
30,2 |
|
19 |
58 |
32 |
|
20 |
60 |
33 |
Задание 2. Определите,
имеется ли связь между временем работы
спортивного тренажера для фитнеса (тыс.
часов) и стоимость его ремонта (тыс.
руб.):
-
Время
работа тренажера (тыс. часов)Стоимость
ремонта (тыс. руб.)0,50
7,50
0,60
7,75
0,70
7,25
0,80
7,40
0,90
7,90
1,00
8,00
1,10
8,50
1,20
8,40
1,30
8,35
1,40
8,55
1,50
8,70
1,60
9,05
1,70
8,80
1,80
9,10
1,90
9,30
2,00
9,25
2,10
9,45
1.2
Множественная корреляция в MS Excel
При большом числе наблюдений,
когда коэффициенты корреляции необходимо
последовательно вычислять для нескольких
выборок, для удобства получаемые
коэффициенты сводят в таблицы, называемые
корреляционными
матрицами.
Корреляционная матрица — это
квадратная таблица, в которой на
пересечении соответствующих строк и
столбцов находятся коэффициент корреляции
между соответствующими параметрами.
В MS Excel для вычисления
корреляционных матриц используется
процедура Корреляция
из пакета Анализ
данных. Процедура
позволяет получить корреляционную
матрицу, содержащую коэффициенты
корреляции между различными параметрами.
Для реализации процедуры необходимо:
1. выполнить команду Сервис
— Анализ
данных;
2. в появившемся списке
Инструменты анализа
выбрать строку Корреляция
и нажать кнопку ОК;
3. в появившемся диалоговом
окне указать Входной
интервал, то есть
ввести ссылку на ячейки, содержащие
анализируемые данные. Входной интервал
должен содержать не менее двух столбцов.
4. в разделе Группировка
переключатель установить в соответствии
с введенными данными (по столбцам или
по строкам);
5. указать выходной
интервал,
то есть ввести ссылку на ячейку, начиная
с которой будут показаны результаты
анализа. Размер выходного диапазона
будет определен автоматически, и на
экран будет выведено сообщение в случае
возможного наложения выходного диапазона
на исходные данные. Нажать кнопку ОК.
В
выходной диапазон будет выведена
корреляционная матрица, в которой
на пересечении каждых строки и столбца
находится коэффициент корреляции
между соответствующими параметрами.
Ячейки выходного диапазона, имеющие
совпадающие координаты строк и столбцов,
содержат значение 1, так как каждый
столбец во входном диапазоне полностью
коррелирует сам с собой
Пример 2.
Имеются ежемесячные данные наблюдений
за состоянием погоды и посещаемостью
музеев и парков (см. табл. 3). Необходимо
определить, существует ли взаимосвязь
между состоянием погоды и посещаемостью
музеев и парков.
Таблица 3. Результаты наблюдений
-
Число
ясных днейКоличество
посетителей музеяКоличество
посетителей парка8
495
132
14
503
348
20
380
643
25
305
865
20
348
743
15
465
541
Решение.
Для выполнения корреляционного анализа
введите в диапазон A1:G3 исходные данные
(рис. 2). Затем в меню Сервис
выберите пункт Анализ
данных
и далее укажите строку Корреляция.
В появившемся диалоговом окне укажите
Входной интервал
(А2:С7). Укажите, что данные рассматриваются
по столбцам. Укажите выходной диапазон
(Е1) и нажмите кнопку ОК.
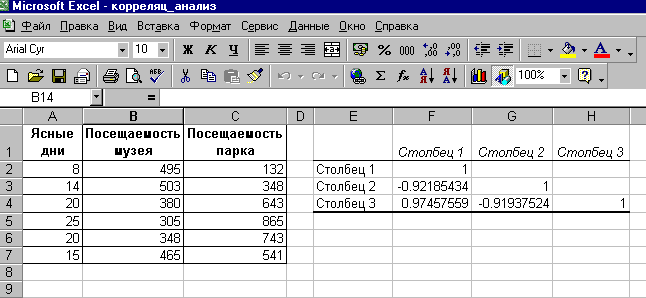
На рис. 33 видно, что корреляция
между состоянием погоды и посещаемостью
музея равна -0,92, а между состоянием
погоды и посещаемостью парка — 0,97,
между посещаемостью парка и музея —
0,92.
Таким образом, в результате
анализа выявлены зависимости: сильная
степень обратной линейной взаимосвязи
между посещаемостью музея и количеством
солнечных дней и практически линейная
(очень сильная прямая) связь между
посещаемостью парка и состоянием погоды.
Между посещаемостью музея и парка
имеется сильная обратная взаимосвязь.
Рис. 2. Результаты вычисления
корреляционной матрицы из примера 2
Задание 3. 10 менеджеров
оценивались по методике экспертных
оценок психологических характеристик
личности руководителя. 15 экспертов
производили оценку каждой психологической
характеристики по пятибальной системе
(см. табл. 4). Психолога интересует вопрос,
в какой взаимосвязи находятся эти
характеристики руководителя между
собой.
Таблица 4. Результаты исследования
|
Испытуемые п/п |
тактичность |
требовательность |
критичность |
|
1 |
70 |
18 |
36 |
|
2 |
60 |
17 |
29 |
|
3 |
70 |
22 |
40 |
|
4 |
46 |
10 |
12 |
|
5 |
58 |
16 |
31 |
|
6 |
69 |
18 |
32 |
|
7 |
32 |
9 |
13 |
|
8 |
62 |
18 |
35 |
|
9 |
46 |
15 |
30 |
|
10 |
62 |
22 |
36 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: дипломная работа.docx, практ работа +++.doc, Практическая работа №1.docx, Курсовая работа похищение человека.docx, Практическая работа №1.docx, Самостоятельная работа по теме 1.2.docx, Контрольная Работа.. (пп).docx, Практическая работа по Теории организации Марчук ЮП.docx, практическая работа №6 ответ.docx, Лабораторная работа по биологии_ Определение по спилу возраста п
ЛАБОРАТОРНАЯ РАБОТА
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ В EXCEL
1.1 Корреляционный анализ в MS Excel
Корреляционный анализ состоит в определении степени связи между двумя случайными величинами X и Y. В качестве меры такой связи используется коэффициент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (xi, yi) из совместной генеральной совокупности X и Y. Для оценки степени взаимосвязи величин X и Y, измеренных в количественных шкалах, используется коэффициент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки X и Y распределены по нормальному закону.
Коэффициент корреляции изменяется от -1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорциональная зависимость). При значении 0 линейной зависимости между двумя выборками нет.
Общая классификация корреляционных связей (по Ивантер Э.В., Коросову А.В., 1992):
Существует несколько типов коэффициентов корреляции, что зависит от переменных Х и Y, которые могут быть измерены в разных шкалах. Именно этот факт и определяет выбор соответствующего коэффициента корреляции (см. табл. 13):
В MS Excel для вычисления парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ (массив1; массив2),
| № испытуемых | X | Y |
| 1 | 19 | 17 |
| 2 | 32 | 7 |
| 3 | 33 | 17 |
| 4 | 44 | 28 |
| 5 | 28 | 27 |
| 6 | 35 | 31 |
| 7 | 39 | 20 |
| 8 | 39 | 17 |
| 9 | 44 | 35 |
| 10 | 44 | 43 |
где массив1 – ссылка на диапазон ячеек первой выборки (X);
массив2 – ссылка на диапазон ячеек второй выборки (Y).
Пример 1: 10 школьникам были даны тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Исследователя интересует вопрос: существует ли взаимосвязь между временем решения этих задач? Переменная X — обозначает среднее время решения наглядно-образных, а переменная Y— среднее время решения вербальных заданий тестов.
Р
В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию КОРРЕЛ, после чего нажмите кнопку ОК. Указателем мыши введите диапазон данных выборки Х в поле массив1 (А1:А10). В поле массив2 введите диапазон данных выборки У (В1:В10). Нажмите кнопку ОК. В ячейке С1 появится значение коэффициента корреляции — 0,54119. Далее необходимо посмотреть на абсолютное число коэффициента корреляции и определить тип связи (тесная, слабая, средняя и т.д.)
Рис. 1. Результаты вычисления коэффициента корреляции
Таким образом, связь между временем решения наглядно-образных и вербальных заданий теста не доказана.
Задание 1. Имеются данные по 20 сельскохозяйственным хозяйствам. Найти коэффициент корреляции между величинами урожайности зерновых культур и качеством земли и оценить его значимость. Данные приведены в таблице.
Таблица 2. Зависимость урожайности зерновых культур от качества земли
| Номер хозяйства | Качество земли, балл | Урожайность, ц/га |
| 1 | 32 | 19,5 |
| 2 | 33 | 19 |
| 3 | 35 | 20,5 |
| 4 | 37 | 21 |
| 5 | 38 | 20,8 |
| 6 | 39 | 21,4 |
| 7 | 40 | 23 |
| 8 | 41 | 23,3 |
| 9 | 42 | 24 |
| 10 | 44 | 24,5 |
| 11 | 45 | 24,2 |
| 12 | 46 | 25 |
| 13 | 47 | 27 |
| 14 | 49 | 26,8 |
| 15 | 50 | 27,2 |
| 16 | 52 | 28 |
| 17 | 54 | 30 |
| 18 | 55 | 30,2 |
| 19 | 58 | 32 |
| 20 | 60 | 33 |
Задание 2. Определите, имеется ли связь между временем работы спортивного тренажера для фитнеса (тыс. часов) и стоимость его ремонта (тыс. руб.):
-
Время работа тренажера (тыс. часов) Стоимость ремонта (тыс. руб.) 0,50 7,50 0,60 7,75 0,70 7,25 0,80 7,40 0,90 7,90 1,00 8,00 1,10 8,50 1,20 8,40 1,30 8,35 1,40 8,55 1,50 8,70 1,60 9,05 1,70 8,80 1,80 9,10 1,90 9,30 2,00 9,25 2,10 9,45
1.2 Множественная корреляция в MS Excel
При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять для нескольких выборок, для удобства получаемые коэффициенты сводят в таблицы, называемые корреляционными матрицами.
Корреляционная матрица — это квадратная таблица, в которой на пересечении соответствующих строк и столбцов находятся коэффициент корреляции между соответствующими параметрами.
В MS Excel для вычисления корреляционных матриц используется процедура Корреляция из пакета Анализ данных. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.
Для реализации процедуры необходимо:
1. выполнить команду Сервис_-_Анализ_данных_;2._в_появившемся_списке_Инструменты_анализа’>Сервис — Анализ данных;
2. в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку ОК;
3. в появившемся диалоговом окне указать Входной интервал, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Входной интервал должен содержать не менее двух столбцов.
4. в разделе Группировка переключатель установить в соответствии с введенными данными (по столбцам или по строкам);
5. указать выходной интервал, то есть ввести ссылку на ячейку, начиная с которой будут показаны результаты анализа. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные. Нажать кнопку ОК.
В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует сам с собой
Пример 2. Имеются ежемесячные данные наблюдений за состоянием погоды и посещаемостью музеев и парков (см. табл. 3). Необходимо определить, существует ли взаимосвязь между состоянием погоды и посещаемостью музеев и парков.
Таблица 3. Результаты наблюдений
-
Число ясных дней Количество посетителей музея Количество посетителей парка 8 495 132 14 503 348 20 380 643 25 305 865 20 348 743 15 465 541
Решение. Для выполнения корреляционного анализа введите в диапазон A1:G3 исходные данные (рис. 2). Затем в меню Сервис выберите пункт Анализ данных и далее укажите строку Корреляция. В появившемся диалоговом окне укажите Входной интервал (А2:С7). Укажите, что данные рассматриваются по столбцам. Укажите выходной диапазон (Е1) и нажмите кнопку ОК.
На рис. 33 видно, что корреляция между состоянием погоды и посещаемостью музея равна -0,92, а между состоянием погоды и посещаемостью парка — 0,97, между посещаемостью парка и музея — 0,92.
Таким образом, в результате анализа выявлены зависимости: сильная степень обратной линейной взаимосвязи между посещаемостью музея и количеством солнечных дней и практически линейная (очень сильная прямая) связь между посещаемостью парка и состоянием погоды. Между посещаемостью музея и парка имеется сильная обратная взаимосвязь.
Рис. 2. Результаты вычисления корреляционной матрицы из примера 2
Задание 3. 10 менеджеров оценивались по методике экспертных оценок психологических характеристик личности руководителя. 15 экспертов производили оценку каждой психологической характеристики по пятибальной системе (см. табл. 4). Психолога интересует вопрос, в какой взаимосвязи находятся эти характеристики руководителя между собой.
Таблица 4. Результаты исследования
| Испытуемые п/п | тактичность | требовательность | критичность |
| 1 | 70 | 18 | 36 |
| 2 | 60 | 17 | 29 |
| 3 | 70 | 22 | 40 |
| 4 | 46 | 10 | 12 |
| 5 | 58 | 16 | 31 |
| 6 | 69 | 18 | 32 |
| 7 | 32 | 9 | 13 |
| 8 | 62 | 18 | 35 |
| 9 | 46 | 15 | 30 |
| 10 | 62 | 22 | 36 |
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.