Лабораторная работа excel поиск решения в excel

Лабораторная работа №15.
Подбор параметра, поиск решения в MS
Excel

Цель работы:

Научиться использованию подбора
параметра для анализа данных, научится
решать задачи на оптимизацию, с помощью
надстройки «поиск решения».

Теоретическая часть

Использование подбора параметра
для анализа данных.

Подбор параметра определяет значение
одной входной ячейки, которое требуется
для получения желаемого результата в
ячейке результата.

Задача 1.

  1. На «Лист 1» введите данные калькуляции
    цены книги, приведённые в таблице (рис.
    1). Константами должны быть (в таблице
    эти значения показаны на сером фоне
    жирным шрифтом):

  • количество экземпляров;

  • проценты накладных расходов;

  • затраты на зарплату;

  • затраты на рекламу;

  • цена продукции;

  • себестоимость продукции.

Остальные данные должны быть представлены
в виде расчётных формул:

  • Доход = Цена продукции * Количество
    экземпляров;

  • Себестоимость реализованной
    продукции = Себестоимость продукции *
    Количество экземпляров;

  • Валовая прибыль = Доход – Себестоимость
    реализованной продукции;

  • Накладные расходы = Доход * Проценты
    накладных расходов;

  • Валовые издержки = Накладные расходы
    + Затраты на зарплату + Затраты на
    рекламу;

  • Прибыль от продукции = Валовая
    прибыль – Валовые издержки.

Введите формулы и сверьте результаты
расчёта по ним с данными, приведёнными
в таблице:

Рис. 1. Таблица калькуляции цены
книги.

  1. Переименуйте «Лист 1» в «Калькуляция»
    и скопируйте таблицу с формулами на
    «Лист 2». Исследуйте информацию,
    представленную в таблице листа
    «Калькуляция». Увеличение прибыли
    может быть достигнуто за счёт изменения
    количества экземпляров, себестоимости,
    валовых издержек и уровня накладных
    расходов.

  2. Подберите такую цену книги, чтобы
    прибыль от продукции составила 1500000
    рублей. Для этого:

  • на вкладке Данные (группа Работа
    с данными    , кнопка Анализ «что
    если»    ) выберите Подбор параметра;

  • в диалоговом окне Подбор параметра
    в поле Установить в ячейке
    укажите целевую ячейку, содержащую
    значение прибыли от продукции ($C$10), в
    поле Значение укажите то
    значение, которое должно быть достигнуто
    (1500000) и в поле Изменяя значение
    ячейки     введите абсолютную ссылку
    на ячейку, содержащую значение цены
    (($C$11);

  • нажмите кнопку ОК.

  1. Ознакомьтесь с результатами выполнения
    операции подбора параметра в окне
    Результат подбора параметра и
    нажмите кнопку ОК для изменения
    значений ячеек таблицы в соответствии
    с найденным решением.

  2. Вернитесь к исходному состоянию таблицы,
    используя описанный в пунктах 3 и 4
    способ подбора параметра.

  3. Самостоятельно определите, каков должен
    быть показатель процентов накладных
    расходов, чтобы прибыль за продукцию
    составила 100000 рублей.

Задача 2. В приведенной таблице
(рис. 2), используя средство Подбор
параметра определите:

  • насколько нужно снизить транспортные
    расходы, чтобы они составили не более
    40% от общих расходов компании;

  • насколько нужно снизить стоимость
    работ, чтобы она составляла не более
    20% от общих затрат.

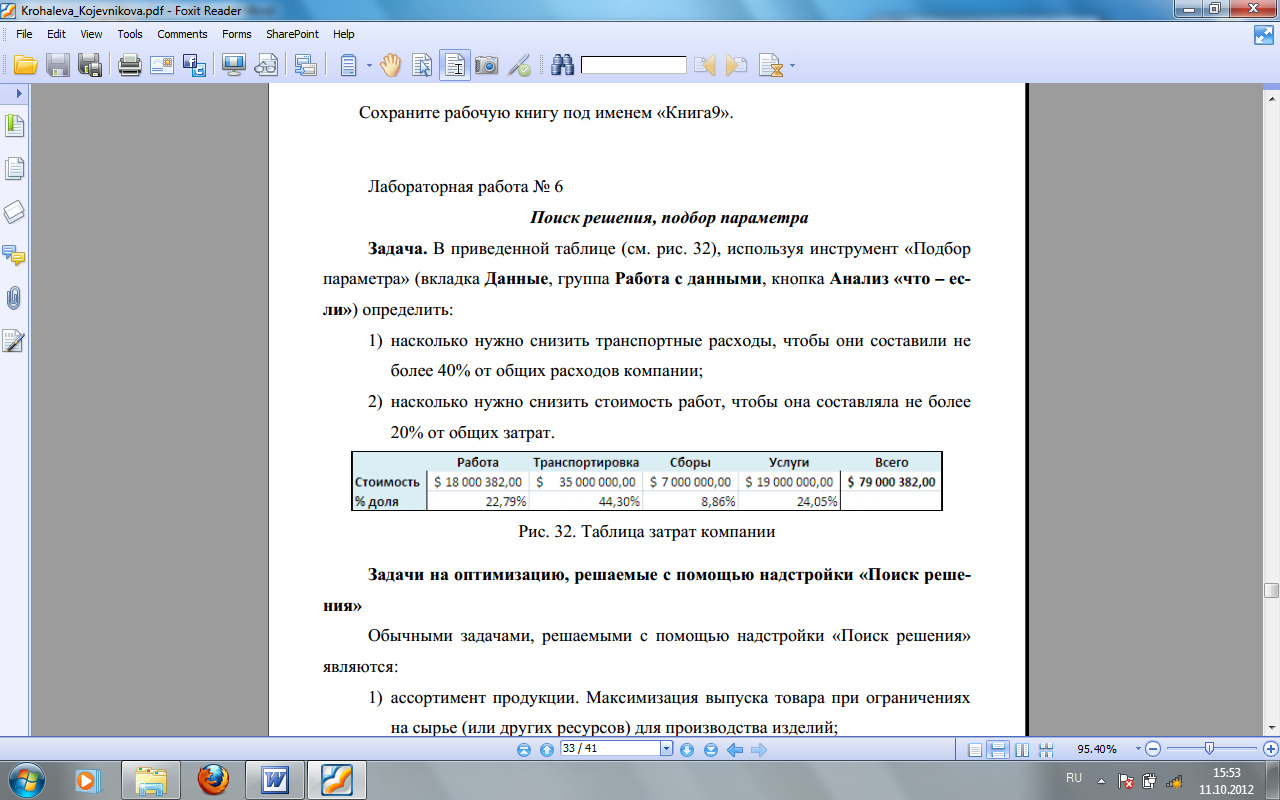
Рис. 2. Таблица затрат компании.

Задачи на оптимизацию, решаемые с
помощью надстройки «Поиск решения».

Обычными задачами, решаемыми с помощью
надстройки Поиск решения
являются:

  • ассортимент продукции (например,
    максимизация выпуска товара при
    ограничениях на сырье (или других
    ресурсов) для производства изделий);

  • планирование перевозок (например,
    минимизация затрат на транспортировку);

  • оптимизация финансовых показателей
    (например, максимизация доходов за счет
    оптимизации средств на разные
    инвестиционные проекты);

  • и т. д.

Задачи, которые лучше всего решаются
данным средством, имеют три свойства:

  • имеется единственная минимизируемая
    или максимизируемая цель;

  • имеются ограничения, выражаемые, как
    правило, в виде неравенств;

  • имеется набор входных значений-переменных,
    прямо или косвенно влияющих на ограничения
    и на оптимизируемые величины.

Задача 3. Из приведенной таблицы
(рис. 3), используя опцию Поиск решения,
определите количество товара разных
наименований, так чтобы количество
каждого товара было не менее 100 шт. и при
общих издержках (т.е. сумме по Суммарным
издержкам) не более 1000000 р. Прибыль
предприятия должна быть максимальной.
Столбцы D, F, G должны быть заполнены с
помощью формул.

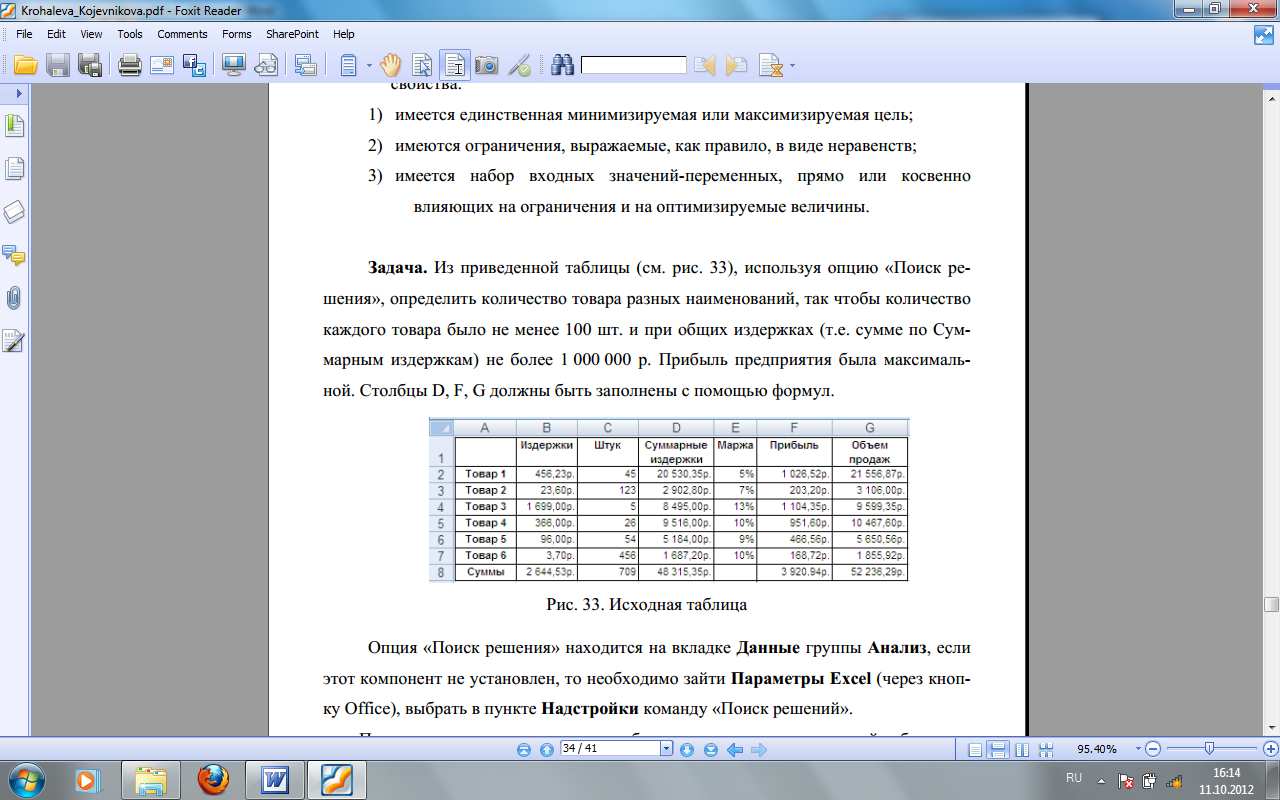
Рис. 3. Исходная таблица.

Опция Поиск решения находится
на вкладке Данные группы Анализ.
Если этот компонент не установлен, то
необходимо открыть Параметры Excel
(через кнопку Office), выбрать в
пункте Надстройки команду Поиск
решений.

Перед началом решения задачи необходимо
определить, какая ячейка будет целевой,
какие ячейки будут изменяться, и на
какие ячейки будут накладываться
условия.

В данной задаче ячейка F8 будет целевой,
так как необходимо максимизировать
прибыль предприятия.

Ячейки С2:С7 могут изменяться. А условия
необходимо наложить, во-первых, на ячейки
С2:С7, они должны быть все не менее 100,
во-вторых, числа в этих же ячейках должны
быть все целые, в-третьих, ячейка D8 должна
быть меньше 1000000. Таким образом, окно
поиска решения должно быть заполнено
следующим образом (рис. 4):

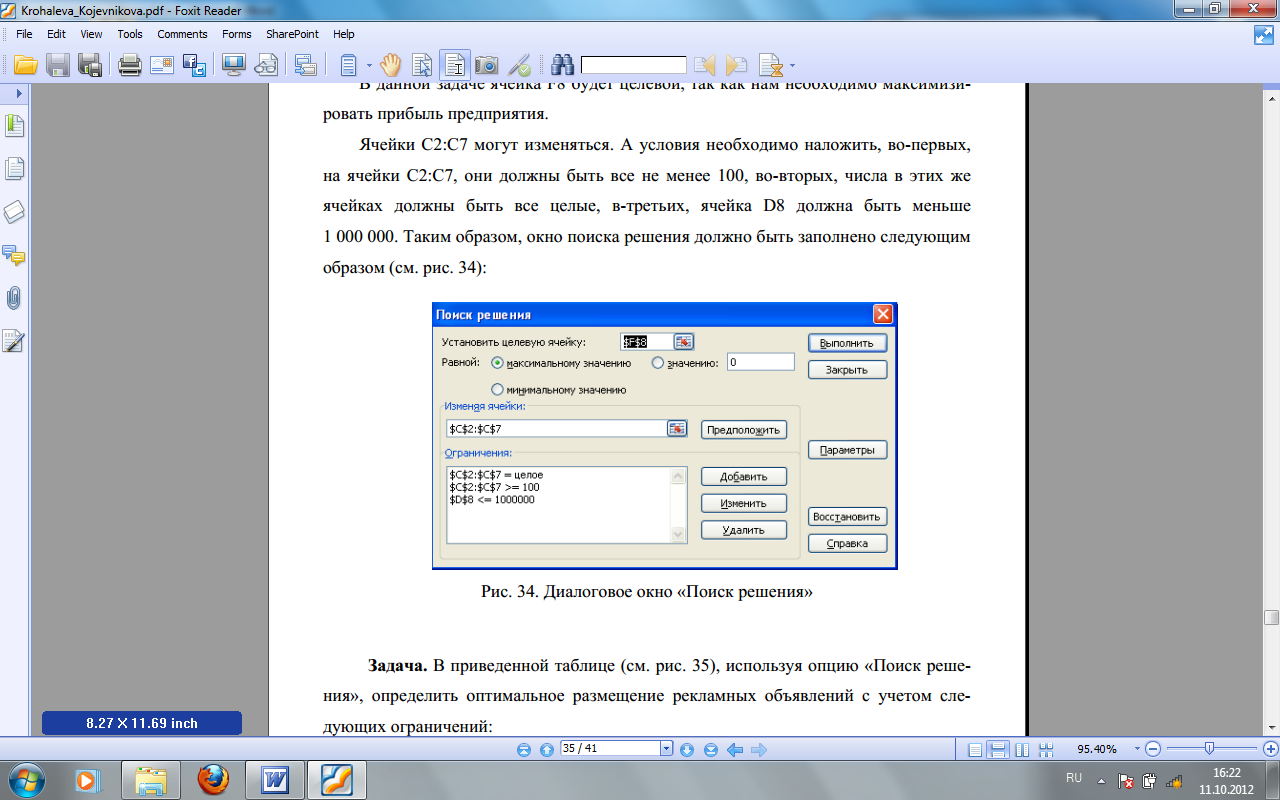
Рис. 4. Диалоговое окно «Поиск решения».

Задача 4. В приведенной таблице
(рис. 5), используя опцию Поиск решения,
определите оптимальное размещение
рекламных объявлений с учетом следующих
ограничений:

  • необходимо обеспечить максимальную
    читательскую аудитории для объявлений;

  • нужно заказать как минимум 8 объявлений
    в трех журналах и хотя бы 10 в четвертом;

  • в одном журнале должно быть не более
    20 объявлений;

  • аудитория должна быть не менее 10 млн.
    человек;

  • бюджет рекламной компании должен
    составлять 3 млн.р.

Общая постановка
задачи

Изучить возможности программы MS
Excel для
выполнения следующих операций над
документом: создание таблицы с константами
и расчетными формулами, средство «подбор
параметра», использование надстройки
«поиск решения».

Список индивидуальных
данных

Номер варианта и задания, если это
требуется в лабораторной работе,
определяется преподавателем.

Пример выполнения
работы

Каждое задание должно быть выполнено,
сохранено в файле .xlsx.

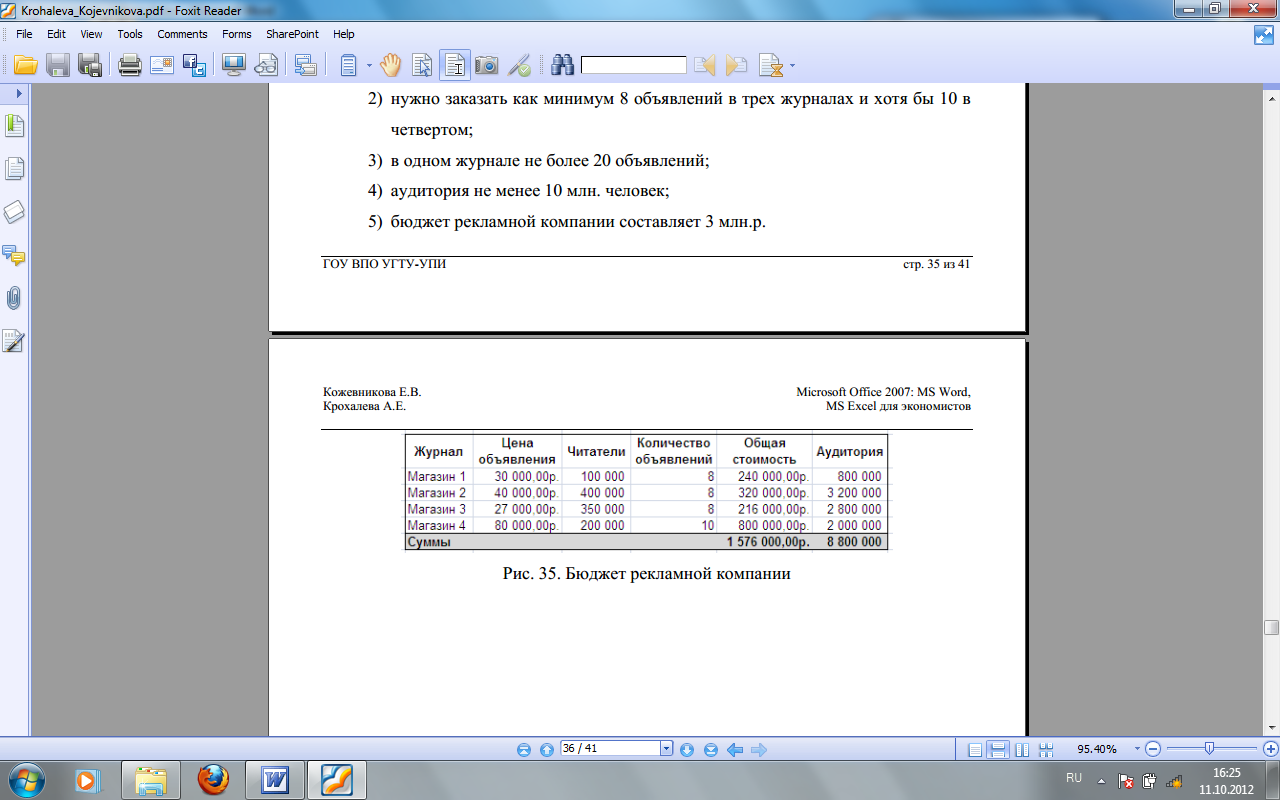
Рис. 5. Бюджет рекламной компании.

Контрольные вопросы
к защите

  1. Для чего нужно средство подбор параметра?

  2. Каким образом можно ознакомиться с
    результатом подбора параметра?

  3. Какие виды задач можно решить с помощью
    надстройки «поиск решения»?

  4. Какие свойства имеют задачи, решаемые
    с помощью средства «поиск решения»?

  5. Какие параметры необходимо определить
    для использования надстройки «поиск
    решения»?

Соседние файлы в предмете Информатика

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Лабораторная работа 3. Поиск решения в Microsoft Excel

Целью лабораторной работы является
изучение возможностей средства Поиск решения MS Excel для решения
оптимизационных задач.

К защите лабораторной работы студент
должен предоставить файл ЛР3_ФамилияИО.xlsx с решенными задачами
на листах: Задача1, Задача2, Задача3, Задача4.

Сохраните рабочую книгу MS Excel в своей папке под именем
ЛР3_ФамилияИО.xlsx.

Задача 1. Транспортная
задача

Постановка задачи

Некоторая
фирма имеет 4 фабрики и пять центров распределения товаров. Фабрики
располагаются в Витебске, Гомеле, Могилеве и Полоцке и имеют производственные
мощности для выпуска соответственно 200, 150, 225 и 175 единиц продукции
ежедневно. Центры распределения товаров располагаются в Минске, Бресте, Пинске,
Гродно и Лиде и имеют ежедневные потребности в продукции 100, 200, 50, 250 и
150 единиц соответственно. Стоимость перевозки единицы продукции с фабрик в
пункты распределения приведена в таблице 1.

Таблица 1 – Транспортные расходы

Стоимость перевозок

                                         Фабрики          Склады

                                                                                             Минск      Брест      Пинск     Гродно      Лида

                                        Витебск                              $2,00      $2,00      $1,75      $2,25      $2,25

                                        Гомель                               $2,50      $0,50      $1,50      $1,00      $1,50

                                        Могилев                              $1,50      $1,50      $1,75      $1,75      $1,75

                                         Полоцк                               $2,00      $2,00      $1,75      $1,75      $1,75

Необходимо так
спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.

Оценка информации. Данная модель
сбалансирована, т.е. суммарный объем произведенной продукции (750) равен суммарному
объему потребностей в ней (750).

Введем обозначения:

•      
xij – объем перевозок с i-й фабрики в j-й
центр распределения;

•      
cij – стоимость перевозки единицы продукции с i-й
фабрики в j-й центр распределения;        ai – объем
производства на i-й фабрике;

•      
bj – спрос в j-м центре распределения.

Математическая модель этой задачи состоит из трех
ограничений:

               4                                                              5


xij
bj, j 1,5;          

xij
ai,  i 1,4;          
xij
0,  i 1,4,
j 1,5

              i1                                                                  j1

4 5

и целевой функции, минимизирующей транспортные расходы: cij
xij
min .

i 1 j 1

Порядок выполнения:

Переименуйте Лист1 рабочей книги,
новое имя листа – Задача1. Сохраните файл. Выполните следующую подготовительную
работу для решения транспортной задачи с помощью средства Поиск решения
(рисунок 1).

 

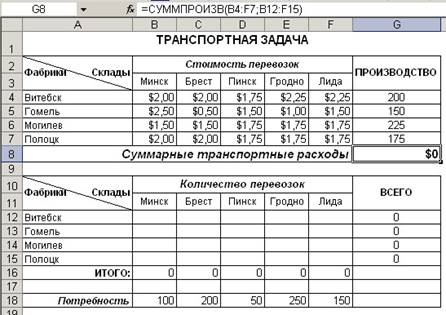
Рисунок
1 – Исходные данные транспортной задачи

В ячейки диапазона G12:G15 введите
формулы, вычисляющие суммарный объем товаров по каждой фабрике,  а в ячейки B16:F16
– формулы, вычисляющие объемы доставляемой продукции в пункты распределения. В целевую
ячейку G8 введите формулу, вычисляющую суммарные транспортные расходы.

При создании вычислительной модели используем
инструмент Поиск решения и заполняем диалоговое окно, как показано на рисунке
2. Нажмите кнопку Параметры диалогового окна Поиск решения. Откроется
диалоговое окно Параметры поиска решения, в котором необходимо установить
Линейность модели (рисунок 3).

После нажатия кнопки Найти
решение будут найдены оптимальный план поставок продукции и соответствующие
ему транспортные расходы (рисунок 4). Сохраните найденное решение.

 

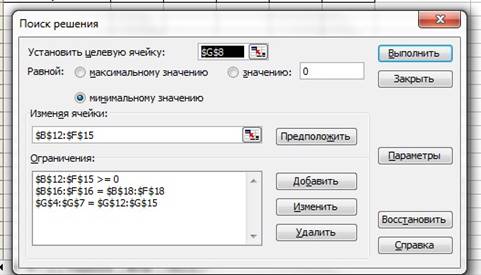
Рисунок
2 – Окно Поиск решения после заполнения для транспортной задачи

 

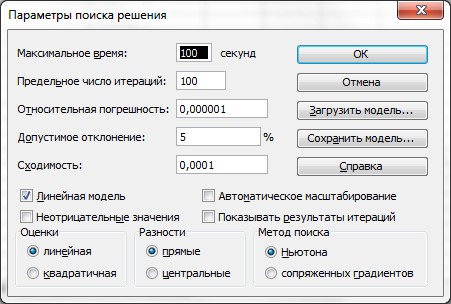
Рисунок
3 – Окно Параметры поиска решения после заполнения для транспортной задачи

 

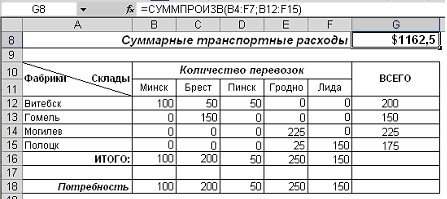
Рисунок 4 – Решенная транспортная задача

Задача 2. О
планировании производства

Постановка задачи

Предприятие электронной
промышленности выпускает две модели радиоприемников, причем каждая модель
производится на отдельной технической линии. Суточный объем производства первой
линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели
расходуется 10 однотипных элементов электронных схем, на радиоприемник второй
модели – 8 таких элементов. Максимальный суточный запас используемых элементов
равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй
модели равна 30 и 20 у.е. соответственно. Определите оптимальный суточный объем
производства первой и второй моделей.

Оценка информации. Предприятию
необходимо спланировать объем выпуска радиоприемников так, чтобы максимизировать
прибыль.

Введем обозначения:

•      
x1 – суточный объем выпуска радиоприемников
первой модели;

•      
x2 – суточный объем выпуска радиоприемников
второй модели.

Математическая модель этой задачи состоит из ограничений:

              x1 60                                                 

                                                        x
j
0,  j
1,2

              x2 75                                                          

10x1 8x2 800

Кроме того, на x1 и x2 налагаются
условия целочисленности, т.е. полученные в результате расчетов значения объемов
выпуска должны быть целыми числами.

Целевая функция 30x1 20x2 max .

Порядок выполнения:

Выполните следующую подготовительную
работу для решения задачи о планировании производства с помощью средства Поиск
решения (рисунок 5).

 

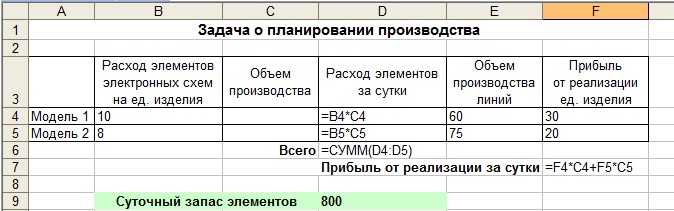
Рисунок 
5 — Таблица с исходными данными и формулами

Введите в ячейки С4 и С5
данные об объемах выпуска радиоприемников, удовлетворяющие условиям задачи (допустимый
план задачи), равные 40 единицам. Просмотрите полученные результаты.

При создании вычислительной модели используем
инструмент Поиск решения и заполняем диалоговое окно, как показано на рисунке
6.

 

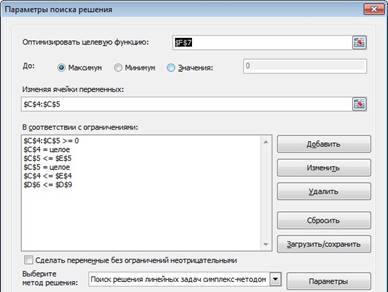
Рисунок
6 — Окно Поиск решения для задачи о планировании производства

После нажатия кнопки Найти
решение будут найдены оптимальный план производства. Проанализируйте изменения
в таблице.

Переименуйте Лист2 с решенной задачей,
новое имя листа – Задача2. Сохраните файл. (Впоследствии каждую задачу необходимо
решать на новом листе рабочей книги, листы называть соответственно задачам).

Задача 3. О снабжении

Постановка задачи

Некоторое
учреждение приняло решение одеть своих сотрудников в фирменные костюмы. Оно
получило предложения от фирм f1, f2 и f3 на поставку фирменных костюмов трех
размеров: s1, s2 и s3. Стоимость костюмов приведена в таблице 2.

Таблица 2 – Стоимость костюмов

s1

s2

s3

фирма f1

110

115

126

фирма f2

107

115

130

фирма f3

104

109

116

Будут заключены
контракты на покупку 1000 костюмов размера s1, 1500 костюмов размера s2 и 1200
костюмов размера s3. Производственные мощности фирм позволяют выпускать 1000
костюмов разных размеров фирме f1, 1500 костюмов фирме f2 и 2500 костюмов фирме
f3.

Как следует распределить заказы, чтобы
контракты были заключены с минимизацией общей стоимости?

Оценка информации. Заметим,
что общее предложение (5000) превосходит общий спрос (3700), т.е. налицо некоторая
избыточная производственная мощность. Мы понимаем, что учреждение должно получить
ровно столько костюмов, сколько работников оно собирается ими обеспечить. А вот
с какой фирмы и сколько будет взято костюмов, выяснится в результате решения задачи.
Введем обозначения:

•             
a1, a2, a3 – количество костюмов размера s1, выпускаемых соответственно
фирмами f1, f2 и f3;

•             
b1, b2, b3 – количество костюмов размера s2, выпускаемых соответственно
фирмами f1, f2 и f3; c1, c2, c3 – количество костюмов
размера s3, выпускаемых соответственно фирмами f1, f2 и f3. Математическая
модель этой задачи состоит из шести ограничений:

a1 + a2
+ a3 = 1000, b1 + b2 + b3 = 1500, c1 + c2 + c3 = 1200, a1 + b1 + c1 <= 1000,
a2 + b2 + c2 <= 1500, a3 + b3 + c3 <= 2500

и целевой функции, минимизирующей общую стоимость:

110a1 + 107a2
+ 104a3 + 115b1 + 115b2 + 109b3 + 126c1 + 130c2 + 116c3 → min.

Порядок выполнения:

Выполните следующую подготовительную работу для решения
задачи (рисунок 7).

 

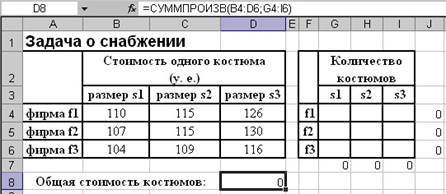
Рисунок
7 – Исходные данные для задачи о снабжении

В ячейки J4:J6 введите формулы
для расчета общего объема поставок от фирм f1, f2 и f3 соответственно, используя
функцию СУММ. В ячейки G7:I7 введите формулы, подсчитывающие общее
количество костюмов s1, s2 и s3. В целевой ячейке D8 подсчитайте общую стоимость
костюмов.

При создании вычислительной модели используем
инструмент Поиск решения, т.к. задача имеет достаточно много переменных
(9). При этом для изменяемых ячеек (переменных) необходимо будет добавить два ограничения.
Значения их должны быть целочисленными и неотрицательными (рисунок 8). Всего должно
быть 8 ограничений.

 

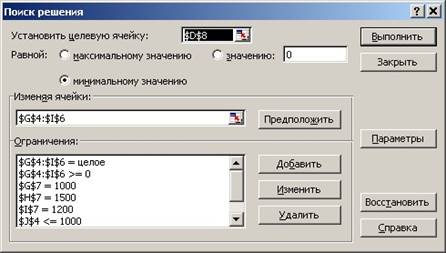
Рисунок
8 – Окно Поиск решения после заполнения для задачи о снабжении

После нажатия кнопки Найти
решение получим оптимальный план распределения заказов (рисунок 9). Сохраните
файл.

 

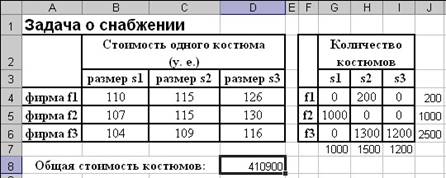
Рисунок
9 – Решенная задача о снабжении

Задача 4. О назначениях

Постановка задачи

Имеются
четыре рабочих и четыре вида работ. Стоимости cij выполнения i-м рабочим j-й работы
приведены  в таблице 3, где под строкой понимается рабочий, а под столбцом –
работа

Таблица 3 – Стоимость выполнения работ

1

4

6

3

9

10

7

9

4

5

11

7

8

7

8

5

Рабочие

                                                                                                                             Виды
работ

Необходимо
составить план выполнения работ так, чтобы все работы оказались выполненными,
каждый рабочий был загружен только на одной работе, а суммарная стоимость
выполнения всех работ была минимальной.

Оценка информации. Данная задача
является сбалансированной, т.е. число работ совпадает с числом рабочих. Если задача
не сбалансирована, то перед началом решения ее необходимо сбалансировать, введя
недостающее число фиктивных строчек или столбцов с достаточно большими штрафными
стоимостями работ. Введем обозначения:

•      
xij
– переменная, имеющая только два допустимых значения: 0 или 1 (такие
переменные называются двоичными);       xij=1, если i—м рабочим выполняется j-я работа;

•      
xij=0,
если i—м рабочим не
выполняется j-я работа.

Математическая модель этой задачи состоит из ограничений: 

                4                                                                                                 4                                                                                                  

xij 1, j 1,4;

i1

xij 1,  i 1,4;

j1

xij {0,1},i 1,4, j 1,4

                                                                                                                                                                        4       4

и целевой функции, минимизирующей суммарную стоимость выполнения
всех работ: cij xij
min .

i
1 j 1 Порядок выполнения:

Выполните следующую подготовительную
работу для решения задачи о назначениях с помощью средства Поиск решения
(рисунок 10).

 

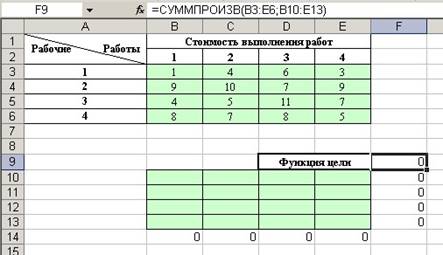
Рисунок
10 – Исходные данные задачи о назначениях

В ячейки диапазона B14:E14 и F10:F13 введите следующие
формулы, задающие левые части ограничений:

Ячейка

Формула

Ячейка

Формула

B14

=СУММ(B10:B13)

F10

=СУММ(B10:E10)

C14

=СУММ(C10:C13)

F11

=СУММ(B11:E11)

D14

=СУММ(D10:D13)

F12

=СУММ(B12:E12)

E14

=СУММ(E10:E13)

F13

=СУММ(B13:E13)

В целевую ячейку F9 введите формулу, вычисляющую
суммарную стоимость выполнения работ.

При создании вычислительной модели используем
инструмент Поиск решения и заполняем диалоговое окно, как показано на рисунке
11.

 

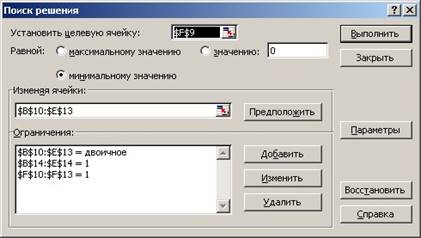
Рисунок
11 – Окно Поиск решения после заполнения для задачи о назначениях

После нажатия кнопки Найти решение получим оптимальный
план выполнения работ. Сохраните файл.

ЗАДАЧИ ДЛЯ
САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Задача 5. Транспортная задача

Постановка задачи

Имеются n пунктов производства
и m пунктов распределения продукции. Стоимость перевозки единицы продукции
с i-го пункта производства в j-й центр распределения cij
приведена в таблице, где под строкой понимается пункт производства, а под столбцом
– пункт распределения. Кроме того, в этой таблице в i-й строке указан объем
производства  в i-м пункте производства, а в j-м столбце указан спрос
в j-м центре распределения. Необходимо составить план перевозок продукции
в пункты распределения, минимизирующий суммарные транспортные расходы.

Задача 6. Транспортная
задача

Постановка задачи

На складах w1, w2, w3 хранятся соответственно
15, 25, 20 кроватей, которые должны быть распределены по четырем магазинам ml,
m2, mЗ, m4, где требуется 20, 12, 5 и 9 кроватей. Пусть стоимость перевозки одной
кровати со склада  в магазин задается следующей таблицей в условных единицах:

Склад

Магазин 

ml 

m2 

m3 

m4 

w1

2

2

2

4

w2

3

1

1

3

w3

3

6

3

4

Как следует планировать перевозку для минимизации стоимости?

Задача 7. Транспортная
задача

Постановка задачи

Компания владеет тремя заводами А, В,
С. Объем их производства равен соответственно 6000, 3000 и 3000 единиц. Компания
обязалась поставлять соответственно 1500, 2500, 2700 и 3300 единиц продукции в города
W, X, Y, Z. При заданных стоимостях перевозок составьте оптимальный план распределения.

 

Задача 8. Задача о
назначениях

Постановка задачи

Имеются n рабочих мест и m
видов работ. Стоимость cij выполнения i-м рабочим j-й
работы приведена в таблице, где под строкой понимается рабочий, а под столбцом
– работа. Необходимо составить план работ так, чтобы все работы были выполнены,
каждый рабочий был занят только на одной работе, а суммарная стоимость работ была
минимальной.

Вариант 1.

Стоимость выполнения работ

3

6

2

5

1

2

7

11

5

12

11

9

2

4

2

10

Рабочие

                                                                                                       Виды
работ

Вариант 2.

Стоимость выполнения работ

1

3

6

5

5

2

7

8

3

5

1

9

6

4

2

10

Рабочие

                                                                                                       Виды
работ

Задача 9.
Производственная задача

Постановка задачи

Фирма производит две модели А и В сборных
книжных полок. Их производство ограничено наличием сырья (высококачественных досок)
и временем машинной обработки. Для каждого изделия модели А требуется 3м2
досок, а для изделия модели В – 4м2. Фирма может получать до 1700м2
досок в неделю. Для каждого изделия модели А требуется 12 минут машинного времени,
а для изделия модели В – 30 минут. В неделю можно использовать 160 часов
машинного времени.

Сколько изделий каждой модели следует
фирме выпускать в неделю, чтобы получить максимальную прибыль, если каждое изделие
модели А приносит 2 условные единицы прибыли, а каждое изделие модели В – 4 условные
единицы прибыли?

Задача 10.
Производственная задача

Постановка задачи

Фирма производит два продукта А и В,
рынок сбыта которых неограничен. Каждый продукт должен быть обработан каждой из
машин I, II, III. Время обработки в часах для каждого из продуктов А и В приведено
в таблице. Время работы машин I, II, III соответственно равно 40, 36 и 36 часов
в неделю. Прибыль от изделий А и В составляет соответственно 5 и 5 условных единиц.
Фирме надо определить недельные нормы выпуска продуктов А и В, максимизирующие прибыль.

Машины 

I

II

III

продукт А

продукт В

0,5

0,25

0,4

0,3

0,2

0,4

Задача 11.
Производственная задача

Постановка задачи

Процесс изготовления изделий двух видов
А и В некоторым заводом требует, во-первых, последовательной обработки на токарных
и фрезерных станках, во-вторых, затрат двух видов сырья: стали и цветных металлов.
В таблице приводятся данные о потребности каждого ресурса на единицу выпускаемого
изделия, общие запасы ресурсов и прибыль от реализации каждой единицы изделия. Определить
такой план выпуска продукции, который обеспечивает максимальную прибыль при условии,
что время работы фрезерных станков должно быть использовано полностью.

 

Задача 12.
Производственная задача

Постановка задачи

Производитель безалкогольных напитков
располагает двумя разливочными машинами А и В. Машина А спроектирована для пол-литровых
бутылок, а машина В — для литровых, но каждая из них может использоваться для обоих
типов бутылок с некоторой потерей эффективности в соответствии с приведенными в
таблице сведениями о работе машин, каждая из машин работает ежедневно по 6 часов
при пятидневной рабочей неделе. Прибыль от поллитровой бутылки составляет 4 цента,
а от литровой — 10 центов. Недельная продукция не может превосходить 50000 л; рынок
принимает не более 44000 пол-литровых бутылок и 30000 литровых. Требуется максимизировать
прибыль.

Машина 

Количество бутылок,
производимых в 1 мин.

пол-литровые

литровые

А

В 

50 40 

20 30 

Источник

Лабораторная работа №11.

Тема: ЗАДАЧИ ОПТИМИЗАЦИИ (ПОИСК РЕШЕНИЯ)

Цель:
Формирование практических навыков технологии поиска решения для задач
оптимизации (минимизации, максимизации) в Excel.

Задача 1.

В ходе
производственного процесса из листов материала получают заготовки деталей двух
типов различными способами, при этом количество получаемых заготовок при каждом
методе различается.

Способы раскроя заготовок

Тип заготовки

Количество заготовок

Способ 1

Способ 2

Способ 3

А

10

3

8

Б

3

6

4

Необходимо выбрать оптимальное сочетание способов раскроя, для того
чтобы получить 500 заготовок первого типа и 300 заготовок второго типа при
расходовании наименьшего количества листов материала.

2. Поисковые
переменные

Параметрами, значения
которых необходимо определить, являются количества листов материала, которые
будут раскроены различными способами:

•      Х1 – количество листов, раскроенные способом
1;

•      Х2 – количество листов, раскроенные способом
2;

•      Х3 – количество листов, раскроенные способом
3;

3. Математическая
модель

Тогда целевая
функция, значением которой является общее количество листов материала, примет
вид:           F=X1+X2+X2

4. Ограничения

Ограничения
определяются значениями требуемых количеств заготовок типа А и Б, тогда с
учетом количества заготовок, получаемых различными способами, должны
выполняться два равенства:

10Х1+3Х2+8Х3=500

3Х1+6Х2+4Х3=800

Кроме того,
количества листов не могут быть отрицательными, поэтому должны выполняться
неравенства: Х1>=0; Х2>=0; Х3>=0;

5. Критерии
оптимизации

Таким образом,
необходимо найти удовлетворяющие ограничениям значения параметров, при которых
целевая функция принимает минимальное значение.

6. Решение на
компьютере.

Заполнить таблицу на
компьютере, занести в ячейки формулы.

Найти оптимальное решение. Для этого:

а) выделить целевую
ячейку B7;

б) выбрать Данные,
Поиск решения;

в) установить целевую ячейку, равную минимальному
значению;

г) указать мышью диапазон изменяемых ячеек;

д) выбрать кнопку
Добавить для записи ограничений;

е) после записи
ограничения нажать Добавить (для последнего ограничения – ОК);

ж) нажать кнопку
Найти решение;

з) выбрать Тип
отчёта, Результаты и нажать ОК.

На новом листе Отчёт
по результатам1 можно увидеть

7. Анализ полученных результатов

В электронных таблицах найдено оптимальное
решение:

Наименьшее количество раскроенных листов
равно 69, первым способом – 0, вторым -11, третьим – 58.

Тип
заготовки

Количество
заготовок

Всего
заготовок

общее
колличество листов

Способ 1

Способ 2

Способ 3

А

10

3

8

500

Б

3

6

4

300

Колличество листов

0

11

58

69

Задача решена.

Задание 2. Фирма производит
несколько видов продукции из одного и того же сырья — А, В, С. Реализация
продукции А дает прибыль 10р., В-15р. и С-20р. на единицу изделия.

Продукцию можно производить в любых количествах,
поскольку из­вестно, что сбыт, обеспечен,
но ограничены запасы сырья. Необходимо опре­делить, какой продукции, из
какого сырья (одного из трех видов) и сколько надо произвести, чтобы общая
прибыль от реализации была максимальной.

Нормы расхода сырья на
производство продукции каждого вида.   Таб.2

Сырье

Нормы расхода сырья

Запас сырья

А

В

С

Сырье 1

18

15

12

350

Сырье 2

6

4

8

200

Сырье 3

5

3

3

100

Прибыль

10

15

20

— Создайте расчетную таблицу (Таб.2.) Введите исходные данные и формулы в электронную таблицу. Расчетные формулы
имеют вид: Рас­ход сырья 1= (количество сырья 1) * (норма расхода сырья А) +
(количество сырья) * (норма расхода сырья
В) + (количество сырья 1) * (норма расхода сырья С).

Итоговая общая прибыль =
(Общая прибыль по А) + (Общая прибыль по В) + (Общая прибыль по С),
значит в ячейку ЕЮ следует ввести формулу = CУMM (B10:D10).

it_6ex5

— В меню Данные активизируйте
команду Поиск решения и введите па­раметры поиска.   В   качестве  
целевой   ячейки   укажите   ячейку   «Итого­вая   общая прибыль» (Е10), в
качестве изменяемых ячеек — ячейки количества сырья — (B9:D9 пока пустые). Не
забудьте задать максимальное значение сум­марной прибыли и указать ограничения
на запас сырья:

Расход сырья 1<=350; расход сырья 2<=200; расход сырья
3<=100, а также положительные значения количества сырья А, В, С>=0

— Кнопкой Найти решение запустите Поиск
решения.

Задача 3. Используя файл «План производства» (Задача 2) определите план
выгодного производства, т.е. какой продукции и сколько необходимо произвести,
чтобы общая прибыль от реализации была максимальной. Выберите нормы расхода
сырья на производство продукции каждого вида и ограничения по запасам сырья из
таблицы соответствующего варианта (5 вариантов):

it_6ex1var

it_6ex2var

it_6ex3var

it_6ex4varit_6ex5var

Контрольные
вопросы:

1.    
Перечислите этапы решения
задач оптимизации.

2.    
С помощью какой команды
(кнопки) в EXCEL решаются задачи оптимизации?

Источник

Применение команды «Поиск решений»

в работе с профессионально-ориентированными задачами

Постановка задачи

В ресторане установлены 7 графиков работы официантов:

График

Выходные

1

Суббота. Воскресение

2

Воскресение, Понедельник

3

Понедельник, Вторник

4

Вторник, Среда

5

Среда,

Четверг

6

Четверг, Пятница

7

Пятница, Суббота

Количество работающих по ним соответственно – №1, №2, №3, №4, №5, №6, №7. Опытным путём было определено требуемое  количество официантов на каждый день недели:

День недели

Пн

Вт

Ср

ЧТ

Пт

Сб

Вс

Требуется, чел.

11

10

9

10

12

12

13

Необходимо распределить работающих официантов по каждому графику таким образом, чтобы затраты на еженедельную зарплату всем официантам были минимальными (найти N1, N2, N3, N4, N5, N6, N7). При этом нужно учитывать следующие факторы:

  1. Ежедневно фактическое количество работающих официантов должно быть не менее ежедневной потребности.
  2. Число работников, работающих по каждому графику, не может быть отрицательным.
  3. Число работников, работающих по каждому графику, должно быть целочисленным.

Рассмотреть ситуацию, когда по графику 1 обязательно должно работать 3 человека.

Создание таблицы для анализа данных

Исходя из условий постановки задачи, создадим в табличном процессоре Excel таблицу, где будем потом рассматривать и анализировать ситуации.

  1. Открываем программу Excel, например, щёлкнув два раза её ярлык на рабочем столе или через Пуск – Программы – Microsoft Excel.
  2. Устанавливаем поля документа через Файл — Параметры страницы:
  3. Сохраняем книгу (файл в Excel) через Файл – Сохранить как под именем Анализ графиков работы.xls.
  4. Начиная с ячейки A1, оформляем таблицу (см. следующий лист). В те дни недели, где предусмотрен по графику рабочий день, ставим 1, а где  выходной – 0. при этом формат данных в этих  ячейках оставляем по умолчанию – Общий.
  5. После заполнения таблицы данными, отформатируем ячейки так, чтобы текст и числа в них располагались по горизонтали и вертикали По центру. Для этого выделим мышкой всю таблицу и используем меню Формат – Ячейки – вкладка Выравнивание (или по правой клавише мыши).
  6. Оформим  внешние и внутренние границы ячеек.
  7. Получим таблицу следующего вида:

Здесь A2…G2 – количество официантов, работающих в соответствующий день недели, A1..G1 – требуемое (определённое опытным путём, меньше нельзя).

Всего работников – N.

K – дневная заработная плата одного официанта, она составляет, к примеру, 200 рублей.

  1. Поскольку файл в программе Excel называется книга, а каждая книга состоит из листов, переименуем ярлычок первого листа книги, где создана таблица, и назовём его Заготовка. Переименовать можно щелчком правой клавишей по ярлычку листа, выбрать пункт Переименовать или просто два раза щёлкнуть по ярлычку листа, название Лист1 выделиться, можно вводить новое название.
  2. Мышкой выделим всю таблицу и скопируем её в Буфер обмена.
  3. Перейдём на Лист2 книги, щёлкнув ярлычок этого листа.
  4. Вставим из буфера скопированную таблицу: щёлкнем значок  на панели Стандартная.
  5. В ячейках C2:C8 удалим набранный текст. В этих ячейках будут вычисляться значения при применении команды Поиск решения.
  6. В ячейки D10:J10 введём определённое опытном путём минимальное количество официантов по дням недели.

Требуется (определено опыт. путём)

11

10

9

10

12

12

13

Цвет шрифта этих ячеек для лучшей наглядности сделаем синим.    

  1. В ячейках D9:J9 также удалим текст. Сюда необходимо вписать формулы.
  2. В ячейку C12 запишем 200, изменим формат данных в ячейке на Денежный в рублях, получим 200р.
  3. Переименуем Лист2 в Ситуация 1.

Таблица для проведения анализа готова.

Ввод формул для получения решения

Чтобы в дальнейшем проанализировать ситуации, необходимо в ячейки D9:J9 ввести формулы. рассчитывающие фактическое количество официантов по дням недели и по графикам работы.

Формулы для вычислений могут быть простыми, такими как сложение содержимого двух ячеек, а могут быть сложными, такими как определение отклонения какой-либо величины от других значений последовательности.

Ввод формулы в Excel начинается со знака =. За ним записывается функция, потом в скобках () аргументы. Некоторые функции, например, многие статистические, финансовые используют несколько аргументов. Тогда аргументы отделяются друг от друга запятыми.

Простейшие формулы, такие как сложение, вычитание, умножение, деление состоят из двух частей: арифметического оператора и хотя бы одного адреса ячейки.

При составлении формул для вычислений или преобразований данных необходимо указать содержимое каких именно ячеек используется в формулах.

Введём в ячейку D9 формулу =D2*C2+D5*C5+D6*C6+D7*C7+C8.

 Она рассчитывает сколько официантов должно работать в понедельник с учётом графиков их работы. Там, где в таблице 0, т.е. выходной, ячейки не обсчитываем.

Для подсчёта работников во вторник в ячейку E9 запишем формулу

=C2*E2+E3*C3+E6*C6+E7*C7+E8*C8.

Для ячейки F9 – =F2*C2+F3*C3+F4*C4+F7*C7+F8*C8. Среда.

Для ячейки G9 – =G2*C2+G3*C3+G4*C4+G5*C5+G8*C8. Четверг.

Для ячейки H9 – =H2*C2+H3*C3+H4*C4+H5*C5+H6*C6. Пятница.

Для ячейки I9 – =I3*C3+I4*C4+I5*C5+I6*C6+I7*C7. Суббота.

Для ячейки J9 – =J4*C4+J5*C5+J6*C6+J7*C7+J8*C8. Воскресенье.

В ячейку C11 нужно записать формулу подсчёта общего количества официантов с учётом всех семи графиков работы: =СУММ(C2:C8), т.е. просуммировать всех официантов, работающих по графикам 1…7.

В ячейку C13 введём формулу подсчёта недельной зарплаты всех официантов:

=(C11*C12).

 Все необходимые формулы  и данные введены в таблицу. Теперь можно приступать к поиску решения поставленной задачи.

Поиск решения

Команда Поиск решения из меню Сервис анализирует ситуацию с учётом ограничений, накладываемых на отдельные ячейки, рассчитывает значение целевой ячейки, изменяя значения указанных нами ячеек.

При поиски решения  целевая ячейка должна содержать формулу, но ячейки, которые будут изменяться, должны содержать значения, а не формулу.

Для решения нашей задачи выполним следующие действия:

  1. Выделим ячейку C13. (Еженедельная зарплата, она должна быть минимальной.)
  2. Сервис — Поиск решения.
  3. Установим целевую ячейку $C$13 равной минимальному значению.

  1. Укажем, что будут меняться значения ячеек $C$2:$C$8. Это можно сделать, щёлкнув по красной стрелке в правом углу окошечка, перейдя в таблицу и выделив нужные ячейки.
  2. Введём ограничения на значения отдельных ячеек: в ячейках C2…C8 должно быть целое число; ячейка D9>=11, E9>=10, F9>=9, G9>=10, H9>=12, I9>=12, J9>=13. Ввод ограничений проводим через кнопку.
  3. Через кнопку Параметры установим, что значения в изменяемых ячейках должны быть неотрицательными. Другие параметры в открывшемся окне Параметры поиска решения оставляем внесёнными по умолчанию.
  1. Нажимаем кнопку Выполнить. Получаем решение задачи для первой ситуации, когда определяем минимальное количество официантов с учётом всех графиков их работы при условии, что ежедневно фактическое количество работающих официантов должно быть не менее ежедневной потребности. Решение представлено в Приложении.
  2. В ситуации 2 официантов, работающих по графику №1, должно быть обязательно 3. Для учёта этого обстоятельства при новом поиске решения введём ещё одно ограничение: $C$2 =3.  Тогда после нажатия кнопки Выполнить получим решение для этой ситуации. Это решение представлено также в Приложении.
  3. Проанализировав обе ситуации видим, что общее количество официантов одинаково (16). Это минимальное количество при заданных условиях. Соответственно подсчитана и еженедельная зарплата всех официантов. Но в ситуации 2 распределение официантов по графикам работы другое. Фактическое количество работающих по дням недели  также изменилось.

Заключение

Табличный процессор Excel обладает удобными возможностями для анализа и обработки данных. Такие команды или средства программы как Подбор параметров и Поиск решения можно использовать для решения задач прогнозирования различных ситуаций в работе менеджера, финансиста и других специалистов, гибкого подбора новых параметров при изменении ситуации, поиска более гибкого и многовариантного решения задачи с учётом различных обстоятельств и ограничений.

Приложение

Решение задачи, найденное с помощью программы MS Excel

Ситуация 1

Ситуация 2

Источник

Подборка по базе: Противотанковые средства советской пехоты (часть 4).pdf, Jценочные средства-музыка.docx, Сайфиев С.Х Лабораторная работа.docx, Интегральные средства.docx, практическая работа4 нормальная земля.docx, Тема 9. Управление силами и средствами на пожарев.docx, «Организация управления силами и средствами на пожаре и при пров, Современные средства обучения иностранному языку 2.docx, Управленческие решения 3 семестр 2.docx, 1 лабораторная.docx

Лабораторная работа№4: Средства поиска решения в MS Excel
Цель работы: освоение специального инструментария MS Excel для решения оптимизационных задач.

Порядок работы:

  1. Ознакомиться с механизмом поиска решения в Excel.
  2. Выполнить задание для самостоятельной работы.
  3. Ответить на контрольные вопросы.

Ежедневно специалисты в области экономики и менеджмента сталкиваются с задачами оптимизации. Наиболее легкими и показательными являются задачи линейной оптимизации.

Типы задач оптимизации:

  • Задачи о перевозках: например, минимизация расходов по доставке товаров с нескольких фабрик в несколько магазинов с учетом спроса;
  • Задачи распределения рабочих мест: например, минимизация расходов на содержание штата с соблюдением требований, определенных законодательством;
  • Управление ассортиментом товаров: извлечение максимальной прибыли с помощью варьирования ассортиментным набором товаров (при соблюдении требований клиентов). Аналогичная задача возникает при продаже товаров с разной структурой затрат, рентабельностью и показателями спроса.
  • Замена или смешивание материалов: например. Манипуляция материалами с целью снижения себестоимости, поддержания необходимого уровня качества и соблюдения требований потребителей.
  • Задачи линейной алгебры: решение линейных уравнений.

Для решения такого вида задач существует инструмент «Поиск решения».
Процедуру поиска решения можно использовать для определения значения влияющей ячейки, которое соответствует экстремуму зависимой ячейки — например, расходы на рекламу, обеспечивающие максимальную прибыль. Влияющая и целевая ячейки должны быть связаны формулой, иначе при изменении значения одной не будет изменяться другая.

Задачи, решаемые с помощью оптимизатора, имеют три характерных признака:

  • Имеется единственная целевая ячейка. В нее пользователь должен ввести формулу, указав позднее в программном диалоге какой экстремум необходим (максимум или минимум). После завершения построения модели и инициализации расчета программа автоматически должна добиться для этой ячейки экстремального результата.
  • В формуле целевой ячейки должны быть сделаны ссылки на одну или более изменяемых ячеек, от значений которых зависит результат. Они могут быть названы также неизвестными или переменными для решения. Поиск решения устанавливает значения изменяемых ячеек так, чтобы найти для формулы целевой ячейки оптимальное решение.
  • Ограничивающих ячеек может быть не менее одной на каждую изменяемую ячейку. Может существовать и некоторое количество дополнительных ячеек ограничений, например, ограничение по объему ресурса и ограничения по спросу (минимальный спрос, максимальный спрос).

Пример 1 .

Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:

Ресурсы

 Нормы затрат ресурсов на одно изделие (куб.м) Общее количество ресурсов
стол шкаф
Древесина 1 вида 0,2 0,1 40
Древесина 2 вида 0,1 0,3 60
Трудоемкость (человеко-часов) 1,2 1,5 371,4
Прибыль от реализации одного изделия (руб.) 6 8

Определить, сколько столов и шкафов фабрике следует изготовлять, чтобы прибыль от их реализации была максимальной. Подготовка исходных данных для решения задачи

1.Формализация задачи

Для решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса:

  1. Для определения каких величин строится модель?
  2. В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?
  3. Каким ограничениям должны удовлетворять неизвестные?

В нашем случае мебельной фабрике необходимо спланировать объем производства столов и шкафов так, чтобы максимизировать прибыль. Поэтому переменными являются: x1 – количество столов, х2 – количество шкафов.

Суммарная прибыль от производства столов и шкафов равна z = 6*x1 + 8*x2. Целью фабрики является определение среди всех допустимых значений х1 и х2 таких, которые максимизируют суммарную прибыль, т.е. целевую функцию z.

Перейдем к ограничениям, которые налагаются на х1 и х2. Объем производства шкафов и столов не может быть отрицательным, следовательно:

Нормы затрат древесины на столы и шкафы не может превосходить максимально возможный запас данного исходного продукта, следовательно:

Кроме того, ограничение на трудоемкость не превышает количества затрачиваемых ресурсов

Таким образом, математическая модель данной задачи имеет следующий вид:

Максимизировать

при следующих ограничениях:

Заметим, что данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.

2.Поиск решения

Решим данную задачу с помощью команды Поиск решения (Tools, Solver). Средство поиска решений является одной из надстроек Excel. Если в меню Сервис(Tools) отсутствует команда Поиск решения (Solver), то для ее установки необходимо выполнить команду

Сервис -> Надстройки -> Поиск решения (Tools ->Add-ins -> Solver).

Отведем ячейки А3 и В3 под значения переменных х1 и х2 (рис. 1).
В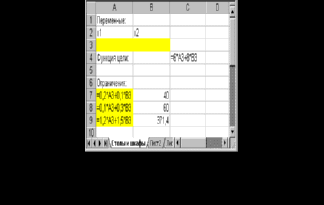 ячейку С4 введем функцию цели: =6*А3+8*В3, в ячейки А7:А9 введем левые части ограничений:

=0,2*А1+0,1*В3

=0,1*А3+0,3*В3

=1,2*А3+1,5*В3,

а в ячейки В7:В9 – правые части ограничений.

Теперь выберем команду Сервис, Поиск решения (Tools, Solver) и заполним открывшееся диалоговое окно Поиск решения (Solver), как показано на рис. 2.

Не забудьте в диалоговом окне Параметры поиска решения (Solver Options) установить флажок Линейная модель (Assume Linear Model).

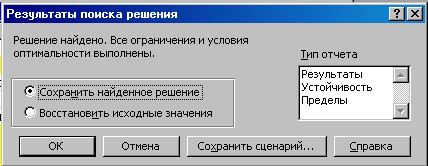
После нажатия кнопки Выполнить (Solve) открывается окно Результаты поиска решения (Solver Results), которое сообщает, что решение найдено:

Рис. 3. Диалоговое окно Результаты поиска решения
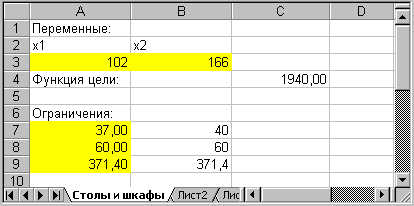
Результаты расчета задачи представлены на рис. 4, из которого видно, что оптимальным является производство 102 столов и 166 шкафов. Этот объем производства принесет фабрике 1940 руб. прибыли.

Рис. 4. Результаты расчета с помощью средства поиска решений для задачи максимизации выпуска столов и шкафов

Задание для самостоятельной работы

Вариант1
Для производства двух видов изделий А и В используется токарное, фрезерное и шлифовальное оборудование. Нормы затрат времени для каждого из типов оборудования на одно изделие данного вида приведены в таблице. В ней же указан общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия.

Тип оборудования Затраты времени (станко-часов) на обработку одного изделия Общий фонд полезного рабочего времени
А В
Фрезерное 10 8 168
Токарное 5 10 180
Шлифовальное 6 12 144
Прибыль от реализации одного изделия (руб.) 14 18

Найти план выпуска изделий вида А и В, обеспечивающий максимальную прибыль от их реализации.

Задание для самостоятельной работы

Вариант2
На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое должны ежедневно получать лисицы и песцы, приведено в таблице. В ней же указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца.

Найти оптимальное соотношение количества кормов и численности поголовья лис и песцов.

Вид корма Количество единиц корма, которое ежедневно должны получать Общее количество корма
А В
Вид 1 2 3 180
Вид 2 4 1 240
Вид 3 6 7 426
Прибыль от реализации одной шкурки (руб.) 16 12

Задание для самостоятельной работы

Вариант3

Для изготовления различных изделий А, В и С предприятие использует три различных видов сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице:

Вид сырья Норма затрат сырья (кг) на одно изделие Общее количество сырья (кг)
А В С
Вид 1 18 15 12 360
Вид 2 6 4 8 192
Вид 3 5 3 3 180
Цена одного изделия (руб.) 9 10 16

Изделия А, В и С могут производится в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида.

Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.

Задание для самостоятельной работы

Вариант4
На швейной фабрике для изготовления четырех видов изделий может быть использована ткань трех артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия приведены в таблице. В ней же указаны имеющиеся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида. Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной.

Артикул ткани Норма расхода ткани (м) на одно изделие вида Общее количество ткани (м)
Вид 1 Вид 2 Вид 3 Вид 4
Артикул 1 1 — 2 1 180
Артикул 2 — 1 3 2 210
Артикул 3 4 2 — 4 800
Цена одного изделия (руб.) 9 6 4 7

Задание для самостоятельной работы

Вариант 5
Фабрика «GRM pie» выпускает два вида каш для завтрака — «Crunchy» и «Chewy». Используемые для производства обоих продуктов ингредиенты в основном одинаковы и, как правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики.

Управляющему производством Джою Дисону необходимо разработать план производства на месяц. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта.

Цех Необходимый фонд рабочего времени, чел.-ч/г Общий фонд рабочего времени, чел.-ч. в месяц
«Crunchy» «Chewy»
А. Производство

В. Добавка приправ

С. Упаковка

 10

3

2

 4

2

5

 1000

360

600

Доход от производства 1 т «Crunchy» составляет 150 ф. ст., а от производства «Chewy» — 75 ф. ст. На настоящий момент нет никаких ограничений на возможные объемы продаж. Имеется возможность продать всю произведенную продукцию.

Требуется: сформулировать модель линейного программирования, максимизирующую общий доход фабрики за месяц и реализовать решение этой модели.

Задание для самостоятельной работы

Вариант6
Оливер А. Петерс скоро выйдет на пенсию, и ему предстоит решить, как поступить с единовременным пособием, которое в соответствии с пенсионной программой будет предоставлено ему фирмой. М-р Петерс и его супруга намерены предпринять длительный визит в Австралию к своей дочери сроком на два года, поэтому любые сделанные в настоящий момент инвестиции будут свободны для использования на данный период. Очевидно, цель м-ра Петерса состоит в максимизации общего дохода от вложений, полученного за двухлетний период.

Мистера Петерса проконсультировали, что наилучшим вариантом вложения инвестиций был бы инвестиционный фонд, и в настоящее время он рассматривает возможность помещения инвестиций в один из таких фондов, состоящий из инвестиций трех типов — А, В и С. Сумма единовременного пособия составит 25000 ф. ст., однако, мистер Петере считает, что нет необходимости вкладывать в данный инвестиционный фонд все деньги; часть из них он намерен перевести на свой счет жилищно-строительного кооператива, который гарантирует ему 9% годовых.

По мнению бухгалтера фирмы, мистеру Петерсу следует попытаться распределить свои инвестиции таким образом, чтобы обеспечить как получение дохода, так и рост капитала. Поэтому ему посоветовали не менее 40% от общей суммы вложить в вариант А и перевести на свой счет. Для обеспечения значительного роста капитала не менее 25% общей суммы денежных средств, вложенных в инвестиционный фонд, необходимо поместить в проект В, однако, вложения в В не должны превышать 35% общего объема вложений в инвестиционный фонд ввиду высокой вероятности риска, соответствующей проекту В. Кроме того, для сохранности капитала в проекты А и С следует вложить не менее 50% средств, помещаемых в инвестиционный фонд.

В настоящее время проект А позволяет получать 10 % годовых и обеспечивает 1% роста капитала; проект В предполагает рост капитала в 15%; проект С дает 4% годовых и 5%-ный рост капитала.

Требуется: учитывая цель м-ра Петерса, сформулировать модель линейного программирования, показывающую, как следует распределить сумму единовременного пособия между различными проектами инвестиций.

Задание для самостоятельной работы

Вариант7
Китайская компания с ограниченной ответственностью по производству гусеничных механизмов выпускает пять сходных друг с другом товаров — А, В, С, D и Е. В нижеследующей таблице представлены расходы ресурсов, необходимых для выпуска единицы каждого товара, а также недельные запасы каждого ресурса и цены продажи единицы каждого продукта.

Ресурсы. Товар Недельный запас ресурсов
А В С D Е
Сырье, кг

Сборка, ч

Обжиг, ч

Упаковка,ч

 6,00 1,00

3

0,50

 6,50 0,75 4,50 0,50 6,10 1,25

6

0,50

 6,10 1,00

6

0,75

 6,40 1,00 4,50 1,00 35000

6000

30000

4000
Цена продажи, ф.ст. 40 42 44 48 52

Известны также издержки, связанные с использованием каждого вида ресурсов:

сырье — 2,10 ф. ст. за 1 кг;

сборка —. 3,00 ф. ст. за 1 ч;

обжиг — 1,30 ф. ст. за 1 ч;

упаковка — 8,00 ф. ст. за 1 ч.

Требуется:

Сформулировать задачу линейного программирования таким образом, чтобы в качестве переменных как целевой функции, так и ограничений выступали ресурсы. Кратко сформулировать предпосылки применения модели. Для максимизации элементов, составляющих прибыль за неделю, следует использовать компьютерный пакет прикладных программ.

Задание для самостоятельной работы

Вариант8
Нефтяная компания «РТ» для улучшения эксплуатационных качеств и снижения точки замораживания дизельного топлива, которое она производит, добавляет в него определенные химикаты. В каждом бензобаке объемом 1000 л должно содержаться не менее 40 мг химической добавки X, не менее 14 мг химической добавки Y и не менее 18 мг химической добавки Z. Необходимые химические добавки в форме готовых смесей поставляют «РТ» две химические компании А и В. В нижеследующей таблице приведено содержание химических добавок в каждом продукте, поставляемом указанными компаниями.

Продукт Химические добавки, мг/л
Х У Z
А

В

 4

5

 2

1

 3

1

Стоимость продукта А — 1,50 ф. ст. за 1 л, а продукта В — 3,00 ф. ст. за 1 л.

Требуется: найти ассортиментный набор продуктов А и В, минимизирующий общую стоимость добавленных в топливо химикатов.

Задание для самостоятельной работы

Вариант9
Администрация компании «Nemesis Company», осуществляя рационализаторскую программу корпорации, приняла решение о слиянии двух своих заводов в Аббатсфилде и Берчвуде. Предусматривается закрытие завода в Аббатсфилде и за счет этого — расширение производственных мощностей предприятия в Берчвуде. На настоящий момент распределение рабочих высокой и низкой квалификации, занятых на обоих заводах, является следующим:

Квалификация рабочих Аббатсфилд Берчвуд
Высокая

Низкая

 200

300

 100

200
Итого 500 300

В то же время после слияния завод в Берчвуде должен насчитывать 240 рабочих высокой и 320 рабочих низкой квалификации.

После проведения всесторонних переговоров с привлечением руководителей профсоюзов были выработаны следующие финансовые соглашения:

1. Все рабочие, которые попали под сокращение штатов, получат выходные пособия следующих размеров:

Квалифицированные рабочие — 2000 ф. ст.;

Неквалифицированные рабочие — 1500 ф. ст.

2. Рабочие завода в Аббатсфилде, которые должны будут переехать, получат пособие по переезду в размере 2000 ф. ст.

3. Во избежание каких-либо преимуществ для рабочих Берчвудского завода доля бывших рабочих завода в Аббатсфилде на новом предприятии должна совпадать с долей бывших рабочих Берчвудского завода.

Требуется: Построить модель линейного программирования, в которой определяется, как осуществить выбор работников нового предприятия из числа рабочих двух бывших заводов таким образом, чтобы минимизировать общие издержки, связанные с увольнением и переменой места жительства части рабочих. В процессе формализации следует использовать следующие переменные:

S1 — число квалифицированных рабочих, переведенных на новую работу с завода в Аббатсфилде;

S2 — число квалифицированных рабочих, переведенных на новую работу с завода в Берчвуде;

Ui — число неквалифицированных рабочих, переведенных на новую работу с завода в Аббатсфилде;

U2 — число неквалифицированных рабочих, переведенных на новую работу с завода в Берчвуде.

Задание для самостоятельной работы

Вариант10
Компания «Bermuda Paint» — частная промышленная фирма, специализирующаяся на производстве технических лаков. Представленная ниже таблица содержит информацию о ценах продажи и соответствующих издержках производства единицы полировочного и матового лаков.

Лак Цена продажи 1 галлона, ф.ст Издержки производства 1 галлона, ф. ст.
Матовый

Полировочный

 13,0

16,0

 9,0

10,0

Для производства 1 галлона матового лака необходимо затратить 6 мин трудозатрат, а для производства одного галлона полировочного лака — 12 мин. Резерв фонда рабочего времени составляет 400 чел.-ч. в день. Размер ежедневного запаса необходимой химической смеси равен 100 унциям, тогда как ее расход на один галлон матового и полировочного лаков составляет .0,05 и 0,02 унции соответственно. Технологические возможности завода позволяют выпускать не более 3000 галлонов лака в день.

В соответствии с соглашением с основным оптовым покупателем компания должна поставлять ему 5000 галлонов матового лака и 2500 Галлонов полировочного лака за каждую рабочую неделю (состоящую из 5 дней). Кроме того, существует профсоюзное соглашение, в котором оговаривается минимальный объем производства в день, равный 2000 галлонов. Администрации данной компании необходимо определить ежедневные объемы производства каждого вида лаков, которые позволяют получать максимальный общий доход.

Требуется: Построить и решить линейную модель для производственной проблемы, с которой столкнулась компания. Для исходной задачи (не учитывающей сверхурочные работы) определить промежуток изменений показателя единичного дохода за 1 галлон полировочного лака, в котором исходное оптимальное решение остается прежним.

Источник

Понравилась статья? Поделить с друзьями:
  • Лабораторная работа excel подбор параметра
  • Лабораторная работа на тему работа в текстовом редакторе microsoft word
  • Лабораторная работа excel на заказ
  • Лабораторная работа excel графики функций
  • Лабораторная работа математической статистики excel