Инфоурок
›
Информатика
›Другие методич. материалы›Лабораторная работа по информатике: «Построение графиков функций в программе MS Excel»
Скачать материал
Скачать материал


- Курс добавлен 19.01.2023




- Сейчас обучается 122 человека из 48 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 211 165 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
-
Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы




- 09.02.2018
- 669
- 8

- 09.02.2018
- 1320
- 7


- 08.02.2018
- 746
- 0

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»
-
Скачать материал
-
11.02.2018
2253
-
DOCX
57.5 кбайт -
14
скачиваний -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Трофимова Татьяна Михайловна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 2318
-
Всего материалов:
1
Файлы
Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….
Лабораторная работа № 6
MS
Excel. Построение графиков
функций
Цель работы
Получить
практические навыки работы в приложении
MS
Excel,
а именно: по настройке рабочей книги,
по работе с данными различных типов и
оформлению рабочего листа Microsoft
Excel.
Освоить приёмы автозаполнения и
форматирования таблиц, ввода и
редактирования формул, использования
математических функций, построения
графиков (диаграмм).
Порядок выполнения работы
Общее
задание. Пример построения графиков
функций y1
= sinx и y2
= cosx на интервале от 0 до
2
-
Создайте
в своей папке папку под названием
«Таблицы Excel».
Запустите программу Microsoft
Excel. -
Открывшийся
файл имеет три пустых листа. Переименуйте
эти листы следующим образом:
Лист 1
– Титульный
лист
Лист 2
– sinxcosx
Лист 3
– Функция
№ < укажите номер своего варианта>
-
Сохраните
файл в папке «Таблицы Excel»
с именем Графики. -
Перейдите
на лист sinx
cos
x.
В первой строке сделайте заголовок:
Построение
графиков функций y1
= sinx
и y2
= cosx
-
В ячейках
А5,
А6,
А7
сделайте заголовки таблицы исходных
данных:
x,
y1,
y2. -
С помощью
автозаполнения заполните строку
значений аргумента х,
начиная с ячейки В5:
х
= 0; 0,6; … ; 6,6. -
В ячейку
В6
запишите формулу: =SIN(В5) -
Скопируйте
эту формулу на остальные ячейки строки
6
– до М6. -
На
вкладке Вставка
в группе Диаграммы
выберите тип диаграммы – Точечная
с гладкими кривыми. -
MS
Excel
построит диаграмму и откроет дополнительные
вкладки Работа
с диаграммами
(Конструктор,
Макет
и Формат).
На вкладке Конструктор
в группе Данные
нажмите Выбрать
данные.
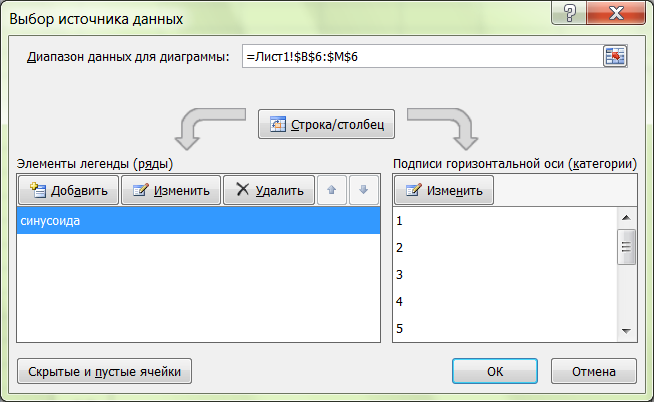
В диалоговом окне Выбор
источника данных
в группе Элементы
легенды (ряды)
измените имя ряд1
на синусоида.
-
Перейдите
на вкладку Макет
и задайте название осей диаграммы,
линии сетки. Посмотрите, какие еще
элементы диаграммы можно настроить. -
Добавьте
к этому графику график косинусоиды.
Для этого заполните в таблице исходных
данных строку 7
– в ячейку В7
запишите формулу =COS(В5)
и скопируйте её на остальные ячейки
строки до М7
включительно. -
Вызовите
окно Выбор
источника данных
(Работа
с диаграммами / Конструктор / Выбрать
данные).
Щёлкните по кнопке Добавить
под списком Элементы
диаграммы (ряды).
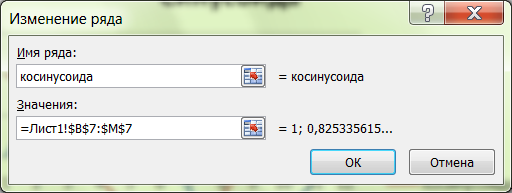
В диалоговом окне Изменение
ряда
задайте имя ряда – косинусоида,
а в поле ввода Значения
укажите диапазон ячеек со значениями
cos(x)
(вручную или с помощью мыши).
-
Измените
название диаграммы – Синусоида
и косинусоида. -
Изучите
вкладки Конструктор,
Макет
и Формат.
Попробуйте применить готовые макет и
стиль диаграммы и настроить их вручную,
изменив макет и форматирование отдельных
элементов диаграммы, например области
диаграммы, области построения диаграммы,
рядов данных или легенды. -
Сохраните
результаты своей работы.
Построение графика функции
Перейдите
на лист Функция
№
. Постройте график функции своего
варианта задания. Действия при построении
графика аналогичны рассмотренным выше
при построении синусоиды. Сделайте
заголовки к таблице исходных данных,
укажите вид функции. Константы,
встречающиеся в некоторых вариантах
функций (коэффициенты а,
в,
с,
k),
записывайте в отдельных ячейках и
делайте на них абсолютные
ссылки.
Это даст вам возможность легко варьировать
их и наблюдать поведение вашей функции
при различных значениях коэффициентов.
Построение поверхности
Добавьте
ещё один лист в рабочий файл Графики.
Назовите его «Исходные
данные».
Запишите название и вид своей функции
(см. свой вариант), используя редактор
формул Microsoft
Equation
(меню Вставка
/Текст /Объект).
Заполните таблицу исходных данных для
построения графика функции. Выполните
построение поверхности (пример построения
поверхности рассмотрен ниже). Разместите
диаграмму на отдельном листе, назовите
этот лист «Поверхность
№ <укажите номер варианта>».
Сохраните файл.
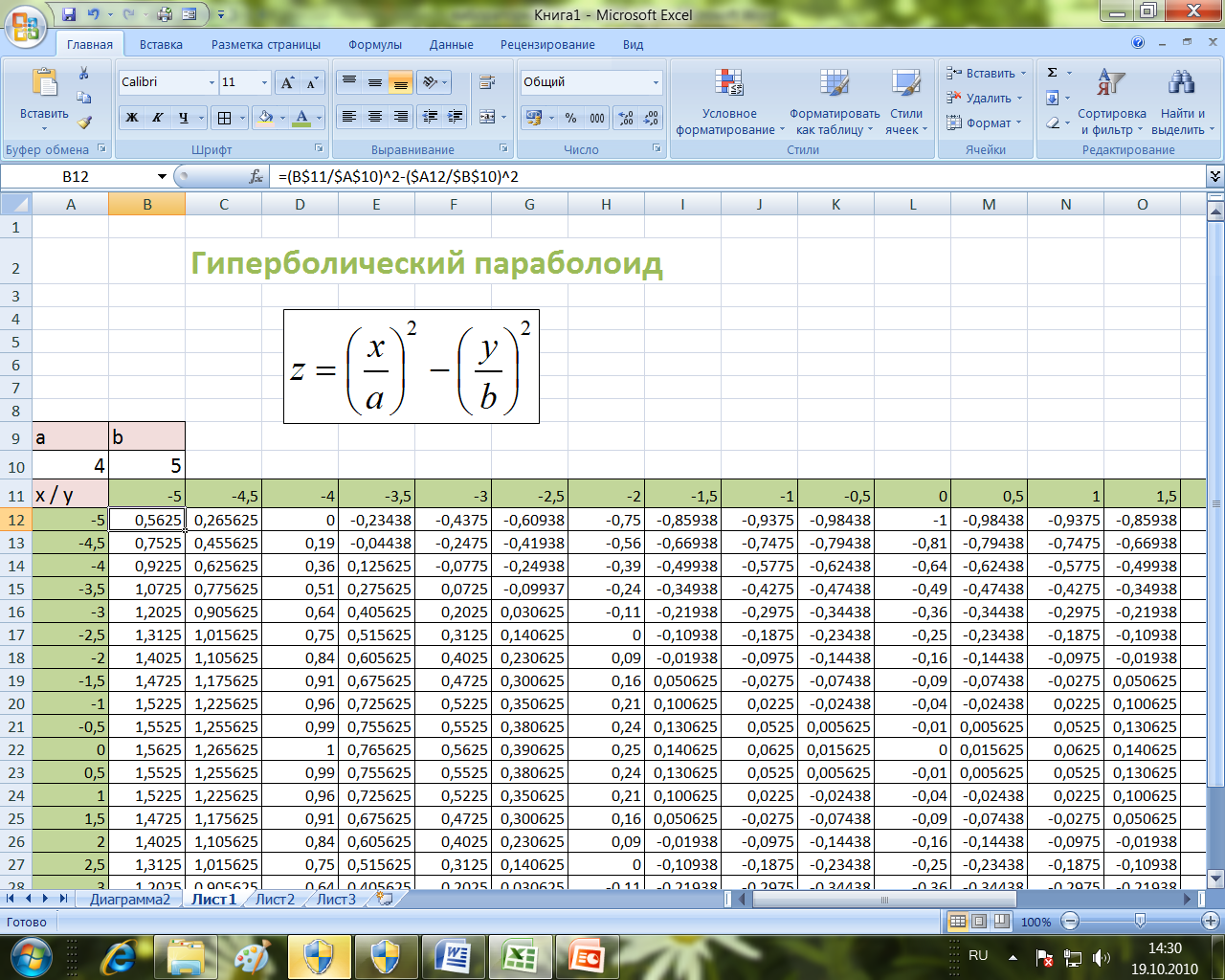
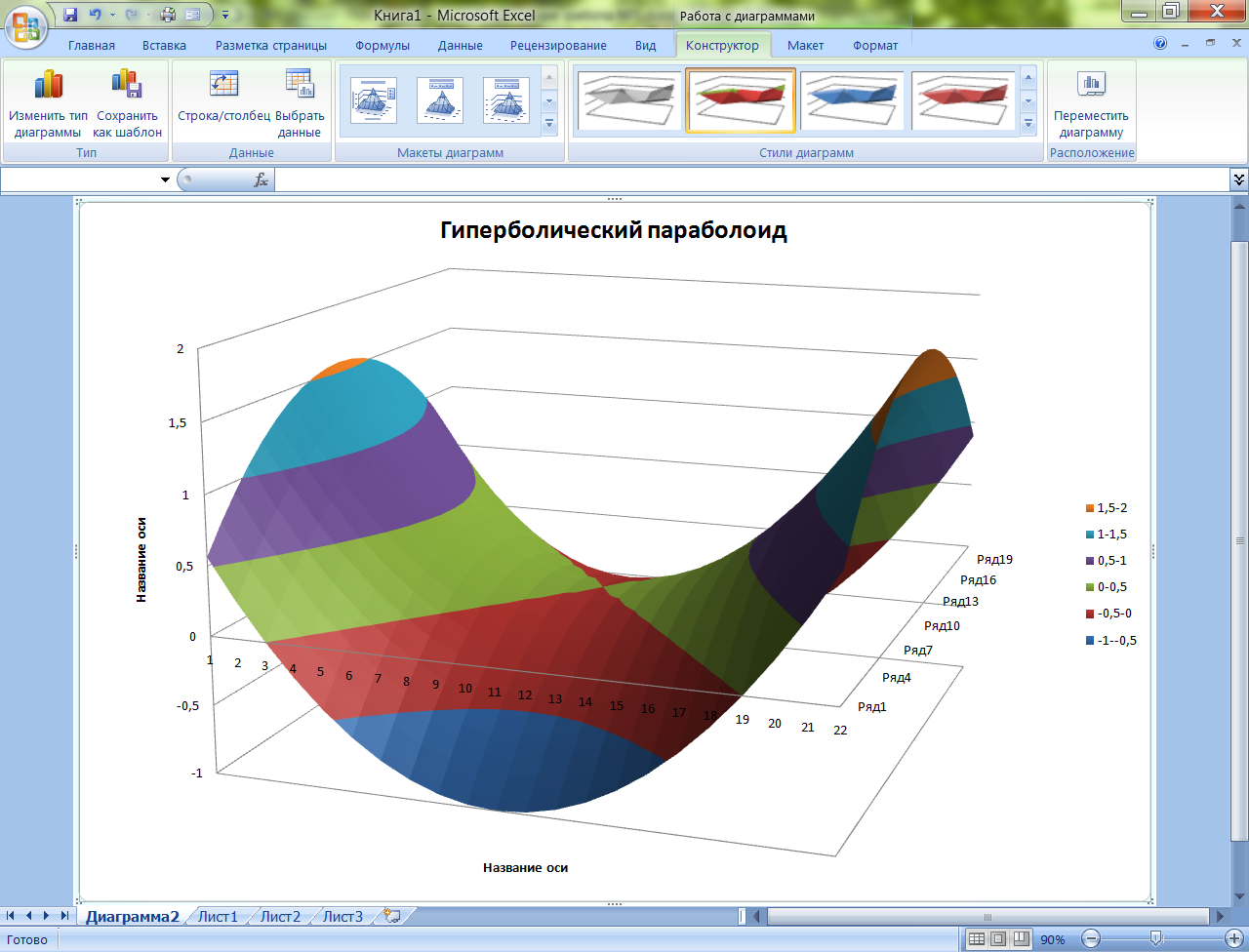
Пример построения поверхности
гиперболического параболоида
-
Оставьте
сверху 8 строк под заголовок. В ячейках
А9
и В9
сделайте заголовки для коэффициентов
a
и b,
а в ячейки А10
и В10
запишите значения коэффициентов 4
и 5
соответственно (пусть a
= 4, b
= 5) (см. рис. 5.1). -
Заполните
строку значений аргумента х,
начиная с ячейки В11,
х
= -5 до 5, с шагом 0,5 (используйте
автозаполнение по строке). -
Заполните
столбец значений аргумента y,
начиная с ячейки А12,
у
= -5 до 5, с шагом 0,5 (используйте
автозаполнение по столбцу). -
В ячейку
В12
запишите формулу =(B$11/$A$10)^2-($A12/$B$10)^2
. -
Скопируйте
эту формулу на все ячейки диапазона
В12:V32
с помощью автозаполнения (сначала
выполните автозаполнение, например,
по столбцу, а затем – по строкам). -
Не
снимая выделение с диапазона, укажите
тип диаграммы – Поверхность
(Вставка/Диаграммы/Другие диаграммы/Поверхность).
Далее выполните действия аналогичные
рассмотренным в общем задании (т.е.
задайте макет, название, стиль диаграммы
и т.п.). -
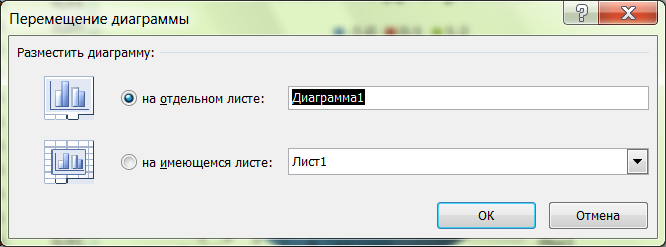
Переместите
диаграмму на отдельный лист. Для этого
выберите вариант На
отдельном листе
в диалоговом окне Перемещение
диаграммы
(Работа
с диаграммами/Конструктор/Расположение).
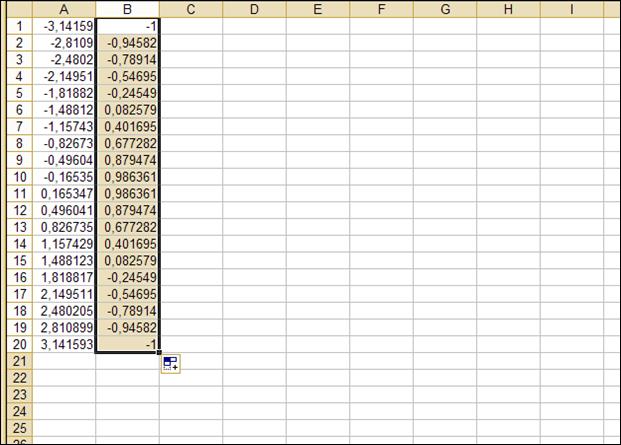
Пример
листа с исходными данными для построения
поверхности и вид поверхности показаны
ниже.
Оформление титульного листа
Перейдите
на первый (титульный) лист книги. Сделайте
титульный лист к своей работе. Используйте
средства рисования: автофигуры, заливку,
обрамление, объекты WordArt
и т.п. Пример оформления титульного
листа приведен далее. Желательно создать
свои элементы оформления, а не копировать
оформление образца.
Результаты работы
В
результате выполненной лабораторной
работы студент должен продемонстрировать
преподавателю готовый файл Графики.xls,
содержащий 5 листов:
-
Лист 1
(Титульный
лист)
– титульный лист к работе, на котором
указаны название работы, номер варианта,
фамилия И.О. студента, номер группы,
дата выполнения работы; -
Лист 2
(sinxcosx)
– таблица исходных данных и графики
функций у1
= sin
x,
у2
= cos
x; -
Лист 3
(Функция
№…)
– таблица исходных данных и график
функции своего варианта; -
Лист 4
(Исходные
данные)
– таблица исходных данных для построения
поверхности; -
Лист 5
(Поверхность
№…)
– диаграмма, содержащая поверхность
(в соответствии с вариантом задания).
Приложение
Варианты функций
-
Парабола:
y
= ax2
+
bx
+
c;
x = -5,-4,…,4,5. a
=
100, b
= 20, c
= 10 -
y
= Asin
kx,
A
= mx;
x
= 0, 0,8,…,12; m
=
10, k
= 4 -
Локон
Аньези
,
x=-5,-4,…,4,5;
a-
варьировать, смотреть изменения графика
(a=2;4;0,5
и т.п.) -
y
= a(x
— sinx);
x
=
0, 0,8, 1,6,…,12; a
– любое -
Затухающие
колебания
y
= A
sin kx,
A
= e-x;
k
= 20; x
= 0, 0,8, 1,6,…,12 -
y=axbecx,
x=0,
0,2,…,1,8, 2; a,
b,
c
— варьировать, смотреть изменения
графика -
y=a
exp(bx+cx2);
x=0,
0,5,…,5,5, 6; a,
b,
c
— варьировать, смотреть изменения
графика -
y=ax3+bx2+cx+d;
x=-5,-4,…,9,10; a=3, b=4, c=5, d=6 -
y=(sin kx)/kx; x=0,1, 0,6,
….,10,1; k=0,5 -
Ареа-синус
;
x=-10, -9,5,…,10; c=1 -
Ареа-тангенс
;
x=1,1, 1,2, ….. ,6; c=0,5 -
;
x=-8,
-7, … , 7, 8; a-
варьировать, смотреть изменения графика
(a=2;4;0,5
и т.п.) -
x=a(
t-sin t ), y=a( 1-cos t ); t=0, 0,8, 1,6, … , 12; a – любое -
y=(sin x)/x; x=0,1, 0,6,
….,10,1
Варианты поверхностей
-
z=ax2-axy+ay2-ax+2ay;
x=[-5;5] шаг
0,5; y=[-5,5] шаг
0,5; a=4 -
z=ax2+axy+(a+2)y2-5ax;
x=[-5;5] шаг
1; y=[-5,5] шаг
1; a=4 -
;
x=[-5;5] шаг 0,5; y=[-5,5] шаг 0,5 -
z=a/x
+ x/y
+ y;
x=[-5;5]
шаг 0,5; y=[-5,5]
шаг 0,5; исключить точки x=0
и y=0 -
;
a=2, b=4; x=[-5;5] шаг
0,5; y=[-5;5] шаг
0,5; y=[-5;5] шаг
0,5 -
z=x3+ay3-bxy+1;
a=8, b=6; x=[-5;5] шаг
0,5; y=[-5;5] шаг
0,5 -
z=(ax-x2)*(ay-y2);
a=2; x=[-5;5] шаг
0,5; y=[-5;5] шаг
0,5 -
z=x3+y3-axy;
a=3; x=[-2;2] шаг
0,2; y=[-2;2] шаг
0,2 -
z=sin x*
sin y*ln (a+x+y); a=10; x=[0; 4] шаг
0,2; y=[0; 4] шаг
0,2 -
z=a sin
x* sin y/(xy); a=3; x=[0,01; 4,01] шаг
0,2; y=[0,01; 4,01] шаг
0,2 -
z=a sin
(bx2y2);
a=2; b=1,5; x=[-1,5; 1,5] шаг
0,15; y=[-1,5; 1,5] шаг
0,15 -
;
x=[-5;5] шаг
0,5; y=[0,1; 1,1] шаг
0,05; a=4, b=5 -
z=exp(x-y)
(x2-2y2);
x=[-3;3] шаг
0,3; y=[-5; 5] шаг
0,5 -
z=x3+axy2-5ax-4ay;
x=[-5;5] шаг
0,5; y=[-5,5] шаг
0,5; a=3 -
z=ax2-axy+by2+x-by;
x=[-5;5] шаг 0,5; y=[-5,5] шаг 0,5; a=2, b=3 -
z=sin x +
sin y + sin(x+y); x=[0; 4] шаг
0,2; y=[0; 4] шаг
0,2 -
z=exp(x/2)
(x+y2);
x=[-5;5] шаг
0,5; y=[-5,5] шаг
0,5 -
z=(sin x+
sin y)*ln (a+x+y); a=10; x=[0; 4] шаг
0,2; y=[0; 4] шаг
0,2 -
z= a sin
(x2+y2);
a=0,5; x=[0; 2] шаг
0,1; y=[0; 2] шаг
0,1 -
z= a*ln
(bx2y2+c);
a=2, b=3, c=0,01; x=[-2; 2] шаг
0,2; y=[-2; 2] шаг
0,2 -
z=x4+y4-ax2-bxy-ay2
; a=2, b=4; x=[-2; 2] шаг
0,2; y=[-2; 2] шаг
0,2 -
z= a*tg
(bx2y2+c);
a=2, b=1,5, c=0,01; x=[-2; 2] шаг
0,2; y=[-2; 2] шаг
0,2
Содержание
Лабораторная
работа № 6 1
MS Excel. Построение
графиков функций 1
Цель работы 1
Порядок выполнения
работы 1
Общее задание.
Пример построения графиков функций y1
= sinx и y2 = cosx на интервале от 0 до 2 1
Построение
графика функции 3
Построение
поверхности 3
Пример построения
поверхности гиперболического
параболоида 3
Оформление
титульного листа 5
Результаты работы 6
Приложение 7
Варианты функций 7
Варианты
поверхностей 7
Содержание 10
10
Информационные технологии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лабораторная работа 3.5. Графики
функций и поверхности
1 Откройте рабочую книгу Лабораторные.xls. Вставьте новый
лист График 1. Постройте на этом листе график функции y=cos(x) при .
Выполнение:
1.1 Сначала необходимо построить таблицу
значений функции при различных значениях аргумента, который изменяется с
фиксированным шагом. Столбец А будет содержать значения х, а столбец В — значения y.
1.2 Введите в ячейку А1 формулу =-ПИ(), в
ячейку А20 формулу =ПИ().
1.3 Выделите диапазон А1:А20 и выберите меню Правка
/ Заполнить / Прогрессия (рис. 3.22). Выберите автоматическое
определение шага и нажмите ОК.
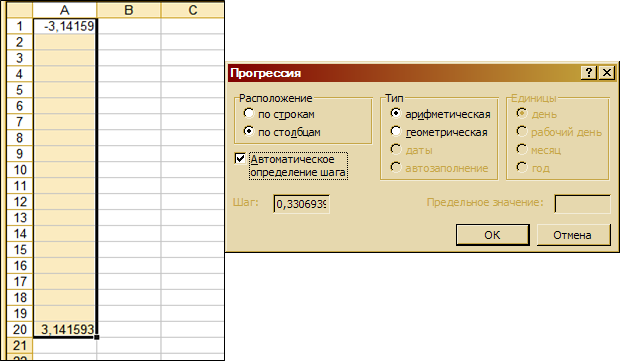 |
Рис. 3.22. Заполнение столбца А значениями
аргумента
1.4 Далее необходимо в диапазон В1:В20 ввести
значения функции. Для этого в ячейку В1 внесите формулу =COS(A1). Эту формулу
«протащите» на весь диапазон В1:В20.
1.5 Выделите диапазон В1:В20, вызовите мастер
диаграмм. На первом шаге мастера выберите вкладку Нестандартные, тип Гладкие
графики. Нажмите Готово (рис. 3.23).
2 Постройте график функции y(x) при :
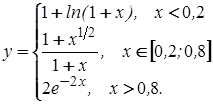
Выполнение:
2.1 В рабочую книгу Лабораторные.xls вставьте новый
лист График 2. В столбец А будем заносить значения аргумента х,
который также изменяется с фиксированным шагом. Его значение целесообразно
сделать небольшим. В нашем случае будем считать, что шаг изменения аргумента
равен 0,1.
2.2 В ячейку А1 введите первое значение
аргумента х: 0.
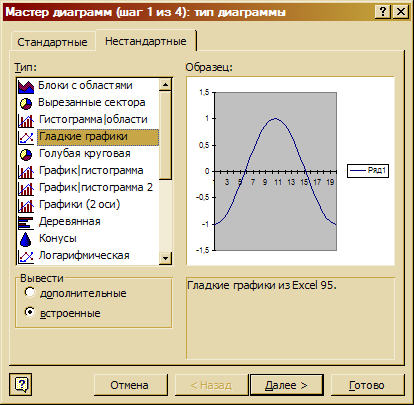 |
Рис.
3.23. Построение графика функции y=cos(x)
2.3 В ячейку А2 введите второе значение х:
0,1 — первое значение,
увеличенное на величину шага: 0 + 0,1 = 0,1 (рис. 3.24).
Рис.
3.24. Ввод первых двух значений аргумента
2.4 Выделите обе ячейки А1:А2,
подведите курсор мыши к правому нижнему углу выделенного диапазона, курсор
примет знак черного крестика; «протащите» черный крестик вниз, пока значение в
ячейке не станет равным 1 (ячейка А11).
2.5 Введите значения функции в столбец В: в
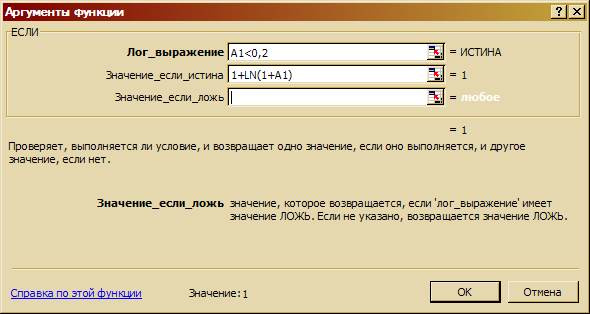
ячейку В1 поставьте знак «равно» и вызовите функцию ЕСЛИ. В открывшемся
окне Аргументы функции в поле Лог_выражение введите А1<0,2, в поле Значение_если истина
— 1+LN(1+A1) (рис. 3.25).
Поставьте курсор в поле Значение_если ложь и еще раз войдите в функцию ЕСЛИ.
Рис.
3.25. Окно внешней функции ЕСЛИ
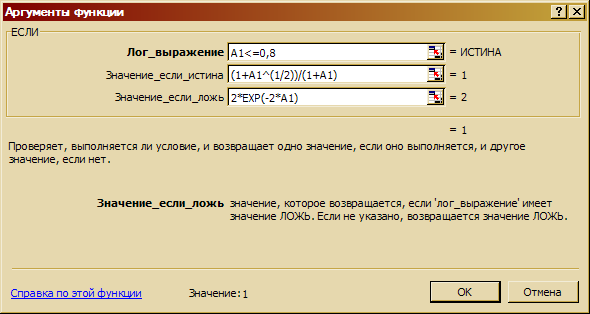
2.6 В открывшемся окне новой функции ЕСЛИ,
которая будет вложена в предыдущую, в поле Лог_выражение введите А1<=0,8, в поле Значение_если
истина — (1+А1^(1/2))/(1+A1), в поле Значение_если
ложь — 2*EXP(-2*A1) (рис. 3.26). Нажмите ОК.
Рис.
3.26. Окно вложенной функции ЕСЛИ
2.7 «Протащите» за маркер автозаполнения
получившуюся формулу =ЕСЛИ(A1<0,2;1+LN(1+A1);ЕСЛИ(A1<=0,8;(1+A1^(1/2))/(1+A1);2*EXP(‑2*A1))) до ячейки В11.
2.8 Выделите диапазон В1:В11 и вызовите
мастер диаграмм. Выберите тип диаграммы График, щелкните по нужному
образцу. Нажмите Далее.
2.9 Перейдите на вкладку Ряд. Войдите
в поле Подписи оси Х и выделите мышью на рабочем листе диапазон А1:А11
(то есть весь столбец значений х). Нажмите Далее.
2.10 При настройке параметров диаграммы
укажите заголовки осей (Ось Х и Ось Y), удалите легенду и линии сетки.
2.11 Разместите график на имеющемся
листе. В области построения диаграммы установите невидимую рамку и прозрачную
заливку.
2.12 Выполните двойной щелчок мышью на
оси Х диаграммы (оси категорий), в появившемся диалоговом окне Формат оси
перейдите на вкладку Шкала, снимите флажок Пересечение с осью Y (значений) между
категориями.
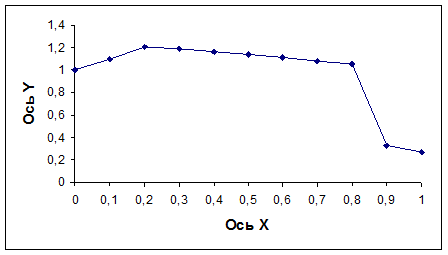
Это позволит разместить подписи на оси Х под делениями. Нажмите ОК.
График примет вид (рис. 3.27).
Рис.
3.27. График функции для задания 2
3 Постройте графики функций:
а)
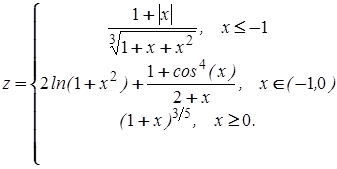
.
б) 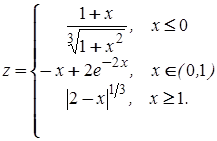
.
в) 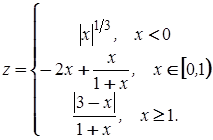
.
Указания:
• При написании формул используйте
следующие правила записи функций (табл. 3.6); всегда ставьте знаки умножения.
Таблица 3.6
Примеры функций
|
|
ABS(x) |
|
|
x^(1/n) |
|
|
(cos(x))^ m |
|
ex |
EXP(x) |
4 Постройте поверхность z = x2 – y2 при .
Выполнение:
4.1 В книгу Лабораторные.xls вставьте новый
лист Поверхности.
4.2 В диапазон ячеек B1:L1 введите
последовательность значений: ‑1; ‑0,8;…;1 переменной у,
а в диапазон ячеек А2:А12 – последовательность значений: -1; -0,8; …; 1
переменной х.
4.3 В ячейку В2 введите формулу =$A2^2-B$1^2. Выделите эту
ячейку, установите указатель мыши на ее маркере заполнения и «протащите» его
так, чтобы заполнить весь диапазон B2:L12.
При работе с формулой в ячейке В2
использовались смешанные ссылки. Если знак $ поставить перед именем
столбца ($A2), то фиксируется
этот столбец (А); если перед номером строки (B$1), то фиксируется
вся эта строка и при копировании формула будет ссылаться на ячейки в этой
строке (в нашем случае в строке 1).
4.4 Выделите диапазон ячеек А1:L12, содержащий
таблицу значений функции и ее аргументов, и вызовите мастер диаграмм. Выберите
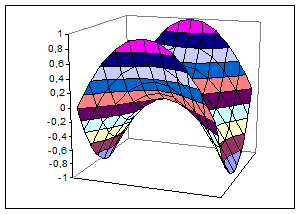
тип диаграммы – Поверхность. В итоге поверхность примет вид (рис. 3.28).
Рис.
3.28. Вид поверхности для задания 4
5 Постройте поверхности:
а) при
.
б) при
.
с) при
.
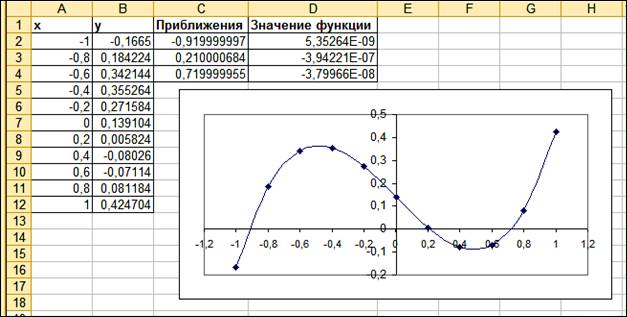
6 Найдите корни уравнения: х3 –
0,01х2 – 0,7044х + 0,139104 = 0.
Выполнение:
6.1 В рабочую книгу вставьте новый лист Корни
уравнения.
6.2 Вещественных корней у полинома третьей
степени может быть не более трех, необходимо их локализовать. Для этого
постройте график функции, где аргумент изменяется, например, на отрезке с шагом 0,2. Запишите в ячейку А1
слово х, в В1 — слово y. Заполните
диапазон А2:А12 значениями х, в ячейку В2 введите формулу =А2^3-0,01*A2^2-0,7044*A2+0,139104 и протяните вниз
до В12. Постройте график полученной функции. Из него видно, что полином меняет
знак на интервалах (-1;-0,8), (0,2;0,4), (0,6;0,8). Значит, корни находятся в
этих интервалах. Введите также заголовки: в ячейку С1 — слово Приближения, в D1 — Значение функции.
6.3 Войдите в меню Сервис / Параметры /
Вычисления, задайте предельное число итераций и относительную погрешность
(1000 и 0,00001).
6.4 В качестве начальных значений
(приближенных) корней задают любые точки из отрезков локализации корней.
Например, возьмите -0,9 (из первого интервала), 0,3 (из второго) и 0,7 (из
третьего). Введите их в С2:С4.
6.5 Для вычисления значений функции,
соответствующих приближенным решениям, в ячейку D2 введите
следующую формулу:
=C2^3‑0,01*C2^2‑0,7044*C2+0,139104. Протяните эту
формулу вниз на D2:D4.
6.6 Таким образом, получены три пары значений
«приближенный корень – уравнение для него» в ячейках C2:D2, C3:D3, C4:D4. Для каждой из
этих пар примените функцию Excel Сервис / Подбор
параметра,
которая позволяет по известному результату (значение уравнения равно нулю)
подобрать неизвестное значение параметра (здесь — аргумента х, корня). Начните с первой пары:
—
вызовите меню Сервис / Подбор параметра, в окне заполните:
Установить в ячейке: $D$2 (где формула с
вычислением левой части уравнения);
Значение: 0 (значение
правой части уравнения);
Изменяя значение ячейки: $C$2 (где искомый
аргумент х).
Нажмите кнопку ОК.
Результат (значение первого корня)
появится в ячейке С2. Аналогичную процедуру проделайте для каждой из оставшихся
пар. В итоге в ячейках С2, С3 и С4 появятся значения всех корней (рис. 3.29).
Рис.
3.29. Нахождение корней заданного уравнения
7 Найдите корни уравнения 0,3х3 –
0,8756х2 + 0,0021х – 0,44 = 0.
Цель работы:
- научиться строить графики в Excel;
- развить самостоятельность;
- развить навыки мыслительной деятельности, включая каждого учащегося в учебно – познавательный процесс и создавая условия для работы каждого в индивидуальном темпе;
Оборудование:
- ПЭВМ, сеть, проектор;
- опорный конспект, план практической работы, варианты для самостоятельной работы учащихся.
| Этапы | План урока + опорный конспект | Средства обучения |
| I | Подготовительный. Постановка учебных задач. Устное разъяснение порядка работы на уроке, тема урока. |
— |
| II | Повторение.
Фронтальный опрос изученного материала. Вопросы:
|
проектор |
| III | Объяснение нового материала и подготовка к практической работе:
|
Проектор, раздаточный материал |
| IV | Выполнение проектной практической работы:
|
Компьютер |
| V | Итоги:
|
Проектор, раздаточный материал, компьютер |
Опорный конспект
Построение совмещенных графиков в Microsoft Office Excel -2007.
Для построения графиков функций Y(X) в Microsoft Office Excel используется тип диаграммы Точечная:
Для этого требуется два ряда значений: Х и Y значения, которые должны быть соответственно расположены в левом и правом столбцах.
Можно совместить построение нескольких графиков. Такая возможность используется для графического решения систем уравнений с двумя переменными, при проведении сравнения анализа значений y при одних и тех же значениях x.
ПРИМЕР.
(Используется при объяснении материала через проектор.)
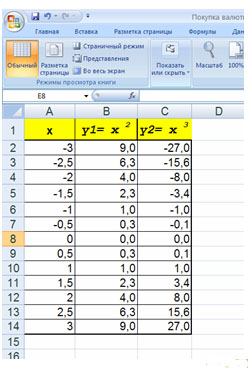
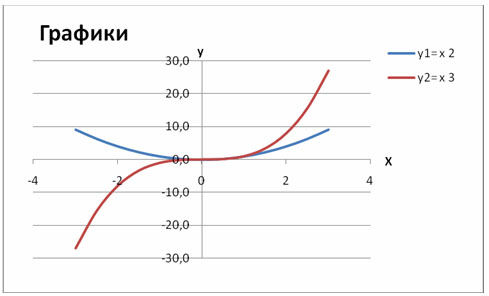
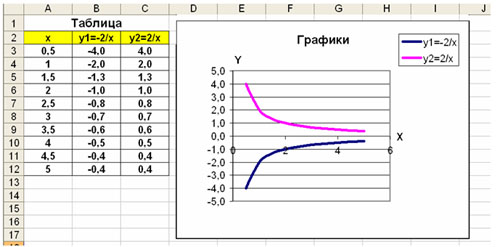
Построить графики функций y1= x 2 и y2= x 3 на интервале [- 3 ; 3] с шагом 0,5.
Алгоритм выполнения задания:
1. Заполнить таблицу значений:
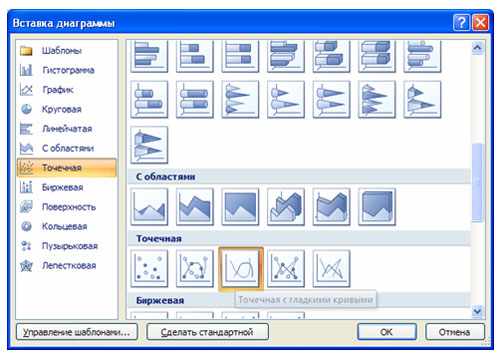
2. Выделить таблицу и указать тип диаграммы Точечная.
3. Выбрать формат точечной диаграммы с гладкими кривыми.
4. В Макете указать название диаграммы «Графики», дать название осей: X и Y
5. Должен получиться график:
P.S. В версии 97-2003 для получения графика, представленного на рисунке надо провести редактирование.
Раздаточный материал
Варианты
ВАРИАНТ 1
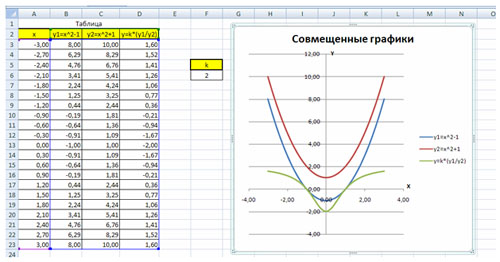
Построить графики функций y1= x 2 -1, y2= x 2+1 иy=К·(y1/ y2)на интервале [- 3 ; 3] с шагом 0,3.
ВАРИАНТ 2
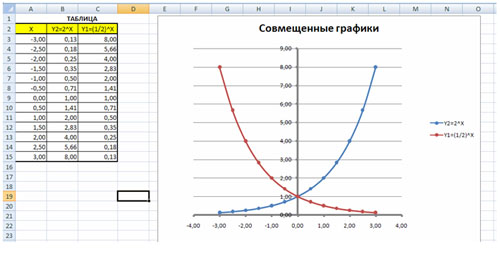
Построить графики функций y1= и y2= 2х на интервале [- 3 ; 3] с шагом 0,5.
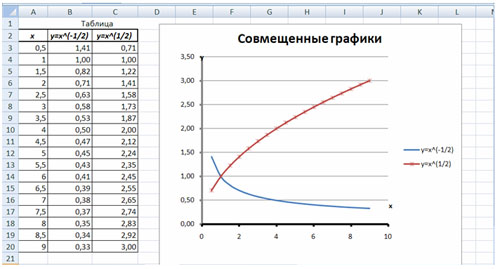
ВАРИАНТ 3
Построить графики функций y1= , y2=
на интервале [- 0,5 ; 9] с шагом 0,5.
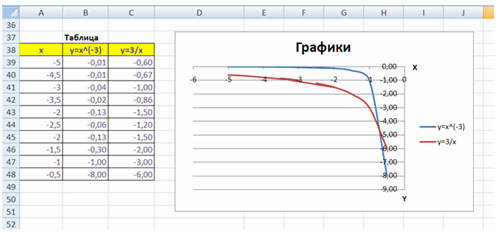
ВАРИАНТ 4
Построить графики функций y1=, y2=
на интервале [- 5 ; -0,5] с шагом 0,5.
ВАРИАНТ 5
Построить графики функций y1= , y2=
на интервале [0,5 ; 5] с шагом 0,5.


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Был в сети 07.04.2023 09:00

Куликовский Максим Юрьевич
преподаватель
10 546
2 245
13.12.2018 08:46
Просмотр содержимого документа
«Практическая работа в MS Excel «Графики»»
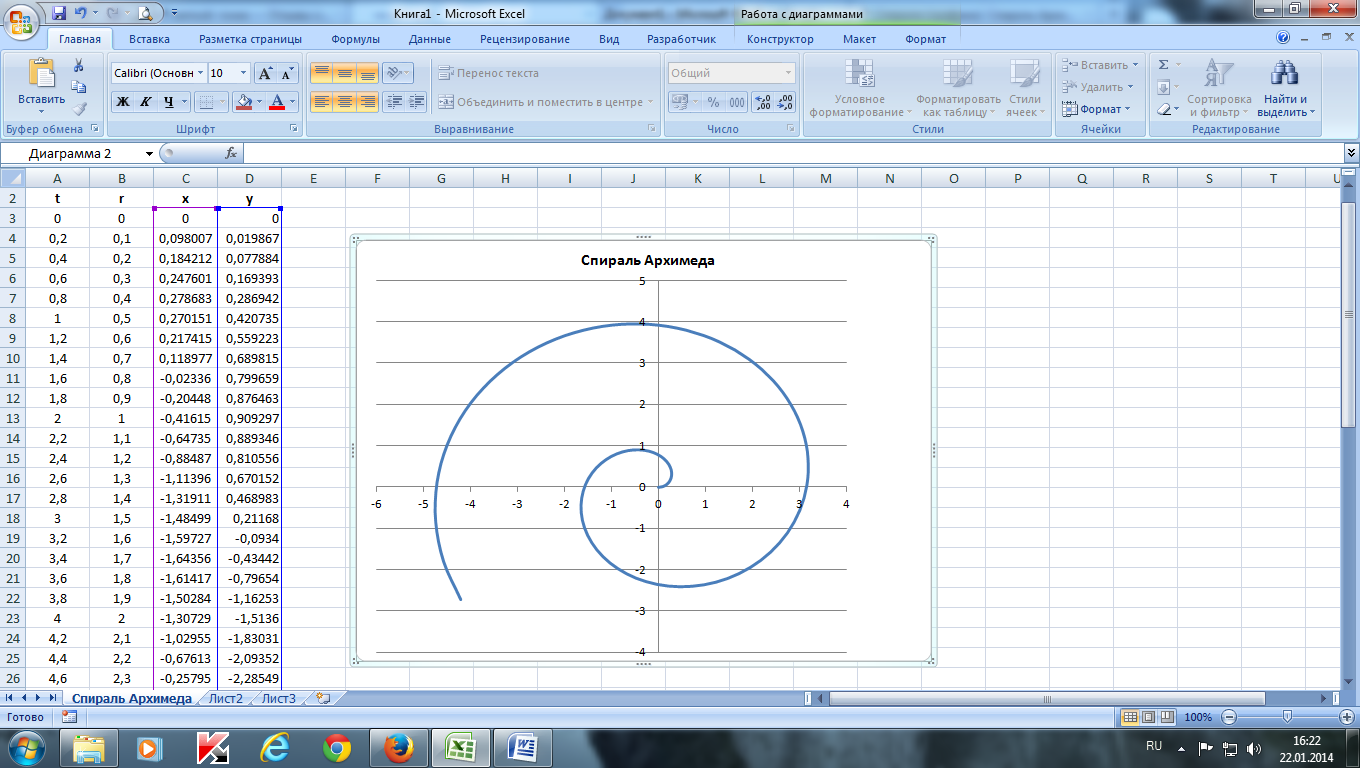
Практическая работа «Красивые графики функций»
-
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5*t
— в столбце С – значения х = r*cos(t)
— в столбце D – значения y = r*sin(t)
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми)
-
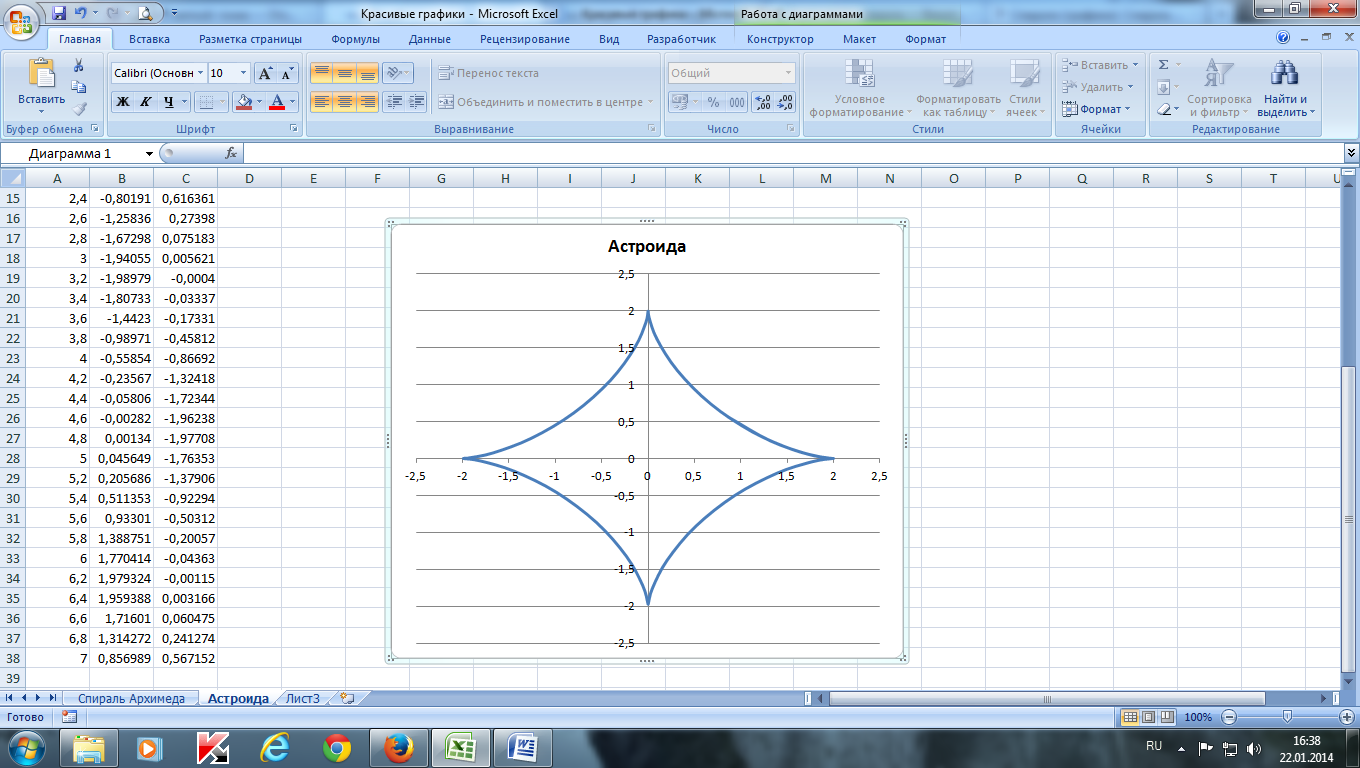
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*(cos (t))3
— в столбце С – значения y = 2*(sin (t))3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми)
-
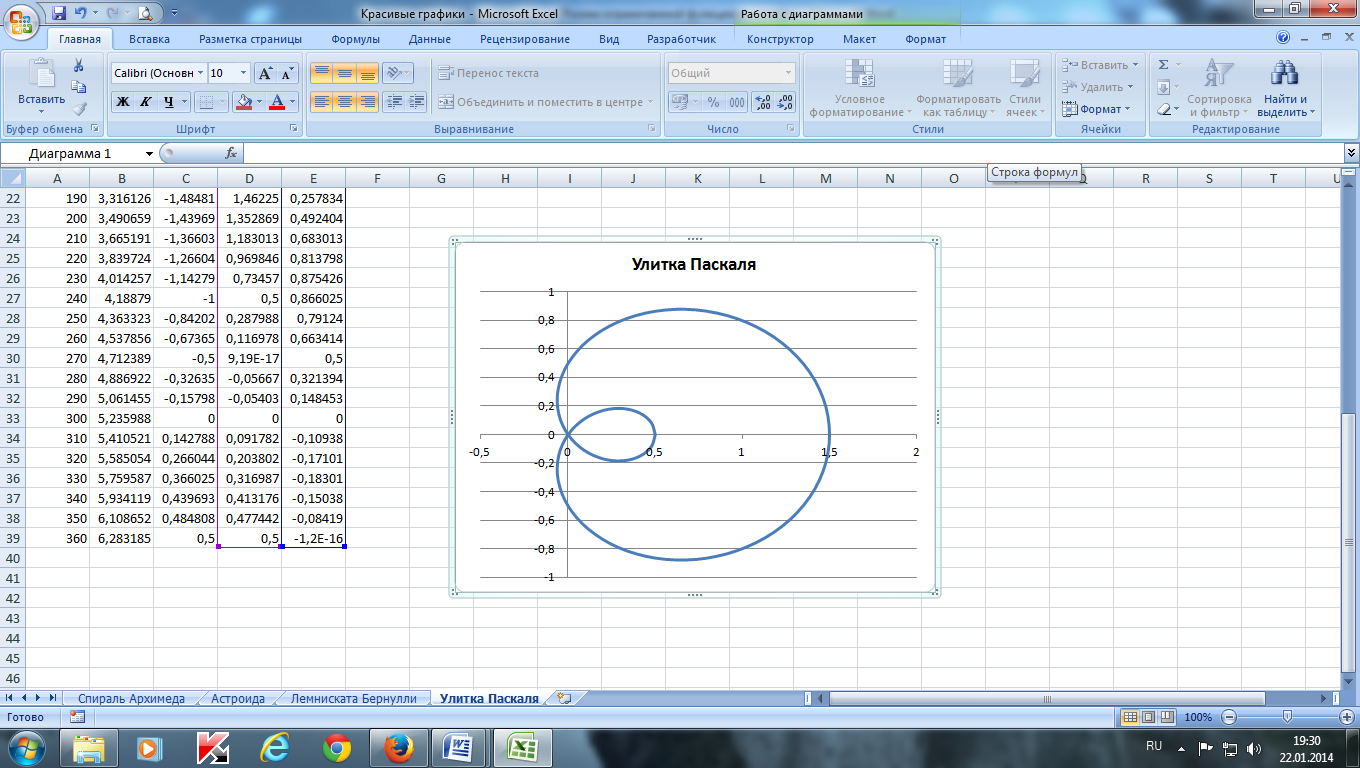
Построить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения p = cos(t)–0,5
— в столбце D – значения x = p*cos(t)
— в столбце Е – значения у = p*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми) -
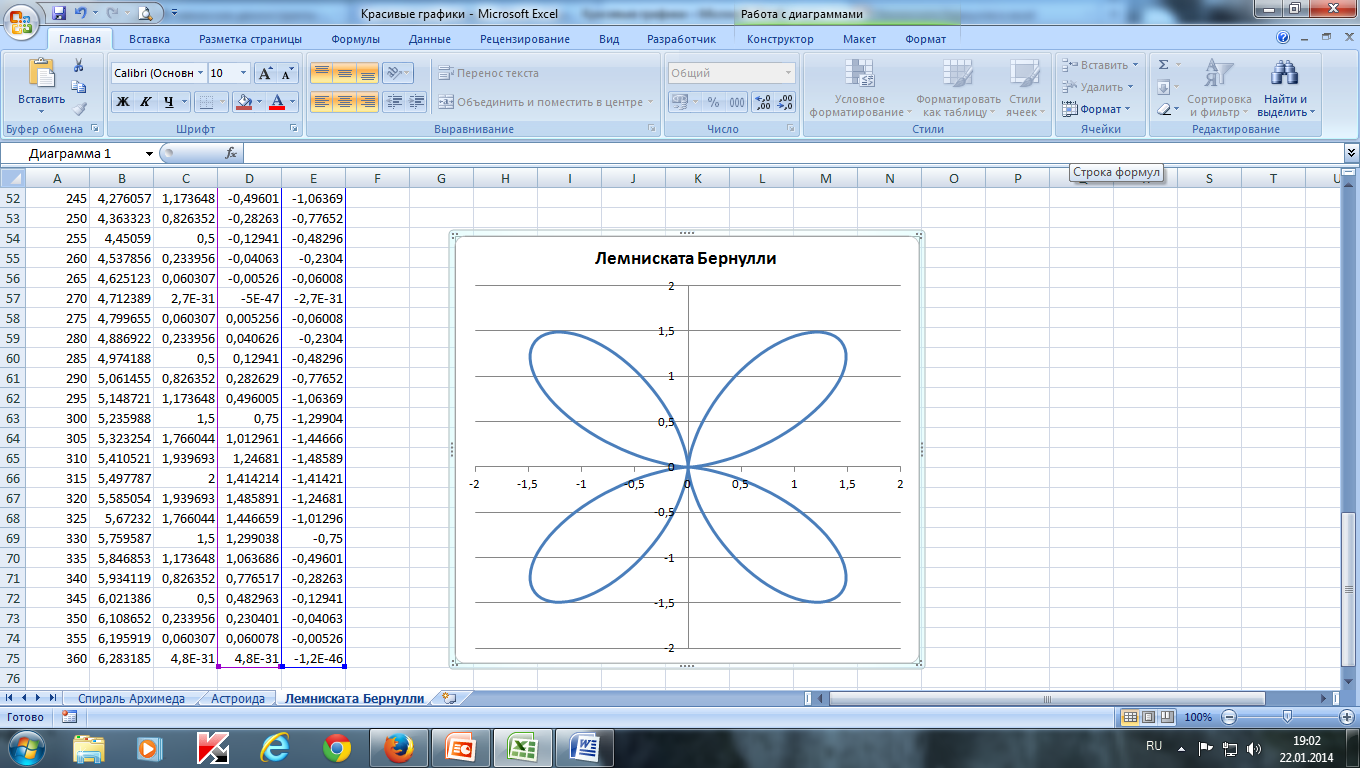
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения r = 2*sin(2*t)2
— в столбце D – значения x = r*cos(t)
— в столбце E – значения y = r*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
-
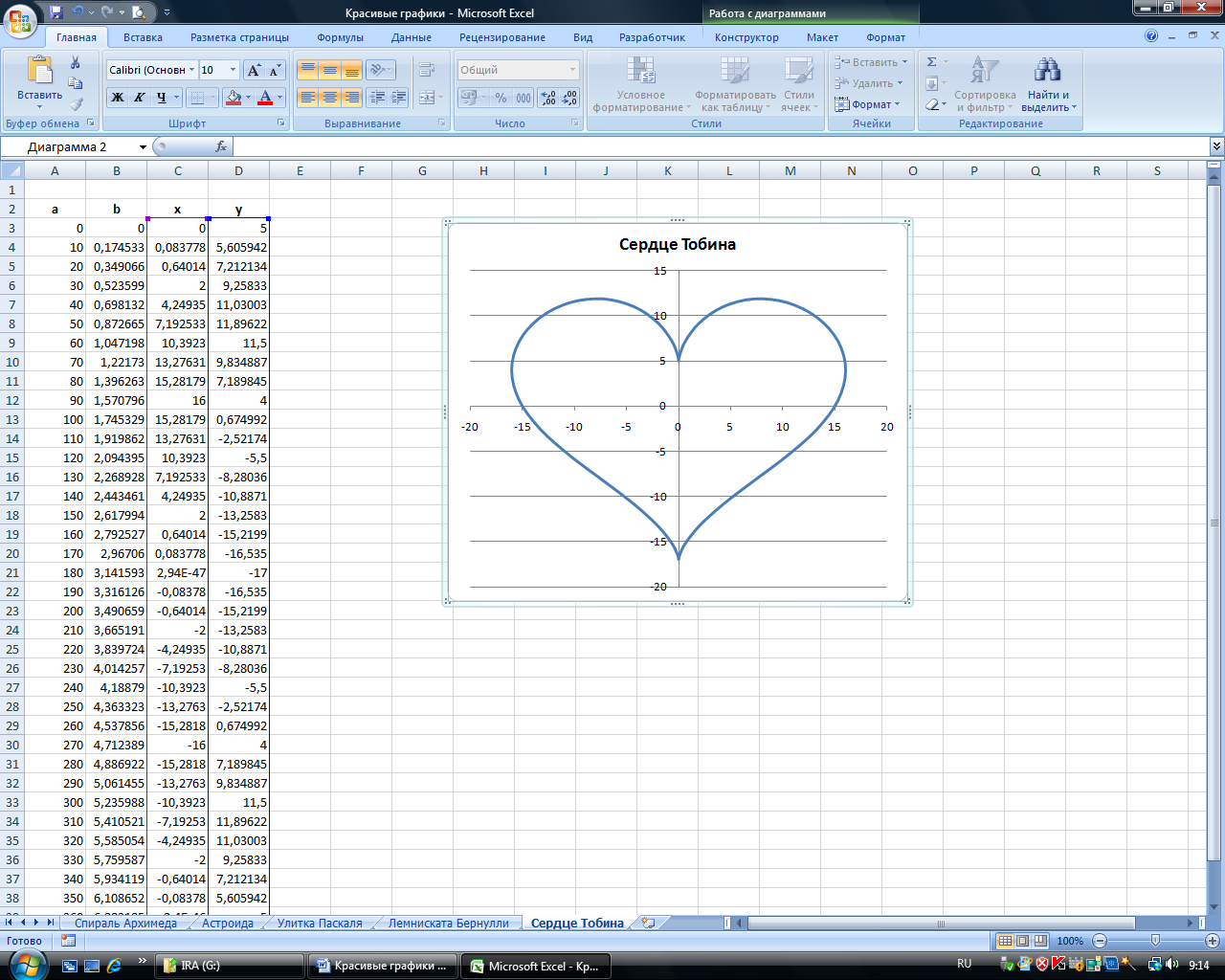
Построить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения x = 16*(sin(t))3
— в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми)