Лабораторная работа 3 решение задачи табулирования функции в excel решение - Word и Excel

Лабораторная работа №3

«Решение задачи табулирования функции в Excel»

Цели
работы:

·
закрепить навыки заполнения и
редактирования таблиц;

·
познакомиться со способами
адресации;

·
освоить некоторые приемы
оформления таблиц.

Для
дальнейшего знакомства с Excel рассмотрим задачу табулирования функции.

Постановка
задачи: вычислить значения функции y=kx(x²-1)/(x²+1) для
всех x на интервале [-2; 2 ] с шагом 0,2 при k=10.

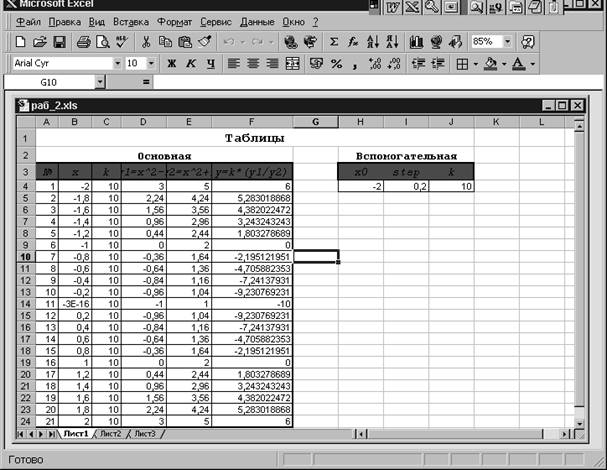
Решение
должно быть получено в виде таблицы:

№	x	K	y1=x^2-1	Y2=x^2+1	y=k*(y1/y2)

Задание
1. Прежде чем перейти к выполнению
задачи, познакомтесь со способами адресации в Excel.

Абсолютная, относительная и смешанная
адресации ячеек и

блоков (диапазонов)

При
обращении к ячейке можно использовать описанные ранее способы: B3, A1: G9 и
т. д. Такая адресация называется относительной. При её использовании в формулах
Excel запоминает расположение относительно текущей ячейки.
Так, например, когда вы вводите формулу =B1+B2 в
ячейку B4, то Excel интерпретирует формулу как “прибавить содержимое
ячейки, расположенной тремя рядами выше, к содержимому ячейки, расположенной
двумя рядами выше”.

Если
вы скопировали формулу =В1+B2 из ячейки B4 в С4, Excel также
интерпретирует формулу как “прибавить содержимое ячейки, расположенной тремя
рядами выше, к содержимому ячейки двумя рядами выше”. Таким образом, формула в
ячейке С4 примет вид =С1+С2.

Если
при копировании формул вы пожелаете сохранить ссылку на конкретную ячейку или
область, то вам необходимо воспользоваться абсолютной адресацией. Для её задания
необходимо перед именем столбца и перед номером строки ввести символ $.
Например: B$4 или $C2. Тогда при копировании один параметр адреса
изменяется, а другой — нет.

Задание
2. Заполните основную и вспомогательную таблицы

·
2. 1. Заполните шапку основной
таблицы начиная с ячейки А1:

в
ячейку А1 занесите N;

в
ячейку B1 занесите X;

в
ячейку C1 занесите K и т.д.

установите
ширину столбцов такой, чтобы надписи были видны полностью.

·
2.2. Заполните вспомогательную
таблицу начальными исходными данными начиная с ячейки H1:

Где
х0 — начальное значение х, step — шаг изменения х, k
— коэффициент (константа).

Данный
пункт при решении задачи табулирования функции является не обязательным и
введен искусственно — для демонстрации способов адресации.

·
2. 3. Используя функцию
автозаполнения, заполните столбец А числами от 1 до 21, начиная с ячейки А2 и
заканчивая ячейкой А22.

·
2. 4. Заполните столбец В
значениями х:

·
в ячейку В2 занесите $H$2.

Это означает, что в ячейку В2 заносится значение из
ячейки Н2 (начальное значение х), знак $ указывает на абсолютную адресацию;

·
в ячейку В3 занесите =В2 + $I$2.

Это
означает, что начальное значение х будет увеличено на величину шага, который
берется из ячейки I2;

·
скопируйте формулы из ячейки В3
в ячейки В4 ; В22.

Столбец
заполнится значениями х от 2 до -2 шагом 0,2.

·
2. 5. Заполните столбец С
значениями коэффициента k:

·
в ячейку С2 занесите =$J$2;

·
в ячейку С3 занесите =С2.

Посмотрите
на введенные формулы. Почему они так записаны?

·
скопируйте формулу из ячейки
С3 в ячейки С4: С22.

Весь
столбец заполнится значением 10.

·
2. 6. Заполните столбец D
значениями функции y1 =x^2-1:

·
в ячейку D2
занесите =B2 *B2-1;

·
скопируйте формулу из ячейки D2
в ячейки D3: D 22.

Столбец
заполнится как положительными, так и отрицательными значениями функции у1.
Начальное и конечное значения равны 3.

·
2. 7. Аналогичным образом
заполните столбец Е значениями функции у2=х^2+1.

Проверьте!
Все значения положительные; начальное
и конечное значения равны 5.

·
2. 8. Заполните столбец F
значениями функции y = k*(x^2-1)/(x^2+1):

·
в ячейку F2
занесите =С2*(D2/E2);

·
скопируйте формулу из F2
в ячейки F2 :F22.

Проверьте!
Значения функции как положительные,
так и отрицательные; начальное и конечное значения равны 6.

Задание
3. Понаблюдайте за изменениями в основной таблице при смене данных во
вспомогательной.

·
3. 1. Измените во
вспомогательной таблице начальное значение х: в ячейку Н2 занесите -5.

·
3. 2. Измените значение шага: в
ячейку I2 занесите 2.

·
3. 3. Измените значение
коэффициента: в ячейку J2 занесите 1.

Внимание!
При всех изменениях данных во
вспомогательной таблице в основной таблице пересчет производится автоматически.

·
3. 4. Прежде чем продолжить
работу, верните прежние начальные значения во вспомогательной таблице: х0 = –2,
step = 0,2, k=10.

Задание
4. Оформить основную и вспомогательную таблицы.

·
4. 1. Вставьте две пустые
строки для оформления заголовков:

·
установите курсор на строку
номер 1;

·
выполните команды меню Вставка,
Строки (2 раза).

·
4. 2. Введите заголовки:

·
в ячейку А1 «Таблицы»;

·
в ячейку А2 «Основная»;

·
в ячейку Н2 «Вспомогательная».

·
4. 3. Объедините ячейки А1:J1
и разместите заголовок «Таблицы» по центру:

·
выделите блок А1:J1;

·
кнопку Центрировать используйте
ко столбцам панели инструментов Форматирование.

·
4. 4. Аналогичным образом
разместите по центру заголовки «основная» и «вспомогательная».

·
4. 5. Оформите заголовки
определенными шрифтами.

Шрифтовое оформление текста.

Символы любой ячейки или блока можно оформить
разными шрифтами. Для этого необходимо выделить ячейку или блок, а затем
воспользоваться кнопками из панели Форматирование или командой меню Формат,
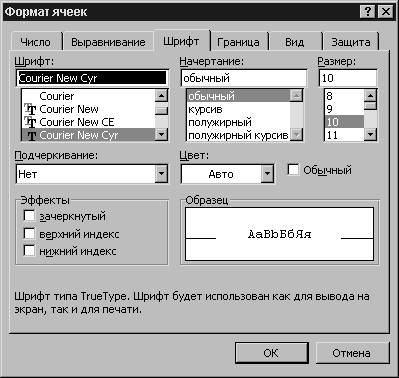
Ячейки, Шрифт. При использовании команды появится диалоговое окно вида:

Рис. 3. 1.

·
для заголовка «Таблицы» задайте
шрифт Courier New Cyr, размер шрифта 14, полужирный.

Используйте
кнопки панели инструментов Форматирование;

·
Для заголовков «основная» и
«вспомогательная» задайте шрифт Courier New Cyr,
размер шрифта 12, полужирный.

Используя
команды меню Формат, Ячейки, Шрифт;

·
для шапок таблиц установите
шрифт Courier New Cyr, размер шрифта 12, курсив.

Любым
способом.

·
4. 6. Подгоните ширину столбцов
так, чтобы текст помещался полностью.

·
4. 7. Произведите выравнивание
надписей шапок по центру.

Выравнивание.

Содержимое
любой ячейки можно выровнять по левому или правому краю, по центру (по
горизонтали и вертикали), а так же можно задать необходимую ориентацию текста
(снизу вверх, сверху вниз и т. д.).

Для
задания необходимой ориентации используют кнопки в панели Форматирование или
команды меню Формат, Ячейки, Выравнивание.

·
4.8. Задайте рамки для основной
и вспомогательной таблиц, используя кнопку панели инструментов Форматирование.

Для
задания рамки используется кнопка в панели Форматирование или команда меню
Формат, Ячейки, Рамка

·
Задайте фон заполнения внутри
таблиц – желтый, фон заполнения шапок таблиц – малиновый.

Фон

Содержимое
любой ячейки или блока может иметь необходимый фон (тип штриховки, цвет
штриховки, цвет фона.)

Для
задания фона используется кнопка в панели Форматирование или команда
мену Формат, Ячейка, Вид.

Вид
экрана после выполнения работы представлен на рис. 3. 2.

Рис. 3. 2.

Задание 5. Сохранить
результаты работы на дискете в личном каталоге файле

Задание
6. Завершите работу.

Задание
7. Подведите итоги.

Проверьте:

§
знаете ли вы, что такое относительная адресация; абсолютная;
смешанная;

§
умеете ли вы: использовать различные способы адресации при
обращении к ячейкам, оформлять символы, производить выравнивание, задавать
рамку, изменять фон.

Если
нет, то еще раз внимательно перечитайте соответствующие разделы работы.

Предьявите преподавателю:

§
краткий конспект;

§
файл раб_2.xls на экране и на рабочем диске в личном каталоге.

Источник

Лабораторная
работа
№ 2 (1).

Решение задачи табулирования функции

Цели работы:

закрепить навыки заполнения и
редактирования таблиц;

познакомитъся со способами адресации;

освоить некоторые приемы оформления
таблиц.

Для дальнейшего знакомства с Excelрассмотрим задачу табулирования
функции.

Постановка задачи:вычислить значения
функцииy=k*(x²—l)/(х²+1)
для всех х на интервале [—2,2] с шагом 0,2
приk=10.

Решение должно быть получено в виде
таблицы:

№	x	k	у1=х^2-1	у2=х^2+1	y=k*(yl/y2)

Задание 1.Прежде чем перейти к
выполнению задачи, познакомьтесь со
способами адресации в Excel.

Абсолютная, относительная и смешанная адресации ячеек и блоков

При обращении к ячейке можно использовать
описанные ранее способы: ВЗ, А1:G9
и т. д. Такая адресация называется
относительной. При ее использовании в
формулахExcelзапоминает
расположение относительно текущей
ячейки. Так, например, когда вы вводите
формулу =B1+B2 в ячейку В4, тоExcelинтерпретирует формулу как «прибавить
содержимое ячейки, расположенной тремя
рядами выше, к содержимому ячейки,
расположенной двумя рядами выше».

Если вы скопировали формулу =В1+В2 из
ячейки В4 в С4, Excelтакже
интерпретирует формулу как «прибавить
содержимое ячейки, расположенной тремя
рядами выше, к содержимому ячейки
двумя рядами выше». Таким образом,
формула в ячейке С 4 примет вид =С1+С2.

Если при копировании формул вы пожелаете
сохранить ссылку на конкретную ячейку
или область, то вам необходимо
воспользоваться абсолютной адресацией.
Для ее задания необходимо перед именем
столбца и перед номером строки ввести
символ $. Например: $В$4 или $C$2:$F$48
и т. д.

Смешанная адресация. Символ $ ставится
только там, где он необходим. Например:
В$4 или $С2. Тогда при копировании один
параметр адреса изменяется. а другой —
нет.

Задание 2.
Заполните
основную и вспомогательную таблицы.

>
2.1. Заполните шапку основной таблицы
начиная с ячейки А1:

в
ячейку А1 занесите N;

в ячейку В1 занесите
X;

в ячейку С1 занесите К
и т. д.

установите ширину
столбцов такой, чтобы надписи были видны
полностью.

> 2.2. Заполните
вспомогательную таблицу начальными
исходными данными начиная с ячейки H1:

X0	Step	k
-2	0,2	10

где х0 — начальное значение х, step
— шаг изменения х, г — коэффициент
(константа).

Данный пункт при решении задачи
табулирования функции является не
обязательным и введен искусственно
— для демонстрации способов адресации.

> 2.3. Используя функцию автозаполнения,
заполните столбец А числами от 1 до 21,
начиная с ячейки А2 и заканчивая ячейкой
А22.

> 2.4. Заполните столбец
В значениями х:

> в ячейку В2 занесите
=$Н$2.

Это означает, что в ячейку В2 заносится
значение из ячейки Н2 (начальное значение
х), знак $ указывает на абсолютную
адресацию;

> в ячейку ВЗ занесите
=В2+$1$2.

Это означает, что начальное значение х
будет увеличено на величину шага. которая
берется из ячейки 12;

> скопируйте формулу из ячейки ВЗ в
ячейки В4:В22.

Столбец заполнится значениями х от —2
до 2 с шагом 0,2.

> 2.5. Заполните столбец С значениями
коэффициента k:

> в ячейку С2 занесите =$J$2;

> а ячейку СЗ занесите =С2.

Посмотрите на введенные формулы. Почему
они так записаны? > скопируйте формулу
из ячейки СЗ в ячейки С4:С22.

Весь столбец заполнился значением 10. >
2.6. Заполните столбец Dзначениями функции у1=х^2-1:

> в ячейку D2 занесите
=В2*В2-1;

> скопируйте формулу из ячейки D2 в
ячейки 03: D22.

Столбец заполнился как положительными,
так и отрицательными значениями функции
у1. Начальное и конечное значения равны
3.

> 2.7. Аналогичным образом заполните
столбец Е значениями функции у2=х^2+1.
Проверьте! Все значения положительные;
начальное и конечное значения равны 5.

> 2.8. Заполните столбец Fзначениями функцииy=k*(x^2-1)/(x^2+1):

> в ячейку F2 занесите
=C2*(D2/E2);

> скопируйте формулу из F2 в ячейки F2:
F22.

Проверьте!Значения функции как
положительные, так и отрицательные;
начальное и конечное значения равны
6.

Задание 3.
Понаблюдайте
за изменениями в основной таблице при
смене данных во вспомогательной.

>
3.1. Измените во вспомогательной таблице
начальное значение х: в ячейку Н2 занесите
-5.

> 3.2. Измените
значение шага: в ячейку l2 занесите 2. >
3.3. Измените значение коэффициента: в
ячейку J2
занесите 1.

Внимание!
При всех изменениях данных во
вспомогательной таблице в основной
таблице пересчет производится
автоматически.

> 3.4. Прежде чем
продолжить работу, верните прежние
начальные значения во вспомогательной
таблице: х0=-2, step=0,2,
k=10.

Задание 4.
Оформите
основную и вспомогательную таблицы.

>
4.1. Вставьте две пустые строки сверху
для оформления заголовков:

> установите
курсор на строку номер 1;

> выполните
команды меню
Вставка, Строки
(2 раза)

>
4.2. Введите заголовки:

>
в ячейку А1«Таблицы»;

>
в ячейку А2
«основная»;

>
в ячейку Н2
«вспомогательная».

>
4.3. Объедините ячейки А1:J1 и разместите
заголовок «Таблицы» по центру:

>
выделите блок А1:J1;

>
используйте кнопку
Центрировать по столбцам
панели инструментов
Форматирование.

> 4.4. Аналогичным образом разместите
по центру заголовки «основная» и
«вспомогательная».

>
4.5. Оформите заголовки определенными
шрифтами.

Соседние файлы в предмете Информатика

Источник

Обновлено: 15.04.2023

Для дальнейшего знакомства с Excelрассмотрим задачу табулирования функции.

Постановка задачи:вычислить значения функцииy=k*(x 2 —l)/(х 2 +1) для всех х на интервале [—2,2] с шагом 0,2 приk=10.

Решение должно быть получено в виде таблицы:

Задание 1.Прежде чем перейти к выполнению задачи, познакомьтесь со способами адресации в Excel.

Абсолютная, относительная и смешанная адресации ячеек и блоков

При обращении к ячейке можно использовать описанные ранее способы: ВЗ, А1:G9 и т. д. Такая адресация называется относительной. При ее использовании в формулахExcelзапоминает расположение относительно текущей ячейки. Так, например, когда вы вводите формулу =B1+B2 в ячейку В4, тоExcelинтерпретирует формулу как «прибавить содержимое ячейки, расположенной тремя рядами выше, к содержимому ячейки, расположенной двумя рядами выше».

Если вы скопировали формулу =В1+В2 из ячейки В4 в С4, Excelтакже интерпретирует формулу как «прибавить содержимое ячейки, расположенной тремя рядами выше, к содержимому ячейки двумя рядами выше». Таким образом, формула в ячейке С 4 примет вид =С1+С2.

Если при копировании формул вы пожелаете сохранить ссылку на конкретную ячейку или область, то вам необходимо воспользоваться абсолютной адресацией. Для ее задания необходимо перед именем столбца и перед номером строки ввести символ $. Например: $В$4 или $C$2:$F$48 и т. д.

Смешанная адресация. Символ $ ставится только там, где он необходим. Например: В$4 или $С2. Тогда при копировании один параметр адреса изменяется. а другой — нет.

Задание 2. Заполните основную и вспомогательную таблицы.

> 2.1. Заполните шапку основной таблицы начиная с ячейки А1:

в ячейку А1 занесите N;

в ячейку В1 занесите X;

в ячейку С1 занесите К и т. д.

установите ширину столбцов такой, чтобы надписи были видны полностью.

> 2.2. Заполните вспомогательную таблицу начальными исходными данными начиная с ячейки H1:

где х0 — начальное значение х, step — шаг изменения х, г — коэффициент (константа).

Данный пункт при решении задачи табулирования функции является не обязательным и введен искусственно — для демонстрации способов адресации.

> 2.3. Используя функцию автозаполнения, заполните столбец А числами от 1 до 21, начиная с ячейки А2 и заканчивая ячейкой А22.

> 2.4. Заполните столбец В значениями х:

> в ячейку В2 занесите =$Н$2.

Это означает, что в ячейку В2 заносится значение из ячейки Н2 (начальное значение х), знак $ указывает на абсолютную адресацию;

> в ячейку ВЗ занесите =В2+$1$2.

Это означает, что начальное значение х будет увеличено на величину шага. которая берется из ячейки 12;

> скопируйте формулу из ячейки ВЗ в ячейки В4:В22.

Столбец заполнится значениями х от —2 до 2 с шагом 0,2.

> 2.5. Заполните столбец С значениями коэффициента k:

> в ячейку С2 занесите =$J$2;

> а ячейку СЗ занесите =С2.

Посмотрите на введенные формулы. Почему они так записаны? > скопируйте формулу из ячейки СЗ в ячейки С4:С22.

Весь столбец заполнился значением 10. > 2.6. Заполните столбец Dзначениями функции у1=х^2-1:

> в ячейку D2 занесите =В2*В2-1;

> скопируйте формулу из ячейки D2 в ячейки 03: D22.

Столбец заполнился как положительными, так и отрицательными значениями функции у1. Начальное и конечное значения равны 3.

> 2.7. Аналогичным образом заполните столбец Е значениями функции у2=х^2+1. Проверьте! Все значения положительные; начальное и конечное значения равны 5.

> 2.8. Заполните столбец Fзначениями функцииy=k*(x^2-1)/(x^2+1):

> в ячейку F2 занесите =C2*(D2/E2);

> скопируйте формулу из F2 в ячейки F2: F22.

Проверьте!Значения функции как положительные, так и отрицательные; начальное и конечное значения равны 6.

Задание 3. Понаблюдайте за изменениями в основной таблице при смене данных во вспомогательной.

> 3.1. Измените во вспомогательной таблице начальное значение х: в ячейку Н2 занесите -5.

> 3.2. Измените значение шага: в ячейку l2 занесите 2. > 3.3. Измените значение коэффициента: в ячейку J2 занесите 1.

Внимание! При всех изменениях данных во вспомогательной таблице в основной таблице пересчет производится автоматически.

> 3.4. Прежде чем продолжить работу, верните прежние начальные значения во вспомогательной таблице: х0=-2, step=0,2, k=10.

Задание 4. Оформите основную и вспомогательную таблицы.

> 4.1. Вставьте две пустые строки сверху для оформления заголовков:

> установите курсор на строку номер 1;

> выполните команды меню Вставка, Строки (2 раза)

> 4.2. Введите заголовки:

> в ячейку А1«Таблицы»;

> в ячейку А2 «основная»;

> в ячейку Н2 «вспомогательная».

> 4.3. Объедините ячейки А1:J1 и разместите заголовок «Таблицы» по центру:

> выделите блок А1:J1;

> используйте кнопку Центрировать по столбцам панели инструментов Форматирование.

> 4.4. Аналогичным образом разместите по центру заголовки «основная» и «вспомогательная».

> 4.5. Оформите заголовки определенными шрифтами.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Постановка задачи: вычислить значения функции y = kx ( x 2 -1)/( x 2 +1) для всех x на интервале [-2; 2 ] с шагом 0,2 при k =10.

Решение должно быть получено в виде таблицы:

Задание 1. Прежде чем перейти к выполнению задачи, познакомтесь со способами адресации в Excel .

Абсолютная, относительная и смешанная адресации ячеек и

блоков (диапазонов)

При обращении к ячейке можно использовать описанные ранее способы: B 3, A 1: G 9 и т. д. Такая адресация называется относительной. При её использовании в формулах Excel запоминает расположение относительно текущей ячейки. Так, например, когда вы вводите формулу = B 1+ B 2 в ячейку B 4, то Excel интерпретирует формулу как “прибавить содержимое ячейки, расположенной тремя рядами выше, к содержимому ячейки, расположенной двумя рядами выше”.

Если вы скопировали формулу =В1+ B 2 из ячейки B 4 в С4, Excel также интерпретирует формулу как “прибавить содержимое ячейки, расположенной тремя рядами выше, к содержимому ячейки двумя рядами выше”. Таким образом, формула в ячейке С4 примет вид =С1+С2.

Если при копировании формул вы пожелаете сохранить ссылку на конкретную ячейку или область, то вам необходимо воспользоваться абсолютной адресацией. Для её задания необходимо перед именем столбца и перед номером строки ввести символ $. Например: B $4 или $ C 2. Тогда при копировании один параметр адреса изменяется, а другой — нет.

Задание 2. Заполните основную и вспомогательную таблицы

2. 1. Заполните шапку основной таблицы начиная с ячейки А1:

в ячейку А1 занесите N ;

в ячейку B 1 занесите X ;

в ячейку C 1 занесите K и т.д.

установите ширину столбцов такой, чтобы надписи были видны полностью.

2.2. Заполните вспомогательную таблицу начальными исходными данными начиная с ячейки H 1:

Где х0 — начальное значение х, step — шаг изменения х, k — коэффициент (константа).

Данный пункт при решении задачи табулирования функции является не обязательным и введен искусственно — для демонстрации способов адресации.

2. 3. Используя функцию автозаполнения, заполните столбец А числами от 1 до 21, начиная с ячейки А2 и заканчивая ячейкой А22.

2. 4. Заполните столбец В значениями х:

в ячейку В2 занесите $ H $2.

Это означает, что в ячейку В2 заносится значение из ячейки Н2 (начальное значение х), знак $ указывает на абсолютную адресацию;

в ячейку В3 занесите =В2 + $ I $2.

Это означает, что начальное значение х будет увеличено на величину шага, который берется из ячейки I 2;

скопируйте формулы из ячейки В3 в ячейки В4 ; В22.

Столбец заполнится значениями х от 2 до -2 шагом 0,2.

2. 5. Заполните столбец С значениями коэффициента k :

в ячейку С2 занесите =$ J $2;

в ячейку С3 занесите =С2.

Посмотрите на введенные формулы. Почему они так записаны?

скопируйте формулу из ячейки С3 в ячейки С4: С22.

Весь столбец заполнится значением 10.

2. 6. Заполните столбец D значениями функции y 1 = x ^2-1:

в ячейку D 2 занесите = B 2 * B 2-1;

скопируйте формулу из ячейки D 2 в ячейки D 3: D 22.

Столбец заполнится как положительными, так и отрицательными значениями функции у1. Начальное и конечное значения равны 3.

2. 7. Аналогичным образом заполните столбец Е значениями функции у2=х^2+1.

Проверьте! Все значения положительные; начальное и конечное значения равны 5.

2. 8. Заполните столбец F значениями функции y = k *( x ^2-1)/( x ^2+1):

в ячейку F 2 занесите =С2*( D 2/ E 2);

скопируйте формулу из F 2 в ячейки F 2 : F 22.

Проверьте! Значения функции как положительные, так и отрицательные; начальное и конечное значения равны 6.

Задание 3. Понаблюдайте за изменениями в основной таблице при смене данных во вспомогательной.

3. 1. Измените во вспомогательной таблице начальное значение х: в ячейку Н2 занесите -5.

3. 2. Измените значение шага: в ячейку I 2 занесите 2.

3. 3. Измените значение коэффициента: в ячейку J 2 занесите 1.

3. 4. Прежде чем продолжить работу, верните прежние начальные значения во вспомогательной таблице: х0 = –2, step = 0,2, k =10.

Задание 4. Оформить основную и вспомогательную таблицы.

4. 1. Вставьте две пустые строки для оформления заголовков:

установите курсор на строку номер 1;

выполните команды меню Вставка, Строки (2 раза).

4. 2. Введите заголовки:

в ячейку А1 «Таблицы»;

в ячейку А2 «Основная»;

в ячейку Н2 «Вспомогательная».

4. 3. Объедините ячейки А1: J 1 и разместите заголовок «Таблицы» по центру:

выделите блок А1: J 1;

кнопку Центрировать используйте ко столбцам панели инструментов Форматирование.

4. 4. Аналогичным образом разместите по центру заголовки «основная» и «вспомогательная».

4. 5. Оформите заголовки определенными шрифтами.

Шрифтовое оформление текста.

С
имволы любой ячейки или блока можно оформить разными шрифтами. Для этого необходимо выделить ячейку или блок, а затем воспользоваться кнопками из панели Форматирование или командой меню Формат, Ячейки, Шрифт. При использовании команды появится диалоговое окно вида:

для заголовка «Таблицы» задайте шрифт Courier New Cyr , размер шрифта 14, полужирный.

Используйте кнопки панели инструментов Форматирование;

Для заголовков «основная» и «вспомогательная» задайте шрифт Courier New Cyr , размер шрифта 12, полужирный.

Используя команды меню Формат, Ячейки, Шрифт;

для шапок таблиц установите шрифт Courier New Cyr , размер шрифта 12, курсив.

4. 6. Подгоните ширину столбцов так, чтобы текст помещался полностью.

4. 7. Произведите выравнивание надписей шапок по центру.

Выравнивание.

Содержимое любой ячейки можно выровнять по левому или правому краю, по центру (по горизонтали и вертикали), а так же можно задать необходимую ориентацию текста (снизу вверх, сверху вниз и т. д.).

Для задания необходимой ориентации используют кнопки в панели Форматирование или команды меню Формат, Ячейки, Выравнивание.

4.8. Задайте рамки для основной и вспомогательной таблиц, используя кнопку панели инструментов Форматирование.

Для задания рамки используется кнопка в панели Форматирование или команда меню Формат, Ячейки, Рамка

Задайте фон заполнения внутри таблиц – желтый, фон заполнения шапок таблиц – малиновый.

Содержимое любой ячейки или блока может иметь необходимый фон (тип штриховки, цвет штриховки, цвет фона.)

Для задания фона используется кнопка в панели Форматирование или команда мену Формат, Ячейка, Вид.

Вид экрана после выполнения работы представлен на рис. 3. 2.

Р
ис. 3. 2.

Задание 5. Сохранить результаты работы на дискете в личном каталоге файле

Задание 6. Завершите работу.

Задание 7. Подведите итоги.

знаете ли вы, что такое относительная адресация; абсолютная; смешанная;

умеете ли вы: использовать различные способы адресации при обращении к ячейкам, оформлять символы, производить выравнивание, задавать рамку, изменять фон.

Если нет, то еще раз внимательно перечитайте соответствующие разделы работы.

Предьявите преподавателю:

краткий конспект;

файл раб_2. xls на экране и на рабочем диске в личном каталоге.

Постановка задачи: вычислить значения функции y = kx ( x 2 -1)/( x 2 +1) для всех x на интервале [-2; 2 ] с шагом 0,2 при k =10.

Решение должно быть получено в виде таблицы:

Задание 1. Прежде чем перейти к выполнению задачи, познакомтесь со способами адресации в Excel .

Абсолютная, относительная и смешанная адресации ячеек и

блоков (диапазонов)

При обращении к ячейке можно использовать описанные ранее способы: B 3, A 1: G 9 и т. д. Такая адресация называется относительной. При её использовании в формулах Excel запоминает расположение относительно текущей ячейки. Так, например, когда вы вводите формулу = B 1+ B 2 в ячейку B 4, то Excel интерпретирует формулу как “прибавить содержимое ячейки, расположенной тремя рядами выше, к содержимому ячейки, расположенной двумя рядами выше”.

Если вы скопировали формулу =В1+ B 2 из ячейки B 4 в С4, Excel также интерпретирует формулу как “прибавить содержимое ячейки, расположенной тремя рядами выше, к содержимому ячейки двумя рядами выше”. Таким образом, формула в ячейке С4 примет вид =С1+С2.

Если при копировании формул вы пожелаете сохранить ссылку на конкретную ячейку или область, то вам необходимо воспользоваться абсолютной адресацией. Для её задания необходимо перед именем столбца и перед номером строки ввести символ $. Например: B $4 или $ C 2. Тогда при копировании один параметр адреса изменяется, а другой — нет.

Задание 2. Заполните основную и вспомогательную таблицы

· 2. 1. Заполните шапку основной таблицы начиная с ячейки А1:

в ячейку А1 занесите N ;

в ячейку B 1 занесите X ;

в ячейку C 1 занесите K и т.д.

установите ширину столбцов такой, чтобы надписи были видны полностью.

· 2.2. Заполните вспомогательную таблицу начальными исходными данными начиная с ячейки H 1:

Табулирование функции представляет собой вычисление значения функции для каждого соответствующего аргумента, заданного с определенным шагом, в четко установленных границах. Эта процедура является инструментом для решения целого ряда задач. С её помощью можно локализовать корни уравнения, найти максимумы и минимумы, решать другие задачи. С помощью программы Excel выполнять табулирование намного проще, чем используя бумагу, ручку и калькулятор. Давайте выясним, как это делается в данном приложении.

Использование табулирования

Создание таблицы

Создаем шапку таблицы с колонками x, в которой будет указано значение аргумента, и f(x), где отобразится соответствующее значение функции. Для примера возьмем функцию f(x)=x^2+2x, хотя для процедуры табулирования может использоваться функция любого вида. Устанавливаем шаг (h) в размере 2. Граница от -10 до 10. Теперь нам нужно заполнить столбец аргументов, придерживаясь шага 2 в заданных границах.

В первую ячейку столбца «x» вписываем значение «-10». Сразу после этого жмем на кнопку Enter. Это очень важно, так как если вы попытаетесь произвести манипуляцию мышкой, то значение в ячейке превратится в формулу, а в данном случае это не нужно.

Таким образом, табуляция функции была проведена. На её основе мы можем выяснить, например, что минимум функции (0) достигается при значениях аргумента -2 и 0. Максимум функции в границах вариации аргумента от -10 до 10 достигается в точке, соответствующей аргументу 10, и составляет 120.

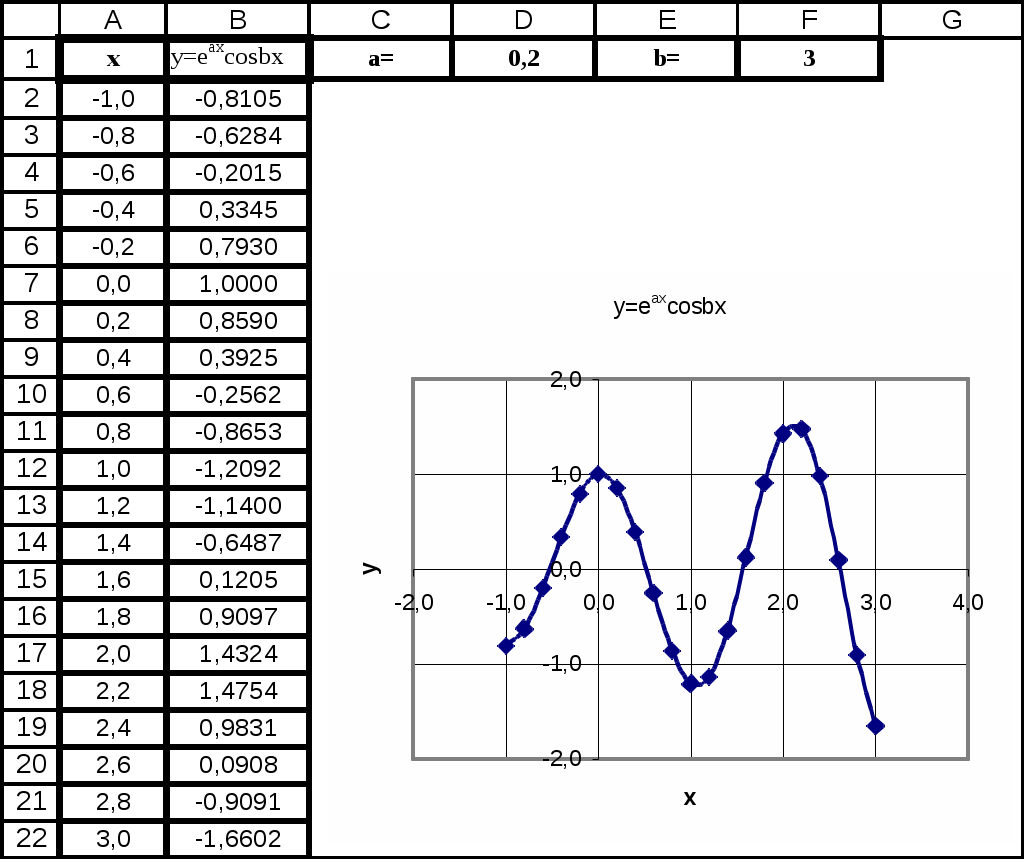
Построение графика

На основе произведенной табуляции в таблице можно построить график функции.

«Вставка»

«Диаграммы»

«Графики»

Далее по желанию пользователь может отредактировать график так, как считает нужным, используя для этих целей инструменты Excel. Можно добавить названия осей координат и графика в целом, убрать или переименовать легенду, удалить линию аргументов, и т.д.

Как видим, табулирование функции, в общем, процесс несложный. Правда, вычисления могут занять довольно большое время. Особенно, если границы аргументов очень широкие, а шаг маленький. Значительно сэкономить время помогут инструменты автозаполнения Excel. Кроме того, в этой же программе на основе полученного результата можно построить график для наглядного представления.

Мы рады, что смогли помочь Вам в решении проблемы.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Напомним, что ссылка вида A1 называется относительной. Относительная ссылка меняется при копировании формулы из одной ячейки в другую, так что сохраняется относительное расположение влияющих на формулу ячеек и ячейки, содержащей формулу. Это позволяет создать расчетные таблицы, содержащие повторяющиеся вычисления для данных, находящихся в различных ячейках.

Пример. В ячейку C3 введена формула =(A2+A3+A4)/3. При ее копировании в ячейку С4 получим формулу =(A3+A4+A5)/3. При копировании в ячейку F10 получим формулу =(D9+D10+D11)/3.
Просмотреть зависимые и влияющие ячейки можно с помощью панели Зависимости. Она вызывается по команде Вид|Панели инструментов|Настройка, вкладка Панели инструментов, установить флажок Зависимости. Затем выделяется ячейка с формулой. При нажатии кнопки Влияющие ячейки появляются стрелки от влияющих ячеек к зависимым. Кнопка Зависимые ячейки показывает, на какие ячейки с формулами влияет данная ячейка. Для снятия стрелок используется кнопка Убрать все стрелки.

Ссылка вида $A$1 называется абсолютной. При копировании формул абсолютные ссылки не меняются. Это позволяет использовать константы в повторяющихся вычислениях. Ссылка вида $A1 называется смешанной. При копировании формулы со ссылкой данного типа не меняется заголовок столбца, а номер строки может меняться. Наоборот, при использовании другой смешанной ссылки типа A$1 не меняется номер строки, а заголовок столбца может меняться.

1.2. Заполнение ячеек

Вычисление значений аргумента по типу арифметической или геометрической прогрессии. Порядок работы следующий: ввести первое значение в требуемую ячейку и выделить эту ячейку, вызвать команду Правка|Заполнить|Прогрессия . В ее диалоговом окне установить расположение данных (строки, столбцы), тип прогрессии, шаг изменения аргумента, предельное значение аргумента. После подтверждения команды (OK) столбец (или строка) будет заполнен. в направлении увеличения адресов.
Заполнение ячеек заголовками строк или столбцов вида Урок 1, Урок 2, и т.д. выполняется так: вводится первый заголовок, выделяется заполняемый диапазон ячеек и выполняется команда Правка|Заполнить|Прогрессия. В диалоговом окне команды выбирается Автозаполнение.
Возможно заполнение последовательных ячеек датами с заданным интервалом, названиями месяцев, дней недели, годов, часов. Предлагаем эту операцию освоить самостоятельно экспериментальным путем с помощью все той же команды Правка|Заполнить |Прогрессия.
Заполнение ячеек формулами разберем на примере построения таблицы значений функции. Предварительно отметим следующее: при копировании формул из одних ячеек в другие, обычные (так называемые относительные) ссылки на ячейки изменяются с сохранением структуры зависимости от исходных данных. Например, введем в ячейку B1 формулу =A1+5. При копировании формулы в нижележащую ячейку B2 она превращается в формулу =A2+5. Заполнение ячеек формулами есть не что иное, как копирование формул в последовательные ячейки таблицы. Оно выполняется следующим образом: формула вводится в первую ячейку ряда, затем нужно выделить диапазон для ввода формул и применить команду Правка|Заполнить| Вниз (или Вправо).

Замечание. Если ссылка на ячейку в формуле является абсолютной ($A$10), то при копировании формулы она не меняется. Например, формула =$A$10+A1 при копировании изменит ссылку лишь на ячейку A1.

Добавление . Можно быстрее выполнять команду заполнения с помощью Маркера заполнения. Данные типа арифметической прогрессии вводятся в две первые ячейки заполняемого ряда. Затем, выделив эти ячейки, нужно установить указатель мыши на Маркер заполнения — маленький черный квадрат в правом нижнем углу выделенного диапазона и протащить указатель вдоль заполняемого столбца до появления последнего значения. При отпускании мыши ряд будет заполнен данными. Заполнение ячеек формулой выполняется аналогично, но только еще проще — достаточно протащить формулу за маркер заполнения вдоль требуемого ряда.

2. Примеры построения таблиц значений и графиков функций

Пример 1. ( Функция одной переменной для шагового аргумента). Построить таблицу значений функции для аргумента x, изменяющегося от 0 до 1,5 с шагом 0,1. Построить график функции.

Решение. Решение разбивается на два основных этапа: построение таблицы значений функции и построение графика функции.

Наберем заголовки столбцов для x и y в ячейках A1, B1.
Наберем первое значение x, равное 0, в ячейку A2.
Выполним команду Правка|Заполнить|Прогрессия, зададим в диалоге Расположение в столбце, Арифметическая прогрессия, Шаг 0,1, Предельное значение 2. Заполнятся ячейки A4:A22.
В ячейку B2 введем формулу: =SIN(4*A2)^2/(A2+1) и скопируем ее в ячейки B3:B22
Выполним форматирование данных (чисел) и обрамление таблицы. Фрагмент рабочего листа с таблицей показан на рис.1.

Рис.1. Таблица значений функции для примера 1

Рис. 2. График (точечная диаграмма) примера 1
Рис. 2. График (точечная диаграмма) примера 1

Пример 2. (Функция, заданная различными аналитическими выражениями (сложная функция)). Построить таблицу значений и график функции

для аргумента x , изменяющегося от -2 до 2 с шагом 0,2

Решение

Построение таблицы. Решение выполним в том же файле, что и предыдущий пример, но на новом листе Excel. Последовательность заполнения ячеек аналогична примеру 1.

В ячейку B2 введем формулу:

=ЕСЛИ(A2 Рис . .4. График сложной функции

Рис. 3. Таблица значений сложной функции

остроение графика функции также полностью аналогично построению предыдущего примера, если заданная функция непрерывна.

Замечание. Если функция терпит разрыв при переходе от одного аналитического выражения к другому, то нужно построить на одной диаграмме два графика, каждый из которых отвечает области непрерывности функции. В случае разрывной функции можно строить один график, если выбрать вид графика из отдельных точек
Пример 3. (Функция, зависящая от параметра). Построить таблицу значений и график функции для аргумента x, изменяющегося от -1 до 3 с шагом 0,2 при заданных значениях a и b.

Решение

Введем заголовки столбцов для x и y в ячейки A1, B1 и значения a, b в отдельные ячейки D1, F1.
Заполним столбец A2:A22 значениями x.
Введем формулу для y в ячейку B2

Перейдем на новый рабочий лист.
Зададим заголовки столбцов t,x,y.
Заполним первый столбец значениями t, применив еще один способ задания аргумента: каждое последующее значение вычислим через предыдущее, добавляя шаг. В ячейке D2 вычислим по формуле =ПИ()/16. В ячейку A2 введем 0, в ячейку A3 введем формулу =A2+$D$2, которую копируем вниз до значения 2.
Введем в ячейку B2 формулу =COS(A2); в ячейку C2 формулу =SIN(A2)
Выделим ячейки B2, C2 и копируем их для всех значений t с помощью заполнения.
Форматируем таблицу по образцу.

Выделим диапазон B2:C23
Вызовем Мастер диаграмм и построим точечную диаграмму. В процессе построения зададим заголовки диаграммы и осей, уберем легенду, назначим линии сетки.
Затем отредактируем диаграмму: по команде Формат оси зададим точность – один знак после запятой, по команде Формат области построения укажем рамку Невидимая.
Выполним растяжение-сжатие диаграммы, так чтобы получилась окружность, а не эллипс.

Рис. 7. График функции, заданной параметрическими уравнениями

Рис.6. Таблица функции, заданной параметрическими уравнениями

Замечания

1. Несколько изменив уравнения (1) можем получить и параметрические уравнения эллипса. Как работать с функциями, содержащими постоянные параметры, было рассмотрено в предыдущем примере. Итак, эллипс с осями a, bзадается уравнениями:

где a, b — положительные константы

2. В примерах 1-3 были рассмотрены функции, заданные аналитически в явном виде, т.е. формулой, в которой зависимая переменная yвычислялась через независимую переменнуюx. Существует другой способ задания функции, в котором обе этих величины являются функциями одного и того же параметра t. Тогда каждому значению t соответствует пара значений (x, y), определяемых формулой

Предположим, что по каждому значению x=f(t) можно найти единственное значение t, которому в свою очередь можно сопоставить y=g(t). Тогда можно считать y функцией x. Такой способ задания функции называется параметрическим. Если рассматривать множество пар (x,y), определяемых уравнением (2) как множество точек на плоскости, то уже нет необходимости требовать единственности решения tпо x. И в этом случае считаем, что задана функция yот x параметрическими уравнениями (2). Может оказаться, что одному значению xсоответствует два или даже несколько значений y. В ряде случаев простые параметрические уравнения позволяют задать функции, для которых явные уравнения очень сложны или не существуют.

3. Функция, заданная в полярной системе координат, легко преобразуется к параметрической форме. Действительно, декартовы координаты x, yсвязаны с полярными координатами ,  уравнениями
(3)
Если задано уравнение кривой в полярной системе координат , то подставив это выражение в уравнения (3), получим параметрические уравнения кривой с полярным углом  в качестве параметра.

Читайте также:

Neoline x cop 9500 прошивка через usb

Mediatek da usb vcom port как прошить

Как из паттерна сделать сэмпл в fl studio

Как в эксель написать число без формулы

1с супа что это

Источник

Лабораторная работа №1 — Решение задачи табулирования функции с использованием Excel

Цель работы:
• закрепление навыков по заполнению и редактированию таблицы,
• ознакомление со способами адресации;
• освоение основных приемов оформления таблиц. Дальнейшее знакомство с Excel осуществим на примере задачи
табулирования функции. Постановка задачи:
Вычислить значения функции у=k*(х^{^}2-1)/(х^{^}2+1) всех х на интервале [-2,2] с шагом 0,2 при к=10.
Решение должно быть получено в виде таблицы:

1. Прежде чем перейти к выполнению задачи, познакомтись со способами адресации в Excel.
Абсолютная, относительная и смешанная адресация ячеек и блоков.
Относительная адресация. При обращении к ячейке можно использовать такие ссылки как D3, А1:Н9 и т.д. Такая адресация называется относительной. Относительные ссылки удобны при перемещении формул. При использовании подобной адресации в формулах, Excel запоминает расположение относительно текущей ячейки. Так, например, когда вы вводите формулу =D1+D2 в ячейку D4, то Excel интерпретирует формулу как «прибавить содержимое ячейки, расположенной тремя рядами выше, к содержимому ячейки двумя рядами выше».
Если вы скопировали формулу =D1+D2 из ячейки D4 в С4, Excel также интерпретирует формулу как «прибавить содержимое ячейки, расположенной тремя рядами выше». Таким образом, формула в ячейке С4 изменит свой вид на =С1+С2. Если вы скопировали формулу =D1+D2 из ячейки D4 в С4, Excel также интерпретирует формулу как «прибавить содержимое ячейки, расположенной тремя рядами выше». Таким образом, формула в ячейке С4 изменит свой вид на =С1+С2.
Абсолютная адресация. Если при копировании формул вы пожелаете сохранить ссылку на конкретную ячейку или область, вам необходимо воспользоваться абсолютной адресацией. Абсолютная ссылка формируется с помощью знака $. Запись $С$15 означает, что независимо от того, куда вы потом переместите формулу, она всегда будет искать значение, помешенное в ячейку С15.
Смешанная адресация. Символ $ ставится только там, где он необходим, например $C15 или C$15. Таким образом, можно зафиксировать столбец значений, но по мере перемещения менять строки ($С15) или зафиксировать строку и менять столбцы (С$15).
2. Заполните основную и вспомогательную таблицы.
2.1. Заполните шапку основной таблицы, начиная с ячейки A1:
Шапка — это верхняя строка таблицы с названием столбцов (см. постановку задачи):
• в ячейку А1 занесите № (название первого столбца таблицы);
• в ячейку B1 занесите х (название второго столбца таблицы);
• в ячейку С1 занесите k (название третьего столбца таблицы)
• в ячейку D1 занесите у1 =х^2-1 (название четвертого столбца таблицы);
• в ячейку E1 занесите у2=х^{^}2+1 (название пятого столбца таблицы);
• в ячейку F1 занесите y=k*(y1/y2) (название шестого столбца таблицы).
• установите ширину столбцов такой, чтобы надписи были видны полностью.
2.2. Заполните вспомогательную таблицу начальными исходными данными, начиная с ячейки H1:

где х0 — начальное значение x;
step — шаг изменения X;
k — коэффициент (const).
При решении задачи данный пункт табулирования функции является необязательным и введен искусственно для демонстрации способов адресации.
2.3. Используя функцию автозаполнения, заполните столбец А числами от 1 до 21, начиная с ячейки A2 и заканчивая ячейкой А22.
• Для этого в А2 наберите число 1, а в А3 число 2;
• Выделите блок А2:А3, затем установив указатель мыши в правый нижний угол этого блока, добейтесь появления черного крестика и, дотащив его до ячейки А22, отпустите.
2.4. Заполните столбец В значениями х:
• В ячейку В2 занесите =$h$2
Это означает, что в ячейку В2 заносится значение из ячейки Н2 (начальное значение х), знак $ указывает на абсолютную адресацию.
• В ячейку В3 занесите формулу =b2+$i$2
• В ячейку В4 занесите формулу =b3+$i$2
Это означает, что начальное значение будет увеличено на величину шага, которая берется из ячейки i2.
• Выделите блок B3:B4, заполните этой формулой ячейки В5:В22 (можно использовать функцию автозаполнения или перекопировать с помощью меню Правка/Копировать и Правка/Вставить, а также можно использовать кнопки Копирования и Вставки на панели инструментов Стандартная).
Столбец заполнится значениями x от -2 до 2 с шагом 0,2.
2.5. Заполните столбец С значениями коэффициента k:
• В ячейку С2 занесите =$j$2
• В ячейку С3 занесите формулу =c2
• заполните этой формулой ячейки С4:С22.
Весь столбец заполнился значением 10.
2.6. Заполните столбец D значениями функции у1=х^2-1
• в ячейку D2 занесите =b2*b2-1,
• заполните этой формулой ячейки D3:D22.
Столбец заполнился как положительными, так и отрицательными значениями функции y1. Начальное значение 3 и конечное значение 3.
2.7. Аналогичным образом заполните столбец Е значениями функции у2=х^{^}2+1.
Проверьте! Все значения положительные: начальное 5, конечное 5.
2.8. Заполните столбец F значениями функции у=k*(х^{^}2-1)/(х^{^}2+1)
• в ячейку F2 занесите =c2*(d2/e2),
• заполните этой формулой ячейки F2:F22.
Проверьте! Значение функции как положительные, так и отрицательные. Начальное значение 6, конечное 6.
3. Понаблюдайте за изменениями в основной таблице при смене данных во вспомогательной.
3.1. Смените во вспомогательной таблице начальное значение x, в ячейку H2 занесите -5.
3.1. Смените значение шага, для этого в ячейку i2 занесите 2.
3.3. Смените значение коэффициента, для этого в ячейку J2 занесите 1.
Внимание! При всех изменениях данных во вспомогательной таблице в основной таблице пересчет производится автоматически.
3.4. Прежде чем продолжим работу, верните прежние начальные значения во вспомогательной таблице:
x0 = -2 step = 0,2 k = 10

4. Оформите основную и вспомогательную таблицы.
4.1. Вставьте 2 пустые строки сверху дли оформления заголовков:
• установите курсор на 1 строку;
• выполните команды меню Вставить, Строки на лист (2 раза) или нажмите на первую строку правой кнопкай мыщи, команда Вставить.
4.2. Занесите заголовки:
• в ячейку А1 занесите слово «Таблицы»,
• в ячейку А2 занесите слово «Основная»,
• в ячейку H2 зaнесите слово «Вспомогательная».
4.3. Объедините ячейки A1:J1 и центрируйте заголовок «Таблицы»:
• выделите блок А1:J1, используйте кнопку «центрировать по столбцам» панели инструментов форматирование
4.4. Аналогичным образом центрируйте заголовки: «основная» и «вспомогательная».
4.5. Оформите заголовки определенными шрифтами:
Символы (шрифты)
(Символы любой ячейки или блока можно оформить различными шрифтами, начертанием, высотой и т.д. Дли выполнения этих действий необходимо выделить ячейку или блок, а затем воспользоваться кнопками из панели инструментов
Тип шрифта –
Размер –
Форматирование: Начертание
(жирный, курсив,

подчеркивание

)
• для заголовка «Таблицы» установите шрифт Arial, высота шрифта 14, полужирный.
• для заголовка «Основная» и «Вспомогательная» установите шрифт Arial, высота шрифта 12, полужирный.
• Для шапок таблиц установите шрифт Arial, высота шрифта 12, курсив. Используйте контекстное меню.
4.6. Подгоните ширину столбцов так, чтобы текст помешался полностью.
4.7. Произведите выравнивание надписей шапок по центру.
Выравнивание.
Содержимое любой ячейки можно выровнять внутри по одному из краев или по центру, как по горизонтали, так и по вертикали, а также можно задать необходимую ориентацию текста (снизу-вверх, сверху вниз и т.д.)
Для задания необходимой ориентации используются кнопки на панели инструментов Форматирование
(Выровнить влево, Выровнить по центру, Выровнить вправо).
Можно воспользоваться командой меню Формат, Ячейки или щелкнуть правой кнопкой мыши и выбрать эту команду из контекстного меню. На экране появится диалоговое окно Формат ячеек. В нем необходимо раскрыть вкладку Выравнивание.
4.8. Обрамите основную вспомогательную таблицы.
Обрамление
Для задания обрамления используется кнопка па панели Форматированы;
Можно использовать команду меню Формат, Ячейки, вкладка Рамка или аналогичную команду контекстного меню.
4.9. Задайте фон заполнения внутри таблиц — желтый, фон заполнения шапок таблиц-малиновый.
Фон
Содержимое любой ячейки или блока может иметь необходимый фон (тип штриховки, цвет штриховки, цвет фона).
Для задания фона используется кнопка панели Форматирование
Можно использовать команду меню Формат, Ячейки, вкладка Вид, или
аналогичную команду контекстного меню.
5. Сохраните результаты своей работы на диске, в личном каталоге. Имя файла — Задание1_1.xls
6. Завершите работу в excel
В результате должна получится следующая таблица:
Самоконтроль. Проверьте, что такое:
• относительная адресация;
• абсолютная адресация;
• смешанная адресация.
Умеете ли вы:
• использовать различные способы адресации;
• оформлять символы;
• производить выравнивание и обрамление;
• изменять фон.
Рекомендации с целью закрепления темы:
• внимательно перечитайте соответствующие разделы работы.
Представьте учителю:
1. краткий конспект;
2. файл Задание1_1.xls на экране и на рабочем диске в личном каталоге.

Лабораторная работа № 2 — Функции в Excel. Форматирование чисел. Защита информации в таблицах.

Цель работы:
• познакомиться с использованием функций в Excel;
• познакомиться с форматами чисел;
• научиться осуществлять защиту информации в таблице;
1. Откройте файл Задание1_1.xls, созданный при выполнении лабораторной работы №1.
2. Защитите в таблице информацию, которая не изменяется (заголовки, полностью основную таблицу, шапку вспомогательной таблицы).
Защита ячеек, листов и книг от несанкционированного доступа.
Если после больших усилий по созданию и форматированию листа, вам не захочется, чтобы кто-то по невнимательности свел эти усилия на нет, если вы не хотите, чтобы случайный пользователь внес путаницу в ваши формы или вы хотели бы держать ваши данные и расчеты в тайне от других пользователей полезно защитить данные.
В Excel можно защитить от изменения всю рабочую книгу, лист или некоторые ячейки. Защита блокирует каждую ячейку и делает невозможным изменение информации, пока защита не будет снята. Обычно защищают данные, которые не должны изменяться (расчетные формулы, заголовки, шапки таблиц).
Иногда возникает необходимость оставить несколько ячеек или диапазоны не защищенными на защищенном листе, например, для ввода исходных данных. Перед тем как защитить лист, необходимо зафиксировать не защищаемые ячейки. Для этого следует выделить ячейку или диапазон, затем зайти в контекстное меню Формат ячеек и перейти на вкладку Защита. По умолчанию для каждой ячейки устанавливается режим Защищаемая ячейка. Надо разблокировать ячейки, убрав метку с этого переключателя. В результате выбранные ячейки останутся незаблокированными после включения защиты всего листа.
Таким образом, установка или снятие защиты выполняется за два действия:
• отключают блокировку или защиту с ячеек, подлежащих последующей корректировке;
• включают защиту листа или книги.
После этих действий можно корректировать и заполнять только те ячейки, которые ранее были разблокированы.
Разблокировки (блокировка) ячеек.
Необходимо выделить необходимый блок и выполним, команду Формат ячеек, Защита, а затем в диалоговом окне выключить (включить) параметр Защищаемая ячейка.
Включение (снятие) защиты с листа или книги.
Далее нужно выполнить команду Рецензирование, Защитить лист (книгу).
На экране предоставляется на выбор несколько вариантов зашиты от несанкционированного доступа:
• Установка метки на переключателе Защитить лист и содержимое защищаемых ячеек.
• Установка метки на переключателе Выделение заблокированных ячеек.
• Установка метки на переключателе Выделение незаблокированных ячеек.
• Установка метки на переключателе Изменение объектов.
• Установка метки на переключателе Изменение сценариев.
В поле пароль можно ввести пароль для защиты. Если лист защищен паролем, то снять защиту без указания пароля будет невозможно. Но если был введен пароль, то следует его запомнить.
После установки этих меток надо нажать на ОК для активизации защиты, (для отклонения — команду Рецензирование, Снять защиту листа (книги)).
• Установка метки на переключателе Окна защищает окно книги, предотвращая перемещение, изменение размеров, скрытие, показ и закрытие окон.
Введение пароля предотвращает несанкционированное снятие защиты с книги, при вводе пароля разрешаются строчные и прописные символы, пароль может содержать до 255 символов и содержать любое сочетание букв, цифр и других символов.
После установки этих меток надо нажать на ОК для активизации защиты.
2.1. Выделите блок H4:J4 и снимите блокировку.
Меню: Формат ячеек, Защита, Выключить параметр Защищаемая ячейка то есть убрать знак ٧ напротив этой записи.
2.2. Защитите лист.
Меню: Рецензирование, Защитить лист, ОК.
В результате действий заблокируется вся основная таблица и шапка вспомогательной.
2.3. Попробуйте изменить значения в ячейках:
• в ячейке А4 с 1 на 10.
Это невозможно.
• значение шага во вспомогательной таблице с 0,2 на 0,5.
Это возможно. В основной таблице произошел пересчет.
• измените текст «step» в ячейке i3 на текст «шаг».
Какой результат? Почему?
• верните начальное значение шага 0,2.
3. Сохраните файл под старым именем
Воспользуйтесь кнопкой Сохранить на панели инструментов.
4. Снимите защиту с листа
Меню: Рецензирование, Снять защиту листа.
5. Познакомьтесь с функциями пакета Excel
Работа с функциями
Большая ценность Excel заключается во встроенном наборе математических, финансовых, статистических и логических функций. Если ввести некоторый набор чисел, то Excel может обработать их более чем 300 различными способами, от простого подсчета среднего значения до вычисления сложных тригонометрических зависимостей.
Функция Excel — это специальная формула хранящаяся в памяти программы. Каждая функция включает две части: имя функции (например, СУММ) и ее аргументы. Аргументы — это данные, которые используются функцией для получения результата. Аргументом функции могут быть ссылки или имена, текст или числа, дата или время. Аргументы всегда появляются в круглых скобках справа от имени функции.
Таким образом, функции предназначены для упрощения расчетов и имеют следующую форму: Y=f(x), где у— результат вычисления функции, x — аргумент, f — функция.
Пример содержимого ячейки с функцией:
=A5 + sin(C7), где
А5-адрес ячейки;
sin — имя функции, в круглых скобках указывается аргумент;
С7 — аргумент (число, текст, и т.д.) в данном случае ссылка на ячейку, содержащую число.
Скобки — обязательная принадлежность функции, даже если у нее нет аргументов. Некоторые функции:

Например, СУММ(А1:А300)=> подсчитает сумму чисел в трехстах ячейках диапазона А1:A300.
Так как функция суммирования часто используется, то за ней закреплена кнопка на панели инструментов
Для вставки функции в формулу можно воспользоваться Мастером функций, вызываемым командой меню Формулы, Вставить функцию. Появится диалоговое окно, в котором необходимо выбрать функцию, а затем нажать на кнопку ОК.
Второе диалоговое окно (второй шаг Мастера функций) позволяет задать аргументы к выбранной функции. Ого панель формул.
На панели отображены определение функции и ее аргументы. В текстовом поле Число 1 можно ввести число, ссылку на ячейку, имя, формулу или другую
функцию.
5.1. Нажмите кнопку или . Выберите категорию Полный алфавитный перечень.
Посмотрите с помощью линейки просмотра, каким огромным арсеналом функции располагает Excel. Закройте окно функций.
5.2. Подсчитайте сумму вычисленных значений y и запишите ее в ячейку F25.
• сделайте текущей ячейку F25;
щелкните по кнопке ;
Вычисление суммы — часто используемая операция. Она закреплена за кнопкой на панели инструментов.
• в ячейку E25 запишите поясняющий текст Сумма у=
5.3. Оформите нахождение среднего арифметического вычисленных значений у.
• сделайте текущей ячейку F26;
щелкните по кнопке ;
в диалоговом окне выберите категорию функции
Полный алфавитный перечень и имя функции СРЗНАЧ;
щелкните по кнопке OK;
• в появившимся диалоговом окне укажите диапазон, в котором вычисляется среднее значение (F4:F24).
Это можно сделать двумя способами:
• набрав диапазон вручную в окне Число1;
• на панели формул щелкните на кнопке с красной стрелкой в правом конце текстового поля Число1, чтобы свернуть панель в одну строку. Затем необходимо выделить нужный диапазон ячеек. И обратно щелкнуть на кнопке с красной стрелкой, чтобы восстановить прежний размер панели.
• щелкните по кнопке ОК;
• занесите в ячейку Е26 поясняющий текст, а в F26- среднее значение.
5.4. Оформите нахождение минимального и максимального значений y, для этого занесите в ячейку Е27 и E28 поясняющий текст, а в ячейки F27 и F28 минимальное и максимальное значения.
Если имя функции известно, то ее можно вставить в формулу без использования Мастера функции, например =MAKC(F4:F24)
6. Оформите блок ячеек E25:F28
6.1. Сделайте обрамление блока E25:F28.
6.2. Заполните этот блок фоном шапки таблицы.
6.3. Поясняющие подписи в ячейках Е25:Е28 оформите жирным шрифтом типа Arial c выравниванием вправо.
7. Сохраните файл под новым именем Задание1_2.
8. Познакомимся с форматами чисел в Excel.
Выбор форматов для чисел
Одним из основных назначений Excel является обработка чисел и представление числовых значений. Поэтому в Excel предусмотрено множество способов отображения чисел. Все эти способы четко классифицированы по категориям. Число в ячейке можно представить в различных форматах.
Например, число 100 будет выглядеть как:
100,00 р. — в денежном формате;
10000% — в процентном выражении;
1,00Е+2 — в экспоненциальной форме, что означает 1 * 10².
Для задания формата числа необходимо выделить ячейку или блок, а затем воспользоваться кнопками из панели инструментов Форматирование
Лучше воспользоваться командой меню Формат ячеек или щелкнуть правой кнопкой мыши и выбрать эту команду из контекстного меню. На экране появится диалоговое окно Формат ячеек. В нем необходимо раскрыть вкладку Число и выбрать желаемый формат.
При изменении формата числа ячейки изменяется только способ представления данных в ячейке. но не сами данные.
Если в ячейке отображается набор символов в виде #####, то это означает, что столбец недостаточно широк для отображения числа целиком в установленном формате. Его следует расширить.
8.1. Установите масштаб 75%.
Для чего надо войти в меню Вид и выбрать команду Масштаб и установить в окне Масштаб переключатель на 75%.
8.2. Скопируйте значения y из столбца F в столбцы K, L, M, N.
Столбец F заполнен формулами, а скопировать требуется значения.
• выделите столбец F;
подведите курсор к границе выделенного (он должен принять форму черного крестика со стрелками на концах);
• нажмите правую кнопку мыши и держите ее;
буксируйте блок с помощью мыши до столбца K;
• отпустите кнопку мыши;
• в открывшемся контекстно-зависимом меню выберите команду Копировать только значения.
При этом столбец К заполнится теми же значениями, что и столбец F, но он не будет содержать формул.
• заполните значениями столбца К столбцы L, М, N.
8.3. В столбце К задайте формат, в котором отражаются 2 значащие цифры после запятой 0,00.
8.4. В столбце L задайте Экспоненциальный формат.
8.5. В столбце М задайте формат Процент.
8.6. В столбце N установите финансовый формат 4 знак после запятой:
Меню: Формат ячеек, Число
В поле Тип следует набрать 0,0000 и OK
8.7. Оформите блок К2:N24 в стиле оформления основной и вспомогательной таблиц (заголовок, обрамление, заполнение, шрифт).
В результате должна получится следующая таблица:

9. Предъявите результат работы преподавателю.

10. Сохраните файл под старым именем Задание1_2.хls

Лабораторная работа №3 — Формирование промежуточных итогов.

Цель: Научиться формировать промежуточные итоги
Задание:
1. Создать табличный документ.
2. Выполнить сортировку диапазона данных.
3. Применить функции, обслуживающие промежуточные итоги.
4. Вывести промежуточные итоги на печать.
Теоретические сведения
Microsoft Excel может автоматически вычислять промежуточные и общие итоги в списке. При вставке автоматических промежуточных итогов Microsoft Excel изменяет разметку списка, что позволяет отображать и скрывать строки каждого промежуточного итога.
Перед тем как вставить промежуточные итоги, необходимо отсортировать список, чтобы сгруппировать строки, по которым нужно подвести итоги. После этого можно подсчитать промежуточные итоги любого столбца, содержащего числа. В Excel для решения подобных задач предназначена функция автоматического вычисления итогов, которая вызывается командой Итоги меню Данные.
Если данные не организованы в виде списка или если требуется подвести один промежуточный итог, вместо автоматических промежуточных итогов можно использовать Автосумму.
Контрольный пример
Задание 1: Создайте табличный документ, содержащий список организаций и товаров, которые они приобретали, на основе рис.1.

Рис.1.
Задание 2. Отсортируйте данные по организациям. Для этого:
— выделите диапазон всей таблицы (А2:F10);
— выполните команду Данные – Сортировка;
— в открывшемся диалоговом окне Сортировка диапазона в поле Сортировать по выберите поле Организация, выберите порядок от А до Я (по возрастанию);
— нажмите кнопку OK.
Задание 3. В созданной таблице вычислите промежуточные итоги сумм, потраченных каждой организацией и итоговой сумме. Для этого:
— выделите диапазон всей таблицы (А2:F10);
— выполните команду Данные – Промежуточные итоги;
— в открывшемся диалоговом окне Промежуточные итоги в поле При каждом изменении в выберите поле Организация;
— в поле Операция выберите операцию Сумма;
— в поле Добавить итоги по поставьте галочку в поле Сумма (тенге);
— поставьте галочки для полей Заменить текущие итоги и Итоги по данным;
— нажмите кнопку OK. В результате ваша таблица примет вид:

Лабораторная работа №4 — Консолидация табличных данных

Цель: Изучить функции консолидации
Задание:
1 Изучить использование меток при консолидации.
2 Задать параметры консолидации.
Теоретические сведения
При консолидации данных объединяются значения из нескольких диапазонов данных. Например, если имеется лист расходов для каждого регионального представительства, консолидацию можно использовать для преобразования этих данных в лист корпоративных расходов.
Консолидация выполняется командой Консолидация меню Данные.
Консолидацию по расположению следует использовать в случае, если данные всех исходных областей находятся в одном месте и размещены в одинаковом порядке; например, если имеются данные из нескольких листов, созданных на основе одного шаблона.
Если установлено автоматическое обновление консолидации при изменении исходных данных, изменить набор ячеек и диапазонов, входящих в консолидацию, невозможно. Данная функция доступна только при обновлении консолидации вручную.
Консолидацию по категории следует использовать в случае, если требуется обобщить набор листов, имеющих одинаковые заголовки рядов и столбцов, но различную организацию данных. Этот способ позволяет консолидировать данные с одинаковыми заголовками со всех листов.
Если установлено автоматическое обновление консолидации при изменении исходных данных, изменить набор ячеек и диапазонов, входящих в консолидацию, невозможно. Данная функция доступна только при обновлении консолидации вручную.
Контрольный пример
Задание 1: Создать консолидацию данных по расположению на основе представленных таблиц (рис 4.1, рис. 4.2). Для этого:

Рис. 4.1. Таблица «Отчет заработной платы за март»

Рис. 4.2. Таблица «Отчет заработной платы за апрель»

— создайте рабочую книгу с именем Консолидация;
— Лист1 переименуйте на Консолидация по расположению и создайте на этом листе две таблицы в соответствии с рис.4.1 и рис. 4.2;
Расчет столбца Проф. взносы: =Оклад*5%;
Расчет столбца Пенсионные отчисления: =Оклад*10%;
Расчет столбца Индивидуальный подоход. налог: =(Оклад-Пенсионные отчисления-МЗП)*10% (МЗП с 2022 года равен 60000тг.);
Расчет столбца Мед. страховка: =Оклад*2%.
— поставьте курсор в ячейку А14;
— выполните команду Данные – Консолидация;
— в поле Функция выберите Сумма;
— поместите курсор в поле Ссылка и выделите диапазон первой таблицы (вместе с «шапкой», A2:H10);
— нажмите кнопку Добавить;
— поместите курсор в поле Ссылка и выделите диапазон второй таблицы (вместе с «шапкой», J2:Q10);
— нажмите кнопку Добавить;
— поставьте галочки Подписи верхней строки и Значения левого столбца;- нажмите кнопку OK.
Задание 2: Создать консолидацию данных по категории. Для этого:
— Лист2 переименуйте на Консолидация по категории и создайте на этом листе две таблицы в соответствии с рис.4.1 и рис. 4.2;
— во вторую таблицу добавьте Маркова и его данные.
— выполните консолидацию, повторив действия из задания 1, но с поправкой на добавленного сотрудника.

Лабораторная работа №5 — ИТ использования таблиц подстановки.

Цель: Научиться разрабатывать таблицу подстановки
Задание:
1. Изучить виды подстановки значений.
2. Создание таблицы подстановки с несколькими переменными.
3. Сохранение таблицу подстановки.
Теоретические сведения
Таблица данных (таблица подстановок) — диапазон ячеек, содержащий результаты подстановки различных значений в одну или несколько формул. Существует два типа таблиц данных: таблицы с одним входом и таблицы с двумя входами.
Создание таблицы подстановки с одной переменной
Следует сформировать таблицу подстановки с одной переменной, чтобы введенные значения были расположены либо в столбце (ориентированные по столбцу), либо в строке (ориентированные по строке). Формулы, используемые в таблицах подстановки с одной переменной, должны ссылаться на ячейку ввода.
1. Либо в отдельный столбец, либо в отдельную строку введите список значений, которые следует подставлять в ячейку ввода.
2. Выполните одно из следующих действий.
— Если значения в таблице подстановки ориентированы по столбцу, введите формулу в ячейку, расположенную на одну строку выше и на одну ячейку правее первого значения. Правее первой формулы введите любые другие формулы.
— Если значения в таблице подстановки ориентированы по строке, введите формулу в ячейку, расположенную на один столбец левее и на одну строку ниже первого значения. В том же столбце, но ниже введите любые другие формулы.
3. Выделите диапазон ячеек, содержащий формулы и значения подстановки.
4. В меню Данные выберите команду Таблица.
5. Выполните одно из следующих действий:
— если значения в таблице расположены по столбцам, введите ссылку на ячейку ввода в поле Подставлять значения по строкам в;
— если значения в таблице расположены по строкам, введите ссылку на ячейку ввода в поле Подставлять значения по столбцам в.
6. Нажмите кнопку OK.
Создание таблицы подстановки с двумя переменными
Таблицы подстановки с двумя переменными используют одну формулу с двумя наборами значений. Формула должна ссылаться на две различные ячейки ввода.
1. В ячейку листа введите формулу, которая ссылается на две ячейки ввода.
2. В том же столбце ниже формулы введите значения подстановки для первой переменной.
3. Введите значения подстановки для второй переменной правее формулы в той же строке.
4. Выделите диапазон ячеек, содержащий формулу и оба набора данных подстановки.
5. В меню Данные выберите команду Таблица подстановки.
6. В поле Подставлять значения по столбцам в введите ссылку на ячейку ввода для значений подстановки в строке.
7. В поле Подставлять значения по строкам в введите ссылку на ячейку ввода для значений подстановки в столбце.
8. Нажмите кнопку OK.

Контрольный пример
Задание 1: Вы берете кредит в 188444,74 тенге на 20 лет с процентной ставкой 3% годовых. Посчитать коэффициент наращивания и сумму выплат при условии, что процентная ставка может варьироваться от 3% до 6,5% годовых. Для этого:
— создайте рабочую книгу с именем и Лист1 переименуйте на Таблица подстановок
— расположите данные задачи в соответствии с рис. 5.1;

Рис. 5.1
— значение ячейки B7 и E2 =(1+В5)^B3;
— значение ячейки B10 =B7*B1;
— значение ячейки F2 =E2*B1;
— столбец процент содержит возможные значения процентной ставки;
— выделите диапазон с подстановками и формулами (D2:F16);
— выполните команду Данные /Анализ «что если»/Таблица данных;
— в поле Подставлять значения по строкам в укажите ячейку с процентной ставкой, т.е. B5;
— нажмите кнопку OK. В результате должно получиться (см. Рис 5.2)

Рис. 5.2

Лабораторная работа № 6 — Графические возможности Excel. Построение диаграмм.

Цель работы:
— Ознакомиться с различными типами диаграмм и графиков и научиться их строить;
— Освоить основные приемы редактирования и оформления диаграмм;
— Научиться выводить на печать диаграммы.
1.1 Используя данные следующей таблицы, построить диаграммы вида а, б.

1.2 Используя данные следующей таблицы, построить диаграммы вида а, б, в и г.

1.3 Используя данные следующей таблицы, построить диаграммы вида а, б, в.

1.4 Используя данные следующей таблицы, построить указанную диаграмму.

Лабораторная работа № 7 — Работа с электронной таблицей как с базой данных.

Цель работы:
— Ознакомиться с использованием электронной таблицы как базы данных;
— Научиться осуществлять поиск информации в базе данных по различным критериям;
— Научится производить сортировку информации.

Заполните таблицу, содержащую информацию о планетах солнечной системы, согласно рисунку 7.1, и сохраните ее на Листе1. Скопируйте данную таблицу в Лист2 по Лист6

Рис. 7.1

Единицы измерения, используемые в таблице:
— Период обращения по орбите;
— Среднее расстояние от Солнца, млн. км.;
— Экваториальный диаметр тыс. км.;
— Масса – х 10²⁴ кг
Основные понятия базы данных
Область таблицы A2:F12 можно рассматривать как базу данных. Столбцы A, B, C, D, E, F этой таблицы называются полями а строки 3-12 называются записями. Область A2:F12 содержит имена полей.
Существуют ограничения накладываемые, на структуру базы данных:
— Первый ряд базы данных должен содержать неповторяющиеся имена полей;
— Остальные ряды базы данных содержат записи, которые не должны быть пустыми рядами;
— Информация по полям (столбцам) должна быть однородной, то есть только цифры или только текст.
Основная функция любой базы данных – поиск информации по определенным критериям. С увеличением количества записей поиск определенной информации затрудняется. Excel позволяет упростить этот процесс путем фильтрации данных.

Фильтрация записей
С помощью команды Главная, Сортировка и фильтр, Фильтр можно выделить (фильтровать) нужные записи. Фильтрацию можно осуществить как через автоматический фильтр Автофильтр, так и через Расширенный фильтр – ручной фильтр.

Автофильтр
При использовании Автофильтра необходимо переместить курсор в область базы данных или выделить ее. Затем следует выполнить команды: Главная, Сортировка и фильтр, Фильтр. На именах полей появятся кнопки с изображением стрелок вниз . Используя эти кнопки можно задавать критерии фильтрации. В появляющемся подменю пункт (Выделить все) отключает фильтрацию (Рис. 7.2), а пункт (Текстовые фильтры) вызывает диалоговое окно, в котором можно установить параметры фильтрации (Рис. 7.3). Для одного поля могут быть заданы два условия одновременно, связанные логическим И или ИЛИ.

Рис. 7.2

Рис. 7.3

Задание 1. Перейти в Лист1. С использованием Автофильтра осуществите поиск планет, начинающиеся на букву «С» или букву «Ю» с массой не менее 600*10²⁴ кг. Для этого:
1.1 Выделите таблицу и выполните команды: Главная, Сортировка и фильтр, Фильтр.
На полях базы данных появились кнопки
1.2 Нажмите на кнопку на поле Планеты и выберите пункт (Текстовые фильтры, Настраиваемый фильтр).
1.3 В диалоговом окне Пользовательский автофильтр задайте критерии согласно рисунку 7.3 и нажмите на кнопку ОК.
Проверьте! В базе данных остались планеты: Солнце, Юпитер и Сатурн.

1.4 Нажмите на кнопку на поле Масса, выберите пункт (Текстовые фильтры, Настраиваемый фильтр).
1.5 В диалоговом окне Пользовательский автофильтр задайте критерии: в поле Масса нажмите на кнопку , следует выделить условие меньше, а справа набрать число 600.
Проверьте! Остался только Сатурн.

Рис. 7.4

Задание 2. Перейти в Лист2. С использованием Автофильтра самостоятельно:
Осуществите поиск планет, имеющих экваториальный диаметр менее 50 тыс. км. и массу менее 4*10²⁴ кг (см. Рис. 7.5 и Рис. 7.6).
Проверьте! В базе данных остались планеты: Меркурий, Марс и Плутон.

Рис. 7.5

Рис. 7.6

Задание 3. Перейти в Лист3. Осуществите поиск планет, находящихся от Солнца на расстоянии не менее 100 млн. км, имеющих массу в диапазоне от 3*10²⁴ до 500*10²⁴ кг, а так же не более 2-х спутников (см. Рис. 7.7, Рис. 7.8 и Рис. 7.9).
Проверьте! В базе данных остались планеты: Венера, Земля и Нептун.

Рис. 7.7

Рис. 7.8

Рис. 7.9
Выполните команды меню: Главная, Сортировка и фильтр, Очистить.

Расширенный фильтр
При использовании Расширенного фильтра необходимо сначала определить (создать) три области (Рис 7.10):
интервал списка – эта область базы данных (A2:F12);
интервал критериев – эта область, где задаются критерии фильтрации (A14:F15);
интервал извлечения – эта область, в котором будет отражаться результаты фильтрации (A17:F21).
Имена полей во всех интервалах должны совпадать.
Для выполнения действий по фильтрации необходимо воспользоваться командами меню: Данные, Фильтр, Дополнительно. В появившемся на экране диалоговом окне Расширенный фильтр (Рис 7.11) надо указать координаты интервалов.
Если необходимо получить результаты фильтрации в интервале извлечения, то нужно установить переключатель – скопировать результат в другое место (Рис 7.11).

Рис. 7.10

Рис. 7.11

Задание 4. Перейти в Лист4. С использованием Расширенного фильтра осуществить поиск планет с периодам обращения более 10 земных лет и количеством спутников не менее 2.
Для этого:
4.1 Создайте интервал критериев и интервал извлечения (см. Рис 7.10).
4.2 Запишите критерии поиска в интервал критериев (см. Рис 7.10).
4.3 Поместите курсор в область базы данных, то есть в интервал A2:F12.
4.4 Выполните команды Данные, Фильтр, Дополнительно.
4.5 В диалоговом окне Расширенный фильтр установите переключатель – скопировать результат в другое место (см. Рис 7.11).
4.6 Проверьте правильность задания интервалов (см. Рис 7.11), и нажмите кнопку ОК.
Проверьте! Найдены планеты: Юпитер, Сатурн, Уран, Нептун.

Задание 5. С использованием Расширенного фильтра самостоятельно:
Перейти в Лист5. Скопируйте имена полей в 14-ю и 17-ю строки (см. Рис 7.10)
Найдите планеты, имеющие период обращения более 2-х земных лет и экваториальный диаметр менее 50 –ти тыс. км.
Проверьте! Найдены планеты: Уран и Плутон. (см. Рис 7.12)

Рис. 7.12

Задание 6. Перейти в Лист6. Скопируйте имена полей в 14-ю и 17-ю строки (см. Рис 7.10)
Осуществите поиск планет, находящихся от Солнца более 1000 млн. км и имеющих более 1-го спутника.
Проверьте! Найдены планеты: Сатурн, Уран и Нептун. (см. Рис 7.13)

Рис. 7.13

Лабораторная работа №8 — Анализ данных с помощью сводных таблиц

Цель: Изучить правила создания сводных таблиц и работы с данными в них.
Задание:
1. Создать табличный документ.
2. Запустить Мастер сводных таблиц.
3. Выполнить работу с данными в сводной таблице.
4. Изучить панель инструментов Запрос и сводная таблица.
5. Выполнить редактирование сценария.
6. Выполнить фильтрацию данных в сводной таблице
Теоретические сведения
Сводная таблица позволяет анализировать, обобщать, манипулировать данными, содержащихся в больших списках, базах данных, рабочих книгах, таблицах или других коллекциях данных. Сводные таблицы предлагают гибкий и интуитивный способ анализа данных. Сводная таблица связана с исходными данными. Однако можно изменить форматирование и произвести вычисления.
Сводная таблица нужна, например, для того чтобы узнать насколько хорошо продается тот или иной товар в каждом регионе. Сводную таблицу можно создать из нескольких источников. Чаще всего она создается на основе списка или базы данных Excel.
Контрольный пример
Задание 1. Создать сводную таблицу для отчетов о том, по какой цене был отдан тот или иной продукт фирмам-потребителям. Для этого:
— создать заданную таблицу в Excel на Лист1 и переименуйте на Сводн_табл. Для ускорения работы использовать копирование и автозаполнение данных. ПосчитайтеСумму;

Рис. 8.1.

— вызовите Мастер сводных таблиц, выполнив команду Данные→Сводная таблица;
— в появившемся окне установите переключатель в положение в списке или базе данных Microsoft Excel, щелкните по кнопке Далее;
— укажите диапазон, содержащий исходные данные (выделите всю таблицу с данными), щелкните по кнопке Далее, в следующем окне выберите переключатель в положение Новый лист;
— нажмите кнопку Макет;
— в появившемся диалоговом окне, в котором создается структура сводной таблицы, выбрать поле, по которому будут подводиться итоги сводных таблиц, и перетащить кнопку, соответствующую этому полю, в область Данные (перетащите кнопку Цена в область Данные);
— двойной щелчок по кнопке Цена в области Данные приведет к отображению диалогового окна Вычисление поля сводной таблицы, которое позволяет установить операцию, на основе которой будут подводиться итоги (выбрать операцию Сумма). Нажмите кнопку OK;
— выбрать поля, которые будут образовывать строки сводной таблицы, и перетащить кнопки, соответствующие этим полям, в область Строка. Перетащить кнопкуПолучатель в область Строка;
— выбрать поля, которые будут образовывать столбцы сводной таблицы, и перетащить кнопки, соответствующие этим полям, в область Столбец. Перетащить кнопку Месяц в область Столбец. Кнопка OK;
— выберите Поместить таблицу в новый лист. Кнопка Готово;
— Получена сводная таблица, в которой рядом с названиями полей есть кнопки, открывающие списки. С их помощью можно производить выбор отображаемых данных в таблице.
— Для перерасчета сводной таблицы, если изменились данные, на основе которых строилась эта сводная таблица, выделить ее и выполнить командуДанные→Обновить данные.
— Проиллюстрируйте данные полученной сводной таблицы на графике.

Лабораторная работа №9 — Использования диспетчера сценариев.

Цель: Изучить правила разработки сценария анализа данных.
Задание:
1. Создать табличный документ.
2. Произвести условный анализ данных.
3. Разработать сценарий.
4. Произвести работу с диспетчером сценариев.
5. Выполнить редактирование сценария.
6. Создать итоговый отчет
Теоретические сведения
Сценарии являются частью блока задач, который иногда называют инструментами анализа «что-если». Сценарий — это набор значений, которые Microsoft Excel сохраняет и может автоматически подставлять на листе. Сценарии можно использовать для прогноза результатов моделей и систем расчетов. Существует возможность создать и сохранить на листе различные группы значений, а затем переключаться на любой из этих новых сценариев для просмотра различных результатов.
Создание сценария
1. Выберите команду Сценарии в меню Данные — Анализ «что-если».
2. Нажмите кнопку Добавить.
3. Введите в поле Название сценария название сценария.
4. В поле Изменяемые ячейки введите ссылки на ячейки, которые требуется изменить.

Примечание

: Для сохранения исходных значений изменяемых ячеек создайте сценарий, который использует исходные значения ячеек, до создания сценария, изменяющего значения.
5. Установите необходимые флажки в наборе флажков Защита.

Примечание

: Если для рабочего листа установлена защита с помощью пароля, то посредством активизации опции Запретить изменения в области Защита диалогового окна Добавление сценарияпользователь может запретить редактирование сценария для других пользователей. При установке в том же поле опции Скрыть имя сценария не будет представлено в окне Диспетчера сценариев.
6. Нажмите кнопку Ok.
7. Введите необходимые значения в диалоговом окне Значения ячеек сценария.
8. Чтобы создать сценарий, нажмите кнопку Ok.
9. Если требуется создать дополнительные сценарии, снова нажмите кнопку Добавить, а затем повторите эту процедуру. После завершения создания сценариев нажмите кнопку Ok, а затем — кнопку Закрыть в диалоговом окне Диспетчер сценариев.
Правка сценария
Если после внесения изменений в сценарий он будет сохранен с первоначальным именем, новые значения изменяемых ячеек заменят значения в исходном сценарии.
1. Выберите команду Сценарии в меню Данные — Анализ «что-если».
2. Выберите название изменяемого сценария, а затем нажмите кнопку Изменить.
3. Внесите требуемые изменения.
4. Введите необходимые значения в диалоговом окне Значения ячеек сценария.
5. Выполните одно из следующих действий:
— чтобы сохранить изменения, нажмите кнопку OK;
— чтобы вернуться в диалоговое окно Диспетчер сценариев без изменения текущего сценария, нажмите кнопку Отмена.
Удаление сценария
1. Выберите команду Сценарии в меню Данные — Анализ «что-если».
2. Выберите название сценария, который требуется удалить, а затем нажмите кнопку Удалить.
Контрольный пример
Задание 1: Разработать сценарий, увеличивающий норму прибыли на 2%. Для этого:
1. В новой рабочей книге Лист 1 переименуйте как Сценарий;
2. Создайте таблицу приведенную ниже:

Рис. 9.1.

3. Значения столбца Всего издержек равно Издержки * Штук;
4. Значения столбца Прибыль равно Всего издержек * Норма прибыли;
5. Значения столбца Объем продаж равно Всего издержек + Прибыль;
6. Для начала создадим сценарий, который будет восстанавливать исходные данные. Для этого:
— выполните команду Данные – Анализ «что-если» — Диспетчер сценариев;
— название сценария – Исходный;
— изменяемые ячейки – F4:F12;
— установите флажок Запретить изменения в области Защита;
— нажмите кнопку Ok;
— в появившемся диалоговом окне будут представлены исходные значения ячеек. Поскольку исходные значения должны быть сохранены в качестве сценария, то в диалоговом окне Значения ячеек сценария следует нажать кнопку Ok.
7. Теперь создадим сценарий, увеличивающий нормы прибыли на 0,25%. Для этого:
— нажмите кнопку Добавить;
— название сценария – Увеличение на 2%;
— изменяемые ячейки – F4:F12;
— установите флажок Запретить изменения в области Защита;
— нажмите кнопку Ok;
— в полях появившегося диалогового окна можно вводить формулы, начиная запись со знака «=». Введите формулы, увеличивающие значения ячеек на 2% (рис. 9.2)
— нажмите кнопку Ok;
— выделите сценарий Увеличить на 2% и нажмите кнопку Вывести;
— просмотрите результат.

Рис. 9.2.

Источник

Подборка по базе: Самостоятельная работа.docx, 2 практическая работа по организаций компьютера.docx, курсовая работа Мещеряков 2301.docx, Практическая работа №3.docx, Практическая работа 3 .docx, Самостоятельная работа 2.5.2.docx, Практическая работа Модуль 1.docx, Курсовая работа.pdf, Проверочная работа РЯ.docx, контрольная работа.docx

Лабораторная работа 3

Табулирование функций и построение графиков

Цель работы:

изучить операцию заполнения ячеек данными;
изучить операцию копирования формул с помощью заполнения;
научиться решать расчетные задачи табулирования функции одной переменной для шагового аргумента;
рассмотреть вопросы вычисления таблиц функций, заданных различными аналитическими выражениями, функций, зависящих от параметра, функций заданных в параметрической форме или в полярной системе координат.

1. Приемы копирования и заполнения ячеек

1.1 Абсолютные, относительные, смешанные ссылки

Пример. В ячейку C3 введена формула =(A2+A3+A4)/3. При ее копировании в ячейку С4 получим формулу =(A3+A4+A5)/3. При копировании в ячейку F10 получим формулу =(D9+D10+D11)/3.
Просмотреть зависимые и влияющие ячейки можно с помощью панели Зависимости. Она вызывается по команде Вид|Панели инструментов|Настройка, вкладка Панели инструментов, установить флажок Зависимости. Затем выделяется ячейка с формулой. При нажатии кнопки Влияющие ячейки появляются стрелки от влияющих ячеек к зависимым. Кнопка Зависимые ячейки показывает, на какие ячейки с формулами влияет данная ячейка. Для снятия стрелок используется кнопка Убрать все стрелки.

1.2. Заполнение ячеек

Заполнение ячеек — это перенос данных из одной ячейки в ряд смежных ячеек строки или столбца с возможностью их изменения по некоторому закону. Операция выполняется по команде Правка|Заполнить…. В диалоговом окне команды можно указать различные варианты заполнения.

Вычисление значений аргумента по типу арифметической или геометрической прогрессии. Порядок работы следующий: ввести первое значение в требуемую ячейку и выделить эту ячейку, вызвать команду Правка|Заполнить|Прогрессия. В ее диалоговом окне установить расположение данных (строки, столбцы), тип прогрессии, шаг изменения аргумента, предельное значение аргумента. После подтверждения команды (OK) столбец (или строка) будет заполнен. в направлении увеличения адресов.
Заполнение ячеек заголовками строк или столбцов вида Урок 1, Урок 2, и т.д. выполняется так: вводится первый заголовок, выделяется заполняемый диапазон ячеек и выполняется команда Правка|Заполнить|Прогрессия. В диалоговом окне команды выбирается Автозаполнение.
Возможно заполнение последовательных ячеек датами с заданным интервалом, названиями месяцев, дней недели, годов, часов. Предлагаем эту операцию освоить самостоятельно экспериментальным путем с помощью все той же команды Правка|Заполнить |Прогрессия.
Заполнение ячеек формулами разберем на примере построения таблицы значений функции. Предварительно отметим следующее: при копировании формул из одних ячеек в другие, обычные (так называемые относительные) ссылки на ячейки изменяются с сохранением структуры зависимости от исходных данных. Например, введем в ячейку B1 формулу =A1+5. При копировании формулы в нижележащую ячейку B2 она превращается в формулу =A2+5. Заполнение ячеек формулами есть не что иное, как копирование формул в последовательные ячейки таблицы. Оно выполняется следующим образом: формула вводится в первую ячейку ряда, затем нужно выделить диапазон для ввода формул и применить команду Правка|Заполнить| Вниз (или Вправо).

Замечание. Если ссылка на ячейку в формуле является абсолютной ($A$10), то при копировании формулы она не меняется. Например, формула =$A$10+A1 при копировании изменит ссылку лишь на ячейку A1.

Добавление. Можно быстрее выполнять команду заполнения с помощью Маркера заполнения. Данные типа арифметической прогрессии вводятся в две первые ячейки заполняемого ряда. Затем, выделив эти ячейки, нужно установить указатель мыши на Маркер заполнения — маленький черный квадрат в правом нижнем углу выделенного диапазона и протащить указатель вдоль заполняемого столбца до появления последнего значения. При отпускании мыши ряд будет заполнен данными. Заполнение ячеек формулой выполняется аналогично, но только еще проще — достаточно протащить формулу за маркер заполнения вдоль требуемого ряда.

2. Примеры построения таблиц значений и графиков функций

Пример 1. ( Функция одной переменной для шагового аргумента). Построить таблицу значений функции для аргумента x, изменяющегося от 0 до 1,5 с шагом 0,1. Построить график функции.

Решение. Решение разбивается на два основных этапа: построение таблицы значений функции и построение графика функции.

Построение таблицы

Наберем заголовки столбцов для x и y в ячейках A1, B1.
Наберем первое значение x, равное 0, в ячейку A2.
Выполним команду Правка|Заполнить|Прогрессия, зададим в диалоге Расположение в столбце, Арифметическая прогрессия, Шаг 0,1, Предельное значение 2. Заполнятся ячейки A4:A22.
В ячейку B2 введем формулу: =SIN(4*A2)^2/(A2+1) и скопируем ее в ячейки B3:B22
Выполним форматирование данных (чисел) и обрамление таблицы. Фрагмент рабочего листа с таблицей показан на рис.1.

Построение графика функции. Для построения графика выделим диапазон данных (ячейки A1:B22) и построим точечную диаграмму, вид которой представлен на рис.2.

Рис.1. Таблица значений функции для примера 1

Рис. 2. График (точечная диаграмма) примера 1
Рис. 2. График (точечная диаграмма) примера 1

Пример 2. (Функция, заданная различными аналитическими выражениями (сложная функция)). Построить таблицу значений и график функции

для аргумента x , изменяющегося от -2 до 2 с шагом 0,2

Решение

Построение таблицы. Решение выполним в том же файле, что и предыдущий пример, но на новом листе Excel. Последовательность заполнения ячеек аналогична примеру 1.

В ячейку B2 введем формулу:

=ЕСЛИ(A2<0;-A2/(ABS(A2)+1);SIN(ПИ()*A2))

и скопируем ее в нижележащие ячейки для всех значений x .

П
Рис..4. График сложной функции

Рис. 3. Таблица значений сложной функции

остроение графика функции

также полностью аналогично построению предыдущего примера, если заданная функция непрерывна.

Замечание. Если функция терпит разрыв при переходе от одного аналитического выражения к другому, то нужно построить на одной диаграмме два графика, каждый из которых отвечает области непрерывности функции. В случае разрывной функции можно строить один график, если выбрать вид графика из отдельных точек
Пример 3. (Функция, зависящая от параметра). Построить таблицу значений и график функции для аргумента x, изменяющегося от -1 до 3 с шагом 0,2 при заданных значениях a и b.

Решение

Введем заголовки столбцов для x и y в ячейки A1, B1 и значения a, b в отдельные ячейки D1, F1.
Заполним столбец A2:A22 значениями x.
Введем формулу для y в ячейку B2

=EXP($D$1*A2)*COS($F$1*A2) и скопируем ее в ячейки B3:B22.

П
Рис..5. Таблица и график функции, зависящей от параметра

остроим график аналогично примеру 1 (см. рис.5.5)

Замечание. Меняя значения параметров, можно получить совершенно другое поведение функции. Рекомендуется проанализировать поведение функции при a>0 и a<0, а также рассмотреть уменьшение и увеличение b.
Пример 4. (Функция, заданная параметрическими уравнениями). Вычислить таблицу значений функции, заданной параметрическими уравнениями и построить ее график. В качестве примера рассмотрим построение окружности.

Параметрические уравнения окружности рассмотрим для значений параметра, пробегающих полный оборот вокруг начала координат:

(1)
Построение таблицы значений функции

Перейдем на новый рабочий лист.
Зададим заголовки столбцов t, x, y.
Заполним первый столбец значениями t, применив еще один способ задания аргумента: каждое последующее значение вычислим через предыдущее, добавляя шаг. В ячейке D2 вычислим по формуле =ПИ()/16. В ячейку A2 введем 0, в ячейку A3 введем формулу =A2+$D$2, которую копируем вниз до значения 2.
Введем в ячейку B2 формулу =COS(A2); в ячейку C2 формулу =SIN(A2)
Выделим ячейки B2, C2 и копируем их для всех значений t с помощью заполнения.
Форматируем таблицу по образцу.

Построение графика функции

Выделим диапазон B2:C23
Вызовем Мастер диаграмм и построим точечную диаграмму. В процессе построения зададим заголовки диаграммы и осей, уберем легенду, назначим линии сетки.
Затем отредактируем диаграмму: по команде Формат оси зададим точность – один знак после запятой, по команде Формат области построения укажем рамку Невидимая.
Выполним растяжение-сжатие диаграммы, так чтобы получилась окружность, а не эллипс.

Результат построения показан на рис.7.

Рис. 7. График функции, заданной параметрическими уравнениями

Рис.6. Таблица функции, заданной параметрическими уравнениями

Замечания

где a, b — положительные константы

(2)

3. Варианты заданий

Задача 1. Вычислить таблицу значений функции для аргумента, изменяющегося с данным шагом в заданном интервале, и построить ее график

Таблица 1
Вариант	Функция	Интервал изменения аргумента	Шаг изменения аргумента
1		[0, 10]	0,5
2		[-1,4]	0,25
3		[-2,2]	0,2
4		[-4,4]	0,5
5		[-2,2]	0,2
6		[0,5]	0,25
7		[0,4]	0,2
8		[-4,2]	0,25
9		[1,10]	0,5
10		[-10,10]	1
11		[-2,3]	0,2
12		[-3,3]	0,25
13		[-3,3]	0,25
14		[-10,10]	1
15		[-5,5]	0,5
16		[1,10]	0,5

Задача №2.

Построить график функции. Значения аргумента задать таким образом, чтобы получить на графике не менее 15 точек. Для автоматизации вычислений использовать функцию ЕСЛИ.

Таблица 2

№	Функция	Интервал
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Задача 3. Вычислить таблицу значений функции, заданной параметрическими уравнениями или уравнением в полярной системе координат, и построить ее график. В случае задания функции в полярной системе координат перейти к параметрическим уравнениям. Константы, входящие в уравнения, являются положительными и, если не задано их конкретное значение, могут быть взяты равными единице.
Таблица 3

№	Название кривой	Уравнения кривой
1	Циклоида
2	Астроида
3	Двухлепестковая роза
4	Кардиоида
5	Конхоида
6	Улитка
7	Гипербола
8	Четырехлепестковая роза
9	Спираль
10	Архимедова спираль
11	Конхоида
12	Астроида
13	Гипербола
14	Улитка
15	Двухлепестковая роза
16	Астроида

Источник