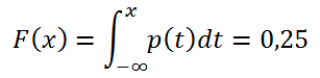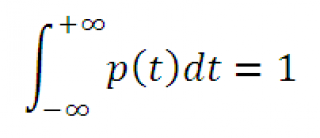Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает квартиль множества данных. Квартиль часто используются при анализе продаж для разбиения генеральной совокупности на группы. Например, можно воспользоваться функцией КВАРТИЛЬ, чтобы найти среди всех предприятий 25 процентов наиболее доходных.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новых функциях см. в разделах Функция КВАРТИЛЬ.ИСКЛ и Функция КВАРТИЛЬ.ВКЛ.
Синтаксис
КВАРТИЛЬ(массив;часть)
Аргументы функции КВАРТИЛЬ описаны ниже.
-
Массив Обязательный. Массив или диапазон ячеек с числовыми значениями, для которых определяется значение квартиля.
-
Часть Обязательный. Значение, которое требуется вернуть.
|
Если часть равна |
КВАРТИЛЬ возвращает |
|---|---|
|
0 |
Минимальное значение |
|
1 |
Первую квартиль (25-ю персентиль) |
|
2 |
Значение медианы (50-ю персентиль) |
|
3 |
Третью квартиль (75-ю персентиль) |
|
4 |
Максимальное значение |
Замечания
-
Если массив пуст, КВАРТИЛЬ возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если значение аргумента «часть» не является целым числом, то оно усекается.
-
Если кварт < 0 или > 4, кВАРТИЛЬ возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Функции МИН, МЕДИАНА и МАКС возвращают то же значение, что и функция КВАРТИЛЬ, если аргумент «часть» равен соответственно 0, 2 или 4.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
1 |
||
|
2 |
||
|
4 |
||
|
7 |
||
|
8 |
||
|
9 |
||
|
10 |
||
|
12 |
||
|
Формула |
Описание (результат) |
Результат |
|
=КВАРТИЛЬ(A2:A9;1) |
Первая квартиль (25-я процентиль) для приведенных выше данных (3,5) |
3,5 |
Нужна дополнительная помощь?
Download Article
Download Article
A quartile is the name for a percentage of data in four parts, or quarters, which is especially helpful for marketing, sales, and teachers scoring tests. Do you have data entered into your Excel sheet and want to see the quartiles (like the top 25%)? This wikiHow will teach you how to calculate quartiles in Excel using a formula.
-
1
Open your project in Excel. If you’re in Excel, you can go to File > Open or you can right-click the file in your file browser.
- This method works for Excel for Microsoft 365, Excel for Microsoft 365 for Mac, Excel for the web, Excel 2019-2007, Excel 2019-2011 for Mac, and Excel Starter 2010.
-
2
Select an empty cell where you want to display your quartile information. This can be anywhere on your spreadsheet.
- For example, you can select cell E7 even if all your data is located in cells A2-A20.
Advertisement
-
3
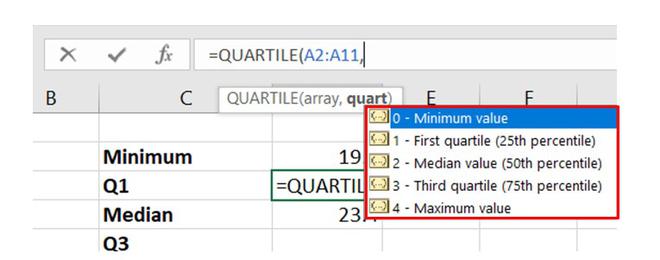
Enter the quartile function: =QUARTILE.INC(. INC stands for «Inclusive,» which will give you results that include 0+100.
-
4
Select the cells containing your data. You can drag your cursor to select the entire range or you can select the first cell then press CTRL + SHIFT + Down arrow.
- After you’ve selected the data set, you’ll see it entered into your formula. It’ll look something like «=QUARTILE.INC(A2:A20». Don’t add the closing parentheses because you’ll need to add more information to the function.
-
5
Enter «,1)» to finish the formula. The number after the data range can represent either Q1, Q2, Q3, or Q4, so you can use any number 1-4 in the function instead of 1.
- The function QUARTILE.INC(A2:A20,1) will show you the first quartile (or 25th percentile) of your data set.[1]
- The function QUARTILE.INC(A2:A20,1) will show you the first quartile (or 25th percentile) of your data set.[1]
-
6
Press ↵ Enter (Windows) or ⏎ Return (Mac). The cell you have selected will display the quartile function result. You can repeat this process using the other quartile function to see the differences.[2]
Advertisement
-
1
Open your project in Excel. If you’re in Excel, you can go to File > Open or you can right-click the file in your file browser.
- This method works for Excel for Microsoft 365, Excel for Microsoft 365 for Mac, Excel for the web, Excel 2019-2007, Excel 2019-2011 for Mac, and Excel Starter 2010.
-
2
Select an empty cell where you want to display your quartile information. This can be anywhere on your spreadsheet.
- For example, you can select cell E7 even if all your data is located in cells A2-A20.
-
3
Enter the quartile function: =QUARTILE.EXC(. .EXC displays exclusive results, not showing you the highest and lowest ranges.
-
4
Select the cells containing your data. You can drag your cursor to select the entire range or you can select the first cell then press CTRL + SHIFT + Down arrow.
- After you’ve selected the data set, you’ll see it entered into your formula. It’ll look something like «=QUARTILE.EXC(A2:A20». Don’t add the closing parentheses because you’ll need to add more information to the function.
-
5
Enter «,1)» to finish the formula. The number after the data range can represent either Q1, Q2, Q3, or Q4, so you can use any number 1-4 in the function instead of 1.
- The function QUARTILE.EXC(A2:A20,1) will show you the position of the first quartile in your data set.[3]
- The function QUARTILE.EXC(A2:A20,1) will show you the position of the first quartile in your data set.[3]
-
6
Press ↵ Enter (Windows) or ⏎ Return (Mac). The cell you have selected will display the quartile function result. You can repeat this process using the other quartile function to see the differences.[4]
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
1. Open your project in Excel.
2. Select an empty cell where you want to display your quartile information.
3. Enter «=QUARTILE.INC(« or «=QUARTILE.EXC(«.
4. Select the cells containing your data.
5. Enter «,1)» to finish the formula.
6. Press Enter (Windows) or Return (Mac).
Did this summary help you?
Thanks to all authors for creating a page that has been read 33,241 times.
Is this article up to date?
Функция КВАРТИЛЬ в Excel используется для расчета квартиля диапазона числовых данных и возвращает соответствующее числовое значение.
Функция КВАРТИЛЬ.ВКЛ вычисляет на основе указанной процентили в качестве второго аргумента функции. Полностью соответствует первой функции. Последняя используется в Excel 2007 и более ранних версиях и оставлена для совместимости.
Функция КВАРТИЛЬ.ИСКЛ используется для расчета квартили диапазона числовых значений на основе известной процентили, за исключением граничных значений (минимального и максимального значения в диапазоне).
Квартили используются для распределения диапазона чисел на четыре равные части:
- Первый квартиль является числом из диапазона исследуемых значений, которое делит данный диапазон на две части так, что около 25% данного диапазона являются числами, которые меньше первого квартиля, а остальные (75%) – больше. Рассматриваемые функции могут возвращать результат интерполяции двух соседних значений из диапазона.
- Второй квартиль эквивалентен медиане выборки (исследуемого числового диапазона), то есть числовому значению, которое делит диапазон на две части: 50% чисел меньше медианы, остальные 50% чисел больше медианы. Так, запись =КВАРТИЛЬ.ВКЛ(A1:A10;2) возвращает значение, эквивалентное результату вычисления функции =МЕДИАНА(A1:A10), при условии, что ячейки из диапазона A1:A10 содержат числовые значения.
- Третий квартиль – числовое значение, делящее диапазон на две части, в первой из которой содержатся 75% чисел диапазона, которые меньше полученного значения, а во второй (25%) – больше.
Функция КВАРТИЛЬ.ВКЛ может быть использована не только для определения медианы выборки (второго квартиля), а и нахождения минимального и максимального значений соответственно. При работе с большими диапазонами чисел для подобных расчетов рекомендуется использовать функции МИН и МАКС соответственно.
Существует несколько алгоритмов расчета квартилей. Все рассмотренные функции используют следующую формулу:
Qp=(1-(x-i)∙Ai+(x-i)∙A(i+1), где:
- Qp – p-й квантиль (является частным случаем квантиля);
- x – индекс квантиля;
- i – индекс элемента из выборки;
- A1,A2…Ai – элементы выборки, отсортированной по возрастанию значений.
Для расчета индекса квантиля (x) функция КВАРТИЛЬ.ВКЛ используют формулу:
x=(n-1)p, где n – количество элементов в диапазоне.
Функция КВАРТИЛЬ.ИСКЛ использует формулу x=(n+1)p.
В Excel принято так, что первые выше указанные 2 функции используют метод N-1-интерполяцию, а третья функция – N+1-интерполяцию.
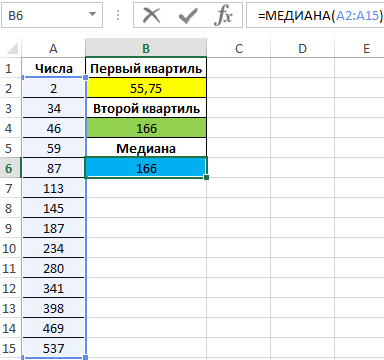
Примеры использования функций КВАРТИЛЬ в Excel
Пример 1. В столбце таблицы содержится числовая последовательность. Определить число, которое делит последовательность на 2 части, 25% первой – числа меньше полученного значения, а 75% — больше. Использовать N+1-интерполяцию.
Вид таблицы данных:
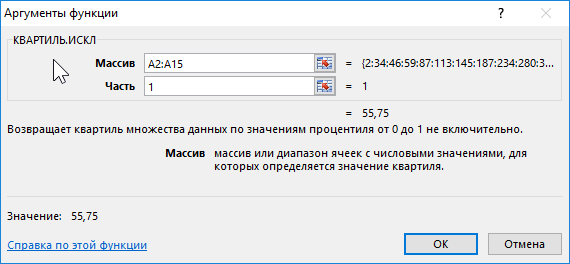
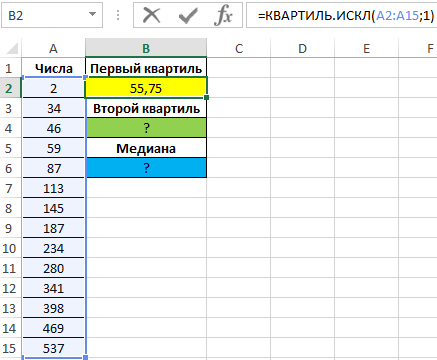
Для определения 1-го квартиля используем функцию:
Описание аргументов:
- A2:A15 – диапазон ячеек с исследуемыми числами;
- 1 – номер вычисляемого квартиля.
Полученный результат:
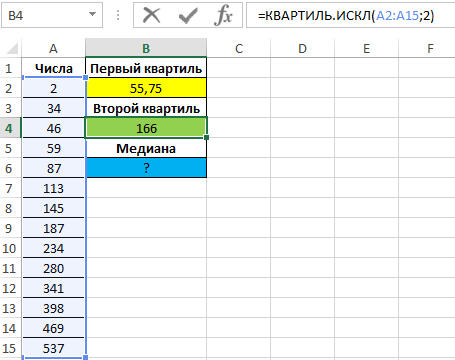
Проверим утверждение о том, что второй квартиль соответствует медиане выборке. Определим 2-й по формуле:
Вычислим медиану:
=МЕДИАНА(A2:A15)
Полученные значения совпадают:
В результате расчетов мы получили первый, второй квартили и медиану для исходного диапазона чисел.
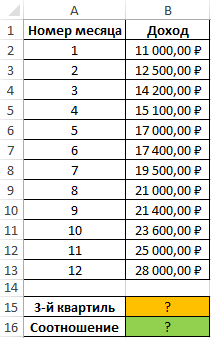
Статистический анализ роста доли дохода в Excel за период
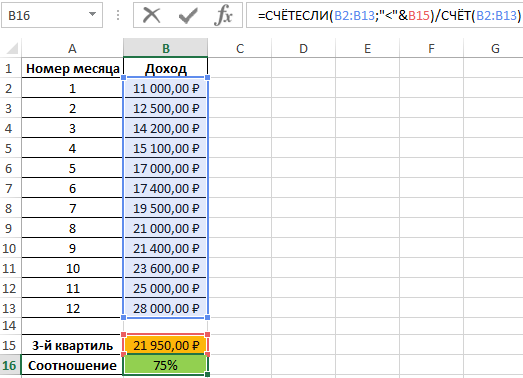
Пример 2. В таблице приведены данные о доходах предпринимателя за год. Доказать, что примерно 75% значений меньше, чем третий квартиль доходов.
Вид исходной таблицы:
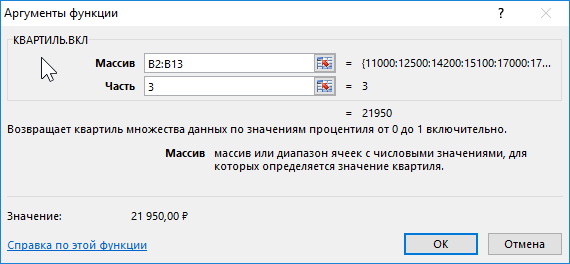
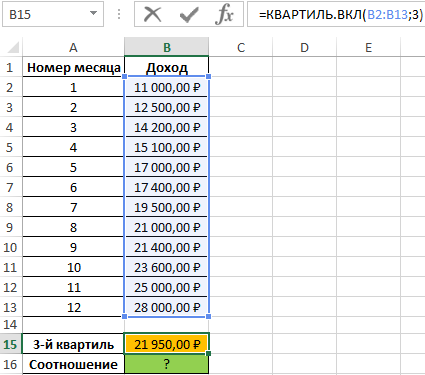
Определим 3-й по формуле:
Определим соотношение чисел, меньше полученного числа, к общему количеству значений по формуле:
=СЧЁТЕСЛИ(B2:B13;»<«&B15)/СЧЁТ(B2:B13)
Полученные результаты:
Анализ статистики случайно сгенерированных чисел в Excel
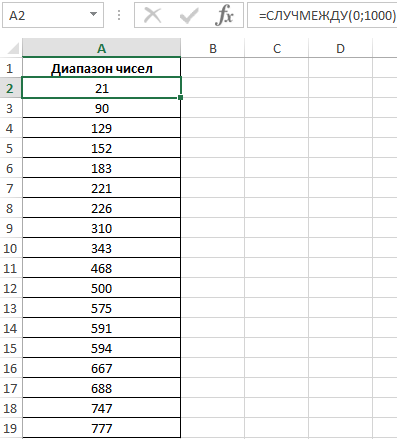
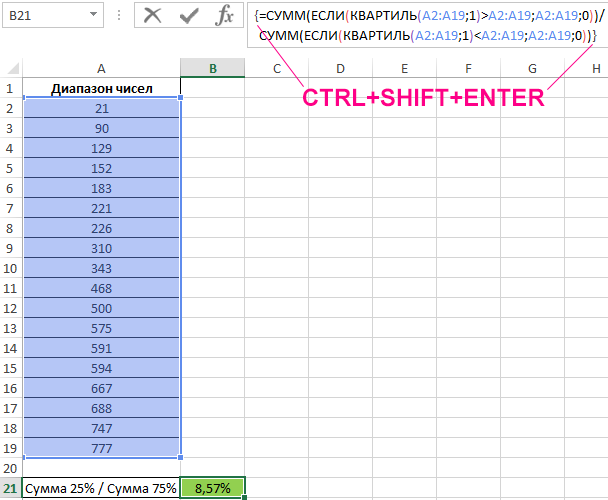
Пример 3. Имеется диапазон случайных чисел, отсортированный в порядке возрастания. Определить соотношение суммы чисел, которые меньше 1-го квартиля, к сумме чисел, которые превышают значение 1-го квартиля.
Чтобы сгенерировать случайное число в Excel воспользуемся функцией:
=СЛУЧМЕЖДУ(0;1000)
После генерации отсортируем случайно сгенерированные числа по возрастанию. Вид исходной таблицы данных со случайными числами:
Формула для расчета имеет следующий вид (формула массива CTRL+SHIFT+ENTER):
Функции СУММ с вложенными функциями ЕСЛИ выполняют расчет суммы только тех чисел, которые меньше и больше соответственно значения, возвращаемого функцией для исследуемого диапазона. Из полученных значений вычисляется частное. Результат расчетов:
Общая сумма чисел исследуемого диапазона, которые меньше 1-го квартиля, составляет всего 8,57% от общей суммы чисел, которые больше 1-го квартиля.
Особенности использования функций расчета квартиля в Excel
Все рассматриваемые функции имеют одни и те же аргументы:
=КВАРТИЛЬ(массив;часть)
Описание аргументов:
- массив – обязательный аргумент, принимающий константу массива или ссылку на диапазон ячеек с числовыми значениями, для которых будет рассчитан требуемый квартиль;
- часть – обязательный аргумент, принимающий числовые значения, указывающие номер возвращаемого квартиля. В зависимости от используемой функции, может принимать числа из диапазонов:
- От 0 до 4 (КВАРТИЛЬ.ВКЛ), при этом числа 0 и 1 характеризуют минимальное и максимальное значения из исследуемого диапазона соответственно. Число 1 соответствует 1-й квартили, 2 – медиане, 3 – 3-й квартили.
- От 1 до 3 (функция КВАРТИЛЬ.ИСКЛ), соответствующие 1-й, 2-й и 3-й квартилям.
Примечания:
- Все рассматриваемые функции не учитывают имена и текстовые строки, которые не могут быть преобразованы к числам, логические значения и пустые ячейки. Ячейки, содержащие значение 0 (нуль), в расчет включаются.
- Если в качестве первого аргумента функций передан пустой массив или ссылка на диапазон пустых значений, все функции вернут код ошибки #ЧИСЛО!.
- Если в качестве второго аргумента функций было передано нецелое число из диапазона допустимых значений, дробная часть будет усечена.
- Если второй аргумент задан числом, взятым из вне диапазона допустимых значений, в результате вычислений будет возвращен код ошибки #ЧИСЛО!.
Для вычисления квартилей в MS EXCEL существует специальная функция
КВАРТИЛЬ()
. В этой статье дадим определение квартилей и научимся их вычислять для выборки и для непрерывного распределения. Также вычислим интерквартильный интервал.
Квартили
(Quartiles) — значения, которые делят
выборку
(набор значений) на четыре части, содержащие приблизительно равное количество наблюдений (по 25%).
Поясним определение
квартиля
на примере. Пусть имеется
выборка
, состоящая из 50 значений в ячейках
А7:А56
(см.
файл примера
, лист Квартиль-выборка). Для наглядности
отсортируем значения по возрастанию
и построим
гистограмму
.
Чтобы разделить
выборку
на 4 части достаточно 3-х
квартилей
.
Первый
квартиль
(или
нижний квартиль
, Q1) делит
выборку
, на 2 части: примерно 25% значений в
выборке
меньше Q1, остальные 75% — больше. Для вычисления
1-го квартиля
используйте формулу
=КВАРТИЛЬ.ВКЛ(A7:A56;1)
. Для нашей выборки формула вернет значение 224. Значения 224 нет в
выборке
, формула произвела интерполяцию на основе 2-х соседних значений 223 и 227.
Примечание
: Функция
КВАРТИЛЬ.ВКЛ()
появилась в MS EXCEL 2010. В более ранних версиях использовалась аналогичная ей функция
КВАРТИЛЬ()
.
Чтобы убедиться, что примерно 25% значений меньше, чем 224, используем формулу
=СЧЁТЕСЛИ(A7:A56;»<«&224)/СЧЁТ(A7:A56)
. В результате получим, что 26% меньше, чем 1-й
квартиль
.
Чем в
выборке
больше значений и меньше
повторов
, тем точнее деление
выборки квартилями
на четверти.
Примечание
: Первый квартиль — это то же самое, что и 25-я
процентиль
. Подробнее см.
статью про процентили
.
Второй
квартиль
(или
медиана
, Q2) также делит
выборку
, на 2 равные части: половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для вычисления 2-го
квартиля
используйте формулу
=КВАРТИЛЬ.ВКЛ(A7:A56;2)
или
=МЕДИАНА(A7:A56)
Третий
квартиль
(или верхний
квартиль
, Q3) делит
выборку
, на 2 части: примерно 75% значений в
выборке
меньше Q3, остальные 25% — больше. Для вычисления 3-го
квартиля
используйте формулу
=КВАРТИЛЬ.ВКЛ(A7:A56;3)
или
=ПРОЦЕНТИЛЬ.ВКЛ(A7:A56;0,75)
Примечание
: Третий
квартиль
— это то же самое, что и 75-я
процентиль
.
Второй аргумент функции
КВАРТИЛЬ.ВКЛ()
может также принимать значения 0 и 4. В первом случае функция вернет
минимальное значение
, во втором –
максимальное
.
Интерквартильный размах
Интерквартильным размахом
или
интерквартильным интервалом
(InterQuartile range, IQR) называется разность между третьим и первым
квартилями
(Q3 — Q1).
Интерквартильный размах
является характеристикой разброса значений в
выборке
.
Примечание
: Характеристикой разброса значений в
выборке
является также
дисперсия и стандартное отклонение
.
Интерквартильный размах
, а также
квартили
используются при построении
Блочной диаграммы
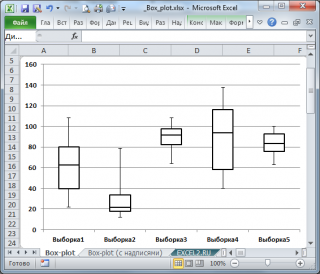
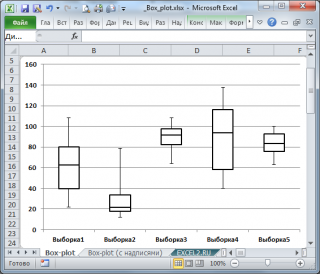
, которая полезна для оценки разброса значений (variation) в небольших
выборках
или для сравнения нескольких
выборок
имеющих сходные распределения.
Подробнее о построении
Блочной диаграммы
см. статью
Блочная диаграмма в MS EXCEL
.
Квартили непрерывного распределения
Если
функция распределения
F
(х)
случайной величины
х
непрерывна, то 1-й
квартиль
является решением уравнения
F(х)
=0,25, второй —
F(х)
=0,5, а третий
F(х)
=0,75.
Примечание
: Подробнее о
Функции распределения
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Если известна
функция плотности вероятности
p
(х)
, то 1-й
квартиль
можно найти из уравнения:
Например, решив аналитическим способом это уравнение для
Логнормального распределения
lnN(μ; σ
2
), получим, что
медиана
(2-й
квартиль
) вычисляется по формуле e
μ
или в MS EXCEL =EXP(μ). При μ=1,
медиана
равна 2,718.
Обратите внимание на точку
Функции распределения
, для которой
F(х)=0,5
(см. картинку выше или
файл примера
, лист Квартиль-распределение)
.
Абсцисса этой точки равна 2,718. Это и есть значение 2-го
квартиля
(
медианы
), что естественно совпадает с ранее вычисленным значением по формуле e
μ
.
Примечание
: Напомним, что интеграл от
функции плотности вероятности
по всей области задания случайной величины равен единице:
Поэтому, линии
квартилей
(
х=квартиль
) делят площадь под графиком
функции плотности вероятности
на 4 равные части.
Квартили в MS EXCEL
Чтобы вычислить в MS EXCEL
квартили
заданного распределения необходимо использовать соответствующую
обратную функцию распределения
.
При вычислении
квартилей
в MS EXCEL используются
обратные функции распределения
:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР()
,
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Например, в MS EXCEL 1-й
квартиль
для
логнормального распределения
LnN(1;1) можно вычислить по формуле
=ЛОГНОРМ.ОБР(0,25;1;1)
, а 3-й
квартиль
для
стандартного нормального распределения
по формуле
=НОРМ.СТ.ОБР(0,75)
.
Содержание
- Обзор функции QUARTILE
- Функция КВАРТИЛЬ Синтаксис и входные данные:
- Что такое функция КВАРТИЛЬ?
- КВАРТИЛЬ — это функция «совместимости»
- Что такое квартиль?
- Как использовать функцию КВАРТИЛЬ
- Создание пятизначной сводки
- QUARTILE.INC
- QUARTILE.EXC
- Функция КВАРТИЛЬ в Google Таблицах
- Примеры QUARTILE в VBA
Скачать пример рабочей книги
Загрузите образец книги
В этом руководстве показано, как использовать Функция Excel QUARTILE в Excel для расчета квартиля.
Функция КВАРТИЛЬ Вычисляет указанное значение квартиля.
Чтобы использовать функцию листа Excel QUARTILE, выберите ячейку и введите:
(Обратите внимание, как появляются входные данные формулы)
Функция КВАРТИЛЬ Синтаксис и входные данные:
| 1 | = КВАРТИЛЬ (массив; кварта) |
множество — Массив чисел.
кварта — Число, представляющее квартиль, который вы хотите вернуть.
Что такое функция КВАРТИЛЬ?
КВАРТИЛЬ — одна из статистических функций Excel. Он возвращает квартиль диапазона данных. Вы можете указать, хотите ли вы: первый, второй или третий квартиль. QUARTILE также может возвращать минимальные и максимальные значения.
КВАРТИЛЬ — это функция «совместимости»
Начиная с Excel 2010, Microsoft заменила QUARTILE двумя вариантами: QUARTILE.INC и QUARTILE. ИСКЛ.
КВАРТИЛЬ по-прежнему работает, поэтому, если у вас есть старые электронные таблицы, которые его используют, они будут продолжать работать в обычном режиме. Однако вы должны использовать QUARTILE.INC или QUARTILE.EXC везде, где это возможно, на тот случай, если Microsoft исключит QUARTILE из будущих версий Excel.
Что такое квартиль?
Квартили делят диапазон данных на четыре приблизительно равные группы по размеру. Excel рассчитывает квартили как процентили:
- Первый квартиль также известен как 25th процентиль — поскольку 25% данных ниже этого значения.
- Второй квартиль — это медиана набора данных, также известная как 50th процентиль, поскольку 50% данных ниже этого значения.
- Третий квартиль также называют 75th процентиль, поскольку 75% данных ниже этого значения.
Квартили вместе с наименьшими и наибольшими числами в наборе создают «пятизначную сводку». Это может помочь вам сразу увидеть, где находится середина данных и насколько они распределены.
Как использовать функцию КВАРТИЛЬ
Используйте QUARTILE так:
Группа учеников эксклюзивной школы сдала важный экзамен. Их оценки хранятся в C4: C13, а диапазон данных — это первый аргумент, который мы передаем в QUARTILE.
Следующий аргумент в функции, который мы называем «кварта”, Определяет значение, которое мы хотим вернуть. Здесь мы выбрали 2, второй квартиль / медиана. Медиана — это среднее число в диапазоне, а поскольку у нас 11 студентов, медиана — это 6th один — 74 балла Жана, которые я выделил в таблице.
Несколько полезных вещей, которые нужно знать о QUARTILE:
- Если кварт не является числом, вы получите # ЗНАЧ! ошибка
- Если в кварте меньше 0 или больше 4, вы получите # ЧИСЛО! ошибка
- Если кварт не является целым числом, КВАРТИЛЬ проигнорирует все, что находится после десятичной точки.
- Пустые или нечисловые ячейки в диапазоне данных игнорируются.
- Если диапазон данных пуст, вы получите # ЧИСЛО! ошибка
Создание пятизначной сводки
Когда вы определяете кварта у вас есть пять вариантов:
- 0 — наименьшее число (эквивалент функции MIN в Excel <>)
- 1 — первый квартиль
- 2 — второй квартиль (эквивалент функции МЕДИАНА Excel <>)
- 3 — третий квартиль
- 4 — наибольшее значение (эквивалент функции Excel MAX <>)
Поэтому, если вы хотите создать сводку из пяти цифр, вы просто создаете пять функций QUARTILE и измените кварта ценность в каждом. Это показано ниже:
QUARTILE.INC
Как я упоминал ранее, Microsoft заменила квартиль двумя функциями — QUARTILE.INC и QUARTILE.EXC. QUARTILE.INC — это то же самое, что QUARTILE. Поэтому, если мы переключим эти функции в нашей сводной таблице из пяти чисел, мы получим точно такие же результаты:
| 1 | = КВАРТИЛЬ.INC (C4: C14; E4) |
Часть функции «INC» является сокращением от «inclusive». Это означает, что QUARTILE.INC включает наименьшие и наибольшие значения в диапазоне данных при вычислении квартилей.
Excel вычисляет квартили как процентили: это может дать несколько отличные результаты от способа вычисления квартилей в других аналитических пакетах (обычно путем разделения данных на две половины и вычисления медианы каждой половины).
Вот как Excel рассчитывает инклюзивные квартили:
| 1 | Расположение квартиля = (n — 1) * (целевой квартиль / 100) + 1 |
Здесь n — количество точек данных в наборе. Итак, давайте заполним уравнение на примере первого квартиля:
| 1 | Расположение Q1 = (11-1) * (25/100) + 1 |
Это означает, что значение Q1 равно 3,5.th значение, другими словами, посередине между третьим и четвертым значением.
Чтобы получить фактическое значение, мы используем следующее:
| 1 | Q1 = 3-е значение + (4-е значение — 3-е значение) * .5 |
Заполняем уравнение нашими значениями:
| 1 | Q1 = 65 + (67-65) * 0,5 |
Более подробное обсуждение того, как рассчитываются процентили в Excel, можно найти на главной странице функции Excel PERCENTILE <>.
QUARTILE.EXC
QUARTILE.EXC очень похож на QUARTILE.INC, за исключением того, что он исключает наименьшие и наибольшие значения в наборе данных при вычислении квартилей.
Вы используете это так:
| 1 | = КВАРТИЛЬ.EXC (C4: C14,2) |
Вот та же сводка из пяти цифр, рассчитанная с помощью QUARTILE.EXC:
Ну, первое, что выскакивает, — это # ЧИСЛО! ошибки, когда мы устанавливаем кварта на 0 или 4. Это связано с тем, что, как упоминалось ранее, QUARTILE.EXC исключает наименьшие и наибольшие значения при создании своих диапазонов. Таким образом, вы не можете создать пятизначную сводку с помощью QUARTILE.EXC.
Вот как Excel рассчитывает эксклюзивные квартили:
| 1 | Расположение квартиля = (n + 1) * (целевой квартиль / 100) |
Давайте заполним это поле, снова используя в качестве примера первый квартиль:
| 1 | Расположение Q1 = (11 + 1) * (25/100) |
Это означает, что значение Q1 является третьим значением: оценка Логана 65.
Если бы в результате мы получили десятичное число, это означало бы, что квартиль находится между двумя значениями, и мы получили бы значение так же, как и с QUARTILE.INC:
| 1 | Квартиль = наименьшее значение + (наибольшее значение — наименьшее значение) * [десятичная дробь из первого уравнения] |
Опять же, для более подробного обсуждения того, как рассчитываются процентили в Excel, см. Главную страницу функции Excel PERCENTILE <>.
Функция КВАРТИЛЬ в Google Таблицах
Функция КВАРТИЛЬ в Google Таблицах работает точно так же, как и в Excel:
Примеры QUARTILE в VBA
Вы также можете использовать функцию QUARTILE в VBA. Тип:application.worksheetfunction.quartile (массив, кварта)
Для аргументов функции (массив и т. Д.) Вы можете либо ввести их непосредственно в функцию, либо определить переменные, которые будут использоваться вместо них.
Вернуться к списку всех функций в Excel
Содержание
- Квартили и интерквартильный интервал (IQR) в EXCEL
- Интерквартильный размах
- Квартили непрерывного распределения
- Квартили в MS EXCEL
- How to Calculate the Interquartile Range (IQR) in Excel
- What is the Interquartile Range?
- How to Calculate the Interquartile Range in Excel
- Example: Finding IQR in Excel
- A Shorter Approach
- Conclusion
- How to Calculate the Interquartile Range in Excel?
- Interquartile Range
- Calculation
- Calculate Interquartile Range (IQR) – Excel & Google Sheets
- What is Interquartile Range (IQR)?
- Calculate Interquartile Range (IQR) in Excel
- Calculate Interquartile Range (IQR) in Google Sheets
Квартили и интерквартильный интервал (IQR) в EXCEL
history 20 ноября 2016 г.
Для вычисления квартилей в MS EXCEL существует специальная функция КВАРТИЛЬ() . В этой статье дадим определение квартилей и научимся их вычислять для выборки и для непрерывного распределения. Также вычислим интерквартильный интервал.
Квартили (Quartiles) — значения, которые делят выборку (набор значений) на четыре части, содержащие приблизительно равное количество наблюдений (по 25%).
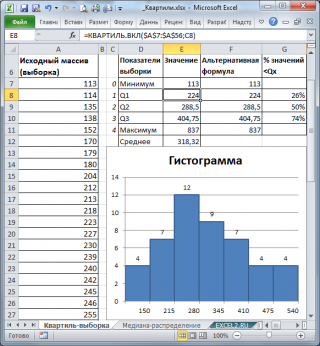
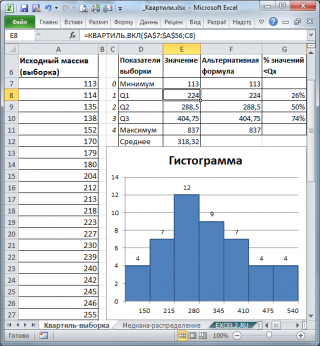
Поясним определение квартиля на примере. Пусть имеется выборка , состоящая из 50 значений в ячейках А7:А56 (см. файл примера , лист Квартиль-выборка). Для наглядности отсортируем значения по возрастанию и построим гистограмму .
Чтобы разделить выборку на 4 части достаточно 3-х квартилей .
Первый квартиль (или нижний квартиль , Q1) делит выборку , на 2 части: примерно 25% значений в выборке меньше Q1, остальные 75% — больше. Для вычисления 1-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;1) . Для нашей выборки формула вернет значение 224. Значения 224 нет в выборке , формула произвела интерполяцию на основе 2-х соседних значений 223 и 227.
Примечание : Функция КВАРТИЛЬ.ВКЛ() появилась в MS EXCEL 2010. В более ранних версиях использовалась аналогичная ей функция КВАРТИЛЬ() .
Чтобы убедиться, что примерно 25% значений меньше, чем 224, используем формулу =СЧЁТЕСЛИ(A7:A56;» . В результате получим, что 26% меньше, чем 1-й квартиль .
Чем в выборке больше значений и меньше повторов , тем точнее деление выборки квартилями на четверти.
Примечание : Первый квартиль — это то же самое, что и 25-я процентиль . Подробнее см. статью про процентили .
Второй квартиль (или медиана , Q2) также делит выборку , на 2 равные части: половина чисел множества больше, чем медиана , а половина чисел меньше, чем медиана . Для вычисления 2-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;2) или =МЕДИАНА(A7:A56)
Третий квартиль (или верхний квартиль , Q3) делит выборку , на 2 части: примерно 75% значений в выборке меньше Q3, остальные 25% — больше. Для вычисления 3-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;3) или =ПРОЦЕНТИЛЬ.ВКЛ(A7:A56;0,75)
Примечание : Третий квартиль — это то же самое, что и 75-я процентиль .
Второй аргумент функции КВАРТИЛЬ.ВКЛ() может также принимать значения 0 и 4. В первом случае функция вернет минимальное значение , во втором – максимальное .
Интерквартильный размах
Интерквартильным размахом или интерквартильным интервалом (InterQuartile range, IQR) называется разность между третьим и первым квартилями (Q3 — Q1). Интерквартильный размах является характеристикой разброса значений в выборке .
Примечание : Характеристикой разброса значений в выборке является также дисперсия и стандартное отклонение .
Интерквартильный размах , а также квартили используются при построении Блочной диаграммы , которая полезна для оценки разброса значений (variation) в небольших выборках или для сравнения нескольких выборок имеющих сходные распределения.
Подробнее о построении Блочной диаграммы см. статью Блочная диаграмма в MS EXCEL .
Квартили непрерывного распределения
Если функция распределения F (х) случайной величины х непрерывна, то 1-й квартиль является решением уравнения F(х) =0,25, второй — F(х) =0,5, а третий F(х) =0,75.
Если известна функция плотности вероятности p (х) , то 1-й квартиль можно найти из уравнения:
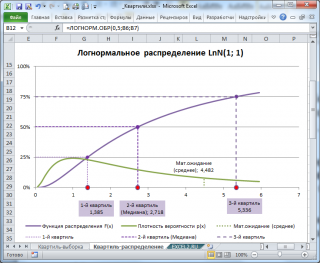
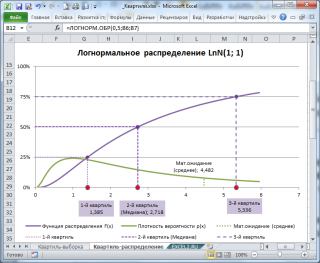
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ 2 ), получим, что медиана (2-й квартиль ) вычисляется по формуле e μ или в MS EXCEL =EXP(μ). При μ=1, медиана равна 2,718.
Обратите внимание на точку Функции распределения , для которой F(х)=0,5 (см. картинку выше или файл примера , лист Квартиль-распределение) . Абсцисса этой точки равна 2,718. Это и есть значение 2-го квартиля ( медианы ), что естественно совпадает с ранее вычисленным значением по формуле e μ .
Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице:
Поэтому, линии квартилей ( х=квартиль ) делят площадь под графиком функции плотности вероятности на 4 равные части.
Квартили в MS EXCEL
Чтобы вычислить в MS EXCEL квартили заданного распределения необходимо использовать соответствующую обратную функцию распределения .
При вычислении квартилей в MS EXCEL используются обратные функции распределения : НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР() , ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .
Например, в MS EXCEL 1-й квартиль для логнормального распределения LnN(1;1) можно вычислить по формуле =ЛОГНОРМ.ОБР(0,25;1;1) , а 3-й квартиль для стандартного нормального распределения по формуле =НОРМ.СТ.ОБР(0,75) .
Источник
How to Calculate the Interquartile Range (IQR) in Excel
This tutorial explains how to calculate the interquartile range of a dataset in Excel.
What is the Interquartile Range?
The interquartile range, often denoted IQR, is a way to measure the spread of the middle 50% of a dataset. It is calculated as the difference between the first quartile* (Q1) and the third quartile (Q3) of a dataset.
*Quartiles are simply values that split up a dataset into four equal parts.
For example, suppose we have the following dataset:
[58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98]
The third quartile turns out to be 91 and the first quartile is 75.5. Thus, the interquartile range (IQR) for this dataset is 91 – 75.5 = 15. This tells us how spread out the middle 50% of the values are in this dataset.
How to Calculate the Interquartile Range in Excel
Microsoft Excel doesn’t have a built-in function to calculate the IQR of a dataset, but we can easily find it by using the QUARTILE() function, which takes the following arguments:
- array: the array of data you’re interested in.
- quart: the quartile you would like to calculate.
Example: Finding IQR in Excel
Suppose we would like to find the IQR for the following dataset:
To find the IQR, we can perform the following steps:
Step 1: Find Q1.
To find the first quartile, we simply type =QUARTILE(A2:A17, 1) into any cell we choose:
Step 2: Find Q3.
To find the third quartile, we type =QUARTILE(A2:A17, 3) into any cell we choose:
Step 3: Find IQR.
To find the interquartile range (IQR), we simply subtract Q1 from Q3:
The IQR turns out to be 39.5 – 23.5 = 16. This tells us how spread out the middle 50% of the values are in this particular dataset.
A Shorter Approach
Note that we could also have found the interquartile range of the dataset in the previous example by using one formula:
=QUARTILE(A2:A17, 3) – QUARTILE(A2:A17, 1)
This would also result in the value 16.
Conclusion
The interquartile range only represents one way of measuring the “spread” of a dataset. Some other ways to measure spread are the range, the standard deviation, and the variance.
The nice part about using the IQR to measure spread is that it’s resistant to outliers. Since it only tells us the spread of the middle 50% of the dataset, it isn’t affect by unusually small or unusually large outliers.
This makes it a preferable way to measure dispersion compared to a metric like the range, which simply tells us the difference between the largest and the smallest values in a dataset.
Источник
How to Calculate the Interquartile Range in Excel?
In statistics, the five-number summary is mostly used as it gives a rough idea about the dataset. It is basically a summary of the dataset describing some key features in statistics. The five key features are :
- Minimum value: It is the minimum value in the data set.
- First Quartile, Q1: It is also known as the lower quartile where 25% of the scores fall below it.
- Median (middle value) or second quartile: It is basically the mid-value in the dataset.
- Third Quartile, Q3: It is also known as the Upper quartile in which 25% of the data is above it and the rest 75% falls below it.
- Maximum value: It is the maximum value in the dataset.
Using two quartiles of the five-number summary we can easily calculate the IQR abbreviated as Interquartile Range.
In this article, we are going to see how to calculate the Interquartile range in Excel using a sample dataset as an example.
Interquartile Range
In terms of Mathematics, it is basically defined as the difference between the third quartile (75th percentile) and the first quartile (25th percentile).
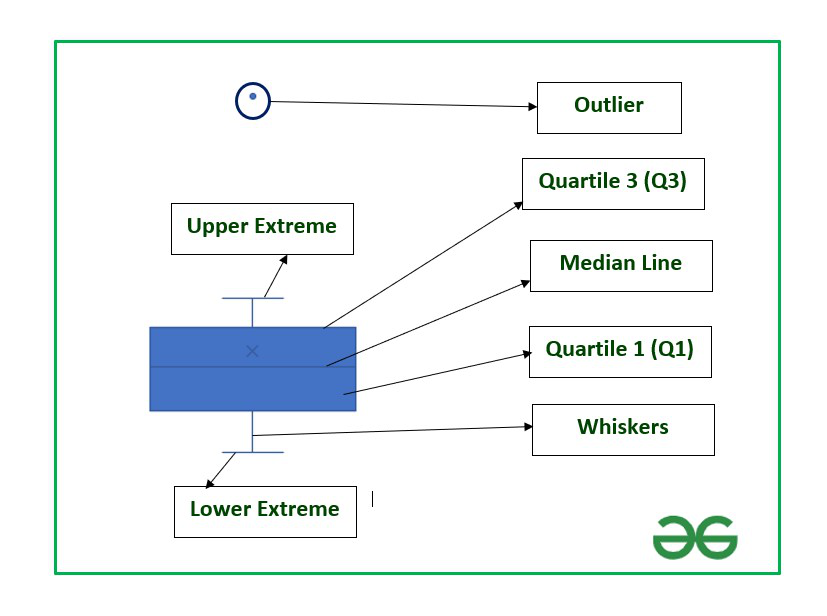
IQR denotes the middle 50% hence also known as midspread or H-spread in statistics. It can be easily observed using a box plot.
The vertical lines of the rectangular box plot denote the Interquartile range which lies between Quartile 1 and Quartile 3.
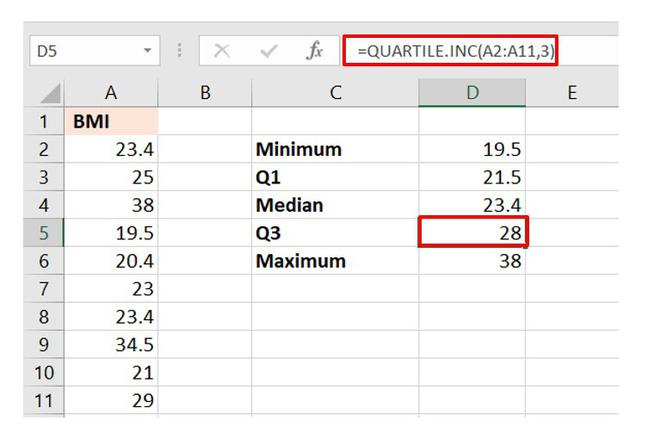
Example: Consider the dataset consisting of the BMI of ten students in a class.
Now, in order to calculate the IQR we need to first calculate the two quartile values Q1 and Q3. The function used is :
quart values
Calculation
Follow the below steps to calculate the same:
Step 1: Insert the dataset.
Step 2: Select any cell where you want to write the formula to calculate the values of Q1, Q3, and IQR.
Step 3: First find the values of Q1 and Q3 using the quart values as 1 and 3 respectively.
The dataset is stored in column “A” of the worksheet and the observations are stored from cell A2 to A11.
So the array will start from A2 and end at A11.
Calculation of Q1
Calculation of Q3
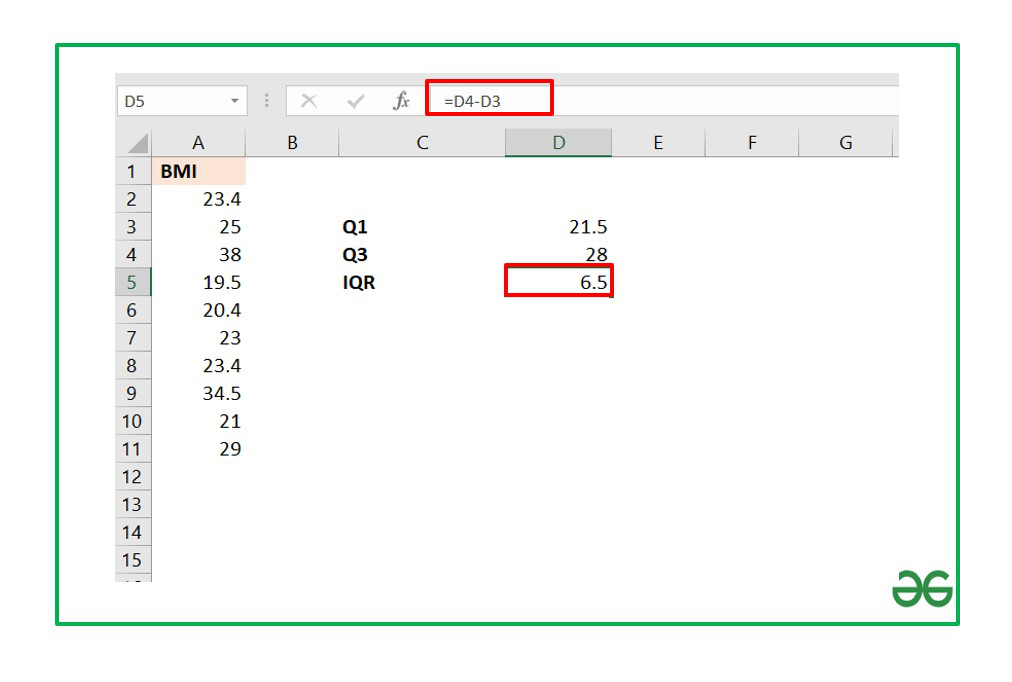
You can also find the remaining three parameters of a five-number summary using the same formula just by changing the quart value. But to find the IQR, we only need the values of Q1 and Q3.
The value of Q3 is stored in cell D4 and that of Q1 in cell D3. The formula will be :
The Interquartile range for the above dataset turns out to be 6.5.
Источник
Calculate Interquartile Range (IQR) – Excel & Google Sheets
This tutorial demonstrates how to calculate interquartile range (IQR) in Excel and Google Sheets.
What is Interquartile Range (IQR)?
The Interquartile range presents a spread of the middle half of the dataset. It is actually the difference between the third and the first quartile. Quartiles are values that split a dataset into 4 equal parts. Say. that you have the following dataset:
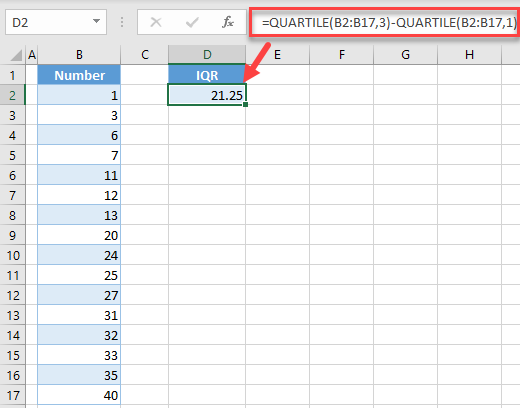
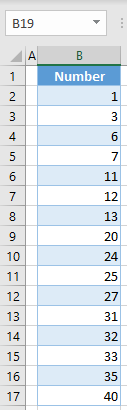
1, 3, 6, 7, 11, 12, 13, 20, 24, 25, 27, 31, 32, 33, 35, 40
In this case, there are 16 values, so quartiles will split it into 4 parts, each containing 4 numbers. Therefore, the first quartile is 10, the second is 22, and the third is 31.25, From this, you can conclude that the IQR is 31.5-9 = 22.5.
Calculate Interquartile Range (IQR) in Excel
Say that you have the same dataset in Excel and want to calculate IQR.
To achieve this, you need to use the QUARTILE Function to get the first and third quartile. Enter the following formula in cell D2:
As you can see the IQR is 21.25
Calculate Interquartile Range (IQR) in Google Sheets
Similar to Excel, to calculate interquartile range in Google Sheets, enter the formula:
Источник
17 авг. 2022 г.
читать 2 мин
Квартили — это значения, которые делят набор данных на четыре равные части.
Есть три разные функции, которые вы можете использовать для вычисления квартилей в Excel:
1. QUARTILE.EXC: Эта функция использует следующий процесс для вычисления квартилей набора данных:
- Используйте медиану, чтобы разделить набор данных на две половины.
- Рассчитайте Q1 как медианное значение в нижней половине и Q3 как медианное значение в верхней половине. Обязательно исключите медиану набора данных при расчете Q1 и Q3.
2. QUARTILE.INC: Эта функция использует следующий процесс для вычисления квартилей набора данных:
- Используйте медиану, чтобы разделить набор данных на две половины.
- Рассчитайте Q1 как медианное значение в нижней половине и Q3 как медианное значение в верхней половине. Не забудьте включить медиану набора данных при расчете Q1 и Q3.
3. КВАРТИЛЬ: Эта функция также вычисляет квартили набора данных. Она вернет то же значение, что и функция КВАРТИЛЬ.ВКЛ .
Например, предположим, что у нас есть следующий набор данных:
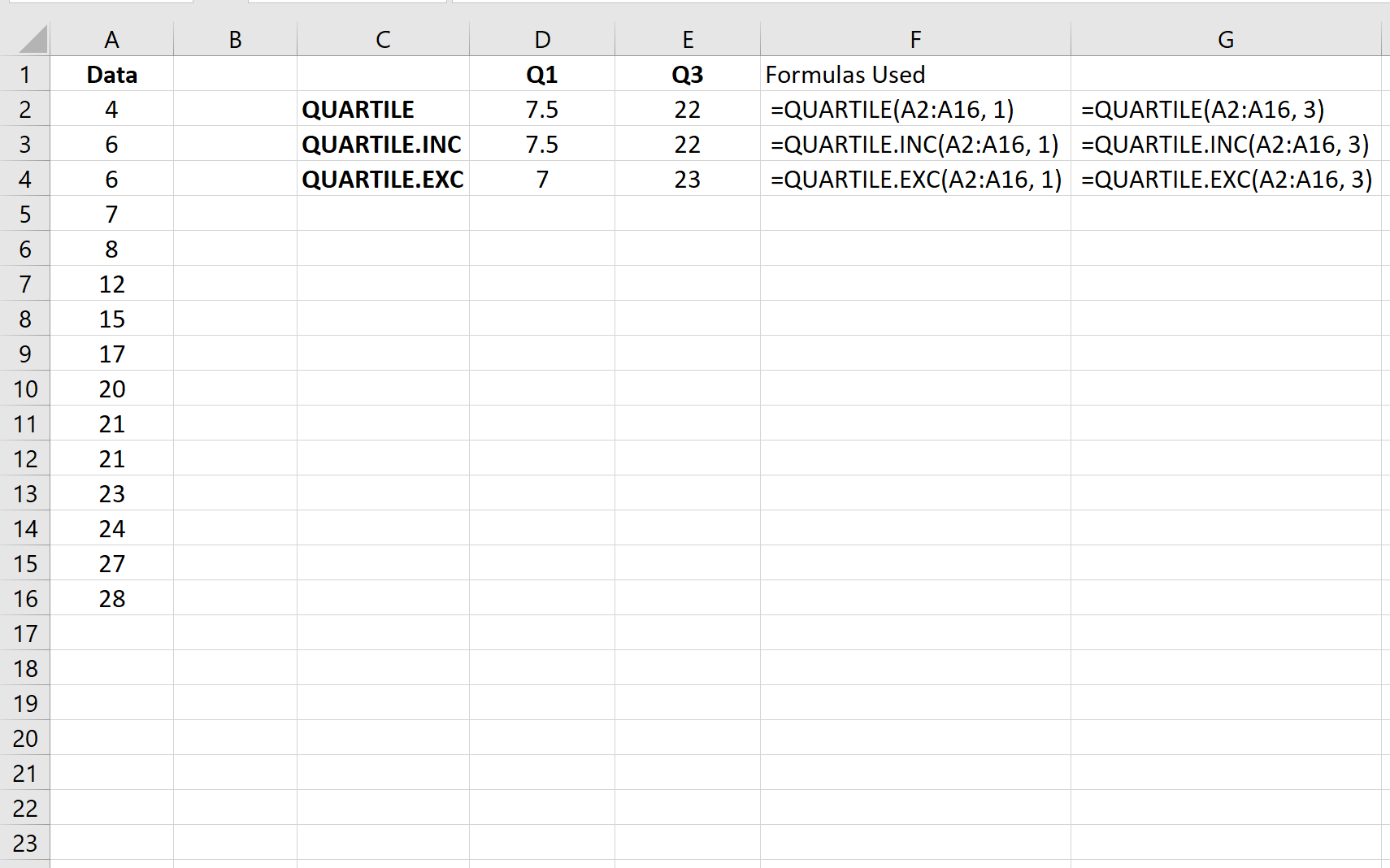
Набор данных: 4, 6, 6, 7, 8, 12, 15, 17, 20, 21, 21, 23, 24, 27, 28
Функция КВАРТИЛЬ.ИСКЛ будет использовать медиану, чтобы разделить набор данных на две половины и вычислить Q1 и Q3 как 7 и 23 соответственно:
- Q1: Медиана 4, 6, 6, 7, 8, 12, 15 = 7
- Q3: Медиана 20, 21, 21, 23, 24, 27, 28 = 23
Функция КВАРТИЛЬ.ВКЛ будет использовать медиану, чтобы разделить набор данных на две половины и вычислить Q1 и Q3 как 7,5 и 22 соответственно:
- Q1: Медиана 4, 6, 6, 7, 8, 12, 15, 17 = 7,5
- Q3: Медиана 17, 20, 21, 21, 23, 24, 27, 28 = 22
В следующем примере показано, как использовать различные функции КВАРТИЛЕЙ в Excel.
Пример: КВАРТИЛЬ.ИСКЛ и КВАРТИЛЬ.ВКЛ в Excel
Предположим, у нас есть следующий набор данных в Excel:
На следующем снимке экрана показано, как рассчитать квартили для набора данных с использованием трех разных формул квартилей:
Используя функции КВАРТИЛЬ или КВАРТИЛЬ.ВКЛ , мы вычисляем нижний и верхний квартили как:
- Q1 : 7,5
- Q3 : 22
И наоборот, используя функцию КВАРТИЛЬ.ИСКЛ , мы вычисляем нижний и верхний квартили следующим образом:
- Q1 : 7
- Q3 : 23
Когда использовать QUARTILE.EXC против QUARTILE.INC
Не существует универсально «правильного» способа расчета квартилей в наборе данных.
На самом деле, разные статистические программы используют разные формулы по умолчанию для расчета квартилей.
В языке программирования R используется формула, соответствующая функции КВАРТИЛЬ.ВКЛ в Excel.
- Как рассчитать межквартильный диапазон в R
Язык программирования Python использует формулу, соответствующую функции КВАРТИЛЬ.ВКЛ в Excel.
- Как рассчитать межквартильный диапазон в Python
Калькуляторы TI-84 используют формулу, соответствующую функции КВАРТИЛЬ.ИСКЛ в Excel.
- Как рассчитать межквартильный размах на калькуляторе TI-84
К счастью, независимо от того, какую функцию вы используете для расчета квартилей, разница между значениями, рассчитанными с помощью КВАРТИЛЬ.ВКЛ и КВАРТИЛЬ.ИСКЛ , в большинстве случаев будет очень похожей.
В некоторых случаях даже возможно, что две функции будут возвращать одни и те же значения в зависимости от последовательности чисел в наборе данных.
Дополнительные ресурсы
STDEV.P и STDEV.S в Excel: в чем разница?
VAR.P и VAR.S в Excel: в чем разница?