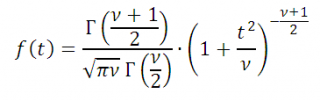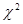Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в
MS
EXCEL
.
Понятие
Квантиля
основано на определении
Функции распределения
. Поэтому, перед изучением
Квантилей
рекомендуем освежить в памяти понятия из статьи
Функция распределения вероятности
.
Содержание статьи:
- Определение
- Квантили специальных видов
- Квантили стандартного нормального распределения
- Квантили распределения Стьюдента
- Квантили распределения ХИ-квадрат
- Квантили F-распределения
- Квантили распределения Вейбулла
- Квантили экспоненциального распределения
Сначала дадим формальное определение
квантиля,
затем приведем примеры их вычисления в MS EXCEL.
Определение
Пусть случайная величина
X
, имеет
функцию распределения
F
(
x
).
α-квантилем
(
альфа-
квантиль,
x
a
,
квантиль
порядка
α, нижний
α-
квантиль
) называют решение уравнения
x
a
=F
-1
(α), где
α
— вероятность, что случайная величина х примет значение меньшее или равное x
a
, т.е. Р(х<= x
a
)=
α.
Из определения ясно, что нахождение
квантиля
распределения является обратной операцией нахождения вероятности. Т.е. если при вычислении
функции распределения
мы находим вероятность
α,
зная x
a
, то при нахождении
квантиля
мы, наоборот, ищем
x
a
зная
α
.
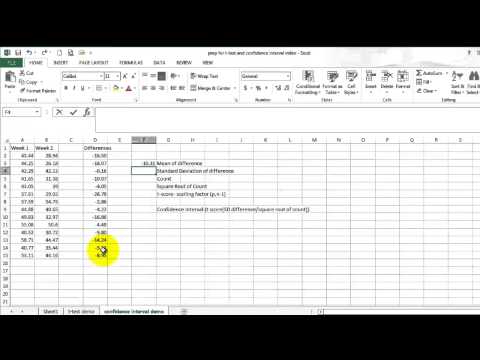
Чтобы пояснить определение, используем график функции
стандартного нормального распределения
(см.
файл примера Лист Определение
):
Примечание
: О построении графиков в MS EXCEL можно прочитать статью
Основные типы диаграмм в MS EXCEL
.
Например, с помощью графика вычислим 0,21-ю
квантиль
, т.е. такое значение случайной величины, что Р(X<=x
0,21
)=0,21.
Для этого найдем точку пересечения горизонтальной линии на уровне вероятности равной 0,21 с
функцией распределения
. Абсцисса этой точки равна -0,81. Соответственно, 0,21-я
квантиль
равна -0,81. Другими словами, вероятность того, что случайная величина, распределенная
стандартному нормальному закону,
примет значение
меньше
-0,81, равна 0,21 (21%).
Примечание
: При вычислении
квантилей
в MS EXCEL используются
обратные функции распределения
:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР(),
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Точное значение
квантиля
в нашем случае можно найти с помощью формулы
=НОРМ.СТ.ОБР(0,21)
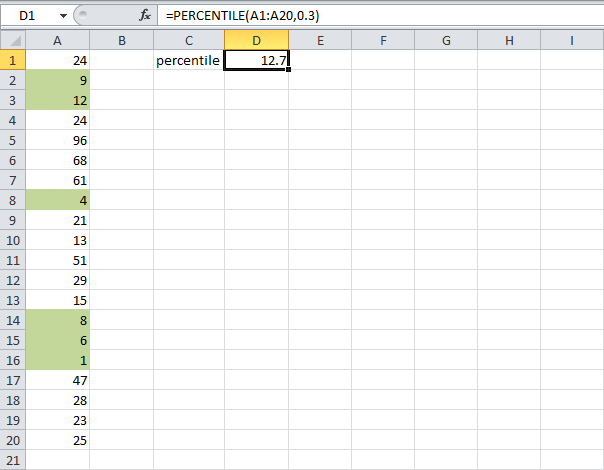
СОВЕТ
: Процедура вычисления
квантилей
имеет много общего с вычислением
процентилей
выборки
(см. статью
Процентили в MS EXCEL
).
Квантили специальных видов
Часто используются
Квантили
специальных видов:
-
процентили
x
p/100
, p=1, 2, 3, …, 99 -
квартили
x
p/4
, p=1, 2, 3 -
медиана
x
1/2
В качестве примера вычислим
медиану (0,5-квантиль)
логнормального распределения
LnN(0;1) (см.
файл примера лист Медиана
).
Это можно сделать с помощью формулы
=ЛОГНОРМ.ОБР(0,5; 0; 1)
Квантили стандартного нормального распределения
Необходимость в вычислении квантилей
стандартного нормального распределения
возникает при
проверке статистических гипотез
и при
построении доверительных интервалов.
Примечание
: Про
проверку статистических гипотез
см. статью
Проверка статистических гипотез в MS EXCEL
. Про
построение доверительных интервалов
см. статью
Доверительные интервалы в MS EXCEL
.
В данных задачах часто используется специальная терминология:
Нижний квантиль уровня
альфа
(
α
percentage point)
;
Верхний квантиль уровня альфа (upper
α
percentage point)
;
Двусторонние квантили уровня
альфа
.
Нижний квантиль уровня альфа
— это обычный
α-квантиль.
Чтобы пояснить название «
нижний» квантиль
, построим график
плотности вероятности
и
функцию вероятности
стандартного нормального
распределения
(см.
файл примера лист Квантили
).
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше
α-квантиля
. Из определения
квантиля
эта вероятность равна
α
. Из графика
функции распределения
становится понятно, откуда происходит название »
нижний квантиль» —
выделенная область расположена в нижней части графика.
Для
α=0,05,
нижний 0,05-квантиль
стандартного нормального распределения
равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:
=НОРМ.СТ.ОБР(0,05)
Однако, при
проверке гипотез
и построении
доверительных интервалов
чаще используется «верхний»
α-квантиль.
Покажем почему.
Верхним
α
—
квантилем
называют такое значение x
α
, для которого вероятность, того что случайная величина X примет значение
больше или равное
x
α
равна
альфа:
P(X>= x
α
)=
α
. Из определения понятно, что
верхний альфа
—
квантиль
любого распределения равен
нижнему (1-
α)
—
квантилю.
А для распределений, у которых
функция плотности распределения
является четной функцией,
верхний
α
—
квантиль
равен
нижнему
α
—
квантилю
со знаком минус
.
Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.
Действительно, для
α=0,05,
верхний 0,05-квантиль
стандартного нормального распределения
равен 1,645. Т.к.
функция плотности вероятности
стандартного нормального
распределения
является четной функцией, то вычисления в MS EXCEL
верхнего квантиля
можно сделать по двум формулам:
=НОРМ.СТ.ОБР(1-0,05)
=-НОРМ.СТ.ОБР(0,05)
Почему применяют понятие
верхний
α
—
квантиль?
Только из соображения удобства, т.к. он при
α<0,5
всегда положительный (в случае
стандартного нормального
распределения
). А при проверке гипотез
α
равно
уровню значимости
, который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре
проверки гипотез
пришлось бы записывать условие отклонения
нулевой гипотезы
μ>μ
0
как Z
0
>Z
1-
α
, подразумевая, что Z
1-
α
–
обычный
квантиль
порядка
1-
α
(или как Z
0
>-Z
α
). C верхнем квантилем эта запись выглядит проще Z
0
>Z
α
.
Примечание
: Z
0
— значение
тестовой статистики
, вычисленное на основе
выборки
. Подробнее см. статью
Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна)
.
Чтобы пояснить название «
верхний»
квантиль
, построим график
плотности вероятности
и
функцию вероятности
стандартного нормального
распределения
для
α=0,05.
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше
верхнего 0,05-квантиля
, т.е.
больше
значения 1,645. Эта вероятность равна 0,05.
На графике
плотности вероятности
площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика
функции распределения
становится понятно, откуда происходит название «верхний»
квантиль
—
выделенная область расположена в верхней части графика. Если Z
0
больше
верхнего квантиля
, т.е. попадает в выделенную область, то
нулевая гипотеза
отклоняется.
Также при
проверке двухсторонних гипотез
и построении соответствующих
доверительных интервалов
иногда используется понятие «двусторонний»
α-квантиль.
В этом случае условие отклонения
нулевой гипотезы
звучит как |Z
0
|>Z
α
/2
, где Z
α
/2
–
верхний
α/2-квантиль
. Чтобы не писать
верхний
α/2-квантиль
, для удобства используют «двусторонний»
α-квантиль.
Почему двусторонний? Как и в предыдущих случаях, построим график
плотности вероятности стандартного нормального распределения
и график
функции распределения
.
Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение
между
нижним квантилем уровня α
/2 и
верхним квантилем
уровня α
/2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z
0
попадает в одну из выделенных областей, то
нулевая гипотеза
отклоняется.
Вычислить
двусторонний
0,05
—
квантиль
это можно с помощью формул MS EXCEL:
=НОРМ.СТ.ОБР(1-0,05/2)
или
=-НОРМ.СТ.ОБР(0,05/2)
Другими словами,
двусторонние α-квантили
задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.
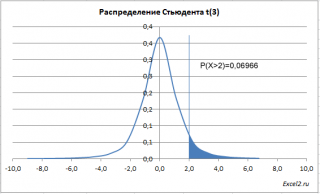
Квантили распределения Стьюдента
Аналогичным образом
квантили
вычисляются и для
распределения Стьюдента
. Например, вычислять
верхний
α/2-
квантиль
распределения Стьюдента с
n
-1 степенью свободы
требуется, если проводится
проверка двухсторонней гипотезы
о
среднем значении
распределения при
неизвестной
дисперсии
(
см. эту статью
).
Для
верхних квантилей
распределения Стьюдента
часто используется запись t
α/2,n-1
. Если такая запись встретилась в статье про
проверку гипотез
или про построение
доверительного интервала
, то это именно
верхний квантиль
.
Примечание
:
Функция плотности вероятности распределения Стьюдента
, как и
стандартного нормального распределения
, является четной функцией.
Чтобы вычислить в MS EXCEL
верхний
0,05/2
—
квантиль
для t-распределения с 10 степенями свободы (или тоже самое
двусторонний
0,05-квантиль
), необходимо записать формулу
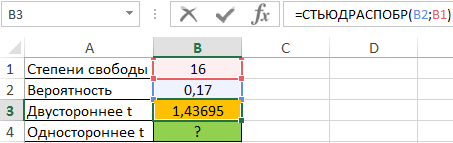
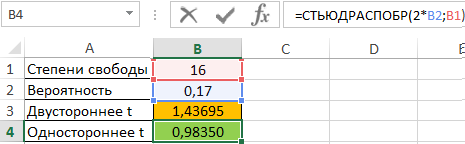
=СТЬЮДЕНТ.ОБР.2Х(0,05; 10)
или
=СТЬЮДРАСПОБР(0,05; 10)
или
=СТЬЮДЕНТ.ОБР(1-0,05/2; 10)
или
=-СТЬЮДЕНТ.ОБР(0,05/2; 10)
.2X означает 2 хвоста, т.е.
двусторонний квантиль
.
Квантили распределения ХИ-квадрат
Вычислять
квантили
распределения ХИ-квадрат
с
n
-1 степенью свободы
требуется, если проводится
проверка гипотезы
о
дисперсии нормального распределения
(см. статью
Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения
).
При
проверке таких гипотез
также используются
верхние квантили.
Например, при
двухсторонней гипотезе
требуется вычислить 2
верхних
квантиля
распределения
ХИ
2
: χ
2
α/2,n-1
и
χ
2
1-
α/2,n-1
. Почему требуется вычислить два
квантиля
, не один, как при
проверке гипотез о среднем
, где используется
стандартное нормальное распределение
или
t-распределение
?
Дело в том, что в отличие от
стандартного нормального распределения
и
распределения Стьюдента
, плотность распределения
ХИ
2
не является четной (симметричной относительно оси х). У него все
квантили
больше 0, поэтому
верхний альфа-квантиль
не равен
нижнему (1-альфа)-квантилю
или по-другому:
верхний альфа-квантиль
не равен
нижнему альфа-квантилю
со знаком минус.
Чтобы вычислить
верхний
0,05/2
—
квантиль
для
ХИ
2
-распределения
с
числом степеней свободы
10, т.е.
χ
2
0,05/2,n-1
, необходимо в MS EXCEL записать формулу
=ХИ2.ОБР.ПХ(0,05/2; 10)
или
=ХИ2.ОБР(1-0,05/2; 10)
Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике
функции распределения
.
Чтобы вычислить
верхний
(1-0,05/2)-
квантиль
при том же
числе степеней свободы
, т.е.
χ
2
1-0,05/2,n-1
и необходимо записать формулу
=ХИ2.ОБР.ПХ(1-0,05/2; 10)
или
=ХИ2.ОБР(0,05/2; 10)
Результат равен 3,25.
Квантили F-распределения
Вычислять
квантили
распределения Фишера
с
n
1
-1 и
n
2
-1 степенями свободы
требуется, если проводится
проверка гипотезы
о равенстве
дисперсий двух нормальных распределений
(см. статью
Двухвыборочный тест для дисперсии: F-тест в MS EXCEL
).
При
проверке таких гипотез
используются, как правило,
верхние квантили.
Например, при
двухсторонней гипотезе
требуется вычислить 2
верхних
квантиля
F
-распределения:
F
α/2,n1-1,
n
2
-1
и
F
1-α/2,n1-1,
n
2
-1
. Почему требуется вычислить два
квантиля
, не один, как при
проверке гипотез о среднем
? Причина та же, что и для распределения ХИ
2
– плотность
F-распределения
не является четной
.
Эти
квантили
нельзя выразить один через другой как для
стандартного нормального распределения
.
Верхний альфа-квантиль
F
-распределения
не равен
нижнему альфа-квантилю
со знаком минус.
Чтобы вычислить
верхний
0,05/2-квантиль
для
F
-распределения
с
числом степеней свободы
10 и 12, необходимо записать формулу
=F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)
Результат равен 3,37. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике
функции распределения
.
Квантили распределения Вейбулла
Иногда
обратная функция распределения
может быть представлена в явном виде с помощью элементарных функций, например как для
распределения Вейбулла
. Напомним, что функция этого распределения задается следующей формулой:
После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:
Примечание
: Вместо обозначения
α-квантиль
может использоваться
p
—
квантиль.
Суть от этого не меняется.
Это и есть обратная функция, которая позволяет вычислить
P
—
квантиль
(
p
—
quantile
). Для его вычисления в формуле нужно подставить известное значение вероятности P и вычислить значение х
p
(вероятность того, что случайная величина Х примет значение меньше или равное х
p
равна P).
Квантили экспоненциального распределения
Задача
:
Случайная величина имеет
экспоненциальное распределение
:
Требуется выразить
p
-квантиль
x
p
через параметр распределения λ и заданную вероятность
p
.
Примечание
: Вместо обозначения
α-квантиль
может использоваться
p-квантиль
. Суть от этого не меняется.
Решение
: Вспоминаем, что
p
-квантиль
– это такое значение x
p
случайной величины X, для которого P(X<=x
p
)=
p
. Т.е. вероятность, что случайная величина X примет значение меньше или равное x
p
равна
p
. Запишем это утверждение с помощью формулы:
По сути, мы записали
функцию вероятности экспоненциального распределения
: F(x
p
)=
p
.
Из определения
квантиля
следует, что для его нахождения нам потребуется
обратная функция распределения
.
Проинтегрировав вышеуказанное выражение, получим:
Используя это уравнение, выразим x
p
через λ и вероятность
p
.
Конечно, явно выразить
обратную функцию распределения
можно не для всех
функций распределений
.
Содержание
- Медиана и квартили
- Математическое описание
- Среднее значение
- Отклонение от среднего
- Квантиль
- Построение интервалов
- Двусторонний доверительный интервал
- Первый квартиль
- Третий квартиль
- Квартили непрерывного распределения
- Квартили в MS EXCEL
- Моменты случайной величины
- Статистический анализ роста доли дохода в Excel за период
- Анализ статистики случайно сгенерированных чисел в Excel
- Расчет квартилей в R и SAS
- Расчет децилей для дискретного ряда
- Квантили специальных видов
- Квантили стандартного нормального распределения
- Квантили распределения Стьюдента
- Квантили распределения ХИ-квадрат
Квантили нормального распределения
Основная статья: Медиана (статистика)
- 0,25-квантиль называется первым (или нижним) квартилем (от лат. quarta — четверть);
- 0,5-квантиль называется медианой (от лат. mediāna — середина) или вторым квартилем
- 0,75-квантиль называется третьим (или верхним) квартилем.
Интерквартильным размахом (англ. Interquartile range) называется разность между третьим и первым квартилями. Интерквартильный размах является характеристикой разброса распределения величины и является робастным аналогом дисперсии. Вместе, медиана и интерквартильный размах могут быть использованы вместо математического ожидания и дисперсии в случае распределений с большими выбросами, либо при невозможности вычисления последних.
Математическое описание
Смотря на закон распределения, мы можем понять, какова вероятность того или иного события, можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы “на глаз” перевести в математически обоснованное утверждение.
Крайне важное определение: математическое ожидание – это площадь под графиком распределения. Если мы говорим о дискретном распределении – это сумма событий умноженных на соответсвующие вероятности, также известно как момент:
(2) E(X) = Σ(pi•Xi) E – от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:
(3) E(X + Y) = E(X) + E(Y)
(4) E(X•Y) = E(X) • E(Y)
Момент степени k:
(5) νk = E(Xk)
Центральный момент степени k:
(6) μk = E[X – E(X)]k
Среднее значение
Среднее значение (μ) закона распределения – это математическое ожидание случайной величины (случайная величина – это событие), например, сколько в среднем посетителей заходит в магазин в час:
| Кол-во посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество наблюдений | 114 | 115 | 52 | 52 | 24 | 13 | 30 |
| Таблица 1. Количество посетителей в час |
График 1. Количество посетителей в час
Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:
μ = (114 • 0 + 115 • 1 + 52 • 2 + 52 • 3 + 24 • 4 + 13 • 5 + 30 • 6) / 400 = 716/400 = 1.79
То же самое мы можем проделать используя формулу 2:
μ = M(X) = Σ(Xi•pi) = 0 • 0.29 + 1 • 0.29 + 2 • 0.13 + 3 • 0.13 + 4 • 0.06 + 5 • 0.03 + 6 • 0.08 = 1.79 Момент первой степени, формула (5)
Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 1.79 посетителя в час
| Количество посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятность (%) | 28.5 | 28.8 | 13 | 13 | 6 | 3.3 | 7.5 |
| Таблица 2. Закон распределения количества посетителей |
Отклонение от среднего
Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:
График 2. График функции вероятности. Распределение ≈ 100±5
Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы использовать в качестве меры удалённости “разность” между средним и случайными величинами:
(7) xi – μ
но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц между величинами и средним значением:
(8) (xi – μ)2
Соответственно, среднее значение удалённости – это математическое ожидание квадратов удалённости:
(9) σ2 = E[(X – E(X))2] Поскольку вероятности любой удалённости равносильны – вероятность каждого из них – 1/n, откуда: (10) σ2 = E[(X – E(X))2] = ∑[(Xi – μ)2]/n Она же формула центрального момента (6) второй степени
σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ2 называется дисперсией. Корень из дисперсии называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:
(11) μ±σ
(12) σ = √(σ2) = √[∑[(Xi – μ)2]/n]
Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:
σ = √(∑(x-μ)2/n) = √{[(90 – 99.95)2 + (91 – 99.95)2 + (92 – 99.95)2 + (93 – 99.95)2 + (94 – 99.95)2 + (95 – 99.95)2 + (96 – 99.95)2 + (97 – 99.95)2 + (98 – 99.95)2 + (99 – 99.95)2 + (100 – 99.95)2 + (101 – 99.95)2 + (102 – 99.95)2 + (103 – 99.95)2 + (104 – 99.95)2 + (105 – 99.95)2 + (106 – 99.95)2 + (107 – 99.95)2 + (108 – 99.95)2 + (109 – 99.95)2 + (110 – 99.95)2]/21} = 6.06
Итак, для графика 2 мы получили:
X = 99.95±6.06 ≈ 100±6 , что немного отличается от полученного “на глаз”
Квантиль
График 3. Функция распределения. Медиана
График 4. Функция распределения. 4-квантиль или квартиль
График 5. Функция распределения. 0.34-квантиль
Для анализа функции распределения ввели понятие квантиль. Квантиль – это случайная величина при заданном уровне вероятности, т.е.: квантиль для уровня вероятности 50% – это случайная величина на графике плотности вероятности, которая имеет вероятность 50%. На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)
- 2-квантиль – медиана
- 4-квантиль – квартиль
- 10-квантиль – дециль
- 100-квантиль – перцентиль
То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям, и для каждого дециля нашли значение случайной величины.
Также, используется обозначение x-квантиль, где х – дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при p = 0.34.
Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.
Построение интервалов
Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например, интерес – случайное число = 98), а для группы событий (например, интерес – случайное число между 96 и 99). Доверительный интервал бывает двух видов: односторонний и двусторонний. Параметр доверительного интервала – уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.
Двусторонний доверительный интервал
Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются “критическая область“
Первый квартиль
Значение квартиля Q1 находится в интервале 68,98 – 71,70, соответствующего частоте fQ1 = 150:4 = 37,5
Третий квартиль
Значение квартиля находится в интервале 68,98 – 71,70, соответствующего частоте fQ3 = (3*150):4 = 112,5
Квартили непрерывного распределения
Если функция распределения F (х) случайной величины х непрерывна, то 1-й квартиль является решением уравнения F(х) =0,25, второй – F(х) =0,5, а третий F(х) =0,75.
Примечание : Подробнее о Функции распределения см. статью Функция распределения и плотность вероятности в MS EXCEL .
Если известна функция плотности вероятности p (х) , то 1-й квартиль можно найти из уравнения:
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ 2 ), получим, что медиана (2-й квартиль ) вычисляется по формуле e μ или в MS EXCEL =EXP(μ). При μ=1, медиана равна 2,718.
Обратите внимание на точку Функции распределения , для которой F(х)=0,5 (см. картинку выше или файл примера , лист Квартиль-распределение) . Абсцисса этой точки равна 2,718. Это и есть значение 2-го квартиля ( медианы ), что естественно совпадает с ранее вычисленным значением по формуле e μ .
Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице:
Поэтому, линии квартилей ( х=квартиль ) делят площадь под графиком функции плотности вероятности на 4 равные части.
Квартили в MS EXCEL
Чтобы вычислить в MS EXCEL квартили заданного распределения необходимо использовать соответствующую обратную функцию распределения .
При вычислении квартилей в MS EXCEL используются обратные функции распределения : НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР() , ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .
Например, в MS EXCEL 1-й квартиль для логнормального распределения LnN(1;1) можно вычислить по формуле =ЛОГНОРМ.ОБР(0,25;1;1) , а 3-й квартиль для стандартного нормального распределения по формуле =НОРМ.СТ.ОБР(0,75) .
Моменты случайной величины
Моменты случайно величины описывают различные аспекты характера и формы нашего распределения.
#1 — первый момент случайной величины — среднее значение данных, которое показывает место распределения.
#2 — второй момент случайной величины — дисперсия, которая показывает разброс распределения. Большие значения имеют больший размах, чем маленькие.
#3 — третий момент случайной величины — коэффициент асимметрии — мера того, насколько неравномерным является распределение. Коэффициент асимметрии положителен, если распределение наклонено влево и левый хвост короче правого. То есть среднее значение находится правее. И наоборот:

#4 — четвертый момент случайной величины — коэффициент эксцесса, который описывает то, насколько толстый хвост и насколько острый пик распределения. Этот коэффициент показывает, насколько вероятно найти точки экстремума в данных. Чем выше значение, тем вероятнее выбросы. Это похоже на разброс (дисперсию), но между ними есть отличия.

Как видно на графике, чем выше значение пики, тем выше коэффициент эксцесса, т.е. у верхней кривой коэффициент эксцесса выше, чем у нижней.
Статистический анализ роста доли дохода в Excel за период
Пример 2. В таблице приведены данные о доходах предпринимателя за год. Доказать, что примерно 75% значений меньше, чем третий квартиль доходов.
Вид исходной таблицы:

Определим 3-й по формуле:


Определим соотношение чисел, меньше полученного числа, к общему количеству значений по формуле:
=СЧЁТЕСЛИ(B2:B13;”<“&B15)/СЧЁТ(B2:B13)
Полученные результаты:

Анализ статистики случайно сгенерированных чисел в Excel
Пример 3. Имеется диапазон случайных чисел, отсортированный в порядке возрастания. Определить соотношение суммы чисел, которые меньше 1-го квартиля, к сумме чисел, которые превышают значение 1-го квартиля.
Чтобы сгенерировать случайное число в Excel воспользуемся функцией:
=СЛУЧМЕЖДУ(0;1000)
После генерации отсортируем случайно сгенерированные числа по возрастанию. Вид исходной таблицы данных со случайными числами:

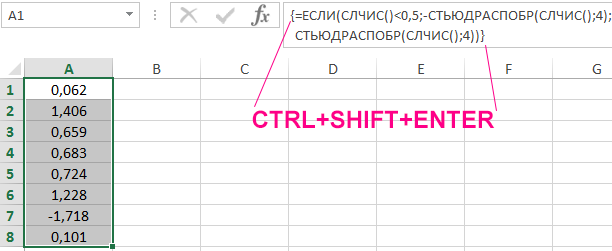
Формула для расчета имеет следующий вид (формула массива CTRL+SHIFT+ENTER):
Функции СУММ с вложенными функциями ЕСЛИ выполняют расчет суммы только тех чисел, которые меньше и больше соответственно значения, возвращаемого функцией для исследуемого диапазона. Из полученных значений вычисляется частное. Результат расчетов:

Общая сумма чисел исследуемого диапазона, которые меньше 1-го квартиля, составляет всего 8,57% от общей суммы чисел, которые больше 1-го квартиля.
Расчет квартилей в R и SAS
Функция quantile в R использует все девять алгоритмов расчета квантилей, в соответствии с нумерацией, предложенной Hyndman and Fan в работе 1996 г. (рис. 15; если вы не знакомы с R, рекомендую начать с Алексей Шипунов. Наглядная статистика. Используем R!). Квантиль при i-м методе расчета:
где i – номер метода, 1 ≤ i ≤ 9, (j–m)/n ≤ p < (j–m+1)/n, хj – j-ый порядковый элемент упорядоченного ряда, n – размер выборки, γ является функцией двух параметров: j = floor(np + m) и g = np + m – j, где floor – функция возвращающая наибольшее целое, но всё еще меньшее, чем аргумент функции (аналог в Excel – ОКРВНИЗ.МАТ), m – константа, определяемая типом алгоритма расчета квантиля. Если вас интересуют подробности, обратитесь к справочной системе R.
SAS предлгает 5 методов расчета квантилей.
Расчет децилей для дискретного ряда
-
Определяем номер дециля по формуле:
,
-
Если номер дециля – целое число, то значение дециля будет равно величине элемента ряда, которое обладает накопленной частотой равной номеру дециля. Например, если номер дециля равен 20, его значение будет равно значению признака с S =20 (накопленной частотой равной 20).
Если номер дециля – нецелое число, то дециль попадает между двумя наблюдениями. Значением дециля будет сумма, состоящая из значения элемента, для которого накопленная частота равна целому значению номера дециля, и указанной части (нецелая часть номера дециля) разности между значением этого элемента и значением следующего элемента.
Например, если номер дециля равна 20,25, дециль попадает между 20-м и 21-м наблюдениями, и его значение будет равно значению 20-го наблюдения плюс 1/4 разности между значением 20-го и 21-го наблюдений.
Квантили специальных видов
Часто используются Квантили специальных видов:
- процентили x p/100 , p=1, 2, 3, …, 99
- квартили x p/4 , p=1, 2, 3
- медиана x 1/2
В качестве примера вычислим медиану (0,5-квантиль) логнормального распределения LnN(0;1) (см. файл примера лист Медиана ).
Это можно сделать с помощью формулы =ЛОГНОРМ.ОБР(0,5; 0; 1)
Квантили стандартного нормального распределения
Необходимость в вычислении квантилей стандартного нормального распределения возникает при проверке статистических гипотез и при построении доверительных интервалов.
Примечание : Про проверку статистических гипотез см. статью Проверка статистических гипотез в MS EXCEL . Про построение доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .
В данных задачах часто используется специальная терминология:
- Нижний квантиль уровня альфа ( α percentage point)
- Верхний квантиль уровня альфа (upper α percentage point)
- Двусторонние квантили уровня альфа .
Нижний квантиль уровня альфа – это обычный α-квантиль. Чтобы пояснить название « нижний» квантиль , построим график плотности вероятности и функцию вероятности стандартного нормального распределения (см. файл примера лист Квантили ).
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше α-квантиля . Из определения квантиля эта вероятность равна α . Из графика функции распределения становится понятно, откуда происходит название ” нижний квантиль” – выделенная область расположена в нижней части графика.
Для α=0,05, нижний 0,05-квантиль стандартного нормального распределения равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:
=НОРМ.СТ.ОБР(0,05)
Однако, при проверке гипотез и построении доверительных интервалов чаще используется “верхний” α-квантиль. Покажем почему.
Верхним α – квантилем называют такое значение x α , для которого вероятность, того что случайная величина X примет значение больше или равное x α равна альфа: P(X>= x α )= α . Из определения понятно, что верхний альфа – квантиль любого распределения равен нижнему (1- α) – квантилю. А для распределений, у которых функция плотности распределения является четной функцией, верхний α – квантиль равен нижнему α – квантилю со знаком минус . Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.
Действительно, для α=0,05, верхний 0,05-квантиль стандартного нормального распределения равен 1,645. Т.к. функция плотности вероятности стандартного нормального распределения является четной функцией, то вычисления в MS EXCEL верхнего квантиля можно сделать по двум формулам:
=НОРМ.СТ.ОБР(1-0,05)
=-НОРМ.СТ.ОБР(0,05)
Почему применяют понятие верхний α – квантиль? Только из соображения удобства, т.к. он при α всегда положительный (в случае стандартного нормального распределения ). А при проверке гипотез α равно уровню значимости , который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре проверки гипотез пришлось бы записывать условие отклонения нулевой гипотезы μ>μ 0 как Z 0 >Z 1- α , подразумевая, что Z 1- α – обычный квантиль порядка 1- α (или как Z 0 >-Z α ). C верхнем квантилем эта запись выглядит проще Z 0 >Z α .
Примечание : Z 0 – значение тестовой статистики , вычисленное на основе выборки . Подробнее см. статью Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна) .
Чтобы пояснить название « верхний» квантиль , построим график плотности вероятности и функцию вероятности стандартного нормального распределения для α=0,05.
Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше верхнего 0,05-квантиля , т.е. больше значения 1,645. Эта вероятность равна 0,05.
На графике плотности вероятности площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика функции распределения становится понятно, откуда происходит название “верхний” квантиль – выделенная область расположена в верхней части графика. Если Z 0 больше верхнего квантиля , т.е. попадает в выделенную область, то нулевая гипотеза отклоняется.
Также при проверке двухсторонних гипотез и построении соответствующих доверительных интервалов иногда используется понятие “двусторонний” α-квантиль. В этом случае условие отклонения нулевой гипотезы звучит как |Z 0 |>Z α /2 , где Z α /2 – верхний α/2-квантиль . Чтобы не писать верхний α/2-квантиль , для удобства используют “двусторонний” α-квантиль. Почему двусторонний? Как и в предыдущих случаях, построим график плотности вероятности стандартного нормального распределения и график функции распределения .
Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение между нижним квантилем уровня α /2 и верхним квантилем уровня α /2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z 0 попадает в одну из выделенных областей, то нулевая гипотеза отклоняется.
Вычислить двусторонний 0,05 – квантиль это можно с помощью формул MS EXCEL: =НОРМ.СТ.ОБР(1-0,05/2) или =-НОРМ.СТ.ОБР(0,05/2)
Другими словами, двусторонние α-квантили задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.
Квантили распределения Стьюдента
Аналогичным образом квантили вычисляются и для распределения Стьюдента . Например, вычислять верхний α/2- квантиль распределения Стьюдента с n -1 степенью свободы требуется, если проводится проверка двухсторонней гипотезы о среднем значении распределения при неизвестной дисперсии ( см. эту статью ).
Для верхних квантилей распределения Стьюдента часто используется запись t α/2,n-1 . Если такая запись встретилась в статье про проверку гипотез или про построение доверительного интервала , то это именно верхний квантиль .
Примечание : Функция плотности вероятности распределения Стьюдента , как и стандартного нормального распределения , является четной функцией.
Чтобы вычислить в MS EXCEL верхний 0,05/2 – квантиль для t-распределения с 10 степенями свободы (или тоже самое двусторонний 0,05-квантиль ), необходимо записать формулу =СТЬЮДЕНТ.ОБР.2Х(0,05; 10) или =СТЬЮДРАСПОБР(0,05; 10) или =СТЬЮДЕНТ.ОБР(1-0,05/2; 10) или =-СТЬЮДЕНТ.ОБР(0,05/2; 10)
.2X означает 2 хвоста, т.е. двусторонний квантиль .
Квантили распределения ХИ-квадрат
Вычислять квантили распределения ХИ-квадрат с n -1 степенью свободы требуется, если проводится проверка гипотезы о дисперсии нормального распределения (см. статью Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения ).
При проверке таких гипотез также используются верхние квантили. Например, при двухсторонней гипотезе требуется вычислить 2 верхних квантиля распределения ХИ 2 : χ 2 α/2,n-1 и χ 2 1- α/2,n-1 . Почему требуется вычислить два квантиля , не один, как при проверке гипотез о среднем , где используется стандартное нормальное распределение или t-распределение ?
Дело в том, что в отличие от стандартного нормального распределения и распределения Стьюдента , плотность распределения ХИ 2 не является четной (симметричной относительно оси х). У него все квантили больше 0, поэтому верхний альфа-квантиль не равен нижнему (1-альфа)-квантилю или по-другому: верхний альфа-квантиль не равен нижнему альфа-квантилю со знаком минус.
Чтобы вычислить верхний 0,05/2 – квантиль для ХИ 2 -распределения с числом степеней свободы 10, т.е. χ 2 0,05/2,n-1 , необходимо в MS EXCEL записать формулу =ХИ2.ОБР.ПХ(0,05/2; 10) или =ХИ2.ОБР(1-0,05/2; 10)
Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике функции распределения .
Чтобы вычислить верхний (1-0,05/2)- квантиль при том же числе степеней свободы , т.е. χ 2 1-0,05/2,n-1 и необходимо записать формулу =ХИ2.ОБР.ПХ(1-0,05/2; 10) или =ХИ2.ОБР(0,05/2; 10)
Результат равен 3,25.
Источники
- https://dic.academic.ru/dic.nsf/ruwiki/291015
- https://k-tree.ru/articles/statistika/analiz_dannyh/svoistva_raspredeleniia
- https://univer-nn.ru/zadachi-po-statistike-primeri/kvartili-v-statistike/
- https://excel2.ru/articles/kvartili-i-interkvartilnyy-interval-iqr-v-ms-excel
- https://nuancesprog.ru/p/3307/
- https://exceltable.com/funkcii-excel/primery-funkcii-kvartil
- https://baguzin.ru/wp/kvartil-kakie-formuly-rascheta-ispol/
- https://studfile.net/preview/5316597/page:4/
- https://excel2.ru/articles/kvantili-raspredeleniy-ms-excel
Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).
Распределение Стьюдента
Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ2. Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией
Тогда случайная величина
имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.
Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:
где
Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96sx̅. Другими словами, являются ли распределения случайных величин
и
эквивалентными.
Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.
Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.
Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:
Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.
Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.
Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.
Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».
У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина
зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.
Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:
1. средняя X̅ и выборочная дисперсия s2 являются независимыми величинами;
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ2(хи-квадрат) с таким же количеством степеней свободы, т.е.
где k – количество степеней свободы (на английском degrees of freedom (d.f.))
Вернемся к распределению средней. Разделим числитель и знаменатель выражения
на σX̅. Получим
Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.
Тогда исходное выражение примет вид
Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.
Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.
Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин
где ξ распределена по стандартному нормальному закону, а χ2k подчиняется распределению χ2 c k степенями свободы.
Таким образом, формула критерия Стьюдента для средней арифметической
есть частный случай стьюдентова отношения
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.
При k > 30 t-критерий практически не отличается от стандартного нормального распределения.
В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel
С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.
Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.
Таким образом, мы решили одну и ту же задачу тремя способами:
1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.
Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.
Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.
Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.
Скачать файл с примером.
Всего доброго, будьте здоровы.
Поделиться в социальных сетях:
Все, рассмотренные в этом разделе инструменты вычисляют значения квантилей как значения функций, обратных соответствующим функциям распределения. Все эти функции – библиотечные функции Excel из группы функций «Статистические»,.
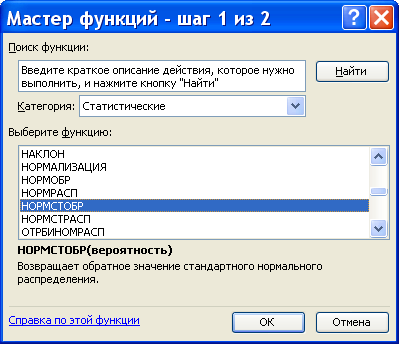
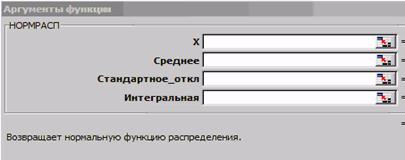
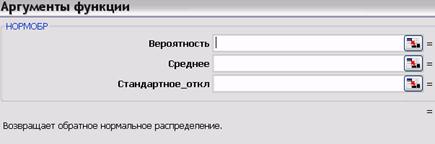
Функция вычисления критических точек распределения Лапласа
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) стандартного нормального распределения.
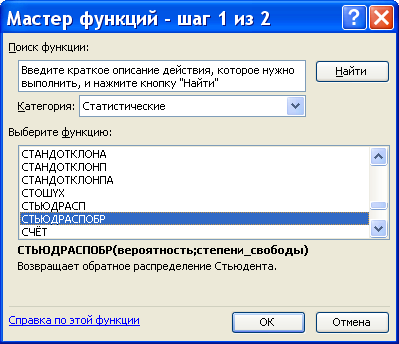
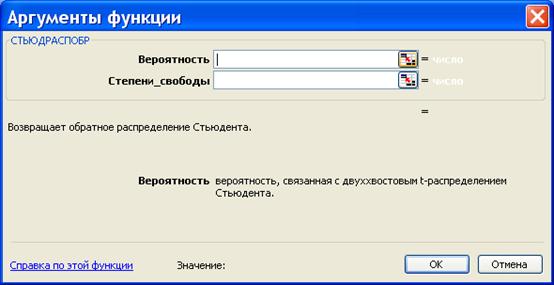
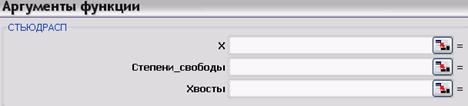
Функция вычисления критических точек распределения Стьюдента
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения Стьюдента с числом степеней свободы, равным значению, введенному в поле «Степени свободы» (понятно, что это натуральное число).
Важно знать, что функция Excel СТЬЮДРАСПОБР( p , k ) возвращает значение t , при котором P (| x | > t ) = p , x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы.
Поэтому решение уравнения в Excel возвращает функция СТЬЮДРАСПОБР( a , n – 1).
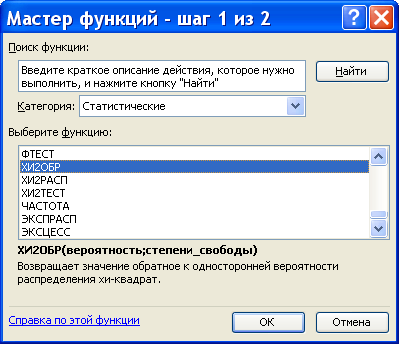
Функция вычисления критических точек распределения
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения с числом степеней свободы, равным значению, введенному в поле «Степени свободы» (понятно, что это натуральное число).
В Excel функция распределения случайной величины определена нестандартно: F x ( x ) = P ( x > x ). Поэтому для вычисления квантиля вводим в качестве аргумента функции ХИ2ОБР значение вероятности, равное , а для вычисления – .
Функция КВАРТИЛЬ
Возвращает квартиль множества данных. Квартиль часто используются при анализе продаж для разбиения генеральной совокупности на группы. Например, можно воспользоваться функцией КВАРТИЛЬ, чтобы найти среди всех предприятий 25 процентов наиболее доходных.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новых функциях см. в разделах Функция КВАРТИЛЬ.ИСКЛ и Функция КВАРТИЛЬ.ВКЛ.
Синтаксис
Аргументы функции КВАРТИЛЬ описаны ниже.
Массив Обязательный. Массив или диапазон ячеек с числовыми значениями, для которых определяется значение квартиля.
Часть Обязательный. Значение, которое требуется вернуть.
Содержание
- Определение термина
- Расчет показателя в Excel
- Способ 1: Мастер функций
- Способ 2: работа со вкладкой «Формулы»
- Способ 3: ручной ввод
- Вопросы и ответы
Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Определение термина
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
- Строим таблицу с двумя рядами переменных.
- Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.
- После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».
- Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».
- Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».
- Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
Способ 3: ручной ввод
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.
После того, как данные введены, жмем кнопку Enter для вывода результата на экран.
Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Еще статьи по данной теме:
Помогла ли Вам статья?
В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами Excel.
Ключевые слова:
безотказная работа, доверительный интервал, испытания, нормальный закон распределения, число отказов.
Определение показателей надёжности необходимо для формулирования требования по надежности к проектируемым устройствам или системам. Показатель надежности — это количественная характеристика одного или нескольких свойств, составляющих надежность объекта [1].
Поскольку отказы и сбои элементов являются случайными событиями, то теория вероятностей и математическая статистика являются основным аппаратом, используемым при исследовании надежности, а сами характеристики надежности должны выбираться из числа показателей, принятых в теории вероятностей [2, с.
13].
Количественные характеристики надежности при нормальном законе распределения отказов могут быть определены из следующих выражений:
(1)
P(t)=
(2)
λ(
)=
(3),
где
нормированная и центрированная функция Лапласа.
Произведем расчет параметров надежности испытаний, проведенных в течение 100 часов на 100 деталях, 34 из которых вышли из строя.
Для построения статистического ряда время испытаний разбивают на интервалы (разряды) и подсчитывают частоту, интенсивность и вероятность отказов, используя выражения (1), (2) и (3). Определяют доверительные интервалы математического ожидания и среднеквадратичного отклонения при нормальном законе распределения отказов и заданном коэффициенте доверия [3, с. 60].
Результаты вычислений представлены в таблице Excel (Таблица 1).
Таблица 1
Результаты расчета основных показателей испытаний
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
5 |
3 |
5 |
2 |
2 |
3 |
3 |
3 |
5 |
3 |
|
|
0,935 |
0,917 |
0,896 |
0,870 |
0,841 |
0,805 |
0,767 |
0,725 |
0,680 |
0,633 |
|
|
0,983 |
0,986 |
0,988 |
0,990 |
0,991 |
0,992 |
0,993 |
0,993 |
0,994 |
0,994 |
|
λн(t) |
1,050 |
1,074 |
1,102 |
1,137 |
1,178 |
1,232 |
1,294 |
1,369 |
1,460 |
1,570 |
|
|
0,064 |
0,082 |
0,103 |
0,129 |
0,158 |
0,194 |
0,232 |
0,274 |
0,319 |
0,366 |
|
|
0,014 |
0,002 |
0,026 |
0,020 |
0,011 |
0,005 |
0,002 |
0,014 |
0,009 |
0,026 |
|
|
0,085065269 |
|||||||||
Листинг фрагмента программы расчета показателей при нормальном законе распределения:
‘Вычислим 43 строку таблицы(45)=============================Рн(t)
СтрокаТаблицы = 45
‘a=(t-Tср)/Сигма
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
a = Abs(Sheets(«ОсновнаяТаблица»).
‘b=Фо
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
If a <= Sheets(«Таблица функции Лапласа»).Cells(2, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(2, 2).Value
GoTo далее
End If
If a >= Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
GoTo далее
End If
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value = a Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
GoTo далее3
End If
If a < Sheets(«Таблица функции Лапласа»).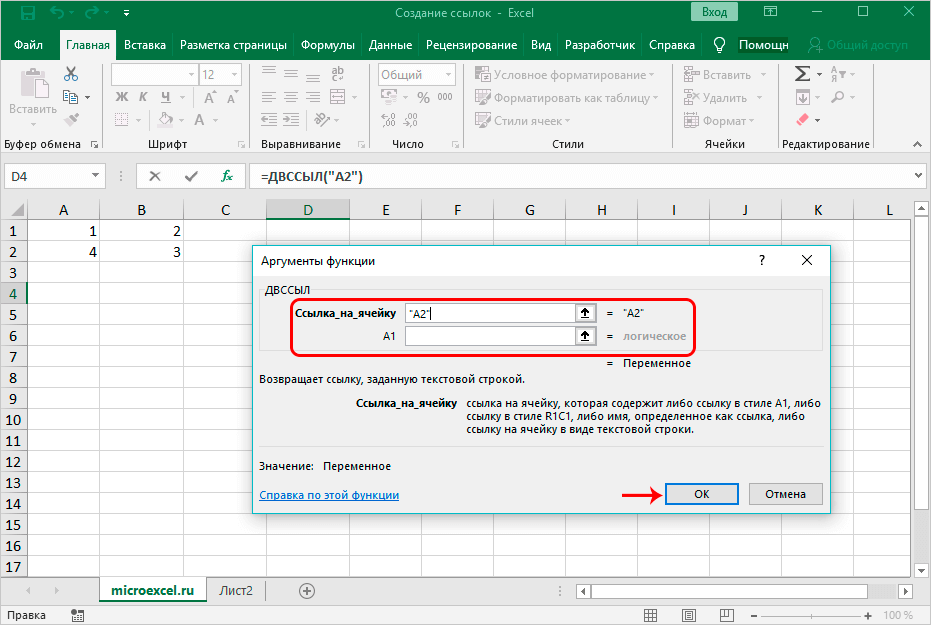
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value — a < a — Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
Else
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
End If
GoTo далее3
End If
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
далее3:
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = 0.5 + ф0
Next
‘Вычислим 44 строку таблицы(46)=============================fн(t)
СтрокаТаблицы = 46
СтолбецТаблицы = 4
Pi = Application.WorksheetFunction.Pi
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»).
Next
‘Заполним 45 строку таблицы(47)=============================Лямбда н(t)
СтрокаТаблицы = 47
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Sheets(«ОсновнаяТаблица»).Cells(46, n).Value / Sheets(«ОсновнаяТаблица»).Cells(45, n).Value
Next
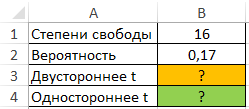
Для определения доверительного интервала для математического ожидания по таблице квантилей распределения Стьюдента находят квантиль вероятности. Используя выражения (4) и (5) проводят расчеты
(4)
(5)
‘Заполним 30 строку таблицы(32)=============================Tср min
СтрокаТаблицы = 32
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).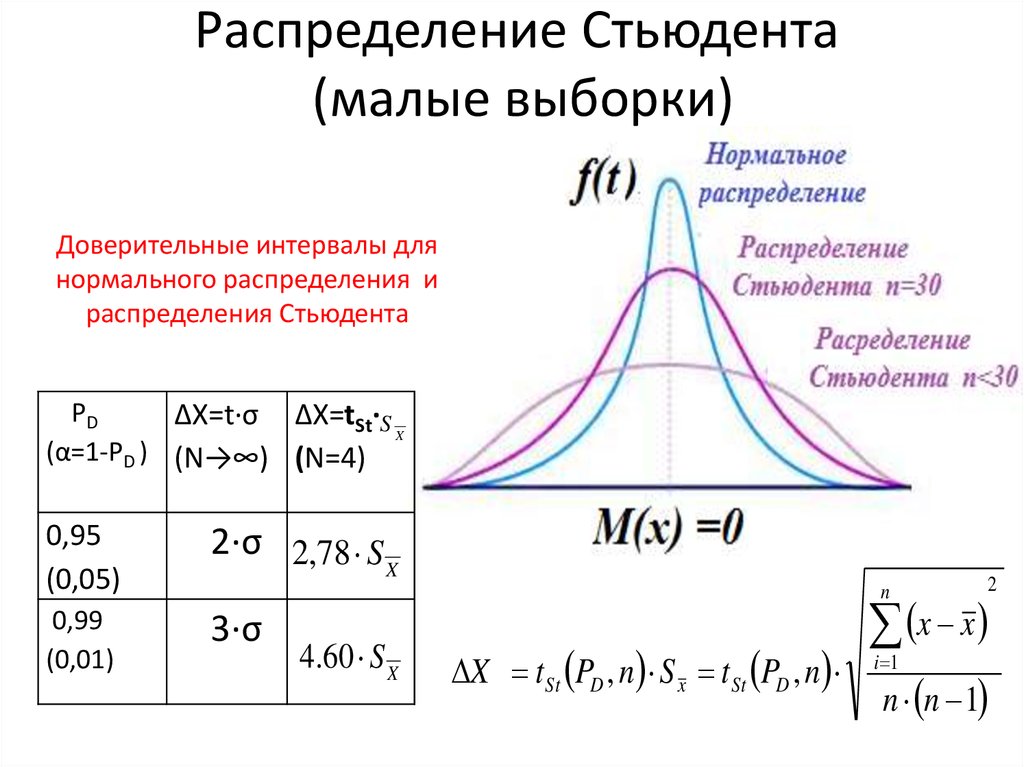
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 31 строку таблицы(33)=============================Tср max
СтрокаТаблицы = 33
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Tcp + Sheets(«ОсновнаяТаблица»).Cells(31, 4).Value * Сигма / Sqr(СтепеньСвободыПриНормРаспред)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
|
Тср, min = |
79,29380755 ч. |
|
Тср, max = |
172,43129 ч. |
Для определения доверительного интервала для среднеквадратичного отклонения по таблице квантилей χ
2
– квадрат распределения определяют квантили для заданных вероятностей
P
1
и
P
2
.
|
(0,05) = |
3,32511 |
|
(0,95) = |
16,919 |
‘Заполним 32 строку таблицы(34)=============================X1(0,05)
СтрокаОсновнойТаблицы = 34
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»).
СтрокаТабл = 4
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»).
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск10:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0.05
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск11
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск11
End If
СледующийПоиск11:
СтолбецТаблКвантили = 11
While Sheets(«Квантили распределения хи»).
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск12
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value And ВходнаяВертикальнаяВеличина > Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск12
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск12:
x1 = Sheets(«Квантили распределения хи»).
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 33 строку таблицы(35)=============================X2(0,95)
СтрокаОсновнойТаблицы = 35
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(4, 1).Value Then
СтрокаТабл = 4
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»).
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск13:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0.
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск14
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск14
End If
СледующийПоиск14:
СтолбецТаблКвантили = 2
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск15
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).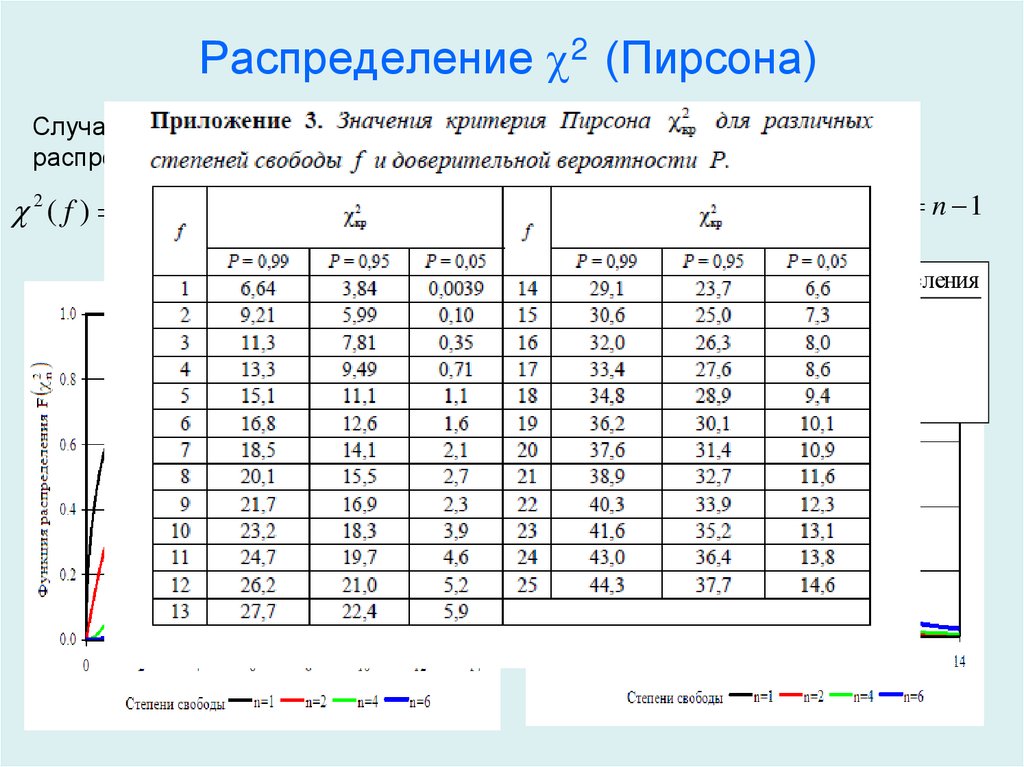
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск15
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск15:
x1 = Sheets(«Квантили распределения хи»).Cells(СтрокаТабл, СтолбецТабл).Value
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).
Получим минимальное σ
min
и максимальное σ
max
значения среднеквадратического отклонения:
(6)
(7)
‘Заполним 34 строку таблицы(36)=============================Сигма min
СтрокаТаблицы = 36
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Сигма * Sqr((СтепеньСвободыПриНормРаспред — 1) / Sheets(«ОсновнаяТаблица»).Cells(35, 4).Value)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 35 строку таблицы(37)=============================Сигма max
СтрокаТаблицы = 37
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»).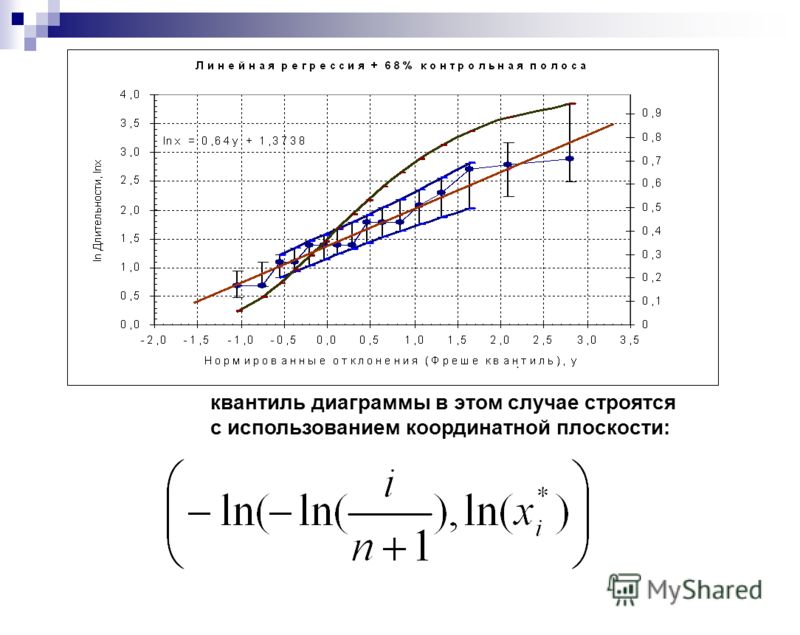
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
Число разрядов, на которые следует группировать статистический ряд, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и часто в нем обнаруживают незакономерные колебания), с другой стороны, оно не должен быть слишком малым (свойства распределения при этом описываются статистическим рядом слишком грубо).
Литература:
-
ГОСТ 27.
002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
- Федотов, А. В. Основы теории надежности и технической диагностики: конспект лекций / А. В. Федотов, Н. Г. Скабкин. – Омск : Изд-во ОмГТУ, 2010 – 64 с.
- Коваленко, В. Н. Надежность устройств железнодорожной автоматики, телемеханики : учеб. пособие / В. Н. Коваленко. – Екатеринбург : Изд-во УрГУПС, 2013. – 87 с.
Основные термины (генерируются автоматически): Таблица функции, строка таблицы, доверительный интервал, Сигма, математическое ожидание, распределение отказов, среднеквадратичное отклонение, статистический ряд, таблица, теория вероятностей.
КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ В EXCEL
1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПАРНОЙ
КОРРЕЛЯЦИИ В ПРОГРАММЕ EXCEL
t-статистика=0,99*(КОРЕНЬ(20-2)/КОРЕНЬ(1-0,99*0,99))=29,7745296027549
Коэффициент корреляции=0,991477169252612
Распределение Стьюдента=2,10092204024104
Расчетное значение t-статистики больше квантиля распределения Стьюдента, следовательно величина коэффициента корреляции является значимой.
2. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ СВЯЗИ
МЕЖДУ ДВУМЯ ВЕЛИЧИНАМИ
1-ый способ
| a1= 0,5014 | a0= 2,5326 |
| Se1= 0,0155 | Se0= 0,7075 |
| R2= 0,9830 | Se= 0,5561 |
| Se= 0,5561 | n-k-1= 18 |
| QR= 322,4250 | Qe= 5,5670 |
Для проверки адекватности
модели нашли квантиль распределения Фишера Ff. с помощью функции FРАСПОБР
FРАСПОБР=4,4139
Проверили адекватность
построенной модели, используя расчетный уровень значимости (P):
2,18499711496499E-17
2 –й способ
|
а=2,532579627 |
|
в=0,50139175 |
Для данного примера
уравнение модели имеет вид:Y=2,53+0,5X
Проверка адекватности модели выполняется по расчетному уровню значимости P,
указанному в столбце Значимость F.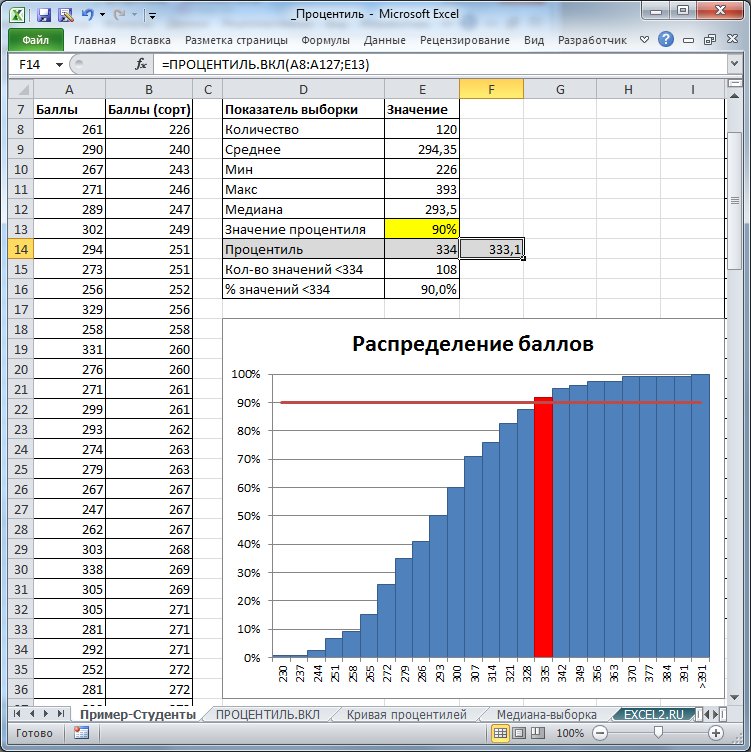
расчетный уровень значимости меньше заданного уровня значимости α =0,05, то модель адекватна.
Проверка статистической значимости коэффициентов модели выполняется по расчетным
уровням значимости P, указанным в столбце P-значение. Если расчетный уровень значимости меньше заданного
уровня значимости α =0,05, то соответствующий
коэффициент модели статистически значим.
Множественный R – коэффициент корреляции. Чем ближе его величина к 1, тем более
тесная связь между изучаемыми показателями. Для данного примера R= 0,99. Это позволяет сделать
вывод, что качество земли – один из основных факторов, от которого зависит
урожайность зерновых культур.
R-квадрат – коэффициент
детерминации. Он получается возведением в квадрат коэффициента корреляции –
R2=0,98. Он
показывает, что урожайность зерновых культур на 98% зависит от качества почвы,
а на долю других факторов приходится 0,02%.
3-ий способ (графический)
Расчет квантилей или процентилей в Excel
В этом руководстве показано, как вычислять квантили или процентили, связанные с доверительными интервалами, в Excel с помощью программного обеспечения XLSTAT.
Квантиль и процентили
XLSTAT имеет полный инструмент для вычисления квантилей или процентилей, их доверительного интервала и графического представления.
Квантили являются важными статистическими показателями, их легко понять. Квантиль 0,5 — это значение, при котором половина выборки находится ниже, а другая половина — выше. Его еще называют средним. Квантиль называется процентилем, если он основан на шкале от 0 до 100. 0,95-квантиль эквивалентен 95-процентилю и таков, что 95 % выборки ниже его значения, а 5 % выше.
Набор данных для создания квантиля
Набор данных был получен от [Lewis T. and Taylor L.R. (1967). Введение в экспериментальную экологию, Нью-Йорк: Academic Press, Inc. Это касается 237 детей, описанных по полу и росту в сантиметрах (1 см = 0,4 дюйма).
Настройка расчета определенного квантиля
После открытия XLSTAT выберите XLSTAT / Description / Quantiles , или нажмите на соответствующую кнопку панели инструментов «Описание» (см.
После нажатия кнопки появится диалоговое окно Quantile . Выберите данные на листе Excel.
В нашем случае; переменная — это «Высота». Данные должны быть количественными .
Поскольку для переменных был выбран заголовок столбца, необходимо активировать опцию Метки переменных .
Мы выбираем метод оценки по умолчанию ( средневзвешенное значение при x(Np) ) и оба типа доверительных интервалов с доверительной вероятностью 95 % .
Подробную информацию о статистических методах можно найти в справке XLSTAT.
Во вкладке диаграммы выбираем все диаграммы и нас интересует 67-процентиль (две трети детей меньше, а одна треть выше).
Вычисления начинаются после того, как вы нажмете на ОК . Затем будут отображены результаты.
Интерпретация результатов генерации квантилей
В первой таблице показаны некоторые описательные статистические данные о переменной высоты.
Затем отображается значение 67-процентиля. Две трети детей меньше 164,58 см.
Первый график (см. ниже) позволяет нам визуализировать эмпирическую кумулятивную функцию распределения со значением 67-го процентиля.
Вторая и третья диаграммы представляют собой коробчатую диаграмму и диаграмму рассеяния. 67-процентиль отображается синей линией.
Вы также можете использовать подвыборки, например пол можно использовать в качестве групповой переменной. Веса, связанные с наблюдениями, также могут быть включены.
Была ли эта статья полезной?
- Да
- №
Квантиль (квартиль, дециль и процентиль): расчет вручную + Microsoft
Квантиль — важная статистическая концепция, позволяющая разделить данные на равные группы.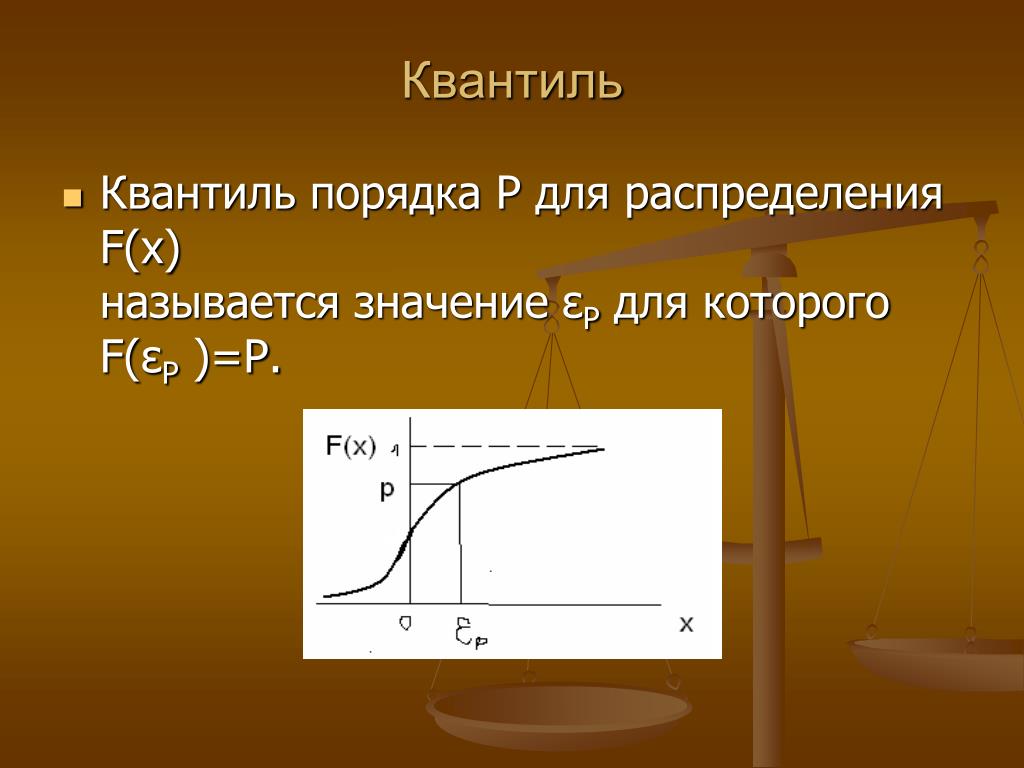
Квантиль
Квантиль — это мера, указывающая значение, ниже которого падает определенная доля наблюдений в группе наблюдений. Квантиль используется в статистике для разделения группы наблюдений на группы одинакового размера. Например, квантиль 0,25 — это значение, ниже которого падают 25% наблюдений; квантиль 0,50 — это значение, ниже которого падает 50%, и так далее. Другим родственным измерением является медиана, которая совпадает с квантилем 0,50, поскольку 50% данных находятся ниже медианы.
Какие общие квантили существуют?
Некоторые распространенные квантили включают:
1. Квартиль
Квартиль — это тип квантиля, который делит группу наблюдений на четыре группы одинакового размера.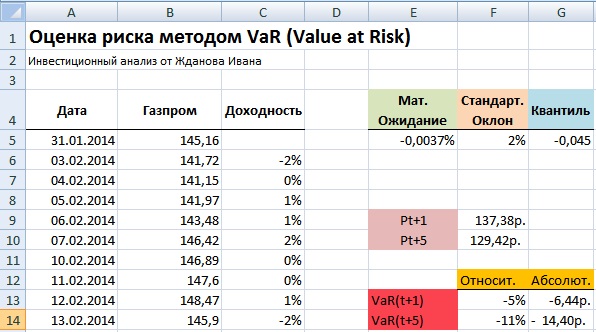
2. Дециль
Дециль – это мера, которая делит группу наблюдений на десять групп одинакового размера. Например, в группе наблюдений первый дециль (D1) — это значение, ниже которого попадают первые 10% наблюдений, второй дециль (D2) — это значение, ниже которого попадают первые 20% наблюдений, и скоро. 9-й дециль (D9) — это значение, ниже которого опускаются последние 10% наблюдений.
3. Процентиль
Процентиль — это мера, указывающая значение, ниже которого находится определенный процент наблюдений в группе наблюдений. Например, в группе наблюдений 20-й процентиль (P20) — это значение, ниже которого опускаются первые 20% наблюдений, 50-й процентиль (P50) — это значение, ниже которого опускаются средние 50% наблюдений, и 95-й процентиль (P95) — это значение, ниже которого падают последние 95% наблюдений.
50-й процентиль также является медианой, вторым квартилем и 5-м децилем.
Процентиль: Расчет вручную / Microsoft Excel
Процентиль — это мера, используемая в статистике для указания значения, ниже которого находится определенный процент наблюдений в группе наблюдений.
Чтобы найти местоположение определенного процентиля, такие программы, как Minitab, Python, R и Excel, используют следующие шаги:
- Расположите наблюдения в порядке возрастания.
- Используйте формулу для определения положения процентиля, чтобы вычислить положение, в котором будет располагаться значение процентиля, используя желаемое значение процентиля и общее количество наблюдений в качестве входных данных. Существует два подхода: EXC (Exclusive) и INC (Inclusive). Процентное положение в подходе EXC определяется формулой (K(N+1)), а положение в подходе INC определяется формулой (K(N-1)+1).
- Если местоположение процентиля является целым числом, значение в этой позиции в упорядоченном списке наблюдений является значением процентиля.
- Если местоположение процентиля не является целым числом, значение процентиля рассчитывается путем вычисления значения на пропорциональной основе между этими двумя числами.
Чтобы найти 65-й процентиль в группе из 8 наблюдений, вы должны сначала расположить наблюдения в порядке возрастания: 8, 9, 12, 22, 23, 33, 55, 61.
Затем вы должны использовать формулу для местоположения процентиля, чтобы вычислить положение, в котором будет расположен 65-й процентиль:
Для ПРОЦЕНТИЛЬ.ИСКЛ рассчитанный ранг равен (K(N+1)).
Расположение в процентиле (с использованием эксклюзивного подхода) = (left(frac{65}{100}right)(8+1)) = 5,85
Поскольку положение в процентиле не является целым числом, 65-й процентиль будет между 5-м пунктом (номер 23) и 6-м пунктом (номер 33) на пропорциональной основе. Это будет (23+0,85(33-23) = 31,5).
Для PERCENTILE.INC (и PERCENTILE) рассчитанный ранг равен (K(N-1)+1).
Расположение в процентах (с использованием инклюзивного подхода) = ((65/100) (8-1)+1) = 5,55
Поскольку местоположение процентиля не является целым числом, 65-й процентиль будет почти посередине между 5-м элементом (число 23) и 6-м элементом (число 33).
Квартиль: пример расчета вручную
Квартиль — это статистическое значение, которое делит набор данных на четыре равные части или четверти. Первый квартиль, также известный как нижний квартиль или Q1, — это значение, которое отделяет самые низкие 25 % данных от остальных. Второй квартиль, также известный как медиана или Q2, представляет собой значение, которое отделяет самые низкие 50% данных от самых высоких 50% данных. Третий квартиль, также известный как верхний квартиль или Q3, — это значение, которое отделяет самые высокие 25% данных от остальных.
Например, если у нас есть следующие числа: 14, 9, 10, 11, 11 и 6, мы можем разделить данные на четыре равные группы, найдя первый, второй и третий квартили.
Чтобы найти квартили набора данных, нам сначала нужно расположить данные в порядке возрастания следующим образом: 6, 9, 10, 11, 11, 14.
Затем нам нужно найти медиану, или Q2, которая является средним значением в наборе данных.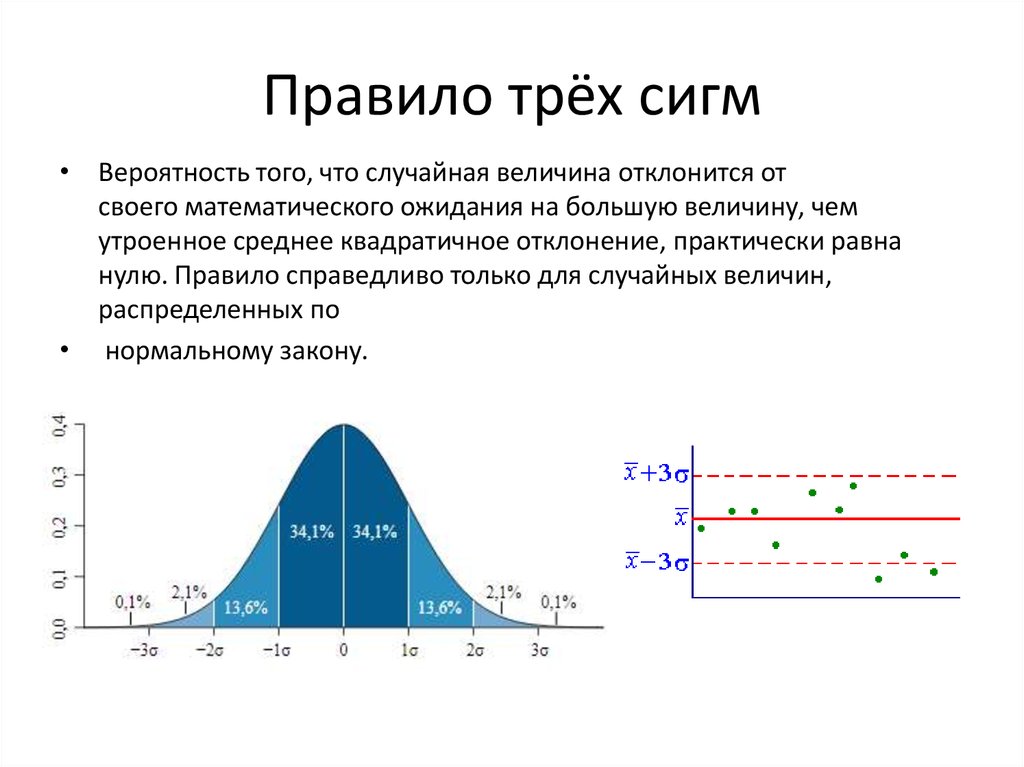
Чтобы найти нижний квартиль или Q1, мы берем медиану значений ниже медианы. В данном случае это будет медиана 9. Чтобы найти верхнюю квартиль или Q3, мы берем медиану значений выше медианы. В данном случае это будет медиана 11, 11 и 14, что равно 11.
Таким образом, для этого набора данных квартили: эти числа расчета квартиля не совпадают с расчетом Excel?
Квартиль Использование Excel:
Для расчета квартилей такие программы, как Microsoft Excel и Minitab, используют метод процентилей, как объяснялось ранее. Q1 рассчитывается как 25-й процентиль, Q2 — как 50-й и Q3 — как 75-й процентиль. Это приводит к тому, что значение квартиля иногда отличается от значения, рассчитанного с использованием обычного ручного метода расчета.
Возьмем тот же пример, который мы использовали ранее в ручном расчете для расчета первого квартиля (Q1).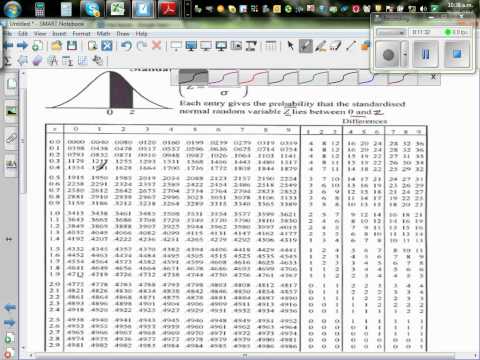
Чтобы найти квартили набора данных, нам сначала нужно расположить данные в порядке возрастания следующим образом: 6, 9, 10, 11, 11, 14.
Вы можете использовать функцию КВАРТИЛЬ.ИСКЛ или КВАРТИЛЬ.ВКЛ. найти квартили набора чисел в Excel.
Quartile.Exc
Для QUARTILE.EXC расчетный ранг равен K*(N+1). Чтобы рассчитать положение Q1 (или 25-го процентиля), подставим в эту формулу соответствующие значения.
Местоположение 1-го квартиля (с использованием эксклюзивного подхода) = (25/100) * (6+1) = 1,75
Поскольку положение процентиля не является целым числом, 1-й квартиль будет между 1-м элементом (номер 6) и 2-м элементом (номер 9) на пропорциональной основе. Получится (6 + (9-6)*0,75) = 8,25.
Использование Minitab: Если вы используете Minitab для расчета Q1, это значение (8,25), которое вы получите в описательной статистике. Minitab использует метод EXC для расчета процентилей и квартилей.
Квартиль.Вкл
Для КВАРТИЛЬ.
Все, рассмотренные в этом разделе инструменты вычисляют значения квантилей как значения функций, обратных соответствующим функциям распределения. Все эти функции – библиотечные функции Excel из группы функций «Статистические»,.
Функция вычисления критических точек распределения Лапласа
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) стандартного нормального распределения.
Функция вычисления критических точек распределения Стьюдента
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения Стьюдента с числом степеней свободы, равным значению, введенному в поле «Степени свободы» (понятно, что это натуральное число).
Важно знать, что функция Excel СТЬЮДРАСПОБР(p, k) возвращает значение t, при котором P(|x| > t) = p, x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы.
Поэтому решение уравнения в Excel возвращает функция СТЬЮДРАСПОБР(a, n – 1).
Функция вычисления критических точек распределения
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения с числом степеней свободы, равным значению, введенному в поле «Степени свободы» (понятно, что это натуральное число).
В Excel функция распределения случайной величины определена нестандартно: Fx(x) = P(x > x). Поэтому для вычисления квантиля вводим в качестве аргумента функции ХИ2ОБР значение вероятности, равное
, а для вычисления
–
.
Методология работы в программе MS EXCEL с функциями нормального распределения и распределения Стьюдента
Функция НОРМРАСП(рис. 5.8) определяет плотность f и интегральную функцию F нормального распределения при заданных аргументах:
— «x» — значение X, для которого определяются значения f или F.
— «Среднее» — математическое ожидание (или его оценка), представленное самим значением или ссылкой на ячейку, содержащую результат его расчёта.
— «Стандартное откл» — стандартное отклонение распределения (или оценка стандартного отклонения) или ссылка на ячейку, содержащую результат его расчёта.
— «Интегральная» — направление расчёта: плотность f или интегральная функция F распределения, см. § 2.4.
Рис. 5.8. Аргументы функции НОРМРАСП
Например, поставлена задача определения вероятности попадания некоторой характеристики (размера, какого-либо механического свойства и т.д.) в поле допуска с границами (x1, x2), если известна выборка значений этой характеристики. Тогда, подставляя в аргументы функции НОРМРАСП рассчитанные «Среднее» и «Стандартное откл», в «Интегральная» — значение ИСТИНА, а в «x» — последовательно x1 и x2, определяют интегральную функцию 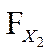
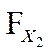
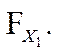
Функция НОРМСТРАСП определяет интегральное функцию стандартного нормального распределения (здесь не представлена). Эта функция используется вместо справочной таблицы для стандартной нормальной кривой (приложение ….). Поскольку для стандартного нормального распределения =0 и σ=1 известны, в функции НОРМСТРАСП представлен лишь один аргумент — z.
НОРМОБР — функция, обратная функции НОРМРАСП, определяющей по заданному значению x интегральную функцию F. НОРМОБР (рис. 5.9) для указанного среднего и стандартного отклонения по заданному значению вероятности ищет значение x, используя метод итераций. (Такую же операцию выполняет и не представленная здесь функция НОРМСТОБР, но для стандартного нормального распределения.)
Рис. 5.9. Аргументы функции НОРМОБР
Как правило, работа технолога состоит в разработке процесса производства, обеспечивающего попадание с максимальной вероятностью характеристик качества в заданные границы допусков. Но бывают случаи, особенно в мелкосерийном производстве, когда необходимо исходить из возможностей уже существующего процесса: определить какие границы допуска при неизменной настройке можно обеспечить с заданной степенью достоверности (или уровня значимости). Именно тогда функцию НОРМОБР удобно использовать для нахождения границ доверительного интервала, обеспечивающих необходимую вероятность попадания в этот интервал контролируемой характеристики, см. § 6.6. Для этого уровень значимости α, например 0,05, делят на две части, обычно равные. Для нахождения нижней границы интервала в качестве аргумента «Вероятность» (см. рис. 5.9) ставят величину α/2 (= 0,025). Для определения верхней границы в качестве аргумента «Вероятность» ставят величину 1,0 — α/2 (= 0,975).
Но бывают случаи, когда выпады за пределы нижней и верхней границы доверительного интервала неравноценны по своим последствиям. Например, при изготовлении детали выпад в одну сторону от допуска может означать исправимый, а в другую — неисправимый брак, см. § 6.6. В этом случае по сравнению с предыдущим уровень значимости α, например 0,05, делят на две неравные части. Меньшую часть назначают в сторону области неисправимого брака (например, при обработке вала — в сторону меньших размеров). Наоборот, бóльшую часть α назначают в сторону исправимого брака, то есть при обработке вала в сторону бóльших размеров.
Таким образом, будучи родственной функции ДОВЕРИТ (см. ниже § 6.3), устанавливающей только ширину доверительного интервала, функция НОРМОБР имеет более широкие возможности в отношении установления расположения доверительного интервала, см. ниже § 6.6.
Функция СТЬЮДРАСП (рис. 5.10) определяет процентные точки (вероятность) для t-распределения Стьюдента, используемого для проверки гипотез при малом объеме выборки. При увеличении n оно приближается к нормальному распределению. (В аргументах функции СТЬЮДРАСП, как и в аргументах функции НОРМСТРАСПотсутствуют математическое ожидание и дисперсия.)
Рис. 5.10. Аргументы функции СТЬЮДРАСП
В качестве аргументов функции используются:
— «x» — это значение, для которого вычисляются вероятности;
— «Степени_свободы» — целое, указывающее число степеней свободы k;
— «Хвосты» — число, которое может быть равно 1 или 2 и определяет следующим образом характер распределения: если «Хвосты» = 1, то функция СТЬЮДРАСП определяет одностороннее распределение; если «Хвосты» = 2, то функция СТЬЮДРАСП определяет двухстороннее распределение.
Расчет производится только для x ³ 0. Но следует помнить, что для одностороннего распределения: СТЬЮДРАСП(-x,df,1) = 1 – СТЬЮДРАСП(x,df,1) и для двустороннего распределения: СТЬЮДРАСП(-x,df,2) = СТЬЮДРАСП(x df,2). То есть распределение Стьюдента можно «достроить» и для области x
Распределение Стьюдента (t-распределение). Распределения математической статистики в EXCEL
Рассмотрим Распределение Стьюдента (t-распределение). С помощью функции MS EXCEL СТЬЮДЕНТ.РАСП() построим графики функции распределения и плотности вероятности, поясним применение этого распределения для целей математической статистики.
Распределение Стьюдента (также называется t -распределением ) применяется в различных методах математической статистики:
- при построении доверительных интервалов для среднего (используется функция ДОВЕРИТ.СТЬЮДЕНТ() );
- для оценки различия двух выборочных средних (используется функция СТЬЮДЕНТ.ТЕСТ() );
- при проверке гипотез (выборка небольшого размера, стандартное отклонение не известно) ,
- в линейном регрессионном анализе (при проверке гипотез на значимость отдельных регрессионных коэффициентов).
Определение : Если случайная величина Z распределена по стандартному нормальному закону N(0;1) и случайная величина U имеет распределение ХИ-квадрат с ν степенями свободы, то случайная величина T=Z/√(U/v) имеет t-распределение .
Плотность распределения Стьюдента выражается формулой:
при −∞ x) или даже P(|X| > x).
Очевидно, что справедливо равенство
=СТЬЮДЕНТ.РАСП.ПХ(x;n)+СТЬЮДЕНТ.РАСП(x;n;ИСТИНА)=1 т.к. первое слагаемое вычисляет вероятность P(X > x), а второе P(X x)) и объединяет возможности нескольких новых функций MS EXCEL 2010: СТЬЮДЕНТ.РАСП(x; n; ЛОЖЬ) , СТЬЮДЕНТ.РАСП.ПХ() , СТЬЮДЕНТ.РАСП.2Х() . Функция СТЬЮДРАСП() оставлена в MS EXCEL 2010 для совместимости.
- Если значение аргумента «хвосты» = 1, функция СТЬЮДРАСП() вычисляет правостороннюю вероятность P(X > x), где X — случайная переменная, соответствующая t-распределению. Под термином «хвост» подразумевается «хвост» распределения, в данном случае правый. На графике плотности вероятности этому «хвосту» будет соответствовать площадь фигуры под графиком (выделена синим), которая ограничена слева вертикальной линией X = x.
- Если значение аргумента «хвосты» = 2, функция СТЬЮДРАСП() вычисляет вероятность P(|X| > x) или другими словами P(X > x или X 0;СТЬЮДРАСП(x;n;1);1-СТЬЮДРАСП(-x;n;1)) .
Примеры
Найдем вероятность, что случайная величина Х примет значение меньше или равное заданного x : P(X x), так называемую правостороннюю вероятность, поэтому, чтобы найти P(X x).
Аналогичные вычисления для P(X > x) и P(|X| > x) приведены в файле примера на листе Функции , в том числе и для x
Генерация дискретного случайного числа с произвольной функцией распределения в MS EXCEL
Функция распределения и плотность вероятности в MS EXCEL
Функция стьюдраспобр в excel
Функция НОРМРАСП(рис. 5.8) определяет плотность f и интегральную функцию F нормального распределения при заданных аргументах:
– «x» – значение X, для которого определяются значения f или F.
– «Среднее» – математическое ожидание (или его оценка), представленное самим значением или ссылкой на ячейку, содержащую результат его расчёта.
– «Стандартное откл» – стандартное отклонение распределения (или оценка стандартного отклонения) или ссылка на ячейку, содержащую результат его расчёта.
– «Интегральная» – направление расчёта: плотность f или интегральная функция F распределения, см. § 2.4.
Рис. 5.8. Аргументы функции НОРМРАСП
Например, поставлена задача определения вероятности попадания некоторой характеристики (размера, какого-либо механического свойства и т.д.) в поле допуска с границами (x1, x2), если известна выборка значений этой характеристики. Тогда, подставляя в аргументы функции НОРМРАСП рассчитанные «Среднее» и «Стандартное откл», в «Интегральная» – значение ИСТИНА, а в «x» – последовательно x1 и x2, определяют интегральную функцию 


Функция НОРМСТРАСП определяет интегральное функцию стандартного нормального распределения (здесь не представлена). Эта функция используется вместо справочной таблицы для стандартной нормальной кривой (приложение ….). Поскольку для стандартного нормального распределения =0 и σ=1 известны, в функции НОРМСТРАСП представлен лишь один аргумент – z.
НОРМОБР – функция, обратная функции НОРМРАСП, определяющей по заданному значению x интегральную функцию F. НОРМОБР (рис. 5.9) для указанного среднего и стандартного отклонения по заданному значению вероятности ищет значение x, используя метод итераций. (Такую же операцию выполняет и не представленная здесь функция НОРМСТОБР, но для стандартного нормального распределения.)
Рис. 5.9. Аргументы функции НОРМОБР
Как правило, работа технолога состоит в разработке процесса производства, обеспечивающего попадание с максимальной вероятностью характеристик качества в заданные границы допусков. Но бывают случаи, особенно в мелкосерийном производстве, когда необходимо исходить из возможностей уже существующего процесса: определить какие границы допуска при неизменной настройке можно обеспечить с заданной степенью достоверности (или уровня значимости). Именно тогда функцию НОРМОБР удобно использовать для нахождения границ доверительного интервала, обеспечивающих необходимую вероятность попадания в этот интервал контролируемой характеристики, см. § 6.6. Для этого уровень значимости α, например 0,05, делят на две части, обычно равные. Для нахождения нижней границы интервала в качестве аргумента «Вероятность» (см. рис. 5.9) ставят величину α/2 (= 0,025). Для определения верхней границы в качестве аргумента «Вероятность» ставят величину 1,0 – α/2 (= 0,975).
Но бывают случаи, когда выпады за пределы нижней и верхней границы доверительного интервала неравноценны по своим последствиям. Например, при изготовлении детали выпад в одну сторону от допуска может означать исправимый, а в другую – неисправимый брак, см. § 6.6. В этом случае по сравнению с предыдущим уровень значимости α, например 0,05, делят на две неравные части. Меньшую часть назначают в сторону области неисправимого брака (например, при обработке вала – в сторону меньших размеров). Наоборот, бóльшую часть α назначают в сторону исправимого брака, то есть при обработке вала в сторону бóльших размеров.
Таким образом, будучи родственной функции ДОВЕРИТ (см. ниже § 6.3), устанавливающей только ширину доверительного интервала, функция НОРМОБР имеет более широкие возможности в отношении установления расположения доверительного интервала, см. ниже § 6.6.
Функция СТЬЮДРАСП (рис. 5.10) определяет процентные точки (вероятность) для t-распределения Стьюдента, используемого для проверки гипотез при малом объеме выборки. При увеличении n оно приближается к нормальному распределению. (В аргументах функции СТЬЮДРАСП, как и в аргументах функции НОРМСТРАСПотсутствуют математическое ожидание и дисперсия.)
Рис. 5.10. Аргументы функции СТЬЮДРАСП
В качестве аргументов функции используются:
– «x» – это значение, для которого вычисляются вероятности;
– «Степени_свободы» – целое, указывающее число степеней свободы k;
– «Хвосты» – число, которое может быть равно 1 или 2 и определяет следующим образом характер распределения: если «Хвосты» = 1, то функция СТЬЮДРАСП определяет одностороннее распределение; если «Хвосты» = 2, то функция СТЬЮДРАСП определяет двухстороннее распределение.
Расчет производится только для x ³ 0. Но следует помнить, что для одностороннего распределения: СТЬЮДРАСП(-x,df,1) = 1 – СТЬЮДРАСП(x,df,1) и для двустороннего распределения: СТЬЮДРАСП(-x,df,2) = СТЬЮДРАСП(x df,2). То есть распределение Стьюдента можно «достроить» и для области x
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10236 – 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Функция СТЮДРАСПОБР предназначена для расчета значения квантиля уровня, соответствующего известной вероятности (указывается в качестве первого аргумента), распределения Стьюдента для известных степеней свободы и возвращает обратное t-распределение.
Распределение Стьюдента и нормальное распределение в Excel
Рассматриваемая функция возвращает значение t, соответствующее условию P(|x|>t)=p. Здесь x является значением некоторой случайной величины с распределением Стьюдента, у которого число степеней свобод соответствует k (второй аргумент функции СТЮДРАСПОБР).
- Распределение Стьюдента является одним из видов распределения случайной величины, близкое к нормальному распределению с характерным отличием – сниженная концентрацией отклонений в средней части распределения. Иное название – t-распределение.
- Квантилем считается некоторое значение, которое с определенной вероятностью (фиксированной) не будет превышено случайной величиной.
- Функция СТЮДРАСПОБР считается устаревшей начиная с версии MS Office 2010. Она оставлена для обеспечения совместимости с другими табличными редакторами и документами, созданными в более старых версиях табличного редактора. В новых версиях следует использовать усовершенствованные аналоги: СТЬЮДЕНТ.ОБР.2Х или СТЬЮДЕНТ.ОБР.
Ниже рассмотрим примеры использования функции СТЮДРАСПОБР в Excel.
Определение одностороннего и двустороннего t распределение Стьюдента
Пример 1. Определить односторонне и двустороннее t-значения для распределения Стьюдента, характеризующееся вероятностью 0,17 и числом степени свобод 16.
Вид таблицы данных:
Для расчета двустороннего t-значения используем функцию:
Для двустороннего t используем удвоенное значение вероятности:
В результате получим:
Число степеней свободы в распределении Стьюдента
Пример 2. Сгенерировать 8 случайных чисел с использованием функции СЛЧИС, для которых распределение Стьюдента имеет 4 степени свободы.
Поскольку вероятность того, что случайна величина примет как отрицательное, так и положительное значение является одинаковой и равна 0,5 (распределение Стьюдента симметрично относительно вертикальной оси графика), используем функцию ЕСЛИ для проверки значений.
Выделим 8 ячеек и запишем следующую функцию (вводить как формулу массива CTRL+SHIFT+Enter):
То есть, если случайное значение вероятности, сгенерированное функцией СЛЧИС меньше 0,5, будет сгенерировано отрицательное t-значение, иначе – положительное.
Как пользоваться функцией распределения Стьюдента СТЮДРАСПОБР В EXCEL
Функция имеет следующий синтаксис:
- вероятность – обязательный для заполнения, принимает числовое значение вероятности для двустороннего распределения Стьюдента из диапазона от 0 (не включительно) до 1.
- степени_свободы – обязательный для заполнения, принимает числовое значение степеней свободы, которые определяют исследуемое распределение.
- Если один из аргументов функции указан в виде значения нечислового типа данных, результатом выполнения рассматриваемой функции будет код ошибки #ЗНАЧ!. Логические значения, имена и текстовые строки, преобразуемые в числа, не приводят к возникновению ошибки. Например, функция =СТЮДРАСПОБР(“0,4”;ИСТИНА) вернет значение 1,32638.
- Если аргумент вероятность задан числом, не находящимся в промежутке от 0 (не включительно) до 1, функция СТЮДРАСПОБР вернет код ошибки #ЧИСЛО!. Аналогичная ошибка возникает, если аргумент степени_свободы задан числом, которое меньше 1.
- Для расчета односторонней t-величины следует в качестве аргумента вероятность указать значение удвоенной вероятности.
Возвращает двустороннее обратное t-распределения Стьюдента.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новых функциях см. в разделах Функция СТЬЮДЕНТ.ОБР.2Х и Функция СТЬЮДЕНТ.ОБР.
Синтаксис
Аргументы функции СТЬЮДРАСПОБР описаны ниже.
Вероятность Обязательный. Вероятность, соответствующая двустороннему распределению Стьюдента.
Степени_свободы Обязательный. Число степеней свободы, характеризующее распределение.
Замечания
Если любой из аргументов не является числом, то функция СТЬЮДРАСПОБР возвращает значение ошибки #ЗНАЧ!.
Если «вероятность» 1, функция СТЬЮДРАСПОБР возвращает значение ошибки #ЧИСЛО!.
Если значение «степени_свободы» не является целым, оно усекается.
Если значение «степени_свободы» t) = вероятность, где X — случайная величина, соответствующая t-распределению, и P(|X| > t) = P(X t).
Одностороннее t-значение может быть получено при замене аргумента «вероятность» на 2*вероятность. Для вероятности 0,05 и 10 степеней свободы двустороннее значение вычисляется по формуле СТЬЮДРАСПОБР(0,05;10) и равно 2,28139. Одностороннее значение для той же вероятности и числа степеней свободы может быть вычислено по формуле СТЬЮДРАСПОБР(2*0,05;10), возвращающей значение 1,812462.
Примечание: В некоторых таблицах вероятность описана как (1-p).
Если задано значение вероятности, то функция СТЬЮДРАСПОБР ищет значение x, для которого функция СТЬЮДРАСП(x, степени_свободы, 2) = вероятность. Однако точность функции СТЬЮДРАСПОБР зависит от точности СТЬЮДРАСП. В функции СТЬЮДРАСПОБР для поиска применяется метод итераций. Если поиск не закончился после 100 итераций, функция возвращает значение ошибки #Н/Д.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Вероятность, соответствующая двустороннему распределению Стьюдента.
Инструменты Excel для построения интервальных оценок параметров распределений
Все, рассмотренные в этом разделе инструменты вычисляют значения квантилей как значения функций, обратных соответствующим функциям распределения. Все эти функции – библиотечные функции Excel из группы функций «Статистические»,.
Функция вычисления критических точек распределения Лапласа
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) стандартного нормального распределения.
Функция вычисления критических точек распределения Стьюдента
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения Стьюдента с числом степеней свободы, равным значению, введенному в поле «Степени свободы» (понятно, что это натуральное число).
Важно знать, что функция Excel СТЬЮДРАСПОБР( p , k ) возвращает значение t , при котором P (| x | > t ) = p , x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы.
Поэтому решение уравнения 
Функция вычисления критических точек распределения
Функция возвращает (вычисляет) значения квантили уровня, равного значению, введенному в поле «Вероятность» (понятно, что это число из промежутка (0б 1)) распределения 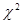
В Excel функция распределения случайной величины определена нестандартно: F x ( x ) = P ( x > x ). Поэтому для вычисления квантиля 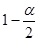
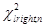
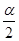
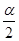
Функции t-распределения (распределения Стьюдента)
Функция СТЬЮДРАСП
См. также ДОВЕРИТ, СТЬЮДРАСПОБР, ТТЕСТ.
СТЬЮДРАСП (x; степени свободы; хвосты)
Рассчитывает t-распределение (распределение Стьюдента).
x: значение, для которого вычисляется t-распределение;
степени свободы: число степеней свободы;
хвосты: число рассчитываемых хвостов распределения. Если аргумент хвосты = 1, то функция СТЬЮДРАСП рассчитывает одностороннее t-распределение; если аргумент хвосты = 2 — двустороннее t-распределение.
При большом числе единиц выборочной совокупности (n >100) распределение случайных ошибок выборочной средней в соответствии с теоремой Ляпунова нормально (или приближается к нормальному) по мере увеличения числа наблюдений. Вероятность выхода ошибки за определенные пределы оценивается на основе таблиц интеграла Лапласа (см. описание функции ДОВЕРИТ в подразд. 6.3.1).
Однако в практике статистических исследований часто приходится сталкиваться с так называемыми малыми выборками, объем которых не превышает 30 ед. и может доходить до 4-5 ед.
Разработка теории малой выборки была начата в 1908 г. английским статистиком Госсетом, печатавшимся под псевдонимом Стьюдент. Он доказал, что оценка расхождения между средней малой выборки и генеральной средней имеет особый закон распределения, получивший название распределения Стьюдента. Для определения возможных пределов ошибки пользуются так называемым t-критерием (критерием Стьюдента), вычисляемым по формуле
t =
где 


Величина 

где величина 

Предельная ошибка малой выборки ΔМВ связана со средней ошибки малой выборки 
ΔМВ = t
В данном случае величина t связана не с нормальным распределением, а с распределением Стьюдента, которое при небольшом объеме выборки отличается от нормального: большие величины критерия имеют здесь большую вероятность, чем при нормальном распределении.
При увеличении n распределение Стьюдента стремится к нормальному и при n 

Пример 6.15. При контрольной проверке качества поставленного в торговлю маргарина получены следующие данные о содержании консерванта Е205 в 10 пробах, %: 4,3; 4,2; 3,8; 4,3; 3,7; 3,9; 4,5; 4,4; 4,0; 3,9. Какова вероятность того, что среднее содержание консерванта Е205 во всей партии не выйдет за пределы 0,1% его среднего содержания в представленных пробах?
Рассмотрим решение задачи в среде Microsoft Excel (табл. 6.7).
Содержимое ячеек в табл. 6.7:
массив С2:С11 содержит исходные данные задачи;
ячейка С12 содержит формулу =СРЗНАЧ(С2:С11) — рассчитывается значение выборочной средней 
ячейка С13 содержит формулу =С12 — 0,1 — определяется нижняя граница генеральной средней;
ячейка С14 содержит формулу =С12 + 0,1 — определяется верхняя граница генеральной средней;
ячейка С15 содержит формулу =СТАНДОТКЛОНП(С2:С11) — вычисляется стандартное отклонение 
ячейка С16 содержит формулу =С15/КОРЕНЬ(10-1) — рассчитывается значение средней ошибки выборки 
ячейка С17 содержит формулу =0,1/С16 — рассчитывает значение коэффициента доверия t (здесь величина 0,1 — значение предельной ошибки выборки ΔМВ, заданное в условии задачи);
ячейка С18 содержит формулу =1- СТЬЮДРАСП(С17;9;2) — рассчитывается значение доверительной вероятности γ.
Примечание. Аргументом функции СТЬЮДРАСП является число степеней свободы k = n — 1. Для рассматриваемой задачи k = 10 — 1 = 9.
Таким образом, на основании проведенного выборочного контроля качества продукции можно заключить, что среднее содержание консерванта Е205 во всей партии будет находиться в пределах от 4,0 до 4,2% с уровнем надежности 72%.
Функция СТЬЮДРАСПОБР
См. также СТЬЮДРАСП, ТТЕСТ
СТЬЮДРАСПОБР (вероятность; степени свободы)
Рассчитывает обратное t-распределение.
вероятность: вероятность, соответствующая двустороннему t-распределению (уровень значимости α);
степени свободы: число степеней свободы.
См. описание функции СТЬЮДРАСП.
Функция обратного распределения Стьюдента используется в ситуациях, когда известен уровень надежности (или уровень значимости) и необходимо рассчитать значение t-критерия.
Например, формула =СТЬЮДРАСПОБР(0,05;4) рассчитывает значение 2,78 (сравните с формулой =СТЬЮДРАСП(2,78;4;2), вычисляющей значение 0,05).
Пример 6.16. В задаче, рассмотренной в примере 6.15, с уровнем надежности 95 % требуется определить границы интервала, в котором находится средний процент содержания консерванта Е205 в партии маргарина.
Исходя из числа степеней свободы k(k=n-1=10-1=9) и заданного уровня надежности 95 % (уровня значимости α = 0,05) находим значение коэффициента доверия, равное 2,26 (формула =СТЬЮДРАСПОБР(0,05;9)). По формуле Δ МВ = t 

Следовательно, с уровнем надежности 95% можно предположить, что во всей партии маргарина содержание консерванта Е205 находится в пределах 4,1+0,2%, т. е. от 3,9 до 4,3 %.
Функция СТЮДРАСПОБР предназначена для расчета значения квантиля уровня, соответствующего известной вероятности (указывается в качестве первого аргумента), распределения Стьюдента для известных степеней свободы и возвращает обратное t-распределение.
Распределение Стьюдента и нормальное распределение в Excel
Рассматриваемая функция возвращает значение t, соответствующее условию P(|x|>t)=p. Здесь x является значением некоторой случайной величины с распределением Стьюдента, у которого число степеней свобод соответствует k (второй аргумент функции СТЮДРАСПОБР).
Примечания:
- Распределение Стьюдента является одним из видов распределения случайной величины, близкое к нормальному распределению с характерным отличием – сниженная концентрацией отклонений в средней части распределения. Иное название – t-распределение.
- Квантилем считается некоторое значение, которое с определенной вероятностью (фиксированной) не будет превышено случайной величиной.
- Функция СТЮДРАСПОБР считается устаревшей начиная с версии MS Office 2010. Она оставлена для обеспечения совместимости с другими табличными редакторами и документами, созданными в более старых версиях табличного редактора. В новых версиях следует использовать усовершенствованные аналоги: СТЬЮДЕНТ.ОБР.2Х или СТЬЮДЕНТ.ОБР.
Подробнее о нормальном распределении читайте: НОРМСТРАСП функция стандартного нормального распределения в Excel.
Ниже рассмотрим примеры использования функции СТЮДРАСПОБР в Excel.
Определение одностороннего и двустороннего t распределение Стьюдента
Пример 1. Определить односторонне и двустороннее t-значения для распределения Стьюдента, характеризующееся вероятностью 0,17 и числом степени свобод 16.
Вид таблицы данных:
Для расчета двустороннего t-значения используем функцию:
=СТЬЮДРАСПОБР(B2;B1)
Результат вычислений:
Для двустороннего t используем удвоенное значение вероятности:
=СТЬЮДРАСПОБР(2*B2;B1)
В результате получим:
Число степеней свободы в распределении Стьюдента
Пример 2. Сгенерировать 8 случайных чисел с использованием функции СЛЧИС, для которых распределение Стьюдента имеет 4 степени свободы.
Поскольку вероятность того, что случайна величина примет как отрицательное, так и положительное значение является одинаковой и равна 0,5 (распределение Стьюдента симметрично относительно вертикальной оси графика), используем функцию ЕСЛИ для проверки значений.
Выделим 8 ячеек и запишем следующую функцию (вводить как формулу массива CTRL+SHIFT+Enter):
То есть, если случайное значение вероятности, сгенерированное функцией СЛЧИС меньше 0,5, будет сгенерировано отрицательное t-значение, иначе – положительное.
Результат вычислений:
Как пользоваться функцией распределения Стьюдента СТЮДРАСПОБР В EXCEL
Функция имеет следующий синтаксис:
=СТЬЮДРАСПОБР(вероятность;степени_свободы)
Описание аргументов:
- вероятность – обязательный для заполнения, принимает числовое значение вероятности для двустороннего распределения Стьюдента из диапазона от 0 (не включительно) до 1.
- степени_свободы – обязательный для заполнения, принимает числовое значение степеней свободы, которые определяют исследуемое распределение.
Примечания:
- Если один из аргументов функции указан в виде значения нечислового типа данных, результатом выполнения рассматриваемой функции будет код ошибки #ЗНАЧ!. Логические значения, имена и текстовые строки, преобразуемые в числа, не приводят к возникновению ошибки. Например, функция =СТЮДРАСПОБР(“0,4”;ИСТИНА) вернет значение 1,32638.
- Если аргумент вероятность задан числом, не находящимся в промежутке от 0 (не включительно) до 1, функция СТЮДРАСПОБР вернет код ошибки #ЧИСЛО!. Аналогичная ошибка возникает, если аргумент степени_свободы задан числом, которое меньше 1.
- Для расчета односторонней t-величины следует в качестве аргумента вероятность указать значение удвоенной вероятности.

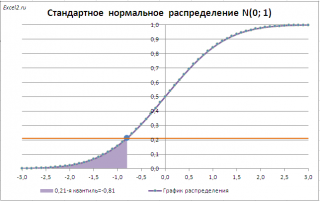
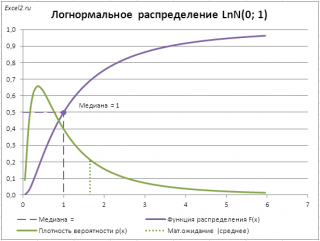
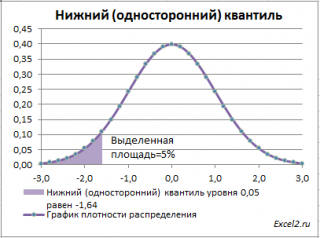
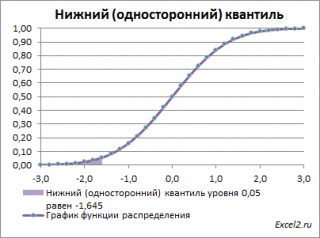
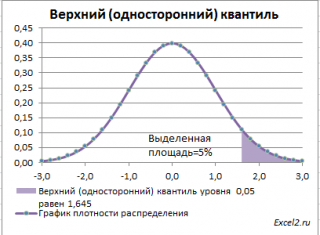
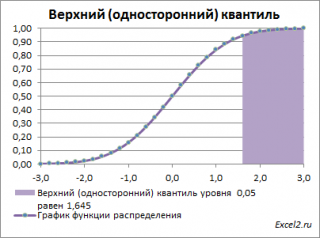
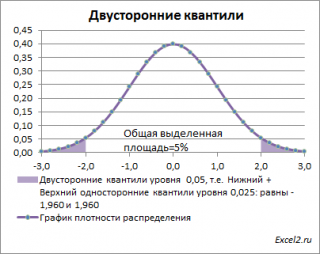
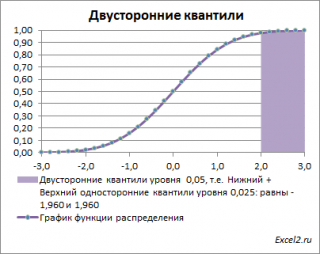



 ,
,






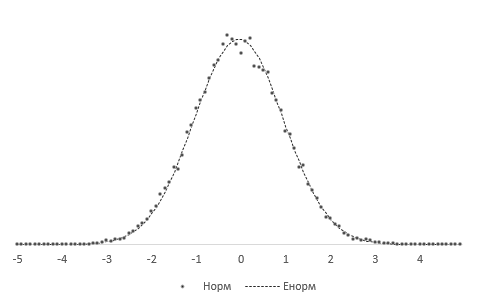
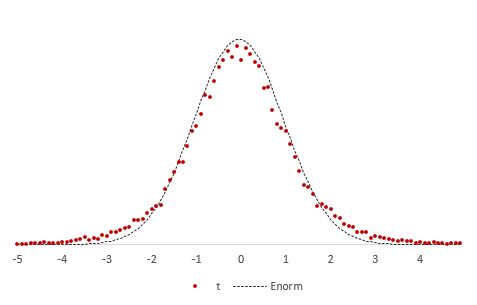
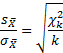
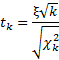
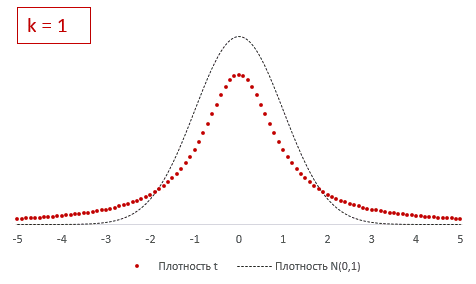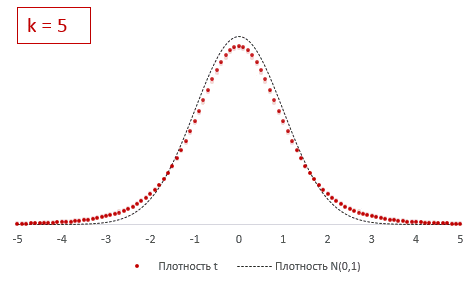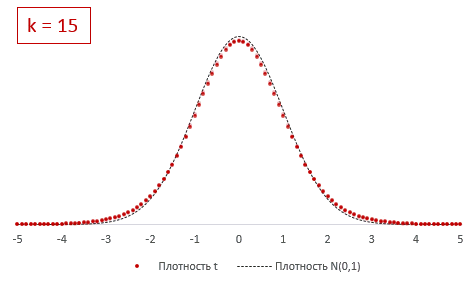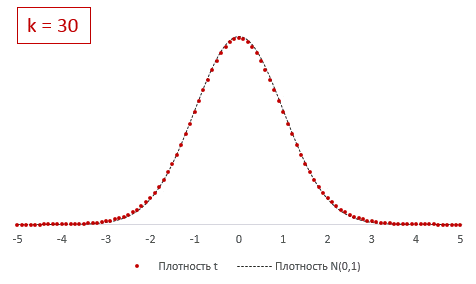
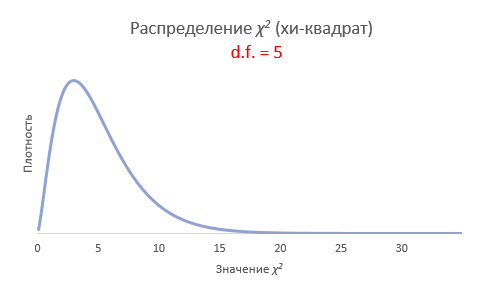
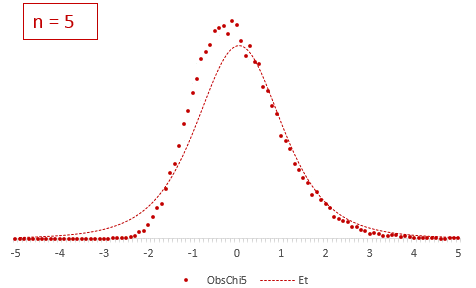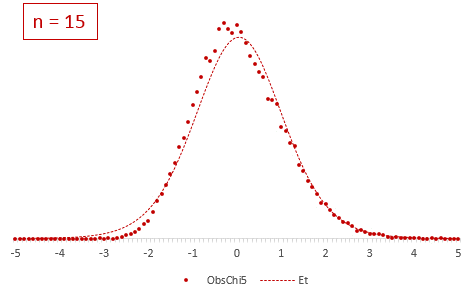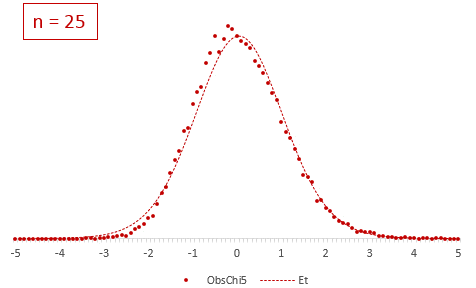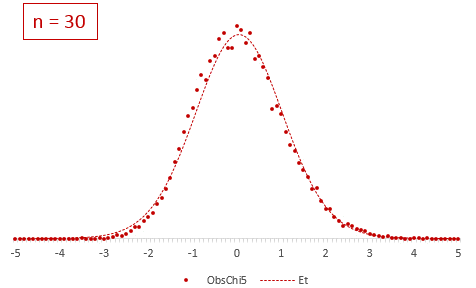
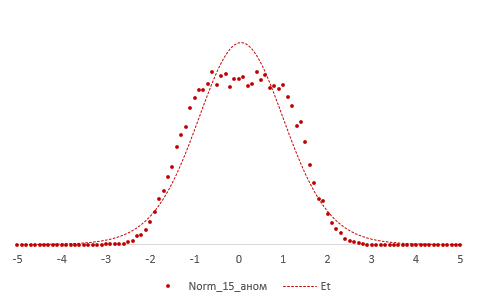
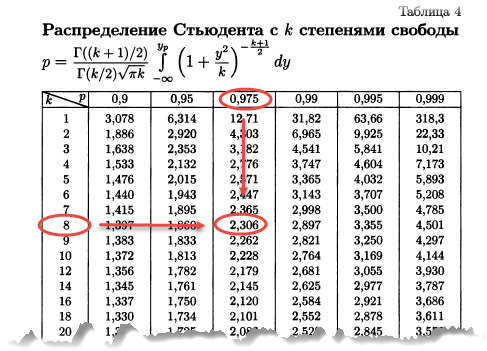
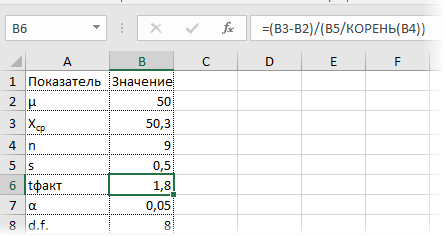
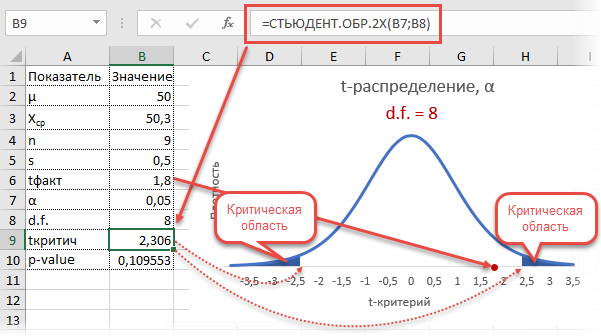
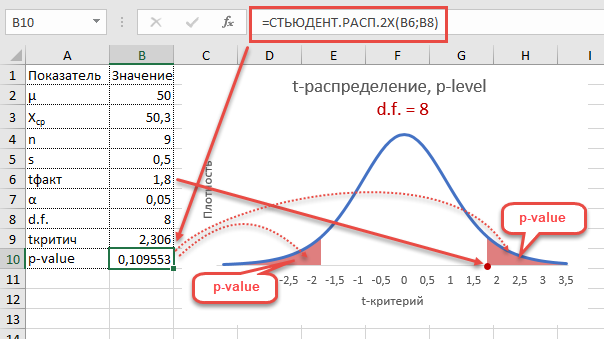
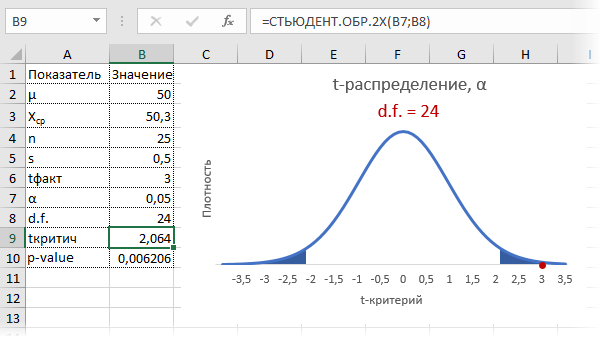
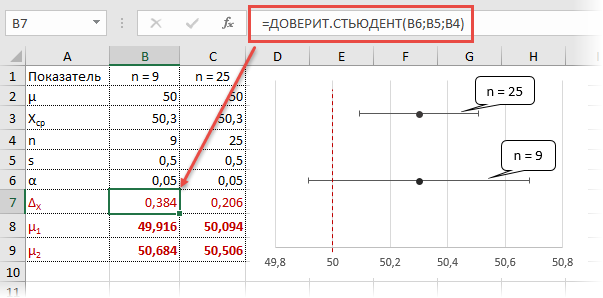












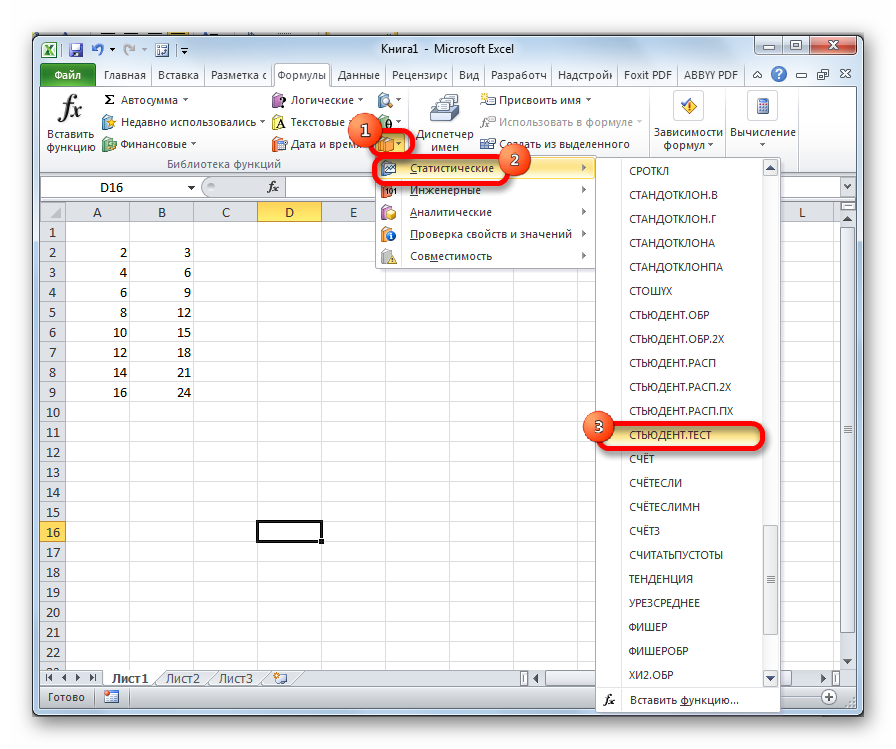

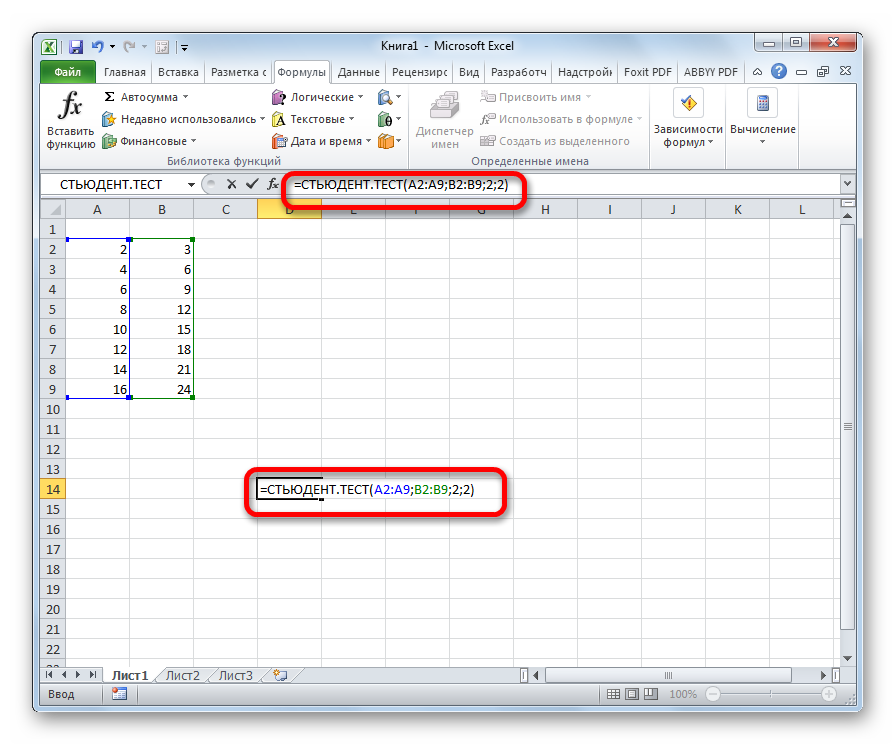
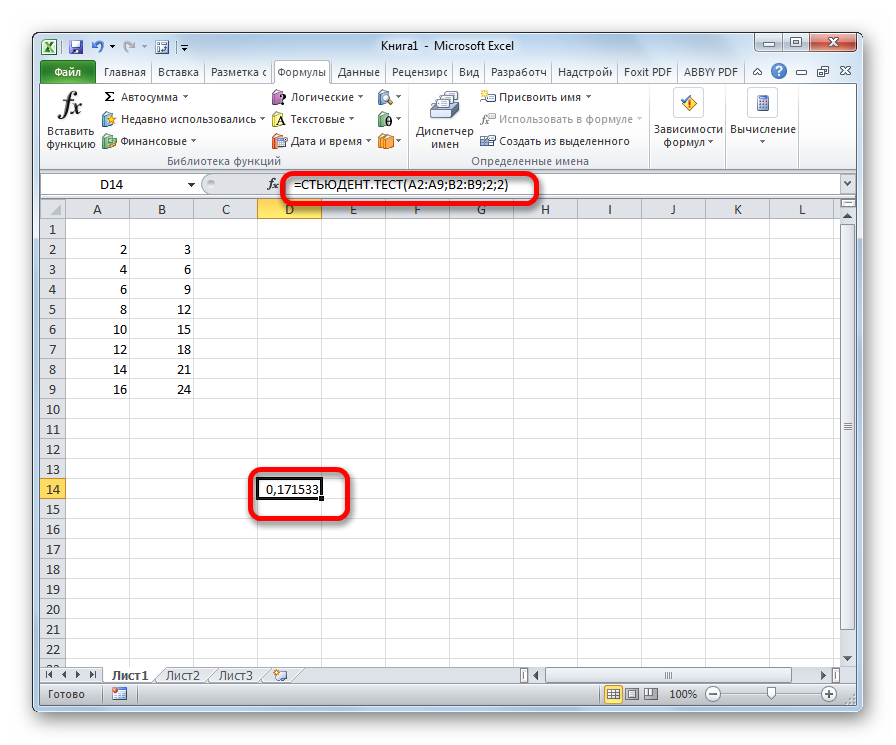
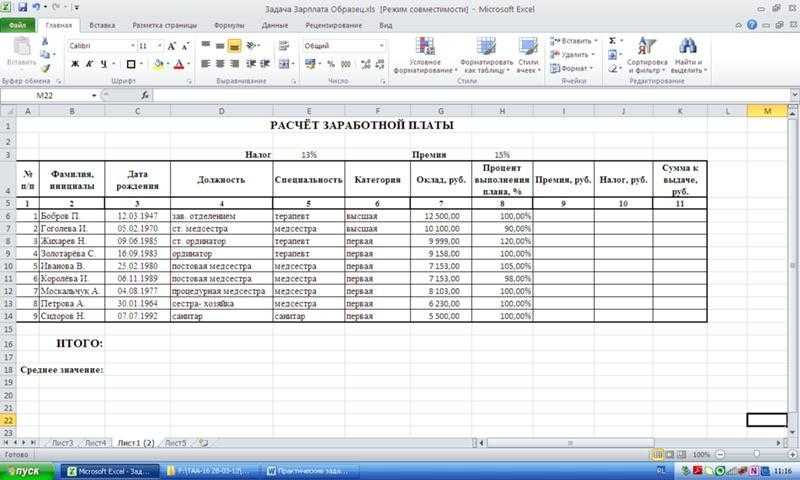
 002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.