Квадратичная линия тренда в excel

---

Если связь между двумя переменными является квадратичной, вы можете использовать квадратичную линию тренда, чтобы зафиксировать их связь на графике.

В этом руководстве представлен пошаговый пример того, как добавить квадратичную линию тренда на диаграмму рассеивания в Excel.

Шаг 1: Создайте данные

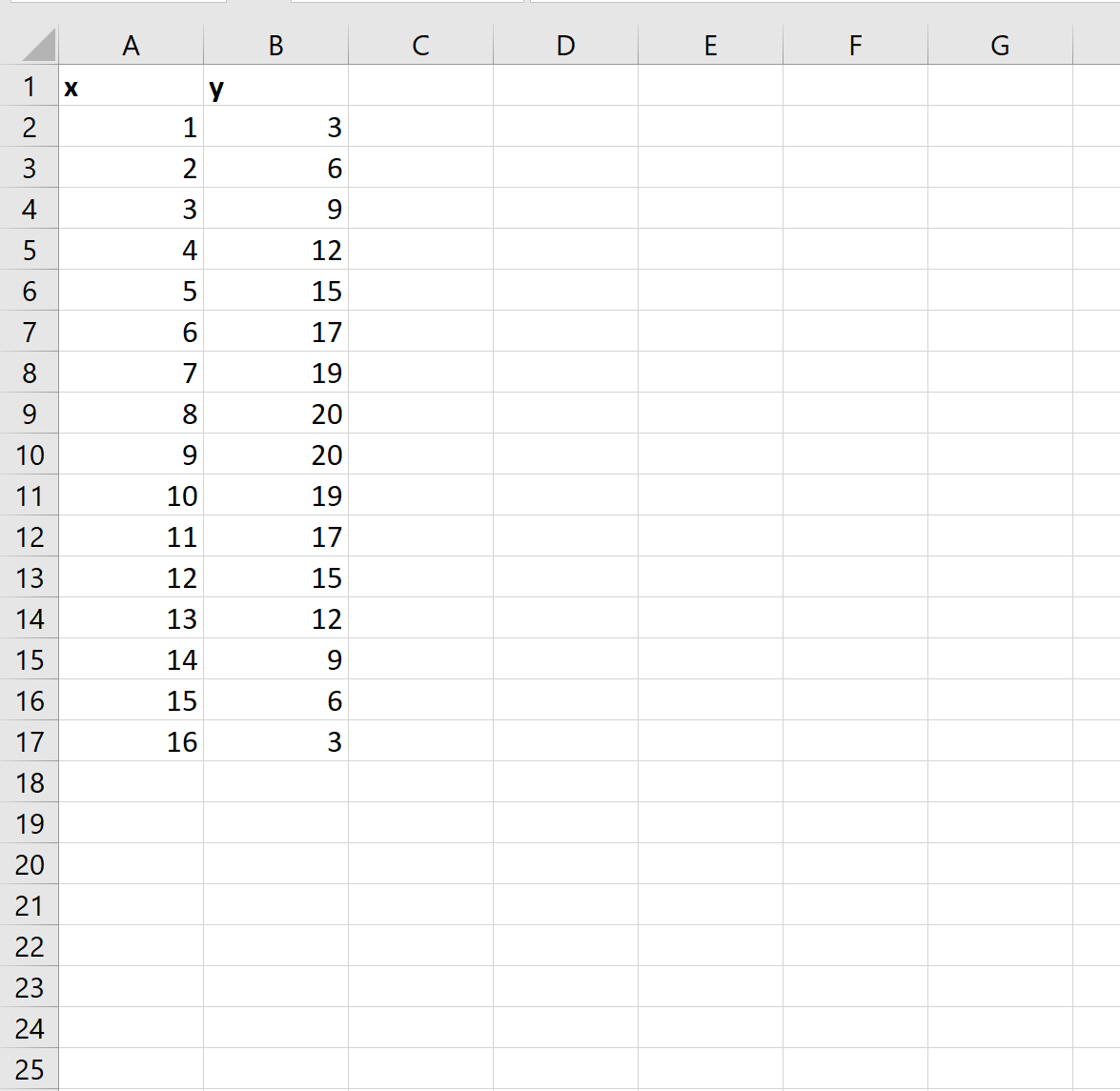
Во-первых, давайте создадим некоторые данные для работы:

Шаг 2: Создайте диаграмму рассеивания

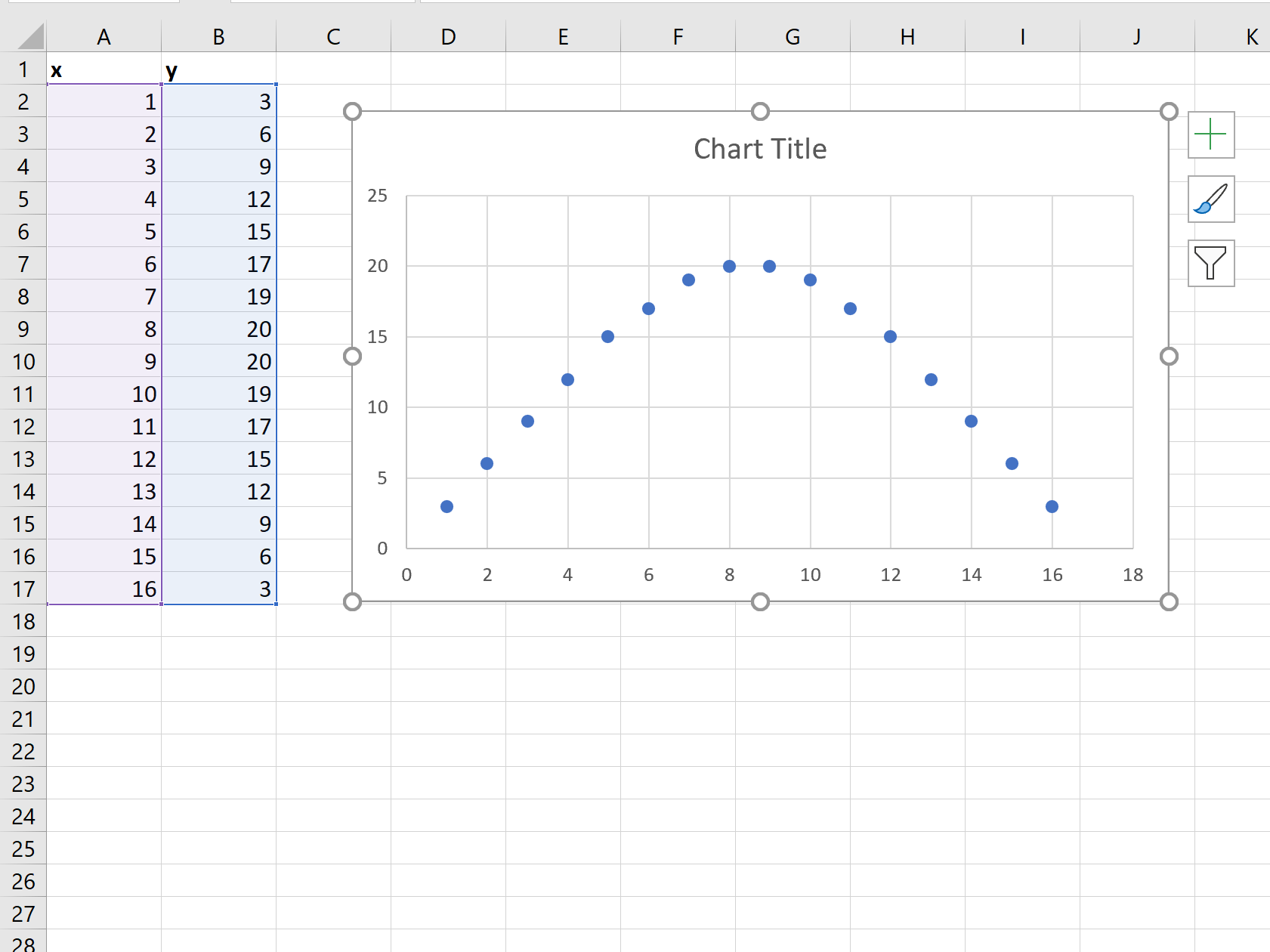
Затем выделите ячейки A2:B17.Щелкните вкладку « Вставка » на верхней ленте, затем щелкните первый вариант диаграммы в разделе « Вставить точечный » в группе « Диаграммы ».

Автоматически отобразится следующая диаграмма рассеяния:

Шаг 3: Добавьте квадратичную линию тренда

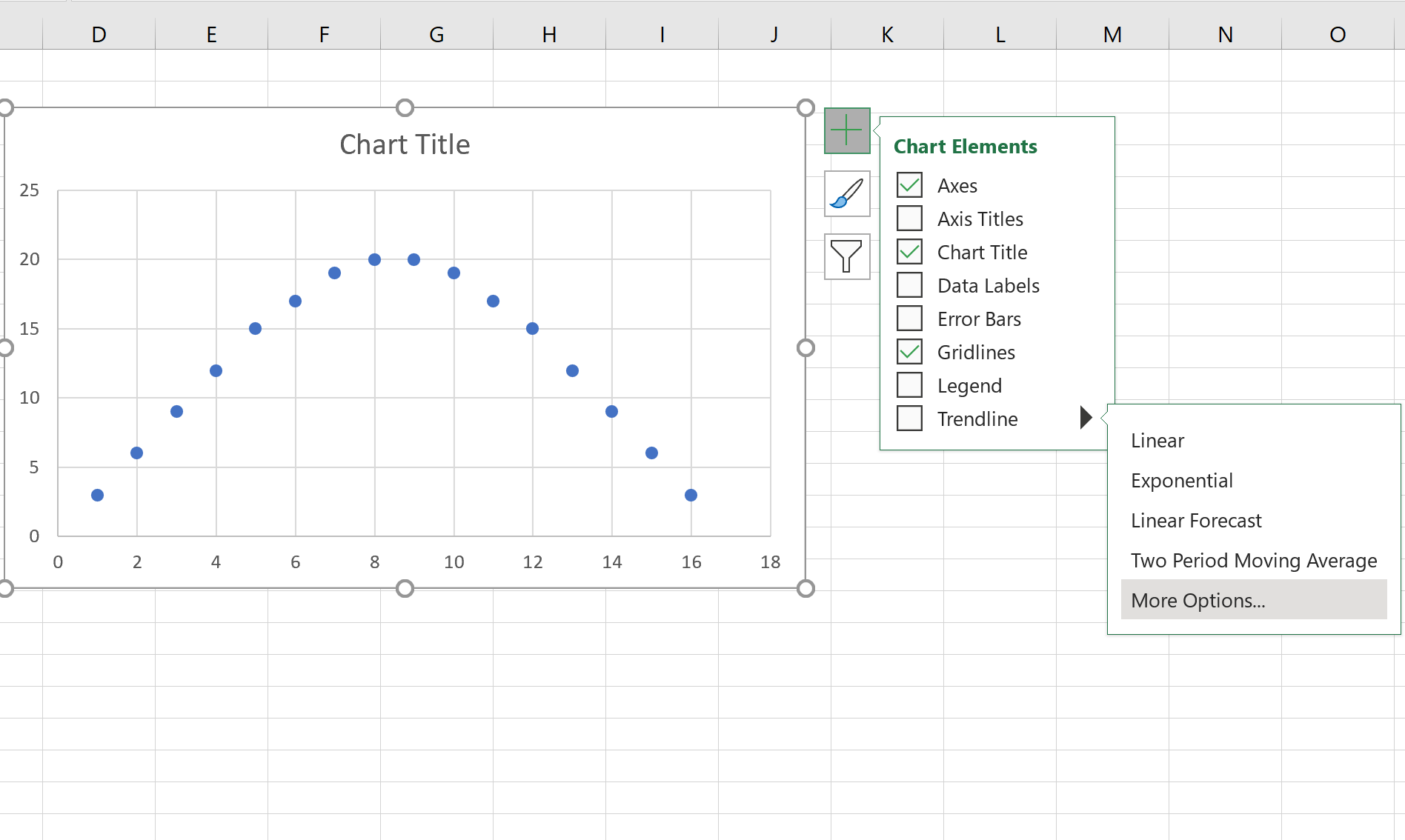
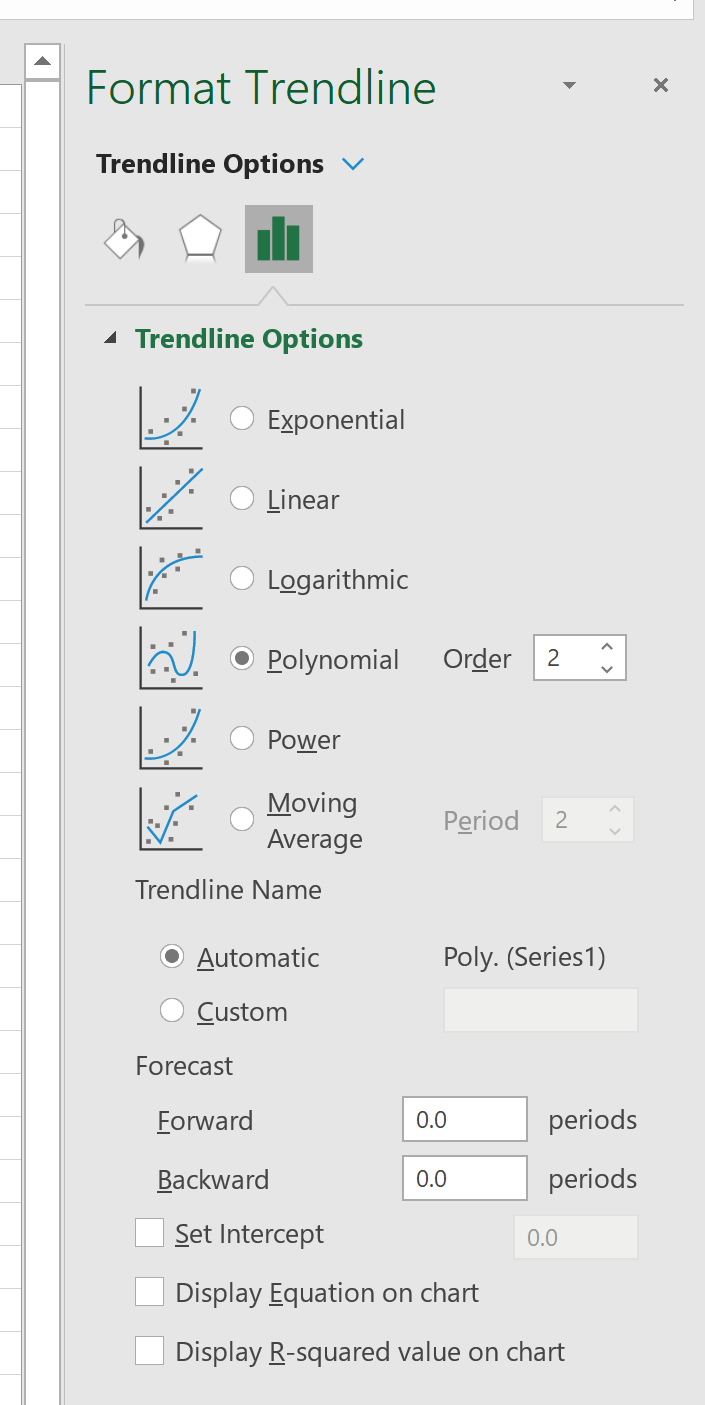
Затем щелкните зеленый значок плюса « + » в правом верхнем углу графика. Щелкните стрелку справа от линии тренда , затем щелкните Дополнительные параметры .

В появившемся справа окне нажмите Polynomial и выберите 2 для Order:

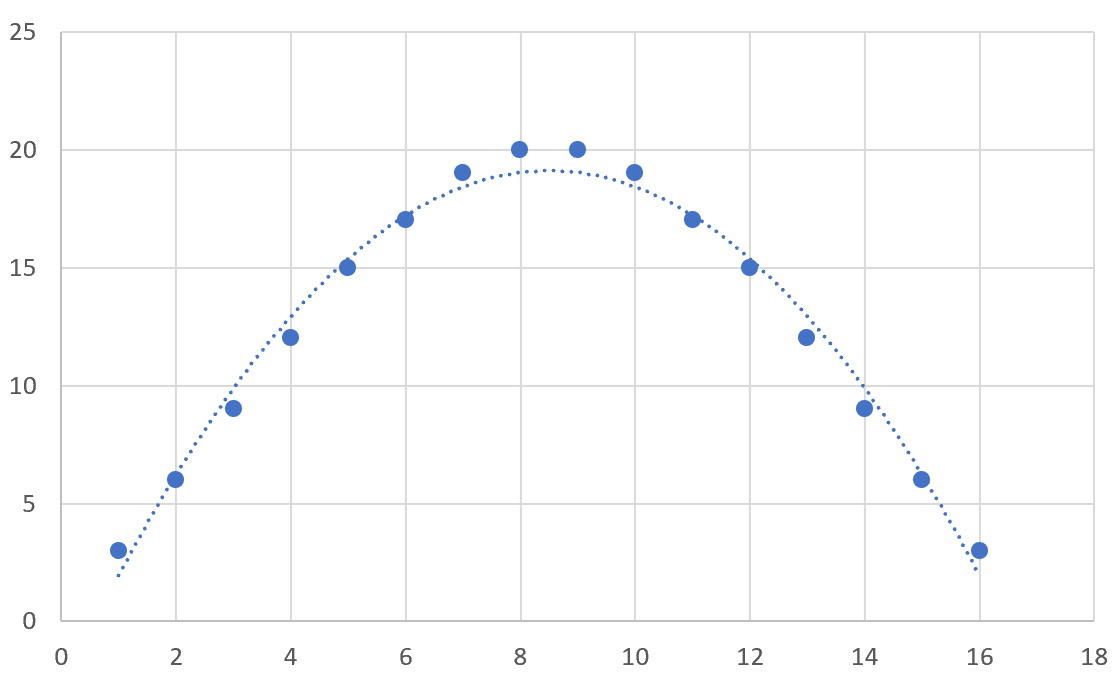
На графике автоматически отобразится следующая квадратичная линия тренда:

Не стесняйтесь нажимать на саму линию тренда, чтобы изменить стиль или цвет.

Дополнительные ресурсы

Как выполнить квадратичную регрессию в Excel
Подбор кривой в Excel (с примерами)

Вычисление трендов с помощью метода наименьших квадратов и прогнозирование

Среди компонентов временного ряда чаще других исследуется тренд. Именно тренд позволяет делать краткосрочные и долгосрочные прогнозы. Для выявления долговременной тенденции изменения временного ряда обычно строят график, на котором наблюдаемые данные (значения зависимой переменной) откладываются на вертикальной оси, а временные интервалы (значения независимой переменной) — на горизонтальной. В этом разделе мы опишем процедуру выявления линейного, квадратичного и экспоненциального тренда с помощью метода наименьших квадратов.

Модель линейного трендаявляется простейшей моделью, применяемой для прогнозирования: Y_i = β₀ + β₁X_i + ε_i. Уравнение линейного тренда:

Напомним, что метод линейного регрессионного анализа используется для вычисления выборочного наклона b₁ и сдвига b₀. Вычислив уравнение Ŷ_i = b₀ + b₁X_i, в него можно подставлять значения X, чтобы определять отклик Y.

Если при аппроксимации временного ряда с помощью метода наименьших квадратов первое наблюдение расположить в начале координат, поставив его в соответствие значению X = 0, интерпретация коэффициентов упрощается. Все последующие наблюдения получают целочисленные номера: 1, 2, 3, так что n-е (последнее) наблюдение будет иметь номер n – 1. Например, если временной ряд записывается на протяжении 20 лет, первый год обозначается цифрой 0, второй— цифрой 1, третий — цифрой 2 и так далее, а последний (20-й) год — числом 19.

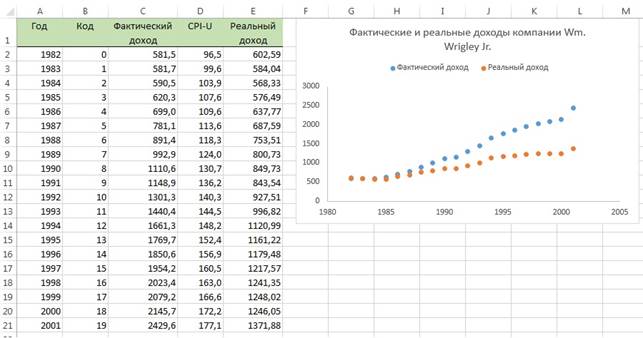
В сценарии была упомянута компания Wm. Wrigley Jr. Company, являющаяся крупнейшим производителем жевательной резинки в США. Акции компании котируются на Нью-Йоркской фондовой бирже под аббревиатурой WWY. Рыночная стоимость компании составляет 13 млрд. долл. Фактические доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах приведены на рис. 7. Затем с помощью индекса потребительских цен (Consumer Price Index — CPI), вычисляемого Бюро статистики Министерства труда США, фактические доходы были преобразованы в реальные. Для этого следует умножить величину фактического дохода на коэффициент 100/CPI.

Рис. 7. Фактические и реальные доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах

Обозначим последовательные значения переменной X с помощью целых чисел от 0 до 19, а затем выполним регрессионный анализ с помощью Пакета анализа (рис. 8).

Рис. 8. Модель линейной регрессии для предсказания реального дохода компании Wm. Wrigley Jr.; построена с помощью Пакета анализа Excel

Уравнение линейной регрессии имеет следующий вид (см. ячейки Е17, Е18 на рис. 8): Ŷ_i = 498,656 + 45,485Х_i, где началом координат является 1982 год, а шаг переменной X равен одному году. Регрессионные коэффициенты интерпретируются следующим образом:

• Сдвиг b₀ = 498,656 представляет собой предсказанное среднее значение реальных доходов компании Wm. Wrigley Jr. Company в 1982 году.

• Наклон b₁ = 45,485 представляет собой предсказанное увеличение реальных доходов компании в среднем на 45,485 млрд. долл. в год.

Линия тренда и временной ряд реальных доходов показаны на рис. 9. График можно построить на основании уравнения линейной регрессии (колонка D; рис. 9а) или простым добавлением линии тренда на ранее построенный график доходов (рис. 9б). Видно, что на протяжении ряда лет доходы компании линейно возрастали. Скорректированный коэффициент r 2 равен 0,966 (ячейка Е6 на рис. 8). Следовательно, все изменения реальных доходов хорошо описываются линейным трендом. Возникает вопрос: а нельзя ли выбрать еще более точную модель? Для ответа на него рассмотрим еще две модели — квадратичную и экспоненциальную.

Рис. 9. Линия тренда реальных доходов компании Wm. Wrigley Jr., вычисленная с помощью метода наименьших квадратов, построенная: (а) на основании уравнения линейной регрессии; (б) добавлением линии тренда на график

Модель квадратичного тренда, или полиномиальная модель второй степени является простейшей нелинейной моделью, применяемой для прогнозирования: . Уравнение квадратичного тренда:

где b₀ – оценка сдвига отклика Y, b₁ – оценка линейного эффекта, b₂ – оценка квадратичного эффекта.

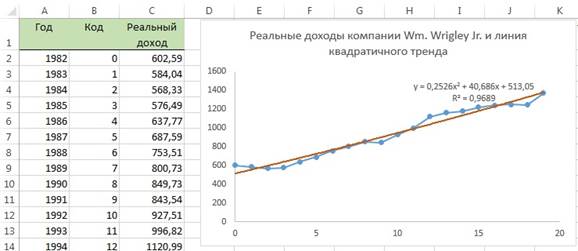
Построим квадратичный тренд путем добавления линии тренда на график с исходными данными (рис. 10).

Рис. 10. График квадратичного тренда для предсказания реальных доходов компании Wm. Wrigley Jr.

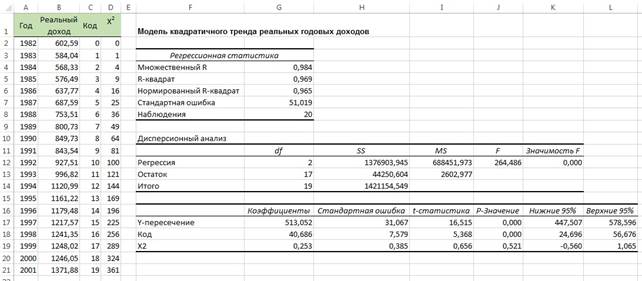
Как показано на рис. 10, уравнение линейной регрессии: Y =513,05 + 40,686Х + 0,2526Х 2 , где началом координат является 1982 год, а шаг переменной X равен одному году. Этот график аппроксимирует временной ряд почти так же, как и линейный тренд. Скорректированный коэффициент r 2 равен 0,965 (рис. 11), а t-статистика, учитывающая вклад квадратичного эффекта, равна 0,656 (соответствующее р-значение равно 0,521).

Рис. 11. Модель квадратичного тренда реальных годовых доходов

Модель экспоненциального тренда.Если временной ряд является возрастающим, а относительное изменение данных — постоянным, можно применять модель экспоненциального тренда. Учитывая сложность формул ограничимся только графическим анализом. Для этого на график с исходными данными добавим линию экспоненциального тренда, а также выведем на график уравнение тренда и параметр r 2 (рис. 12).

Рис. 12. График экспоненциального тренда для предсказания реальных доходов компании Wm. Wrigley Jr.

Экспоненциальная модель аппроксимирует временной ряд почти так же, как линейная и квадратичная модель. Скорректированный коэффициент r 2 равен 0,960, в то время как для линейной модели этот коэффициент равен 0,966, а для квадратичной – 0,965.

Дата добавления: 2015-08-17 ; просмотров: 1106 | Нарушение авторских прав

Расчет параметров линейного и квадратического тренда для показателей x и y

Для расчета параметров уравнений линейного и квадратического тренда построим вспомогательную таблицу.

Таблица 9. Вспомогательная таблица для расчета параметров линейного и квадратического тренда

Условное обозначение времени

Формулы для расчета параметров линейного тренда:

Формулы для расчета параметров квадратичного тренда:

Подставляя в эти формулы все суммы, рассчитанные в последней (итоговой) строке вспомогательной таблицы 4 (Σy =7200320 , Σt 2 = 28 Σt 4 =196, Σyt = 10549215, Σyt 2 = 35198473 ) , получаем следующие результаты:

Линейный тренд y

Квадратический тренд y

Аналогичным образом рассчитаем параметры уравнений линейного и квадратического тренда для показателя x.

Таблица 10. Вспомогательная таблица для расчета параметров линейного и квадратического тренда

Условное обозначение времени

x*t

x*t 2

x

Линейный тренд x

Квадратический тренд x

х^^ = b₀ + b₁* t + b*t 2

Чтобы выбрать, какое из уравнений тренда (линейное или квадратическое) лучше описывает исходный ряд данных, строится вспомогательная таблица для расчета так называемой ошибки аппроксимации, которая находится по формуле:

– исходные значения уровня ряда;

– расчетные значения уровня ряда; т.е. f(t), где f(t) – уравнение соответствующей функции.

Таблица 11. Вспомогательная таблица для расчета ошибок аппроксимации

Линия тренда в Excel на разных графиках

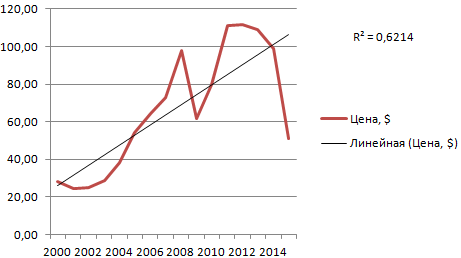
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.

Рассмотрим, как добавить линию тренда на график в Excel.

Добавление линии тренда на график

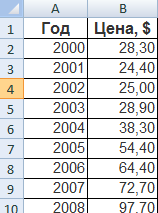
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:

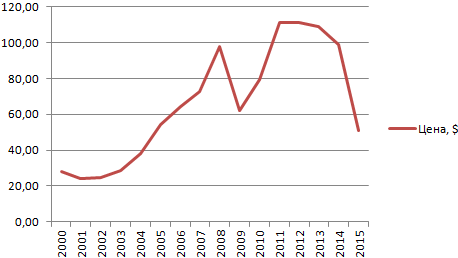
1. Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
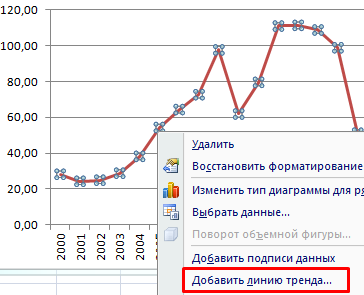
2. Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
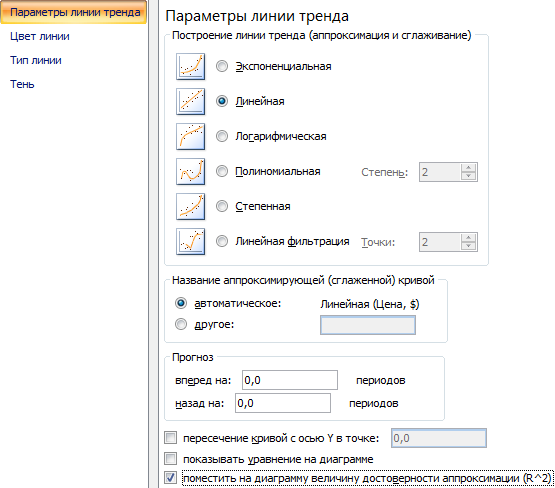
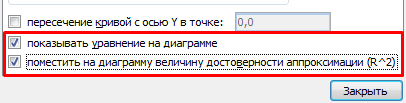
3. Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
4. На графике появляется косая линия.

Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.

Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.

Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:

• лепестковый;
• круговой;
• поверхностный;
• кольцевой;
• объемный;
• с накоплением.

Уравнение линии тренда в Excel

В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.

Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.

Линейная аппроксимация

Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.

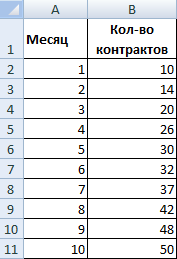
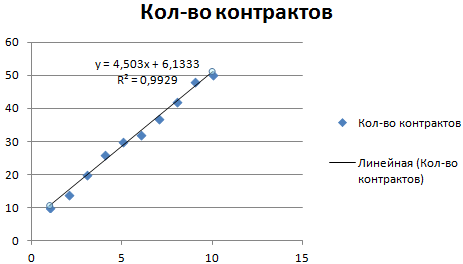
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:

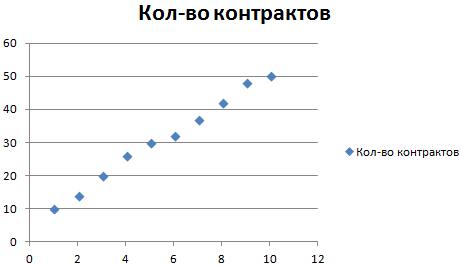
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):

Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).

Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:

y = 4,503x + 6,1333

• где 4,503 – показатель наклона;
• 6,1333 – смещения;
• y – последовательность значений,
• х – номер периода.

Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.

Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.

Экспоненциальная линия тренда

Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.

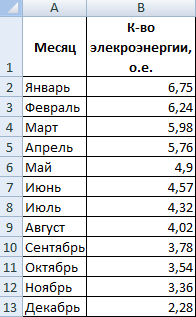
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:

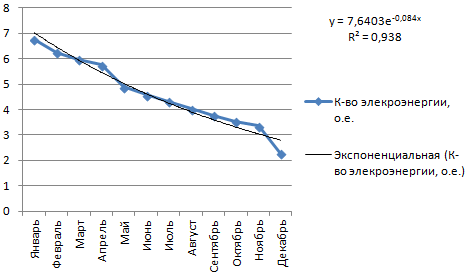
Строим график. Добавляем экспоненциальную линию.

Уравнение имеет следующий вид:

• где 7,6403 и -0,084 – константы;
• е – основание натурального логарифма.

Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.

Логарифмическая линия тренда в Excel

Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.

На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.

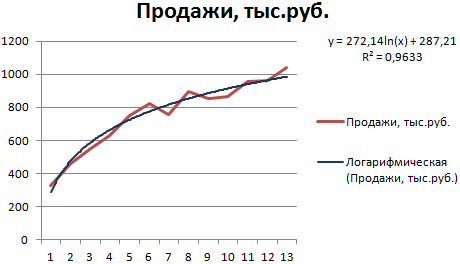
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:

R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.

Период	14	15	16	17	18	19	20
Прогноз	1005,4	1024,18	1041,74	1058,24	1073,8	1088,51	1102,47

Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.

Полиномиальная линия тренда в Excel

Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.

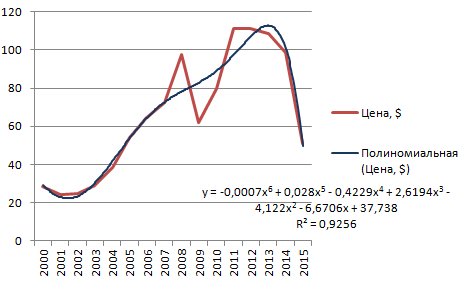
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).

Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.

Зато такой тренд позволяет составлять более-менее точные прогнозы.

Аппроксимируемая
функция у может зависеть от одной или
нескольких переменных.

В Excel для построения
регрессий имеются две возможности.

1. Добавление выбранных
регрессий (линий тренда – trendlines) в
диаграмму, построенную на основе таблицы
данных для исследуемой характеристики
процесса (доступно лишь при наличии
построенной диаграммы).

2. Использование
встроенных статистических функций
рабочего листа Excel, позволяющих получать
регрессии (линии тренда) непосредственно
на основе таблицы исходных данных.

1. Линейная
регрессия
хороша при моделировании характеристик,
значения которых увеличиваются или
убывают с постоянной скоростью. Это
наиболее простая в построении модель
исследуемого процесса. Она строится в
соответствии с уравнением

y = mx +
b,                                                      
(2)

где
m – тангенс угла наклона линейной
регрессии к оси абсцисс; b – координата
точки пересечения линейной регрессии
с осью ординат.

2. Полиномиальная
линия тренда
полезна для описания характеристик,
имеющих несколько ярко выраженных
экстремумов (максимумов и минимумов).
Выбор степени полинома определяется
количеством экстремумов исследуемой
характеристики. Так, полином второй
степени может хорошо описать процесс,
имеющий только один максимум или минимум;
полином третьей степени – не более двух
экстремумов; полином четвертой степени
– не более трех экстремумов и т. д.

В этом случае линия
тренда строится в соответствии с
уравнением

y = c₀
+ c₁x
+ c₂x²
+ c₃x³
+ c₄x⁴
+ c₅x⁵
+ c₆x⁶,            
           (3)

где
коэффициенты c₀,
c₁,
c₂,
…, c₆
– константы, значения которых определяются
в ходе построения.

3. Логарифмическая
линия тренда
с успехом применяется при моделировании
характеристик, значения которых вначале
быстро меняются, а затем постепенно
стабилизируются.

Данная линия тренда
строится в соответствии с уравнением

y = c ln(x) +
b,                                                
(4)

где
коэффициенты b, с – константы.

4.
Степенная
линия тренда
дает хорошие результаты, если значения
исследуемой зависимости характеризуются
постоянным изменением скорости роста.
Примером такой зависимости может служить
график равноускоренного движения
автомобиля. Если среди данных встречаются
нулевые или отрицательные значения,
использовать степенную линию тренда
нельзя.

Линия строится в
соответствии с уравнением

y = c
x^b,                                                      
(5)

где
коэффициенты b, с – константы.

5. Экспоненциальную
линию тренда
следует использовать в том случае, если
скорость изменения данных непрерывно
возрастает. Для данных, содержащих
нулевые или отрицательные значения,
этот вид приближения также неприменим.

Линия тренда строится
в соответствии с уравнением

y =
ce^bx,                                                      
(6)

где
коэффициенты b, с – константы.

 Трендом называется
общая тенденция изменения данных в
зависимости от времени.

При подборе линии
тренда Excel автоматически рассчитывает
значение величины R2 (коэффициент
детерминации), которая характеризует
достоверность аппроксимации (степень
близости линии тренда к исходным данным):
чем ближе значение R2 к единице, тем
надежнее линия тренда аппроксимирует
исследуемый процесс. При
необходимости значение R2 всегда можно
отобразить на диаграмме.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

A line that bounds a particular chart and shows the behavior as it propagates is known as a trend line. It is generally used for analytics purposes to get a close approximate idea from the chart. The chart can be of any type like Bar Chart, Scattered Chart, Line Chart, etc.

In this article, we are going to see different types of Trendlines in Excel using some practical real-life examples :

1. Linear Trendline : Linear trendlines are mostly used when the data sets are linear in nature. It can be linearly increasing which describes a rise in the data or linearly decreasing which describes a fall in the data. It is of the type :

m : Slope of the line y
c : Intercept of the line

Example: The below linear trendline shows the performance of a batsman in a T20 match. The linear trendline is rising with the number of matches played. This shows the player performed well gradually in all the matches and the runs scored kept on increasing.

2. Polynomial Trendline: Polynomial trendline is used when the dataset is changing values rapidly i.e. sometimes increasing or decreasing more than once. It is of the type :

The degree of a polynomial is the largest power of x. In the trendline the number of bends is dependent on the degree number. By default, the order will be 2 as we can see in “Order”. The number of bends or hills will increase as you increase the Order value.

Example : The below polynomial trendline shows the performance of a batsman in eight contiguous matches. We can see a rise in the number of runs scored and then reached a peak value and again fallen. So for such types of data sets the polynomial trendline is mostly used.

3. Exponential Trendline: It is mostly used when there is a rise or fall in the dataset exponentially. It is of the type :

Example : Consider a survey which consists of the number of people suffering from a deadly disease. The number of positive cases per month from January to July is the data set here. We can infer from the below chart that the number of cases are exponentially declining till July.

4. Logarithmic Trendline: The best-fit line is mostly used for datasets that either increase or decrease and then maintain a constant level. It is basically the inverse of the exponential trendline. It is of the type :

Example: Consider a survey about the number of people taking vaccines per month. We can see that it is growing and then level off in June and July. We can infer from the below chart that by June maximum people have started to take vaccines.

5. Power Trendline: It is mostly used for datasets that increase at a particular rate, It is more symmetrical and is somewhat similar to the exponential type of curve. It is of the type :

Example: Consider the runs scored by a batsman in ten consecutive test matches. We can infer from the below chart that the performance of the player has increased gradually as he played more matches. 

6. Moving Average Trendline : When there are a lot of oscillations i.e. rapid up and down in the values of the datasets, the moving average trendline can be used to make a smooth and effective line around the chart to see the growth and fall of the data. In Excel by default, the Period of the trendline is set to 2. As we increase the value of the Period the line becomes more effective and surrounds the chart. It gets a smooth bend and curves on increasing the Period value.

For example: Consider the performance of a batsman in ten consecutive IPL matches. We can see the performance of the player is not constant and there is rise or fall in the runs scored and also in one of the matches he was out for a duck.