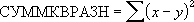Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СУММКВРАЗН в Microsoft Excel.
Описание
Возвращает сумму квадратов разностей соответствующих значений в двух массивах.
Синтаксис
СУММКВРАЗН(массив_x;массив_y)
Аргументы функции СУММКВРАЗН описаны ниже.
-
Массив_x Обязательный. Первый массив или диапазон значений.
-
Массив_y Обязательный. Второй массив или диапазон значений.
Замечания
-
Аргументы могут быть числами либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Если количество значений в аргументах «массив_x» и «массив_y» не совпадает, то функция СУММКВРАЗН возвращает значение ошибки #Н/Д.
-
Уравнение суммы квадратов разностей имеет следующий вид:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
Первый массив |
Второй массив |
|
|
2 |
6 |
|
|
3 |
5 |
|
|
9 |
11 |
|
|
1 |
7 |
|
|
8 |
5 |
|
|
7 |
4 |
|
|
5 |
4 |
|
|
Формула |
Описание (результат) |
Результат |
|
=СУММКВРАЗН(A3:A9;B3:B9) |
Сумма квадратов разностей двух приведенных выше массивов (79) |
79 |
|
=СУММКВРАЗН({2; 3; 9; 1; 8; 7; 5}; {6; 5; 11; 7; 5; 4; 4}) |
Сумма квадратов разностей двух массивов констант (79) |
79 |
Нужна дополнительная помощь?
Функция СУММКВРАЗН возвращает сумму квадратов разностей соответствующих значений в двух массивах.
Описание функции
Возвращает сумму квадратов разностей соответствующих значений в двух массивах.
Синтаксис
=СУММКВРАЗН(массив_x; массив_y)Аргументы
массив_xмассив_y
Обязательный. Первый массив или диапазон значений.
Обязательный. Второй массив или диапазон значений.
Замечания
- Аргументы должны быть либо числами, либо содержащими числа именами, массивами или ссылками.
- Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
- Если количество значений в аргументах «массив_x» и «массив_y» не совпадает, то функция СУММКВРАЗН возвращает значение ошибки #Н/Д.
- Уравнение суммы квадратов разностей имеет следующий вид:
Пример
В этом учебном материале вы узнаете, как использовать Excel функцию СУММКВРАЗН с синтаксисом и примерами.
Описание
Microsoft Excel функция СУММКВРАЗН вычисляет сумму квадратов разностей между соответствующими элементами в массивах и возвращает сумму результатов.
Функция СУММКВРАЗН — это встроенная в Excel функция, которая относится к категории математических / тригонометрических функций.
Её можно использовать как функцию рабочего листа (WS) в Excel.
Как функцию рабочего листа, функцию СУММКВРАЗН можно ввести как часть формулы в ячейку рабочего листа.
Синтаксис
Синтаксис функции СУММКВРАЗН в Microsoft Excel:
СУММКВРАЗН(массив_x;массив_y)
Аргументы или параметры
- массив_x
- Первый диапазон или массив, используемый в вычислении.
- массив_y
- Второй диапазон или массив, используемый при вычислении.
Возвращаемое значение
Функция СУММКВРАЗН возвращает числовое значение.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000
Тип функции
- Функция рабочего листа (WS)
Пример (как функция рабочего листа)
Рассмотрим несколько примеров функции СУММКВРАЗН, чтобы понять, как использовать Excel функцию СУММКВРАЗН в качестве функции рабочего листа в Microsoft Excel:
|
=СУММКВРАЗН({1;2:3;4};{5;6:7;8}) Результат: 64 |
В приведенном выше примере будет возвращено 64.
Вы также можете ссылаться на диапазоны в Excel.
На основе приведенной выше электронной таблицы Excel вы можете ввести следующую формулу:
|
=СУММКВРАЗН(A1:B2; D1:E2) Результат: 64 |
Это также вернет значение 64.
Применение метода наименьших квадратов в Excel
Метод наименьших квадратов представляет собой математическую процедуру построения линейного уравнения, которое бы наиболее точно соответствовало набору двух рядов чисел. Целью применения данного способа является минимизация общей квадратичной ошибки. В программе Excel имеются инструменты, с помощью которых можно применять данный метод при вычислениях. Давайте разберемся, как это делается.
Использование метода в Экселе
Метод наименьших квадратов (МНК) является математическим описанием зависимости одной переменной от второй. Его можно использовать при прогнозировании.
Включение надстройки «Поиск решения»
Для того, чтобы использовать МНК в Экселе, нужно включить надстройку «Поиск решения», которая по умолчанию отключена.
- Переходим во вкладку «Файл».
Кликаем по наименованию раздела «Параметры».
В открывшемся окне останавливаем выбор на подразделе «Надстройки».
Теперь функция Поиск решения в Excel активирована, а её инструменты появились на ленте.
Условия задачи
Опишем применение МНК на конкретном примере. Имеем два ряда чисел x и y, последовательность которых представлена на изображении ниже.
Наиболее точно данную зависимость может описать функция:
При этом, известно что при x=0 y тоже равно . Поэтому данное уравнение можно описать зависимостью y=nx.
Нам предстоит найти минимальную сумму квадратов разности.
Решение
Перейдем к описанию непосредственного применения метода.
- Слева от первого значения x ставим цифру 1. Это будет приближенная величина первого значения коэффициента n.
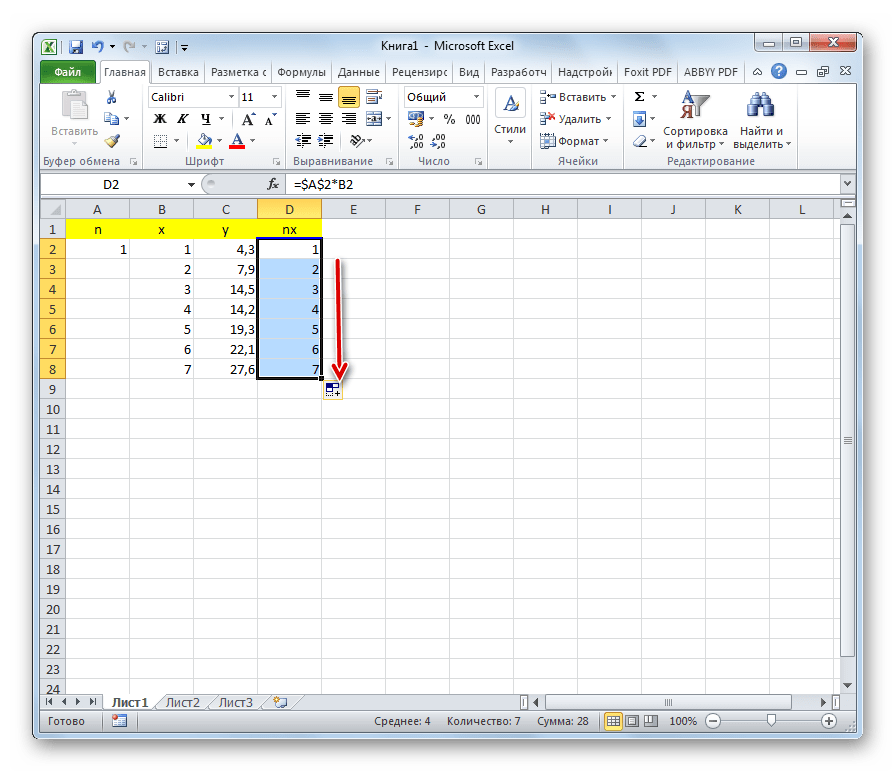
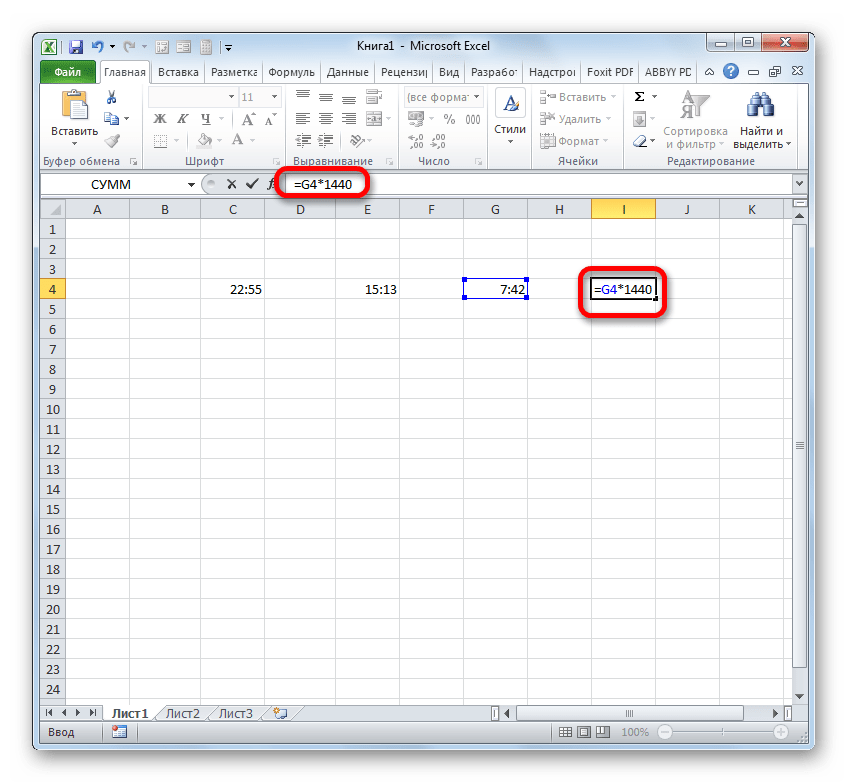
Справа от столбца y добавляем ещё одну колонку – nx. В первую ячейку данного столбца записываем формулу умножения коэффициента n на ячейку первой переменной x. При этом, ссылку на поле с коэффициентом делаем абсолютной, так как это значение меняться не будет. Кликаем по кнопке Enter.
Используя маркер заполнения, копируем данную формулу на весь диапазон таблицы в столбце ниже.
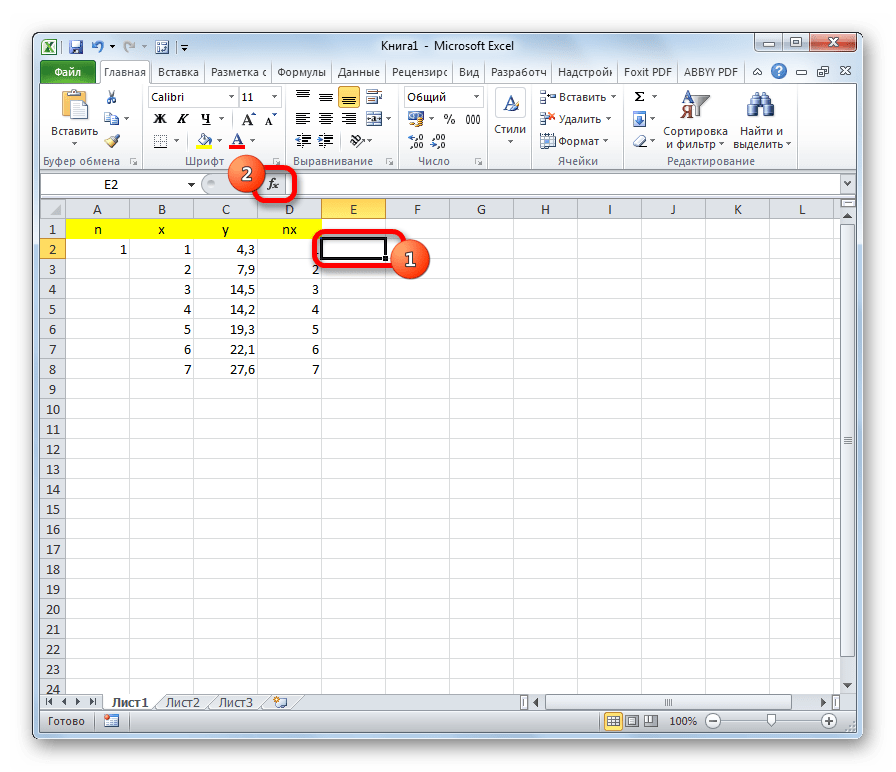
В отдельной ячейке высчитываем сумму разностей квадратов значений y и nx. Для этого кликаем по кнопке «Вставить функцию».
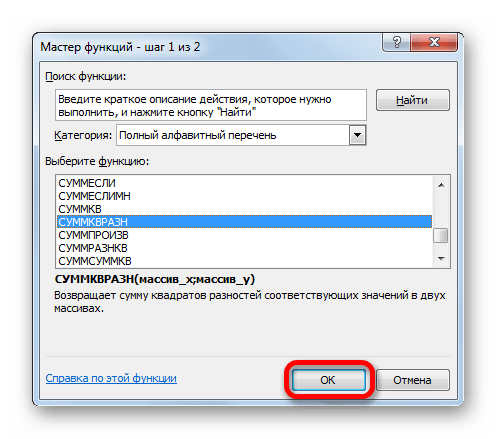
В открывшемся «Мастере функций» ищем запись «СУММКВРАЗН». Выбираем её и жмем на кнопку «OK».
Открывается окно аргументов. В поле «Массив_x» вводим диапазон ячеек столбца y. В поле «Массив_y» вводим диапазон ячеек столбца nx. Для того, чтобы ввести значения, просто устанавливаем курсор в поле и выделяем соответствующий диапазон на листе. После ввода жмем на кнопку «OK».
Переходим во вкладку «Данные». На ленте в блоке инструментов «Анализ» жмем на кнопку «Поиск решения».
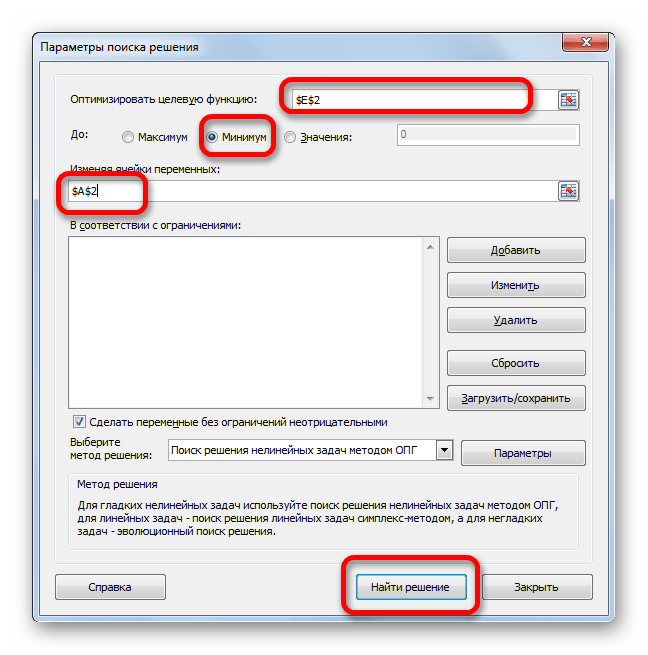
Открывается окно параметров данного инструмента. В поле «Оптимизировать целевую функцию» указываем адрес ячейки с формулой «СУММКВРАЗН». В параметре «До» обязательно выставляем переключатель в позицию «Минимум». В поле «Изменяя ячейки» указываем адрес со значением коэффициента n. Жмем на кнопку «Найти решение».
Как видим, применение метода наименьших квадратов довольно сложная математическая процедура. Мы показали её в действии на простейшем примере, а существуют гораздо более сложные случаи. Впрочем, инструментарий Microsoft Excel призван максимально упростить производимые вычисления.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Метод наименьших квадратов в Excel
Программа Excel – мощный табличный редактор, позволяющий выполнять огромное количество различных операций и задач. В данной статье мы разберем, как можно применить метод наименьших квадратов (МНК), который используется для решения различных задач с минимизацией суммы квадратов отклонений некоторых функций от искомых переменных.
Подготовительный этап: активируем надстройку “Поиск Решения”
Прежде, чем приступить к решению основной задачи, потребуется активировать надстройку “Поиск решения” в программе.
- Идем в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В правой части подраздела “Надстройки” выбираем для параметра “Управление” вариант “Надстройки Excel” и жмем “Перейти”.
- Появится окно для выбора нужных надстроек. Устанавливаем галочку напротив пункта “Поиск решения” и щелкаем OK.
Этап 1: исходные данные
Давайте разберем применение метода наименьших квадратов, решив конкретный пример. Допустим, у нас есть два ряда числовых значений – X и Y.
Данная зависимость может быть описана уравнением ниже:
Также, мы знаем, что если X=0, то и Y=0. А значит, данное уравнение можно записать так:
Приступим к выполнению нашей задачи, которая заключается в нахождении суммы квадратов разности.
Этап 2: решаем задачу с применением МНК
- Столбцу, находящемся слева от X, задаем имя N пишем число “1” (примерное значение первого коэф. N) напротив первого значения ряда X.
- Столбцу с правой стороны от Y задаем название NX. Затем в самой верхней ячейке (напротив первых значений рядов X и Y) пишем формулу произведения коэф. N на соответствующее ему значение из столбца X. При этом адрес ячейки с коэффициентом нужно сделать абсолютным, чтобы он не менялся при копировании формулы. По готовности жмем Enter.
- Наводим указатель мыши на ячейку с полученным результатом. Как только появится черный плюсик (маркер заполнения), зажав левую кнопку мыши тянем его вниз до последней строки таблицы.
- Получаем результаты расчетов в каждой ячейке столбца NX.
- Теперь нужно посчитать сумму разностей квадратов значений Y и NX. Встаем в самую верхнюю ячейку столбца справа от NX (не считая шапки таблицы) и щелкаем по значку “Вставить функцию” (fx).
- В окне вставки функции выбираем категорию “Математические”, находим оператор “СУММКВРАЗН” и щелкаем OK.
- Теперь нужно заполнить аргументы функции:
- в поле “Массив_x” указываем координаты диапазона ячеек столбца Y (без шапки). Адреса ячеек можно указать как вручную, напечатав их с клавиатуры, так и путем выделения с помощью зажатой левой кнопки мыши в самой таблице.
- в поле “Массив_y” указываем диапазон ячеек столбца NX.
- жмем Enter, когда все готово.
- Переключаемся во вкладку “Данные”. В группе “Анализ” щелкаем по функции “Поиск решения”.
- Нам предстоит заполнить параметры поиска решения:
- в поле “Оптимизировать целевую функцию” следует указать ссылку на ячейку с функцией “СУММКВРАЗН”. Сделать это можно вручную или выбрав элемент в таблице.
- для опции “До” выбираем вариант – “Минимум”.
- в поле “Изменяя ячейки переменных” нужно указать координаты ячейки, в которой находится соответствующее значение коэф. N.
- по готовности нажимаем “Найти решение”.
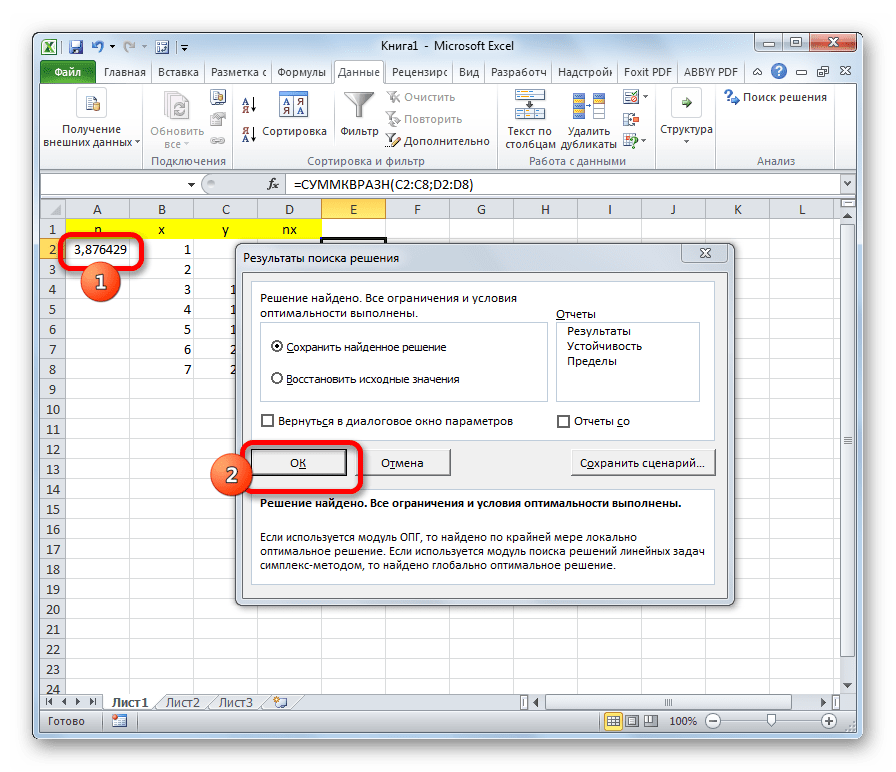
- После выполнения функции появится окно с результатами поиска решения и произойдет замена значения в столбце N. Найденная величина является наименьшим квадратом функции. Нажимаем OK, если полученный результат удовлетворителен.
Заключение
Итак, мы только что разобрали на практическом примере, каким образом можно применить метод наименьших квадратов в Эксель. На практике могут встречаться более сложные задачи, однако, в целом логика действий схожа с той, что мы описали.
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна (нулю).
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Метод наименьших квадратов и поиск решения в Excel
Ну вот, на работе перед инспекцией отчитались, статья дома для конференции написана — можно теперь и в блог писать. Пока данные свои обрабатывал, понял, что не могу не написать про очень классную и нужную надстройку в Excel, которая называется «поиск решения». Так что статья будет посвящена именно этой надстройке, и расскажу я о ней на примере использования метода наименьших квадратов (МНК) для поиска неизвестных коэффициентов уравнения при описании экспериментальных данных.
Как включить надстройку «поиск решения»
Для начала разберемся, как эту надстройку включить.
1. Идем в меню «Файл» и выбираем пункт «Параметры Excel»
2. В появившемся окне выбираем «Поиск решения» и нажимаем «перейти».
3. В следующем окне ставим галочку напротив пункта «поиск решения» и нажимаем «ОК».
4. Надстройка активирована — теперь ее можно найти в пункте меню «Данные».
Метод наименьших квадратов
Теперь вкратце о методе наименьших квадратов (МНК) и о том, где его можно применять.
Допустим, у нас есть набор данных после совершения нами какого-то эксперимента, где мы изучали влияния величины Х на величину Y.
Мы хотим это влияние описать математически, чтобы потом этой формулой пользоваться и знать, что, если мы поменяем величину Х на столько-то , получим величину Y такую-то.
Возьму супер-простой пример (см. рис.).
Ежу понятно, что точки расположились друг за другом как будто по прямой, а потому мы смело предполагаем, что наша зависимость описывается линейной функцией y=kx+b. При этом мы точно уверены, что при X равном нулю значение Y тоже равно нулю. Значит, функция, описывающая зависимость, будет еще проще: y=kx (вспоминаем школьную программу).
В общем, нам предстоит найти коэффициент k. Вот это мы и сделаем с помощью МНК с применением надстройки «поиск решения».
Метод заключается в том, чтобы (здесь — внимание: нужно вдуматься) сумма квадратов разностей экспериментально полученных и соответствующих расчетных значений была минимальной. То есть когда X1=1 реально измеренное значение Y1=4,6, а расчетное y1=f (x1) равно 4, квадрат разности будет (y1-Y1)^2=(4-4,6)^2=0,36. Со следующими так же: когда X2=2, реально измеренное значение Y2=8,1, а расчетное у2 равно 8, квадрат разности будет (y2-Y2)^2=(8-8,1)^2=0,01. И сумма всех этих квадратов должна быть минимально возможной.
Итак, приступим к тренировке по использованию МНК и надстройки Excel «поиск решения».
Применение надстройки поиск решения
1. Если не включили надстройку «поиск решения», то возвращаемся к пункту Как включить надстройку «поиск решения» и включаем 🙂
2. В ячейку А1 введем значение «1». Эта единица будет первым приближением к реальному значению коэффициента (k) нашей функциональной зависимости y=kx.
3. В столбце B у нас расположились значения параметра X, в столбце C — значения параметра Y. В ячейках столбца D вводим формулу: «коэффициент k умножить на значение Х». Например, в ячейке D1 вводим «=A1*B1», в ячейке D2 вводим «=A1*B2» и т.д.
4. Мы считаем, что коэффициент к равен единице и функция f (x)=у=1*х – это первое приближение к нашему решению. Можем рассчитать сумму квадратов разностей между измеренными значениями величины Y и рассчитанными по формуле y=1*х . Можем все это сделать вручную, вбивая в формулу соответствующие ссылки на ячейки: «=(D2-C2)^2+(D3-C3)^2+(D4-C4)^2. и т.д. В конце концов ошибаемся и понимаем, что потеряли кучу времени. В Excel для расчета суммы квадратов разностей есть специальная формула, «СУММКВРАЗН», которая все за нас и сделает. Введем ее в ячейку А2 и зададим исходные данные: диапазон измеренных значений Y (столбец C) и диапазон рассчитанных значений Y (столбец D).
4. Сумму разностей квадратов рассчитали – теперь идем во вкладку «Данные» и выбираем «Поиск решения».
5. В появившемся меню в качестве изменяемой ячейки выбираем ячейку A1 (та, что с коэффициентом k).
6. В качестве целевой выбираем ячейку A2 и задаем условие «установить равной минимальному значению». Помним, что это ячейка, где у нас производится расчёт суммы квадратов разностей расчетного и измеренного значений, и сумма эта должна быть минимальной. Нажимаем «выполнить».
7. Коэффициент k подобран. Теперь можно убедиться, что рассчитанные значения теперь очень близки к измеренным.
Вообще, конечно, для аппроксимации экспериментальных данных в Excel существуют специальные инструменты, которые позволяют осуществлять описание данных с помощью линейной, экспоненциальной, степенной и полиномиальной функцией, поэтому часто можно обойтись и без надстройки «поиск решения». Обо всех этих способах апппроксимации я рассказывал в своем бесплатном курсе по Excel: «10 инструментов Excel для быстрого анализа данных», так что если интересно, скачайте — посмотрите. А вот когда дело касается какой-нибудь экзотической функции с одним неизвестным коэффициентом или задач оптимизации, то здесь надстройка «поиск решения» как нельзя кстати.
Надстройку «поиск решения» можно использовать и для других задач, главное — понять суть: есть ячейка, где мы подбираем значение, а есть целевая ячейка, в которой задано условие для подбора неизвестного параметра.
Вот и все! В следующей статье расскажу сказку про отпуск, так что, чтобы не проворонить выход статьи, подписывайтесь на обновления блога.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Как в эксель посчитать разницу между двумя числами
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Предположим, вы хотите узнать, сколько складских запасов невыгодно (вычитайте прибыльные позиции из общего запаса). Или, возможно, вам нужно узнать, сколько сотрудников приближаются к возрасту выхода на пенсию (вычесть из общего числа сотрудников количество сотрудников в возрасте до 55 лет).
Что необходимо сделать
Существует несколько способов вычитания чисел, в том числе:
Вычитание чисел в ячейке
Для простого вычитания используйте арифметические операторы — (минус).
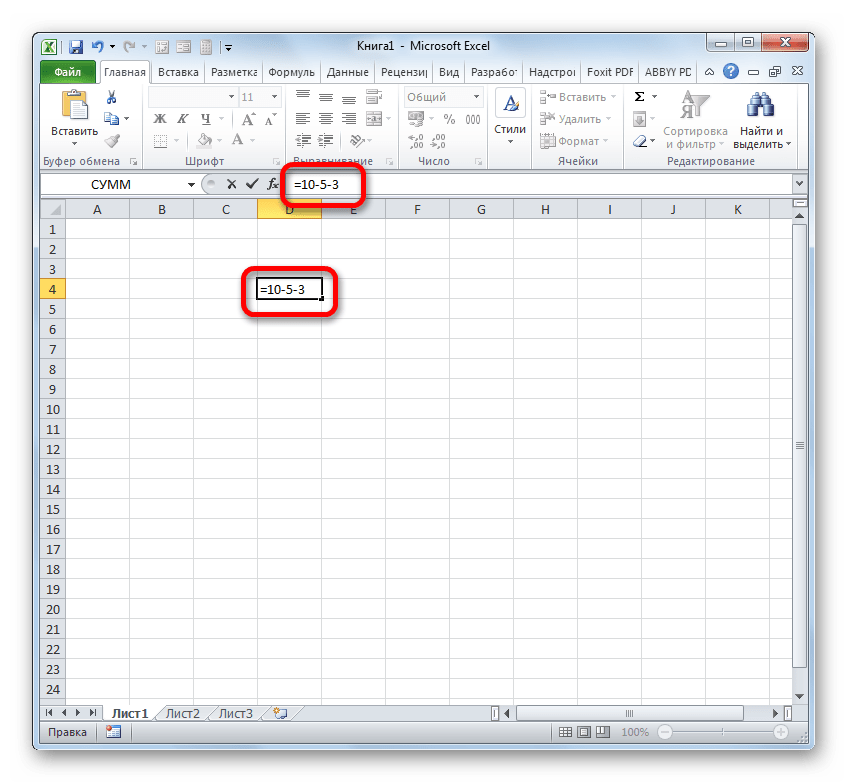
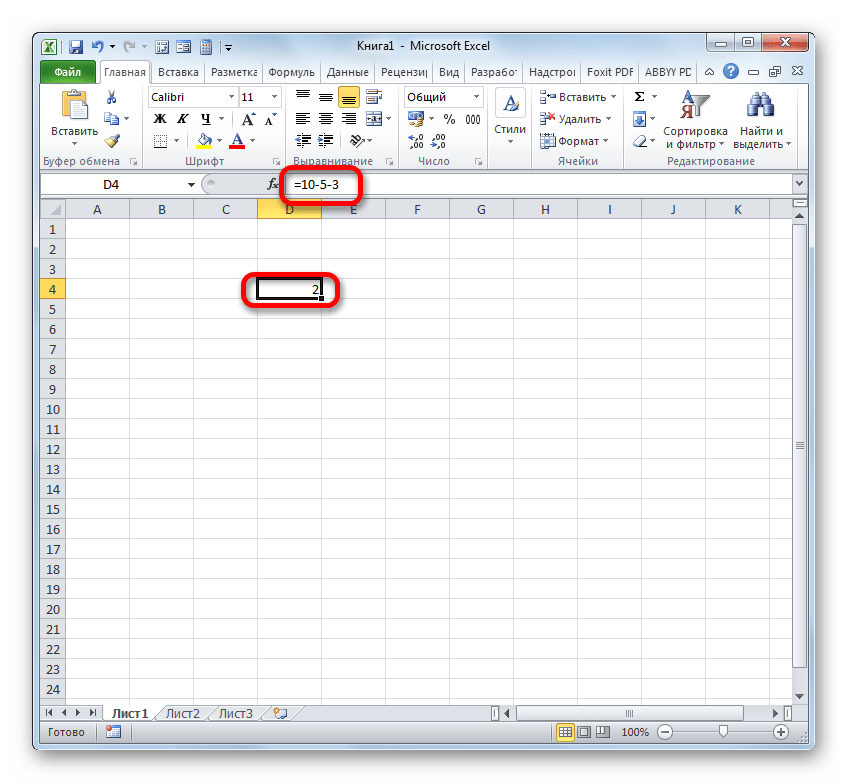
Например, если ввести в ячейку формулу =10-5, в результате в ячейке отобразится 5.
Вычитание чисел в диапазоне
При добавлении отрицательного числа все равно, что вычитать одно число из другого. С помощью функции СУММ можно складывать отрицательные числа в диапазоне.
Примечание: В Excel не существует функции ВЫЧЕСТЬ. Используйте функцию СУММ, преобразуя все числа, которые необходимо вычесть, в их отрицательные значения. Например, функция СУММ(100,-32,15,-6) возвращает результат 77.
Пример
Чтобы вычесть числа различными способами, выполните указанные здесь действия.
Выберите все строки в приведенной ниже таблице, а затем нажмите клавиши CTRL+C.
Вычитает 9000 из 15000 (что равно 6000).
Добавляет все число в списке, включая отрицательные (чистый результат — 16 000).
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
Чтобы переключиться между просмотром результатов и просмотром формул, нажмите клавиши CTRL+’ (ударение) на клавиатуре. Можно также нажать кнопку Показать формулы (на вкладке Формулы).
Использование функции СУММ
Функция СУММ суммирует все числа, которые вы указали в качестве аргументов. Каждый аргумент может быть диапазон, ссылка на ячейку, массив, константа или формулалибо результатом выполнения другой функции. Например, СУММ(A1:A5) суммирует все числа в диапазоне ячеек A1–A5. Другим примером является сумм(A1, A3, A5), которая суммирует числа, содержащиеся в ячейках A1, A3 и A5 (аргументы — A1, A3 и A5).
Как в экселе посчитать разницу в процентах между двумя числами?
Посчитать разницу в процентах между двумя числами, довольно часто встречающаяся задача в повседневной жизни. Рассмотрим подробный пошаговый алгоритм, как решить подобную задачу.
Перед нами представлена таблица, в которой есть два столбца: «число №1» и «Число №2». Задача посчитать разниму между двумя этими числами с помощью программы эксель.
Добавляем в таблицу четвертый столбец и называем его «Разница в процентах».
Рассчитаем разницу в процентах между числами, для этого ячейки «D3» пишем формулу: =(B3-C3)/B3, где «B3» — это первое число, а «C3» — это второе число. Копируем данную формулу на другие ячейки, получаем первый результат.
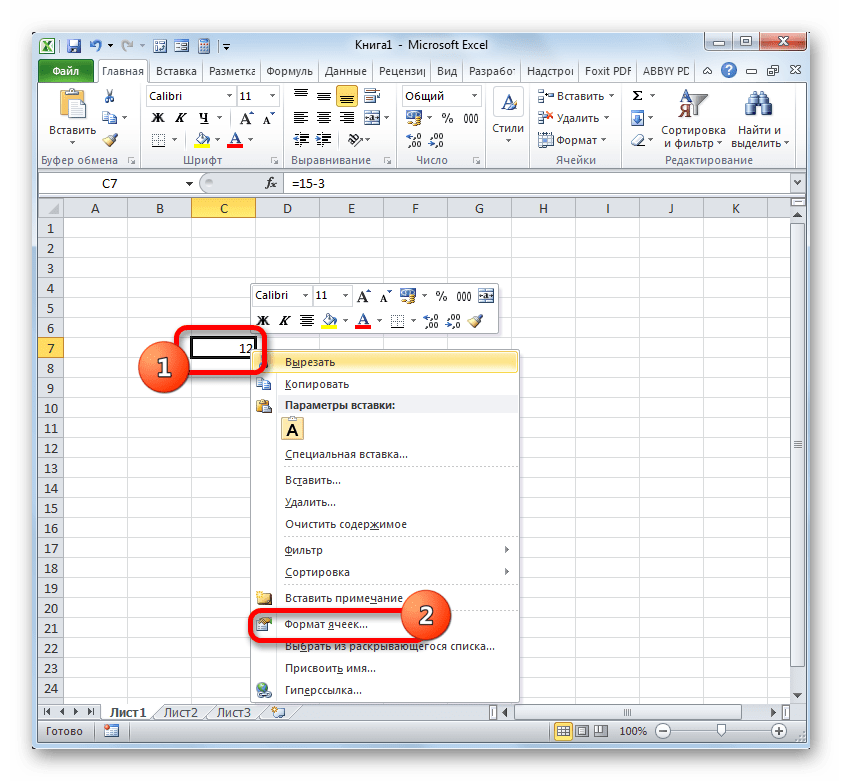
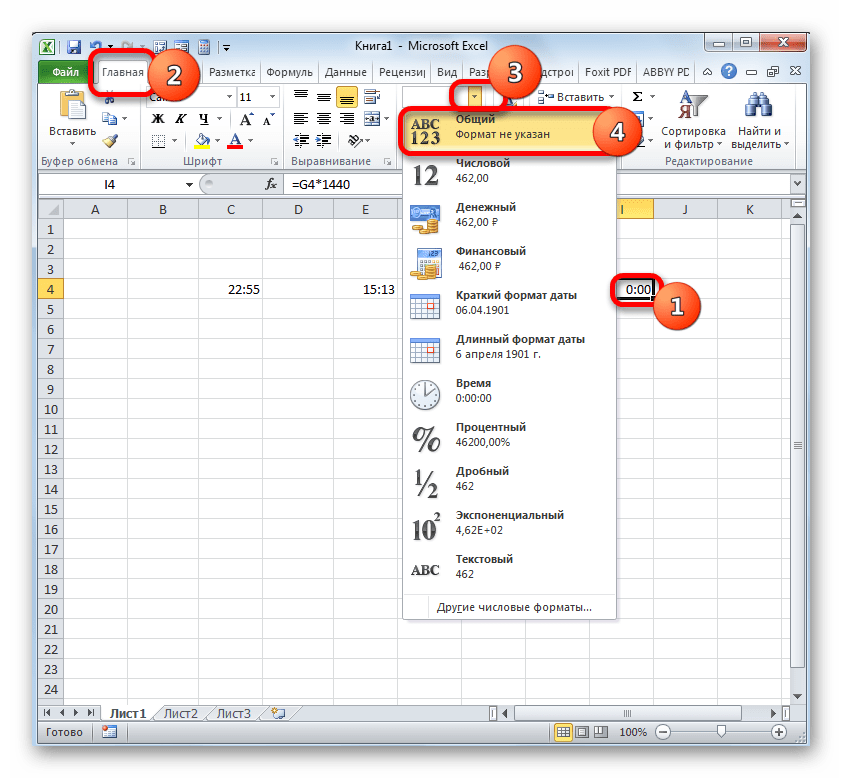
Теперь нужно настроить отображение в процентах, для этого выделяем диапазон ячеек с «D3» по «D8», наводим курсор на выделенную область и жмем правую кнопку мыши. Появившемся в новом меню, выбираем: «Формат ячейки».
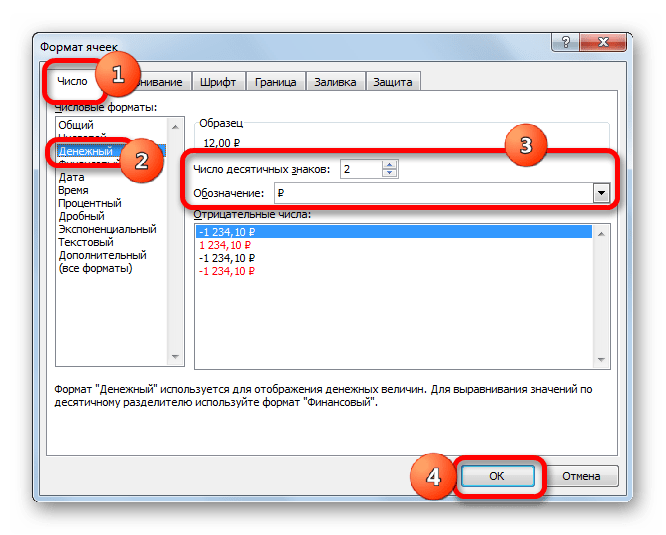
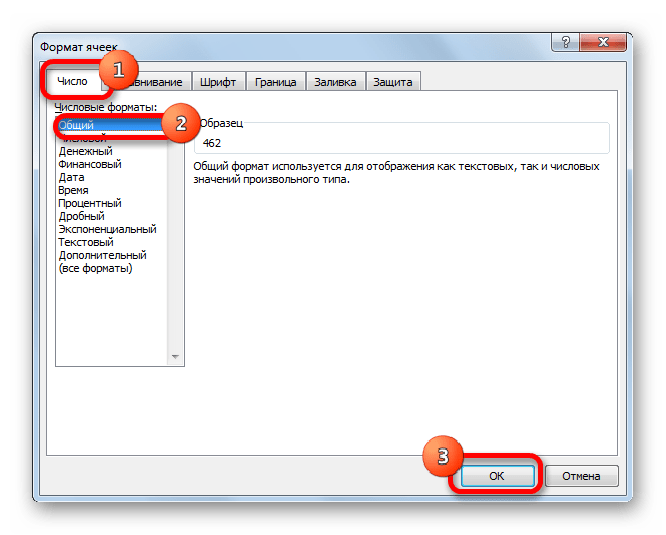
Откроется панель настроек «Формат ячеек», в которой активируем закладку «Число» и в качестве формата чисел выбираем процентный.
После нажатия кнопки «Ок», информация обновиться и мы сделали расчет разницы в процентах между двумя числами в программе эксель.
Вычисление разницы в Microsoft Excel
Вычисление разности является одним из самых популярных действий в математике. Но данное вычисление применяется не только в науке. Мы его постоянно выполняем, даже не задумываясь, и в повседневной жизни. Например, для того, чтобы посчитать сдачу от покупки в магазине также применяется расчет нахождения разницы между суммой, которую дал продавцу покупатель, и стоимостью товара. Давайте посмотрим, как высчитать разницу в Excel при использовании различных форматов данных.
Вычисление разницы
Учитывая, что Эксель работает с различными форматами данных, при вычитании одного значения из другого применяются различные варианты формул. Но в целом их все можно свести к единому типу:
А теперь давайте рассмотрим, как производится вычитание значений различных форматов: числового, денежного, даты и времени.
Способ 1: вычитание чисел
Сразу давайте рассмотрим наиболее часто применимый вариант подсчета разности, а именно вычитание числовых значений. Для этих целей в Экселе можно применить обычную математическую формулу со знаком «-».
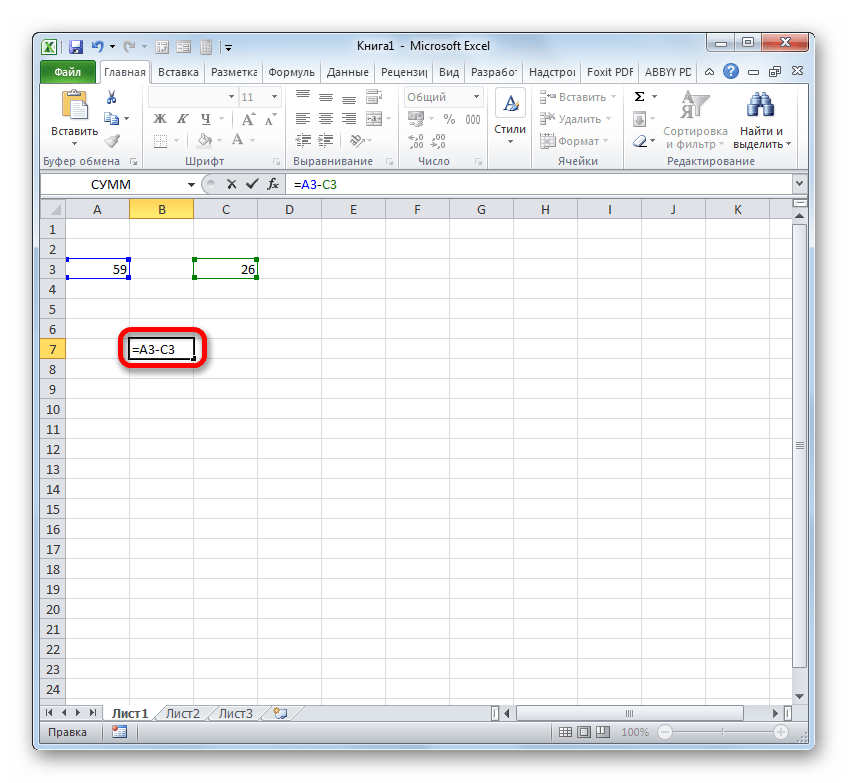
- Если вам нужно произвести обычное вычитание чисел, воспользовавшись Excel, как калькулятором, то установите в ячейку символ «=». Затем сразу после этого символа следует записать уменьшаемое число с клавиатуры, поставить символ «-», а потом записать вычитаемое. Если вычитаемых несколько, то нужно опять поставить символ «-» и записать требуемое число. Процедуру чередования математического знака и чисел следует проводить до тех пор, пока не будут введены все вычитаемые. Например, чтобы из числа 10 вычесть 5 и 3, нужно в элемент листа Excel записать следующую формулу:
Но значительно чаще процесс вычитания в Экселе применяется между числами, размещенными в ячейках. При этом алгоритм самого математического действия практически не меняется, только теперь вместо конкретных числовых выражений применяются ссылки на ячейки, где они расположены. Результат же выводится в отдельный элемент листа, где установлен символ «=».
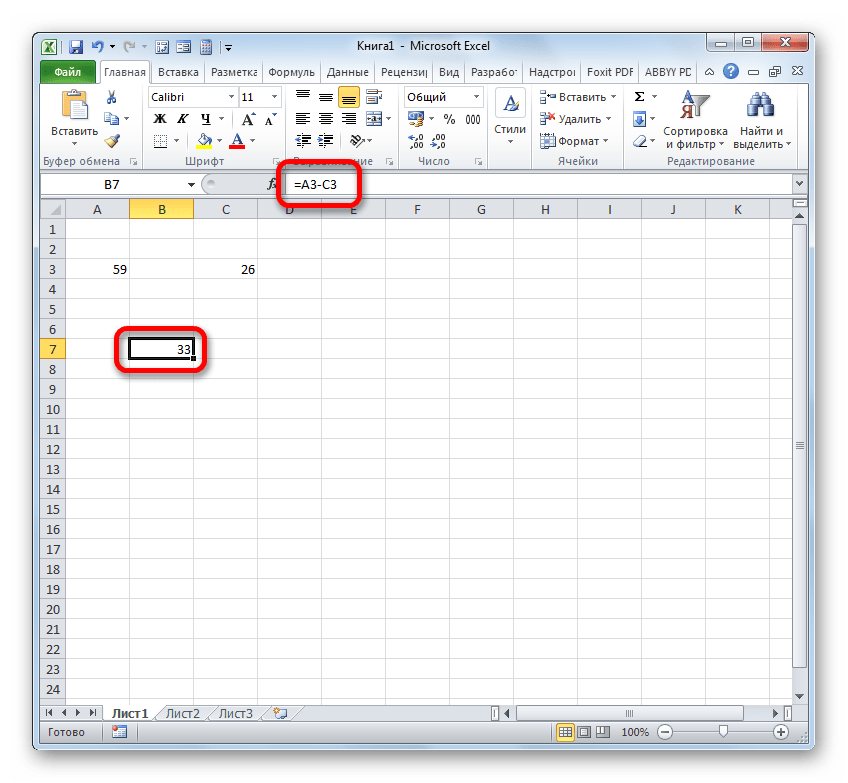
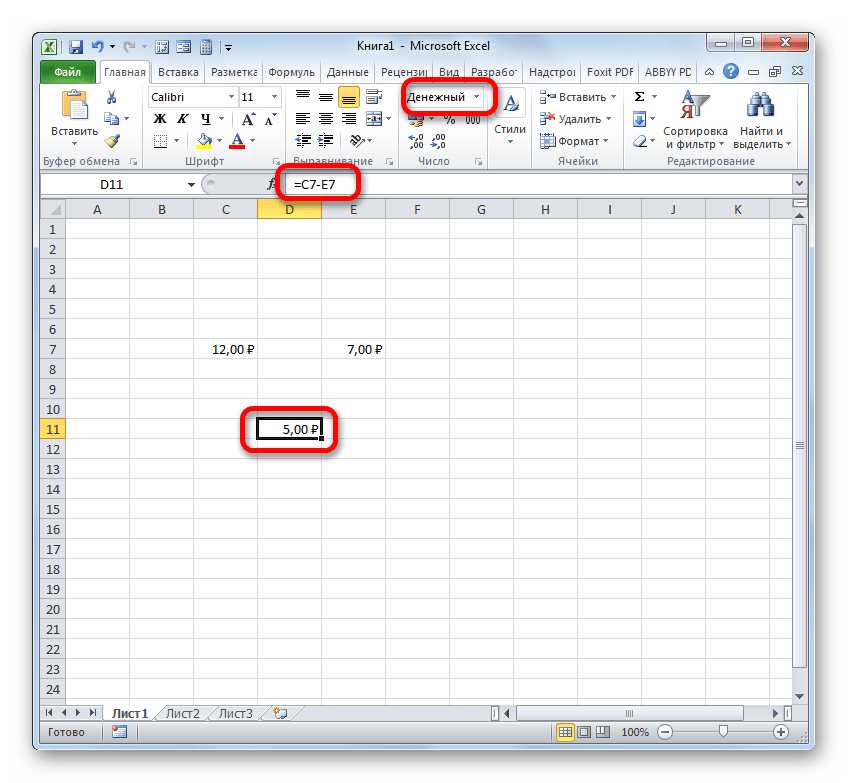
Посмотрим, как рассчитать разницу между числами 59 и 26, расположенными соответственно в элементах листа с координатами A3 и С3.
- Выделяем пустой элемент книги, в который планируем выводить результат подсчета разности. Ставим в ней символ «=». После этого кликаем по ячейке A3. Ставим символ «-». Далее выполняем клик по элементу листа С3. В элементе листа для вывода результата должна появиться формула следующего вида:
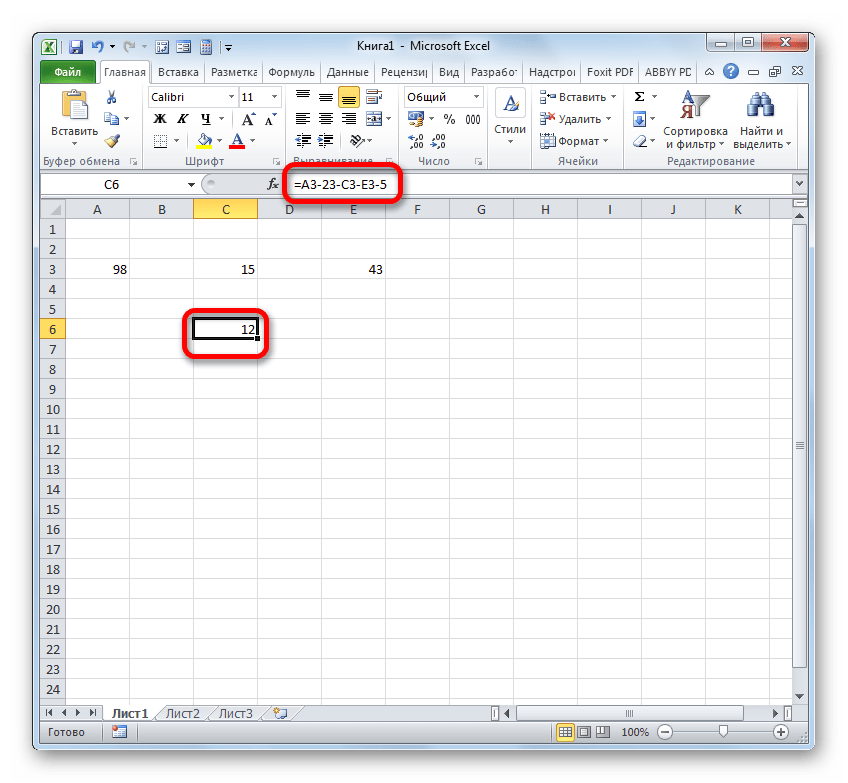
Но на самом деле в некоторых случаях требуется произвести вычитание, в котором будут принимать участие, как непосредственно числовые значения, так и ссылки на ячейки, где они расположены. Поэтому вполне вероятно встретить и выражение, например, следующего вида:
Способ 2: денежный формат
Вычисление величин в денежном формате практически ничем не отличается от числового. Применяются те же приёмы, так как, по большому счету, данный формат является одним из вариантов числового. Разница состоит лишь в том, что в конце величин, принимающих участие в расчетах, установлен денежный символ конкретной валюты.
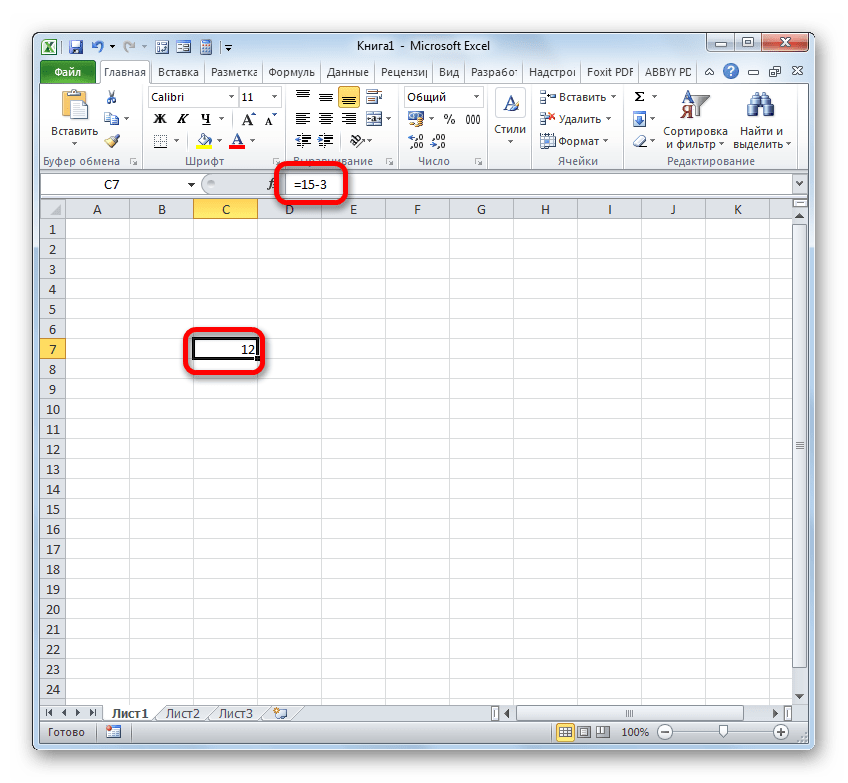
- Собственно можно провести операцию, как обычное вычитание чисел, и только потом отформатировать итоговый результат под денежный формат. Итак, производим вычисление. Например, вычтем из 15 число 3.
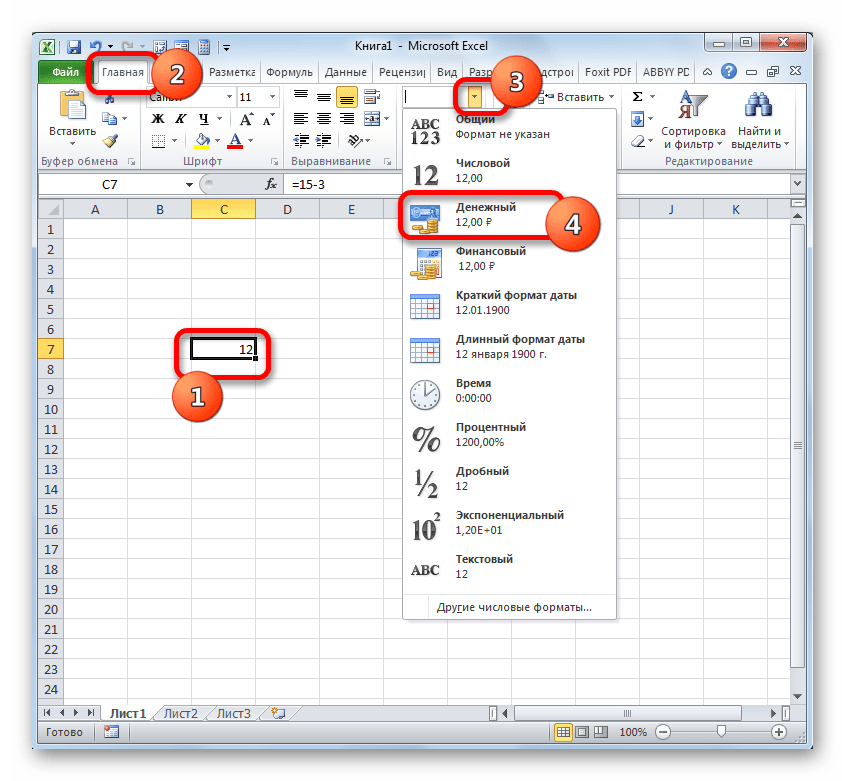
Существует ещё один вариант отформатировать полученный итог вычитания под денежный формат. Для этого нужно на ленте во вкладке «Главная» кликнуть по треугольнику, находящемуся справа от поля отображения действующего формата ячейки в группе инструментов «Число». Из открывшегося списка следует выбрать вариант «Денежный». Числовые значения будут преобразованы в денежные. Правда в этом случае отсутствует возможность выбора валюты и количества десятичных знаков. Будет применен вариант, который выставлен в системе по умолчанию, или настроен через окно форматирования, описанное нами выше.
Если же вы высчитываете разность между значениями, находящимися в ячейках, которые уже отформатированы под денежный формат, то форматировать элемент листа для вывода результата даже не обязательно. Он будет автоматически отформатирован под соответствующий формат после того, как будет введена формула со ссылками на элементы, содержащие уменьшаемое и вычитаемые числа, а также произведен щелчок по клавише Enter.
Способ 3: даты
А вот вычисление разности дат имеет существенные нюансы, отличные от предыдущих вариантов.
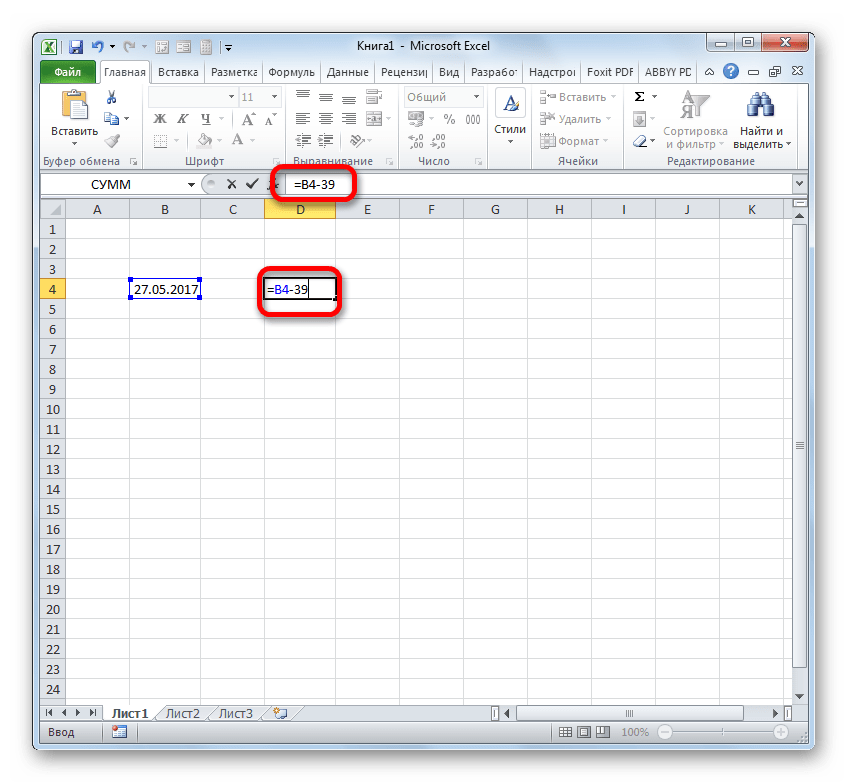
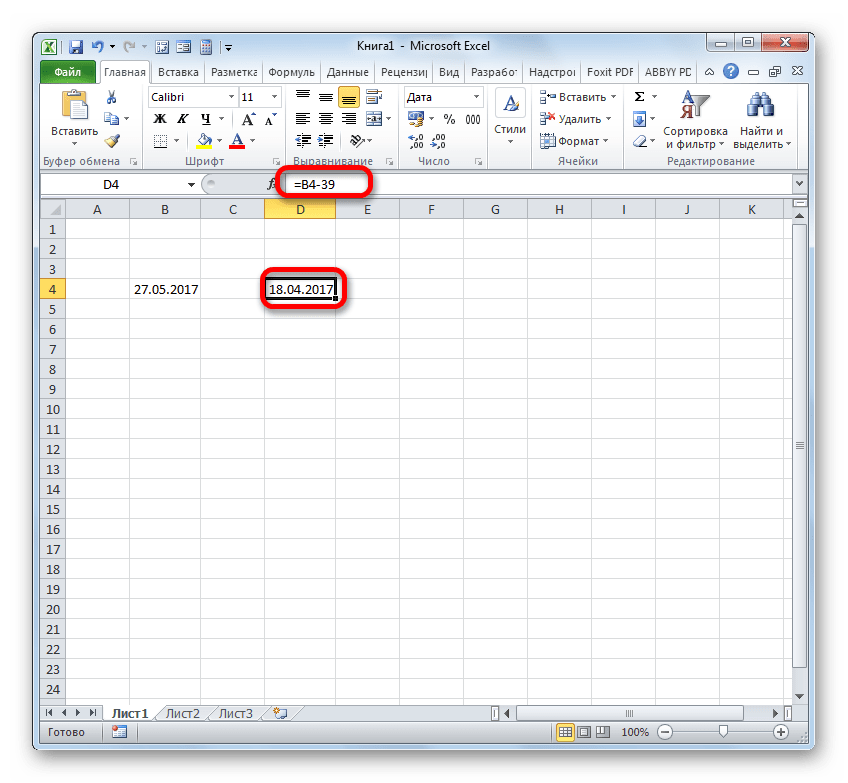
- Если нам нужно вычесть определенное количество дней от даты, указанной в одном из элементов на листе, то прежде всего устанавливаем символ «=» в элемент, где будет отображен итоговый результат. После этого кликаем по элементу листа, где содержится дата. Его адрес отобразится в элементе вывода и в строке формул. Далее ставим символ «-» и вбиваем с клавиатуры численность дней, которую нужно отнять. Для того, чтобы совершить подсчет клацаем по Enter.
Существует и обратная ситуация, когда требуется из одной даты вычесть другую и определить разность между ними в днях.
- Устанавливаем символ «=» в ячейку, где будет отображен результат. После этого клацаем по элементу листа, где содержится более поздняя дата. После того, как её адрес отобразился в формуле, ставим символ «-». Клацаем по ячейке, содержащей раннюю дату. Затем клацаем по Enter.
Также разность между датами можно вычислить при помощи функции РАЗНДАТ. Она хороша тем, что позволяет настроить с помощью дополнительного аргумента, в каких именно единицах измерения будет выводиться разница: месяцы, дни и т.д. Недостаток данного способа заключается в том, что работа с функциями все-таки сложнее, чем с обычными формулами. К тому же, оператор РАЗНДАТ отсутствует в списке Мастера функций, а поэтому его придется вводить вручную, применив следующий синтаксис:
«Начальная дата» — аргумент, представляющий собой раннюю дату или ссылку на неё, расположенную в элементе на листе.
«Конечная дата» — это аргумент в виде более поздней даты или ссылки на неё.
Самый интересный аргумент «Единица». С его помощью можно выбрать вариант, как именно будет отображаться результат. Его можно регулировать при помощи следующих значений:
- «d» — результат отображается в днях;
- «m» — в полных месяцах;
- «y» — в полных годах;
- «YD» — разность в днях (без учета годов);
- «MD» — разность в днях (без учета месяцев и годов);
- «YM» — разница в месяцах.
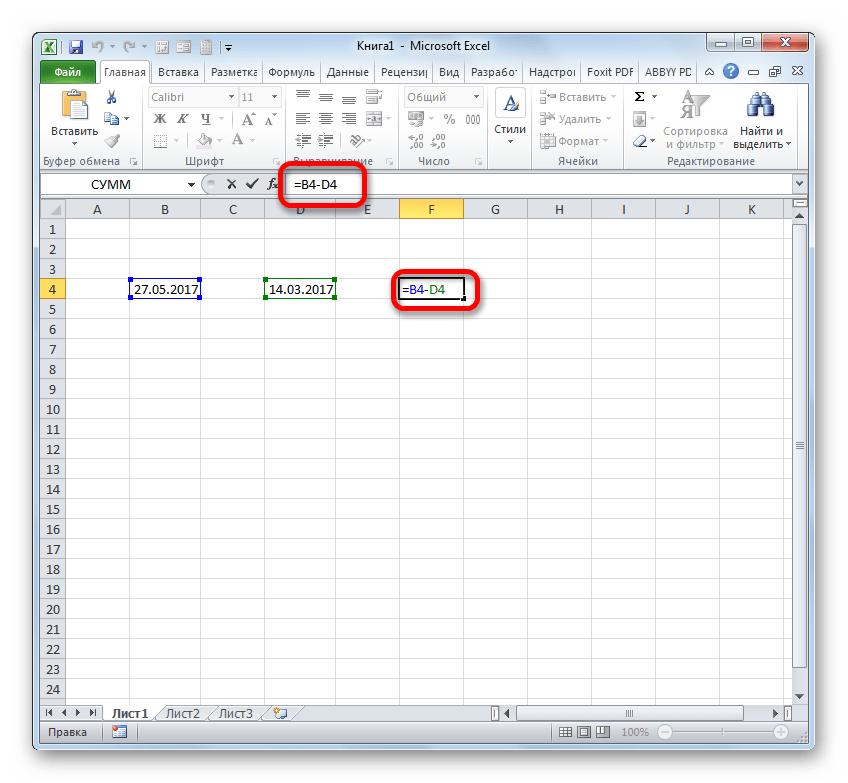
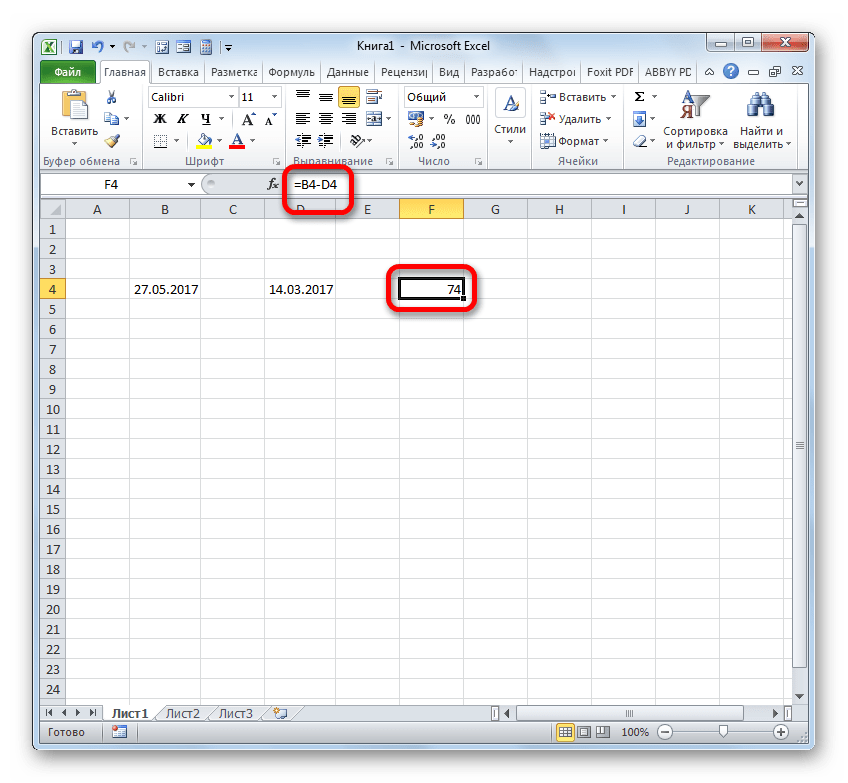
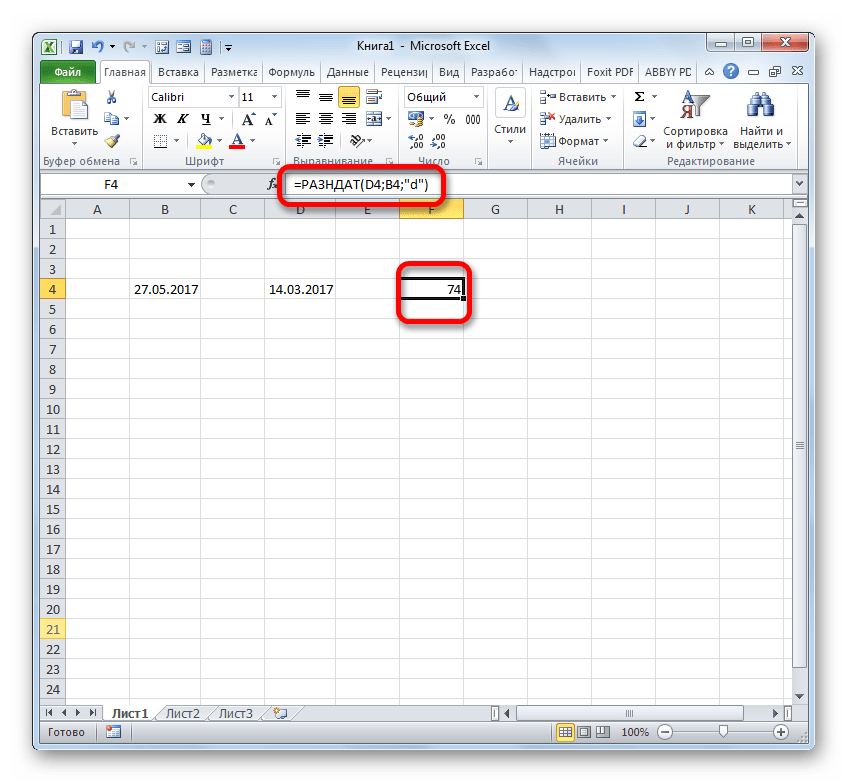
Итак, в нашем случае требуется вычислить разницу в днях между 27 мая и 14 марта 2017 года. Эти даты расположены в ячейках с координатами B4 и D4, соответственно. Устанавливаем курсор в любой пустой элемент листа, где хотим видеть итоги расчета, и записываем следующую формулу:
Жмем на Enter и получаем итоговый результат подсчета разности 74. Действительно, между этими датами лежит 74 дня.
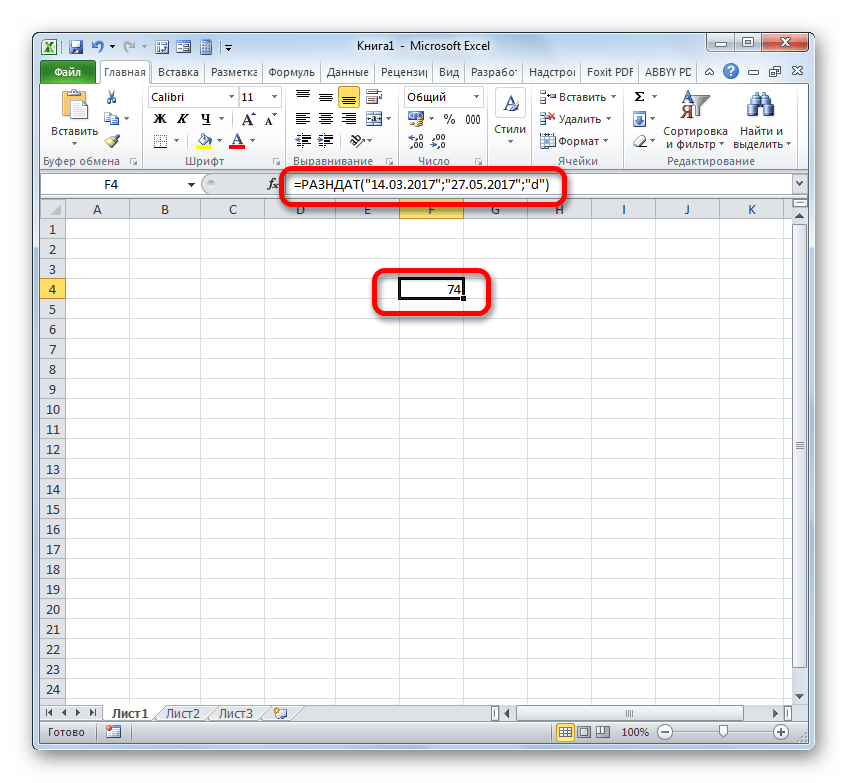
Если же требуется произвести вычитание этих же дат, но не вписывая их в ячейки листа, то в этом случае применяем следующую формулу:
Опять жмем кнопку Enter. Как видим, результат закономерно тот же, только полученный немного другим способом.
Способ 4: время
Теперь мы подошли к изучению алгоритма процедуры вычитания времени в Экселе. Основной принцип при этом остается тот же, что и при вычитании дат. Нужно из более позднего времени отнять раннее.
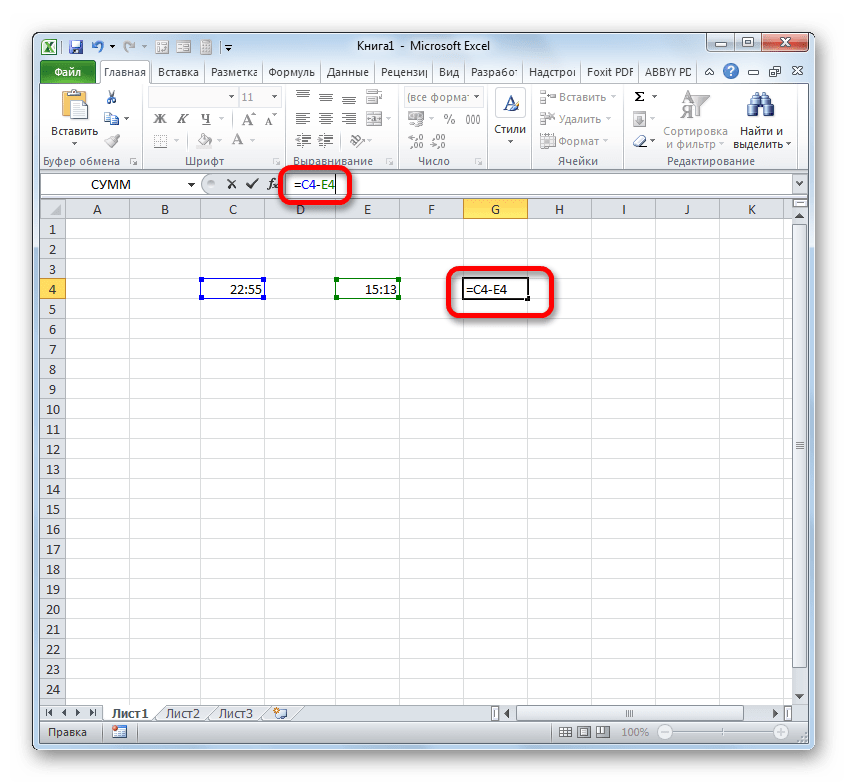
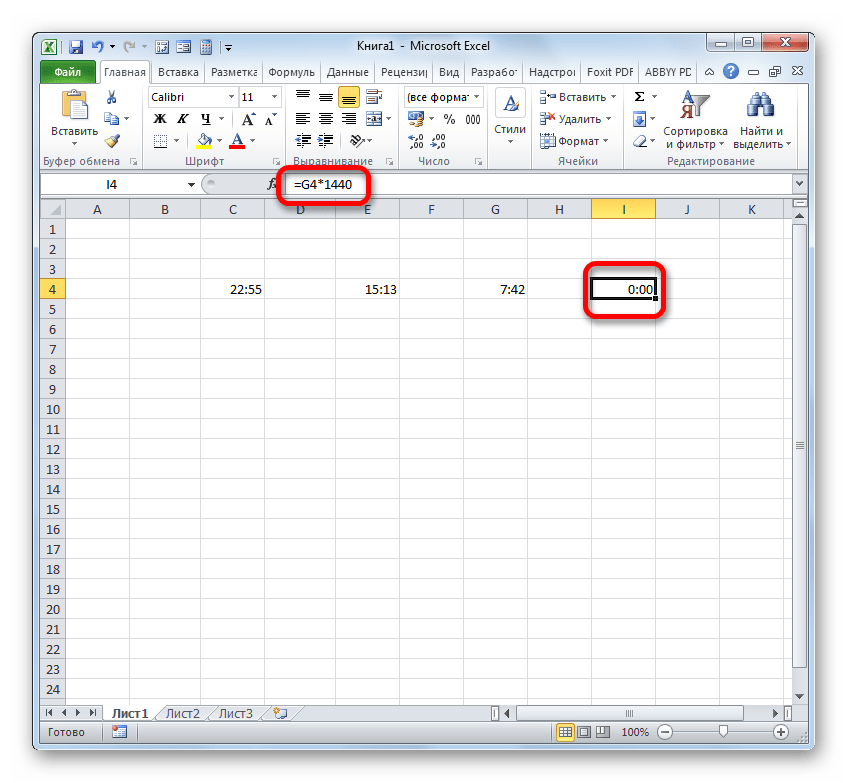
- Итак, перед нами стоит задача узнать, сколько минут прошло с 15:13 по 22:55. Записываем эти значения времени в отдельные ячейки на листе. Что интересно, после ввода данных элементы листа будут автоматически отформатированы под содержимое, если они до этого не форматировались. В обратном случае их придется отформатировать под дату вручную. В ту ячейку, в которой будет выводиться итог вычитания, ставим символ «=». Затем клацаем по элементу, содержащему более позднее время (22:55). После того, как адрес отобразился в формуле, вводим символ «-». Теперь клацаем по элементу на листе, в котором расположилось более раннее время (15:13). В нашем случае получилась формула вида:
Как видим, нюансы подсчета разности в Excel зависят от того, с данными какого формата пользователь работает. Но, тем не менее, общий принцип подхода к данному математическому действию остается неизменным. Нужно из одного числа вычесть другое. Это удается достичь при помощи математических формул, которые применяются с учетом специального синтаксиса Excel, а также при помощи встроенных функций.