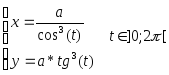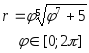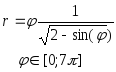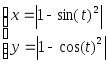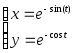Цели:
- Ознакомление учащихся с методом поиска подхода к решению задач и умелое
применение данного метода в решении любых задач; - Умение ставить вопросы, работать по алгоритму;
- Развитие математической речи учащихся в ходе комментирования,
объяснения, аргументации смысла вопросов; - Развитие навыков сотрудничества и взаимопомощи при работе в группе;
- Сформировать у учащихся понятие “точечная диаграмма”;
- Научить заполнять таблицу с учетом заданного интервала и шага.
План проведения мастерской:
- Организационный момент.
- Актуализация знаний.
- Подготовительная работа.
- Поиск подхода к решению задачи.
- Работа в группах.
- Обсуждение в мастерской.
- Оценочно-рефлексивная деятельность.
- Итог урока.
Оборудование урока: доска, экран, проектор, компьютер учителя, компьютеры
для учащихся (кол-во 12), раздаточный материал. (Памятка 1 , памятка 2, конверт
с заданием)
1. Организационный момент.
Учащиеся проходят в класс. Занимают свои места. Учителя приветствуют их.
2. Актуализация знаний.
На доске записано слово “Функция”. Учитель математики просит учащихся назвать
ассоциации, связанные с этим словом.
3. Подготовительная работа.
Задание 1.
Учащимся предлагается 4 вида графиков и варианты функций. Соотнести графики
функций с их алгебраической записью.
Графики и алгебраические записи размещены на маркерной доске.
Задание 2.
Учащимся предлагается 4 вида преобразования графиков. Необходимо объяснить,
какой вид преобразования используется (данное задание учитель математики
иллюстрирует, используя электронное сопровождение курса “Алгебра – 8” под
редакцией А.Г.Мордковича).
4. Поиск подхода к
решению задачи.
Каждый ученик получает карточку определённого цвета, на которой представлена
часть того или иного графика. Учащиеся делятся на группы по цветам.
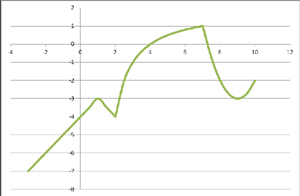
– Соедините части и скажите, что у Вас получилось? (График кусочной функции)
– Как построить график кусочной функции? Попробуйте вспомнить алгоритм.
Группа 1.
Группа 2.
Группа 3.
Группа 4.
5. Работа в группах.
Каждая группа получает конверты с заданиями. Учащиеся внутри группы сами
определяют, кто и какую часть будет строить. Построив каждый кусочек функции на
листе, учащийся выполняет построение на компьютере под руководством учителя
информатики.
Необходимо построить таблицу значений “х” и “у”, заполнить для заданного
интервала, самостоятельно выбрав шаг.
(Памятка 1.)
Для заполнения значений “у” необходимо правильно внести формулы в ячейку
таблицы. (Памятка 2.)
Каждый ученик строит согласно своему заданию функцию и сохраняет работу на
отдельном листе книги Excel, переименовав его согласно номеру задания.
Далее все части собираются на одном листе, а затем на компьютере. Если группы
справились с заданием, то и на листе, и на компьютере графики одинаковы.
Раздаточный материал:
Конверт 1.
Конверт 2.

Конверт 3.
Конверт 4.
Приложение 1.
Приложение 2.
6. Обсуждение в мастерской.
Работы вывешиваются на доску. Учащиеся сравнивают полученный график с
макетом, собранным ими в начале урока. Оценивают работы друг друга. Высказывают
свои мнения.
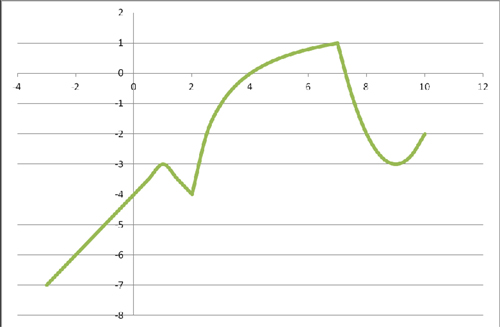
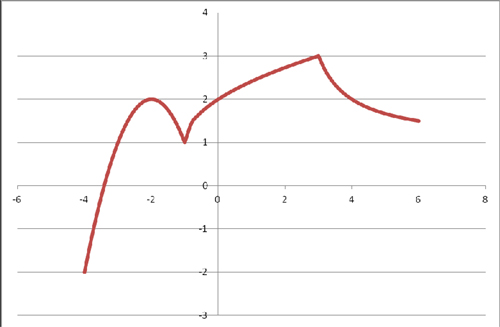
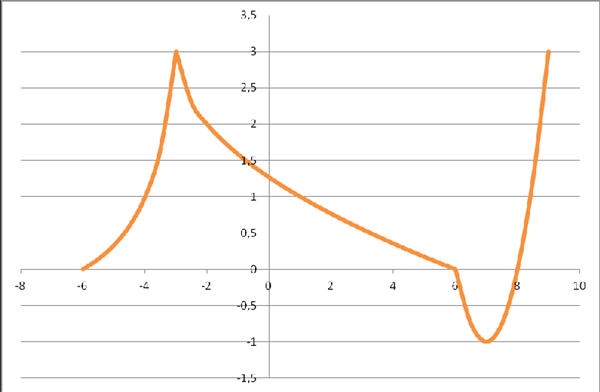
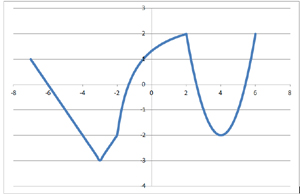
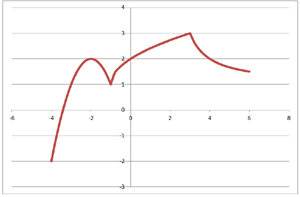
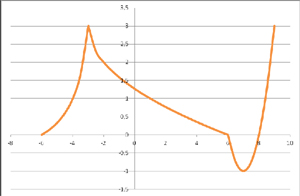
Группа 1 получила после выполнения задания график вида:
Группа 2 получила после выполнения задания график вида:
Группа 3 получила после выполнения задания график вида:
Группа 4 получила после выполнения задания график вида:
7. Оценочно-рефлексивная деятельность.
Каждому ученику предлагается оценить свои чувства после выполнения работы.
Для этого, на доске расположены 3 рисунка. Каждый ученик подходит к доске и
прикрепляет к выбранному им рисунку клейкую бумагу. В конце подсчитывается
количество прикреплённых бумажек к тому или иному рисунку. Обсуждается, почему
выбрано то или иное настроение.
8. Итог урока.
В конце урока каждому ученику вручается сертификат и выполненная им работа.
Список используемой литературы:
- Мордкович А.Г., Семенов П.В. методическое пособие для учителей
“Алгебра и начало математического анализа 8 класс” М: “Мнемозина”, 2010 –
203 с. - Мордкович А.Г., Семенов П.В. “Алгебра. Задачник. Часть 2 8 класс”
М: “Мнемозина”, 2011 – 272 с. - Семенов А.Л., Ященко И.В. “ГИА – 2013 ФИПИ “Математика: типовые
экзаменационные варианты: 30 вариантов”” – М: “Национальное образование” ,
2013 192 с. М: “Мнемозина”, 2010 – 203 с. - Мордкович А.Г., Семенов П.В. “Алгебра 8 класс. Электронное
сопровождение курса” – М: “Мнемозина”, 2008. - Анеликова Л.А., Гусев О.Б. “ Информатика и
информационно-коммуникационные технологии. Базовый уровень. 9 класс” – М:
“Солон-пресс”, 2009–400с. - Крылов С.С., Чуркина Т.Е. “ГИА – 2013 ФИПИ “Информатика и ИКТ
типовые экзаменационные варианты: 10 вариантов”” М: “Национальное
образование” , 2013 – 144 с. - Угринович Н.Д. “информатика и ИКТ.9 класс” – М: БИНОМ лаборатория
знаний, 2011 – 295c. - Горностаева А.М. “Информатика 8 класс. Поурочные планы по
учебнику Угриновича Н.Д.” Волгоград: Учитель,2008 – 185 с. - Лапчик М.П. и др. “Методика преподавания информатики: Учебное
пособие для студентов пед ВУЗов” – издательский центр “Академия”, 2001 – 624
с.
Электронные Образовательные Ресурсы
- Федеральный институт педагогических измерений: http\
www.fipi.ru - Методическая копилка учителя информатики: http \
www.metod-kopilka.ru - Электронные учебники: http\
www.agtu.ru - Единая коллекция цифровых образовательных ресурсов: http \
school-collection.edu.ru - Информационный образовательный портал для учителей информатики и ИКТ:
http \
www.klyaksa.net - Сайт для учителей видео уроки: http\
www.videouroki.net
-
Скачать презентацию (0.12 Мб)
-
65 загрузок -
1.7 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Интересует тема «Кусочно-заданная функция в Excel»? Лучшая powerpoint презентация на эту тему представлена здесь! Данная презентация состоит из 11 слайдов. Средняя оценка: 1.7 балла из 5. Также представлены другие презентации по информатике для 8 класса. Скачивайте бесплатно.
-
Формат
pptx (powerpoint)
-
Количество слайдов
11
-
Аудитория
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Кусочно-заданная функция
-
Слайд 2
Кусочно-заданная функция — функция, заданная несколькими формулами, в зависимости от значений аргумента, например:
y=
-
Слайд 3
Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками. Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями. Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.
-
Слайд 4
Рассмотрим кусочно-заданную функцию
y=
-
Слайд 5
Создание графиков в программе Exel
Любые функции можно оформлять в виде графиков в Exel.
Данную кусочно-заданную функцию нужно прописывать через условие ЕСЛИ.
ОБЯЗАТЕЛЬНО нужно учитывать все ОДЗ функций для грамотного оформления графика.
Удобно следовать блок-схеме при написании условия -
Слайд 6
Блок схема кусочно-заданной функции
Начало
Усл 1
Итог 1
Усл 2
Усл 3
Итог 2
Нет реш
Итог 3
Конец
да
нет
да
нет
да
нет -
Слайд 7
Создание графика кусочно-заданной функции вExel
Кусочно-заданная функция строится с помощью команды ЕСЛИ
1. Создаем значения x с необходимым нам шагом( возьмем от-10 до 10,шаг 1)
2. Записываем необходимые нам данные для построения(значения постоянных,x при которых не существует функция)
3. Далее в ячейке значения функции y вызываем команду ЕСЛИ
Значения,являющиеся постоянными(например a=5),следует «замораживать» кнопкой F4 -
Слайд 8
Работа с командой ЕСЛИ
Общий вид функции =ЕСЛИ(логическое выражение, [значение если ИСТИНА], [значение если ЛОЖЬ])
В логическом выражении можно применять операторы сравнения:
> больше
= больше или равно
не равно
Удобно использовать блок-схему при прописывании условий функции -
Слайд 9
Прописанное Условие для нашей функции
=ЕСЛИ(И(B40);КОРЕНЬ(SIN(B4));ЕСЛИ(И(B4>-3;B41;B4-1);10/((B4*B4)-5);ЕСЛИ(B4>4;B4*B4*B4;»net»)))
Красный-условие первой функции
Зеленый – условие второй функции
Синий – условие третьей функции
Фиолетовый – условие,если ни одна функция не выполняется -
Слайд 10
Создание графика по данным функции
Выделяем область значений и определений функции,в которых она существует
Вставка->Точечный график
Далее открываем контекстное меню, нажав правой кнопкой на графике, и выбираем «Выбрать данные»
В открывшемся окне нажимаем кнопку «добавить» и добавляем допустимые значения X и Y в соответствующие строки -
Слайд 11
Конечный вид Exel c функцией
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации












Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте
Ответ:
В самом простом случае нужно задать таблицу, где будет переменная (первый столбец) и значения функции для это переменной (второй столбец), важно не менять порядок, Excel по умолчанию думает, что первый столбец переменная, второй значение функции.
Потом выделить таблицу прямо вместе с названиями переменных, если указали заголовок таблицы, щёлкнув по верхней левой ячейке таблицы и потянув рамочку на всю таблицу. Если не получилось выделить с первого раза, не страшно, щелчок по любой другой ячейке сбросит выделение и можно заново попробовать,
А потом в меню Вставка нужно нажать График и выбрать из выпавшей менюшки вид этого графика. И, вот здорово-то, где-то на листе расчётов появится график функции таким маленьким обособленным окошком. Его можно переместить туда, где лучше он будет смотреться, можно в нём исправлять названия осей, задавать координатную сетку и цвета линий, можно строить несколько графиков в одном рисунке, но база выглядит так.
Объяснение:
Построить
график кусочной функции на участке
[a;b]
с шагом 0,5.
|
№ Вар |
Функция |
[a;b] |
|
1. |
|
[-7;7] |
|
2. |
|
[-7;7] |
|
3. |
|
[-5;5] |
|
4. |
|
[-5;5] |
|
5. |
|
|
|
6. |
|
[-7;7] |
|
7. |
|
[-10;10] |
|
8. |
|
[-10;10] |
|
9. |
|
[-4;10] a-коэф-т |
|
10. |
|
[-10;10] |
|
11. |
|
[-5;8] с-коэф-т |
|
12. |
|
[-4;4] a-коэф-т |
|
13. |
|
[-4;4] |
|
14. |
|
[-10;10] с-коэф-т |
|
15. |
|
[-10;10] d-коэф-т |
|
16. |
|
[-7;7] |
|
17. |
|
[-7;7] |
|
18. |
|
[-30;30] |
|
19 |
|
[-30;30] |
|
20. |
|
|
|
21. |
|
[-10;10] |
|
22. |
|
[-3;3] |
|
23. |
|
[-10;10] |
|
24. |
|
[-10;10] |
|
25. |
|
[-5;6] a-коэф-т |
|
26. |
|
[-5;5] b-коэф-т |
|
27. |
|
[-10;10] |
|
28. |
|
[-8;8] d-коэф-т |
|
29. |
|
[-5;6] a-коэф-т |
|
30. |
|
[-7;7] d-коэф-т |
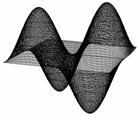
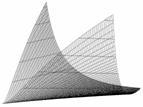
Задание по Excel № 3 «Построение трехмерной поверхности»
-
Получить
матрицу значений функции в виде двумерной
таблицы. Для этого задать изменение
двух аргументов функции в виде числовых
рядов, расположенных под прямым углом
друг к другу. Вычислить значение функции
для каждой пары аргументов. Шаг 0,1xy
-4
-3.5
-3
….
0
0.5
1
Z(x,y)
1.5
…
-
Внимание!
Формула для вычисления значения функции
должна быть набрана один раз, затем
скопирована. -
Выполнить
построение трехмерной поверхности.
Сравнить получившийся результат с
образцом.
|
№ |
Уравнение |
Вид |
№ |
Уравнение |
Вид |
|
1 |
x=[-5;5] y=[-5;5] a=2 b=7 |
|
8 |
x=[-2;2] y=[—2×p ; 2×p] a=2 |
|
|
2 |
x=[-5;5] y=[-5;5] a=2 b=5 |
|
9 |
x=[-1;1] y=[—2×p ; 2×p] a=10 b=2 |
|
|
3 |
x=[-5
y=[-2 ; a=1.5 b=0.5 |
|
10 |
x=[—p ; p] y=[—p ; p] a=2 |
|
|
4 |
x=[-5;5] y=[-5;5] a=0.7 |
|
11 |
x=[—p ; p] y=[—p ; p] a=0.5 |
|
|
5 |
x=[—2×p ; 2×p] y=[—2×p ; 2×p] a=2 b=5 |
|
12 |
x=[—p ; p] y=[—p ; p] a=4 |
|
|
6 |
x=[—p ; p] y=[—p ; p] a=3 |
|
13 |
x=[-2;2] y=[-2;2] a=0.5 |
|
|
7 |
x=[ —p ; p] y=[ —p ; p] a=3 |
|
14 |
x=[-2;2] y=[-2;2] a=2 |
|
|
15 |
x=[-2;2] y=[-2;2] a=2 |
|
22 |
x=[0.01 ; 2×p] y=[0.01 ; 2×p] a=200 |
|
|
16 |
x=[-5;5] y=[-5;5] a=2 b=1 |
|
23 |
x=[0.01 ; 2×p] y=[0.01 ; p] a=200 |
|
|
17 |
x=[-5;5] y=[-5;5] a=0.3 |
|
24 |
x=[-3’3] y=[-1;6] a=50 |
|
|
18 |
x=[-5;5] y=[-5;5] a=0.3 |
|
25 |
x=[-3;3] y=[-3;3] a=0.5 |
|
|
19 |
x=[-5;5] y=[-5;5] a=5 |
|
26 |
x=[-3;3] y=[-3;3] a=2 b=3 |
|
|
20 |
x=[-5;5] y=[-5;5] a=0.1 |
|
x=[—p/2
y=[—p/2 a=0.1 b=2 |
|
|
|
21 |
x[0.1;1] y[0.1;1] a=0.1 |
|
28 |
x[—p/4
y[—p/4 a=2 b=1 |
|
y=
Задание
№1 по MathCAD
«Двумерные графики, заданные в
параметрическом виде, и графики, заданные
в полярных координатах»
Задание:
1.
Построить
два графика;
2.
Вывести
таблицу значений функции, заданной в
параметрическом виде;
3.
При
сдаче работы уметь:
перевести
полярные координаты в декартовы;
отобразить
несколько зависимостей на одном графике.
Указания
к работе:
1.
Для
построения XY-графика,
заданного в параметрическом виде
необходимо:
указать
диапазон и шаг изменения параметра в
виде
.
Знак «:=»
вводится с помощью английского знака
«:».
Символ «..»
вводится с помощью символа «;»
|
№ Вар |
Функция, |
Функция, |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
задать
зависимость
;
“Graph”à
“Create
XY-Plot”.
2.
В
полярной системе координат каждая точка
задается углом и радиусом определенной
длины. Длина радиуса находится в
определенной зависимости от полярного
угла. Для построения графика, заданного
в полярных координатах необходимо:
указать
диапазон и шаг изменения полярного угла
в радианах , например
;
задать
зависимость
“Graph”à
“Create
Polar
Plot”.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
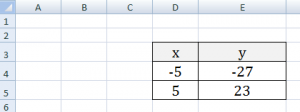
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
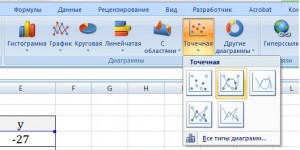
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
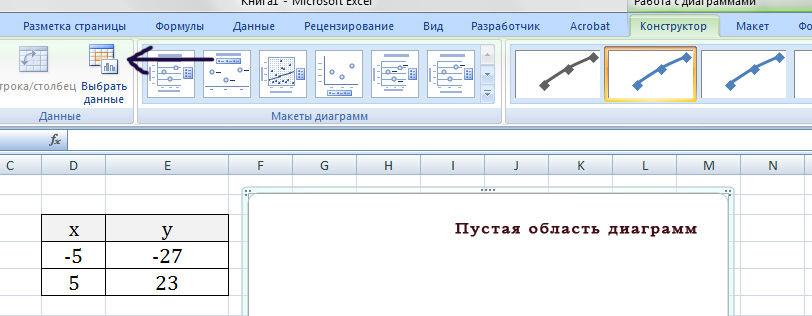
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
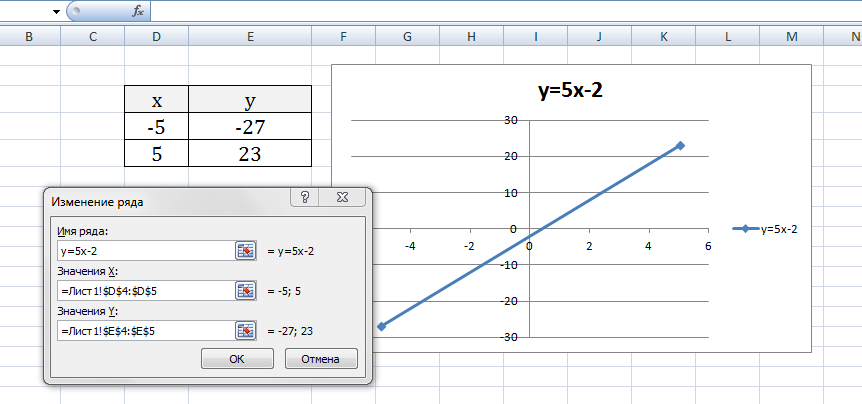
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
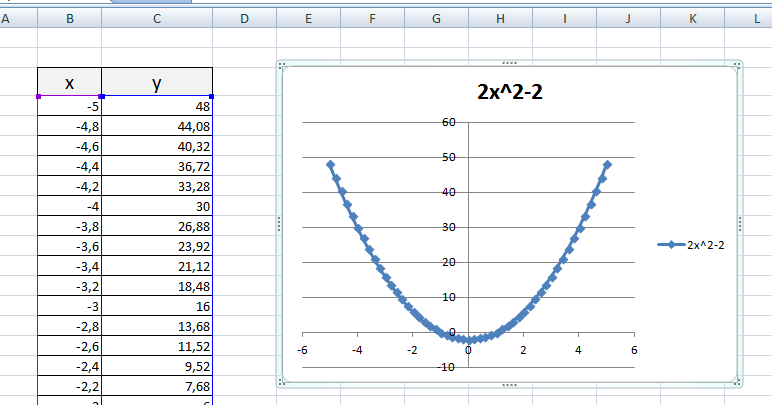
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
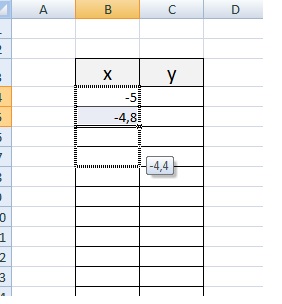
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
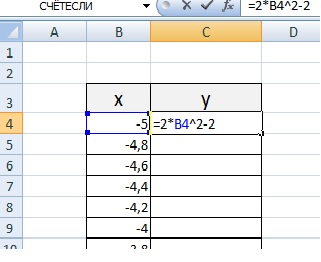
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
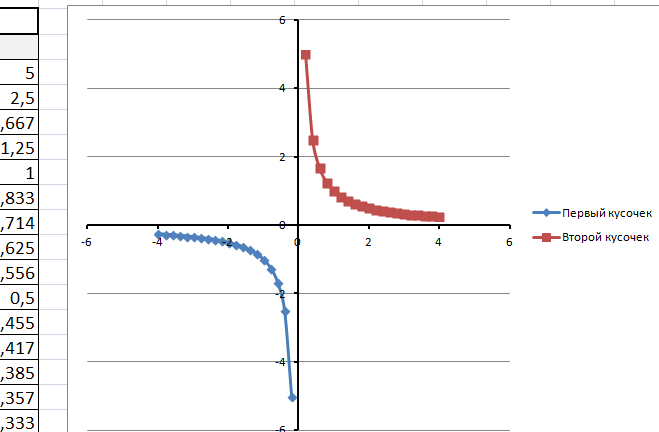
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
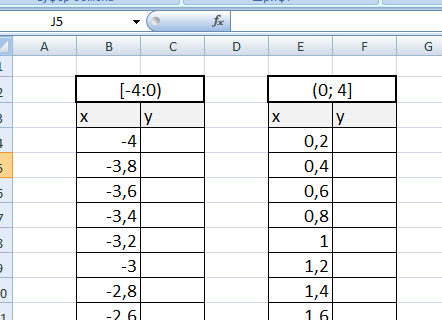
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
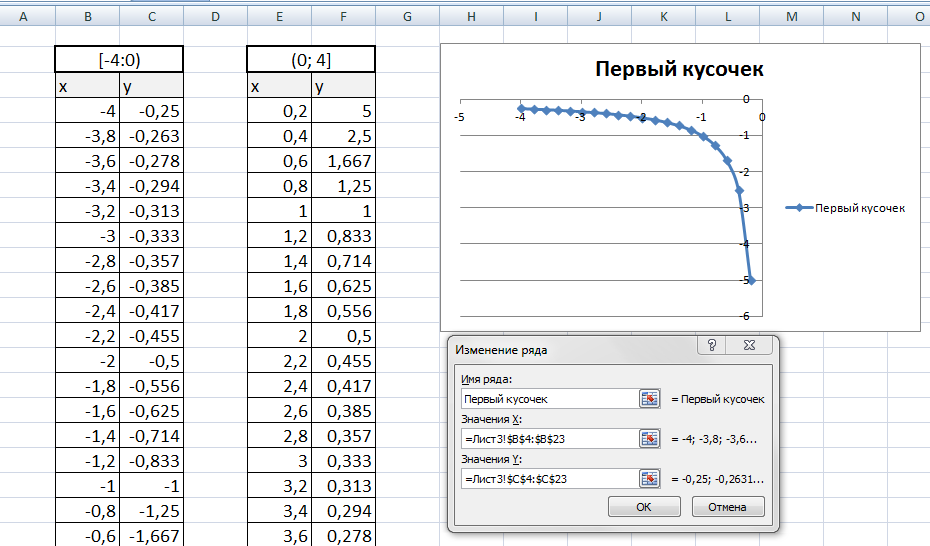
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
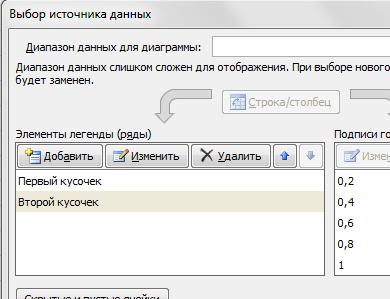
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
Вы можете оставить комментарий, или ссылку на Ваш сайт.
Душевые термостаты, лучшие модели на http://tools-ricambi.ru/ изготавливаются из материалов высшего качества


















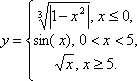




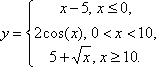







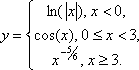






 <
<