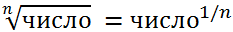Егорова Елена 
Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии
«Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы
делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому
ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С
начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у
нас пока нет, одни благодарности. Очень простая и понятная инструкция, что
немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда
коллеги понимают, как можно «упростить» работу учителя.
Наговицина Ольга Витальевна 
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология.
Очень облегчило аналитическую работу, выявляются узкие места в подготовке к
экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит
время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования
занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз
разобраться. Большое спасибо за качественный анализатор.
Лосеева Татьяна Борисовна 
учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво.
Мой ученик доволен, свой сертификат он вложил в портфолио.
Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной
информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь
полезными материалами вебинара. Спасибо большое лектору за то, что она
поделилась своим опытом!
Арапханова Ашат 
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень
аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и
приобрела у вас этот табель. Благодаря Вам сэкономила время, сейчас же
составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Дамбаа Айсуу 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и
особенно радует, что есть варианты с сочинением, без сочинения, только анализ
сочинения! Превосходно!
Для извлечения корня в Excel и возведения числа в степень используются встроенные функции и математические операторы. Рассмотрим на примерах.
Примеры функции КОРЕНЬ в Excel
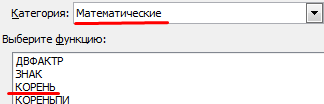
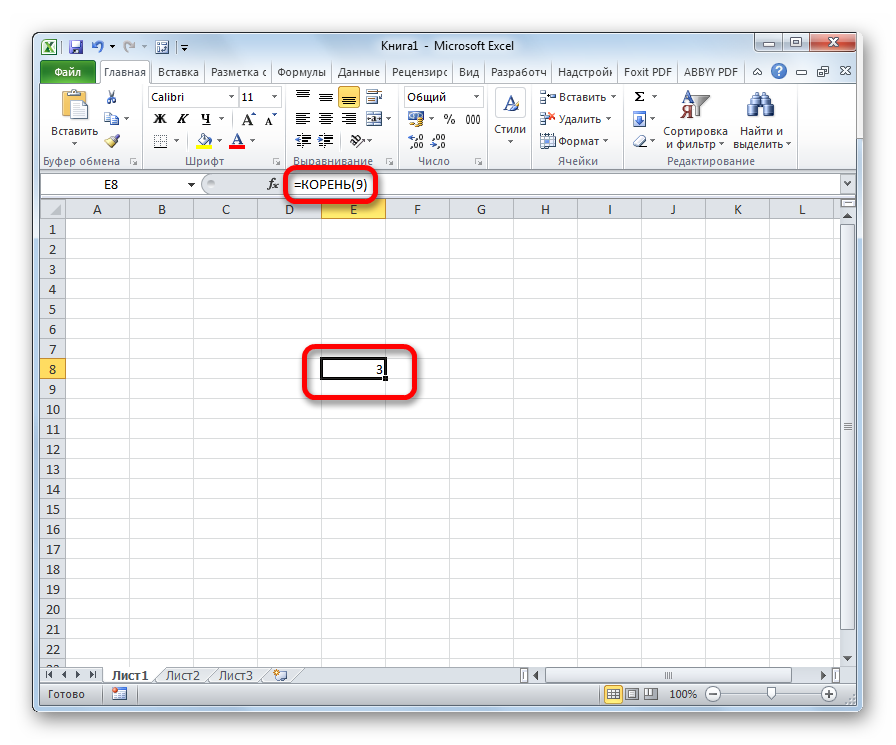
Встроенная функция КОРЕНЬ возвращает положительное значение квадратного корня. В меню «Функции» она находится в категории «Математические».
Синтаксис функции: =КОРЕНЬ(число).
Единственный и обязательный аргумент представляет собой положительное число, для которого функция вычисляет квадратный корень. Если аргумент имеет отрицательное значение, Excel вернет ошибку #ЧИСЛО!.
В качестве аргумента можно указывать конкретное значение либо ссылку на ячейку с числовым значением.
Рассмотрим примеры.
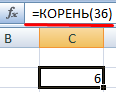
Функция вернула квадратный корень числа 36. Аргумент – определенное значение.
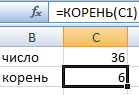
Аргумент функции – ссылка на ячейку с положительным значением 36.
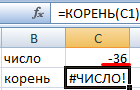
Функция вернула ошибку, т.к. аргумент – ссылка на ячейку с отрицательным значением.
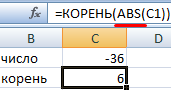
Функция ABS возвращает абсолютное значение числа -36. Ее использование позволило избежать ошибки при извлечении квадратного корня из отрицательного числа.
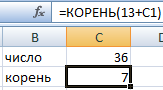
Функция извлекла квадратный корень от суммы 13 и значения ячейки C1.
Функция возведения в степень в Excel
Синтаксис функции: =СТЕПЕНЬ(значение; число). Оба аргумента обязательные.
Значение – любое вещественное числовое значение. Число – показатель степени, в которую нужно возвести заданное значение.
Рассмотрим примеры.
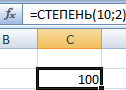
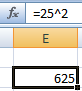
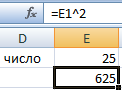
В ячейке C2 – результат возведения числа 10 в квадрат.
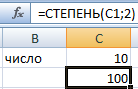
В качестве основания указана ссылка на ячейку с положительным значением 10.
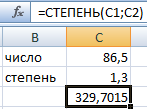
Аргументы функции – ссылки на ячейки с дробными значениями. Результат – число 86,5, возведенное в степень 1,3.
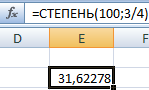
Функция вернула число 100, возведенное к ¾.
Возведение к степени с помощью оператора
Для возведения числа к степени в Excel, можно воспользоваться математическим оператором «^». Для его введения нажать Shift + 6 (с английской раскладкой клавиатуры).
Чтобы Excel воспринимал вводимую информацию как формулу, сначала ставится знак «=». Далее водится цифра, которую нужно возвести в степень. А после значка «^» – значение степени.
Вместо любого значения данной математической формулы можно использовать ссылки на ячейки с цифрами.
Это удобно, если нужно возвести множество значений.
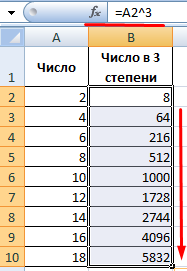
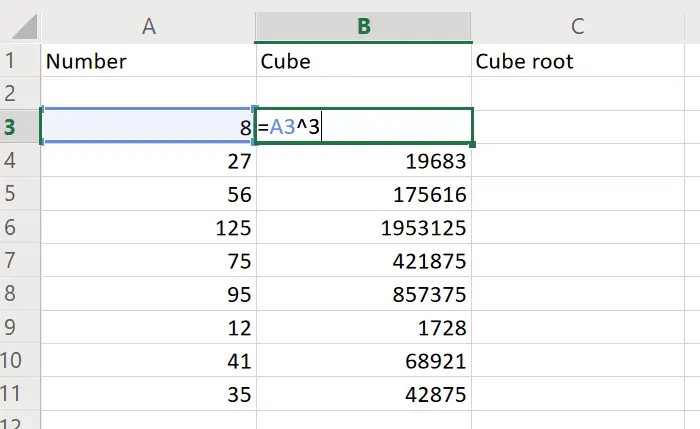
Скопировав формулу на весь столбец, быстро получили результаты возведения чисел в столбце A в третью степень.
Извлечение корней n-й степени
КОРЕНЬ – это функция квадратного корня в Excel. А как извлекать корень 3-й, 4-й и иной степеней?
Вспомним один из математических законов: чтобы извлечь корень n-й степени, необходимо возвести число в степень 1/n.
Например, чтобы извлечь кубический корень, возводим число в степень 1/3.
Воспользуемся формулой для извлечения корней разных степеней в Excel.
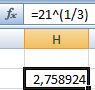
Формула вернула значение кубического корня из числа 21. Для возведения в дробную степень использовали оператор «^».
Обратите внимание! Дробная степень пишется в скобках.
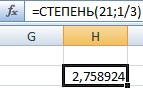
Выполнили ту же задачу, но с использованием функции СТЕПЕНЬ.
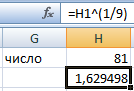
Извлекли корень девятой степени из значения ячейки H1.
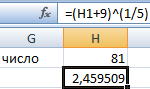
Извлекли корень пятой степени из суммы числа 9 и значения ячейки H1.
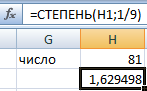
Те же математические операции можно выполнить с помощью функции СТЕПЕНЬ:
Таким образом, возвести в степень и извлечь корень n-й степени в Excel можно с помощью одной функции.
Как написать число в степени
Для корректного отображения числа в степени при демонстрации файла или его печати, необходимо произвести ряд манипуляций:
- Щелкаем по ячейке с числом правой кнопкой мыши. Выбираем «Формат ячеек» (или нажмите CTRL+1).
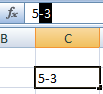
- В открывшемся меню переходим на вкладку «Число». Задаем «Текстовый» формат. Текстовый формат для значения в ячейке можно также задать через панель инструментов («Главная» – «Число»). После установки текстового формата цифра в ячейке становится слева.
- Рядом с цифрой вводим в ячейку значение со знаком «минус».
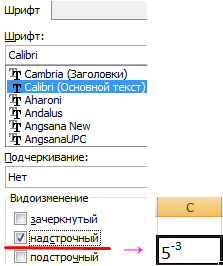
- Выделяем только значение степени («-3»). Вызываем меню «Формат ячеек». Устанавливаем видоизменение «Надстрочный». И нажимаем ОК.
Получили корректное отображение числа 5 в -3 степени.
Среди базовых математических вычислений помимо сложения, вычитания, умножения и деления можно выделить возведение в степень и обратное действие – извлечение корня. Давайте посмотрим, каким образом можно выполнить последнее действие в Эксель разными способами.
- Метод 1: использование функции КОРЕНЬ
- Метод 2: нахождение корня путем возведения в степень
- Заключение
Метод 1: использование функции КОРЕНЬ
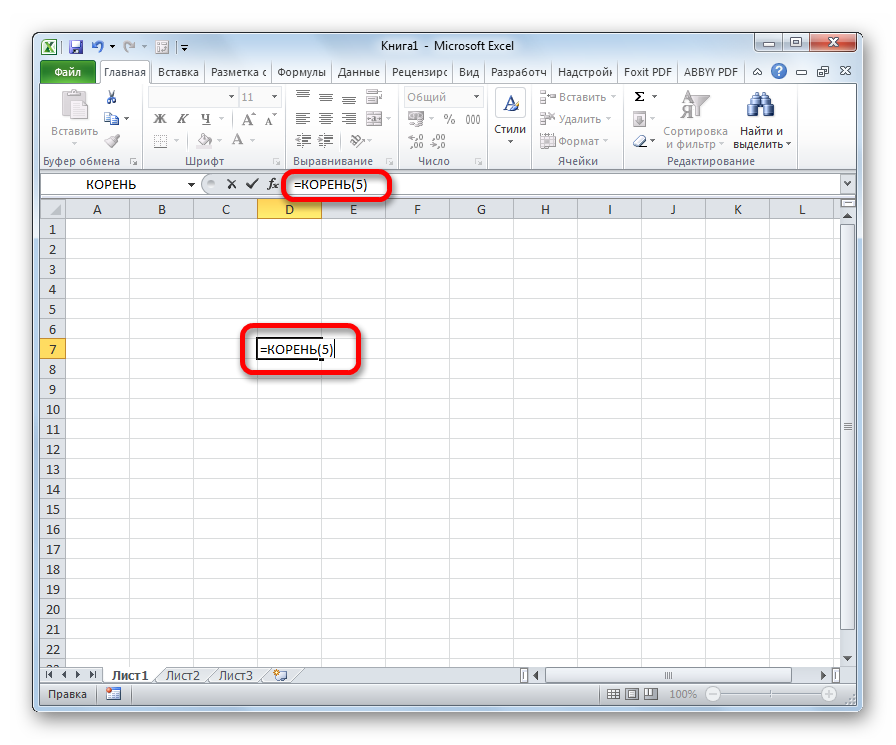
Множество операций в программе реализуется с помощью специальных функций, и извлечение корня – не исключение. В данном случае нам нужен оператор КОРЕНЬ, формула которого выглядит так:
=КОРЕНЬ(число)
Для выполнения расчета достаточно написать данную формулу в любой свободной ячейке (или в строке формул, предварительно выбрав нужную ячейку). Слово “число”, соответственно, меняем на числовое значение, корень которого нужно найти.
Когда все готово, щелкаем клавишу Enter и получаем требуемый результат.
Вместо числа можно, также, указать адрес ячейки, содержащей число.
Указать координаты ячейки можно как вручную, прописав их с помощью клавиш на клавиатуре, так и просто щелкнув по ней, когда курсор находится в положенном месте в формуле.
Вставка формулы через Мастер функций
Воспользоваться формулой для извлечения корня можно через окно вставки функций. Вот, как это делается:
- Выбрав ячейку, в которой мы хотим выполнить расчеты, щелкаем по кнопке “Вставить функцию” (fx).
- В окне мастера функций выбираем категорию “Математические”, отмечаем оператор “КОРЕНЬ” и щелкаем OK.
- Перед нами появится окно с аргументом функции для заполнения. Как и при ручном написании формулы можно указать конкретное число или ссылку на ячейку, содержащую числовое значение. При этом, координаты можно указать, напечатав их с помощью клавиатуры или просто кликнуть по нужному элементу в самой таблице.
- Щелкнув кнопку OK мы получим результат в ячейке с функцией.
Вставка функции через вкладку “Формулы
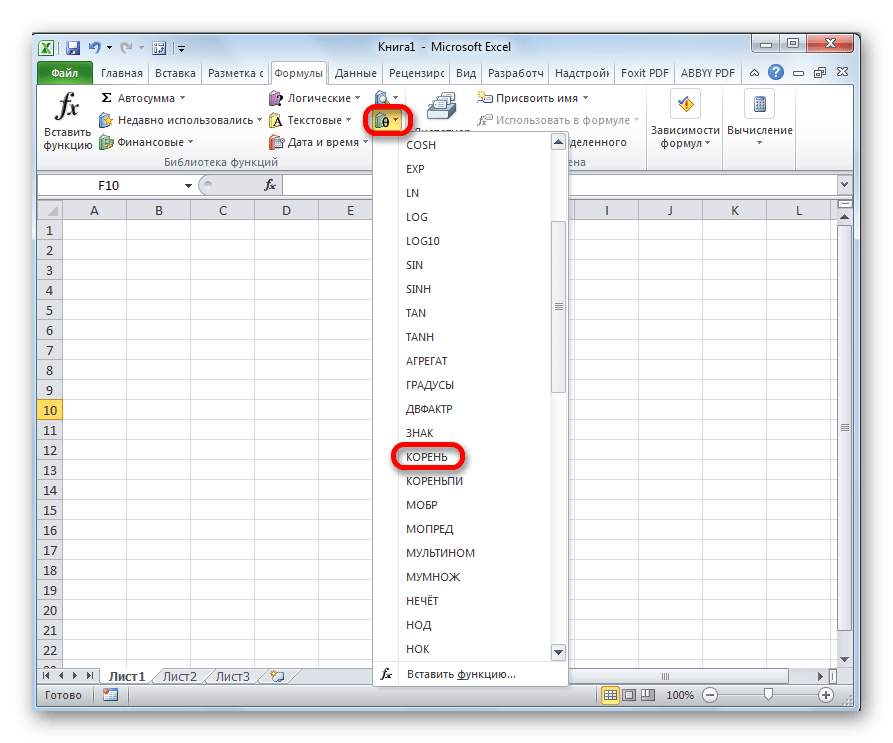
- Встаем в ячейку, в которой хотим произвести вычисления. Щелкаем по кнопке “Математические” в разделе инструментов “Библиотека функций”.
- Пролистав предложенный перечень находим и кликаем по пункту “КОРЕНЬ”.
- На экране отобразится уже знакомое окно с аргументом, который нужно заполнить, после чего нажать кнопку OK.
Метод 2: нахождение корня путем возведения в степень
Описанный выше метод позволяет с легкостью извлекать квадратный корень из числа, однако, для кубического уже не подходит. Но и эта задача в Excel реализуема. Для этого числовое значение нужно возвести в дробную степень, где в числителе будет стоять “1”, а в знаменателе – цифра, означающая степень корня (n).
В общем виде, формула выглядит так:
=(Число)^(1/n)
Безусловным преимуществом такого способа является то, что мы можем извлечь корень любой степени, заменив букву “n” в знаменателе дроби на требуемую цифру.
Для начала давайте рассмотрим формулу для извлечения квадратного корня. Она выглядит следующим образом: =(Число)^(1/2).
Соответственно, для расчета кубического корня будет использоваться выражение ниже:
=(Число)^(1/3)
Допустим, нам нужно извлечь кубический корень из числа 27. В этом случае нужно записать в ячейке такую формулу: =27^(1/3).
Нажав Enter, получаем результат вычислений.
Аналогично работе с функцией КОРЕНЬ, вместо конкретного числа можно указать ссылку на ячейку.
Заключение
Таким образом, в Excel можно без особых усилий извлечь корень из любого числа, и сделать это можно разными способами. К тому же, возможности программы позволяют выполнять расчеты для извлечения не только квадратного, но и кубического корня. В редких случаях требуется найти корень n-степени, но и эта задача достаточно просто выполняется в программе.
Содержание
- Способы извлечения
- Способ 1: применение функции
- Способ 2: возведение в степень
- Вопросы и ответы
Извлечение корня из числа является довольно распространенным математическим действием. Оно применяется и для различных расчетов в таблицах. В Microsoft Excel есть несколько способов посчитать данное значение. Давайте подробно рассмотрим различные варианты осуществления подобных расчетов в этой программе.
Способы извлечения
Существуют два основных способа расчета данного показателя. Один из них подходит исключительно для вычисления квадратного корня, а второй можно использовать для расчета величины любой степени.
Способ 1: применение функции
Для того, чтобы извлечь квадратный корень используется функция, которая так и называется КОРЕНЬ. Её синтаксис выглядит следующим образом:
=КОРЕНЬ(число)
Для того, чтобы воспользоваться данным вариантом, достаточно записать в ячейку или в строку функций программы это выражение, заменив слово «число» на конкретную цифру или на адрес ячейки, где она расположена.
Для выполнения расчета и вывода результата на экран жмем кнопку ENTER.
Кроме того, можно применить данную формулу через мастер функций.
- Кликаем по ячейке на листе, куда будет выводиться результат вычислений. Переходим по кнопке «Вставить функцию», размещенную около строки функций.
- В открывшемся списке выбираем пункт «КОРЕНЬ». Кликаем по кнопку «OK».
- Открывается окно аргументов. В единственном поле данного окна нужно ввести либо конкретную величину, из которой будет происходить извлечение, либо координаты ячейки, где она расположена. Достаточно кликнуть по этой ячейке, чтобы её адрес был внесен в поле. После ввода данных жмем на кнопку «OK».
В итоге в указанной ячейке будет отображаться результат вычислений.
Также функцию можно вызвать через вкладку «Формулы».
- Выделяем ячейку для отображения результата расчета. Переходим во вкладку «Формулы».
- В блоке инструментов «Библиотека функций» на ленте кликаем по кнопке «Математические». В появившемся списке выбираем значение «КОРЕНЬ».
- Открывается окно аргументов. Все дальнейшие действия в точности такие же, как и при действии через кнопку «Вставить функцию».
Способ 2: возведение в степень
Рассчитать кубический корень использование указанного выше варианта не поможет. В этом случае величину нужно возвести в дробную степень. Общий вид формулы для расчета таков:
=(число)^1/3
То есть, формально это даже не извлечение, а возведение величины в степень 1/3. Но данная степень и является корнем кубическим, поэтому именно такое действие в Эксель используется для его получения. В эту формулу вместо конкретного числа также можно вписать координаты ячейки с числовыми данными. Запись производится в любой области листа или в строке формул.
Не стоит думать, что данный способ можно применять только для извлечения кубического корня из числа. Таким же образом можно рассчитать квадратный и любой другой корень. Но только в этом случае придется использовать следующую формулу:
=(число)^1/n
n – это степень возведения.
Таким образом, этот вариант является намного универсальнее, чем использование первого способа.
Как видим, несмотря на то, что в Excel нет специализированной функции для извлечения кубического корня, данное вычисление можно провести, используя возведение в дробную степень, а именно — 1/3. Для извлечения квадратного корня можно воспользоваться специальной функцией, но существует также возможность сделать это путем возведения числа в степень. На этот раз нужно будет возвести в степень 1/2. Пользователь сам должен определить, какой способ вычислений для него удобнее.
Еще статьи по данной теме:
Помогла ли Вам статья?
Нахождение квадратного и кубического корня с помощью функций и формул
При работе с Microsoft Excel вы можете найти квадратный корень из чисел двумя способами. Вы можете использовать функцию, которая уже запрограммирована в формате Excel, которая называется функцией «КОРЕНЬ». И второй метод — это вручную добавить формулу квадратного корня из числа, для которого вы хотите получить значение квадратного корня. Давайте посмотрим, как можно использовать оба метода.
Но прежде чем мы перейдем к тому, как можно работать с обоими методами нахождения квадратного корня из числа, вам необходимо знать основы работы с таблицами Excel. Иногда мы допускаем незначительные ошибки в наших записях в таблице Excel, которые могут дать нам неточные или ожидаемые ответы. Чтобы избежать таких ошибок, необходимо всегда помнить следующие важные основы использования листов Excel. И даже если вы забыли их использовать и обнаружили ошибку, вы можете перепроверить список ниже, чтобы убедиться, что ошибка возникла из-за пропуска этих шагов.
- Знак «=». Знак равенства — самая важная часть формулы. Вы упустите это, и введенная вами формула или функция будет просто отображаться как простой текст. Добавление знака «=» в ячейку перед вводом формулы или функции является частью реализации формулы в этой ячейке.
- Скобки (). Скобки играют очень важную роль в формулах и функциях Excel. Поэтому убедитесь, что вы добавили скобки в свою функцию, поскольку они должны быть добавлены. Для большинства функций скобки обычно содержат значение или номера ячеек, по которым будет реализована формула.
- Наконец, клавиша ввода. Нажмите клавишу ввода после закрытия скобок или заполнения формулы, чтобы наконец сделать функцию функцией.
Важно отметить, что пропуск любого из них не даст вам ответов по существу или даже может привести к ошибке. Так что запомните это.
Способ 1
Функция SQRT в Microsoft Excel
- Откройте лист Excel на пустой странице. Или, если вы уже создали файл данных, откройте его. Основная идея — иметь числа, для которых нужен квадратный корень.
Работа с Microsoft Excel может быть хорошим опытом. Он помогает своим пользователям во многих отношениях.
- Теперь, например, я хочу узнать квадратный корень из числа 7. Я напишу функцию, как показано на рисунке ниже.
= sqrt (число)
Я начну со знака равенства, и после добавления этого значения в ячейку, в которой я хочу отображать квадратный корень значений, я начну набирать «sqrt». Через минуту введите s, список формул начнет появляться в раскрывающемся списке для этой ячейки. Теперь, когда я вижу формулу sqrt, я дважды щелкаю по ней, и она отображается в выбранной ячейке.
Начните вводить функцию
Открывающая скобка появляется автоматически, когда вы дважды щелкаете по формуле, вы добавляете сюда номер / значение ячейки, закрываете скобку и нажимаете ввод.
Двойной щелчок по формуле, которая появляется в раскрывающемся списке ячейки, открывает саму скобку.
После открытой скобки вы вводите либо номер ячейки, либо само число / значение
Добавление числа, для которого вы хотите найти квадратный корень, в скобках функции.
Ответ в обоих случаях будет одним и тем же независимо от того, добавляете ли вы само значение или номер ячейки.
Квадратный корень из числа 7.
Это ваш квадратный корень для 7. Если вы не уверены, следует ли вам добавлять номер ячейки или значение напрямую, я бы посоветовал вам добавить номер ячейки. Потому что существует высокая вероятность того, что вам, возможно, придется внести некоторые изменения в свой лист Excel. Если число в ячейке A2 изменилось, и если вы написали A2 в формуле функций, значение квадратного корня изменится автоматически. В противном случае вам придется вручную изменить значение для каждой ячейки, в которую вы добавили «7» вместо «A2».
Способ 2
Добавление формулы для квадратного корня вручную
Формула, которую вы должны ввести вручную в ячейку для нахождения квадратного корня из числа, выглядит следующим образом:
= число ^ (1/2)
или же
= число ^ 0,5
Вы можете увидеть следующие изображения, чтобы убедиться, как это можно сделать.
= число ^ (1/2) Скобки здесь будут играть очень важную роль, поэтому не перемещайте скобки.
Квадратный корень после добавления формулы вручную = число ^ (1/2)
= число ^ 0,5
квадратный корень, используя = число ^ 0,5
Кубический корень
Чтобы найти корень куба, вы можете вручную ввести = число ^ (1/3). Единственное отличие здесь — число 3. Вы также можете использовать функцию Power, как показано на изображении ниже, чтобы найти кубический корень числа.
Использование функции Power в Excel, чтобы найти Cub Root
Мощность (количество ячеек, мощность)
Ответ на кубический корень.
Download PC Repair Tool to quickly find & fix Windows errors automatically
Finding cubes and cube roots have plenty of real-life applications. They are essential as a part of many mathematical functions. Even more, they are used for estimating the volume of vessels. If you wish to find the cube and cube root of numbers in a cell or a range of cells in Excel, please read through this article.
There is no specific known function for finding the cube or cube root in Excel, so you could use the exponential function instead. That is seemingly the easiest option.
The syntax of the formula for finding the cube of a number in Excel is as follows:
=<first cell with number>^3
Where, <first cell with number> is the first cell in the range of cells from which you start counting the cube for the range of cells.
Eg. Let us consider an example where you have a range of numbers across column A from cell A3 to cell A11. You need the cube of these numbers in the respective columns across column B, from cells B3 to B11. To do so, enter the following formula in cell B3:
=A3^3
When you hit Enter, Excel will return the value of the cube of the number in cell A3 to the cell B3. Then, you can use the Fill function to pull the formula down to cell B11. To do so, click on any cell outside cell B3 (which contains the formula) and then back on it.
This will highlight the Fill function which is represented by a small dot at the right-bottom corner of the selected cell. Now, hover your mouse over that dot, click it, and without releasing the click, pull the formula down to cell B11.
How to find the Cube Root in Excel
The syntax of the formula for finding the cube of a number in Excel is as follows:
=<first cell with number>^(1/3)
Where, <first cell with number> is the first cell in the range of cells from which you start counting the cube for the range of cells.
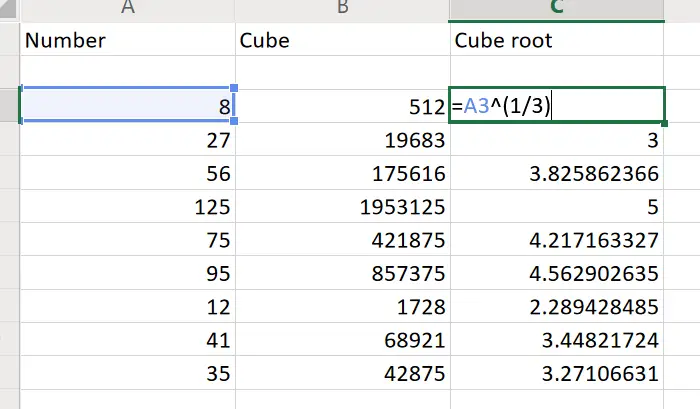
Eg. Let us consider the previous example and add that you need the list of cube roots in column C, from C3 to C11. So, the formula you would have to enter the following formula in cell C3:
=A3^(1/3)
Hit Enter to get the cube root for the number in cell A3 in cell C3 and then use the Fill function to pull the formula down till cell C11.
Read: How to find the Square and Square Root of a number in Excel.
Hope it helps!
Karan is a B.Tech, with several years of experience as an IT Analyst. He is a passionate Windows user who loves troubleshooting problems and writing about Microsoft technologies.
Автор:
Обновлено: 09.10.2022
Пользователи электронных таблиц широко используют функцию по извлечению корня числа. Поскольку работа с данными обычно требуют обработки больших чисел, считать вручную бывает довольно сложно. В этой статье вы найдете подробный разбор вопроса об извлечении корня любой степени в Excel.
Как извлечь корень любой степени в Excel 2010-2013?
Содержание
- Извлечение квадратного корня
- Извлечение корней 3-ей, 4-ой и других степеней.
- Извлечение корня любой степени с помощью функции
- Извлечение корня любой степени с использованием значка степени «^»
- Примеры записи выражений
- Видео — Как извлечь корень любой степени в Excel
Извлечение квадратного корня
Довольно легкая задача, поскольку в программе присутствует отдельная функция, которую можно взять из перечня. Для этого вам нужно сделать следующее:
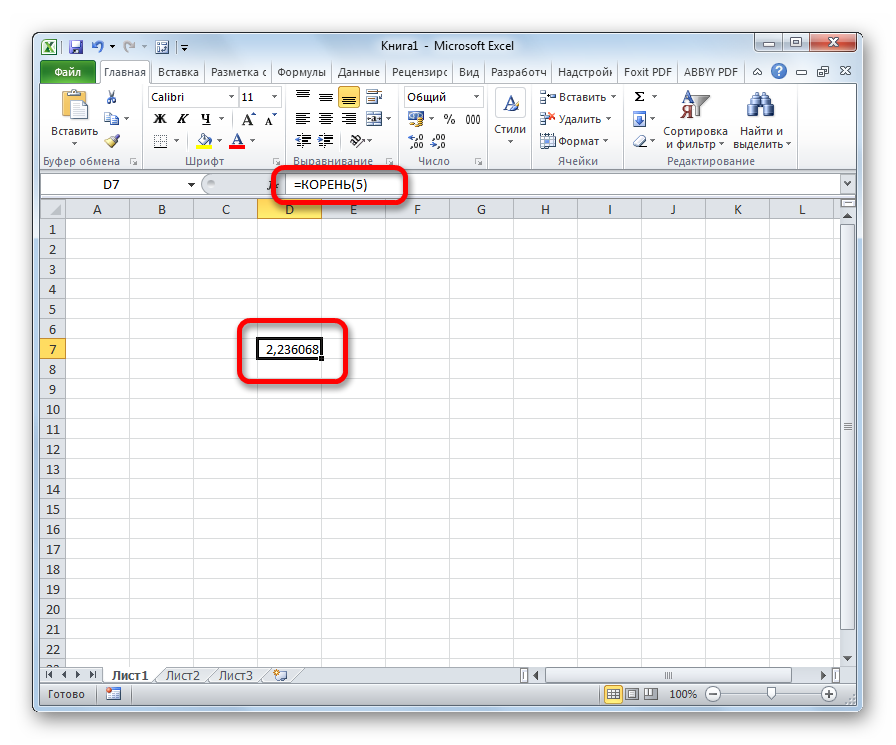
- Выберите ячейку, в которой хотите прописать функцию, кликнув на нее один раз левой кнопкой мыши. Появится черная обводка, оранжевым подсветятся активная строка и столбец, а в адресной ячейке появится имя.
Левой кнопкой мышки щелкаем по нужной ячейке
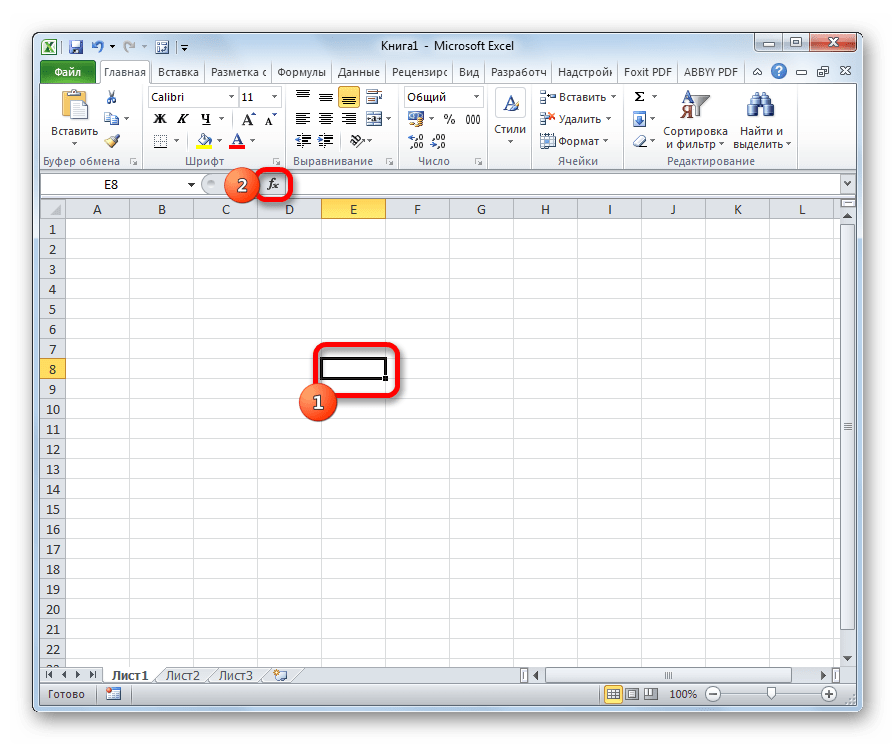
- Нажмите на кнопку «fx» («Вставить функцию»), которая расположена выше названий столбцов, после адресной ячейки, перед строкой формул.
Щелкаем по кнопке «fx» («Вставить функцию»)
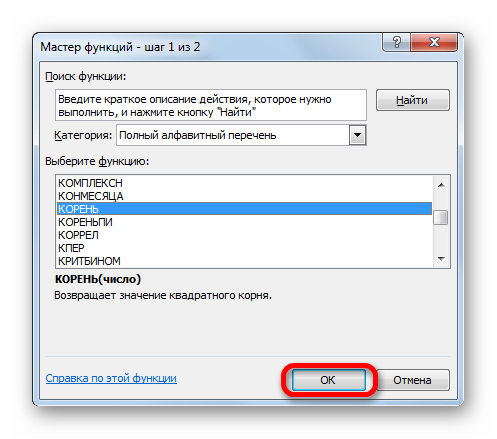
- Появится ниспадающее меню, в котором нужно найти функцию «Корень». Это можно сделать в категории «Математические» или в «Полном алфавитном перечне», прокрутив мышкой меню чуть ниже.
В разделе «Категория» выбираем из списка «Полный алфавитный перечень» или «Математические»
- Выберите пункт «Корень», нажав один раз левой кнопкой мыши, далее – кнопку «ОК».
В окне «Выберите функцию» пролистываем мышкой ниже, находим и выделяем функцию «Корень», нажимаем «ОК»
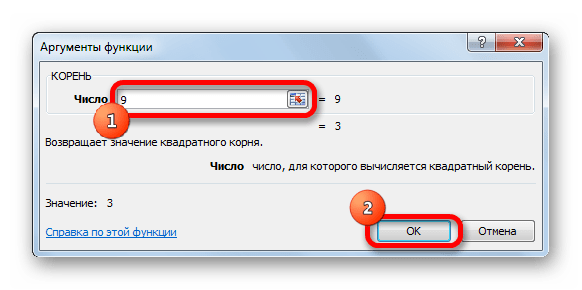
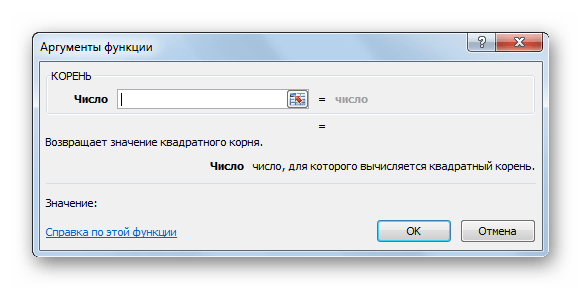
- Появится следующее меню – «Аргументы функции».
Окно «Аргументы функции»
- Введите число или выберите ячейку, в которой заранее было написано данное выражение или формула, для этого один раз кликните левой кнопкой по строке «Число», далее наведите курсор на нужную вам ячейку и нажмите на нее. Имя ячейки будет автоматически забито в строку.
В поле «Число» вводим число, из которого извлекаем квадратный корень
- Нажмите на кнопку «ОК».
Кликаем по кнопке «ОК»
- И все готово, функция посчитала квадратный корень, записав результат в выбранную ячейку.
Посчитанный результат функцией в выбранной ячейке
Читайте подробную инструкцию в нашей новой статье — «Как написать формулу в Excel?Обучение азам работы в Excel».
Существует также возможность извлечь квадратный корень из суммы числа и ячейки (данных, которые забиты в данной ячейке) или двух ячеек, для этого введите значения в строку «Число». Напишите число и кликните один раз по ячейке, программа сама поставит знак сложения.
На заметку! Эту функцию можно вписать и вручную. В строку формул введите следующее выражение: «=КОРЕНЬ(x)», где х – искомое число.
В ячейке вводим значение «=КОРЕНЬ(64)» вручную, нажимаем «Enter»
Извлечение корней 3-ей, 4-ой и других степеней.
Отдельной функции для решения этого выражения в Excel нет. Для извлечения корня n-ой степени необходимо для начала рассмотреть его с математической точки зрения.
Корень n-ой степени равен возведению числа в противоположную степень (1/n). То есть, квадратный корень соответствует числу в степени ½ (или 0.5).
Например:
- корень четвертой степени из 16 равен 16 в степень ¼;
- кубический корень из 64 = 64 в степени 1/3;
Выполнить данное действие в программе электронных таблиц можно двумя способами:
- С помощью функции.
- Используя значок степени «^», ввести выражение вручную.
Извлечение корня любой степени с помощью функции
- Выберите нужную ячейку и кликните на «Вставить функцию» во вкладке «Формулы».
Выделяем ячейку, переходим во вкладку «Формулы», щелкаем по опции «Вставить функцию»
- Раскройте список в пункте «Категория», в категории «Математические» или «Полный алфавитный перечень» найдите функцию «Степень».
В разделе «Категория» выбираем из списка «Полный алфавитный перечень» или «Математические»
Находим и выделяем функцию «Степень», нажимаем «ОК»
- В строке «Число» введите цифру (в нашем случае – это число 64) или имя ячейки, кликнув на нее один раз.
Вводим число в строке «Число»
- В строчке «Степень» напечатайте степень, в которую вы хотите возвести корень (1/3).
В поле «Степень» вводим значение степени, в которую хотим возвести корень
Важно! Для обозначения знака деления необходимо использовать значок «/», а не стандартный знак деления «:».
- Нажмите «ОК», и результат действия появится в изначально выбранной ячейке.
Щелкаем «ОК»
Результат извлечения корня любой степени с помощью функции
Примечание! Наиболее подробную инструкцию с фото по работе с функциями смотри в статье выше.
Извлечение корня любой степени с использованием значка степени «^»
- Выберите ячейку и наведите курсор на строку формул, нажав единожды левой кнопкой мыши.
Щелкаем по ячейке, затем левой кнопкой мышки кликаем по строке формул
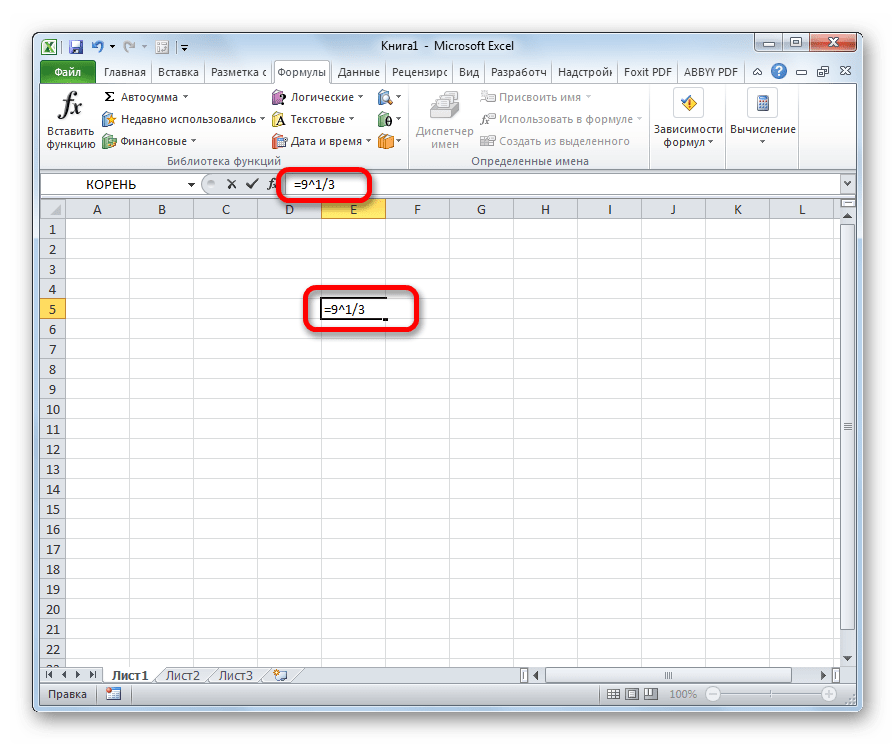
- Введите выражение, начиная со знака «=» (тогда программа воспримет текст как математическое выражение), и занесите степень в круглые скобки. В нашем случае: =64^(1/3). Получается, формула имеет общий вид: «Корень n-ой степени из x = x^(1/n)».
Вводим в поле формулу, начиная со знака «=»
- Переключитесь на другую ячейку, кликнув 1 раз левой кнопкой мыши, программа сама выведет результат.
Кликаем левой кнопкой мышки по пустой ячейке, в ячейке с формулой автоматически появится результат
Примечание! Записывать степень можно как дробью, так и десятичным числом. Например, дробь ¼ можно записать как 0,25. Для отделения десятых, сотых, тысячных и так далее разрядов используйте запятую, как принято в математике.
Пример ввода степени десятичным числом
Примеры записи выражений
- «=16^(1/4)» – извлечение корня 4-ой степени из 16;
Результат извлечение корня 4-ой степени из 16
- «=А1^(0,5)» – кубический корень из выражения, записанного в ячейке «А1»;
Результат кубического корня из выражения, записанного в ячейке «А1»
- «=(B1+30)^(1/3)» – извлечение кубического корня из суммы числа 30 и значения ячейки «B1».
Результат извлечения кубического корня из суммы числа 30 и значения ячейки «B1»
Читайте также подробную инструкцию в новой статье — «Как посчитать сумму в EXcel? Как сложить числа в ячейках».
С наглядной пошаговой инструкцией вы можете ознакомиться по видео.
Видео — Как извлечь корень любой степени в Excel
Рекомендуем похожие статьи
2007-2022 «Педагогическое сообщество Екатерины Пашковой — PEDSOVET.SU».
12+ Свидетельство о регистрации СМИ: Эл №ФС77-41726 от 20.08.2010 г. Выдано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций.
Адрес редакции: 603111, г. Нижний Новгород, ул. Раевского 15-45
Адрес учредителя: 603111, г. Нижний Новгород, ул. Раевского 15-45
Учредитель, главный редактор: Пашкова Екатерина Ивановна
Контакты: +7-920-0-777-397, info@pedsovet.su
Домен: https://pedsovet.su/
Копирование материалов сайта строго запрещено, регулярно отслеживается и преследуется по закону.
Отправляя материал на сайт, автор безвозмездно, без требования авторского вознаграждения, передает редакции права на использование материалов в коммерческих или некоммерческих целях, в частности, право на воспроизведение, публичный показ, перевод и переработку произведения, доведение до всеобщего сведения — в соотв. с ГК РФ. (ст. 1270 и др.). См. также Правила публикации конкретного типа материала. Мнение редакции может не совпадать с точкой зрения авторов.
Для подтверждения подлинности выданных сайтом документов сделайте запрос в редакцию.
- Опубликовать урок
- Опубликовать статью
- Дать объявление
- Подписаться на новости
- Частые вопросы
сервис вебинаров —>
О работе с сайтом
Мы используем cookie.
Публикуя материалы на сайте (комментарии, статьи, разработки и др.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьми лицами.
При этом редакция сайта готова оказывать всяческую поддержку как в публикации, так и других вопросах.
Если вы обнаружили, что на нашем сайте незаконно используются материалы, сообщите администратору — материалы будут удалены. 
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
источники:
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
http://exceltable.com/otchety/reshenie-uravneniy