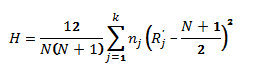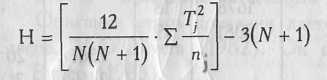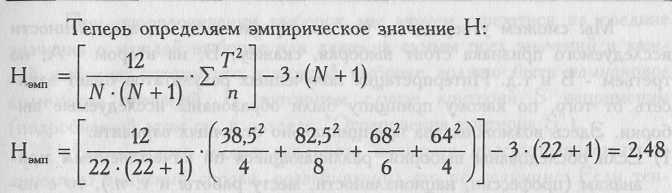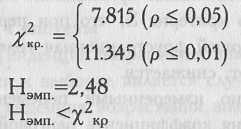17 авг. 2022 г.
читать 2 мин
Критерий Крускала-Уоллиса используется для определения наличия статистически значимой разницы между медианами трех или более независимых групп. Он считается непараметрическим эквивалентом однофакторного дисперсионного анализа.
В этом руководстве объясняется, как провести тест Крускала-Уоллиса в Excel.
Пример: тест Крускала-Уоллиса в Excel
Исследователи хотят знать, приводят ли три разных удобрения к разным уровням роста растений. Они случайным образом выбирают 30 разных растений и делят их на три группы по 10 штук, применяя к каждой группе разные удобрения. В конце месяца измеряют высоту каждого растения.
Используйте следующие шаги, чтобы выполнить тест Крускала-Уоллиса, чтобы определить, одинаков ли медианный рост в трех группах.
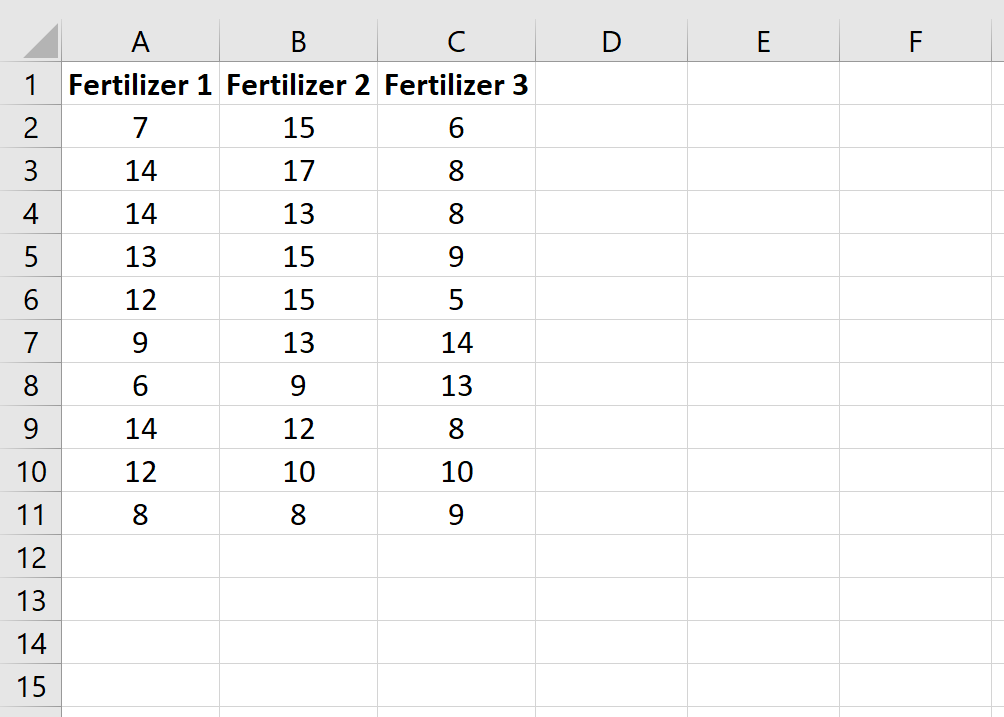
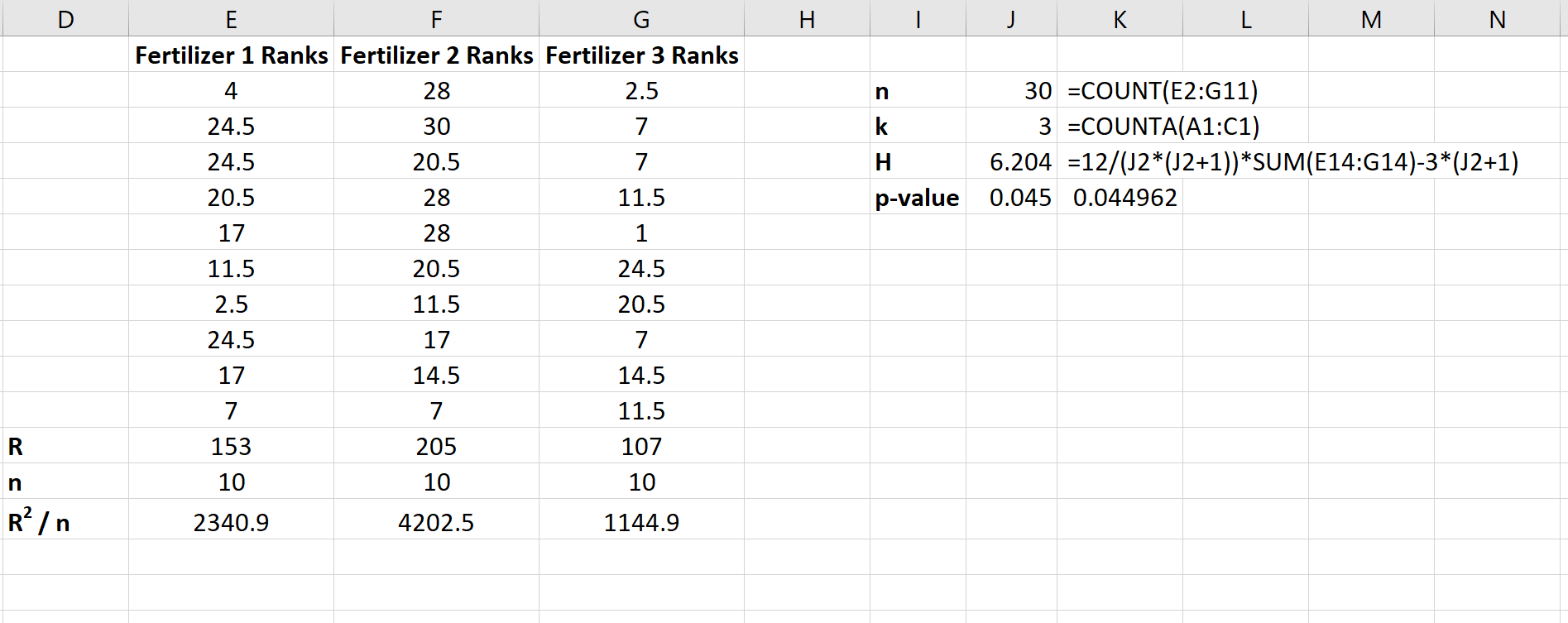
Шаг 1: Введите данные.
Введите следующие данные, которые показывают общий рост (в дюймах) для каждого из 10 растений в каждой группе:
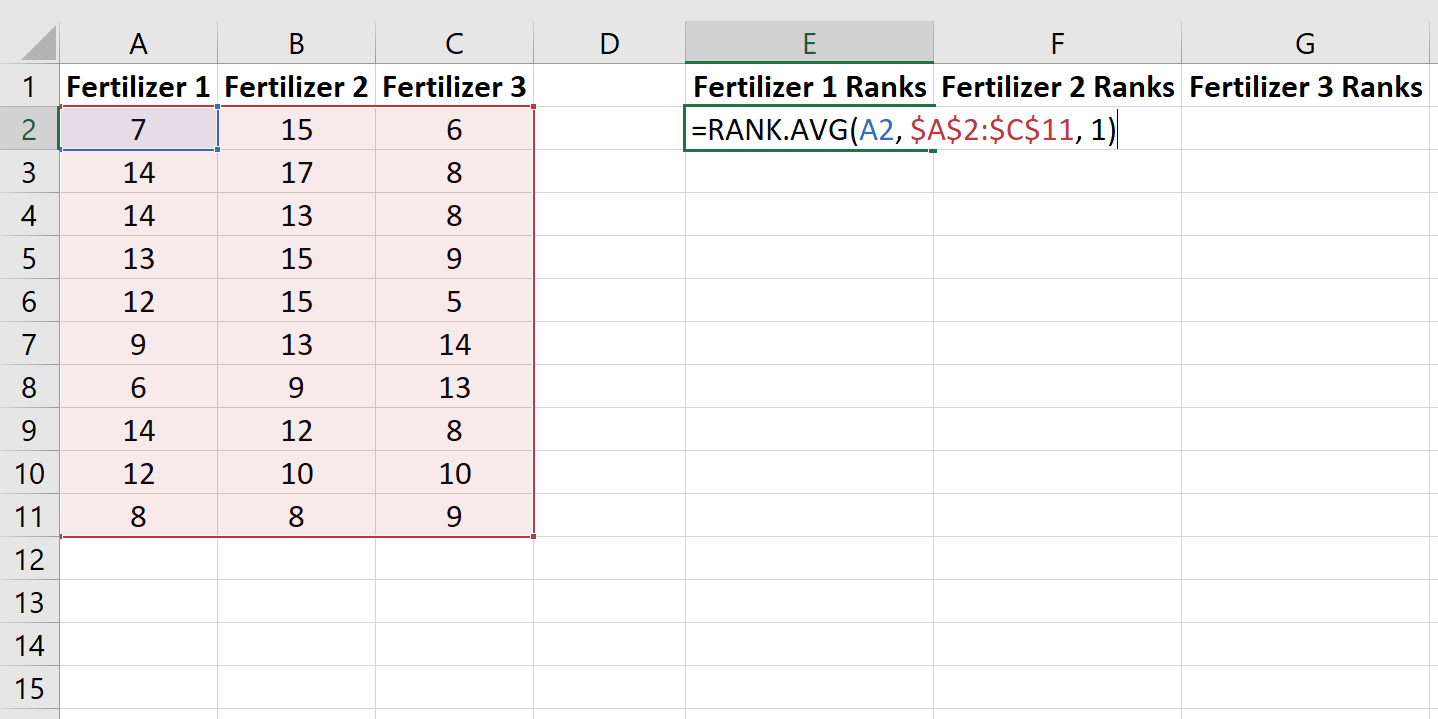
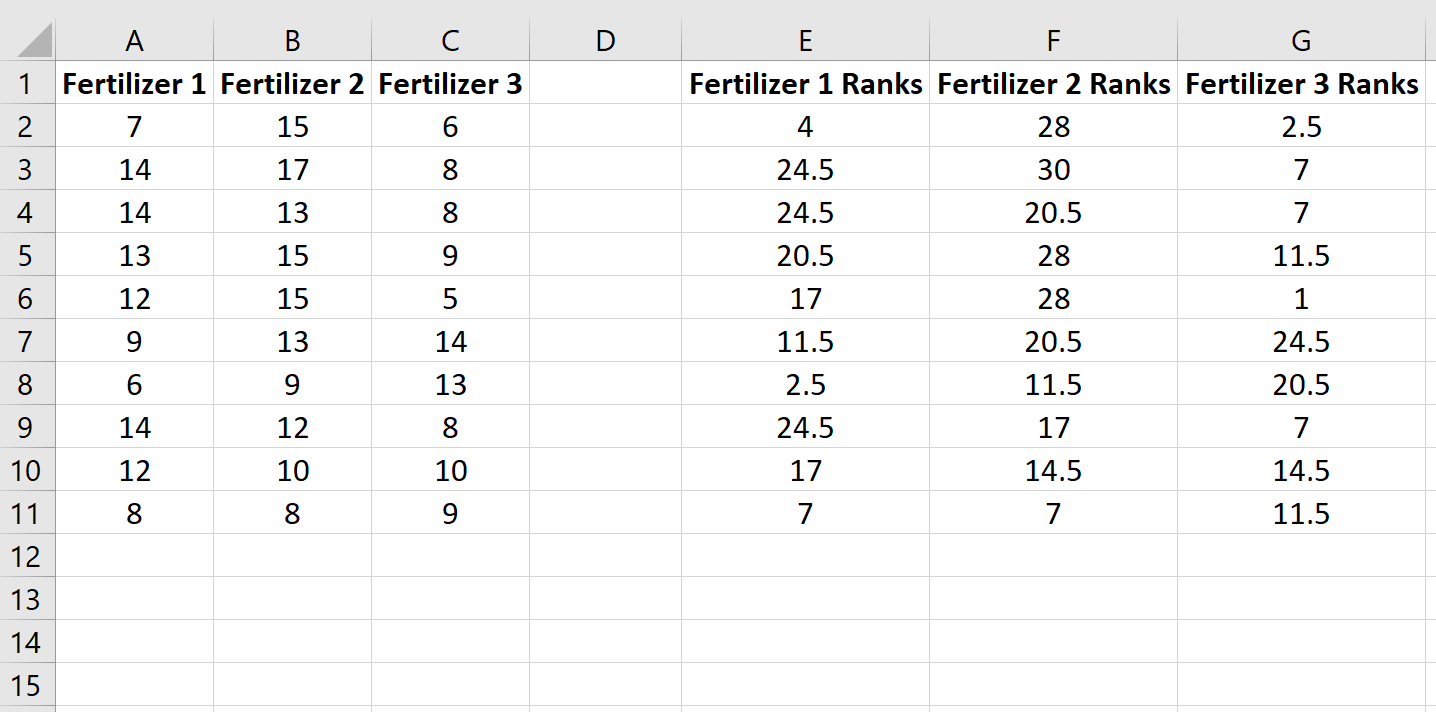
Шаг 2: Ранжируйте данные.
Далее мы воспользуемся функцией RANK.AVG() , чтобы присвоить ранг росту каждого растения из всех 30 растений. Следующая формула показывает, как рассчитать ранг первого растения в первой группе:
Скопируйте эту формулу в остальные ячейки:
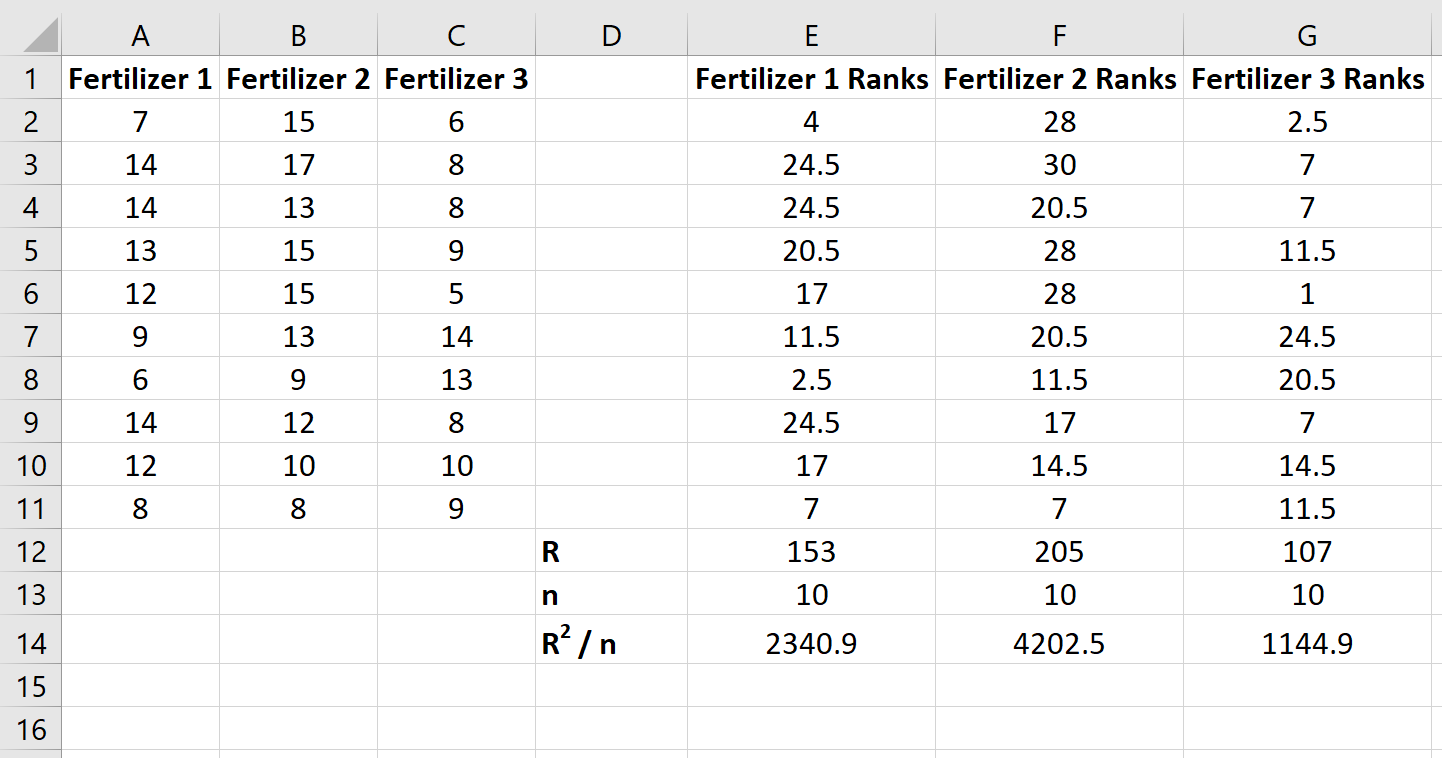
Затем вычислите сумму рангов для каждого столбца вместе с размером выборки и квадратом суммы рангов, деленной на размер выборки:
Шаг 3: Рассчитайте статистику теста и соответствующее значение p.
Статистика теста определяется как:
H = 12/(n(n+1)) * ΣR j 2 /n j – 3(n+1)
куда:
- n = общий размер выборки
- R j 2 = сумма рангов для j -й группы
- n j = размер выборки j -й группы
При нулевой гипотезе H следует распределению хи-квадрат с k-1 степенями свободы.
На следующем снимке экрана показаны формулы, используемые для расчета статистики теста, H и соответствующего значения p:
Статистика теста составляет H = 6,204, а соответствующее значение p равно p = 0,045.Поскольку это p-значение меньше 0,05, мы можем отвергнуть нулевую гипотезу о том, что средний рост растений одинаков для всех трех удобрений. У нас есть достаточно доказательств, чтобы заключить, что тип используемого удобрения приводит к статистически значимым различиям в росте растений.
Шаг 4: Сообщите о результатах.
Наконец, мы хотим сообщить о результатах теста Крускала-Уоллиса. Вот пример того, как это сделать:
Был проведен тест Крускала-Уоллиста, чтобы определить, был ли средний рост растений одинаковым для трех разных удобрений для растений. Всего в анализе было использовано 30 растений. Каждое удобрение применялось к 10 разным растениям.
Тест показал, что средний рост растений не был одинаковым (H = 6,204, p = 0,045) среди трех удобрений. То есть имелась статистически значимая разница в среднем росте растений между двумя или более удобрениями.
A Kruskal-Wallis Test is used to determine whether or not there is a statistically significant difference between the medians of three or more independent groups. It is considered to be the non-parametric equivalent of the One-Way ANOVA.
This tutorial explains how to conduct a Kruskal-Wallis Test in Excel.
Example: Kruskal-Wallis Test in Excel
Researchers want to know if three different fertilizers lead to different levels of plant growth. They randomly select 30 different plants and split them into three groups of 10, applying a different fertilizer to each group. At the end of one month they measure the height of each plant.
Use the following steps to perform a Kruskal-Wallis Test to determine if the median growth is the same across the three groups.
Step 1: Enter the data.
Enter the following data, which shows the total growth (in inches) for each of the 10 plants in each group:
Step 2: Rank the data.
Next, we will use the RANK.AVG() function to assign a rank to the growth of each plant out of all 30 plants. The following formula shows how to calculate the rank for the first plant in the first group:
Copy this formula to the rest of the cells:
Then, calculate the sum of the ranks for each column along with the sample size and the squared sum of ranks divided by the sample size:
Step 3: Calculate the test statistic and the corresponding p-value.
The test statistic is defined as:
H = 12/(n(n+1)) * ΣRj2/nj – 3(n+1)
where:
- n = total sample size
- Rj2 =sum of ranks for the jth group
- nj =sample size of jth group
Under the null hypothesis, H follows a Chi-square distribution with k-1 degrees of freedom.
The following screenshot shows the formulas used to calculate the test statistic, H, and the corresponding p-value:
The test statistic is H = 6.204 and the corresponding p-value is p = 0.045. Since this p-value is less than 0.05, we can reject the null hypothesis that the median plant growth is the same for all three fertilizers. We have sufficient evidence to conclude that the type of fertilizer used leads to statistically significant differences in plant growth.
Step 4: Report the results.
Lastly, we want to report the results of the Kruskal-Wallis Test. Here is an example of how to do so:
A Kruskal-Wallist Test was performed to determine if median plant growth was the same for three different plant fertilizers. A total of 30 plants were used in the analysis. Each fertilizer was applied to 10 different plants.
The test revealed that the median plant growth was not the same (H = 6.204, p = 0.045) among the three fertilizers. That is, there was a statistically significant difference in median plant growth among two or more of the fertilizers.
Omnibus Test
The Kruskal-Wallis H test is a non-parametric test that is used in place of a one-way ANOVA. Essentially it is an extension of the Wilcoxon Rank-Sum test to more than two independent samples.
Although, as explained in Assumptions for ANOVA, one-way ANOVA is usually quite robust, there are many situations where the assumptions are sufficiently violated and so the Kruskal-Wallis test becomes quite useful: in particular, when:
- Group samples strongly deviate from normal; this is especially relevant when sample sizes are small and unequal and data are not symmetric.
- Group variances are quite different because of the presence of outliers
If the assumptions of ANOVA are satisfied, then the Kruskal-Wallis test is less powerful than ANOVA, and so you should use ANOVA. This is also the case when a transformation can be used to meet the ANOVA assumptions. When the homogeneity assumption fails, Welch’s ANOVA is often preferred over the Kruskal-Wallis test.
Some characteristics of Kruskal-Wallis test are:
- The assumptions are similar to those for the Mann-Whitney test: independent group samples, data in each group is randomly selected and data is at least ordinal
- No assumptions are made about the type of underlying distribution, although see below
- Each group sample has at least 5 elements.
- No population parameters are estimated, and so there are no confidence intervals.
The Kruskal-Wallis test is actually testing the null hypothesis that the populations from which the group samples are selected are equal in the sense that none of the group populations is dominant over any of the others. A group is dominant over the others if when one element is drawn at random from each of the group populations, it is more likely that the largest element is in that group.
H0: the group populations have equal dominance; i.e. when one element is drawn at random from each group population, the largest (or smallest, or second smallest, etc.) element is equally likely to come from any one of the group populations
H1: At least one of the group populations is dominant over the others
When the group samples have the same shape (and so presumably this is reflective of the corresponding population distributions), then the null hypothesis can be viewed as a statement about the group medians.
H0: the group population medians are equal
H1: the group population medians are not equal
An indication that the population distributions have the same shape (except that possibly there is a shift to the right or left among them) is that the box plots are similar, except that the box and whiskers among them may be at different heights. Another indication is that the group histograms or QQ plots look similar (although not necessarily indicating normality).
Property 1: Define the test statistic
where k = the number of groups, nj is the size of the jth group, Rj is the rank sum for the jth group and n is the total sample size, i.e.
Then
provided nj ≥ 5 based on the following null hypothesis:
H0: The distribution of scores is equal across all groups
Observation: If the assumptions of ANOVA are satisfied, then the Kruskal-Wallis test is less powerful than ANOVA.
An alternative expression for H is given by
where is the sum of squares between groups using the ranks instead of raw data. This is based on the fact that
is the expected value (i.e. mean) of the distribution of
.
If there are small sample sizes and many ties, a corrected Kruskal-Wallis test statistic H’ = H/T gives better results where
Here the sum is taken over all scores where ties exist and f is the number of ties at that level.
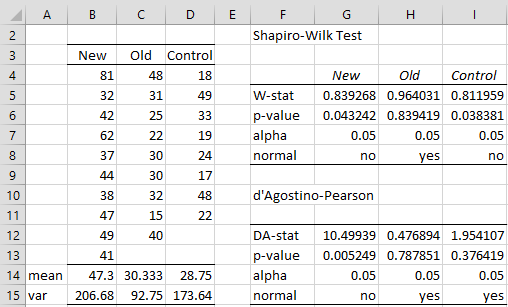
Example 1: A cosmetic company created a small trial of a new cream for treating skin blemishes. It measured the effectiveness of the new cream compared to the leading cream on the market and a placebo. Thirty people were put into three groups of 10 at random, although just before the trial began 2 people from the control group and 1 person from the test group for the existing cream dropped out. The left side of Figure 1 shows the number of blemishes removed from each person during the trial.
Figure 1 – Blemish treatment data
Based on the Shapiro-Wilk test, shown on the right side of the figure, we see that two of the groups are not normally distributed. This conclusion is confirmed from the QQ plots (not shown here). We, therefore decide to use the Kruskal-Wallis test instead of ANOVA.
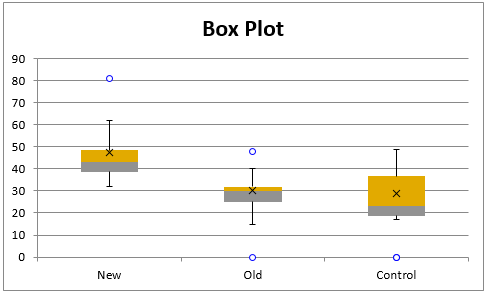
From the box plots shown in Figure 2, we observe, that although the group distributions don’t have the exact same shape (consistent with the fact that two are not normally distributed, while one is normally distributed), their shapes are fairly similar (although the values for the New group are larger than for the other two groups). Thus, we can use Kruskal-Wallis to test the null hypothesis that none of the groups is dominant over the others, and perhaps even that the group medians are equal.
Figure 2 – Box plot comparisons
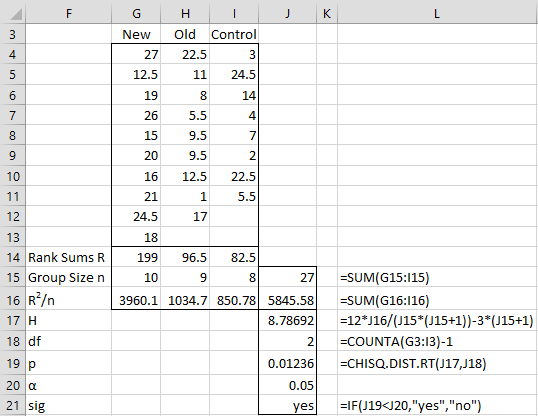
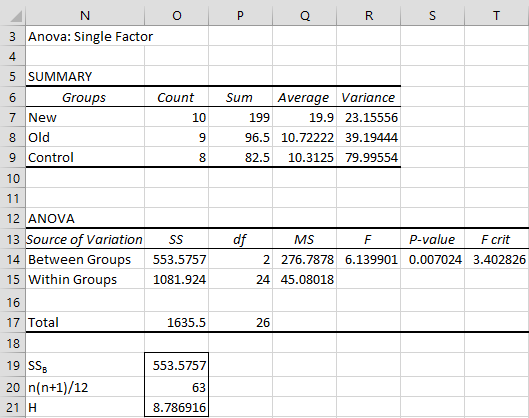
We now carry out the Kruskal-Wallis test as shown in Figure 3. Using the RANK.AVG function (or the RANK_AVG function for Excel 2007 users), we obtain the ranks of each of the raw scores, as shown in range G4:I13. E.g. cell I4 contains =IF(ISNUMBER(D4), RANK.AVG(D4,$B$4:$D$13,1),””).
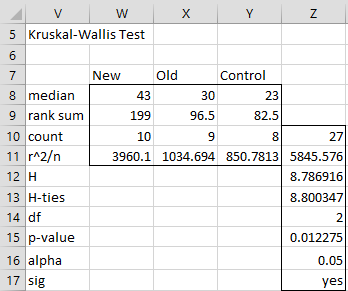
We next calculate the sum of the ranks for each group, namely R1 = 199, R2 = 96.5 and R3 = 82.5. Next, we square each of these values and divide by the number of elements in the corresponding group to obtain the figures shown in range G16:I16. The remaining formulas in the figure are shown in column L (corresponding to formulas in column J).
Figure 3 – Kruskal-Wallis test
Since p-value = .01236 < .05 = α, we reject the null hypothesis, and conclude there is significant difference between the three cosmetics.
Note that we can perform a one-way ANOVA on the ranks (i.e. the data in range G3:I13) using Excel’s ANOVA: One Factor data analysis tool (or the Real Statistic data analysis tool) to find SSB. This provides an alternative way of calculating H (see Figure 4) since H is equal to
Figure 4 – ANOVA on ranked data
Real Statistics Functions: The Real Statistics Resource Pack contains the following functions:
KRUSKAL(R1, ties) = value of H on the data (without headings) contained in range R1 (organized by columns).
KTEST(R1, ties) = p-value of the Kruskal-Wallis test on the data (without headings) contained in range R1 (organized by columns).
When ties = TRUE (default) then a ties correction is applied.
For Example 1, KRUSKAL(B5:D14) = 8.7869 and KTEST(B5:D14) = .01236.
The resource pack also provides the following array function:
KW_TEST(R1, lab, ties) = the 4 × 1 range consisting of the values for H, H′, df, p-value. If lab = TRUE then an extra column is added containing labels. If ties = TRUE (default) then H’ is used to calculate the p-value; otherwise, H is used to calculate the p-value.
Real Statistics Data Analysis Tool: The Real Statistics Resource Pack provides a data analysis tool to perform the Kruskal-Wallis test.
To use the tool for Example 1, press Ctrl-m and double click on Analysis of Variance (or click on the Anova tab if using the Multipage interface) and select Single Factor Anova. When a dialog box similar to that shown in Figure 1 of ANOVA Analysis Tool appears, enter B3:D13 in the Input Range, check Column headings included with data, select the Kruskal-Wallis option and click on OK.
The output is shown in Figure 5.
Figure 5 – Kruskal-Wallis data analysis
The H′ value (including a ties correction) can be calculated by =KRUSKAL(B4:D13) and the corresponding p-value by =KTEST(B4:D13). In fact, the range Z12:Z15 can be calculated by =KW_TEST(B4:D13).
Follow-up Tests
If the Kruskal-Wallis Test shows a significant difference between the groups, then pairwise comparisons or contrasts can be used to pinpoint the difference(s) as described following a single factor ANOVA. It is important to reduce familywise Type I error.
For more information about these follow-up tests and how to perform them in Excel, click on any of the following links:
- Nemenyi Test
- Dunn’s Test
- Schaich-Hamerle Test
- Conover Test
- Steel Test
- Pairwise Mann-Whitney tests
- Contrasts
Сравнение трех и более независимых групп. Критерий Краскела — Уоллиса
Введение
В этой статье речь пойдет о непараметрическом статистическом критерии Краскела-Уоллиса. Что это за критерий? Каковы условия его применения? Где используют? Как рассчитать? Ответы на эти и другие вопросы Вы найдете ниже.
Критерий Краскела-Уоллиса – непараметрический статистический критерий, используемый для сравнения 3-ех и более независимых выборок по количественному или порядковому признаку.
Критерий был разработан американскими математиками. Уильям Краскел и Аллен Уоллис представили критерий в своей работе «Use of ranks in one-criterion variance analysis» в 1952 году. Отсюда и название критерия.
Условия применения критерия
- Не менее трех выборок испытуемых объектов
- Зависимая переменная должна измеряться в порядковой или непрерывной шкале
- Наблюдения должны быть независимыми (не должно быть никаких отношений между двумя группами или внутри каждой группы)
- Наблюдения не распределяются нормально
Критерий Краскела-Уоллиса подходит для сравнения небольших выборок. Желательно, чтобы в каждой выборке было не менее 5 наблюдений.
Использование Краскела-Уоллиса
Непараметрический критерий Краскела-Уоллиса используется во многих областях. Чаще всего его можно встретить в психологии, здравоохранении и бизнесе.
Примеры задач, которые решает критерий Краскела-Уоллиса:
- Оказывают ли три препарата разное влияние на боль пациентов?
- Приводят ли четыре разных видов удобрения к разным уровням роста растений?
- Различаются ли уровни выгорания в группах: преподаватели, врачи, шахтеры?
Как рассчитать критерий Краскела-Уоллиса
- Определите нулевую и альтернативную гипотезы.
H0: Между выборками 1, 2, 3 и т. д. существуют лишь случайные различия по уровню исследуемого признака.
Н1: Между выборками 1, 2, 3 и т. д. существуют неслучайные различия по уровню исследуемого признака.
- Вычислите величину статистики критерия (нулевой гипотезы).
- Определите критические значения и соответствующий им уровень значимости.
- Интерпретируйте величину р и результаты.
Важно, отклонение нулевой гипотезы не указывает, какая из групп отличается. Для того, чтобы это выяснить, необходимо проводить апостериорные (попарные) сравнения между группами.
Существует много критериев для осуществления попарных сравнений, мы, чаще всего, используем метод Неменьи, который был предложен Петром Неменьи в 1963 году.
В современном мире, когда все вокруг автоматизировано, для расчета критерия используют готовые статистические программы, в основе которых уже заложены специальные алгоритмы для расчетов, минуя ручные вычисления.
Мы выполняем расчеты критерием Краскела-Уоллиса в Python с использованием пакетов pandas, numpy, matplotlib.pyplot, seaborn, scipy.stats.
Почему вы выбрали для расчета критерий Краскела-Уоллиса?
Перед защитой работы, очень многих студентов, аспирантов пугает именно этот вопрос.
Мы, обычно, в качестве примера предлагаем следующий ответ:
«Нами был выбран критерий Краскела-Уоллиса ввиду того, что наши данные подходят под условия применения данного теста.» И далее ссылаемся на условия применения.
Пример результата сравнения трех групп
Смотреть отчет — сравнение трех независимых групп
О проекте BIRDYX
У нас Вы можете заказать услугу статистического анализа и помощи в статистических расчетах для научных статей, диссертаций или маркетинговых исследований. Свяжитесь с нами одним из удобных способов, чтобы обсудить детали:
WhatsApp: +7 (919) 882-93-67
Telegram: birdyx_ru
E-mail: mail@birdyx.ru
Мы растем, развиваемся, постоянно работаем над автоматизацией аналитических процессов, чтобы предоставлять Вам качественную аналитику оперативно и по доступной цене.
Ранговый критерий Крускала-Уоллиса для оценки разностей между с медианами (с > 2) представляет собой обобщение рангового критерия Уилкоксона для двух независимых выборок (см. также Однофакторный дисперсионный анализ). Таким образом, критерий Крускала-Уоллиса является непараметрической альтернативой F-критерию в однофакторном дисперсионном анализе, аналогично тому, как критерий Уилкоксона представляет собой непараметрическую альтернативу t-критерию, использующему суммарную дисперсию при сравнении двух независимых выборок. Если выполняются условия, необходимые для применения F-критерия в однофакторном дисперсионном анализе, критерий Крускала-Уоллиса обладает той же мощностью. [1]
Ранговый критерий Крускала-Уоллиса применяется для проверки гипотезы, что с независимых выборок извлечены из генеральных совокупностей, имеющих одинаковые медианы. Иначе говоря, нулевая и альтернативная гипотезы формулируются следующим образом:
Н0: М1 = М2 = … =Mc
H1: не все Mj (j = 1, 2, …, с) являются одинаковыми
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Для этого необходимо знать ранги, вычисленные по всем выборкам, а с генеральных совокупностей, из которых они извлечены, должны иметь одинаковые изменчивость и вид. Для того чтобы применить критерий Крускала-Уоллиса, сначала необходимо заменить наблюдения в с выборках их объединенными рангами. При этом первый ранг соответствует наименьшему наблюдению, а ранг n — наибольшему (n = n1 + n2 + … + nc). Если некоторые значения повторяются, им присваивается среднее значение их рангов.
Критерий Крускала-Уоллиса является альтернативой F-критерию в однофакторном дисперсионном анализе. H-статистика, применяемая в критерии Крускала-Уоллиса, аналогична величине SSA— межгрупповой вариации (подробнее см. Однофакторный дисперсионный анализ), по которой вычисляется F-статистика. Вместо сравнения средних значений j всех с групп с общим средним значением
, в критерии Крускала-Уоллиса средние ранги каждой из с групп сравниваются с общим рангом, вычисленным на основе всех n наблюдений. Если существует статистически значимый эффект эксперимента, средние ранги каждой группы будут значительно отличаться друг от друга и от общего ранга. При возведении этих разностей в квадрат Н-статистика увеличивается. С другой стороны, если эффект эксперимента не наблюдается, статистика Н теоретически должна быть равной нулю. Однако на практике вследствие случайных изменений статистика Н будет ненулевой, но достаточно малой.
Критерий Крускала-Уоллиса для разностей между с медианами:
где n — общее количество наблюдений в объединенных выборках, nj — количество наблюдений в j-й выборке (j = 1, 2, … , с), Tj — сумма рангов j-й выборки.
При достаточно большом объеме выборок (больше пяти) H-статистику можно аппроксимировать χ2-распределением с с – 1 степенями свободы. Таком образом, при заданном уровне значимости α решающее правило формулируется так: гипотеза Н0 отклоняется, если H > χU2 (рис. 1), в противном случае гипотеза Н0 не отклоняется. Критические значения χ2-распределения вычисляются с помощью функции Excel =ХИ2.ОБР(вероятность;степени_свободы).
Рис. 1. Критическая область критерия Крускала-Уоллиса
Продемонстрируем критерий Крускала-Уоллиса на примере оценки прочности парашютов в зависимости от поставщика синтетических волокон. Если прочность парашютов не является нормально распределенной случайной величиной, для оценки различий между медианами четырех генеральных совокупностей можно применить непараметрический критерий Крускала-Уоллиса.
Нулевая гипотеза заключается в том, что прочность всех парашютов одинакова: Н0: М1 = М2 = М3 =M4. Альтернативная гипотеза утверждает, что по крайней мере один поставщик отличается от других: H1: не все Mj (j = 1, 2, 3, 4) являются одинаковыми. Результаты эксперимента, ранги и вычисления приведены на рис. 2.
Рис. 2. Прочность и ранги парашютов, сшитых из синтетической ткани, приобретенной у четырех разных поставщиков
В процессе преобразования 20 показателей прочности в объединенные ранги, выясняется, что третий парашют, произведенный из синтетического волокна первого поставщика, имеет наименьшую прочность, равную 17,2. Он получает ранг 1. Четвертый парашют, произведенный из синтетического волокна первого поставщика, и второй парашют, сотканный из волокон четвертого поставщика, имеют одинаковую прочность, равную 19,9. Поскольку им соответствуют ранги 5 и 6, обоим парашютам присваивается ранг 5,5, равный среднему значению рангов 5 и 6. И, наконец, ранг 20 присваивается первому парашюту, сотканному из волокон второго поставщика, поскольку величина 26,3 является наибольшей. После присвоения рангов вычисляется их сумма в каждой группе: Т1 = 27,0; Т2 = 76,5; Т3 = 62,0; Т4 = 44,5. Для проверки рангов просуммируем эти величины:
Используя формулу (1), вычислим Н-статистику:
Статистика Н имеет приближенное χ2-распределение с с – 1 степенями свободы. При уровне значимости α, равном 0,05, определяем величину χU2 — верхнего критического значения χ2-распределения с с – 1 = 3 степенями свободы с использованием функции =ХИ2.ОБР(1 – α;с –1) = 7,815 (рис. 2). Поскольку вычисленная Н-статистика равна 7,889 и превышает критическое значение 7,815, нулевая гипотеза отклоняется. Следовательно, не все фирмы поставляют синтетическое волокно, прочность которого имеет одинаковую медиану. Аналогичный вывод можно сделать, вычислив р-значение по формуле р(Н=7,889) =1-ХИ2.РАСП(7,889;3;ИСТИНА) =0,048 (рис. 2). р-значение равно 0,048, т.е. меньше уровня значимости 0,05. Поскольку нулевая гипотеза отклоняется, приходим к выводу, что фирмы поставляют волокна разной прочности. На следующем этапе необходимо попарно сравнить всех поставщиков и определить, какие из них отличаются друг от друга. Для этого можно применить апостериорную процедуру множественного сравнения, предложенную Дж. Данном.
Для применения критерия Крускала-Уоллиса должны выполняться следующие условия.
- Все с выборок случайно и независимо друг от друга извлекаются из соответствующих генеральных совокупностей.
- Анализируемая переменная является непрерывной.
- Наблюдения допускают ранжирование как внутри, так и между группами.
- Все с генеральных совокупностей имеют одинаковую изменчивость.
- Все с генеральных совокупностей имеют одинаковый вид.
Процедура Крускала-Уоллиса имеет меньше ограничений, чем F-критерий. Процедура Крускала-Уоллиса предусматривает ранжирование только по всем выборкам в совокупности. Общее распределение должно быть непрерывным, но его вид значения не имеет. Если эти условия не выполняются, критерий Крускала-Уоллиса по-прежнему можно применять для проверки гипотезы о различиях между с генеральными совокупностями. Альтернативная гипотеза утверждает, что среди с генеральных совокупностей существует хотя бы одна, которая отличается от остальных какой-нибудь характеристикой — либо средним значением, либо видом. С другой стороны, для применения F-критерия переменная должна быть числовой, а с выборок должны извлекаться из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию.
В полностью рандомизированных экспериментах, для которых выполняются условия F-критерия, следует применять именно его, а не процедуру Крускала-Уоллиса, поскольку мощность F-критерия в этой ситуации выше. С другой стороны, если эти условия не выполняются, более мощным становится критерий Крускала-Уоллиса, и следует предпочесть именно его.
Предыдущая заметка Непараметрические критерии. Ранговый критерий Уилкоксона
Следующая заметка Критерий «хи-квадрат» для дисперсий
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 748–751
The Kruskal–Wallis test in R Programming Language is a rank-based test that is similar to the Mann–Whitney U test but can be applied to one-way data with more than two groups. It is a non-parametric alternative to the one-way ANOVA test, which extends the two-samples Wilcoxon test. A group of data samples is independent if they come from unrelated populations and the samples do not affect each other. Using the Kruskal-Wallis Test, it can be decided whether the population distributions are similar without assuming them to follow the normal distribution. It is very much easy to perform Kruskal-Wallis test in the R language.
Note: The outcome of the Kruskal–Wallis test tells that if there are differences among the groups, but doesn’t tell which groups are different from other groups.
Examples:
- Let one wants to find out how socioeconomic status influences attitude towards sales tax hikes. Here the independent variable is “socioeconomic status” with three levels: working-class, middle-class, and wealthy. The dependent variable is measured on a 5-point Likert scale from strongly agree to strongly disagree.
- If one wants to find out how test anxiety influences actual test scores. The independent variable “test anxiety” has three levels: no anxiety, low-medium anxiety, and high anxiety. The dependent variable is the exam score and it is rated from 0 to 100%.
Assumptions for the Kruskal-Wallis test in R
The variables should have:
- One independent variable with two or more levels. The test is more commonly used when there are three or more levels. For two levels instead of the Kruskal-Wallis test consider using the Mann Whitney U Test.
- The dependent variable should be the Ordinal scale, Ratio Scale, or Interval scale.
- The observations should be independent. In other words, there should be no correlation between the members in every group or within groups.
- All groups should have identical shape distributions.
Implementation in R
R provides a method kruskal.test() which is available in the stats package to perform a Kruskal-Wallis rank-sum test.
Syntax: kruskal.test(x, g, formula, data, subset, na.action, …)
Parameters:
- x: a numeric vector of data values, or a list of numeric data vectors.
- g: a vector or factor object giving the group for the corresponding elements of x
- formula: a formula of the form response ~ group where response gives the data values and group a vector or factor of the corresponding groups.
- data: an optional matrix or data frame containing the variables in the formula .
- subset: an optional vector specifying a subset of observations to be used.
- na.action: a function which indicates what should happen when the data contain NA
…: further arguments to be passed to or from methods.
Example:
Let’s use the built-in R data set named PlantGrowth. It contains the weight of plants obtained under control and two different treatment conditions.
R
myData = PlantGrowth
print(myData)
print(levels(myData$group))
Output:
weight group 1 4.17 ctrl 2 5.58 ctrl 3 5.18 ctrl 4 6.11 ctrl 5 4.50 ctrl 6 4.61 ctrl 7 5.17 ctrl 8 4.53 ctrl 9 5.33 ctrl 10 5.14 ctrl 11 4.81 trt1 12 4.17 trt1 13 4.41 trt1 14 3.59 trt1 15 5.87 trt1 16 3.83 trt1 17 6.03 trt1 18 4.89 trt1 19 4.32 trt1 20 4.69 trt1 21 6.31 trt2 22 5.12 trt2 23 5.54 trt2 24 5.50 trt2 25 5.37 trt2 26 5.29 trt2 27 4.92 trt2 28 6.15 trt2 29 5.80 trt2 30 5.26 trt2 [1] "ctrl" "trt1" "trt2"
Here the column “group” is called factor and the different categories (“ctr”, “trt1”, “trt2”) are named factor levels. The levels are ordered alphabetically. The problem statement is we want to know if there is any significant difference between the average weights of plants in the 3 experimental conditions. And the test can be performed using the function kruskal.test() as given below.
R
myData = PlantGrowth
result = kruskal.test(weight ~ group,
data = myData)
print(result)
Output:
Kruskal-Wallis rank sum test
data: weight by group
Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842
Explanation:
As the p-value is less than the significance level 0.05, it can be concluded that there are significant differences between the treatment groups.
Порой, чтобы провести качественное исследование, получить достоверные результаты, необходимо пользоваться не только общими, всем известными приемами, но и осваивать новые инструменты. Для сравнения трех и более элементов, различных по характеру или содержанию, можно воспользоваться непараметрическим критерием Краскела-Уоллеса (критерий Н), который успешно применяют в статистических и психологических научных работах.
Когда целесообразно применение методики?
Любые параметрические и непараметрические критерии, используемые в психологических исследованиях, имеют ряд ограничений и условий. Методика Краскела-Уоллеса не является исключением из данного правила.
По сути, этот инструмент является достойным и надежным аналогом однофакторной модели дисперсионного анализа. Его использование целесообразно, если исследователь намерен изучать несколько выборок, групп или элементов (3,4 и более). Эксперты рекомендуют прибегать к нему в том случае, если результаты проведенного эксперимента возможно представить в виде последовательной шкалы.
Критерий Н позволяет оценить различия между объектами исследования, его элементами по конкретному признаку. Важно отметить, что применение этого непараметрического исследовательского инструмента возможно к несвязным выборкам и группам.
В основе методики Краскела-Уоллеса лежит ранжирование.
Условия применения критерия Краскела-Уоллеса
Смысл критерий Н заключается в следующем: исследователь может перейти от собранных эмпирических данных к их значениям после ранжирования.
Методика применима в следующих случаях:
- Автор сумел выбрать не менее трех выборок испытуемых объектов;
- Исследователь должен провести не менее 4 наблюдений за объектами исследования первой выборки, и не менее двух наблюдений за остальными испытуемыми группами для получения достоверных эмпирических данных. Важно соблюдение соотношения 4/2/2. Количество испытуемых в каждой выборке не играет роли.
- Для оценки полученных результатов необходимо пользоваться специально разработанной таблицей критических значений.
- Если какие-либо различия становятся «стертыми», то можно выявить их посредством попарного сравнения испытуемых между собой.
Возникли сложности?
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Этапы применения методики Краскела-Уоллеса
Чтобы провести исследование, важно знать правильную последовательность действий, которая приведет к успеху и достоверному результату. Сейчас мы расскажем порядок «эксплуатации» критерия Н.
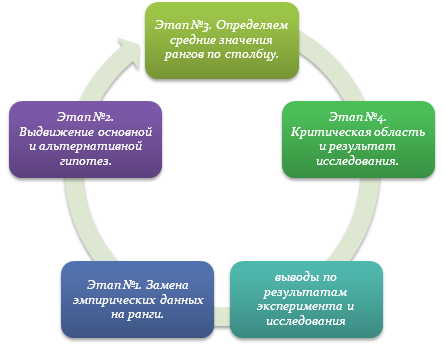
Этап №1. Замена эмпирических данных на ранги.
Для начала необходимо обработать все полученные сведения и преобразовать их в числовой (математический) вид. Лучше всего при этом ввести систему обозначений каждого элемента и признака. Допустим, все данные эксперимента были обозначены xij, а их ранги – rij. Далее необходимо проранжировать все полученные значения и сформировать «ранговую таблицу», в которой все элементы будут располагаться по возрастанию или убыванию ранга.
Этап №2. Выдвижение основной и альтернативной гипотез.
Здесь исследователь должен принять определенную позицию и выдвинуть идею, а затем сразу же предложить достойную альтернативу (на случай, если основная гипотеза не найдет своего подтверждения и буде опровергнута). Важным условием при формулировании гипотез является то, что основная гипотеза и ранжирование по ней должно отличаться от ранжирования альтернативной идеи (допускаются минимальные совпадения).
Этап №3. Определяем средние значения рангов по столбцу.
С их помощью исследователь «оптимизирует и стабилизирует» разбросанные значения. В целях анализа более точных данных, также необходимо учесть случайную величину (которая минимизирует погрешности отклонения):
Где — характеризует общее количество числе в таблице.
Этап №4. Критическая область и результат исследования.
Далее исследователю останется лишь сравнить полученные данные с табличными (таблица критических областей). Для наглядности можно построить графическую зависимость и проследить, каким образом пересекаются выборки, есть ли сходства и различия.
Если количество испытуемых небольшое, то можно воспользоваться готовыми таблицами, но при проведении исследования над тремя и более выборками – расчеты и анализ неизбежны.
Пример применения критерия Краскела-Уоллиса
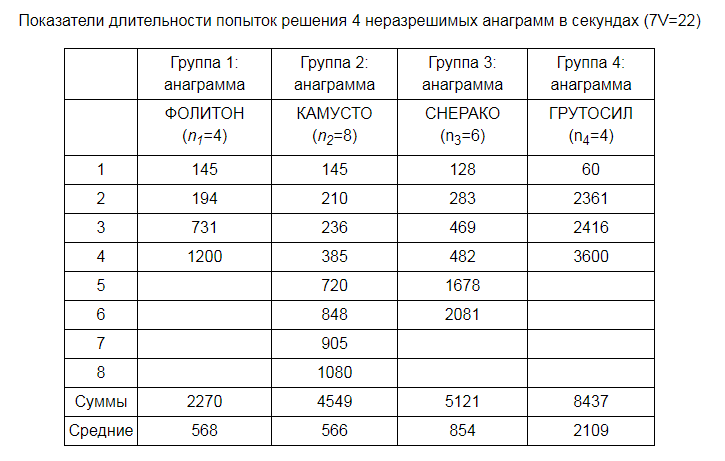
Автор исследования проводил эксперимент над молодыми людьми в возрасте 20-22 лет, которые обучались в техническом ВУЗе. Эксперимент посвящался оценке интеллектуальной настойчивости. Он предполагал оценку навыков студентов по работе с анаграммами. Всего было определено 4 анаграммы разного уровня сложности. Работа с каждым испытуемым проходила в индивидуальном порядке. Время на проведение эксперимента не ограничивалось.
Исследователь заметил, что над некоторыми неразрешимыми анаграммами студенты работали дольше, чем над остальными. Поэтому было принято решение оценить, какая анаграмма для каждого из них была неразрешимой.
Автор намерен проверить: длительность попыток решить каждую анаграмму примерно одинакова. В связи с этим он выдвинул следующие гипотезы:
На текущий момент он располагает следующими данными:
Рассмотрим порядок дальнейших действия и расчетов.
Далее необходимо сделать следующее:
1. Перенести все
показатели испытуемых на индивидуальные
карточки.
2. Пометить карточки
испытуемых группы 1 определенным цветом,
например красным, карточки испытуемых
группы 2 — синим, карточки испытуемых
групп 3 и 4 — соответственно, зеленым и
желтым цветом и т. д. (Можно использовать,
естественно, и любые другие обозначения.)
3. Разложить все
карточки в единый ряд по степени
нарастания признака, не считаясь с тем,
к какой группе относятся карточки, как
если бы мы работали с одной объединенной
выборкой.
4. Проранжировать
значения на карточках, приписывая
меньшему значению меньший ранг. Надписать
на каждой карточке ее ранг. Общее
количество рангов будет равняться
количеству испытуемых в объединенной
выборке.
5. Вновь разложить
карточки по группам, ориентируясь на
цветные или другие принятые обозначения.
6. Подсчитать суммы
рангов отдельно по каждой группе.
Проверить совпадение общей суммы рангов
с расчетной.
7. Подсчитать
значение критерия Н по формуле:
где N
— общее
количество испытуемых в объединенной
выборке;
n
— количество испытуемых в каждой группе;
Т —
суммы
рангов по каждой группе.
8а. При
количестве групп с=3, n1•n2•n3≤5
определить
критические значения и соответствующий
им уровень значимости по Табл. IV
Приложения 1.
Если
Нэмп
равен или превышает критическое значение
H0,05,
H0
отвергается.
8б. При
количестве групп с>3 или количестве
испытуемых n1•n2•n3>5,
определить
критические значения χ2
по
Табл. IX
Приложения 1.
Если
Нэмп
равен или превышает критическое значение
χ2,
H0
отвергается.
Воспользуемся
этим алгоритмом при решении задачи о
неразрешимых анаграммах. Результаты
работы по 1-6 шагам алгоритма представлены
в Табл. 2.6.
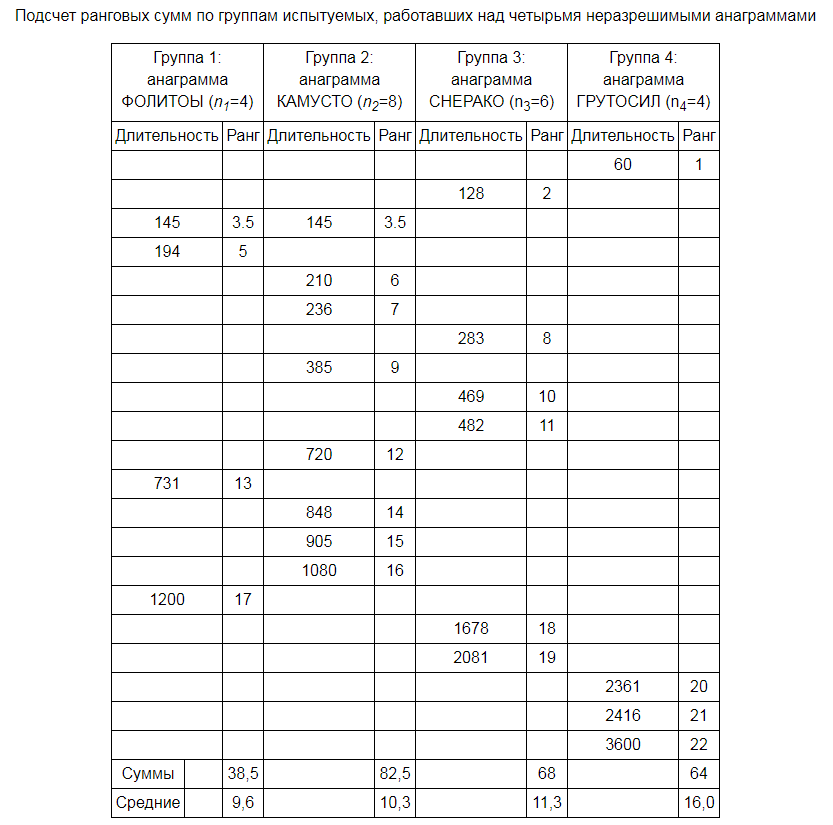
Таблица 2.6
Подсчет ранговых
сумм по группам испытуемых, работавших
над четырьмя неразрешимыми анаграммами
|
Группа 1: анаграмма ФОЛИТОЫ (n1=4) |
Группа 2: анаграмма КАМУСТО (n2=8) |
Группа 3: анаграмма СНЕРАКО (n3=6) |
Группа 4: анаграмма
ГРУТОСИЛ |
|||||
|
Длительность |
Ранг |
Длительность |
Ранг |
Длительность |
Ранг |
Длительность |
Ранг |
|
|
60 |
1 |
|||||||
|
128 |
2 |
|||||||
|
145 |
3.5 |
145 |
3.5 |
|||||
|
194 |
5 |
|||||||
|
210 |
6 |
|||||||
|
236 |
7 |
|||||||
|
283 |
8 |
|||||||
|
385 |
9 |
|||||||
|
469 |
10 |
|||||||
|
482 |
11 |
|||||||
|
720 |
12 |
|||||||
|
731 |
13 |
|||||||
|
848 |
14 |
|||||||
|
905 |
15 |
|||||||
|
1080 |
16 |
|||||||
|
1200 |
17 |
|||||||
|
1678 |
18 |
|||||||
|
2081 |
19 |
|||||||
|
2361 |
20 |
|||||||
|
2416 |
21 |
|||||||
|
3600 |
22 |
|||||||
|
Суммы |
38,5 |
82,5 |
68 |
64 |
||||
|
Средние |
9,6 |
10,3 |
11,3 |
16,0 |
Общая
сумма рангов =38,5+82,5+68+64=253. Расчетная
сумма рангов:
Равенство реальной
и расчетной сумм соблюдено.
Поскольку
таблицы критических значений критерия
Н предусмотрены только для количества
групп с = 3, а в данном случае у нас 4
группы, придется сопоставлять полученное
эмпирическое значение Н с критическими
значениями у}.
Для
этого вначале определим количество
степеней свободы V
для c=4:
v=c-
1 = 4 — 1 = 3
Теперь
определим критические значения по Табл.
IX
Приложения 1 для v=3:
Ответ:
Н0
принимается: 4 группы испытуемых,
получившие разные неразрешимые анаграммы,
не различаются по длительности попыток
их решения.
2.5.
S
—
критерий
тенденций Джонкира
Описание
этого критерия дается с использованием
руководства J.Greene,
M.D’Olivera
(1982). Он описан также у М. Холлендера,
Д.А. Вулфа (1983).
Назначение
критерия S
Критерий
S
предназначен для выявления тенденций
изменения
признака при переходе от выборки к
выборке при сопоставлении трех
и более выборок.
Описание
критерия S
Критерий
S
позволяет нам упорядочить обследованные
выборки по какому-либо признаку, например,
по креативности, фрустрационной
толерантности, гибкости и т.п.
Мы сможем утверждать,
что на первом месте по выраженности
исследуемого признака стоит выборка,
скажем, Б, на втором — А, на третьем — В и
т.д. Интерпретация полученных результатов
будет зависеть от того, по какому
принципу были образованы исследуемые
выборки. Здесь возможны два принципиально
отличных варианта.
1) Если
обследованы выборки, различающиеся по
качественным
признакам
(профессии, национальности, месту работы
и т. п.), то с помощью критерия S
мы сможем упорядочить выборки по
количественно
измеряемому
признаку (креативности, фрустрационной
толерантности, гибкости и т.п.).
2) Если
обследованы выборки, различающиеся или
специально сгруппированные по
количественному
признаку
(возрасту, стажу работы, социометрическому
статусу и др.), то, упорядочивая их теперь
уже по другому количественному
признаку,
мы фактически устанавливаем меру
связи между
двумя количественными признаками.
Например, мы можем показать с помощью
критерия S,
что при переходе от младшей возрастной
группы к старшей фрустрационная
толерантность возрастает, а гибкость,
наоборот, снижается.
Меру
связи между количественно измеренными
переменными можно установить с помощью
вычисления коэффициента ранговой
корреляции или линейной корреляции
(см. Главу 6). Однако критерий тенденций
S
имеет следующие преимущества перед
коэффициентами корреляции:
а)
критерий тенденций S
более прост в подсчете;
б) он применим и в
тех случаях, когда один из признаков
варьирует в узком диапазоне, например,
принимает всего 3 или 4 значения, в то
время как при подсчете ранговой корреляции
в этом случае мы получаем огрубленный
результат, нуждающийся в поправке на
одинаковые ранги.
Критерий
S
основан на способе расчета, близком к
принципу критерия Q
Розенбаума. Все выборки располагаются
в порядке возрастания исследуемого
признака, при этом выборку, в которой
значения в общем ниже, мы помещаем слева,
выборку, в которой значения выше, правее,
и так далее в порядке возрастания
значений. Таким образом, все выборки
выстраиваются слева направо в порядке
возрастания значений исследуемого
признака.
При
упорядочивании выборок мы можем опираться
на средние значения в каждой выборке
или даже на суммы всех значений в каждой
выборке, потому что в каждой выборке
должно быть одинаковое
1 количество
значений. В противном случае критерий
S
неприменим j
(подробнее об этом см. в разделе
«Ограничения критерия S»).
Для
каждого индивидуального значения
подсчитывается ко-личество значений
справа, превышающих его по величине.
Если
тенденция возрастания признака слева
направо существенна, то большая [часть
значений справа должна быть выше.
Критерий S
позволяет определить, преобладают ли
справа более высокие значения или нет.
Статистика S
отражает степень этого преобладания.
Чем выше эмпирическое [значение S,
тем тенденция возрастания признака
является более существенной.
Следовательно,
если Sэмп
равняется критическому значению или
превышает его, нулевая гипотеза может
быть отвергнута.
Гипотезы
Н0:
Тенденция возрастания значений признака
при переходе от выборки к выборке
является случайной.
H1:
Тенденция возрастания значений признака
при переходе от выборки к выборке не
является случайной.
Графическое
представление критерия
Фактически
критерий S
позволяет определить, достаточно ли
ве-&
лика
суммарная зона неперекрещивающихся
значений в сопоставляемых (выборках:
действительно ли в первом ряду значения
в общем ниже, чем 1в последующих, во
втором — ниже, чем в оставшихся справа
последующих и т. д.
Графически это
представлено на Рис. 2.7.
На Рис. 2.7(а) у
сопоставляемых рядов значений есть
непере* 1крещивающиеся зоны, но их
суммарная площадь может оказаться 1
слишком небольшой, чтобы признать
тенденцию возрастания признака |
существенной.
На
рис. 2.7(6) сумма неперекрещивающихся зон,
по-видимому, достаточно велика, чтобы
тенденция возрастания признака была
признана достоверной. Точно определить
это мы сможем лишь с помощью критерия
S.
Ограничения
критерия S
1. В каждой из
сопоставляемых выборок должно быть
одинаковое число наблюдений. Если
число наблюдений неодинаково, то придется
искусственно уравнивать выборки,
утрачивая при этом часть полученных
наблюдений.
Например,
если в двух выборках по 7 наблюдений, а
в третьей — И, то 4 из них необходимо
отсеять. Для этого карточки с
индивидуальными значениями
переворачиваются лицевой стороной вниз
и перемешиваются, а затем из них
случайным образом извлекается 7 карточек.
Оставшиеся 4 карточки с индивидуальными
значениями не включаются в дальнейшее
рассмотрение и в подсчет критерия S.
Ясно, что при таком подходе часть
информации утрачивается, и общая
картина может быть искажена.
Если исследователь
хочет избежать этого, ему следует
воспользоваться критерием Н,
позволяющим выявить различия между
тремя и более выборками без указания
на направление этих различий (см. параграф
2.4).
2.
Нижний порог: не менее 3 выборок и не
менее 2 наблюдений в каждой выборке.
Верхний порог в существующих таблицах:
не более 6 выборок и не более 10 наблюдений
в каждой выборке (см. Табл. III
Приложения 1 для определения критических
значений S).
При большем количестве выборок или
наблюдений в них придется пользоваться
критерием Н Крускала-Уоллиса.
Пример
Выборка претендентов
на должность коммерческого директора
в Санкт-Петербургском филиале зарубежной
фирмы была обследована с помощью
Оксфордской методики экспресс-видеодиагностики,
использующей диагностические ролевые
игры. Были обследованы 20 мужчин в возрасте
от 25 до 40 лет, средний возраст 31,5 года.
Оценки производились по 15 значимым,
с точки зрения зарубежной фирмы,
психологическим качествам,
обеспечивающим эффективную деятельность
на посту коммерческого директора. Одним
из этих качеств была «Авторитетность».
В конце 8-часового сеанса диагностических
ролевых игр и упражнений проводился
социометрический опрос участников
группы, в котором они должны были ответить
на вопрос: «Если бы я сам был
представителем фирмы, я выбрал бы на
должность коммерческого директора:
1)…. 2)…. 3)….» Участники знали, что
каждый их шаг является материалом для
диагностики, и что в данном случае, в
частности, проверяется, помимо
прочего, их способность к объективному
суждению о людях. В результате этой
процедуры каждый участник получил
то или иное количество выборов от других
участников, отражающее его социометрический
статус в группе претендентов.
Результаты
исследования представлены в Табл. 2.7
(данные Е. В. Сидоренко, И. В. Дермановой,
1991).
Можно ли считать,
что группы с разным статусом различаются
и по уровню авторитетности, определявшейся
независимо от социометрии с помощью
экспресс-видеодиагностики?
Таблица 2.7
Показатели по
шкале Авторитетности в группах с разным
социометрическим статусом (N=20)
|
Номера испытуемых |
Группа 1: 0 выборов (n1=5) |
Группа 2: 1 выбор (n2=5) |
Группа 3: 2-3 выбора (n3=5) |
Группа 4: 4 и более выборов |
|
1 2 3 4 5 |
5 5 2 5 4 |
5 6 7 6 4 |
5 6 7 7 5 |
9 9 8 8 7 |
|
Суммы |
21 |
28 |
30 |
41 |
|
Средние |
4,2 |
5,6 |
6,0 |
8,2 |
Сформулируем
гипотезы.
H0:
Тенденция
повышения значений по шкале Авторитетности
при переходе от группы к группе (слева
направо) случайна.
Н1:
Тенденция повышения значений по шкале
Авторитетности при переходе от группы
к группе (слева направо) неслучайна.
Для
того, чтобы нам было удобнее подсчитывать
количества более высоких значений
(S1),
лучше упорядочить значения в каждой
группе по их возрастанию (Табл. 2.8).
Таблица 2.8
Расчет
критерия S
при сопоставлении групп с разным
социометрическим статусом по
показателю Авторитетности (N=20)
|
Места испытуемых |
Группа 1: 0 выборов (n1=5) |
Группа 2: 1 выбор (n2=5) |
Группа 3: 2-3 выбора (n3=5) |
Группа 47: |
|||
|
Индивидуальные значения |
Si |
Индивидуальные значения |
Si |
Индивидуальные значения |
Si |
Индивидуальные значения |
|
|
1 2 3 4 5 |
2 4 5 5 5 |
(15) (14) (11) (11) (11) |
4 5 6 6 7 |
(10) (8) (7) (7) (4) |
5 5 6 7 7 |
(5) (5) (5) (4) (4) |
7 8 8 9 9 |
|
Суммы |
(62) |
(36) |
(23) |
После того, как
все индивидуальные значения расположены
в порядке возрастания, легко подсчитать,
сколько значений справа превышают
данное значение слева. Начнем с крайнего
левого столбца. Значение «2» превышают
все 15 значений из трех правых столбцов;
значение «4» — 14 значений из трех
правых столбцов; значение «5»
превышают 11 значений из трех правых
столбцов. Полученные количества
«превышений» запишем в скобках
слева от каждого индивидуального
значения, как это сделано в Табл. 2.8.
Расчет для второго
столбца производим по тому же принципу.
Мы видим, что значение «4» превышают
все 10 значений из оставшихся столбцов
справа; значение «5» — 8 значений из
столбцов справа и т.д.
Сумма
всех чисел в скобках (Si)
составит величину А, которую нам нужно
будет подставить в формулу для подсчета
критерия S.
Однако вначале определим максимально
возможное значение А, которое мы получили
бы, если бы все значения справа были
больше значений слева. Эта величина
называется величиной В и вычисляется
по формуле:
где с — количество
столбцов (групп);
п —
количество
испытуемых в каждом столбце (группе). В
данном случае:
Эмпирическое
значение критерия S
вычисляется по формуле:
S
= 2·А — В
где А
— сумма всех «превышений» по всем
значениям;
В —
максимально возможное количество всех
«превышений».
В
данном
случае:
По
Табл. III
Приложения 1 определяем критические
значения S
для с=4, n=5:
Построим «ось
значимости».
Мы
помним, что критерий S
построен на подсчете количества
превышающих значений. Чем это количество
больше, тем более достоверные различия
мы сможем констатировать. Поэтому «зона
значимости» простирается вправо,
в область более высоких значений, а
«зона незначимости» — влево, в
область более низких значений.
Sэмп>Sкp.
(p
≤0,01)
Ответ:
H0
отвергается. Принимается H1.
Тенденция повышения значений по шкале
Авторитетности при переходе от группы
к группе не случайна (р<0,01).
Отвечая
на вопрос задачи, мы можем сказать, что
группы с разным статусом различаются
по показателю Авторитетности,
определявшемуся независимо от
социометрической процедуры. Критерий
S
позволяет указать на тенденцию этих
изменении: с ростом статуса растут и
показатели по шкале Авторитетности.
Однако мы имеем дело здесь, конечно же,
не с причинно-следственными связями, а
с сопряженными изменениями двух
признаков. Возможно, оба они изменяются
под влиянием одних и тех же общих
факторов, например, последовательно
проявляющейся в поведении привычки
к лидерству, внушающей способности
или «харизмы».
Теперь
мы можем суммировать все сказанное,
алгоритмизировав процесс подсчета
критерия S.