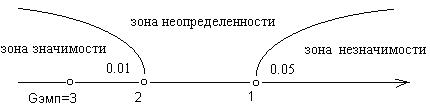Постановка
задачи.
Двухвыборочный
вариант.
Имеются две выборки
одинакового объема. Известно, что каждое
-ое
наблюдение
в 1-ой выборке зависит (в вероятностном
смысле) от соответствующего
-ого
наблюдения
во второй выборке. Распределение выборок
неизвестно. Требуется проверить гипотезу
однородности выборок.
Одновыборочный
вариант. Имеется
одна выборка. Требуется проверить
гипотезу, что некоторое фиксированное
событие происходит чаще, чем противоположное
к этому событию утверждение (например,
лечение чаще приводит к выздоровлению).
Теоретические
основы.
См.
стр. 40-42 пособия [4].
Вычисления.
При
малых значениях
критический уровень значимости может
быть вычислен с использованием простого
калькулятора. Например, если в эксперименте
наблюдалось
в
испытаниях, то критический уровень
значимости можно вычислить так:
|
m |
8 |
9 |
10 |
Сумма |
210 |
|
|
|
45 |
10 |
1 |
56 |
1024 |
56/1024≈ |
Пакет
Excel
имеет встроенную функцию БИНОМРАСП
(см. стр. 74), которая позволяет вычислять
вероятность
для биномиального распределения. Нам
необходима вероятность противоположного
события, причем значениеm
должно быть учтено при вычислении этой
вероятности. Таким образом, для вычисления
следует использовать функцию
=1-БИНОМРАСП(m
-1; n;
0,5; 1)
(единица
отнимается с целью учета значения m).
Пример.
Рассмотрим
данные, которые использовались для
иллюстрации одновыборочного критерия
Стьюдента.
|
A |
B |
C |
D |
E |
F |
|
|
1 |
До |
После |
Эффект |
|||
|
2 |
162,8 |
139 |
1 |
Число n |
10 |
|
|
3 |
186,9 |
189 |
0 |
Число |
8 |
|
|
4 |
167,2 |
162 |
1 |
|||
|
5 |
166,5 |
168,6 |
0 |
Уровень |
||
|
6 |
173 |
164,9 |
1 |
|
0,055 |
|
|
7 |
164,1 |
137,9 |
1 |
|||
|
8 |
158,3 |
121,7 |
1 |
Наличие |
||
|
9 |
168,4 |
129,9 |
1 |
слабо |
||
|
10 |
174,8 |
160,5 |
1 |
Вывод: способствует |
||
|
11 |
167,4 |
155,3 |
1 |
Порядок
вычислений.
-
В
столбце С
указать наличие эффекта для каждой
пары данных; -
в
ячейке F2
вычислить количество пар данных; -
в
ячейке F3
подсчитать число пар с наличием эффекта; -
в
ячейке F6
вычислить критический уровень значимости
-
=1-БИНОМРАСП(F3-1;
F2;
0,5; 1)
сделать
вывод о степени влиянии лечения на
артериальное давление.
Замечание
1. Проведенные
вычисления можно разместить на том же
листе, где строился одновыборочный
критерий Стьюдента.
Замечание
2. Если для
этих данных построить нижнюю
95%-доверительную границу для вероятности
эффекта (см. Задание 13), то получим
,
что говорит в пользу гипотезы, поскольку
интервал
не попадает полностью в область
альтернативы
(см. способ проверки гипотезы, основанный
на доверительной границе, описанный в
[4]). Если же построить 90%-ю границу, то
получим
,
свидетельствующее в пользу альтернативы.
Это объясняет тот странный вывод, что
сделан нами по результатам статистической
обработки.
Замечание
3. Описанную
схему можно применять также для проверки
гипотезы о вероятности “успеха” при
биномиальных испытаниях – одновыборочный
вариант критерия. Это связано с тем, что
при применении критерия знаков вывод
основывается исключительно на количестве
положительных эффектов и не зависит от
того, как это количество было подсчитано.
Например,
если бы перед исследователем стояла
задача окончательного излечения больных
гипертонией, то для представленных
данных мы имели бы лишь один положительный
эффект:
.
В этом случае
=1-БИНОМРАСП(0;
10; 0,5; 1)=0,999.
То
есть, несколько преждевременно говорить,
что лечение приводит к выздоровлению.
В
качестве другого примера
рассмотрим ситуацию, когда при составлении
договора купли-продажи заказчиком была
оговорена верхняя граница в 8% для доли
бракованной продукции. При поступлении
товара заказчик проводит контрольные
измерения n
единиц продукции. По результатам
испытаний требуется проверить гипотезу
(опять же гипотеза противоположна
ожиданиям). Все вычисления в данном
случае будут аналогичны вышеприведенным.
Единственное отличие возникнет при
нахождении критического уровня значимости
– здесь нужно, во-первых, вычислять не
функцию надежности, а функцию распределения
биномиального закона (объясните
самостоятельно), и, во-вторых, заменить
граничное значение гипотезы 0,5 на
значение 0,08. Например, если среди 37
проконтролированных изделий было
обнаружено 1 некондиционное (т.е. 2,7% от
объема контроля), то критический уровень
значимости равен
=БИНОМРАСП(1;
37; 0,08; 1)=0,193.
Другими
словами, нет достаточных оснований
утверждать, что продукция удовлетворяет
требованиям заказчика (гипотеза
не отвергается). Может быть, надо провести
еще ряд контрольных замеров.
Еще
один пример
см. пособие [4] стр. 42.
Контрольные
вопросы.
-
Сформулируйте
статистическую задачу. -
Чему равна
статистика критерия знаков?-
41.
-
-
Чему
равен критический уровень значимости
критерия знаков?-
41.
-
-
Когда следует
применять критерий Стьюдента, а когда
критерий знаков?-
38, 40.
-
-
Чем,
как Вы думаете, обусловлен неоднозначный
вывод в нашем первом примере? -
Вычислите
с помощью калькулятора значение
критического уровня значимости, если
число успехов равно 6 при 9 испытаниях.-
33.
-
-
Проверьте
гипотезу о том, что вероятность рождения
мальчика равна 0,515, если среди 1000
новорожденных детей 509 оказались
мальчики.-
41-42.
-
Соседние файлы в папке Матстат
- #
- #
Содержание
- Алгоритм расчета G-критерия знаков
- Задание 6. Критерий знаков.
- G — критерий знаков
Алгоритм расчета G-критерия знаков
1. Проверить применимость критерия к данным выборкам.
2. Сформулировать гипотезы:
Н0: Преобладание типичного направления сдвига является случайным.
H1: Преобладание типичного направления сдвига не является случайным
3. Подсчитать сдвиги. Подсчитать количество нулевых реакций и исключить их из рассмотрения. В результате п уменьшится на количество нулевых реакций.
4. Определить преобладающее направление изменений. Считать сдвиги в преобладающем направлении «типичными».
Определить количество «нетипичных» сдвигов. Считать это число эмпирическим значением G критерия знаков: G эмп
5. По таблице Критические значения G-критерия знаков определить критические значения G кр. 1 для p≤ 0.05 и G кр.2 для p≤ 0.01
6. Построить ось значимости, отметить на ней G кр. 1, G кр.2 и G эмп. В соответствии с правилом принятия решения сформулировать принятую гипотезу.
7. Сделать выводы.
Психолог проводит с младшими школьниками коррекционную работу по формированию навыков внимания. Будет ли уменьшаться количество ошибок внимания у младших школьников после специальных коррекционных упражнений?
Используем G-критерия знаков.
1. Проверим применимость критерия к данным выборкам.
а) Используется порядковая, интервальная или абсолютная шкала. В данном исследовании присутствует шкала не менее, чем интервальная. Условие выполнено.
б) Число элементов в выборках должно быть равным. Условие выполнено.
в) Количество испытуемых в каждой выборке находится в интервале от 5 до 500. Количество испытуемых в выборках находится в указанном интервале. Условие выполнено.
Итак, данный критерий применим к указанным выборкам.
2. Сформулируем гипотезы:
Н0: Преобладание типичного направления сдвига в формировании навыков внимания является случайным.
H1: Преобладание типичного направления сдвига в формировании навыков внимания не является случайным
3. Подсчитаем сдвиги.
| после | ||||||||
| до | ||||||||
| сдвиг | -4 | -12 | -8 | -6 | -7 | -12 | -11 | -2 |
Нулевых сдвигов 1, исключим их из рассмотрения. Тогда объем выборки уменьшится на 1. Теперь п = 12 – 1 = 11
4. Определим типичные и нетипичные сдвиги.
Положительных сдвигов – 3
Отрицательных сдвигов – 8
Так как отрицательных сдвигов больше, чем положительных, то отрицательный сдвиг является типичным, а положительный – нетипичный. Тогда G эмп = 3
5. По таблице Критические значения G-критерия знаков определим критические значения G кр. 1 для p≤ 0.05 и G кр.2 для p≤ 0.01
Так как G эмп > G кр. 1, то принимаем гипотезу Н0: преобладание типичного направления сдвига в формировании навыков внимания является случайным
7. Сделаем выводы.
Так как мы приняли гипотезу H 0, то можно утверждать, что уменьшение количества ошибок внимания у младших школьников после специальных коррекционных упражнений было случайным.
Т — критерий Вилкоксона
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник
Задание 6. Критерий знаков.
Двухвыборочный вариант. Имеются две выборки 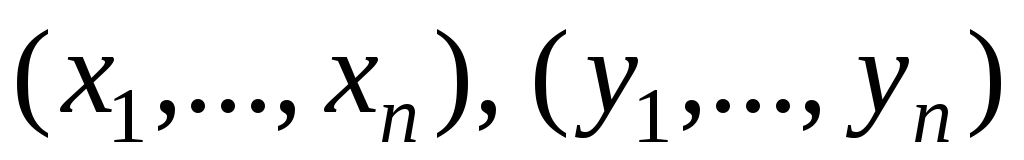одинакового объема. Известно, что каждое-ое наблюдениев 1-ой выборке зависит (в вероятностном смысле) от соответствующего-ого наблюденияво второй выборке. Распределение выборок неизвестно. Требуется проверить гипотезу однородности выборок.
Одновыборочный вариант. Имеется одна выборка. Требуется проверить гипотезу, что некоторое фиксированное событие происходит чаще, чем противоположное к этому событию утверждение (например, лечение чаще приводит к выздоровлению).
См. стр. 40-42 пособия [4].
При малых значениях критический уровень значимости может быть вычислен с использованием простого калькулятора. Например, если в эксперименте наблюдалосьв испытаниях, то критический уровень значимости можно вычислить так:
Пакет Excel имеет встроенную функцию БИНОМРАСП (см. стр. 74), которая позволяет вычислять вероятность для биномиального распределения. Нам необходима вероятность противоположного события, причем значениеm должно быть учтено при вычислении этой вероятности. Таким образом, для вычисления следует использовать функцию
(единица отнимается с целью учета значения m).
Рассмотрим данные, которые использовались для иллюстрации одновыборочного критерия Стьюдента.
Число наблюдений n
Число успехов m
=
Вывод: по-видимому, препарат
способствует уменьшению давления. Для уточнения необходимо провести дополнительное исследование.
В столбце С указать наличие эффекта для каждой пары данных;
в ячейке F2 вычислить количество пар данных;
в ячейке F3 подсчитать число пар с наличием эффекта;
в ячейке F6 вычислить критический уровень значимости
=1-БИНОМРАСП(F3-1; F2; 0,5; 1)
сделать вывод о степени влиянии лечения на артериальное давление.
Замечание 1. Проведенные вычисления можно разместить на том же листе, где строился одновыборочный критерий Стьюдента.
Замечание 2. Если для этих данных построить нижнюю 95%-доверительную границу для вероятности эффекта (см. Задание 13), то получим , что говорит в пользу гипотезы, поскольку интервалне попадает полностью в область альтернативы(см. способ проверки гипотезы, основанный на доверительной границе, описанный в [4]). Если же построить 90%-ю границу, то получим, свидетельствующее в пользу альтернативы. Это объясняет тот странный вывод, что сделан нами по результатам статистической обработки.
Замечание 3. Описанную схему можно применять также для проверки гипотезы о вероятности “успеха” при биномиальных испытаниях – одновыборочный вариант критерия. Это связано с тем, что при применении критерия знаков вывод основывается исключительно на количестве положительных эффектов и не зависит от того, как это количество было подсчитано.
Например, если бы перед исследователем стояла задача окончательного излечения больных гипертонией, то для представленных данных мы имели бы лишь один положительный эффект: . В этом случае
=1-БИНОМРАСП(0; 10; 0,5; 1)=0,999.
То есть, несколько преждевременно говорить, что лечение приводит к выздоровлению.
В качестве другого примера рассмотрим ситуацию, когда при составлении договора купли-продажи заказчиком была оговорена верхняя граница в 8% для доли бракованной продукции. При поступлении товара заказчик проводит контрольные измерения n единиц продукции. По результатам испытаний требуется проверить гипотезу (опять же гипотеза противоположна ожиданиям). Все вычисления в данном случае будут аналогичны вышеприведенным. Единственное отличие возникнет при нахождении критического уровня значимости – здесь нужно, во-первых, вычислять не функцию надежности, а функцию распределения биномиального закона (объясните самостоятельно), и, во-вторых, заменить граничное значение гипотезы 0,5 на значение 0,08. Например, если среди 37 проконтролированных изделий было обнаружено 1 некондиционное (т.е. 2,7% от объема контроля), то критический уровень значимости равен
=БИНОМРАСП(1; 37; 0,08; 1)=0,193.
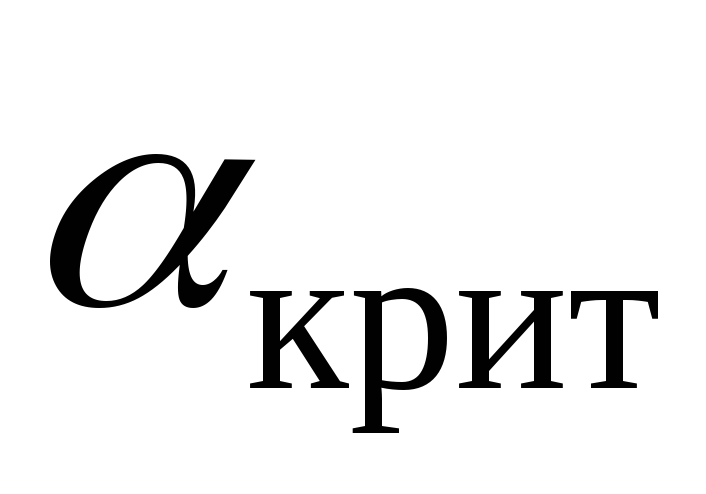
Другими словами, нет достаточных оснований утверждать, что продукция удовлетворяет требованиям заказчика (гипотеза не отвергается). Может быть, надо провести еще ряд контрольных замеров.
Еще один пример см. пособие [4] стр. 42.
Сформулируйте статистическую задачу.
Чему равна статистика критерия знаков?
Чему равен критический уровень значимости критерия знаков?
Когда следует применять критерий Стьюдента, а когда критерий знаков?
Чем, как Вы думаете, обусловлен неоднозначный вывод в нашем первом примере?
Вычислите с помощью калькулятора значение критического уровня значимости, если число успехов равно 6 при 9 испытаниях.
Проверьте гипотезу о том, что вероятность рождения мальчика равна 0,515, если среди 1000 новорожденных детей 509 оказались мальчики.
Источник
G — критерий знаков
Предназначен для установления общего направления сдвига изучаемого признака (сдвигом называют разность между вторым и первым измерениями). Критерий знаков позволяет установить, в какую сторону в выборке в целом произошли изменения (произошло увеличение значений, уменьшение или значения не изменились).
Суть метода: Если попарно сравниваемые значения двух выборок существенно не отличаются друг от друга, то число «+» и «-» будет примерно одинаковым. Если заметно преобладают «+» или «-», это указывает на положительное или отрицательное действие фактора.
Критерий знаков может быть применим не только к количественным признакам, но и к качественным, имеющим не менее трех градаций.
Чтобы обработать экспериментальные данные с помощью критерия знаков, в таблицу выписывают результаты первого и второго измерений. Первое измерение проводится до действия фактора на изучаемую величину, второе измерение – после воздействия фактора. В столбце, обозначенном «сдвиг», указывается величина и направление сдвига (в случае количественного признака) или только направление (в случае качественного признака).
Примеры таблиц для количественного и качественного признаков:
| № измерения | Х («до») | Y («после») | сдвиг | № измерения | Х («до») | Y ( «после») | сдвиг |
| 1
После заполнения таблицы подсчитывается общее число положительных и отрицательных сдвигов и вводятся следующие понятия:
По таблице критических точек находим значение Gкр(α;n’) , где n’ — объем выборки за вычетом нулевых сдвигов. Осуществляем выбор гипотезы, учитывая, что критерий знаков является левосторонним. Если Gн Gк, то нет оснований отвергать гипотезу Н0; нетипичных сдвигов много, преобладание типичного сдвига является случайным. Ограничения критерия:
Источник Adblock |
17 авг. 2022 г.
читать 2 мин
Критерий знака — это непараметрический критерий, который используется для определения того, равна ли медиана генеральной совокупности некоторому значению.
В следующем пошаговом примере показано, как выполнить проверку знака в Excel.
Шаг 1: введите данные
Предположим, завод-изготовитель заявляет, что выпускает изделия весом 50 фунтов. Чтобы проверить это, инспектор выходит на завод и случайным образом измеряет вес 20 штук.
Затем он вводит следующие веса для каждого виджета:
Мы можем выполнить знаковый тест, чтобы определить, значительно ли средний вес отличается от 50 фунтов.
Шаг 2: Рассчитайте знаки
Далее рассчитаем признаки каждого виджета по следующим правилам:
- Если вес виджета меньше 50, присвойте ему знак -1
- Если вес виджета равен 50, присвоить ему знак 0
- Если вес виджета больше 50, присвойте ему знак 1
Для этого мы будем использовать следующую формулу в Excel:
Шаг 3: Рассчитайте P-значение теста
Наконец, мы будем использовать следующие формулы для расчета общего количества положительных и отрицательных знаков и расчета соответствующего значения p теста знака:
Знаковый тест использует следующие нулевые и альтернативные гипотезы:
- H 0 : Средний вес населения = 20 фунтов.
- H A : средний вес населения ≠ 20 фунтов.
Поскольку p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств того, что истинный средний вес произведенных изделий отличается от 50 фунтов.
Примечание. В этом примере мы умножили p-значение на два, так как провели двусторонний тест. Мы также использовали меньшее из отрицательных и положительных значений, поскольку мы использовали двусторонний тест.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные статистические тесты в Excel:
Как провести одновыборочный t-тест в Excel
Как провести двухвыборочный t-тест в Excel
Как провести t-тест для парных выборок в Excel
Как выполнить тест на нормальность в Excel
Написано
Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Допустим мы сравниваем между собой уровень тревожности подростков до и после тренинга уверенности в себе.
Шаг 1. Запишем значения в таблицу.
Шаг 2. Рассчитаем разность значений. Для данного случае типичным сдвигом будет считаться сдвиг в отрицательную сторону (7 значений, красный цвет заливки), а нетипичным в положительную сторону (3 значения, зеленый цвет заливки).
| № | Уровень тревожности (до тренинга) | Уровень тревожности (после тренинга) | Шаг 2: Разность (после-до) |
| 1 | 15 | 14 | -1 |
| 2 | 14 | 11 | -3 |
| 3 | 16 | 17 | 1 |
| 4 | 18 | 19 | 1 |
| 5 | 21 | 20 | -1 |
| 6 | 21 | 18 | -3 |
| 7 | 20 | 15 | -5 |
| 8 | 15 | 17 | 2 |
| 9 | 17 | 14 | -3 |
| 10 | 13 | 12 | -1 |
Шаг 3. Найдем G эмпирическое как сумма нетипичных сдвигов:
G-эмп = 3
Шаг 4. Используя таблицу критических значений определим G-критическое:
4.1. Находим количество человек в выборке. n=10
4.2. Определяем G-критическое справа от значения количества человек в выборке. для p<0,05 G=1; для p<0,01 G=0
Шаг 5. Сравниваем G-критическо и G-эмпирическое.
G-эмп = 3 > G-кр = 1
Шаг 6. Делаем выводы.
В Excel всего 3 подстановочных символа (звездочка, вопросительный знак и тильда), и с их помощью можно многое сделать.
В этом уроке я покажу вам четыре примера, в которых эти подстановочные знаки Excel — настоящие спасители.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Процент рассчитывается путём деления, где в числителе дроби находится искомая часть, а в знаменателе целое, и далее результат умножается на 100. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Я хочу показать Вам некоторые интересные формулы для работы с данными, представленными в виде процентов. Это, например, формула вычисления процентного прироста, формула для вычисления процента от общей суммы и ещё некоторые формулы, на которые стоит обратить внимание.
Как посчитать размах в excel
- * (звездочка) — Он представляет собой любое количество символов. Например, Ex * может означать Excel, Excel, Пример, Эксперт и т. Д.
- ? (вопросительный знак) — Он представляет собой один-единственный персонаж. Например, Tr? Mp может означать Трампа или Бродяги.
- ~ (тильда) — Он используется для обозначения подстановочного знака (~, *,?) В тексте. Например, допустим, вы хотите найти точную фразу Excel * в списке. Если вы используете Excel * в качестве строки поиска, он даст вам любое слово, в начале которого есть Excel, за которым следует любое количество символов (например, Excel, Excels, Excellent). Чтобы специально искать excel *, нам нужно использовать ~. Таким образом, наша строка поиска будет выглядеть следующим образом: excel ~ *. Здесь наличие ~ гарантирует, что excel прочитает следующий символ как есть, а не как подстановочный знак.
Подстановочные знаки в Excel также можно использовать для поиска и замены текстовых значений в инструменте «Найти и заменить» (комбинация клавиш Ctrl + F для поиска и Ctrl + H для замены).
Как посчитать для нескольких ячеек
Если нужно посчитать среднее значение в Excel для большой группы ячеек, можно использовать «Мастер функций». Он позволяет считать среднее значение в Excel с помощью озвученной выше формулы, но сам процесс проходит немного проще. Алгоритм действий следующий:
Если нужно высчитать среднее значение в Excel от цифр, которые расположены в разных ячейках, сделайте рассмотренные выше действия, но в графе «Число 2». Действовать нужно до тех пор, пока все группы не окажутся выделенными. Результат указывается в той ячейке, которая была выделена перед входом в «Мастер функций».
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
И даже, если проценты никогда не были Вашим любимым разделом математики, владея этими формулами и приёмами, Вы заставите Excel проделать за Вас всю работу. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Эти способы помогут Вам в вычислении процентов в Excel. И даже, если проценты никогда не были Вашим любимым разделом математики, владея этими формулами и приёмами, Вы заставите Excel проделать за Вас всю работу.
П.12. Решение прикладных задач средствами EXCEL. УМК Математ основы пс
- Выделите группу числе в столбце, для которых нужно рассчитать среднее значение в Экселе.
- Перейдите в раздел «Главная».
- Найдите значок «∑» на рабочей панели в блоке редактирования.
- В выпадающем списке жмите на «Среднее».
- Получите результат, который выводится в качестве усредненного арифметического набора чисел.
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
С определенным текстом или значением
Функция СЧЁТЕСЛИ – позволяет рассчитать количество блоков, которые соответствуют заданному критерию. В качестве аргумента прописывается диапазон – В2:В13 , и через «;» указывается критерий – «>5» .
Например, есть таблица, в которой указано, сколько килограмм определенного товара было продано за день. Посчитаем, сколько товаров было продано весом больше 5 килограмм. Для этого нужно посчитать сколько блоков в столбце Вес, где значение больше пяти. Функция будет выглядеть следующим образом: =СЧЁТЕСЛИ(В2:В13;»>5″) . Она рассчитает количество блоков, содержимое в которых больше пяти.
Для того чтобы растянуть функцию на другие блоки, и скажем поменять условия, необходимо закрепить выбранный диапазон. Сделать Вы это сможете, используя абсолютные ссылки в Excel.
– количество ячеек с отрицательными значениями: =СЧЁТЕСЛИ(В2:В13;» <0″) ;
– количество блоков, содержимое в которых больше (меньше) чем в А10 (для примера): =СЧЁТЕСЛИ(В2:В13;»>»&A10) ;
– ячейки, значение в которых больше 0: =СЧЁТЕСЛИ(В2:В13;»>0″) ;
– непустые блоки из выделенного диапазона: =СЧЁТЕСЛИ(В2:В13;»») .
Применять функцию СЧЁТЕСЛИ можно и для расчета ячеек в Excel, содержащих текст. Например, рассчитаем, сколько в таблице фруктов. Выделим область и в качестве критерия укажем «фрукт». Будут посчитаны все блоки, с данным словом. Можно не писать текст, а просто выделить прямоугольник, который его содержит, например С2 .
Для формулы СЧЁТЕСЛИ регистр не имеет значения, будут подсчитаны ячейки содержащие текст «Фрукт» и «фрукт».
В качестве критерия также можно использовать специальные символы: «*» и «?» . Они применяются только к тексту.
Посчитаем сколько товаров начинается на букву А: «А*» . Если указать «абрикос*» , то учтутся все товары, которые начинаются с «абрикос»: абрикосовый сок, абрикосовое варенье, абрикосовый пирог.
Символом «?» можно заменить любую букву в слове. Написав в критерии «ф?укт» – учтутся слова фрукт, фуукт, фыукт.
Чтобы посчитать слова в ячейках, которые состоят из определенного количества букв, поставьте знаки вопросов подряд. Для подсчета товаров, в названии которых 5 букв, поставим в качестве критерия «. » .
Если в качестве критерия поставить звездочку, из выбранного диапазона будут посчитаны все блоки, содержащие текст.
Подстановочные знаки Excel — почему вы их не используете?
Как видно из сказанного, посчитать среднее значение в Excel можно разными способами — через формулы, путем ввода ручные или с помощью мастера. При этом в некоторых случаях может потребоваться применение дополнительных функций.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
В такой ситуации для расчета берутся лишь те цифры из диапазона, соответствующего определенному условию, к примеру, если параметр больше или меньше определенного числа. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
С наступлением курортного сезона Вы замечаете определённые изменения в Ваших привычных еженедельных статьях расходов. Возможно, Вы захотите ввести некоторые дополнительные корректировки к расчёту своих лимитов на расходы.
Как посчитать проценты в (Excel): как посчитать разницу или средневзвешенную наценку, ее значение и динамика повышения цены
Примечание: если вы вручную вводите в ячейке числовое значение и после него ставите знак %, то Excel применяет к данной ячейке процентный формат и воспринимает это число как его сотую часть. Например, если в ячейку ввести 18%, то для расчётов Excel будет использовать значение 0,18.