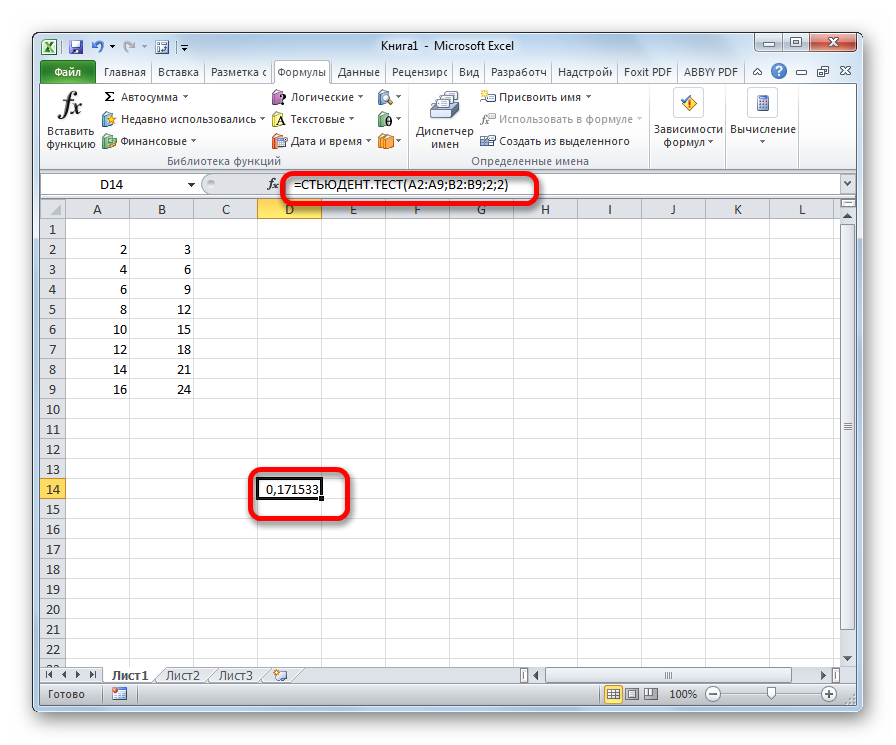
Для того, чтобы рассчитать t-критерий Стьюдента (для зависимых и для независимых выборок) в Excell необходимо сделать следующие шаги:
1.Вносим значения для двух переменных в таблицу (Например Переменная 1 и Переменная 2)
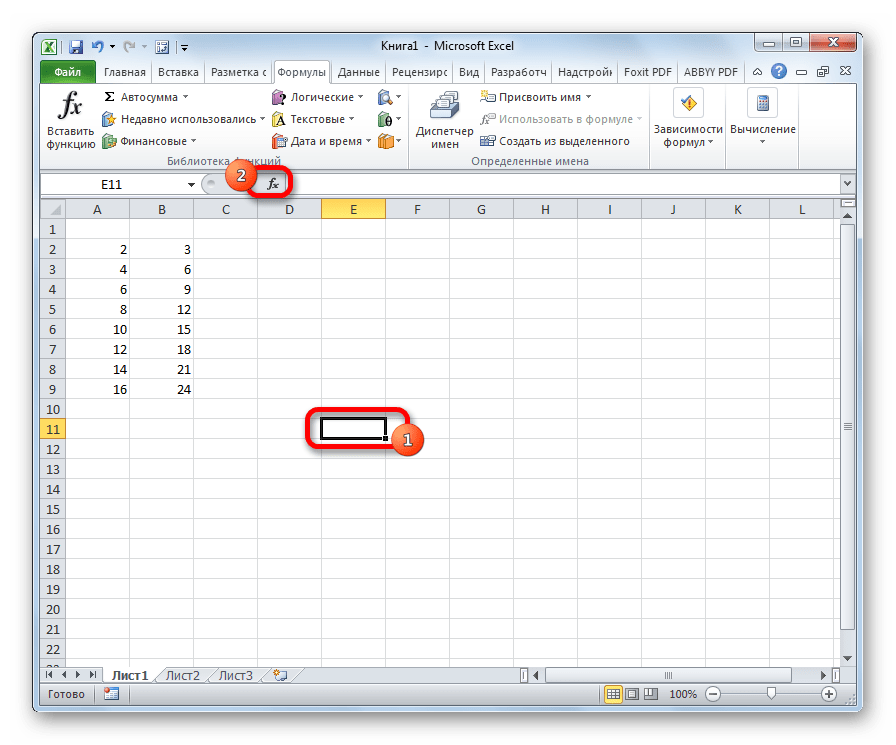
2. Ставим курсор в пустую ячейку
3. На панеле инструментов нажимаем кнопку fx (вставить формулу)
4. В открывшемся окне «Мастер функций» в поле «Категории» выбираем Полный алфавитный перечень
5. Затем в поле «Выберите функцию» находим функцию TTECT, которая возвращает вероятность, соответствующую критерию Стьюдента.
5.1. Нажимаем Ок
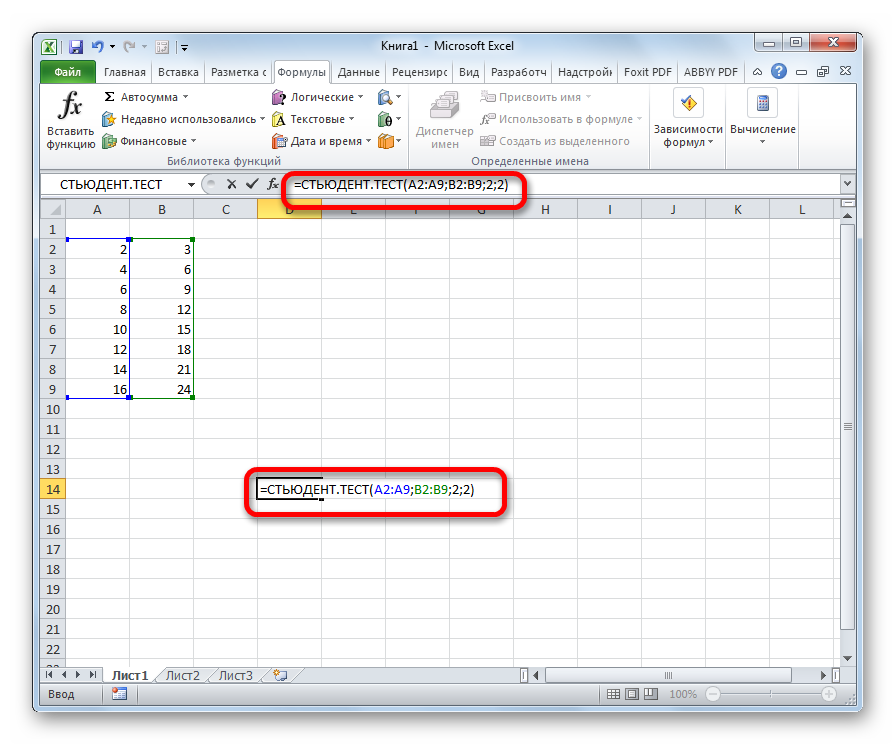
6. В открывшемся окне «Аргументы функции» в поле Массив1 вносим номера ячеек, содержащие значения Переменной 1, в поле Массив2 вносим номера ячеек, содержащие значения Переменной2.
7. В поле «Хвосты» пишем 2 (критерий будет рассчитываться используя двустороннее распределение, как и в SPSS); либо 1 (критерий будет рассчитываться используя одностороннее распределение).
Важно!
8. В поле «Тип» пишем 1 (рассчитывается, если выборки зависимые); либо 2 или 3 (если выборки независимые).
9. Нажимаем Ок
10. Смотрим получившийся результат
Содержание
- Определение термина
- Расчет показателя в Excel
- Способ 1: Мастер функций
- Способ 2: работа со вкладкой «Формулы»
- Способ 3: ручной ввод
- Вопросы и ответы
Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Определение термина
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
- Строим таблицу с двумя рядами переменных.
- Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.
- После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».
- Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
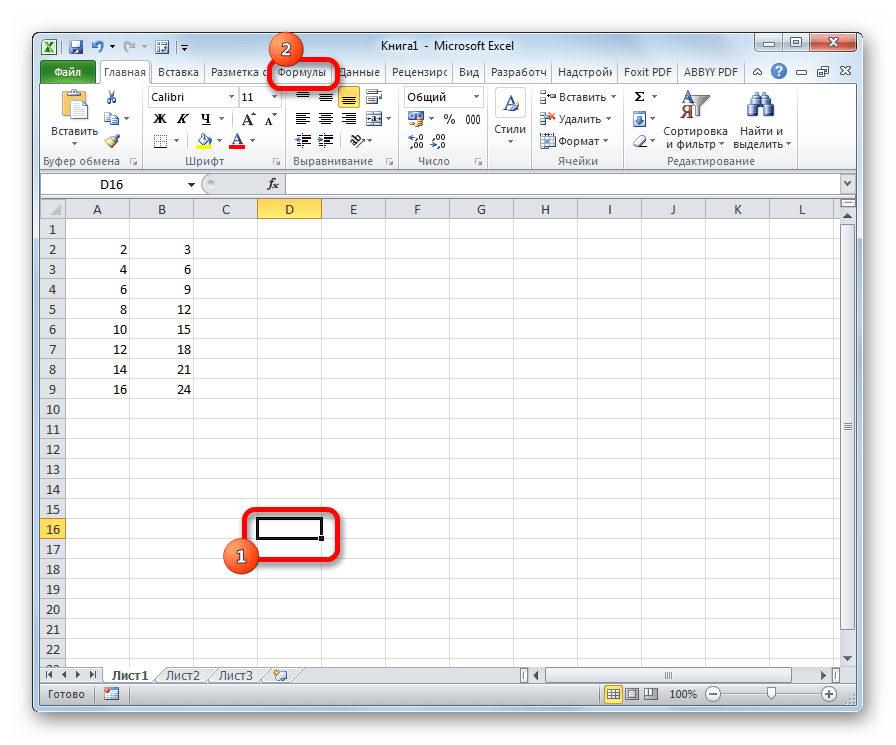
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».
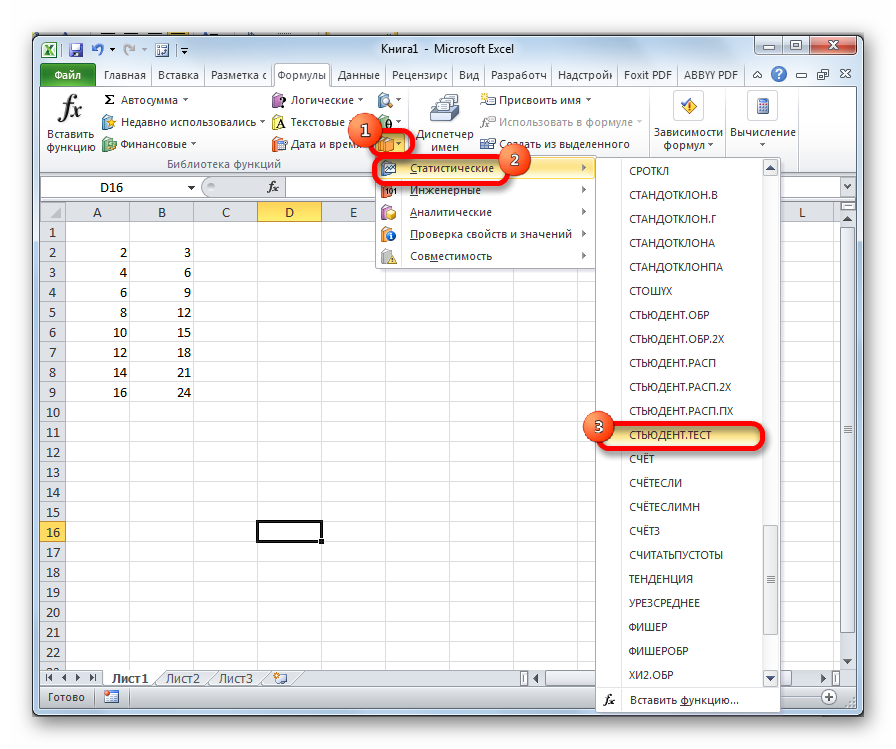
- Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».
- Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
Способ 3: ручной ввод
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.
После того, как данные введены, жмем кнопку Enter для вывода результата на экран.
Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Еще статьи по данной теме:
Помогла ли Вам статья?
Критерий Стьюдента – обобщенное название группы статистических тестов (обычно перед словом “критерий” добавляется латинская буква “t”). Чаще всего он применяется для проверки равенства средних значений в двух выборках. Давайте посмотрим, как рассчитать данный критерий в программе Excel с помощью специальной функции.
-
Расчет t-критерия Стьюдента
- Метод 1: пользуемся Мастером функций
- Метод 2: вставляем функцию через “Формулы”
- Метод 3: ручной ввод формулы
-
Заключение
Для того, чтобы выполнить соответствующие расчеты, понадобится функция “СТЬЮДЕНТ.ТЕСТ”, в ранних версиях Excel (2007 и старше) – “ТТЕСТ”, которая есть и в современных редакциях для сохранения совместимости со старыми документам.
Использовать функцию можно по-разному. Давайте разберем каждый вариант отдельно на примере таблицы с двумя рядами-столбцами числовых значений.
Метод 1: пользуемся Мастером функций
Этот способ хорош тем, что не нужно запоминать формулу функции (список ее аргументов). Итак, алгоритм действий следующий:
- Встаем в любую свободную ячейку, затем щелкаем по значку “Вставить функцию” слева от строки формул.
- В открывшемся окне Мастера функций выбираем категорию “Полный алфавитный перечень”, в списке ниже находим оператор “СТЬЮДЕНТ.ТЕСТ”, отмечаем его и щелкаем OK.
- На экране отобразится окно, в котором заполняем аргументы функции, после чего нажимаем OK:
- “Массив1” и “Массив2” – указываем диапазоны ячеек, содержащие ряды чисел (в нашем случае это “A2:A7” и “B2:B7”). Мы можем сделать это вручную, введя координаты с клавиатуры, или просто выделяем нужные элементы в самой таблице.
- “Хвосты” – пишем цифру “1”, если требуется выполнить расчет методом одностороннего распределения, или “2” – для двухстороннего.
- “Тип” – в этом поле указываем: “1” – если выборка состоит из зависимых величин; “2” – из независимых; “3” – из независимых величин с неравным отклонением.
- В результате в нашей ячейке с функцией появится рассчитанное значение критерия.
Метод 2: вставляем функцию через “Формулы”
- Переключаемся во вкладку “Формулы”, где также представлена кнопка “Вставить функцию”, которая нам и нужна.
- В результате откроется Мастер функций, дальнейшие действия в котором аналогичны описанным выше.
Через вкладку “Формулы” функцию “СТЬЮДЕНТ.ТЕСТ” можно запустить по-другому:
- В группе инструментов “Библиотека функций” жмем по значку “Другие функции”, после чего раскроется список, в котором выбираем раздел “Статистические”. Пролистав предложенный перечень мы сможем найти нужный нам оператор.
- На экране отобразится окно для заполнения аргументов, с которым мы уже познакомились ранее.
Метод 3: ручной ввод формулы
Опытные пользователи могут обходиться без Мастера функций и в требуемой ячейке сразу вводить формулу со ссылками на нужные диапазоны данных и прочими параметрами. Синтаксис функции в общем виде выглядит так:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Каждый из аргументов мы разобрали в первом разделе публикации. Все, что остается сделать после набора формулы – нажать Enter для выполнения расчета.
Заключение
Таким образом, рассчитать t-критерий Стьюдента в программе Excel можно с помощью специальной функции, которую можно запустить разными способами. Также у пользователя есть возможность сразу ввести формулу функции в нужной ячейке, однако в этом случае придется запоминать ее синтаксис, что может быть хлопотно из-за того, что применяется она не так часто.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает вероятность, соответствующую t-тесту Стьюдента. Функция СТЬЮДЕНТ.ТЕСТ позволяет определить вероятность того, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.
Синтаксис
СТЬЮДЕНТ.ТЕСТ(массив1;массив2;хвосты;тип)
Аргументы функции СТЬЮДЕНТ.ТЕСТ описаны ниже.
-
Массив1 Обязательный. Первый набор данных.
-
Массив2 Обязательный. Второй набор данных.
-
Хвосты Обязательный. Число хвостов распределения. Если значение «хвосты» = 1, функция СТЬЮДЕНТ.ТЕСТ возвращает одностороннее распределение. Если значение «хвосты» = 2, функция СТЬЮДЕНТ.ТЕСТ возвращает двустороннее распределение.
-
Тип Обязательный. Вид выполняемого t-теста.
Параметры
|
Тип |
Выполняемый тест |
|
1 |
Парный |
|
2 |
Двухвыборочный с равными дисперсиями (гомоскедастический) |
|
3 |
Двухвыборочный с неравными дисперсиями (гетероскедастический) |
Замечания
-
Если аргументы «массив1» и «массив2» имеют различное число точек данных, а «тип» = 1 (парный), то функция СТЬЮДЕНТ.ТЕСТ возвращает значение ошибки #Н/Д.
-
Аргументы «хвосты» и «тип» усекаются до целых значений.
-
Если «хвосты» или «тип» не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.
-
Если «хвосты» — любое значение, кроме 1 или 2, возвращается значение #NUM! значение ошибки #ЗНАЧ!.
-
Функция СТЬЮДЕНТ.ТЕСТ использует данные аргументов «массив1» и «массив2» для вычисления неотрицательной t-статистики. Если «хвосты» = 1, СТЬЮДЕНТ.ТЕСТ возвращает вероятность более высокого значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими к генеральной совокупности с одним и тем же средним. Значение, возвращаемое функцией СТЬЮДЕНТ.ТЕСТ в случае, когда «хвосты» = 2, вдвое больше значения, возвращаемого, когда «хвосты» = 1, и соответствует вероятности более высокого абсолютного значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими к генеральной совокупности с одним и тем же средним.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные 1 |
Данные 2 |
|
|
3 |
6 |
|
|
4 |
19 |
|
|
5 |
3 |
|
|
8 |
2 |
|
|
9 |
14 |
|
|
1 |
4 |
|
|
2 |
5 |
|
|
4 |
17 |
|
|
5 |
1 |
|
|
Формула |
Описание |
Результат |
|
=СТЬЮДЕНТ.ТЕСТ(A2:A10;B2:B10;2;1) |
Вероятность, соответствующая парному критерию Стьюдента, с двусторонним распределением |
0,196016 |
Нужна дополнительная помощь?
Рассматриваемая функция возвращает значение t, соответствующее условию P(|x|>t)=p. Здесь x является значением некоторой случайной величины с распределением Стьюдента, у которого число степеней свобод соответствует k (второй аргумент функции СТЮДРАСПОБР).
Пример 1. Определить односторонне и двустороннее t-значения для распределения Стьюдента, характеризующееся вероятностью 0,17 и числом степени свобод 16.
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Проще всего производить вычисления данного показателя через Мастер функций.
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
Этапы статистического вывода (statistic inference)
- Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
- Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
- Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
- Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
- Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.
Пример использования т-критерия Стьюдента
А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.
Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.
Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.
Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅1914 и в 2014 году x̅2014. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅1914≠x̅2014). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅1914=x̅2014), то есть о том, что все эти находки случайны, и я, по сути, не прав.
Для чего используется t-критерий Стьюдента?
t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента
В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча (Welch’s t).
При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни.
Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
f = (n1 + n2) – 2
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
- Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
- Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
Внесите исходные данные группы
Вы можете внести данные для расчета критерия Т-Стьюдента поочередно вручную или скопировать их из вашего Excel файла.
Внесите исходные данные группы
Вы можете внести данные поочередно вручную или скопировать их из вашего Excel файла.
Критические точки распределения Стьюдента
| Число степеней свободы k |
Уровень значимости α (двусторонняя критическая область) | |||||
| 0.10 | 0.05 | 0.02 | 0.01 | 0.002 | 0.001 | |
| 1 | 6.31 | 12.7 | 31.82 | 63.7 | 318.3 | 637.0 |
| 2 | 2.92 | 4.30 | 6.97 | 9.92 | 22.33 | 31.6 |
| 3 | 2.35 | 3.18 | 4.54 | 5.84 | 10.22 | 12.9 |
| 4 | 2.13 | 2.78 | 3.75 | 4.60 | 7.17 | 8.61 |
| 5 | 2.01 | 2.57 | 3.37 | 4.03 | 5.89 | 6.86 |
| 6 | 1.94 | 2.45 | 3.14 | 3.71 | 5.21 | 5.96 |
| 7 | 1.89 | 2.36 | 3.00 | 3.50 | 4.79 | 5.40 |
| 8 | 1.86 | 2.31 | 2.90 | 3.36 | 4.50 | 5.04 |
| 9 | 1.83 | 2.26 | 2.82 | 3.25 | 4.30 | 4.78 |
| 10 | 1.81 | 2.23 | 2.76 | 3.17 | 4.14 | 4.59 |
| 11 | 1.80 | 2.20 | 2.72 | 3.11 | 4.03 | 4.44 |
| 12 | 1.78 | 2.18 | 2.68 | 3.05 | 3.93 | 4.32 |
| 13 | 1.77 | 2.16 | 2.65 | 3.01 | 3.85 | 4.22 |
| 14 | 1.76 | 2.14 | 2.62 | 2.98 | 3.79 | 4.14 |
| 15 | 1.75 | 2.13 | 2.60 | 2.95 | 3.73 | 4.07 |
| 16 | 1.75 | 2.12 | 2.58 | 2.92 | 3.69 | 4.01 |
| 17 | 1.74 | 2.11 | 2.57 | 2.90 | 3.65 | 3.95 |
| 18 | 1.73 | 2.10 | 2.55 | 2.88 | 3.61 | 3.92 |
| 19 | 1.73 | 2.09 | 2.54 | 2.86 | 3.58 | 3.88 |
| 20 | 1.73 | 2.09 | 2.53 | 2.85 | 3.55 | 3.85 |
| 21 | 1.72 | 2.08 | 2.52 | 2.83 | 3.53 | 3.82 |
| 22 | 1.72 | 2.07 | 2.51 | 2.82 | 3.51 | 3.79 |
| 23 | 1.71 | 2.07 | 2.50 | 2.81 | 3.59 | 3.77 |
| 24 | 1.71 | 2.06 | 2.49 | 2.80 | 3.47 | 3.74 |
| 25 | 1.71 | 2.06 | 2.49 | 2.79 | 3.45 | 3.72 |
| 26 | 1.71 | 2.06 | 2.48 | 2.78 | 3.44 | 3.71 |
| 27 | 1.71 | 2.05 | 2.47 | 2.77 | 3.42 | 3.69 |
| 28 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 29 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 30 | 1.70 | 2.04 | 2.46 | 2.75 | 3.39 | 3.65 |
| 40 | 1.68 | 2.02 | 2.42 | 2.70 | 3.31 | 3.55 |
| 60 | 1.67 | 2.00 | 2.39 | 2.66 | 3.23 | 3.46 |
| 120 | 1.66 | 1.98 | 2.36 | 2.62 | 3.17 | 3.37 |
| ∞ | 1.64 | 1.96 | 2.33 | 2.58 | 3.09 | 3.29 |
| 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | 0.0005 | |
| Уровень значимости α (односторонняя критическая область) |
Условия применения t-критерия Стьюдента
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.

Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.

Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.

Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).

По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.

Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.

Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.

P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.

Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Источники
- https://exceltable.com/funkcii-excel/raspredeleniya-styudenta-styudraspobr
- https://lumpics.ru/calculation-student-test-in-excel/
- https://lit-review.ru/biostatistika/t-kriterijj-styudenta-za-12-minut/
- https://medstatistic.ru/methods/methods.html
- https://statpsy.ru/t-student/onlajn-raschet-kriteriya-t-styudenta-dlya-nezavisimyh-vyborok/
- https://math.semestr.ru/corel/table-student.php
- https://statanaliz.info/statistica/proverka-gipotez/raspredelenie-t-kriteriya-styudenta-dlya-proverki-gipotezy-i-rascheta-doveritelnogo-intervala-v-ms-excel/