17 авг. 2022 г.
читать 2 мин
Многие статистические тесты предполагают, что значения в наборе данных имеют нормальное распределение .
Один из самых простых способов проверить это предположение — выполнить тест Харке-Бера , который представляет собой тест согласия, который определяет, имеют ли выборочные данные асимметрию и эксцесс, соответствующие нормальному распределению.
В этом тесте используются следующие гипотезы:
H 0 : Данные нормально распределены.
H A : Данные не распределены нормально.
Тестовая статистика JB определяется как:
JB = (n/6) * (S 2 + (C 2 /4))
куда:
- n: количество наблюдений в выборке
- S: асимметрия выборки
- C: образец эксцесса
При нулевой гипотезе нормальности JB ~ X 2 (2).
Если значение p , соответствующее тестовой статистике, меньше некоторого уровня значимости (например, α = 0,05), то мы можем отклонить нулевую гипотезу и сделать вывод, что данные не распределены нормально.
В этом руководстве представлен пошаговый пример того, как выполнить тест Харке-Бера для заданного набора данных в Excel.
Шаг 1: Создайте данные
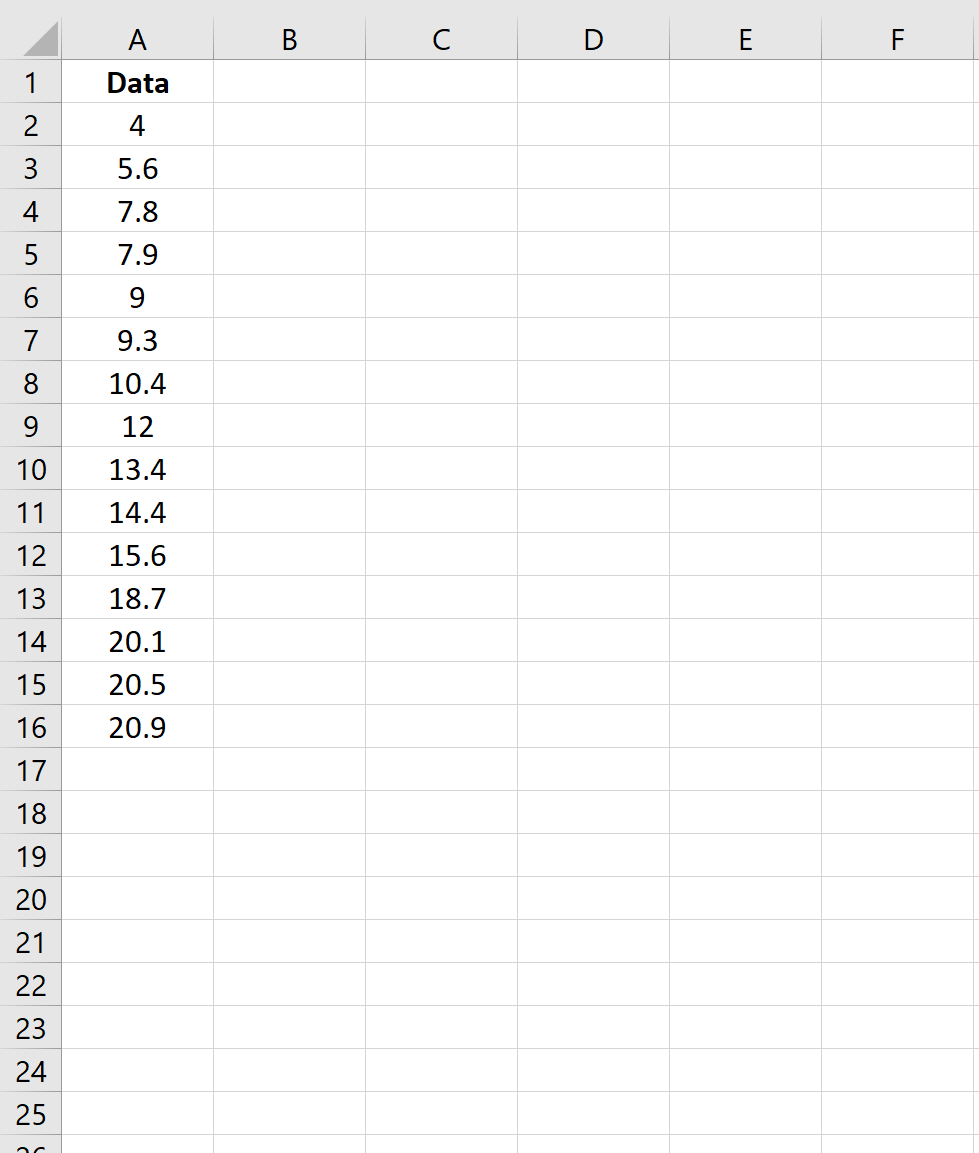
Во-первых, давайте создадим поддельный набор данных с 15 значениями:
Шаг 2: Рассчитайте тестовую статистику
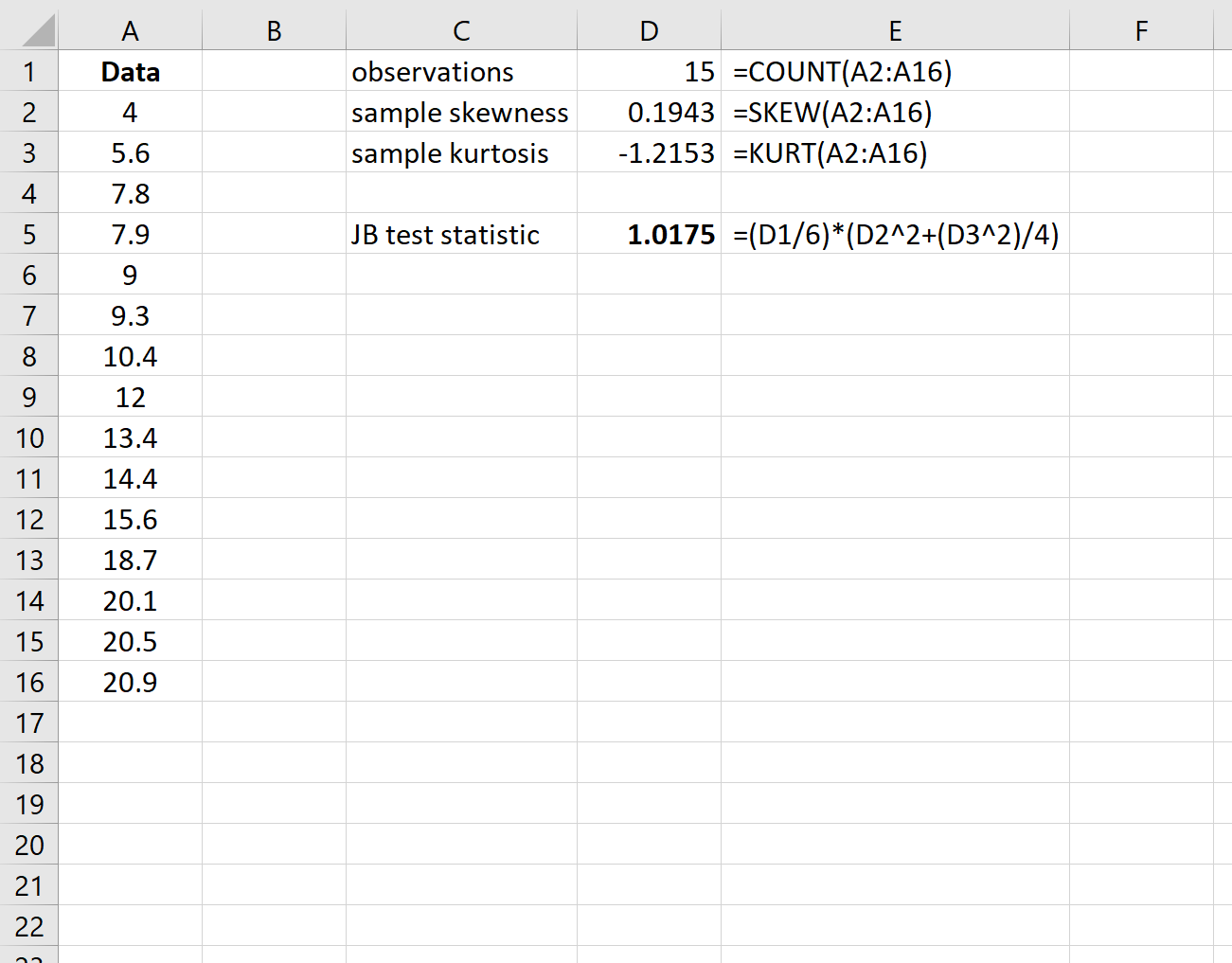
Затем рассчитайте статистику теста JB. В столбце E показаны используемые формулы:
Тестовая статистика оказывается 1,0175 .
Шаг 3: Рассчитайте P-значение
При нулевой гипотезе нормальности тестовая статистика JB следует распределению хи-квадрат с 2 степенями свободы.
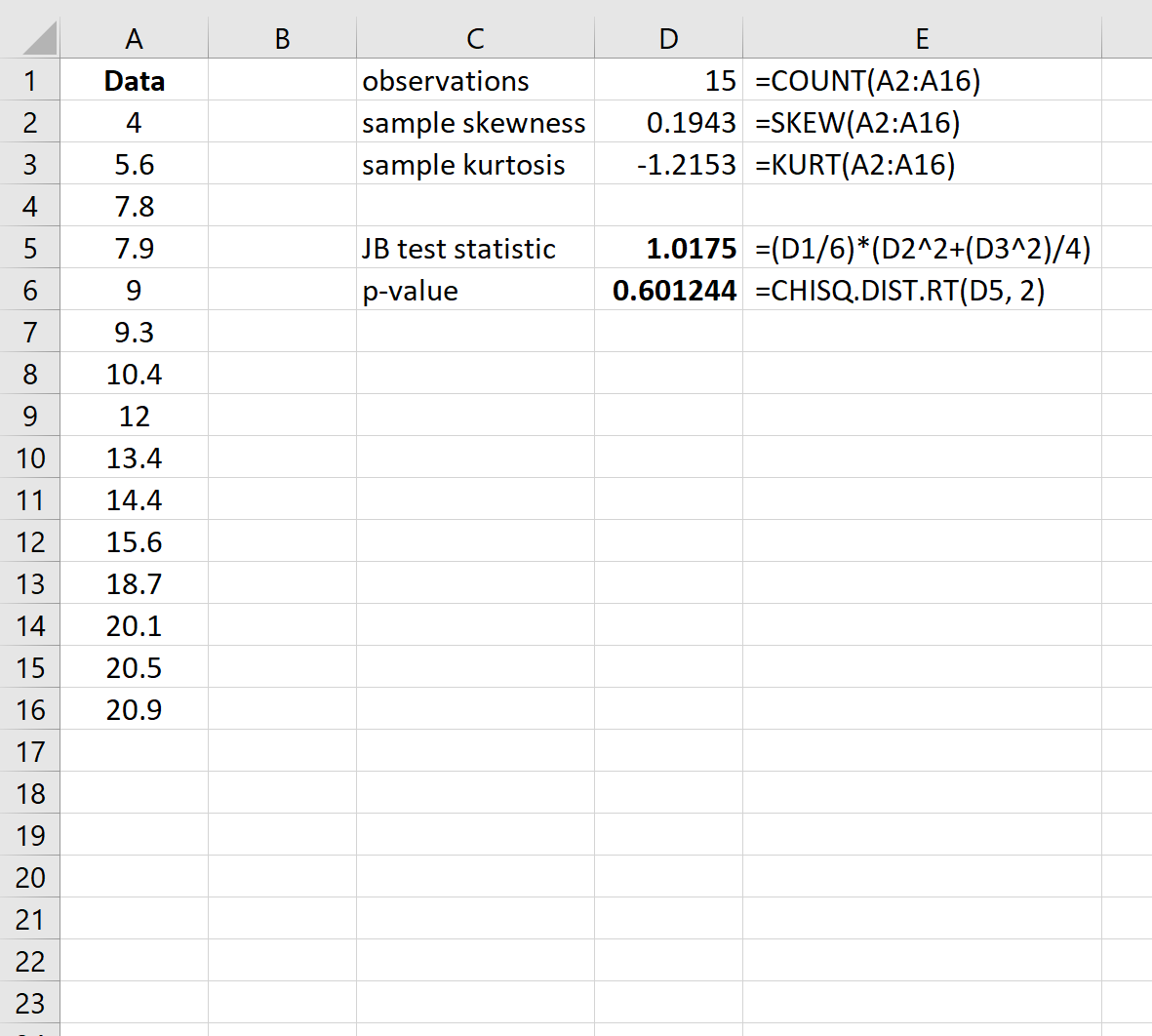
Итак, чтобы найти p-значение для теста, мы будем использовать следующую функцию в Excel: =CHISQ.DIST.RT(статистика теста JB, 2)
Значение p теста составляет 0,601244.Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств того, что набор данных не имеет нормального распределения.
Другими словами, мы можем предположить, что данные распределены нормально.
Дополнительные ресурсы
Как создать график QQ в Excel
Как выполнить критерий согласия хи-квадрат в Excel
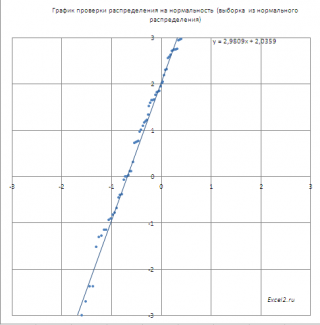
Построение графика проверки распределения на нормальность (
Normal
Probability
Plot
) является графическим методом определения соответствия значений выборки нормальному распределению.
Предположим, что имеется некий набор данных. Требуется оценить, соответствует ли данная
выборка
нормальному распределению
.
Рассмотренный ниже графический метод основан на субъективной визуальной оценке данных. Объективным же подходом является, например,
анализ степени согласия гипотетического распределения с наблюдаемыми данными
(goodness-of-fit test), который рассмотрен в статье
Проверка простых гипотез критерием Пирсона ХИ-квадрат
.
Из-за наличия неустранимой статистической ошибки выборки, присущей случайной величине, невозможно однозначно ответить на вопрос «Взята ли данная выборка из
нормального распределения
или нет». Поэтому, рассмотренный графический метод, скорее, дает ответ на вопрос «Разумно ли предположение, что оцениваемая выборка взята из
нормального распределения
»?
Рассмотрим алгоритм построения графика проверки распределения на нормальность (
Normal
Probability
Plot
)
:
-
Отсортируйте значения выборки по возрастанию
(значения выборки x
j
будут отложены по горизонтальной оси Х); -
Каждому значению x
j
выборки
поставьте в соответствие значения (j-0,5)/n, где n – количество значений в
выборке
, j –порядковый номер
значения от 1 до n. Этот массив будет содержать значения от 0,5/n до (n-0,5)/n. Таким образом, диапазон от 0 до 1 будет разбит на равномерные отрезки. Этот диапазон соответствует
вероятности наблюдения значений случайной величины
Z<=z
j
; -
Преобразуем значения массива, полученные на предыдущем шаге, с помощью
обратной функции
стандартного нормального распределения
НОРМ.СТ.ОБР()
и отложим их по вертикальной оси Y.
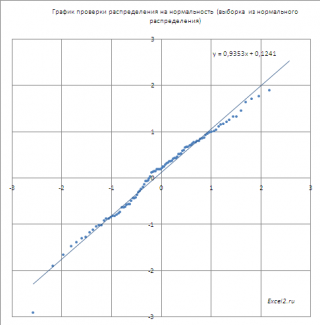
Если значения
выборки
, откладываемые по оси Х, взяты из
стандартного нормального распределения
, то на графике мы получим приблизительно прямую линию, проходящую примерно через 0 и под углом 45 градусов к оси х (если масштабы осей совпадают).
Расчеты и графики приведены в
файле примера на листе Нормальное
. О построении диаграмм см. статью
Основные типы диаграмм в MS EXCEL
.
Примечание
: Значения
выборки
в
файле примера
сгенерированы с помощью формулы
=НОРМ.СТ.ОБР(СЛЧИС())
. При перерасчете листа или нажатии клавиши
F9
происходит обновление данных в
выборке
. О генерации чисел, распределенных по
нормальному закону
см. статью
Нормальное распределение. Непрерывные распределения в MS EXCEL
. Таже значения выборки могут быть сгенерированы с помощью надстройки
Пакет анализа
.
Если значения
выборки
взяты из
нормального распределения
(μ не обязательно равно 0, σ не обязательно равно 1), то угол наклона кривой даст оценку
стандартного отклонения
σ, а ордината точки пересечения оси Y – оценку
среднего значения
μ.
Данные оценки несколько отличаются от оценок параметров, полученных с помощью функций
СРЗНАЧ()
и
СТАНДОТКЛОН.В()
, т.к. они получены
методом наименьших квадратов
, рассмотренного в статье про регрессионный анализ.
Примечание
: Рассмотренный выше метод в отечественной литературе имеет название
Метод номограмм
. Номограмма – это листы бумаги, разлинованные определенным образом. Номограмма используется в различных областях знаний. В
математической статистике
номограмма называется вероятностной бумагой. Такую «вероятностную бумагу» мы практически построили самостоятельно, когда нелинейно изменили масштаб шкалы ординат:
=НОРМ.СТ.ОБР((j-0,5)/n)
Интересно посмотреть, как будут выглядеть на диаграмме данные, полученные из
выборок
из других распределений (не из
нормального
). В
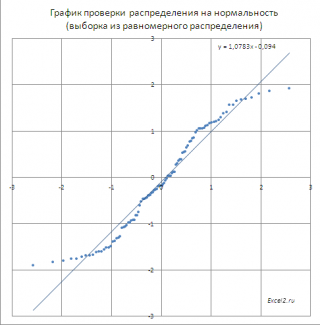
файле примера на листе Равномерное
приведен график, построенный на основе
выборки
из непрерывного равномерного распределения.
Очевидно, что значения
выборки
совсем не ложатся на прямую линию и предположение о
нормальности выборки
должно быть отвергнуто.
Подобная визуальная проверка
выборки
на соответствие другим распределениям может быть сделана при наличии соответствующих
обратных функций
. В статье
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
приведены
графики
для следующих распределений:
Стьюдента
,
ХИ-квадрат распределения
,
F-распределения
. Подобный график также приведен в статье про
распределение Вейбулла
.
Many statistical tests make the assumption that the values in a dataset are normally distributed.
One of the easiest ways to test this assumption is to perform a Jarque-Bera test, which is a goodness-of-fit test that determines whether or not sample data have skewness and kurtosis that matches a normal distribution.
This test uses the following hypotheses:
H0: The data is normally distributed.
HA: The data is not normally distributed.
The test statistic JB is defined as:
JB =(n/6) * (S2 + (C2/4))
where:
- n: the number of observations in the sample
- S: the sample skewness
- C: the sample kurtosis
Under the null hypothesis of normality, JB ~ X2(2).
If the p-value that corresponds to the test statistic is less than some significance level (e.g. α = .05), then we can reject the null hypothesis and conclude that the data is not normally distributed.
This tutorial provides a step-by-step example of how to perform a Jarque-Bera test for a given dataset in Excel.
Step 1: Create the Data
First, let’s create a fake dataset with 15 values:
Step 2: Calculate the Test Statistic
Next, calculate the JB test statistic. Column E shows the formulas used:
The test statistic turns out to be 1.0175.
Step 3: Calculate the P-Value
Under the null hypothesis of normality, the test statistic JB follows a Chi-Square distribution with 2 degrees of freedom.
So, to find the p-value for the test we will use the following function in Excel: =CHISQ.DIST.RT(JB test statistic, 2)
The p-value of the test is 0.601244. Since this p-value is not less than 0.05, we fail to reject the null hypothesis. We don’t have sufficient evidence to say that the dataset is not normally distributed.
In other words, we can assume that the data is normally distributed.
Additional Resources
How to Create a Q-Q Plot in Excel
How to Perform a Chi-Square Goodness of Fit Test in Excel
Решения задач на проверку статистических гипотез
Проверка статистических гипотез включает в себя большой пласт задач математической статистики. Зная некоторые характеристики выборки (или имея просто выборочные данные), мы можем проверять гипотезы о виде распределении случайной величины или ее параметрах (примеры этих задач на странице Проверка гипотез о параметрах распределения).
Ниже в примерах мы разберем основные учебные задачи на проверку гипотез о виде распределения. Чаще всего для этого используется критерий согласия $chi^2$ Пирсона, а также критерий Колмогорова-Смирнова.
Критерий согласия Пирсона (или критерий $chi^2$ — «хи квадрат») — наиболее часто употребляемый для проверки гипотезы о принадлежности некоторой выборки теоретическому закону распределения (в учебных задачах чаще всего проверяют «нормальность» — распределение по нормальному закону).
В учебных задачах обычно используется следующий алгоритм:
- Выбор теоретического закона распределения (обычно задан заранее, если не задан — анализируем выборку, например с помощью гистограммы относительных частот, которая имитирует плотность распределения).
- Оцениваем параметры распределения по выборке (для этого вычисляется математическое ожидание и дисперсия): $a, sigma$ для нормального, $a,b$ — для равномерного, $lambda$ — для распределения Пуассона и т.д.
- Вычисляются теоретические значения частот (через теоретические вероятности попадания в интервал) и сравниваются с исходными (выборочными).
- Анализируется значение статистики $chi^2$ и делается вывод о соответствии (или нет) теоретическому закону распределения.
Подробные примеры на разные распределения и критерии вы найдете ниже.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
73 Наблюдаемое значение статистики Пирсона попадает в критическую область Кнабл Kkp, поэтому есть основания отвергать основную гипотезу. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Пример . Имеются следующие данные о количестве заявок на автомобили технической помощи по дням. Помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Скачать решение
Нормальное распределение (Normal Distribution)
Пример 1. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X по результатам выборки:
X 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3
N 7 9 28 27 30 26 21 25 22 9 5
Свойства нормального распределения
Кривая стандартного нормального распределения симметрична относительно Среднего арифметического (Mean), Медианы (Median) и Моды (Mode). Более того, также являются нормальным распределением произведение двух нормальных распределений и их сумма. Магия, не правда ли? Существуют и другие, более сложные закономерности, пока обойдемся самыми понятными.
Вы слышали об эмпирическом правиле? Оно часто используется в статистике и гласит: «68,27% наблюдений случайной Выборки (Sample) лежат в пределах одного Стандартного отклонения (Standard Deviation), 95,45% – в пределах двух, а 99,73 – в пределах трех стандартных отклонений от среднего»:
Это правило позволяет нам идентифицировать Выбросы (Outlier) и очень полезно при Проверке на нормальность (Normality Test).
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Преимущество его заключается в том, что тот же подход можно использовать для сравнения любого распределения, не обязательно только нормального распределения. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Если копнуть глубже, то нормальное распределение можно найти в распределении многих показателях в системах связи (сигналы, шумы, помехи и другие), под нормальное распределение подгоняют многие финансовые показатели. Хотя следует подчеркнуть, что именно подгоняют, поскольку признаки нормальности в этих случаях часто бывают смещены.
Проверка гипотезы о нормальном распределении по критерию Пирсона. Подробный пример решения
Стандартное отклонение (σ), может принимать значения от нуля до плюс бесконечности. При увеличении стандартного отклонения график плотности нормального распределения становится более растянутым вдоль оси Ox, а при уменьшении — наоборот, сжимается. Это показано на графике снизу.
Проверка гипотезы о нормальном распределении
Критерий согласия Пирсона:
| Группы | xi | Кол-во, fi | xi * fi | Накопленная частота, S | |x — xср|*f | (x — xср) 2 *f | Частота, fi/n |
| 43 — 45.83 | 44.42 | 1 | 44.42 | 1 | 8.88 | 78.91 | 0.0278 |
| 45.83 — 48.66 | 47.25 | 1 | 47.25 | 2 | 6.05 | 36.64 | 0.0278 |
| 48.66 — 51.49 | 50.08 | 6 | 300.45 | 8 | 19.34 | 62.33 | 0.17 |
| 51.49 — 54.32 | 52.91 | 18 | 952.29 | 26 | 7.07 | 2.78 | 0.5 |
| 54.32 — 57.15 | 55.74 | 4 | 222.94 | 30 | 9.75 | 23.75 | 0.11 |
| 57.15 — 59.98 | 58.57 | 6 | 351.39 | 36 | 31.6 | 166.44 | 0.17 |
| 36 | 1918.73 | 82.7 | 370.86 | 1 |
| Интервалы группировки | Наблюдаемая частота ni | x1 = (xi— x )/s | x2 = (xi+1— x )/s | Ф(x1) | Ф(x2) | Вероятность попадания в i-й интервал, pi = Ф(x2) — Ф(x1) | Ожидаемая частота, 36pi | Слагаемые статистики Пирсона, Ki |
| 43 — 45.83 | 1 | -3.16 | -2.29 | -0.5 | -0.49 | 0.01 | 0.36 | 1.14 |
| 45.83 — 48.66 | 1 | -2.29 | -1.42 | -0.49 | -0.42 | 0.0657 | 2.37 | 0.79 |
| 48.66 — 51.49 | 6 | -1.42 | -0.56 | -0.42 | -0.21 | 0.21 | 7.61 | 0.34 |
| 51.49 — 54.32 | 18 | -0.56 | 0.31 | -0.21 | 0.13 | 0.34 | 12.16 | 2.8 |
| 54.32 — 57.15 | 4 | 0.31 | 1.18 | 0.13 | 0.38 | 0.26 | 9.27 | 3 |
| 57.15 — 59.98 | 6 | 1.18 | 2.06 | 0.38 | 0.48 | 0.0973 | 3.5 | 1.78 |
| 36 | 9.84 |
Пример №2 . Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение находим с помощью калькулятора.
Таблица для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x- x )·f | (x- x ) 2 ·f | (x- x ) 3 ·f | Частота, fi/n |
| 5 | 15 | 75 | 15 | 114.45 | 873.25 | -6662.92 | 0.075 |
| 7 | 26 | 182 | 41 | 146.38 | 824.12 | -4639.79 | 0.13 |
| 9 | 25 | 225 | 66 | 90.75 | 329.42 | -1195.8 | 0.13 |
| 11 | 30 | 330 | 96 | 48.9 | 79.71 | -129.92 | 0.15 |
| 13 | 26 | 338 | 122 | 9.62 | 3.56 | 1.32 | 0.13 |
| 15 | 21 | 315 | 143 | 49.77 | 117.95 | 279.55 | 0.11 |
| 17 | 24 | 408 | 167 | 104.88 | 458.33 | 2002.88 | 0.12 |
| 19 | 20 | 380 | 187 | 127.4 | 811.54 | 5169.5 | 0.1 |
| 21 | 13 | 273 | 200 | 108.81 | 910.74 | 7622.89 | 0.065 |
| 200 | 2526 | 800.96 | 4408.62 | 2447.7 | 1 |
Пример 2. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение.
Таблица для расчета показателей.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Естественно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия, и, следовательно, он характеризует близость эмпирического и теоретического распределений. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Имеется несколько критериев согласия. Наиболее часто используется критерий согласия К.Пирсона («хи-квадрат»). Здесь мы ограничимся применением критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности.
Проверка гипотезы о виде распределения онлайн
Если наблюдаемые данные полностью соответствуют нормальному распределению, значение статистики KS будет равно 0. Значение P используется, чтобы решить, достаточно ли велика разница, чтобы отклонить нулевую гипотезу:
| Группы | xi | Кол-во, fi | xi * fi | Накопленная частота, S | |x — xср|*f | (x — xср) 2 *f | Частота, fi/n |
| 43 — 45.83 | 44.42 | 1 | 44.42 | 1 | 8.88 | 78.91 | 0.0278 |
| 45.83 — 48.66 | 47.25 | 1 | 47.25 | 2 | 6.05 | 36.64 | 0.0278 |
| 48.66 — 51.49 | 50.08 | 6 | 300.45 | 8 | 19.34 | 62.33 | 0.17 |
| 51.49 — 54.32 | 52.91 | 18 | 952.29 | 26 | 7.07 | 2.78 | 0.5 |
| 54.32 — 57.15 | 55.74 | 4 | 222.94 | 30 | 9.75 | 23.75 | 0.11 |
| 57.15 — 59.98 | 58.57 | 6 | 351.39 | 36 | 31.6 | 166.44 | 0.17 |
| 36 | 1918.73 | 82.7 | 370.86 | 1 |
В статье описывается алгоритм обработки статистических данных на основе процедуры проверки нормальности распределения значений результатов измерения по критерию Пирсона с помощью программы Excel. Рассматриваются преимущества автоматического счета показателей по сравнению с ручным.
Ключевые слова: Excel, обработка данных, критерий согласия Пирсона, гистограмма, кривая распределения.
В эконометрических и экономико-математических моделях, применяемых, в частности, при изучении и оптимизации процессов маркетинга и менеджмента, управления предприятием и регионом, точности и стабильности технологических процессов, в задачах надежности, обеспечения безопасности, в том числе экологической, функционирования технических устройств и объектов, разработки организационных схем, часто применяют понятия и результаты теории вероятностей и математической статистики. При этом зачастую используют те или иные параметрические семейства распределений вероятностей. Наиболее популярным является нормальное распределение. Используют также логарифмически нормальное распределение, экспоненциальное распределение, гамма-распределение, распределение Вейбулла-Гнеденко и т. д.
Очевидно, что всегда необходимо проверять соответствие моделей реальности. Возникают два вопроса. Отличаются ли реальные распределения от используемых в модели? Насколько это отличие влияет на выводы?
Есть ли основания априори предполагать нормальность результатов измерений?
Иногда утверждают, что в случае, когда погрешность измерения (или иная случайная величина) определяется в результате совокупного действия многих малых факторов, то в силу Центральной предельной теоремы (ЦПТ) теории вероятностей эта величина хорошо приближается (по распределению) к нормальной случайной величине. Это утверждение, вообще говоря, неверно [1].
При обработке конкретных данных иногда считают, что погрешности измерений имеют нормальное распределение. На предположении нормальности построены классические модели регрессионного, дисперсионного, факторного анализов, метрологические модели, которые еще продолжают встречаться как в отечественной нормативно-технической документации, так и в международных стандартах. На то же предположение опираются модели расчетов максимально достигаемых уровней тех или иных характеристик, применяемые при проектировании систем обеспечения безопасности функционирования экономических структур, технических устройств и объектов. Однако теоретических оснований для такого предположения нет. Необходимо экспериментально изучать распределения погрешностей [1].
Представляется достаточно очевидным необходимость проверки используемых моделей на соответствие реальности, что возможно сделать уже на этапе первичной обработки данных экспериментальных наблюдений. Таким образом, можно сказать, что целью первичной обработки экспериментальных наблюдений является выбор закона распределения, описывающего случайную величину, выборку которой наблюдают. Проверка того, насколько хорошо наблюдаемая выборка описывается теоретическим законом, осуществляется с использованием различных критериев согласия.
Целью проверки гипотезы о согласии опытного распределения с теоретическим, является стремление удостовериться в том, что данная модель теоретического закона не противоречит наблюдаемым данным, и использование ее не приведет к существенным ошибкам при вероятностных расчетах. Некорректное использование критериев согласия может приводить к необоснованному принятию или необоснованному отклонению проверяемой гипотезы [2, с. 31]. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.
Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными. Сама процедура проверки нормальности распределения относится к распространенной стандартной задаче обработки данных и достаточно подробно и широко описана в различной литературе по метрологии и статистической обработке данных измерений [3].
Данные, получаемые в результате измерений при контроле технологических процессов, оценке характеристик различных объектов и др. для дальнейшей обработки, желательно представлять в виде теоретического распределения, максимально соответствующего экспериментальному распределению. Как правило, теоретические и эмпирические частоты различаются и расхождения могут быть не случайными, что возможно объясняется неверно выбранной гипотезой.
Приведенные описания экспериментальных данных показывают, что погрешности измерений в большинстве случаев имеют распределения, отличные от нормальных. Это означает, в частности, что большинство применений критерия Стьюдента, классического регрессионного анализа и других статистических методов, основанных на нормальной теории, строго говоря, не является обоснованным, поскольку неверна лежащая в их основе аксиома нормальности распределений соответствующих случайных величин.
Очевидно, для оправдания или обоснованного изменения существующей практики анализа статистических данных требуется изучить свойства процедур анализа данных при «незаконном» применении. Изучение процедур отбраковки показало, что они крайне неустойчивы к отклонениям от нормальности, а потому применять их для обработки реальных данных нецелесообразно; поэтому нельзя утверждать, что произвольно взятая процедура устойчива к отклонениям от нормальности.
Иногда предлагают перед применением, например, критерия Стьюдента однородности двух выборок, проверять нормальность. Хотя для этого имеется много критериев, но проверка нормальности — более сложная и трудоемкая статистическая процедура, чем проверка однородности (как с помощью статистик типа Стьюдента, так и с помощью непараметрических критериев). Для достаточно надежного установления нормальности требуется весьма большое число наблюдений. Так, чтобы гарантировать, что функция распределения результатов наблюдений отличается от некоторой нормальной не более, чем на 0,01 (при любом значении аргумента), требуется порядка 2500 наблюдений [4].
В большинстве экономических, технических, медико-биологических и других прикладных исследований число наблюдений существенно меньше. Особенно это справедливо для данных, используемых при изучении проблем, связанных с обеспечением безопасности функционирования экономических структур и технических объектов.
Проверку гипотезы о виде функции распределения в настоящее время проводят в соответствии с новым разработанным нормативным документом — ГОСТ Р 8.736–2011 по различным критериям согласия — Пирсона, Колмогорова, Мизеса — Смирнова и другим [5, с. 13].
Наиболее часто используется критерий Пирсона
χ
2
. Критерий Пирсона отвечает на поставленный вопрос, но, как и любой критерий он ничего не доказывает, а лишь устанавливает на принятом уровне значимости её согласие или несогласие с данными наблюдений. Критерий
χ
2
отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях. Преимущество метода состоит в том, что он позволяет сопоставлять распределения признаков, представленных в любой шкале, начиная от шкалы наименований. В самом простом случае альтернативного распределения «да — нет», «допущен брак — не допущен брак», «решена задача — не решена задача» и т. п. мы уже можем применить критерий
χ
2
.
Применение критериев согласия требует обычно довольно значительного объёма данных. Так, критерий Пирсона обычно рекомендуется использовать при объёме выборки не менее 50…100. Поэтому при небольшом объёме выборки проверку гипотезы о виде функции распределения проводят приближёнными методами — графическим методом или по асимметрии и эксцессу.
Применение критерия Пирсона для ручной обработки данных очень подробно было рассмотрено в известной работе [3, с. 161]. Как свидетельствует опыт проверок согласия экспериментальных данных с теоретическими по различным критериям, с использованием классических известных таблиц математической статистики [6, с. 15, с. 139], эта процедура является трудоемкой, и как правило, не исключает ошибок в работе.
Решение задач статистического анализа связано со значительными объемами вычислений. Проведение реальных многовариантных статистических расчетов в ручном режиме является очень громоздкой и трудоемкой задачей и без использования компьютера в настоящее время практически невозможно.
В целях облегчения решения данной задачи авторами предлагается для использования достаточно простая и эффективная модель в виде некоторого шаблона на основе среды Ехсе1 для практически мгновенного построения гистограммы и кривой распределения, которые сразу же после загрузки данных в шаблон дают исследователю предварительное визуальное представление о законе распределения значений результатов измерений.
По полученному виду гистограммы и кривой распределения можно предположить то, что выборка из 100 шт. реальных результатов измерений подчиняется нормальному закону распределения. Далее, для того чтобы убедиться в правильности выбранной гипотезы надо, первое — построить график гипотетического нормального закона распределения, выбрав в качестве параметров (математического ожидания и среднего квадратического отклонения) их оценки (среднее и стандартное отклонение), и совместить график гипотетического распределения с графиком гистограммы. И, второе — используя в данном случае один из известных критериев, например, критерий согласия Пирсона, установить справедливость выбранной гипотезы.
Рассмотрим порядок действий при работе с моделью в среде Ехсе1.
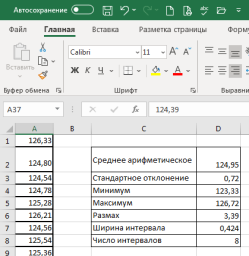
1. Полученные в итоге проведения эксперимента значения 100 случайных результатов измерений вносим в ячейки А1:А100 листа Ехсе1 и создаем таблицу, в которую посредством формул Ехсе1 вносим основные расчетные величины, используемые для построения гистограммы и кривой Гаусса: среднее арифметическое, стандартное отклонение, минимальное и максимальное значения выборки, размах, ширина интервала. Внешний вид таблицы с исходными данными показан на рис. 1.
В таблице исходных данных в ячейку D2 вносим формулу =СРЗНАЧ (А1:А100), D3: =СТАНДОТКЛОН (А1:А100), D4: =МИН (А1:А100), D5: =МАКС (А1:А100), D6: =D5-D4, D7: =D6/D8. В ячейку D8 вводится любое принятое на первом этапе число интервалов от 7 до 12.
2. Затем на этом же листе Ехсе1приступаем к построению гистограммы на основе данных, назначая длину интервала (карман) и выбирая необходимое число интервалов, которое для числа измерений, равного 100, может быть принято от 7 до 12.
Рис. 1. Фрагмент шаблона Ехсе1 с таблицей исходных данных
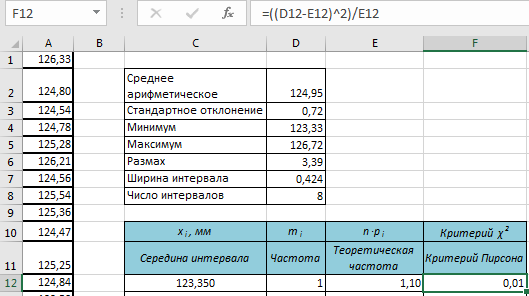
Для дальнейших расчетов построим расчетную таблицу с данными по столбцам по форме, показанной на рис. 2.
В ячейки столбца, помеченного как «Критерий Пирсона», вводим формулу (
m
i
—
np
i
)
2
/
np
i
для расчета критерия Пирсона для каждого интервала в соответствии с требованиями ГОСТ 8.736–2011 [5, с. 11] (рис. 2).
Рис. 2. Построение столбца расчетной таблицы для расчета статистики
U
Далее размножим формулу, показанную на рис. 2 в ячейке F12, для критерия
χ
2
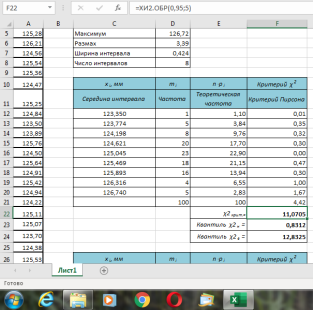
в диапазонах ячеек [F12; F20] и [F28; F38]. В ячейке F21 получим сумму содержимого ячеек [F12; F20] (рис. 3).
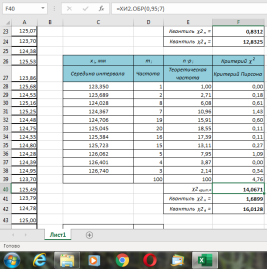
В ячейке F39 получим сумму содержимого ячеек [F28; F38] (рис. 4).
Рис. 3. Заполненная таблица для числа интервалов n = 8
Далее проводим проверку согласия эмпирического и теоретического законов распределения по критерию хи-квадрат Пирсона с использованием таблиц данных, изображенных на рис. 3 и рис. 4, как это было показано ранее в работе [7, с. 144].
Рис. 4. Заполненная таблица для числа интервалов n = 10
Критическое значение статистики
U
, которая имеет распределение
χ
2
с
f
степенями свободы (для нормального распределения число степеней свободы определяется как число частичных интервалов минус 3 в соответствии с указаниями стандарта [5, с. 11]), определяется при помощи функции ХИ2. ОБР.
Функция ХИ2. ОБР вызывается следующим образом. В главном меню Excel выбирается закладка Формулы, вставить функцию, в диалоговом окне Мастер функций — шаг 1 из 2 в категории Статистические ХИ2. ОБР (рис. 5).
Рис. 5. Диалоговое окно выбора функции ХИ2. ОБР
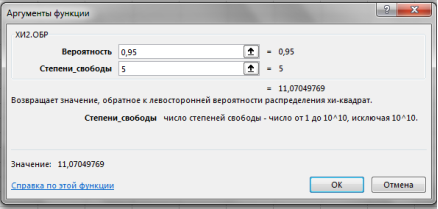
В диалоговом окне Аргументы функции ХИ2. ОБР заполняются поля, как показано на рис. 6, задаваясь доверительной вероятностью, например, Р = 0,95 и вводя значение числа степеней свободы, равным 5, при выбранном, например, числе интервалов
n
= 8, предварительно выбрав ячейку для результата вычисления функции.
Рис. 6. Диалоговое окно функции ХИ2. ОБР с заполненными полями ввода
Теперь с помощью стандартного инструмента для построения гистограмм («вставка/гистограмма» и т. д.) на этом же листе Ехсе1 можно построить гистограммы распределения с кривой Гаусса для выбранных разных чисел интервалов (в данном случае
n
= 8 и
n
= 10) (рис. 7 и 
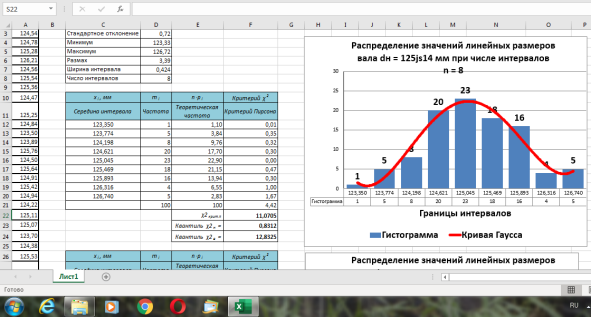
Рис. 7. Вид гистограммы и кривой распределения размеров при числе интервалов
n
= 8 (пример)
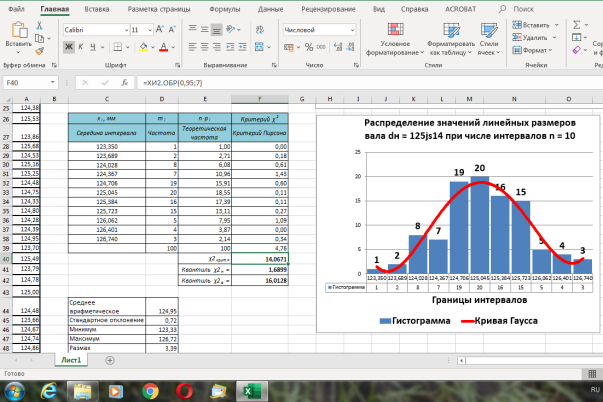
Рис. 8. Вид гистограммы и кривой распределения размеров при числе интервалов
n
= 10 (пример)
В приведенном примере в качестве исходных данных рассмотрено распределение линейных размеров вала номинальным значением диаметра 125js14, выполненного при его изготовлении по 14 квалитету точности.
Применяемая модель позволяет варьировать (т. е., как бы «играть») числом интервалов, началом первого интервала и шириной интервалов (карманов), при осуществлении этих действий исследователем он может визуально наблюдать автоматическое изменение внешнего вида гистограммы и кривой нормального распределения. Экспериментатор, изменяя указанные параметры графиков, по своему усмотрению может подобрать наиболее «красивый» вид гистограммы и аппроксимирующей кривой Гаусса, одновременно назначая требующееся значение доверительной вероятности и числа степеней свободы и добиваясь при этом выполнения критерия
χ
2
Пирсона.
Если значение статистики оказалось меньше критического значения
χ
2
при заданной доверительной вероятности, то можно утверждать, что нулевая гипотеза, состоящая в том, что исследуемая выборка подчиняется нормальному закону распределения, является правдоподобной и не отклоняется, т. е., не противоречит опытным данным.
В ячейке F21 получено значение статистики:
U
= 4,42 (рис. 7), а в ячейке F39 —
U
= 4,76 (рис. 8).
В указанных таблицах в соответствии с рекомендациями приложения в ГОСТ Р 8.736–2011 определены значения нижнего и верхнего квантилей
χ
2
н
и
χ
2
в
. Как видно из таблиц, вычисленный по результатам измерений квантиль
χ
2
находится между нижним и верхним значениями квантиля.
В данном примере значение обеих статистик
U
оказалось меньше критического значения
χ
2
(0,95; 5) =11,07 и
χ
2
(0,95; 7) =14,07. Следовательно, в данном случае, мы можем с указанной доверительной вероятностью
Р
= 0,95 распространить данный закон распределения на всю генеральную совокупность исследуемых объектов (партию изделий, сменную выработку, месячный план и т. д.) для принятия последующих решений о качестве оцениваемой продукции.
Проверка нормальности распределения результатов наблюдений, несмотря на кажущуюся тривиальность задачи, остаётся одним из актуальных методов первичной статистической обработки данных в различных областях современной науки, имеющих дело с большими массивами данных.
Другие известные критерии (Колмогорова-Смирнова, Лилиефорса, Шапиро-Уилка), применяемые в медицине, биологии и др., являются мощным инструментом, могут быть реализованы в программном пакете IBM SPSS Statiscs, в то же время достаточно сложны в применении и рассчитаны на подготовленного пользователя [8], поэтому применение описанной модели для простейшей первичной обработки данных является вполне оправданным.
Данная методика прошла экспериментальную проверку в учебном процессе в Государственном университете управления по ряду дисциплин, начиная с 2016 г. По мнению авторов, её можно рекомендовать к использованию и для исследования других законов распределений (Пуассона, биномиального, равномерного и т. п.).
Выводы
-
Критерий хи-квадрат Пирсона является одним из множества известных статистике критериев, применяемых при проверке нормальности распределения при большом объеме данных (
n
> 50) и вполне пригоден для решения несложных задач. - Появление пакетов офисных программ, в частности, Excel, позволяет оптимизировать скорость обработки данных и повысить научный уровень работы, минимизируя появление ошибок в расчетах.
- Использование метода и шаблона Excel, рассмотренного в статье, позволяет производить предварительную экспресс-оценку нормальности распределения данных измерений путем их «загрузки» в программу непосредственно после получения результатов до принятия последующего решения об их тщательной статистической обработке.
Литература:
1. Орлов А. И. Распределения реальных статистических данных не являются нормальными — Научный журнал КубГАУ, 2016, № 117 (03).
2. Иванов О. В. Статистика / Учебный курс для социологов и менеджеров. Часть 2. Доверительные интервалы. Проверка гипотез. Методы и их применение. — М.: Изд. МГУ им. М. В. Ломоносова, 2005.- 220 с.
3. Бурдун Г. Д., Марков Б. Н. Основы метрологии. Учебное пособие для вузов
.
—
М.: Изд. стандартов, 1975.- 336 с.
4. Орлов А. И. Прикладная статистика. — М.: Экзамен, 2006. — 671 с.
5. ГОСТ Р 8.736–2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения
.
—
М.: ФГУП «Стандартинформ», 2013.- 24 с.
6. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, Главная редакция физико-математической литературы, 1983.- 416 с.
7. Фаюстов А. А. Шаблон Ехсеl для проверки законов распределения данных наблюдений по критерию согласия Пирсона. — Молодой ученый, 2019, № 13(251). С. 142–147
.
8. Щелыкалина С. П. Проверка нормальности выборочных данных измерения переменных в непрерывной шкале. — РНИМУ им. Н. И. Пирогова / http://do.rsmu.ru/fileadmin/user_upload/mbf/c_kibernetiki/23.10.2020_Lek_Proverka_normalnosti_vyborochnykh_dannykh_izmerenija_peremennykh_v_nepreryvnoi_.pdf (Дата обращения 16.11.2021).
Основные термины (генерируются автоматически): число интервалов, данные, критерий, распределение, нормальное распределение, выбранная гипотеза, критерий согласия, ячейка, диалоговое окно, доверительная вероятность.