17 авг. 2022 г.
читать 2 мин
Критерий Крускала-Уоллиса используется для определения наличия статистически значимой разницы между медианами трех или более независимых групп. Он считается непараметрическим эквивалентом однофакторного дисперсионного анализа.
В этом руководстве объясняется, как провести тест Крускала-Уоллиса в Excel.
Пример: тест Крускала-Уоллиса в Excel
Исследователи хотят знать, приводят ли три разных удобрения к разным уровням роста растений. Они случайным образом выбирают 30 разных растений и делят их на три группы по 10 штук, применяя к каждой группе разные удобрения. В конце месяца измеряют высоту каждого растения.
Используйте следующие шаги, чтобы выполнить тест Крускала-Уоллиса, чтобы определить, одинаков ли медианный рост в трех группах.
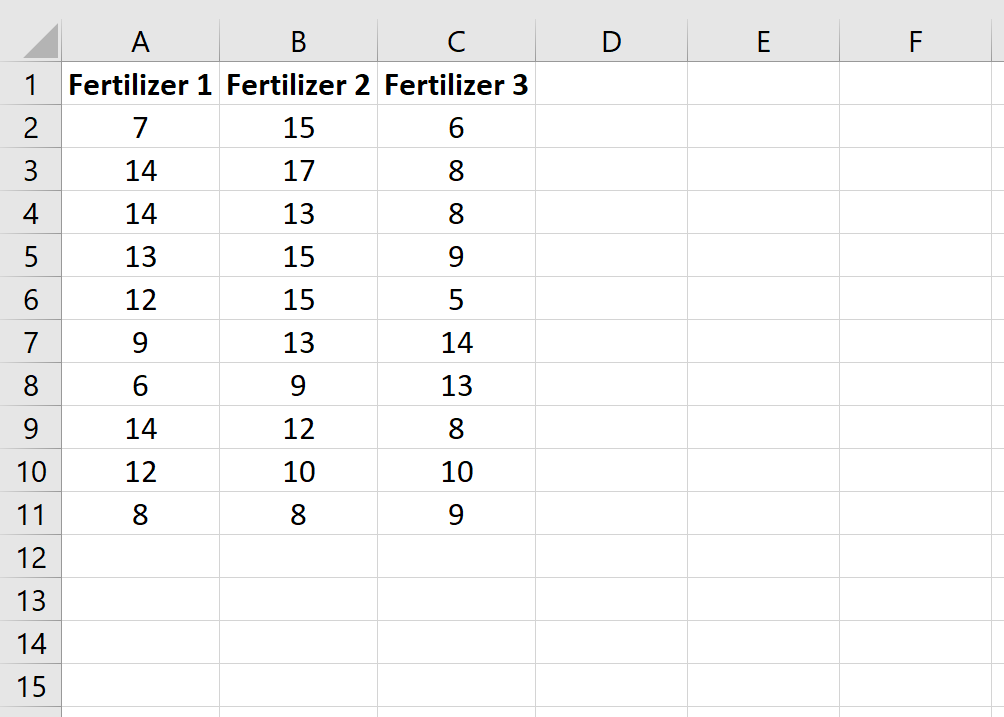
Шаг 1: Введите данные.
Введите следующие данные, которые показывают общий рост (в дюймах) для каждого из 10 растений в каждой группе:
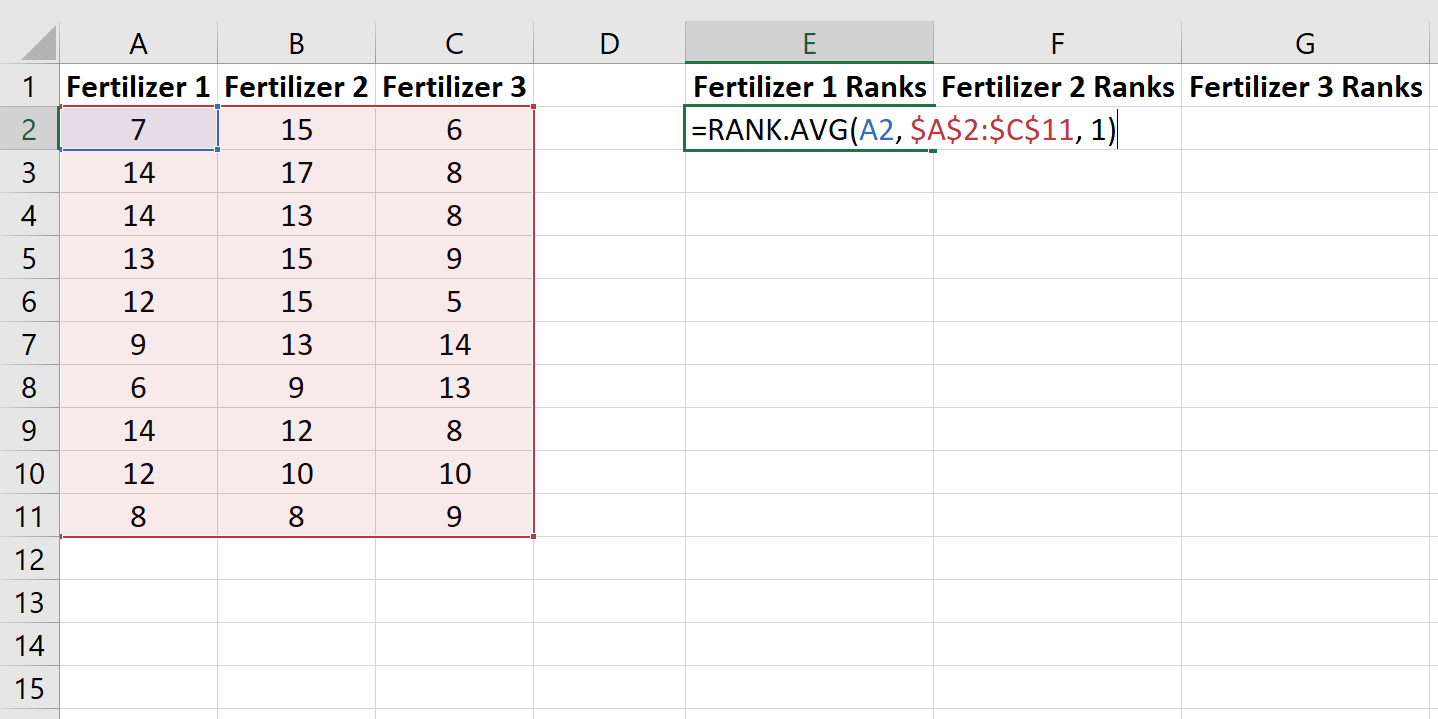
Шаг 2: Ранжируйте данные.
Далее мы воспользуемся функцией RANK.AVG() , чтобы присвоить ранг росту каждого растения из всех 30 растений. Следующая формула показывает, как рассчитать ранг первого растения в первой группе:
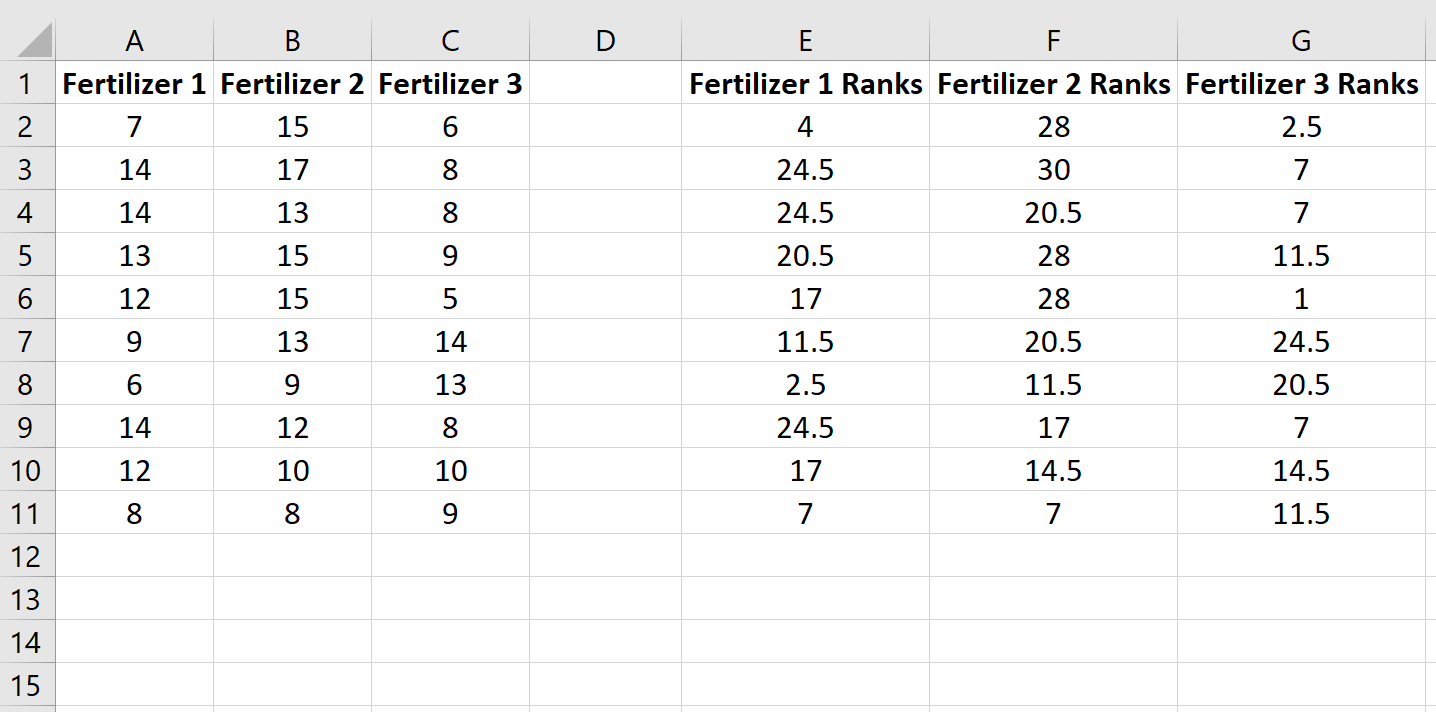
Скопируйте эту формулу в остальные ячейки:
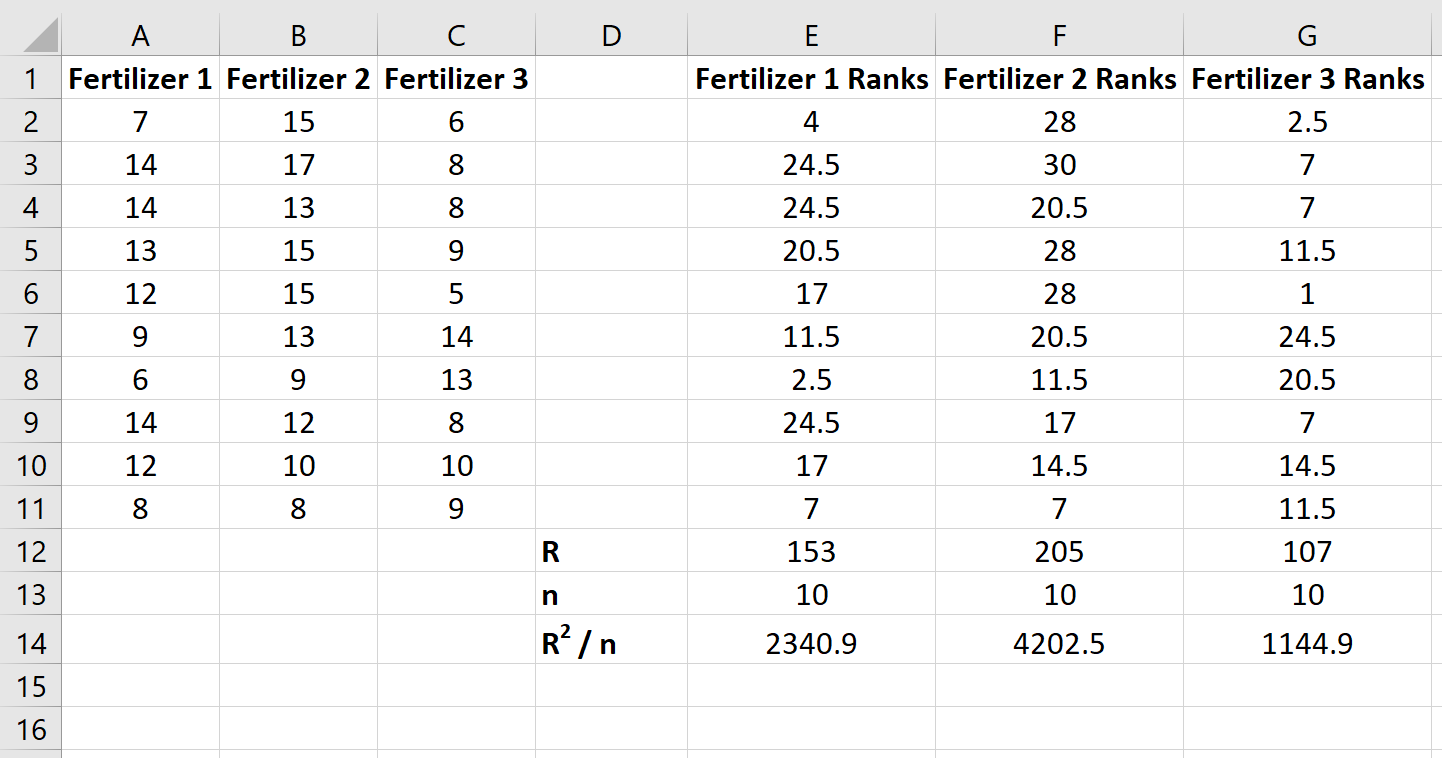
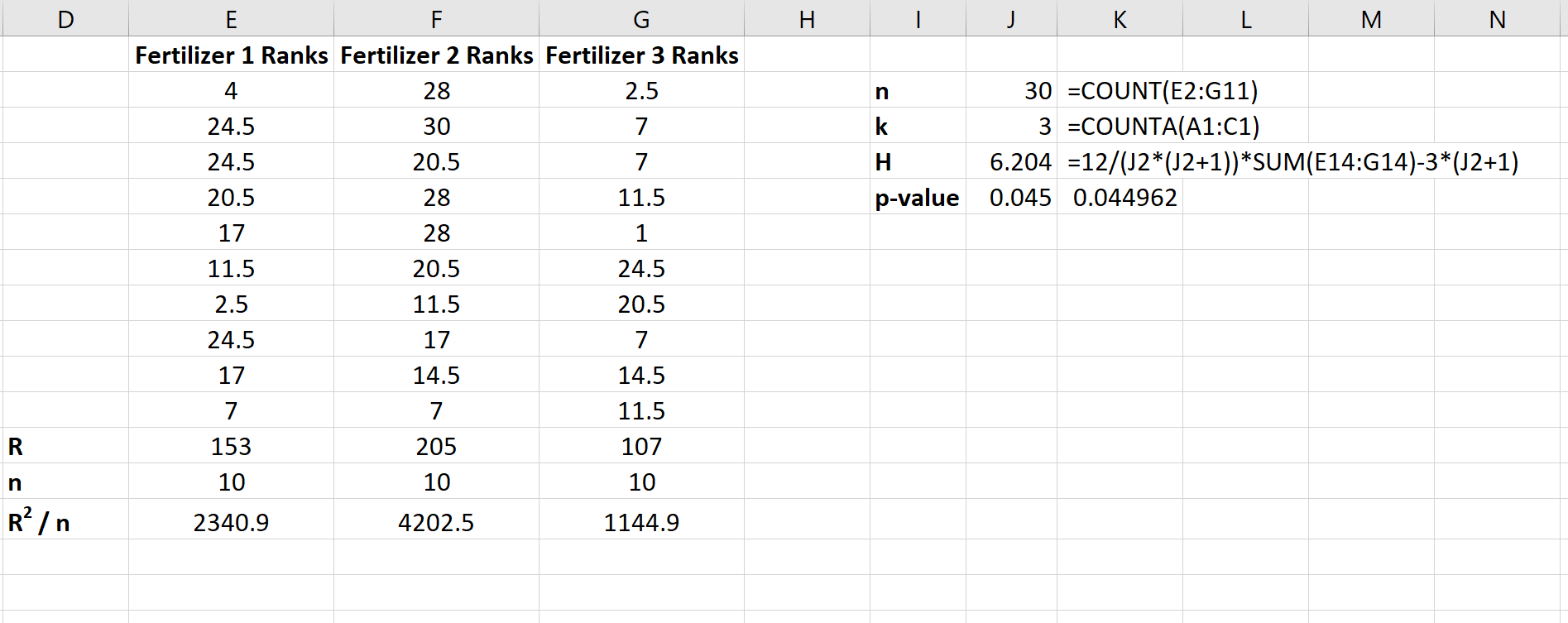
Затем вычислите сумму рангов для каждого столбца вместе с размером выборки и квадратом суммы рангов, деленной на размер выборки:
Шаг 3: Рассчитайте статистику теста и соответствующее значение p.
Статистика теста определяется как:
H = 12/(n(n+1)) * ΣR j 2 /n j – 3(n+1)
куда:
- n = общий размер выборки
- R j 2 = сумма рангов для j -й группы
- n j = размер выборки j -й группы
При нулевой гипотезе H следует распределению хи-квадрат с k-1 степенями свободы.
На следующем снимке экрана показаны формулы, используемые для расчета статистики теста, H и соответствующего значения p:
Статистика теста составляет H = 6,204, а соответствующее значение p равно p = 0,045.Поскольку это p-значение меньше 0,05, мы можем отвергнуть нулевую гипотезу о том, что средний рост растений одинаков для всех трех удобрений. У нас есть достаточно доказательств, чтобы заключить, что тип используемого удобрения приводит к статистически значимым различиям в росте растений.
Шаг 4: Сообщите о результатах.
Наконец, мы хотим сообщить о результатах теста Крускала-Уоллиса. Вот пример того, как это сделать:
Был проведен тест Крускала-Уоллиста, чтобы определить, был ли средний рост растений одинаковым для трех разных удобрений для растений. Всего в анализе было использовано 30 растений. Каждое удобрение применялось к 10 разным растениям.
Тест показал, что средний рост растений не был одинаковым (H = 6,204, p = 0,045) среди трех удобрений. То есть имелась статистически значимая разница в среднем росте растений между двумя или более удобрениями.
A Kruskal-Wallis Test is used to determine whether or not there is a statistically significant difference between the medians of three or more independent groups. It is considered to be the non-parametric equivalent of the One-Way ANOVA.
This tutorial explains how to conduct a Kruskal-Wallis Test in Excel.
Example: Kruskal-Wallis Test in Excel
Researchers want to know if three different fertilizers lead to different levels of plant growth. They randomly select 30 different plants and split them into three groups of 10, applying a different fertilizer to each group. At the end of one month they measure the height of each plant.
Use the following steps to perform a Kruskal-Wallis Test to determine if the median growth is the same across the three groups.
Step 1: Enter the data.
Enter the following data, which shows the total growth (in inches) for each of the 10 plants in each group:
Step 2: Rank the data.
Next, we will use the RANK.AVG() function to assign a rank to the growth of each plant out of all 30 plants. The following formula shows how to calculate the rank for the first plant in the first group:
Copy this formula to the rest of the cells:
Then, calculate the sum of the ranks for each column along with the sample size and the squared sum of ranks divided by the sample size:
Step 3: Calculate the test statistic and the corresponding p-value.
The test statistic is defined as:
H = 12/(n(n+1)) * ΣRj2/nj – 3(n+1)
where:
- n = total sample size
- Rj2 =sum of ranks for the jth group
- nj =sample size of jth group
Under the null hypothesis, H follows a Chi-square distribution with k-1 degrees of freedom.
The following screenshot shows the formulas used to calculate the test statistic, H, and the corresponding p-value:
The test statistic is H = 6.204 and the corresponding p-value is p = 0.045. Since this p-value is less than 0.05, we can reject the null hypothesis that the median plant growth is the same for all three fertilizers. We have sufficient evidence to conclude that the type of fertilizer used leads to statistically significant differences in plant growth.
Step 4: Report the results.
Lastly, we want to report the results of the Kruskal-Wallis Test. Here is an example of how to do so:
A Kruskal-Wallist Test was performed to determine if median plant growth was the same for three different plant fertilizers. A total of 30 plants were used in the analysis. Each fertilizer was applied to 10 different plants.
The test revealed that the median plant growth was not the same (H = 6.204, p = 0.045) among the three fertilizers. That is, there was a statistically significant difference in median plant growth among two or more of the fertilizers.
Сравнение трех и более независимых групп. Критерий Краскела — Уоллиса
Введение
В этой статье речь пойдет о непараметрическом статистическом критерии Краскела-Уоллиса. Что это за критерий? Каковы условия его применения? Где используют? Как рассчитать? Ответы на эти и другие вопросы Вы найдете ниже.
Критерий Краскела-Уоллиса – непараметрический статистический критерий, используемый для сравнения 3-ех и более независимых выборок по количественному или порядковому признаку.
Критерий был разработан американскими математиками. Уильям Краскел и Аллен Уоллис представили критерий в своей работе «Use of ranks in one-criterion variance analysis» в 1952 году. Отсюда и название критерия.
Условия применения критерия
- Не менее трех выборок испытуемых объектов
- Зависимая переменная должна измеряться в порядковой или непрерывной шкале
- Наблюдения должны быть независимыми (не должно быть никаких отношений между двумя группами или внутри каждой группы)
- Наблюдения не распределяются нормально
Критерий Краскела-Уоллиса подходит для сравнения небольших выборок. Желательно, чтобы в каждой выборке было не менее 5 наблюдений.
Использование Краскела-Уоллиса
Непараметрический критерий Краскела-Уоллиса используется во многих областях. Чаще всего его можно встретить в психологии, здравоохранении и бизнесе.
Примеры задач, которые решает критерий Краскела-Уоллиса:
- Оказывают ли три препарата разное влияние на боль пациентов?
- Приводят ли четыре разных видов удобрения к разным уровням роста растений?
- Различаются ли уровни выгорания в группах: преподаватели, врачи, шахтеры?
Как рассчитать критерий Краскела-Уоллиса
- Определите нулевую и альтернативную гипотезы.
H0: Между выборками 1, 2, 3 и т. д. существуют лишь случайные различия по уровню исследуемого признака.
Н1: Между выборками 1, 2, 3 и т. д. существуют неслучайные различия по уровню исследуемого признака.
- Вычислите величину статистики критерия (нулевой гипотезы).
- Определите критические значения и соответствующий им уровень значимости.
- Интерпретируйте величину р и результаты.
Важно, отклонение нулевой гипотезы не указывает, какая из групп отличается. Для того, чтобы это выяснить, необходимо проводить апостериорные (попарные) сравнения между группами.
Существует много критериев для осуществления попарных сравнений, мы, чаще всего, используем метод Неменьи, который был предложен Петром Неменьи в 1963 году.
В современном мире, когда все вокруг автоматизировано, для расчета критерия используют готовые статистические программы, в основе которых уже заложены специальные алгоритмы для расчетов, минуя ручные вычисления.
Мы выполняем расчеты критерием Краскела-Уоллиса в Python с использованием пакетов pandas, numpy, matplotlib.pyplot, seaborn, scipy.stats.
Почему вы выбрали для расчета критерий Краскела-Уоллиса?
Перед защитой работы, очень многих студентов, аспирантов пугает именно этот вопрос.
Мы, обычно, в качестве примера предлагаем следующий ответ:
«Нами был выбран критерий Краскела-Уоллиса ввиду того, что наши данные подходят под условия применения данного теста.» И далее ссылаемся на условия применения.
Пример результата сравнения трех групп
Смотреть отчет — сравнение трех независимых групп
О проекте BIRDYX
У нас Вы можете заказать услугу статистического анализа и помощи в статистических расчетах для научных статей, диссертаций или маркетинговых исследований. Свяжитесь с нами одним из удобных способов, чтобы обсудить детали:
WhatsApp: +7 (919) 882-93-67
Telegram: birdyx_ru
E-mail: mail@birdyx.ru
Мы растем, развиваемся, постоянно работаем над автоматизацией аналитических процессов, чтобы предоставлять Вам качественную аналитику оперативно и по доступной цене.
Ранговый критерий Крускала-Уоллиса для оценки разностей между с медианами (с > 2) представляет собой обобщение рангового критерия Уилкоксона для двух независимых выборок (см. также Однофакторный дисперсионный анализ). Таким образом, критерий Крускала-Уоллиса является непараметрической альтернативой F-критерию в однофакторном дисперсионном анализе, аналогично тому, как критерий Уилкоксона представляет собой непараметрическую альтернативу t-критерию, использующему суммарную дисперсию при сравнении двух независимых выборок. Если выполняются условия, необходимые для применения F-критерия в однофакторном дисперсионном анализе, критерий Крускала-Уоллиса обладает той же мощностью. [1]
Ранговый критерий Крускала-Уоллиса применяется для проверки гипотезы, что с независимых выборок извлечены из генеральных совокупностей, имеющих одинаковые медианы. Иначе говоря, нулевая и альтернативная гипотезы формулируются следующим образом:
Н0: М1 = М2 = … =Mc
H1: не все Mj (j = 1, 2, …, с) являются одинаковыми
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Для этого необходимо знать ранги, вычисленные по всем выборкам, а с генеральных совокупностей, из которых они извлечены, должны иметь одинаковые изменчивость и вид. Для того чтобы применить критерий Крускала-Уоллиса, сначала необходимо заменить наблюдения в с выборках их объединенными рангами. При этом первый ранг соответствует наименьшему наблюдению, а ранг n — наибольшему (n = n1 + n2 + … + nc). Если некоторые значения повторяются, им присваивается среднее значение их рангов.
Критерий Крускала-Уоллиса является альтернативой F-критерию в однофакторном дисперсионном анализе. H-статистика, применяемая в критерии Крускала-Уоллиса, аналогична величине SSA— межгрупповой вариации (подробнее см. Однофакторный дисперсионный анализ), по которой вычисляется F-статистика. Вместо сравнения средних значений j всех с групп с общим средним значением
, в критерии Крускала-Уоллиса средние ранги каждой из с групп сравниваются с общим рангом, вычисленным на основе всех n наблюдений. Если существует статистически значимый эффект эксперимента, средние ранги каждой группы будут значительно отличаться друг от друга и от общего ранга. При возведении этих разностей в квадрат Н-статистика увеличивается. С другой стороны, если эффект эксперимента не наблюдается, статистика Н теоретически должна быть равной нулю. Однако на практике вследствие случайных изменений статистика Н будет ненулевой, но достаточно малой.
Критерий Крускала-Уоллиса для разностей между с медианами:
где n — общее количество наблюдений в объединенных выборках, nj — количество наблюдений в j-й выборке (j = 1, 2, … , с), Tj — сумма рангов j-й выборки.
При достаточно большом объеме выборок (больше пяти) H-статистику можно аппроксимировать χ2-распределением с с – 1 степенями свободы. Таком образом, при заданном уровне значимости α решающее правило формулируется так: гипотеза Н0 отклоняется, если H > χU2 (рис. 1), в противном случае гипотеза Н0 не отклоняется. Критические значения χ2-распределения вычисляются с помощью функции Excel =ХИ2.ОБР(вероятность;степени_свободы).
Рис. 1. Критическая область критерия Крускала-Уоллиса
Продемонстрируем критерий Крускала-Уоллиса на примере оценки прочности парашютов в зависимости от поставщика синтетических волокон. Если прочность парашютов не является нормально распределенной случайной величиной, для оценки различий между медианами четырех генеральных совокупностей можно применить непараметрический критерий Крускала-Уоллиса.
Нулевая гипотеза заключается в том, что прочность всех парашютов одинакова: Н0: М1 = М2 = М3 =M4. Альтернативная гипотеза утверждает, что по крайней мере один поставщик отличается от других: H1: не все Mj (j = 1, 2, 3, 4) являются одинаковыми. Результаты эксперимента, ранги и вычисления приведены на рис. 2.
Рис. 2. Прочность и ранги парашютов, сшитых из синтетической ткани, приобретенной у четырех разных поставщиков
В процессе преобразования 20 показателей прочности в объединенные ранги, выясняется, что третий парашют, произведенный из синтетического волокна первого поставщика, имеет наименьшую прочность, равную 17,2. Он получает ранг 1. Четвертый парашют, произведенный из синтетического волокна первого поставщика, и второй парашют, сотканный из волокон четвертого поставщика, имеют одинаковую прочность, равную 19,9. Поскольку им соответствуют ранги 5 и 6, обоим парашютам присваивается ранг 5,5, равный среднему значению рангов 5 и 6. И, наконец, ранг 20 присваивается первому парашюту, сотканному из волокон второго поставщика, поскольку величина 26,3 является наибольшей. После присвоения рангов вычисляется их сумма в каждой группе: Т1 = 27,0; Т2 = 76,5; Т3 = 62,0; Т4 = 44,5. Для проверки рангов просуммируем эти величины:
Используя формулу (1), вычислим Н-статистику:
Статистика Н имеет приближенное χ2-распределение с с – 1 степенями свободы. При уровне значимости α, равном 0,05, определяем величину χU2 — верхнего критического значения χ2-распределения с с – 1 = 3 степенями свободы с использованием функции =ХИ2.ОБР(1 – α;с –1) = 7,815 (рис. 2). Поскольку вычисленная Н-статистика равна 7,889 и превышает критическое значение 7,815, нулевая гипотеза отклоняется. Следовательно, не все фирмы поставляют синтетическое волокно, прочность которого имеет одинаковую медиану. Аналогичный вывод можно сделать, вычислив р-значение по формуле р(Н=7,889) =1-ХИ2.РАСП(7,889;3;ИСТИНА) =0,048 (рис. 2). р-значение равно 0,048, т.е. меньше уровня значимости 0,05. Поскольку нулевая гипотеза отклоняется, приходим к выводу, что фирмы поставляют волокна разной прочности. На следующем этапе необходимо попарно сравнить всех поставщиков и определить, какие из них отличаются друг от друга. Для этого можно применить апостериорную процедуру множественного сравнения, предложенную Дж. Данном.
Для применения критерия Крускала-Уоллиса должны выполняться следующие условия.
- Все с выборок случайно и независимо друг от друга извлекаются из соответствующих генеральных совокупностей.
- Анализируемая переменная является непрерывной.
- Наблюдения допускают ранжирование как внутри, так и между группами.
- Все с генеральных совокупностей имеют одинаковую изменчивость.
- Все с генеральных совокупностей имеют одинаковый вид.
Процедура Крускала-Уоллиса имеет меньше ограничений, чем F-критерий. Процедура Крускала-Уоллиса предусматривает ранжирование только по всем выборкам в совокупности. Общее распределение должно быть непрерывным, но его вид значения не имеет. Если эти условия не выполняются, критерий Крускала-Уоллиса по-прежнему можно применять для проверки гипотезы о различиях между с генеральными совокупностями. Альтернативная гипотеза утверждает, что среди с генеральных совокупностей существует хотя бы одна, которая отличается от остальных какой-нибудь характеристикой — либо средним значением, либо видом. С другой стороны, для применения F-критерия переменная должна быть числовой, а с выборок должны извлекаться из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию.
В полностью рандомизированных экспериментах, для которых выполняются условия F-критерия, следует применять именно его, а не процедуру Крускала-Уоллиса, поскольку мощность F-критерия в этой ситуации выше. С другой стороны, если эти условия не выполняются, более мощным становится критерий Крускала-Уоллиса, и следует предпочесть именно его.
Предыдущая заметка Непараметрические критерии. Ранговый критерий Уилкоксона
Следующая заметка Критерий «хи-квадрат» для дисперсий
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 748–751
Для того, чтобы рассчитать критерий Н-КрускалаУоллеса используя статистически пакет SPSS необходимо сделать следующий шаги:
1.Внести в таблицу Data Editor значения нескольких переменных. (Например var1, var2, var3)
1.1 Переменная var1 должна содержать значения всех выборок
1.2. Переменная var2 должна содержать условные обозначения выборок, которые ставятся напротив соответствующих значений var1(например 1 — для первой выборки, 2 — для второй выборки, 3- для третьей выборки)
2. Выбрать Analyze -> Nonparametric Tests -> K-independent Samples
3. В открывшемся окне выделяем переменную var1 и переносим ее в Test Variables (правое верхнее окно)
4. Переменную var2 переносим в Grouping Variable (второе окно сверху)
5. Нажимаем кнопку Define Group
6. Вносим минимальное и максимальное значение существующее в переменной var2. В нашем примере это будут 1 и 3
7. Нажимаем Continue
8. Нажимаем кнопку Ok
9. Смотрим получившиеся результаты
| Расчет критерия H-Крускалла-Уоллеса | Пример расчета критерия H-Крускалла-Уоллеса |
| Расчет критерия H-Крускалла-Уоллеса в Excell | Пример расчет критерия H-Крускалла-Уоллеса в Excell |
| Пример расчета критерия H-Крускалла-Уоллеса в SPSS | |
| Критерий H-Крускалла-Уоллеса |