-
Понятие
информации. Термин «информация»
происходит от латинского informatio что
означает разъяснение,
осведомление, изложение. Понятие
«информация» многозначно, и поэтому
строго определено быть не может. В
широком смысле информация — это
отражение реального (материального,
предметного) мира, выражаемого в виде
сигналов и знаков.
В
информатике понятие «информация»
означает сведения об объектах и явлениях
окружающей среды, их параметрах,
свойствах и состоянии, которые уменьшают
имеющуюся о них степень неопределенности,
неполноты знаний.
Свойства
информации (требования к информации). При
этом, чтобы информация способствовала
принятию на ее основе правильных
решений, она должна характеризоваться
такими свойствами, как достоверность,
полнота, актуальность, полезность,
понятность. Обратим
внимание еще на такое свойство
информации, как адекватность
— определенный
уровень соответствия создаваемого с
помощью полученной информации образа
реальному объекту, процессу, явлению
и т.п., что позволяет говорить о
возможности уточнения, расширения
объема информации, приближения в
процессе познания к ее большей
достоверности.
Единица
измерения информации называется
бит (bit) –
сокращение от английских слов binary
digit, что означает двоичная цифра.
Содержит 0 или 1. Более употребим для
ПК термин байт(состоит из 8 бит) и
являющийся основной единицей хранения
информации в памяти ПК.
Бит —
слишком мелкая единица измерения.
На практике чаще применяется более
крупная единица — байт, равная восьми
битам.
Именно
восемь битов требуется для того, чтобы
закодировать любой из 256 символов
алфавита клавиатуры компьютера.Также
используются такие единицы измерения,как
Килобайт,Гигабайт,Терабайт и т.д.
2.История создания
ЭВМ.
ЭВМ
— одно из величайших изобретений
середины XX века, изменивших человеческую
жизнь во многих ее проявлениях
.Основы построения ЭВМ в их современном
понимании были заложены в 30-40 года 20-го
века.
С точки зрения архитектуры ЭВМ с хранимой
в памяти программой революционными
были идеи американского математика,
Члена Национальной АН США и американской
академии искусств и наук Джона фон
Неймана (1903—1957). Эти идеи были изложены
в статье «Предварительное рассмотрение
логической конструкции электронного
вычислительного устройства», написанная
вместе с А. Берксом и Г. Голдстайном и
опубликованная в 1946 году.,который
впоследствии заложил все основы развития
вычислительной техники на несколько
десятилетий вперед.
Принципы Неймана:
1.Двоичное
кодирование.Вся информация кодируется
с помощью двух символов.
2.Однородность
памяти.Все программы и файлы хранятся
в одном месте.
3.Адресация
памяти.Память состоит из пронумерованных
ячеек,процессу доступна любая из них.
4.Последовательное
программное управление.Программы
состоят из набора команд,котрые выполняет
процессор автоматически один за другим.
3.Принип работы и
структура ПК.
ПК-настольная или
переносная ЭВМ,которая удовлетворяет
общедоступные универсальные требования.
Компьютеры являются
преобразователями информации,в них
исходные задачи преобразуются в
результат ее решения, и относятся к
классу дискретного действия-цифровому.
Работу ПК можно
охарактеризовать следующим образом-при
включении компьютера в процессе
начальной загрузки все компоненты ПК
тестируется специальной программой,находящяяся
в ПЗУ(постоянное запоминающее
устройство)-Bios.Эта
программа также тестирует периферийные
устройства.После этого начинает
загружаться ОС,задающая последовательность
работы устройств ПК и порядок ввода
данных,алгоритмы их работы и вывод
результата.
Как правило,данные
берутся из ячеек памяти ОЗ,обрабатываются
все микропроцессы и пересылаются в
другие ячейки памяти.
4. Понятие
периферийного устройства персонального
компьютера Устройства ввода и вывода
информации.
Периферийные
устройства-понимается любое
устройство,конструктивно отделенное
от центральной части ПК,и имеющее
собственное управление.По назначению
можно выделить следующие внешние
устройства ПК:
1.устройства ввода
информации(клавиатура)
2.устройства вывода
информации(монитор,принтер)
3.устройства связи
и коммуникации(модем,сетевой адаптер)
Внешняя память
используется для долговременного
хранения различной информации,которая
может потребоваться при решении
каких-либо задач.В частности,именно во
внешней памяти компьютера содержится
все программное обеспечение
компьютера.(винчестер,USB)
5.Память персонального
компьютера: виды, основные характеристики
В компьютере
существует 2 основных видов памяти-
основная и внешняя.
1.Основная
память ПК.
Предназначена для
хранения и оперативного обмена
информацией с прочими блоками ЭВМ,включая
2 вида запоминающего устройства –основное
запоминающее устройство и постоянное
запоминающее устройство.
ПЗУ имеет вид
микросхемы, запаянную в материнскую
плату и не подлежит замене.Информация,которая
содержится в ПЗУ,не является
пользовательской.В ней храняться
программы,тестируемые при запуске
ПК,загрузке ОС и обсуживании операций
по вводу и выводу данных.Эта память
энергозависима.
ОЗУ предназначено
для хранения информации,участвующей
в вычислительных процессах на текущем
этапе функционирования ПК.
2.Внешняя
память.
Внешняя память
используется для долговременного
хранения различной информации,которая
может потребоваться при решении
каких-либо задач.В частности,именно во
внешней памяти компьютера содержится
все программное обеспечение
компьютера.(винчестер,USB)
6.Файлы и папки, их
имена. Структура файловой системы. Путь
доступа к файлу.
Вся информация
(программы, документы, таблицы, рисунки
и пр.) хранится в файлах.Под файлом понимают
логически связанную совокупность
однотипных данных или программ, для
размещения которой во внешней памяти
выделяется именованная область.
Файловая система обеспечивает
возможность доступа к конкретному
файлу и позволяет найти свободное место
при записи нового файла. Она определяет
схему записи информации, содержащейся
в файлах, на физический диск. Каждый
файл имеет имя и расширение.
Расширение указывает на тип файла.
Файловая
структура может быть одноуровневой —
это простая последовательность
файлов. Многоуровневая
файловая структура —
древовидный способ организации файлов
на диске. При этом существуют специальные
файлы, которые в одних операционных
системах называют каталогами (directory)
(в других — папками),
назначение которых — регистрация в
них файлов (в том числе и других
каталогов). Наличие поддержки каталогов
в операционной системе позволяет
выстроить иерархическую (многоуровневую)
организацию размещения файлов на
носителе. В этом случае файлы, имеющие
одинаковую природу (файлы операционной
системы, документы, офисные программы,
игровые программы, результаты расчетов,
домашние задания, рисунки и т.д.),
размещаются в отдельных каталогах.
Файлы и каталоги,
зарегистрированные в одном каталоге, должны
иметь уникальные имена.
Файлы (или каталоги),
зарегистрированные на одном и том же
носителе информации, но в разных
каталогах, могут иметь совпадающие
имена.
Полное
имя файла однозначно
определяет местоположение любого файла
на носителе. Оно состоит из пути
к файлу,
включающемулогическое
имя устройства и
иерархическую систему каталогов, от
корневого каталога до того, в котором
содержится файл, исобственно
имени файла и расширения.
Правила
задания имени файла определяются
операционной
системой и используемой файловой
системой.
7.Программное
обеспечение ПК. Структура программного
обеспечения ПК.
В узком смысле ПО
ПК-совокупность программ (Программа-это
описание,воспринимаемое ЭВМ и достаточное
для решения определенной задачи)
В широком смысле
ПО ПК включает в себя различные
языки,процедуры,правила и
документацию,необходимую для эксплуатации
программных продуктов.
Классификация
ПО,основным признаком которой является
сфера применения,подразделяется на :
1.Системное ПО.
Используется для
создания программ,а также для
предоставлению пользователю необходимых
ему услуг.Является необходимым
дополнением ЭВМ,без нее ЭВМ безжизненна.
2.Прикладное ПО
Предназначено для
решения какой-либо определенной задачи
или класса задач.К ним относят производство
различных вычислений по алгоритмам,подготовка
текстовых документов к работе и т.д.
3.Средства
программирования
Различные программные
комплексы,необходимые для поддержки
созданных программ.
8. Операционные
системы: понятие, основные функции,
характеристики. ОС семейства Windows.
ОС-комплекс
программ,входящих в состав ПО
ПК,обеспечивающих управление работы
аппаратных средств компьютера,обменом
данными между аппаратными узлами ПК
,а также организацию диалога компьютера
с пользователем.
ОС могут
классифицироваться на :
1.по количеству
пользователей (однопользовательские
и многопользовательские)
2.по количеству
решаемых задач (однозадачные и
многозадачные)
3..по доступу
(пакетные,интерактивные,системы
реального времени)
Примеры
ОС-Windows
(95,98,ME,NT,2000,XP,Vista,7,8);Unix,Mac OS,ets
ОС отвечает за
управление всех устройств и обеспечивает
пользователя необходимыми ему для
решения задач и работы с аппаратурой
программами,
ОС семейства
Windows
являются многозадачными, имеют
графический интерфейс. Переход от
работы в одном приложении в другое
осуществляется с помощью перехода от
одного открытого окна к другому. Также
графический интерфейс реализован с
помощью функции Drag-and-Drop.В
этой ОС организована иерархическая
структура подчинения папок, а пусть
доступа к файлу является цепочкой
папок, которую необходимо пройти по
иерархической структуре к папке, где
зарегистрирован необходимый файл.
9. Особенности
обмена данными между приложениями ОС
Windows.
Обмен
данными между приложениями. Кроме
того возможен обмен данными между
приложениями, что позволяет, например,
информацию созданную в электронной
таблице, перенести в текстовый документ
через буфер обмена.
10.Понятие
форматирования текстового документа.
Способы выделения текста. Форматирование
символов, абзацев в MS Word.
С
понятием форматирования документа в
Word связываются три основные операции:
-
форматирование
символов; -
форматирование
абзацев; -
форматирование
страниц.
Word
может самостоятельно улучшать внешний
вид документов. Для этого после ввода
всего текста нужно воспользоваться
командой Автоформат меню Формат. Эта
команда накладывает на абзацы документа
набор атрибутов формата, что улучшает
его внешний вид и придает единый стиль.
Кроме того, команда Автоформат может
автоматически произвести некоторые
замены текста в документе, например,
заменить прямые кавычки парными. После
применения команды Автоформат можно
быстро подправить общий вид документа
с помощью библиотеки стилей Word.Команда
Автоформат формирует документ, анализируя
каждый абзац и назначая ему подходящий
стиль, который представляет собой набор
атрибутов формата с уникальным именем.Для
того чтобы автоматически отформатировать
только некоторую часть документа,
следует выделить эту часть перед
выполнением команды Автоформат.
Word
может автоматически изменять некоторые
атрибуты формата во время ввода
документа. Для этого следует выполнить
команду Параметры команды Автоформат
меню Формат или команду Автозамена
меню Сервис и в появившемся диалоговом
окне выбрать вкладку Автоформат при
вводе.
На
отдельные символы можно накладывать
следующие атрибуты формата:
-
шрифт
— общий дизайн символов (вид шрифта); -
размер
— высота символов, измеряемая в пунктах
(1 пункт = 1/72 дюйма); -
начертание
— внешний вид (обычный, полужирный,
курсив и т. д.); -
подчеркивание
символа — одинарное, двойное, пунктирное
или только слова (пробелы не
подчеркиваются); -
эффекты
— выделение символов: зачеркивание,
верхний индекс, нижний индекс, скрытый,
малые прописные и все прописные; -
цвет
— цвет символов на экране монитора
или на цветном принтере; -
интервал
— расстояние добавляемое или отнимаемое
от межсимвольного интервала для
получения растянутого или сжатого
текста;
Для
форматирования символов используется
команда Шрифт меню Формат или контекстного
меню. Диалоговое окно этой команды
содержит три вкладки для настройки
шрифта, интервалов между символами и
анимации.
1.Создание таблиц
в MS Word. Вставка/удаление строк и столбцов.
Таблица Word
состоит из строк и столбцов ячеек.
Таблицы Word могут содержать цифры, текст
и рисунки. Таблицы Word используются для
упорядочения и представления данных.
Они позволяют выстроить числа в столбцы,
а затем отсортировать их, а также
выполнить различные вычисления. Границы
и линии сетки
Таблица
Word имеет границу в виде тонкой сплошной
линии черного цвета. Граница сохраняется
при печати, а в случае удаления границы
линии сетки отображаются на экране.
Удаление (восстановление) границы
осуществляется командой Формат / Границы
и заливка, на вкладке Границы или
командой Внешние границы на панели
инструментов. Линии сетки не печатаются,
но их тоже можно удалить (восстановить)
командой Таблица / Скрыть сетку
(Отображать сетку).
Концевые
символы
Символ
ячейки и символ строки являются
непечатаемыми знаками, которые
обозначают, соответственно, конец
ячейки и конец строки.
Поля
ячеек и интервалы между ячейками
Поля
ячеек – это расстояние между границей
ячейки и текстом внутри ячейки. Интервалы
между ячейками и поля ячеек можно
изменить в окне диалога Параметры
таблицы, которое можно вызвать командой
Таблица / Свойства таблицы, нажав кнопку
Параметры.
Маркер
перемещения и маркер изменения размера
таблицы
Маркер
перемещения таблицы служит для
перемещения таблицы в другое место
страницы, а маркер изменения размера
таблицы позволяет изменить размер
таблицы.
Создание
таблицы Word
Создание
новой таблицы Word можно осуществить
тремя способами:
Нарисовать
Вставить
Создание на
основе существующих данных (текста,
чисел)
-
Нарисовать
(создать) таблицу Word
Для
создания таблицы Word со сложным заголовком
целесообразно использовать способ
Нарисовать таблицу. Для этого надо
выбрать команду Таблица / Нарисовать
таблицу. Появится плавающая панель
инструментов Таблицы и границы. С
помощью этой панели можно создать
таблицу и осуществить ее редактирование
и форматирование. -
2.
Вставка (создание) таблицы Word
Чтобы
быстро создать простую таблицу в Word,
необходимо воспользоваться командой
Таблица/Вставить/Таблица. Появится
диалоговое окно Вставка таблицы
3. Преобразование
существующего текста в таблицу
При
преобразовании текста в таблицу
необходимо указать, в каком месте должен
начинаться каждый столбец. Для этого
используют символы разделителей. В
качестве разделителя может быть выбран
знак абзаца, знак табуляции, точка с
запятой или другой.
Ввод
текста в ячейку
Для
ввода текста в ячейку, необходимо
щелкнуть на ячейке и ввести текст с
клавиатуры или вставить из буфера
обмена при копировании текста. Если
текст не помещается в строке , то он
переносится на другую строку и увеличивает
высоту строки.
Для
изменения ориентации текста в ячейке
необходимо установить курсор в ячейку
и в меню Формат выбрать команду
Направление текста. Для изменения
выравнивания текста в ячейке на панели
инструментов Таблицы и границы выберите
параметр выравнивания по вертикали и
горизонтали.
Для
перемещения, копирования и удаления
текста в ячейках необходимо выделить
этот текст. Выделенный текст можно
удалять клавишей Delete или Backspace, а также
копировать и перемещать как с помощью
буфера обмена, так и методом перемещения
при помощи мыши (при нажатой левой или
правой клавиши).
Форматирование
текста в ячейках осуществляется методами
форматирования обычного текста. Добавить
текст перед таблицей в начале страницы
можно, если установить курсор в начале
первой строки и нажать клавишу Enter.
К
операциям редактирования таблиц Word
относится:
Вставить и
удалить строки и столбцы
Объединить и разбить ячейки
Разбить
таблицу
Для
редактирования элементов (ячеек, строк,
столбцов) необходимо выделить эти
элементы, а затем использовать меню
Таблица или контекстное меню.
12.Создание формул
в MS Word.
Для
работы с формулами
в комплект Microsoft Office входит
«Редактор формул» («Equation editor»
в английской версии).
13.
Структура окна MS Excel.
После запуска Ех.
Появляется окно следующей структуры:
1.Заголовок программы
2.Панель быстрого
доступа
3.Ленты
3.1.Вкладки(главная,вставка,разметка,и
т.д.)
3.2.Способы
сворачивания ленты(2 щелчка по Главная)
4.Вкладка (Меню
файлов.Всегда расположена в ленте
первой слева.Меню содержит набор
команд,необходимых для работы с
файлами,для настойки Ех и т.д.)
5.Мини-панель
инструментов
6.Строка формул
7.Координатная
строка (содержит имена столбцов)
7.1.Координатный
столбец.
8.Ярлычки листов
8.1. Кнопки для
быстрого перемещения по листам.
9.Строка
состояния(Готово,Ввод,Правка)
10.Линейка масштаба
11.Клавиши режима
отображения документов.
14.Основные объекты
MS Excel. Типы данных.
1.Столбец.
Таблица Ех содержит
16384 стоблца.
2.Строка.
1048576 строк.
3.Ячейка.
Место пересечения
строки и стоблца.
4.Блок ячеек.
Прямоугольник,в
котором указываются адреса ячеек
верхнего и нижнего правого углов.
5.Рабочий лист.
Созданная таблица
для решения задач,построения диаграмм
и т.д.
6.Стандартное имя
листа
Книга-файл,хранящийся
на диске и содержащий в себе 1 или более
листов.
Типы данных.
1.Текст.
2.Число.(целые,дробные
с фиксированной запятой,с плавающей
запятой(например: 1,5Е-03=1,5*10^-3))
3.Формула.
4.Функция.
5.Даты.
15.Построение рядов
данных.
-
Заполнение рядов
с помощью мыши. -
Использование
правой кнопки мыши при перетаскивании
маркера заполнения. -
Создание
пользовательских списков.
Заполнение рядов с помощью мыши
Можно использовать
маркер заполнения для быстрого заполнения
ячеек и создания рядов.
После выделения
одной ячейки надо установить указатель
на маркере заполнения и затем перетащить
его в любом направлении. Содержимое
этой ячейки копируется в выделенный
диапазон.
Использование правой кнопки мыши при перетаскивании маркера заполнения
Если использовать
правую кнопку мыши для заполнения
диапазона или расширения ряда, то при
отпускании кнопки появляется контекстное
меню.
Команды из этого
контекстного меню можно использовать
для изменения способа заполнения
диапазонов или рядов.
Команда «Копировать
ячейки» —
просто копирует выделенные исходные
ячейки в конечный диапазон, повторяя
при необходимости значения ячеек из
исходного диапазона.
При
выборе команды «Заполнить»,
последовательность выделенных чисел
расширится, как если бы мы перетаскивали
маркер заполнения при нажатой левой
кнопке мыши.
Создание пользовательских списков
Иногда приходится
повторять ввод конкретной последовательности
в рабочем листе, например списка имен.
В таком случае можно создать
пользовательский список. После создания
такого списка его можно ввести в диапазон
ячеек простым вводом в ячейку любого
элемента этого списка с последующим
перетаскиванием маркера заполнения.
Чтобы создать
пользовательский список, надо выполнить
следующие действия:
1. В меню «Сервис»
выбрать команду «Параметры» и в
открывшемся окне диалога щелкнуть на
вкладке «Списки».
2. В списке
«Списки» выбрать пункт НОВЫЙ СПИСОК
и в списке «Элементы списка» ввести
значения, которые надо включить в данный
список. Обязательно надо вводить в том
порядке, в котором они должны появляться
в рабочем листе.
3. Нажать кнопку
«Добавить», чтобы включить свой
список в перечень пользовательских
списков.
4. Нажать ОК.
16. Операции с
рабочими листами. Одномерное и многомерное
связывание.
???
17.
18. Абсолютная и
относительная адресация ячеек MS Excel.
Присвоение имени ячейки.
Автоматически в
новых формулах Ех использует относительные
ссылки.В этом случае при копировании
ячейки с формулой адреса копируются в
соответствии перемещению.
Абсолютная
адресация-ссылки на ячейки,остающиеся
неизменными при их копировании вдоль
строк и стоблцов.Для задания такой
адресации ставится знак $,например
$D$2.
Эквивалентными
абсолютной адресации являются ячейки
с присвоенными им именами..
19.Стандартные
функции MS Excel: математические,
статистические, логические.
Функция-запрограммированная
последовательность стандартных
вычислений.Используется для упрощения
формулы в ячейке,особенно когда функция
большая и сложная.Функции содержат в
себе имя и аргументы(которыми могут
быть числа,тексты,логические значения
и т.д.).
Существуют также
функции без аргумента,например,функции
СЕГОДНЯ или ПИ.
Стандартные
функции.Категории.
1.Математические.
СУММ,СУММЕСЛИ(суммирует
ячейки в указанном
диапазоне),ПРОИЗВЕД,СТЕПЕНЬ,СЛУЧМЕЖДУ(возвращает
случайное число между 2-мя заданными
числами),ЕХР,Ln
и т.д.
2.Статические
функции
СРЗНАЧ,МИН,МАКС,СЧЕТ,СЧЕТЕСЛИ,РАНГ.РВ.((число/ссылка/порядок);где
ссылка-массив/ссылка на список чисел,с
которыми сравнивается число,а
порядок-число от 0 до 1,определяет способ
ранга)
3.Логические
ЕСЛИ,И,ИЛИ,НЕ(меняет
истину на ложь и наоборот).
20.Матричные операции
в Ех.
Как и
над числами, над матрицами можно
проводить ряд операций. Способов
вычислений существует также несколько.
Например, вычисления с помощью MS Excel.
Одной
из операций является операция
транспонирования. Для осуществления
транспонирования в Excel используется
функция ТРАНСП, которая позволяет
поменять ориентацию массива на рабочем
листе с вертикальной на горизонтальную
и наоборот. Данная функция будет иметь
вид ТРАНСП (массив). Здесь массив – это
транспонируемый массив или диапазон
ячеек на рабочем листе. Транспонирование
массива заключается в том, что первая
строка массива становится первым
столбцом нового массива, вторая строка
массива становится вторым столбцом
нового массива и т.д.
Одной
из важных характеристик квадратных
матриц является их определитель.
Определитель матрицы – это число,
вычисляемое на основе значений элементов
массива. В MS Excel для вычисления определителя
квадратной матрицы используется функция
МОПРЕД. Функция имеет вид МОПРЕД
(массив). В этом случае массив – это
числовой массив, в котором хранится
матрица с равным количеством строк и
столбцов.
Для нахождения
обратной матрицы в MS Excel используется
функция МОБР, которая вычисляет обратную
матрицу для матрицы, хранящей в таблице
в виде массива. Функция имеет вид МОБР
(массив). Здесь массив – это числовой
массив с равным количеством строк и
столбцов. Массив может быть задан как
диапазон ячеек, например А1:С3; как массив
констант, например (1;2;3;4;5;6;7;8;9) или как
имя диапазона или массива.
Для нахождения
произведения двух матриц в Excel используется
функция МУМНОЖ, которая вычисляет
произведения матриц (матрицы хранятся
в массивах). Функция имеет вид МУМНОЖ
(массив1;массив2). Здесь массив1 и массив2
– это перемножаемые массивы.
21. Форматирование
ячеек и данных таблицы.
Содержание
- Применение критериев
- СЧЁТЕСЛИ
- СЧЁТЕСЛИМН
- СУММЕСЛИ
- СУММЕСЛИМН
- Условное форматирование
- Вопросы и ответы
Программа Microsoft Excel является не просто табличным редактором, а ещё и мощнейшим приложением для различных вычислений. Не в последнюю очередь такая возможность появилась благодаря встроенным функциям. С помощью некоторых функций (операторов) можно задавать даже условия вычисления, которые принято называть критериями. Давайте подробнее узнаем, каким образом можно их использовать при работе в Экселе.
Применение критериев
Критерии представляют собой условия, при которых программа выполняет определенные действия. Они применяются в целом ряде встроенных функций. В их названии чаще всего присутствует выражение «ЕСЛИ». К данной группе операторов, прежде всего, нужно отнести СЧЁТЕСЛИ, СЧЁТЕСЛИМН, СУММЕСЛИ, СУММЕСЛИМН. Кроме встроенных операторов, критерии в Excel используются также при условном форматировании. Рассмотрим их применение при работе с различными инструментами данного табличного процессора более подробно.
СЧЁТЕСЛИ
Главной задачей оператора СЧЁТЕСЛИ, относящегося к статистической группе, является подсчет занятых различными значениями ячеек, которые удовлетворяют определенному заданному условию. Его синтаксис следующий:
=СЧЁТЕСЛИ(диапазон;критерий)
Как видим, у данного оператора два аргумента. «Диапазон» представляет собой адрес массива элементов на листе, в которых следует произвести подсчет.
«Критерий» — это аргумент, который задаёт условие, что именно должны содержать ячейки указанной области, чтобы быть включенными в подсчет. В качестве параметра может быть использовано числовое выражение, текст или ссылка на ячейку, в которой критерий содержится. При этом, для указания критерия можно использовать следующие знаки: «<» («меньше»), «>» («больше»), «=» («равно»), «<>» («не равно»). Например, если задать выражение «<50», то при подсчете будут учитываться только элементы, заданные аргументом «Диапазон», в которых находятся числовые значения менее 50. Использование данных знаков для указания параметров будут актуальными и для всех других вариантов, о которых пойдет речь в данном уроке ниже.
А теперь давайте на конкретном примере посмотрим, как работает данный оператор на практике.
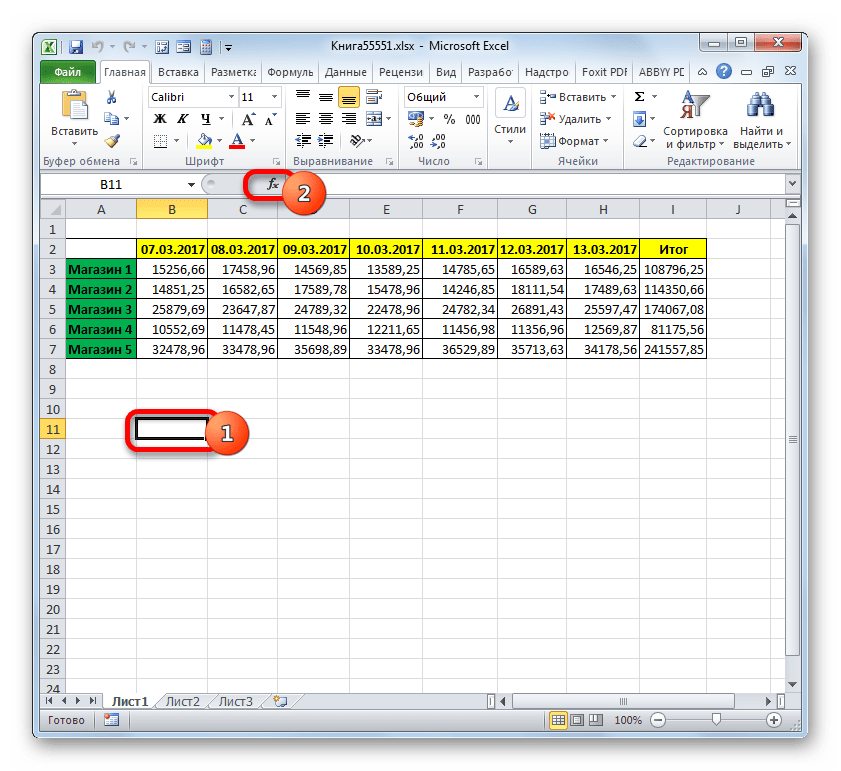
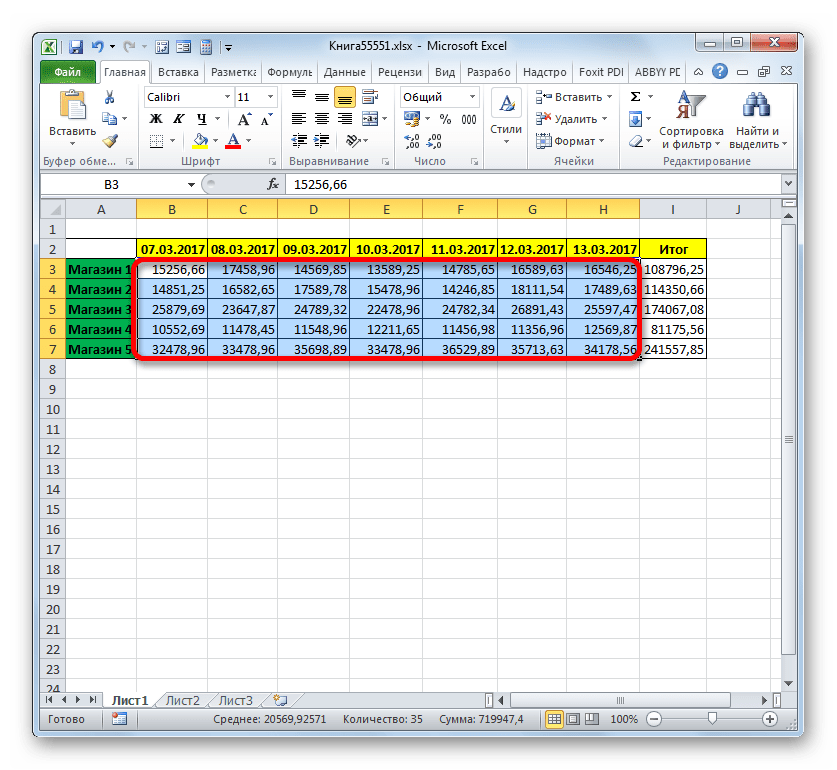
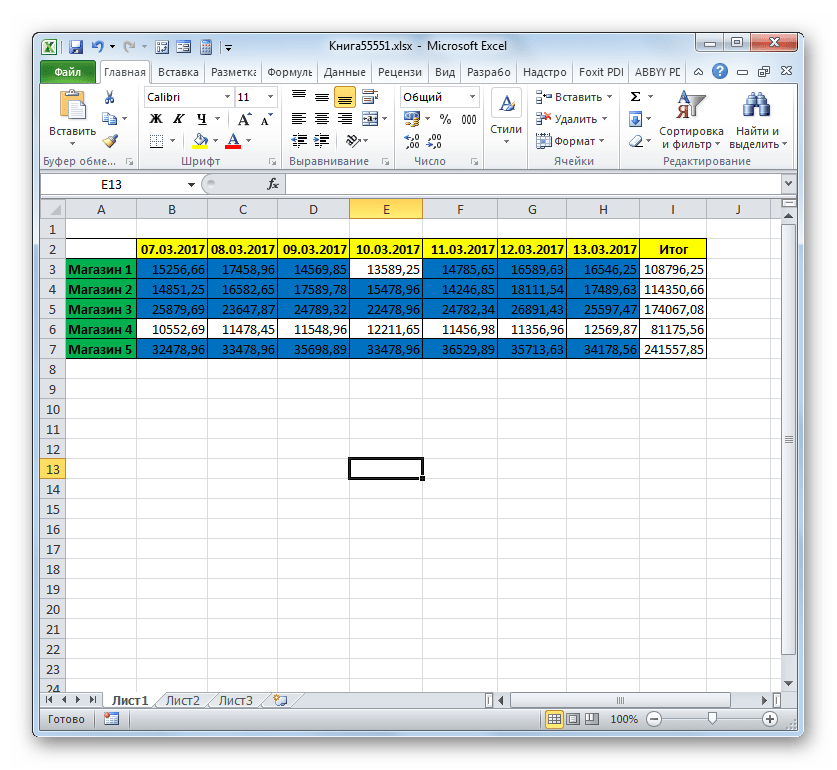
Итак, имеется таблица, где представлена выручка по пяти магазинам за неделю. Нам нужно узнать количество дней за этот период, в которых в Магазине 2 доход от реализации превысил 15000 рублей.
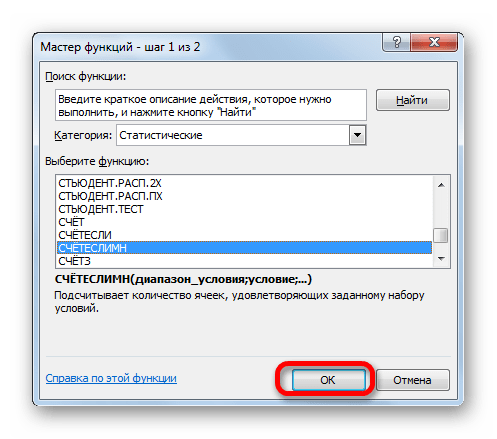
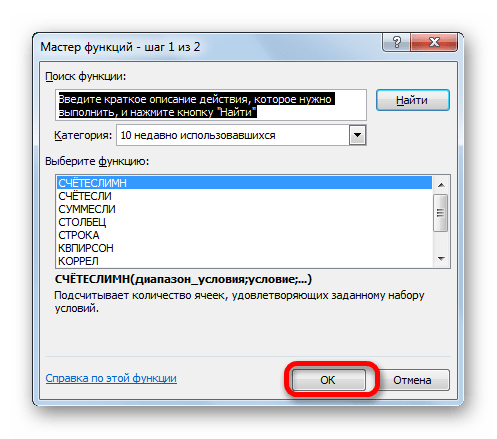
- Выделяем элемент листа, в который оператор будет выводить результат вычисления. После этого щелкаем по пиктограмме «Вставить функцию».
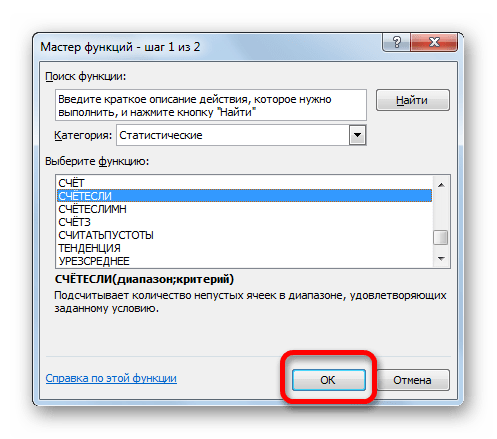
- Производится запуск Мастера функций. Совершаем перемещение в блок «Статистические». Там находим и выделяем наименование «СЧЁТЕСЛИ». Затем следует клацнуть по кнопке «OK».
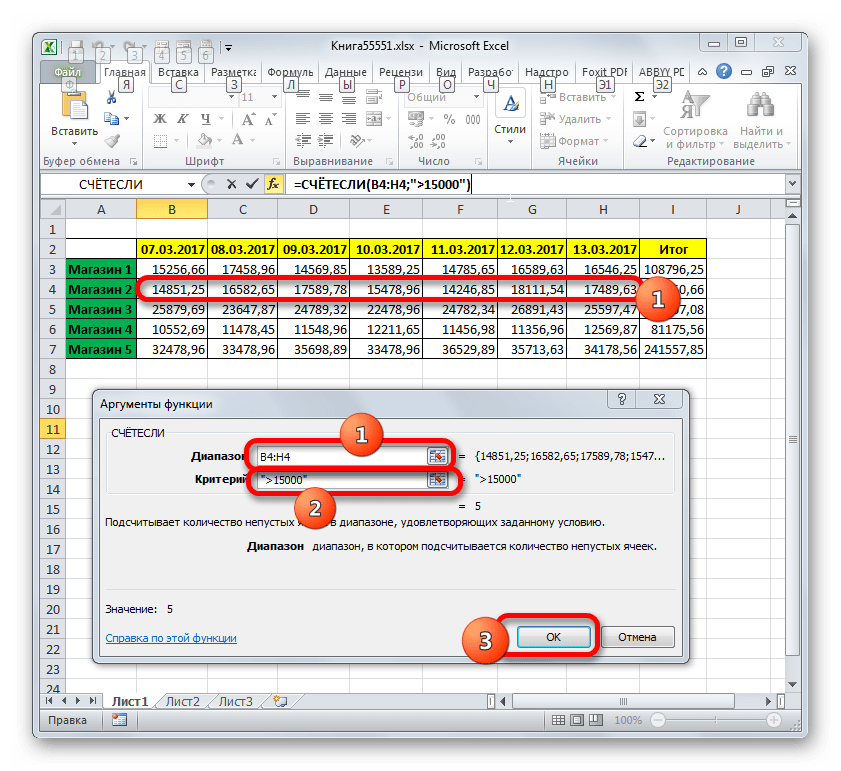
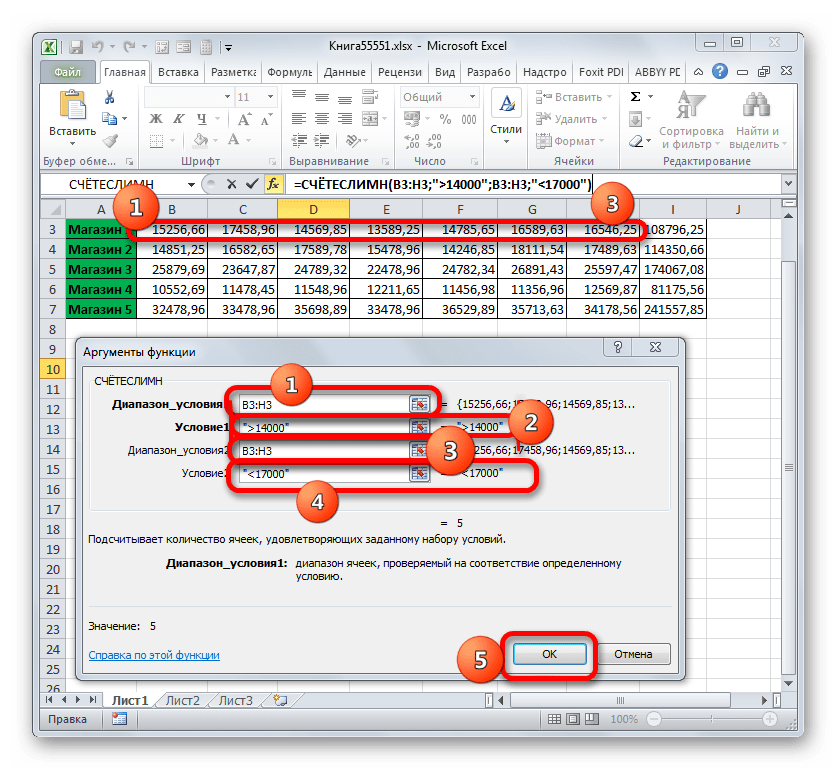
- Происходит активация окна аргументов вышеуказанного оператора. В поле «Диапазон» следует указать область ячеек, среди которых будет производиться подсчет. В нашем случае следует выделить содержимое строки «Магазин 2», в которой расположены значения выручки по дням. Ставим курсор в указанное поле и, зажав левую кнопку мыши, выделяем соответствующий массив в таблице. Адрес выделенного массива отобразится в окне.
В следующем поле «Критерий» как раз нужно задать непосредственный параметр отбора. В нашем случае нужно подсчитать только те элементы таблицы, в которых значение превышает 15000. Поэтому с помощью клавиатуры вбиваем в указанное поле выражение «>15000».
После того, как все вышеуказанные манипуляции произведены, клацаем по кнопке «OK».
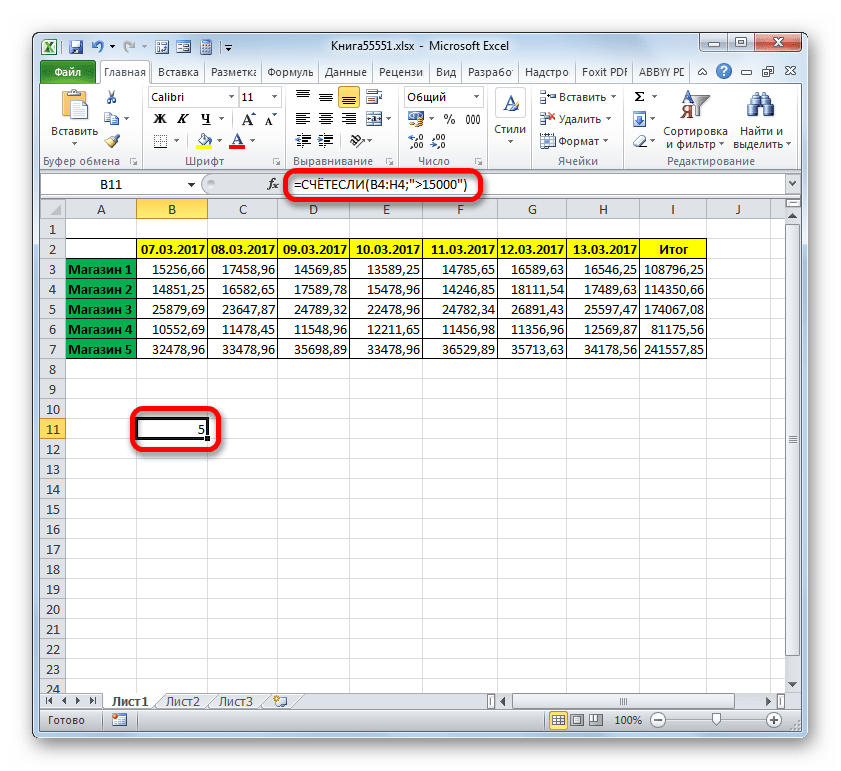
- Программа производит подсчет и выводит результат в элемент листа, который был выделен перед активацией Мастера функций. Как видим, в данном случае результат равен числу 5. Это означает, что в выделенном массиве в пяти ячейках находятся значения превышающие 15000. То есть, можно сделать вывод, что в Магазине 2 в пяти днях из анализируемых семи выручка превысила 15000 рублей.
Урок: Мастер функций в программе Эксель
СЧЁТЕСЛИМН
Следующей функцией, которая оперирует критериями, является СЧЁТЕСЛИМН. Она также относится к статистической группе операторов. Задачей СЧЁТЕСЛИМН является подсчет ячеек в указанном массиве, которые удовлетворяют определенному набору условий. Именно тот факт, что можно задать не один, а несколько параметров, и отличает этого оператора от предыдущего. Синтаксис следующий:
=СЧЁТЕСЛИМН(диапазон_условия1;условие1;диапазон_условия2;условие2;…)
«Диапазон условия» является идентичным первому аргументу предыдущего оператора. То есть, он представляет собой ссылку на область, в которой будет производиться подсчет ячеек, удовлетворяющих указанным условиям. Данный оператор позволяет задать сразу несколько таких областей.
«Условие» представляет собой критерий, который определяет, какие элементы из соответствующего массива данных войдут в подсчет, а какие не войдут. Каждой заданной области данных нужно указывать условие отдельно, даже в том случае, если оно совпадает. Обязательно требуется, чтобы все массивы, используемые в качестве областей условия, имели одинаковое количество строк и столбцов.
Для того, чтобы задать несколько параметров одной и той же области данных, например, чтобы подсчитать количество ячеек, в которых расположены величины больше определенного числа, но меньше другого числа, следует в качестве аргумента «Диапазон условия» несколько раз указать один и тот же массив. Но при этом в качестве соответствующих аргументов «Условие» следует указывать разные критерии.
На примере все той же таблицы с недельной выручкой магазинов посмотрим, как это работает. Нам нужно узнать количество дней недели, когда доход во всех указанных торговых точках достигал установленной для них нормы. Нормы выручки следующие:
- Магазин 1 – 14000 рублей;
- Магазин 2 – 15000 рублей;
- Магазин 3 – 24000 рублей;
- Магазин 4 – 11000 рублей;
- Магазин 5 – 32000 рублей.
- Для выполнения вышеуказанной задачи, выделяем курсором элемент рабочего листа, куда будет выводиться итог обработки данных СЧЁТЕСЛИМН. Клацаем по иконке «Вставить функцию».
- Перейдя в Мастер функций, снова перемещаемся в блок «Статистические». В перечне следует отыскать наименование СЧЁТЕСЛИМН и произвести его выделение. После выполнения указанного действия требуется произвести нажатие на кнопку «OK».
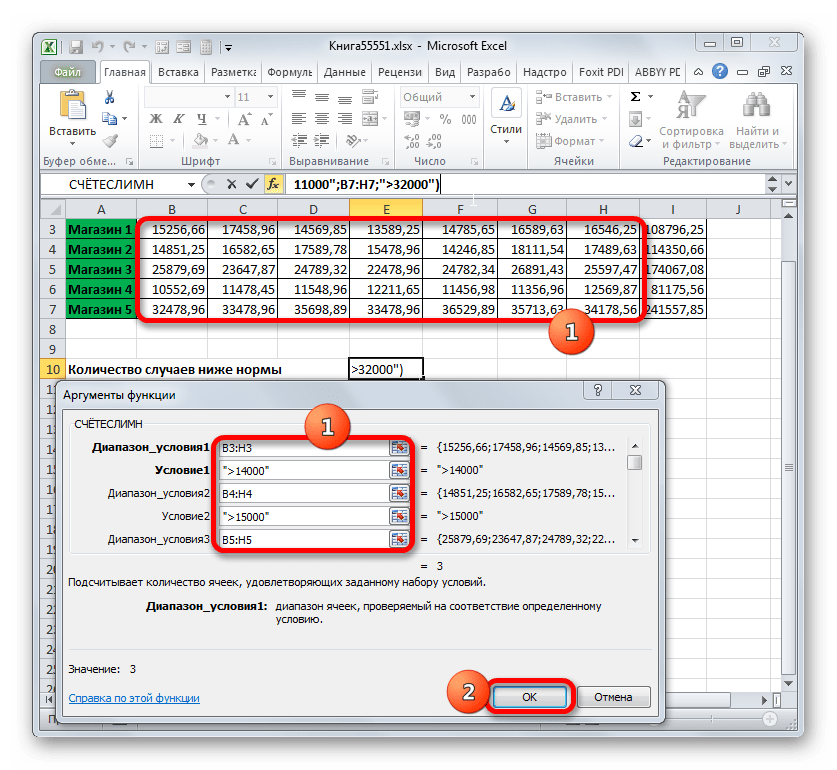
- Вслед за выполнением вышеуказанного алгоритма действий открывается окно аргументов СЧЁТЕСЛИМН.
В поле «Диапазон условия1» следует ввести адрес строки, в которой расположены данные по выручке Магазина 1 за неделю. Для этого ставим курсор в поле и выделяем соответствующую строку в таблице. Координаты отображаются в окне.
Учитывая, что для Магазина 1 дневная норма выручки составляет 14000 рублей, то в поле «Условие 1» вписываем выражение «>14000».
В поля «Диапазон условия2 (3,4,5)» следует внести координаты строк с недельной выручкой соответственно Магазина 2, Магазина 3, Магазина 4 и Магазина 5. Действие выполняем по тому же алгоритму, что и для первого аргумента данной группы.
В поля «Условие2», «Условие3», «Условие4» и «Условие5» вносим соответственно значения «>15000», «>24000», «>11000» и «>32000». Как нетрудно догадаться, эти значения соответствуют интервалу выручки, превышающую норму для соответствующего магазина.
После того, как был произведен ввод всех необходимых данных (всего 10 полей), жмем на кнопку «OK».
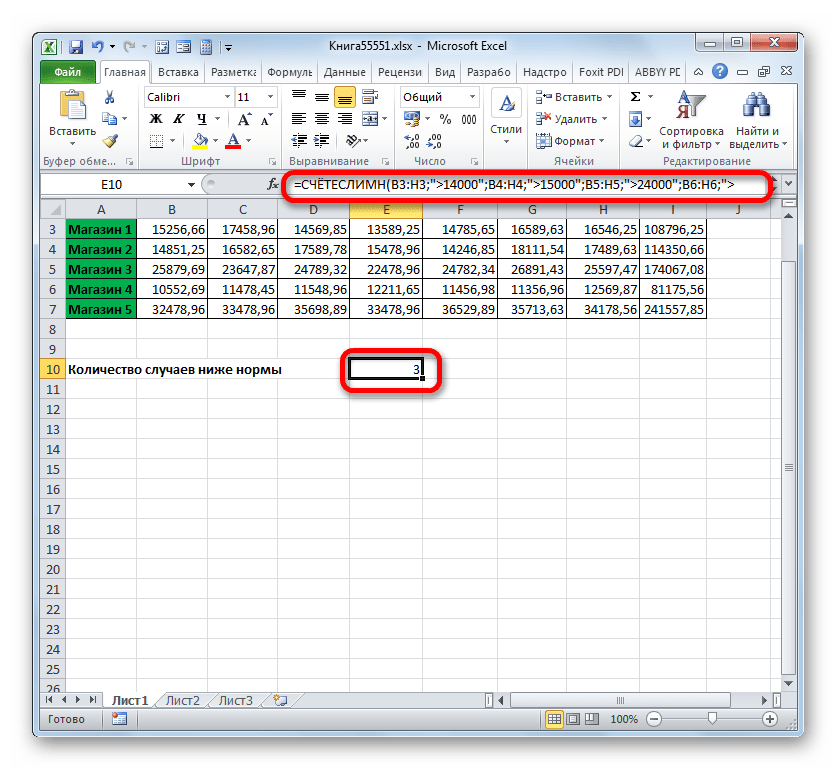
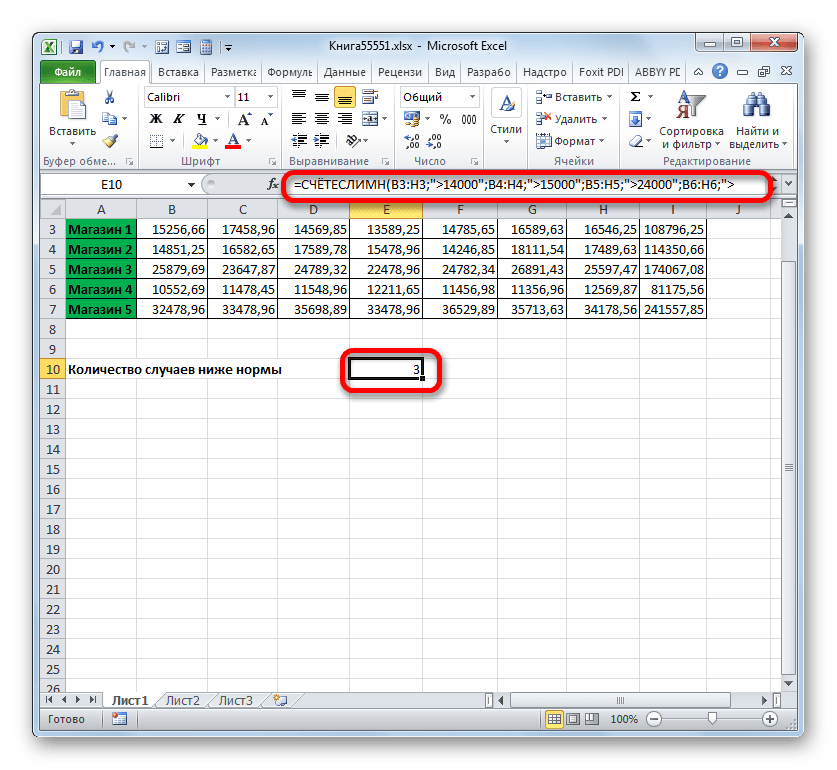
- Программа производит подсчет и выводит результат на экран. Как видим, он равен числу 3. Это означает, что в трех днях из анализируемой недели выручка во всех торговых точках превышала установленную для них норму.
Теперь несколько изменим задачу. Нам следует посчитать количество дней, в которых Магазин 1 получил выручку, превышающую 14000 рублей, но меньшую, чем 17000 рублей.
- Ставим курсор в элемент, где будет произведен вывод на лист результатов подсчета. Клацаем по пиктограмме «Вставить функцию» над рабочей площадью листа.
- Так как мы совсем недавно применяли формулу СЧЁТЕСЛИМН, то теперь не обязательно переходить в группу «Статистические» Мастера функций. Наименование данного оператора можно найти в категории «10 недавно использовавшихся». Выделяем его и щелкаем по кнопке «OK».
- Открывается уже знакомое нам окошко аргументов оператора СЧЁТЕСЛИМН. Ставим курсор в поле «Диапазон условия1» и, произведя зажим левой кнопки мыши, выделяем все ячейки, в которых содержится выручка по дням Магазина 1. Они расположены в строке, которая так и называется «Магазин 1». После этого координаты указанной области будут отражены в окне.
Далее устанавливаем курсор в поле «Условие1». Тут нам нужно указать нижнюю границу значений в ячейках, которые будут принимать участие в подсчете. Указываем выражение «>14000».
В поле «Диапазон условия2» вводим тот же адрес тем же способом, который вводили в поле «Диапазон условия1», то есть, опять вносим координаты ячеек со значениями выручки по первой торговой точке.
В поле «Условие2» указываем верхнюю границу отбора: «<17000».
После того, как все указанные действия произведены, клацаем по кнопке «OK».
- Программа выдает результат расчета. Как видим, итоговое значение равно 5. Это значит, что в 5 днях из исследуемых семи выручка в первом магазине была в интервале от 14000 до 17000 рублей.
СУММЕСЛИ
Ещё одним оператором, который использует критерии, является СУММЕСЛИ. В отличие от предыдущих функций, он относится к математическому блоку операторов. Его задачей является суммирование данных в ячейках, которые соответствуют определенному условию. Синтаксис таков:
=СУММЕСЛИ(диапазон;критерий;[диапазон_суммирования])
Аргумент «Диапазон» указывает на область ячеек, которые будут проверяться на соблюдение условия. По сути, он задается по тому же принципу, что и одноименный аргумент функции СЧЁТЕСЛИ.
«Критерий» — является обязательным аргументом, задающим параметр отбора ячеек из указанной области данных, которые будут суммироваться. Принципы указания те же, что и у аналогичных аргументов предыдущих операторов, которые были рассмотрены нами выше.
«Диапазон суммирования» — это необязательный аргумент. Он указывает на конкретную область массива, в которой будет производиться суммирование. Если его опустить и не указывать, то по умолчанию считается, что он равен значению обязательного аргумента «Диапазон».
Теперь, как всегда, рассмотрим применение данного оператора на практике. На основе той же таблицы перед нами стоит задача подсчитать сумму выручки в Магазине 1 за период, начиная с 11.03.2017.
- Выделяем ячейку, в которой будет производиться вывод результата. Щелкаем по пиктограмме «Вставить функцию».
- Перейдя в Мастер функций в блоке «Математические» находим и выделяем наименование «СУММЕСЛИ». Клацаем по кнопке «OK».
- Запускается окно аргументов функции СУММЕСЛИ. В нём имеется три поля, соответствующих аргументам указанного оператора.
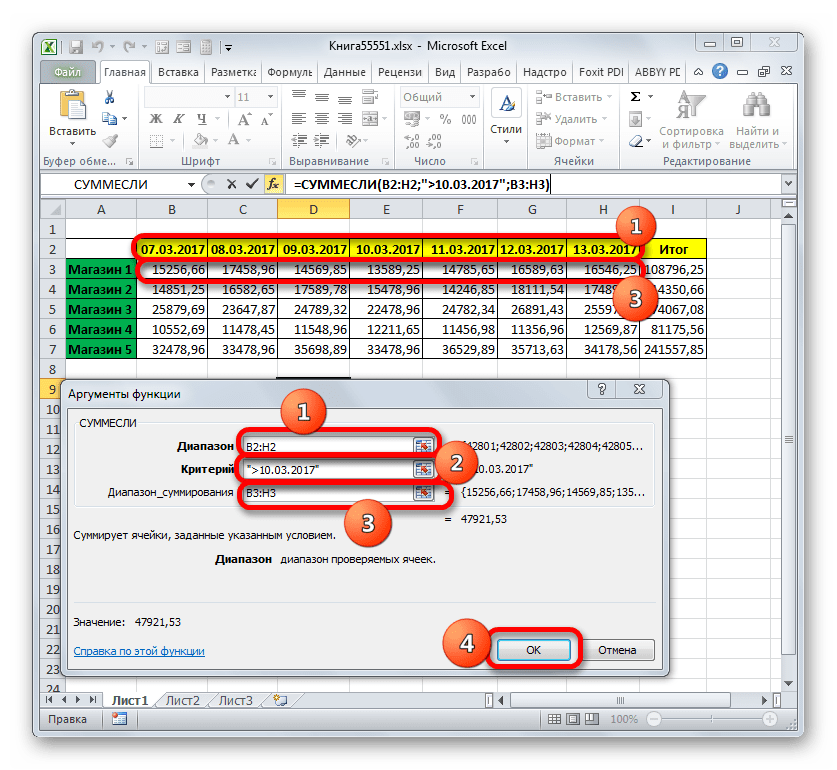
В поле «Диапазон» вводим область таблицы, в которой будут располагаться значения, проверяемые на соблюдение условий. В нашем случае это будет строка дат. Ставим курсор в данное поле и выделяем все ячейки, в которых содержатся даты.
Так как нам нужно сложить только суммы выручки, начиная с 11 марта, то в поле «Критерий» вбиваем значение «>10.03.2017».
В поле «Диапазон суммирования» нужно указать область, значения которой, отвечающие указанным критериям, будут суммироваться. В нашем случае это значения выручки строки «Магазин1». Выделяем соответствующий массив элементов листа.
После того, как произведено введение всех указанных данных, жмем на кнопку «OK».
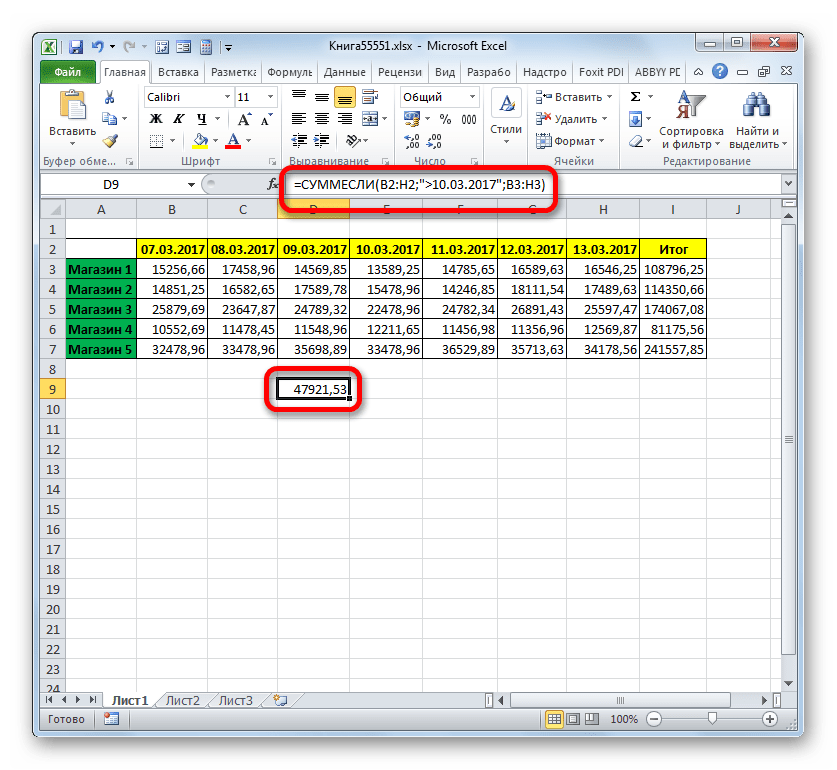
- После этого в предварительно указанный элемент рабочего листа будет выведен результат обработки данных функцией СУММЕСЛИ. В нашем случае он равен 47921,53. Это означает, что начиная с 11.03.2017, и до конца анализируемого периода, общая выручка по Магазину 1 составила 47921,53 рубля.
СУММЕСЛИМН
Завершим изучение операторов, которые используют критерии, остановившись на функции СУММЕСЛИМН. Задачей данной математической функции является суммирование значений указанных областей таблицы, отобранных по нескольким параметрам. Синтаксис указанного оператора таков:
=СУММЕСЛИМН(диапазон_суммирования;диапазон_условия1;условие1;диапазон_условия2;условие2;…)
«Диапазон суммирования» — это аргумент, являющийся адресом того массива, ячейки в котором, отвечающие определенному критерию, будут складываться.
«Диапазон условия» — аргумент, представляющий собой массив данных, проверяемый на соответствие условию;
«Условие» — аргумент, представляющий собой критерий отбора для сложения.
Данная функция подразумевает операции сразу с несколькими наборами подобных операторов.
Посмотрим, как данный оператор применим для решения задач в контексте нашей таблицы выручки от реализации в торговых точках. Нам нужно будет подсчитать доход, который принес Магазин 1 за период с 09 по 13 марта 2017 года. При этом при суммировании дохода должны учитываться только те дни, выручка в которых превысила 14000 рублей.
- Снова выделяем ячейку для вывода итога и клацаем по пиктограмме «Вставить функцию».
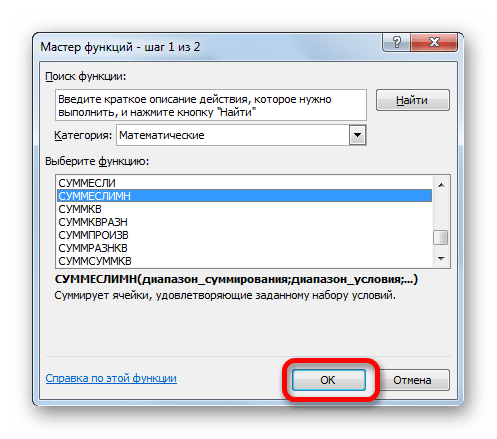
- В Мастере функций, прежде всего, выполняем перемещение в блок «Математические», а там выделяем пункт под названием «СУММЕСЛИМН». Производим клик по кнопке «OK».
- Производится запуск окошка аргументов оператора, наименование которого было указано выше.
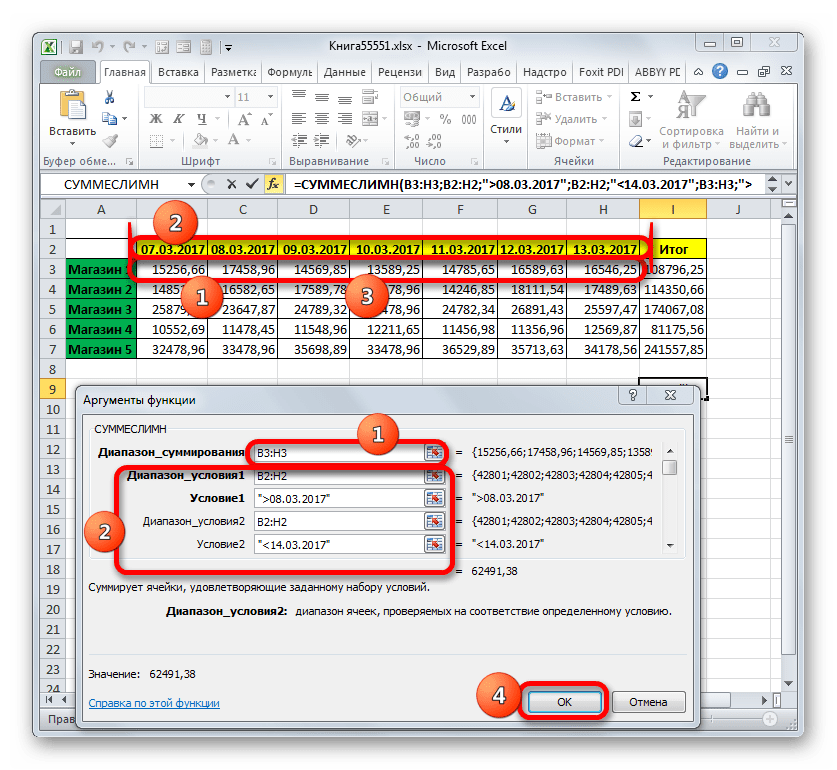
Устанавливаем курсор в поле «Диапазон суммирования». В отличие от последующих аргументов, этот единственный в своем роде и указывает на тот массив значений, где будет производиться суммирование подошедших под указанные критерии данных. Затем выделяем область строки «Магазин1», в которой размещены значения выручки по соответствующей торговой точке.
После того, как адрес отобразился в окне, переходим к полю «Диапазон условия1». Тут нам нужно будет отобразить координаты строки с датами. Производим зажим левой кнопки мыши и выделяем все даты в таблице.
Ставим курсор в поле «Условие1». Первым условием является то, что нами будут суммироваться данные не ранее 09 марта. Поэтому вводим значение «>08.03.2017».
Перемещаемся к аргументу «Диапазон условия2». Тут нужно внести те же координаты, которые были записаны в поле «Диапазон условия1». Делаем это тем же способом, то есть, путем выделения строчки с датами.
Устанавливаем курсор в поле «Условие2». Вторым условием является то, что дни, за которые будет суммироваться выручка, должны быть не позже 13 марта. Поэтому записываем следующее выражение: «<14.03.2017».
Переходим в поле «Диапазон условия2». В данном случае нам нужно выделить тот самый массив, адрес которого был внесен, как массив суммирования.
После того, как адрес указанного массива отобразился в окне, переходим к полю «Условие3». Учитывая, что в суммировании будут принимать участие только значения, величина которых превышает 14000 рублей, вносим запись следующего характера: «>14000».
После выполнения последнего действия клацаем по кнопке «OK».
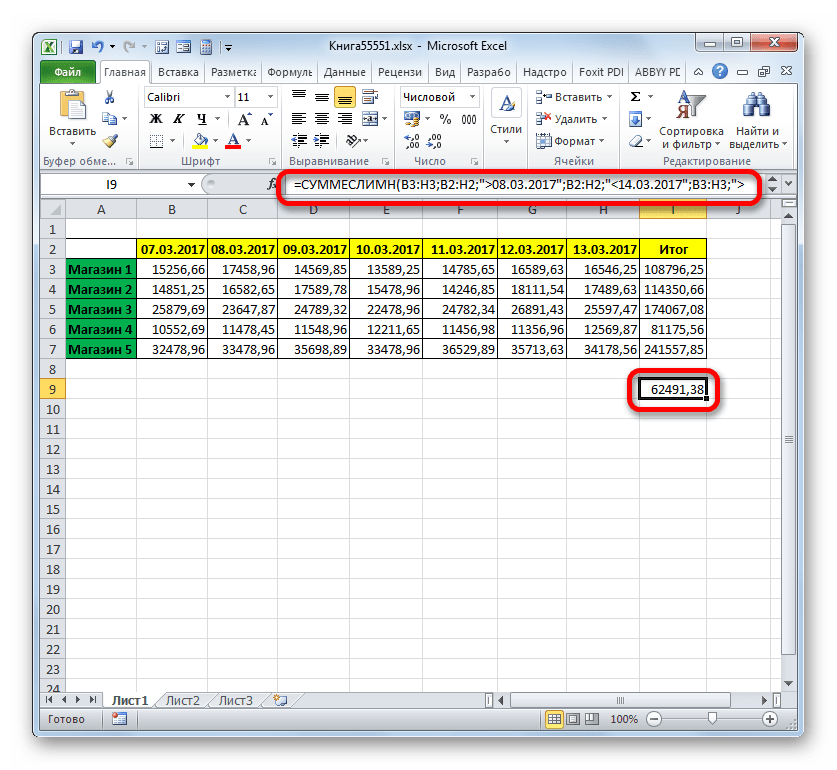
- Программа выводит результат на лист. Он равен 62491,38. Это означает, что за период с 09 по 13 марта 2017 года сумма выручки при сложении её за дни, в которых она превышает 14000 рублей, составила 62491,38 рубля.
Условное форматирование
Последним, описанным нами, инструментом, при работе с которым используются критерии, является условное форматирование. Он выполняет указанный вид форматирования ячеек, которые отвечают заданным условиям. Взглянем на пример работы с условным форматированием.
Выделим те ячейки таблицы синим цветом, где значения за день превышают 14000 рублей.
- Выделяем весь массив элементов в таблице, в котором указана выручка торговых точек по дням.
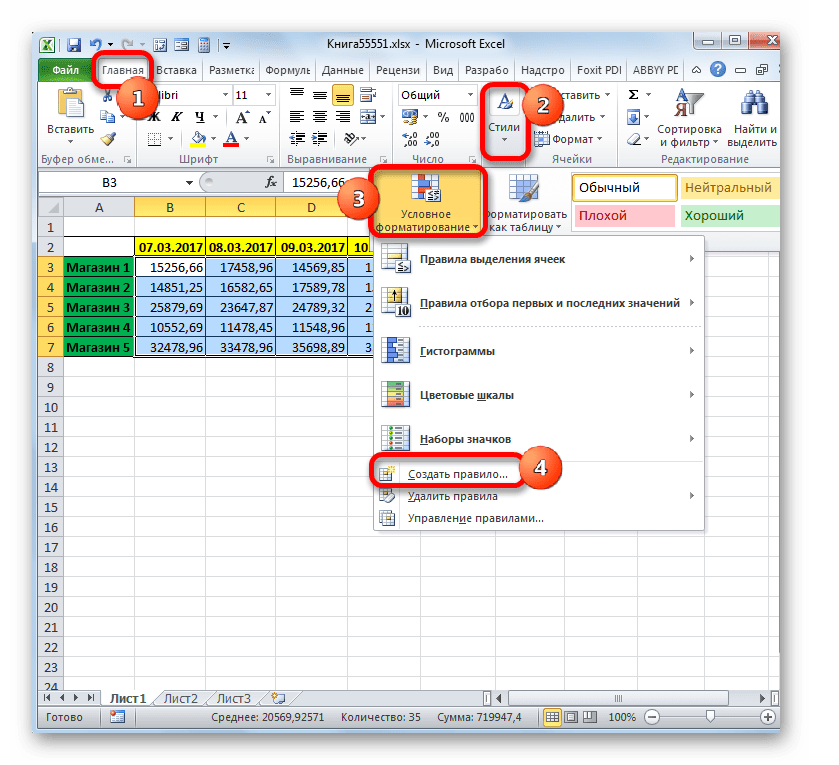
- Передвигаемся во вкладку «Главная». Клацаем по пиктограмме «Условное форматирование», размещенной в блоке «Стили» на ленте. Открывается список действий. Клацаем в нём по позиции «Создать правило…».
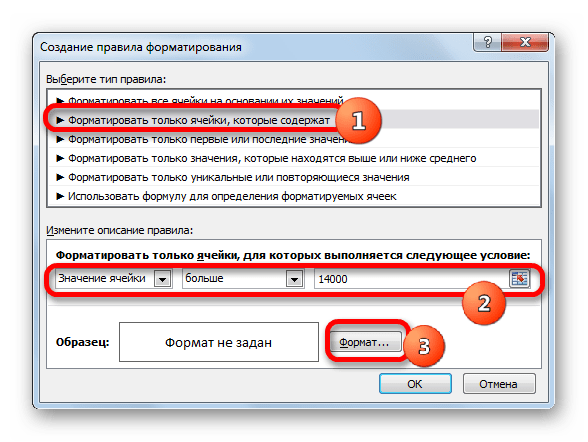
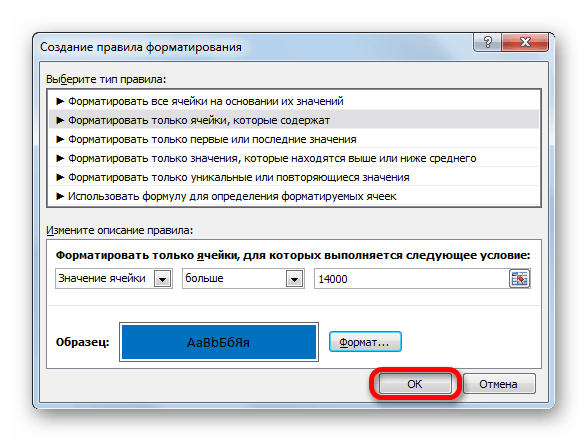
- Активируется окошко генерации правила форматирования. В области выбора типа правила выделяем наименование «Форматировать только ячейки, которые содержат». В первом поле блока условий из списка возможных вариантов выбираем «Значение ячейки». В следующем поле выбираем позицию «Больше». В последнем — указываем само значение, больше которого требуется отформатировать элементы таблицы. У нас это 14000. Чтобы выбрать тип форматирования, клацаем по кнопке «Формат…».
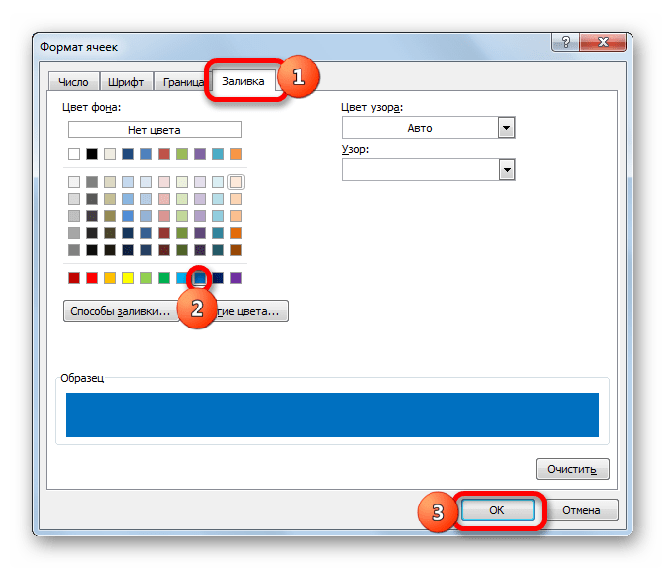
- Активируется окно форматирования. Передвигаемся во вкладку «Заливка». Из предложенных вариантов цветов заливки выбираем синий, щелкая по нему левой кнопкой мыши. После того, как выбранный цвет отобразился в области «Образец», клацаем по кнопке «OK».
- Автоматически происходит возврат к окну генерации правила форматирования. В нём также в области «Образец» отображается синий цвет. Тут нам нужно произвести одно единственное действие: клацнуть по кнопке «OK».
- После выполнения последнего действия, все ячейки выделенного массива, где содержится число большее, чем 14000, будут залиты синим цветом.
Более подробно о возможностях условного форматирования рассказывается в отдельной статье.
Урок: Условное форматирование в программе Эксель
Как видим, с помощью инструментов, использующих при своей работе критерии, в Экселе можно решать довольно разноплановые задачи. Это может быть, как подсчет сумм и значений, так и форматирование, а также выполнение многих других задач. Основными инструментами, работающими в данной программе с критериями, то есть, с определенными условиями, при выполнении которых активируется указанное действие, является набор встроенных функций, а также условное форматирование.
Если вы выберите ряд данных какой-нибудь диаграммы и взгляните на строку формул, вы увидите, что ряд данных генерируется с помощью функции РЯД. РЯД – это специальный вид функции, который используется только в контексте создания диаграммы и определяет значения рядов данных. Вы не сможете использовать ее на рабочем листе Excel и не сможете включить стандартные функции в ее аргументы.
Про аргументы функции РЯД
Для всех видов диаграмм, кроме пузырьковой, функция РЯД имеет список аргументов, представленных ниже. Для пузырьковой диаграммы, требуется дополнительный аргумент, который определяет размер пузыря.
| АРГУМЕНТ | ОБЯЗАТЕЛЬНЫЙ/ НЕ ОБЯЗАТЕЛЬНЫЙ | ОПРЕДЕЛЕНИЕ |
| Имя | Не обязательный | Имя ряда данных, которое отображается в легенде |
| Подписи_категорий | Не обязательный | Подписи, которые появляются на оси категорий (если не указано, Excel использует последовательные целые числа в качестве меток) |
| Значения | Обязательный | Значения, используемые для построения диаграммы |
| Порядок | Обязательный | Порядок ряда данных |
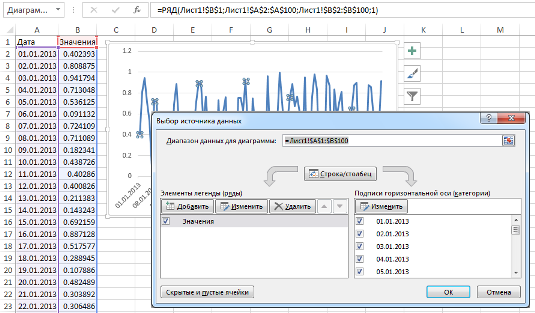
Каждый из этих аргументов соответствует конкретным данным в полях диалогового окна Выбор источника данных (Правый щелчок мыши по ряду данных, во всплывающем меню выбрать Выбор данных).
В строке формул Excel вы можете увидеть примерно такую формулу:
=РЯД(Diag!$B$1;Diag!$A$2:$A$100;Diag!$B$2:$B$100;1)
Аргументами функции РЯД являются данные, которые можно найти в диалоговом окне Выбор источника данных:
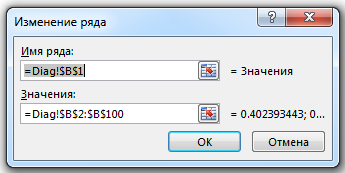
Имя – аргумент Diag!$B$1 можно найти, если щелкнуть по кнопке Изменить, во вкладке Элементы легенды (ряды) диалогового окна Выбор источника данных. Так как ячейка B1 имеет подпись Значение, ряд данных будет называться соответственно.
Подпись_категорий – аргумент Diag!$A$2:$A$100 находится в поле Подписи горизонтальной оси (категории).
Значения – аргумент значений ряда данных Diag!$B$2:$B$100 находится там же, где мы указали имя ряда.
Порядок – так как наша диаграмма имеет всего один ряд данных, то и порядок будет равен 1. Порядок рядов данных отражается в списке поля Элементы легенды (ряды)
Применение именованных диапазонов в функции РЯД
Прелесть использования функции РЯД заключается в возможности использования именованных диапазонов в ее аргументах. Используя именованные диапазоны, вы можете легко переключаться между данными одного ряда данных. Что более важно, используя именованные диапазоны в качестве аргументов функции РЯД, можно создавать динамические диаграммы. Вообще, все диаграммы динамические, в том смысле, что при изменении данных, диаграммы меняют свой внешний вид. Но используя именованные диапазоны вы можете сделать так, чтобы график автоматически обновлялся при добавлении новых данных в книгу или выбирал какое-нибудь подмножество данных, например, последние 30 значений.
Методика создания динамических диаграмм на основе именованных диапазонов была описана мной в одной из предыдущих статей.
Содержание
- 1 Применение критериев
- 1.1 СЧЁТЕСЛИ
- 1.2 СЧЁТЕСЛИМН
- 1.3 СУММЕСЛИМН
- 1.4 Условное форматирование
- 1.5 Помогла ли вам эта статья?
- 2 Синтаксис и особенности функции
- 3 Функция СЧЕТЕСЛИ в Excel: примеры
- 4 ПРОМЕЖУТОЧНЫЕ.ИТОГИ и СЧЕТЕСЛИ
Программа Microsoft Excel является не просто табличным редактором, а ещё и мощнейшим приложением для различных вычислений. Не в последнюю очередь такая возможность появилась благодаря встроенным функциям. С помощью некоторых функций (операторов) можно задавать даже условия вычисления, которые принято называть критериями. Давайте подробнее узнаем, каким образом можно их использовать при работе в Экселе.
Применение критериев
Критерии представляют собой условия, при которых программа выполняет определенные действия. Они применяются в целом ряде встроенных функций. В их названии чаще всего присутствует выражение «ЕСЛИ». К данной группе операторов, прежде всего, нужно отнести СЧЁТЕСЛИ, СЧЁТЕСЛИМН, СУММЕСЛИ, СУММЕСЛИМН. Кроме встроенных операторов, критерии в Excel используются также при условном форматировании. Рассмотрим их применение при работе с различными инструментами данного табличного процессора более подробно.
СЧЁТЕСЛИ
Главной задачей оператора СЧЁТЕСЛИ, относящегося к статистической группе, является подсчет занятых различными значениями ячеек, которые удовлетворяют определенному заданному условию. Его синтаксис следующий:
=СЧЁТЕСЛИ(диапазон;критерий)
Как видим, у данного оператора два аргумента. «Диапазон» представляет собой адрес массива элементов на листе, в которых следует произвести подсчет.
«Критерий» — это аргумент, который задаёт условие, что именно должны содержать ячейки указанной области, чтобы быть включенными в подсчет. В качестве параметра может быть использовано числовое выражение, текст или ссылка на ячейку, в которой критерий содержится. При этом, для указания критерия можно использовать следующие знаки: «» («больше»), «=» («равно»), «» («не равно»). Например, если задать выражение «15000».
После того, как все вышеуказанные манипуляции произведены, клацаем по кнопке «OK».
Программа производит подсчет и выводит результат в элемент листа, который был выделен перед активацией Мастера функций. Как видим, в данном случае результат равен числу 5. Это означает, что в выделенном массиве в пяти ячейках находятся значения превышающие 15000. То есть, можно сделать вывод, что в Магазине 2 в пяти днях из анализируемых семи выручка превысила 15000 рублей.
Урок: Мастер функций в программе Эксель
СЧЁТЕСЛИМН
Следующей функцией, которая оперирует критериями, является СЧЁТЕСЛИМН. Она также относится к статистической группе операторов. Задачей СЧЁТЕСЛИМН является подсчет ячеек в указанном массиве, которые удовлетворяют определенному набору условий. Именно тот факт, что можно задать не один, а несколько параметров, и отличает этого оператора от предыдущего. Синтаксис следующий:
=СЧЁТЕСЛИМН(диапазон_условия1;условие1;диапазон_условия2;условие2;…)
«Диапазон условия» является идентичным первому аргументу предыдущего оператора. То есть, он представляет собой ссылку на область, в которой будет производиться подсчет ячеек, удовлетворяющих указанным условиям. Данный оператор позволяет задать сразу несколько таких областей.
«Условие» представляет собой критерий, который определяет, какие элементы из соответствующего массива данных войдут в подсчет, а какие не войдут. Каждой заданной области данных нужно указывать условие отдельно, даже в том случае, если оно совпадает. Обязательно требуется, чтобы все массивы, используемые в качестве областей условия, имели одинаковое количество строк и столбцов.
Для того, чтобы задать несколько параметров одной и той же области данных, например, чтобы подсчитать количество ячеек, в которых расположены величины больше определенного числа, но меньше другого числа, следует в качестве аргумента «Диапазон условия» несколько раз указать один и тот же массив. Но при этом в качестве соответствующих аргументов «Условие» следует указывать разные критерии.
На примере все той же таблицы с недельной выручкой магазинов посмотрим, как это работает. Нам нужно узнать количество дней недели, когда доход во всех указанных торговых точках достигал установленной для них нормы. Нормы выручки следующие:
- Магазин 1 – 14000 рублей;
- Магазин 2 – 15000 рублей;
- Магазин 3 – 24000 рублей;
- Магазин 4 – 11000 рублей;
- Магазин 5 – 32000 рублей.
- Для выполнения вышеуказанной задачи, выделяем курсором элемент рабочего листа, куда будет выводиться итог обработки данных СЧЁТЕСЛИМН. Клацаем по иконке «Вставить функцию».
- Перейдя в Мастер функций, снова перемещаемся в блок «Статистические». В перечне следует отыскать наименование СЧЁТЕСЛИМН и произвести его выделение. После выполнения указанного действия требуется произвести нажатие на кнопку «OK».
- Вслед за выполнением вышеуказанного алгоритма действий открывается окно аргументов СЧЁТЕСЛИМН.
В поле «Диапазон условия1» следует ввести адрес строки, в которой расположены данные по выручке Магазина 1 за неделю. Для этого ставим курсор в поле и выделяем соответствующую строку в таблице. Координаты отображаются в окне.
Учитывая, что для Магазина 1 дневная норма выручки составляет 14000 рублей, то в поле «Условие 1» вписываем выражение «>14000».
В поля «Диапазон условия2 (3,4,5)» следует внести координаты строк с недельной выручкой соответственно Магазина 2, Магазина 3, Магазина 4 и Магазина 5. Действие выполняем по тому же алгоритму, что и для первого аргумента данной группы.
В поля «Условие2», «Условие3», «Условие4» и «Условие5» вносим соответственно значения «>15000», «>24000», «>11000» и «>32000». Как нетрудно догадаться, эти значения соответствуют интервалу выручки, превышающую норму для соответствующего магазина.
После того, как был произведен ввод всех необходимых данных (всего 10 полей), жмем на кнопку «OK».
- Программа производит подсчет и выводит результат на экран. Как видим, он равен числу 3. Это означает, что в трех днях из анализируемой недели выручка во всех торговых точках превышала установленную для них норму.
Теперь несколько изменим задачу. Нам следует посчитать количество дней, в которых Магазин 1 получил выручку, превышающую 14000 рублей, но меньшую, чем 17000 рублей.
- Ставим курсор в элемент, где будет произведен вывод на лист результатов подсчета. Клацаем по пиктограмме «Вставить функцию» над рабочей площадью листа.
- Так как мы совсем недавно применяли формулу СЧЁТЕСЛИМН, то теперь не обязательно переходить в группу «Статистические» Мастера функций. Наименование данного оператора можно найти в категории «10 недавно использовавшихся». Выделяем его и щелкаем по кнопке «OK».
- Открывается уже знакомое нам окошко аргументов оператора СЧЁТЕСЛИМН. Ставим курсор в поле «Диапазон условия1» и, произведя зажим левой кнопки мыши, выделяем все ячейки, в которых содержится выручка по дням Магазина 1. Они расположены в строке, которая так и называется «Магазин 1». После этого координаты указанной области будут отражены в окне.
Далее устанавливаем курсор в поле «Условие1». Тут нам нужно указать нижнюю границу значений в ячейках, которые будут принимать участие в подсчете. Указываем выражение «>14000».
В поле «Диапазон условия2» вводим тот же адрес тем же способом, который вводили в поле «Диапазон условия1», то есть, опять вносим координаты ячеек со значениями выручки по первой торговой точке.
В поле «Условие2» указываем верхнюю границу отбора: «10.03.2017».
В поле «Диапазон суммирования» нужно указать область, значения которой, отвечающие указанным критериям, будут суммироваться. В нашем случае это значения выручки строки «Магазин1». Выделяем соответствующий массив элементов листа.
После того, как произведено введение всех указанных данных, жмем на кнопку «OK».
- После этого в предварительно указанный элемент рабочего листа будет выведен результат обработки данных функцией СУММЕСЛИ. В нашем случае он равен 47921,53. Это означает, что начиная с 11.03.2017, и до конца анализируемого периода, общая выручка по Магазину 1 составила 47921,53 рубля.
СУММЕСЛИМН
Завершим изучение операторов, которые используют критерии, остановившись на функции СУММЕСЛИМН. Задачей данной математической функции является суммирование значений указанных областей таблицы, отобранных по нескольким параметрам. Синтаксис указанного оператора таков:
=СУММЕСЛИМН(диапазон_суммирования;диапазон_условия1;условие1;диапазон_условия2;условие2;…)
«Диапазон суммирования» — это аргумент, являющийся адресом того массива, ячейки в котором, отвечающие определенному критерию, будут складываться.
«Диапазон условия» — аргумент, представляющий собой массив данных, проверяемый на соответствие условию;
«Условие» — аргумент, представляющий собой критерий отбора для сложения.
Данная функция подразумевает операции сразу с несколькими наборами подобных операторов.
Посмотрим, как данный оператор применим для решения задач в контексте нашей таблицы выручки от реализации в торговых точках. Нам нужно будет подсчитать доход, который принес Магазин 1 за период с 09 по 13 марта 2017 года. При этом при суммировании дохода должны учитываться только те дни, выручка в которых превысила 14000 рублей.
- Снова выделяем ячейку для вывода итога и клацаем по пиктограмме «Вставить функцию».
- В Мастере функций, прежде всего, выполняем перемещение в блок «Математические», а там выделяем пункт под названием «СУММЕСЛИМН». Производим клик по кнопке «OK».
- Производится запуск окошка аргументов оператора, наименование которого было указано выше.
Устанавливаем курсор в поле «Диапазон суммирования». В отличие от последующих аргументов, этот единственный в своем роде и указывает на тот массив значений, где будет производиться суммирование подошедших под указанные критерии данных. Затем выделяем область строки «Магазин1», в которой размещены значения выручки по соответствующей торговой точке.
После того, как адрес отобразился в окне, переходим к полю «Диапазон условия1». Тут нам нужно будет отобразить координаты строки с датами. Производим зажим левой кнопки мыши и выделяем все даты в таблице.
Ставим курсор в поле «Условие1». Первым условием является то, что нами будут суммироваться данные не ранее 09 марта. Поэтому вводим значение «>08.03.2017».
Перемещаемся к аргументу «Диапазон условия2». Тут нужно внести те же координаты, которые были записаны в поле «Диапазон условия1». Делаем это тем же способом, то есть, путем выделения строчки с датами.
Устанавливаем курсор в поле «Условие2». Вторым условием является то, что дни, за которые будет суммироваться выручка, должны быть не позже 13 марта. Поэтому записываем следующее выражение: «14000».
После выполнения последнего действия клацаем по кнопке «OK».
- Программа выводит результат на лист. Он равен 62491,38. Это означает, что за период с 09 по 13 марта 2017 года сумма выручки при сложении её за дни, в которых она превышает 14000 рублей, составила 62491,38 рубля.
Условное форматирование
Последним, описанным нами, инструментом, при работе с которым используются критерии, является условное форматирование. Он выполняет указанный вид форматирования ячеек, которые отвечают заданным условиям. Взглянем на пример работы с условным форматированием.
Выделим те ячейки таблицы синим цветом, где значения за день превышают 14000 рублей.
- Выделяем весь массив элементов в таблице, в котором указана выручка торговых точек по дням.
- Передвигаемся во вкладку «Главная». Клацаем по пиктограмме «Условное форматирование», размещенной в блоке «Стили» на ленте. Открывается список действий. Клацаем в нём по позиции «Создать правило…».
- Активируется окошко генерации правила форматирования. В области выбора типа правила выделяем наименование «Форматировать только ячейки, которые содержат». В первом поле блока условий из списка возможных вариантов выбираем «Значение ячейки». В следующем поле выбираем позицию «Больше». В последнем — указываем само значение, больше которого требуется отформатировать элементы таблицы. У нас это 14000. Чтобы выбрать тип форматирования, клацаем по кнопке «Формат…».
- Активируется окно форматирования. Передвигаемся во вкладку «Заливка». Из предложенных вариантов цветов заливки выбираем синий, щелкая по нему левой кнопкой мыши. После того, как выбранный цвет отобразился в области «Образец», клацаем по кнопке «OK».
- Автоматически происходит возврат к окну генерации правила форматирования. В нём также в области «Образец» отображается синий цвет. Тут нам нужно произвести одно единственное действие: клацнуть по кнопке «OK».
- После выполнения последнего действия, все ячейки выделенного массива, где содержится число большее, чем 14000, будут залиты синим цветом.
Более подробно о возможностях условного форматирования рассказывается в отдельной статье.
Урок: Условное форматирование в программе Эксель
Как видим, с помощью инструментов, использующих при своей работе критерии, в Экселе можно решать довольно разноплановые задачи. Это может быть, как подсчет сумм и значений, так и форматирование, а также выполнение многих других задач. Основными инструментами, работающими в данной программе с критериями, то есть, с определенными условиями, при выполнении которых активируется указанное действие, является набор встроенных функций, а также условное форматирование.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Функция СЧЕТЕСЛИ входит в группу статистических функций. Позволяет найти число ячеек по определенному критерию. Работает с числовыми и текстовыми значениями, датами.
Синтаксис и особенности функции
Сначала рассмотрим аргументы функции:
- Диапазон – группа значений для анализа и подсчета (обязательный).
- Критерий – условие, по которому нужно подсчитать ячейки (обязательный).
В диапазоне ячеек могут находиться текстовые, числовые значения, даты, массивы, ссылки на числа. Пустые ячейки функция игнорирует.
В качестве критерия может быть ссылка, число, текстовая строка, выражение. Функция СЧЕТЕСЛИ работает только с одним условием (по умолчанию). Но можно ее «заставить» проанализировать 2 критерия одновременно.
Рекомендации для правильной работы функции:
- Если функция СЧЕТЕСЛИ ссылается на диапазон в другой книге, то необходимо, чтобы эта книга была открыта.
- Аргумент «Критерий» нужно заключать в кавычки (кроме ссылок).
- Функция не учитывает регистр текстовых значений.
- При формулировании условия подсчета можно использовать подстановочные знаки. «?» — любой символ. «*» — любая последовательность символов. Чтобы формула искала непосредственно эти знаки, ставим перед ними знак тильды (~).
- Для нормального функционирования формулы в ячейках с текстовыми значениями не должно пробелов или непечатаемых знаков.
Посчитаем числовые значения в одном диапазоне. Условие подсчета – один критерий.
У нас есть такая таблица:
Посчитаем количество ячеек с числами больше 100. Формула: =СЧЁТЕСЛИ(B1:B11;»>100″). Диапазон – В1:В11. Критерий подсчета – «>100». Результат:
Если условие подсчета внести в отдельную ячейку, можно в качестве критерия использовать ссылку:
Посчитаем текстовые значения в одном диапазоне. Условие поиска – один критерий.
Формула: =СЧЁТЕСЛИ(A1:A11;»табуреты»). Или:
Во втором случае в качестве критерия использовали ссылку на ячейку.
Формула с применением знака подстановки: =СЧЁТЕСЛИ(A1:A11;»таб*»).
Для расчета количества значений, оканчивающихся на «и», в которых содержится любое число знаков: =СЧЁТЕСЛИ(A1:A11;»*и»). Получаем:
Формула посчитала «кровати» и «банкетки».
Используем в функции СЧЕТЕСЛИ условие поиска «не равно».
Формула: =СЧЁТЕСЛИ(A1:A11;»»&»стулья»). Оператор «» означает «не равно». Знак амперсанда (&) объединяет данный оператор и значение «стулья».
При применении ссылки формула будет выглядеть так:
Часто требуется выполнять функцию СЧЕТЕСЛИ в Excel по двум критериям. Таким способом можно существенно расширить ее возможности. Рассмотрим специальные случаи применения СЧЕТЕСЛИ в Excel и примеры с двумя условиями.
- Посчитаем, сколько ячеек содержат текст «столы» и «стулья». Формула: =СЧЁТЕСЛИ(A1:A11;»столы»)+СЧЁТЕСЛИ(A1:A11;»стулья»). Для указания нескольких условий используется несколько выражений СЧЕТЕСЛИ. Они объединены между собой оператором «+».
- Условия – ссылки на ячейки. Формула: =СЧЁТЕСЛИ(A1:A11;A1)+СЧЁТЕСЛИ(A1:A11;A2). Текст «столы» функция ищет в ячейке А1. Текст «стулья» — на базе критерия в ячейке А2.
- Посчитаем число ячеек в диапазоне В1:В11 со значением большим или равным 100 и меньшим или равным 200. Формула: =СЧЁТЕСЛИ(B1:B11;»>=100″)-СЧЁТЕСЛИ(B1:B11;»>200″).
- Применим в формуле СЧЕТЕСЛИ несколько диапазонов. Это возможно, если диапазоны являются смежными. Формула: =СЧЁТЕСЛИ(A1:B11;»>=100″)-СЧЁТЕСЛИ(A1:B11;»>200″). Ищет значения по двум критериям сразу в двух столбцах. Если диапазоны несмежные, то применяется функция СЧЕТЕСЛИМН.
- Когда в качестве критерия указывается ссылка на диапазон ячеек с условиями, функция возвращает массив. Для ввода формулы нужно выделить такое количество ячеек, как в диапазоне с критериями. После введения аргументов нажать одновременно сочетание клавиш Shift + Ctrl + Enter. Excel распознает формулу массива.
СЧЕТЕСЛИ с двумя условиями в Excel очень часто используется для автоматизированной и эффективной работы с данными. Поэтому продвинутому пользователю настоятельно рекомендуется внимательно изучить все приведенные выше примеры.
ПРОМЕЖУТОЧНЫЕ.ИТОГИ и СЧЕТЕСЛИ
Посчитаем количество реализованных товаров по группам.
- Сначала отсортируем таблицу так, чтобы одинаковые значения оказались рядом.
- Первый аргумент формулы «ПРОМЕЖУТОЧНЫЕ.ИТОГИ» — «Номер функции». Это числа от 1 до 11, указывающие статистическую функцию для расчета промежуточного результата. Подсчет количества ячеек осуществляется под цифрой «2» (функция «СЧЕТ»).
Скачать примеры функции СЧЕТЕСЛИ в Excel
Формула нашла количество значений для группы «Стулья». При большом числе строк (больше тысячи) подобное сочетание функций может оказаться полезным.
Эксель: Счетесли критерий формула. Есть возможность задать определенные условия, называемые критериями. Это происходит благодаря встроенным функциям. Самые распространенные из них СЧЁТЕСЛИ, СЧЁТЕСЛИМН, СУММЕСЛИ, СУММЕСЛИМН. Можно заметить, что их объединяет слово Если. Как они работают, рассмотрим далее.
СЧЕТЕСЛИ.
Данный критерий применяется, когда необходимо подсчитать значения занятые несколькими ячейками, объединенное некоторым условием, то есть критерием. Пишется это так:
=СЧЁТЕСЛИ(диапазон;критерий)
Здесь мы видим два аргумента. «диапазан»- задает адрес ячеек с которыми необходимо проводить расчеты. «критерий»- задает условие, которое должна содержать ячейка, для того что бы быть включенной в расчет. При этом для указания критерия можно использовать следующие знаки: «» («больше»), «=» («равно»), «» («не равно»).
Например, если задать выражение «15000».
После того, как все вышеуказанные манипуляции произведены, нажимаем на кнопку «OK».
4. Программа производит подсчет и выводит результат в элемент листа, который был выделен перед активацией Мастера функций. Как видим, в данном случае результат равен числу 5. Это означает, что в выделенном массиве в пяти ячейках находятся значения превышающие 15000. То есть, можно сделать вывод, что в Магазине 2 в пяти днях из анализируемых семи выручка превысила 15000 рублей.
СЧЁТЕСЛИМН
Следующей функцией, которая оперирует критериями, является СЧЁТЕСЛИМН.
Она также относится к статистической группе операторов. Задачей СЧЁТЕСЛИМН является подсчет ячеек в указанном массиве, которые удовлетворяют определенному набору условий. Именно тот факт, что можно задать не один, а несколько параметров, и отличает этого оператора от предыдущего. Синтаксис следующий:
=СЧЁТЕСЛИМН(диапазон_условия1;условие1;диапазон_условия2;условие2;…)
«Диапазон условия» является идентичным первому аргументу предыдущего оператора. То есть, он представляет собой ссылку на область, в которой будет производиться подсчет ячеек, удовлетворяющих указанным условиям. Данный оператор позволяет задать сразу несколько таких областей.
«Условие» представляет собой критерий, который определяет, какие элементы из соответствующего массива данных войдут в подсчет, а какие не войдут. Каждой заданной области данных нужно указывать условие отдельно, даже в том случае, если оно совпадает. Обязательно требуется, чтобы все массивы, используемые в качестве областей условия, имели одинаковое количество строк и столбцов.
Для того, чтобы задать несколько параметров одной и той же области данных, например, чтобы подсчитать количество ячеек, в которых расположены величины больше определенного числа, но меньше другого числа, следует в качестве аргумента «Диапазон условия» несколько раз указать один и тот же массив.
Но при этом в качестве соответствующих аргументов «Условие» следует указывать разные критерии.
На примере все той же таблицы с недельной выручкой магазинов посмотрим, как это работает. Нам нужно узнать количество дней недели, когда доход во всех указанных торговых точках достигал установленной для них нормы. Нормы выручки следующие:
• Магазин 1 – 14000 рублей;
• Магазин 2 – 15000 рублей;
• Магазин 3 – 24000 рублей;
• Магазин 4 – 11000 рублей;
• Магазин 5 – 32000 рублей.
1. Для выполнения вышеуказанной задачи, выделяем курсором элемент рабочего листа, куда будет выводиться итог обработки данных СЧЁТЕСЛИМН. Нажимаем на иконку «Вставить функцию».
2. Перейдя в Мастер функций, снова перемещаемся в блок «Статистические». В перечне следует отыскать наименование СЧЁТЕСЛИМН и произвести его выделение. После выполнения указанного действия требуется произвести нажатие на кнопку «OK».
3. Вслед за выполнением вышеуказанного алгоритма действий открывается окно аргументов СЧЁТЕСЛИМН.
В поле «Диапазон условия1» следует ввести адрес строки, в которой расположены данные по выручке Магазина 1 за неделю. Для этого ставим курсор в поле и выделяем соответствующую строку в таблице. Координаты отображаются в окне.
Учитывая, что для Магазина 1 дневная норма выручки составляет 14000 рублей, то в поле «Условие 1» вписываем выражение «>14000».
В поля «Диапазон условия2 (3,4,5)» следует внести координаты строк с недельной выручкой соответственно Магазина 2, Магазина 3, Магазина 4 и Магазина 5. Действие выполняем по тому же алгоритму, что и для первого аргумента данной группы.
В поля «Условие2», «Условие3», «Условие4» и «Условие5» вносим соответственно значения «>15000», «>24000», «>11000» и «>32000». Как нетрудно догадаться, эти значения соответствуют интервалу выручки, превышающую норму для соответствующего магазина.
После того, как был произведен ввод всех необходимых данных (всего 10 полей), жмем на кнопку «OK».
4. Программа производит подсчет и выводит результат на экран. Как видим, он равен числу 3.
Это означает, что в трех днях из анализируемой недели выручка во всех торговых точках превышала установленную для них норму.
Теперь несколько изменим задачу. Нам следует посчитать количество дней, в которых Магазин 1 получил выручку, превышающую 14000 рублей, но меньшую, чем 17000 рублей.
1. Ставим курсор в элемент, где будет произведен вывод на лист результатов подсчета. Нажимаем на пиктограмму «Вставить функцию» над рабочей площадью листа.
2. Так как мы совсем недавно применяли формулу СЧЁТЕСЛИМН, то теперь не обязательно переходить в группу «Статистические» Мастера функций. Наименование данного оператора можно найти в категории «10 недавно использовавшихся». Выделяем его и щелкаем по кнопке «OK».
3. Открывается уже знакомое нам окошко аргументов оператора СЧЁТЕСЛИМН. Ставим курсор в поле «Диапазон условия1» и, произведя зажим левой кнопки мыши, выделяем все ячейки, в которых содержится выручка по дням Магазина 1.
Они расположены в строке, которая так и называется «Магазин 1».
После этого координаты указанной области будут отражены в окне.
Далее устанавливаем курсор в поле «Условие1». Тут нам нужно указать нижнюю границу значений в ячейках, которые будут принимать участие в подсчете. Указываем выражение «>14000».
В поле «Диапазон условия2» вводим тот же адрес тем же способом, который вводили в поле «Диапазон условия1», то есть, опять вносим координаты ячеек со значениями выручки по первой торговой точке.
В поле «Условие2» указываем верхнюю границу отбора: «10.03.2017».
В поле «Диапазон суммирования» нужно указать область, значения которой, отвечающие указанным критериям, будут суммироваться. В нашем случае это значения выручки строки «Магазин1». Выделяем соответствующий массив элементов листа.
После того, как произведено введение всех указанных данных, жмем на кнопку «OK».
4. После этого в предварительно указанный элемент рабочего листа будет выведен результат обработки данных функцией СУММЕСЛИ. В нашем случае он равен 47921,53. Это означает, что начиная с 11.03.2017, и до конца анализируемого периода, общая выручка по Магазину 1 составила 47921,53 рубля.
СУММЕСЛИМН
Завершим изучение операторов, которые используют критерии, остановившись на функции СУММЕСЛИМН. Задачей данной математической функции является суммирование значений указанных областей таблицы, отобранных по нескольким параметрам. Синтаксис указанного оператора таков:
=СУММЕСЛИМН(диапазон_суммирования;диапазон_условия1;условие1;диапазон_условия2;условие2;…)
«Диапазон суммирования» — это аргумент, являющийся адресом того массива, ячейки в котором, отвечающие определенному критерию, будут складываться.
«Диапазон условия» — аргумент, представляющий собой массив данных, проверяемый на соответствие условию;
«Условие» — аргумент, представляющий собой критерий отбора для сложения.
Данная функция подразумевает операции сразу с несколькими наборами подобных операторов.
Посмотрим, как данный оператор применим для решения задач в контексте нашей таблицы выручки от реализации в торговых точках. Нам нужно будет подсчитать доход, который принес Магазин 1 за период с 09 по 13 марта 2017 года. При этом при суммировании дохода должны учитываться только те дни, выручка в которых превысила 14000 рублей.
1. Снова выделяем ячейку для вывода итога и нажимаем на пиктограмму «Вставить функцию».
2. В Мастере функций, прежде всего, выполняем перемещение в блок «Математические», а там выделяем пункт под названием «СУММЕСЛИМН». Производим клик по кнопке «OK».
3. Производится запуск окошка аргументов оператора, наименование которого было указано выше.
Устанавливаем курсор в поле «Диапазон суммирования». В отличие от последующих аргументов, этот единственный в своем роде и указывает на тот массив значений, где будет производиться суммирование подошедших под указанные критерии данных.
Затем выделяем область строки «Магазин1», в которой размещены значения выручки по соответствующей торговой точке.
После того, как адрес отобразился в окне, переходим к полю «Диапазон условия1». Тут нам нужно будет отобразить координаты строки с датами. Производим зажим левой кнопки мыши и выделяем все даты в таблице.
Ставим курсор в поле «Условие1». Первым условием является то, что нами будут суммироваться данные не ранее 09 марта. Поэтому вводим значение «>08.03.2017».
Перемещаемся к аргументу «Диапазон условия2».
Тут нужно внести те же координаты, которые были записаны в поле «Диапазон условия1». Делаем это тем же способом, то есть, путем выделения строчки с датами.
Устанавливаем курсор в поле «Условие2».
Вторым условием является то, что дни, за которые будет суммироваться выручка, должны быть не позже 13 марта. Поэтому записываем следующее выражение: «14000».
После выполнения последнего действия нажимаем на кнопку «OK».
4. Программа выводит результат на лист. Он равен 62491,38. Это означает, что за период с 09 по 13 марта 2017 года сумма выручки при
сложении её за дни, в которых она превышает 14000 рублей, составила 62491,38 рубля.
Все очень просто!
Подсчет с критерием «ИЛИ» в Excel может оказаться сложнее, чем кажется на первый взгляд. В этой статье вы найдёте несколько нетрудных, но полезных примеров.
- Начнем с простого. Требуется подсчитать количество ячеек, содержащих «Google» или «Facebook» (первый столбец). Вот формула, которая сделает это:
=COUNTIF(A1:A8,"Google")+COUNTIF(A1:A8,"Facebook")=СЧЁТЕСЛИ(A1:A8;"Google")+СЧЁТЕСЛИ(A1:A8;"Facebook") - Однако, если потребуется подсчитать количество строк, которые содержат или «Google» или «Stanford» (рассматриваем сразу два столбца), то мы не сможем просто использовать формулу, дважды содержащюю функцию COUNTIF (СЧЕТЕСЛИ) (см. рисунок ниже). В этом случае строки, которые содержат и «Google» и «Stanford» (в одной строке) подсчитываются дважды, а они должны учитываться только один раз. 4 – вот ответ, который нам нужен.
=COUNTIF(A1:A8,"Google")+COUNTIF(B1:B8,"Stanford")=СЧЁТЕСЛИ(A1:A8;"Google")+СЧЁТЕСЛИ(B1:B8;"Stanford") - Вот почему нам нужна формула массива. Мы используем функцию IF (ЕСЛИ), чтобы проверить, попадается ли в строке «Google» или «Stanford»:
=IF((A1="Google")+(B1="Stanford"),1,0)=ЕСЛИ((A1="Google")+(B1="Stanford");1;0)
- Пояснение:
- Вспомним, что ИСТИНА = 1, а ЛОЖЬ = 0.
- Для строки 1:
=ЕСЛИ(ИСТИНА+ИСТИНА;1;0) ► =ЕСЛИ(2;1;0) ► 1, т.е. первая строка будет учитываться. - Для строки 2:
=ЕСЛИ(ЛОЖЬ+ЛОЖЬ;1;0) ► =ЕСЛИ(0;1;0) ► 0, т.е. вторая строка учитываться не будет. - Для строки 3:
=ЕСЛИ(ЛОЖЬ+ИСТИНА;1;0) ► =ЕСЛИ(1;1;0) ► 1, т.е. третья строка будет учитываться, и т.д.
- Теперь все, что нам нужно – это функция SUM (СУММ), которая сосчитает единицы. Для достижения этой цели мы добавляем функцию SUM (СУММ) и заменяем A1 на A1:A8, а B1 на B1:B8.
=SUM(IF((A1:A8="Google")+(B1:B8="Stanford"),1,0)))=СУММ(ЕСЛИ((A1:A8="Google")+(B1:B8="Stanford");1;0)) - Ввод формулы закончим нажатием Ctrl+Shift+Enter.
Примечание: Строка формул указывает, что это формула массива, заключая её в фигурные скобки {}. Их не нужно вводить самостоятельно. Они исчезнут, когда вы начнете редактировать формулу.
- Пояснение:
- Диапазон (массив констант), созданный с помощью функции IF (ЕСЛИ) хранится в памяти Excel, а не в ячейках листа.
- Массив констант выглядит следующим образом: {1;0;1;0;1;0;1;0}.
- Этот массив констант используется в качестве аргумента для функции SUM (СУММ), давая результат 4.
- Мы можем сделать ещё один шаг вперёд. К примеру, подсчитать количество строк, которые содержат «Google» и «Stanford», либо «Columbia».
=SUM(IF((A1:A8="Google")*(B1:B8="Stanford")+(B1:B8="Columbia"),1,0))=СУММ(ЕСЛИ((A1:A8="Google")*(B1:B8="Stanford")+(B1:B8="Columbia");1;0))
Урок подготовлен для Вас командой сайта office-guru.ru
Источник: /> Перевела: Ольга Гелих
Правила перепечаткиЕще больше уроков по Microsoft Excel
Оцените качество статьи. Нам важно ваше мнение:
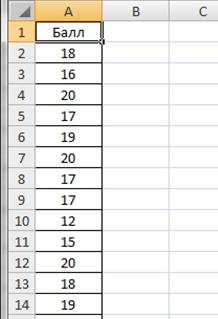
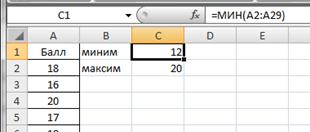
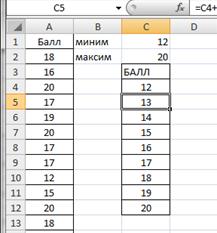
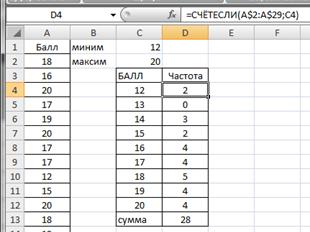
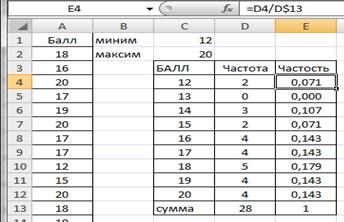
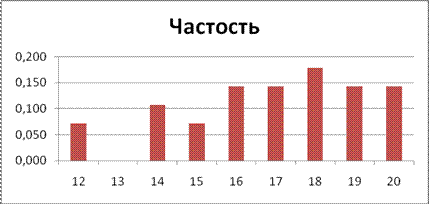
Как построить вариационный ряд в Excel
Вариационный ряд может быть:
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Решение.
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel
Следующая тема: Построение интервального вариационного ряда в Excel.
Download Article
You can automatically add sequential numbers to cells using AutoFill or the ROW function.
Download Article
- Choosing Increments
- Using the Fill Handle
- Using a Formula
- Video
- Q&A
- Tips
|
|
|
|
|
It’s easy and fast to create a number series in Microsoft Excel. Understanding how to use the spreadsheet correctly to generate an automatic number series will save you a lot of time, especially if you are working with a large amount of data.
Things You Should Know
- To use AutoFill, type the first number in your series, then click and drag the square at the cell’s bottom right corner down the column.
- You can use the =ROW() function to start a new series from any cell value.
- To create a series of dates, type the first date into a cell, then drag the AutoFill handle to instantly generate a series of sequential dates.
-
1
Click on the cell that you want to start the number series in. A cell is one of the individual blocks that make up an Excel spreadsheet.
- Type the number that you want to start the series with in that cell and hit enter. By way of example, type “1.” This is called a “value” in Excel terminology.[1]
- Now, write the first few numbers of your series in adjacent cells. You could write them in the vertical columns or horizontally in a row.[2]
- Type the number that you want to start the series with in that cell and hit enter. By way of example, type “1.” This is called a “value” in Excel terminology.[1]
-
2
Figure out the increment for your number series. For example, if you want cells to increase by the same increment (say by “1”), then type two numbers with that increment. Thus, you would type “1” in the first cell and “2” in the cell beneath it.
- If you want the number series to increase by increments of 2, you would type 2 and then 4.
- If you want the series to use more complicated increments (say, “2, 4, 8, 16”) type the first three numbers so it doesn’t assume you are asking it for increments of 2.
Advertisement
-
1
Click and hold to highlight all the cells with your numbers. To do so, hold your cursor in the top left of the first cell, and drag it down to the last cell with a number in it (in the first example, the cell with the “2” in it.)[3]
- Do this without letting your finger off the cursor. This will highlight the 2 (or 3) numbers that you have already typed into the cells.
- Remember that, in Excel, cells form vertical columns but horizontal rows. You can create the number series vertically down a column, or horizontally across a row.
-
2
Hover your cursor over the little black (or green) square in the bottom right cell. The square will appear in the bottom right of the last cell you typed a number in (in the first example, the cell with the “2.»)
- The little black square will turn into a small black plus sign in the bottom right corner of that cell. This is called the fill handle. The key to creating a number series in MS Excel is the fill handle.
- When you look at the individual cell, notice the green or black border around the cell. That means you are working in the active cell.[4]
[5]
-
3
Left click on your mouse while hovering your cursor over the plus sign. Drag the cursor down the vertical column. Excel will automatically create a number series for as long as you drag your cursor.
- Use the same process with a number series in a horizontal row. But drag your cursor horizontally. Remember, by default, Excel uses a linear growth pattern to determine these values.
- If you already have a sequence of numbers and you just want to add to it, select the last two in the sequence and drag the fill handle to the new selection, and it will continue the list.
Advertisement
-
1
Use an Excel formula to generate a number series. Put your cursor in the cell at A1. This means the block that is located where Column A meets Row 1.
- In A1, type =ROW(). This formula should generate the first number in your series. Select the fill handle on the bottom right of the A1 cell, and drag down or across to create the number series.
- If you want to find the number of any cell, you can put your cursor in it, and type =ROW(C10), replacing C10 with the coordinates of that cell. Hit enter.
-
2
Right click on the plus sign with your mouse, and drag the fill handle. This will open a shortcut menu that allows you to perform other functions with the number series.
- To fill the series in increasing order, drag down or to the right. To fill in decreasing order, drag up or to the left.
- In the shortcut menu, you can choose such options as fill series to populate the numbers or copy series.
-
3
Count days in Excel. This same trick also allows you to count up by days. To make this work, type a date in any recognizable format in any one cell.
- Drag the fill handle to the adjacent cells, and it will add the days as you go.
- You can skip days, for example, showing every other day or every third day, as long as the sequence is repetitive.
Advertisement
Add New Question
-
Question
Why do I need to enter the first two values of a number series?
You need to enter two values of a number series in Excel to create the pattern. Using only one number, you can’t get a unique pattern of numbers, so two numbers are required.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
You could import Excel into Microsoft Access, and create a field to generate unique identifiers.[6]
-
These numbers are not automatically updated when you add, move, or remove rows.
Thanks for submitting a tip for review!
Advertisement
About This Article
Thanks to all authors for creating a page that has been read 138,974 times.
Is this article up to date?
При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение – это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, – генеральной совокупностью.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Элементами выборки (x1 х2, . хп) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.
Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Пример 2.1.
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):
| 18 | 16 | 20 | 17 | 19 | 20 | 17 |
| 17 | 12 | 15 | 20 | 18 | 19 | 18 |
| 18 | 16 | 18 | 14 | 14 | 17 | 19 |
| 16 | 14 | 19 | 12 | 15 | 16 | 20 |
Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.
Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).
Рисунок 2.6. Баллы успеваемости студентов
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
Рисунок 2.7. Минимальный и максимальный балл
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.
Рисунок 2.8. Значения признака
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).
Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.
Рис.2.9. Частоты вариационного ряда
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
Рисунок 2.10. Частости ряда распределения
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).
Рисунок 2.11. Накопленные частоты ряда
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.
Рисунок 2.12. Накопленные частости ряда
Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частот представлен на рисунке 2.13.
Рисунок 2.13. Полигон распределения частот
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.
Рисунок 2.14. Полигон распределения частостей
Построим гистограмму распределения частостей, для чего выделим диапазон Е4:Е12, выберем тип диаграммы «Гистограмма». Щелкнем правой кнопкой в области диаграммы, выберем «Выбрать данные», выберете «Ряд» – «Изменить», левой кнопкой щелкнем в строке «Подписи оси Х» и выделим диапазон С4:С12 (рис.2.15).
Рисунок 2.15. Гистограмма распределения частостей
Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.
Рисунок 2.16. Кумулята
Пример 2.2.
В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.
Банковские процентные ставки
| № Банка | Процентная ставка, % |
| 1 | 20,3 |
| 2 | 17,1 |
| 3 | 14,2 |
| 4 | 11,0 |
| 5 | 17,3 |
| 6 | 19,6 |
| 7 | 20,5 |
| 8 | 23,6 |
| 9 | 14,6 |
| 10 | 17,5 |
| 11 | 20,8 |
| 12 | 13,6 |
| 13 | 24,0 |
| 14 | 17,5 |
| 15 | 15,0 |
| 16 | 21,1 |
| 17 | 17,6 |
| 18 | 15,8 |
| 19 | 18,8 |
| 20 | 22,4 |
| 21 | 16,1 |
| 22 | 17,9 |
| 23 | 21,7 |
| 24 | 18,0 |
| 25 | 16,4 |
| 26 | 26,0 |
| 27 | 18,4 |
| 28 | 16,7 |
| 29 | 12,2 |
| 30 | 13,9 |
Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).
Рисунок 2.17. Процентные ставки банков
Рисунок 2.18. Число интервалов
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).
Рисунок 2.19. Длина интервала
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).
Рисунок 2.20. Границы интервалов
Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.
Воспользуемся функцией ЧАСТОТА. Для этого в ячейке F2 введем формулу =ЧАСТОТА(A2:A31;E2:E7). Протянем F2 маркером заполнения вниз до F8.
Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).
Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.
Рисунок 2.21. Частоты значений признака
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).
Рисунок 2.22. Построение гистограммы
Полученная гистограмма представлена на рис.2.23.
Рис.2.23. Гистограмма частот
Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Дата добавления: 2018-11-12 ; просмотров: 1065 | Нарушение авторских прав
Вариационный ряд может быть:
– дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
– интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения
Решение .
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда

7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа – в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
В реальных социально-экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений — это в общем случае ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжи- ровать).
Операция, заключающаяся в расположении значений признака по возрастанию, называется ранжированием опытных данных.
После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (х,). Число элементов в каждой группе называется частотой варианта («,).
Размахом вариации называется число
где хтах — наибольший вариант;
x min — наименьший вариант.
Сумма всех частот равна определенному числу л, которое называется объемом совокупности:
Отношение частоты данного варианта к объему совокупности называется относительной частотой, или частостью, этого варианта:
Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация — изменение).
Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.
Пример 1. В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 1, 2, 1, 2. Построить дискретный вариационный ряд.
Решение. Проранжируем исходный ряд, подсчитаем частоту и частость вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4.
В результате получим дискретный вариационный ряд (табл. 3.10).
Ранжированный ряд успеваемости
Число студентов, л,
Относительная частота, А
В Excel проранжируем исходный ряд. Для этого введем все данные в диапазон А1 :А24 и воспользуемся кнопкой Щ (Сортировка по возрастанию).
Подсчитаем частоту и частость вариант. Построим таблицу в диапазоне D2:G7 (рис. 3.13).
Рис. 3.13. Контекстное меню строки состояния
Рассмотрим два варианта подсчета частот:
- 1) выделим диапазон, в котором находятся нули. Щелкнем в нижней правой части окна Excel правой кнопкой мыши и выберем в контекстном меню вид итога, который по умолчанию будет появляться в итоговой строке при выделении произвольного диапазона (см. рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
- 2) выполним команду Сервис — Анализ данных — Гистограмма. Заполним диалоговое окно в соответствии с рис. 3.14.
Рис. 3.14. Диалоговое окно инструмента пакета анализа «Гистограмма»
В результате получим таблицу с частотами вариантов и соответствующий график (рис. 3.15).
Рис. 3.15. Результаты применения инструмента «Гистограмма)
Найдем объем выборки, заполнив все частоты вариант в диапазоне ЕЗ:Е7, выделим его левой кнопкой мыши и щелкнем по кнопке ? (автосумма).
В ячейку F3 введем формулу «=ЕЗ/$Е$8», за маркер заполнения (крест в правом нижнем углу ячейки) с помощью мыши скопируем до F7 и выберем кнопку автосумма, в результате получим частоты вариантов и их сумму (1). В ячейку G3 введем частоту варианта 0 — цифру 6 (или ссылку на ячейку, ее содержащую — ЕЗ), в ячейку G4 введем формулу «=G3+E4» и скопируем ее до ячейки G7, в результате получим накопленные частоты. Таким образом, мы получили дискретный вариационный ряд. Естественно, частоты необходимо округлить, но таким образом, чтобы их сумма равнялась 1. Для этого выделим левой кнопкой мыши диапазон частот (F3:F7), щелкнув по правой кнопке, откроем контекстное меню и выполним команду Формат ячеек — Числовой — Число знаков 3 — ОК. Преобразовав обозначения, получим дискретный вариационный ряд, представленный в табл. 3.11.
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Размах вариации
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Простая формула для расчета объема выборки
- Пример расчета объема выборки
- Задачи о генеральной доле
- По части судить о целом
- Как рассчитать объем выборки
- Как определить статистические выбросы и сделать выборку для их удаления в Excel
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- СРЗНАЧ()
- СРЗНАЧЕСЛИ()
- МАКС()
- МИН()
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;
p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = (1 – p);
e – допустимая ошибка, в долях.
Пример расчета объема выборки
Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле
|
Гипотеза |
H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |  |
|
| Статистика K |  |
 |
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при
достаточном числе наблюдений
. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:
С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.
Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.
Как рассчитать объем выборки
Достаточный размер выборки зависит от следующих составляющих:
- изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
- размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
- уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)
ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента
Формулы для расчета объема выборки:
Формулы расчета объема выборки
Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.
График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.
Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Способ 1: применение расширенного автофильтра
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
Источники
- https://lumpics.ru/descriptive-statistics-in-excel/
- https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
- https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
- http://galyautdinov.ru/post/formula-vyborki-prostaya
- https://math.semestr.ru/group/interval-estimation-share.php
- https://tidydata.ru/sample-size
- https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
- https://lumpics.ru/how-to-make-a-sample-in-excel/
- https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html