Функция ПИРСОН (вводить следует PEARSON на английском) предназначена для вычисления коэффициента корреляции Пирсона r. Данную функцию используют в работе в том случае, когда необходимо отразить степень линейной зависимости между двумя массивами данных. В Excel имеется несколько функций с помощью которых можно получить такой же результат, однако универсальность и простота функции Пирсон делают выбор в ее пользу.
Как работает функция ПИРСОН в Excel?
Рассмотрим пример расчета корреляции Пирсона между двумя массивами данных при помощи функции PEARSON в MS EXCEL. Первый массив представляет собой значения температур, второй давление в определенный летний период. Пример заполненной таблицы изображен на рисунке:
Задача следующая: необходимо определить взаимосвязь между температурой и давлением за июнь месяц.
Пример решения с функцией ПИРСОН при анализе в Excel
- Выберем ячейку С17 в которой должен будет посчитаться критерий Пирсона как результат и нажмем кнопку мастер функций «fx» или комбинацию горячих клавиш (SHIFT+F3). Откроется мастер функций, в поле Категория необходимо выбрать «Статистические». В списке статистических функций выбрать PEARSON и нажать Ok:
- В меню аргументов выбрать Массив 1, в примере это утренняя температура воздуха, а затем массив 2 – атмосферное давление.
- В результате в ячейке С17 получим коэффициент корреляции Пирсона. В нашем случае он отрицательный и приблизительно равен -0,14.
Данный показатель -0,14 по Пирсону, который вернула функция, говорит об неблагоприятной зависимости температуры и давления в раннее время суток.
Функция ПИРСОН пошаговая инструкция
Коэффициент корреляции является самым удобным показателем сопряженности количественных признаков.
Задача: Определить линейный коэффициент корреляции Пирсона.
Пример решения:
- В таблице приведены данные для группы курящих людей. Первый массив х — представляет собой возраст курящего, второй массив y представляет собой количество сигарет, выкуренных в день.
- Выберем ячейку В4 в которой должен будет посчитаться результат и нажмем кнопку мастер функций fx (SHIFT+F3).
- В группе Статистические выберем функцию PEARSON.
- Выделим Массив 1 – возраст курящего, затем Массив 2 – число сигарет, выкуренных в день.
- Нажмем кнопку ОК и увидим критерий нормального распределения Пирсона в ячейке В4.

Таким образом, по результату вычисления статистическим выводом эксперимента выявлена отрицательная зависимость между возрастом и количеством выкуренных сигарет в день.
Корреляционный анализ по Пирсону в Excel
Задача: школьникам были даны тесты на наглядное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли взаимосвязь между временем решения этих задач?
Пример решения: представим исходные данные в виде таблицы:
- Переходим курсором в ячейку F2. Откроем мастер функций fx (SHIFT+F3) или вводим вручную.
- Выберем функцию PEARSON.
- Выделим мышкой Массив1, затем Массив 2.
- Нажмем ОК и в ячейке F2 получим критерий согласия Пирсона.
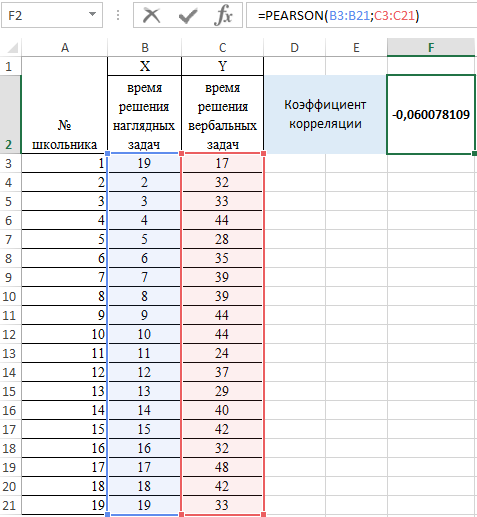
Интерпретация результата вычисления по Пирсону
Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 – являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 – следовательно, произошла ошибка в вычислениях.
Если коэффициент корреляции по модулю оказывается близким к 1, то это соответствует высокому уровню связи между переменными.
Скачать примеры функции ПИРСОН для корреляции в Excel
Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости. Эти положения очень важно четко усвоить для правильной интерпретации полученной корреляционной зависимости.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции PEARSON в Microsoft Excel.
Описание
Возвращает коэффициент корреляции Пирсона (r) — безразмерный индекс в интервале от -1,0 до 1,0 включительно, который отражает степень линейной зависимости между двумя множествами данных.
Синтаксис
PEARSON(массив1;массив2)
Аргументы функции PEARSON описаны ниже.
-
Массив1 Обязательный. Множество независимых значений.
-
Массив2 Обязательный. Множество зависимых значений.
Замечания
-
Аргументы должны быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Если массив1 или массив2 пуст, либо число точек данных в этих массивах не совпадает, функция PEARSON возвращает значение ошибки #Н/Д.
-
Коэффициента корреляции Пирсона (r) вычисляется по следующей формуле:
где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
Независимые значения |
Зависимые значения |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Формула |
Описание (результат) |
Результат |
|
=PEARSON(A3:A7;B3:B7) |
Коэффициент корреляции Пирсона для приведенных выше данных (0,699379) |
0,699379 |
Нужна дополнительная помощь?
Рассмотрим применение в
MS
EXCEL
критерия хи-квадрат Пирсона для проверки простых гипотез.
После получения экспериментальных данных (т.е. когда имеется некая
выборка
) обычно производится выбор закона распределения, наиболее хорошо описывающего случайную величину, представленную данной
выборкой
. Проверка того, насколько хорошо экспериментальные данные описываются выбранным теоретическим законом распределения, осуществляется с использованием
критериев согласия
.
Нулевой гипотезой
, обычно выступает гипотеза о равенстве распределения случайной величины некоторому теоретическому закону.
Сначала рассмотрим применение
критерия согласия Пирсона Х
2
(хи-квадрат)
в отношении простых гипотез (параметры теоретического распределения считаются известными). Затем —
применение критерияв случае сложных гипотез
, когда задается только форма распределения, а параметры этого распределения и значение
статистики
Х
2
оцениваются/рассчитываются на основании одной и той же
выборки
.
Примечание
: Применение
критерия согласия Пирсона
Х
2
в отношении сложных гипотез см. статью
Проверка сложных гипотез критерием хи-квадрат Пирсона в MS EXCEL
.
Примечание
: В англоязычной литературе процедура применения
критерия согласия Пирсона
Х
2
имеет название
The chi-square goodness of fit test
.
Напомним процедуру проверки гипотез:
-
на основе
выборки
вычисляется значение
статистики
, которая соответствует типу проверяемой гипотезы. Например, дляпроверки гипотезы о равенстве среднего μ некоторому заданному значению μ
0
используется
t
-статистика
(еслистандартное отклонение
не известно);
-
при условии истинности
нулевой гипотезы
, распределение этой
статистики
известно и может быть использовано для вычисления вероятностей (например, для
t
-статистики
этораспределение Стьюдента
);
-
вычисленное на основе
выборки
значение
статистики
сравнивается с критическим для заданногоуровня значимости
значением (
α-квантилем
);
нулевую гипотезу
отвергают, если значение
статистики
больше критического (или если вероятность получить это значение
статистики
(p-значение
) меньше
уровня значимости
, что является эквивалентным подходом).
Проведем
проверку гипотез
для различных распределений.
Дискретный случай
Предположим, что два человека играют в кости. У каждого игрока свой набор костей. Игроки по очереди кидают сразу по 3 кубика. Каждый раунд выигрывает тот, кто выкинет за раз больше шестерок. Результаты записываются. У одного из игроков после 100 раундов возникло подозрение, что кости его соперника – несимметричные, т.к. тот часто выигрывает (часто выбрасывает шестерки). Он решил проанализировать насколько вероятно такое количество исходов противника.
Примечание
: Т.к. кубиков 3, то за раз можно выкинуть 0; 1; 2 или 3 шестерки, т.е. случайная величина может принимать 4 значения.
Из теории вероятности нам известно, что если кубики симметричные, то вероятность выпадения шестерок подчиняется
биномиальному закону
. Поэтому, после 100 раундов частоты выпадения шестерок могут быть вычислены с помощью формулы
=БИНОМ.РАСП(A7;3;1/6;ЛОЖЬ)*100
В формуле предполагается, что в ячейке
А7
содержится соответствующее количество выпавших шестерок в одном раунде.
Примечание
: Расчеты приведены в
файле примера на листе Дискретное
.
Для сравнения
наблюденных
(Observed) и
теоретических частот
(Expected) удобно пользоваться
гистограммой
.
При значительном отклонении наблюденных частот от теоретического распределения,
нулевая гипотеза
о распределении случайной величины по теоретическому закону, должна быть отклонена. Т.е., если игральные кости соперника несимметричны, то наблюденные частоты будут «существенно отличаться» от
биномиального распределения
.
В нашем случае на первый взгляд частоты достаточно близки и без вычислений сложно сделать однозначный вывод. Применим
критерий согласия Пирсона Х
2
, чтобы вместо субъективного высказывания «существенно отличаться», которое можно сделать на основании сравнения
гистограмм
, использовать математически корректное утверждение.
Используем тот факт, что в силу
закона больших чисел
наблюденная частота (Observed) с ростом объема
выборки
n стремится к вероятности, соответствующей теоретическому закону (в нашем случае,
биномиальному закону
). В нашем случае объем выборки n равен 100.
Введем
тестовую
статистику
, которую обозначим Х
2
:
где O
l
– это наблюденная частота событий, что случайная величина приняла определенные допустимые значения, E
l
– это соответствующая теоретическая частота (Expected). L – это количество значений, которые может принимать случайная величина (в нашем случае равна 4).
Примечание
: Вышеуказанная
статистика
является частным случаем
статистики
используемой для вычисления
критерия независимости хи-квадрат
(см. статью
Критерий независимости хи-квадрат в MS EXCEL
).
Как видно из формулы, эта
статистика
является мерой близости наблюденных частот к теоретическим, т.е. с помощью нее можно оценить «расстояния» между этими частотами. Если сумма этих «расстояний» «слишком велика», то эти частоты «существенно отличаются». Понятно, что если наш кубик симметричный (т.е. применим
биномиальный закон
), то вероятность того, что сумма «расстояний» будет «слишком велика» будет малой. Чтобы вычислить эту вероятность нам необходимо знать распределение
статистики
Х
2
(
статистика
Х
2
вычислена на основе случайной
выборки
, поэтому она является случайной величиной и, следовательно, имеет свое
распределение вероятностей
).
Из многомерного аналога
интегральной теоремы Муавра-Лапласа
известно, что при n—>∞ наша случайная величина Х
2
асимптотически
распределена по закону Х
2
с L — 1 степенями свободы.
Итак, если вычисленное значение
статистики
Х
2
(сумма «расстояний» между частотами) будет больше чем некое предельное значение, то у нас будет основание отвергнуть
нулевую гипотезу
. Как и при проверке
параметрических гипотез
, предельное значение задается через
уровень значимости
. Если вероятность того, что статистика Х
2
примет значение меньше или равное вычисленному (
p
-значение
), будет меньше
уровня значимости
, то
нулевую гипотезу
можно отвергнуть.
В нашем случае, значение статистики равно 22,757. Вероятность, что статистика Х
2
примет значение больше или равное 22,757 очень мала (0,000045) и может быть вычислена по формулам
=ХИ2.РАСП.ПХ(22,757;4-1)
или
=ХИ2.ТЕСТ(Observed; Expected)
Примечание
: Функция
ХИ2.ТЕСТ()
специально создана для проверки связи между двумя категориальными переменными (см.
статью про критерий независимости
).
Вероятность 0,000045 существенно меньше обычного
уровня значимости
0,05. Так что, у игрока есть все основания подозревать своего противника в нечестности (
нулевая гипотеза
о его честности отвергается).
При применении
критерия Х
2
необходимо следить за тем, чтобы объем
выборки
n был достаточно большой, иначе будет неправомочна аппроксимация
Х
2
-распределением
распределения
статистики Х
2
. Обычно считается, что для этого достаточно, чтобы наблюденные частоты (Observed) были больше 5. Если это не так, то малые частоты объединяются в одно или присоединяются к другим частотам, причем объединенному значению приписывается суммарная вероятность и, соответственно, уменьшается число степеней свободы
Х
2
-распределения
.
Для того чтобы улучшить качество применения
критерия Х
2
(
увеличить его мощность
), необходимо уменьшать интервалы разбиения (увеличивать L и, соответственно, увеличивать количество
степеней свободы
), однако этому препятствует ограничение на количество попавших в каждый интервал наблюдений (д.б.>5).
Примечание
: Рассмотренный выше пример является частным случаем применения
критерия независимости хи-квадрат
(chi-square test), который позволяет определить есть ли связь между двумя категориальными переменными (см. статью
Критерий независимости хи-квадрат в MS EXCEL
).
СОВЕТ
: О проверке других видов гипотез см. статью
Проверка статистических гипотез в MS EXCEL
.
Непрерывный случай
Критерий согласия Пирсона
Х
2
можно применить так же в случае
непрерывного распределения
.
Рассмотрим некую
выборку
, состоящую из 200 значений.
Нулевая гипотеза
утверждает, что
выборка
сделана из
стандартного нормального распределения
.
Примечание
: Cлучайные величины в
файле примера на листе Непрерывное
сгенерированы с помощью формулы
=НОРМ.СТ.ОБР(СЛЧИС())
. Поэтому, новые значения
выборки
генерируются при каждом пересчете листа.
Соответствует ли имеющийся набор данных
нормальному распределению
можно визуально оценить
с помощью графика проверки на нормальность (normal probability plot)
.
Как видно из диаграммы, значения выборки довольно хорошо укладываются вдоль прямой. Однако, как и в
дискретном случае
для
проверки гипотезы
применим
Критерий согласия Пирсона Х
2
.
Для этого разобьем диапазон изменения случайной величины на интервалы с шагом 0,5
стандартных отклонений
. Вычислим наблюденные и теоретические частоты. Наблюденные частоты вычислим с помощью функции
ЧАСТОТА()
, а теоретические – с помощью функции
НОРМ.СТ.РАСП()
.
Примечание
: Как и для
дискретного случая
, необходимо следить, чтобы
выборка
была достаточно большая, а в интервал попадало >5 значений.
Вычислим статистику Х
2
и сравним ее с критическим значением для заданного
уровня значимости
(0,05). Т.к. мы разбили диапазон изменения случайной величины на 10 интервалов, то число степеней свободы равно 9. Критическое значение можно вычислить по формуле
=ХИ2.ОБР.ПХ(0,05;9)
или
=ХИ2.ОБР(1-0,05;9)
На диаграмме выше видно, что значение статистики равно 8,19, что существенно выше
критического значения
–
нулевая гипотеза
не отвергается.
Ниже приведена
диаграмма
, на которой
выборка
приняла маловероятное значение и на основании
критерия
согласия Пирсона Х
2
нулевая гипотеза была отклонена (не смотря на то, что случайные значения были сгенерированы с помощью формулы
=НОРМ.СТ.ОБР(СЛЧИС())
, обеспечивающей
выборку
из
стандартного нормального распределения
).
Нулевая гипотеза
отклонена, хотя визуально данные располагаются довольно близко к прямой линии.
В качестве примера также возьмем
выборку
из
непрерывного равномерного распределения
U(-3; 3). В этом случае, даже из графика очевидно, что
нулевая гипотеза
должна быть отклонена.
Критерий
согласия Пирсона Х
2
также подтверждает, что
нулевая гипотеза
должна быть отклонена.
Содержание
- Характеристики распределений
- Равномерное распределение
- Нормальное распределение
- Что такое корреляция
- Численное выражение корреляционной зависимости
- Прямая и обратная
- Сильная и слабая
- Корреляционный анализ в психологии
- Как работает функция ПИРСОН в Excel?
- Пример решения с функцией ПИРСОН при анализе в Excel
- Для чего нужен коэффициент корреляции?
- Свойства коэффициента корреляции
- Значения коэффициента корреляции
- История разработки критерия корреляции
- Для чего используется критерий корреляции Пирсона?
- Условия и ограничения применения критерия хи-квадрат Пирсона
- Выборочный коэффициент корреляции
- Как посчитать коэффициент корреляции в Excel
- Расчет доверительного интервала для коэффициента корреляции в Excel
- Примеры расчета хи-квадрата Пирсона
- Первый этап
- Второй этап
- Третий этап
- Четвертый этап
Характеристики распределений
Основная задача анализа вариационных рядов – это выявление подлинной закономерности распределения, которая достигается увеличением объема исследуемой совокупности при одновременном уменьшении интервала ряда.
Равномерное распределение
Нормальное распределение
Что такое корреляция
Корреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере.
Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше».
Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна).
Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект. Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие?
Правильно, между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная.
В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность.
Численное выражение корреляционной зависимости
Итак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение.
Например, изучается роль чтения в жизни людей. Исследователи взяли группу из 40 человек и измерили у каждого испытуемого два показателя: 1) сколько времени он читает в неделю; 2) в какой мере он считает себя благополучным (по шкале от 1 до 10). Ученые занесли эти данные в два столбика и с помощью статистической программы рассчитали корреляцию между чтением и благополучием. Предположим, они получили следующий результат -0,76. Но что значит это число? Как его проинтерпретировать? Давайте разбираться.
Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:
- Знак «+» или «-» отражает направление зависимости.
- Величина коэффициента отражает силу зависимости.
Прямая и обратная
Знак плюс перед коэффициентом указывает на то, что связь между явлениями или показателями прямая. То есть, чем больше один показатель, тем больше и другой. Выше оклад – выше продажи. Такая корреляция называется прямой, или положительной.
Если коэффициент имеет знак минус, значит, корреляция обратная, или отрицательная. В этом случае чем выше один показатель, тем ниже другой. В примере с чтением и благополучием мы получили -0,76, и это значит, что, чем больше люди читают, тем ниже уровень их благополучия.
Сильная и слабая
Корреляционная связь в численном выражении – это число в диапазоне от -1 до +1. Обозначается буквой «r». Чем выше число (без учета знака), тем корреляционная связь сильнее.
Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше.
Максимально возможная сила зависимости – это 1 или -1. Как это понять и представить?
Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов.
|
Испытуемый |
IQ |
Успеваемость (баллы) |
|
1 |
90 |
4,0 |
|
2 |
91 |
4,1 |
|
3 |
92 |
4,2 |
|
4 |
93 |
4,3 |
|
5 |
94 |
4,4 |
|
6 |
95 |
4,5 |
|
7 |
96 |
4,6 |
|
8 |
97 |
4,7 |
|
9 |
98 |
4,8 |
|
10 |
99 |
4,9 |
Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет.
Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость между интеллектом и успеваемостью равна 1.
Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10).
|
Испытуемый |
IQ |
Успех в общении с противоположным полом (баллы) |
|
1 |
90 |
10 |
|
2 |
91 |
9 |
|
3 |
92 |
8 |
|
4 |
93 |
7 |
|
5 |
94 |
6 |
|
6 |
95 |
5 |
|
7 |
96 |
4 |
|
8 |
97 |
3 |
|
9 |
98 |
2 |
|
10 |
99 |
1 |
Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет.
Это пример полной согласованности изменения двух показателей в группе – максимально возможная отрицательная взаимосвязь. Корреляционная связь между IQ и успешностью общения с противоположным полом равна -1.
А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места.
|
Испытуемый |
IQ |
Длина прыжка с места (м) |
|
1 |
90 |
2,5 |
|
2 |
91 |
1,2 |
|
3 |
92 |
2,0 |
|
4 |
93 |
1,7 |
|
5 |
94 |
1,9 |
|
6 |
95 |
1,3 |
|
7 |
96 |
1,7 |
|
8 |
97 |
2,3 |
|
9 |
98 |
1,1 |
|
10 |
99 |
2,6 |
Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0.
Мы рассмотрели крайние случаи. В реальных измерениях коэффициенты редко бывают равны точно 1 или 0. При этом принята следующая шкала:
- если коэффициент больше 0,70 – связь между показателями сильная;
- от 0,30 до 0,70 – связь умеренная,
- меньше 0,30 – связь слабая.
Если оценить по этой шкале полученную нами выше корреляцию между чтением и благополучием, то окажется, что эта зависимость сильная и отрицательная -0,76. То есть, наблюдается сильная отрицательная связь между начитанностью и благополучием. Что еще раз подтверждает библейскую мудрость о соотношении мудрости и печали.
Приведенная градация дает очень приблизительные оценки и в таком виде редко используются в исследованиях.
Чаще используются градации коэффициентов по уровням значимости. В этом случае реально полученный коэффициент может быть значимым или не значимым. Определить это можно, сравнив его значение с критическим значением коэффициента корреляции, взятым из специальной таблицы. Причем эти критические значения зависят от численности выборки (чем больше объем, тем ниже критическое значение).
Корреляционный анализ в психологии
Корреляционный метод выступает одним из основных в психологических исследованиях. И это не случайно, ведь психология стремится быть точной наукой. Получается ли?
В чем особенность законов в точных науках. Например, закон тяготения в физике действует без исключений: чем больше масса тела, тем сильнее оно притягивает другие тела. Этот физический закон отражает связь массы тела и силы притяжения.
В психологии иная ситуация. Например, психологи публикуют данные о связи теплых отношений в детстве с родителями и уровня креативности во взрослом возрасте. Означает ли это, что любой из испытуемых с очень теплыми отношениями с родителями в детстве будет иметь очень высокие творческие способности? Ответ однозначный – нет. Здесь нет закона, подобного физическому. Нет механизма влияния детского опыта на креативность взрослых. Это наши фантазии! Есть согласованность данных (отношения – креативность), но за ними нет закона. А есть лишь корреляционная связь. Психологи часто называют выявляемые взаимосвязи психологическими закономерностями, подчеркивая их вероятностный характер – не жесткость.
Пример исследования на студентах из предыдущего раздела хорошо иллюстрирует использование корреляций в психологии:
- Анализ взаимосвязи между психологическими показателями. В нашем примере IQ и успешность общения с противоположным полом – это психологические параметры. Выявление корреляции между ними расширяет представления о психической организации человека, о взаимосвязях между различными сторонами его личности – в данном случае между интеллектом и сферой общения.
- Анализ взаимосвязей IQ с успеваемостью и прыжками – пример связи психологического параметра с непсихологическими. Полученные результаты раскрывают особенности влияния интеллекта на учебную и спортивную деятельность.
Вот как могли выглядеть краткие выводы по результатам придуманного исследования на студентах:
- Выявлена значимая положительная зависимость интеллекта студентов и их успеваемости.
- Существует отрицательная значимая взаимосвязь IQ с успешностью общения с противоположным полом.
- Не выявлено связи IQ студентов с умением прыгать с места.
Таким образом, уровень интеллекта студентов выступает позитивным фактором их академической успеваемости, в то же время негативно сказываясь на отношениях с противоположным полом и не оказывая значимого влияния на спортивные успехи, в частности, способность к прыгать с места.
Как видим, интеллект помогает студентам учиться, но мешает строить отношения с противоположным полом. При этом не влияет на их спортивные успехи.
Неоднозначное влияние интеллекта на личность и деятельность студентов отражает сложность этого феномена в структуре личностных особенностей и важность продолжения исследований в этом направлении. В частности, представляется важным провести анализ взаимосвязей интеллекта с психологическими особенностями и деятельностью студентов с учетом их пола.
Как работает функция ПИРСОН в Excel?
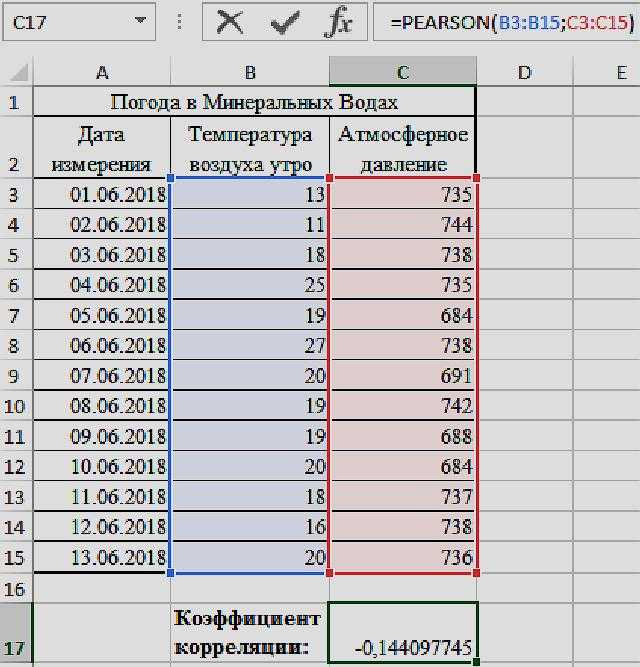
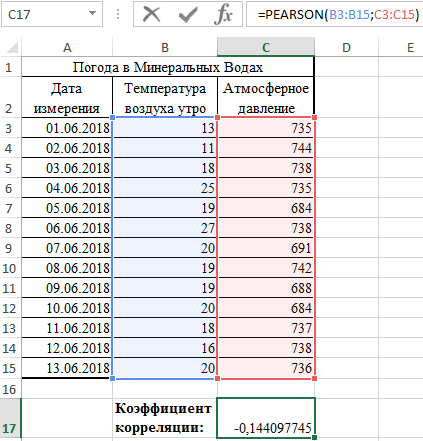
Рассмотрим пример расчета корреляции Пирсона между двумя массивами данных при помощи функции PEARSON в MS EXCEL. Первый массив представляет собой значения температур, второй давление в определенный летний период. Пример заполненной таблицы изображен на рисунке:

Пример решения с функцией ПИРСОН при анализе в Excel
- Выберем ячейку С17 в которой должен будет посчитаться критерий Пирсона как результат и нажмем кнопку мастер функций «fx» или комбинацию горячих клавиш (SHIFT+F3). Откроется мастер функций, в поле Категория необходимо выбрать «Статистические». В списке статистических функций выбрать PEARSON и нажать Ok:
- В меню аргументов выбрать Массив 1, в примере это утренняя температура воздуха, а затем массив 2 – атмосферное давление.
- В результате в ячейке С17 получим коэффициент корреляции Пирсона. В нашем случае он отрицательный и приблизительно равен -0,14.



Данный показатель -0,14 по Пирсону, который вернула функция, говорит об неблагоприятной зависимости температуры и давления в раннее время суток.
Для чего нужен коэффициент корреляции?
Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.
Случайные величины, связанные между собой, могут иметь совершенно разную природу этой связи. Не обязательно она будет функциональной, случай, когда прослеживается прямая зависимость между величинами. Чаще всего на обе величины действует целая совокупность разнообразных факторов, в случаях, когда они являются общими для обеих величин, наблюдается формирование связанных закономерностей.
Это значит, что доказанный статистически факт наличия связи между величинами не является подтверждением того, что установлена причина наблюдаемых изменений. Как правило, исследователь делает вывод о наличии двух взаимосвязанных следствий.
Свойства коэффициента корреляции

- значение коэффициента располагается в диапазоне от -1 до +1. Чем ближе к крайним значениям, тем сильнее положительная либо отрицательная связь между линейными параметрами. В случае нулевого значения речь идет об отсутствии корреляции между признаками;
- положительное значение коэффициента свидетельствует о том, что в случае увеличения значения одного признака наблюдается увеличение второго (положительная корреляция);
- отрицательное значение – в случае увеличения значения одного признака наблюдается уменьшение второго (отрицательная корреляция);
- приближение значения показателя к крайним точкам (либо -1, либо +1) свидетельствует о наличии очень сильной линейной связи;
- показатели признака могут изменяться при неизменном значении коэффициента;
- корреляционный коэффициент является безразмерной величиной;
- наличие корреляционной связи не является обязательным подтверждением причинно-следственной связи.
Значения коэффициента корреляции
Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока, в которой определенному числовому значению соответствует качественная характеристика.

- 0-0,3 – корреляционная связь очень слабая;
- 0,3-0,5 – слабая;
- 0,5-0,7 – средней силы;
- 0,7-0,9 – высокая;
- 0,9-1 – очень высокая сила корреляции.
Шкала может использоваться и для отрицательной корреляции. В этом случае качественные характеристики заменяются на противоположные.
Можно воспользоваться упрощенной шкалой Челдока, в которой выделяется всего 3 градации силы корреляционной связи:
- очень сильная – показатели ±0,7 — ±1;
- средняя – показатели ±0,3 — ±0,699;
- очень слабая – показатели 0 — ±0,299.
Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.
История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
Условия и ограничения применения критерия хи-квадрат Пирсона
- Сопоставляемые показатели должны быть измерены в количественной шкале (например, частота сердечных сокращений, температура тела, содержание лейкоцитов в 1 мл крови, систолическое артериальное давление).
- Посредством критерия корреляции Пирсона можно определить лишь наличие и силу линейной взаимосвязи между величинами. Прочие характеристики связи, в том числе направление (прямая или обратная), характер изменений (прямолинейный или криволинейный), а также наличие зависимости одной переменной от другой – определяются при помощи регрессионного анализа.
- Количество сопоставляемых величин должно быть равно двум. В случае анализ взаимосвязи трех и более параметров следует воспользоваться методом факторного анализа.
- Критерий корреляции Пирсона является параметрическим, в связи с чем условием его применения служит нормальное распределение каждой из сопоставляемых переменных. В случае необходимости корреляционного анализа показателей, распределение которых отличается от нормального, в том числе измеренных в порядковой шкале, следует использовать коэффициент ранговой корреляции Спирмена.
- Следует четко различать понятия зависимости и корреляции. Зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.

Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.
В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:

Распределение z для тех же r имеет следующий вид.

Намного ближе к нормальному. Стандартная ошибка z равна:

Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.

cγ – квантиль стандартного нормального распределения;
N-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.
Нижняя граница z:

Верхняя граница z:

Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:

Верхняя граница r:

Это была теоретическая часть. Переходим к практике расчетов.
Как посчитать коэффициент корреляции в Excel
Корреляционный анализ в Excel лучше начинать с визуализации.

На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.

Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:
— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.

Стандартная ошибка z легко подсчитывается с помощью формулы.

Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.

Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.

Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.

Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.
Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.
Примеры расчета хи-квадрата Пирсона
Пример 1:
Необходимо определить наличие влияния предшествующей степени нарушения кровообращения на исход комиссуротомии (хирургическое разделение спаек при стенозе клапанного отверстия сердца). Пациенты поступали на комиссуротомию с различными исходными уровнями нарушения кровообращения. После комиссуротомии пациенты были выписаны с различными исходами операции.
Таблица: наблюдаемые (Observed) частоты распределения влияния степени нарушения кровообращения на результаты операции комиссуротомии
| Степень нарушения кровообращения | Всего больных | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 30 | 20 | 8 | 2 |
| III | 80 | 43 | 20 | 17 |
| IV | 60 | 10 | 40 | 10 |
| Всего | 170 | 73 | 68 | 29 |
| H0-гипотеза | 100% | 43% | 40% | 17% |
Первый этап
Расчет ожидаемых (Expected) величин (на основании групповых частот)
Второй этап
Сопоставление наблюдаемых и ожидаемых частот с нахождением их разницы (O-E)
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | +7 | -4 | -3 |
| III | +9 | -12 | +3 |
| IV | -16 | +16 | 0 |
| Всего | 0 | 0 | 0 |
Третий этап
Рассчитываем сумму отношений квадрата разности значений и делим ожидаемые данные (хи-квадрат) (O-E)2/E
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 49/13=3,77 | 16/12=1,33 | 9/5=1,80 |
| III | 81/34=2,38 | 144/32=4,50 | 9/14=0,64 |
| IV | 256/26=9,85 | 256/24=10,66 | 0/10*=0,10 |
| Всего | 16 | 16,49 | 2,54 |
как видно из данной таблицы одно из ожидаемых значений равно 0, в данном случае будет подставлена 1, корректнее применить точный критерий Фишера (см. Условия применения хи-квадрата Пирсона)
Четвертый этап
Необходимо соотнести полученное значение хи-квадрата с критическим значением хи-квадрата.Возникает вопрос, откуда брать критическое значение? Критическое значение хи-квадрата, как и для большинства, статистических критериев зависит от степени свободы и уровня достоверности (alpha), который Вы выбираете.В нашем случае, наше количество степеней свободы равно (3-1)*(3-1)=4, уровень значимости, который мы хотим соблюсти равен 0,05Обратимся к таблице критических значение хи-квадрата:
- Xи-квадрат (для d.f.=4 p=0.05) = 9.488
- Xи-квадрат (для d.f.=4 p=0.01) = 13.27735,03 > 13,277;
- p<0,01
Пример корректной интерпретации: Предшествующая степень нарушения кровообращения влияет на исход комиссуротомии (однако! Мы не можем говорить о направленности связи, то есть: улучшает-ухудшает сказать не можем), оптимально указать степень свободы, точное значение хи-квадрата, если есть возможность рассчитать точное значение достоверности, то так же стоит указать и его или остановиться на критическом значении достоверности (p<0,05 или p<0,01 и так далее).В нашем случае:d.f.=4, x2=35,03, p< 0.01
Пример 2: Вернемся к нашему примеру с влиянием курения на развитие артериальной гипертензии:Исходная четырехпольная таблица:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
Для четырехпольных таблиц существует упрощенная формула расчета значения хи-квадрата:
| Исход + | Исход 0 | Всего | |
| Фактор + | a | b | a+b |
| Фактор 0 | c | d | c+d |
| Всего | a+c | b+d | N |
- x2= (40х48 – 32х30)х150 / (70)(80)(72)(78) = (1920 – 960)2х150/31449600 = 138240000/31449600 = 4,395
- Сравним полученное значение хи-квадрата с критическим значением (для степени свободы 1, и уровнем значимости 3,841)
Правильная интерпретация: Курение оказывает влияние на формирование повышенного артериального давления df=1, x2= 4,395, p<0,05
Источники
- https://math.semestr.ru/group/hypothesis-testing.php
- http://xn--c1abdmpkibfqehdkeh3a.xn--p1ai/stati/article_post/o-korrelyatsii-prostymi-slovami
- https://exceltable.com/funkcii-excel/koefficient-korrelyacii-pirsona
- https://forex365.ru/indicators/koef-korrelyacii-v-excell.html
- https://medstatistic.ru/methods/methods8.html
- https://statanaliz.info/statistica/korrelyaciya-i-regressiya/linejnyj-koefficient-korrelyacii-pirsona/
- https://lit-review.ru/biostatistika/kriterijj-khi-kvadrat-pirsona/
В статье рассматривается процедура создания шаблона Excel и опыт его применения для автоматического построения гистограмм и кривых Гаусса по результатам данных экспериментальных наблюдений с одновременной оценкой согласия по критерию Пирсона в учебном процессе. Показываются преимущества данного метода перед ручным счетом по проверке рассмотренного критерия.
Ключевые слова: шаблон Excel, гистограмма, кривая распределения, критерий согласия Пирсона
В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: металлургии, а также в экономике, биологии, политике, социологии и т. д. Рассмотрим использование некоторых средств статистического анализа, а именно — гистограмм для обработки больших массивов данных.
Целью первичной обработки экспериментальных наблюдений обычно является выбор закона распределения, наиболее хорошо описывающего случайную величину, выборку которой мы наблюдали. Проверка того, насколько хорошо наблюдаемая выборка описывается теоретическим законом, осуществляется с использованием различных критериев согласия. Целью проверки гипотезы о согласии опытного распределения с теоретическим является стремление удостовериться в том, что данная модель теоретического закона не противоречит наблюдаемым данным, и использование ее не приведет к существенным ошибкам при вероятностных расчетах. Некорректное использование критериев согласия может приводить к необоснованному принятию или необоснованному отклонению проверяемой гипотезы [1].
Сходимость результатов наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.
Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными. Сама процедура проверки нормальности распределения относится к распространенной стандартной и довольно тривиальной задаче обработки данных и достаточно подробно и широко описана в различной литературе по метрологии и статистической обработке данных измерений [2- 4].
Данные, получаемые в результате измерений при контроле технологических процессов, оценке характеристик различных объектов и др. для дальнейшей обработки желательно представлять в виде теоретического распределения, максимально соответствующего экспериментальному распределению. Проверку гипотезы о виде функции распределения в настоящее время проводят по различным критериям согласия — Пирсона, Колмогорова, Смирнова и другим в соответствии с новыми разработанными нормативными документами — рекомендациями по стандартизации [5, 6].
Наиболее часто используется критерий Пирсона 2. Однако применение критериев согласия требует обычно довольно значительного объёма данных. Так, критерий Пирсона обычно рекомендуется использовать при объёме выборки не менее 50…100. Поэтому при небольшом объёме выборки проверку гипотезы о виде функции распределения проводят приближёнными методами — графическим методом или по асимметрии и эксцессу. Применение критерия Пирсона для ручной обработки данных очень подробно было изложено в известной работе [2]. Как свидетельствует опыт проверок согласия экспериментальных данных с теоретическими по различным критериям, эта процедура является очень трудоемкой, требует некоторой усидчивости и особого внимания при обработке от исследователя, как правило, не исключает ошибок в работе и не вызывает особого энтузиазма у выполняющего эту работу.
Решение задач статистического анализа связано со значительными объемами вычислений. Проведение реальных многовариантных статистических расчетов в ручном режиме является очень громоздкой и трудоемкой задачей и без использования компьютера в настоящее время практически невозможно. В настоящее время разработано достаточное количество универсальных и специализированных программных средств для статистического анализа и обработки экспериментальных данных. Автор предлагает к рассмотрению достаточно простой и эффективный шаблон для быстрого построения гистограммы и кривой нормального распределения.
По виду гистограммы можно предположить (принять гипотезу) о том, что выборка случайных чисел подчиняется нормальному закону распределения. Далее, для того чтобы убедиться в правильности выбранной гипотезы надо, первое — построить график гипотетического нормального закона распределения, выбрав в качестве параметров (математического ожидания и среднего квадратического отклонения) их оценки (среднее и стандартное отклонение), и совместить график гипотетического распределения с графиком гистограммы. И, второе — используя в данном случае, как пример, критерий согласия Пирсона, установить справедливость выбранной гипотезы.
Рассмотрим порядок действий при работе с критерием Пирсона в среде Excel.
1. Полученные в результате измерений значения 100 случайных результатов измерений внести в ячейки A1:A100 шаблона Excel и приступить к построению гистограммы на основе данных, назначая длину интервала (карман) и выбирая необходимое число интервалов.
2. Затем на этом же листе создается таблица, в которую посредством формул Excel вносятся основные расчетные величины, используемые для построения гистограммы и кривой Гаусса: среднее арифметическое, стандартное отклонение, минимальное и максимальное значения выборки, размах, величина кармана (рис. 1).
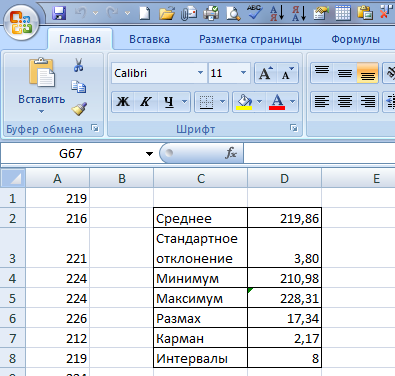
Рис. 1. Фрагмент таблицы с исходными данными
В ячейку D2 вносится формула =СРЗНАЧ(A1:A100), D3: =СТАНДОТКЛОН(A1:A100), D4: =МИН(A1:A100), D5: =МАКС(A1:A100), D6: =D5-D4, D7: =D6/D8. В ячейку D8 вводится число интервалов, которое для числа измерений, равным 100, может быть принято от 7 до 12.
Для оценки оптимального для нашего массива данных количества интервалов можно воспользоваться формулой Стерджесса: k~1+3,322lgN, где N— количество всех значений величины. Например, для N = 100, n = 7,6, которое должно быль округлено до целого числа, округляем до n = 8.
3. Интервал карманов вычисляют так: разность максимального и минимального значений массива, деленная на количество интервалов: .
4. Теперь в каждой ячейке шаг за шагом прибавляем полученное значение ширины кармана: сначала к минимальному значению нашего массива (ячейка D4), затем в следующей ячейке ниже — к полученной сумме и т. д. Так постепенно доходим до максимального значения. Таким образом, мы и построили интервалы карманов в виде столбца значений.
Интервалом считается следующий диапазон: (i-1; i] или i<значения<=i (нестрогая верхняя граница интервала — это значение в ячейке, нижняя строгая граница — значение в предыдущей ячейке).
5. Выделяем столбец рядом с нашими карманами, нажимаем «F2» и вводим функцию: =ЧАСТОТА (массив данных; диапазон карманов) и нажимаем Ctr+Shift+Enter.
6. В выделенном нами столбце напротив границ интервалов (а мы знаем, что это нестрогие верхние границы) появилось количество значений исходного массива, которые попадают в интервал (рис. 2).
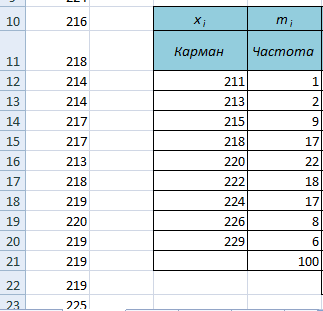
Рис. 2. Количество значений исходного массива, попавших в интервалы (частоты)
Построение теоретического закона распределения
Для построения теоретического закона распределения совместно с гистограммой и проверкой согласия по критерию хи-квадрат Пирсона автоматически заполняется таблица 1 после ввода экспериментальных данных в ячейки A1:A100.
Таблица 1
|
xi |
mi |
n∙pi |
|
|
карманы |
частота |
теоретическая частота |
статистика U |
Для построения этой таблицы надо воспользоваться таблицей карман — частота процедуры Гистограмма. В этой таблице обозначены:
xi — границы интервалов группировки (карманы — получены как результат выполнения процедуры Гистограмма);
mi — количество элементов выборки, попавших в i–ый интервал (частота — получена в результате процедуры Гистограмма).
Для построения этой таблицы в Excel к столбцам карман — частота процедуры Гистограмма надо добавить столбцы n∙pi (теоретическая частота) и (статистика U).
Проверка согласия эмпирического и теоретического законов распределения по критерию хи-квадрат Пирсона.
В ячейку столбца, помеченного именем U, вводим формулу,
, (1)
Критическое значение статистики U, которая имеет распределениес r степенями свободы (число степеней свободы определяется как число частичных интервалов минус 1), определяется при помощи функции ХИ2ОБР.
Функция ХИ2ОБР вызывается следующим образом. В главном меню Excel выбирается закладка Формулы → Вставить функцию →в диалоговом окне Мастер функций— шаг 1 из 2 вкатегории Статистические →ХИ2ОБР (рис. 3).
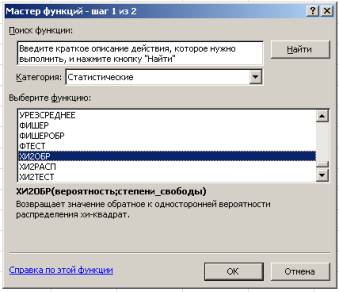
Рис. 3. Диалоговое окно выбора функции ХИ2ОБР
В диалоговом окне Аргументы функции ХИ2ОБР заполняются поля как показано на рис. 4, задаваясь уровнем значимости (например, 0,05, что соответствует доверительной вероятности Р = 0,95) и предварительно выбрав ячейку для результата вычисления функции.
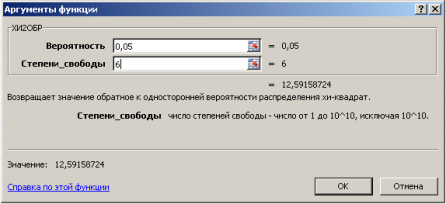
Рис. 4. Диалоговое окно функции ХИ2ОБР с заполненными полями ввода
Размножим формулу (1) в диапазонах ячеек [F12; F20] и [F51; F61]. В ячейке F21 получим сумму содержимого ячеек F12; F20 (рис. 5). В ячейке F62 получим сумму содержимого ячеек F51; F61 (рис. 6).
В ячейке F21 получено значение статистики: U = 2,09, а в ячейке F62 — U = 3,43 при доверительной вероятности Р = 0,95.
Теперь с помощью стандартного инструмента для построения гистограмм («вставка/гистограмма» и т. д.) на этом же листе Excel можно построить гистограммы распределения с кривой Гаусса для разных чисел интервалов (в данном случае n = 8 и n = 10) (рис. 5 и 6).
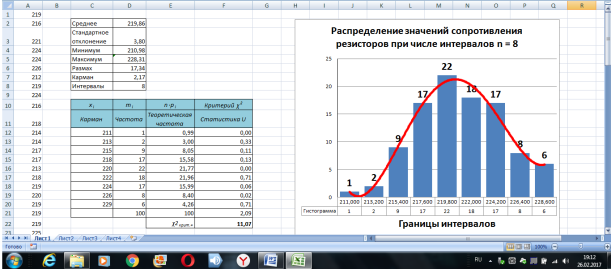
Рис. 5. Вид гистограммы и кривой распределения при числе интервалов n = 8 (пример)
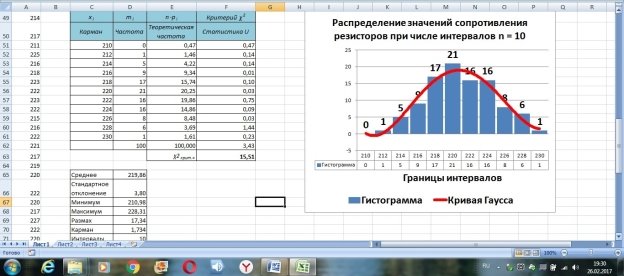
Рис. 6. Вид гистограммы и кривой распределения при числе интервалов n = 10 (пример)
Шаблон позволяет варьировать числом интервалов и величиной кармана, при этом автоматически изменяется внешний вид гистограммы и кривой нормального распределения. Исследователь может подобрать наиболее «красивый» вид гистограммы и аппроксимирующей кривой Гаусса, одновременно изменив значение доверительной вероятности и числа степеней свободы и добившись при этом выполнения критерия Пирсона.
Если значение статистики U оказалось меньше критического значения при заданной доверительной вероятности, то гипотеза, состоящая в том, что исследуемая выборка подчиняется нормальному закону распределения, принимается. Вданном примере значение обеих статистик U оказалось меньше критического значения
и
Следовательно, мы можем распространить данный закон распределения на всю генеральную совокупность исследуемых объектов (партию изделий, сменную выработку, месячный план и т. д.).
Более подробно указанная тема была рассмотрена в статье автора в сборнике «Законодательная и прикладная метрология» [7].
Выводы
- Существовавшая ранее традиционная «ручная» обработка данных при проверке нормального (и других) законов распределения и построении гистограмм являлась достаточно трудоемкой задачей, не исключавшей появление ошибок, обнаружение которых зачастую требовало значительных затрат времени и моральных сил исследователя.
- Появление пакетов офисных программ, в частности Excel 2010 и ее последующих версий, позволяет значительно сократить трудоемкость обработки данных и практически исключает появление ошибок в расчетах.
Литература:
1. Лемешко Б. Ю., Постовалов С. Н. О правилах проверки согласия опытного распределения с теоретическим. — Методы менеджмента качества. Надежность и контроль качества. — 1999, № 11. — С. 34–43.
2. Бурдун Г. Д., Марков Б. Н. Основы метрологии. Учебное пособие для вузов. — М.: Изд. стандартов, 1975. — 336 с.
3. Сулицкий В. Н. Методы статистического анализа в управлении: Учеб. пособие. — М.: Дело, 2002. — 520 с.
4. Иванов О. В. Статистика / Учебный курс для социологов и менеджеров. Часть 2. Доверительные интервалы. Проверка гипотез. Методы и их применение. — М.: Изд. МГУ им. М. В. Ломоносова, 2005. — 220 с.
5. Рекомендации по стандартизации Р 50.1.033–2001. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть 1. Критерии типа хи-квадрат. — М.: ФГУП «Стандартинформ», 2006. — 87 с.
6. Рекомендации по стандартизации Р 50.1.037–2002. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. — М.: ИПК Изд. стандартов, 2002. — 62 с.
7. Фаюстов А. А. Проверка гипотезы о нормальном распределении выборки по критерию согласия Пирсона средствами приложения Excel. — Законодательная и прикладная метрология, 2016, № 6. — С. 3–9.
Основные термины (генерируются автоматически): статистический анализ, критерий согласия, массив данных, вид функции распределения, интервал карманов, максимальное значение, минимальное значение, построение гистограммы, различный критерий согласия, стандартное отклонение.
До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.
Так был изобретен критерий χ2 (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.
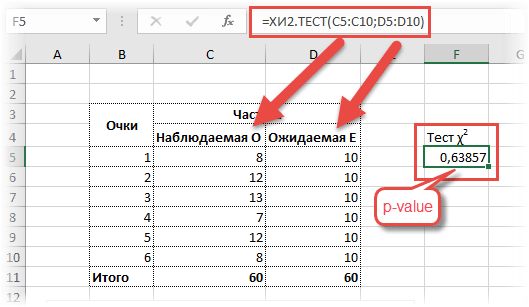
Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.
- Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
- Распределение этой меры при справедливости гипотезы о том, что различий нет.
Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.
Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной Ei будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение
имеет стандартное нормальное распределение.
Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.
У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.
Это и есть статистика для критерия Хи-квадрат Пирсона. Если частоты действительно соответствуют ожидаемым, то значение статистики Хи-квадрат будет относительно не большим (отклонения находятся близко к нулю). Большое значение статистики свидетельствует в пользу существенных различий между частотами.
«Большой» статистика Хи-квадрат становится тогда, когда появление наблюдаемого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение статистики Хи-квадрат при многократном повторении эксперимента, когда гипотеза о согласии частот верна.
Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем больше слагаемых, тем больше ожидается значение статистики, ведь каждое слагаемое вносит свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ2 – это целое семейство распределений.
И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.
По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам Хи-квадрат).
Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.
Примерно также распределение статистики может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.
Таким образом, распределение хи квадрат (χ2) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. Формальное определение следующее. Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.
Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).
Проверка гипотезы по критерию Хи квадрат Пирсона
Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по статистике Хи-квадрат. Далее либо полученную статистику сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда статистика окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.
Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение статистики критерия хи-квадрат.
Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ20,05; 5 = 11,1.
Сравним фактическое и табличное значение. 3,4 (χ2) < 11,1 (χ20,05; 5). Расчетный значение оказалось меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.
Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.
Ниже их краткое описание.
ХИ2.ОБР – критическое значение Хи-квадрат при заданной вероятности слева (как в статистических таблицах)
ХИ2.ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.
ХИ2.РАСП – p-value слева (можно рассчитать плотность).
ХИ2.РАСП.ПХ – p-value справа.
ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.
Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:
=ХИ2.ОБР(0,95;5)
Или так
=ХИ2.ОБР.ПХ(0,05;5)
Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).
Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ2 = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)
=ХИ2.РАСП.ПХ(3,4;5) = 0,63857
Значит, при 5-ти степенях свободы вероятность получить значение критерия χ2 = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.
А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.
Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.
Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.
Статистика критерия хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).
Надеюсь, мне удалось объяснить, что такое критерий согласия χ2 (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.
Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.
Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.
Скачать файл с примером.
Поделиться в социальных сетях:
Для того, чтобы рассчитать коэффициент корреляции Пирсона в Excell необходимо сделать следующие шаги:
1.Вносим значения для двух переменных в таблицу (Например Переменная 1 и Переменная 2)
2. Ставим курсор в пустую ячейку
3. На панеле инструментов нажимаем кнопку fx (вставить формулу)
4. В открывшемся окне «Мастер функций» в поле «Категории» выбираем Полный алфавитный перечень
5. Затем в поле «Выберите функцию» находим функцию ПИРСОН
5.1. Нажимаем Ок
6. В открывшемся окне «Аргументы функции» в поле Массив1 вносим номера ячеек, содержащие значения Переменной 1, в поле Массив2 вносим номера ячеек, содержащие значения Переменной2.
7. Нажимаем Ок
8. Смотрим получившийся результат
Correlations are important in many areas of science. Although correlation doesn’t equal causation, it’s often the first step to understanding the true relationship between two variables and can give a valuable hint that there is a causal relationship somewhere.
Learning to calculate a correlation is crucial, and you can easily find the “r value” in Excel using either built-in functions or by working through the calculation in pieces using the more basic functions of the program. The simplest way is using the built-in function, but understanding the calculation is helpful if you ever need to use a different program to find it.
What Is Pearson’s Correlation Coefficient?
Pearson’s correlation coefficient is a simple way of calculating the degree of correlation between two variables, returning a value (called r) ranging from −1 to 1. A perfect correlation (r = 1) between two variables would be where an increase in one variable by a certain amount leads to a correspondingly-sized increase in the other, or vice-versa.
A perfect negative correlation (r = −1) is basically the same, except an increase in one variable leads to a correspondingly-sized decrease in the other. Finally, no correlation whatsoever means there is no relationship at all between two things.
In practice, you’ll almost never see a perfect correlation, and most values will be some decimal value between −1 and 1. So when you find the Pearson r in Excel, the result will usually be some decimal value, where the magnitude of the number tells you the strength of the correlation between your variables.
Pearson Correlation in Excel
The easiest method for finding the Pearson correlation in Excel is using the built-in “Pearson” function or (equivalently) the “Correl” function. The function has a simple syntax: PEARSON(array 1, array 2).
In short, you just need two arrays of values (i.e. columns of results, for example, age and blood pressure arranged so there is a row for each individual patient) that are equal in length, then type “=PEARSON(” into an empty cell, followed by the range of values for the first array, a comma, then the range of values for the second. Then you close out the brackets, hit “Enter” and it will return the r value.
As always, you can highlight the values you want to search for correlations with your mouse or by navigating to the relevant cells with the arrow keys on your keyboard.
You can also use the “Correl” function, which performs the same calculation as “Pearson” and on versions of Excel from 2003 onward, leads to the exact same result. However, if you have an older version of Excel, you should use the “Correl” function because there can be rounding errors with “Pearson.”
Finding Pearson’s r “By Hand”
You can also calculate the r value in Excel in the more traditional method but with the help of the automatic calculations from the program. First, put the values for your variables (which can be referred to as x and y for clarity) in two columns, then create three more columns: xy, x2 and y2. Now multiply each value in the x column by the y column in the xy column (using the cell numbers in the calculation so you can drag it down for the rest of the column), square the x values for the next column, and square the y values for the final one.
Create a “sum” row underneath your data, and take the sum of all the values for each column. You can then use the formula to calculate your r value:
Here, n is the number of pairs of values you have. You can follow this through in pieces: Take the number of pairs of values, multiply it by the sum of your xy column, and then subtract the product of the sums of the x and y values.
Then, multiply the sum of your x2 column by n, subtract the sum of your x column squared, do the same thing for y and multiply these together, then take the square root of the whole thing. Finally, divide the first result by the second to get your r value.
Home » Misc » Критерий пирсона в excel
Функция ПИРСОН расчета коэффициента корреляции Пирсона в Excel
Функция ПИРСОН (вводить следует PEARSON на английском) предназначена для вычисления коэффициента корреляции Пирсона r. Данную функцию используют в работе в том случае, когда необходимо отразить степень линейной зависимости между двумя массивами данных. В Excel имеется несколько функций с помощью которых можно получить такой же результат, однако универсальность и простота функции Пирсон делают выбор в ее пользу.
Как работает функция ПИРСОН в Excel?
Рассмотрим пример расчета корреляции Пирсона между двумя массивами данных при помощи функции PEARSON в MS EXCEL. Первый массив представляет собой значения температур, второй давление в определенный летний период. Пример заполненной таблицы изображен на рисунке:
Задача следующая: необходимо определить взаимосвязь между температурой и давлением за июнь месяц.
Пример решения с функцией ПИРСОН при анализе в Excel
- Выберем ячейку С17 в которой должен будет посчитаться критерий Пирсона как результат и нажмем кнопку мастер функций «fx» или комбинацию горячих клавиш (SHIFT+F3).
Откроется мастер функций, в поле Категория необходимо выбрать «Статистические». В списке статистических функций выбрать PEARSON и нажать Ok:
- В меню аргументов выбрать Массив 1, в примере это утренняя температура воздуха, а затем массив 2 – атмосферное давление.
- В результате в ячейке С17 получим коэффициент корреляции Пирсона. В нашем случае он отрицательный и приблизительно равен -0,14.
Данный показатель -0,14 по Пирсону, который вернула функция, говорит об неблагоприятной зависимости температуры и давления в раннее время суток.
Функция ПИРСОН пошаговая инструкция
Коэффициент корреляции является самым удобным показателем сопряженности количественных признаков.
Задача: Определить линейный коэффициент корреляции Пирсона.
Пример решения:
- В таблице приведены данные для группы курящих людей. Первый массив х — представляет собой возраст курящего, второй массив y представляет собой количество сигарет, выкуренных в день.
- Выберем ячейку В4 в которой должен будет посчитаться результат и нажмем кнопку мастер функций fx (SHIFT+F3).
- В группе Статистические выберем функцию PEARSON.
- Выделим Массив 1 – возраст курящего, затем Массив 2 – число сигарет, выкуренных в день.
- Нажмем кнопку ОК и увидим критерий нормального распределения Пирсона в ячейке В4.
Таким образом, по результату вычисления статистическим выводом эксперимента выявлена отрицательная зависимость между возрастом и количеством выкуренных сигарет в день.
Корреляционный анализ по Пирсону в Excel
Задача: школьникам были даны тесты на наглядное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли взаимосвязь между временем решения этих задач?
Пример решения: представим исходные данные в виде таблицы:
- Переходим курсором в ячейку F2. Откроем мастер функций fx (SHIFT+F3) или вводим вручную.
- Выберем функцию PEARSON.
- Выделим мышкой Массив1, затем Массив 2.
- Нажмем ОК и в ячейке F2 получим критерий согласия Пирсона.
Интерпретация результата вычисления по Пирсону
Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 – являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 – следовательно, произошла ошибка в вычислениях.
Если коэффициент корреляции по модулю оказывается близким к 1, то это соответствует высокому уровню связи между переменными.
Скачать примеры функции ПИРСОН для корреляции в Excel
Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости. Эти положения очень важно четко усвоить для правильной интерпретации полученной корреляционной зависимости.
Функция ПИРСОН — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции PEARSON в Microsoft Excel.
Описание
Возвращает коэффициент корреляции Пирсона (r) — безразмерный индекс в интервале от -1,0 до 1,0 включительно, который отражает степень линейной зависимости между двумя множествами данных.
Синтаксис
PEARSON(массив1;массив2)
Аргументы функции PEARSON описаны ниже.
Замечания
-
Аргументы должны быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Если массив1 или массив2 пуст, либо число точек данных в этих массивах не совпадает, функция PEARSON возвращает значение ошибки #Н/Д.
-
Коэффициента корреляции Пирсона (r) вычисляется по следующей формуле:
где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
Независимые значения |
Зависимые значения |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Формула |
Описание (результат) |
Результат |
|
=PEARSON(A3:A7;B3:B7) |
Коэффициент корреляции Пирсона для приведенных выше данных (0,699379) |
0,699379 |
функция PEARSON — служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Дополнительно.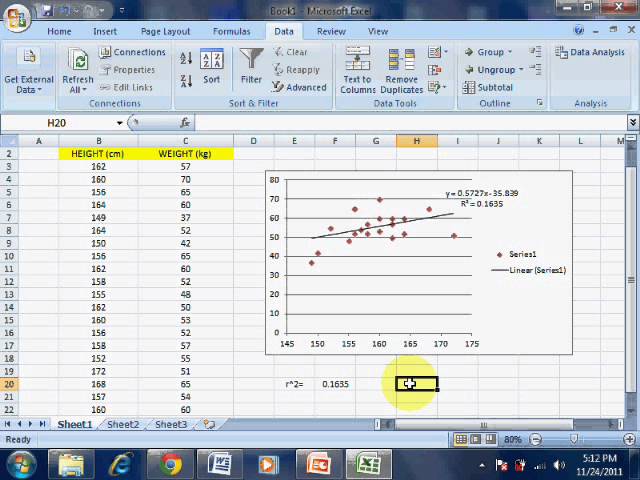
В этой статье описаны синтаксис формулы и использование функции PEARSON в Microsoft Excel.
Описание
Возвращает коэффициент корреляции момента продукта Пирсона, r, безразмерный индекс, который находится в диапазоне от -1,0 до 1,0 включительно и отражает степень линейной зависимости между двумя наборами данных.
Синтаксис
ПИРСОН (массив1, массив2)
Синтаксис функции ПИРСОН имеет следующие аргументы:
Замечания
-
Аргументы должны быть либо числами, либо именами, константами массива или ссылками, содержащими числа.
-
Если аргумент массива или ссылки содержит текст, логические значения или пустые ячейки, эти значения игнорируются; однако включаются ячейки с нулевым значением.
-
Если массивы1 и массив2 пусты или содержат разное количество точек данных, PEARSON возвращает значение ошибки #Н/Д.
-
Формула для коэффициента корреляции момента продукта Пирсона, r, выглядит следующим образом:
, где x и y — выборочные значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
|
Данные |
||
|
Независимые значения |
Зависимые значения |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Формула |
Описание (Результат) |
Р результат |
|
=ПИРСОН(A3:A7;B3:B7) |
Коэффициент корреляции момента продукта Пирсона для наборов данных выше (0,699379) |
0,699379 |
Функция ПИРСОН для расчета коэффициента корреляции Пирсона в Excel
Функция ПИРСОН используется для расчета коэффициента корреляции Пирсона r.
Как PEARSON работает в Excel?
Рассмотрим пример вычисления корреляции Пирсона между двумя массивами данных с помощью функции ПИРСОН в MS EXCEL. Первый массив представляет собой значения температуры, второй – давления в определенный летний период. Пример заполненной таблицы показан на рисунке:
Задача следующая: необходимо определить зависимость между температурой и давлением для месяца июнь.
Пример решения с функцией ПИРСОН при анализе в Excel
- Выберите ячейку C17, в которой должен быть рассчитан критерий Пирсона как результат, и нажмите мастер-кнопку функции «fx» или комбинацию горячих клавиш (SHIFT+F3). Откроется мастер функций, в поле «Категория» выберите «Статистические».
В списке статистических функций выберите и нажмите Ok:
- В меню аргументов выберите Массив 1; в примере это утренняя температура воздуха, а затем Массив 2 — атмосферное давление.
- В результате в ячейке С17 получаем коэффициент корреляции Пирсона. В нашем случае он отрицательный и примерно равен -0,14.
Этот показатель -0,14 по Пирсону, вернувшему функцию, свидетельствует о неблагоприятной зависимости температуры и давления в раннее время суток.
Пошаговая инструкция функции ПИРСОНА
Коэффициент корреляции является наиболее удобным показателем сопряженности количественных признаков.
Задача: Определить коэффициент линейной корреляции Пирсона.
Пример решения:
- В таблице приведены данные для группы курильщиков. Первый массив x — представляет возраст курильщика, второй массив y — количество выкуриваемых сигарет в день.
- Выберите ячейку B4, в которой будет вычисляться результат, и нажмите главную кнопку функции fx (SHIFT + F3).
- В группе Статистические выберите функцию ПИРСОН.
- Выберите Массив 1 — возраст курения, затем Массив 2 — количество выкуриваемых сигарет в день.
- Нажмите кнопку ОК и посмотрите критерий нормального распределения Пирсона в ячейке B4.
Таким образом, по результату расчета статистический вывод эксперимента выявил отрицательную связь между возрастом и количеством выкуриваемых сигарет в день.
Корреляционный анализ по Пирсону в Excel
Задание: учащимся были даны тесты на наглядное и вербальное мышление. Измерялось среднее время решения тестовых задач в секундах. Психолога интересует вопрос: есть ли связь между временем решения этих задач?
Пример решения: исходные данные представляем в виде таблицы:
- Подводим курсор к ячейке F2. Откройте мастер функций fx (SHIFT+F3) или введите его вручную.
- Выберите функцию.
- Выберите массив 1 B3:B21 с помощью мыши, затем массив 2 C3:C21.
- Нажимаем ОК и в ячейке F2 получаем критерий совместимости Пирсона.
Learn more

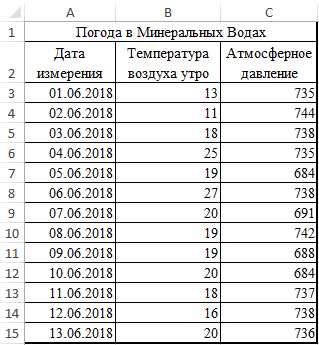
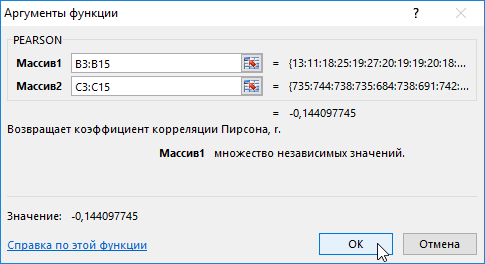

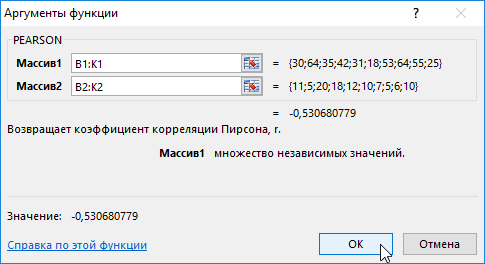
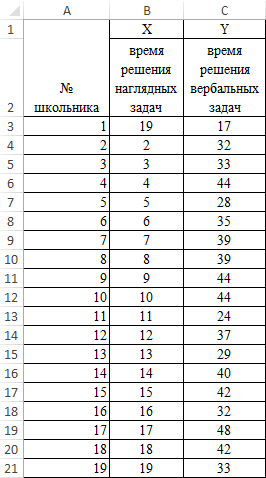
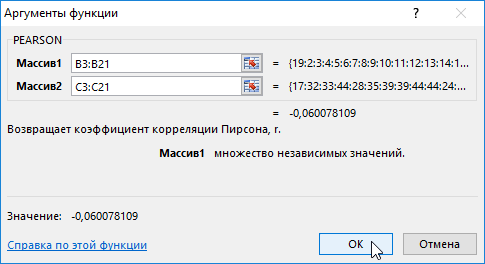
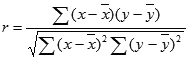
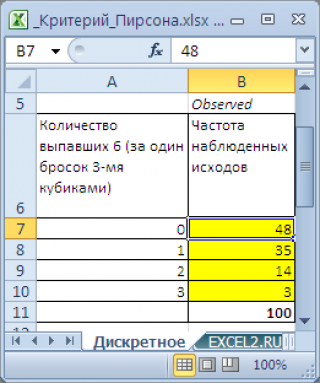
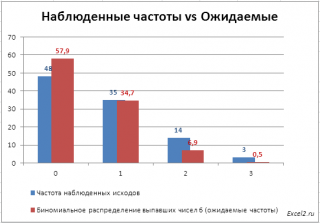
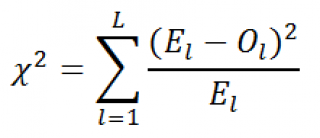
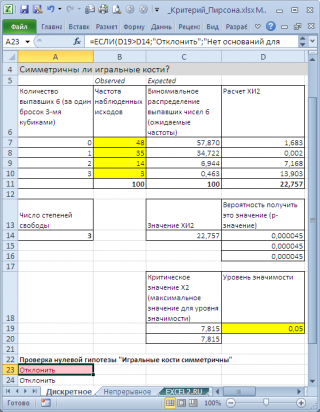
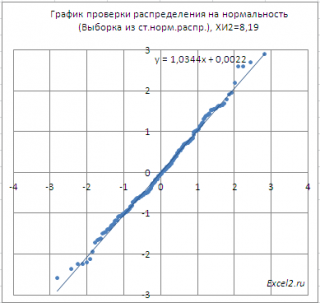
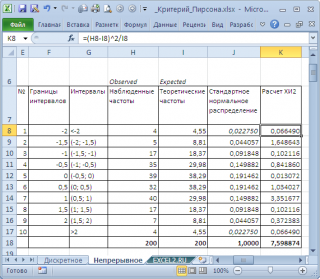
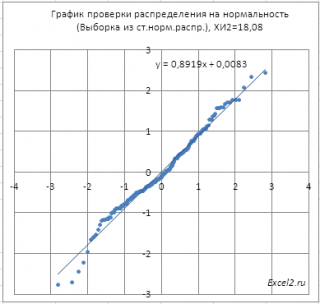
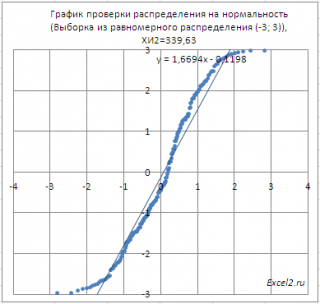





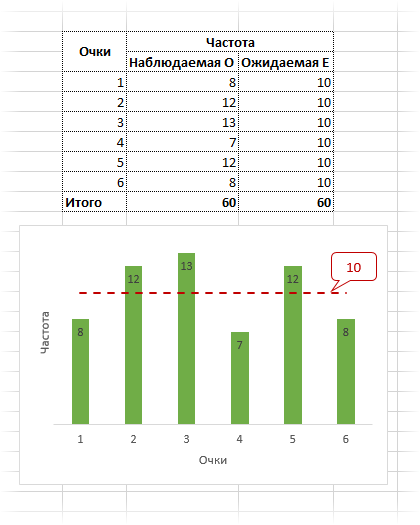
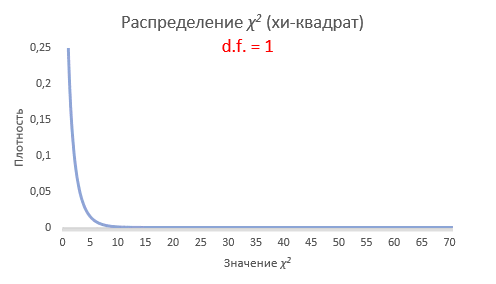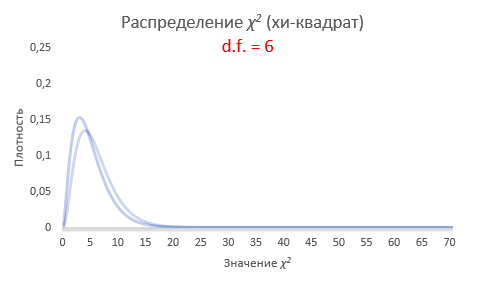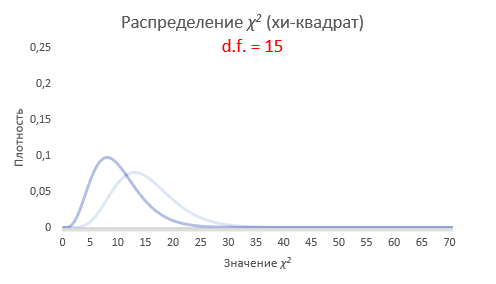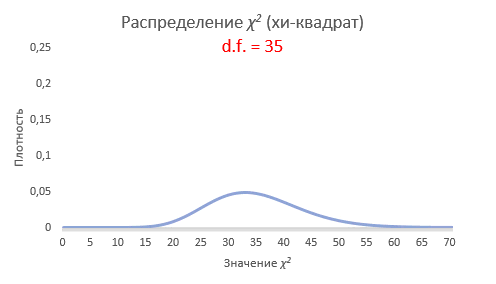
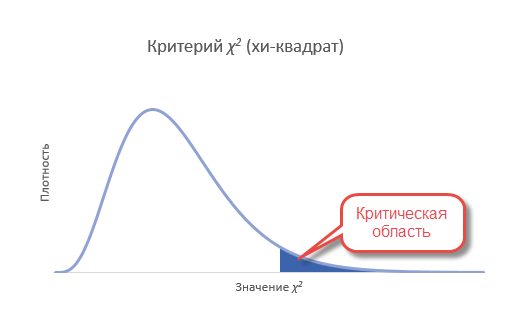
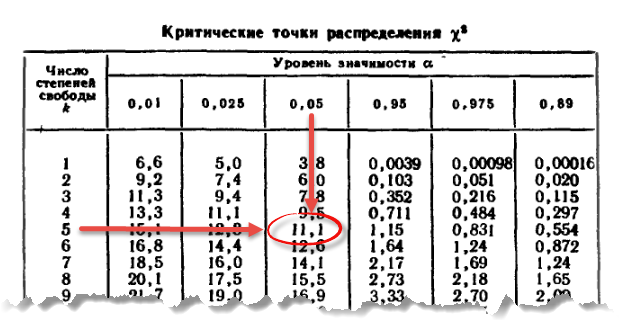
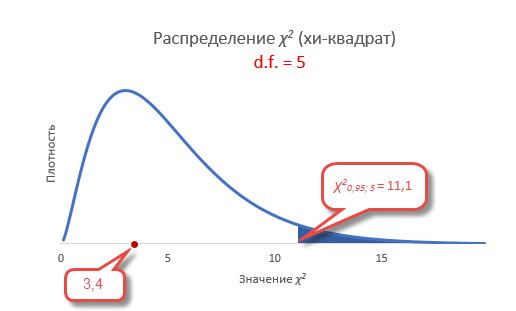
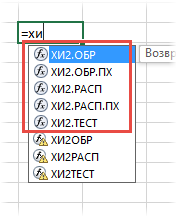
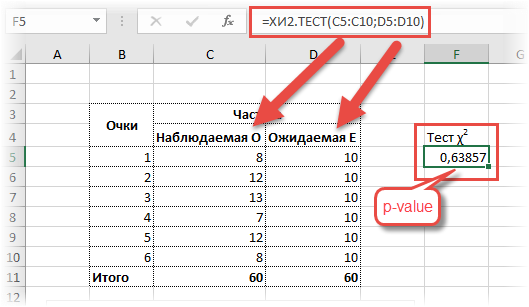
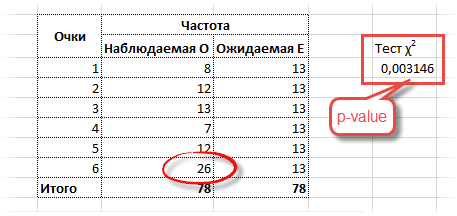
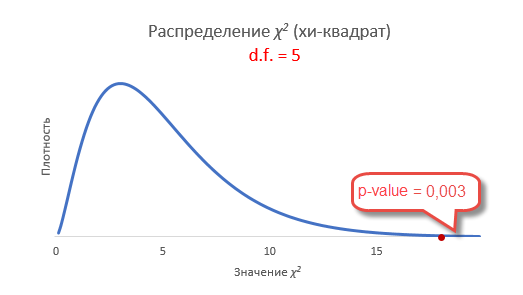
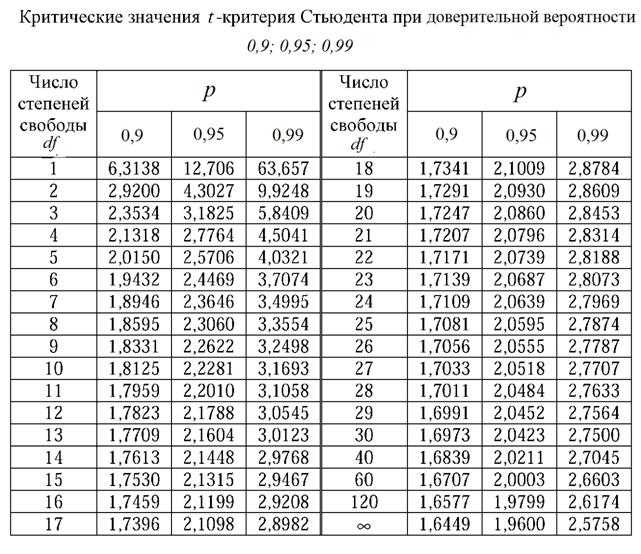
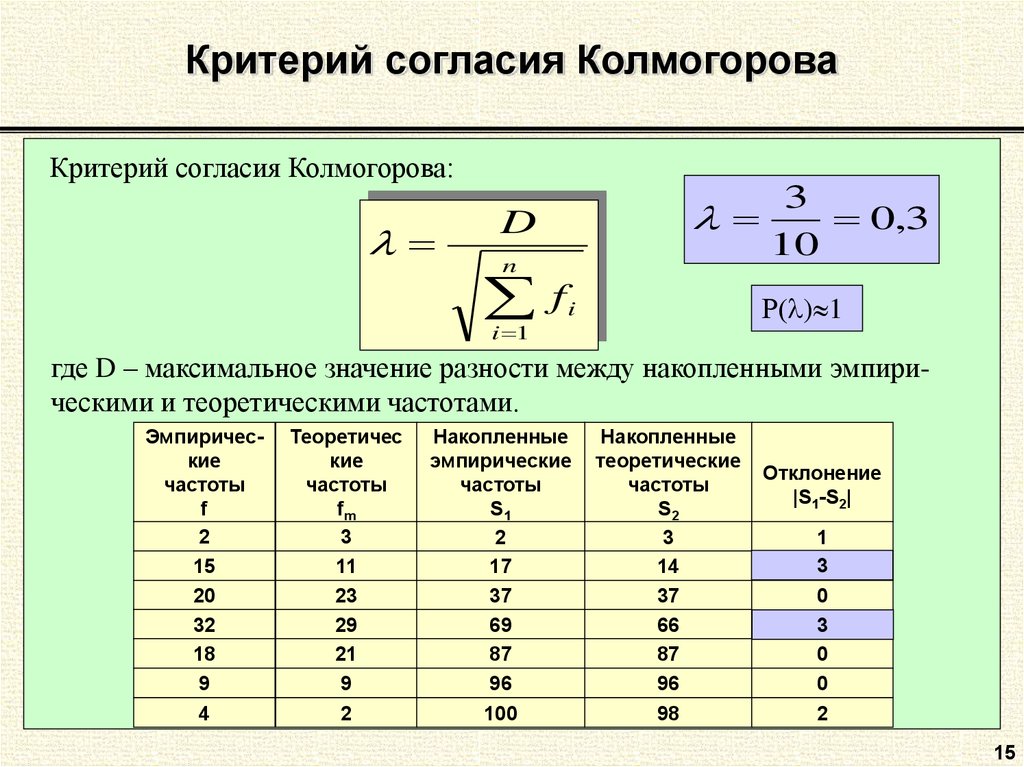



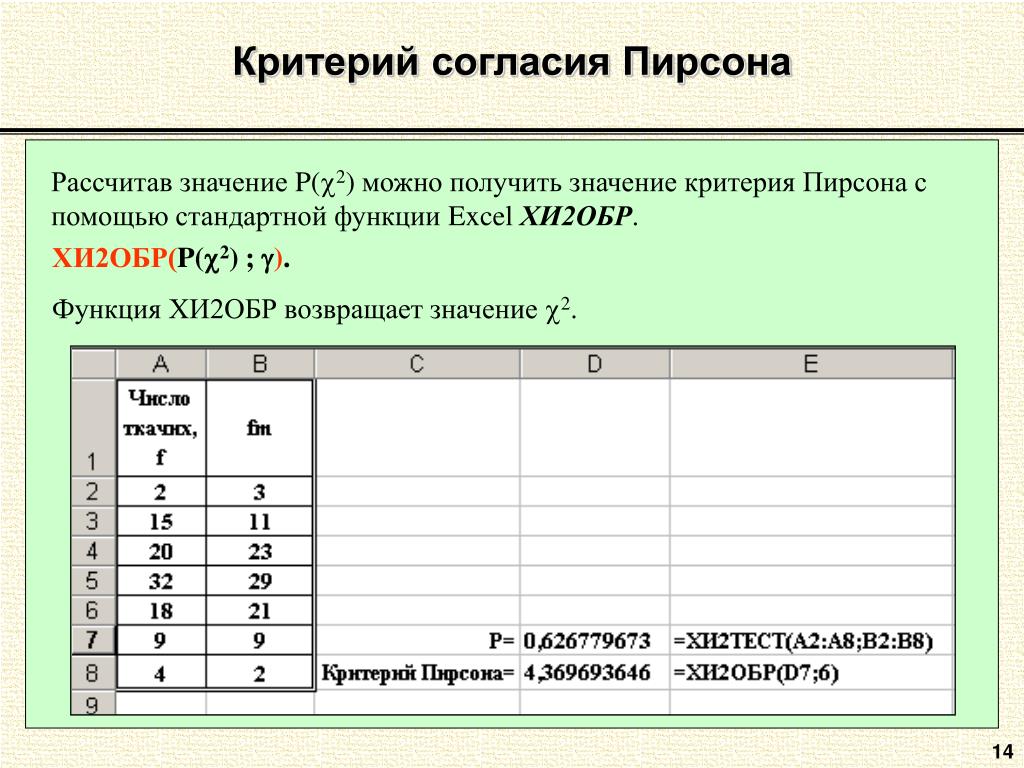 В списке статистических функций выберите и нажмите Ok:
В списке статистических функций выберите и нажмите Ok: