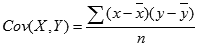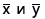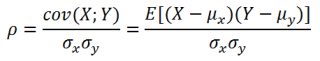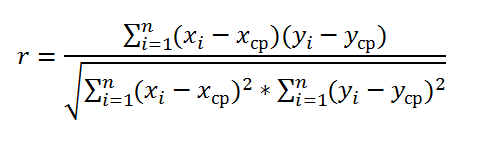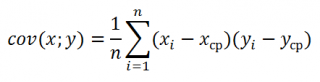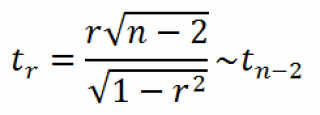Ковариация в excel анализ данных

В этой статье описаны синтаксис формулы и использование функции КОВАРИАЦИЯ.Г в Microsoft Excel.

Возвращает коварианс по численности населения, то есть среднее точки отклонений для каждой пары точек данных в двух наборах данных. Ковариация используется для определения отношения между двумя множествами данных. Например, можно проверить, соответствует ли более высокому уровню доходов более высокий уровень образования.

Синтаксис

КОВАРИАЦИЯ.Г(массив1;массив2)

Аргументы функции КОВАРИАЦИЯ.Г описаны ниже.

• Массив1     — обязательный аргумент. Первый диапазон ячеек с целыми числами.

• Массив2     — обязательный аргумент. Второй диапазон ячеек с целыми числами.

Замечания

• Аргументы должны быть числами, именами, массивами или ссылками, содержащими числа.

• Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.

• Если массив1 и массив2 имеют различное число точек данных, функция КОВАРИАЦИЯ.Г возвращает значение ошибки #Н/Д.

• Если массив1 или массив2 пуст, коВАРИАНА. P возвращает #DIV/0! значение ошибки #ЗНАЧ!.

• Ковариация определяется следующим образом:

  

  где

  

  являются выборочными средними значениями СРЗНАЧ(массив1) и СРЗНАЧ(массив2), а n — размер выборки.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные1	Данные2
3	9
2	7
4	12
5	15
6	17
Формула	Описание	Результат
=КОВАРИАЦИЯ.Г(A2:A6;B2:B6)	Ковариация, т. е. среднее произведений отклонений для каждой пары точек приведенных выше данных.	5,2

Функция КОВАРИАЦИЯ.В в Excel предназначена для расчета коэффициента ковариации двух наборов данных (массивов или диапазонов ячеек, хранящих числовые значения), являющихся выборками соответствующих диапазонов данных, и возвращает соответствующее числовое значение.

Функция КОВАРИАЦИЯ.Г в Excel используется для расчета коэффициента ковариации всей совокупности двух диапазонов данных (генеральной совокупности) и возвращает соответствующее значение.

Функция КОВАР в Excel предназначена для расчета коэффициента ковариации двух любых наборов числовых данных, являющихся генеральными совокупностями.

Использование функций КОВАР, КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г в Excel

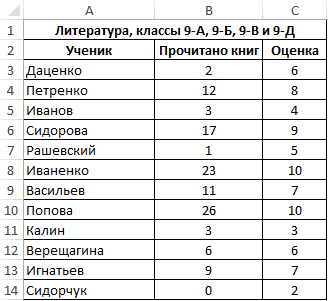
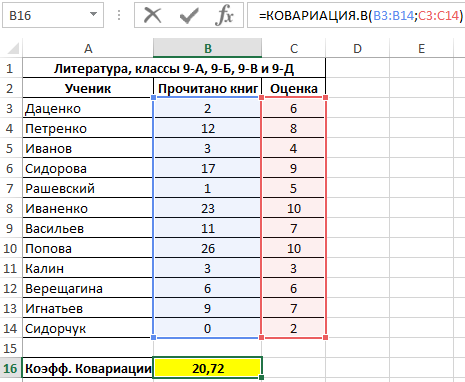
Пример 1. В таблице Excel содержится два диапазона данных, значения первого из которых характеризуют количество прочитанных книг за год каждым учеником, отобранным из нескольких классов школы, а второй – итоговую оценку по литературе по 10-бальной шкале. Определить коэффициент ковариации двух диапазонов данных.

Вид исходной таблицы:

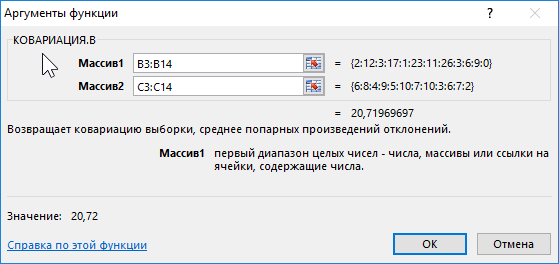
Поскольку для анализа были отобраны по несколько учеников различных классов, оба диапазона можно считать выборками из генеральной совокупности, которой являются все ученики 9-го класса данной школы. Используем следующую функцию:

Описание аргументов:

• B3:B14 – диапазон ячеек, содержащих данные о количестве прочитанных книг;
• C3:C14 – диапазон ячеек с итоговыми оценками по предмету.

Полученный результат:

Полученное значение свидетельствует о наличии прямой связи между значениями из двух диапазонов. То есть, можно полагать, что ученик, прочитавший большее количество книг, получит более высокую оценку за предмет.



Расчет ковариации роста и падения цен двух видов акций в Excel

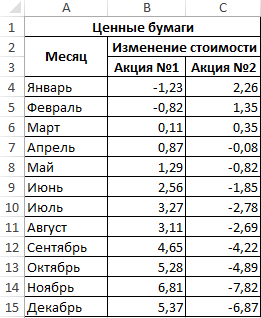
Пример 2. В таблице Excel внесены данные роста (положительное число) или падения цены (отрицательное) двух различных ценных бумаг на протяжении 12 месяцев года относительно некоторой начальной величины. Определить ковариацию двух диапазонов данных и сделать выводы. Сделать отчет доступным для пользователей Excel 2007.

Вид исходной таблицы:

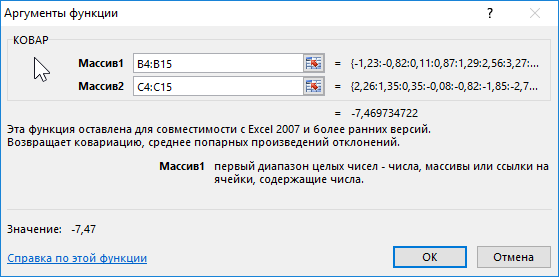
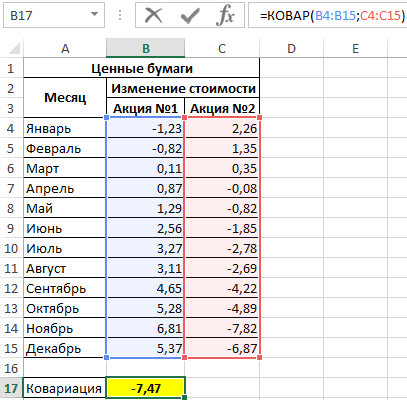
В данном примере исследуется вся генеральная выборка. Для расчета можно использовать функцию КОВАРИАЦИЯ.Г, однако результаты не будут доступны для пользователей более старых версий Excel. Применим следующую формулу:

В результате получим:

Это значение свидетельствует о достаточно большой взаимосвязи между исследуемыми значениями. Поскольку число отрицательное, данная взаимосвязь является обратной. То есть, с ростом цены одной акции наблюдается падение цены второй и наоборот. Можно предположить, что эти акции принадлежат двум конкурирующим компаниям.

Статистический анализ ковариации показателей в Excel

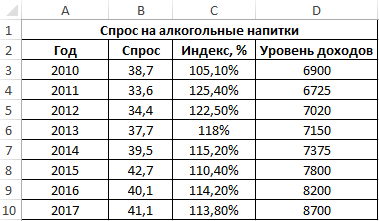
Пример 3. В таблице Excel введены данные о спросе на алкогольные напитки, индексе цен и уровне дохода населения государства. Проанализировать взаимосвязи между имеющимися данными.

Вид исходной таблицы данных:

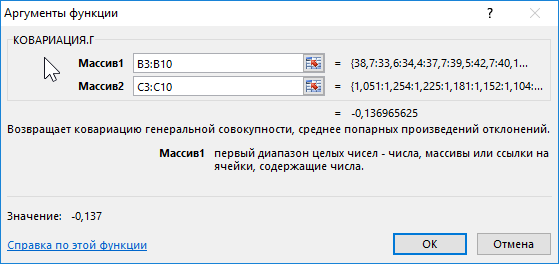
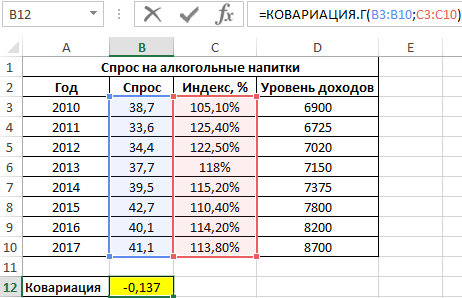
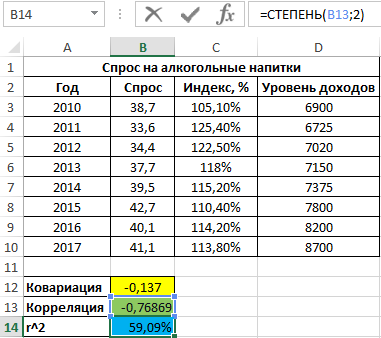
Вначале рассчитаем ковариацию между спросом и индексом цен по формуле:

Полученный результат:

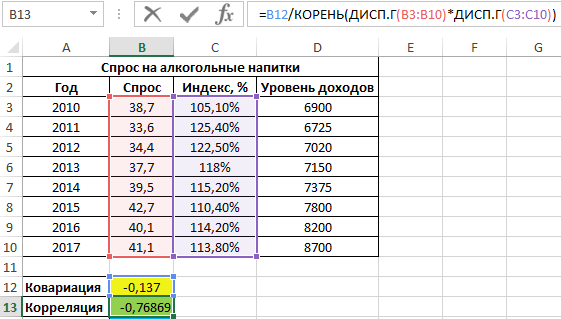
Для оценки степени взаимосвязи двух диапазонов данных удобнее использовать коэффициент корреляции, который можно рассчитать без использования функции КОРРЕЛ следующим способом:

=B12/КОРЕНЬ(ДИСП.Г(B3:B10)*ДИСП.Г(C3:C10))

Функция ДИСП.Г используется для расчета дисперсии генеральной совокупности. Приведенная выше формула наглядно демонстрирует взаимосвязь между коэффициентами ковариации и корреляции.

Полученный результат:

Как видно, между ценами и спросом существует довольно сильная обратная связь. Однако для определения степени влияния спроса определим коэффициент детерминации r2 по формуле:

=СТЕПЕНЬ(B13;2)

Полученное значение, выраженное в процентах:

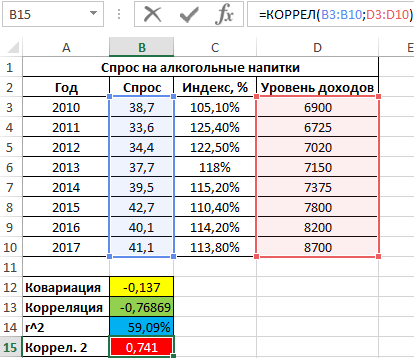
То есть, примерно 59% вариации спроса за исследуемый период обусловлены изменчивостью цены. Остальные 41% — прочими факторами. А еще одним фактором в данном примере является уровень дохода. Рассчитаем коэффициент корреляции между спросом и доходами с помощью следующей функции:

=КОРРЕЛ(B3:B10;D3:D10)

Результат:

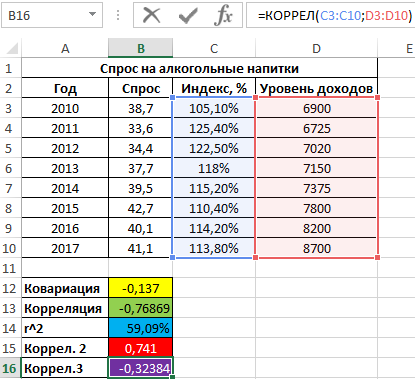
Положительное значение 0,741 соответствует о наличии довольно сильной зависимости между ростом уровня доходов и спросом. Чтобы определить общий коэффициент корреляции и сделать выводы, найдем коэффициент корреляции между индексом цен и уровнем доходов:

=КОРРЕЛ(C3:C10;D3:D10)

Результат:

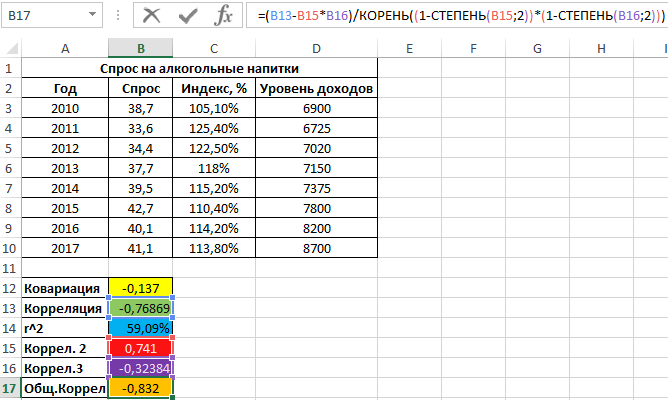
Имеем не сильно выраженную обратную взаимосвязь. Теперь выполним расчет общего коэффициента корреляции по формуле:

=(B13-B15*B16)/КОРЕНЬ((1-СТЕПЕНЬ(B15;2))*(1-СТЕПЕНЬ(B16;2)))

Результат:

Расчеты показывают, что влияние роста цен на уровень спроса «сглаживается» благодаря росту уровня дохода населения. Корень квадратный из последнего значения, взятого по модулю, равен примерно 91%, показывая, насколько вариация цен определяла вариация спроса на алкогольные напитки, если не брать в учет параллельное изменение уровня дохода.

Особенности использования функций КОВАР, КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г в Excel

Функция КОВАР имеет следующий синтаксис:

= КОВАР(массив1;массив2)

Функция КОВАРИАЦИЯ.В имеет следующую синтаксическую запись:

= КОВАРИАЦИЯ.В(массив1;массив2)

Синтаксис функции КОВАРИАЦИЯ.Г:

= КОВАРИАЦИЯ.Г(массив1;массив2)

Все рассматриваемые функции принимают на вход следующие аргументы:

• массив1 – обязательный аргумент, характеризующий первый массив или диапазон ячеек, содержащих данные числового типа, которые являются всей генеральной совокупностью данных (для функций КОВАРИАЦИЯ.Г и КОВАР) или выборкой (для функции КОВАРИАЦИЯ.В);
• массив2 – обязательный аргумент, характеризующий второй массив или диапазон ячеек с числовыми значениями (генеральная совокупность либо выборка, чем обусловлен выбор функции для расчета).

Примечания 1:

1. Все рассматриваемые функции принимают в качестве аргументов массивы или ссылки на диапазоны ячеек, содержащие текстовые, логические, числовые и данные других типов.
2. Число элементов в диапазонах или массивах, переданных в качестве аргументов массив1 и массив2 должны совпадать. В противном случае все рассматриваемые функции вернут код ошибки #Н/Д.
3. При расчете не учитываются значения типа Текст, Имя, логические значения (ИСТИНА, ЛОЖЬ), ссылки на пустые ячейки. Однако ячейки, содержащие числовое значения 0 (нуль), будут учтены.
4. Если рассматриваемые функции в качестве аргументов принимают:

• Диапазоны пустых ячеек, результатом их выполнения будет код ошибки #ЗНАЧ! (принимают по одной пустой ячейке в качестве каждого аргумента) или #ДЕЛ/0! (принимают по несколько пустых ячеек в качестве аргументов);
• Массивы, состоящие из одного элемента или по одной ячейке в качестве каждого аргумента, функции КОВАРИАЦИЯ.Г и КОВАР вернут числовое значение 0, а функция КОВАРИАЦИЯ.В – код ошибки #ДЕЛ/0!.

Примечания 2:

1. Ковариация – величина, характеризующая линейную зависимость, установившуюся между двумя рядами случайных величин X и Y. Она соответствует математическому ожиданию произведения отклонений X и Y от их центров распределений. Коэффициент ковариации может быть выражен отрицательным, положительным числами и нулем, при этом:

• Если с ростом значений X более вероятные появления больших значений Y и наоборот, между двумя диапазонами существует прямая связь, о чем свидетельствует положительное значение коэффициента ковариации;
• Если с ростом X величина Y имеет тенденцию к снижению и наоборот, устанавливается обратная зависимость, выражаемая отрицательным значением коэффициента ковариации;
• Если между X и Y устанавливается слабая взаимосвязь (при изменениях X изменения Y являются непоследовательными, хаотичными), значение коэффициента ковариации стремится к нулю.

Примечания 3:

1. Функция КОВАР являлась стандартной функцией для расчета ковариации в ранних версиях Excel (2007 и более старых) и оставлена для обеспечения совместимости. В последующих версиях Excel она может отсутствовать, поэтому рекомендуется использовать функции КОВАРИАЦИЯ.В и КОВАРИАЦИЯ.Г.
2. Выборка – это подмножество величин одного множества, называемого генеральной совокупностью. Другими словами, выборкой считается результат ограниченного ряда наблюдений какого-либо одно или нескольких признаков. Например, при изучении банковской системы государства генеральной совокупностью являются все банковские организации страны, а выборкой – банки города Санкт-Петербург.
3. В отличие от коэффициента корреляции, значение коэффициента ковариации не ограничено диапазоном чисел от -1 до 1.
4. При определении коэффициента ковариации одних и тех же двух диапазонов чисел функции КОВАР и КОВАРИАЦИЯ.Г вернут одинаковый результат, отличающийся от числового значения, которое вернет функция КОВАРИАЦИЯ.В, поскольку они используют разные алгоритмы расчетов.

Covariance is a statistical term that signifies the direction of the linear relationship between two variables. The direction usually refers to whether the variables vary directly or inversely to each other. It should be remembered that covariance only measures how two variables change together, it does not explain the dependency of one variable over another variable. When the two variables vary in the same direction (directly) then the covariance is said to be positive covariance. Conversely, when the two variables vary in the opposite direction (inversely) then the covariance is said to be negative covariance.

The mathematical formula for Covariance of a population is given as:

 

Where, x,y is the array of first and second variable respectively,  and  are the mean values of x and y respectively and n is the no. of elements in the array.

On the other hand, the mathematical formula for Covariance of a sample is given as:

The value of covariance lies in the range . The crux of the matter is the numerical value of significance holds no value since it is unit dependent, hence only the sign/polarity associated with the numerical value matters. If the sign is positive, both the variables vary in the same direction else if the sign is negative, we can infer both the variables vary inversely with one another.

What is a covariance matrix?

A covariance matrix is typically a square matrix representing covariance between each pair of elements in a random array. The covariance matrix is symmetrical along the diagonals.

Creating a covariance matrix in Excel 

We can create a covariance matrix in Excel using the Covariance function present inside the data analysis tool available under the data analysis the toolpak add-in package.

Suppose, we have a group of students and we want to create a covariance matrix for finding the covariance between marks obtained by each student in various subjects. The marks obtained by each student in the different subject is given as :

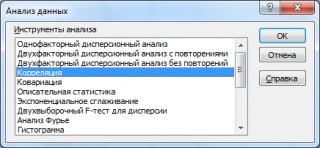
Step 1: Click the Data ribbon in the excel menu and select the Data Analysis tool option.

Step 2: A data analysis tool dialog box will appear on the screen. From all the available options in the dialog box, select the Covariance option and click OK.

Step 3: A Covariance dialog box will pop up on the screen. Inside the dialog box, in the input range field pass the data array. Here, We want to compare the marks, hence, the cell range from B1 to D7 is passed. Now, since our data is grouped by columns, therefore, we select the Columns radio button under the Grouped by field and our data has labels in the first row, therefore, we click the appropriate checkbox. Now, we want to place the covariance matrix in the same worksheet, we will select the cell in which we want to place the covariance matrix and give the cell address in the output range field here cell A10 is passed.  Then click the OK button.

Step 4: The covariance matrix will get generated from the A10 cell as shown in the figure below. 

So this is how we create a covariance matrix in Excel.

• 

Вычислим коэффициент корреляции и ковариацию для разных типов взаимосвязей случайных величин.

Коэффициент корреляции

(

критерий корреляции

Пирсона, англ. Pearson Product Moment correlation coefficient)

определяет степень

линейной

взаимосвязи между случайными величинами.

где Е[…] – оператор

математического ожидания

, μ и σ –

среднее

случайной величины и ее

стандартное отклонение

.

Как следует из определения, для вычисления

коэффициента корреляции

требуется знать распределение случайных величин Х и Y. Если распределения неизвестны, то для оценки

коэффициента корреляции

используется

выборочный коэффициент корреляции

r

(

еще он обозначается как

R

_xy

или

r

_xy

)

:

Как видно из формулы для расчета

корреляции

, знаменатель (произведение стандартных отклонений с точностью до безразмерного множителя) просто нормирует числитель таким образом, что

корреляция

оказывается безразмерным числом от -1 до 1.

Корреляция

и

ковариация

предоставляют одну и туже информацию, но

корреляцией

удобнее пользоваться, т.к. она является безразмерной величиной.

Рассчитать

коэффициент корреляции

и

ковариацию выборки

в MS EXCEL не представляет труда, так как для этого имеются специальные функции

КОРРЕЛ()

и

КОВАР()

. Гораздо сложнее разобраться, как интерпретировать полученные значения, большая часть статьи посвящена именно этому.

Теоретическое отступление

Напомним, что

корреляционной связью

называют статистическую связь, состоящую в том, что различным значениям одной переменной соответствуют различные

средние

значения другой (с изменением значения Х

среднее значение

Y изменяется закономерным образом). Предполагается, что

обе

переменные Х и Y являются

случайными

величинами и имеют некий случайный разброс относительно их

среднего значения

.

Примечание

. Если случайную природу имеет только одна переменная, например, Y, а значения другой являются детерминированными (задаваемыми исследователем), то можно говорить только о регрессии.

Таким образом, например, при исследовании зависимости среднегодовой температуры нельзя говорить о

корреляции

температуры и года наблюдения и, соответственно, применять показатели

корреляции

с соответствующей их интерпретацией.

Корреляционная связь

между переменными может возникнуть несколькими путями:

1. Наличие причинной зависимости между переменными. Например, количество инвестиций в научные исследования (переменная Х) и количество полученных патентов (Y). Первая переменная выступает как
   
   независимая переменная (фактор)
   
   , вторая —
   
   зависимая переменная (результат)
   
   . Необходимо помнить, что зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.
2. Наличие сопряженности (общей причины). Например, с ростом организации растет фонд оплаты труда (ФОТ) и затраты на аренду помещений. Очевидно, что неправильно предполагать, что аренда помещений зависит от ФОТ. Обе этих переменных во многих случаях линейно зависят от количества персонала.
3. Взаимовлияние переменных (при изменении одной, вторая переменная изменяется, и наоборот). При таком подходе допустимы две постановки задачи; любая переменная может выступать как в роли независимой переменной и в роли зависимой.

Таким образом,

показатель корреляции

показывает, насколько сильна

линейная взаимосвязь

между двумя факторами (если она есть), а регрессия позволяет прогнозировать один фактор на основе другого.

Корреляция

, как и любой другой статистический показатель, при правильном применении может быть полезной, но она также имеет и ограничения по использованию. Если

диаграмма рассеяния

показывает четко выраженную линейную зависимость или полное отсутствие взаимосвязи, то

корреляция

замечательно это отразит. Но, если данные показывают нелинейную взаимосвязь (например, квадратичную), наличие отдельных групп значений или выбросов, то вычисленное значение

коэффициента корреляции

может ввести в заблуждение (см.

файл примера

).

Корреляция

близкая к 1 или -1 (т.е. близкая по модулю к 1) показывает сильную линейную взаимосвязь переменных, значение близкое к 0 показывает отсутствие взаимосвязи. Положительная

корреляция

означает, что с ростом одного показателя другой в среднем увеличивается, а при отрицательной – уменьшается.

Для вычисления коэффициента корреляции требуется, чтобы сопоставляемые переменные удовлетворяли следующим условиям:

• количество переменных должно быть равно двум;
• переменные должны быть количественными (например, частота, вес, цена). Вычисленное среднее значение этих переменных имеет понятный смысл: средняя цена или средний вес пациента. В отличие от количественных, качественные (номинальные) переменные принимают значения лишь из конечного набора категорий (например, пол или группа крови). Этим значениям условно сопоставлены числовые значения (например, женский пол – 1, а мужской – 2). Понятно, что в этом случае вычисление
  
  среднего значения
  
  , которое требуется для нахождения
  
  корреляции
  
  , некорректно, а значит некорректно и вычисление самой
  
  корреляции
  
  ;
• переменные должны быть случайными величинами и иметь

  нормальное распределение
  
  .
  

Двумерные данные могут иметь различную структуру. Для работы с некоторыми из них требуются определенные подходы:

• Для данных с нелинейной связью
  
  корреляцию
  
  нужно использовать с осторожностью. Для некоторых задач бывает полезно преобразовать одну или обе переменных так, чтобы получить линейную взаимосвязь (для этого требуется сделать предположение о виде нелинейной связи, чтобы предложить нужный тип преобразования).
• С помощью
  
  диаграммы рассеяния
  
  у некоторых данных можно наблюдать неравную вариацию (разброс). Проблема неодинаковой вариации состоит в том, что места с высокой вариацией не только предоставляют наименее точную информацию, но и оказывают наибольшее влияние при расчете статистических показателей. Эту проблему также часто решают с помощью преобразования данных, например, с помощью логарифмирования.
• У некоторых данных можно наблюдать разделение на группы (clustering), что может свидетельствовать о необходимости разделения совокупности на части.
• Выброс (резко отклоняющееся значение) может исказить вычисленное значение коэффициента корреляции. Выброс может быть причиной случайности, ошибки при сборе данных или могут действительно отражать некую особенность взаимосвязи. Так как выброс сильно отклоняется от среднего значения, то он вносит большой вклад при расчете показателя. Часто расчет статистических показателей производят с и без учета выбросов.

Использование MS EXCEL для расчета корреляции

В качестве примера возьмем 2 переменные

Х

и

Y

и, соответственно,

выборку

состоящую из нескольких пар значений (Х

_i

; Y

_i

). Для наглядности построим

диаграмму рассеяния

.

Примечание

: Подробнее о построении диаграмм см. статью

Основы построения диаграмм

. В

файле примера

для построения

диаграммы рассеяния

использована

диаграмма График

, т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).

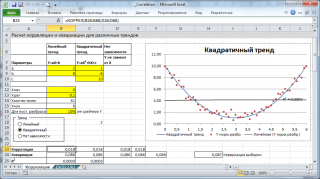
Расчеты

корреляции

проведем для различных случаев взаимосвязи между переменными:

линейной, квадратичной

и при

отсутствии связи

.

Примечание

: В

файле примера

можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.

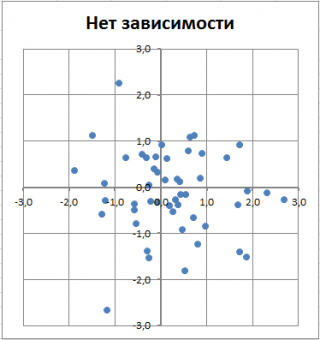
В

файле примера

для построения

диаграммы рассеяния

в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.

Примечание

: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми.

Как было сказано выше, для расчета

коэффициента корреляции

в MS EXCEL существует функций

КОРРЕЛ()

. Также можно воспользоваться аналогичной функцией

PEARSON()

, которая возвращает тот же результат.

Для того, чтобы удостовериться, что вычисления

корреляции

производятся функцией

КОРРЕЛ()

по вышеуказанным формулам, в

файле примера

приведено вычисление

корреляции

с помощью более подробных формул:

=

КОВАРИАЦИЯ.Г(B28:B88;D28:D88)/СТАНДОТКЛОН.Г(B28:B88)/СТАНДОТКЛОН.Г(D28:D88)

=

КОВАРИАЦИЯ.В(B28:B88;D28:D88)/СТАНДОТКЛОН.В(B28:B88)/СТАНДОТКЛОН.В(D28:D88)

Примечание

: Квадрат

коэффициента корреляции

r равен

коэффициенту детерминации

R2, который вычисляется при построении линии регрессии с помощью функции

КВПИРСОН()

. Значение R2 также можно вывести на

диаграмме рассеяния

, построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладку

Макет

, затем в группе

Анализ

нажмите кнопку

Линия тренда

и выберите

Линейное приближение

). Подробнее о построении линии тренда см., например, в

статье о методе наименьших квадратов

.

Использование MS EXCEL для расчета ковариации

Ковариация

близка по смыслу с

дисперсией

(также является мерой разброса) с тем отличием, что она определена для 2-х переменных, а

дисперсия

— для одной. Поэтому, cov(x;x)=VAR(x).

Для вычисления ковариации в MS EXCEL (начиная с версии 2010 года) используются функции

КОВАРИАЦИЯ.Г()

и

КОВАРИАЦИЯ.В()

. В первом случае формула для вычисления аналогична вышеуказанной (окончание

.Г

обозначает

Генеральная совокупность

), во втором – вместо множителя 1/n используется 1/(n-1), т.е. окончание

.В

обозначает

Выборка

.

Примечание

: Функция

КОВАР()

, которая присутствует в MS EXCEL более ранних версий, аналогична функции

КОВАРИАЦИЯ.Г()

.

Примечание

: Функции

КОРРЕЛ()

и

КОВАР()

в английской версии представлены как CORREL и COVAR. Функции

КОВАРИАЦИЯ.Г()

и

КОВАРИАЦИЯ.В()

как COVARIANCE.P и COVARIANCE.S.

Дополнительные формулы для расчета

ковариации

:

=

СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88-СРЗНАЧ(D28:D88)))/СЧЁТ(D28:D88)

=

СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88))/СЧЁТ(D28:D88)

=

СУММПРОИЗВ(B28:B88;D28:D88)/СЧЁТ(D28:D88)-СРЗНАЧ(B28:B88)*СРЗНАЧ(D28:D88)

Эти формулы используют свойство

ковариации

:

Если переменные

x

и

y

независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:

VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)

А

дисперсия

их разности равна

VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)

Оценка статистической значимости коэффициента корреляции

При проверке значимости

коэффициента корреляции

нулевая гипотеза состоит в том, что

коэффициент корреляции

равен нулю, альтернативная — не равен нулю (про

проверку гипотез

см. статью

Проверка гипотез

).

Для того чтобы проверить гипотезу, мы должны знать распределение случайной величины, т.е.

коэффициента корреляции

r. Обычно, проверку гипотезы осуществляют не для r, а для случайной величины t

_r

:

которая имеет

распределение Стьюдента

с n-2 степенями свободы.

Если вычисленное значение случайной величины |t

_r

| больше, чем критическое значение t

_α,n-2

(α- заданный

уровень значимости

), то нулевую гипотезу отклоняют (взаимосвязь величин является статистически значимой).

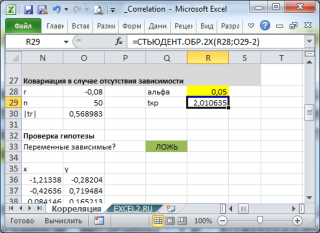
Надстройка Пакет анализа

В

надстройке Пакет анализа

для вычисления ковариации и корреляции

имеются одноименные инструменты

анализа

.

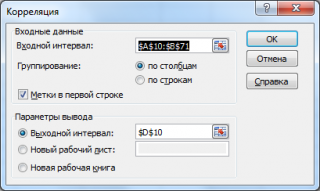
После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:

• 
  Входной интервал
  
  : нужно ввести ссылку на диапазон с исходными данными для 2-х переменных
• 
  Группирование
  
  : как правило, исходные данные вводятся в 2 столбца
• 
  Метки в первой строке
  
  : если установлена галочка, то
  
  Входной интервал
  
  должен содержать заголовки столбцов. Рекомендуется устанавливать галочку, чтобы результат работы Надстройки содержал информативные столбцы
• 
  Выходной интервал
  
  : диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.

Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).