Компьютерное моделирование свободного падения в excel 11 класс семакин

Выберите документ из архива для просмотра:

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Математическая модель свободного падения тела Глава 3.2 §3.2.1 10 класс

• 

  2 слайд

  Вы часто наблюдали   падение тел, то есть движения тяжелого тела, падающего с некоторой высоты. Над закономерностями свободного падения размышляли многие великие   умы —   Аристотель, Галилео Галилей, Исаак   Ньютон. Свободное падение — движение, при котором на тело не действуют никакие силы (силы сопротивления, реактивные силы, и т. п.), кроме силы тяжести. В частности парашютист, в течении прыжка, до раскрытия парашюта, находится практически в свободном падении. Под действием силы, тело движется с ускорением. Силиванов А.А.

• 

  3 слайд

  Аристотель (384-22 до н.э.) – древнегреческий философ и ученый. Родился в Стагире. В 367-347 до н.э. учился в академии Платона в Афинах, в 343-335 у царя Македонии Филиппа был воспитателем его сына Александра. В 335 возвратился в Афины, где основал свою философскую школу – перипатептиков. Аристотель утверждал, что в реальных условиях движение конечно и тела падают с разной скоростью. Он полагал, что чем тяжелее тело, тем быстрее оно падает.

• 

  4 слайд

  Галилео Галилей (1564-1642) – выдающийся итальянский физик и астроном, один из основателей точного естествознания, член Академии деи Линчеи. Родился в Пизе. В 1581 поступил в Пизанский университет, где изучал медицину. Но, увлекся геометрией и механикой, оставил университет и вернулся во Флоренцию, где четыре года самостоятельно изучал математику. С 1589 – профессор Пизанского университета, в 1592-1610 – Падуанского, а в дальнейшем – придворный философ герцога Козимо II Медичи. Будучи в Пизе, Галилей опроверг учение о пропорциональности скорости падения тела силе тяжести. Он наблюдал за колебаниями маятника в Пизанском соборе, изучал скатывания шаров по наклонной плоскости (с разной амплитудой). Сбрасывал шары со знаменитой Пизанской башни (деревянный и чугунный, одинакового размера упали практически одновременно). Галилео Галилей в результате тщательно проведенных опытов и размышлений сделал вывод о том, что ускорения всех свободно падающих тел одинаковы и постоянны, если пренебречь сопротивлением воздуха.

• 

  5 слайд

  Ньютон Исаак (1643-1727) – выдающийся английский ученый, заложивший основы современного естествознания, создатель классической физики, член Лондонского королевского общества (16720, президент ( с 1703). Родился в Вулсторпе. Окончил Кембриджский университет. В 1669-1701возглавлял в нем кафедру. С 1695 – смотритель, с 1699 – директор Монетного двора. Вскоре после Галилея были созданы воздушные насосы, позволяющие проводить опыты со свободным падением в вакууме. С этой целью Ньютон откачал из длинной стеклянной трубки воздух и бросал сверху одновременно птичье перо и монету. Оба тела падали с одной скоростью. Именно этот опыт дал решающую проверку предположению Галилея.

• 

• 

  7 слайд

  Движение в воздухе

• 

  8 слайд

  Движение в безвоздушном пространстве

• 

• 

  10 слайд

  УСКОРЕНИИЕ СВОБОДНОГО ПАДЕНИЯ g = 9,8 ≈ 10м/с² Направлено всегда вниз Величина ускорения зависит: а) от географической широты (9,78÷9,83) б) от высоты над поверхностью Земли 3) g > 0, если тело движется вниз g < 0, если тело движется вверх

• 

  11 слайд

  Ускорение свободного падения На полюсе g=9,832 м/с2 На экваторе g=9,780 м/с2 На высоте 100км над полюсом g=9,53 м/с2 На Луне g=1,623 м/с2

• 

• 

  13 слайд

  Действующие силы FА – архимедова сила, направленная вертикально вверх mg – сила тяжести, направленная вертикально вниз Fс — сила сопротивления движению, направленная против движения

• 

  14 слайд

  Анализ объекта Архимедова сила FА < mg (плотность газа много меньше плотности тела, но плотность воды следует учесть) Сила сопротивления среды Зависит от плотности среды и зависит от скорости, но… Если движение происходит в газе, плотность которого много меньше плотности тела, вязкость невелика и высота падения небольшая, то Fс можно пренебречь

• 

  15 слайд

  Математическая формализация Уравнение закона Ньютона ma = mg + FА + Fс Проектируем данное векторное уравнение на ось Y FА + Fс — mg a = m

• 

  16 слайд

  Задача На высоте Н над поверхностью Земли находится тело массой m. В момент времени t=0 начинается свободное падение тела на Землю. Требуется определить время падения и скорость, которую будет иметь тело в момент удара о Землю

• 

  17 слайд

  Анализ параметров Неизменные параметры m – масса тела H – высота, с которой началось движение g – ускорение свободного падения Переменные параметры t – время движения v – скорость падения Y — координата

• 

  18 слайд

  Свободное падение без учета сил противодействия Пример: падение свинцового шарика в воздухе FА =0 Fс =0 a = — g Движение равноускоренное.

• 

  19 слайд

  ФОРМУЛЫ a = -g Основныеформулы V0=0 Другиеформулы

• 

  20 слайд

  Графики Изменение скорости Изменение координаты

• 

  21 слайд

  Задача 1 Какую скорость и координату (высоту над землей) будет иметь тело через 1 сек после начала падения? Решение.

• 

  22 слайд

  Задача 2 Через сколько времени и с какой скоростью тело упадет на Землю? Решение. Выразим t из формулы при y=0 Подставим в формулу

• 

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Математическая модель Глава 3.2 §3.2.2 11 класс Свободное падение с учетом сопротивления среды

• 

  2 слайд

  Действующие силы FА – архимедова сила, направленная вертикально вверх mg – сила тяжести, направленная вертикально вниз Fс — сила сопротивления движению, направленная против движения

• 

  3 слайд

  Анализ объекта Архимедова сила FА < mg (плотность газа много меньше плотности тела, но плотность воды следует учесть) Сила сопротивления среды Зависит от плотности среды и зависит от скорости, но… Очевидно, что на предмет, падающий с большой высоты, действует Fс увеличивающаяся по мере роста скорости v пренебрегаем

• 

  4 слайд

  Сила сопротивления F V – малая – преобладает вязкое трение жидкости или газа F пропорциональна V С ростом V – возрастает лобовое сопротивление (парусный эффект) F пропорциональна V F = k ∙ v + k ∙ v c c c 2 c 1 2 2

• 

  5 слайд

  Математическая формализация Из уравнения закона Ньютона ma = mg + FА + Fс Проектируем данное векторное уравнение на ось Y Fс (t)- mg k1 v(t) + k2 v(t) — mg a(t) = = m m Ф1* 2

• 

  6 слайд

  Численный подход к моделированию процессов vi+1 – vi t vi+1 = vi + ai t Из Ф1* выразим ai k1 v(t) + k2 v(t) – mg m Δ Δ t – малый шаг изменения времени a = Δ Δ t vi+1 = vi + 2

• 

  7 слайд

  Численный подход к моделированию процессов yi+1 = yi + vi t — координата y, где i = 0,1,2,… По условию задачи падение происходит с высоты Н с нулевой начальной скоростью => v(0) = v0 = 0 y(0) = y0 = Н Δ

• 

  8 слайд

  Математическая модель Исходные данные v(0) = v0 = 0 y(0) = y0 = Н Рекуррентные формулы k1 v(t) + k2 v(t) – mg m yi+1 = yi + vi t vi+1 = vi + Δ t Δ 2

• 

  9 слайд

  у H g v0=0 Свободное падение тела с высоты H С учетом силы сопротивления Без учета силы сопротивления vi+1=v1+ k1 –коэффициент вязкого трения k1vi+k2 vi2-mg m k2 – коэффициент лобового сопротивления yi+1=yi + vi t а = -g v y=y0-gt2/2 v =-gt y=H-gt2/2 0 y0 Δ a(t)= k1vi+k2 vi2-mg m Δ t

• 

  10 слайд

  Предельная скорость свободного падения С возрастанием скорости падения v возрастает сила сопротивления Fc => Fc – mg уменьшается. Когда Fc = mg, скорость выйдет на постоянное предельное значение v*. Находим из уравнения k1 v + k2 v – mg = 0 2

• 

  11 слайд

  Параметры модели Определим k1 для конкретных ситуаций. k1 – пропорциональная динамической вязкости среды (μ) k1 = с1 ∙μ∙ b с1 – определяется формой тела b – характерный размер тела в направлении, │ потоку, обтекающего газа или жидкости. Для тела сферической формы k1 = 6π ∙ μ ∙ r

• 

  12 слайд

  Параметры модели

• 

  13 слайд

  Коэффициенты лобового сопротивления Шар с2 = 0,4 Полусфера с2 = 1,1 Диск с2 = 0,55

• 

  14 слайд

  Полный набор параметров Масса тела m Начальная высота H Динамическая вязкость среды μ Плотность среды ρ Начальная скорость движения тела v0 Характерный размер тела b в направлении перпендикулярном потоку ( δ ) Параметры с1 и с2 (отражающие форму тела)

• 

  15 слайд

  ФОРМУЛЫ a(t)= k1vi+k2 vi2-mg m yi+1=yi + vi t k1vi+k2 vi2-mg m vi+1=v1+ Δ Δ t Безучета сопротивления С учетом сопротивления

• 

  16 слайд

  Задача 1 Определите при какой скорости падения в воздухе железного шара радиусом 10 см сравняются силы вязкого трения и лобового сопротивления.

• 

  17 слайд

  Задача 2 Определите максимальную скорость падения железного шара радиусом 10 см в воде (μ = 1,002 н∙с/м ρ= 1000 кг/м ); в глицерине (μ = 1480 н∙с/м ρ= 1260 кг/м ). 2 3 3 2

• 

  18 слайд

  Задача 3 Постройте численную модель падения твердого шара в воде с учетом архимедовой силы.

• 

  19 слайд

  Задача 5 Парашютист массой 90 кг разгоняется в свободном падении до скорости 10 м/с и на высоте 50 м раскрывает парашют, площадь которого 55 м2. Коэффициент сопротивления парашюта равен 0,9. Выполните следующие задания: постройте графики изменения скорости и высоты полета в течение первых 4 секунд; определите, с какой скоростью приземлится парашютист? сравните результаты моделирования с установившимся значением скорости, вычисленным теоретически.   теоретически моделирование Скорость приземления, м/с    

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Компьютерное моделирование свободного падения Гл 3.2 §3.2.3 11 класс

• 

  2 слайд

  Задача 1 Сопоставить процессы падения твердого шара радиуса r с одной и той же высоты в разных средах: в пустоте (без сопротивления) в воздухе в воде

• 

  3 слайд

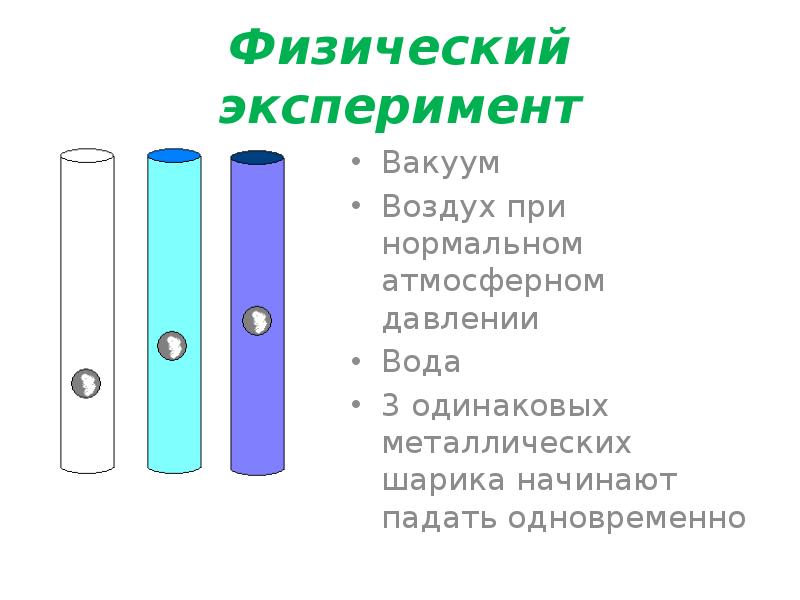
  Физический эксперимент Вакуум Воздух при нормальном атмосферном давлении Вода 3 одинаковых металлических шарика начинают падать одновременно

• 

  4 слайд

  Математическая модель на ПК 2 3 3

• 

  5 слайд

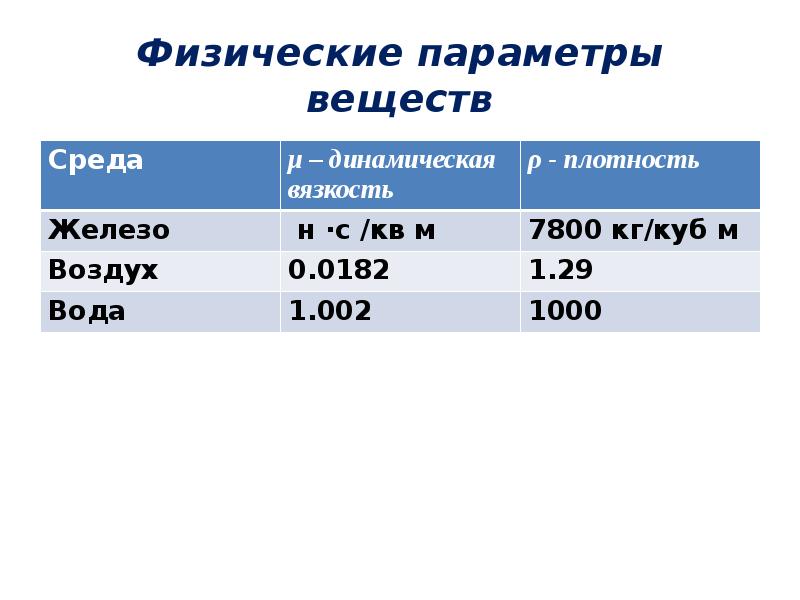
  Физические параметры веществ Среда μ– динамическая вязкость ρ- плотность Железо н ∙с/квм 7800 кг/куб м Воздух 0.0182 1.29 Вода 1.002 1000

• 

  6 слайд

  ФОРМУЛЫ a(t)= k1vi+k2 vi2-mg m yi+1=yi + vi t k1vi+k2 vi2-mg m vi+1=v1+ Δ Δ t Безучета сопротивления С учетом сопротивления

• 

  7 слайд

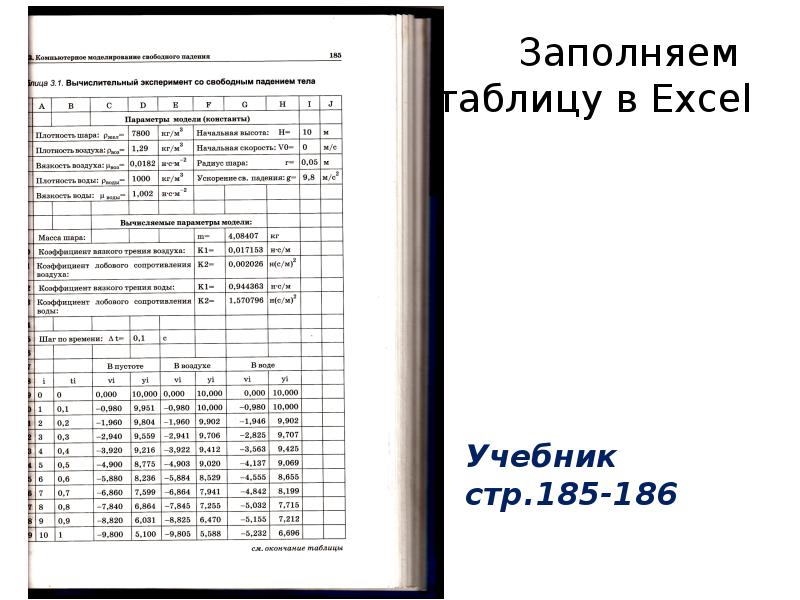
  Заполняем таблицу в Excel Учебник стр.185-186

• 

  8 слайд

  Формулы в Excel E20 =E19+($G$10*E19 +$G$11*E19^2-$G$9*$I$5) *$D$15/$G$9 -v1 F20 =F19+E19*$D$15 -yi

• 

  9 слайд

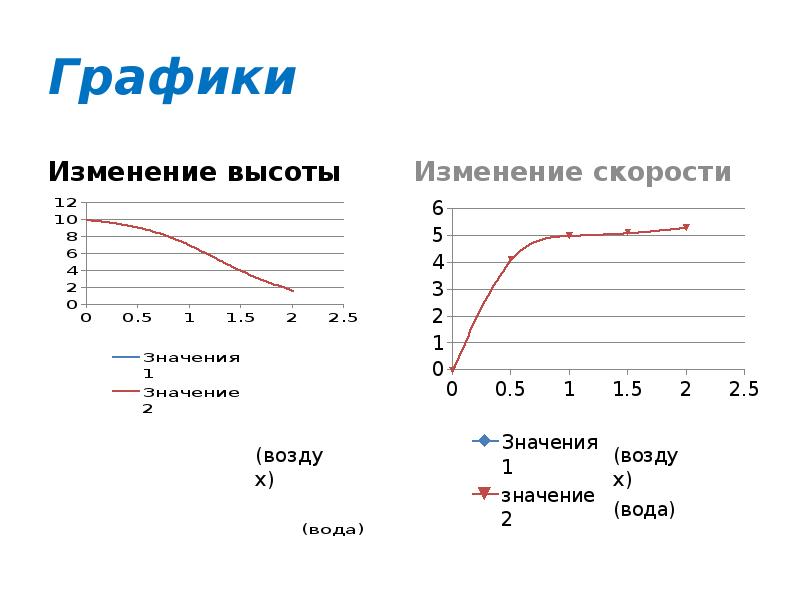
  Графики Изменение высоты Изменение скорости (воздух)

• 

  10 слайд

  Задача 2 Рассчитать время падения шара в воде с точностью до 0,01 сек. Метод: приближенные численные вычисления с точностью 0,001 (dt) Число шагов вычислений n = 100 Результат округлить до 0,01 Программа на Pascal

• 

  11 слайд

  Программа Const Ro_shar=7800; Ro_sreda=1000; Mju=1.02; h=10; v0=0; r=0.05; g=9.8; Var i,n: integer; t, y, dt, m, V, k1, k2:real; Begin k1:=6*Pi*Mju*r; k2:=0.2*Pi*r*r*Ro_sreda; m:=4/3*Pi*r*r*r*Ro_shar; Write (‘шаг по времени:’);readln (dt); Write (‘Число шагов’);readln (n);

• 

  12 слайд

  Программа продолжение i:=0; t:=0; v:=v0; y:=h+v*dt; While y>0 do Begin i:=i+1; t:=t+dt; v:=v+(k1*V+k2*v*v-m*g)/m*dt; If I mad n=0 then writeln (t:7:4,abs(V):7:4,y:7:4); y:=y+V*dt; End; writeln (‘Tmax=‘,t:7:4,’Vmax=‘,abs(V):7:4) End.

• 

  13 слайд

  Результаты При t=0,001 Tmax = 2,23 сек Vmax = 5,355 мс Δ

• 

  14 слайд

  Погрешности Основное правило: Точность результата не может быть выше точности исходных данных. Абсолютная погрешность Х ± ΔХ Относительная погрешность δХ = ΔХ/Х

• 

  15 слайд

  пример Если g = 9,8 ± 0,01, то Δg = 0,01/9,8 ≈ 0,1% Следовательно ΔTmax = 2,23 ∙ 0,001 ≈ 0,003 Δ Vmax = 5,355 ∙ 0,001 ≈ 0,006 ИТОГО: Tmax = 2,23 ±0,003 сек Vmax = 5,355 ±0,006 мс

• 

Краткое описание документа:

Предлагаю материалы к учебнику Семакина И.Г. «Информатика и ИКТ» для 11 класса (профильный уровень) Глава 3. Компьютерное моделирование 3.2 «Моделирование движения тел в поле силы тяжести».

Материал данной главы их этого учебника я использую на уроках кружка «Моделирование на компьютере», так как по моему мнению он достаточно сложен для всех учащихся, но интересен для ребят с математическим складом ума, тем более тем, кто интересуется физикой. Разработанные презентации и раздаточный материал для практической работы уже опробован и, возможно, значительно облегчит работу учителям информатики, не обладающим достаточной подготовкой по физике.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 211 138 материалов в базе

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»

• Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»

• Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»

• Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»

• Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»

• Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Современные тенденции цифровизации образования»

• Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»

• Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»