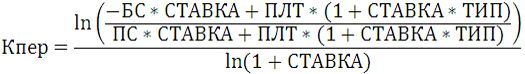Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Mobile Еще…Меньше
Управление личными финансами может быть сложной задачей, особенно если вам нужно планировать свои платежи и сбережения. Excel формулы и шаблоны бюджетов помогут вам вычислить будущую стоимость своих задолженности и инвестиций, что упростит расчет времени, необходимого для достижения целей. Используйте следующие функции:
-
ПЛТ: возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и процентной ставки.
-
КПЕР: возвращает количество периодов выплаты для инвестиции на основе регулярных постоянных выплат и постоянной процентной ставки.
-
ПВ: возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат.
-
БС: возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки.
Расчет ежемесячных платежей для погашения задолженности по кредитной карте
Предположим, остаток к оплате составляет 5400 долларов США под 17% годовых. Пока задолженность не будет погашена полностью, вы не сможете рассчитываться картой за покупки.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
=ПЛТ(17%/12;2*12;5400)
получаем ежемесячный платеж в размере 266,99 долларов США, который позволит погасить задолженность за два года.
-
Аргумент «ставка» — это процентная ставка на период погашения кредита. Например, в данной формуле ставка 17% годовых делится на 12 — количество месяцев в году.
-
Аргумент КПЕР 2*12 — это общее количество периодов выплат по кредиту.
-
Аргумент ПС или приведенной стоимости составляет 5400 долларов США.
Расчет ежемесячных платежей по ипотеке
Представьте дом стоимостью 180 000 долларов США под 5% годовых на 30 лет.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
=ПЛТ(5%/12;30*12;180000)
получена сумма ежемесячного платежа (без учета страховки и налогов) в размере 966,28 долларов США.
-
Аргумент «ставка» составляет 5%, разделенных на 12 месяцев в году.
-
Аргумент КПЕР составляет 30*12 для ипотечного кредита сроком на 30 лет с 12 ежемесячными платежами, оплачиваемыми в течение года.
-
Аргумент ПС составляет 180 000 (нынешняя величина кредита).
Расчет суммы ежемесячных сбережений, необходимой для отпуска
Необходимо собрать деньги на отпуск стоимостью 8500 долларов США за три года. Процентная ставка сбережений составляет 1,5%.
С помощью функции ПЛТ(ставка;КПЕР;ПС;БС)
=ПЛТ(1,5%/12;3*12;0;8500)
получаем, что чтобы собрать 8500 долларов США за три года, необходимо откладывать по 230,99 долларов США ежемесячно.
-
Аргумент «ставка» составляет 1,5%, разделенных на 12 месяцев — количество месяцев в году.
-
Аргумент КПЕР составляет 3*12 для двенадцати ежемесячных платежей за три года.
-
Аргумент ПС (приведенная стоимость) составляет 0, поскольку отсчет начинается с нуля.
-
Аргумент БС (будущая стоимость), которую необходимо достичь, составляет 8500 долларов США.
Теперь допустим, вы хотите собрать 8500 долларов США на отпуск за три года, и вам интересно, какую сумму необходимо положить на счет, чтобы ежемесячный взнос составлял 175,00 долларов США. Функция ПС рассчитает размер начального депозита, который позволит собрать желаемую сумму.
С помощью функции ПС(ставка;КПЕР;ПЛТ;БС)
=ПС(1,5%/12;3*12;-175;8500)
мы узнаем, что необходим начальный депозит в размере 1969,62 долларов США, чтобы можно было откладывать по 175,00 долларов США в месяц и собрать 8500 долларов США за три года.
-
Аргумент «Ставка» составляет 1,5%/12.
-
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
-
Аргумент ПЛТ составляет -175 (необходимо откладывать по 175 долларов США в месяц).
-
Аргумент БС (будущая стоимость) составляет 8500.
Расчет срока погашения потребительского кредита
Представьте, что вы взяли потребительский кредит на сумму 2500 долларов США и согласились выплачивать по 150 долларов США ежемесячно под 3% годовых.
С помощью функции КПЕР(ставка;ПЛТ;ПС)
=КПЕР(3%/12;-150;2500)
выясняем, что для погашения кредита необходимо 17 месяцев и несколько дней.
-
Аргумент «Ставка» составляет 3%/12 ежемесячных платежей за год.
-
Аргумент ПЛТ составляет -150.
-
Аргумент ПС (приведенная стоимость) составляет 2500.
Расчет суммы первого взноса
Скажем, вы хотите приобрести автомобиль стоимостью 19 000 долларов США под 2,9 % годовых за три года. Вы хотите, чтобы ежемесячные платежи были на уровне 3500 долларов США в месяц, поэтому вам нужно выяснить сумму своего взноса. В этой формуле результатом функции ПС является сумма займа, которая затем вычитается из цены покупки, чтобы получить первый взнос.
С помощью функции ПС(ставка;КПЕР;ПЛТ)
= 19000-ПС(2,9%/12; 3*12;-350)
выясняем, что первый взнос должен составлять 6946,48 долларов США.
-
Сначала в формуле указывается цена покупки в размере 19 000 долларов США. Результат функции ПС будет вычтен из цены покупки.
-
Аргумент «Ставка» составляет 2,9%, разделенных на 12.
-
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
-
Аргумент ПЛТ составляет -350 (необходимо будет выплачивать по 350 долларов США в месяц).
Оценка динамики увеличения сбережений
Начиная с 500 долларов США на счету, сколько можно собрать за 10 месяцев, если класть на депозит по 200 долларов США в месяц под 1,5% годовых?
С помощью функции БС(ставка;КПЕР;ПЛТ;ПС)
=БС(1,5%/12;10;-200;-500)
получаем, что за 10 месяцев выйдет сумма 2517,57 долларов США.
-
Аргумент «Ставка» составляет 1,5%/12.
-
Аргумент КПЕР составляет 10 (месяцев).
-
Аргумент ПЛТ составляет -200.
-
Аргумент ПС (приведенная стоимость) составляет -500.
См. также
ПЛТ
КПЕР
ПС
БС
Нужна дополнительная помощь?
Функция КПЕР в Excel предназначена для расчета количества периодов выплат погашения определенной суммы задолженности при известных значениях процентной ставки (простые проценты), суммы платежа для каждого периода (фиксированное значение), начальной суммы задолженности или общей суммы долга с учетом процентов, и возвращает соответствующее числовое значение.
Примеры как использовать функцию КПЕР в Excel
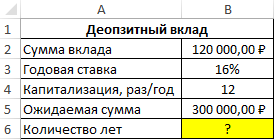
Пример 1. Вкладчик внес депозит под 16% годовых на сумму 120000 рублей с ежемесячной капитализацией вклада (простые проценты). Сколько лет потребуется для накопления 300000 рублей?
Исходные данные:
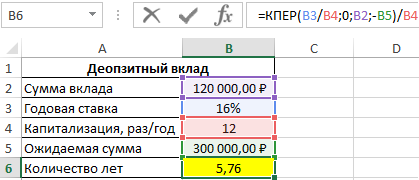
Формула для расчета:
=КПЕР(B3/B4;0;B2;-B5)/B4
Описание аргументов:
- B3/B4 – процентная ставка за период капитализации;
- 0 – числовое значение, характеризующее ежемесячный платеж (дополнительное пополнение депозитного счета не производится);
- B2 – начальная инвестиция;
- -B5 – конечная сумма по окончанию договора.
Возвращенный функцией КПЕР результат разделен на количество периодов капитализации в году для расчета числа лет, необходимых для накопления требуемой суммы. Результат расчетов:
Вкладчик должен оставлять деньги на депозитном счете на протяжении почти 6 лет.
Расчет реальной суммы долга с процентами и переплатой в Excel
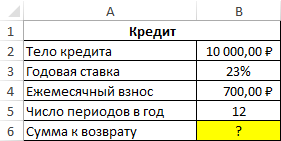
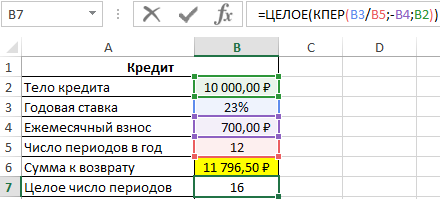
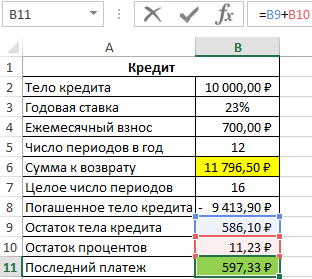
Пример 2. Клиенту банка был выдан кредит на сумму 10000 рублей под 23% годовых с ежемесячной оплатой 700 рублей. Сколько всего денег получит банк по окончанию срока кредитного договора?
Исходные данные:
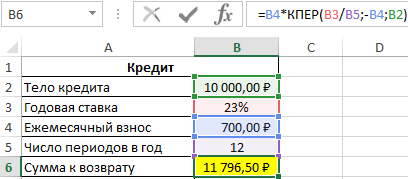
Формула для расчета:
=B4*КПЕР(B3/B5;-B4;B2)
Общая сумма кредита рассчитывается как произведение фиксированной суммы ежемесячного платежа и количества периодов выплат. В данном случае количество периодов равно 16,85 (нецелое число), значит, последняя выплата должна составить меньше 700 рублей. Найдем целое число периодов:
=ЦЕЛОЕ(КПЕР(B3/B5;-B4;B2))
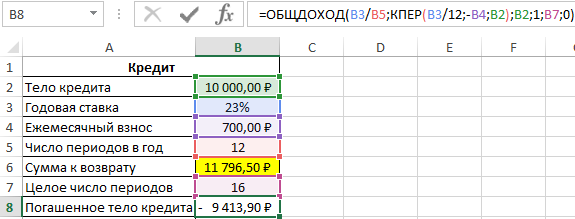
Чтобы определить, какую часть тела кредита было погашено за 16 целых периодов выплат, воспользуемся следующей функцией:
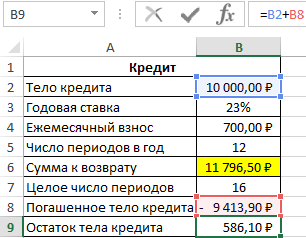
За последний неполный период необходимо вернуть следующую часть тела кредита:
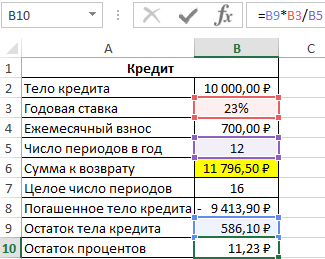
Рассчитаем оставшиеся проценты к уплате:
Так как платеж включает в себя оплату тела кредита и процентов, насчитанных за период, определим размер последнего платежа по формуле:
Общая сумма, которую получит банк, составит 11796 рублей, а размер последнего платежа – 597 рублей.
Расчет сроков погашения кредита с помощью функции КПЕР
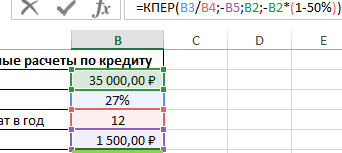
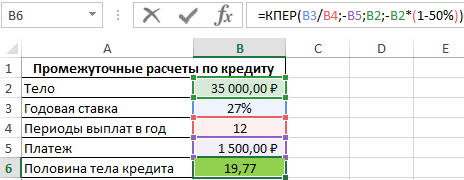
Пример 3. Банк выдал кредит на сумму 35000 рублей под 27% годовых. Размер ежемесячного платежа составляет 1500 рублей. Через сколько месяцев клиент выплатить 50% кредита?
Исходная таблица данных:
На основании тождества аннуитетных платежей (сумма величины платежа в погашение тела кредита за все периоды, тела кредита и будущей стоимости равна нулю, то есть ОБЩДОХОД+ПС+БС=0) используем следующую формулу:
=КПЕР(B3/B4;-B5;B2;-B2*(1-50%))
Выражение -B2*(1-50%)) характеризует будущую стоимость и было получено из уравнения:
-35000*50%+35000=-БС
Результат расчета:
Для выплаты 50% кредита потребуется вносить ежемесячный платеж на протяжении примерно 20 месяцев.
Особенности использования функции КПЕР в Excel
Функция КПЕР используется для решения финансовых задач совместно с функциями ПЛТ, БС, СТАВКА, ПС и имеет следующую синтаксическую запись:
=КПЕР(ставка;плт;пс;[бс];[тип])
Описание аргументов (первые три аргумента – обязательные для заполнения):
- ставка – числовое значение, характеризующее ставку за 1 период выплат (для ссуд) или капитализации (для депозитных вкладов). Аргумент может быть указан в виде дробного числа или в качестве значения в процентном формате (например, 14,5% или 0,145 – эквивалентные варианты записи). Если в условии задачи указана годовая ставка, необходимо выполнить пересчет по формуле Rп=Rг/12, где Rп – ставка за период, Rg – годовая ставка, 12 – число месяцев в году.
- плт – числовое значение, соответствующее сумме выплаты за период, которая является фиксированной величиной (простые проценты).
- пс – числовое значение, характеризующее текущую стоимость инвестиции (например, сумма, выданная кредитной организацией в долг клиенту, или сумма средств, положенных на депозитный счет в банк).
- [бс] – числовое значение, соответствующее будущей стоимости инвестиции. Например, данный аргумент может характеризовать сумму, которую получит вкладчик по окончанию действия договора по депозитному вкладу. Если аргумент явно не указан или принимает значение 0 (нуль), функция КПЕР вернет количество периодов выплат до полного погашения задолженности. Аргумент необязателен для заполнения, по умолчанию принимается значение 0.
- [тип] – необязательный аргумент, характеризующий способ выплат (0 – выплата на конец периода, 1 – выплата на начало периода).
Примечания 1:
- Функция КПЕР возвращает код ошибки #ЧИСЛО! В случае, если сумма платежа за каждый период меньше, чем произведение начальной суммы инвестиции и ставки за период, при этом будущая стоимость инвестиции равна 0 (ситуация при расчете количества периодов для полного возврата задолженности), а выплата производится в конце периода (то есть, аргумент [тип] или явно указан как 0 (нуль).
- Указанная выше особенность работы функции КПЕР вытекает из алгоритма, который она использует для расчета:
- Все аргументы функции КПЕР должны указываться в виде числовых значений или конвертируемых в числа текстовых срок. Иначе рассматриваемая функция будет возвращать код ошибки #ЗНАЧ!.
Примечания 2:
- Фактически, функция КПЕР позволяет определить количество периодов, по окончанию последнего из которых будущая стоимость инвестиции примет указанное значение.
- В случае с кредитом, считается, что задолженность погашена полностью, если будущая стоимость инвестиции равна 0 (нулю).
- Также функция КПЕР позволяет вычислить количество периодов капитализации депозитного вклада, необходимых для достижения требуемой суммы накоплений.
- Для расчета количества периодов выплаты задолженности с нулевой процентной ставкой можно использовать формулу =A1/A2, где A1 – будущая стоимость, A2 – фиксированная сумма выплат за период.
В
пакете Excel
существует группа функций, предназначенных
для расчета финансовых операций по
кредитам, ссудам, займам. Эти расчеты
основаны на концепции временной стоимости
денег и предполагают неравноценность
денег, относящихся к разным моментам
времени. Эта группа функций охватывает
следующие расчеты:
-
определение
наращенной суммы (будущей стоимости), -
определение
начального значения (текущей стоимости), -
определение
срока платежа и процентной ставки, -
расчет
периодических платежей, связанных с
погашением займов.
Общая
формула расчета, которуюExcel
использует при вычислении финансовых
аргументов, связанных с денежными
потоками, имеет вид:
где
pmt
– фиксированная
(неизменная) периодическая сумма платежа;
n
– общее
число периодов выплат,
r
– процентная
ставка за один период,
type
– число 0
или 1, обозначающее, когда производится
выплата (1 – в начале периода, 0 – в конце
периода),
—
текущая стоимость вклада (займа), по
которому начисляются проценты по ставке
r%
n—ное
число периодов или текущая стоимость
серии фиксированных платежей,
—будущая стоимость вклада (займа) или
будущая стоимость серии фиксированных
периодических платежей.
Если
процентная ставка за период начисления
r=0, то используется следующая формула:
Эти
формулы используют встроенные функцииБC,
КПЕР, ПC,
ПЛТ, ЭФФЕКТ и
другие.
ПС
— текущий объём вклада
Позволяет
рассчитать текущий объем вклада.
Синтаксис
ПС
(норма;кпер;выплата;бс;тип)
норма
— процентная
ставка за период. Так, если Вы получили
ссуду под станок под 15% годовых и делаете
ежемесячные выплаты, то ставка
процента за месяц составит 15%/12, или
1,25%. Аргумент норма
в данном
случае может принимать значения 15%/12
или 1,25% или 0,0125.
кпер
— общее число
периодов выплат годовых процентов. Так,
если Вы получили ссуду на 3 года под
станок и делаете ежемесячные платежи,
то Ваша ссуда имеет 3*12 (или 36) периодов.
Аргумент кпер
в данном случае принимает значение 36.
выплата
—
размер выплаты, производимой в каждом
периоде и не меняющейся в течение всего
времени выплаты процентов. Обычно,
выплата включает основные платежи и
платежи по процентам без учета других
сборов или налогов. Например,
ежемесячная выплата по четырехгодичному
займу в 10 000 руб. под 12% годовых составит
308,3 руб. Аргумент выплата
в данном случае принимает значение
-308,3.
бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
Если бс
опущено, оно полагается равным 0 (будущая
стоимость займа, например, равна 0).
Например, если Вы хотите накопить 50000
руб. в течение18 лет, то 50 000 руб. это и
есть будущая стоимость. Вы можете сделать
предположение о сохранении заданной
процентной ставки и определить, сколько
нужно откладывать каждый месяц.
тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 означает — выплата в конце периода,
1 — выплата в начале периода.
-
Выбранные
единицы измерения для аргументов норма
и кпер
должны соответствовать друг другу.
Если Вы делаете ежемесячные выплаты
по четырехгодичному займу под 12% годовых,
то используйте 12%/12 для задания аргумента
норма,
4*12 для задания аргумента кпер.
Если Вы делаете ежегодные платежи по
тому же займу, то используйте 12% для
задания аргумента норма
и 4 для задания аргумента кпер. -
В
функциях, связанных с интервалами
выплат, выплачиваемые деньги
представляются отрицательным числом,
а получаемые деньги представляются
положительным числом. Например, депозит
в банк на сумму 1 000 руб. представляется
для вкладчика аргументом -1000, а для
банка аргументом 1000.
Пример
Фирме
потребуется 5000 руб. через 12 лет. В
настоящее время фирма располагает
деньгами и готова положить их на депозит
единым вкладом, чтобы через 12 лет он
достиг 5000 руб. Определим необходимую
сумму текущего вклада, если ставка
процента по нему составляет 12% годовых.
Необходимая
сумма текущего вклада составит:
ПС
(12%;12;;5000)=-1283.38 руб.
БС
— стоимость постоянных платежей в
определенные периоды на основе постоянной
процентной ставки
Позволяет
рассчитать объем вклада через определенный
промежуток времени на основе периодических
постоянных платежей и постоянной
процентной ставки.
Синтаксис
БС(норма;кпер;выплата;пс;тип)
ставка
— процентная
ставка за период.
кпер
— количество
периодов, в которые производится выплата
годовых процентов.
выплата—
размер выплаты, производимой в каждом
периоде; это значение постоянно в течение
всего времени выплат. Обычно плата
состоит из основного платежа и платежа
по процентам без учета других налогов
и сборов.
пс
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент пс
опущен,
то он полагается равным 0.
тип
— число,
определяющее когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплата в конце периода, 1 — выплата
в начале периода.
Более
подробная информация об аргументах
функции БЗ и о других функциях выплат
по процентным вкладам приведена в
описании функции ПЗ.
-
Единицы
измерения для аргументов норма
и кпер
должны быть согласованы. Если производятся
ежемесячные платежи по четырехгодичному
займу из расчета 12% годовых, то норма
должна быть 12%/12 , а кпер
должно быть 4*12. Если производятся
ежегодные платежи по тому же займу, то
норма
должна быть
12%, а кпер
должно быть 4. -
Ваш
вклад представляется отрицательным
числом, а деньги, которые вы получите,
представляются положительным числом.
Пример
Определим,
сколько денег будет на счету через год,
если вы собираетесь вложить 1000 рублей
под 6% годовых (что составит в месяц
6%/12 или 0,5%). Причем вы собираетесь
вкладывать по 100 рублей в начале каждого
следующего месяца в течение года.
Через
год на счете будет:
БС
(0,5%;12;-100;-1000;1)=2301,40 р.
ПРПЛТ
— платежи по процентам за период на
основе постоянных периодических выплат
и постоянной процентной ставки
С
помощью данной функции можно рассчитать
процентные платежи за текущий период
при периодических постоянных выплатах
и постоянной процентной ставке. Полное
описание аргументов функции ПРПЛТ
и более подробная информация о функциях,
связанных с ежегодными выплатами,
приведены в описании функции ПС.
Синтаксис
ПРПЛТ(норма;период;кпер;тс;бс;тип)
норма
—
процентная ставка за период.
период
— текущий
период, в котором требуется определить
прибыль (может принимать значения от 1
до кпер).
кпер
— общее число
периодов выплат.
тс
— сумма,
которую составят будущие платежи с
настоящего момента.
бс
— баланс
платежей, который нужно достичь после
последней выплаты.
тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплаты в конце периода, 1 — выплаты
в начале периода.
-
Единицы
измерения для аргументов норма
и кпер
должны быть согласованы. Если производятся
ежемесячные платежи по трехгодичному
займу из расчета 10% годовых, то норма
должна быть 10%/12 , а кпер
должно быть 3*12. Если производятся
ежегодные платежи по тому же займу, то
норма
должна быть 10%, а кпер
должно быть 3. -
Выплачиваемые
денежные средства представляются
отрицательным числом, а получаемые
денежные средства представляются
положительным числом.
Пример
Требуется
определить доход за первый месяц от
четырехгодичного займа в 1000000 рублей
из расчета 15% годовых:
ПРПЛТ(0,15/12;1;48;1000000)
равняется -12500 рублей.
ПЛТ
— расчет постоянных периодических
выплат
Функция
вычисляет величину выплаты за один
период на основе фиксированных
периодических выплат и постоянной
процентной ставки. Выплаты, рассчитанные
функцией ПЛТ, включают основные платежи
и платежи по процентам.
Синтаксис
ПЛТ(норма;кпер;нз;бс;тип)
норма
– норма
прибыли за период займа.
кпер
– общее
число периодов выплат годовой ренты
нз
– текущая стоимость: общая сумма всех
будущих платежей с настоящего момента.
бс
– будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты.
тип
— число,
определяющее, когда должна производиться
выплата.
Пример
Предположим,
что необходимо накопить 4000 руб. за 3
года, откладывая постоянную сумму в
конце каждого месяца. Какой должна быть
эта сумма, если норма процента по вкладу
составляет 12% годовых?
Величина
ежемесячных выплат составит:
ПЛТ(12%/12;12*3;;4000)=-92.86
руб.
ОСПЛТ
— расчет основных платежей по займу
Функция
вычисляет величину основного платежа
(выплаты задолженности) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
на указанный период.
Синтаксис
ОСПЛТ(норма;период;кпер;тс;бс;тип)
норма
– норма
прибыли за период.
период
– период,
который должен быть в интервале от 1 до
кпер.
кпер
– общее
число периодов выплат годовой ренты.
тс
– текущая
стоимость: общая сумма всех будущих
платежей с настоящего периода.
бс
– будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
тип
—
число,
определяющее, когда должна производиться
выплата.
Пример
Банком
выдан кредит в 7000 руб. на 3 года под 17%
годовых, начисляемых один раз в конце
каждого периода.
Определите
размер ежегодных основных выплат по
займу.
Основная
часть платежа на каждый из трех периодов
составит соответственно:
ОСПЛТ(17%;1;3;-70000)=19780.16
руб.
ОСПЛТ(17%;2;3;-70000)=23142.78
руб.
ОСПЛТ(17%;3;3;-70000)=27077.06
руб.
ОБЩПЛТ
— расчет суммы платежей по процентам
по займу между двумя периодами выплат
Функция
вычисляет накопленный доход (сумму
платежей по процентам) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
между двумя периодами выплат.
Синтаксис
ОБЩПЛТ(ставка;кол_пер;нз;нач_период;кон_период;тип)
ставка
– процентная ставка.
кол_пер
– общее
количество периодов выплат.
нз
– текущее
значение.
нач_период
– первый
период.
кон_период
— последний период.
Пример
Пусть
заем под недвижимость сделан на следующих
условиях: процентная ставка –9% годовых;
срок-30 лет, размер ссуды – 125000 руб.,
проценты начисляются ежемесячно.
Найти
сумму выплат по процентам за 2-й год и
за 1-й месяц займа.
Общая
выплата по процентам за второй год
составит:
ОБЩПЛТ(9%/12;30*12;125000;13;24)=-11135.23
руб.
Одна
выплата за первый месяц составит:
ОБЩПЛТ(9%/12;30*12;125000;1;1)=-937.50
руб.
ОБЩДОХОД
— расчет суммы основных выплат по займу
между двумя периодами
Функция
вычисляет сумму основных выплат по
займу, который погашается равными
платежами в конце или начале каждого
расчетного периода, между двумя периодами.
Синтаксис
ОБЩДОХОД
(ставка;кол_пер;нз;нач_период; нач_период;)
ставка
– процентная ставка.
кол_пер
– общее
количество периодов выплат.
нз
– текущее
значение.
нач_период
– первый
период.
кон_период
— последний период.
Пример
Выдана
ссуда размером 1000$ сроком на 6 лет под
15% годовых; проценты начисляются
ежеквартально.
Определите
величину основных выплат за 5 год.
Если
ссуда погашается равными платежами в
конце каждого расчетного периода, то
размер выплаты задолженности за пятый
год составит:
ОБЩДОХОД(15%/4;6*4;1000;17;20)=-201.43$.
Комплексный
пример
Банком
выдан кредит в 10000$ на 5 лет под 12% годовых,
начисляемых один раз в конце каждого
периода. По условиям договора кредит
должен быть погашен равными долями в
течение указанного срока, выплачиваемыми
в конце каждого периода.
Разработать
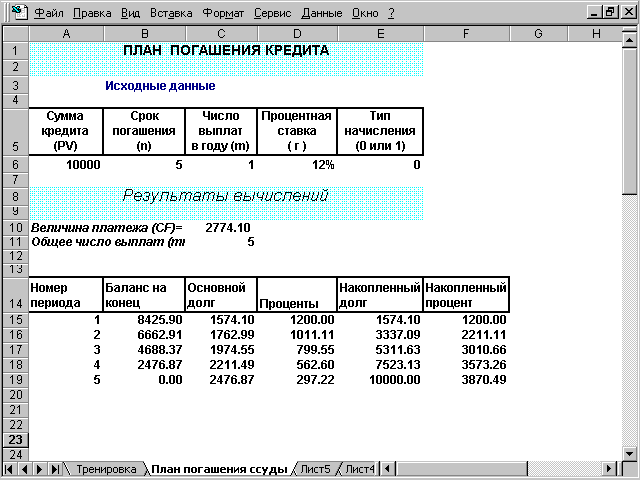
план погашения кредита.
Периодический
платеж по данной операции составит:
ПЛТ(12%;5;-10000)=2774.10$.
Процентная
часть платежа на первый период составит:
ПРПЛТ(12%;1;5;-10000)=1200,00$.
Основная
часть платежа, направленная на погашение
долга за первый период, составит:
ОСПЛТ(12%;1;5;-10000)=1574.10$.
Как
видно выполняется тождество:
ПРПЛТ()+ОСПЛТ()=ПЛТ()=2774.10$.
Будущее
значение суммы, которую банк получит в
результате проведения операции:
ПЛТ(12%;5;-10000)*5=13870.50$.
Накопленная
сумма процентов за весь период составит:
ОБЩПЛТ(12%;5;10000;1;5;0)=-3870,49$.
Накопленная
сумма в счет погашения по займу за 5 лет
составит:
ОБЩДОХОД(12%;5;10;1;5;0)=-10000.00$.
Как
видно, сумма полученных величин равна
общей сумме, выплаченной по данному
займу:
ОБЩДОХОД()+ОБЩПЛАТ()=13870.49$.
(В
силу заложенного алгоритма расчета
функции ОБЩДОХОД() и ОБЩПЛАТ возвращают
отрицательные значения. Для получения
положительных значений можно задать
их со знаком минус).
На
рис. 1 приведена таблица с планом погашения
кредита.
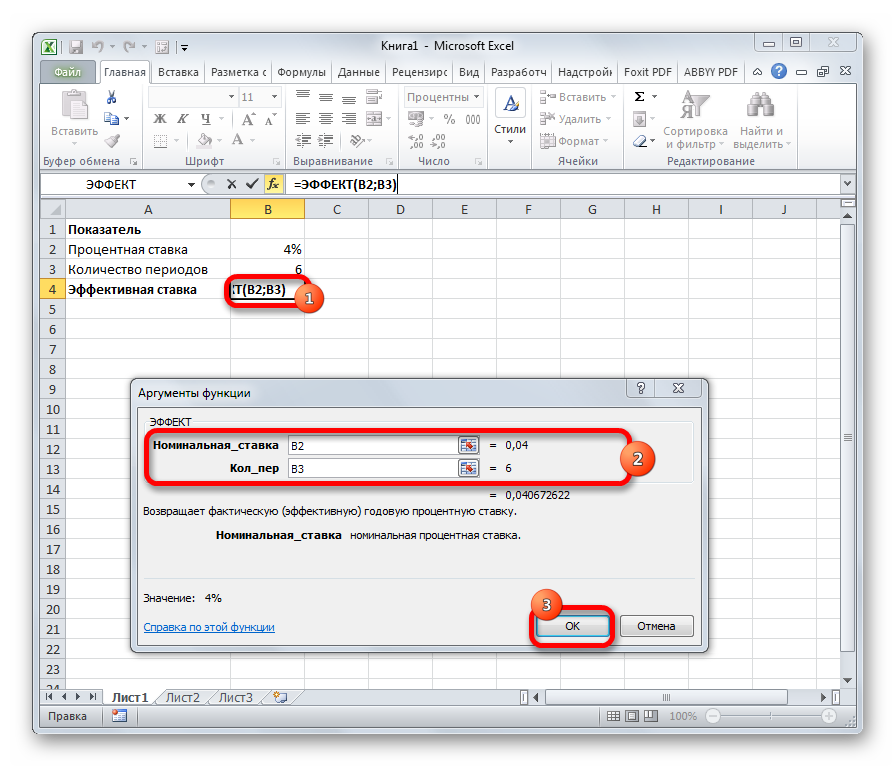
ЭФФЕКТ
— эффективная годовая процентная ставка
Позволяет
рассчитать фактическую годовую процентную
ставку, если известны годовая процентная
ставка и количество периодов в году.
Синтаксис
ЭФФЕКТ(нoмuнaльнaя_cmaвкa;кол_пep)
номинальная_ставка
—
номинальная годовая процентная ставка.
кол_пер
— количество
периодов в году.
Рис.
1. План погашения кредита
-
Число
периодов в году округляется до целого. -
Функция
ЭФФЕКТ
выдает значение ошибки #ЗНАЧ! в случае,
если один из аргументов — не число либо,
если номинальная_ставка
меньше 0 или
кол_пер
меньше 1.
Пример
Рассчитаем
эффективную годовую процентную ставку
при ставке 5,25% и четырех периодах в
году.
ЭФФЕКТ(5,25%;4)
равняется 0,053543 или 5,35%.
КПЕР
— определение срока платежа
Эта
функция вычисляет общее число периодов
выплат как для единой суммы вклада
(займа), так и для периодических постоянных
выплат на основе постоянной процентной
ставки. Если платежи производятся
несколько раз в год, найденное значение
необходимо разделить на число расчетных
периодов в году, чтобы найти число лет
выплат.
Синтаксис
КПЕР(норма;выплата;нз;бс;тип)
норма
– норма
прибыли за период.
выплата—
размер выплаты, производимой в каждом
периоде.
нз
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент нз опущен, то он
полагается равным 0.
бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
тип
— число,
определяющее, когда должна производиться
выплата.
Пример
Ожидается,
что ежегодные доходы от реализации
проекта составят 33 млн. руб. Необходимо
рассчитать срок окупаемости проекта,
если инвестиции к началу поступления
доходов составят 100 млн. руб., норма
дисконтирования 12.11%.
Срок
окупаемости проекта составит:
КПЕР(12.11%;33;-100)=4года.
Определение
скорости оборота инвестиций
ВНДОХ
— процентная ставка дохода для ряда
последовательных периодических
выплат или поступлений
Позволяет
рассчитать процентную ставку дохода
от инвестиций для ряда последовательных
операций с денежными средствами,
представленными числовыми значениями.
Объемы операций могут быть различны.
Однако они должны происходить через
равные промежутки времени, например,
ежемесячно или ежегодно. Процентная
ставка дохода, полученного от инвестиции,
состоит из выплат (отрицательные
значения) и поступлений (положительные
значения), которые происходят в регулярные
периоды времени.
Синтаксис
ВНДОХ
(значения;предположение)
значения
— массив или
ссылка на ячейки, содержащие числа, для
которых вычисляется процентная ставка
инвестиций.
предположение
—
прогнозируемая величина.
-
Аргумент
значения
должен включать в себя по крайней мере
одно положительное значение и одно
отрицательное значение, для того, чтобы
можно было вычислить процентную ставку. -
Начиная
со значения прогноз, функция ВНДОХ
выполняет
циклические вычисления, пока не получит
результат с точностью 0,00001 процента
(такой метод вычисления называется
методом итераций). -
Функция
ВНДОХ выдает значение ошибки #ЧИСЛО! в
том случае, если не может получить
результат после 20 попыток. -
Обычно
нет необходимости задавать аргумент
прогноз
для вычислений с помощью функции ВНДОХ.
Если прогноз
опущен, то
он полагается равным 0,1 (10 процентов).
Если ВНДОХ
выдает значение ошибки
#ЧИСЛО!,
можно попытаться выполнить вычисления
еще раз с другим значением аргумента
прогноз.
Пример
Предположим,
что затраты по проекту составят 500 тыс.
руб. Ожидаемые доходы составят 50 , 100 ,
300 и 200 тыс. руб. в течение последующих
4 лет. Оценим
экономическую целесообразность проекта
по скорости оборота инвестиций, если
рыночная норма дохода 12%.
Ячейки
А1:А5 содержат следующие значения: -500,
50, 100, 300 и 200 соответственно.
Внутренняя
скорость оборота инвестиций составит:
ВНДОХ(А1:А5)=9.25%.
Это
меньше, чем рыночная норма, поэтому
проект должен быть отвергнут.
В
том случае, если эта какая-либо из
финансовых функций недоступна из Excel,
следует установить надстройку Пакет
Анализа (Analysis
ToolPak),
а затем подключить его с помощью команды
Сервис
— Надстройки…
ЗАДАЧИ
Для Google Docs эти формулы тоже подходят.
1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.
Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.
Какие данные нужны
Для начала надо правильно написать формулу — в любой свободной ячейке.
=ПЛТ(ставка;кпер;пс)
В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:
- Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
- Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
- Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.
Как всё посчитать
Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.
Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.
2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
Какие данные нужны
Формула расчёта довольно простая:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
В ней всего две переменные:
- Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
- Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).
Как всё посчитать
Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:
Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.
3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.
Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.
Какие данные нужны
Формула состоит из трёх компонентов:
=ЧИСТНЗ(ставка;значения;даты)
Второй и третий достаточно ясны:
2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.
Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.
Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.
Как всё посчитать
Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.
Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.
4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.
Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.
Какие данные нужны
Чтобы определить более выгодное предложение, применим формулу:
=ЧИСТВНДОХ(значения;даты)
Достаточно знать всего две переменные:
- Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
- Даты — график платежей, по которым будут выплачивать прибыль.
Как всё посчитать
Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.
5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.
Какие данные нужны
Полезной будет эта формула:
=СТАВКА(кпер;плт;пс)
Три переменных в ней означают следующее:
- Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
- Плт — размер платежей. Считаются и основной долг, и проценты.
- Пс — общая сумма займа. В нашем примере это 100 000 рублей.
Как всё посчитать
Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.
6. PV (ПС) — подсказывает, сколько денег можно взять в долг
Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.
Какие данные нужны
Пригодится формула расчёта текущей стоимости:
=ПС(ставка; кпер; плт)
Для этого потребуется информация, которая есть на сайте любого банка:
- Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
- Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
- Плт — размер комфортного платежа.
Как всё посчитать
Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.
Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.
7. NPER (КПЕР) — помогает рассчитать время накоплений
Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.
Какие данные нужны
Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:
=КПЕР(ставка/периоды_капитализации;плт;пс;бс)
Она состоит из четырёх основных значений и одного дополнительного:
- Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
- Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
- Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
- Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
- Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.
Как всё посчитать
Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.
Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.
Читайте также 🧐
- Как вести бюджет, если у вас непостоянный доход
- 20 полезных шаблонов «Google Таблиц» на все случаи жизни
- 10 крутых приложений, чтобы взять финансы под контроль
В Microsoft Excel предусмотрено огромное количество разнообразных функций, позволяющих справляться с математическими, экономическими, финансовыми и другими задачами. Программа является одним из основных инструментов, использующихся в малых, средних и больших организациях для ведения различных видов учета, выполнения расчетов и т.д. Ниже мы рассмотрим финансовые функции, которые наиболее востребованы в Экселе.
- Вставка функции
-
Популярные финансовые функции
- БС
- ВСД
- ДОХОД
- МВСД
- ИНОРМА
- ПЛТ
- ПОЛУЧЕНО
- ПС
- СТАВКА
- ЦЕНА
- ЧПС
- Заключение
Вставка функции
Для начала вспомним, как вставить функцию в ячейку таблицы. Сделать это можно по-разному:
- Выбрав нужную ячейку щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- Или переключаемся во вкладку “Формулы” и жмем аналогичную кнопку, расположенную в левом углу ленты программы.
Независимо от выбранного варианта, откроется окно вставки функции, в котором требуется выбрать категорию “Финансовые”, определиться с нужным оператором (например, ДОХОД), после чего нажать кнопку OK.
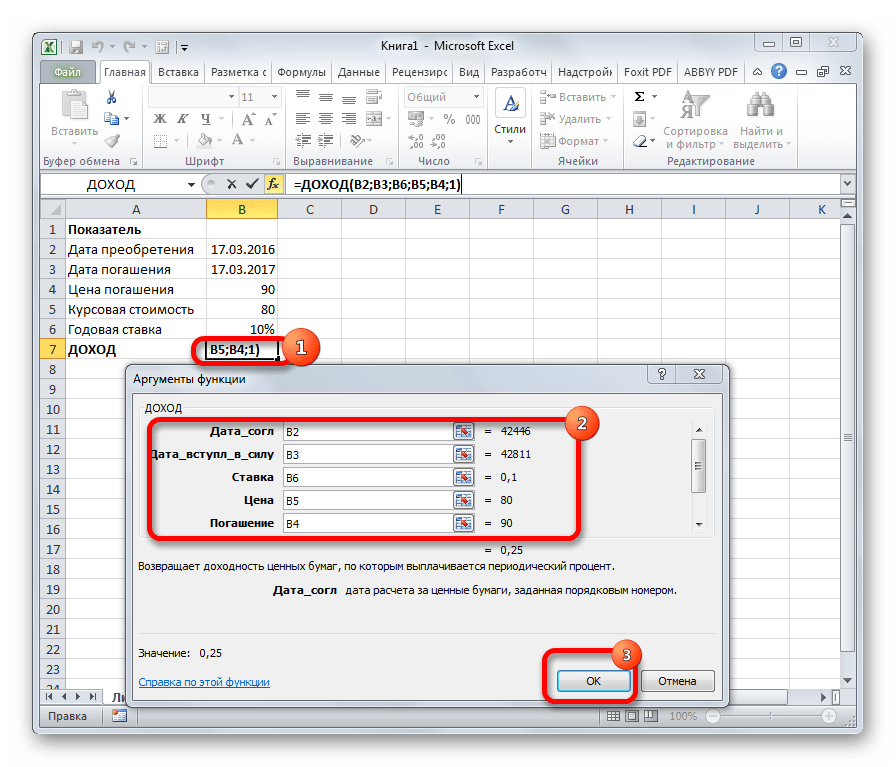
На экране отобразится окно с аргументами функции, которые требуется заполнить, после чего нажать кнопку OK, чтобы добавить ее в выбранную ячейку и получить результат.
Указывать данные можно вручную, используя клавиши клавиатуры (конкретные значения или ссылки на ячейки), либо встав в поле напротив нужного аргумента, выбирать соответствующие элементы в самой таблице (ячейки, диапазон ячеек) с помощью левой кнопки мыши (если это допустимо).
Обратите внимание, что некоторые аргументы могут не показываться и необходимо пролистать область вниз для получения доступа к ним (с помощью вертикального ползункам справа).
Альтернативный способ
Находясь во вкладке “Формулы” можно нажать кнопку “Финансовые” в группе “Библиотека функций”. Раскроется список доступных вариантов, среди которых просто кликаем по нужному.
После этого сразу же откроется окно с аргументами функции для заполнения.
Популярные финансовые функции
Теперь, когда мы разобрались с тем, каким образом функция вставляется в ячейку таблицы Excel, давайте перейдем к перечню финансовых операторов (представлены в алфавитном порядке).
БС
Данный оператор применяется для вычисления будущей стоимости инвестиции исходя из периодических равных платежей (постоянных) и размера процентной ставки (постоянной).
Обязательными аргументами (параметрами) для заполнения являются:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы:
- Пс – приведенная (нынешняя) стоимость. Если не заполнять, будет принято значение, равное “0”;
- Тип – здесь указывается:
- 0 – выплата в конце периода;
- 1 – выплата в начале периода
- если поле оставить пустым, по умолчанию будет принято нулевое значение.
Также есть возможность вручную ввести формулу функции сразу в выбранной ячейке, минуя окна вставки функции и аргументов.
Синтаксис функции:
=БС(ставка;кпер;плт;[пс];[тип])
Результат в ячейке и выражение в строке формул:
ВСД
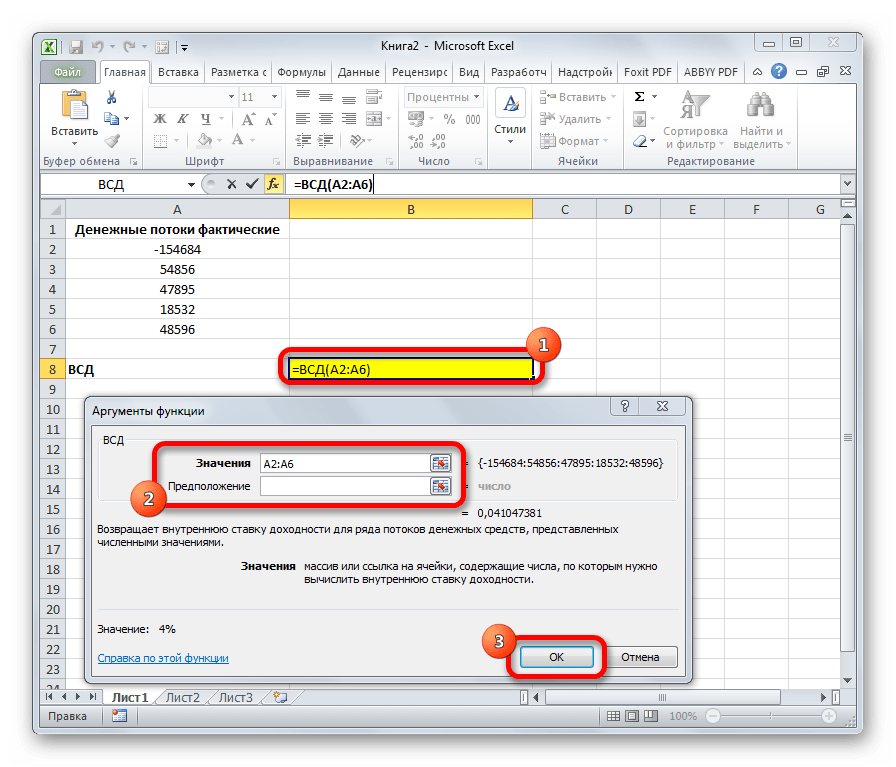
Функция позволяет вычислить внутреннюю ставку доходности для ряда денежных потоков, выраженных числами.
Обязательный аргумент всего один – “Значения”, в котором нужно указать массив или координаты диапазона ячеек с числовыми значениями (по крайней мере, одно отрицательное и одно положительное число), по которым будет выполняться расчет.
Необязательный аргумент – “Предположение”. Здесь указывается предполагаемая величина, которая близка к результату ВСД. Если не заполнять данное поле, по умолчанию будет принято значение, равное 10% (или 0,1).
Синтаксис функции:
=ВСД(значения;[предположение])
Результат в ячейке и выражение в строке формул:
ДОХОД
С помощью данного оператора можно посчитать доходность ценных бумаг, по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата соглашения/расчета по ценным бумагам (далее – ц.б.);
- Дата_вступл_в_силу – дата вступления в силу/погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Цена – цена ц.б. за 100 рублей номинальной стоимости;
- Погашение – суммы погашения или выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” является необязательным, в нем задается способ вычисления дня:
- 0 или не заполнен – армериканский (NASD) 30/360;
- 1 – фактический/фактический;
- 2 – фактический/360;
- 3 – фактический/365;
- 4 – европейский 30/360.
Синтаксис функции:
=ДОХОД(дата_согл;дата_вступл_в_силу;ставка;цена;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
МВСД
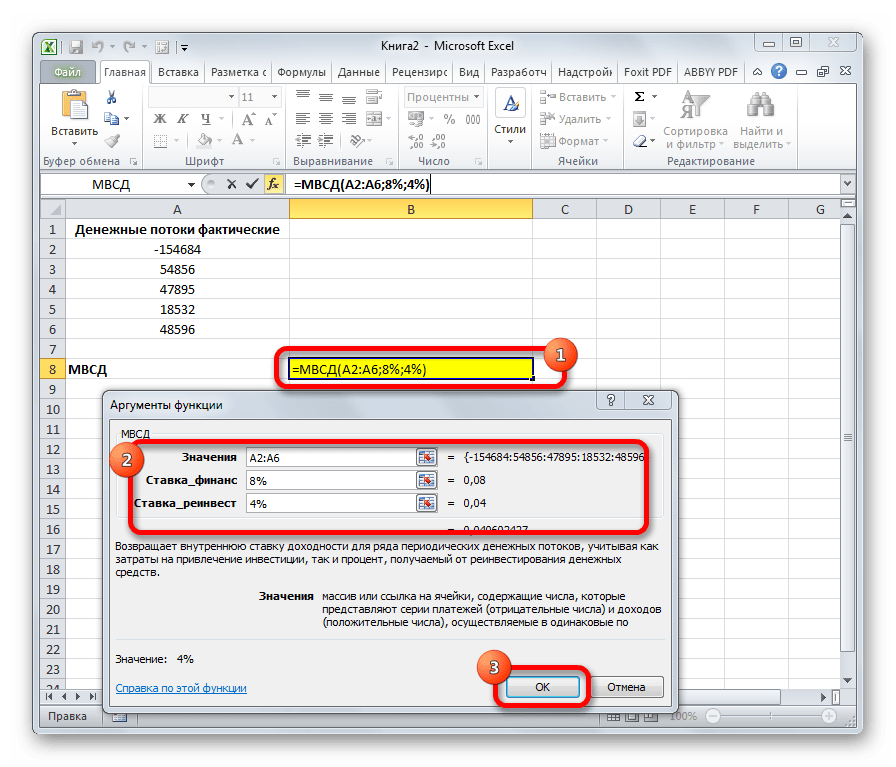
Оператор используется для расчета внутренней ставки доходности для ряда периодических потоков денежных средств исходя из затрат на привлечение инвестиций, а также процента от реинвестирования денег.
У функции только обязательные аргументы, к которым относятся:
- Значения – указываются отрицательные (платежи) и положительные числа (поступления), представленные в виде массива или ссылок на ячейки. Соответственно, здесь должно быть указано, как минимум, одно положительное и одно отрицательное числовое значение;
- Ставка_финанс – выплачиваемая процентная ставка за оборачиваемые средства;
- Ставка _реинвест – процентная ставка при реинвестировании за оборачиваемые средства.
Синтаксис функции:
=МВСД(значения;ставка_финанс;ставка_реинвест)
Результат в ячейке и выражение в строке формул:
ИНОРМА
Оператор позволяет вычислить процентную ставку для полностью инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, вложенная в ц.б.;
- Погашение – сумма к получению при погашении ц.б.;
- аргумент “Базис” как и для функции ДОХОД является необязательным.
Синтаксис функции:
=ИНОРМА(дата_согл;дата_вступл_в_силу;инвестиция;погашение;[базис])
Результат в ячейке и выражение в строке формул:
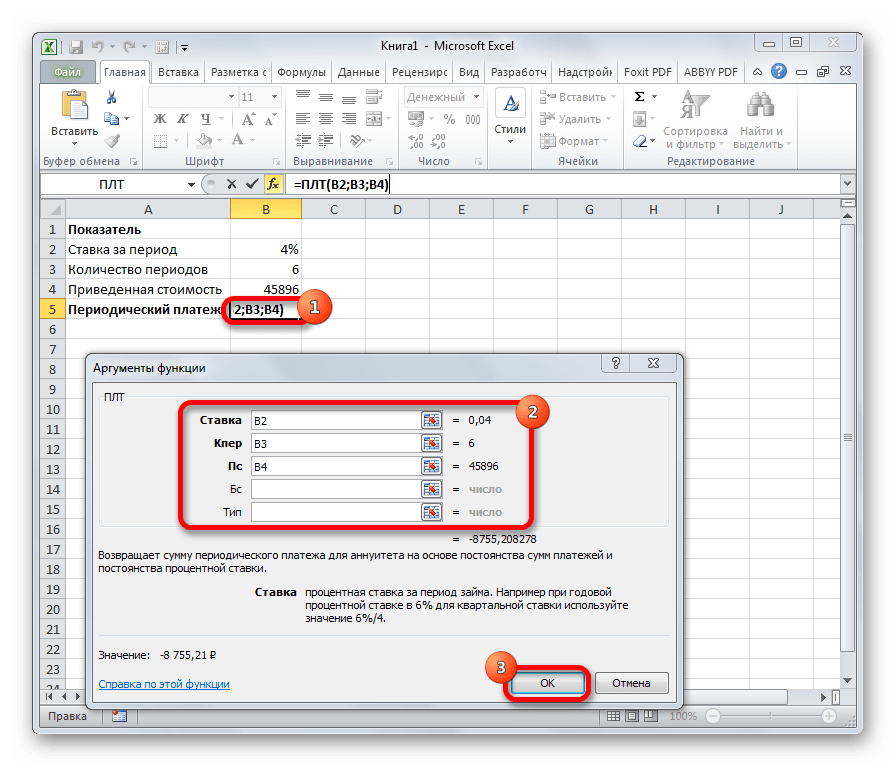
ПЛТ
С помощью этой функции рассчитывается сумма периодического платежа по займу исходя из постоянства платежей и процентной ставки.
Обязательные аргументы:
- Ставка – процентная ставка за период займа;
- Кпер – общее количество периодов выплат;
- Пс – приведенная (нынешняя) стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (баланс после последней выплаты). Если поле оставить незаполненным, по умолчанию будет принято значение, равное “0”.
- Тип – здесь указывается, как будет производиться выплата:
- “0” или не указано – в конце периода;
- “1” – в начале периода.
Синтаксис функции:
=ПЛТ(ставка;кпер;пс;[бс];[тип])
Результат в ячейке и выражение в строке формул:
ПОЛУЧЕНО
Применяется для нахождения суммы, которая будет получена к сроку погашения инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, инвестированная в ц.б.;
- Дисконт – ставка дисконтирования ц.б.;
- “Базис” – необязательный аргумент (см. функцию ДОХОД).
Синтаксис функции:
=ПОЛУЧЕНО(дата_согл;дата_вступл_в_силу;инвестиция;дисконт;[базис])
Результат в ячейке и выражение в строке формул:
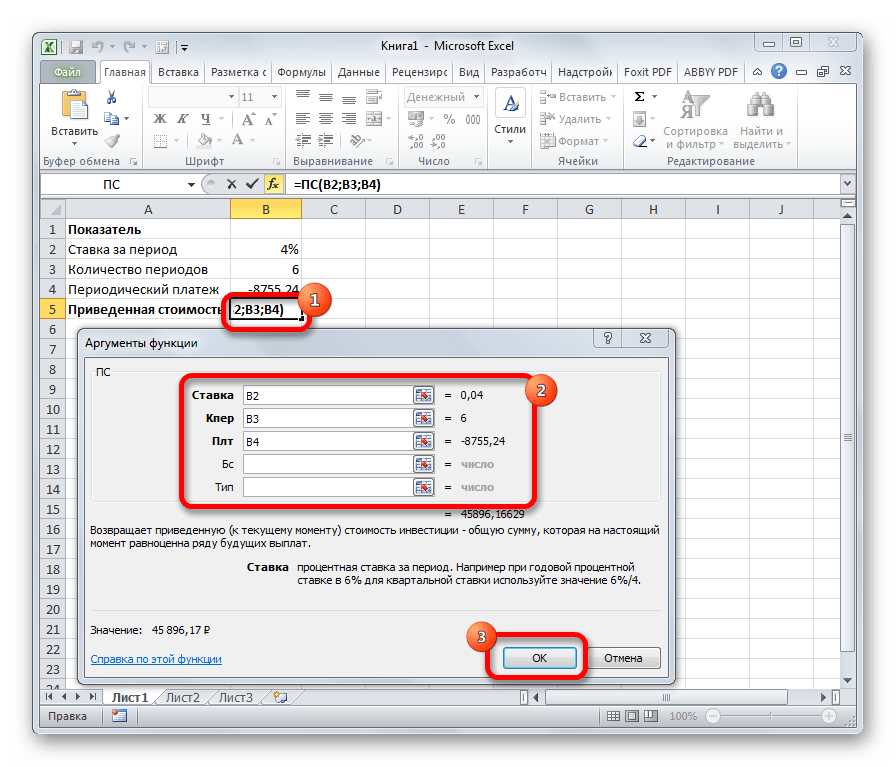
ПС
Оператор используется для нахождения приведенной (т.е. к настоящему моменту) стоимости инвестиции, которая соответствует ряду будущих выплат.
Обязательные аргументы:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы – такие же как и для функции “ПЛТ”:
- Бс – будущая стоимость;
- Тип.
Синтаксис функции:
=ПС(ставка;кпер;плт;[бс];[тип])
Результат в ячейке и выражение в строке формул:
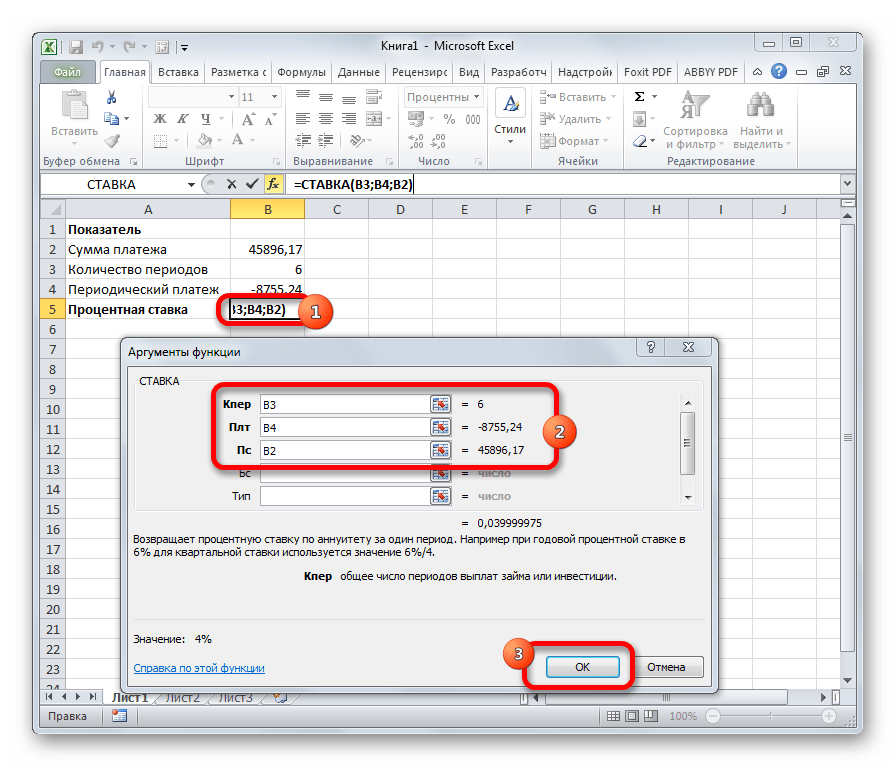
СТАВКА
Оператор поможет найти процентную ставку по аннуитету (финансовой ренте) за 1 период.
Обязательные аргументы:
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период;
- Пс – приведенная стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (см. функцию ПЛТ);
- Тип (см. функцию ПЛТ);
- Предположение – предполагаемая величина ставки. Если не указывать, будет принято значение по умолчанию – 10% (или 0,1).
Синтаксис функции:
=СТАВКА(кпер;;плт;пс;[бс];[тип];[предположение])
Результат в ячейке и выражение в строке формул:
ЦЕНА
Оператор позволяет найти цену за 100 рублей номинальной стоимости ц.б., по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Доход – годовой доход по ц.б.;
- Погашение – выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” как и для оператора ДОХОД является необязательным.
Синтаксис функции:
=ЦЕНА(дата_согл;дата_вступл_в_силу;ставка;доход;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
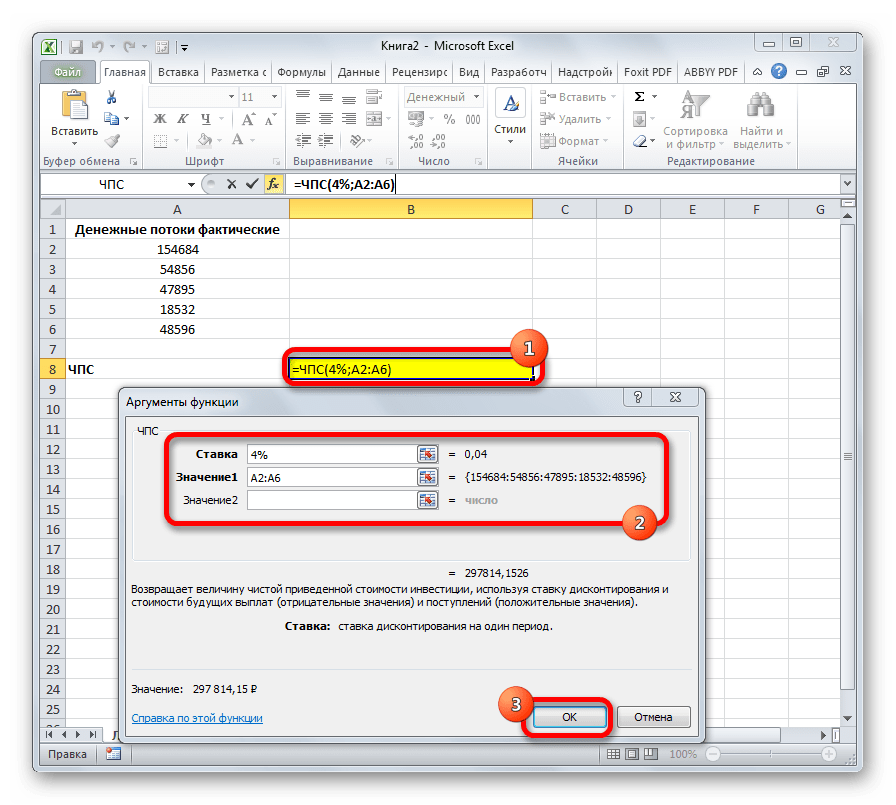
ЧПС
С помощью данной функции можно определить чистую приведенную стоимость инвестиции исходя из ставки дисконтирования, а также размера будущих поступлений и платежей.
Аргументы функции:
- Ставка – ставка дисконтирования за 1 период;
- Значение1 – здесь указываются выплаты (отрицательные значения) и поступления (положительные значения) в конце каждого периода. Поле может содержать до 254 значений.
- Если лимит аргумента “Значение 1” исчерпан, можно перейти к заполнению следующих – “Значение2”, “Значение3” и т.д.
Синтаксис функции:
=ЧПС(ставка;значение1;[значение2];...)
Результат в ячейке и выражение в строке формул:
Заключение
Категория “Финансовые” в программе Excel насчитывает свыше 50 различных функций, но многие из них специфичны и узконаправлены, из-за чего используются редко. Мы же рассмотрели 11 самых востребованных, по нашему мнению.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Мы подумали, что блок статей о формулах Excel просто не сможет обойтись без обозревания таких удобных и востребованных функций, как финансовые. Поэтому представляем вашему вниманию небольшой экскурс в мир «денежных» функций.
По «старой» традиции начнем с того, как найти финансовые формулы в программе. Сделать это очень просто: на главной панели найти кнопку «Формулы», нажать на нее и выбрать в появившемся списке название раздела «Финансовые».
Дальше выпадет перечень формул, которые вы можете использовать:

В данном разделе больше 50 функций, которые могут помочь специалистам упростить расчеты и сэкономить время на составление формул.
Разумеется, рассказать о всех возможностях в рамках этой статьи мы не успеем, но рассмотрим некоторые их них. Если вы хотите узнать о функционале математических функций в Excel, то скачивайте бесплатный гайд «Математические функции Excel».
1. Функция ДОХОД()
Очень популярная формула у финансистов. Она позволяет высчитать доход от ценных бумаг, по которым происходят выплаты процентов за определенный период.
Аргументов у функции много, поэтому медленно и по порядку со всеми разберемся!
Дата_согл – дата покупки ценных бумаг.
Дата_вступл_в_силу – дата, показывающая истечение срока действия бумаг.
Ставка – купонная ставка ценных бумаг за год.
Цена – цена бумаг на 100 руб. номинальной стоимости.
Погашение – выкупная стоимость ценных бумаг на 100 руб. номинальной стоимости.
Частота – цифра, показывающая количество выплат в год. Ежегодные выплаты – 1, полугодовые – 2, ежеквартальные – 4.
Помимо перечисленных обязательных аргументов есть один необязательный:
Базис – число, характеризующее способ вычисления дня. По умолчанию ставится 0.
Примечание. Обязательные аргументы выделены жирным шрифтом, а необязательные – обычным.

Замечание. Не рекомендуется вводить дату как текстовую запись. Лучше использовать функцию ДАТА во избежание ошибок и проблем с работой функции.
Например, число 21 сентября 2013 г. лучше записать так: ДАТА(2013,09,21).
2. Функция ПЛТ()
Функция ПЛТ() помогает высчитать сумму, которую нужно платить периодически для погашения ссуды с учетом процентных переплат за один расчетный период. Предполагается, что объем платежей и ставка не меняются.
У функции 3 обязательных аргумента и 2 – необязательных. Разберемся со всеми по порядку.
Ставка – процент, на который возрастает сумма платежа за один период.
Кпер – количество выплат или периодов.
Пс – общая сумма, которую нужно выплатить.
БС – показывает, сколько останется выплатить после последней выплаты. По умолчанию подразумевается 0 (то есть после последней выплаты стоимость ссуды составит 0 руб.).
Тип – аргумент, который принимает значения: 0 – когда платежи совершаются в конце периода, 1 – если в начале.
Рассмотрим пример.
Нужно рассчитать ежемесячный платеж по кредиту в размере 500 000 руб., взятого на 4 года под 6% годовых:

Так как в условиях задачи была дана процентная ставка за год, то, чтобы рассчитать ставку за один месяц, мы разделили 6% на 12 месяцев.
Так как выплаты производятся каждый месяц, то количество периодов рассчитываем так: 4 * 12 = 48:

Обратим внимание на то, то результат получился отрицательным. Знак «-» показывает, что эту сумму нужно отдать (вычесть из задолженности).
3. Формула ПС()
Формулу ПС() необходима для нахождения приведенной стоимости (то есть общей суммы, которую нужно выплатить на текущий момент).
Её можно назвать обратной к предыдущему оператору ПЛТ(). У неё точно такие же аргументы, только вместо «Пс» – «Плт» – сумма периодической выплаты.
Функция записывается следующим образом:
ПС(Ставка; Кпер; Плт; Бс; Тип)
Рассмотрим пример:


Мы получили сумму, которую в итоге заплатил бы человек, взявший кредит под 6% годовых на 4 года с ежемесячными выплатами в размере 12 000 руб.
4. Формула ОСПЛТ()
Данная формула в качестве результата выводит основную часть выплат по кредиту за заданный период (то есть ту часть платежа, которая уходит на оплату именно ссуды, а не процентов).
При этом учитывается, что параметры Ставка и размер выплат не меняются.
У функции ОСПЛТ() такие же аргументы, как и предыдущая формула: Ставка, Кпер, Пс, БС, Тип.
Еще добавляется Период (обязательный аргумент) – число от 1 до Кпер.
Посмотрим результат функции на предыдущем примере. Нужно рассчитать, сколько денег от первого платежа идет на погашение ссуды, не учитывая оплату процентов:


Мы видим, что основная часть первого платежа равна 9 242,51 руб – это примерно 79% от ежемесячной выплаты.
Если посмотреть результат формулы за 48-ой период, то получим уже 11 684,1 – это 99,5%. Заметная разница говорит о том, что процентные начисления в большей степени выплачиваются в первые расчетные периоды.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
5. Формулы ПРПЛТ(), ОБЩПЛАТ()
Функция очень похожа на ОСПЛТ() с небольшой оговоркой: она помогает высчитать размер выплат по процентам за выбранный период, предполагая неизменяемыми размер платежей и ставку.
У функция ПРПЛТ() точно такие же аргументы, как и у ОСПЛТ(), и выглядит в строке ввода формул так:
ПРПЛТ(Ставка; Период; Кпер; Пс; БС; Тип)
Применим формулу к нашему примеру:


Получили, что за первый период сумма выплат по процентам составит 2 500 руб., а в 48 месяце – всего 58,4 руб.
То есть данная формула еще раз подтверждает факт, что большая часть выплат по процентам осуществляется в начальные периоды платежей.
Замечание. Чтобы рассчитать, какая сумма из ваших платежей ушла на оплату процентов между любыми периодами, нужно использовать формулу:
ОБЩПЛАТ(Ставка;Кпер; Пс; Нач_пер;Кон_пер)
Ниже представлен пример применения функции ОБЩПЛАТ(), где в качестве Нач_пер берем первый период и Кон_пер – второй.
Выплаты происходят в конце месяца:

С помощью этих формул даже рядовой пользователь сможет рассчитать самые выгодные условия кредитования!
6. Формула СТАВКА()
Мы уже узнали, как считать объем ежемесячных выплат, процентные переплаты, число будущих выплат и так далее. Помимо этих действий в Excel можно вычислить ставку по кредиту, используя одноименную функцию СТАВКА().
В качестве аргументов выступают хорошо известные нам критерии: Кпер, Плт, Пс, Бс, Тип.
Два последних аргумента – необязательные:


7. Формула БС()
Теперь поговорим о функции БС() – высчитывает стоимость инвестиций после определенного количества периодов при условии неизменной ставки.
Формула записывается следующим образом:
БС(Ставка; Кпер; Плт; Пс; Тип).
Здесь аргумент Пс является необязательным.
Рассмотрим пример:
Пусть 12% – годовая ставка, количество платежей – 12, каждая выплата – 1 000 руб. (знаком минус покажем, что эти деньги нужно отдавать).
Посчитаем стоимость инвестиций при таких условиях:


Отметим, что «сумму выплат» мы специально сделали отрицательной, чтобы показать, что эти деньги вычитаются, и что сумма инвестиций не может быть отрицательной.
Заключение
Мы с вами проделали большую работу и познакомились с базовыми финансовыми формулами, которые могут применять не только специалисты в узкой области, но и простые пользователи Excel.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Investment Banking
Как работает сотрудник одной из компаний «большой тройки»?
Ты работаешь в компании «большой тройки (имеются в виду три крупнейших консалтинговых компании: McKinsey, Boston Consulting Group и Bain & Company), в которых мечтают работать тысячи подписчиков наших каналов и читателей vc.ru. Что это значит для тебя?
12 необходимых для работы с данными математических функций в Excel
Содержание статьи Microsoft Excel– одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп…
10 популярных финансовых функций в Microsoft Excel
Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.
Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
Запускается Мастер функций. Выполняем клик по полю «Категории».
Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:
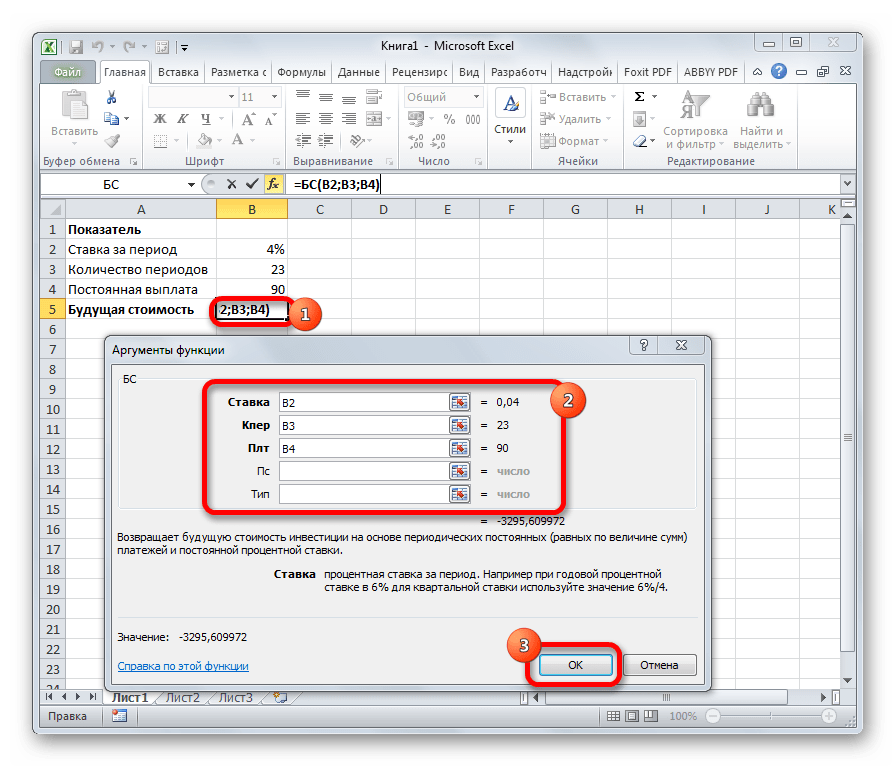
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
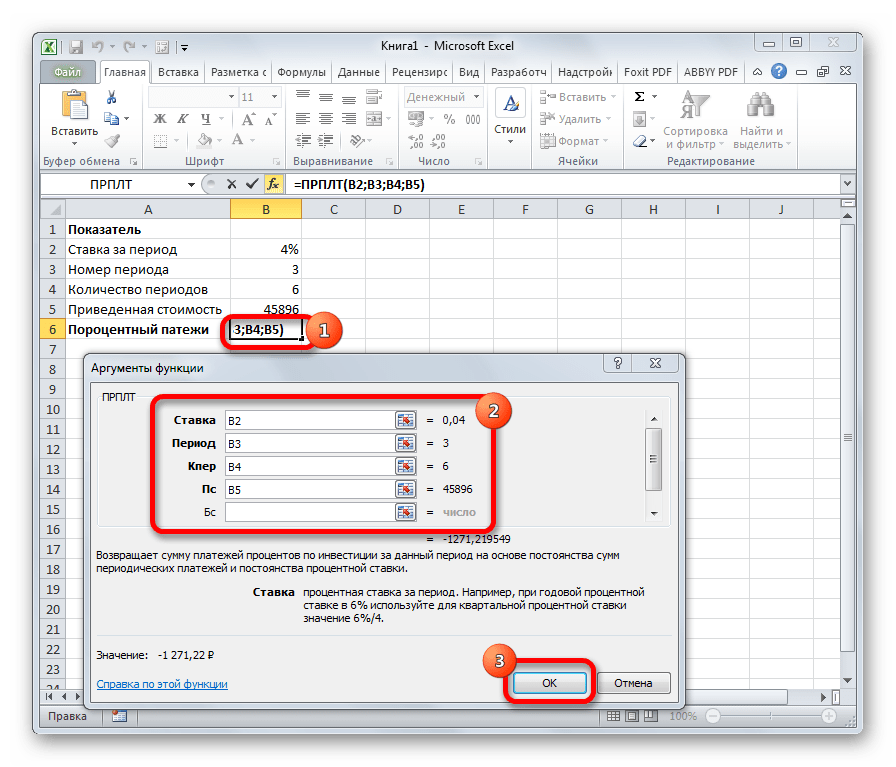
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Лабораторная работа № 4. Некоторые финансовые функции Excel
Работа с финансовыми функциями в MS Excel предполагает использование следующей методики:
1. Подготовить на рабочем листе значения основных аргументов функции
2. Перейти к ячейке в которую вводиться формула, использующая встроенную финансовую функцию
3. Вызвать мастер функций и в списке финансовых функций выбрать необходимую финансовую функцию.
4. Если аргумент финансовой функции является результатом расчета другой вложенной функции, используйте повторный вызов мастера функций для данного аргумента
5. После ввода всех аргументов нажмите кнопку ОК и MS Excel произведет расчет по формуле.
При задании аргументов для финансовых функций необходимо помнить следующее:
− Все аргументы, означающие расходы денежных средств (например, ежегодные платежи), представляются отрицательными числами, а аргументы, означающие поступления, (например, дивиденды) – положительными;
− Все даты, как аргументы функции имеют числовой формат
− Для логических аргументов используются константы ИСТИНА или ЛОЖЬ, либо функции категории Логические
− Каждый аргумент должен находиться на своем месте. Если аргументы пропускаются, то следует поставить соответствующее число разделительных знаков.
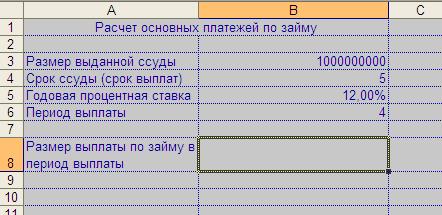
Задание №1.
Определить величину основного платежа за четвертый год, если выдана ссуда размером 1 000 000 000 сроком на 5 лет под 12% годовых.
Для основных платежей по займу, который погашается равными платежами в конце или в начале каждого расчетного периода используется функция ОСПЛТ, которая возвращает величину платежа в погашение основной суммы по инвестиции за данный период на основе постоянства периодических платежей и постоянства процентной ставки.
ОСПЛТ(Ставка, Период, Кпер, Пс Бс)
Ставка — процентная ставка за период.
Период — задает период, значение должно быть в интервале от 1 до «кпер».
Кпер — общее число периодов платежей по аннуитету. Например, если получена ссуда на 4 года под автомобиль и делаются ежемесячные платежи, то ссуда имеет 4*12 (или 48) периодов. В качестве значения аргумента кпер в формулу нужно ввести число 48.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.
Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0). Например, если предполагается накопить 50000 руб. для оплаты специального проекта в течение 18 лет, то 50 000 руб. это и есть будущая стоимость. Можно сделать предположение о сохранении заданной процентной ставки и определить, сколько нужно откладывать каждый месяц.
Ввод данных и расчеты производятся в соответствии с рисунком
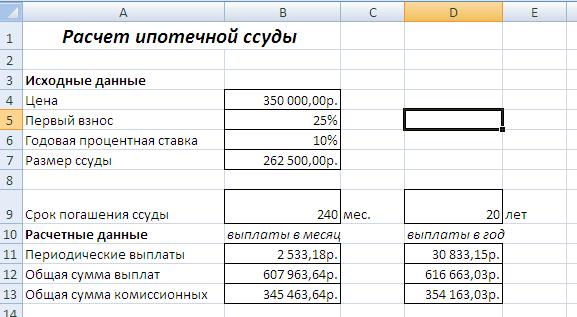
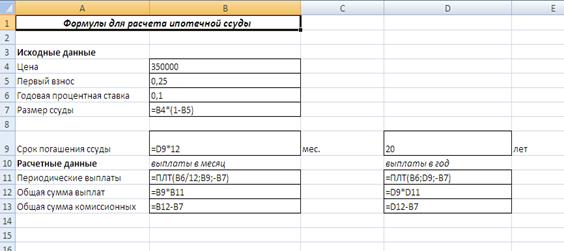
Задание №2.
Рассчитать 20-летнюю ипотечную ссуду со ставкой 10% годовых при начальном взносе 25% и ежемесячной (ежегодной) выплате.
Для вычисления величины постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянной процентной ставке используется функция ПЛТ, которая возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки.
ПЛТ(Ставка; Кпер; Бс; Пс; Тип).
Ставка — процентная ставка по ссуде.
Кпер — общее число выплат по ссуде.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.
Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нолю), т. е. для займа, например, значение бс равно 0.
Тип — число 0 (ноль) или 1, обозначающее, когда должна производиться выплата.
В нашем случае функция ПЛТ имеет вид:
ПЛТ(10%/12;20*12;-(350000*(1-25%))) – ежемесячные выплаты;
ПЛТ(10%;20;-(350000*(1-25%))) – ежегодные выплаты.
Решение задачи приведено на рисунках.
Задание №3.
Определить, какая сумма окажется на счете, если 52000 руб. положены на 20 лет под 11% годовых. Проценты начисляются ежемесячно.
Для расчета будущей стоимости единой суммы вклада используются сложные проценты, а расчетная формула основана на функции БС, которая возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постянной процентной ставки.
Ставка — процентная ставка за период.
Кпер — общее число периодов платежей по аннуитету.
Плт — выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент «пс» опущен, предполагается значение 0. В этом случае аргумент «плт» является обязательным.
Тип — число 0 или 1, обозначающее срок выплаты. Если аргумент «тип» опущен, предполагается значение 0.
Для нашей задачи функция БС примет вид:
Решение задачи приведено на рисунке, а формула для расчета ячейки В30:
Задание №4.
Ожидается, что ежегодные доходы от реализации проекта составят 54000000 руб. Рассчитать срок окупаемости проекта, если инвестиции к началу поступления доходов составят 140000000 руб., а норма дисконтирования 7,67.
Для определения срока платежа используется функция КПЕР, которая возвращает общее количество периодов выплаты для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки.
Ставка — процентная ставка за период.
Плт — выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно платеж состоит из основного платежа и платежа по процентам и не включает налогов и сборов.
Пс — приведенная к текущему моменту стоимость, т. е. общая сумма, которая на текущий момент равноценна ряду будущих платежей.
Бс — значение будущей стоимости, т. е. желаемого остатка средств после последней выплаты. Если аргумент «бс» опущен, предполагается, что он равен 0 (например, бс для займа равна 0).
Тип — число 0 или 1, обозначающее срок выплаты.
В нашей задаче функция выглядит следующим образом:
Задание №5.
Облигация номиналом 200000 руб. выпущена на 7 лет. Предусматривается следующий порядок начисления процентов: в первый год начисляется 11%,последующие три года – по 16%, в оставшиеся три года по 20%. Рассчитать будущую (наращенную) стоимость облигации по сложной процентной ставке.
Для расчета наращенной стоимости облигации по сложной процентной ставке используется функция БЗРАСПИС, которая возвращает будущую стоимость первоначальной основной суммы после применения ряда (плана) ставок сложных процентов. Функция БЗРАСПИС используется для вычисления будущей стоимости инвестиции с переменной процентной ставкой.
Первичное — стоимость инвестиции на текущий момент.
План — массив применяемых процентных ставок.
Решение приведено на рисунке
Формула для расчета примет следующий вид:
Задание №6.
Затраты по проекту составят 600 млн. руб. Ожидаемые доходы в течение последующих 5 лет составят, соответственно, 50, 100,300,200, 300 млн. руб. Оценить экономическую целесообразность проекта по скорости оборота инвестиций, если рыночная норма дохода 15%.
Для вычисления внутренней скорости оборота инвестиции (внутренней нормы доходности) используется функция ВСД, Возвращает внутреннюю ставку доходности для ряда потоков денежных средств представленных их численными значениями. В отличие от аннуитета, денежные суммы в пределах этих потоков могут колебаться. Однако обязательным условием является регулярность поступлений (например, ежемесячных или ежегодных). Внутренняя ставка доходности — это процентная ставка, принимаемая для инвестиции, состоящей из платежей (отрицательные величины) и доходов (положительные величины), которые имеют место в следующие друг за другом и одинаковые по продолжительности периоды.
Значения — массив или ссылка на ячейки, содержащие числа, для которых требуется подсчитать внутреннюю ставку доходности.
Значения должны содержать по крайней мере одно положительное и одно отрицательное значение.
В функции ВСД для интерпретации порядка денежных выплат или поступлений используется порядок значений. Убедитесь, что значения выплат и поступлений введены в нужном порядке.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, такие значения игнорируются.
Предположение — величина, предположительно близкая к результату ВСД.
В нашем случае функция для решения задачи использует только аргумент Значения, один из которых обязательно отрицателен. Если внутренняя скорость оборота инвестиций будет больше рыночной нормы доходности, то проект считается экономически целесообразным. В противном случае проект должен быть отвергнут.
Для принятия решения о экономической целесообразности проекта используйте логическую функцию ЕСЛИ:
Решение приведено на рисунке:
Задание №7.
Предполагается, что доходы по проекту в течение 5 лет составят 120000000 руб., 200000000., 300000000 руб., 250000000 руб., 320000000 руб. Определить первоначальные затраты на проект, чтобы обеспечить скорость оборота 12%.
Расчет внутренней скорости оборота инвестиций производится с помощью функции ВСД. Ввод исходных данных производиться в соответствии с рисунком:
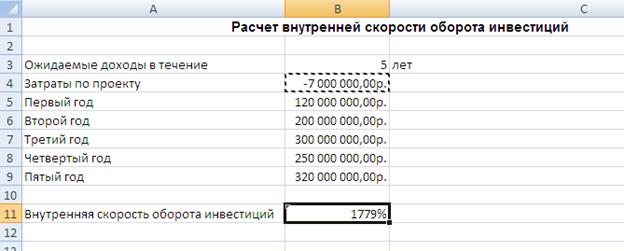
Далее, на вкладке Данные в группе Средства обработки данных выберите команду Анализ условия, а затем выберите в списке пункт Подбор параметра. Находим величину первоначальных затрат на проект, обеспечивающих скорость обороты инвестиций в 12%:
93.79.221.197 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Примеры функции БС в Excel с фиксированной процентной ставкой
Функция БС в Excel рассчитывает будущую стоимость инвестиции при условии, что процентная ставка является константой (не меняется с течением времени), и возвращает соответствующее значение. Функцию можно использовать в случаях, когда по окончанию срока выполняется единый платеж, а также при разбиении общей суммы на несколько фиксированных платежей.
Примеры использования финансовой функции БС в Excel
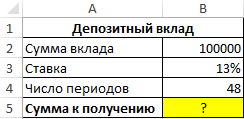
Пример 1. Вкладчик сделал депозит с ежемесячной капитализацией на сумму 100 000 рублей под 13% годовых сроком на 4 года. Какую сумму средств он сможет снять со своего депозитного счета по окончанию действия договора с банком?
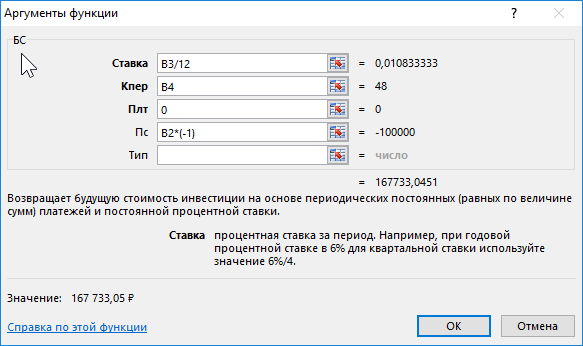
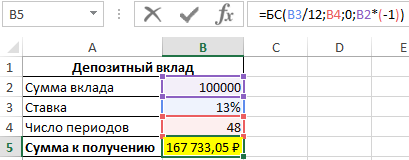
Формула для расчета:
- B3/12 – ставка за период (капитализация выполняется ежемесячно);
- B4 – число периодов капитализации вклада;
- 0 – сумма выплаты за период капитализации (неизвестная величина в рамках данной задачи, поэтому значение 0);
- B2*(-1) – начальная сумма вклада (инвестиция, которая должна являться отрицательным числом).
Спустя 4 года вкладчик получит 167 733 рубля.
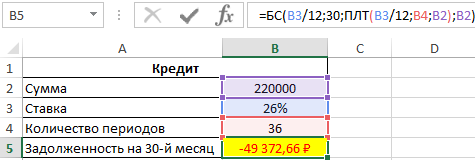
Расчет суммы долга по кредиту по состоянию на 30-й период погашения
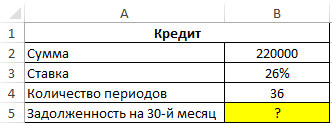
Пример 2. Заемщик взял кредит в банке под 26% годовых на сумму 220 000 рублей сроком на 3 года с ежемесячным фиксированным платежом. Какой будет сумма задолженности заемщика по окончанию 30-го периода выплат?
Формула для расчета:
- B3/12 – месячная процентная ставка;
- 30 – номер периода для расчета остатка задолженности;
- ПЛТ(B3/12;B4;B2) – функция, возвращающая сумму ежемесячного платежа;
- B2 – тело кредита.
Фактическая задолженность за кредит по окончанию 30-го месяца составит примерно 49372 рубля.
Сравнительный инвестиционный анализ условий депозита в банке
Пример 3. Вкладчик получил предложения по депозитному вкладу от двух банков с различными условиями:
- Ставка – 12% годовых, капитализация – ежемесячная.
- Ставка – 33% годовых, капитализация – ежеквартальная.
Определить, какое из предложений является более выгодным, если сумма вклада – 100000 рублей, срок действия договора – 2 года.
Формула для расчета:
БС(B3/12;B5;0;B6*(-1));»Первый банк»;»Второй банк»)’ class=’formula’>
С помощью функции ЕСЛИ определяем, в каком случае будущая стоимость окажется больше и возвращаем соответствующее значение. Полученный результат:
Выведем результаты расчетов функций БС и разницу сумм:
Как видно, несмотря на высокую годовую ставку, первый банк сделал более выгодное предложение, поскольку по условиям предложенного договора капитализация является ежемесячной. То есть, чем чаще происходит капитализация, тем быстрее увеличивается сумма вклада.
Особенности использования финансовой функции БС в Excel
Функция БС используется наряду с прочими финансовыми функциями (ПС, ПЛТ, КПЕР и другими) и имеет следующий синтаксис:
=БС( ставка;кпер;плт ;[пс];[тип])
- ставка – аргумент, принимающий числовое или процентное значение ставки за указанный период. Обязательный для заполнения. Если по условию используется годовая ставка, необходимо выполнить пересчет по следующей формуле: R=Rg/n, где Rg – годовая ставка, n – число периодов.
- кпер – числовое значение, характеризующее число периодов оплаты. Аргумент обязателен для заполнения. Если кредит был взят на период 3 года, выплаты по которому должны производиться каждый месяц, аргумент кпер должен принять значение 3*12=36 (12 – месяцы в году).
- плт – числовое значение, характеризующее фиксированную сумму выплаты за каждый период. Аргумент обязателен для заполнения. Если выплата за период является неизвестной величиной, аргумент плт может принимать значение 0, но при этом следующий аргумент задается явно.
- [пс] – приведенная стоимость на данный момент. Например, когда заемщик берет кредит у финансовой организации, тело кредита является приведенной на текущий момент стоимостью. По умолчанию аргумент [пс] принимает значение 0, а плт должен иметь отличное от нуля значение.
- [тип] – числовое значение, характеризующее тип выплат: в конце или начале периода. Принимает только два значения: 0 (если явно не указан) и 1.
- При указании аргумента ставка можно использовать процентный формат данных (например 17%) и числовой аналог (0,17).
- Расходные операции (текущая стоимость, выплата за период) должны быть указаны со знаком «-», то есть являться отрицательными числами.
- Функция БС использует в расчетах следующую формулу:
- Данная функция может быть использована для расчета баланса на конец периода и остаточной суммы задолженности по кредиту на текущий момент.
- Если процентная ставка меняется со временем, для расчетов следует использовать формулу БЗРАСПИС.
- Аргументы функции могут являться числовыми значениями или текстовыми данными, которые могут быть преобразованы в числа. Если один или несколько аргументов функции БС принимают текстовые строки, не содержащие числовые значения, будет возвращен код ошибки #ЗНАЧ!.
Примечание 2: функция БС также применяется для определения остатка задолженности по кредиту с аннуитетным графиком выплат, при этом дополнительные проценты и комиссии учтены не будут. Аннуитетный график предполагает фиксированную сумму погашения для каждого периода выплат (состоит из процентов и тела кредита).
Финансовые функции Excel
Финансовые функции — это совокупность необходимых процессов, циклов и подразделений, которые взятые вместе:
- · способствуют получению выручки на всех стадиях с помощью проведения финансового анализа;
- · управляют расходами с помощью анализа необходимости закупок, утверждения всех расходов (включая капиталовложения) в масштабе всего предприятия;
- · следят за имеющимися финансовыми средствами и обязательствами;
- · управляют поступлениями и расходованиями денежных средств, включая оплату налогов;
- · ведут поиск оптимальных источников и условий финансирования;
- · способствуют проведению бартерных операций;
- · осуществляет финансовый анализ проектов на всех этапах;
- · выполняют работу по составлению бюджета, планированию и прогнозированию как для предприятия, так и его подразделений;
- · учитывают и регистрируют каждую операцию, проводимую предприятием;
- · способствуют распределению заработанного между сотрудниками и акционерами.
Основная роль финансовой функции состоит в оптимизации использования предприятием своих ресурсов.
Перечень финансовых функций:
АМОРУВ — возвращает величину амортизации для каждого периода.
НАКОПДОХОД — данная функция возвращает накопленный процент по ценным бумагам с периодической выплатой процентов.
НАКОПДОХОДПОГАШ — возвращает накопленный процент по ценным бумагам, процент по которым выплачивается в срок погашения.
АМОРУМ — возвращает величину амортизации для каждого периода.
ДНЕЙКУПОНДО — возвращает количество дней от начала действия купона до даты соглашения.
ДНЕЙКУПОН — вычисляет число дней в периоде купона, содержащем дату расчета.
ДНЕЙКУПОНПОСЛЕ — возвращает число дней от даты расчета до срока следующего купона.
ДАТАКУПОНДО — возвращает число, представляющее дату следующего купона от даты соглашения.
ЧИСЛКУПОН — возвращает количество купонов, которые могут быть оплачены между датой соглашения и датой вступления в силу, округленное до ближайшего целого купона.
ОБЩПЛАТ — вычисляет кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат. exсel финансовый электронный таблица
ОБЩДОХОД — вычисляет кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами.
ФУО — определяет величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка.
ДДОБ — определяет значение амортизации актива за данный период, используя метод двойного уменьшения остатка или иной явно указанный метод.
СКИДКА — определяет ставку дисконтирования (норму скидки) для ценных бумаг.
РУБЛЬ.ДЕС — преобразует цену в рублях, представленную в виде дроби, в цену в рублях, выраженную десятичным числом. Функция РУБЛЬ.ДЕС используется для преобразования дробных значений денежных сумм, например стоимости ценных бумаг, в десятичное число.
РУБЛЬ.ДРОБЬ — преобразует цену в рублях, выраженную десятичным числом, в цену в рублях, представленную в виде дроби. Функция РУБЛЬ.ДРОБЬ используется для преобразования десятичных чисел, например стоимости ценных бумаг, в дробные цены.
ДЛИТ — находит ежегодную продолжительность действия ценных бумаг с периодическими выплатами по процентам.
ЭФФЕКТ — определяет эффективную (фактическую) годовую процентную ставку, если заданы номинальная годовая процентная ставка и количество периодов в году, за которые начисляются сложные проценты.
ЭФФЕКТ вычисляется следующим образом:
БС — вычисляет будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки.
БЗРАСПИС — вычисляет будущее значение начального вклада при изменяющихся сложных процентных ставках.
ИНОРМА — определяет ставку доходности полностью обеспеченной ценной бумаги.
ПРПЛТ — определяет сумму платежей процентов по инвестиции за данный период на основе постоянства сумм периодических платежей и постоянства процентной ставки.
ВСД — вычисляет внутреннюю ставку доходности (отдачи) для серии потоков денежных средств.
ПРОЦПЛАТ — вычисляет проценты, выплачиваемые за определенный инвестиционный период.
МДЛИТ — определяет модифицированную длительность Маколея для ценных бумаг с предполагаемой номинальной стоимостью 100 рублей.
МВСД — определяет внутреннюю ставку доходности, при которой положительные и отрицательные денежные потоки имеют разную ставку.
НОМИНАЛ — определяет номинальную годовую процентную ставку.
КПЕР — определяет общее количество периодов выплаты для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки.
ЧПС — определяет величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).
ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции. ЧПС связана также с функцией ВСД (внутренняя ставка доходности). ВСД — это ставка, для которой ЧПС равняется нулю: ЧПС(ВСД(. ); . ) = 0.
ЦЕНАПЕРВНЕРЕГ — находит цену за 100 рублей нарицательной стоимости ценных бумаг с нерегулярным первым периодом.
ДОХОДПЕРВНЕРЕГ — находит доход по ценным бумагам с нерегулярным (коротким или длинным) первым периодом.
ЦЕНАПОСЛНЕРЕГ — определяет цену за 100 рублей нарицательной стоимости ценных бумаг для нерегулярного (короткого или длинного) последнего периода купона.
ДОХОДПОСЛНЕРЕГ — определяет доход по ценным бумагам с нерегулярным последним периодом.
ПЛТ — Вычисляет величину выплаты по ссуде за один период.
ОСПЛТ — Вычисляет величину выплат на основной капитал для вклада в заданный период.
ЦЕНА — вычисляет цену за 100 рублей нарицательной стоимости ценных бумаг, по которым производится периодическая выплата процентов.
ЦЕНАПОГАШ — вычисляет цену за 100 рублей номинальной стоимости ценных бумаг, по которым процент выплачивается в срок погашения.
ЦЕНАСКИДКА — определяет цену за 100 рублей номинальной стоимости ценных бумаг, на которые сделана скидка.
ПС — определяет приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат. Например, в момент займа его сумма является приведенной (нынешней) стоимостью для заимодавца.
СТАВКА — определяет процентную ставку по аннуитету за один период
ПОЛУЧЕНО — вычисляет сумму, полученную в срок вступления в силу полностью обеспеченных ценных бумаг.
АПЛ — определяет величину амортизации актива за один период, рассчитанную линейным методом.
АСЧ — определяет величину амортизации актива за данный период, рассчитанную по сумме чисел лет срока полезного использования.
РАВНОКЧЕК — вычисляет эквивалентный облигации доход по казначейскому векселю.
ЦЕНАКЧЕК — вычисляет цену на 100 рублей номинальной стоимости для казначейского векселя.
ЦЕНАКЧЕК вычисляется следующим образом:
ДОХОДКЧЕК — вычисляет доходность по казначейскому векселю.
ПУО — определяет величину амортизации актива для любого выбранного периода, в том числе для частичных периодов, с использованием метода двойного уменьшения остатка или иного указанного метода.
ЧИСТВНДОХ — вычисляет внутреннюю ставку доходности запланированных непериодических денежных потоков.
ЧИСТНЗ — вычисляет чистую текущую стоимость инвестиции, вычисляемую на основе ряда поступлений наличных, которые не обязательно являются периодическими.
Функция ЧИСТНЗ вычисляется следующим образом:
ДОХОД — вычисляет доходность ценных бумаг, по которым производятся периодические выплаты процентов. Функция ДОХОД используется для вычисления доходности облигаций.
ДОХОДСКИДКА — вычисляет годовую доходность по ценным бумагам, на которые сделана скидка.
ДОХОДПОГАШ — определяет годовую доходность ценных бумаг, по которым проценты выплачиваются при наступлении срока погашения.
Финансовые функции (справка)
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
Возвращает накопленный процент по ценным бумагам с периодической выплатой процентов.
Возвращает накопленный процент по ценным бумагам, процент по которым выплачивается в срок погашения.
Возвращает величину амортизации для каждого учетного периода, используя коэффициент амортизации.
Возвращает величину амортизации для каждого учетного периода.
Возвращает количество дней от начала действия купона до даты соглашения.
Возвращает количество дней в периоде купона, который содержит дату расчета.
Возвращает количество дней от даты расчета до срока следующего купона.
Возвращает порядковый номер даты следующего купона после даты соглашения.
Возвращает количество купонов между датой соглашения и сроком вступления в силу.
Возвращает порядковый номер даты предыдущего купона до даты соглашения.
Возвращает кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат.
Возвращает кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами.
Возвращает величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка.
Возвращает величину амортизации актива за данный период, используя метод двойного уменьшения остатка или иной явно указанный метод.
Возвращает ставку дисконтирования для ценных бумаг.
Преобразует цену в рублях, выраженную в виде дроби, в цену в рублях, выраженную десятичным числом.
Преобразует цену в рублях, выраженную десятичным числом, в цену в рублях, выраженную в виде дроби.
Возвращает продолжительность Маколея для ценных бумаг, по которым выплачивается периодический процент.
Возвращает фактическую (эффективную) годовую процентную ставку.
Возвращает будущую стоимость инвестиции.
Возвращает будущее значение первоначальной основной суммы после применения ряда (плана) ставок сложных процентов.
Возвращает процентную ставку для полностью инвестированных ценных бумаг.
Возвращает проценты по вкладу за данный период.
Возвращает внутреннюю ставку доходности для ряда потоков денежных средств.
Вычисляет выплаты за указанный период инвестиции.
Возвращает модифицированную продолжительность Маколея для ценных бумаг с предполагаемой номинальной стоимостью 100 рублей.
Возвращает внутреннюю ставку доходности, при которой положительные и отрицательные денежные потоки имеют разные значения ставки.
Возвращает номинальную годовую процентную ставку.
Возвращает общее количество периодов выплаты для инвестиции.
Возвращает чистую приведенную стоимость инвестиции, основанной на серии периодических денежных потоков и ставке дисконтирования.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг с нерегулярным (коротким или длинным) первым периодом купона.
Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) первым периодом купона.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг с нерегулярным (коротким или длинным) последним периодом купона.
Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) последним периодом купона.
ПДЛИТ
Возвращает количество периодов, необходимых инвестиции для достижения заданного значения.
Возвращает регулярный платеж годичной ренты.
Возвращает платеж с основного вложенного капитала за данный период.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым выплачивается периодический процент.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, на которые сделана скидка.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым процент выплачивается в срок погашения.
Возвращает приведенную (к текущему моменту) стоимость инвестиции.
Возвращает процентную ставку по аннуитету за один период.
Возвращает сумму, полученную к сроку погашения полностью инвестированных ценных бумаг.
ЭКВ.СТАВКА
Возвращает эквивалентную процентную ставку для роста инвестиции.
Возвращает величину амортизации актива за один период, рассчитанную линейным методом.
Возвращает величину амортизации актива за данный период, рассчитанную методом суммы годовых чисел.
Возвращает эквивалентный облигации доход по казначейскому векселю.
Возвращает цену за 100 рублей номинальной стоимости для казначейского векселя.
Возвращает доходность по казначейскому векселю.
Возвращает величину амортизации актива для указанного или частичного периода при использовании метода сокращающегося баланса.
Возвращает внутреннюю ставку доходности для графика денежных потоков, не обязательно носящих периодический характер.
Возвращает чистую приведенную стоимость для денежных потоков, не обязательно носящих периодический характер.
Возвращает доход по ценным бумагам, по которым производятся периодические выплаты процентов.
Возвращает годовой доход по ценным бумагам, на которые сделана скидка (например, по казначейским векселям).
Возвращает годовую доходность ценных бумаг, по которым процент выплачивается в срок погашения.
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Рассчитаем в MS EXCEL сколько времени потребуется для погашения кредита в случае равных ежемесячных платежей (по аннуитетной схеме). Процентная ставка и величина платежа — известны, начисление процентов за пользование кредитом – ежемесячное. Также в статье разберем случай накопления вклада.
Аннуитетная схема
предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат. В статье
Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)
показано как рассчитать величину регулярной суммы для погашения кредита или ссуды. Расчет количества периодов, необходимых для погашения кредита произведем сначала с помощью финансовой функции MS EXCEL КПЕР(), затем приведем расчет с помощью эквивалентной формулы (см.
файл примера
).
Функция КПЕР(ставка; плт; пс; [бс]; [тип])
позволяет вычислить количество периодов, через которое
текущая сумма вклада
(пс) станет равной заданной сумме (бс) при известной процентной ставке за период (ставка) и известной величине пополнения вклада (плт). Бс (
будущая стоимость
) может быть =0 или опущена. Тип – это число 0 или 1, обозначающее, когда должна производиться выплата (и соответственно начисление процентов): 0 – в конце периода, 1 – в начале. Также функцию
КПЕР()
можно использовать для определения количества периодов, необходимых для погашения долга по ссуде.
Примечание
. Обзор всех функций аннуитета
найдете здесь
.
Эквивалентная формула для расчета количества периодов:
Если ставка равна 0, то: Кпер = (Пс + Бс) /ПЛТ
Задача1
Сколько времени потребуется для погашения кредита 1 млн. рублей в случае равных ежемесячных взносов. Начисление процентов за пользование кредитом – ежемесячное, годовая процентная ставка = 10%. Ежемесячный платеж 50 000р.
Решение
1
Так как погашение кредита производится ежемесячно (12 раз в году), то ставка за период составит 10%/12. Формула
=КПЕР(10%/12;-50000;1000000;0;0)
вернет количество периодов, после которых кредит будет возвращен в полном размере. Знак минус перед 2-м аргументом функции (величина ежемесячного платежа) показывает, что разнонаправленные денежные потоки должны иметь разные знаки (+1000000 – это деньги, которые
банк
дал
нам, -50000 – это деньги, которые мы
возвращаем банку
). Конечно, можно и наоборот: деньги, которые банк дал нам учитывать со знаком минус, а те деньги, которые мы отдаем банку учитывать со знаком +. Формула вернет 21,97, т.е. потребуется 22 месяца, чтобы полностью вернуть 1 млн. руб., возвращая ежемесячно по 50 тыс. руб. (последний платеж будет несколько меньше, о том, как его рассчитать – читайте ниже).
Расчет последнего платежа
При расчете количества периодов погашения ссуды может получиться нецелое количество периодов. В этом случае, последний платеж будет несколько меньше, чем предыдущие. Найдем величину этого платежа. Учтем, что в последнем периоде нам будет необходимо погасить оставшуюся задолженность и заплатить % банку (% от суммы оставшейся задолженности). Найдем сначала количество полных периодов
=ЦЕЛОЕ(КПЕР(10%/12;-50000;1000000;0;0))
и поместим результат в ячейку G21. Чтобы вычислить сколько было погашено основной суммы долга за все целые периоды можно использовать формулу
=СУММПРОИЗВ(ОСПЛТ(10%/12;СТРОКА(ДВССЫЛ(«1:»&G21)); КПЕР(10%/12;-50000;1000000;0;0);1000000;0;0))
(Альтернатива –
используйте функцию
ОБЩДОХОД()
)
Примечание
. Сумму платежа, идущую на оплату основной суммы долга в один определенный период, можно вычислить с помощью функции
ОСПЛТ()
. Складывая результат
ОСПЛТ()
для всех целых периодов с помощью функции
СУММПРОИЗВ()
получим сколько было погашено основной суммы долга.
Далее вычтем из суммы кредита выплаченную сумму за все целые периоды (с учетом знаков). Затем вычислим проценты за последний период = СУММПРОИЗВ(…)*10%/12 Сложим остаток основной суммы долга и проценты за последний (неполный) период (см.
файл примера
). В результате получим -48487,18р. (это несколько меньше регулярного платежа -50000р.)
Если функция КПЕР() возвращает ошибку
В некоторых случаях функция
КПЕР()
возвращает значение ошибки #ЧИСЛО! Разобраться, почему это происходит, можно, вспомнив альтернативную формулу (см. выше). Понятно, что логарифм числа может быть вычислен только для положительного числа, а это означает, что величина платежа ПЛТ должна быть больше величины ежемесячных процентов начисляемых на остаток тела кредита, т.е. больше ПС*СТАВКА (это справедливо только при БС=0 и ТИП=0). Оно и понятно, нам нужно ежемесячно не только оплачивать проценты, но и возвращать основную сумму долга.
Количество периодов, через которое будет погашено 80% кредита
Сколько времени потребуется, чтобы погасить кредит не полностью, а например, на 80%? Записав формулу
=КПЕР(10%/12;-50000;1000000;-1000000*(1-80%);0)
получим, что для этого потребуется 17,88 периодов (месяцев). Величину БС = -1000000*(1-80%) мы нашли пользуясь тождеством для аннуитета (справедливо, если Тип=0): СУММ(ОСПЛТ(за все периоды)) + ПС + БС = 0 Из условий задачи ПС = 1000000 (начальная сумма кредита), выплаченная сумма кредита, т.е. СУММ(ОСПЛТ(за все периоды)) равна -1000000*80%. Решая уравнение, получим, что БС = -1000000*(1-80%). БС в данном случае – это непогашенная сумма кредита (конечно, чтобы найти, что БС=20% от суммы кредита, не требует использования тождества. Но важен знак БС).
Задача2
Рассчитать, через сколько времени вклад размером 200 000 руб. достигнет 1 000 000 руб., если годовая процентная ставка по вкладу 10% годовых, начисление процентов производится ежеквартально, также ежеквартально вклад пополняется на 10 000 руб.
Решение2
Так как взносы и начисление процентов происходит ежеквартально (4 раза в год), то ставка за период составит 10%/4. Формула
=КПЕР(10%/4;-10000;-200000;1000000;0)
вернет количество периодов, после которых вклад достигнет 1 млн. руб., т.е. 34,31 квартал (см.
файл примера, лист Задача2
).
Как посчитать в программе Microsoft Excel
Программа Microsoft Excel это не только большая таблица, но еще и суперсовременный калькулятор с множеством функций и возможностей. В этом уроке мы научимся пользоваться им по назначению.
Все вычисления в Excel называются формулы , и все они начинаются со знака равно (=).
Например, я хочу посчитать сумму 3+2. Если я нажму на любую ячейку и внутри напечатаю 3+2, а затем нажму кнопку Enter на клавиатуре, то ничего не посчитается – в ячейке будет написано 3+2. А вот если я напечатаю =3+2 и нажму Enter, то в всё посчитается и будет показан результат.
После того, как ввели формулу, нужно нажать кнопку Enter на клавиатуре
А теперь о знаках, при помощи которых мы будем считать. Также они называются арифметические операторы:
/ деление. Есть еще палочка с наклоном в другую сторону. Так вот, она нам не подходит.
^ возведение в степень. Например, 3^2 читать как три в квадрате (во второй степени).
% процент. Если мы ставим этот знак после какого-либо числа, то оно делится на 100. Например, 5% получится 0,05.
При помощи этого знака можно высчитывать проценты. Если нам нужно вычислить пять процентов из двадцати, то формула будет выглядеть следующим образом: =20*5%
Все эти знаки есть на клавиатуре либо вверху (над буквами, вместе с цифрами), либо справа (в отдельном блоке кнопок).
Для печати знаков вверху клавиатуры нужно нажать и держать кнопку с надписью Shift и вместе с ней нажимать на кнопку с нужным знаком.
А теперь попробуем посчитать. Допустим, нам нужно сложить число 122596 с числом 14830. Для этого щелкните левой кнопкой мышки по любой ячейке. Как я уже говорил, все вычисления в Excel начинаются со знака «=». Значит, в ячейке нужно напечатать =122596+14830
И для того, чтобы получить ответ, нужно нажать кнопку Enter на клавиатуре. После чего в ячейке будет уже не формула, а результат.
А теперь обратите внимание вот на такое верхнее поле в программе Эксель:
Это «Строка формул». Она нам нужна для того, чтобы проверять и изменять наши формулы.
Для примера нажмите на ячейку, в которой мы только что посчитали сумму.
И посмотрите на строку формул. В ней будет показано, как именно мы получили данное значение.
То есть, в строке формул мы видим не само число, а формулу, при помощи которой это число получилось.
Попробуйте в какой-нибудь другой ячейке напечатать цифру 5 и нажать Enter на клавиатуре. Затем щелкните по этой ячейке и посмотрите в строку формул.
Так как это число мы просто напечатали, а не вычислили при помощи формулы, то только оно и будет в строке формул.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Для этого в ячейке В6 пишем формулу себестоимости B2 B4, а в ячейке В7 считаем валовую прибыль B5-B6, аналогично считаем для второго клиента. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
После ввода этой формулы необходимо нажать не Enter , как обычно, а Ctrl + Shift + Enter — тогда Excel воспримет ее как формулу массива и сам добавит фигурные скобки. Вводить скобки с клавиатуры не надо. Легко сообразить, что этот способ (как и предыдущий) легко масштабируется на три, четыре и т.д. условий без каких-либо ограничений.
Получаем, что продажи уменьшились (знак минус) на 9996 рублей. Теперь необходимо посчитать сколько это в процентах. Наш начальный показатель это 2014 год. Именно с этим годом мы сравниваем на сколько изменились продажи, поэтому 2014 год — это 100%
Как сложить листы в Excel?
Вариант 1. Ручной ввод.
Начнем с одной стороны с медленного варианта, но с другой стороны с более понятного и наглядного способа.
Для примера возьмем простую задачу и сложим данные ячейки A1 с трех листов: Лист1, Лист2 и Лист3. Для этого поочередно в формулу записываем ссылки на ячейку с разных листов и знаки сложения «+»:
Это совсем простой вариант. Еще один вариант записи можно аналогично реализовать с помощью функции СУММ:
В реализуемых нами вариантах в общем и целом все хорошо, за исключением большой ручной работы при прощелкивании всех нужных для суммирования ячеек.
Как это часто бывает если нужно посчитать сумму для двух или трех листов, то вышеописанный способ отлично подойдет. Но если усложнить задачу и представить подобный пример не для 3, а, например, для 30 листов, то процесс уже несколько затянется.
Поэтому перейдем к чуть более сложному на первый взгляд варианту, но гораздо более быстрому с точки зрения трудовых и временных затрат.
Вариант 2. Полуавтоматический ввод.
Повторно воспользуемся функцией СУММ, но в этот раз запишем ссылку на листы через двоеточие:
В этом случае общее количество суммируемых листов для нас уже не так важно, главное знать только начальный и конечный.
Поэтому запись для сложения 10 или 20 листов будет примерно такой же — ИмяПервогоЛиста:ИмяПоследнегоЛиста!Диапазон.
При добавлении еще одной размерности в виде листов мы получаем так называемую трехмерную ссылку. К примеру, диапазон Лист1:Лист3!A1:A10 содержит все ячейки от Лист1!A1:A10 до Лист3!A1:A10.
Таким образом в нашем примере суммируются все ячейки A1 от Лист1 до Лист3. Но при применении такого способа суммирования есть некоторые тонкости, которые желательно нужно помнить, чтобы случайно не допустить ошибку, давайте подробнее про них поговорим.
Как посчитать в Excel (эксель)
Как вы, наверное, уже могли догадаться, вместо ручного ввода адресов ячеек и их диапазонов можно просто выделять необходимые элементы с помощью мышки. Главное, не забывать при этом удерживать клавишу «CTRL», когда вы переходите от выделения одного элемента к другому.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Как мы уже говорили ранее, при применении трехмерных ссылок нужен только первый и последний лист, промежуточные листы между ними в записи никак не участвуют. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Прежде всего, это позволит избежать возможных ошибок в процессе выделения диапазона или отдельных ячеек, которые нужно просуммировать. Кроме того, даже если совершить ошибку на каком-либо этапе, то исправить ее так же легко, как и простую опечатку в набранном тексте, поэтому не придется выполнять всю работу с самого начала, и можно обойтись лишь незначительной корректировкой данных.
Как посчитать сумму всего столбца в excel
- Добавление/копирование листа. Если добавить новый лист или скопировать уже существующий и вставить его между первым и последним (используемых в формуле), то он автоматически будет участвовать в расчете.
Т.е. сама формула не поменяется, а значение вполне может измениться, если на новом листе в тех же ячейках содержатся данные; - Удаление листа. Аналогичный случай примеру выше. При удалении листа формула не изменится, а расчет поменяется в зависимости от удаленных данных (если удалить начальный или конечный листы, то формула изменится, промежуточный — формула останется неизменной);
- Перемещение листа. При перемещении листа в другое место книги формула не изменится, но поменяется набор листов между ними (либо добавятся новые, либо удалятся текущие).
А сейчас (барабанная дробь) испытайте чувство гордости за себя. Потому что теперь вы можете рассчитать это в Excel. Для этого вызовите функцию Кпер, заполните данные из нашего примера (10% годовых, 5 лет, выплата процентов в конце года) и добавьте в поле БС ожидаемую сумму вклада в размере 20 000 руб. (10 000 руб. х 2). Вуаля!