ЛАБОРАТОРНАЯ РАБОТА
«Статистические функции MS Excel 2013. Построение рядов данных»
Цели работы:
-
научиться применять статистические функции для обработки данных; закрепить навыки форматирования таблицы;
-
воспитывать в себе аккуратность и внимательность при выполнении работ с электронными таблицами;
-
развивать логическое мышление, необходимое для работы с большими массивами информации
Задание:
-
изучите п.1 «Учебный материал»;
-
выполните задания, приведенные в п.2;
-
ответьте на контрольные вопросы (п.3).
-
Учебный материал
-
-
Функции категории Статистические
-
Статистические функции позволяют выполнять статистический анализ диапазонов данных: нахождение минимального и максимального значения среди исходных чисел, выполнение элементарного подсчёта числовых значений, подсчёт числовых значений в соответствии с определённым условием и т.д. Статистические функции входят в категорию Статистические Мастера функций (рис.1).
Рис.1. Окно Мастера функций с выбранное категорией функций Статистические
Рассмотрим ряд статистических функций, встречающихся в простейших вычислениях.
-
Нахождение минимального значения (среди числовых значений) в списке аргументов с помощью функции МИН. Формат записи функции:
МИН (число1; число2;…)
Количество допустимых аргументов, среди которых находится минимальное значение, равно 255.
Пример. Найти наименьшее значение цены на книгу «Гарри Поттер и дары смерти» среди магазинов города. Пусть в ячейках B3:B7 внесены значения цены (рис.2). Установите курсор в ячейку В9, вызовите Мастер функций и из категории Статистические выберите функцию МИН. Укажите исходные значения и нажмите OK.
-
Нахождение максимального значения (среди числовых значений) в списке аргументов с помощью функции МАКС. Формат записи функции:
МАКС (число1; число2;…)
Количество допустимых аргументов, среди которых находится максимальное значение, равно 255.
Пример. Найти максимальное значение цены на книгу «Гарри Поттер и дары смерти» среди магазинов города. Пусть в ячейках B3:B7 внесены значения цены (рис.3). Установите курсор в ячейку В9, вызовите Мастер функций и из категории Статистические выберите функцию МАКС. Укажите исходные значения и нажмите OK.
Рис. 2. Нахождение минимального значения среди аргументов
Рис. 3. Нахождение максимального значения среди аргументов
-
Нахождение среднего арифметического значения с помощью функции СРЗНАЧ. Формат записи функции:
СРЗНАЧ(число1; число2;…)
Количество допустимых аргументов, среди которых находится среднее значение, равно 255.
Пример. Найти среднее значение цены на книгу «Гарри Поттер и дары смерти» в магазинах города. Пусть в ячейках B3:B7 внесены значения цены (рис. 4). Установите курсор в ячейку В9, вызовите Мастер функций и из категории Статистические выберите функцию СРЗНАЧ. Укажите исходные данные и нажмите OK.
Рис. 4. Нахождение среднего значения среди аргументов
-
Подсчет количества значений в списке аргументов осуществляется с помощью функции СЧЕТ. Формат записи функции:
СЧЕТ(число1; число2;…)
Количество допустимых аргументов, среди которых находится среднее значение, равно 255.
Пример. Найти количество студентов, получающих стипендию. Пусть в ячейках B3:B7 внесены сведения о стипендии студентов группы (рис.5). Установите курсор в ячейку В9, вызовите Мастер функций и из категории Статистические выберите функцию СЧЕТ. Укажите исходные данные и нажмите OK. В ячейке В9 будет найдено искомое значение.
Рис. 5. Нахождение количества числовых значений среди аргументов
-
Нахождение количества значений, удовлетворяющих заданному условию, выполняется с помощью функции СЧЕТЕСЛИ. Формат записи функции:
СЧЕТЕСЛИ(диапазон; критерий),
где диапазон – диапазон, в котором подсчитывается количество непустых ячеек;
критерий – проверяемое условие в заданном интервале (в форме числа, выражения, текста).
Примеры записи функции:
-
=СЧЕТЕСЛИ(А1:А9; 85) – подсчитывает, сколько раз число 85 встречается в интервале А1:А9;
-
=СЧЕТЕСЛИ(А1:А9; “>85”) – подсчитывает, сколько раз в интервале А1:А9 встречаются числа, большие 85;
-
=СЧЕТЕСЛИ(А1:А9; “высший”) – подсчитывает, сколько раз в интервале А1:А9 встречается слово «высший»;
-
=СЧЕТЕСЛИ(А1:А9; “в*”) – подсчитывает, сколько раз в интервале А1:А9 встречаются слова, начинающиеся на букву «в».
Обратите внимание на то, что если в качестве критерия указываются не числовые значения, а текст или символы, то они заключаются в кавычки.
-
Определение ранга (номера позиции) числа в списке других чисел (т.е. порядкового номера относительно других чисел списка) выполняется с помощью функции РАНГ. РВ. Формат записи функции:
РАНГ.РВ(число; ссылка; порядок),
где число – число, для которого определяется ранг (порядковый номер);
ссылка – массив или ссылка на список чисел, с которым сравнивается число;
порядок – число (0 либо отличное от 0), определяющее способ ранжирования (в порядке убывания или возрастания).
Пример. Используем функцию РАНГ.РВ, которая присвоит номер места каждой марке автомобиля в зависимости от определенного параметра. Пусть в ячейки В3:В8 занесены значения расхода топлива на 100 км пробега (рис.6). Наилучшим будем считать автомобиль, имеющий минимальный расход. В ячейку С3 занесем формулу
=РАНГ.РВ(B3;$B$3:$B$8;1)
и скопируем ее в оставшиеся ячейки С4:С8. Аргументы в этой формуле означают следующее: В3 – адрес ячейки, которой присваиваем в ячейке С3 номер искомого места; $B$3:$B$8 – блок ячеек, в который занесены все известные значения расхода топлива и среди которых мы выясняем ранг. Здесь используем абсолютную адресацию ($) для того, чтобы при копировании формулы из ячейки С3 адрес участвующих в вычислении ячеек В3:В8 не изменялся. Последний аргумент функции 1 указывает на то, что сравнение результатов происходит в порядке возрастания, т.е. наилучшим результатом считаем наименьший. Если поставим 0, то лучшим результатом будет наибольший, как, например, в случае с объемом двигателя (рис.7).
Рис. 22. Нахождение ранга числа в порядке возрастания значений
Рис.7. Нахождение ранга числа в порядке убывания значений
-
-
Построение рядов данных
-
Для ввода в смежные ячейки повторяющейся с определенной закономерностью информации (текст, даты, числа), т.е. построения рядов данных, существует несколько способов.
-
Использование маркера заполнения и перетаскивания ячеек.
Пусть необходимо построить ряд чисел от 1 до 5,5 с шагом 0,5, т.е. получить арифметическую прогрессию. Для этого:
-
в окне открытого листа введите данные в первую ячейку диапазона (рис.8);
-
наведите курсор мыши на правый нижний угол ячейки (там располагается маркер заполнения) и, когда курсор станет тонким черным крестом, при нажатой левой кнопке мыши протащите маркер заполнения вниз по столбцу;
-
в конце нужного диапазона отпустите левую кнопку мыши. Оцените результат.
В данном случае в новые ячейки заносятся соответствующие значения, а также форматы исходной ячейки.
Рис.8. Использование маркера заполнения для получения арифметической прогрессии
Если после ввода первых двух значений потянуть за маркер заполнения при нажатой клавише <Ctrl>, то будет реализован принцип автозаполнения, а не получение арифметической прогрессии, и во всех ячейках получится чередование чисел 1 и 1,5 (рис.9).
Рис.9. Использование маркера заполнения для автозаполнения ячеек
-
Использование команды Прогрессия.
-
Занесите в ячейку А1 число 1;
-
выберите команду Прогрессия…, находящуюся в группе Редактирование вкладки Главная (рис.10), которая позволяет заполнить ряд соответствующим образом;
Рис.10. Команда Прогрессия для заполнения рядов данных
-
в появившемся диалоговом окне установите параметры, как показано на рис.11.
Рис.11. Диалоговое окно для построения рядов данных
-
нажмите ОК. Оцените результат.
3) Использование формул.
-
Занесите в ячейку А1 число 1;
-
по условию задачи, каждое следующее число отличается от предыдущего на 0,5, поэтому для построения ряда чисел воспользуемся формулой: =А1+0,5, которую внесем в ячейку А2 и с помощью маркера скопируем по столбцу вниз (рис.12).
Рис.12. Построение ряда чисел с использованием формулы
4) Использование параметров автозаполнения.
-
Введите данные в первую ячейку диапазона;
-
наведите курсор мыши на правый нижний угол ячейки и, когда курсор станет тонким черным крестом, при нажатой правой кнопке мыши протащите маркер заполнения, верх или вниз по столбцу либо вправо или влево по строке;
-
в конце нужного диапазона отпустите правую кнопку мыши;
-
в контекстном меню выберите соответствующий пункт:
-
«Копировать ячейки» – будут копироваться и значения, и форматы исходной ячейки;
-
«Заполнить только форматы» – будет копироваться только формат исходной ячейки;
-
«Заполнить только значения» – будет копироваться только значение исходной ячейки.
-
Задание к лабораторной работе
Для выполнения лабораторной работы введите исходные данные в соответствии с выданным номером задания. Отформатируйте таблицу по приведенным ниже параметрам.
-
-
Заголовок таблицы Применение статистических функций сделайте жирным шрифтом, размер шрифта – 12 пт. Для центрирования заголовка таблицы необходимо выделить ячейки A1:G2 и нажать на кнопку Объединить и поместить в центре
, расположенную в группе Выравнивание вкладки Главная. Затем, не убирая курсора с объединенных ячеек, в контекстном меню выберите команду Формат ячеек и в открывшемся диалоговом окне выберите: вкладка Выравнивание→область Выравнивание→по горизонтали – по центру; по вертикали — по центру;
-
Заголовки столбцов таблицы (№ п/п; ФИО студента; Рост (см); Вес (кг)… и т.д. в зависимости от варианта задания) – по центру, полужирным шрифтом, размер шрифта – 10 пт). Возможность отображать текст внутри ячейки таблицы в несколько строк добивается следующим образом:
-
-
-
выделить ячейки A3:G3, формат которых требуется изменить;
-
в контекстном меню выберите команду Формат ячеек и в открывшемся диалоговом окне выберите: вкладка Выравнивание→область Выравнивание→по горизонтали – по центру; по вертикали — по центру;
-
в области Отображение установить флажок переносить по словам.
-
-
-
Ячейки А4:А13 заполните значениями от 1 до 10 одним из способов, описанных в п.1.2 «Построение рядов данных».
-
К тексту ячеек B15:B22 примените начертание курсив и сделайте перенос по словам.
-
Выделите ячейки A1:G13 таблицы. С помощью кнопки Границы→Все границы
группы Шрифт измените границы таблицы.
-
Символ, соответствующий степени 2 числа, можно вставить с помощью команды Символ группы Символы вкладки Вставка. Другой способ указания символа степени: написать степень числа, выделить его, нажать кнопку группы Шрифт и в появившемся диалоговом окне во вкладке Шрифт в области Видоизменение установить флажок надстрочный.
-
Задание 1
Задание. Для данной группы студентов определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.13. На вашем рабочем листе цвет ячеек изменять не обязательно):
-
минимальное значение роста, веса и бега на 100 м;
-
максимальное значение роста, веса и бега на 100 м;
-
среднее значение роста, веса и бега на 100 м;
-
количество студентов, имеющих рост < 180 см;
-
количество студентов, имеющих рост > 185 см;
-
количество студентов, имеющих вес < 80 кг;
-
количество студентов, имеющих вес > 85 кг;
-
количество студентов, участвовавших в соревновании;
-
ранг студентов (порядковый номер относительно друг друга) в беге на 100 м.
Рис.13. Исходные данные для выполнения лабораторной работы
Задание 2
Задание. Для данной группы продуктов определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.14. На вашем рабочем листе цвет ячеек изменять не обязательно):
-
минимальное значение цен в магазинах;
-
максимальное значение цен в магазинах;
-
среднее значение цен в магазинах;
-
количество продуктов, название которых начинается на букву «м»;
-
количество продуктов, название которых начинается на букву «к»;
-
количество продуктов дороже 25 руб.;
-
количество продуктов дешевле 25 руб.;
-
количество продуктов, ассортимент которых обновлялся;
-
ранг продуктов магазина «Рублик» (порядковый номер относительно стоимости друг друга).
Рис.14. Исходные данные для выполнения лабораторной работы
Задание 3
Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.15. На вашем рабочем листе цвет ячеек изменять не обязательно):
-
минимальное значение цен в парикмахерских;
-
максимальное значение цен в парикмахерских;
-
среднее значение цен на услуги парикмахерских;
-
количество услуг со стоимостью < 200 руб.;
-
количество услуг со стоимостью ≥200 руб.;
-
среднее значение стоимости стрижек в парикмахерской «Люкс»;
-
средняя стоимость других услуг (отличных от стрижек) парикмахерской «Люкс»;
-
количество скидок;
-
ранг стоимости услуг парикмахерской «Аванта» (порядковый номер стоимости относительно друг друга).
Рис.15. Исходные данные для выполнения лабораторной работы
Задание 4
Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.16. На вашем рабочем листе цвет ячеек изменять не обязательно):
-
минимальное значение цен на услуги компаний сотовой связи;
-
максимальное значение цен на услуги компаний сотовой связи;
-
среднее значение цен на услуги компаний сотовой связи;
-
количество услуг со стоимостью < 2 руб.;
-
количество услуг со стоимостью ≥2 руб.;
-
среднее значение стоимости звонков оператора «МТС»;
-
средняя стоимость других услуг (отличных от звонков) оператора «МТС»;
-
количество скидок именинникам;
-
ранг стоимости услуг оператора «МТС» (порядковый номер стоимости относительно друг друга).
Рис.16. Исходные данные для выполнения лабораторной работы
Задание 5
Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.17. На вашем рабочем листе цвет ячеек изменять не обязательно):
-
минимальное значение населения, площади территории страны, количества городов-миллионеров;
-
максимальное значение населения, площади территории страны, количества городов-миллионеров;
-
среднее значение населения, площади территории страны, количества городов-миллионеров;
-
количество стран с населением < 100 млн. чел.;
-
количество стран с населением ≥ 100 млн. чел.;
-
количество стран площадью территории >5 млн. км2;
-
количество стран площадью территории <1 млн. км2;
-
количество стран, берега которых омываются океанами;
-
ранг стран по площади территории (порядковый номер страны относительно значений площадей).
Рис.17. Исходные данные для выполнения лабораторной работы
Задание 6
Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.18. На вашем рабочем листе цвет ячеек изменять не обязательно):
-
минимальное значение населения, площади территории страны, количества городов-миллионеров;
-
максимальное значение населения, площади территории страны, количества городов-миллионеров;
-
среднее значение населения, площади территории страны, количества городов-миллионеров;
-
количество стран с населением < 100 млн. чел.;
-
количество стран с населением ≥ 100 млн. чел.;
-
количество стран площадью территории >10 млн. км2;
-
количество стран площадью территории <1 млн. км2;
-
количество стран с океанами;
-
ранг стран по населению (порядковый номер страны относительно значений количества человек).
Рис.18. Исходные данные для выполнения лабораторной работы
Задание 7
Задание. Для данной группы услуг определить (искомые значения разместить в соответствующих выделенных ячейках, как показано на рис.19. На вашем рабочем листе цвет ячеек изменять не обязательно):
-
минимальное значение длины реки, площади бассейна реки и количества крупных городов, где эти реки протекают;
-
максимальное значение длины реки, площади бассейна реки и количества крупных городов;
-
среднее значение длины рек, площади бассейна и количества крупных городов;
-
количество рек длиной < 5000 км;
-
количество рек длиной ≥ 5000 км;
-
количество рек с площадью бассейна >1000 тыс. км²;
-
количество рек с площадью бассейна ≤ 1000 тыс. км²;
-
количество стран с указанными реками;
-
ранг рек по длине (порядковый номер реки относительно значений длины).
Рис.19. Исходные данные для выполнения лабораторной работы
-
Контрольные вопросы
-
Назовите известные вам функции из категорий Статистические и их аргументы.
-
Сколько аргументов могут иметь функции МИН и МАКС?
-
Каковы отличия функций СЧЕТ и СЧЕТЕСЛИ. Назовите аргументы этих функций.
-
С какой целью в функции РАНГ.РВ используется абсолютная адресация ячеек?
-
Самостоятельно выясните назначение и работу функций НАИМЕНЬШИЙ, НАИБОЛЬШИЙ, ТЕНДЕНЦИЯ категории Статистические, используя справку по каждой из них. Приведите примеры.
Задание.
Для данной группы студентов определить
(искомые значения разместить в
соответствующих выделенных ячейках,
как показано на рис. 29. На вашем рабочем
листе цвет ячеек изменять не нужно):
-
минимальное
значение роста, веса и бега на 100 м; -
максимальное
значение роста, веса и бега на 100 м; -
среднее значение
роста, веса и бега на 100 м; -
количество
студентов, имеющих рост < 180 см; -
количество
студентов, имеющих рост > 185 см; -
количество
студентов, имеющих вес < 80 кг; -
количество
студентов, имеющих вес > 85 кг; -
количество
студентов, участвовавших в соревновании; -
ранг студентов
(порядковый номер относительно друг
друга) в беге на 100 м.
Рис. 29. Исходные данные для выполнения
лабораторной работы
Вариант 2
Задание.
Для данной группы продуктов определить
(искомые значения разместить в
соответствующих выделенных ячейках,
как показано на рис.30. На вашем рабочем
листе цвет ячеек изменять не нужно):
-
минимальное
значение цен в магазинах; -
максимальное
значение цен в магазинах; -
среднее значение
цен в магазинах; -
количество
продуктов, название которых начинается
на букву «м»; -
количество
продуктов, название которых начинается
на букву «к»; -
количество
продуктов дороже 25 руб.; -
количество
продуктов дешевле 25 руб.; -
количество
продуктов, ассортимент которых
обновлялся; -
ранг продуктов
магазина «Рублик» (порядковый номер
относительно стоимости друг друга).
Рис. 30. Исходные данные для выполнения
лабораторной работы
Вариант 3
Задание.
Для данной группы услуг определить
(искомые значения разместить в
соответствующих выделенных ячейках,
как показано на рис.31. На вашем рабочем
листе цвет ячеек изменять не нужно):
-
минимальное
значение цен в парикмахерских; -
максимальное
значение цен в парикмахерских; -
среднее значение
цен на услуги парикмахерских; -
количество услуг
со стоимостью < 200 руб.; -
количество услуг
со стоимостью ≥200 руб.; -
среднее значение
стоимости стрижек в парикмахерской
«Люкс»; -
средняя стоимость
других услуг (отличных от стрижек)
парикмахерской «Люкс»; -
количество скидок;
-
ранг стоимости
услуг парикмахерской «Аванта» (порядковый
номер стоимости относительно друг
друга).
Рис. 31. Исходные данные для выполнения
лабораторной работы
Вариант 4
Задание.
Для данной группы услуг определить
(искомые значения разместить в
соответствующих выделенных ячейках,
как показано на рис.32. На вашем рабочем
листе цвет ячеек изменять не нужно):
-
минимальное
значение цен на услуги компаний сотовой
связи; -
максимальное
значение цен на услуги компаний сотовой
связи; -
среднее значение
цен на услуги компаний сотовой связи; -
количество услуг
со стоимостью < 2 руб.; -
количество услуг
со стоимостью ≥2 руб.; -
среднее значение
стоимости звонков оператора «МТС»; -
средняя стоимость
других услуг (отличных от звонков)
оператора «МТС»; -
количество скидок
именинникам; -
ранг стоимости
услуг оператора «МТС» (порядковый номер
стоимости относительно друг друга).
Рис. 32. Исходные данные для выполнения
лабораторной работы
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В медицинском кабинете измеряли рост и вес учеников с 5 по 11 классы. Результаты занесли в электронную таблицу. Ниже приведены первые пять строк таблицы:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | Фамилия | Имя | Класс | Рост | Вес |
| 2 | Абашкина | Елена | 9 | 168 | 50 |
| 3 | Аксенова | Мария | 9 | 183 | 71 |
| 4 | Александров | Константин | 7 | 170 | 68 |
| 5 | Алексеева | Анастасия | 8 | 162 | 58 |
| 6 | Алиев | Ариф | 7 | 171 | 57 |
Каждая строка таблицы содержит запись об одном ученике. В столбце А записана фамилия, в столбце В — имя; в столбце С — класс; в столбце D — рост, в столбце Е — вес учеников. Всего в электронную таблицу были занесены данные по 211 ученикам в алфавитном порядке.
Выполните задание.
Откройте файл с данной электронной таблицей (расположение файла Вам сообщат организаторы экзамена). На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
1. Каков вес самого тяжёлого ученика 10 класса? Ответ на этот вопрос запишите в ячейку Н2 таблицы.
2. Какой процент учеников 9 класса имеет рост больше 180? Ответ на этот вопрос с точностью не менее 2 знаков после запятой запишите в ячейку НЗ таблицы.
task19.xls
Высчитать «Численность студентов»
30.03.2020, 21:51. Показов 4643. Ответов 1

НУЖНО ДОДЕЛАТЬ НАЧИНАЯ С 11 пункта
За годы обучения студентов происходят изменения их численности. Для этого существуют различные причины. К ним относятся отчисление студентов, восстановление ранее отчисленных студентов, перевод студентов из одного вуза в другой, предоставление студентам отпуска или повторного обучения. В последнем случае студент продолжает обучение вместе со студентами следующего года приема. Процент, который составляет каждая из перечисленных категорий студентов вуза от их общего количества, от года к году практически не изменяется. В этом задании приведены вполне реальные данные. Выполните предлагаемое ниже исследование. Обратите внимание на полученные результаты и сделайте для себя необходимые выводы.
Порядок выполнения работы:
1. Запустите Excel и щелкните на кнопке Сохранить.
2. С помощь кнопки Создать папку в появившемся окне Сохранение документа создайте свою рабочую папку и сохраните в ней файл Книга1 под именем Контингент.xls.
3. Создайте электронную таблицу, соответствующую рис. 2. В таблице применяйте шрифт Times New Roman размером 12. Напомним порядок выполнения некоторых операций, которые Вам при этом придется применять:
Объединение ячеек. Для этого необходимо выделить подлежащие объединению ячейки, выполнить команду меню Формат, Ячейки, установить на вкладке Выравнивание флажок в поле Объединение ячеек и щелкнуть на кнопке ОК.
Форматирование текста. Чтобы текст в одной ячейке (или нескольких ячейках) мог занимать не одну, а несколько строк, необходимо выделить ячейку (или соответственно несколько ячеек), выполнить команду Формат, Ячейки, включить на вкладке Выравнивание флажок в поле Переносить по словам и щелкнуть на кнопке ОК.
Изображение границ ячеек, строк, столбцов, таблицы. Сначала следует выделить совокупность ячеек, для которой Вы хотите изобразить границу. Границы могут быть изображены с помощью кнопки Границы панели инструментов, которую можно увидеть, щелкнув на кнопке панели инструментов Другие кнопки. Можно изобразить границы с помощью команды меню Формат, Ячейки. В появившемся окне Формат ячеек открыть вкладку Граница. Эта вкладка позволяет выбрать тип линии границы, а также положение границы относительно выделенной совокупности ячеек.
Рис.2. Исходные данные
4. Введите в ячейку D4 очевидную формулу =C4–C6–C8–C10+D12+D13 для вычисления численности студентов в начале второго семестра.
5. Для вычисления численности студентов в начале каждого из
3 – 12 семестров обеспечьте появление аналогичных формул в ячейках E4:N4. Для этого следует копировать формулу из ячейки D4 в ячейки E4:N4.
6. Форматируйте ячейки C5:N5, установив один разряд дробной части.
7. Приступите к вводу в ячейки C5:N5 необходимых формул для вычисления величины в процентах, которую составляет количество студентов в начале каждого из 1 – 12 семестров по сравнению с количеством студентов в начале первого семестра. Сначала эту очевидную формулу =C4/$C4*100 надо ввести в ячейку С5. Ссылка на ячейку С4 в знаменателе введенной формулы должна быть абсолютной, иначе возникнет ошибка при копировании формулы в другие ячейки пятой строки. Затем содержимое ячейки С5 следует копировать в ячейки D5:N5.
8. Введите в ячейки C7:N7 формулу для вычисления величины в процентах, которую составляет количество отчисленных студентов в 1-12 семестрах, по отношению к численности студентов на начало соответствующего семестра.
9. Введите в ячейки J9 и N9 формулы для вычисления величины в процентах, которую составляет количество отчисленных студентов в связи с успешным окончанием обучения в 8 и 12 семестрах, по отношению к численности студентов на начало соответствующего семестра.
10. Введите в ячейки C11:N11 формулы для вычисления величины в процентах, которую составляет количество студентов, оставленных в течение семестра на второй год в 1 – 12 семестрах по отношению к численности студентов на начало семестра.
11. Вычислите долю в процентах, которую составляет суммарное число студентов, успешно окончивших ВУЗ за 12 семестров обучения, по отношению к числу студентов, начавших обучение на первом курсе. Для этого в ячейку F14 введите текст «Суммарный выпуск составляет» и выровняйте его по правому краю ячейки. Затем в ячейку H14 введите текст
«% от начальной численности студентов» и, если необходимо, выровняйте его по левому краю. Установите в ячейке G14 один разряд дробной части. Теперь Вам осталось в ячейку G14 записать нужную формулу.
12. Вычислите долю в процентах, которую составляет суммарное число студентов, за весь срок обучения отчисленных из вуза или оставленных на второй год, по отношению к числу студентов, начавших обучение на первом курсе. Для этого в ячейку F15 введите текст «Суммарный отсев составляет» и выровняйте его по правому краю ячейки. Затем в ячейку H15 введите текст «% от начальной численности студентов» и, если необходимо, выровняйте его по левому краю. Установите в ячейке G15 один разряд дробной части. Теперь Вам осталось записать очевидную формулу в ячейку G15. Если до сих пор Вы не ошибались, то Ваша таблица должна соответствовать рис. 3.
13. Постройте с помощью мастера диаграмм объемный вариант обычной гистограммы для отображения выраженного в процентах количества студентов на начало каждого семестра (строка 5). До обращения к мастеру диаграмм следует выделить подлежащий отображению числовой ряд (в данном случае это ячейки C5:N5). Результат, который Вы должны получить, сравните с рис. 4.
Рис.3. Результаты вычислений
Рис.4. Изменение численности студентов за время обучения
14. Постройте с помощью мастера диаграмм графики отсева студентов в процессе обучения (отчисление, оставление на второй год). До обращения к мастеру диаграмм выделите подлежащий отображению числовой ряд (в данном случае – это ячейки C7:N7 и C11:N11). Выделить участки таблицы, не являющиеся смежными, возможно с помощью мыши при нажатой клавише Ctrl. Результат, который Вы должны получить, сравните с рис. 5.
Рис.5. График отсева студентов
1
Задание 19 ОГЭ информатика по теме «Обработка большого массива данных (электронные таблицы)»
Часть теоретического материала этой темы рассмотрена в задании 5.
Ниже рассмотрены наиболее часто встречающиеся функции и их смысл. Наводите курсор на пример для просмотра ответа.
| русский | англ. | действие | синтаксис |
|---|---|---|---|
| СУММ | SUM | Суммирует все числа в интервале ячеек | СУММ(число1;число2) |
| Пример: | |||
| =СУММ(3; 2) =СУММ(A2:A4) |
|||
| СЧЁТ | COUNT | Подсчитывает количество всех непустых значений указанных ячеек | СЧЁТ(значение1, [значение2],…) |
| Пример: | |||
| =СЧЁТ(A5:A8) | |||
| СРЗНАЧ | AVERAGE | Возвращает среднее значение всех непустых значений указанных ячеек | СРЕДНЕЕ(число1, [число2],…) |
| Пример: | |||
| =СРЗНАЧ(A2:A6) | |||
| МАКС | MAX | Возвращает наибольшее значение из набора значений | МАКС(число1;число2; …) |
| Пример: | |||
| =МАКС(A2:A6) | |||
| МИН | MIN | Возвращает наименьшее значение из набора значений | МИН(число1;число2; …) |
| Пример: | |||
| =МИН(A2:A6) | |||
| ЕСЛИ | IF | Проверка условия. Функция с тремя аргументами: первый аргумент — логическое выражение; если значение первого аргумента — истина, то результатом выполнения функции является второй аргумент. Если ложно — третий аргумент. | ЕСЛИ(лог_выражение; значение_если_истина; значение_если_ложь) |
| Пример: | |||
| =ЕСЛИ(A2>B2;»Превышение»;»ОК») | |||
| СЧЁТЕСЛИ | COUNTIF | Количество непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. | СЧЁТЕСЛИ(диапазон, критерий) |
| Пример: | |||
| =СЧЁТЕСЛИ(A2:A5;»яблоки») | |||
| СУММЕСЛИ | SUMIF | Сумма непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. | СУММЕСЛИ (диапазон, критерий, [диапазон_суммирования]) |
| Пример: | |||
| =СУММЕСЛИ(B2:B25;»>5″) |
ОГЭ по информатике 19 задание разбор, практическая часть
Разбор задания 19.1:
В электронную таблицу занесли данные о тестировании учеников. Ниже приведены первые пять строк таблицы:
В столбце А записан округ, в котором учится ученик;
в столбце В — фамилия;
в столбце С — любимый предмет;
в столбце D — тестовый балл.
Всего в электронную таблицу были занесены данные по 1000 ученикам.
Выполните задание:
Откройте файл с данной электронной таблицей (расположение файла Вам сообщат организаторы экзамена). На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Сколько учеников в Северо-Восточном округе (СВ) выбрали в качестве любимого предмета математику? Ответ на этот вопрос запишите в ячейку Н2 таблицы.
- Каков средний тестовый балл у учеников Южного округа (Ю)? Ответ на этот вопрос запишите в ячейку Н3 таблицы с точностью не менее двух знаков после запятой.
Ответ: 17
Возможны и другие варианты решения.
Разбор задания 19.2 (демоверсия ОГЭ 2018):
В электронную таблицу занесли данные о калорийности продуктов. Ниже приведены первые пять строк таблицы.
В столбце A записан продукт;
в столбце B – содержание в нём жиров;
в столбце C – содержание белков;
в столбце D – содержание углеводов и
в столбце Е – калорийность этого продукта.
Всего в электронную таблицу были занесены данные по 1000 продуктам.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Сколько продуктов в таблице содержат меньше 50 г углеводов и меньше 50 г белков? Запишите число, обозначающее количество этих продуктов, в ячейку H2 таблицы.
- Какова средняя калорийность продуктов с содержанием жиров менее 1 г? Запишите значение в ячейку H3 таблицы с точностью не менее двух знаков после запятой.
Ответ: 864
Возможны и другие варианты решения.
Разбор задания 19.4:
В электронную таблицу занесли информацию о грузоперевозках, совершённых некоторым автопредприятием с 1 по 9 октября.
alt=»решение ОГЭ с таблицей excel» width=»500″ height=»87″ />Каждая строка таблицы содержит запись об одной перевозке. В столбце A записана дата перевозки (от «1 октября» до «9 октября»); в столбце B — название населённого пункта отправления перевозки; в столбце C — название населённого пункта назначения перевозки; в столбце D — расстояние, на которое была осуществлена перевозка (в километрах); в столбце E — расход бензина на всю перевозку (в литрах); в столбце F — масса перевезённого груза (в килограммах).
Всего в электронную таблицу были занесены данные по 370 перевозкам в хронологическом порядке.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- На какое суммарное расстояние были произведены перевозки с 1 по 3 октября? Ответ на этот вопрос запишите в ячейку H2 таблицы.
- Какова средняя масса груза при автоперевозках, осуществлённых из города Липки? Ответ на этот вопрос запишите в ячейку H3 таблицы с точностью не менее одного знака после запятой.
- Задание 1 первый способ:
Ответ: 28468
Задание 1 второй способ:
Ответ: 28468
Возможны и другие варианты решения, например, сортировка строк по значению столбца B с дальнейшим выбором необходимых диапазонов для функций.
Разбор задания 19.5:
В электронную таблицу занесли результаты тестирования учащихся по географии и информатике. Вот первые строки получившейся таблицы:
В столбце А указаны фамилия и имя учащегося; в столбце В — номер школы учащегося; в столбцах С, D — баллы, полученные, соответственно, по географии и информатике. По каждому предмету можно было набрать от 0 до 100 баллов.
Всего в электронную таблицу были занесены данные по 272 учащимся. Порядок записей в таблице произвольный.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Сколько учащихся школы № 2 набрали по информатике больше баллов, чем по географии? Ответ на этот вопрос запишите в ячейку F2 таблицы.
- Сколько процентов от общего числа участников составили ученики, получившие по географии больше 50 баллов? Ответ с точностью до одного знака после запятой запишите в ячейку F3 таблицы.
Возможны и другие варианты решения.
Разбор задания 19.6:
В электронную таблицу занесли результаты тестирования учащихся по физике и информатике. Вот первые строки получившейся таблицы:
В столбце А указаны фамилия и имя учащегося; в столбце В — округ учащегося; в столбцах С, D — баллы, полученные, соответственно, по физике и информатике. По каждому предмету можно было набрать от 0 до 100 баллов.
Всего в электронную таблицу были занесены данные по 266 учащимся. Порядок записей в таблице произвольный.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Чему равна средняя сумма баллов по двум предметам среди учащихся школ округа «Южный»? Ответ на этот вопрос запишите в ячейку F2 таблицы.
- Сколько процентов от общего числа участников составили ученики школ округа «Западный»? Ответ с точностью до одного знака после запятой запишите в ячейку F3 таблицы.
Ответ: 117,15;
Ответ: 15,4.
Каждая строка таблицы содержит запись об одном поэте. В столбце А записана фамилия, в столбце В — имя, в столбце С — отчество, в столбце D — год рождения, в столбце Е — год смерти.
Всего в электронную таблицу были занесены данные по 150 поэтам Серебряного века в алфавитном порядке.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Определите количество поэтов, родившихся в 1889 году. Ответ на этот вопрос запишите в ячейку H2 таблицы.
- Определите в процентах, сколько поэтов, умерших позже 1940 года, носили имя Сергей. Ответ с точностью не менее 2 знаков после запятой запишите в ячейку НЗ таблицы.
Ответ: 8.
Ответ: 6,02.
Каждая строка таблицы содержит запись об одном ученике. В столбце А записана фамилия, в столбце В — имя; в столбце С — класс; в столбце D — рост, в столбце Е — вес учеников.
Всего в электронную таблицу были занесены данные по 211 ученикам в алфавитном порядке.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Каков рост самого высокого ученика 10 класса? Ответ на этот вопрос запишите в ячейку H2 таблицы.
- Какой процент учеников 8 класса имеет вес больше 65? Ответ с точностью не менее 2 знаков после запятой запишите в ячейку НЗ таблицы.
Ответ: 1) 199; 2) 53,85.
В столбце А указана фамилия; в столбце В — имя; в столбце С — пол; в столбце D — год рождения; в столбце Е — результаты в беге на 1000 метров; в столбце F — результаты в беге на 30 метров; в столбце G — результаты по прыжкам в длину с места.
Всего в электронную таблицу были занесены данные по 1000 учащимся.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Сколько процентов участников пробежало дистанцию в 1000 м меньше, чем за 5 минут? Ответ запишите в ячейку L1 таблицы.
- Найдите разницу в см с точностью до десятых между средним результатом у мальчиков и средним результатом у девочек в прыжках в длину. Ответ на этот вопрос запишите в ячейку L2 таблицы.
Ответ: 1) 59,4; 2)6,4.
Результаты сдачи выпускных экзаменов по алгебре, русскому языку, физике и информатике учащимися 9 класса некоторого города были занесены в электронную таблицу. На рисунке приведены первые строки получившейся таблицы:
Всего в электронную таблицу были занесены результаты 1000 учащихся.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
Как посчитать количество людей в экселе?
Работа со списками людей в программе эксель довольно часто встречается. Часто нужно просто посчитать количество людей, когда список маленький, сделать это можно вручную, когда их много, то нужно использовать специальные инструменты программы эксель.
Рассмотрим подробно все возможные варианты, как посчитать количество людей.
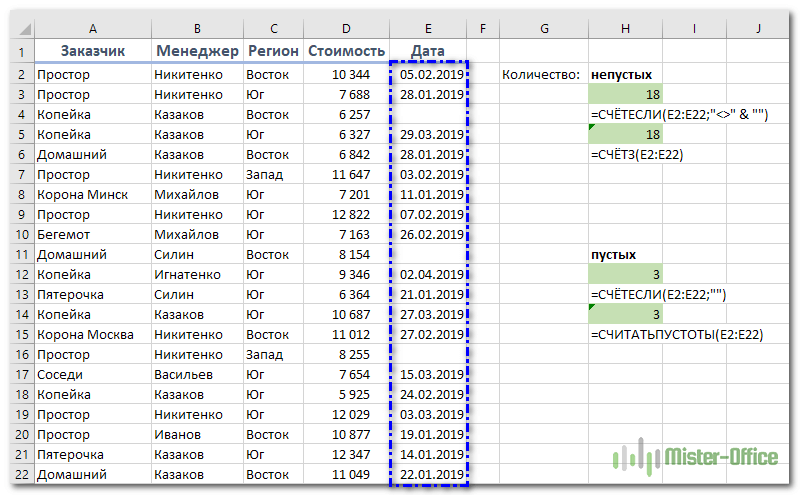
Перед нами небольшая таблица, состоящая из двух столбцов: ФИО и даты рождения. Нужно посчитать количество людей с помощью программы эксель.
Первый вариант.
Выделим диапазон, ячеек, в которых указаны ФИО, это получается ячейки с «D2» по «D8». После смотрите на нижний правый угол, там имеется строка «количество», где подсчитано количество значений в выделенном диапазоне ячеек.
Второй вариант.
Произвести подсчет количества людей, с помощью функции СЧЁТ, а если присутствуют какие-то ограничения, например, возраст людей, то функцией СЧЁТЕСЛИ.
В ячейке «D9» подсчитаем общее количество людей, для этого напишем формулу =СЧЁТ(D2:D8) .
В ячейке «D10» посчитаем количество людей старше 01.01.2000, для этого напишем формулу =СЧЁТЕСЛИ(D2:D8;»>01.01.2000″).
СЧЕТЕСЛИ в Excel — примеры функции с одним и несколькими условиями
В этой статье мы сосредоточимся на функции Excel СЧЕТЕСЛИ (COUNTIF в английском варианте), которая предназначена для подсчета ячеек с определённым условием. Сначала мы кратко рассмотрим синтаксис и общее использование, а затем я приведу ряд примеров и предупрежу о возможных причудах при подсчете по нескольким критериям одновременно или же с определёнными типами данных.
По сути,они одинаковы во всех версиях, поэтому вы можете использовать примеры в MS Excel 2016, 2013, 2010 и 2007.
Функция Excel СЧЕТЕСЛИ применяется для подсчета количества ячеек в указанном диапазоне, которые соответствуют определенному условию.
Например, вы можете воспользоваться ею, чтобы узнать, сколько ячеек в вашей рабочей таблице содержит число, больше или меньше указанной вами величины. Другое стандартное использование — для подсчета ячеек с определенным словом или с определенной буквой (буквами).
СЧЕТЕСЛИ(диапазон; критерий)
Как видите, здесь только 2 аргумента, оба из которых являются обязательными:
- диапазон — определяет одну или несколько клеток для подсчета. Вы помещаете диапазон в формулу, как обычно, например, A1: A20.
- критерий — определяет условие, которое определяет, что именно считать. Это может быть число, текстовая строка, ссылка или выражение. Например, вы можете употребить следующие критерии: «10», A2, «> = 10», «какой-то текст».
Что нужно обязательно запомнить?
- В аргументе «критерий» условие всегда нужно записывать в кавычках, кроме случая, когда используется ссылка либо какая-то функция.
- Любой из аргументов ссылается на диапазон из другой книги Excel, то эта книга должна быть открыта.
- Регистр букв не учитывается.
- Также можно применить знаки подстановки * и ? (о них далее – подробнее).
- Чтобы избежать ошибок, в тексте не должно быть непечатаемых знаков.
Как видите, синтаксис очень прост. Однако, он допускает множество возможных вариаций условий, в том числе символы подстановки, значения других ячеек и даже другие функции Excel. Это разнообразие делает функцию СЧЕТЕСЛИ действительно мощной и пригодной для многих задач, как вы увидите в следующих примерах.
Примеры работы функции СЧЕТЕСЛИ.
Для подсчета текста.
Давайте разбираться, как это работает. На рисунке ниже вы видите список заказов, выполненных менеджерами. Выражение =СЧЕТЕСЛИ(В2:В22,»Никитенко») подсчитывает, сколько раз этот работник присутствует в списке:
Замечание. Критерий не чувствителен к регистру букв, поэтому можно вводить как прописные, так и строчные буквы.
Если ваши данные содержат несколько вариантов слов, которые вы хотите сосчитать, то вы можете использовать подстановочные знаки для подсчета всех ячеек, содержащих определенное слово, фразу или буквы, как часть их содержимого.
К примеру, в нашей таблице есть несколько заказчиков «Корона» из разных городов. Нам необходимо подсчитать общее количество заказов «Корона» независимо от города.
Мы подсчитали количество заказов, где в наименовании заказчика встречается «коро» в любом регистре. Звездочка (*) используется для поиска ячеек с любой последовательностью начальных и конечных символов, как показано в приведенном выше примере. Если вам нужно заменить какой-либо один символ, введите вместо него знак вопроса (?).
Кроме того, указывать условие прямо в формуле не совсем рационально, так как при необходимости подсчитать какие-то другие значения вам придется корректировать её. А это не слишком удобно.
Рекомендуется условие записывать в какую-либо ячейку и затем ссылаться на нее. Так мы сделали в H9. Также можно употребить подстановочные знаки со ссылками с помощью оператора конкатенации (&). Например, вместо того, чтобы указывать «* Коро *» непосредственно в формуле, вы можете записать его куда-нибудь, и использовать следующую конструкцию для подсчета ячеек, содержащих «Коро»:
Подсчет ячеек, начинающихся или заканчивающихся определенными символами
Вы можете употребить подстановочный знак звездочку (*) или знак вопроса (?) в зависимости от того, какого именно результата вы хотите достичь.
Если вы хотите узнать количество ячеек, которые начинаются или заканчиваются определенным текстом, независимо от того, сколько имеется других символов, используйте:
=СЧЁТЕСЛИ(A2:A22;»К*») — считать значения, которые начинаются с « К» .
=СЧЁТЕСЛИ(A2:A22;»*р») — считать заканчивающиеся буквой «р».
Если вы ищете количество ячеек, которые начинаются или заканчиваются определенными буквами и содержат точное количество символов, то поставьте вопросительный знак (?):
=СЧЁТЕСЛИ(С2:С22;». д») — находит количество буквой «д» в конце и текст в которых состоит из 5 букв, включая пробелы.
= СЧЁТЕСЛИ(С2:С22,»??») — считает количество состоящих из 2 символов, включая пробелы.
Примечание. Чтобы узнать количество клеток, содержащих в тексте знак вопроса или звездочку, введите тильду (
) перед символом ? или *.
?*») будут подсчитаны все позиции, содержащие знак вопроса в диапазоне С2:С22.
Подсчет чисел по условию.
В отношении чисел редко случается, что нужно подсчитать количество их, равных какому-то определённому числу. Тем не менее, укажем, что записать нужно примерно следующее:
Гораздо чаще нужно высчитать количество значений, больших либо меньших определенной величины.
Чтобы подсчитать значения, которые больше, меньше или равны указанному вами числу, вы просто добавляете соответствующий критерий, как показано в таблице ниже.
Обратите внимание, что математический оператор вместе с числом всегда заключен в кавычки .
критерии
Описание
Если больше, чем
Подсчитайте, где значение больше 5.
Если меньше чем
Подсчет со числами менее 5.
Определите, сколько раз значение равно 5.
Подсчитайте, сколько раз не равно 5.
Если больше или равно
Подсчет, когда больше или равно 5.
Если меньше или равно
Подсчет, где меньше или равно 5.
В нашем примере
Считаем количество крупных заказов на сумму более 10 000. Обратите внимание, что условие подсчета мы записываем здесь в виде текстовой строки и поэтому заключаем его в двойные кавычки.
Вы также можете использовать все вышеприведенные варианты для подсчета ячеек на основе значения другой ячейки. Вам просто нужно заменить число ссылкой.
Замечание. В случае использования ссылки, вы должны заключить математический оператор в кавычки и добавить амперсанд (&) перед ним. Например, чтобы подсчитать числа в диапазоне D2: D9, превышающие D3, используйте =СЧЕТЕСЛИ(D2:D9,»>»&D3)
Если вы хотите сосчитать записи, которые содержат математический оператор, как часть их содержимого, то есть символ «>», «<» или «=», то употребите в условиях подстановочный знак с оператором. Такие критерии будут рассматриваться как текстовая строка, а не числовое выражение.
Например, =СЧЕТЕСЛИ(D2:D9,»*>5*») будет подсчитывать все позиции в диапазоне D2: D9 с таким содержимым, как «Доставка >5 дней» или «>5 единиц в наличии».
Примеры с датами.
Если вы хотите сосчитать клетки с датами, которые больше, меньше или равны указанной вами дате, вы можете воспользоваться уже знакомым способом, используя формулы, аналогичные тем, которые мы обсуждали чуть выше. Все вышеприведенное работает как для дат, так и для чисел.
Позвольте привести несколько примеров:
критерии
Описание
Даты, равные указанной дате.
Подсчитывает количество ячеек в диапазоне E2:E22 с датой 1 июня 2014 года.
Даты больше или равные другой дате.
Сосчитайте количество ячеек в диапазоне E2:E22 с датой, большей или равной 01.06.2014.
Даты, которые больше или равны дате в другой ячейке, минус X дней.
=СЧЕТЕСЛИ(E2:E22,»> font-family: inherit; font-size: inherit; font-weight: inherit; letter-spacing: 0px;»>
Определите количество ячеек в диапазоне E2:E22 с датой, большей или равной дате в H2, минус 7 дней.
Помимо этих стандартных способов, вы можете употребить функцию СЧЕТЕСЛИ в сочетании с функциями даты и времени, например, СЕГОДНЯ(), для подсчета ячеек на основе текущей даты.
критерии
Равные текущей дате.
До текущей даты, то есть меньше, чем сегодня.
После текущей даты, т.е. больше, чем сегодня.
Даты, которые должны наступить через неделю.
= СЧЕТЕСЛИ(E2:E22,» font-family: inherit; font-size: inherit; font-weight: inherit; letter-spacing: 0px;»>
В определенном диапазоне времени.
Как посчитать количество пустых и непустых ячеек?
Посмотрим, как можно применить функцию СЧЕТЕСЛИ в Excel для подсчета количества пустых или непустых ячеек в указанном диапазоне.
Непустые.
В некоторых руководствах по работе с СЧЕТЕСЛИ вы можете встретить предложения для подсчета непустых ячеек, подобные этому:
Но дело в том, что приведенное выше выражение подсчитывает только клетки, содержащие любые текстовые значения. А это означает, что те из них, что включают даты и числа, будут обрабатываться как пустые (игнорироваться) и не войдут в общий итог!
Если вам нужно универсальное решение для подсчета всех непустых ячеек в указанном диапазоне, то введите:
Это корректно работает со всеми типами значений — текстом, датами и числами — как вы можете видеть на рисунке ниже.
Также непустые ячейки в диапазоне можно подсчитать:
Пустые.
Если вы хотите сосчитать пустые позиции в определенном диапазоне, вы должны придерживаться того же подхода — используйте в условиях символ подстановки для текстовых значений и параметр “” для подсчета всех пустых ячеек.
Считаем клетки, не содержащие текст:
Поскольку звездочка (*) соответствует любой последовательности текстовых символов, в расчет принимаются клетки, не равные *, т.е. не содержащие текста в указанном диапазоне.
Для подсчета пустых клеток (все типы значений):
Конечно, для таких случаев есть и специальная функция
Но не все знают о ее существовании. Но вы теперь в курсе …
Нулевые строки.
Также имейте в виду, что СЧЕТЕСЛИ и СЧИТАТЬПУСТОТЫ считают ячейки с пустыми строками, которые только на первый взгляд выглядят пустыми.
Что такое эти пустые строки? Они также часто возникают при импорте данных из других программ (например, 1С). Внешне в них ничего нет, но на самом деле это не так. Если попробовать найти такие «пустышки» (F5 -Выделить — Пустые ячейки) — они не определяются. Но фильтр данных при этом их видит как пустые и фильтрует как пустые.
Дело в том, что существует такое понятие, как «строка нулевой длины» (или «нулевая строка»). Нулевая строка возникает, когда программе нужно вставить какое-то значение, а вставить нечего.
Проблемы начинаются тогда, когда вы пытаетесь с ней произвести какие-то математические вычисления (вычитание, деление, умножение и т.д.). Получите сообщение об ошибке #ЗНАЧ!. При этом функции СУММ и СЧЕТ их игнорируют, как будто там находится текст. А внешне там его нет.
И самое интересное — если указать на нее мышкой и нажать Delete (или вкладка Главная — Редактирование — Очистить содержимое) — то она становится действительно пустой, и с ней начинают работать формулы и другие функции Excel без всяких ошибок.
Если вы не хотите рассматривать их как пустые, используйте для подсчета реально пустых клеток следующее выражение:
Откуда могут появиться нулевые строки в ячейках? Здесь может быть несколько вариантов:
- Он есть там изначально, потому что именно так настроена выгрузка и создание файлов в сторонней программе (вроде 1С). В некоторых случаях такие выгрузки настроены таким образом, что как таковых пустых ячеек нет — они просто заполняются строкой нулевой длины.
- Была создана формула, результатом которой стал текст нулевой длины. Самый простой случай:
В итоге, если в Е1 записано что угодно, отличное от 1, программа вернет строку нулевой длины. И если впоследствии формулу заменять значением (Специальная вставка – Значения), то получим нашу псевдо-пустую позицию.
Если вы проверяете какие-то условия при помощи функции ЕСЛИ и в дальнейшем планируете производить с результатами математические действия, то лучше вместо «» ставьте 0. Тогда проблем не будет. Нули всегда можно заменить или скрыть: Файл -Параметры -Дополнительно — Показывать нули в позициях, которые содержат нулевые значения.
СЧЕТЕСЛИ с несколькими условиями.
На самом деле функция Эксель СЧЕТЕСЛИ не предназначена для расчета количества ячеек по нескольким условиям. В большинстве случаев я рекомендую использовать его множественный аналог — функцию СЧЕТЕСЛИМН. Она как раз и предназначена для вычисления количества ячеек, которые соответствуют двум или более условиям (логика И). Однако, некоторые задачи могут быть решены путем объединения двух или более функций СЧЕТЕСЛИ в одно выражение.
Количество чисел в диапазоне
Одним из наиболее распространенных применений функции СЧЕТЕСЛИ с двумя критериями является определение количества чисел в определенном интервале, т.е. меньше X, но больше Y.
Например, вы можете использовать для вычисления ячеек в диапазоне B2: B9, где значение больше 5 и меньше или равно 15:
Количество ячеек с несколькими условиями ИЛИ.
Обратите внимание, что мы включили подстановочный знак (*) во второй критерий. Он используется для вычисления количества всех видов сока в списке.
Как вы понимаете, сюда можно добавить и больше условий.
Использование СЧЕТЕСЛИ для подсчета дубликатов.
Другое возможное использование функции СЧЕТЕСЛИ в Excel — для поиска дубликатов в одном столбце, между двумя столбцами или в строке.
1. Ищем дубликаты в одном столбце
Эта простое выражение СЧЁТЕСЛИ($A$2:$A$24;A2)>1 найдет все одинаковые записи в A2: A24.
А другая формула СЧЁТЕСЛИ(B2:B24;ИСТИНА) сообщит вам, сколько существует дубликатов:
Для более наглядного представления найденных совпадений я использовал условное форматирование значения ИСТИНА.
2. Сколько совпадений между двумя столбцами?
Сравним список2 со списком1. В столбце Е берем последовательно каждое значение из списка2 и считаем, сколько раз оно встречается в списке1. Если совпадений ноль, значит это уникальное значение. На рисунке такие выделены цветом при помощи условного форматирования.
Выражение =СЧЁТЕСЛИ($A$2:$A$24;C2) копируем вниз по столбцу Е.
Аналогичный расчет можно сделать и наоборот – брать значения из первого списка и искать дубликаты во втором.
Для того, чтобы просто определить количество дубликатов, можно использовать комбинацию функций СУММПРОИЗВ и СЧЕТЕСЛИ.
Подсчитаем количество уникальных значений в списке2:
Получаем 7 уникальных записей и 16 дубликатов, что и видно на рисунке.
Полезное. Если вы хотите выделить дублирующиеся позиции или целые строки, содержащие повторяющиеся записи, вы можете создать правила условного форматирования на основе формул СЧЕТЕСЛИ, как показано в этом руководстве — правила условного форматирования Excel.
3. Сколько дубликатов и уникальных значений в строке?
Если нужно сосчитать дубликаты или уникальные значения в определенной строке, а не в столбце, используйте одну из следующих формул. Они могут быть полезны, например, для анализа истории розыгрыша лотереи.
Считаем количество дубликатов:
Видим, что 13 выпадало 2 раза.
Подсчитать уникальные значения:
Часто задаваемые вопросы и проблемы.
Я надеюсь, что эти примеры помогли вам почувствовать функцию Excel СЧЕТЕСЛИ. Если вы попробовали какую-либо из приведенных выше формул в своих данных и не смогли заставить их работать или у вас возникла проблема, взгляните на следующие 5 наиболее распространенных проблем. Есть большая вероятность, что вы найдете там ответ или же полезный совет.
- Возможен ли подсчет в несмежном диапазоне клеток?
Вопрос: Как я могу использовать СЧЕТЕСЛИ для несмежного диапазона или ячеек?
Ответ: Она не работает с несмежными диапазонами, синтаксис не позволяет указывать несколько отдельных ячеек в качестве первого параметра. Вместо этого вы можете использовать комбинацию нескольких функций СЧЕТЕСЛИ:
Правильно: = СЧЕТЕСЛИ (A2;»>0″) + СЧЕТЕСЛИ (B3;»>0″) + СЧЕТЕСЛИ (C4;»>0″)
Альтернативный способ — использовать функцию ДВССЫЛ (INDIRECT) для создания массива из несмежных клеток. Например, оба приведенных ниже варианта дают одинаковый результат, который вы видите на картинке:
- Амперсанд и кавычки в формулах СЧЕТЕСЛИ
Вопрос: когда мне нужно использовать амперсанд?
Ответ: Это, пожалуй, самая сложная часть функции СЧЕТЕСЛИ, что лично меня тоже смущает. Хотя, если вы подумаете об этом, вы увидите — амперсанд и кавычки необходимы для построения текстовой строки для аргумента.
Итак, вы можете придерживаться этих правил:
- Если вы используете число или ссылку на ячейку в критериях точного соответствия, вам не нужны ни амперсанд, ни кавычки. Например:
= СЧЕТЕСЛИ(A1:A10;10) или = СЧЕТЕСЛИ(A1:A10;C1)
- Если ваши условия содержат текст, подстановочный знак или логический оператор с числом, заключите его в кавычки. Например:
= СЧЕТЕСЛИ(A2:A10;»яблоко») или = СЧЕТЕСЛИ(A2:A10;»*») или = СЧЕТЕСЛИ(A2:A10;»>5″)
- Если ваши критерии — это выражение со ссылкой или же какая-то другая функция Excel, вы должны использовать кавычки («») для начала текстовой строки и амперсанд (&) для конкатенации (объединения) и завершения строки. Например:
Вопрос: Как подсчитать клетки по цвету заливки или шрифта, а не по значениям?
Ответ: К сожалению, синтаксис функции не позволяет использовать форматы в качестве условия. Единственный возможный способ суммирования ячеек на основе их цвета — использование макроса или, точнее, пользовательской функции Excel VBA.
- Ошибка #ИМЯ?
Проблема: все время получаю ошибку #ИМЯ? Как я могу это исправить?
Ответ: Скорее всего, вы указали неверный диапазон. Пожалуйста, проверьте пункт 1 выше.
- Формула не работает
Проблема: моя формула не работает! Что я сделал не так?
Ответ: Если вы написали формулу, которая на первый взгляд верна, но она не работает или дает неправильный результат, начните с проверки наиболее очевидных вещей, таких как диапазон, условия, ссылки, использование амперсанда и кавычек.
Будьте очень осторожны с использованием пробелов. При создании одной из формул для этой статьи я был уже готов рвать волосы, потому что правильная конструкция (я точно знал, что это правильно!) не срабатывала. Как оказалось, проблема была на самом виду. Например, посмотрите на это: =СЧЁТЕСЛИ(A4:A13;» Лимонад»). На первый взгляд, нет ничего плохого, кроме дополнительного пробела после открывающей кавычки. Программа отлично проглотит всё без сообщения об ошибке, предупреждения или каких-либо других указаний. Но если вы действительно хотите посчитать товары, содержащие слово «Лимонад» и начальный пробел, то будете очень разочарованы….
Если вы используете функцию с несколькими критериями, разделите формулу на несколько частей и проверьте каждую из них отдельно.
И это все на сегодня. В следующей статье мы рассмотрим несколько способов подсчитывания ячеек в Excel с несколькими условиями.
Ещё примеры расчета суммы:







8 простых способов как посчитать в Excel сумму столбца — Как посчитать сумму в Excel быстро и просто? Чаще всего нас интересует итог по столбцу либо строке. Попробуйте различные способы найти сумму по столбцу, используйте функцию СУММ или же преобразуйте…
Функция СЧЁТЕСЛИ в Excel используется для подсчета количества ячеек в рассматриваемом диапазоне, содержащиеся данные в которых соответствуют критерию, переданному в качестве второго аргумента данной функции, и возвращает соответствующее числовое значение.
Функция СЧЁТЕСЛИ может быть использована для анализа числовых значений, текстовых строк, дат и данных другого типа. С ее помощью можно определить количество неповторяющихся значений в диапазоне ячеек, а также число ячеек с данными, которые совпадают с указанным критерием лишь частично. Например, таблица Excel содержит столбец с ФИО клиентов. Для определения количества клиентов-однофамильцев с фамилией Иванов можно ввести функцию =СЧЁТЕСЛИ(A1:A300;”*Иванов*”). Символ «*» указывает на любое количество любых символов до и после подстроки «Иванов».
Примеры использования функции СЧЁТЕСЛИ в Excel
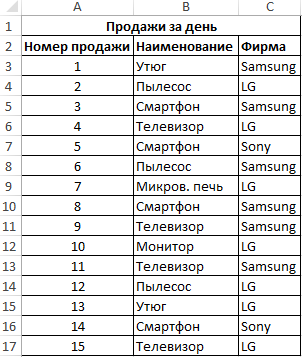
Пример 1. В таблице Excel содержатся данные о продажах товаров в магазине бытовой техники за день. Определить, какую часть от проданной продукции составляет техника фирмы Samsung.
Вид исходной таблицы данных:
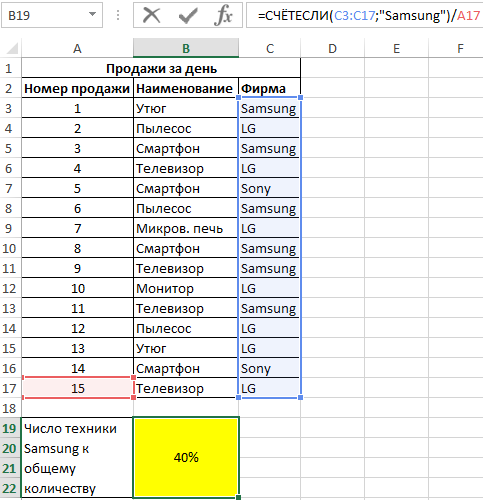
Для расчета используем формулу:
=СЧЁТЕСЛИ(C3:C17;»Samsung»)/A17
Описание аргументов:
- C3:C17 – диапазон ячеек, содержащих названия фирм проданной техники;
- «Samsung» – критерий поиска (точное совпадение);
- A17 – ячейка, хранящая номер последней продажи, соответствующий общему числу продаж.
Результат расчета:
Доля проданной продукции техники фирмы Samsung в процентах составляет – 40%.
Подсчет количества определенного значения ячейки в Excel при условии
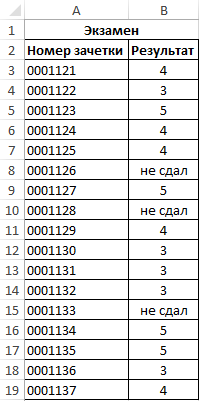
Пример 2. По итогам сдачи экзаменов необходимо составить таблицу, в которой содержатся данные о количестве студентов, сдавших предмет на 5, 4, 3 балла соответственно, а также тех, кто не сдал предмет.
Вид исходной таблицы:
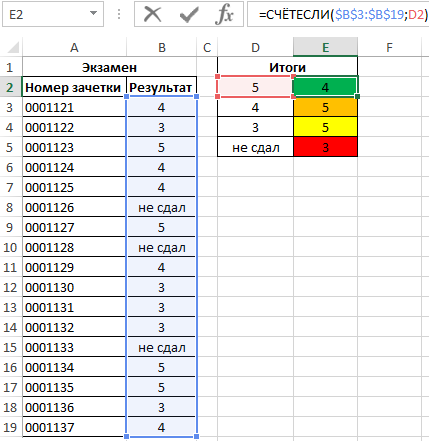
Предварительно выделим ячейки E2:E5, введем приведенную ниже формулу:
=СЧЁТЕСЛИ(B3:B19;D2:D5)
Описание аргументов:
- B3:B19 – диапазон ячеек с оценками за экзамен;
- D2:D5 – диапазон ячеек, содержащих критерии для подсчета числа совпадений.
В результате получим таблицу:
Статистический анализ посещаемости с помощью функции СЧЁТЕСЛИ в Excel
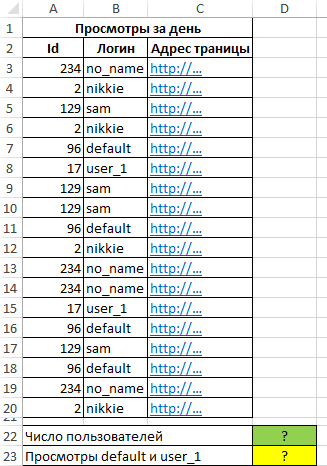
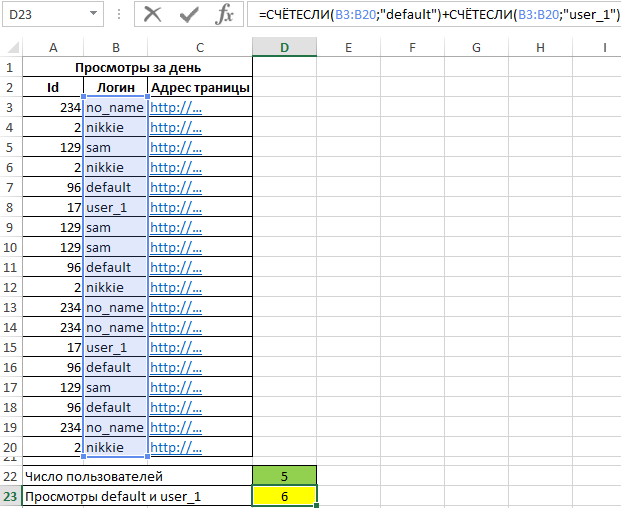
Пример 3. В таблице Excel хранятся данные о просмотрах страниц сайта за день пользователями. Определить число пользователей сайта за день, а также сколько раз за день на сайт заходили пользователи с логинами default и user_1.
Вид исходной таблицы:
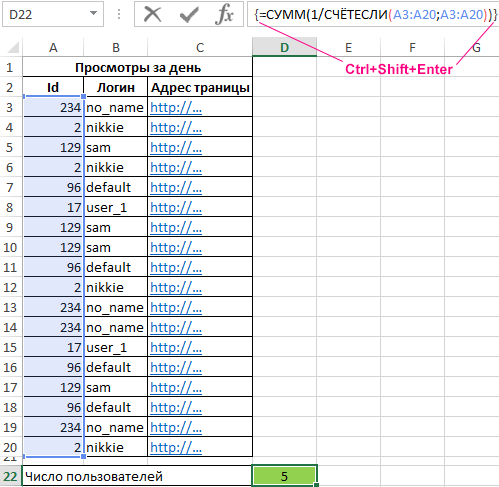
Поскольку каждый пользователь имеет свой уникальный идентификатор в базе данных (Id), выполним расчет числа пользователей сайта за день по следующей формуле массива и для ее вычислений нажмем комбинацию клавиш Ctrl+Shift+Enter:
Выражение 1/СЧЁТЕСЛИ(A3:A20;A3:A20) возвращает массив дробных чисел 1/количество_вхождений, например, для пользователя с ником sam это значение равно 0,25 (4 вхождения). Общая сумма таких значений, вычисляемая функцией СУММ, соответствует количеству уникальных вхождений, то есть, числу пользователей на сайте. Полученное значение:
Для определения количества просмотренных страниц пользователями default и user_1 запишем формулу:
В результате расчета получим:
Особенности использования функции СЧЁТЕСЛИ в Excel
Функция имеет следующую синтаксическую запись:
=СЧЕТЕСЛИ(диапазон; критерий)
Описание аргументов:
- диапазон – обязательный аргумент, принимающий ссылку на одну либо несколько ячеек, в которых требуется определить число совпадений с указанным критерием.
- критерий – условие, согласно которому выполняется расчет количества совпадений в рассматриваемом диапазоне. Условием могут являться логическое выражение, числовое значение, текстовая строка, значение типа Дата, ссылка на ячейку.
Примечания:
- При подсчете числа вхождений в диапазон в соответствии с двумя различными условиями, диапазон ячеек можно рассматривать как множество, содержащее два и более непересекающихся подмножеств. Например, в таблице «Мебель» необходимо найти количество столов и стульев. Для вычислений используем выражение =СЧЁТЕСЛИ(B3:B200;»*стол*»)+СЧЁТЕСЛИ(B3:B200;»*стул*»).
- Если в качестве критерия указана текстовая строка, следует учитывать, что регистр символов не имеет значения. Например, функция СЧЁТЕСЛИ(A1:A2;»Петров») вернет значение 2, если в ячейках A1 и A2 записаны строки «петров» и «Петров» соответственно.
- Если в качестве аргумента критерий передана ссылка на пустую ячейку или пустая строка «», результат вычисления для любого диапазона ячеек будет числовое значение 0 (нуль).
- Функция может быть использована в качестве формулы массива, если требуется выполнить расчет числа ячеек с данными, удовлетворяющим сразу нескольким критериям. Данная особенность будет рассмотрена в одном из примеров.
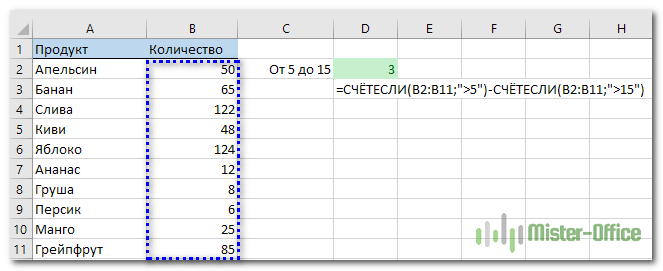
- Рассматриваемая функция может быть использована для определения количества совпадений как по одному, так и сразу по нескольким критериям поиска. В последнем случае используют две и более функции СЧЁТЕСЛИ, возвращаемые результаты которых складывают или вычитают. Например, в ячейках A1:A10 хранится последовательность значений от 1 до 10. Для расчета количества ячеек с числами больше 3 и менее 8 необходимо выполнить следующие действия:
Скачать примеры функции СЧЁТЕСЛИ для подсчета ячеек в Excel
- записать первую функцию СЧЁТЕСЛИ с критерием «>3»;
- записать вторую функцию с критерием «>=8»;
- определить разницу между возвращаемыми значениями =СЧЁТЕСЛИ(A1:10;»>3″)-СЧЁТЕСЛИ(A1:A10;»>=8″). То есть, вычесть из множества (3;+∞) подмножество [8;+∞).
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Размах вариации
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Простая формула для расчета объема выборки
- Пример расчета объема выборки
- Задачи о генеральной доле
- По части судить о целом
- Как рассчитать объем выборки
- Как определить статистические выбросы и сделать выборку для их удаления в Excel
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- СРЗНАЧ()
- СРЗНАЧЕСЛИ()
- МАКС()
- МИН()
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;
p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = (1 – p);
e – допустимая ошибка, в долях.
Пример расчета объема выборки
Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле
|
Гипотеза |
H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |  |
|
| Статистика K |  |
 |
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при
достаточном числе наблюдений
. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:
С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.
Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.
Как рассчитать объем выборки
Достаточный размер выборки зависит от следующих составляющих:
- изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
- размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
- уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)
ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента
Формулы для расчета объема выборки:
Формулы расчета объема выборки
Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.
График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.
Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Способ 1: применение расширенного автофильтра
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
Источники
- https://lumpics.ru/descriptive-statistics-in-excel/
- https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
- https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
- http://galyautdinov.ru/post/formula-vyborki-prostaya
- https://math.semestr.ru/group/interval-estimation-share.php
- https://tidydata.ru/sample-size
- https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
- https://lumpics.ru/how-to-make-a-sample-in-excel/
- https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html
Лабораторная работа
Статистические функции Excel
Цель работы: Освоение приемов работы с функциями массивов (табличными функциями). Изучение элементарных статистических функций Excel
- Формулы массивов (табличные формулы)
Массивом называют блок ячеек электронной таблицы, который используется для создания формул, возвращающих некоторое множество результатов или оперирующих множеством значений, а не отдельными значениями.
Формулы массивов (иногда их называют табличными формулами), используют несколько множеств значений (массивов аргументов), и возвращают одно или несколько значений. Такие формулы позволяют обращаться с блоками, как с обычной ячейкой.
Рассмотрим работу с использованием массивов на следующем примере. Требуется определить прибыль для каждого года деятельности отеля, представленного в таблице 1.
Таблица 1.
Пример использования функций массива
|
A |
B |
C |
D |
|
|
1 |
Год |
Приход |
Расход |
Прибыль |
|
2 |
2005 |
200 |
150 |
{B2:B5-C2:C5} |
|
3 |
2006 |
360 |
230 |
{B2:B5-C2:C5} |
|
4 |
2007 |
410 |
250 |
{B2:B5-C2:C5} |
|
5 |
2008 |
200 |
180 |
{B2:B5-C2:C5} |
Выделим блок D2:D5. Начнем ввод формулы – наберем знак =. Выделим блок B2:B5, наберем знак минус -, выделим блок С2:С5. Ввод формул массива заканчивается комбинацией клавиш Ctrl+Shift+Enter. После нажатия такой комбинации во всех ячейках блока D2:D5 появится формула {B2:B5-C2:C5}.
- Основные правила работы с формулами массива:
- перед вводом формулы нужно выделить ячейку или диапазон для результатов, если формула возвращает несколько значений, то диапазон результатов должен быть того же размера, что и диапазон исходных данных;
- фигурные скобки, отмечающие формулу массива, вводятся при завершении ввода формулы клавишами Ctrl+Shift+Enter, если фигурные скобки ввести вручную, такой ввод будет воспринят Excel как текст.
- для редактирования формулы массива необходимо выделить блок, активировать строку формул, внести изменения и завершить редактированием клавишами Ctrl+Shift+Enter;
- блок ячеек может указываться присвоенным ему именем (клавиша F3 и выбор имени в диалоге «Вставка имени»;
- массив исходных данных и массив результатов могут быть многомерными, т.е. включать несколько строк и столбцов.
- Функции Excel, используемые для статистического анализа
Статистический анализ данных необходим для оценки деятельности фирмы и прогноза ее работы на какой-то срок. Такой анализ основывается на сборе информации, определении по представленным массивам данных оценок, статистических показателей и тенденций развития фирмы.
В категорию статистических функций Excel входит около 80 функций, кроме того, значительное число функций статистического анализа входят в надстройку «Пакет анализа».
Для выполнения задания потребуются статистические функции, полное описание которых приведено ниже.
- МАКС(число1;число2; …) — возвращает наибольшее значение из набора значений.
- Число1, число2,…— от 1 до 30 чисел, среди которых требуется найти наибольшее.
- Можно задавать аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел. Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, вызывают значения ошибок.
- Если аргумент является массивом или ссылкой, то в нем учитываются только числа. Пустые ячейки, логические значения или текст в массиве или ссылке игнорируются. Если логические значения или текст не должны игнорироваться, следует использовать функцию МАКСА. Если аргументы не содержат чисел, то функция МАКС возвращает 0 (ноль);
- МИН(число1;число2; …) — возвращает наименьшее значение из набора значений, в остальном полностью аналогична функции ^ МАКС;
- СРЗНАЧ(число1; число2; …) — возвращает среднее (арифметическое) своих аргументов.
- Число1, число2, … — это от 1 до 30 аргументов, для которых вычисляется среднее.
- Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.
- Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются;
ТЕНДЕНЦИЯ (известные_значения_y; известные_значения_x; новые значения_x; конст) — возвращает значения в соответствии с линейным трендом, т.е. аппроксимирует прямой линией (по методу наименьших квадратов) массивы ”известные_значения_y” и “известные_значения_x”. Возвращает значения y, в соответствии с этой прямой для заданного массива новые_значения_x.
- Известные_значения_y — множество значений y, которые уже известны для соотношения y = mx + b.
- Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная. - Известные_значения_x — необязательное множество значений x, которые уже известны для соотношения y = mx + b.
- Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные_значения_y и известные_значения_x могут иметь любую форму, при условии, что они имеют одинаковую размерность.
- Если используется более одной переменной, то известные_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец).
Если известные_значения_x опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_y. - Новые_значения_x — новые значения x, для которых ТЕНДЕНЦИЯ возвращает соответствующие значения y. Новые_значения_x должны содержать столбец (или строку) для каждой независимой переменной, как иизвестные_значения_x. Таким образом, если известные_значения_y — это один столбец, то известные_значения_x и новые_значения_x должны иметь такое же количество столбцов. Если известные_значения_y — это одна строка, то известные_значения_x и новые_значения_x должны иметь такое же количество строк.
- Если новые_значения_x опущены, то предполагается, что они совпадают с известные_значения_x.
- Если опущены оба массива известные_значения_x и новые_значения_x, то предполагается, что это массив {1;2;3;…} такого же размера, что и известные_значения_y.
- Конст — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
- Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.
- Если конст имеет значение ЛОЖЬ, то b полагается равным 0, и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
РОСТ(известные_значения_y;известные_значения_x;новые_значения_x; конст) — возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих x- и y-значений, т.е. функция рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных.
- Известные_значения_y — это множество значений y, которые уже известны в соотношении y = b*mx. Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная. Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
- Известные_значения_x — это необязательное множество значений x, которые уже известны для соотношения y=b*mx. Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_xинтерпретируется как отдельная переменная. Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные_значения_y иизвестные_значения_x могут иметь любую форму, при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец). Если известные_значения_x опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_y.
- Новые_значения_x — это новые значения x, для которых РОСТ возвращает соответствующие значения y. Новые_значения_x должны содержать столбец (или строку) для каждой независимой переменной, как иизвестные_значения_x. Таким образом, если известные_значения_y — это один столбец, то известные_значения_x и новые_значения_x должны иметь такое же количество столбцов. Если известные_значения_y — это одна строка, то известные_значения_x и новые_значения_x должны иметь такое же количество строк. Если аргумент новые_значения_x опущен, то предполагается, что он совпадает с аргументом известные_значения_x. Если оба аргумента известные_значения_x и новые_значения_x опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_y.
- Конст — это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 1. Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если конст имеет значение ЛОЖЬ, то b полагается равным 1, а значения m подбираются так, чтобы y = mx.
ПРЕДСКАЗ(x, известные_значения_y, известные_значения_x) – вычисляет или предсказывает будущее значение по существующим значениям. Предсказываемое значение — это значение y, соответствующее заданному значению x. Значения x и y известны; новое значение предсказывается с использованием линейной регрессии. Эту функцию можно использовать для прогнозирования будущих продаж, потребностей в оборудовании или тенденций потребления.
- Функция ПРЕДСКАЗ имеет аргументы, указанные ниже.
- x — обязательный аргумент. Точка данных, для которой предсказывается значение.
- Известные_значения_y — обязательный аргумент. Зависимый массив или интервал данных.
- Известные_значения_x — обязательный аргумент. Независимый массив или интервал данных.
- Если x не является числом, функция ПРЕДСКАЗ возвращает значение ошибки #ЗНАЧ!.
- Если аргументы «известные_значения_y» и «известные_значения_x» пусты или количество точек данных в этих аргументах не совпадает, функция ПРЕДСКАЗ возвращает значение ошибки #Н/Д.
- Если дисперсия аргумента «известные_значения_x» равна 0, функция ПРЕДСКАЗ возвращает значение ошибки #ДЕЛ/0!.
- Замечания
- 1) Формулы, которые возвращают массивы, должны быть введены как формулы массива.
2) При вводе константы массива для аргумента, такого как известные_значения_x, следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк.
- Задание
Для приведенных в таблице 2 данных о реализации гостиничных услуг сетью отелей «Европа» вычислить:
- минимальные, максимальные и среднее показатели по каждому кварталу;
- средние показатели по каждому отелю;
- вычислить средний доход по всей сети отелей за отчетный период;
- дать оценку работы каждого отеля: «хорошо», если доход отеля превышает средний по сети, и «плохо», если доход меньше среднего по сети;
- построить линейную и экспоненциальную модель деятельности сети отелей и дать прогноз для двух следующих кварталов;
- оценить относительные отклонения для среднего значения и «Тенденции», для среднего значения и «Роста».
^ Таблица 2.
Исходные данные
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Отель |
1 кв. |
2 кв. |
3 кв. |
4 кв. |
Среднее по |
Оценка |
|
отелю |
|||||||
|
2 |
Швеция |
1500 |
2000 |
6000 |
8000 |
||
|
3 |
Дания |
1400 |
5000 |
4100 |
5000 |
||
|
4 |
Норвегия |
3600 |
3600 |
3000 |
4500 |
||
|
5 |
Финляндия |
1100 |
1045 |
9100 |
7800 |
||
|
6 |
Германия |
3850 |
3650 |
7800 |
11000 |
||
|
7 |
Польша |
6800 |
7250 |
8122 |
9450 |
||
|
8 |
Чехия |
6590 |
7050 |
6400 |
6440 |
||
|
9 |
Словакия |
930 |
3970 |
4512 |
4600 |
||
|
10 |
Венгрия |
8912 |
7490 |
3570 |
8000 |
||
|
11 |
Болгария |
3590 |
3800 |
5464 |
5954 |
||
|
12 |
Мин |
||||||
|
13 |
Мах |
||||||
|
14 |
Среднее |
||||||
|
15 |
1 |
2 |
3 |
4 |
|||
|
16 |
Тенденция по среднему |
||||||
|
17 |
Рост по среднему |
||||||
|
18 |
Погрешность |
||||||
|
тенденции |
|||||||
|
19 |
Погрешность |
||||||
|
роста |
|||||||
|
20 |
Лучший отель по сети |
||||||
|
Доход |
- Технология выполнения
- Минимальные, максимальные и средние значения по кварталам и средние значения по турам подсчитываются с помощью Мастера функций.
- Для оценки работы отеля используется среднее значение дохода по сети и функция ЕСЛИ().
- Функция Тенденция показывает динамику изменения данных и позволяет получить прогноз на будущее. При этом изменение данных описывается линейным уравнением. Для определения Тенденции:
- Выделить новый диапазон ячеек для размещения результатов (B16:E16);
- В строке формул вставить функцию Тенденция и в Мастере функций в поле аргумента известные_значения_y указать диапазон средних по кварталу значений.
- Известные_значения_x можно не устанавливать, т.к. это 1, 2, 3, 4 кварталы.
- Выйти из Мастера функций – Ok.
- Установить курсор в строке формул, нажать комбинацию клавиш Ctrl+Shift+Enter, в выделенном новом массиве появятся результаты.
- Функция Тенденция показывает линейную модель изменения показателей, экспоненциальная модель строится функцией Рост.
- Самостоятельно вычислите функцию Рост для средних по кварталам, подобно тому, как вычислялась функция Тенденция.
- Вычислить прогноз развития событий на ближайшие два квартала, используя функцию Тенденция:
- Справа от ячейки со значением Тенденция для 4-го квартала выделить две свободные ячейки.
- Вставить функцию Тенденция и в Мастере функций указать:
- в поле известные_значения_y вычисленные ранее значения Тенденция за четыре квартала (диапазон B16:E16);
- в поле новые_значения_x – диапазон F15:G15 – кварталы 5 и 6, для которых выполняется прогноз.
- Завершить работу Мастера – Ok, завершить ввод функции массива Ctrl+Shift+Enter, в выделенных ячейках появятся предсказанные по линейной модели значения для 5 и 6 кварталов.
- Таким же образом рассчитать прогноз по экспоненциальной модели с помощью функции Рост.
- Оценить относительные отклонения в процентах для среднего значения и Тенденции, для среднего значения и Роста (для каждого из четырех кварталов) по формуле:
Относительное отклонение=(yфакт — yмодели)/yмодели,
где yфакт — среднее значение;
yмодели – значение, определенное с помощью Тенденции или Роста.
Пример расчета показателей работы отелей по первому кварталу приведен в таблице 3.
Таблица 3.
Пример расчета показателей работы отелей по первому кварталу
|
A |
B |
|
|
13 |
Мин |
=МИН(В3:В12) |
|
14 |
Мах |
=МАКС(В3:В12) |
|
15 |
Среднее |
=СРЗНАЧ(В3:В12) |
|
17 |
Тенденция по среднему |
=ТЕНДЕНЦИЯ(В15:Е15) |
|
18 |
Рост по среднему |
=РОСТ(В15:Е15) |
|
19 |
Погрешность |
=(В15-В17)/В17 |
|
тенденции |
||
|
20 |
Погрешность |
=(В15-В18)/В18 |
|
роста |
||
|
21 |
Лучший отель по сети |
=ИНДЕКС($А$3:В12;ПОИСКПОЗ(МАКС(В3:В12);В3:В12;0);1) |
|
22 |
Доход |
=ИНДЕКС($А$3:В12;ПОИСКПОЗ(МАКС(В3:В12);В3:В12;0);2) |
Результаты расчетов приведены в таблице 4.
Таблица 4.
Результаты расчетов
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Отель |
1 кв. |
2 кв. |
3 кв. |
4 кв. |
Среднее по |
Оценка |
|
отелю |
|||||||
|
2 |
Швеция |
1500 |
2000 |
6000 |
8000 |
4375 |
Плохо |
|
3 |
Дания |
1400 |
5000 |
4100 |
5000 |
3875 |
Плохо |
|
4 |
Норвегия |
3600 |
3600 |
3000 |
4500 |
3675 |
Плохо |
|
5 |
Финляндия |
1100 |
1045 |
9100 |
7800 |
4761,25 |
Плохо |
|
6 |
Германия |
3850 |
3650 |
7800 |
11000 |
6575 |
Хорошо |
|
7 |
Польша |
6800 |
7250 |
8122 |
9450 |
7905,5 |
Хорошо |
|
8 |
Чехия |
6590 |
7050 |
6400 |
6440 |
6620 |
Хорошо |
|
9 |
Словакия |
930 |
3970 |
4512 |
4600 |
3503 |
Плохо |
|
10 |
Венгрия |
8912 |
7490 |
3570 |
8000 |
6993 |
Хорошо |
|
11 |
Болгария |
3590 |
3800 |
5464 |
5954 |
4702 |
Плохо |
|
12 |
Мин |
930 |
1045 |
3000 |
4500 |
||
|
13 |
Мах |
8912 |
7490 |
9100 |
11000 |
||
|
14 |
Среднее |
3827 |
4486 |
5807 |
7074 |
5298 |
|
|
15 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
16 |
Тенденция по среднему |
3639 |
4745 |
5852 |
6958 |
8064 |
9170 |
|
17 |
Рост по среднему |
3760 |
4639 |
5724 |
7063 |
8714 |
10752 |
|
18 |
Погрешность |
5,17% |
-5,48% |
-0,77% |
1,67% |
||
|
тенденции |
|||||||
|
19 |
Погрешность |
1,79% |
-3,32% |
1,44% |
0,17% |
||
|
роста |
|||||||
|
20 |
Лучший отель по сети |
Венгрия |
Венгрия |
Финляндия |
Германия |
||
|
21 |
Доход |
8912 |
7490 |
9100 |
11000 |
Дополнительные задания
- Выполнить условное форматирование Столбца Оценка – выделить красным цветом отели, доход которых меньше среднего.
- Определить лучший отель по сети за квартал и его доход.
- Дополнить таблицу строкой Предсказание для 5 и 6 кварталов.
- Построить диаграмму – график изменения доходов по кварталам и тенденцию изменения доходов по кварталам, включая прогноз на два следующие квартала, а также рост изменения доходов по кварталам.
Пример для отеля «Венгрия» представлен на диаграмме 1.
Диаграмма 1.
- Добавить на график линию тренда.
- Проще всего построить график функции тренда непосредственно сразу после внесения имеющихся данных в массив. Для этого на листе с таблицей данных выделите не менее двух ячеек диапазона, для которого будет построен график, и сразу после этого вставьте диаграмму. Вы можете воспользоваться такими видами диаграмм, как график, точечная, гистограмма, пузырьковая, биржевая. Остальные виды диаграмм не поддерживают функцию построения тренда.
- В меню «Диаграмма» выберите пункт «Добавить линию тренда». В открывшемся окне на вкладке «Тип» выберите необходимый тип линии тренда, что в математическом эквиваленте также означает и способ аппроксимации данных. При использовании описываемого метода вам придется делать это «на глаз», т.к. никаких математических вычислений для построения графика вы не проводили.
- Поэтому просто прикиньте, какому типу функции более всего соответствует график имеющихся данных: линейной, логарифмической, экспоненциальной, степенной или иной. Если же вы сомневаетесь в выборе типа аппроксимации, можете построить несколько линий, а для большей точности прогноза на вкладке «Параметры» этого же окна отметить флажком пункт «поместить на диаграмму величину достоверности аппроксимации (R^2)».
- Сравнивая значения R^2 для разных линий, вы сможете выбрать тот тип графика, который характеризует ваши данные наиболее точно, а, следовательно, строит наиболее достоверный прогноз. Чем ближе значение R^2 к единице, тем точнее вы выбрали тип линии. Здесь же, на вкладке «Параметры», вам необходимо указать период, на который делается прогноз.
- Такой способ построения тренда является весьма приблизительным, поэтому лучше все-таки произвести хотя бы самую примитивную статистическую обработку имеющихся данных. Это позволит построить прогноз более точно.
- Если вы предполагаете, что имеющиеся данные описываются линейным уравнением, просто выделите их курсором и произведите автозаполнение на необходимое число периодов, или количество ячеек. В данном случае нет необходимости находить значение R^2, т.к. вы заранее подогнали прогноз к уравнению прямой.
- Если же вы считаете, что известные значения переменной лучше всего могут быть описаны с помощью экспоненциального уравнения, также выделите исходный диапазон и произведите автозаполнение необходимого количества ячеек, удерживая правую клавишу мыши. При помощи автозаполнения вы не сможете построить других типов линий, кроме двух указанных.
Рабочее окно для построения линии тренда представлено на рисунке 1.
Рисунок 1.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5