Количество разрядов значащих цифр для хранения чисел в ms excel - Word и Excel

Содержание

Отображение в EXCEL ЧИСЕЛ с точностью более 15 значащих цифр
Последние цифры заменяются на ноли при введении длинных чисел в ячейки Excel
Симптомы
Причина
Обходной путь
Добавить кавычку
Формат ячеек
Дополнительная информация
Длинные числа отображаются неправильно в Excel
Симптомы
Обходной путь
Способ 1. Форматирование ячейки как текста
Способ 2. Использование одинарной кавычки
Связанные статьи
как в Excel Отключить обрезание чисел больших [закрыт]
1 ответ 1
Как уменьшить разрядность числа в excel
Как округлить числа в Excel — разные способы
Как сделать, чтобы Эксель не округлял числа, когда не надо
Как отключить округление в Эксель
Увеличение разрядности
Настройка формата
Изменение формата
Как сделать, чтобы данные в таблице Эксель округлялись
Кнопки в ленте
Округление через форматирование
Задание точности расчетов
Изменение функции
Дополнительный метод

Отображение в EXCEL ЧИСЕЛ с точностью более 15 значащих цифр

history 3 апреля 2013 г.

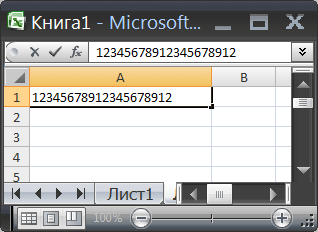
EXCEL хранит и выполняет вычисления с точностью 15 значащих цифр. Поэтому, не получится ввести 20-и значное число без того, чтобы EXCEL автоматически округлил его с точностью до 100 тыс. Используем текстовый формат для отображения таких чисел.

То, что вычисления в EXCEL производятся с точностью 15 значащих цифр, проявляется, например, при записи в ячейку целого двадцатизначного числа.

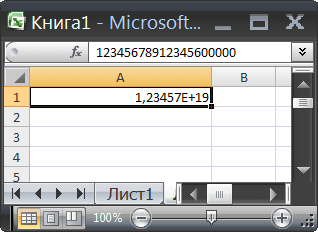
После нажатия клавиши ENTER происходит округление целого числа до 15 значащих цифр, последние цифры заменяются нулями (см. Строку формул на рисунке ниже). К числу будет применен экспоненциальный формат (см. ячейку А1 на рисунке ниже).

Увеличить точность вычислений в EXCEL нельзя. Однако, если не предполагается участие чисел в математических операциях, то для их хранения можно использовать текстовый формат. Такое решение подходит, например, для хранения номеров банковских счетов.

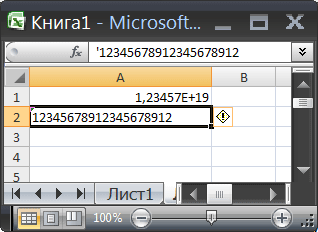
Для перевода ячейки в текстовый формат достаточно поставить перед значением апостроф (‘) или перед вводом изменить формат ячейки ( CTRL+1 ) на Текстовый .

Примечание . При подсчете таких значений могут возникнуть сложности (см. статью Подсчет ТЕКСТовых значений с единственным критерием в MS EXCEL ).

Источник

Последние цифры заменяются на ноли при введении длинных чисел в ячейки Excel

Симптомы

При введении числа, содержащего более 15 цифр в ячейку в Microsoft Excel, Excel заменяет любые цифры после пятнадцатого разряда на ноли. Например, введите идентификационный номер кредитной карты в следующем формате:

В этом случае Excel заменяет последнюю цифру на ноль.

Причина

Excel следует спецификации IEEE 754 в отношении хранения и вычисления чисел с плавающей точкой. Excel сохраняет только 15 значащих цифр числа и изменяет цифры после пятнадцатого разряда на ноль

Обходной путь

Добавить кавычку

Чтобы предотвратить изменение цифр на ноли, добавьте одинарную кавычку перед вводом числа.

Для этого выделите пустую ячейку, введите одну кавычку (‘), а затем введите число. Все цифры отображаются в ячейке.

Формат ячеек

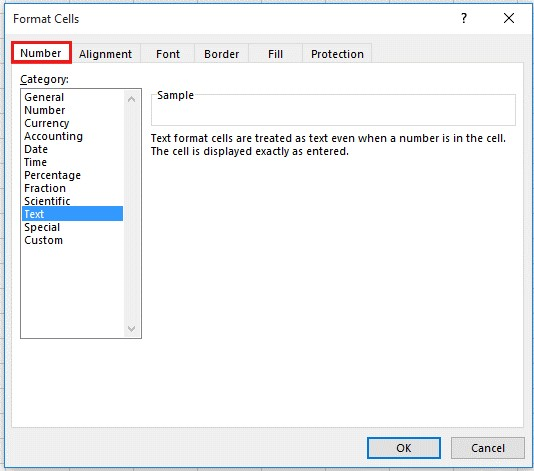
Чтобы не вводить кавычку в каждой ячейке, перед вводом каких-либо данных можно задать для этих ячеек текстовый формат.

Выберите все затронутые ячейки и нажмите Ctrl+1, чтобы открыть диалоговое окно Формат ячеек.

На вкладке Число выберите Текст из списка Категория, а затем выберите ОК.

Дополнительная информация

Это происходит только в том случае, если для ячейки задан формат Число, а введенное число содержит более 15 цифр. В форматированные в виде текста ячейки можно ввести до 32 767 символов. На листе Excel отображается до 1024 символов.

Так как настраиваемые форматы чисел предназначены для работы в основном с числами, невозможно создать настраиваемый формат номеров, который хранит более 15 цифр. Например, нельзя использовать следующий формат для хранения 16-символьного удостоверения кредитной карты в виде числа:

Однако, если ввести такое число в ячейке, которая форматирована как текст, все символы остаются в том виде, в котором они введены, так как Excel сохраняет это число в виде текста, а не числа.

Требуется дополнительная помощь? Зайдите на сайт сообщества Майкрософт.

Источник

Длинные числа отображаются неправильно в Excel

Симптомы

После ввода длинного номера (например, номера кредитной карты) в ячейке Excel номер отображается неправильно в Excel. Например,

Числовой формат по умолчанию в Excel является общим, поэтому вы можете отображать до 11 цифр в ячейке.

Обходной путь

Для решения проблемы используйте один из указанных ниже способов.

Способ 1. Форматирование ячейки как текста

Для этого выполните следующие действия:

Щелкните правой кнопкой мыши поле со списком и выберите пункт Формат ячеек.

На вкладке Число выберите Текст, а затем нажмите ОК.

Затем введите длинное число. (Не забудьте установить формат ячейки, прежде чем ввести число)

Если вы не хотите видеть предупреждающие стрелки, нажмите на маленькую стрелку, а затем Пропустить ошибку.

Способ 2. Использование одинарной кавычки

При вводе длинного числа сначала введите одинарную кавычку (‘) в ячейке, а затем длинное число.

Например, введите ‘1234567890123456789, и одинарная кавычка не будет отображаться после нажатия ENTER.

Связанные статьи

Ваше мнение важно для нас! Не стесняйтесь сообщать, что вы думаете об этой статье, используя поле комментария, расположенное внизу документа. Это позволит нам улучшить содержимое. Заранее спасибо!

Источник

как в Excel Отключить обрезание чисел больших [закрыт]

Скорее всего, данный вопрос не соответствует тематике Stack Overflow на русском, согласно правилам описанным в справке.

Закрыт 4 года назад .

Чтобы они отображались не так в графике 2E+09 а нормально в десятиричной системе без сокращений

1 ответ 1

Первое, что нужно учитывать: формат значения и формат ячейки — не одно и то же.

То, что видим (2E+09) — экспоненциальная форма записи числа 2000000000 (не только этого, см. ниже). Это же число можно получить:

Число не обрезано, но отображается в другом виде. Значение в нормальном его виде можно посмотреть в строке формул.

Но вот незадача. 2100000000 в экспоненциальной форме будет иметь ту же запись — 2E+09. А все потому, что формат ячейки выставлен Экспоненциальный, да еще и с нулевым количеством знаков в дробной части. Ставим два знака после запятой — получаем 2,10E+09

Excel сравнивает значение с заданными форматами и сам определяет, как его отображать. Иногда «зло шутит». Например, запись 1.02 (не в текстовой ячейке) воспринимается как дата день.месяц.(текущий_год), 11.22 — как дата месяц.день.(текущий_год). При этом Excel меняет не только формат отображения — он еще и значение изменит! Вместо введенного 1.02 получим дату 01.02.2018. Или, если установим формат ячейки Общий, увидим 43132 (количество дней после 01.01.1900)

Формат ячейки мог автоматически измениться на экспоненциальный в случае, когда ширина ячейки была недостаточна для отображения полного числа. Мог подтянуться при копировании данных.

Исправить «обрезанное» просто: задать достаточную ширину ячейки, задать ей формат Общий или Числовой с необходимым количеством знаков после запятой.

Важное примечание. Большие числа все же обрезаются, но это не связано с экспоненциальной формой записи.

Excel имеет ограничение при работе с числовыми данными — не более 15 разрядов. Если в ячейку вписать число 12345678901234567890, получим значение с обнуленными младшими разрядами — 12345678901234500000, от 1,2345678901234567890 останется 1,23456789012345.

Избежать обрезания можно, если установить текстовый формат ячейки. Текстом может храниться и длинное число. Это тоже бывает нужно: банковские счета, инвентарные номера. Т.е. фатически не числа, а текст, состоящий из цифр. Но использовать такие значения в качестве чисел не получится — при первой же попытке младшие разряды обнулятся.

Ради справедливости нужно отметить, что работать можно и с очень большими числами, разрядность которых превышает 15: хранить значения как текст, при использовании делить на допустимые фрагменты. Но это непросто и выходит за рамки вопроса.

Источник

Как уменьшить разрядность числа в excel

Как округлить числа в Excel — разные способы

Первый способ. Выделить одну или несколько ячеек, содержащих цифры, которые следует округлить. На вкладке «Главная» в разделе «Число» выбрать кнопку «Уменьшить разрядность». Нажать нужное количество раз. С каждым нажатием после запятой останется на одну цифру меньше.

Второй способ. Выделить одну или несколько ячеек, содержащих цифры, которые следует округлить. Нажать правую кнопку мыши, выбрать «Формат ячеек». На вкладке «Число» выбрать формат «Числовой», указать необходимое число десятичных знаков (количество знаков после запятой).

Третий способ. Использование функции «ОКРУГЛ». Ставим курсор в ячейку, где желаем получить результат – например, рядом с первоначальным числом. Набираем формулу: =ОКРУГЛ(число; число_разрядов), где число – ссылка на первоначальное число, число_разрядов – число цифр после запятой. При этом если число разрядов поставить отрицательное, цифра будет округляться до определенного разряда. Например, в ячейке А1 стоит число 314. Если запишем формулу =ОКРУГЛ(А1;-1), результат будет 310, если запишем формулу =ОКРУГЛ(А1;-2), результат будет 300.

Четвертый способ. Использование функции «ОКРУГЛТ» округляет число до желаемой точности. Например, при заданной формуле =ОКРУГЛТ(А1;10) наше число 314 округлится до 310, при заданной формуле =ОКРУГЛТ(А1;100) число 314 округлится до 300.

Как сделать, чтобы Эксель не округлял числа, когда не надо

Как сделать, чтобы Эксель не округлял числа? Воспользуйтесь функцией увеличения разрядности, используйте настройку или изменение формата ячеек. Выберите подходящую секцию, войдите в раздел «Число», и жмите на кнопку «Увеличить разрядность». После контролируйте изменения и учтите, что после выключения округления каждый последующий знак будет ноль. Ниже рассмотрим, как сделать, чтобы Эксель не округлял числа, и каким образом можно на место вернуть настройки.

Как отключить округление в Эксель

В процессе пользования Эксель часто возникает ситуации, когда при вводе данных цифры округляются. Это может влиять на точность расчеты и визуальное восприятие информации. В таком случае выделяется несколько вариантов, как сделать, чтобы Excel не округлял числа. Рассмотрим основные решения.

Увеличение разрядности

Наиболее простой метод выключения — применение опции увеличения разрядности, которая работает по принципу добавления чисел после запятой. Для решения задачи сделайте следующие шаги:

Определитесь, в какой ячейке не нужно округлять числа в Excel.
В разделе «Число» разверните список форматов и примите решение, какой хотите использовать.

Кликните по кнопке «Увеличить разрядность» в Эксель нужное число раз.

Контролируйте правки путем просмотра состояния секции и учтите, что после установки нужной функции округление выключиться. При добавлении нового знака будет «0».

В более новых версиях Excel этот метод будет иметь другой вид:

Зайдите на кладку «Главная».
Жмите на символ стрелки вниз справа от надписи «Число».
В разделе «Категория» выберите нужный числовой вариант и убедитесь, что он имеет десятичные разряды.
Найдите поле «Число десятичных» и введите нужную цифру, а после жмите «ОК».

Настройка формата

Еще один способ сделать так, чтобы Эксель не округлял — настроить формат и установить точное количество знаков после запятой. В настройках можно с легкостью увеличить цифру до требуемого, выключив округление. Для этого потребуется специальное меню в программе:

Выделите место в таблице, где нужно внести соответствующие изменения.
Разверните меню «Ячейки» и кликните на «Формат».

Выберите «Формат …».
Выделите с помощью левой кнопкой мышки ту цифру, которая применяется для выделенных ранее секций.
Установите количество знаков, вписав его в отведенное поле, используйте новые настройки и покиньте меню.

Посмотрите на выделенные ячейки и убедитесь в правильности отображения.

Изменение формата

Чтобы в Экселе не округлять числа, можно изменить формат. Этот вариант наиболее привлекательный в ситуации, когда в ячейке не хватает места для установки всех знаков. Можно использовать рассмотренный выше метод и поменять формат, но результат будет виден только после выхода из меню. Лучше войти в раздел «Число», как отмечалось в первом способе, и посмотреть представление цифр для других форматов. Выберите тот, который вам подходит, и сразу оцените изменения.

Как сделать, чтобы данные в таблице Эксель округлялись

Рассмотренные выше шаги позволяют сделать, чтоб Эксель не округлял числа. Но бывают ситуации, когда выполнение такого шага является обязательным для пользователя. В таком случае нужно снова включить опцию одним из доступных способов. Ниже рассмотрим наиболее востребованные варианты.

Кнопки в ленте

Наиболее простой метод, как сделать, чтобы Excel снова округлял, выделить одну / несколько ячеек, а после пройти такие шаги:

Войдите в «Главная».
Жмите на ленте кнопку «Увеличить / уменьшить разрядность». В первом случае количество знаков увеличивается, а во втором уменьшается на одну цифру.

Округление через форматирование

Выше мы разобрали, как не округлять в Экселе с помощью форматирования. Этот же метод можно использовать для включения опции. Сделайте следующие шаги:

Выделите диапазон ячеек на листе, жмите правой кнопкой мышки и кликните «Формат …».

Перейдите в раздел «Число». Если выбран не числовой вариант, выберите его. В ином случае сделать так, чтобы Эксель округлял, не получится.
В «Число десятичных знаков» внесите нужные данные.

Задание точности расчетов

Рассмотренные выше методы в Эксель оказывают влияние только на внешнее отображение в Эксель, а при расчетах использовались только точные показатели (до 15-ти знаков). При необходимости можно поменять точность вычислений. Сделайте следующее:

Войдите в «Файл», а далее «Параметры».

Найдите «Дополнительно», отыщите блок настроек «При пересчете этой книги».
Поставьте отметку возле параметра «Задать точность как на экране».

После выполнения этой задачи система будет округлять величину и использовать ее для вычислений.

Изменение функции

Для изменения размера округления при расчете одной, двух или более ячеек без уменьшения точности расчетов нужно использовать функцию округления «ОКРУГЛ» и разные ее варианты. К наиболее популярным относится «ОКРУГЛ» или округление до указанного числа десятичных знаков, «ОКРУГЛВВЕРХ» — до ближайшего верхнего, а «ОКРУГЛВНИЗ» — до ближайшего нижнего. Также можно сделать, чтобы Эксель округлял с заданной точностью с помощью «ОКРУГЛТ», или до ближайшего четного / нечетного параметра — «ЧЕТН», «НЕЧЕТН». Интересующую функцию можно вводить как в ячейку, так и в строку.

Дополнительный метод

Можно выделить еще один метод, как сделать, чтобы Excel округлял числа. Он подходит для случаев, когда в таблице находятся параметры, требующие преобразования. Сделайте следующие шаги:

Войдите во вкладку «Формулы».
Жмите на «Математические».
В появившемся списке выберите «ОКРУГЛ».
В окне аргументов в поле «Число» введите вручную нужный параметр.
Жмите по ячейке, где нужно, чтобы Эксель округлял цифры.
Откройте окно аргументов в поле «Число разрядов».
Укажите разрядность, до которой нужно сократить дробь.

Теперь вы знаете, как сделать, чтобы Excel не округлял, какие методы для этого существуют, и как вернуть нужные настройки обратно.

Источник

     MS Excel оперирует числами в двоичной системе счисления, при этом для хранения каждого двоичного числа используется 8 байт (64 двоичных разряда). Поэтому любое десятичное число в MS Excel может содержать не более 15 значащих цифр. Если ввести десятичное число, содержащее более 15 значащих цифр, то «лишние» цифры просто отбрасываются или заменяются нулями, но число не округляется.
     Если во введённом числе целая часть состоит более чем из 15 цифр, то нулями заменяются младшие разряды числа, а само число отображается в экспоненциальном формате.
     Если вводится дробное число, у которого целая часть имеет менее 15 цифр, то отбрасываются все цифры, начиная с 16-й, которые отсчитываются от старшего разряда числа, при этом число будет отображаться в обычном или экспоненциальном формате (если целая часть состоит из более чем 12 цифр).
     Если вводится дробное число с нулевой целой частью, то 15 цифр, которые сохраняются в числе, отсчитываются вправо от десятичной запятой, при этом число будет отображаться в экспоненциальном формате.
     Следует понимать, что при использовании различных встроенных форматов Excel, в отличии от отбрасывания «лишних» цифр, происходит округление отображаемых значений чисел, хотя в ячейке по-прежнему хранятся первоначально введённые числа.
     Точность отображения результатов вычисления функций Excel так же определяется 15-ю значащими цифрами. Но это, конечно, ничего не говорит о точности вычисленного значения, возвращаемого функцией, которая определяется используемыми алгоритмами вычисления функций. Однако, какие бы алгоритмы не использовались, точность вычислений опять же не может превышать 10^-15.
     Отмечу так же, что функции, которые должны возвращать целочисленные значения (например, функции подсчёта количества в заданном диапазоне с определённым содержимым), всегда возвращают именно целые числа, а не дробные числа, округлённые до целых.

Ниже приведена таблица технических характеристик и ограничений вычислений MS Excel:

Параметр	Значение
Точность представления чисел, разрядов, не более	15
Допустимое отрицательное число, не менее	-2,2251E+308
Допустимое положительное число, не менее	2,23E-308
Допустимое положительное число, не более	1,00E+308
Допустимое отрицательное число, не более	-1,00E+308
Наибольшее положительное число, получаемое в формуле	1,7976931348623158E+308
Наибольшее отрицательное число, получаемое в формуле	-1,7976931348623158E+308
Длина записи формулы, знаков, не более*	8 192
Внутренняя длина формулы, байт, не более	16 384 байт
Количество итераций, не более	32 767
Количество массивов в книге	Ограничено объемом доступной оперативной памяти
Количество выделенных диапазонов, не более	2 048
Количество аргументов функции, не более**	255
Количество уровней вложенности функций, не более***	64
Количество категорий пользовательских функций, не более	255
Количество доступных функций листа Microsoft Excel, не более****	341
Размер стека операндов, не более	1 024
Перекрестная зависимость листов, не более	64 000 листов, которые могут ссылаться на другие листы
Перекрестная зависимость формул массива на разных листах	Ограничена объемом доступной оперативной памяти
Зависимость областей	Ограничена объемом доступной оперативной памяти
Зависимость областей на каждом листе	Ограничена объемом доступной оперативной памяти
Зависимости одной ячейки, не более	4 миллиарда формул, зависящих от одной ячейки
Длина содержимого связанной ячейки из закрытых книг, не более	32 767
Допустимая в расчетах дата, не ранее	1 января 1900 г. (1 января 1904 г. для системы дат 1904)
Допустимая в расчетах дата, не позднее	31 декабря 9999 г.
Интервал времени, который можно ввести, не более	9999:59:59

Примечания:
* — В версиях ранее Excel 2007 — не более 1024 знаков;
** — В версиях ранее Excel 2007 — не более 30;
*** — В версиях ранее Excel 2007 — не более 7, в версии Excel 2010 — не более 128 уровней;
**** — В версиях ранее Excel 2007 — не более 329.

Источник

Подборка по базе: ари вопросы.docx, Уголовное вопросы.docx, 30 вопрос.docx, Дифференциальная психология 59 вопросов.docx, упп до 150 вопроса(Данияр).docx, тестовые вопросы для РК1 Бизнес (копия).docx, SERM-продвижение 58 вопросов.docx, Задание 2 к теме 5 (исправленный) + ответы на вопросы в коммента, Тема № 10. Страницы воинской доблести (о мужестве и верности …, 10 билет, 2 вопрос.pptx

Вопрос 19

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Формулу =СУММЕСЛИ(A1:C1;»<0″;A3:C3) из ячейки D1 скопировали в ячейку D2. Результат вычислений: …

Ответ:

Вопрос 20

Неверно

Баллов: 0,00 из 1,00

Отметить вопрос

Текст вопроса

Тип данных, который автоматически выравнивается по левой границе в ячейках MS Excel:

Выберите один ответ:

a. формула

b. числовой

c. дата и время

d. текстовый

Вопрос 21

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Диаграмма, изображенная на рисунке :

Выберите один ответ:

a. график

b. круговая

c. линейчатая

d. гистограмма

Вопрос 22

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Дата в MS Excel хранится как целое число, обозначающее количество дней:

Выберите один ответ:

a. оставшихся до 31 декабря 3000 года

b. прошедших с 1 января 1950 года

c. прошедших с 1 января 1900 года

d. оставшихся до 31 декабря 2050 года

Вопрос 23

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Максимально количество листов в рабочей книге MS Excel:

Выберите один ответ:

a. 3

b. нет ограничений

c. 255

d. 1000

Вопрос 24

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Чтобы текст, вводимый в ячейку листа MS Excel, полностью отображался в ней, нужно:

Выберите один ответ:

a. занять текстом две соседние ячейки

b. установить для ячейки атрибут «Переносить по словам»

c. увеличить ширину этой ячейки

d. текст всегда отображается полностью

Вопрос 25

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Инструмент, позволяющий создавать в MS Excel произвольные числовые последовательности, арифметические и геометрические прогрессии, ряды дат и времени – это:

Выберите один ответ:

a. автозамена

b. автофильтр

c. автозавершение

d. автозаполнение

Вопрос 26

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Книгой в MS Office называют:

Выберите один ответ:

a. шаблон MS Word

b. файл электронной таблицы

c. файл СУБД Access

d. документ MS Word

Вопрос 27

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Инструменты, которые можно использовать при работе со списками MS Excel:

Выберите один или несколько ответов:

a. автофильтр

b. промежуточные итоги

c. расширенный фильтр

d. создание последовательностей

Вопрос 28

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Количество разрядов (значащих цифр) для хранения чисел в MS Excel:

Выберите один ответ:

a. нет ограничений

b. 6

c. 15

d. 10

Вопрос 29

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Интерактивная таблица рабочего листа, позволяющая быстро суммировать большие объемы данных с применением выбранного пользователем формата и метода вычисления, – это … таблица.

Ответ:

Вопрос 30

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Неверный формат числовых данных в MS Excel:

Выберите один ответ:

a. денежный

b. строковый

c. финансовый

d. числовой

Вопрос 1

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Для вызова редактора VBA следует нажать комбинацию клавиш:

Выберите один ответ:

a. Ctrl+Alt

b. Alt+F11

c. F1

d. Ctrl+Alt+Del

Вопрос 2

Частично правильный

Баллов: 0,33 из 1,00

Отметить вопрос

Текст вопроса

К объектам приложения MS Excel относятся:

Выберите один или несколько ответов:

a. Range

b. Application

c. Cell

d. VBA

Вопрос 3

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Последовательность действий пользователя, записанная в виде программы, — это:

Выберите один ответ:

a. шаблон

b. форма

c. макрос

d. модуль

Вопрос 4

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Записанная последовательность команд, которая может быть воспроизведена для автоматизации часто повторяемых действий, — это:

Выберите один ответ:

a. модуль

b. макрос

c. формула

d. функция

Вопрос 5

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Для выполнения процедуры в редакторе VBA нужно нажать клавишу:

Выберите один ответ:

a. Alt+F11

b. F5

c. F11

d. F1

Вопрос 6

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

К элементам управления, которые можно размещать на форме (пользовательское окно диалога) относятся:

Выберите один или несколько ответов:

a. надпись

b. кнопка

c. поле вывода

d. список

Вопрос 7

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Для работы в редакторе VBA на ленте должна присутствовать вкладка:

Выберите один ответ:

a. Сервис

b. Данные

c. Разработчик

d. Главная

Вопрос 8

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Набор программ, связанных с основным документом приложения, хранящийся с данными документа в одном файле, -это:

Выберите один ответ:

a. форма

b. процедура

c. функция

d. проект

Вопрос 9

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Совокупность объявлений и процедур, собранных вместе и составляющих самостоятельную программную единицу проекта, — это:

Выберите один ответ:

a. модуль

b. форма

c. функция

d. класс

Вопрос 10

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Встроенный язык программирования в среде MS Office — это:

Выберите один ответ:

a. Паскаль

b. С++

c. Пролог

d. VBA

Вопрос 1

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Для установления соответствия между таблицами базы данных необходимо:

Выберите один ответ:

a. индексирование

b. связывание данных

c. группировка

d. сортировка

Вопрос 2

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Для ввода, отображения и редактирования данных в MS Access служит объект базы данных:

Выберите один ответ:

a. форма

b. запрос

c. модуль

d. отчет

Вопрос 3

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Свойство «маска ввода» предназначено для задания:

Выберите один ответ:

a. типа поля

b. признака ключевого поля

c. размера поля

d. формата представления данных

Вопрос 4

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

База данных — это:

Выберите один ответ:

a. набор программ, обеспечивающих автоматизацию профессиональной деятельности

b. структурированная совокупность данных, предназначенных для хранения и использования

c. прикладная программа для обработки данных пользователя

d. таблица, позволяющая хранить и обрабатывать данные и формулы

Вопрос 5

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Объекты базы данных, на основе которых можно формировать запросы, — это:

Выберите один ответ:

a. таблицы и запросы

b. формы

c. модули

d. отчеты

Вопрос 6

Неверно

Баллов: 0,00 из 1,00

Отметить вопрос

Текст вопроса

Элементарной единицей логической организации данных, которая соответствует неделимой единице информации в MS Access, является:

Выберите один ответ:

a. формула

b. запись

c. таблица

d. поле

Вопрос 7

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Одно или несколько полей, комбинация значений которых однозначно определяет каждую запись в таблице базы данных, называются:

Выберите один ответ:

a. надпись

b. индекс

c. ключ

d. маска

Вопрос 8

Неверно

Баллов: 0,00 из 1,00

Отметить вопрос

Текст вопроса

Объект базы данных MS Access, предназначенный для хранения данных:

Выберите один ответ:

a. таблица

b. форма

c. модуль

d. отчет

Вопрос 9

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Элемент управления, предназначенный для выполнения вычислений в MS Access:

Выберите один ответ:

a. надпись

b. поле

c. присоединенная рамка объекта

d. свободная рамка объекта

Вопрос 10

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

В основе построения баз, с которыми работает MS Access лежит модель данных:

Выберите один ответ:

a. реляционная

b. иерархическая

c. даталогическая

d. сетевая

Вопрос 1

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

К сервисам Интернета можно отнести:

Выберите один или несколько ответов:

a. WWW

b. E-mail

c. TCP/IP

d. FTP

Вопрос 2

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Протокольной основой Интернета является:

Выберите один ответ:

a. адресная книга

b. система IP-адресов

c. протоколы тестирования сетевого компьютера

d. последовательность адресов

Вопрос 3

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Программа для просмотра web-страниц — это…

Ответ:

Вопрос 4

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

К способам конфигурации (топологии) компьютерных сетей относятся:

Выберите один или несколько ответов:

a. звезда

b. кольцо

c. последовательность

d. шина

Вопрос 5

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Протокол — это:

Выберите один ответ:

a. структуризация данных в сети

b. правила хранения данных в сети

c. правила организации передачи данных в сети

d. пакет данных

Вопрос 6

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Online — это:

Выберите один ответ:

a. информационная сеть

b. команда

c. режим реального времени

d. утилита

Вопрос 7

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Домен — это:

Выберите один ответ:

a. почтовый ящик узловой станции

b. код страны

c. название файла в почтовом ящике

d. группа компьютеров,имеющая общую часть в интернет-адресе

Вопрос 8

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Сервер — это:

Выберите один ответ:

a. один или несколько мощных компьютеров для обслуживания сети

b. мультимедийный компьютер с модемом

c. высокопроизводительный компьютер

d. хранитель программы начальной загрузки

Вопрос 9

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

IP-адрес состоит :

Выберите один ответ:

a. из адреса сети

b. из протокола

c. из последовательности адресов

d. из адреса сети и номера хоста

Вопрос 10

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Модем — это:

Выберите один ответ:

a. хранилище информации

b. транспортная основа сети

c. устройство, которое управляет процессом передачи информации

d. устройство преобразования цифровых сигналов в аналоговые и наоборот

Вопрос 11

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Какие протоколы поддерживает Интернет:

Выберите один ответ:

a. SCP

b. SCP/IP

c. TCP/IP

d. QCP/IP

Вопрос 12

Частично правильный

Баллов: 0,50 из 1,00

Отметить вопрос

Текст вопроса

Транспортная основа глобальной сети — это:

Выберите один или несколько ответов:

a. коаксиальный кабель

b. витая пара

c. телеграф

d. телефонные линии и спутниковые каналы

Вопрос 13

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

WWW — это:

Выберите один ответ:

a. электронная книга

b. информационная среда обмена файлами

c. протокол размещения информации в Интернет

d. распределенная информационная система мультимедиа, основанная на гипертексте

Вопрос 14

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Наиболее важным для организации компьютерной сети является:

Выберите один ответ:

a. несколько сетевых операционных систем

b. высокоскоростные модемы

c. наличие большого количества компьютеров

d. система протоколов

Вопрос 15

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Основная функция сервера:

Выберите один ответ:

a. хранит информацию

b. пересылает информацию от клиента к клиенту

c. выполняет специфические действия по запросам клиентов

d. кодирует информацию, предоставляемую клиентом

Вопрос 16

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

HTML — это:

Выберите один ответ:

a. прикладная программа

b. язык разметки гипертекста

c. программа просмотра www-документов

d. протокол взаимодействия клиент-сервер

Вопрос 17

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Программы, не являющиеся браузерами:

Выберите один ответ:

a. Google Chrome

b. Internet Explorer

c. Google

d. Opera

Вопрос 18

Неверно

Баллов: 0,00 из 1,00

Отметить вопрос

Текст вопроса

Гипертекст — это:

Выберите один ответ:

a. хранилище информации

b. банк данных

c. информационная оболочка

d. информация в виде документов, имеющих ссылки на другие документы

Вопрос 19

Неверно

Баллов: 0,00 из 1,00

Отметить вопрос

Текст вопроса

Линии связи, используемые для построения локальных сетей:

Выберите один ответ:

a. только оптоволокно

b. витая пара, коаксиальный кабель, оптоволокно и беспроводные линии связи

c. только витая пара

d. толстый и тонкий коаксиальный кабель

Вопрос 20

Неверно

Баллов: 0,00 из 1,00

Отметить вопрос

Текст вопроса

Хост-машина — это:

Выберите один ответ:

a. банк информации

b. компьютерный узел связи

c. мультимедийный компьютер

d. машина-хранилище информации

Вопрос 1

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Антивирусные программы — это:

Выберите один ответ:

a. специальные программы для обнаружения вирусов

b. специальные программы для просмотра вирусов

c. специальные программы для удаления вирусов

d. специальные программы для обнаружения и удаления вирусов

Вопрос 2

Неверно

Баллов: 0,00 из 1,00

Отметить вопрос

Текст вопроса

Аутентификация — это:

Выберите один ответ:

a. подтверждение целостности и неизменности данных

b. дешифрование информации

c. шифрование информации

d. подтверждение личности отправителя

Вопрос 3

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Для профилактики заражения компьютера вирусом через flash-карту нужно с помощью антивирусной программы:

Выберите один ответ:

a. проверить дискету на наличие вирусов

b. проверить жесткий диск на наличие вирусов

c. проверить компьютер на наличие вирусов

d. проверить flash-карту на наличие вирусов

Вопрос 4

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

К основным классам антивирусных программ относятся:

Выберите один или несколько ответов:

a. программы-детекторы

b. программы-сторожа

c. программы-архиваторы

d. программы-доктора

Вопрос 5

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Главной задачей криптографии является:

Выберите один ответ:

a. шифрование и кодирование информации с целью ее защиты от несанкционированного прочтения

b. шифрование информации

c. кодирование информации

d. передача данных в компьютерной сети

Вопрос 6

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Компьютерные вирусы -это:

Выберите один ответ:

a. программы, способные создавать текстовые документы

b. программы, которые позволяют обрабатывать табличные данные

c. макросы

d. специально написанные программы, способные внедряться в файлы и системные области компьютера и создавать копии

Вопрос 7

Неверно

Баллов: 0,00 из 1,00

Отметить вопрос

Текст вопроса

Несуществующий тип компьютерных вирусов — это:

Выберите один ответ:

a. макровирусы

b. файловые вирусы

c. загрузочные вирусы

d. микровирусы

Вопрос 8

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Косвенными признаками, указывающими на наличие компьютерного вируса, могут служить:

Выберите один или несколько ответов:

a. самопроизвольный запуск программ

b. частые зависания компьютера

c. медленная работа компьютера

d. появление заставки

Вопрос 9

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Сетевые вирусы могут распространяться и заражать компьютеры:

Выберите один ответ:

a. через программу MS Word

b. через диски

c. через программу MS Excel

d. через компьютерные сети

Вопрос 10

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Источником заражения компьютерными вирусами является в основном:

Выберите один ответ:

a. программа Nod32

b. винчестер

c. сеть Интернет

d. Doctor Web

Источник

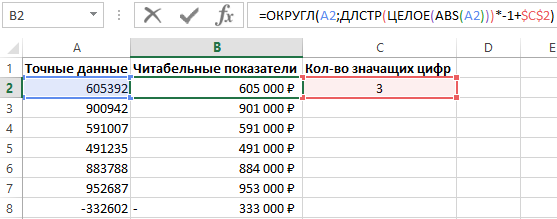
В некоторых финансовых отчетах данные показателей представлены с точностью округления до определенных значащих цифр. Что значит значащая цифра? Дело в том, что при визуальном анализе презентаций отчетов с миллионами не нужно засорять точными числовыми значениями отображая каждую цифру в числе (единицы, десятки, сотни и тысячи), чтобы не ухудшить читабельность данных.

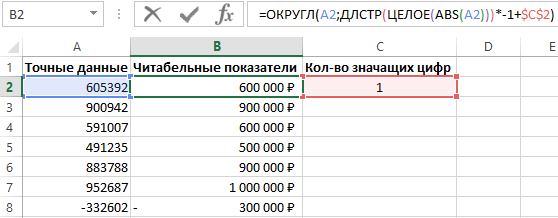
Например, вместо того чтобы в презентации отчета указывать сумму 883 788 $, можно округлить до одной значащей цифры. Это значит, что после округления будет отображена сумма легкая к восприятию 900 000 $. Если округлить исходное число до двух значащих цифр, в результате получим значение числа 880 000 $.

Как округлить до трех значащих цифр в Excel

В Excel все решает пользователь. Программа округлит дробные или даже целые числа в зависимости какое число значащих цифр удовлетворит потребность пользователя. Несомненно, на первый взгляд такое округление может вызывать сомнение в рациональности решения. Однако в презентациях есть место быть как точным показателям, так и относительным. И в других ситуациях это также применимо. Например, в стратегическом планировании более важные относительные показатели, так как сколько не планируй никогда не угадаешь точные результирующие числа. В тактическом планировании более важны точные значения чтобы избежать серьезных просчетов. В стратегическом планировании где показатели достигают миллионов, каждое значение ниже определенного числа значащих цифр – не существенно.

Ниже на рисунке показано, как составить формулу, которая округляет миллионные числовые значения до заданного числа значащих цифр:

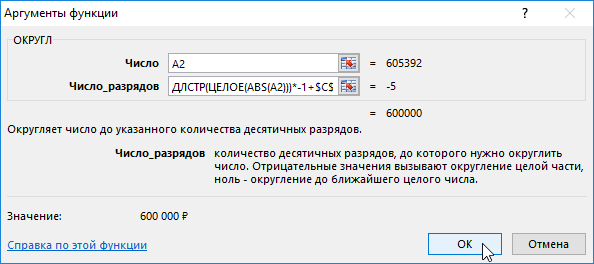
Функция ОКРУГЛ используется для округления исходного числового значения до определенного количества разрядов после запятой. Функция содержит 2 аргумента:

Число – ссылка на исходное значение, которое необходимо округлить.
Число-разрядов – количество разрядов, которое необходимо оставить после округления исходного числа.

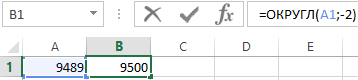
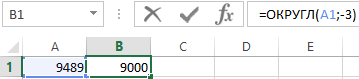
Если во втором аргументе функции ОКРУГЛ указать отрицательное число, тогда Excel округлит исходное числовое значение в соответствии цифр по левой стороне запятой. Например, следующая формула возвращает в результате вычисления число 9500:

А если указать во втором аргументе значение -3, тогда функция ОКРУГЛ возвращает результат 9000:

Такая формула прекрасно работает, но не всегда. Например, что будет если исходные числовые значения будут разных величин числовых радов? Одни будут более миллиона, другие едва превышают сотни тысяч. Если возникнет необходимость округлить все такие исходные значения до одной и той же значащей цифры используя при этом одну и туже формулу (как обычно принято в Excel). Применять для отдельных групп исходных значений функцию ОКГРУГЛ с разными значениями в аргументах – это не правильное, а точнее не наилучшее решение. Хотя теоретически все может сработать.

Для красивого решения данной задачи следует использовать постоянное неизменяемое число значащих цифр в формуле, которая вычислит соответствующие значения.

Как узнать количество значащих цифр в Excel

Допустим исходное значение — это число -2330,45. Для вычисления числа значащих цифр в функции ОКРУГЛ можно использовать такую формулу:

Данная формула сначала преобразовывает заданное исходное отрицательно число в положительное используя функцию ABS (уберет знак минус спереди при его наличии). Полученный результат далее обрабатывается функцией ЦЕЛОЕ, котаря убирает все разряды после запятой. Далее полученный результат обрабатывается функцией ДЛСТР с целью подсчета количества символов из которых состоит исходное числовое значение без знака минуса и запятой.

В данном случаи функция ДЛСТР возвращает значение 4. Если из числа -2330,45 убрать знак минус и числа после запятой мы получим 4 цифры.

Далее результат функции умножается на отрицательное число -1, чтобы получить отрицательное значение (для второго аргумента функции ОКГРУГЛ). А после добавляется желаемое количесвто значащих цифр. В данном примере вычисление выглядит следующим образом: 4*(-1)+2=-2.

Подобно как в предыдущих примерах данная формула будет использоваться в качестве второго аргумента для функции ОКРУГЛ. Введите в Excel следующую формулу и округлите исходные данные -2330,45 до -2300:

Округляем до 3 значащих цифр в Excel

Число 2 указанное в аргументе данной формулы можно заменить на ссылку с ячейкой в которой будет указано желаемое число заданных значащих цифр пользователем. Как на рисунке с примером.

Таким образом можно округлить до 3 или 5 значащих цифр. Просто укажите необходимое значение в ячейке C2.

Источник

Как и другие электронные таблицы, Microsoft Excel работает только с ограниченной точностью, поскольку сохраняет только определенное количество цифр для описания чисел (имеет ограниченную точность ). За некоторыми исключениями, касающимися ошибочных значений, бесконечностей и денормализованных чисел, Excel выполняет вычисления в формате с плавающей запятой двойной точности из спецификации IEEE 754 (помимо чисел Excel использует несколько других типов данных). Хотя Excel может отображать 30 десятичных разрядов, его точность для указанного числа ограничена 15 значащими цифрами , а точность вычислений может быть еще меньше из-за пяти проблем: округление , усечение и двоичное хранение , накопление отклонений от операнды в вычислениях, и хуже всего: отмена при вычитании соотв. «Катастрофическая отмена» при вычитании значений с аналогичной величиной.

Точность и двоичная память

Excel поддерживает 15 цифр в своих числах, но они не всегда точны: математически нижняя строка должна быть такой же, как и верхняя строка, в ‘fp-math’ шаг ‘1 + 1/9000’ приводит к округлению в большую сторону, так как первый бит 14-битного хвоста ‘10111000110010’ мантиссы, выпадающий из таблицы при добавлении 1, равен ‘1’, это округление в сторону увеличения не отменяется при повторном вычитании 1, поскольку нет информации о происхождении значений на этом этапе. Таким образом, «повторное вычитание» 1 оставляет мантиссу, оканчивающуюся на «100000000000000» вместо «010111000110010», представляющую значение «1.1111111111117289E-4», округленное ex $ el до 15 значащих цифр: «1.11111111111173E-4».

Конечно, математический 1 + x — 1 = x, «математика с плавающей запятой» иногда немного отличается, в этом нельзя винить Excel. Несоответствие указывает на ошибку. Все ошибки выходят за пределы 15-й значащей цифры промежуточного значения 1 + x, все ошибки относятся к разрядам высокого значения окончательного результата, что является проблемным эффектом «отмены».

На верхнем рисунке отображается дробь 1/9000 в Excel. Хотя это число имеет десятичное представление, представляющее собой бесконечную строку единиц, Excel отображает только первые 15 цифр. Во второй строке к дроби добавляется цифра один, и снова Excel отображает только 15 цифр. В третьей строке вычитается единица из суммы с помощью Excel. Поскольку в сумме после десятичной дроби всего одиннадцать единиц, истинная разница после вычитания «1» составляет три нуля, за которыми следует строка из одиннадцати единиц. Однако разница, о которой сообщает Excel, составляет три нуля, за которыми следует 15-значная строка из тринадцати единиц и двух дополнительных ошибочных цифр. Таким образом, числа, которые вычисляет Excel, не являются числами, которые он отображает. Более того, ошибка в ответе Excel — это не просто ошибка округления, это результат вычислений с плавающей запятой, называемый «отменой».

Погрешность расчетов в Excel сложнее ошибок из-за точности до 15 значащих цифр. Хранение чисел в двоичном формате в Excel также влияет на его точность. В качестве иллюстрации на нижнем рисунке представлена таблица простого сложения 1 + x — 1 для нескольких значений x . Все значения x начинаются с 15-го десятичного знака, поэтому Excel должен их учитывать. Перед вычислением суммы 1 + x Excel сначала приближает x как двоичное число. Если эта двоичная версия x представляет собой простую степень двойки , 15-значное десятичное приближение к x сохраняется в сумме, а два верхних примера на рисунке указывают на восстановление x без ошибок. В третьем примере x — более сложное двоичное число, x = 1,1 · 10111 111 × 2 ⁻⁴⁹ (всего 15 бит). Здесь двойное значение IEEE 754, полученное в результате 15-битного числа, составляет 3,330560653658221E-15, которое Excel округляет для «пользовательского интерфейса» до 15 цифр 3,33056065365822E-15, а затем отображается с 30-ю десятичными цифрами и получает одно «поддельное». ноль », поэтому« двоичные »и« десятичные »значения в образце идентичны только на дисплее, значения, связанные с ячейками, различаются (1,1101111111111100000000000000000000000000000000000000 × 2 ^{−49 по} сравнению с 1.1101111111111011111111111111111111111111111111111101 × 2 ⁻⁴⁹ ). То же самое делают и другие электронные таблицы, обрабатывая различное количество десятичных цифр, которые могут быть точно сохранены в 53-битной мантиссе двойного числа (например, 16 цифр между 1 и 8, но только 15 цифр между 0,5 и 1 и между 8 и 10) довольно сложно и решается «неоптимально». В четвертом примере x — десятичное число, не эквивалентное простому двоичному разряду (хотя оно согласуется с двоичным кодом третьего примера относительно отображаемой точности). Десятичный ввод аппроксимируется двоичным, а затем используется это десятичное число. Эти два средних примера на рисунке показывают, что вносится некоторая ошибка.

Последние два примера иллюстрируют, что происходит, если x — довольно небольшое число. Во втором из последнего примера x = 1,110111 111 × 2 ⁻⁵⁰ ; Всего 15 бит. Двоичный код очень грубо заменяется одной степенью двойки (в этом примере ^2–49 ) и используется ее десятичный эквивалент. В нижнем примере десятичное число, идентичное приведенному выше двоичному с указанной точностью, тем не менее аппроксимируется иначе, чем двоичное, и исключается путем усечения до 15 значащих цифр, не влияя на 1 + x — 1 , что приводит к x = 0. .

Для x ′ s, которые не являются простыми степенями 2, заметная ошибка в 1 + x — 1 может возникнуть, даже если x довольно велико. Например, если x = 1/1000, то 1 + x — 1 = 9,99999999999 89 × 10 ⁻⁴ , ошибка в 13-й значащей цифре. В этом случае, если бы Excel просто добавлял и вычитал десятичные числа, избегая преобразования в двоичное и обратно в десятичное, ошибки округления не возникало бы, и точность фактически была бы лучше. В Excel есть опция «Установить точность как отображаемую». С этим вариантом, в зависимости от обстоятельств, точность может быть лучше или хуже, но вы будете точно знать, что делает Excel. (Сохраняется только выбранная точность, и нельзя восстановить дополнительные цифры, изменив эту опцию.) Некоторые похожие примеры можно найти по этой ссылке.

Короче говоря, разнообразие поведения точности вводится путем комбинации представления числа с ограниченным количеством двоичных цифр, наряду с усечением чисел после пятнадцатой значащей цифры. Обработка в Excel чисел, превышающих 15 значащих цифр, иногда способствует большей точности последних нескольких значащих цифр в вычислении, чем прямая работа только с 15 значащими цифрами, а иногда и нет.

Обоснование преобразования в двоичное представление и обратно в десятичное, а также дополнительные сведения о точности в Excel и VBA см. По этим ссылкам.

1. Недостатки в задачах «= 1 + x — 1» представляют собой комбинацию «слабых сторон fp-math» и «того, как Excel справляется с этим», особенно округления Excel. Excel выполняет округление и / или «привязку к нулю» для большинства своих результатов, в среднем отбрасывая последние 3 бита двойного представления IEEE. Это поведение можно отключить, задав формулу в скобках: ‘= (1 + 2 ^ -52-1)’. Вы увидите, что даже эта небольшая ценность сохраняется. Меньшие значения исчезнут, поскольку для представления значения имеется только 53 бита, в этом случае 1.0000000000 0000000000 0000000000 0000000000 0000000000 01, первый представляет «1», а последний — «2 ^ -52».

2. Это не только чистые степени двух выживших, но и любая комбинация значений, состоящая из битов, которые будут в пределах 53 бит после добавления десятичной единицы. Поскольку большинство десятичных значений не имеют четкого конечного представления в двоичном формате, они будут страдать от «округления» и «отмены» в задачах, подобных приведенным выше.

Например, десятичная дробь 0,1 имеет двойное представление IEEE 0 (1). 1001100110011001100110011001100110011001100110011010 умножить на 2 ^ -4, а добавление к 140737488355328.0 (то есть 2 ^ 47) потеряет все свои биты, кроме первых двух. Таким образом, из ‘= (140737488355328.0 + 0,1 — 140737488355328.0) он вернется как 0,09375, рассчитанный с помощью www.weitz.de/ieee (64 бит), а также в Excel с круглыми скобками вокруг формулы. Этим эффектом в основном можно управлять с помощью значимого округления, которое Excel не применяет, это зависит от пользователя.

Излишне говорить: другие электронные таблицы имеют аналогичные проблемы, LibreOffice Calc использует более агрессивное округление, в то время как gnumeric пытается сохранить точность и сделать так же точность, как и «отсутствие», видимым для пользователя.

Примеры, в которых точность не является показателем точности

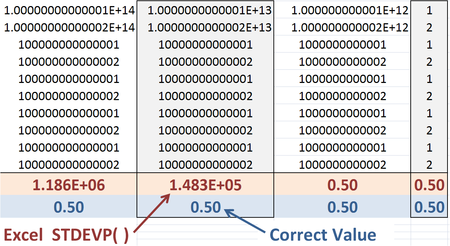
Статистические функции

Ошибка в расчете стандартного отклонения в Excel 2007. Все четыре столбца имеют одинаковое отклонение 0,5.

Точность функций, предоставляемых Excel, может быть проблемой. Мика Альтман и др. представьте этот пример: Стандартное отклонение совокупности, определяемое по формуле:

${ sqrt {{ frac { Sigma (x - { bar {x}}) ^ {2}} {n}}}} = { sqrt {{ frac { Sigma left [x- left] ( Sigma x right) / n right] ^ {2}} {n}}}} ,$

математически эквивалентно:

${ displaystyle { sqrt { frac {n Sigma x ^ {2} - left ( Sigma x right) ^ {2}} {n ^ {2}}}} .}$

Однако первая форма сохраняет лучшую числовую точность для больших значений x , поскольку квадраты разностей между x и x _av приводят к меньшему округлению, чем различия между гораздо большими числами Σx ² и (Σx) ² . Однако встроенная функция Excel STDEVP () использует менее точную формулировку, поскольку она быстрее в вычислительном отношении.

И функция «совместимости» STDEVP, и функция «согласованности» STDEV.P в Excel 2010 возвращают стандартное отклонение генеральной совокупности 0,5 для данного набора значений. Однако числовую неточность все же можно показать на этом примере, расширив существующее число до 10 ¹⁵ , после чего ошибочное стандартное отклонение, обнаруженное Excel 2010, будет равно нулю.

Вычитание результатов вычитания

Выполнение простых вычитаний может привести к ошибкам, поскольку две ячейки могут отображать одно и то же числовое значение при сохранении двух отдельных значений. Пример этого происходит на листе, где для следующих ячеек заданы следующие числовые значения:

и следующие ячейки содержат следующие формулы

Обе ячейки и дисплей . Однако, если ячейка содержит формулу ,
то не показывает , как можно было бы ожидать, но дисплеи вместо этого.
Би 2 1,1530

Вышеупомянутое не ограничивается вычитаниями, попробуйте ‘= 1 + 1,405 * 2 ^ -48’ в одной ячейке, Excel округлит отображение до 1,00000000000000000000 и ‘= 0,9 + 225179982494413 * 2 ^ -51’ в другой, тот же дисплей (в диапазоне выше 1 / ниже 1 округление отличается, что затрагивает большинство изменений десятичной или двоичной величины) выше, другое округление для значения и отображения нарушает одно из элементарных требований Голдберга: « Что должен знать каждый компьютерный ученый » Об арифметике с плавающей точкой » (более или менее« священной книге »fp-math) там сказано:« важно убедиться, что ее использование прозрачно для пользователя. Например, на калькуляторе, если внутреннее представление отображаемого значения не округлено до той же точности, что и отображение, то результат дальнейших операций будет зависеть от скрытых цифр и будет казаться пользователю непредсказуемым »(проблема не в ограничивается Excel, например, LibreOffice calc действует аналогично).

Ошибка округления

Пользовательские вычисления должны быть тщательно организованы, чтобы ошибка округления не стала проблемой. Пример возникает при решении квадратного уравнения :

$ах ^ {2} + Ьх + с = 0 .$

Решения (корни) этого уравнения точно определяются квадратной формулой :

${ displaystyle x = { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}.}$

Когда один из этих корней очень велик по сравнению с другим, то есть когда квадратный корень близок к значению b , оценка корня, соответствующего вычитанию двух членов, становится очень неточной из-за округления (отмены? ).

Погрешность округления можно определить, используя формулу ряда Тейлора для квадратного корня:

${ displaystyle { sqrt {b ^ {2} -4ac}} = b { sqrt {1 - { frac {4ac} {b ^ {2}}}}} приблизительно b left (1- { frac {2ac} {b ^ {2}}} + { frac {2a ^ {2} c ^ {2}} {b ^ {4}}} + cdots right).}$

Как следствие,

$b - { sqrt {b ^ {2} -4ac}} приблизительно b left ({ frac {2ac} {b ^ {2}}} - { frac {2a ^ {2} c ^ {2} } {b ^ {4}}} + cdots right),$

что указывает на то, что по мере увеличения b первый оставшийся член, скажем, ε:

$varepsilon = { frac {2ac} {b}},$

становится все меньше и меньше. Числа для b и квадратного корня становятся почти одинаковыми, и разница становится небольшой:

${ displaystyle b - { sqrt {b ^ {2} -4ac}} приблизительно b-b + varepsilon.}$

В этих условиях все значащие цифры выражают b . Например, если точность составляет 15 цифр, и эти два числа, b и квадратный корень, совпадают с 15 цифрами, разница будет равна нулю, а не разнице ε.

Лучшую точность можно получить с помощью другого подхода, описанного ниже. Если мы обозначим два корня через r ₁ и r ₂ , квадратное уравнение можно записать:

${ displaystyle left (x-r_ {1} right) left (x-r_ {2} right) = x ^ {2} - left (r_ {1} + r_ {2} right) x + r_ {1} r_ {2} = 0.}$

Когда корень r ₁ >> r ₂ , сумма ( r ₁ + r ₂ ) ≈ r ₁ и сравнение двух форм приблизительно показывает:

$r_ {1} приблизительно - { frac {b} {a}},$

в то время как

${ displaystyle r_ {1} r_ {2} = { frac {c} {a}}.}$

Таким образом, находим примерный вид:

${ displaystyle r_ {2} = { frac {c} {a r_ {1}}} приблизительно - { frac {c} {b}}.}$

Эти результаты не подвержены ошибке округления, но они не точны, если b ² не велико по сравнению с ac .

График в Excel разницы между двумя оценками наименьшего корня квадратичного: прямое вычисление с использованием формулы квадратичного уравнения (с точностью до меньшего b ) и аппроксимация для широко разнесенных корней (с точностью до большего b ). Разница достигает минимума в больших точках, а округление приводит к появлению волнистых линий на кривых за пределами этого минимума.

Суть в том, что при выполнении этого расчета с использованием Excel, поскольку корни становятся все дальше друг от друга по величине, метод расчета должен будет переключиться с прямого вычисления квадратной формулы на какой-либо другой метод, чтобы ограничить ошибку округления. Точка переключения методов зависит от размера коэффициентов a и b .

На рисунке Excel используется для нахождения наименьшего корня квадратного уравнения x ² + bx + c = 0 для c = 4 и c = 4 × 10 ⁵ . Разница между прямой оценкой с использованием квадратичной формулы и приближением, описанным выше для широко разнесенных корней, отображается в зависимости от b . Первоначально разница между методами уменьшается, потому что метод широко разнесенного корня становится более точным при больших значениях b . Однако за пределами некоторого b- значения разница увеличивается, потому что квадратичная формула (подходит для меньших b- значений) становится хуже из-за округления, в то время как метод широко разнесенных корней (хороший для больших b- значений) продолжает улучшаться. Точка переключения методов обозначена большими точками и больше для больших значений c . При больших значениях b наклонная вверх кривая представляет собой ошибку округления Excel в квадратной формуле, неустойчивое поведение которой приводит к изгибу кривых.

Другая область, где точность является проблемой, — это область численного вычисления интегралов и решения дифференциальных уравнений . Примерами являются правило Симпсона , метод Рунге – Кутта и алгоритм Нумерова для уравнения Шредингера . Используя Visual Basic для приложений, любой из этих методов можно реализовать в Excel. В численных методах используется сетка, на которой вычисляются функции. Функции могут быть интерполированы между точками сетки или экстраполированы для определения местоположения соседних точек сетки. Эти формулы включают сравнение соседних значений. Если сетка разнесена очень мелко, произойдет ошибка округления, и чем меньше используемая точность, тем хуже ошибка округления. При большом расстоянии пострадает точность. Если числовую процедуру рассматривать как систему обратной связи , этот вычислительный шум можно рассматривать как сигнал, который подается в систему, что приведет к нестабильности, если система не будет тщательно спроектирована.

Точность в VBA

Хотя Excel номинально работает с 8-байтовыми числами по умолчанию, VBA имеет множество типов данных. Тип данных Double составляет 8 байтов, тип данных Integer — 2 байта, а 16-байтовый тип данных Variant общего назначения может быть преобразован в 12-байтовый тип данных Decimal с помощью функции преобразования VBA CDec . Выбор типов переменных при вычислении VBA требует учета требований к хранилищу, точности и скорости.

использованная литература

Источник

As with other spreadsheets, Microsoft Excel works only to limited accuracy because it retains only a certain number of figures to describe numbers (it has limited precision). With some exceptions regarding erroneous values, infinities, and denormalized numbers, Excel calculates in double-precision floating-point format from the IEEE 754 specification^[1] (besides numbers, Excel uses a few other data types^[2]). Although Excel allows display of up to 30 decimal places, its precision for any specific number is no more than 15 significant figures, and calculations may have an accuracy that is even less due to five issues: round off,^[a]
truncation, and binary storage, accumulation of the deviations of the operands in calculations, and worst: cancellation at subtractions resp. ‘Catastrophic cancellation’ at subtraction of values with similar magnitude.

Accuracy and binary storage[edit]

Excel maintains 15 figures in its numbers, but they are not always accurate; mathematically, the bottom line should be the same as the top line, in ‘fp-math’ the step ‘1 + 1/9000’ leads to a rounding up as the first bit of the 14 bit tail ‘10111000110010’ of the mantissa falling off the table when adding 1 is a ‘1’, this up-rounding is not undone when subtracting the 1 again, since there is no information about the origin of the values in this step. Thus the ‘re-subtracting’ of 1 leaves a mantissa ending in ‘100000000000000’ instead of ‘010111000110010’, representing a value of ‘1.1111111111117289E-4’ rounded by Excel to 15 significant digits: ‘1.11111111111173E-4’.

Of course mathematical 1 + x − 1 = x , ‘floating point math’ is sometimes a little different, that is not to be blamed on Excel. The discrepancy indicates the error. All errors are beyond the 15 th significant digit of the intermediate 1+x value, all errors are in high value digits of the final result, that is the problematic effect of ‘cancellation’.

In the top figure the fraction 1/9000 in Excel is displayed. Although this number has a decimal representation that is an infinite string of ones, Excel displays only the leading 15 figures. In the second line, the number one is added to the fraction, and again Excel displays only 15 figures. In the third line, one is subtracted from the sum using Excel. Because the sum has only eleven 1s after the decimal, the true difference when ‘1’ is subtracted is three 0s followed by a string of eleven 1s. However, the difference reported by Excel is three 0s followed by a 15 digit string of thirteen 1s and two extra erroneous digits. Thus, the numbers Excel calculates with are not the numbers that it displays. Moreover, the error in Excel’s answer is not simply round-off error, it is an effect in floating point calculations called ‘cancellation’.

The inaccuracy in Excel calculations is more complicated than errors due to a precision of 15 significant figures. Excel’s storage of numbers in binary format also affects its accuracy.^[3]
To illustrate, the lower figure tabulates the simple addition 1 + x − 1 for several values of x. All the values of x begin at the 15 th decimal, so Excel must take them into account. Before calculating the sum 1 + x , Excel first approximates x as a binary number. If this binary version of x is a simple power of 2, the 15 digit decimal approximation to x is stored in the sum, and the top two examples of the figure indicate recovery of x without error. In the third example, x is a more complicated binary number, {{nobr| x = 1.110111⋯111 × 2⁻⁴⁹ (15 bits altogether). Here the ‘IEEE 754 double value’ resulting of the 15 bit figure is 3.330560653658221E-15, which is rounded by Excel for the ‘user interface’ to 15 digits 3.33056065365822E-15, and then displayed with 30 decimals digits gets one ‘fake zero’ added, thus the ‘binary’ and ‘decimal’ values in the sample are identical only in display, the values associated with the cells are different (1.1101111111111100000000000000000000000000000000000000 × 2⁻⁴⁹ vs. 1.1101111111111011111111111111111111111111111111111101 × 2⁻⁴⁹). Similar is done by other spreadsheets, the handling of the different amount of decimal digits which can be exactly stored in the 53 bit mantissa of a ‘double’ (e.g. 16 digits between 1 and 8, but only 15 between 1/2 and 1 and between 8 and 10) is somewhat difficult and solved ‘suboptimal’. In the fourth example, x is a decimal number not equivalent to a simple binary (although it agrees with the binary of the third example to the precision displayed). The decimal input is approximated by a binary and then that decimal is used. These two middle examples in the figure show that some error is introduced.

The last two examples illustrate what happens if x is a rather small number. In the second from last example, x = 1.110111⋯111 × 2⁻⁵⁰ ; 15 bits altogether. The binary is replaced very crudely by a single power of 2 (in this example, 2⁻⁴⁹) and its decimal equivalent is used. In the bottom example, a decimal identical with the binary above to the precision shown, is nonetheless approximated differently from the binary, and is eliminated by truncation to 15 significant figures, making no contribution to 1 + x − 1 , leading to x = 0 .^[b]

For x′s that are not simple powers of 2, a noticeable error in 1 + x − 1 can occur even when x is quite large. For example, if x = 1/1000 , then 1 + x − 1 = 9.9999999999989 × 10⁻⁴ , an error in the 13 th significant figure. In this case, if Excel simply added and subtracted the decimal numbers, avoiding the conversion to binary and back again to decimal, no round-off error would occur and accuracy actually would be better. Excel has the option to «Set precision as displayed».^[c]
With this option, depending upon circumstance, accuracy may turn out to be better or worse, but you will know exactly what Excel is doing. (Only the selected precision is retained, and one cannot recover extra digits by reversing this option.) Some similar examples can be found at this link.^[4]

In short, a variety of accuracy behavior is introduced by the combination of representing a number with a limited number of binary digits, along with truncating numbers beyond the fifteenth significant figure.^[5] Excel’s treatment of numbers beyond 15 significant figures sometimes contributes better accuracy to the final few significant figures of a computation than working directly with only 15 significant figures, and sometimes not.

For the reasoning behind the conversion to binary representation and back to decimal, and for more detail about accuracy in Excel and VBA consult these links.^[6]

1. The shortcomings in the = 1 + x - 1 tasks are a combination of ‘fp-math weaknesses’ and ‘how Excel handles it’, especially Excel’s rounding. Excel does some rounding and / or ‘snap to zero’ for most of its results, in average chopping the last 3 bits of the IEEE double representation. This behavior can be switched of by setting the formula in parentheses: = ( 1 + 2^-52 - 1 ). You will see that even that small value survives. Smaller values will pass away as there are only 53 bits to represent the value, for this case 1.0000000000 0000000000 0000000000 0000000000 0000000000 01, the first representing the 1, and the last the 2^-52.

2. It is not only clean powers of two surviving, but any combination of values constructed of bits which will be within the 53 bits once the decimal 1 is added. As most decimal values do not have a clean finite representation in binary they will suffer from ’round off’ and ‘cancellation’ in tasks like the above.

E.g. decimal 0.1 has the IEEE double representation 0 (1).1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 × 2^(-4); when added to 140737488355328.0 (which is 2⁺⁴⁷) it will lose all of its bits, except the first two. Thus from ‘= ( 140737488355328.0 + 0.1 — 140737488355328.0) it will come back as 0.09375 instead of 0.1 when calculated with www.weitz.de/ieee (64 bit) as well as in Excel with the parentheses around the formula. This effect mostly can be managed by meaningful rounding, which Excel does not apply: It is up to the user.

Needless to say, other spreadsheets have similar problems, LibreOffice Calc uses a more aggressive rounding, while gnumeric tries to keep precision and make as well the precision as the ‘lack of’ visible for the user.

Examples where precision is no indicator of accuracy

This section needs expansion. You can help by adding to it. (April 2010)

Statistical functions[edit]

Error in Excel 2007 calculation of standard deviation. All four columns have the same deviation of 0.5

Accuracy in Excel-provided functions can be an issue. Altman et al. (2004) provide this example:^[7] The population standard deviation given by:

${sqrt {{frac {Sigma (x-{bar {x}})^{2}}{n}}}}={sqrt {{frac {Sigma left[x-left(Sigma xright)/nright]^{2}}{n}}}} ,$

is mathematically equivalent to:

${displaystyle {sqrt {frac {nSigma x^{2}-left(Sigma xright)^{2}}{n^{2}}}} .}$

However, the first form keeps better numerical accuracy for large values of x, because squares of differences between x and x leads to less round-off than the differences between the much larger numbers Σ(x²) and (Σx)² . The built-in Excel function STDEVP, however, uses the less accurate formulation because it is faster computationally.^[5]

Both the «compatibility» function STDEVP and the «consistency» function STDEV.P in Excel 2010 return the 0.5 population standard deviation for the given set of values. However, numerical inaccuracy still can be shown using this example by extending the existing figure to include 10¹⁵, whereupon the erroneous standard deviation found by Excel 2010 will be zero.

Subtraction of Subtraction Results[edit]

Doing simple subtractions may lead to errors as two cells may display the same numeric value while storing two separate values.
An example of this occurs in a sheet where the following cells are set to the following numeric values:

and the following cells contain the following formulas

Both cells and display 1.1530 .
However, if cell contains the formula
then does not display as would be expected,
but displays instead.

The above is not limited to subtractions, try = 1 + 1.405*2^(-48) in one cell, Excel rounds the display to 1,00000000000000000000, and = 0.9 + 225179982494413×2^(-51) in another, same display^[d]
above, different rounding for value and display, violates one of the elementary requirements in Goldberg (1991)^[8]
who states:

… ‘it is important to make sure that its use is transparent to the user. For example, on a calculator, if the internal representation of a displayed value is not rounded to the same precision as the display, then the result of further operations will depend on the hidden digits and appear unpredictable to the user’ …

The problem is not limited to Excel, e.g. LibreOffice calc acts similarly.

Round-off error[edit]

User computations must be carefully organized to ensure round-off error does not become an issue. An example occurs in solving a quadratic equation:

$ax^{2}+bx+c=0 .$

The solutions (the roots) of this equation are exactly determined by the quadratic formula:

${displaystyle x={frac {-bpm {sqrt {b^{2}-4ac}}}{2a}}.}$

When one of these roots is very large compared to the other, that is, when the square root is close to the value b, the evaluation of the root corresponding to subtraction of the two terms becomes very inaccurate due to round-off (cancellation?).

It is possible to determine the round-off error by using the Taylor series formula for the square root:
^[9]

${displaystyle {sqrt {b^{2}-4ac}}=b {sqrt {1-{frac {4ac}{b^{2}}}}}approx bleft(1-{frac {2ac}{b^{2}}}+{frac {2a^{2}c^{2}}{b^{4}}}+cdots right).}$

Consequently,

$b-{sqrt {b^{2}-4ac}}approx bleft({frac {2ac}{b^{2}}}-{frac {2a^{2}c^{2}}{b^{4}}}+cdots right),$

indicating that, as b becomes larger, the first surviving term, say ε:

$varepsilon ={frac {2ac}{b}},$

becomes smaller and smaller. The numbers for b and the square root become nearly the same, and the difference becomes small:

${displaystyle b-{sqrt {b^{2}-4ac}}approx b-b+varepsilon .}$

Under these circumstances, all the significant figures go into expressing b. For example, if the precision is 15 figures, and these two numbers, b and the square root, are the same to 15 figures, the difference will be zero instead of the difference ε.

A better accuracy can be obtained from a different approach, outlined below.^[e]
If we denote the two roots by r ₁ and r ₂, the quadratic equation can be written:

${displaystyle left(x-r_{1}right)left(x-r_{2}right)=x^{2}-left(r_{1}+r_{2}right)x+r_{1} r_{2}=0.}$

When the root r ₁ >> r ₂, the sum (r ₁ + r ₂ ) ≈ r ₁ and comparison of the two forms shows approximately:

$r_{1}approx -{frac {b}{a}},$

while

${displaystyle r_{1} r_{2}={frac {c}{a}}.}$

Thus, we find the approximate form:

${displaystyle r_{2}={frac {c}{a r_{1}}}approx -{frac {c}{b}}.}$

These results are not subject to round-off error, but they are not accurate unless b² is large compared to ac.

Excel graph of the difference between two evaluations of the smallest root of a quadratic: direct evaluation using the quadratic formula (accurate at smaller b) and an approximation for widely spaced roots (accurate for larger b). The difference reaches a minimum at the large dots, and round-off causes squiggles in the curves beyond this minimum.

The bottom line is that in doing this calculation using Excel, as the roots become farther apart in value, the method of calculation will have to switch from direct evaluation of the quadratic formula to some other method so as to limit round-off error. The point to switch methods varies according to the size of coefficients a and b.

In the figure, Excel is used to find the smallest root of the quadratic equation x² + bx + c = 0 for c = 4 and c = 4 × 10⁵. The difference between direct evaluation using the quadratic formula and the approximation described above for widely spaced roots is plotted vs. b. Initially the difference between the methods declines because the widely spaced root method becomes more accurate at larger b-values. However, beyond some b-value the difference increases because the quadratic formula (good for smaller b-values) becomes worse due to round-off, while the widely spaced root method (good for large b-values) continues to improve. The point to switch methods is indicated by large dots, and is larger for larger c-values. At large b-values, the upward sloping curve is Excel’s round-off error in the quadratic formula, whose erratic behavior causes the curves to squiggle.

A different field where accuracy is an issue is the area of numerical computing of integrals and the solution of differential equations. Examples are Simpson’s rule, the Runge–Kutta method, and the Numerov algorithm for the Schrödinger equation.^[10]
Using Visual Basic for Applications, any of these methods can be implemented in Excel. Numerical methods use a grid where functions are evaluated. The functions may be interpolated between grid points or extrapolated to locate adjacent grid points. These formulas involve comparisons of adjacent values. If the grid is spaced very finely, round-off error will occur, and the less the precision used, the worse the round-off error. If spaced widely, accuracy will suffer. If the numerical procedure is thought of as a feedback system, this calculation noise may be viewed as a signal that is applied to the system, which will lead to instability unless the system is carefully designed.^[11]

Accuracy within VBA[edit]

Although Excel nominally works with 8-byte numbers by default, VBA has a variety of data types. The Double data type is 8 bytes, the Integer data type is 2 bytes, and the general purpose 16 byte Variant data type can be converted to a 12 byte Decimal data type using the VBA conversion function CDec.^[12]
Choice of variable types in a VBA calculation involves consideration of storage requirements, accuracy and speed.

Footnotes[edit]

^
Round-off is the loss of accuracy when numbers that differ by small amounts are subtracted. Because each number has only fifteen significant digits, their difference is inaccurate when there aren’t enough significant digits to express the difference.
^
To input a number as binary, the number is submitted as a string of powers of 2: 2^(−50)*(2^0 + 2^−1 + ⋯). To input a number as decimal, the decimal number is typed in directly.
^
This option is found on the «Excel options»
^
Rounding is different in the range above 1 vs. below 1, which impacts on most decimal or binary magnitude changes.
^
This approximate method is used often in the design of feedback amplifiers, where the two roots represent the response times of the system. See the article on step response.

References[edit]

^
«Floating-point arithmetic may give inaccurate results in Excel». Microsoft support. June 30, 2010. Revision 8.2 ; article ID: 78113. Retrieved 2010-07-02.
^
Dalton, Steve (2007). «Table 2.3: Worksheet data types and limits». Financial Applications Using Excel Add-in Development in C/C++ (2nd ed.). Wiley. pp. 13–14. ISBN 978-0-470-02797-4.
^
de Levie, Robert (2004). «Algorithmic accuracy». Advanced Excel for scientific data analysis. Oxford University Press. p. 44. ISBN 0-19-515275-1.
^
«Excel addition strangeness». office-watch.com.
^ ^a ^b
de Levie, Robert (2004). Advanced Excel for scientific data analysis. Oxford University Press. pp. 45–46. ISBN 0-19-515275-1.
^
Accuracy in Excel:
- «Floating point arithmetic may give inaccurate results». Microsoft support. KB 78113. — A detailed explanation with examples of the binary/15 sig fig storage consequences.
- «Why does Excel seem to give wrong answers?». Microsoft Developers’ Network (blog). Understanding floating point precision. 10 April 2008. Archived from the original on 30 March 2010. — Another detailed discussion with examples and some fixes.
- Goldberg, David (March 1991). «What every computer scientist should know about floating point». Computing Surveys (edited reprint). E19957-01 / 806-3568 – via Sun Microsystems. — Focuses upon examples of floating point representations of numbers.
- «Visual Basic and arithmetic precision». Microsoft support. Q279 / 7 / 55. — Oriented toward VBA, which does things a bit differently.
- Liengme, Bernard V. (2008). «Mathematical limitations of Excel». A guide to Microsoft Excel 2007 for scientists and engineers. Academic Press. p. 31 ff. ISBN 978-0-12-374623-8 – via Google Books.
^
Altman, Micah; Gill, Jeff; McDonald, Michael (2004). «§2.1.1 Revealing example: Computing the coefficient standard deviation». Numerical Issues in Statistical Computing for the Social Scientist. Wiley-IEEE. p. 12. ISBN 0-471-23633-0.
^
Goldberg, David (March 1991). «What every computer scientist should know about floating point». Computing Surveys (edited reprint). E19957-01 / 806-3568 – via Sun Microsystems. — more or less ‘the holy book’ of fp-math
^
Gradshteyn, I.S.; Ryzhik, I.M.; Geronimus, Yu.V.; Tseytlin, M.Yu.; Jeffrey, A. (2015) [October 2014]. «1.112. Power series». In Zwillinger, Daniel; Moll, Victor Hugo (eds.). Tables of Integrals, Series, and Products. Translated by Scripta Technica, Inc. (8 ed.). Academic Press, Inc. p. 25. ISBN 978-0-12-384933-5. LCCN 2014010276. ISBN 0-12-384933-0
^
Blom, Anders (2002). Computer algorithms for solving the Schrödinger and Poisson equations (PDF) (Report). Department of Physics. Lund University.
^
Hamming, R.W. (1986). «Chapter 21 – Indefinite integrals – feedback». Numerical Methods for Scientists and Engineers (2nd ed.). Courier Dover Publications. p. 357. ISBN 0-486-65241-6. — This book discusses round-off, truncation and stability extensively. For example, see chapter 21, page 357.
^
Walkenbach, John (2010). «Defining data types». Excel 2010 Power Programming with VBA. Wiley. pp. 198 ff & Table 8-1. ISBN 978-0-470-47535-5.

Источник

Друзья… такой, наверно, глупый вопрос.
Уверен, что есть решение, но что-то поиск мне не помог.
Простой вопрос… есть любое число (целое или дробное). Нужно определить число разрядов до и после запятой.
Например:
103,97 — 3 и 2
21,7589 — 2 и 4
Собственно, может быть есть функция готовая?

Спасибо.

Sanja Пользователь Сообщений: 14838 Регистрация: 10.01.2013	=ДЛСТР(ЦЕЛОЕ(A1)) =ДЛСТР(ПСТР(A1;ПОИСК(«,»;A1)+1;999)) Согласие есть продукт при полном непротивлении сторон.

	Kirill Gureev, готовых нет, но вычислить — не проблема Sanja, напишите в А1 1 или 0.1 Программисты — это люди, решающие проблемы, о существовании которых Вы не подозревали, методами, которых Вы не понимаете!

ZVI

Пользователь

Сообщений: 4328
Регистрация: 23.12.2012

Дополнение: во 2-й формуле, предложенной Sanja, чтобы не зависеть от символа разделителя целой и дробной части удобно вместо «.» использовать ПСТР(1/2;2;1)
а в 1-й формуле вместо A1 лучше использовать ABS(A1), чтобы не зависеть от знака числа

Изменено: ZVI — 25.02.2018 00:35:36

Kirill Gureev

Пользователь

Сообщений: 653
Регистрация: 01.01.1970

25.02.2018 00:49:49

Цитата
ZVI написал: ПСТР(1/2;2;1)

А Вы не подскажете, что это такое?
Честно говоря, не очень понятно, как будет выглядеть готовая формула?

Изменено: Kirill Gureev — 25.02.2018 01:03:55

Ігор Гончаренко

Пользователь

Сообщений: 13746
Регистрация: 01.01.1970

25.02.2018 01:01:30

Цитата
Чем, собственно, «ЦЕЛОЕ» отличается от «ABS»?

приблизительно тем же, чем sin отличается от exp — это просто разные функции, выполняющие разные задачи
почитать о каждой из них можно по F1

Изменено: Ігор Гончаренко — 25.02.2018 01:02:37

Программисты — это люди, решающие проблемы, о существовании которых Вы не подозревали, методами, которых Вы не понимаете!

	Простите, что-то затупил)

ZVI

Пользователь

Сообщений: 4328
Регистрация: 23.12.2012

=ПСТР(1/2;2;1) выдаст точку или запятую, в зависимости от установленного разделителя целой и дробной части. Целое число бывает как положительным, так и отрицательным, ABS(A1) всегда выдаст положительное число. Предложенные формулы имеют ограничения, например, если в A1 ввести число 1,1E+20, то выдаст 5, что неверно. И выдаст ошибку на нуле и небольших целых числах.

Изменено: ZVI — 25.02.2018 01:10:39

Kirill Gureev

Пользователь

Сообщений: 653
Регистрация: 01.01.1970

25.02.2018 01:14:01

Цитата
ZVI написал: =ПСТР(1/2;2;1) выдаст точку или запятую

А как Вы вообще об этом узнали?

ZVI Пользователь Сообщений: 4328 Регистрация: 23.12.2012	1/2 = 0,5 или 0.5 в зависимости от символа разделителя целой и дробной части. Второй символ и есть символ этого разделителя.

Ігор Гончаренко

Пользователь

Сообщений: 13746
Регистрация: 01.01.1970

#11

25.02.2018 01:36:25

Код
=ЕСЛИ(ABS(A1)<1;;ЦЕЛОЕ(LN(ABS(A1))/LN(10))+1) =ЕСЛИ(ЦЕЛОЕ(A1)=A1;;ДЛСТР(A1)-ПОИСК(ПСТР(1/2;2;1);A1))

Anchoret Пользователь Сообщений: 1061 Регистрация: 01.01.1970 Anchoret	Каждый разряд числа — степень числа 2, вот и считайте. Но это про компьютерное представление чисел)

	Друзья, спасибо…. Познавательно

ZVI

Пользователь

Сообщений: 4328
Регистрация: 23.12.2012

Для корректного вычисления количества десятичных знаков числа формула в одной ячейке будет громоздкой. Поэтому приложил вариант вычисления с помощью пользовательской функции =ДЛДРОБ(A2). Макросы должны быть разрешены, а приложенный файл должен быть скопирован на диск и

разблокирован

.
В столбце A — тестовые числа, в столбце B — результат функции ДЛДРОБ.
В столбцах C:F для наглядности формулами показаны шаги вычисления этой функции.
В столбцах H:I показаны результаты предложенных здесь формульных вариантов, видно, что они на некоторых числах ошибаются.

Прикрепленные файлы

ДЛДРОБ.xlsb (14.04 КБ)

Изменено: ZVI — 25.02.2018 02:14:37

vikttur

Пользователь

Сообщений: 47199
Регистрация: 15.09.2012

ЦЕЛОЕ может дать ошибку на отрицательных значениях (пример: ЦЕЛОЕ(-0,6)=-1).
=ДЛСТР(ABS(ОТБР(A1)))-(ОТБР(A1)=0)
Если ноль нужно учитывать как 1 символ, удалить из формулы правую часть.
Количество знаков после запятой:
=МАКС(;(ДЛСТР(ABS(A1-ОТБР(A1)))-2))

ZVI

Пользователь

Сообщений: 4328
Регистрация: 23.12.2012

#16

25.02.2018 16:39:13

Цитата
vikttur написал: …

Виктор, добрый день!
ДЛСТР(число) конвертирует число в текст, при этом использует экспоненциальный формат для очень больших и малых чисел.
Поэтому и возникает проблема — проверьте Ваши формулы на 3-х последних числах приложенного мной примера в сообщении #14.

vikttur Пользователь Сообщений: 47199 Регистрация: 15.09.2012	#17 25.02.2018 17:44:40 Пример я видел, но не стал додумывать для экспоненциальных…

Источник