Кобб дуглас производственная функция excel

Один из важных методов анализа и исследования экономической системы является применение математических моделей. Они позволяют прогнозировать различные сценарии развития экономики, предугадывать кризисы и рассчитывать риски. Использование математических моделей в экономике помогает расставлять приоритеты в правовой и социальной политике.

---

Понятие производственной функции и её свойства

Простейшим описанием процесса производства можно считать производственную функцию, описывающую зависимость объема производства (или дохода) от сочетания таких производственных факторов как труд (интеллектуальный и физический и капитал в материальном выражении

Часто процессы
производства продукции в реально функционирующих в течение определенного
времени хозяйственных системах являются непосредственным объектом моделирования
с использованием производственных функций (ПФ). В зависимости от характера производственного
процесса, целей и средств моделирования в качестве ПФ могут использоваться
неотрицательные функции разнообразного вида.

Производственная функция (ПФ) – зависимость между объемами затрачиваемых в производстве ресурсов и объемом выпускаемой продукции.

Термин «производство» в
обычном сознании связан с товарами или услугами — материальными или
нематериальными благами. Однако в экономической науке данный термин имеет более
широкое понятие. Экономисты называют производство любой деятельностью по использованию
природных ресурсов, включая ресурсы самого человека, для получения как
материальных, так и нематериальных выгод. До настоящего времени между
производством продуктов питания и информацией, информацией и энергетикой так
много технологических различий, которые создают общую теорию производства.
Из-за исторической традиции основную роль в таких теориях играет теория
материального производства, которая понимается как процесс преобразования
производственных ресурсов в производство продукта или услуг.

В экономической теории выделяются основные факторы производства, которые в соответствии с теорией создают новую ценность. К ним относятся трудовые, капитальные, земельные и предпринимательские способности. Вторичные факторы, напротив, не создают нового значения. В особенности, современном производстве роль энергии и информации возрастает, они характеризуются признаками первичных и вторичных факторов.

Производственная функция называется независимой переменной, которая принимает значения объемов потраченного или использованного ресурса, а зависимая переменная — значения выходных объемов.

Для производственных функций характерны следующие свойства:

1) Повышение объемов
выпуска за счет одного производственного фактора всегда предельно (в одном цехе
может работать ограниченное число рабочих).

2) Производственные
факторы бывают взаимозаменяемыми (человеческие ресурсы заменяются машинными) и взаимодополняемыми
(работники нуждаются в инструментах).

В самом общем виде
производственная функция выглядит как:

Q = f (K, L, M, T, N)

где Q — объем
произведенных товаров;

K — оборудование
(капитал);

М — затраты на материалы
и сырье;

Т — используемые
технологии;

N — предпринимательские
способности.

Но это не единственный вид функции производства, существует множество типов этой зависимости, которые учитывают влияние как одного, так и нескольких наиболее важных факторов.

Рассмотрим
двухфакторную производственную функцию: пусть K — объем основных фондов в
стоимостном выражении или в количественном, L – числовое выражение объема
трудовых ресурсов, Y – объем выпущенной продукции в стоимостном выражении.

Тогда производственная
функция имеет вид:

𝑌 = 𝐹(𝐾, 𝐿)

Довольно часто для анализа этой модели используется изоквантная группа, то есть кривая, которая соединяет все возможные точки комбинаций факторов производства, которые позволяют выпускать определенный объем определенных товаров (рисунок 1).

На оси X обычно отмечают затраты труда, а на оси Y – капитала. На одном и том же графике рисуют несколько изоквант, каждая из которых соответствует определенному объему продукции, при использовании конкретной технологии. В итоге получается карта изоквант с разными количествами изготавливаемых товаров.

Для изоквант характерны
такие общие свойства, как:

1) чем дальше находится
кривая от начала координат, тем выше объем выпускаемой продукции;

2) вогнутый и
нисходящий вид изокванты связан с тем, что уменьшение использования капитала
при стабильном объеме выпускаемых товаров вызывает рост затрат труда;

3) вогнутая форма кривой изокванты зависит от предельно допустимой нормы технологического замещения (то количество капитала, которое может заменить 1 дополнительная единица труда).

Одной из наиболее
распространенных производственных функций является функция Кобба–Дугласа
(рисунок 2). В 1928 г. математик Д. Кобб и экономист П. Дуглас определили, как
влияет на объем выпускаемой продукции величины вложенного в производство труда
и капитала. Было сделано предположение, что функция выглядит так:

𝑌 = 𝐹(𝐾, 𝐿) = 𝐴𝐾𝛼𝐿𝛽

где A > 0 – константа, α, β ≥ 0, α + β = 1.

Функция Кобба-Дугласа
может использоваться для любой конкретной фирмы.

После логарифмирования
получена система уравнений:

𝑙𝑛𝑌𝑡 = 𝑙𝑛𝐴 + 𝛼 𝑙𝑛𝐾𝑡 + 𝛽 𝑙𝑛𝐿𝑡

где Yt, Kt, Lt –
фактические значения соответствующих величин в год t.

С помощью МНК
находились значения A, α, β из условия минимизации:

∑(𝑙𝑛𝑌𝑡 − 𝑙𝑛𝐴 − 𝛼 𝑙𝑛𝐾𝑡 − 𝛽 𝑙𝑛𝐿𝑡)² → 𝑚𝑖𝑛

В математической
статистике эффективной статистической оценкой экономической величины называется
характеристика оценки, достигающая некоторого экстремума, например, имеющая
минимальную дисперсию, сумму модулей отклоний и т.д. В экономической теории и
прикладных экономических исследованиях для оценки эффективности организации
используются производственные функции разных типов. Традиционно учитываемые в
них факторы производства подразделяются на следующие составляющие: трудовые
ресурсы, или труд (Т); инвестиционные ресурсы, или капитал (К); природные
ресурсы, или земля (З); предпринимательский талант, или предпринимательские
способности (П); информация (И), специфической формой которой являются,
например, управленческие и производственные технологии.

Категория «труд»
описывает собой целесообразную деятельность человека по созданию экономических
благ, накоплению потенциала производственных факторов, вложение в результат
деятельности совокупности умственных и физических способностей коллектива
людей, включая синергетический эффект их взаимодействия.

Капитал включает в себя
совокупность созданных прошлым трудом человека благ и средств производства, в
том числе акции, облигации, деньги, банковские депозиты.

Земля как фактор
производства охватывает все сельскохозяйственные угодья и городские земли,
которые отведены под жилищную или промышленную застройку, используются для
развития инфраструктуры бизнеса (транспортные коммуникации, логистические
площадки и пр.), а также совокупность природных условий, необходимых для
производства товаров и услуг (полезные ископаемые, географическое положение,
климатические условия).

Предпринимательский
талант предполагает особые способности человека, заключающиеся в его умении
организовывать производство и бизнес-деятельность путем соединения всех
необходимых факторов производства.

Предприниматель
принимает обоснованные решения по управлению производством и ведению бизнеса,
рискует денежными средствами, временем, трудом, деловой репутацией.

Модель производственной функции можно задать в общей аналитической форме: функционально, описательно и таблично с минимальными ограничениями. Все допущения и ограничения на производственную функцию обусловлены экономическими законами и условиями.

Следующим важнейшим экономическим ресурсом на современном этапе развития общества является информация. Обладание достоверной информацией о рынке (спрос и предложение, конкуренты) является необходимым условием для решения стоящих перед экономическим субъектом проблем. Именно этот ресурс дает наибольшую отдачу в бизнесе.

В работе Н.С.
Шишмаковой проводится сравнительный анализ применимости нескольких вариантов
производственных функций для анализа экономики России в целом и ряда ее
отраслей. Учитывая влияние цен на нефть на мировых рынках на динамику ВВП
России, в производственную функцию вводится значение цены на нефть:

𝑌 = 𝐴𝐾^𝛼𝐿^𝛽𝑃^𝛾𝑒^𝜁 

где P – значение цены
на нефть, γ – коэффициент, характеризующий степенную зависимость ВВП от мировых
цен на нефть, ζ – коэффициент, характеризующий экспоненциальных временной
тренд.

Среди выводов работы стоит выделить, то что введение временного тренда не является важным для модели с переменной отдачей, а также не стоит переоценивать влияние цен на нефть. Однако, производственная функция с постоянной отдачей (α + β=1) не применима для экономики России.

Модели формирования производственных функций для микроэкономических систем часто отражают не только производственные и трудовые факторы, описываемые в виде затратной функции, но и содержат еще один интегральный элемент – технологические функции производства.

---

Практический пример построения производственной функции Кобба-Дугласа с использованием программы MS Excel

Функция Кобба–Дугласа (зависимость объёма производства от создающих его факторов производства – затрат труда и капитала) предполагает, что эти факторы могут дополнять друг друга и даже заменять.

Производственная
функция Кобба-Дугласа строится на основе исходных статистических данных о
динамике выпуска продукции и использованных производственных факторах
(основного капитала и трудовых ресурсов).

Для начала выберем объект исследования (предприятие, фирму). На наш взгляд, наиболее подходящим вариантом является производственное предприятие. Поэтому выбираем СПК «Береговой».

В таблице 1. представлена динамика
обобщенных экономических показателей деятельности СПК «Береговой» за 2015-2017
гг.

Таблица 1 – Основные экономические показатели деятельности  СПК «Береговой» за 2015-2017 гг.

Показатели	2015 г.	2016 г.	2017 г.
Выручка от продажи с/х продукции,  тыс. руб.	412030	345846	393250
Себестоимость с/х продукции,  тыс. руб.	356898	341249	374817
Прибыль от продаж, тыс. руб.	55132	4597	18433
Чистая прибыль, тыс. руб.	45052	441	6940
Дебиторская задолженность, тыс. руб.	34857	35463	33145
Кредиторская задолженность тыс. руб.	13493	21009	15051
Численность персонала, чел.	451	444	406
Среднегодовая стоимость основных средств, тыс. руб.	273060	264497	250645
Среднегодовая стоимость оборотных активов, тыс. руб.	274119	290857	297495
Средняя заработная плата, тыс. руб.	15,91	17,15	20,04
Площадь сельскохозяйственных угодий, га, всего, в т.ч.	5287	5287	5287
— пашня, га	4102	4102	5280
Урожайность зерновых, ц/га	24	26	28,3
Численность КРС, ед.	1936	1855	1860
Производительность труда, тыс. руб. / чел.	913,6	778,9	968,6
Фондоотдача, руб./руб.	0,66	0,76	0,64
Рентабельность продаж, %	13,38	1,33	4,69
Рентабельность продукции, %	15,45	1,35	4,92

[flat_ab id=»5″]

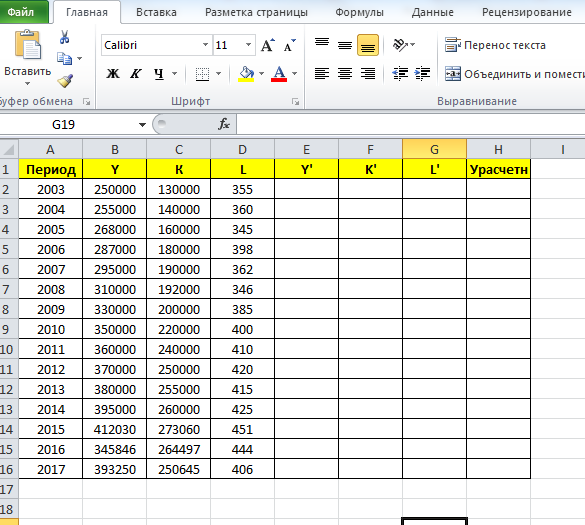
Как было показано в таблице 1, у нас имеются данные по среднегодовой величине основного капитала и численности работников, а также объемам продажи (условно производства) сельскохозяйственной продукции, для этого используем программу MS Excel. Сразу стоит отметить, что т.к. данные имеются всего за 3 года, предшествующие периоды с 2003 по 2014 гг. вставим приблизительные данные (рисунок 3).

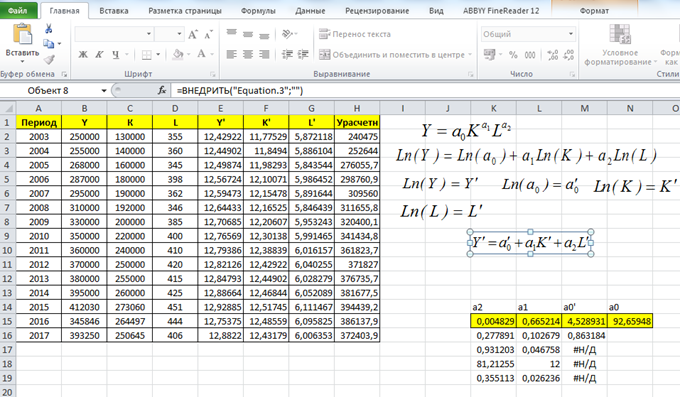
Далее используем представленные формулы и производим согласно лекции расчетные операции (рисунок 4).

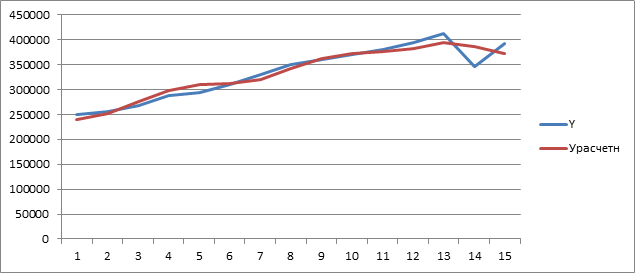
Далее с помощью этой же программы формируем графически рисунок для сравнения фактических и расчетных значений (рисунок 5).

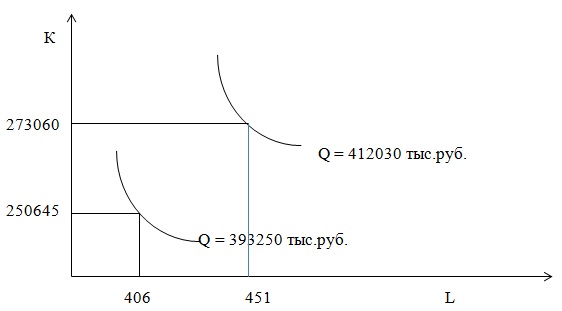
Построим производственную функцию графически (рисунок 6)

[flat_ab id=»5″]

Мы построили
производственную функцию для 2015 и 2017 года, где показано, что рост капитала
и рост количества работников является фактором роста объемов производства
продукции.

В 2016 году, ситуация была обратная, в этот период по сравнению с 2017 годом на предприятии было больше работников, а также больше основных средств, но это не привело к высокому уровню объемов производства, из чего следует сделать вывод, что на объем производства влияют также другие факторы, особенно это может проявляться в сельском хозяйстве. К таким факторам можно отнести (климатические условия, урожайность, внесение удобрений и т.п.).

---

Видео-инструкция по построению производственной функции

Просмотров 13 544

— у нас имеются
исходные данные: годы (или что-либо
другое), У, К, L

— строим еще столбцы:
lnYi,
ln
Ki,
ln
Li,
Утеор

— Yтеор(Ki,Li)=A*Ki
в степени альфа 1*Li
в степени альфа 2

у теор(х1i,x2i)=а
со звезд + b1
со звезд*х1i+b2
со звезд*х2i(1)

ln
Yi=lnA+lnKi
в степени альфа1+lnLi
в степени альфа2

ln
Yi=lnA+альфа1*lnKi+альфа2*lnLi(2)

Сравним (1) и (2):
обозначим через а и b
и получим уравнение множественной
регрессии.

-сервис-анализ
данных-регрессия: находим а со звезд
=lnA,
b1
со звезд=альфа1, b2
со звезд=альфа2

-подставляем и
находим Утеор

Чтобы построить диаграмму нужно
построить таблицу вида…

Ki /Li	5	25	45
10	5,25184766	19,25641	30,94933
40	7,254780778	26,60036	42,75269
70	8,265424355	30,30599	48,70845
100	8,981845819	32,93282	52,93035
130	9,548177635	35,00933	56,26777

-затем мастер
диаграмм-поверхность-1

9. Оценка параметров уравнения множественной регрессии (мр).

Оцениваются, как
и в парной регрессии, методом наименьших
квадратов (МНК). При его применении
строится система нормальных уравнений,
решение которой и позволяет получить
оценки параметров регрессии.

Так, для уравнения
y=a+b1*x1+b2*x2+…+bp*xp+E
система нормальных уравнений составит:

∑y=n*a+b1*∑x1+b2*∑x2+…+bp*∑xp,

∑y*x1=a*∑x1+b1*∑x1^2+b2*∑x1*x2+…+bp*∑xp*x1,

………………………………………………

∑y*xp=a*∑xp+b1*∑x1*xp+b2*∑x2*xp+…+bp*∑xp^2.

Ее решение может
быть осуществлено методом определителей:

a=∆a/∆,
b1=∆b1/∆,
…bp=∆bp/∆.

Г
де
∆ — определитель системы; ∆a,
∆b1,…
∆bp
— частные определители

При этом:

n
∑x1
∑x2
…. ∑xp

∑x1
∑x1^2
∑x2*x1…
∑xp*x1

∆= ∑x2
∑x1*x2
∑x2^2
… ∑xp*x2

…………………………….

∑xp
∑x1*xp
∑x2*xp
….∑xp^2

a
∆a,
∆b1…∆bp
получаются путем замены соответствующего
столбца матрицы определителя системы
данными левой части системы.

Возможен иной
подход к определению параметров, когда
на основе матрицы парных коэффициентов
корреляции строится уравнение регрессии
в стандартизованном масштабе:

t_y=B1*t_x1+B2*t_x2+…+b_p*t_xp+E

Где t_y,
t_x1…t_xp
-стандартизованные переменные: t_y=(y-y
_cp)/σ_y,
t_x1=(xi-xi
_cp)/σ_x1,

для которых среднее
значение равно нулю: t_y
cp
= t_xi
=0,

a
ср. квадратическое отклонение равно
единице: σ_ty=
σ_tx
=1;

β
— стандартизованные коэффициенты
регрессии.

Применяя МНК к
уравнению МР в стандартизованном
масштабе, после соответствующих
преобразований получим систему
нормальных уравнений вида

Ryx1=B1+B2*Rx2x1+B3*Rx3x1+…+Bp*Rxpx1,

Ryx2=B1*Rx2x1+B2+B3*Rx3x2+…+Bp*Rxpx2,

…………………………………………………………..

Ryxp=B1*Rxpx1+B2*Rxpx2+B3*Rx3xp+…+Bp.

Решая ее методом
определителей, найдем параметры –
стандартизованные коэффициенты
регрессии (В-коэффициенты). Они
показывают, на сколько сигм изменится
в среднем результат, если соответствующий
фактор хi
изменится на одну сигму при неизменном
среднем уровне других факторов. В силу
того, что все переменные заданы как
центрированные и нормированные,
стандартизованные коэффициенты
регрессии Вi
сравнимы между собой. Сравнивая их друг
с другом, можно ранжировать факторы по
силе их воздействия на результат. В
этом основное достоинство стандартизованных
коэффициентов регрессии в отличие от
коэффициентов «чистой» регрессии,
которые несравнимы между собой.

Рассмотренный
смысл стандартизованных коэффициентов
регрессии позволяет их использовать
при отсеве факторов — из модели
исключаются факторы с наименьшим
значением Вj

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Я использую Excel для построения визуализации производственных функций Кобба-Дугласа.

Производственная функция представляет собой выпуск любой данной компании как функцию двух затрат (труда и капитала) и параметров (α и β). Когда сумма α и β равна 1, можно доказать, что они представляют собой доли труда и капитала в выпуске соответственно.

Эта ситуация также означает, что масштабы деятельности компании продолжают расти. Когда компания увеличивает объем ввода на определенный процент, выпуск увеличивается на такую ​​же величину.

Если мы укажем альфа и бета, мы можем отобразить каждый труд, капитал и выпуск в пространстве xyz.

Мы делаем это для труда и капитала в диапазоне от 1 до 100, альфа = бета = 0,5. В результате Cobb-Douglas производит поверхность, причем на капитал и рабочую силу приходится 50% затрат.

Обратите внимание, что линии, разделяющие области разного цвета, расположены на одинаковом расстоянии. Это характеристика увеличения отдачи от масштаба.

Когда рабочая сила и капитал расширяются, уровень полезности увеличивается неуклонно и пропорционально.

Также полезно смотреть на поверхность сверху.

 

Эти L-образные кривые называются гиперболами равной длины или прямоугольными. Они представляют собой различные комбинации труда и капитала, которые производят одинаковый («iso») выпуск («Quant»). Например, L = 4 и K = 4, L = 16 и K = 1, L = 1 и K = 16 все производят выходной уровень O = 4. При Q = 4 L-образная кривая просто соединяет эти точки. Когда кривая перемещается на северо-запад, они рисуют комбинацию для получения более высокого выходного значения.

 Любой вопрос? свяжитесь с нами!

Племя больших данных -Профессиональный сторонний поставщик услуг обработки данных в Китае, предоставляющий индивидуальные универсальные консультационные услуги по интеллектуальному анализу данных и статистическому анализу.

Консультационные услуги по статистическому анализу и интеллектуальному анализу данных:y0.cn/teradat(По вопросам консультационных услуг обращайтесьОфициальный сайт службы поддержки клиентов）

QQ：3025393450

[Служебная сцена]

Научно-исследовательские проекты; аутсорсинг проектов компании; индивидуальное обучение онлайн и офлайн; сбор данных; академические исследования; написание отчетов; исследования рынка.

【Племя больших данных】Предоставлять индивидуальные комплексные консультационные услуги по интеллектуальному анализу данных и статистическому анализу

ТЕМА 6. ПРОИЗВОДСТВО

Под производством понимается деятельность по использованию факторов производства (ресурсов) с целью достижения наилучшего результата. Если объем использования ресурсов известен, то максимизируется результат и наоборот, если известен результат, которого необходимо достичь, то максимизируется объем ресурсов.

Под затратами понимается все, что фирма (производитель) закупает для дальнейшего использования в целях получения необходимого результата.

Выпуск подразумевает любое благо (продукция или услуга), изготовленное фирмой для продажи. Деятельность фирмы может означать как производственную, так и коммерческую деятельность.

В рамках теории фирмы в целях упрощения представления деятельности принято считать, что фирма производит одно благо.

Поэтому экономическая деятельность фирмы описывается производственной функцией, включающей в себя переменные для выпуска одного вида товара или услуги:

Q = f (F₁, F₂, F₃, … F_n), где

Q – максимальный объем производства при заданных затратах;

F₁, F₂, F₃, … F_n – количество использованных факторов.

В затраты включаются все используемые факторы производства (труд, материалы, оборудование, уровень технико-организационных знаний, при рассмотрении с/х производства учитывается еще один фактор – земля).

При микроэкономическом анализе предполагается, что уровень организационно–технических знаний фиксирован, а все материальные факторы объединяют в один фактор – капитал. Поэтому производственная функция включает в себя два фактора, от которых зависит выпуск продукции: труд и капитал.

Q = f (L, K)

Следовательно, производственная функция характеризует техническую зависимость между количеством применяемых ресурсов и максимальным объемом выпуска продукции в единицу времени.

Производственная функция описывает множество технологически эффективных способов производства, каждый из которых характеризуется определенной комбинацией ресурсов, необходимых для получения единицы продукции при данном уровне технологии. Как технологическое соотношение производственная функция может быть определена только эмпирическим путем посредством изменения фактических показателей.

Производственная функция имеет ряд особенностей или свойств:

1) факторы производства являются взаимодополняющими;

2) отсутствие одного из факторов делает производство невозможным;

3) производственная функция, использующаяся на макроуровне, именуется функцией Кобба-Дугласа:

Q = f (k*Ka*Lb), где

Q — максимальный объём выпуска продукции;

K — затраты капитала;

L – затраты труда;

a, b — эластичность выпуска по затратам соответствующих факторов (капитала и труда); k – коэффициент пропорциональности или масштабности в отрасли.

4) производственная функция непрерывна и не имеет ограничений по времени, а следовательно, свидетельствует о непрерывности производственного процесса.

Виды производственных функций:

Производственные функции бывают статические и динамические.

Статические производственные функции имеют следующий вид:

Y = f (x₁,x₂,…x_n)

Они не включают в себя показатель времени, т.е. не содержат время как фактор, изменяющий основные производственные характеристики изучаемой зависимости.

Среди статических производственных функций наиболее часто встречаются линейные функции (y = a + a₁x₁ + a₂x₂) и функция Кобба-Дугласа.

Динамические производственные функции имеют следующий вид:

y = f (t , x_i (t) …х_n(t)), где:

x_i (t) – представляет собой динамику изменения определенного производственного фактора в зависимости от времени;

t – представляет собой временную независимую переменную, которая в неявном виде отражает воздействие всех неучтенных факторов на результативность показателя у.

Рассмотрим графическое представление производственной функции. Графиком двухфакторной функции Q = f (L,K) является изокванта, которая представляет собой линию постоянного уровня выпуска. Т.е. изокванта — есть кривая равного продукта или множество возможных комбинаций факторов труда и капитала, при котором достигается один и тот же выпуск продукции.

Рис. 1.6. Двухфакторная производственная функция

Чем дальше от начала координат расположена кривая, тем больше выпуск продукции.

Карта изоквант представляет собой набор изоквант, каждая из которых показывает максимальный объем выпуска продукции при использовании определенного сочетания факторов производства.

Рис. 2.6. Карта изоквант

К свойствам изоквант относят:

1) отрицательный наклон;

2) вогнутость к началу координат;

3) никогда не пересекаются;

4) показывают различные уровни производства.

Чем дальше от начала координат расположена изокванта, тем больший объем выпуска продукции она показывает.

Свойства производственной функции

1. Производственная функция должна задаваться положительно определенной, дважды дифференцируемой по всем своим аргументам функцией.
2. Производственная функция обращается в нуль, если отсутствует хотя бы один из ресурсов x₁, x₂, … ,x_n.
   Невозможно полностью заменить один фактор производства комбинацией других факторов. Возможно лишь частичное замещение одного фактора другими в некоторой ограниченной области.
3. С увеличением любого из ресурсов объем производства возрастает dY/dx_i.
4. При увеличении любого из ресурсов предельная эффективность является убывающей функцией.
5. Производство должно обладать свойством масштабируемости: при одновременном увеличении всех затрат в λ раз количество произведенного продукта также должно увеличиться в λ раз.

Примернеоклассическими0.4040.803

Степень однородности этой производственной функции γ = 0.404 + 0.803 = 1.207. Это означает, что при увеличении капитальных и трудовых затрат в λ раз объем производства увеличится в λ1.207 раз, что характерно для развивающейся экономики.
Средняя фондоотдача AY_K равна отношению произведенного продукта к величине затраченного капитала:
Средняя производительность труда AY_L равна отношению произведенного продукта к величине  затраченного труда L:
Предельная фондоотдача находится как производная объема произведенного продукта Y по величине затраченного капитала K:
Предельную производительность труда, или предельный продукт труда, MY_L определим как частную производную продукта Y по величине затраченного труда L:
Эластичность продукта по фактору.
Коэффициентом эластичности продукта по i-фактору называется относительное изменение продукта, выраженное в процентах, при относительном увеличении i-фактора на 1%.
Эластичность по i-фактору равна отношению предельного продукта к среднему продукту по этому фактору.
эластичность производственной функции по фондам равна ε_K = α = 0.404
эластичность производственной функции по труду равна ε_L = β = 0.803
Если эластичность выпуска по фондам α больше эластичности выпуска по труду, экономика имеет трудосберегающий (интенсивный) рост. Если выполняется обратное неравенство и β > α, то имеет место фондосберегающий (экстенсивный) рост экономики, когда увеличение  трудовых ресурсов на 1% приводит к большему росту объема производства, нежели такое же увеличении фондов.
Эластичность масштаба производства.
Средним продуктом масштаба производства называется отношение продукта, полученное при увеличении факторов производства в λ раз, к коэффициенту масштабирования λ :
AY_λ = λ0.2072.248K0.404L0.803Предельный продукт масштаба производства определяется как прирост продукции при изменении масштаба производства на единицу:
MY_λ = 0.207 λ0.2072.248K0.404L0.803Коэффициентом эластичности масштаба производства называется отношение предельного продукта масштаба к среднему продукту масштаба:
Таким образом, коэффициент эластичности масштаба производства всегда равен степени однородности производственной функции.
Предельная норма замещения факторов производства.
Предельную норму замещения i-фактора производства j-фактором M_ij определим соотношением:
Для нашей модели:

Норма замещения фондов трудовыми ресурсами в явном виде: RST_K,L = L / K

Норма замещения трудовых ресурсов производственными фондами в явном виде: RST_L,K = K / L

Назовем изоклиной множество точек области определения производственной функции, для которых предельная норма замещения i-го фактора производства j-м постоянна.
Для наших данных получаем искомое уравнение семейства изоклин:
K = 1.988M_LK • L
Как и следовало ожидать, семейство изоклин является семейством прямых линий, выходящих из начала координат. Каждому значению предельной нормы замещения труда капиталом соответствует своя линия.

На рис. изображены две изоклины семейства для значений M_LK = 5 и M_LK = 2.

Рис. Изокванты и изоклины для производственной функции Y = 2.248K0.404L0.803

Практический пример построения производственной функции Кобба-Дугласа с использованием программы MS Excel

Функция Кобба–Дугласа (зависимость объёма производства от создающих его факторов производства – затрат труда и капитала) предполагает, что эти факторы могут дополнять друг друга и даже заменять.

Производственная
функция Кобба-Дугласа строится на основе исходных статистических данных о
динамике выпуска продукции и использованных производственных факторах
(основного капитала и трудовых ресурсов).

Для начала выберем объект исследования (предприятие, фирму). На наш взгляд, наиболее подходящим вариантом является производственное предприятие. Поэтому выбираем СПК «Береговой».

В таблице 1. представлена динамика
обобщенных экономических показателей деятельности СПК «Береговой» за 2015-2017
гг.

Таблица 1 – Основные экономические показатели деятельности  СПК «Береговой» за 2015-2017 гг.

Показатели	2015 г.	2016 г.	2017 г.
Выручка от продажи с/х продукции,  тыс. руб.	412030	345846	393250
Себестоимость с/х продукции,  тыс. руб.	356898	341249	374817
Прибыль от продаж, тыс. руб.	55132	4597	18433
Чистая прибыль, тыс. руб.	45052	441	6940
Дебиторская задолженность, тыс. руб.	34857	35463	33145
Кредиторская задолженность тыс. руб.	13493	21009	15051
Численность персонала, чел.	451	444	406
Среднегодовая стоимость основных средств, тыс. руб.	273060	264497	250645
Среднегодовая стоимость оборотных активов, тыс. руб.	274119	290857	297495
Средняя заработная плата, тыс. руб.	15,91	17,15	20,04
Площадь сельскохозяйственных угодий, га, всего, в т.ч.	5287	5287	5287
— пашня, га	4102	4102	5280
Урожайность зерновых, ц/га	24	26	28,3
Численность КРС, ед.	1936	1855	1860
Производительность труда, тыс. руб. / чел.	913,6	778,9	968,6
Фондоотдача, руб./руб.	0,66	0,76	0,64
Рентабельность продаж, %	13,38	1,33	4,69
Рентабельность продукции, %	15,45	1,35	4,92

Как было показано в таблице 1, у нас имеются данные по среднегодовой величине основного капитала и численности работников, а также объемам продажи (условно производства) сельскохозяйственной продукции, для этого используем программу MS Excel. Сразу стоит отметить, что т.к. данные имеются всего за 3 года, предшествующие периоды с 2003 по 2014 гг. вставим приблизительные данные (рисунок 3).

Программа для построения производственной функцииСкачать

Первоначальные данные для построения производственной функции Кобба-Дугласа с использованием программы MS Excel

Далее используем представленные формулы и производим согласно лекции расчетные операции (рисунок 4).

Расчетные итоги для построения производственной функции Кобба-Дугласа с использованием программы MS Excel

Далее с помощью этой же программы формируем графически рисунок для сравнения фактических и расчетных значений (рисунок 5).

Сравнение фактических и расчетных данных

Построим производственную функцию графически (рисунок 6)

Производственная функция для СПК «Береговой»

Мы построили
производственную функцию для 2015 и 2017 года, где показано, что рост капитала
и рост количества работников является фактором роста объемов производства
продукции.

В 2016 году, ситуация была обратная, в этот период по сравнению с 2017 годом на предприятии было больше работников, а также больше основных средств, но это не привело к высокому уровню объемов производства, из чего следует сделать вывод, что на объем производства влияют также другие факторы, особенно это может проявляться в сельском хозяйстве. К таким факторам можно отнести (климатические условия, урожайность, внесение удобрений и т.п.).

Неоклассическая производственная функция

Пусть Y{displaystyle Y} — выпуск, а x=(x1,x2,…,xn){displaystyle x=(x_{1},x_{2},…,x_{n})} — факторы производства (обычно K{displaystyle K} — капитал и L{displaystyle L} — труд). Производственная функция Y=F(x){displaystyle Y=F(x)} является неоклассической, если выполнены следующие условия:

1) Положительная и убывающая предельная производительность факторов :

Fxi′>,Fxi″<{displaystyle F_{x_{i}}^{‘}>0,F_{x_{i}}^{»}<0}

2) Линейная однородность или постоянная отдача от масштаба:

F(λx)=λF(x){displaystyle F(lambda x)=lambda F(x)}

Отсюда следует, в частности, что производственную функцию можно представить как Yxi=f(xxi){displaystyle Y/x_{i}=f(x/x_{i})}, в частности, для двух факторов — капитала и труда, обычно представляют следующим образом: YL=f(KL){displaystyle Y/L=f(K/L)}, то есть как зависимость производительности труда от его капиталовооруженности. Кроме того, выполнена теорема Эйлера об однородных функциях: ∑i=1nFxi′xi=Y{displaystyle sum _{i=1}^{n}F_{x_{i}}^{‘}x_{i}=Y}.

3) Условия Инады:

limxi→Fxi′=∞{displaystyle lim _{x_{i}rightarrow 0}F_{x_{i}}^{‘}=infty }, limxi→∞Fxi′={displaystyle lim _{x_{i}rightarrow infty }F_{x_{i}}^{‘}=0}

Первое условие Инада означает, что все факторы нужны для производства. Второе — что выпуск неограниченно растет при неограниченном росте каждого фактора.

4) Дополнительным свойством является существенность производственного ресурса: ресурс является существенным, если для выпуска требуется положительный объём ресурса:

F(,L)=F(K,)={displaystyle F(0,L)=F(K,0)=0}.

Функция Кобба-Дугласа