Запись от bedvit размещена 01.03.2019 в 20:55
Обновил(-а) bedvit 18.07.2019 в 12:35
То, что вышло — прилагаю.
Функционал:
1. Переключатель «гибель клеток на границе — 0 / закольцованные координаты — 1 «
2. Счетчик поколений
3. Замедление расчета задаваемое в секундах, с дробной частью (к примеру — 0,11 сек.)
4. Выделение ячеек — левой кнопкой, закрашивание выделенного или отдельной ячейки — правой.
5. Поле для жизни 500*500 клеток (поэтому версия №5)
Предустановленная модель в файле и на рис.
1. Стреляет «Планерное ружьё Госпера» -слева и ружье «B-52 bomber» — правее (№2 на рис.)
2. Летящие планеры, поворачивает на 90 градусов — Отражатель «Snark» — №3 на рис.
3. «Планер P60» — представляет собой осциллятор периода 60, состоящий из планера, отраженного двумя пятиугольниками (планер летает между двумя «Pentadecathlon») — №4 на рис.
4. Планеры («Glider»), стрелками указаны направления полета.
5.Что бы планеры не улетали их жрут пожиратели «Eater 1» — №1 на рис.
Запускаем — смотрим движение описанное выше и отмеченное на прилагаемом рисунке.
В дальнейшем развивать посчитал нецелесообразно, все равно, на больших объемах — медленно выходит.
Решил писать свою программу.
Миниатюры
Изображения
Всего комментариев
Модель клеточного автомата, реализованная средствами VBA в Excel (с использованием модуля класса)
В таблице произвольного размера клетки могут быть в трех состояниях: пустая (без цвета), травоядное (зеленый цвет ячейки), хищник (красный цвет ячейки).
Поведение системы характеризуется следующими параметрами:
- особь может переместиться на любую клетку, имеющую с данной общую сторону. Направление выбирается случайно из возможных свободных.
- особь может оставить потомство в той клетке, из которой она переместилась. Потомство появляется периодически, период является параметром.
- если особь является «хищной», то она может поглотить свою жертву, при этом перемещаясь на место жертвы.
- особь живет ограниченное количество времени, называемое временем жизни особи – так же параметр.
- если «хищная» особь не находит себе пищи в течение определенного времени (называемого временем голодной смерти), то она погибает.
- время голодной смерти является параметром.
Для запуска программы нажмите зелёную кнопку.
Предварительно вы можете изменить параметры в желтых ячейках.
Задание:
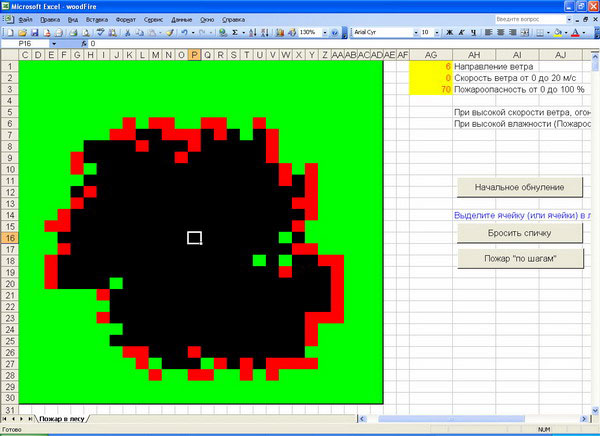
Создать и визуализировать математическую модель распространения лесного пожара в Excel.
- Условия:
- поле 30 на 30 клеток;
- одна клетка — один шаг и одно дерево;
- вокруг горящего дерева есть 8 ближайших клеток, на которые может перейти пожар,
- состояние дерева: горящее — красное, сгоревшее — черное, несгоревшее — зеленое.
- Загорится ли дерево (вероятность) зависит от направления ветра (всего 8 направлений);
- Вероятность возгорания, направление ветра и скорость ветра выставляется произвольно в начале программы,
и являются исходными данными для формирования правил клеточного автомата.
Решение:
- Правила для клеток автомата:
- Зеленая клетка может превратиться только в «красную» по вероятностному закону, если в соседях у нее красная;
- Красная – на следующем шаге, превращается в черную;
- Черная никогда не меняется.
- В теории в автоматах существуют два принципиально разных вида клеток (по параметрам Причина-Следствие):
- Клетка-приемник – использует данные о состояниях своих соседей и в конечном итоге изменяет свое состояние
(как правило, для комплексного учета влияния соседей)
- Клетка-причина – влияет на соседей и, в конечном счете, изменяет их состояние или создает предпосылки
для такого изменения (и не исключено, что и свое).
В нашем случае, проще и удобнее использовать второй вид клеток, а для ускорения процесса расчета провести трансформацию правил.
Самые сложные правила отдадим красной клетке. Матрица вероятностей «поджога соседей» должна учесть
и скорость, и направление ветра, и влажность леса. Такая клетка как бы переводит соседние зеленые клетки
в новое состояние (так более реально выглядит пожар). И сама тут же гаснет. В этом случае правила для
зеленых и черных клеток – пусты.
Процесс пересчета состояний:
Цикл перебора клеток бежит пока не встретит «красную» в массиве. В самом массиве сразу ничего не меняется,
а лишь проверяются соседи и если среди них есть «зеленая», то в нее бросается «Искра» (функция RND).
Клетка, возможно, загорится, а возможно и нет. Изменения, если произойдут, зафиксируются в специальной коллекции.
Матрица вероятностей «поджога соседей» формируется таким образом, что «красные» клетки бросает искры в
основном по направлению ветра – и только на «зеленые» соседние клетки.
После окончания цикла очередного шага, вносим изменения в массив, одновременно очищая «коллекцию изменений».
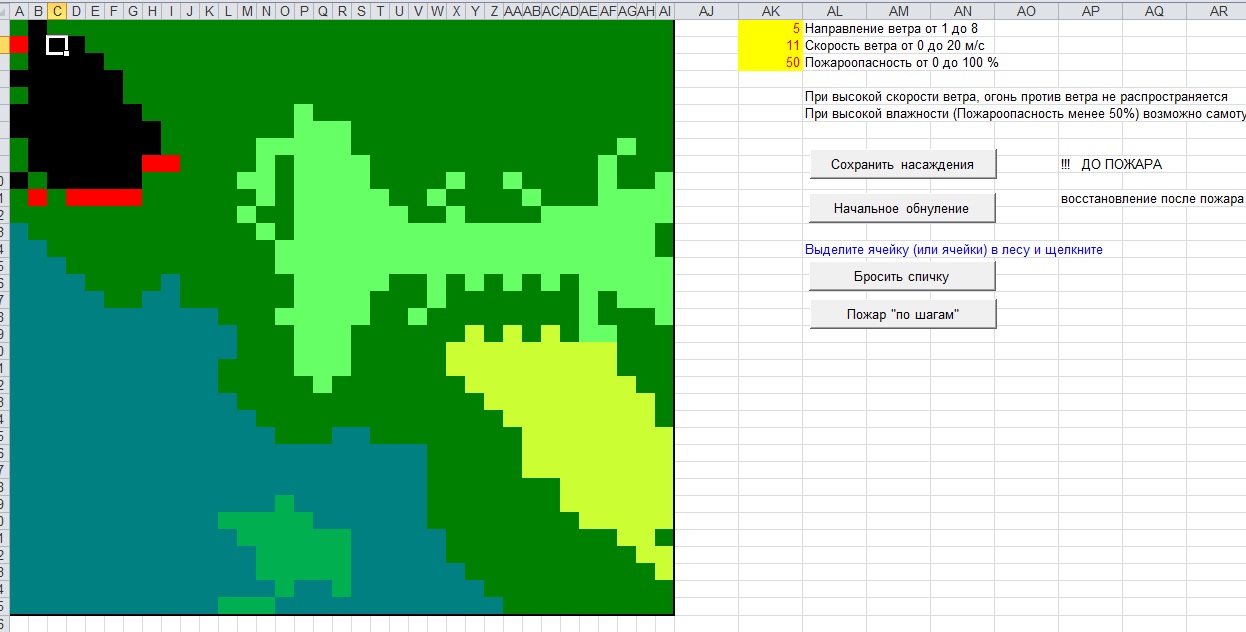
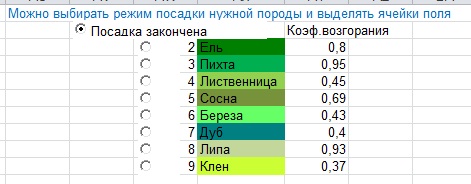
А это чуть усложненный вариант, позволяющий учитывать характер (план) растительности на участке местности и характеристики пород деревьев с точки зрения устойчивости к пожарам…
Большинство лиственных пород имеют пониженный коэффициент возгорания и являются естественным барьером на пути распространения огня в лесу…
Задать схему насаждений для моделирования распространения огня при различных направлениях и скоростях ветра можно при помощи этих не сложных и интуитивно понятных элементов управления
Еще есть Клеточный автомат на Delphi 7 ! Не пожар… Как игра «Жизнь»…
И клеточный автомат для маркетинговых исследований распространения на рынке двух товаров, отличающихся ценой и качеством. Изменяя параметры, можно видеть, как один товар вытесняется с рынка другим… с различной скоростью…
Другие примеры на языке «Delphi»
Если на этой странице не нашлось того, что Вы так искали…
Не расстраивайтесь, не все потеряно… Смело щелкайте…
телефон:
+7(919) 572-59-92
+7(987) 848-79-61
Чтобы
убедить читателя в том, что, используя
возможности электронных
таблиц Excel,
любой
начинающий пользователь может
заниматься клеточным моделированием,
рассмотрим одну из реализаций игры
«Жизнь».
Клетки
в исходной таблице Excel
слишком
велики для нашей
задачи. Поэтому придадим им вид небольших
квадратов. В качестве
примера возьмем игровое поле 5×5,
хотя увеличение размера в несколько
раз не требует никаких усилий. Отведем
для игры клетки В2 : F6.
Если
клетка жива, то в ячейку запишем 1, если
мертва, то О. Зададим
произвольное начальное состояние. Далее
нам понадобятся
две вспомогательные таблицы. В ячейках
Н2 : L6
будет
храниться
«потенциал» клеток. Для вычисления
потенциала клетки
В2 введем в ячейку Н2 следующую формулу:
=
СУММ(А1 : СЗ) — В2 (14.1)
В
данном случае подсчитывается число
живых клеток в окрестности
клетки В2 (окрестность по Муру). Закончив
ввод этой формулы
нажатием клавиши Enter,
установим
курсор на правый нижний
угол клетки Н2 и размножим формулу (14.1)
сначала до ячейки L2,
а
затем вниз, заполнив всю таблицу Н2 : L6.
(Обратите
внима-
266
ние
на то, как следует учитывать состояние
клеток, граничных с таблицей
В2 : F6.
В
данном случае они остаются пустыми, но
возможны
и более сложные формы задания граничных
условий.)
Сложнее
всего задать правило поведения клеточного
автомата.
Запишем в ячейку BlO
правило
поведения автомата В2, используя
логические функции:
=
ЕСЛИ (ИЛИ (Н2 >3;
Н2
<2); О; ЕСЛИ (Н2 = 3; 1;
ЕСЛИ(Н2
= 2;В2;-1))) (14.2)
Первое
ЕСЛИ в (14.2) означает, что клетка будет
мертва при потенциале
Н2 = О, 1, 4, 5, 6, 7; второе ЕСЛИ — что при
потенциале
3 клетка будет живой, третье ЕСЛИ — что
при потенциале 2 состояние автомата в
клетке В2 не меняется. Наконец, выражение
(-1) означает, что при невыполнении всех
предыдущих условий в ячейку BlO
будет
записано значение (-1). (Заметим, что в
данном случае этот вариант невозможен.)
Запись
логической функции требует аккуратности.
Однако следует
учесть, что для освоения Excel
необходимо
умение работать с логическими
функциями.
Функция
(14.2) записывается только в одну ячейку
BlO,
далее
она размножается вправо до ячейки FlO,
а
затем вниз, заполняя всю таблицу
B10:F14.
Таким
образом, если в таблице B2:F6
мы
имеем состояние системы в момент t,
то
в таблице B10:F14
вычисляется
состояние системы в следующий момент
t
+
1. Теперь необходимо скопировать таблицу
B10:F14
в
таблицу
B2:F6.
Делается
это следующим образом.
Шаг
1. Выделяем
таблицу BlO:
F14.
Шаг
2. В
меню «Правка» выбираем команду
«Копировать».
Шаг
3. Устанавливаем
курсор в ячейку В2.
Шаг
4. В
меню «Правка» выбираем команду
«Специальная вставка». В раскрывшейся
дополнительной вкладке следует из
первого
столбца «Вставить» выбрать строку
«Значения» и нажать кнопку
OK.
В
итоге в таблице B2:F6
появится
картинка нового состояния
системы.
Процедуру
копирования можно существенно ускорить,
если подготовить соответствующий
макрос. Делается это очень просто.
В Excel
2000
в меню «Сервис» выбираем «Макрос»,
а затем команду
«Начать запись». В раскрывшейся
вкладке можно дать имя макросу
либо оставить предлагаемый вариант
«Макрос 1». Назначаем макросу
клавишу быстрого вызова, например Ctrl
+
е. Нажимаем OK.
Появится
таблица Excel,
и
на экране возникнет
267
кнопка
«Остановить макрос». Выполним
указанные выше операции (шаги 1-4) и
нажмем кнопку «Остановить». Запись
макроса будет закончена.
Теперь
переход к следующему временному такту
будет происходить
после каждого нажатия комбинации клавиш
Ctrl
+
ей можно
спокойно наблюдать за эволюцией системы.
Столь
подробное описание процесса построения
модели дано лишь
с той целью, чтобы читатель немного
освоил электронные таблицы
и понял, насколько легко могут быть
построены значительно
более сложные и реалистичные модели.
Ясно,
что легко усложнить формулу расчета
потенциала, изменить
окрестность, ввести в расчет случайные
факторы. Учет географических
особенностей региона может заставить
вас отказаться
от простой квадратной решетки. В ней
могут появиться дырки, а
граница вполне может быть извилистой.
Совершенно необязательна
унификация правил поведения автоматов.
Например, вы можете
для центральных клеток задать одни
правила, а для периферийных
— другие.
14.3.
Приложения клеточных моделей
Модель
электорального процесса. В цикле работ
Т.Брауна рассматривается ряд контекстуальных
моделей электорального процесса.
Он считает, что избирательные предпочтения
индивида
определяются установками его ближайшего
окружения [8]. В одной
из моделей предполагается, что индивид
принимает решение голосовать в момент
t
+
1
за республиканцев или демократов в
соответствии с правилом простого
большинства. Учитываются взгляды
индивида и четырех его ближайших соседей
в момент t
(окрестность
фон Неймана). Если из пяти человек трое
или больше
поддерживают демократов, то индивид
также голосует за демократов. Если
большинство составляют республиканцы,
то индивид
и в этом случае разделяет точку зрения
большинства.
В
данном случае клеточный автомат имеет
два состояния: 1 — голосование
за республиканцев; О — голосование за
демократов. Нетрудно
заметить, что указанная модель может
быть реализована
на ЭВМ даже проще, чем рассмотренная
выше игра «Жизнь».
Браун
и его коллеги проводили вычислительные
эксперименты на
решетке 128 х 128, при этом начальное
распределение задавалось
случайным образом. Модель исследовалась
на большом временном
горизонте — до 20 000 тактов. Оказалось,
что партийная
268
борьба
приводит к очень сложным конфигурациям,
существенно зависящим
от исходного распределения. По мнению
Брауна, данная
модель относится к четвертому классу
клеточных автоматов, так же как и
игра «Жизнь». Однако детального
исследования модели пока не проводилось
и нахождение замечательных конфигураций
в политической «Жизни», таких как
«блок», «змея»,
«катапульта», еще впереди.
Рассмотрим
обобщение модели Т.Брауна на случай,
когда учитываются взгляды индивида
и восьми его ближайших соседей
(окрестность
Мура). Если из девяти человек пятеро или
больше поддерживают
демократов, то индивид также голосует
за демократов. Если
большинство составляют республиканцы,
то индивид и в этом случае
разделяет точку зрения большинства.
Покажем,
что данная модель может быть реализована
на ЭВМ с помощью
электронных таблиц даже проще, чем игра
«Жизнь». Придадим
клеткам исходной таблицы Excel
вид
небольших квадратов
(с помощью форматирования). Отведем для
модели поле 10
х 10 (клетки В2: К11) и зададим в нем начальное
состояние.
Перейдем
на лист 2 и введем в ячейку В2 формулу:
=ЕСЛИ
(СУММ (Лист 1!А1 :СЗ) > 4; 1; 0)
Данная
логическая функция вычисляет «потенциал»
ячейки В2
— в нашем случае число сторонников
республиканцев. Если это
число больше 4, то ячейке В2 присваивается
1 (автомат голосует
за республиканцев), в противном случае
присваивается 0 (голосование
за демократов).
Размножим
эту формулу на все ячейки В2:К11. Получим
новое состояние системы, скопируем
его и вставим с помощью команды
«Специальная вставка» только
«значения» в те же ячейки на
листе 1. Запишем процедуру копирования
в виде макроса. (Первым
шагом при записи макроса должен быть
переход с листа 1 на лист
2.) Назначим макросу клавиши быстрого
вызова, например Ctrl+e.
Теперь
переход к следующему временному такту
будет происходить
после каждого нажатия этой комбинации
клавиш [4].
Отметим,
что для длительного прогона модели не
требуется много раз нажимать кнопки.
Достаточно одного нажатия. В
Excel
2000
для выхода в режим редактирования
макроса следует
в меню «Сервис» выбрать команду
«Макрос», затем «Макросы…»
и «Изменить». На экране вы увидите
подпрограмму. Интересно,
что вы составили эту программу сами.
Точнее, это сделал автоматически Excel,
пока
вы формировали макрос. Вставим в этот
макрос цикл следующим образом. После
пер-
269
вой
строки (Sub
Макрос)
вставьте строку For
i =
1 То 100, а перед последней строкой (End
Sub) вставьте
строку Next
i. Теперь
одно нажатие клавиш Ctrl
+
е заставит модель проделать 100 шагов.
Изложенный
подход основан на методологии
иконологичес-кого
моделирования (см. § 12.1). Отметим, что в
данном случае возможности
моделирования существенно расширяются
за счет использования макросов. Умение
слегка скорректировать текст макроса,
вставляя операторы цикла и условного
перехода, дает возможность
пользователю самостоятельно строить
сложные компьютерные
модели, не прибегая к помощи программистов.
Модели
диффузии инноваций. Индийские
ученые предложили
следующую модель клеточных автоматов
[7]. Каждый индивид соответствует одной
клетке, которая может находиться в двух
состояниях:
1 — новинка принята; О — новинка пока
еще не принята.
Предполагается, что автомат, приняв
новинку один раз, остается
ей верен до конца.
Автомат
принимает решение о принятии новинки,
ориентируясь
на мнение ближайших соседей (используется
окрестность Мура).
Пусть в окрестности данной клетки
имеется т
сторонников
новинки. Генерируется случайное число
р
— вероятность
принятия
новинки. Если рт
> г, где
г
— фиксированное
пороговое
значение, то автомат принимает
нововведение, в противном случае новинка
пока отвергается.
Авторы
модели полагают, что вероятность принятия
новинки
со временем должна уменьшаться, так как
степень новизны постепенно
снижается.
Моделирование
проводилось на решетке 10Ox
100.
Эволюция системы
рассматривалась на временном горизонте
в 100 тактов, если
вероятность принятия новинки р
=
0,1, и 130 тактов при р
=
0,05. Для каждого случая осуществлялось
50 прогонов модели.
Проводилось также исследование влияния
на поведение модели начального
распределения сторонников новшества.
Для
каждого временного такта t
подсчитывалось
число автоматов,
принявших инновацию (п().
Приводимые авторами графики
функции п(
показывают хорошую степень совпадения
с моделью
Фишера — Прея (см. § 9.2).
По
мнению индийских ученых, клеточное
моделирование позволяет
строить значительно более реалистические
модели рынка,
чем традиционные подходы к исследованию
диффузии инноваций.
Главное достоинство этого подхода
заключается в возможности эмпирической
оценки фактора р
— вероятности
270
принятия
новинки. Для этого можно использовать
данные социологических опросов и
материалы фокус-групп. Другое преимущество
предлагаемого подхода заключается в
возможности получения оценок необходимого
числа сторонников и их пространственного
распределения в начальный момент
кампании.
»
• »
Исследования
последних лет показывают, что многие
физические
и информационные процессы прекрасно
описываются кле-точно-автоматными
моделями. Оказалось, что если к клетке
приделать
часы, то можно получить новые многообещающие
формы представления
процессов, протекающих в живой и неживой
природе
[1]. Очевидно, что, снабдив клетку даже
примитивным искусственным
интеллектом, можно исследовать более
глубокие слои социальной
реальности. Весьма перспективным
направлением исследований
является клеточное моделирование
процессов кооперации
и конкуренции с использованием для
принятия решений моделей
теории игр.
Читателю
может показаться, что в данной главе
рассматриваются
разрозненные, ничем не связанные модели
из различных областей
науки, практики и сферы развлечений.
Однако более внимательное отношение
к рассматриваемым процессам показывает,
что
они все тесно взаимосвязаны. Игра
становится Жизнью, Жизнь уже стала
Маркетингом, Маркетинг становится
Искусством (может быть единственным).
И все эти процессы можно и нужно
моделировать.
Задачи
и упражнения
1.
Рассмотрите различные определения
понятия «окрестность клетки».
Какие еще модификации «окрестности»
целесообразно исследовать?
2.
Позволяет ли клеточное моделирование
исследовать географические
особенности региона?
3.
Можно ли применить клеточное моделирование
для анализа коммуникативных
процессов?
4.
Реализуйте на ЭВМ модель электорального
поведения Брауна. Используйте в своей
модели различные виды окрестностей.
Как это повлияет на поведение модели?
5.
Бесконечно расширяет возможности
клеточного моделирования использование
цвета. Дж.Касти полагает, что с помощью
клеточных автоматов можно анализировать
творчество художников. В работе [9] он
рассматривает картину известного
голландского абстракциониста Пита
Мондриана «Шахматная доска. Яркие
цвета». Картина представляет
271
собой,
по мнению Касти, прямоугольную решетку
из 256 клеток, раскрашенных в восемь
цветов. Касти формулирует следующие
задачи:
а)
можно ли построить клеточный автомат,
который бы из любой начальной конфигурации
строил картину Мондриана?
б)
можно ли построить «фильтр»,
позволяющий различать индивидуальные
стили художников?
6.
Для освоения нюансов маркетинга
целесообразно поиграть в следующую
игру. Сконструируйте клеточную модель
конкуренции на рынке двух
(или более) новых продуктов. Каждому
продукту должна соответствовать
своя цифра (лучше свой цвет). Начиная со
случайной исходной позиции два игрока
наблюдают за процессами диффузии. Каждый
пятый такт игроки могут вмешиваться в
естественный ход процесса, добавляя по
одному стороннику новинок.
Выработайте
оптимальную маркетинговую стратегию.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Развлекая — поучай.
(Гораций)
Если вы уже имели какой-то опыт программирования в прошлой жизни (привет, Basic, Pascal и т.д.), то, скорее всего, уже прошли этап «игрописательства». Однако, тряхнуть стариной и размять мозги вполне можно. Если же вы никогда не программировали игр, то никогда не поздно начать этот весьма увлекательный процесс. Всё, что нам потребуется — это Excel (любой версии) и 15-20 минут времени для начала.
Тренироваться будем на известной в узких кругах программистов игре «Жизнь» (Life). Её придумал британский математик Джон Конвей еще в 1970 году на основе работ легендарного Джона фон Неймана — прадедушки всех современных компьютеров. Если вы не сталкивались с ней раньше — не проблема, правила можно объяснить за полминуты:
-
Игра идет на большом (иногда даже бесконечном) поле в клеточку («вселенной»). Как вы понимаете, Excel для такого подходит идеально
-
В один момент времени каждая клетка может быть в двух состояниях — живой (обозначим её каким-нибудь значком или просто единичкой) или же мертвой (пустой). Начальное состояние всех клеток в игре называют первым поколением.
-
Если брать блок клеток 3х3 с текущей клеткой в середине, то вокруг неё оказывается 8 клеток-соседей. Дальнейшая судьба клетки зависит от того, сколько именно живых клеток (N) окажется в этой окружающей области. Вариантов несколько:
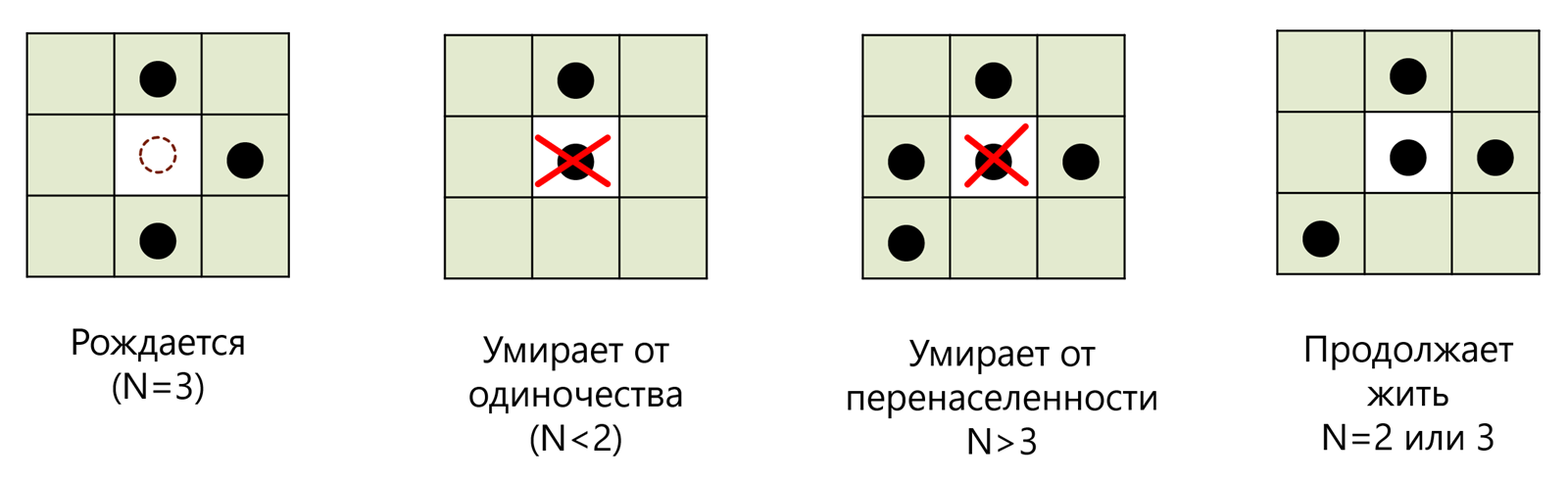
- Если клетка была пустая (мертвая), но у нее есть ровно 3 живых соседа, то в ней зарождается жизнь.
- Если клетка живая, но у неё меньше 2 соседей, то она умирает от одиночества.
- Если клетка живая, но у неё больше 3 соседей, то она умирает от перенаселения.
- Если клетка живая и у нее 2-3 соседа, то клетка продолжает жить.
Вот, собственно, и все правила. Можно даже сказать, что всё это неправильно называть игрой, т.к. здесь нет соперников в привычном понимании. Вы расставляете первое поколение, запускаете процесс и затем просто наблюдаете за развитием вашей «колонии» на протяжении нескольких поколений.
Однако, не стоит недооценивать обманчивую простоту этой логики — количество комбинаций, сценариев игры и многообразие фигур в такой игровой вселенной поражает своим разнообразием и поистине бесконечно. В математике подобные модели называют клеточными автоматами. А самое интересное, что реализовать подобную модель можно в любой версии Excel буквально на 20 строчках кода.
Поехали.
Шаг 1. Готовим игровое пространство
Создадим в новой книге три листа:
- game — это будет основной листы игры, где мы будем наблюдать за развитием нашей «колонии»
- next — этот лист будет формировать следующее поколение, которое затем придет на смену текущему
- start — на этом листе мы будем задавать начальную конфигурацию, т.е. первое поколение в нашей игре
На каждом листе (можно выделить их заранее, удерживая клавишу Shift или Ctrl, чтобы не повторять трижды одни и те же действия), разметим игровое поле размером, допустим, 30 на 30 ячеек. Впоследствии размер поля можно будет подправить в соответствии с вашими аппетитами и мощью вашего ПК:
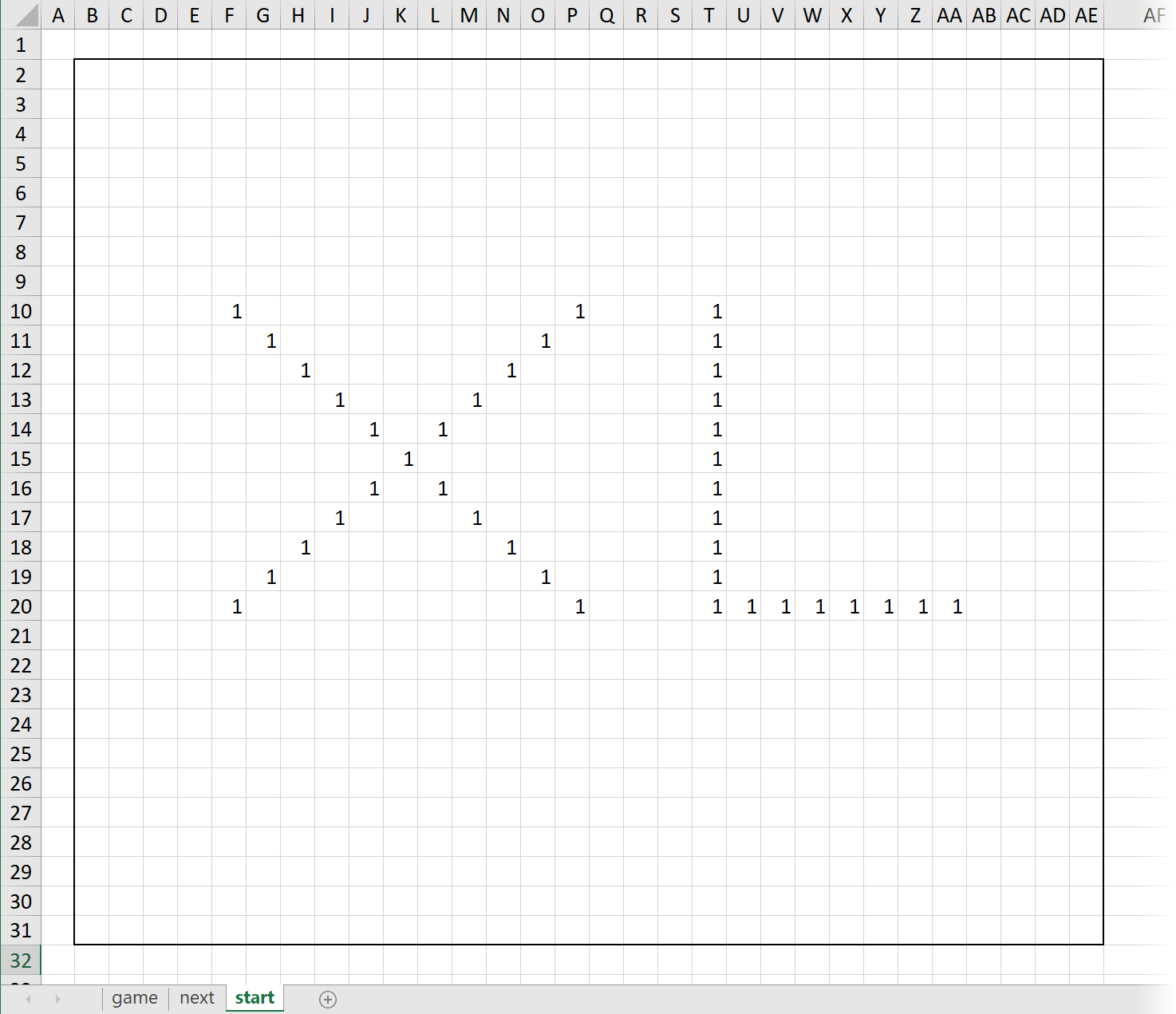
На листе start разметим с помощью единичек первое поколение любым желаемым образом:
Шаг 2. Пишем макрос
Теперь пришла пора расчехлить наш VBA и написать макрос, который и будет делать всю работу, а именно:
- Копировать первое поколение с листа start на лист game.
- Проходить по ячейкам игрового поля на листе game и проверять окружающих соседей (блок 3х3) для каждой из них.
- В зависимости от результатов проверки помечать на листе следующего поколения next ту же ячейку как живую (1) или мертвую (пусто).
- Копировать получившееся новое поколение с листа next вместо текущего на листы игры game.
- Повторять пункты 2-4 несколько раз, сменяя одно поколение другим и отображая на экране изменения в нашей «колонии».
Для начала откроем редактор Visual Basic на вкладке Разработчик (Developer). Если такой вкладки не видно, то её нужно будет сначала отобразить через Файл — Параметры — Настройка ленты (File — Options — Customize Ribbon), включив соответствующий флажок.
В открывшемся окне редактора создадим новый модуль с помощью команды меню Insert — Module, а затем скопируем и вставим туда код нашего макроса:
Sub Life()
Dim cell As Range, n As Integer, i As Integer
Set rGame = Worksheets("Game").Range("B2:AE31")
Set rStart = Worksheets("Start").Range("B2:AE31")
Set rNext = Worksheets("Next").Range("B2:AE31")
Set wNext = Worksheets("Next")
rStart.Copy Destination:=rGame
For i = 1 To 50
rNext.ClearContents
For Each cell In rGame.Cells
n = WorksheetFunction.CountA(cell.Offset(-1, -1).Resize(3, 3)) - cell.value
If cell = "" And n = 3 Then wNext.Cells(cell.Row, cell.Column) = 1
If cell = 1 And (n = 2 Or n = 3) Then wNext.Cells(cell.Row, cell.Column) = 1
If cell = 1 And (n < 2 Or n > 3) Then wNext.Cells(cell.Row, cell.Column) = ""
Next cell
rNext.Copy Destination:=rGame
Next i
End Sub
Теперь давайте разберем его построчно для понятности:
Поскольку в коде нам придется несколько раз ссылаться и много раз работать с диапазонами игрового пространства (B2:AE31) на каждом из трёх листов книги, то имеет смысл сразу оформить их как переменные. Это делается в блоке:
Set rGame = Worksheets("Game").Range("B2:AE31")
Set rStart = Worksheets("Start").Range("B2:AE31")
Set rNext = Worksheets("Next").Range("B2:AE31")
Заодно мы создаем ещё и переменную wNext, которая ссылается на весь лист next целиком — это нам тоже пригодится в будущем:
Set wNext = Worksheets("Next")
Затем, перед началом игры, мы должны перенести первое поколение с листа start на лист game. Это выполяется командой прямого копирования с использованием уже созданных переменных:
rStart.Copy Destination:=rGame
Поскольку мы хотим прокрутить в нашей игре не одно, а несколько (например, 50 для начала) поколений, то дальнейшие действия заключены в цикл:
For i = 1 to 50 ... Next i
А внутри этого цикла мы, во-первых, сначала очищаем рабочее пространство на листе next для формирования следующего поколения:
rNext.ClearContents
А, во-вторых, запускаем вложенный цикл прохода по всем ячейкам игровой вселенной на листе game, чтобы проверить каждую из них — это реализовано циклом прохода по коллекции:
For Each cell in rGame.Cells ... Next cell
Ссылка на очередную проверяемую ячейку будет храниться в переменной cell. Для этой ячейки нам нужно сначала построить окрестность 3х3 с ней в середине. Это выполняется с помощью конструкции:
cell.Offset(-1, -1).Resize(3, 3)
Здесь метод Offset(-1,-1) виртуально сдвигает текущую проверяемую ячейку на одну строку вверх и на один столбец влево, а потом метод Resize(3,3) опять же виртуально растягивает эту одну ячейку до новых размеров 3 на 3:

Чтобы посчитать количество заполненных ячеек в полученной окрестности применяется функция рабочего листа СЧЁТЗ (COUNTA), которую в VBA можно вызвать с помощью объекта WorksheetFunction. Таким образом количество живых соседей в окружающей текущую ячейку области 3 на 3 мы получаем выражением (не забыв вычесть из полученного количества текущую ячейку):
n = WorksheetFunction.CountA(cell.Offset(-1, -1).Resize(3, 3)) - WorksheetFunction.CountA(cell)
Дальше нам нужно проверить полученное количество соседей и пометить на листе следующего поколения текущую ячейку как живую или мертвую, согласно правилам игры. Это выполняет блок из трёх проверок:
If cell = "" And n = 3 Then wNext.Cells(cell.Row, cell.Column) = 1 If cell = 1 And (n = 2 Or n = 3) Then wNext.Cells(cell.Row, cell.Column) = 1 If cell = 1 And (n < 2 Or n > 3) Then wNext.Cells(cell.Row, cell.Column) = ""
Когда цикл прохода по ячейкам будет завершен, то сформированное следующее поколение с листа next нужно скопировать на место текущего на листе game — делаем это уже знакомой конструкцией:
rNext.Copy Destination:=rGame
Вот, собственно, и вся логика.
Осталось вернуться в Excel на лист game, запустить нашу игру через вкладку Разработчик — Макросы (Developer — Macro) и насладиться процессом развития нашей колонии:
Ссылки по теме
- Что такое макросы и как их программировать в Microsoft Excel
- Справочник по игре «Жизнь» — сайт LifeWiki