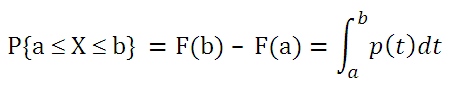Клетчатка вероятности в excel

Comoc Пользователь Сообщений: 3 Регистрация: 27.10.2016	Здравствуйте. Подскажите можно ли так построить график в Excel так что бы координата х выглядела как на рисунке. В приложенном excel есть таблица и график на нем нужно получить такую же ось х. Буду очень благодарен за помощь. Прикрепленные файлы 1111.png (5.39 КБ) 1111.xlsx (16.06 КБ)

vikttur Пользователь Сообщений: 47199 Регистрация: 15.09.2012	Клетчатка — это что-то с биологии И описывать задачу нужно в сообщении, иначе всем нужно открывать файл, чтобы с ним ознакомиться.

Comoc Пользователь Сообщений: 3 Регистрация: 27.10.2016

Chonard Пользователь Сообщений: 132 Регистрация: 01.01.1970	Пока вы  меняете название темы, параллельно попробуйте выделить ряд данных (значение по осиу), потом Вставка-График. Посторится диаграмма по категориям. Идете в Конструктор-Выбрать  Данные- Там меняете подписи по горизонтальной оси на нужные вам *(нужно выделитьзначения по оси х — в верхней строчке вашей таблицы) и будет так, как вы хотите. Прикрепленные файлы 1111.xlsx (17.5 КБ)

Comoc Пользователь Сообщений: 3 Регистрация: 27.10.2016	Спасибо, большое разобрался. Изменено: Comoc — 27.10.2016 17:17:49

С.М. Пользователь Сообщений: 936 Регистрация: 22.12.2012	#6 27.10.2016 23:41:02 Скрытый текст Прикрепленные файлы 111.1.xlsx (16.53 КБ) Изменено: С.М. — 29.10.2016 04:05:15

---

Вероятность описывает вероятность того, что некоторое событие произойдет.

Мы можем рассчитать вероятности в Excel, используя функцию PROB , которая использует следующий синтаксис:

ПРОБ(x_диапазон, вероятностный_диапазон, нижний_предел, [верхний_предел])

куда:

• x_range: диапазон числовых значений x.
• prob_range: диапазон вероятностей, связанных с каждым значением x.
• нижний_предел: нижний предел значения, для которого вы хотите получить вероятность.
• upper_limit: Верхний предел значения, для которого вы хотите получить вероятность. По желанию.

В этом руководстве представлено несколько примеров использования этой функции на практике.

Пример 1: Вероятность игры в кости

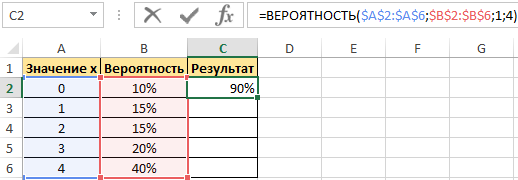
На следующем изображении показана вероятность выпадения кубика с определенным значением при данном броске:

Поскольку кости с одинаковой вероятностью выпадут на каждом значении, вероятность одинакова для каждого значения.

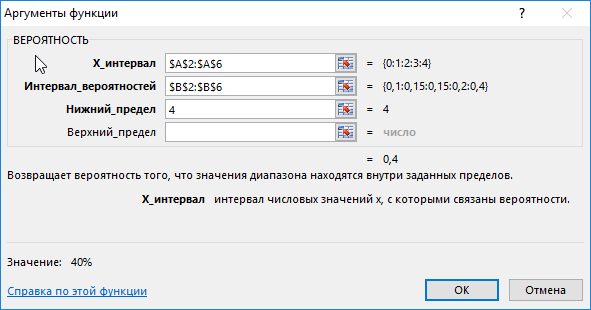
На следующем рисунке показано, как найти вероятность того, что кубик выпадет на число от 3 до 6:

Вероятность оказывается равной 0,5 .

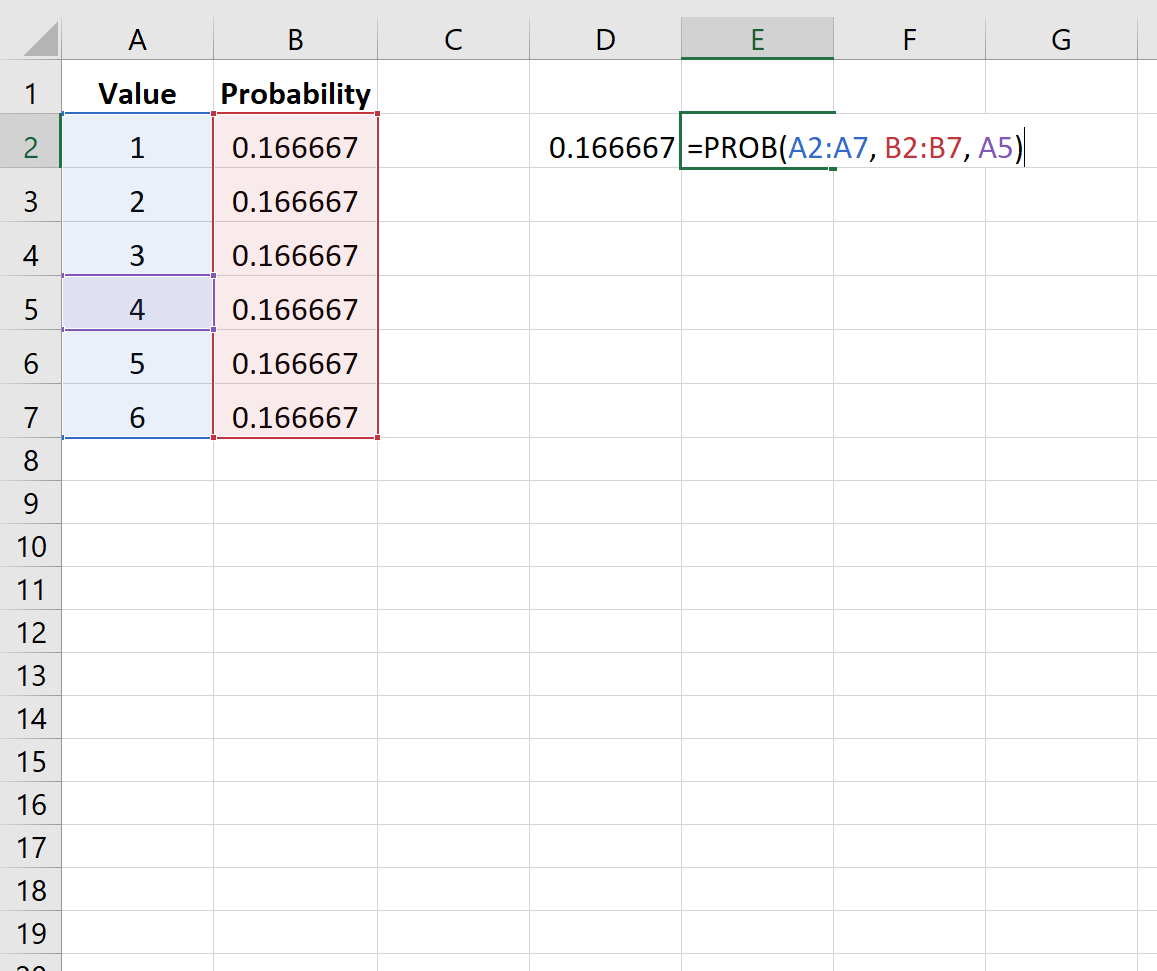
Обратите внимание, что аргумент верхнего предела является необязательным. Таким образом, мы могли бы использовать следующий синтаксис, чтобы найти вероятность того, что кости приземлятся только на 4:

Вероятность оказывается равной 0,166667 .

Пример 2: Вероятность продаж

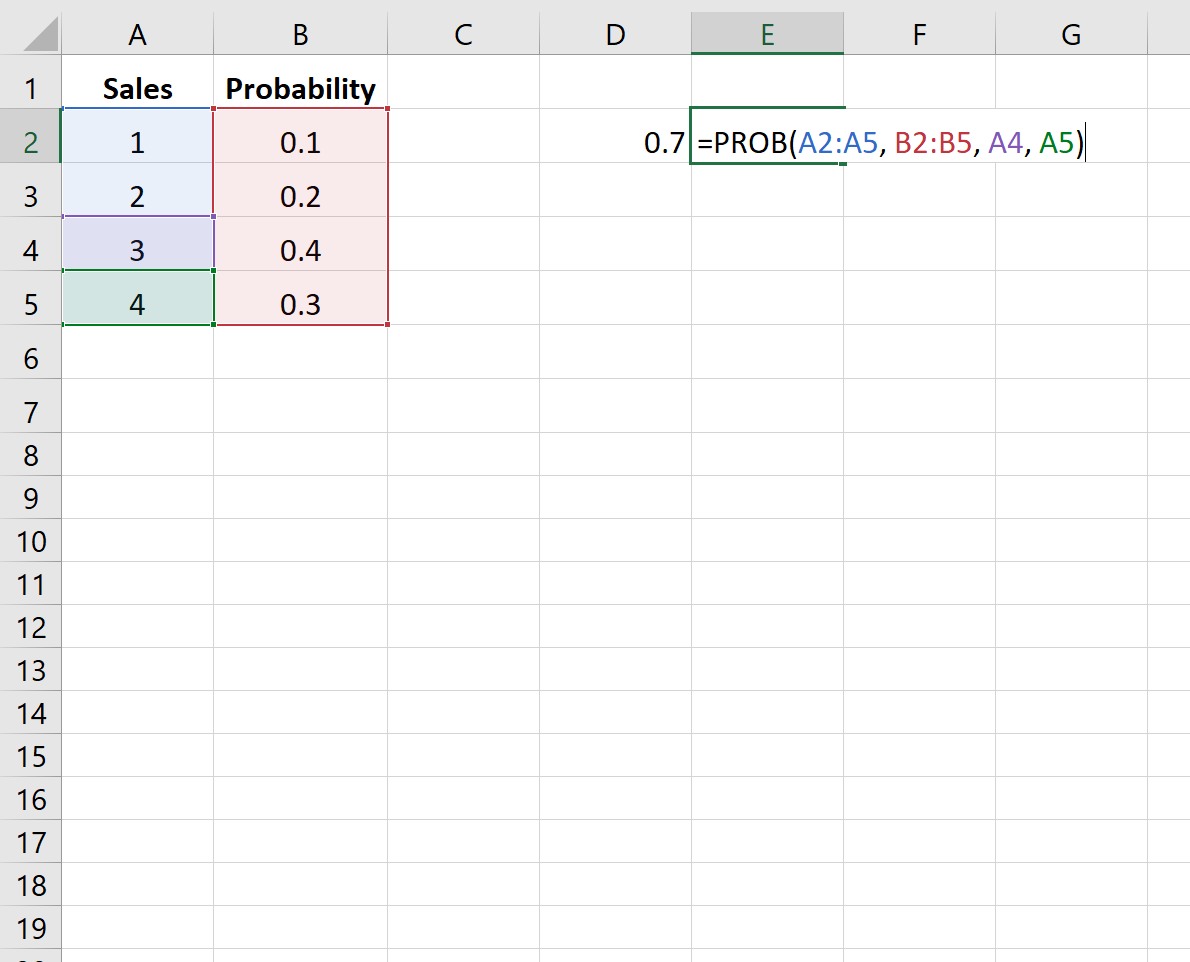
На следующем изображении показана вероятность того, что компания продаст определенное количество товаров в предстоящем квартале:

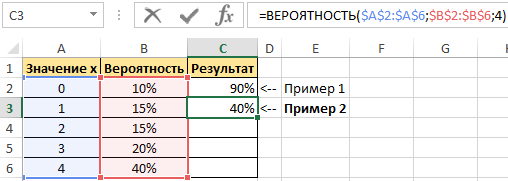
На следующем рисунке показано, как найти вероятность того, что компания совершит 3 или 4 продажи:

Вероятность оказывается равной 0,7 .

Дополнительные ресурсы

Как рассчитать относительную частоту в Excel
Как рассчитать кумулятивную частоту в Excel
Как создать частотное распределение в Excel

Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.

Примеры использования функции вероятность для расчетов в Excel

Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:

• ДИСП;
• ГИПЕРГЕОМ.РАСП;
• СРЗНАЧ и другие.

Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.



Вычисление процента вероятности события в Excel

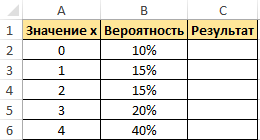
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:

Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].

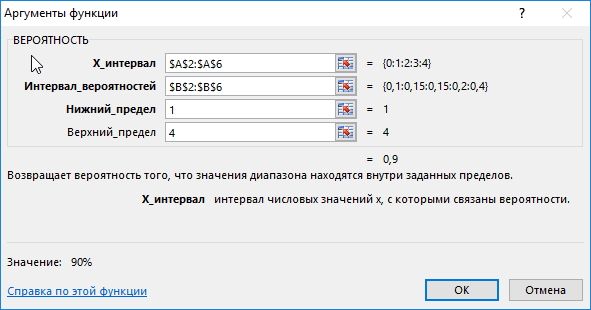
Для этого введем функцию со следующими аргументами:

тут:

• х_интервал – это начальные данные (0, …, 4);
• интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
• нижний предел равен значению 1;
• верхний предел равен 4.

В результате выполненных вычислений получим:

Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».

Введем в ячейку С3 введем функцию с такими аргументами:

тут:

• х_интервал – начальные параметры (0, …, 4);
• интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
• нижний предел – 4;

В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.

Получим:

Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов

Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].

Введем формулу:

Описание формул аналогичные предыдущим примерам.

В результате выполненных вычислений получим:

Скачать примеры функции ВЕРОЯТНОСТЬ в Excel

Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.

Примечание. 1 – биномиальная кривая; 2 –
трехпараметрическая кривая.

По полученным значениям К
и р строят аналитическую кривую обеспеченности на полулогарифмической
сетке, называемой клетчаткой вероятности (см. рис. 6). Данные для построения
горизонтальной шкалы клетчатки вероятностей приведены в табл. 3 приложения. В
ней буквой х  обозначены расстояния от середины шкалы,
соответствующей значению р=50%, до требуемой абсциссы. А вертикальная
шкала клетчатки – равномерная.

4. Аппроксимация эмпирической
кривой трехпараметрической зависимостью (кривая С.М. Крицкого – М.Ф. Менкеля).Из табл. 2 приложения выписывают в табл. 11 величины К_р,
соответствующие условию (10),  вычисленному значению С_v  и выбранным значениям вероятности
превышения  р. Далее  рассчитывают значения расходов, например, для р=1% 
Q_р=2,5 ∙ 3,505 = 8,76 м³/с.
На следующем этапе строят аналитическую кривую обеспеченности.

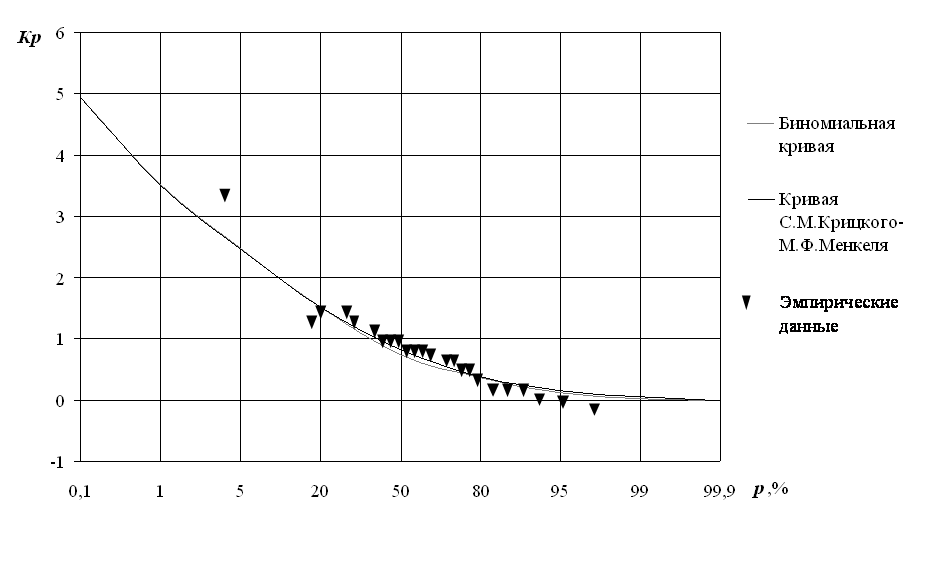
Анализ графиков
показывает, что аналитические кривые практически совпадают в области малых
значений ВП. В области больших значений ВП кривая трехпараметрического
распределения проходит ближе к эмпирической кривой.

ЛАБОРАТОРНАЯ
РАБОТА  4

 ОПРЕДЕЛЕНИЕ 
ХАРАКТЕРИСТИК ТВЕРДОГО СТОКА РЕКИ

Вводные понятия

Речными наносами называются продукты
разрушения земной коры в виде сыпучих материалов, перемещаемых потоком воды в
речном русле. Расход и сток наносов обычно устанавливается одновременно с
определением расхода и стока воды в реке.

В зависимости от
характера передвижения наносы подразделяются на взвешенные и донные. Взвешенные наносы  мелких фракций
подхватываются восходящими струями речного потока и движутся с массой воды.
Донные наносы перемещаются под действием пульсации придонных струй или
находятся в состоянии покоя. Если скорость течения воды увеличивается, донные наносы переходят во
взвешенное состояние и наоборот – при уменьшении скорости часть наиболее
крупных взвешенных наносов начинает перемещаться по дну. Количество взвешенных
наносов, содержащихся в  воде, характеризуется мутностью  р,  г/м³.

Порядок выполнения работы

1. Сбор данных. Для
определения характеристик твердого стока реки из таблицы «Взвешенные наносы»
гидрологического ежегодника  выписывают среднемесячные значения мутности для
всех месяцев года и помещают в табл. 12. В нее же из таблицы «Ежедневные
расходы воды» гидрологического ежегодника записывают  значения среднемесячных
расходов воды.

Таблица 12

Взвешенные
наносы

Месяц	Мутность р, г/м3	Расход  воды  Qp,  м3/с	Массовый расход наносов  Qн.мас, кг/с	Объемный  расход наносов Qн.об, м3/с	Объем наносов Vн,  м3	Накоплен-ная сумма объемов ∑Vн,   м3
I	0	0,99	0	0	0	0
II	0	0,59	0	0	0	0
III	0	0,44	0	0	0	0
IV	20	3,36	67,2	0,061	158,1	158,1
V	80	17,4	1392	1,265	3388,2	3546,3
VI	27	10,6	286	0,26	673,9	4220,2
VII	21	12,3	258	0,234	626,7	4846,9
VIII	28	22,7	635,6	0,578	1547,6	6394,5
IX	10	11,8	118	0,107	277,3	6671,8
X	7,3	6,15	45	0,041	109,8	6781,6
XI	5,7	3,82	21,8	0,02	51,8	6840,6
XII	0	0,87	0	0	0	6840,6

Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта

www.excel2.ru

. Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL

.

Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.

Генеральная совокупность и случайная величина

Пусть у нас имеется

генеральная совокупность

(population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.

Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.

Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения

генеральная совокупность

представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.

В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.

Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является

случайной величиной

. По определению, любая

случайная величина

имеет

функцию распределения

, которая обычно обозначается F(x).

Функция распределения

Функцией распределения

вероятностей

случайной величины

Х называют функцию F(x), значение которой в точке х равно вероятности события X

F(x) = P(X

Поясним на примере нашего станка. Хотя предполагается, что наш станок производит только один тип деталей, но, очевидно, что вес изготовленных деталей будет слегка отличаться друг от друга. Это возможно из-за того, что при изготовлении мог быть использован разный материал, а условия обработки также могли слегка различаться и пр. Пусть самая тяжелая деталь, произведенная станком, весит 200 г, а самая легкая — 190 г. Вероятность того, что случайно выбранная деталь Х будет весить меньше 200 г равна 1. Вероятность того, что будет весить меньше 190 г равна 0. Промежуточные значения определяются формой Функции распределения. Например, если процесс настроен на изготовление деталей весом 195 г, то разумно предположить, что вероятность выбрать деталь легче 195 г равна 0,5.

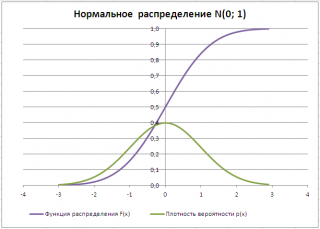
Типичный график

Функции распределения

для непрерывной случайной величины приведен на картинке ниже (фиолетовая кривая, см.

файл примера

):

В справке MS EXCEL

Функцию распределения

называют

Интегральной

функцией распределения

(

Cumulative

Distribution

Function

,

CDF

).

Приведем некоторые свойства

Функции распределения:

• 
  Функция распределения
  
  F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
• 
  Функция распределения
  
  – неубывающая функция;
• Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x
  
  ₁
  <=X
  2

  )=F(x
  
  ₂
  
  )-F(x
  
  ₁
  
  ).

Существует 2 типа распределений:

непрерывные распределения

и

дискретные распределения

.

Дискретные распределения

Если случайная величина может принимать только определенные значения и количество таких значений конечно, то соответствующее распределение называется

дискретным

. Например, при бросании монеты, имеется только 2 элементарных исхода, и, соответственно, случайная величина может принимать только 2 значения. Например, 0 (выпала решка) и 1 (не выпала решка) (см.

схему Бернулли

). Если монета симметричная, то вероятность каждого исхода равна 1/2. При бросании кубика случайная величина принимает значения от 1 до 6. Вероятность каждого исхода равна 1/6. Сумма вероятностей всех возможных значений случайной величины равна 1.

Примечание

: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье

Распределения случайной величины в MS EXCEL

.

Непрерывные распределения и плотность вероятности

В случае

непрерывного распределения

случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для

непрерывной случайной величины

равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой

функции плотности распределения p(x)

. Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение

функции распределения

на этом интервале:

Как видно из формулы выше

плотность распределения

р(х) представляет собой производную

функции распределения

F(x), т.е. р(х) = F’(x).

Типичный график

функции плотности распределения

для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):

Примечание

: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье

Распределения случайной величины в MS EXCEL

.

В литературе

Функция плотности распределения

непрерывной случайной величины может называться:

Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF)

.

Чтобы все усложнить, термин

Распределение

(в литературе на английском языке —

Probability

Distribution

Function

или просто

Distribution

)

в зависимости от контекста может относиться как

Интегральной

функции распределения,

так и кее

Плотности распределения.

Из определения

функции плотности распределения

следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от

Функции распределения,

больше 1. Например, для

непрерывной равномерной величины

, распределенной на интервале [0; 0,5]

плотность вероятности

равна 1/(0,5-0)=2. А для

экспоненциального распределения

с параметром

лямбда

=5, значение

плотности вероятности

в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.

Напомним, что

плотность распределения

является производной от

функции распределения

, т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что

плотность распределения

>1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере

экспоненциального распределения

).

Примечание

: Площадь, целиком заключенная под всей кривой, изображающей

плотность распределения

, равна 1.

Примечание

: Напомним, что функцию распределения F(x) называют в функциях MS EXCEL

интегральной функцией распределения

. Этот термин присутствует в параметрах функций, например в

НОРМ.РАСП

(x; среднее; стандартное_откл;

интегральная

). Если функция MS EXCEL должна вернуть

Функцию распределения,

то параметр

интегральная

, д.б. установлен ИСТИНА. Если требуется вычислить

плотность вероятности

, то параметр

интегральная

, д.б. ЛОЖЬ.

Примечание

: Для

дискретного распределения

вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL

плотность вероятности

может называть даже «функция вероятностной меры» (см. функцию

БИНОМ.РАСП()

).

Вычисление плотности вероятности с использованием функций MS EXCEL

Понятно, что чтобы вычислить

плотность вероятности

для определенного значения случайной величины, нужно знать ее распределение.

Найдем

плотность вероятности

для

стандартного нормального распределения

N(0;1) при x=2. Для этого необходимо записать формулу

=НОРМ.СТ.РАСП(2;ЛОЖЬ)

=0,054 или

=НОРМ.РАСП(2;0;1;ЛОЖЬ)

.

Напомним, что

вероятность

того, что

непрерывная случайная величина

примет конкретное значение x равна 0. Для

непрерывной случайной величины

Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).

Вычисление вероятностей с использованием функций MS EXCEL

1) Найдем вероятность, что случайная величина, распределенная по

стандартному нормальному распределению

(см. картинку выше), приняла положительное значение. Согласно свойству

Функции распределения

вероятность равна F(+∞)-F(0)=1-0,5=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу

=НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА)

=1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).

2) Найдем вероятность, что случайная величина, распределенная по

стандартному нормальному распределению

, приняла отрицательное значение. Согласно определения

Функции распределения,

вероятность равна F(0)=0,5.

В MS EXCEL для нахождения этой вероятности используйте формулу

=НОРМ.СТ.РАСП(0;ИСТИНА)

=0,5.

3) Найдем вероятность того, что случайная величина, распределенная по

стандартному нормальному распределению

, примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу

=НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА)

.

Все расчеты, приведенные выше, относятся к случайной величине, распределенной по

стандартному нормальному закону

N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье

Распределения случайной величины в MS EXCEL

приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.

Обратная функция распределения (Inverse Distribution Function)

Вспомним задачу из предыдущего раздела:

Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.

Вероятность этого события равна 0,5.

Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение
медиану

или 50-ю

процентиль

).

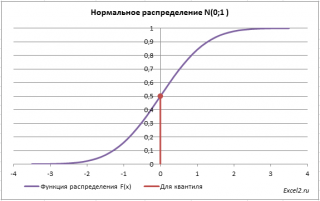
Для этого необходимо на графике

функции распределения

найти точку, для которой F(х)=0,5, а затем найти абсциссу этой точки. Абсцисса точки =0, т.е. вероятность, того что случайная величина Х примет значение <0, равна 0,5.

В MS EXCEL используйте формулу

=НОРМ.СТ.ОБР(0,5)

=0.

Однозначно вычислить значение

случайной величины

позволяет свойство монотонности

функции распределения.

Обратите внимание, что для вычисления обратной функции мы использовали именно

функцию распределения

, а не

плотность распределения

. Поэтому, в аргументах функции

НОРМ.СТ.ОБР()

отсутствует параметр

интегральная

, который подразумевается. Подробнее про функцию

НОРМ.СТ.ОБР()

см. статью про

нормальное распределение

.

Обратная функция распределения

вычисляет

квантили распределения

, которые используются, например, при

построении доверительных интервалов

. Т.е. в нашем случае число 0 является 0,5-квантилем

нормального распределения

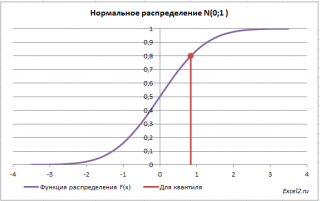
. В

файле примера

можно вычислить и другой

квантиль

этого распределения. Например, 0,8-квантиль равен 0,84.

В англоязычной литературе

обратная функция распределения

часто называется как Percent Point Function (PPF).

Примечание

: При вычислении

квантилей

в MS EXCEL используются функции:

НОРМ.СТ.ОБР()

,

ЛОГНОРМ.ОБР()

,

ХИ2.ОБР(),

ГАММА.ОБР()

и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье

Распределения случайной величины в MS EXCEL

.