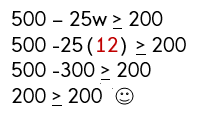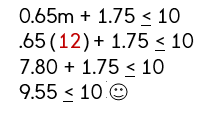|
Lesson Question:How can identifying key words help students solve mathematical word problems? Lesson Overview:In this lesson, students will take turns acting as «math coaches» who will assist other students in solving word problems by identifying key words that usually indicate specific mathematical operations. Length of Lesson:One hour to one hour and a half Instructional Objectives:Students will:
Materials:
Links:
Warm-up:Solving an authentic word problem:
Instruction:Brainstorming key words that indicate mathematical equations:
Mathematical Operations and Key Words
Creating key word flash cards:
Playing the role of «math coach»:
Wrap-up:Sharing word problem answers and strategies:
Extending the Lesson:
Assessment:
Educational Standards:Benchmarks for Mathematics Standard 1. Uses a variety of strategies in the problem-solving process
Click here to read more articles from Lesson Plans. |
 |
Do your students need some help learning those key words when trying to solve word problems? Here is a FREE set of Key Words to use for solving addition and subtraction word problems. (Multiplication and Division Key Words are below) These are a perfect size to hang on your math wall or even on your word wall. Students will be able to tackle word problems with ease using these key words. ******************* Do you need some word problems to practice using key words? Here are some fun and…
Key Words for Word Problems-Freebie Teacher’s Take-Out
Key Words for Word Problems-Freebie Teacher’s Take-Out
Comments
1. A
The ratio between black and blue pens is 7 to 28 or 7:28. Bring to the lowest terms by dividing both sides by 7 gives 1:4.
2. A
At 100% efficiency 1 machine produces 1450/10 = 145 m of cloth.
At 95% efficiency, 4 machines produce 4 * 145 * 95/100 = 551 m of cloth.
At 90% efficiency, 6 machines produce 6 * 145 * 90/100 = 783 m of cloth.
Total cloth produced by all 10 machines = 551 + 783 = 1334 m
Since the information provided and the question are based on 8 hours, we did not need to use time to reach the answer.
3. D
The turnout at polling station A is 945 out of 1270 registered voters. So, the percentage turnout at station A is:
(945/1270) × 100% = 74.41%
The turnout at polling station B is 860 out of 1050 registered voters. So, the percentage turnout at station B is:
(860/1050) × 100% = 81.90%
The turnout at polling station C is 1210 out of 1440 registered voters. So, the percentage turnout at station C is:
(1210/1440) × 100% = 84.03%
To find the total turnout from all three polling stations, we need to add up the total number of voters and the total number of registered voters from all three stations:
Total number of voters = 945 + 860 + 1210 = 3015
Total number of registered voters = 1270 + 1050 + 1440 = 3760
The overall percentage turnout is:
(3015/3760) × 100% = 80.12%
Therefore, the total turnout from all three polling stations is 80.12% — rounding to 80%.
4. D
This is a simple direct proportion problem:
If Lynn can type 1 page in p minutes, then she can type x pages in 5 minutes
We do cross multiplication: x * p = 5 * 1
Then,
x = 5/p
5. A
This is an inverse ratio problem.
1/x = 1/a + 1/b where a is the time Sally can paint a house, b is the time John can paint a house, x is the time Sally and John can together paint a house.
So,
1/x = 1/4 + 1/6 … We use the least common multiple in the denominator that is 24:
1/x = 6/24 + 4/24
1/x = 10/24
x = 24/10
x = 2.4 hours.
In other words; 2 hours + 0.4 hours = 2 hours + 0.4•60 minutes
= 2 hours 24 minutes
6. D
The original price of the dishwasher is $450. During a 15% off sale, the price of the dishwasher will be reduced by:
15% of $450 = 0.15 x $450 = $67.50
So the sale price of the dishwasher will be:
$450 – $67.50 = $382.50
As an employee, the person receives an additional 20% off the lowest price, which is $382.50. We can calculate the additional discount as:
20% of $382.50 = 0.20 x $382.50 = $76.50
So the final price that the employee will pay for the dishwasher is:
$382.50 – $76.50 = $306.00
Therefore, the employee will pay $306.00 for the dishwasher.
7. D
Original price = x,
80/100 = 12590/X,
80X = 1259000,
X = 15,737.50.
8. D
We are given that each of the n employees earns s amount of salary weekly. This means that one employee earns s salary weekly. So; Richard has ‘ns’ amount of money to employ n employees for a week.
We are asked to find the number of days n employees can be employed with x amount of money. We can do simple direct proportion:
If Richard can employ n employees for 7 days with ‘ns’ amount of money,
Richard can employ n employees for y days with x amount of money … y is the number of days we need to find.
We can do cross multiplication:
y = (x * 7)/(ns)
y = 7x/ns
9. B
The distribution is done at three different rates and in three different amounts:
$6.4 per 20 kilograms to 15 shops … 20•15 = 300 kilograms distributed
$3.4 per 10 kilograms to 12 shops … 10•12 = 120 kilograms distributed
550 – (300 + 120) = 550 – 420 = 130 kilograms left. This 50
amount is distributed in 5 kilogram portions. So, this means that there are 130/5 = 26 shops.
$1.8 per 130 kilograms.
We need to find the amount he earned overall these distributions.
$6.4 per 20 kilograms : 6.4•15 = $96 for 300 kilograms
$3.4 per 10 kilograms : 3.4 *12 = $40.8 for 120 kilograms
$1.8 per 5 kilograms : 1.8 * 26 = $46.8 for 130 kilograms
So, he earned 96 + 40.8 + 46.8 = $ 183.6
The total distribution cost is given as $10
The profit is found by: Money earned – money spent … It is important to remember that he bought 550 kilograms of potatoes for $165 at the beginning:
Profit = 183.6 – 10 – 165 = $8.6
10. B
We check the fractions taking place in the question. We see that there is a “half” (that is 1/2) and 3/7. So, we multiply the denominators of these fractions to decide how to name the total money. We say that Mr. Johnson has 14x at the beginning; he gives half of this, meaning 7x, to his family. $250 to his landlord. He has 3/7 of his money left. 3/7 of 14x is equal to:
14x * (3/7) = 6x
So,
Spent money is: 7x + 250
Unspent money is: 6×51
Total money is: 14x
Write an equation: total money = spent money + unspent money
14x = 7x + 250 + 6x
14x – 7x – 6x = 250
x = 250
We are asked to find the total money that is 14x:
14x = 14 * 250 = $3500
11. D
First calculate total square feet, which is 15 * 24 = 360 ft2. Next, convert this value to square yards, (1 yards2 = 9 ft2) which is 360/9 = 40 yards2. At $0.50 per square yard, the total cost is 40 * 0.50 = $20.
Solving Word Problems in Algebra
Inequality Word Problems
How are you with solving word problems in Algebra? Are you ready to
dive into the «real world» of inequalities? I know that solving word
problems in Algebra is probably not your favorite, but there’s no point
in learning the skill if you don’t apply it.
I promise to make this as easy as possible. Pay close attention to
the key words given below, as this will help you to write the
inequality. Once the inequality is written, you can solve the
inequality using the skills you learned in our past lessons.
I’ve tried to provide you with examples that could pertain to your
life and come in handy one day. Think about others ways you might use
inequalities in real world problems. I’d love to hear about them if you do!
Before we look at the examples let’s go over some of the rules and
key words for solving word problems in Algebra (or any math class).
Word Problem Solving Strategies
- Read through the entire problem.
- Highlight the important information and key words that you need to solve the problem.
- Identify your variables.
- Write the equation or inequality.
- Solve.
- Write your answer in a complete sentence.
- Check or justify your answer.
I know it always helps too, if you have key words that help you to write
the equation or inequality. Here are a few key words that we associate
with inequalities! Keep these handy as a reference.
Inequality Key Words
- at least — means greater than or equal to
- no more than — means less than or equal to
- more than — means greater than
- less than — means less than
Ok… let’s put it into action and look at our examples.
Example 1: Inequality Word Problems
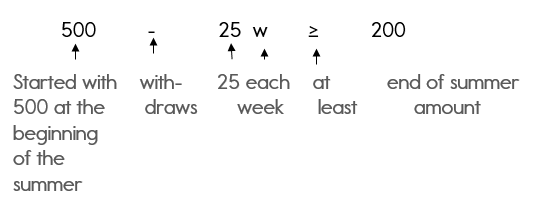
Keith has $500 in a savings account at the beginning of the summer. He wants to have at least $200 in the account by the end of the summer. He withdraws $25 each week for food, clothes, and movie tickets.
- Write an inequality that represents Keith’s situation.
- How many weeks can Keith withdraw money from his account? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: At least is a key word that notes that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know how many weeks.
Let w = the number of weeks
Step 3: Write your inequality.
500 — 25w > 200
I know you are saying, «How did you get that inequality?»
I know the «at least» part is tricky. You would probably think that at least means less than.
But… he wants the amount in his account to be at least $200 which means $200 or greater. So, we must use the greater than or equal to symbol.
Step 4: Solve the inequality.
The number of weeks that Keith can withdraw money from his account is 12 weeks or less.
Step 5: Justify (prove your answer mathematically).
I’m going to prove that the largest number of weeks is 12 by substituting 12 into the inequality for w. You could also substitute any number less than 12.
Since 200 is equal to 200, my answer is correct. Any more than 12 weeks and his account balance would be less than $200. Any number of weeks less than 12 and his account would stay above $200.
That wasn’t too bad, was it? Let’s take a look at another example.
Example 2: More Inequality Word Problems
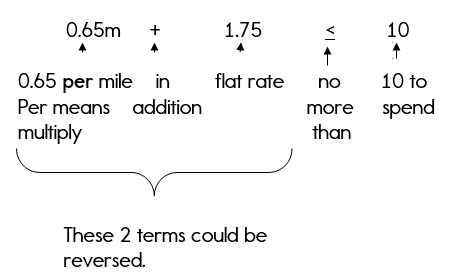
Yellow Cab Taxi charges a $1.75 flat rate in addition to $0.65 per mile. Katie has no more than $10 to spend on a ride.
- Write an inequality that represents Katie’s situation.
- How many miles can Katie travel without exceeding her budget? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: No more than are key words that note that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know the number of miles Katie can travel.
Let m = the number of miles
Step 3: Write the inequality.
0.65m + 1.75 < 10
Are you thinking, «How did you write that inequality?»
The «no more than» can also be tricky. «No more than» means that you can’t have more than something, so that means you must have less than!
Step 4: Solve the inequality.
Since this is a real world problem and taxi’s usually charge by the mile, we can say that Katie can travel 12 miles or less before reaching her limit of $10.
Step 5: Justify (prove your answer mathematically).
Are you ready to try some on your own now? Yes… of course you are! Click here to move onto the word problem practice problems.
Take a look at the questions that other students have submitted:
- Home
- Inequalities
-
Inequality Word Problems
>
>
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Add
- Addition: as in The team needed the addition of three new players …
- Sum: as in The sum of 5, 6, and 8 …
- Total: as in The total of the last two games …
- Plus: as in Three chairs plus five chairs …
- Increase: as in Her pay was increased by $30 …
Subtract
- Difference: as in What is the difference between 8 and 5 …
- Fewer: as in There were ten fewer girls than boys …
- Remainder: as in What is the remainder when … or How many are left when …
- Less: as in A number is six less than another number …
- Reduced: as in His allowance was reduced by $5 …
- Decreased: as in What number decreased by 7 is 5 …
- Minus: as in Seven minus some number is …
Multiply
- Product: as in The product of 3 and 6 is …
- Of: as in One‐half of the people in the room …
- Times: as in Six times as many men as women …
- At: as in The cost of five yards of material at $9 a yard is …
- Total: As in If you spend $20 per week on gas, what is the total for a two‐week period …
- Twice: as in Twice the value of some number … (multiplying by 2)
Divide
- Quotient: as in The final quotient is …
- Divided by: as in Some number divided by 5 is …
- Divided into: as in The coins were divided into groups of …
- Ratio: as in What is the ratio of …
- Half: as in Half of the cards were … (dividing by 2)
As you practice working word problems, you will discover more key words and phrases that give you insight into the solving process.
Example 1
Jack bowled four games for a total score of 500. What was his average score for a game?
- Step 1: Find and underline or circle what the question is asking.
What was his average score for a game?
- Step 2: Focus on and pull out important information.
four games for a total score of 500
- Step 3: Set up the work that is needed.
500 ÷ 4
(The total divided by the number of games gives the average.)
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
Jack’s average score for a game is 125.
- Step 6: Check to make sure that your answer is reasonable.
Since four games of 125 total 500, your answer is reasonable and correct.
Example 2
Judy scored 85, 90, and 95 on her last three algebra tests. What was her average score for these tests?
- Step 1: Find and underline or circle what the question is asking.
What was her average score for these tests?
- Step 2: Focus on and pull out important information.
85, 90, and 95 on three tests
- Step 3: Set up the work that is needed.
(85 + 90 + 95) ÷ 3 =
(The total divided by the number of scores gives the average.)
- Step 4: Do the necessary work or computation carefully.

- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
Judy’s average test score for these tests was 90.
- Step 6: Check to make sure that your answer is reasonable.
Since her scores were 85, 90, and 95, the average should be halfway between 85 and 95. So 90 is a reasonable answer.
Example 3
Frances goes to the market and buys two boxes of cereal at $4 each, three bottles of milk at $2 each, and two cans of soup at $1 each. How much change will Frances get from a $20 bill?
- Step 1: Find and underline or circle what the question is asking.
How much change will Frances get from a $20 bill?
- Step 2: Focus on and pull out important information.
two boxes at $4 each
three bottles at $2 each
two cans at $1 each
$20 bill used
- Step 3: Set up the work that is needed.
2 × 4 =
3 × 2 =
2 × 1 =
$20 – ? =
- Step 4: Do the necessary work or computation carefully.
2 × 4 = 8
3 × 2 = 6
2 × 1 = 2
8 + 6 + 2 = 16
20 – 16 = 4
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
Frances will get $4 change.
- Step 6: Check to make sure that your answer is reasonable.
Since the total expenses were $16, then $4 change from a $20 bill is reasonable.
Example 4
Sarah can purchase a television for $275 cash or for $100 as a down payment and ten monthly payments of $30 each. How much money can Sarah save by paying cash for the television?
- Step 1: Find and underline or circle what the question is asking.
How much money can Sarah save by paying cash for the television?
- Step 2: Focus on and pull out important information.
cash $275
$100 down plus ten payments of $30
- Step 3: Set up the work that is needed.
100 + (10 × 30) =
? – 275 =
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
Sarah can save $125 by paying cash.
Step 6: Check to make sure that your answer is reasonable.
Ten payments of $30 each is $300 plus a $100 down payment gives $400. This is $125 more than $275, so the answer is reasonable.
Example 5
If apples sell for $3.25 per dozen, how many apples can Maria buy for $13.00?
- Step 1: Find and underline or circle what the question is asking.
How many apples can Maria buy for $13.00?
- Step 2: Focus on and pull out important information.
$3.25 per dozen
$13.00
- Step 3: Set up the work that is needed.
$13.00 ÷ 3.25 = ? dozen
= ? apples
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
Maria can buy 48 apples for $13.00.
- Step 6: Check to make sure that your answer is reasonable.
Since Maria could buy 12 apples for about $3, then it is reasonable that she could buy 48 apples for about $13.
Example 6
Sequoia Junior High School has a student enrollment of 2,000. If 30% of the students are seventh graders, how many seventh graders are enrolled at the school?
- Step 1: Find and underline or circle what the question is asking.
How many seventh graders are enrolled at the school?
- Step 2: Focus on and pull out important information.
2,000 students
30% are seventh graders
- Step 3: Set up the work that is needed.
30% of 2,000 =
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
There are 600 seventh graders enrolled at Sequoia Junior High.
- Step 6: Check to make sure that your answer is reasonable.
Since 30% of 1,000 is 300, then 30% of 2,000 is 600. The answer is reasonable.
Example 7
Jim Chamberlain, the center for the West Hills Basketball Stars, makes 75% of his free throws. If Jim attempts 80 free throws in a season, how many of his free throws does he make?
- Step 1: Find and underline or circle what the question is asking.
How many of his free throws does he make?
- Step 2: Focus on and pull out important information.
makes 75%
shoots 80 free throws
- Step 3: Set up the work that is needed.
75% of 80 =
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
Jim makes 60 free throws.
- Step 6: Check to make sure that your answer is reasonable.
Since 50% of his 80 free throws would be 40, then it’s reasonable for 75% to be 60.
Example 8
Each week, John spends $50 of his income on entertainment. If John earns $200 a week, what percent of his income is spent on entertainment?
- Step 1: Find and underline or circle what the question is asking.
What percent of his income is spent on entertainment?
- Step 2: Focus on and pull out important information.
$50 on entertainment
$200 income
- Step 3: Set up the work that is needed.
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
John spends 25% of his income on entertainment.
- Step 6: Check to make sure that your answer is reasonable.
Since 50 is half, or 50% of 100, then 50 would reasonably be 25% of 200.
Example 9
The Gomez family spends 30% of its income for food. If the family spent $6,000 for food last year, what was the family income for last year?
- Step 1: Find and underline or circle what the question is asking.
What was the family income for last year?
- Step 2: Focus on and pull out important information.
30% of income for food
$6,000 spent for food last year
- Step 3: Set up the work that is needed.
30% of income = 6,000
30% x = 6,000
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
The Gomez family income for last year was $20,000.
- Step 6: Check to make sure that your answer is reasonable.
Since 30% of the family income is spent for food, and 30% of $20,000 is $6,000, then the answer is reasonable.
Example 10
A miniature piano keyboard is 

- Step 1: Find and underline or circle what the question is asking.
How many keys are there?
- Step 2: Focus on and pull out important information.


- Step 3: Set up the work that is needed.
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
There are 11 keys on the miniature keyboard.
- Step 6: Check to make sure that your answer is reasonable.
Since 16 divided by 1 is 16, and 16 divided by 2 is 8, the answer of 11 is reasonable.
Example 11
The low temperature on Big Bear mountain was 30 degrees on Monday, 20 degrees on Tuesday, ‐10 degrees on Wednesday, and 15 degrees on Thursday. If you total the changes in low temperature from each day to the next, what is the total number of degrees change?
- Step 1: Find and underline or circle what the question is asking.
What is the total number of degrees change?
- Step 2: Focus on and pull out important information.
30 on Monday
20 on Tuesday
–10 on Wednesday
15 on Thursday
- Step 3: Set up the work that is needed.
30 to 20 =
20 to –10 =
–10 to 15 =
- Step 4: Do the necessary work or computation carefully.
30 to 20 = –10
20 to –10 = –30
–10 to 15 = 25
total change = –10 + –30 + 25
= –15
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
The low temperature changed –15 degrees during the days Monday through Thursday.
- Step 6: Check to make sure that your answer is reasonable.
Since the low temperature dropped 10, dropped 30, and rose 25, the total of –15 is correct and reasonable.
Example 12
The Silverado Flash, a solar‐powered land vehicle, travels at a maximum speed of 97 miles per hour. At this rate, how far will the Silverado Flash travel in 15 hours?
An important formula to remember is d = rt, or distance equals rate times time.
- Step 1: Find and underline or circle what the question is asking.
How far will the Silverado Flash travel in 15 hours?
- Step 2: Focus on and pull out important information.
97 miles per hour
15 hours
- Step 3: Set up the work that is needed.
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
The Silverado Flash will travel 1,455 miles in 15 hours.
- Step 6: Check to make sure that your answer is reasonable.
At 100 miles per hour for 15 hours, the Silverado Flash would have traveled 1,500 miles. So the answer of 1,455 miles is reasonable.
Example 13
Asaf can run around the track, 440 yards, in 65 seconds. At this same rate, how far could Asaf run in 195 seconds?
- Step 1: Find and underline or circle what the question is asking.
How far could Asaf run in 195 seconds?
- Step 2: Focus on and pull out important information.
440 yards in 65 seconds
195 seconds
- Step 3: Set up the work that is needed.
You could set up the proportion
or simply divide 195 by 65 and multiply that result by 440.
(195 ÷ 65) × 440 = ?
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
Asaf could run 1,320 yards in 195 seconds.
- Step 6: Check to make sure that your answer is reasonable.
If Asaf ran 400 yards every 60 seconds, or one minute, and since 195 seconds is just over three minutes, then 3 times 400, or 1,200, would be a good approximation. So 1,320 yards is a reasonable answer.
Example 14
A researcher tagged 100 frogs in a nearby pond. One week later she took a sample and only 5 out of 20 frogs were tagged. Using this method, how many frogs would she approximate are in the pond?
- Step 1: Find and underline or circle what the question is asking.
How many frogs would she approximate are in the pond?
- Step 2: Focus on and pull out important information.
100 tagged
5 out of 20 tagged
- Step 3: Set up the work that is needed.
You could set up the proportion.
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
She would approximate that there are 400 frogs in the pond.
- Step 6: Check to make sure that your answer is reasonable.
Since she tagged 100, and 5 out of 20, or 1 out of 4, came out tagged, then it is reasonable to have a total of 400 frogs in the pond.
Example 15
Julia has $300 in the bank. She works at a bakery and makes $40 per day. If she deposits all of her earnings in the bank and does not make any withdrawals, how many days of work will it take for her to have $740 in the bank?
- Step 1: Find and underline or circle what the question is asking.
How many days of work will it take for her to have $740 in the bank?
- Step 2: Focus on and pull out important information.
$300 in the bank
$40 per day
$740 total
- Step 3: Set up the work that is needed.
Let d stand for the number of days. Then 40 d is the amount of money earned in d days, and 40 d + 300 is the amount of money she would have in the bank at the end of d days. So
40 d + 300 = 740
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
Julia would have to work 11 days to have $740 in the bank.
- Step 6: Check to make sure that your answer is reasonable.
At $40 per day, if she worked 11 days, she would have $440. Add this to the $300 she already had, and the total of $740 is correct and reasonable.
Example 16
A train is 50 miles from Seattle. It is traveling away from Seattle at a speed of 60 miles per hour. In how many hours will the train be 290 miles from Seattle?
- Step 1: Find and underline or circle what the question is asking.
In how many hours will the train be 290 miles from Seattle?
- Step 2: Focus on and pull out important information.
50 miles from Seattle
60 miles per hour
290 miles
- Step 3: Set up the work that is needed.
Let h stand for the number of hours. Then 60 h is the distance traveled in h hours, and 60 h + 50 is the distance from Seattle in h hours. So
60 h + 50 = 290
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
It will take the train four hours to be 290 miles from Seattle.
- Step 6: Check to make sure that your answer is reasonable.
At 60 miles per hour, in four hours the train will travel 240 miles. since it is starting 50 miles from Seattle, the total would be 290 miles.
Example 17
A number n is increased by 25, and the outcome is 57. What is the value of the number n?
- Step 1: Find and underline or circle what the question is asking.
What is the value of the number n ?
- Step 2: Focus on and pull out important information.
n is increased by 25
outcome is 57
- Step 3: Set up the work that is needed.
n + 25 = 57
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
The value of the number is 32.
- Step 6: Check to make sure that your answer is reasonable.
Since 32 plus 25 equals 57, the answer checks and is reasonable.
Example 18
The length of a Lambo Speed Wagon is 75 centimeters less than the length of a Corvette. The Lambo is 410 centimeters long. How long is a Corvette?
- Step 1: Find and underline or circle what the question is asking.
How long is a Corvette?
- Step 2: Focus on and pull out important information.
Lambo is 75 centimeters less
Lambo is 410 centimeters
- Step 3: Set up the work that is needed.
Let c represent the length of a Corvette. Then c –75 is the length of a Lambo. So
c – 75 = 410
- Step 4: Do the necessary work or computation carefully.
- Step 5: Put your answer into a sentence to make sure that you answered the question being asked.
The length of a Corvette is 485 centimeters.
- Step 6: Check to make sure that your answer is reasonable.
Since 485 – 75 is 410, the answer checks and is reasonable.