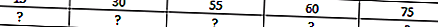Касательная в excel пример - Word и Excel - помощь в работе с программами

Функция TAN Excel (формула, примеры) | Как использовать касательную в Excel?

Функция TAN Excel — это встроенная тригонометрическая функция в Excel, которая используется для вычисления значения косинуса заданного числа или, в терминах тригонометрии, значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.

Функция TAN Excel

Функция TAN Excel — это встроенная функция, относящаяся к категории математических / триггерных функций, которая возвращает значение тангенса угла. Формула для TAN всегда возвращает числовое значение.

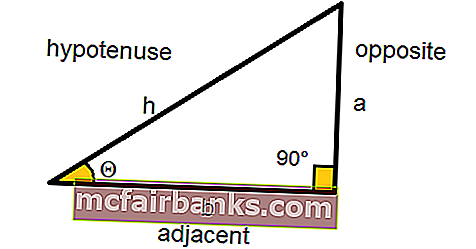
В тригонометрии тангенс угла эквивалентен отношению перпендикуляра к основанию прямоугольного треугольника.

TAN Θ = противоположная сторона / смежная сторона

Следовательно, TAN Θ = a / b

Формула TAN в Excel

Ниже приведена формула TAN в Excel.

Где число — это аргумент, передаваемый функции в радианах.

Угол, который мы указываем в качестве входных данных, распознается функцией Tangent, только если указан как Radians.

Чтобы преобразовать угол в радианы, используйте функцию РАДИАНЫ или преобразуйте угол в радианы с помощью математического соотношения

Радиан = угол в градусах * (π / 180)

π в Excel представлена функцией PI ()

Следовательно, радиан = градус * (PI () / 180)

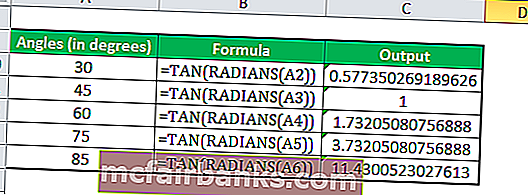
Расчет значения TAN с использованием функции TAN и RADIANS

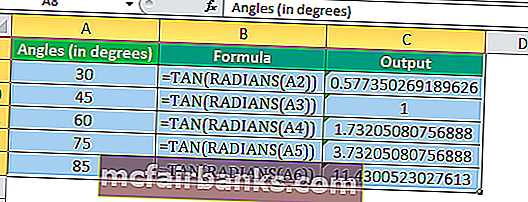
Расчет значения TAN с использованием TAN и функции PI

Функция касания имеет множество реальных приложений; он широко используется в архитектуре для расчета высоты и длины геометрических фигур. Функция касания, используемая в системах навигации и GPS, в аэронавтике.

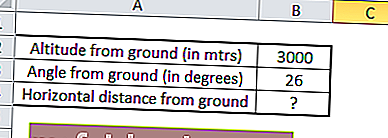
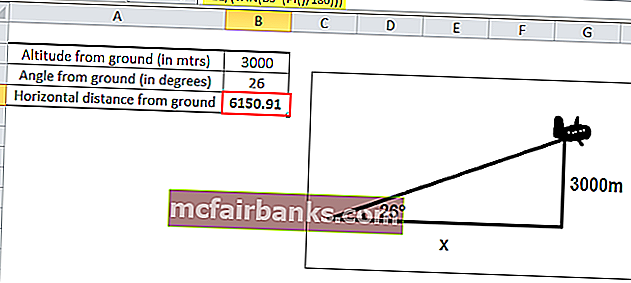
Например, если самолет летит на высоте 3000 м и делает угол к наблюдателю на земле 26 °, и мы хотим найти расстояние от самолета до наблюдателя.

Как мы знаем, TAN Θ = противоположная сторона / смежная сторона

Здесь противоположная сторона = высота самолета от земли, равная 3000 метров.

А прилегающая сторона = горизонтальное расстояние плоскости от земли, которое неизвестно, и нам нужно его вычислить.

Таким образом, используя формулу для TAN, мы имеем

TAN (26 °) = 3000 / x

Следовательно, x = 3000 / (TAN (26 °))

Если взять относительные контрольные значения, которые у нас есть,

X = B2 / (TAN (B3 * (PI () / 180)))

X = 6150,91 метра

Как использовать TAN в Excel?

Функция Excel TAN очень проста и удобна в использовании. Давайте разберемся, как работает формула TAN в Excel на нескольких примерах.

Вы можете скачать этот шаблон Excel с функцией TAN здесь — Шаблон Excel с функцией TAN

Касательная в Excel, пример # 1

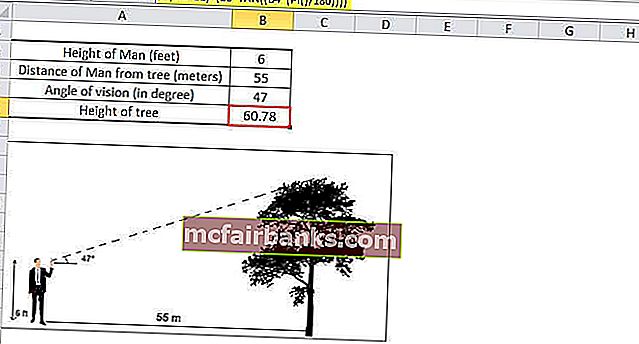
Мужчина ростом 6 футов находится в 55 метрах от дерева. Он делает угол обзора 47 ° параллельно земле. Мы хотим рассчитать высоту дерева.

Чтобы найти высоту дерева, мы будем использовать TAN Θ, в контексте Excel мы будем использовать функцию Tangent.

Высота дерева будет

Высота Человека + Расстояние Человека от дерева * TAN (47 °)

Поскольку рост человека указан в футах, мы переведем его в метры (1 фут = 0,30 метра).

Помещая все относительные значения в Excel, формула для высоты дерева будет

= (0,3 * B2) + (B3 * TAN ((B4 * (PI () / 180))))

Выходные данные TAN Excel:

Высота дерева 60,78 метра.

Касательная в Excel, пример # 2

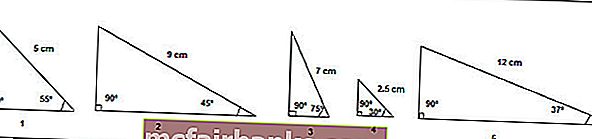
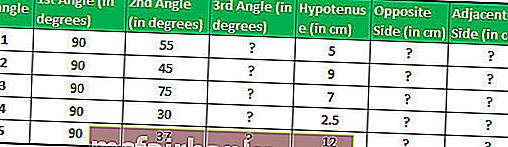
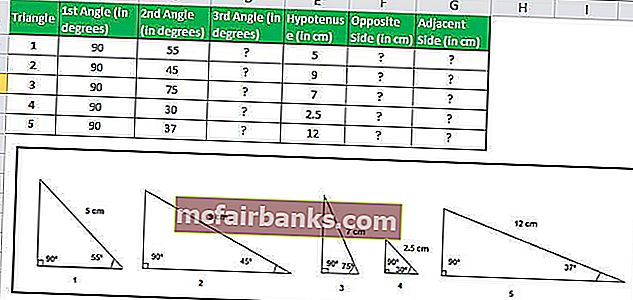
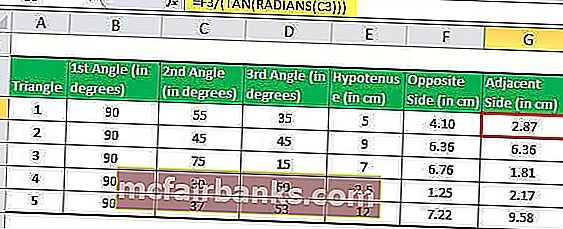
Предположим, у нас есть пять прямоугольных треугольников с указанием их углов и длины с одной стороны, и нам нужно вычислить длину двух других сторон.

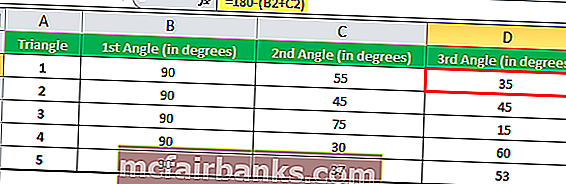
Сумма всех углов на треугольнике равна 180 °, следовательно, мы можем легко вычислить третий угол.

Мы знаем, Sin Θ = противоположное / гипотенуза

Таким образом, длина противоположной стороны будет Sin Θ * гипотенуза

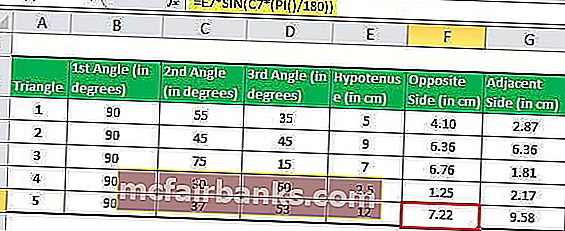
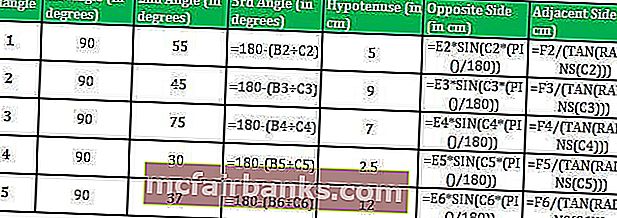
В Excel длина противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле TAN.

= E2 * SIN (C2 * (PI () / 180))

Применяя формулу TAN для пяти треугольников, мы можем получить длину перпендикуляров треугольников

Теперь у нас есть две стороны треугольника, гипотенуза и перпендикулярная сторона, и мы можем легко вычислить третью сторону (основание), используя TAN в Excel.

Мы знаем, что TAN Θ = противоположная сторона / смежная сторона

Таким образом, длина соседней стороны будет Opposite Side / TAN Θ

В Excel длина прилегающей стороны (основания) будет рассчитываться по формуле TAN

= F2 / (TAN (РАДИАНЫ (C2)))

Применяя формулу TAN для пяти треугольников, мы можем получить длину смежной стороны треугольника

TAN в выводе Excel:

Касательная в Excel, пример №3

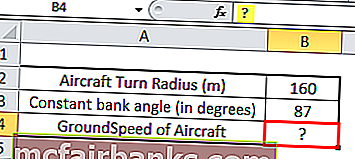
Самолет делает разворот радиусом 160 м и летит с постоянным углом крена 87 °, в идеальных условиях (без колебаний ветра) рассчитайте постоянную путевую скорость самолета.

Радиус поворота определяется формулой

Радиус поворота = V2 / g * TAN Θ

Радиус поворота 160 метров; Постоянный угол крена составляет 87 °, g — ускорение свободного падения, значение которого составляет 9,8 м / с2, поэтому путевая скорость будет равна

V = (Радиус поворота * (g * TAN Θ)) 1/2

Применяя приведенную выше формулу TAN в Excel с эталонными значениями, мы получаем формулу TAN

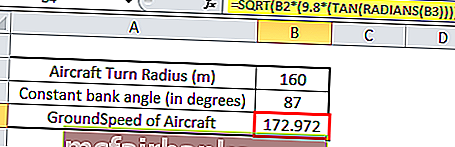
= КОРЕНЬ (B2 * (9,8 * (TAN (РАДИАНЫ (B3)))))

SQRT — это встроенная функция Excel, которая вычисляет квадратный корень из числа.

TAN в выводе Excel:

Итак, путевая скорость самолета составляет 172,97 м / с.

Пример функции касания # 4

У нас есть формула для TAN, обозначаемая f (x) = 2c * TAN2Θ, где c — постоянное значение, равное 0,988. Значение варианта — это значение, а формула для TAN зависит от значения Θ. Нам нужно построить график заданной функции касания.

Затем с помощью функции Excel TAN мы вычислим значения функции, поэтому взяв контрольные значения в качестве входных данных, мы получим формулу TAN,

Источник

Содержание

— Как написать TAN 30 в Excel?
— Какова формула касательной?
— Как писать касательную в Excel?
— Какой тангенс?
— Как получить степень Arctan в Excel?
— Как вы используете e в Excel?

Функция Excel TAN возвращает тангенс угла в радианах. Чтобы указать угол TAN в градусах, умножьте угол на PI () / 180 или используйте функцию РАДИАНЫ для преобразования в радианы. Получите тангенс угла. Значение касательной.

Как написать TAN 30 в Excel?

Как использовать функцию Excel TAN

В этой статье мы узнаем, как использовать функцию TAN в Excel. …
Давайте разберемся с этой функцией на примере. …
A2 / B2: смежная сторона угла делится на противоположную сторону угла. …
Это даст вам загар под углом 30 градусов.

Какова формула касательной?

1. Чему равен загар? Тангенс x определяется как его синус, деленный на его косинус: тангенс х = грех х / соз х. Котангенс x можно определить как косинус x, деленный на синус x: cot x = cos x / sin x.

Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter.
…
Пример.

Формула	Описание (Результат)	Результат
= TAN (45 * PI () / 180)	Касательная 45 градусов (1)	1
= ТАНЬ (РАДИАНЫ (45))	Касательная 45 градусов (1)	1

Какой тангенс?

В любом прямоугольном треугольнике тангенс угла равен длина противоположной стороны (O), деленная на длину соседней стороны (A). В формуле он записывается просто как «загар».

Как получить степень Arctan в Excel?

Чтобы выразить арктангенс в градусах, умножьте результат на 180 / PI () или используйте функцию ГРАДУСЫ.

Как вы используете e в Excel?

В Excel есть экспоненциальная функция и функция натурального журнала. Функция = EXP (значение) и дает результат evalue (это называется синтаксисом). Например, чтобы найти значение e, мы можем написать = EXP (1). Далее, если мы поместим число x в A1, а в A2 мы положим формулу = EXP (A1 ^ 2-1), это даст нам ex2−1.

Интересные материалы:

Как удалить столбец в Word?
Как удалить столбец?
Как удалить страницу компании в Facebook?
Как удалить страницу, которая не удаляется?
Как удалить страницу в конце документа Word?
Как удалить страницу в Word 2010?
Как удалить страницу в Word, которая не удаляет 2010?
Как удалить страницы на принтере Canon?
Как удалить страницы с моего MacBook Air?
Как удалить строку и столбец ячейки в MS Excel?

Источник

Содержание:

1 Шаг 1
2 Шаг 2
3 Шаг 3
4 Шаг 4
5 Шаг 5
6 Шаг 6
- - 6.0.1 Дубликаты не найдены

Тангенциальная линия — это прямая линия на графике, которая проходит по касательной к кривой линии, составленной из точек данных. В Excel есть возможность автоматически создавать линию тренда, или вы можете вручную нарисовать касательную линию на графике. Тангенциальная линия рисуется касаясь изогнутой линии, так что когда кривая отходит от линии, она равноудалена от линии. В то время как функция линии тренда в Excel покажет тренд всей линии, ручное рисование линии создаст истинную касательную.

Кредит: Драган Радоевич / iStock / Getty Images

Шаг 1

Откройте лист Excel, содержащий данные, которые вы хотите использовать для тангенциальной линии. Изогнутый линейный график основан на наборах двух точек данных, например времени и амплитуды.

Шаг 2

Нажмите и перетащите на электронную таблицу, чтобы выделить данные, которые вы хотите показать, включая метки в вашем выборе.

Шаг 3

Нажмите на вкладку «Вставить», а затем нажмите стрелку вниз рядом с кнопкой «Разброс» в области «Диаграмма». Выберите «Разброс с гладкими линиями». Диаграмма создана в вашей электронной таблице.

Шаг 4

Перейдите на вкладку «Инструменты диаграммы: макет», а затем нажмите кнопку «Линия тренда» справа. Выберите «Линейный», чтобы создать прямую линию, которая приближается к прогрессу изогнутой линии. Он будет пересекать кривую в некоторых точках.

Шаг 5

Нажмите на вкладку «Вставка», а затем нажмите «Фигуры». Выберите «Линия» и нарисуйте линию так, чтобы она просто касалась одной из точек на вашей кривой.

Шаг 6

Нажмите на вкладку «Инструменты рисования: Формат» и нажмите кнопку «Повернуть» справа. Выберите «Дополнительные параметры вращения». Нажмите стрелку «Вверх» или «Вниз» рядом с полем «Поворот» в диалоговом окне, которое появляется, чтобы повернуть линию на кривой. Когда линия будет равноудалена от обеих сторон кривой, нажмите «ОК».

Дубликаты не найдены

ЕСЛИ(условие;выполнить_если_истина;выполнить_если_ложь)
[в eng версии соответственно это IF(. )]

Условие — что угодно, что может интерпретироваться как булевская функция. Например, дано, что a=2, b=3. Тогда IF(a>b;»истина»;»ложь») вернёт «ложь».

Сделать разветвление на несколько вариантов — IF(условие1;действие1;IF(условие2;действие2;..))
В качетсве крайнего «ложь» блока ЕСЛИ можно писать что угодно [если уверены, что рассмотрели все возможные варианты].

Вообще, насколько помню, годная в экселе справка была.. Так что традиционное — RTFM.

В математике много задач связано с вычислением производных функций и использованием геометрической интерпретации первой производной функции. Рассмотрим методику построения касательной к заданной точке функции и определения параметров ее уравнения.

Если задана функция f(x), то первая производная функции в заданной точке с координатами хо и уо является угловым коэффициентом касательной в этой точке. Уравнение касательной, проходящей через точку с координатами хо и уо, имеет вид:

где к = /'(хо) — угловой коэффициент;

Требуется построить график функции /(х) и касательную в прямоугольной области диаграммы, ограниченной минимальными и максимальными значениями абсцисс (х_мин и х_макс) и ординат (у_мин и у_макс).

Так как касательная является прямой линией, проходящей через заданную точку, то ее можно построить по координатам двух точек: (х^у-^) и (х₂,у₂), которые располагаются на границах прямоугольника.

Рассмотрим расчет координат точек касательной с учетом значения углового коэффициента к = /'(х) . Значения углового коэффициента

могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.

Пусть к > 0. Остановимся на всех возможных вариантах расположения точек. При х_х = х_мин с учетом формулы у_х = к * (х_мин — х) + у .

Координаты второй точки касательной рассчитываются аналогичным образом. При этом задаем х₂ = х_макс и у₂ = к * (х_макс — х) + у.

Если к Умэкс) П Р И предварительном построении графика заданной функции на основе табулированной функции (В5:С25)

Формируем таблицы начальных условий задачи.

координат заданной точки функции(х, у) (F2 и G2);

углового коэффициента к = /'(х) (Н2);

граничных значений диапазонов (х_мин, х_макс, у_мин, у_макс) (A2:D5).

Отступив одну ячейку от таблицы функции (В5:С25), рассчитываем координаты точек касательной (В27:С28) с учетом приведенных выше рассуждений (на рисунке в примечаниях отображены формулы расчетов). Предварительно для удобства вычисляем во вспомогательных ячейках значения у_г при х_г = х_мин и у₂ при х₂ = х_макс (F8 и G8). Для отображения точки на графике функции добавляем ячейки с ее заданными координатами (ВЗО и СЗО).

Выделив диапазон ячеек (В5:С30), в который включаются ячейки таблицы функции и координат точек касательной, обращаемся к мастеру диаграмм для построения графика функции и касательной. Задаем тип диаграммы — Точечная, а вид — Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Фиксируем минимальные и максимальные значения шкал осей х и у в диалоговом окне Формат оси.

Для заданной точки, к которой строится касательная, можно установить отличительный маркер и вывести ее координат. Чтобы установить цвет и толщину линии касательной нужно аккуратно щелкнуть по линии касательной. При появлении маркеров точек касательной вызвать контекстное меню и щелкнуть по пункту Формат точки данных. В диалоговом окне установить тип, цвет и толщину линии касательной.

Для наглядности одновременно вычисляем параметры уравнения касательной у = а * х + Ь, где из уравнения а = k, b = у — к * х. Эти параметры рассчитываем в соответствующих ячейках, которые соседствуют с ячейками, в которых занесены символы Y,=,* для представления уравнения касательной. Так как значение параметра b могут быть как отрицательными, так и положительными, то в соответствующей ячейке используем функцию ЕСЛИ для отображения символов + и -.

Изменяя значения координаты х, осуществляем исследование поведения касательной в заданной точке функции и изменения параметров уравнения касательной.

При необходимости можно дополнительно построить график производной заданной функции.

Источник

Касательная к графику из определенной точки

Автор mulder777, 29.03.2012, 04:38

« назад — далее »

Ребята, здравствуйте! Несколько лет ломаю голову над вопросом построения касательной к графику из определенной точки. Пример в прикрепленном файле. Только не нужно писать мне об всяких апроксимациях и т.п. Я прошу реальной помощи на основании представленного примера, чтобы посмотрев на ваше решение, смог в дальнейшем использовать ваше уравнение или функцию или т.п.

Нда….. Я так и понял, что на этом сайте и не пахнет реальными мозгами…

mulder777, а вы уверены, что нашли правильную касательную?
например судя по графику, если сильно увеличить масштаб, то прямая не касается графика.

Предположительно касание происходит при х=60, но это не так,
можно проверить формулой:

=ПРЕДСКАЗ(60;{0,04686;0,255};{-23,03;80})
в результате получается значение 0,214596234106571, что выше табличных данных при х=60 (0,213)

Есть вопросы:
откуда взялась точка [-23,03;0,04686]?
если бы график не стал бы опускатся после х=60 (например это была бы парабола), как бы Вы строили касаткльную?

я бы так стал решать

PS: поломал голову минут 10

PPS: на текущий момент исходный файл скачен 2 раза, из них второй раз мной, так что не нужно «брать на слабо»
и неуважительно высказыватся об участниках форума

Если нужна только правая сторона, то так будет лучше

Если нужна касательная к сглаженной линии, то без аппроксимации (интерполяции) не обойтись
Аппроксимирующую (интерполирующую) функцию повзаимствовал у С.М. (все копирайты сохранил)

PS: сдается мне, что здесь «пахнет» игрой на бирже

Качество автоматического построения касательной к сглаженной кривой можете оценить при масштабе 400%

Уважаемый MCH! Здравствуйте!
Этот график представляет собой диаграмму динамической остойчивости судна на плаву. Точка, с которой я провожу касательную — это пересечение этой диаграммы с перпендикуляром, восстановленным из определенного значения угла (амплитуда качки судна), которая тоже расчитывается определенным способом и мне известна. Касательная из этой точки к этой диаграмме мне нужна для определения опрокидывающего плеча судна. В моем случае не обязательно находить значение Y при Х=80, достаточно найти просто координаты места касания к диаграмме. По поводу вашего вопроса о том, как бы я строил касательную, если бы график не опускался после 60-ти — отвечаю, во всех случаях динамической остойчивости судна этот график выглядит однообразно и всегда имеет такую форму. Скачал все ваши варианты, сижу, думаю, анализирую, спасибо за уделенное мне время, о результатах отпишусь. Но в последнем варианте касательной вообще не вижу

P.S. Игрой на бирже тут не пахнет. Я моряк, пытаюсь автоматизировать и без того свой нелегкий труд.

Нда… Вопросов оказывается еще больше…. Откуда вы взяли эти функции типа «MaxRight» и «Non…….»?? При переносе этих функций в свой файл — они не работают!!!??? КАК!?

Цитата: mulder777 от 01.04.2012, 06:33
Откуда вы взяли эти функции типа «MaxRight» и «Non…….»?? При переносе этих функций в свой файл — они не работают!!!??? КАК!?

сами же просили:

ЦитироватьТолько не нужно писать мне об всяких апроксимациях и т.п.

Поэтому промолчу

Смотрите решение, пробуйте в дальнейшем использовать функции MaxRight и NonLinearInterpolation

Определяем точку касания

PS: Все функции можно увидеть нажав Alt+F11

Понятно, видимо все это связано с введением новой нестандартной функции при помощи программирования. Короче я поступил проще, ввел все свои таблицы и расчеты в ваш файл, там они все считают. А как перенести эти новые функции на новую книгу — это для меня дремучий лес! Спасибо за поддержку!

Здравствуйте господа! Вопрос о касательной не совсем полный. Простое построение самой касательной к графику не дает ответ на ее применение. Так, только графическое удовлетворение. Хочется пояснить для чего строится касательная. Дело в том, что кроме создания самой касательной, еще требуется, используя дополнительные построения, вытянуть некие данные из построенного. Возможно ли это вообще? Пользовательские функции не пугают, правда я в них тоже ни-фига… В приложении файл с подробным описанием проблемы. Спасибо!

А в чем вопрос?
Необходимо рассчитать все коэффициенты Kрад, Кзал, Ккас?
Формулу для расчета значения в ячейке S21 можно брать не «с потолка»:

=NonLinearInterpolation($H$11:$T$11;$H$12:$T$12;-$U$12)
расчетное значение получилось: 0,1099736328125

Точка касания: 66,05

=TangentPoint(H11:T11;H12:T12;-U12;U15;0,1)

значение в точке касания = 1,165977702

=NonLinearInterpolation(H11:T11;H12:T12;66,05)

Ккас = 1,47328386794217

=ПРЕДСКАЗ(90;{0,1099736328125:1,165977702};{-16,25:66,05})

Кзал = 0,981850625537781

=ПРЕДСКАЗ(51,7;{0,1099736328125:1,165977702};{-16,25:66,05})

Kрад = 0,84519882314596

=ПРЕДСКАЗ(57,3-16,25;{0,1099736328125:1,165977702};{-16,25:66,05})

Профессиональные приемы работы в Microsoft Excel
►
Обмен опытом
►
Microsoft Excel
►
Касательная к графику из определенной точки

Источник

Функция TAN Excel (касательная)

Функция TAN Excel — это встроенная тригонометрическая функция в excel, которая используется для вычисления значения косинуса заданного числа или, с точки зрения тригонометрии, значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.

Функция TAN Excel

Функция TAN Excel — это встроенная функция, относящаяся к категории Math / Trig function, которая возвращает значение тангенса угла. Формула для TAN всегда возвращает числовое значение.

TAN Θ = противоположная сторона / смежная сторона

Следовательно, TAN Θ = a / b

Формула TAN в Excel

Ниже приведена формула TAN в Excel.

Где число — это аргумент, передаваемый функции в радианах.

Угол, который мы указываем в качестве входных данных, распознается функцией Tangent, только если он указан как Radians.

Радиан = угол в градусах * (π / 180)

π в Excel представлена функцией PI ()

Следовательно, радиан = градус * (PI () / 180)

Расчет значения TAN с использованием функции TAN и RADIANS

Расчет значения TAN с использованием TAN и функции PI

У функции касательной есть много реальных приложений; он широко используется в архитектуре для расчета высоты и длины геометрических фигур. Функция касания, используемая в системах навигации и GPS, в аэронавтике.

Как мы знаем, TAN Θ = противоположная сторона / смежная сторона

Здесь противоположная сторона = высота самолета от земли, равная 3000 метров.

А соседняя сторона = горизонтальное расстояние самолета от земли, которое неизвестно, и нам нужно его вычислить.

Итак, используя формулу для TAN, мы имеем

TAN (26 °) = 3000 / x

Следовательно, x = 3000 / (TAN (26 °))

В Excel, взяв относительные контрольные значения, мы имеем

Икс = B2 / (TAN (B3 * (PI () / 180))))

X = 6150.91 метров

Как использовать TAN в Excel?

Функция Excel TAN очень проста и удобна в использовании. Позвольте мне понять, как работает формула TAN в Excel на нескольких примерах.

Касательная в Excel, пример # 1

Чтобы найти высоту дерева, мы будем использовать TAN Θ. В контексте Excel мы будем использовать функцию Tangent.

Высота дерева будет

Высота Человека + Расстояние Человека от дерева * TAN (47 °)

Поскольку рост человека указан в футах, мы переведем его в метры (1 фут = 0,30 метра).

Поместив все относительные значения в Excel, формула для высоты дерева будет

= (0,3 * B2) + (B3 * TAN ((B4 * (PI () / 180))))

Выходные данные TAN Excel:

Высота дерева 60,78 метра.

Касательная в Excel, пример # 2

Сумма всех углов треугольника равна 180 °; следовательно, мы можем легко вычислить третий угол.

Мы знаем, Sin Θ = противоположное / гипотенуза

Таким образом, длина противоположной стороны будет Sin Θ * гипотенуза

В Excel длина Противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле TAN.

= E2 * SIN (C2 * (PI () / 180))

Применяя формулу TAN для пяти треугольников, мы можем получить длину перпендикуляров треугольников

Теперь у нас есть две стороны треугольника: гипотенуза и перпендикулярная сторона. Мы можем легко вычислить третью сторону (основание), используя TAN в Excel.

Мы знаем, что TAN Θ = противоположная сторона / смежная сторона.

Таким образом, длина прилегающей стороны будет Обратная сторона/ТАН Θ.

В Excel длина прилегающей стороны (основания) будет рассчитываться по формуле TAN.

= F2 / (TAN (РАДИАНЫ (C2)))

Применяя формулу TAN для пяти треугольников, мы можем получить длину смежной стороны треугольника.

TAN в выводе Excel:

Касательная в Excel, пример №3

Радиус поворота задается формулой.

Радиус поворота = V 2 / g * TAN Θ

Радиус поворота 160 метров; Постоянный угол крена 87 °, g — ускорение свободного падения, значение которого составляет 9,8 м / с. 2 , поэтому путевая скорость будет

V = (Радиус поворота * (g * TAN Θ)) 1/2

Применяя приведенную выше формулу TAN в Excel со справочными значениями, мы получаем формулу TAN.

= КОРЕНЬ (B2 * (9,8 * (TAN (РАДИАНЫ (B3)))))

SQRT — это встроенная функция Excel, которая вычисляет квадратный корень из числа.

TAN в выводе Excel:

Итак, путевая скорость самолета составляет 172,97 м / с.

Пример функции касания # 4

У нас есть формула для TAN, обозначенная f (x) = 2c * TAN2Θ, где c — постоянное значение, равное 0,988. Значение варианта — это значение, а формула для TAN зависит от значения. Нам нужно построить график заданной функции касания.

Используя функцию Excel TAN, мы затем вычислим значения функции, поэтому, взяв контрольные значения в качестве входных данных, мы получим формулу TAN,

Как можно провести касательную к графику в экселе?

Excel всё-таки не бумага, чтобы на ней что-то можно было провести.

Вы табулировали некую функцию и отобразили её график. Вам надо выбрать точку и табулировать функцию производной в некой заранее заданной точке.

Уравнение касательной к табулированной функции находят разными способами на выч. методах. В сети можно найти уже готовые формулы. Если хотите сами, то надо выбрать 3 точки, наиболее близкие к заданной, представить функцию параболой, проходящей через них, а потом построить касательную к этой параболе.
Как только у вас будет уравнение прямой, табулируйте её функцию и выведите на график результат.

ЗЫ
Табулировать функцию — найти множесто пар (аргумент, значение) и вывести их в табличном виде.

Как построить касательную в excel к точке

Кредит: Драган Радоевич / iStock / Getty Images

Шаг 1

Шаг 2

Шаг 3

Шаг 4

Шаг 5

Шаг 6

Дубликаты не найдены

ЕСЛИ(условие;выполнить_если_истина;выполнить_если_ложь)
[в eng версии соответственно это IF(. )]

Вообще, насколько помню, годная в экселе справка была.. Так что традиционное — RTFM.

где к = /'(хо) — угловой коэффициент;

Рассмотрим расчет координат точек касательной с учетом значения углового коэффициента к = /'(х ) . Значения углового коэффициента

могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.

Формируем таблицы начальных условий задачи.

координат заданной точки функции(х , у ) (F2 и G2);

углового коэффициента к = /'(х ) (Н2);

граничных значений диапазонов (х_мин, х_макс, у_мин, у_макс) (A2:D5).

Для наглядности одновременно вычисляем параметры уравнения касательной у = а * х + Ь, где из уравнения а = k, b = у — к * х . Эти параметры рассчитываем в соответствующих ячейках, которые соседствуют с ячейками, в которых занесены символы Y,=,* для представления уравнения касательной. Так как значение параметра b могут быть как отрицательными, так и положительными, то в соответствующей ячейке используем функцию ЕСЛИ для отображения символов + и -.

Изменяя значения координаты х , осуществляем исследование поведения касательной в заданной точке функции и изменения параметров уравнения касательной.

При необходимости можно дополнительно построить график производной заданной функции.

Источник