Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см.
файл примера
):
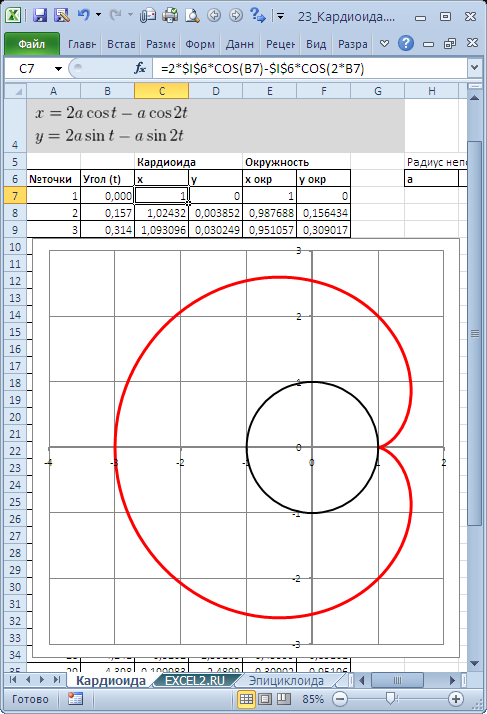
х=2*а*cos(t)-а*cos(2*t)
y=2*а*sin(t)-а*sin(2*t)
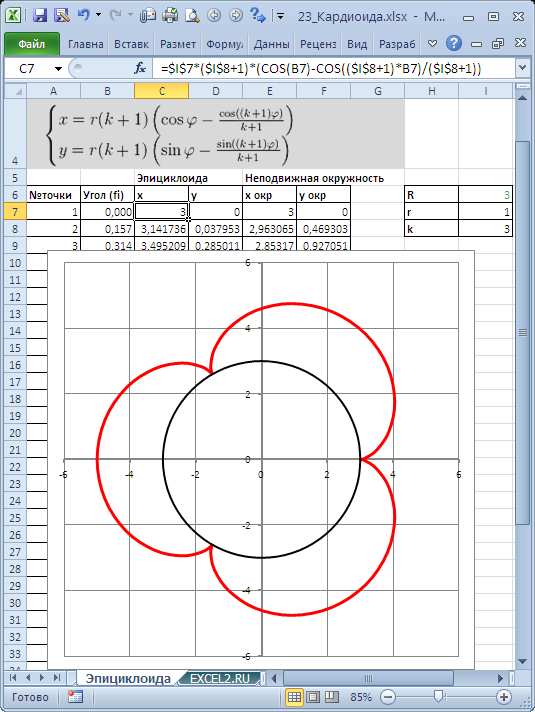
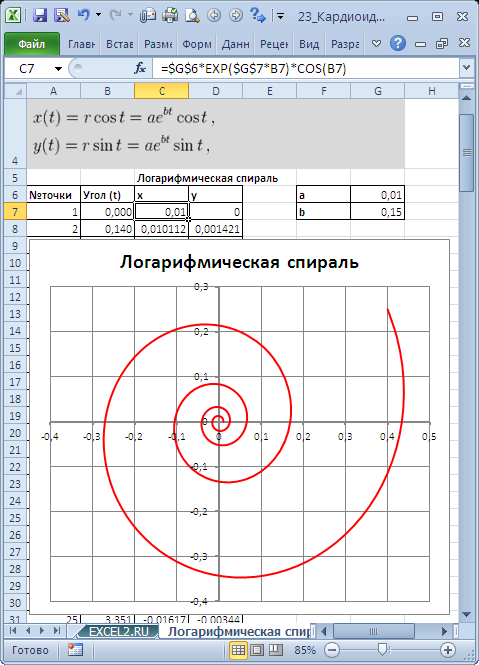
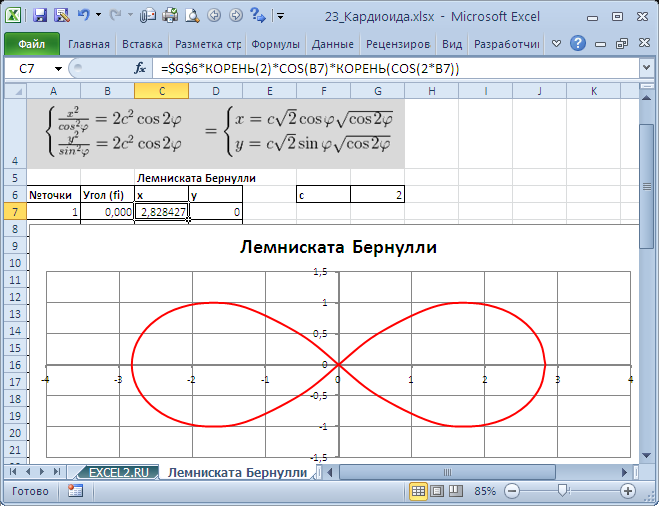
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье
Эллипс и окружность в MS EXCEL
построены окружность и эллипс.
СОВЕТ
: Для начинающих пользователей EXCEL советуем прочитать статью
Основы построения диаграмм в MS EXCEL
, в которой рассказывается о базовых настройках диаграмм, а также
статью об основных типах диаграмм
.
Подборка по базе: Учебник по EXCEL.doc, Работа с программой Excel.pdf, Методическая разработка открытого урока по теме «Microsoft Excel, Отсеивание грубых погрешностей результатов измерений с помощью р, Автоматты есептеулер. Excel бағдарламасындағы функциялар.docx, Excel_5_Работа с базами данных в EXCEL 2007.doc, ВШМ — 8. Решение задач линейной алгебры с помощью пакета Ms Exce, 2.2.2 Выделение ячеек в Excel и Проверка орфографии в Excel.docx, Решение в EXCEL задачи об инвестициях(1).doc, Диаграммы в Microsoft Excel.docx
Как строится Кардиоида в Excel.
1.Нам понадобятся два уравнения в прямоугольных координатах (в параметрической записи):
Для начала создаём точки от 1 до 41
2.Создаём столбец Угол(t) с шагом 0.157 и растягиваем до конца.
3.Создаём таблицу с радиусом неподвижной окружности. В нашем случае он будет равен 1.
4.Создаём два столбца рядом и выделяем их как x и y,они будут координатами кардиоиды.
В столбец x вставляем формулу которую я выделил в самом начале
И растягиваем все значения до конца.
В столбец y вставляем уже другую формулу
5.В конечном итоге у нас получается два таких столбца
6.Теперь добавляем два столбца и выделяем их как “x окр” и “y окр”
В x окр вставляем формулу с косинусом
В y окр вставляем формулу с синусом
И растягиваем до конца.
7.В конечном итоге мы получаем такую таблицу
8.Создаём сначало диаграмму кардиоиды из столбцов x и y
Затем создаём вторую диаграмму окружности из столбцов “x окр” и у “окр”
Теперь берем диаграмму окружности,копируем её и вставляем в диаграмму кардиоиды.
Получается диаграмма Кардиоида
Делаем её красивой
Работа сделана.
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
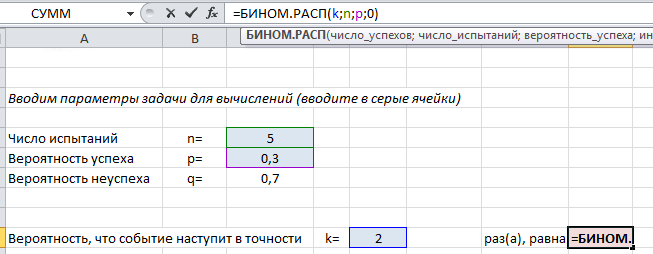
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>right)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>right)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)=\ = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>=\=left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1right)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
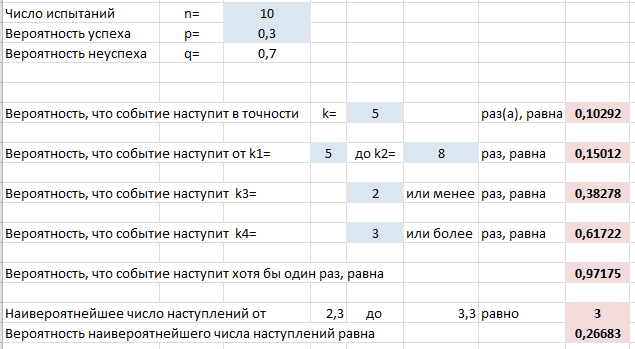
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Плоские алгебраические кривые в EXCEL
history 16 апреля 2015 г.
-
Группы статей
- Диаграммы и графики
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Практическая работа «Красивые графики функций»
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
источники:
http://excel2.ru/articles/ploskie-algebraicheskie-krivye-v-ms-excel
http://pedsovet.su/excel/48255_krasivye_grafiki_v_excel
Изображение слайда
2
Слайд 2: Полярная система координат
Полярная система координат ставит в соответствие каждой точке на плоскости пару чисел.
Основными понятиями этой системы являются точка отсчета – полюс – и луч, начинающийся в этой точке, – полярная ось.
Фигуры в полярных координатах
образуются как след конца
бегающего по кругу полярного
радиуса переменной длины.
Длина радиуса определяется
величиной угла, который он
образует с полярной осью.
Знак «+», если угол против
часовой стрелки, и знак «-»
если угол по часовой стрелки.
Изображение слайда
3
Слайд 3: Переход от ДСК к ПСК
Пусть ( x ; y ) – координаты точки в декартовой системе координат, – в полярной. Тогда очевидно, что:
Формулы обратного перехода:
Замечание:
число в полярной системе
определено не однозначно:
парам чисел соответствует
одна и та же точка при любых
натуральных n.
Переход от ДСК к ПСК
Изображение слайда
4
Слайд 4: Строим график функции y(x)=y=sin(x) пошагово 1 шаг
Изображение слайда
Изображение слайда
Изображение слайда
Изображение слайда
8
Слайд 8: 5 шаг. Мастер диаграммы
Изображение слайда
9
Слайд 9: Мастер диаграммы
Изображение слайда
10
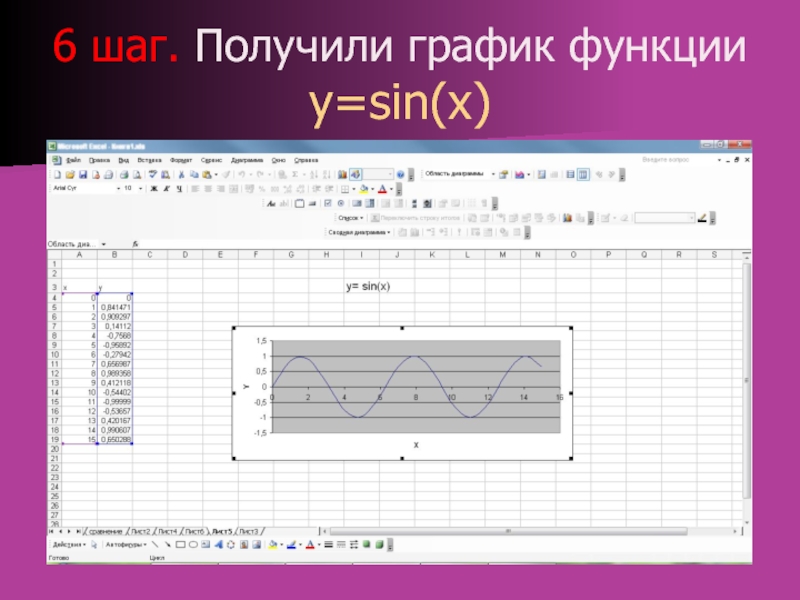
Слайд 10: 6 шаг. Получили график функции y=sin(x)
Изображение слайда
11
Слайд 11: Построим график функции, где x зависит от y, например
Изображение слайда
12
Слайд 12: Инструкция по построению кривых с помощью программы Microsoft Excel
Переведем уравнение из декартовых координат в полярные, используя формулы: X = R * COS ( F ), Y = R * SIN ( F ).
Задача.
Построить кривую, заданную уравнением
Решение. Найдем уравнение линии в полярных координатах
Для программы Microsoft Excel :
R=4*COS(3*F)
Пусть угол
Выберем шаг изменения 0,1
Построим компьютерную модель исследования
Изображение слайда
Внесем данные и получим следующее распре-
деление по столбцам электронной таблицы:
А2 =0,1
А3 =А2+0,1
B2 =4*COS(3*F)
C2 =SIN(А2)
D2 =COS(А2)
E2 =B2*D2
F2 =В2*C2
Для построения графика выделим
информационный блок E2..F63, так как аргумент
F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д.
Изображение слайда
14
Слайд 14: Получим следующую кривую
Изображение слайда
Спираль Архимеда может быть определена как траектория точки, участвующей одновременно в двух равномерных движениях, одно из которых совершается вдоль прямой, а другое – по окружности.
Гиперболическая спираль
По мере роста спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.
Изображение слайда
16
Слайд 16: Получим следующие кривые
Изображение слайда
17
Слайд 17: Построение кардиоиды
Изображение слайда
18
Слайд 18: График астроиды
Изображение слайда
19
Слайд 19: Поверхность 1
Изображение слайда
20
Слайд 20: Поверхность 2
Изображение слайда
Изображение слайда
22
Слайд 22: Кривая Хабеннихта R =1+7 cos8F+ 4(sin8F)^2 + 3 (sin8F)^4
Изображение слайда
23
Слайд 23: Лист клевера R=1+1/3(2 cos3F — cos6F)
Изображение слайда
24
Слайд 24: Пируэты роз»
Изображение слайда
25
Слайд 25: Самостоятельная работа
І Вариант. (x ̸ 7)² + (y ̸ 12)² + (z ̸ 9)² =1 на интервале х,y ∊ [-7;7] с шагом 0.5 ;
ІІ Вариант. x ² ̸ 9 + y² ̸ 4 =2z на интервале х,y ∊ [- 5 ; 5 ] с шагом 0.5 ;
ІІІ Вариант. x ² ̸ (1 ̸ 3)² + y² ̸ (1 ̸ 6)² — z² ̸ (1 ̸ 2)² = 1 на интервале х,y ∊ [- 5 ; 4,5 ] с шагом 0.5 ;
І V Вариант. x ² ̸ 9 + y² ̸ 4 — z² = -1 на интервале х ∊ [- 3 ; 3 ] с шагом 0.5, y ∊[ — 2;2] с шагом 1.
Самостоятельная работа
Изображение слайда
26
Слайд 26: І Вариант. ІІ Вариант
Изображение слайда
27
Последний слайд презентации: ПОСТРОЕНИЕ КРИВЫХ В EXCEL: ІІІ Вариант. І V Вариант
Изображение слайда
Слайд 2Полярная система координат
Полярная система координат ставит в соответствие каждой точке
на плоскости пару чисел .
Основными понятиями этой системы являются
точка отсчета – полюс – и луч, начинающийся в этой точке, – полярная ось.
Фигуры в полярных координатах
образуются как след конца
бегающего по кругу полярного
радиуса переменной длины.
Длина радиуса определяется
величиной угла, который он
образует с полярной осью.
Знак «+», если угол против
часовой стрелки, и знак «-»
если угол по часовой стрелки.

Слайд 3Пусть (x; y) – координаты точки в декартовой системе координат, –
в полярной. Тогда очевидно, что:
Формулы обратного перехода:
Замечание:
число в полярной системе
определено не однозначно:
парам чисел соответствует
одна и та же точка при любых
натуральных n.
Переход от ДСК к ПСК

Слайд 4Строим график функции
y(x)=y=sin(x) пошагово
1 шаг
Слайд 106 шаг. Получили график функции y=sin(x)
Слайд 11Построим график функции, где
x зависит от y, например
Слайд 12Инструкция по построению кривых
с помощью программы Microsoft Excel
Переведем уравнение
из декартовых координат в полярные, используя формулы: X=R*COS(F), Y=R*SIN(F).
Задача.
Построить
кривую, заданную уравнением
Решение. Найдем уравнение линии в полярных координатах
Для программы Microsoft Excel:
R=4*COS(3*F)
Пусть угол
Выберем шаг изменения 0,1
Построим компьютерную модель исследования

Слайд 13Внесем данные и получим следующее распре-
деление по столбцам электронной таблицы:
А2
=0,1
А3 =А2+0,1
B2 =4*COS(3*F)
C2 =SIN(А2)
D2 =COS(А2)
E2 =B2*D2
F2 =В2*C2
Для построения графика выделим
информационный блок E2..F63, так как аргумент
F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д.

Слайд 15Спирали
Спираль Архимеда может быть определена как траектория точки, участвующей одновременно
в двух равномерных движениях, одно из которых совершается вдоль прямой,
а другое – по окружности.
Гиперболическая спираль
По мере роста спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.

Слайд 22
Кривая Хабеннихта
R=1+7 cos8F+ 4(sin8F)^2 + 3 (sin8F)^4

Слайд 23
Лист клевера
R=1+1/3(2 cos3F — cos6F)

Слайд 25І Вариант. (x ̸ 7)² + (y ̸ 12)² +
(z ̸ 9)² =1 на интервале х,y ∊ [-7;7] с
шагом 0.5 ;
ІІ Вариант. x² ̸ 9 + y² ̸ 4 =2z на интервале х,y ∊ [-5;5] с шагом 0.5 ;
ІІІ Вариант. x² ̸ (1 ̸ 3)² + y² ̸ (1 ̸ 6)² — z² ̸ (1 ̸ 2)² = 1 на интервале х,y ∊ [-5;4,5] с шагом 0.5 ;
ІV Вариант. x² ̸ 9 + y² ̸ 4 — z² = -1 на интервале х ∊ [-3;3] с шагом 0.5, y∊[-2;2] с шагом 1.
Самостоятельная работа

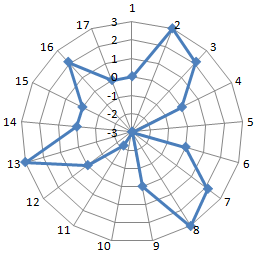
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
Как построить лепестковую диаграмму в Excel
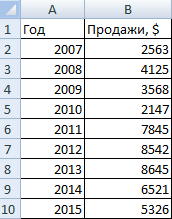
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
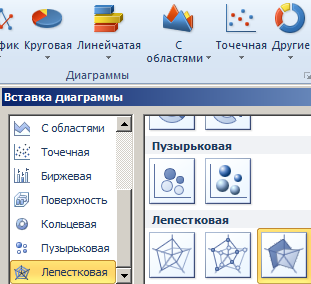
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
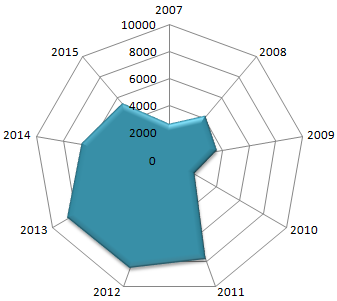
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
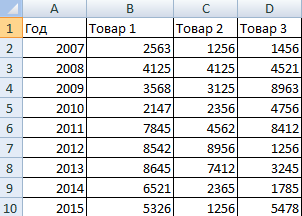
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
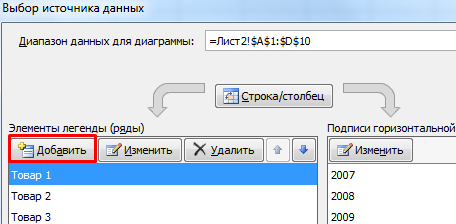
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Уравнение функции:
r = 3 * sin (6 * φ)/
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
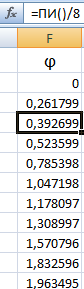
Формулы для заполнения первого столбца берем из таблицы значений точек:
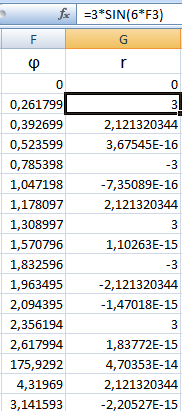
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
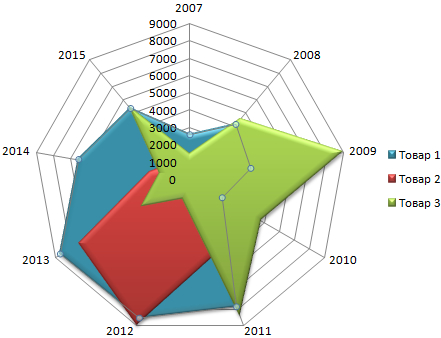
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
history 16 апреля 2015 г.
- Группы статей
- Диаграммы и графики
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Как построить эпициклоиду в excel
0 Спам
Ещё раз про морковь или возвращаясь к непечатному. Доброго здоровья, Денис.
Глядя на процедуру расчёта и вывода циклоиды (Sub DrawCycloide) я задался вопросом: какую часть времени занимает расчёт значений для её вывода, а какую — собственно, графический вывод. Профилировать процедуру напрямую по таймеру в контрольных точках смысла не имело: слишком маленькие интервалы приведут к слишком большим погрешностям. Поэтому решено было нивелировать (свести к нулю) время расчёта, чтобы осталось только время, занимаемое графическим выводом. Как нивелировать? Перевести в машинный код, естественно . Но всё по порядку.
1. Первым делом к ранее выложенному здесь Beauty free.xlsm был прикручен «спидометр» — код, отображающий на форме количество выводимых циклоид в секунду.
Результат здесь: https://yadi.sk/i/EtolJiGL3LhgpJ
2. Далее, через экспорт-импорт, форма из книги Beauty free speed.xlsm была перемещена в «классический» проект VB. Что понравилось: форма встала в проект VB сразу «как влитая», никаких допиливаний и танцев с бубном не понадобилось. Естественно, ссылки на ячейки рабочего листа заменены константами.
Исходник: https://yadi.sk/d/YsNL93Ph3MxWPV
Результат: https://yadi.sk/d/T3u021U-3MxWRv
3. Наконец, была проведена переработка проекта с целью замены объекта UserForm VBA объектом Form VB:
Исходник: https://yadi.sk/d/KCgRKEN33MxYGC
Результат: https://yadi.sk/d/6Odb1BKA3MxYHB
Примечания.
1. Шаги 3 и 4 не имеют отношения к поднятому вопросу, но, раз были проделаны — решил выложить
2. Если у вас нет установленного VB, можно сразу смотреть результаты, вирусов в них нет
Итоги.
Преимущество в скорости компилятора над интерпретатором в доказательствах не нуждалось, вопрос был в количественной оценке. Считая, что время графического вывода в любом случае превалирует над временем расчёта, ожидал прироста быстродействия в 20%-30%. После запуска откомпилированного на шаге 2 проекта получил прирост в скорости в 2,5 раза на своей системе. Медленно: в два с половиной раза. То есть, в коде книги Excel расчёт шёл, примерно, в 1,5 раза дольше вывода. Во сколько именно раз поднялась скорость вычислений данные действия не показывают, но, оценочно — в 8 — 10 раз.
Практический вывод.
Если ваш код VBA содержит сложные расчёты — вынести их в отдельную внешнюю процедуру, подключаемую как DLL или OCX ещё как имеет смысл.
P. S. Всё вышенаписанное стоило писать месяца полтора назад. Руки дошли только сейчас, однако.
0
Аналогично
Чтобы правильно построить линейный график функций в Excel необходимо выбрать точечную диаграмму с прямыми отрезками и маркерами. Естественно это не единственный, но весьма быстрый и удобный способ.
Для разного рода данных нужно использовать разные типы графиков. Убедимся в этом, разобрав практический пример с построением математического графика функций в Excel.
Построение графиков функций в Excel
Начнем из анализа и создания графика функций в Excel. Мы убедимся в том, что линейный график в Excel существенно отличается от графика линейной функции, который преподают в школе.
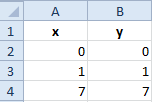
Линейная функция x=y имеет следующие значения: x1=0, x2=1, x3=7. Заполните таблицу этими значениями как показано на рисунке:
Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«График»-«График с маркерами».
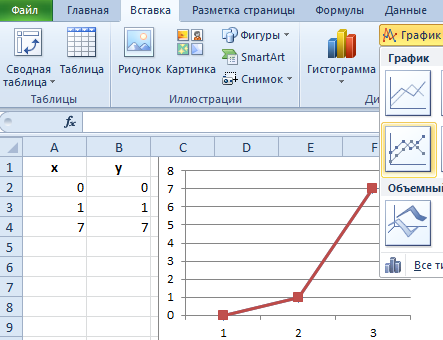
В результате у нас созданы 2 линии на графике, которые наложены одна сверх другой. Так же мы видим, что линии сломаны, а значит, они не соответствуют презентации школьному графику линейной функции. Излом линий, получается, по причине того, что на оси X у нас после значений: 0, 1 сразу идет значение 7 (упущены 2,3,4,5,6).
Вывод один: данный способ графического построения данных нам не подходит. А значит щелкните по нему левой кнопкой мышки (чтобы сделать его активным) и нажмите клавишу DELETE на клавиатуре, чтобы удалить его.
Как построить график линейной функции в Excel
Чтобы создать правильный график функций в Excel выберите подходящий график.
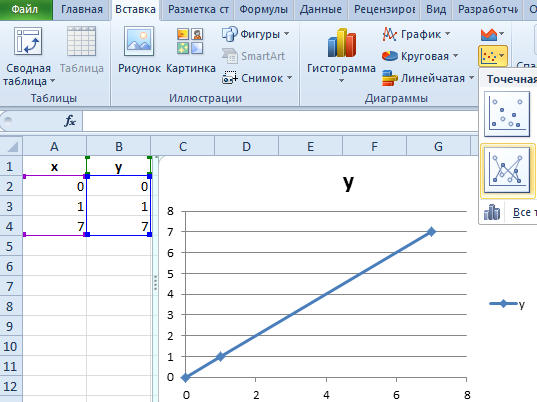
Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с прямыми отрезками и маркерами».
Как видно на рисунке данный график содержит одинаковое количество значений на осях X и Y. По умолчанию в шаблоне данного графика цена делений оси X равна 2. При необходимости ее можно изменить. Для этого:
Теперь у нас отображается одинаковое количество значений по всем осям.
Очень важно понимать разницу в предназначениях графиков Excel. В данном примере мы видим, что далеко не все графики подходят для презентации математических функций.
Примечание. В принципе первый способ можно было-бы оптимизировать под отображение линейной функции, если таблицу заполнить всеми значениями 0-7. Но это не всегда работающее решение, особенно в том случае если вместо значений будут формулы изменяющие данные. Одним словом если нужно забить гвоздь лучше взять молоток, чем микроскоп. Несмотря на то, что теоретически гвозди можно забивать и микроскопом.
Не существует универсальных графиков и диаграмм, которыми можно отобразить любой отчет. Для каждого типа отчета наиболее подходящее то или иное графическое представление данных. Выбор зависит от того что и как мы хотим презентовать. На следующих примерах вы убедитесь, что выбор имеет большое значение. Существует даже целая наука «Инфографика», которая учит лаконично презентовать информацию с максимальным использованием графики вместо текста, насколько это только возможно.
Как сделать систему координат в excel?
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
Как построить лепестковую диаграмму в Excel
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
Формулы для заполнения первого столбца берем из таблицы значений точек:
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке . Называем столбец «х», пишем первое значение «-3», второе – «-2,5». Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
В поле «Элементы легенды» кликаем на кнопочку «Добавить».
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Поделитесь статьёй с друзьями:
Добрый день. А есть возможность в Excele создать график с тремя переменными, но на одном графике? 2 параметра как обычно, координаты х и у, а третий параметр чтоб отражался размером метки? Вот как пример, такой график —
Также статьи о графиках в Экселе:
- Как сделать диаграмму в Эксель?
- Как сделать круговую диаграмму в Экселе?
- Как построить график в Экселе?
- Построение точечной диаграммы в Excel
В Экселе можно результаты расчетов отобразить в виде диаграммы или графика, придавая им большую наглядность, а для сравнения иногда нужно построить два графика рядом. Как построить два графика в Excel на одном поле мы далее и рассмотрим.
Начнем с того, что не каждый тип диаграмм в Экселе сможет отобразить именно тот результат, который мы ожидаем. К примеру, имеются результаты расчетов для нескольких функций на основе одинаковых исходных данных. Если по этим данным строить обычную гистограмму или график, то исходные данные не будут учитываться при построении, а лишь их количество, между которыми будут задаваться одинаковые интервалы.
Выделяем два столбца результатов расчетов и строим обычную гистограмму.
Теперь попробуем добавить еще одну гистограмму к имеющимся с таким же количеством результатов расчетов. Для добавления графика в Экселе делаем активным имеющийся график, выделив его, и на появившейся вкладке «Конструктор» выбираем «Выбрать данные». В появившемся окошке в разделе «Элементы легенды» нажимаем добавить, и указываем ячейки «Имя ряда:» и «Значения:» на листе, в качестве которых будут значения расчета функции «j».
Теперь посмотрим, как будет выглядеть наша диаграмма, если мы к имеющимся гистограммам добавим еще одну, у которой количество значений почти в два раза больше. Добавим к графику значения функции «k».
Как видно, последних добавленных значений гораздо больше, и они настолько малы, что их на гистограмме практически не видно.
Если изменить тип диаграммы с гистограммы на обычный график, результат получится в нашем случае более наглядным.
Если использовать для построения графиков в Экселе точечную диаграмму, то на полученных графиках будет учитываться не только результат расчетов, но и исходные данные, т.е. будет прослеживаться четкая зависимость между величинами.
Для создания точеного графика выделим столбец начальных значений, и пару столбцов результатов для двух разных функций. На вкладке «Вставка» выбираем точечную диаграмму с гладкими кривыми.
Для добавления еще одного графика выделяем имеющиеся, и на вкладке «Конструктор» нажимаем «Выбрать данные».
В новом окошке в графе «Элементы легенды» нажимаем «Добавить», и указываем ячейки для «Имя ряда:», «Значения X:» и «Значения Y:». Добавим таким образом функцию «j» на график.
Теперь добавим функцию «k», у которой совершенно другие исходные данные и их количество.
Как видно, на точечном графике функция «k» практически незаметна, но зато построена с учетом значений по обеим осям.
Построение графиков функций в Excel
Февраль 9th, 2014
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2×2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу .
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу .
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: .
Подготовим две таблички, где х изменяется с шагом :
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
Как сделать координатную плоскость в MS Excel — Наука — 2022
Координатная плоскость образована двумя линиями, которые пересекаются под прямым углом, создавая четыре секции, называемые квадрантами. Координатные плоскости используются для построения графика упорядоченных пар и уравнений или построения диаграмм рассеяния. Вы можете создать координатную плоскость в Microsoft Excel, используя инструменты форматирования и рисования ячеек.
Откройте новый пустой документ Excel. Нажмите «Прямоугольник» в верхнем левом углу электронной таблицы, расположенной на пересечении столбца A и строки 1. Это выберет всю электронную таблицу. Нажмите на вкладку «Вид». В группе «Показать / Скрыть» отмените выбор «Линии сетки».
Поместите курсор на линию между любыми двумя заголовками столбцов. Ваш курсор изменится на вертикальную линию, пересекаемую горизонтальной стрелкой. Перетащите линию влево, пока ширина столбца не станет ровно 20 пикселей. Когда вы отпустите кнопку мыши, все клетки будут квадратными. Нажмите в ячейке «А1», чтобы убрать выделение.
Щелкните ячейку «C3» и перетащите и выделите область из 400 ячеек в ячейку V22. В группе «Шрифт» на вкладке «Главная» нажмите «Стрелка» на инструменте границы. Выберите «Границу», которая напоминает окно с четырьмя панелями.
Нажмите вкладку «Вставить». В группе «Иллюстрации» нажмите стрелку «Фигуры». Выберите линию с двумя стрелками.
Нарисуйте ось X между строкой 12 и строкой 13. Чтобы сделать прямую линию, удерживайте нажатой клавишу «Shift», удерживая ее нажатой и перетаскивая. Нарисуйте ось Y между столбцами L и M.
Как винт похож на наклонную плоскость?
Наклонные плоскости облегчают работу, увеличивая расстояние, которое должен пройти объект, но это приводит к уменьшению количества силы, необходимой для перемещения этого объекта. Толкание мяча вверх по рампе требует меньшего усилия, чем его выброс в воздух.
Как использовать координатную плоскость в реальной жизни
Использование координатных плоскостей в реальной жизни является полезным навыком для составления карты местности, проведения экспериментов или даже планирования повседневных нужд, таких как расстановка мебели в комнате.
Кто изобрел наклонную плоскость?
Наклонная плоскость — это не то, о чем думают люди, когда они думают о машине, потому что наклонные плоскости присутствуют в природе. Посмотрите на склон холма, и вы смотрите на наклонную плоскость. Тем не менее, как механическая концепция, это один из самых фундаментальных принципов в технике, и один из .