Microsoft Office – это стандарт ведения документации в офисе по всему миру. Именно этот офисный пакет сформировал культуру современного документооборота. И Microsoft тщательно работает над тем, чтобы сохранить положение дел. И весьма в этом преуспела. Несмотря на то, что существует множество бесплатных аналогов, а большинство рядовых пользователей даже на 50% не реализуют весь потенциал, заложенный в Office, всё равно люди хотят работать именно в Microsoft Office.
Помню момент, когда Microsoft перевела свои офисные продукты с коробочных продаж на подписочную модель. Под одной из статей на тему в комментариях развернулись нешуточные страсти. Люди жаловались, что не хотят постоянно платить, да и вообще платить не хотят, но скачивать бесплатный аналог не готовы, потому что он не такой удобный.
В какой-то степени такая привязанность понятна: всё-таки Microsoft Office был с нами всегда. Билл Гейтс представил первую версию пакета, состоящего из Word, Excel и PowerPoint, в 1988 году. А в качестве отдельных программ перечисленные приложения появились ещё в 1982-83 годах.
Безусловно, офисный софт от Microsoft не был самым первым. На рынке существовало несколько аналогов, и на первых этапах, например, никто не верил, что тот же Excel (называвшийся тогда Mutiplan) сможет подвинуть VisiCalc или Lotus 1-2-3.
Однако предлагаю немного погрузиться в историю и посмотреть, как вели офисные дела до появления компьютеров.
Презентации до PowerPoint
Планировать продажи, защищать планы развития и выполнять прочие бизнес-задачи требовалось и до создания компьютеров.
В стародавние времена, когда мир был проще, большинство решений принимались на глаз. Например, в 1553 году британский корабль «Эдуард Бонавентура» бросил якорь в Двинском заливе. Так начались торговые отношения между Россией и Британией: группа купцов отправилась в экспедицию, набрав с собой товаров для торговли. Приплыли, нашли клиентов, продали, открыли представительства, наладили поставки.
Однако в XIX-XX веке такой подход уже не работал. Стала появляться так называемая корпоративная культура, когда нужно обучать продажников, защищать планы продаж и так далее.
Это сейчас на каждый митинг лепим по презентации. Раньше презентации делали на века. Зачастую они выглядели как гигантские книги, которые стали называть флипчартами. Например, это флипчарт 1940-х годов с презентацией, посвященной рекламе и продвижению.
Соответственно, когда требовалось обновить какие-то данные, просто меняли листы. В докомпьютерную эпоху флипчарты были презентационным стандартом.
Попутно стоит отметить, что создание презентаций было хлопотным делом, так как требовало сплоченных усилий множества людей. В компаниях существовали целые отделы, задачей которых было создавать презентации по запросу. Там трудились дизайнеры и полиграфисты, у которых всегда было полно работы. Ведь попутно занимались разработкой универсальных дизайнов, которые можно использовать всегда, просто обновляя цифры. Вот пример презентации General Electric 1958 года.
Однако для масштабных событий к сотрудничеству приглашали настоящих гуру-дизайнеров и художников. Как вам презентация IBM тоже из 50-х?
Так как процесс создания слайдов был кропотливым и трудоёмким, то их готовили за несколько дней, а иногда и недель до презентации. А люди тщательно проверяли каждое слово и оттачивали своё выступление. Вследствие такого подхода был несколько иной способ подачи информации. Слайды не пытались утяжелять обилием цифр и текста – всё равно никто не заберет презентацию с собой. Да и сфотографировать не сможет, так что на встрече главным был докладчик, а не презентация.
С развитием полиграфических услуг появились раздаточные материалы. И новый формат презентации, когда всем раздавали вот такой «календарик». Все сидят и перелистывают. Это было в 60-е – 70-е.
Однако в то время никто не называл листы слайдами. Термин «слайд» перекочевал в презентации с развитием проекторов.
Проекционные слайды были сложнее в изготовлении. Однако сами проекторы были гораздо компактнее, а в один проектор можно было зарядить до 80 слайдов. Так что их использовали в командировках. И их очень полюбили разнообразные коммивояжёры. Проектор гораздо удобнее, чем таскать с собой громадные флипчарты или презентационные листы.
Тут следует понимать, что выше были примеры важных презентаций. На рядовых встречах тоже были презентации, но тогда никто не задумывался про оформление, и всё рисовали от руки. Например, вот рядовая презентация IBM 1958 года, которая сохранилась в музее науки.
А вот фотография с пресс-конференции NASA 1961 года. На доске нет реальных вычислений, только базовые уравнения, которые должны были наглядно показать, как ученые NASA ведут работы – куча стремянок и куски мела.
Ну и напоследок посмотрите, как выглядела первая PowerPoint презентация. Черно-белая, на крошечном экране, но сразу было понятно, что это прорыв, будущее, которое приведет к сокращению целых департаментов и банкротству сторонних подрядчиков. Зачем нужен профессиональный дизайнер презентаций, если теперь каждый сам себе дизайнер, правда?
Это произошло во многом из-за того, что та же Microsoft представила ClipArt- наборы картинок, которые каждый мог добавить в свои презентации. Безусловно, электронные презентации простимулировали развитие бизнеса. Однако ушла целая эпоха. Презентации из СОБЫТИЯ, превратились в рядовую вещь с типовым дизайном, то есть стали скучнее и посредственнее.
Таблицы до Excel
Когда в школе только познакомился с Excel, безудержно восхищался, каким же гением надо быть, чтобы придумать такую программу. Гигантская таблица, в которой можно считать и визуализировать любые данные. И только впоследствии я сообразил, что, в отличие от презентации, люди испокон веков пользовались прообразами Excel.
В докомпьютерную эпоху вместо Excel были бухгалтерские книги.
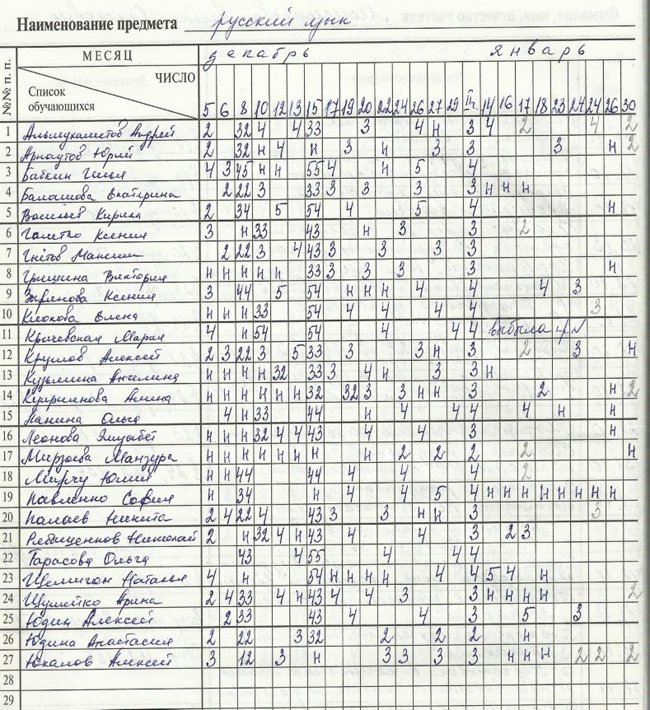
Да и, по сути, любой школьный журнал – это Excel на минималках.
До изобретения Excel жизнь офисных сотрудников была настоящим адом. Изначально им приходилось штудировать все бухгалтерские книги, подбивая цифры вручную. С развитием компьютеров ситуация упростилась, но не сильно.
До появления персональных компьютеров в компании (если она достаточно большая и процветающая) был один компьютер. Этот мейнфрейм мог занимать целый этаж. Это был центр обработки данных. Соответственно, когда требовались какие-то цифры, обращались туда. При этом не следует думать, что можно было просто зайти и попросить скинуть «цифры за прошлую неделю после обеда». Компьютеры были очень большие, но медленные и глупые.
Так что люди делали запросы только тогда, когда это было действительно важные данные. При этом обычно компьютер даже ничего не считал, в него просто заносили все данные, он их лепил вместе и выдавал в виде рулонов тонкой бумаги. Соответственно, в ответ на запрос сотрудник получал громадную простыню цифр, из которой вручную выбирал те, которые ему нужны, а дальше уже считал всё сам. Так что тут нельзя было подойти и попросить статистику продаж по отдельному контрагенту. Выдавали всё скопом. Но и это было лучше, чем бегать по разным департаментам, собирая данные.
Ускорить процесс вычислений стало возможно благодаря изобретению LANPAR, или LANguage for Programming Arrays at Random (язык для программирования случайных массивов).
Только по-настоящему большие компании, такие как General Motors или AT&T, могли себе позволить такое.
Так, LANPAR был разработан по прямому запросу от Bell Canada и AT&T. Компании столкнулись с тем, что им нужно было обновить данные в ячейках формы бюджетирования. Тогда для вычислений использовался язык «Фортран», и местные спецы сказали, что им понадобится от полугода до 2 лет для того, чтобы пересчитать все результаты. А LANPAR позволял пересчитывать автоматически: обновил ячейку — все остальные результаты пересчитались.
Впрочем, для рядовых дел по-прежнему использовали бухгалтерские книги, а вместо компьютеров нанимали студентов, работой которых было остро отточенным карандашом водить по рядам и колонкам цифр, складывая затем на арифмометре.
Если заинтересовало, как такая машина работала, то можно посмотреть вот это видео на YouTube.
Но если подводить итоги, то именно LANPAR стал прообразом современных табличных редакторов, на который все ориентировались. С развитием компьютеров всем хотелось иметь таблицы, в которых данные смогут автоматически пересчитываться.
Заключение
Сегодня мир нельзя представить без компьютеров и Microsoft Office (или другого офисного софта). Офисный софт демократизировал офисы, позволив каждому сотруднику оперировать данными. Забавно, что история идёт по спирали, и мы вернулись практически в исходную точку.
Не верите? Смотрите! Раньше данных было так много, а компьютеры были низкопроизводительными и громадными, из-за чего вычислениями занималась отдельная категория специалистов, к которой рядовые сотрудники обращались с запросами. Потом наступила эпоха, когда каждый на своем компьютере мог складывать цифры и работать с базами данных. Сейчас же опять данных стало так много, что обычному компьютеру не хватает мощности на их обработку, а в Excel — строк и столбцов. И теперь рядовые сотрудники вновь вынуждены обращаться к специализированным сотрудникам, умеющим извлекать нужные данные из массивов.
Интересно, что произойдет в будущем. Будет ли процесс работы с данными снова упрощен, например, можно ли будет просить искусственный интеллект провести в облаке все вычисления и сразу предоставить таблицы и инсайты?
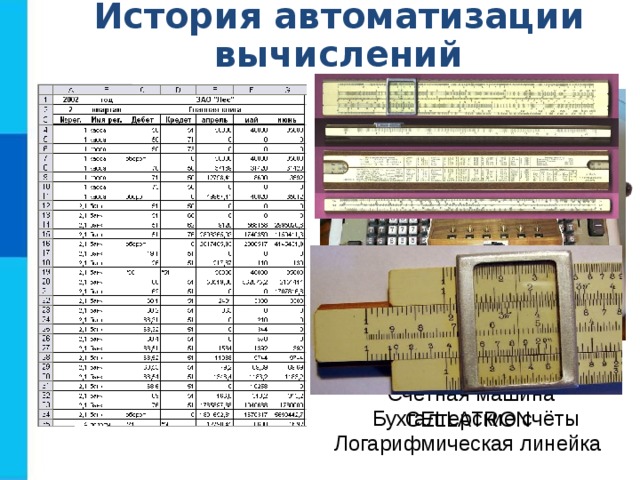
История автоматизации вычислений
Механическая счетная машина Шикарда (1623)
Арифмометр Феликс
Счётная машина CELLATRON
Бухгалтерские счёты
Логарифмическая линейка
С давних пор самыми сложными профессиями считались бухгалтер, инженер и статистик, так как людям этих профессий приходилось выполнять громоздкие вычисления на калькуляторе. При выполнении расчётов нужно было быть очень внимательным и аккуратным, потому что даже из-за незначительной ошибки работа могла остановиться на целые месяцы.
Однажды в 1979г., сидя на лекции в Гарвардском университете студент финансового факультета Дэн Бр и клин наблюдал за преподавателем. Лектору приходилось нелегко. Мало того, что ему нужно было обучить студентов и обеспечить наглядность материала, так ещё и приходилось каждый раз стирать и переписывать большое количество данных в таблице финансовой модели. У Бриклина появилась идея создать компьютерную программу, «электронную таблицу», которая автоматически будет делать перерасчёт всех данных при их изменении.
В 1979г Дэн Бриклин и его друг Роберт Фрэнкстон, который разбирался в программировании, разработали первую программу электронной таблицы, названную ими VisiCalc (Visible Calculator – наглядный вычислитель) .
Даниэль Бриклин
Известен как «отец табличных процессоров».
Основатель компании
Software Arts.
Родился 16 июля 1951 г. (66 лет), Филадельфия, Пенсильвания .
Даниэль Бриклин
Американский программист
Новый существенный шаг в развитии электронных таблиц – появление в 1982г. на рынке программных средств Lotus 1–2–3 .
Времена шли, один табличный процессор сменялся другим, более совершенным, и к настоящему времени наиболее популярным стал табличный процессор Microsoft Excel, а также Calc (модуль электронных таблиц OpenOffice.org).
С английского Excel — « превосходить».
Версия Excel 2007 отличалась от уже привычного нам интерфейса Excel 2003 радикально.
Революционным так же явилось решение разработчиков увеличить рабочий лист
с 65 536 строк и 256 столбцов
до 1 048 576 строк и 16 384 столбцов.
Excel 2007
Excel 2003
Спасибо за внимание!
Используемые ресурсы:
- http://metodist.lbz.ru/authors/informatika/3/eor9.php
- https://videouroki.net/video/23-eliektronnyie-tablitsy-na-primierie-exsel.html
- https://headshotcrew.com/bdicroce/images/29559
- https://home.infomasif.com/7-the-apple-iie-apple-ii-history.html
- https://community.spiceworks.com/topic/1604154-spark-the-birth-of-the-spreadsheet?page=0&pos=5&source=start
- http :// www . bestreferat . ru / referat -414305. html
Example of a spreadsheet holding data about a group of audio tracks.
A spreadsheet is a computer application for computation, organization, analysis and storage of data in tabular form.[1][2][3] Spreadsheets were developed as computerized analogs of paper accounting worksheets.[4] The program operates on data entered in cells of a table. Each cell may contain either numeric or text data, or the results of formulas that automatically calculate and display a value based on the contents of other cells. The term spreadsheet may also refer to one such electronic document.[5][6][7]
Spreadsheet users can adjust any stored value and observe the effects on calculated values. This makes the spreadsheet useful for «what-if» analysis since many cases can be rapidly investigated without manual recalculation. Modern spreadsheet software can have multiple interacting sheets and can display data either as text and numerals or in graphical form.
Besides performing basic arithmetic and mathematical functions, modern spreadsheets provide built-in functions for common financial accountancy and statistical operations. Such calculations as net present value or standard deviation can be applied to tabular data with a pre-programmed function in a formula. Spreadsheet programs also provide conditional expressions, functions to convert between text and numbers, and functions that operate on strings of text.
Spreadsheets have replaced paper-based systems throughout the business world. Although they were first developed for accounting or bookkeeping tasks, they now are used extensively in any context where tabular lists are built, sorted, and shared.
Basics[edit]
LANPAR, available in 1969,[8] was the first electronic spreadsheet on mainframe and time sharing computers. LANPAR was an acronym: LANguage for Programming Arrays at Random.[8] VisiCalc (1979) was the first electronic spreadsheet on a microcomputer,[9] and it helped turn the Apple II computer into a popular and widely used system. Lotus 1-2-3 was the leading spreadsheet when DOS was the dominant operating system.[10] Microsoft Excel now has the largest market share on the Windows and Macintosh platforms.[11][12][13] A spreadsheet program is a standard feature of an office productivity suite; since the advent of web apps, office suites now also exist in web app form.
A spreadsheet consists of a table of cells arranged into rows and columns and referred to by the X and Y locations. X locations, the columns, are normally represented by letters, «A,» «B,» «C,» etc., while rows are normally represented by numbers, 1, 2, 3, etc. A single cell can be referred to by addressing its row and column, «C10». This electronic concept of cell references was first introduced in LANPAR (Language for Programming Arrays at Random) (co-invented by Rene Pardo and Remy Landau) and a variant used in VisiCalc and known as «A1 notation».
Additionally, spreadsheets have the concept of a range, a group of cells, normally contiguous. For instance, one can refer to the first ten cells in the first column with the range «A1:A10». LANPAR innovated forward referencing/natural order calculation which didn’t re-appear until Lotus 123 and Microsoft’s MultiPlan Version 2.
In modern spreadsheet applications, several spreadsheets, often known as worksheets or simply sheets, are gathered together to form a workbook. A workbook is physically represented by a file containing all the data for the book, the sheets, and the cells with the sheets. Worksheets are normally represented by tabs that flip between pages, each one containing one of the sheets, although Numbers changes this model significantly. Cells in a multi-sheet book add the sheet name to their reference, for instance, «Sheet 1!C10». Some systems extend this syntax to allow cell references to different workbooks.
Users interact with sheets primarily through the cells. A given cell can hold data by simply entering it in, or a formula, which is normally created by preceding the text with an equals sign. Data might include the string of text hello world, the number 5 or the date 16-Dec-91. A formula would begin with the equals sign, =5*3, but this would normally be invisible because the display shows the result of the calculation, 15 in this case, not the formula itself. This may lead to confusion in some cases.
The key feature of spreadsheets is the ability for a formula to refer to the contents of other cells, which may, in turn, be the result of a formula. To make such a formula, one replaces a number with a cell reference. For instance, the formula =5*C10 would produce the result of multiplying the value in cell C10 by the number 5. If C10 holds the value 3 the result will be 15. But C10 might also hold its formula referring to other cells, and so on.
The ability to chain formulas together is what gives a spreadsheet its power. Many problems can be broken down into a series of individual mathematical steps, and these can be assigned to individual formulas in cells. Some of these formulas can apply to ranges as well, like the SUM function that adds up all the numbers within a range.
Spreadsheets share many principles and traits of databases, but spreadsheets and databases are not the same things. A spreadsheet is essentially just one table, whereas a database is a collection of many tables with machine-readable semantic relationships. While it is true that a workbook that contains three sheets is indeed a file containing multiple tables that can interact with each other, it lacks the relational structure of a database. Spreadsheets and databases are interoperable—sheets can be imported into databases to become tables within them, and database queries can be exported into spreadsheets for further analysis.
A spreadsheet program is one of the main components of an office productivity suite, which usually also contains a word processor, a presentation program, and a database management system. Programs within a suite use similar commands for similar functions. Usually, sharing data between the components is easier than with a non-integrated collection of functionally equivalent programs. This was particularly an advantage at a time when many personal computer systems used text-mode displays and commands instead of a graphical user interface.
History[edit]
Paper spreadsheets[edit]
The word «spreadsheet» came from «spread» in its sense of a newspaper or magazine item (text or graphics) that covers two facing pages, extending across the centerfold and treating the two pages as one large page. The compound word ‘spread-sheet’ came to mean the format used to present book-keeping ledgers—with columns for categories of expenditures across the top, invoices listed down the left margin, and the amount of each payment in the cell where its row and column intersect—which were, traditionally, a «spread» across facing pages of a bound ledger (book for keeping accounting records) or on oversized sheets of paper (termed ‘analysis paper’) ruled into rows and columns in that format and approximately twice as wide as ordinary paper.[14]
Early implementations[edit]
Batch spreadsheet report generator BSRG[edit]
A batch «spreadsheet» is indistinguishable from a batch compiler with added input data, producing an output report, i.e., a 4GL or conventional, non-interactive, batch computer program. However, this concept of an electronic spreadsheet was outlined in the 1961 paper «Budgeting Models and System Simulation» by Richard Mattessich.[15] The subsequent work by Mattessich (1964a, Chpt. 9, Accounting and Analytical Methods) and its companion volume, Mattessich (1964b, Simulation of the Firm through a Budget Computer Program) applied computerized spreadsheets to accounting and budgeting systems (on mainframe computers programmed in FORTRAN IV). These batch Spreadsheets dealt primarily with the addition or subtraction of entire columns or rows (of input variables), rather than individual cells.
In 1962, this concept of the spreadsheet, called BCL for Business Computer Language, was implemented on an IBM 1130[dubious – discuss] and in 1963 was ported to an IBM 7040 by R. Brian Walsh at Marquette University, Wisconsin. This program was written in Fortran. Primitive timesharing was available on those machines. In 1968 BCL was ported by Walsh to the IBM 360/67 timesharing machine at Washington State University. It was used to assist in the teaching of finance to business students. Students were able to take information prepared by the professor and manipulate it to represent it and show ratios etc. In 1964, a book entitled Business Computer Language was written by Kimball, Stoffells and Walsh and both the book and program were copyrighted in 1966 and years later that copyright was renewed.[16]
Applied Data Resources had a FORTRAN preprocessor called Empires.
In the late 1960s, Xerox used BCL to develop a more sophisticated version for their timesharing system.
LANPAR spreadsheet compiler[edit]
A key invention in the development of electronic spreadsheets was made by Rene K. Pardo and Remy Landau, who filed in 1970 U.S. Patent 4,398,249 on a spreadsheet automatic natural order calculation algorithm. While the patent was initially rejected by the patent office as being a purely mathematical invention, following 12 years of appeals, Pardo and Landau won a landmark court case at the Predecessor Court of the Federal Circuit (CCPA), overturning the Patent Office in 1983 — establishing that «something does not cease to become patentable merely because the point of novelty is in an algorithm.» However, in 1995 the United States Court of Appeals for the Federal Circuit ruled the patent unenforceable.[17]
The actual software was called LANPAR — LANguage for Programming Arrays at Random.[note 1] This was conceived and entirely developed in the summer of 1969, following Pardo and Landau’s recent graduation from Harvard University. Co-inventor Rene Pardo recalls that he felt that one manager at Bell Canada should not have to depend on programmers to program and modify budgeting forms, and he thought of letting users type out forms in any order and having an electronic computer calculate results in the right order («Forward Referencing/Natural Order Calculation»). Pardo and Landau developed and implemented the software in 1969.[18]
LANPAR was used by Bell Canada, AT&T, and the 18 operating telephone companies nationwide for their local and national budgeting operations. LANPAR was also used by General Motors. Its uniqueness was Pardo’s co-invention incorporating forward referencing/natural order calculation (one of the first «non-procedural» computer languages)[19] as opposed to left-to-right, top to bottom sequence for calculating the results in each cell that was used by VisiCalc, SuperCalc, and the first version of MultiPlan. Without forward referencing/natural order calculation, the user had to refresh the spreadsheet until the values in all cells remained unchanged. Once the cell values stayed constant, the user was assured that there were no remaining forward references within the spreadsheet.
Autoplan/Autotab spreadsheet programming language[edit]
In 1968, three former employees from the General Electric computer company headquartered in Phoenix, Arizona set out to start their own software development house. A. Leroy Ellison, Harry N. Cantrell, and Russell E. Edwards found themselves doing a large number of calculations when making tables for the business plans that they were presenting to venture capitalists. They decided to save themselves a lot of effort and wrote a computer program that produced their tables for them. This program, originally conceived as a simple utility for their personal use, would turn out to be the first software product offered by the company that would become known as Capex Corporation. «AutoPlan» ran on GE’s Time-sharing service; afterward, a version that ran on IBM mainframes was introduced under the name AutoTab. (National CSS offered a similar product, CSSTAB, which had a moderate timesharing user base by the early 1970s. A major application was opinion research tabulation.)
AutoPlan/AutoTab was not a WYSIWYG interactive spreadsheet program, it was a simple scripting language for spreadsheets. The user defined the names and labels for the rows and columns, then the formulas that defined each row or column. In 1975, Autotab-II was advertised as extending the original to a maximum of «1,500 rows and columns, combined in any proportion the user requires…«[20]
GE Information Services, which operated the time-sharing service, also launched its own spreadsheet system, Financial Analysis Language (FAL), circa 1974. It was later supplemented by an additional spreadsheet language, TABOL,[21][22] which was developed by an independent author, Oliver Vellacott in the UK. Both FAL and TABOL were integrated with GEIS’s database system, DMS.
IBM Financial Planning and Control System[edit]
The IBM Financial Planning and Control System was developed in 1976, by Brian Ingham at IBM Canada. It was implemented by IBM in at least 30 countries. It ran on an IBM mainframe and was among the first applications for financial planning developed with APL that completely hid the programming language from the end-user. Through IBM’s VM operating system, it was among the first programs to auto-update each copy of the application as new versions were released. Users could specify simple mathematical relationships between rows and between columns. Compared to any contemporary alternatives, it could support very large spreadsheets. It loaded actual financial planning data drawn from the legacy batch system into each user’s spreadsheet monthly. It was designed to optimize the power of APL through object kernels, increasing program efficiency by as much as 50 fold over traditional programming approaches.
APLDOT modeling language[edit]
An example of an early «industrial weight» spreadsheet was APLDOT, developed in 1976 at the United States Railway Association on an IBM 360/91, running at The Johns Hopkins University Applied Physics Laboratory in Laurel, MD.[23] The application was used successfully for many years in developing such applications as financial and costing models for the US Congress and for Conrail. APLDOT was dubbed a «spreadsheet» because financial analysts and strategic planners used it to solve the same problems they addressed with paper spreadsheet pads.
VisiCalc[edit]
VisiCalc running on an Apple II
Because Dan Bricklin and Bob Frankston implemented VisiCalc on the Apple II in 1979 and the IBM PC in 1981, the spreadsheet concept became widely known in the early 1980s. VisiCalc was the first spreadsheet that combined all essential features of modern spreadsheet applications (except for forward referencing/natural order recalculation), such as WYSIWYG interactive user interface, automatic recalculation, status and formula lines, range copying with relative and absolute references, formula building by selecting referenced cells. Unaware of LANPAR at the time PC World magazine called VisiCalc the first electronic spreadsheet.[24]
Bricklin has spoken of watching his university professor create a table of calculation results on a blackboard. When the professor found an error, he had to tediously erase and rewrite several sequential entries in the table, triggering Bricklin to think that he could replicate the process on a computer, using the blackboard as the model to view results of underlying formulas. His idea became VisiCalc, the first application that turned the personal computer from a hobby for computer enthusiasts into a business tool.
VisiCalc went on to become the first «killer application»,[25][26] an application that was so compelling, people would buy a particular computer just to use it. VisiCalc was in no small part responsible for the Apple II’s success. The program was later ported to a number of other early computers, notably CP/M machines, the Atari 8-bit family and various Commodore platforms. Nevertheless, VisiCalc remains best known as an Apple II program.
SuperCalc[edit]
SuperCalc was a spreadsheet application published by Sorcim in 1980, and originally bundled (along with WordStar) as part of the CP/M software package included with the Osborne 1 portable computer. It quickly became the de facto standard spreadsheet for CP/M and was ported to MS-DOS in 1982.
Lotus 1-2-3 and other MS-DOS spreadsheets[edit]
The acceptance of the IBM PC following its introduction in August 1981, began slowly because most of the programs available for it were translations from other computer models. Things changed dramatically with the introduction of Lotus 1-2-3 in November 1982, and release for sale in January 1983. Since it was written especially for the IBM PC, it had a good performance and grew in popularity. Lotus 1-2-3 drove sales of the PC due to the improvements in speed and graphics compared to VisiCalc on the Apple II.[27]
Lotus 1-2-3, along with its competitor Borland Quattro, soon displaced VisiCalc. Lotus 1-2-3 was released on January 26, 1983, started outselling then-most-popular VisiCalc the very same year, and for several years was the leading spreadsheet for DOS.
Microsoft Excel[edit]
Microsoft released the first version of Excel for the Macintosh on September 30, 1985, and then ported[28] it to Windows, with the first version being numbered 2.05 (to synchronize with the Macintosh version 2.2) and released in November 1987. The Windows 3.x platforms of the early 1990s made it possible for Excel to take market share from Lotus. By the time Lotus responded with usable Windows products, Microsoft had begun to assemble their Office suite. By 1995, Excel was the market leader, edging out Lotus 1-2-3,[14] and in 2013, IBM discontinued Lotus 1-2-3 altogether.[29]
Web-based spreadsheets[edit]
Notable current web-based spreadsheet software:
- Collabora Online Calc is a free, open-source and cross-platform enterprise-ready edition of LibreOffice.
- Ethercalc is a simple open-source collaborative spreadsheet that runs in browsers.
- Google Sheets
- Microsoft Excel Online
Mainframe spreadsheets[edit]
- The Works Records System at ICI developed in 1974 on IBM 370/145[30]
- ExecuCalc, from Parallax Systems, Inc.: Released in late 1982,[31] ExecuCalc was the first mainframe «visi-clone» which duplicated the features of VisiCalc on IBM mainframes with 3270 display terminals. Over 150 copies were licensed (35 to Fortune 500 companies). DP managers were attracted to compatibility and avoiding then-expensive PC purchases (see 1983 Computerworld magazine front page article[32] and advertisement[33].)
Other spreadsheets[edit]
Notable current spreadsheet software:
- Apache OpenOffice Calc is a free and open-source.
- Calligra Sheets (formerly KCalc)
- Collabora Online Calc for mobile and desktop apps are free, open-source, cross-platform enterprise-ready editions of LibreOffice.
- Corel Quattro Pro (WordPerfect Office)
- Gnumeric is free and cross-platform, it is part of the GNOME Free Software Desktop Project.
- Kingsoft Spreadsheets
- LibreOffice Calc is free, open-source and cross platform.
- NeoOffice
- Numbers is Apple Inc.’s spreadsheet software, part of iWork.
- PlanMaker (SoftMaker Office)
- Pyspread
Discontinued spreadsheet software:
- 20/20
- 3D-Calc for Atari ST computers
- Framework by Forefront Corporation/Ashton-Tate (1983–84)
- GNU Oleo – A traditional terminal mode spreadsheet for UNIX/UNIX-like systems
- IBM Lotus Symphony (2007)
- Javelin Software
- KCells
- Lucid 3-D
- Lotus Improv[34]
- Lotus Jazz for Macintosh
- Lotus Symphony (1984)
- MultiPlan
- Claris’ Resolve (Macintosh)
- Resolver One
- Borland’s Quattro Pro
- SIAG
- SuperCalc
- T/Maker
- Target Planner Calc for CP/M and TRS-DOS[35][36]
- Trapeze for Macintosh[37]
- Wingz for Macintosh
Other products[edit]
Several companies have attempted to break into the spreadsheet market with programs based on very different paradigms. Lotus introduced what is likely the most successful example, Lotus Improv, which saw some commercial success, notably in the financial world where its powerful data mining capabilities remain well respected to this day.
Spreadsheet 2000 attempted to dramatically simplify formula construction, but was generally not successful.
Concepts[edit]
The main concepts are those of a grid of cells, called a sheet, with either raw data, called values, or formulas in the cells. Formulas say how to mechanically compute new values from existing values. Values are general numbers, but can also be pure text, dates, months, etc. Extensions of these concepts include logical spreadsheets. Various tools for programming sheets, visualizing data, remotely connecting sheets, displaying cells’ dependencies, etc. are commonly provided.
Cells[edit]
A «cell» can be thought of as a box for holding data. A single cell is usually referenced by its column and row (C2 would represent the cell containing the value 30 in the example table below). Usually rows, representing the dependent variables, are referenced in decimal notation starting from 1, while columns representing the independent variables use 26-adic bijective numeration using the letters A-Z as numerals. Its physical size can usually be tailored to its content by dragging its height or width at box intersections (or for entire columns or rows by dragging the column- or row-headers).
| A | B | C | D | |
|---|---|---|---|---|
| 01 | Sales | 100000 | 30000 | 70000 |
| 02 | Purchases | 25490 | 30 | 200 |
An array of cells is called a sheet or worksheet. It is analogous to an array of variables in a conventional computer program (although certain unchanging values, once entered, could be considered, by the same analogy, constants). In most implementations, many worksheets may be located within a single spreadsheet. A worksheet is simply a subset of the spreadsheet divided for the sake of clarity. Functionally, the spreadsheet operates as a whole and all cells operate as global variables within the spreadsheet (each variable having ‘read’ access only except its containing cell).
A cell may contain a value or a formula, or it may simply be left empty.
By convention, formulas usually begin with = sign.
Values[edit]
A value can be entered from the computer keyboard by directly typing into the cell itself. Alternatively, a value can be based on a formula (see below), which might perform a calculation, display the current date or time, or retrieve external data such as a stock quote or a database value.
The Spreadsheet Value Rule
Computer scientist Alan Kay used the term value rule to summarize a spreadsheet’s operation: a cell’s value relies solely on the formula the user has typed into the cell.[38] The formula may rely on the value of other cells, but those cells are likewise restricted to user-entered data or formulas. There are no ‘side effects’ to calculating a formula: the only output is to display the calculated result inside its occupying cell. There is no natural mechanism for permanently modifying the contents of a cell unless the user manually modifies the cell’s contents. In the context of programming languages, this yields a limited form of first-order functional programming.[39]
Automatic recalculation[edit]
A standard of spreadsheets since the 1980s, this optional feature eliminates the need to manually request the spreadsheet program to recalculate values (nowadays typically the default option unless specifically ‘switched off’ for large spreadsheets, usually to improve performance). Some earlier spreadsheets required a manual request to recalculate since the recalculation of large or complex spreadsheets often reduced data entry speed. Many modern spreadsheets still retain this option.
Recalculation generally requires that there are no circular dependencies in a spreadsheet. A dependency graph is a graph that has a vertex for each object to be updated, and an edge connecting two objects whenever one of them needs to be updated earlier than the other. Dependency graphs without circular dependencies form directed acyclic graphs, representations of partial orderings (in this case, across a spreadsheet) that can be relied upon to give a definite result.[40]
Real-time update[edit]
This feature refers to updating a cell’s contents periodically with a value from an external source—such as a cell in a «remote» spreadsheet. For shared, Web-based spreadsheets, it applies to «immediately» updating cells another user has updated. All dependent cells must be updated also.
Locked cell[edit]
Once entered, selected cells (or the entire spreadsheet) can optionally be «locked» to prevent accidental overwriting. Typically this would apply to cells containing formulas but might apply to cells containing «constants» such as a kilogram/pounds conversion factor (2.20462262 to eight decimal places). Even though individual cells are marked as locked, the spreadsheet data are not protected until the feature is activated in the file preferences.
Data format[edit]
A cell or range can optionally be defined to specify how the value is displayed. The default display format is usually set by its initial content if not specifically previously set, so that for example «31/12/2007» or «31 Dec 2007» would default to the cell format of date.
Similarly adding a % sign after a numeric value would tag the cell as a percentage cell format. The cell contents are not changed by this format, only the displayed value.
Some cell formats such as «numeric» or «currency» can also specify the number of decimal places.
This can allow invalid operations (such as doing multiplication on a cell containing a date), resulting in illogical results without an appropriate warning.
Cell formatting[edit]
Depending on the capability of the spreadsheet application, each cell (like its counterpart the «style» in a word processor) can be separately formatted using the attributes of either the content (point size, color, bold or italic) or the cell (border thickness, background shading, color). To aid the readability of a spreadsheet, cell formatting may be conditionally applied to data; for example, a negative number may be displayed in red.
A cell’s formatting does not typically affect its content and depending on how cells are referenced or copied to other worksheets or applications, the formatting may not be carried with the content.
Named cells[edit]
Use of named column variables x & y in Microsoft Excel. Formula for y=x2 resembles Fortran, and Name Manager shows the definitions of x & y.
In most implementations, a cell, or group of cells in a column or row, can be «named» enabling the user to refer to those cells by a name rather than by a grid reference. Names must be unique within the spreadsheet, but when using multiple sheets in a spreadsheet file, an identically named cell range on each sheet can be used if it is distinguished by adding the sheet name. One reason for this usage is for creating or running macros that repeat a command across many sheets. Another reason is that formulas with named variables are readily checked against the algebra they are intended to implement (they resemble Fortran expressions). The use of named variables and named functions also makes the spreadsheet structure more transparent.
Cell reference[edit]
In place of a named cell, an alternative approach is to use a cell (or grid) reference. Most cell references indicate another cell in the same spreadsheet, but a cell reference can also refer to a cell in a different sheet within the same spreadsheet, or (depending on the implementation) to a cell in another spreadsheet entirely, or a value from a remote application.
A typical cell reference in «A1» style consists of one or two case-insensitive letters to identify the column (if there are up to 256 columns: A–Z and AA–IV) followed by a row number (e.g., in the range 1–65536). Either part can be relative (it changes when the formula it is in is moved or copied), or absolute (indicated with $ in front of the part concerned of the cell reference). The alternative «R1C1» reference style consists of the letter R, the row number, the letter C, and the column number; relative row or column numbers are indicated by enclosing the number in square brackets. Most current spreadsheets use the A1 style, some providing the R1C1 style as a compatibility option.
When the computer calculates a formula in one cell to update the displayed value of that cell, cell reference(s) in that cell, naming some other cell(s), causes the computer to fetch the value of the named cell(s).
A cell on the same «sheet» is usually addressed as:
=A1
A cell on a different sheet of the same spreadsheet is usually addressed as:
=SHEET2!A1 (that is; the first cell in sheet 2 of the same spreadsheet).
Some spreadsheet implementations in Excel allow cell references to another spreadsheet (not the currently open and active file) on the same computer or a local network. It may also refer to a cell in another open and active spreadsheet on the same computer or network that is defined as shareable. These references contain the complete filename, such as:
='C:Documents and SettingsUsernameMy spreadsheets[main sheet]Sheet1!A1
In a spreadsheet, references to cells automatically update when new rows or columns are inserted or deleted. Care must be taken, however, when adding a row immediately before a set of column totals to ensure that the totals reflect the values of the additional rows—which they often do not.
A circular reference occurs when the formula in one cell refers—directly, or indirectly through a chain of cell references—to another cell that refers back to the first cell. Many common errors cause circular references. However, some valid techniques use circular references. These techniques, after many spreadsheet recalculations, (usually) converge on the correct values for those cells.
Cell ranges[edit]
Likewise, instead of using a named range of cells, a range reference can be used. Reference to a range of cells is typical of the form (A1:A6), which specifies all the cells in the range A1 through to A6. A formula such as «=SUM(A1:A6)» would add all the cells specified and put the result in the cell containing the formula itself.
Sheets[edit]
In the earliest spreadsheets, cells were a simple two-dimensional grid. Over time, the model has expanded to include a third dimension, and in some cases a series of named grids, called sheets. The most advanced examples allow inversion and rotation operations which can slice and project the data set in various ways.
Formulas[edit]
Animation of a simple spreadsheet that multiplies values in the left column by 2, then sums the calculated values from the right column to the bottom-most cell. In this example, only the values in the A column are entered (10, 20, 30), and the remainder of cells are formulas. Formulas in the B column multiply values from the A column using relative references, and the formula in B4 uses the SUM() function to find the sum of values in the B1:B3 range.
A formula identifies the calculation needed to place the result in the cell it is contained within. A cell containing a formula, therefore, has two display components; the formula itself and the resulting value. The formula is normally only shown when the cell is selected by «clicking» the mouse over a particular cell; otherwise, it contains the result of the calculation.
A formula assigns values to a cell or range of cells, and typically has the format:
where the expression consists of:
- values, such as
2,9.14or6.67E-11; - references to other cells, such as, e.g.,
A1for a single cell orB1:B3for a range; - arithmetic operators, such as
+,-,*,/, and others; - relational operators, such as
>=,<, and others; and, - functions, such as
SUM(),TAN(), and many others.
When a cell contains a formula, it often contains references to other cells. Such a cell reference is a type of variable. Its value is the value of the referenced cell or some derivation of it. If that cell in turn references other cells, the value depends on the values of those. References can be relative (e.g., A1, or B1:B3), absolute (e.g., $A$1, or $B$1:$B$3) or mixed row– or column-wise absolute/relative (e.g., $A1 is column-wise absolute and A$1 is row-wise absolute).
The available options for valid formulas depend on the particular spreadsheet implementation but, in general, most arithmetic operations and quite complex nested conditional operations can be performed by most of today’s commercial spreadsheets. Modern implementations also offer functions to access custom-build functions, remote data, and applications.
A formula may contain a condition (or nested conditions)—with or without an actual calculation—and is sometimes used purely to identify and highlight errors. In the example below, it is assumed the sum of a column of percentages (A1 through A6) is tested for validity and an explicit message put into the adjacent right-hand cell.
- =IF(SUM(A1:A6) > 100, «More than 100%», SUM(A1:A6))
Further examples:
- =IF(AND(A1<>»»,B1<>»»),A1/B1,»») means that if both cells A1 and B1 are not <> empty «», then divide A1 by B1 and display, other do not display anything.
- =IF(AND(A1<>»»,B1<>»»),IF(B1<>0,A1/B1,»Division by zero»),»») means that if cells A1 and B1 are not empty, and B1 is not zero, then divide A1 by B1, if B1 is zero, then display «Division by zero», and do not display anything if either A1 and B1 are empty.
- =IF(OR(A1<>»»,B1<>»»),»Either A1 or B1 show text»,»») means to display the text if either cells A1 or B1 are not empty.
The best way to build up conditional statements is step by step composing followed by trial and error testing and refining code.
A spreadsheet does not have to contain any formulas at all, in which case it could be considered merely a collection of data arranged in rows and columns (a database) like a calendar, timetable, or simple list. Because of its ease of use, formatting, and hyperlinking capabilities, many spreadsheets are used solely for this purpose.
Functions[edit]
Spreadsheets usually contain several supplied functions, such as arithmetic operations (for example, summations, averages, and so forth), trigonometric functions, statistical functions, and so forth. In addition there is often a provision for user-defined functions. In Microsoft Excel, these functions are defined using Visual Basic for Applications in the supplied Visual Basic editor, and such functions are automatically accessible on the worksheet. Also, programs can be written that pull information from the worksheet, perform some calculations, and report the results back to the worksheet. In the figure, the name sq is user-assigned, and the function sq is introduced using the Visual Basic editor supplied with Excel. Name Manager displays the spreadsheet definitions of named variables x & y.
Subroutines[edit]
Functions themselves cannot write into the worksheet but simply return their evaluation. However, in Microsoft Excel, subroutines can write values or text found within the subroutine directly to the spreadsheet. The figure shows the Visual Basic code for a subroutine that reads each member of the named column variable x, calculates its square, and writes this value into the corresponding element of named column variable y. The y column contains no formula because its values are calculated in the subroutine, not on the spreadsheet, and simply are written in.
Remote spreadsheet[edit]
Whenever a reference is made to a cell or group of cells that are not located within the current physical spreadsheet file, it is considered as accessing a «remote» spreadsheet. The contents of the referenced cell may be accessed either on the first reference with a manual update or more recently in the case of web-based spreadsheets, as a near real-time value with a specified automatic refresh interval.
Charts[edit]
Graph made using Microsoft Excel
Many spreadsheet applications permit charts and graphs (e.g., histograms, pie charts) to be generated from specified groups of cells that are dynamically re-built as cell contents change. The generated graphic component can either be embedded within the current sheet or added as a separate object. To create an Excel histogram, a formula based on the REPT function can be used.[41]
Multi-dimensional spreadsheets[edit]
In the late 1980s and early 1990s, first Javelin Software and Lotus Improv appeared. Unlike models in a conventional spreadsheet, they utilized models built on objects called variables, not on data in cells of a report. These multi-dimensional spreadsheets enabled viewing data and algorithms in various self-documenting ways, including simultaneous multiple synchronized views. For example, users of Javelin could move through the connections between variables on a diagram while seeing the logical roots and branches of each variable. This is an example of what is perhaps its primary contribution of the earlier Javelin—the concept of traceability of a user’s logic or model structure through its twelve views. A complex model can be dissected and understood by others who had no role in its creation.
In these programs, a time series, or any variable, was an object in itself, not a collection of cells that happen to appear in a row or column. Variables could have many attributes, including complete awareness of their connections to all other variables, data references, and text and image notes. Calculations were performed on these objects, as opposed to a range of cells, so adding two-time series automatically aligns them in calendar time, or in a user-defined time frame. Data were independent of worksheets—variables, and therefore data, could not be destroyed by deleting a row, column, or entire worksheet. For instance, January’s costs are subtracted from January’s revenues, regardless of where or whether either appears in a worksheet. This permits actions later used in pivot tables, except that flexible manipulation of report tables, was but one of many capabilities supported by variables. Moreover, if costs were entered by week and revenues by month, the program could allocate or interpolate as appropriate. This object design enabled variables and whole models to reference each other with user-defined variable names and to perform multidimensional analysis and massive, but easily editable consolidations.
Trapeze,[37] a spreadsheet on the Mac, went further and explicitly supported
not just table columns, but also matrix operators.
Logical spreadsheets[edit]
Spreadsheets that have a formula language based upon logical expressions, rather than arithmetic expressions are known as logical spreadsheets. Such spreadsheets can be used to reason deductively about their cell values.
Programming issues[edit]
Just as the early programming languages were designed to generate spreadsheet printouts, programming techniques themselves have evolved to process tables (also known as spreadsheets or matrices) of data more efficiently in the computer itself.
End-user development[edit]
Spreadsheets are a popular end-user development tool.[42] EUD denotes activities or techniques in which people who are not professional developers create automated behavior and complex data objects without significant knowledge of a programming language. Many people find it easier to perform calculations in spreadsheets than by writing the equivalent sequential program. This is due to several traits of spreadsheets.
- They use spatial relationships to define program relationships. Humans have highly developed intuitions about spaces, and of dependencies between items. Sequential programming usually requires typing line after line of text, which must be read slowly and carefully to be understood and changed.
- They are forgiving, allowing partial results and functions to work. One or more parts of a program can work correctly, even if other parts are unfinished or broken. This makes writing and debugging programs easier, and faster. Sequential programming usually needs every program line and character to be correct for a program to run. One error usually stops the whole program and prevents any result. Though this user-friendliness is benefit of spreadsheet development, it often comes with increased risk of errors.
- Modern spreadsheets allow for secondary notation. The program can be annotated with colors, typefaces, lines, etc. to provide visual cues about the meaning of elements in the program.
- Extensions that allow users to create new functions can provide the capabilities of a functional language.[43]
- Extensions that allow users to build and apply models from the domain of machine learning.[44][45]
- Spreadsheets are versatile. With their boolean logic and graphics capabilities, even electronic circuit design is possible.[46]
- Spreadsheets can store relational data and spreadsheet formulas can express all queries of SQL. There exists a query translator, which automatically generates the spreadsheet implementation from the SQL code.[47]
Spreadsheet programs[edit]
A «spreadsheet program» is designed to perform general computation tasks using spatial relationships rather than time as the primary organizing principle.
It is often convenient to think of a spreadsheet as a mathematical graph, where the nodes are spreadsheet cells, and the edges are references to other cells specified in formulas. This is often called the dependency graph of the spreadsheet. References between cells can take advantage of spatial concepts such as relative position and absolute position, as well as named locations, to make the spreadsheet formulas easier to understand and manage.
Spreadsheets usually attempt to automatically update cells when the cells depend on change. The earliest spreadsheets used simple tactics like evaluating cells in a particular order, but modern spreadsheets calculate following a minimal recomputation order from the dependency graph. Later spreadsheets also include a limited ability to propagate values in reverse, altering source values so that a particular answer is reached in a certain cell. Since spreadsheet cell formulas are not generally invertible, though, this technique is of somewhat limited value.
Many of the concepts common to sequential programming models have analogs in the spreadsheet world. For example, the sequential model of the indexed loop is usually represented as a table of cells, with similar formulas (normally differing only in which cells they reference).
Spreadsheets have evolved to use scripting programming languages like VBA as a tool for extensibility beyond what the spreadsheet language makes easy.
Shortcomings[edit]
While spreadsheets represented a major step forward in quantitative modeling, they have deficiencies. Their shortcomings include the perceived unfriendliness of alpha-numeric cell addresses.[48]
- Research by ClusterSeven has shown huge discrepancies in the way financial institutions and corporate entities understand, manage and police their often vast estates of spreadsheets and unstructured financial data (including comma-separated values (CSV) files and Microsoft Access databases). One study in early 2011 of nearly 1,500 people in the UK found that 57% of spreadsheet users have never received formal training on the spreadsheet package they use. 72% said that no internal department checks their spreadsheets for accuracy. Only 13% said that Internal Audit reviews their spreadsheets, while a mere 1% receive checks from their risk department.[49]
- Spreadsheets can have reliability problems. Research studies estimate that around 1% of all formulas in operational spreadsheets are in error.[50]
-
- Despite the high error risks often associated with spreadsheet authorship and use, specific steps can be taken to significantly enhance control and reliability by structurally reducing the likelihood of error occurrence at their source.[51]
- The practical expressiveness of spreadsheets can be limited unless their modern features are used. Several factors contribute to this limitation. Implementing a complex model on a cell-at-a-time basis requires tedious attention to detail. Authors have difficulty remembering the meanings of hundreds or thousands of cell addresses that appear in formulas.
-
- These drawbacks are mitigated by the use of named variables for cell designations, and employing variables in formulas rather than cell locations and cell-by-cell manipulations. Graphs can be used to show instantly how results are changed by changes in parameter values. The spreadsheet can be made invisible except for a transparent user interface that requests pertinent input from the user, displays results requested by the user, creates reports, and has built-in error traps to prompt correct input.[52]
- Similarly, formulas expressed in terms of cell addresses are hard to keep straight and hard to audit. Research shows that spreadsheet auditors who check numerical results and cell formulas find no more errors than auditors who only check numerical results.[53] That is another reason to use named variables and formulas employing named variables.
-
- Specifically, spreadsheets typically contain many copies of the same formula. When the formula is modified, the user has to change every cell containing that formula. In contrast, most computer languages allow a formula to appear only once in the code and achieve repetition using loops: making them much easier to implement and audit.
- The alteration of a dimension demands major surgery. When rows (or columns) are added to or deleted from a table, one has to adjust the size of many downstream tables that depend on the table being changed. In the process, it is often necessary to move other cells around to make room for the new columns or rows and to adjust graph data sources. In large spreadsheets, this can be extremely time-consuming.[54][55]
- Adding or removing a dimension is so difficult, one generally has to start over. The spreadsheet as a paradigm forces one to decide on dimensionality right of the beginning of one’s spreadsheet creation, even though it is often most natural to make these choices after one’s spreadsheet model has matured. The desire to add and remove dimensions also arises in parametric and sensitivity analyses.[54][55]
- Collaboration in authoring spreadsheet formulas can be difficult when such collaboration occurs at the level of cells and cell addresses.
Other problems associated with spreadsheets include:[56][57]
- Some sources advocate the use of specialized software instead of spreadsheets for some applications (budgeting, statistics)[58][59][60]
- Many spreadsheet software products, such as Microsoft Excel[61] (versions prior to 2007) and OpenOffice.org Calc[62] (versions prior to 2008), have a capacity limit of 65,536 rows by 256 columns (216 and 28 respectively). This can present a problem for people using very large datasets, and may result in data loss. In spite of the time passed, a recent example is the loss of COVID-19 positives in the British statistics for September and October 2020.[63]
- Lack of auditing and revision control. This makes it difficult to determine who changed what and when. This can cause problems with regulatory compliance. Lack of revision control greatly increases the risk of errors due to the inability to track, isolate and test changes made to a document.[citation needed]
- Lack of security. Spreadsheets lack controls on who can see and modify particular data. This, combined with the lack of auditing above, can make it easy for someone to commit fraud.[64]
- Because they are loosely structured, it is easy for someone to introduce an error, either accidentally or intentionally, by entering information in the wrong place or expressing dependencies among cells (such as in a formula) incorrectly.[54][65][66]
- The results of a formula (example «=A1*B1») applies only to a single cell (that is, the cell the formula is located in—in this case perhaps C1), even though it can «extract» data from many other cells, and even real-time dates and actual times. This means that to cause a similar calculation on an array of cells, an almost identical formula (but residing in its own «output» cell) must be repeated for each row of the «input» array. This differs from a «formula» in a conventional computer program, which typically makes one calculation that it applies to all the input in turn. With current spreadsheets, this forced repetition of near-identical formulas can have detrimental consequences from a quality assurance standpoint and is often the cause of many spreadsheet errors. Some spreadsheets have array formulas to address this issue.
- Trying to manage the sheer volume of spreadsheets that may exist in an organization without proper security, audit trails, the unintentional introduction of errors, and other items listed above can become overwhelming.
While there are built-in and third-party tools for desktop spreadsheet applications that address some of these shortcomings, awareness, and use of these is generally low. A good example of this is that 55% of Capital market professionals «don’t know» how their spreadsheets are audited; only 6% invest in a third-party solution[67]
Spreadsheet risk[edit]
Spreadsheet risk is the risk associated with deriving a materially incorrect value from a spreadsheet application that will be utilized in making a related (usually numerically based) decision. Examples include the valuation of an asset, the determination of financial accounts, the calculation of medicinal doses, or the size of a load-bearing beam for structural engineering. The risk may arise from inputting erroneous or fraudulent data values, from mistakes (or incorrect changes) within the logic of the spreadsheet or the omission of relevant updates (e.g., out of date exchange rates). Some single-instance errors have exceeded US$1 billion.[68][69] Because spreadsheet risk is principally linked to the actions (or inaction) of individuals it is defined as a sub-category of operational risk.
Despite this, research[70] carried out by ClusterSeven revealed that around half (48%) of c-level executives and senior managers at firms reporting annual revenues over £50m said there were either no usage controls at all or poorly applied manual processes over the use of spreadsheets at the firms.[70][71]
In 2013 Thomas Herndon, a graduate student of economics at the University of Massachusetts Amherst found major coding flaws in the spreadsheet used by the economists Carmen Reinhart and Kenneth Rogoff in Growth in a Time of Debt, a very influential 2010 journal article. The Reinhart and Rogoff article was widely used as justification to drive 2010–2013 European austerity programs.[72]
See also[edit]
- Attribute-value system
- Comparison of spreadsheet software
- Moving and copying in spreadsheets
- List of spreadsheet software
- Model audit
Notes[edit]
- ^ This may be a backronym, as «LANPAR is also a portmanteau of the developers’ surnames, «Landau» and «Pardo».
References[edit]
- ^ «spreadsheet». Merriam-Webster Online Dictionary. Retrieved 23 June 2016.
- ^ American Heritage Dictionary of the English Language (5th ed.). Houghton Mifflin Harcourt Publishing Company. 2011.
A software interface consisting of an interactive grid made up of cells in which data or formulas are entered for analysis or presentation.
- ^ Collins English Dictionary – Complete and Unabridged (12th ed.). HarperCollins Publishers. 2014.
(Computer Science) a computer program that allows easy entry and manipulation of figures, equations, and text, used esp for financial planning and budgeting
- ^ «spreadsheet». WhatIs.com. TechTarget. Retrieved 23 June 2016.
- ^ «spreadsheet». Dictionary.com Unabridged. Random House, Inc. Retrieved 23 June 2016.
- ^ Beal, Vangie (September 1996). «spreadsheet». webopedia. QuinStreet. Retrieved 23 June 2016.
- ^ «Spreadsheet». Computer Hope. Retrieved 23 June 2016.
- ^ a b Higgins, Hannah (2009-01-01). The Grid Book. MIT Press. ISBN 9780262512404.
- ^ Charles Babcock, «What’s The Greatest Software Ever Written?», Information Week, 11 Aug 2006 Archived 25 June 2017 at the Wayback Machine. Accessed 25 June 2014
- ^ Lewis, Peter H. (1988-03-13). «The Executive computer; Lotus 1-2-3 Faces Up to the Upstarts». NYTimes.com. The New York Times Company. Retrieved 2012-10-14.
Release 3.0 is being written in the computer language known as C, to provide easy transportability among PCs, Macs and mainframes.
- ^ «Rivals Set Their Sights on Microsoft Office: Can They Topple the Giant? –Knowledge@Wharton». Wharton, University of Pennsylvania. Retrieved 2010-08-20.
- ^ «spreadsheet analysis from winners, losers, and Microsoft». Utdallas.edu. Archived from the original on 2010-07-23. Retrieved 2010-08-20.
- ^ «A». Utdallas.edu. Archived from the original on 2010-08-05. Retrieved 2010-08-20.
- ^ a b Power, D. J. (30 August 2004). «A Brief History of Spreadsheets». DSSResources.COM (3.6 ed.). Retrieved 25 June 2014.
- ^ Mattessich, Richard (1961). «Budgeting Models and System Simulation». The Accounting Review. 36 (3): 384–397. JSTOR 242869.
- ^ Brian Walsh (1996). «Business Computer Language». IT-Directors.com.
- ^ «Refac v. Lotus». Ll.georgetown.edu. Retrieved 2010-08-20.
- ^ «Rene Pardo – Personal Web Page». renepardo.com.
- ^ «Archived copy» (PDF). Archived from the original (PDF) on 2010-08-21. Retrieved 2007-11-03.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ «‘Autotab’ Update Extends Former Matrix Size Limits», 28 May 1975, p19, Computerworld
- ^ «COMPANY HIGHLIGHT: GENERAL ELECTRIC INFORMATION SERVICES COMPANY». INPUT Vendor Analysis Program. INPUT. August 1983.
TABOL Database Manager (TDM), an enhancement to the TABOL financial analysis language, was also introduced in August 1982
- ^ «Package of Features Added to Mark III». Computerworld. IDG Enterprise: 46. 30 August 1982.
- ^ portal.acm.org – APLDOT
- ^ «PC World– Three Minutes: Godfathers of the Spreadsheet». Archived from the original on 2008-07-26. Retrieved 2008-02-22.
- ^ Power, D.J., A Brief History of Spreadsheets Archived 2021-05-06 at the Wayback Machine, DSSResources.COM, v3.6, 8 August 2004
- ^ «Killer Applications» (overview), Partha gawaargupta. Arizona State University in Tempe, Arizona, May 2002, Web page: ASU-killer-app Archived 2011-09-29 at the Wayback Machine.
- ^ Brand, Stewart (1989). Whole Earth Software Catalog. ISBN 9780385233019.
Some say that half of all IBM PCs, in their hundreds of thousands, are running just 1-2-3. Numbers— clever, quick, knowledgeable— boiling the stupidity out of countless business decisions. Interesting how essential the quickness is. It’s 1-2-3’s speed that put it on top.
- ^ Liebowitz, Stan; Margolis, Stephen (2001). «6». In Ellig, Jerome (ed.). Dynamic Competition and Public Policy: Technology, Innovation, and Antitrust Issues. Cambridge: Cambridge University Press. p. 171. ISBN 978-0-521-78250-0.
- ^ Vaughan-Nichols, Steven J. (15 May 2013). «Goodbye, Lotus 1-2-3». zdnet.com. CBS Interactive. Retrieved 24 July 2014.
- ^ «Computing History — Computing History Members».
- ^ «IBM 3270 Terminals Get Spreadsheet Package». Computerworld. November 22, 1982.
- ^ «Do Spreadsheets Mean Micros». Computerworld. December 6, 1982.
- ^ «Advertisement». Computerworld. June 20, 1983.
- ^ «Improv and PowerStep». Archived from the original on 2002-06-06. Retrieved 2010-08-20.
- ^ «THE EXECUTIVE COMPUTER – Lotus 1-2-3 Faces Up to the Upstarts – NYTimes.com». The New York Times. 13 March 1988.
- ^ «Linux Spreadsheets». hex.net. Archived from the original on 6 August 2002.
- ^ a b «Trapeze».
- ^ Kay, Alan; Goldstein, JL (September 1984). «Computer Software». Scientific American. 251 (3): 52–59. Bibcode:1984SciAm.251c..52K. doi:10.1038/scientificamerican0984-52. PMID 6390676. – Value Rule
- ^ Burnett, Margaret; Atwood, J.; Walpole Djang, R.; Reichwein, J.; Gottfried, H.; Yang, S. (March 2001). «Forms/3: A first-order visual language to explore the boundaries of the spreadsheet paradigm». Journal of Functional Programming. 11 (2): 155–206. doi:10.1017/S0956796800003828. S2CID 18730312.
- ^ Al-Mutawa, H. A.; Dietrich, J.; Marsland, S.; McCartin, C. (2014). «On the shape of circular dependencies in Java programs». 23rd Australian Software Engineering Conference. IEEE. pp. 48–57. doi:10.1109/ASWEC.2014.15. ISBN 978-1-4799-3149-1. S2CID 17570052.
- ^ «REPT function: Description, Usage, Syntax, Examples and Explanation October 26, 2021 — Excel Office». 25 February 2019.
- ^ Peter Hornsby. «Empowering Users to Create Their Software».
- ^ Peyton Jones, Simon; Burnett, Margaret; Blackwell, Alan (March 2003). «Improving the world’s most popular functional language: user-defined functions in Excel». Archived from the original on 2005-10-16.
- ^ Sarkar, Advait; Blackwell, Alan; Jamnik, Mateja; Spott, Martin (2014). Teach and Try: A simple interaction technique for exploratory data modelling by end users. 2014 IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC 2014). pp. 53–56. CiteSeerX 10.1.1.695.2025. doi:10.1109/VLHCC.2014.6883022. ISBN 978-1-4799-4035-6. S2CID 14845341.
- ^ Sarkar, A.; Jamnik, M.; Blackwell, A.F.; Spott, M. (2015-10-01). Interactive visual machine learning in spreadsheets. 2015 IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC). pp. 159–163. doi:10.1109/VLHCC.2015.7357211. ISBN 978-1-4673-7457-6. S2CID 17659755.
- ^ Haynes, John L. (Fall 1985). «Circuit Design with Lotus 1-2-3». BYTE. pp. 143–156. Retrieved 19 March 2016.
- ^ Sroka, J.; Panasiuk, A.; Stencel, K.; Tyszkiewicz, J. (2015-02-02). «Translating Relational Queries into Spreadsheets». IEEE Transactions on Knowledge and Data Engineering. 27 (8): 1041–4347. arXiv:1305.2103. doi:10.1109/TKDE.2015.2397440. S2CID 13415694.
- ^ Douglas Butler, «Why are spreadsheets so unfriendly?», The Fifth International Conference on Technology in Mathematics Teaching, August 2001 Archived 2022-01-28 at the Wayback Machine. Accessed 25 June 2014
- ^ «Spreadsheet Risk Management within UK Organisations». July 2011.
- ^ Powell, Stephen G.; Baker, Kenneth R.; Lawson, Barry (July–September 2009). «Errors in Operational spreadsheets» (PDF). Tuck School of Business at Dartmouth College. Retrieved 2022-02-06.
- ^ Richard E. Blaustein (November 2009). «Eliminating Spreadsheet Risks». Internal Auditor Magazine. Institute of Internal Auditors (IIA). Archived from the original on 2010-09-05. Retrieved 2010-05-10. unabridged version Archived 2011-01-18 at the Wayback Machine
- ^ Stephen Bullen, Rob Bovey & John Green (2009). Professional Excel Development (2nd ed.). Addison-Wesley. ISBN 978-0-321-50879-9.
- ^ Powell, Stephen G.; Baker, Kenneth R.; Lawson, Barry (2007-12-01). «A Critical Review of the Literature on Spreadsheet Errors». Tuck School of Business at Dartmouth College. Retrieved 2008-04-18.
- ^ a b c Max Henrion (2004-07-14). «What’s Wrong with Spreadsheets – and How to Fix them with Analytica» (PDF). Retrieved 2010-11-13.
- ^ a b Sam Savage (February 2010). «Weighing the Pros and Cons of Decision Technology in Spreadsheets». OR/MS Today. 24 (1). Retrieved 2010-11-13.
- ^ Philip Howard (2005-04-22). «Managing spreadsheets». IT-Directors.com. Archived from the original on 2006-03-16. Retrieved 2006-06-29.
- ^ Raymond R. Panko (January 2005). «What We Know About Spreadsheet Errors». Archived from the original on 2010-06-15. Retrieved 2006-09-22.
- ^ Is Excel Budgeting a Mistake? Archived 2010-08-03 at the Wayback Machine
Excel’s critics say that Excel is fundamentally unsuited for budgeting, forecasting, and other activities that involve collaboration or consolidation. Are they correct? - ^ http://www.cs.uiowa.edu/~jcryer/JSMTalk2001.pdf Archived 2009-01-26 at the Wayback Machine Problems With Using Microsoft Excel for Statistics
- ^ «Spreadsheet Addiction». burns-stat.com.
- ^ «Excel specifications and limits – Excel – Microsoft Office». Office.microsoft.com. Retrieved 2018-11-06.
- ^ «What’s the maximum number of rows and cells for a spreadsheet file? – OpenOffice.org Wiki». Wiki.services.openoffice.org. 2008-11-26. Archived from the original on 2009-05-04. Retrieved 2010-08-20.
- ^ Kelion, Leo (5 October 2020). «Excel: Why using Microsoft’s tool caused Covid-19 results to be lost». BBC News. Retrieved 20 April 2021.
- ^ «Spreadsheet Management: Not what you figured» (PDF). deloitte.com. Deloitte. 2009. Retrieved 24 July 2014.
- ^ «Excel spreadsheets in School budgeting – a cautionary tale (2001)». AccountingWEB. Archived from the original on 2007-10-07. Retrieved 2007-12-18.
- ^ «European Spreadsheet Risks Interest Group – spreadsheet risk management and solutions conference». eusprig.org.
- ^ «Spreadsheets and Capital Markets» (PDF). June 2009. Archived from the original (PDF) on 2011-06-04. Retrieved 2009-08-13.
- ^ «Excel Financial Model Auditing». Retrieved 20 February 2013.
- ^ Jonathan Glater (30 October 2003). «Fannie Mae Corrects Mistakes In Results». The New York Times. Retrieved 12 June 2012.
- ^ a b Financial Times (18 March 2013). «Finance groups lack spreadsheet controls». Financial Times. Archived from the original on 2022-12-10.
- ^ The Guardian (4 April 2013). «Spreadsheet risk and the threat of cyber attacks in finance». TheGuardian.com.
- ^ «They Said at First That They Hadn’t Made a Spreadsheet Error, When They Had’«. The Chronicle Of Higher Education. 24 April 2013.
External links[edit]
Look up spreadsheet in Wiktionary, the free dictionary.
- comp.apps.spreadsheets FAQ by Russell Schulz
- Extending the Concept of Spreadsheet by Jocelyn Paine
- Spreadsheet at Curlie
- Spreadsheet – Its First Computerization (1961–1964) by Richard Mattessich
- CICS history and introduction of IBM 3270 by Bob Yelavich
- Autoplan & Autotab article by Creative Karma
- Spreadsheets in Science Archived 2020-01-17 at the Wayback Machine
Обновлено: 15.04.2023
Одной из самых продуктивных идей в области компьютерных информационных технологий стала идея электронной таблицы. Многие фирмы разработчики программного обеспечения для ПК создали свои версии табличных процессоров, предназначенных для работы с электронными таблицами.
Цель нашего урока — Получить представление об электронных таблицах, как о классе прикладных программ для ПК. Научиться применять к ним ранее усвоенные приёмы работы с прикладными программами в графическом интерфейсе .
Я предлагаю посмотреть фрагмент видеоролика «Различные расчеты в повседневной жизни» , чтобы ответить на вопрос:
Повторим тему нашего урока: » Что такое электронная таблица «
Из истории: Первая электронная таблица Vizicalc (визуальный компьютер) была создана в 1979 г. Д. Бриклином и Р. Фреэнкстоном , которые на компьютере Apple II создали первую программу электронных таблиц и она получила название VisiCalc от Visible Calculator (наглядный калькулятор). Основная идея программы заключалась в том, чтобы в одни ячейки помещать числа, а в других задавать закон их математического преобразования.
Первыми, кто стал применять ЭТ, были экономисты, которые с восторгом приняли это новшество. Главное назначение ЭТ — выполнять различные расчёты. ЭТ позволяют автоматизировать труд некоторых специалистов: экономистов, бухгалтеров, работников отделов кадров, инженеров, продавцов, т.е. тех, кому приходится работать с таблицами и различными вычислительными расчётами.
Именно для работы с числовой информацией используют специальную программу, называемую электронной таблицей либо табличным процессором. В пакете прикладных программ Offiсe табличный процессор называется Microsoft Exсel. Разработаны различные версии данных программ, но основные приёмы работы остаются неизменными [ Источник 1].
Документ, созданный в электронной таблице, называется рабочей книгой . Каждая книга состоит из рабочих листов . Каждый лист состоит из 65 536 строк и 256 столбцов. Строки нумеруются целыми числами, а столбцы – буквами латинского алфавита. На пересечении столбца и строки располагается – ячейка .
Ч то такое электронная таблица, ч то о бщего и какие различия между таблицами на бумаге и электронными таблицами ?
Идея создания электронной таблицы возникла у студента Гарвардского университета (США) Дэна Бриклина (Dan Bricklin) в 1979 г. Выполняя скучные вычисления экономического характера с помощью бухгалтерской книги, он и его друг Боб Франкстон (Bob Frankston), который разбирался в программировании, разработали первую программу электронной таблицы, названную ими VisiCalc.
VisiCalc скоро стала одной из наиболее успешных программ. Первоначально она предназначалась для компьютеров типа Apple II, но потом была трансформирована для всех типов компьютеров. Многие считают, что резкое повышение продаж компьютеров типа Apple в то время и было связано с возможностью использования на них табличного процессора VisiCalc. В скоропоявившихся электронных таблицах-аналогах (например, SuperCalc) основные идеи VisiCalc были многократно усовершенствованы.
Новый существенный шаг в развитии электронных таблиц — появление в 1982 г. на рынке программных средств Lotus 1-2-3, Lotus был первым табличным процессором, интегрировавшим в своем составе, помимо обычных инструментов, графику и возможность работы с системами управления базами данных.
Поскольку Lotus был разработан для компьютеров типа IBM, он сделал для этой фирмы то же, что VisiCalc в свое время сделал для фирмы Apple. После разработки Lotus 1-2-3 компания Lotus в первый же год повышает свой объем продаж до 50 млн. дол. и становится самой большой независимой компанией — производителем программных средств. Успех компании Lotus привел к ужесточению конкуренции, вызванной появлением на рынке новых электронных таблиц, таких, как VP Planner компании Paperback Software и Quattro Pro компании Borland International, которые предложили пользователю практически тот же набор инструментария, но по значительно более низким ценам.
Следующий шаг — появление в 1987 г. табличного процессора Excel фирмы Microsoft. Эта программа предложила более простой графический интерфейс в комбинации с ниспадающими меню, значительно расширив при этом функциональные возможности пакета и повысив качество выходной информации. Расширение спектра функциональных возможностей электронной таблицы, как правило, ведет к усложнению работы с программой.
Разработчикам Excel удалось найти золотую середину, максимально облегчив пользователю освоение программы и работу с ней. Благодаря этому Excel быстро завоевала популярность среди широкого круга пользователей. В настоящее время, несмотря на выпуск компанией Lotus новой версии электронной таблицы, в которой использована трехмерная таблица с улучшенными возможностями, Excel занимает ведущее место на рынке табличных процессоров.
Имеющиеся сегодня на рынке табличные процессоры способны работать в широком круге экономических приложений и могут удовлетворить практически любого пользователя.
Табличный процессор — категория программного обеспечения, предназначенного для работы с электронными таблицами. Изначально табличные редакторы позволяли обрабатывать исключительно двухмерные таблицы, прежде всего с числовыми данными, но затем появились продукты, обладавшие помимо этого возможностью включать текстовые, графические и другие мультимедийные элементы. Инструментарий электронных таблиц включает мощные математические функции, позволяющие вести сложные статистические, финансовые и прочие расчеты.
Электронные таблицы (или табличные процессоры) — это прикладные программы, предназначенные для проведения табличных расчетов. Появление электронных таблиц исторически совпадает с началом распространения персональных компьютеров. Первая программа для работы с электронными таблицами — табличный процессор, была создана в 1979 году, предназначалась для компьютеров типа Apple II и называлась VisiCalc. В 1982 году появляется знаменитый табличный процессор Lotus 1-2-3, предназначенный для IBM PC. Lotus объединял в себе вычислительные возможности электронных таблиц, деловую графику и функции реляционной СУБД. Популярность табличных процессоров росла очень быстро. Появлялись новые программные продукты этого класса: Multiplan, Quattro Pro, SuperCalc и другие. Одним из самых популярных табличных процессоров сегодня является MS Excel, входящий в состав пакета Microsoft Office.
Что же такое электронная таблица? Это средство информационных технологий, позволяющее решать целый комплекс задач: Прежде всего, выполнение вычислений. Издавна многие расчеты выполняются в табличной форме, особенно в области делопроизводства: многочисленные расчетные ведомости, табуляграммы, сметы расходов и т. п. Кроме того, решение численными методами целого ряда математических задач; удобно выполнять в табличной форме. Электронные таблицы представляют собой удобный инструмент для автоматизации таких вычислений. Решения многих вычислительных задач на ЭВМ, которые раньше можно было осуществить только путем программирования, стало возможно реализовать Математическое моделирование. Использование математических формул в ЭТ позволяет представить взаимосвязь между различными параметрами некоторой реальной системы. Основное свойство ЭТ — мгновенный пересчет формул при изменении значений входящих в них операндов. Благодаря этому свойству, таблица представляет собой удобный инструмент для организации численного эксперимента:
- подбор параметров,
- прогноз поведения моделируемой системы,
- анализ зависимостей,
- планирование.
Дополнительные удобства для моделирования дает возможность графического представления данных (диаграммы); Использование электронной таблицы в качестве базы данных. Конечно, по сравнению с СУБД электронные таблицы имеют меньшие возможности в этой области. Однако некоторые операции манипулирования данными, свойственные реляционным СУБД, в них реализованы. Это поиск информации по заданным условиям и сортировка информации.
В электронных таблицах предусмотрен также графический режим работы, который дает возможность графического представления (в виде графиков, диаграмм) числовой информации, содержащейся в таблице.
Основные типы данных: числа, как в обычном, так и экспоненциальном формате, текст – последовательность символов, состоящая из букв, цифр и пробелов, формулы. Формулы должны начинаться со знака равенства, и могут включать в себя числа, имена ячеек, функции (математические, статистические, финансовые, текстовые, дата и время и т.д.) и знаки математических операций.
Электронные таблицы просты в обращении, быстро осваиваются непрофессиональными пользователями компьютера и во много раз упрощают и ускоряют работу бухгалтеров, экономистов, ученых.
Основные элементы электронных таблиц:
- Столбец,
- Заголовки столбцов,
- Строка,
- Заголовки строк,
- Неактивная ячейка,
- Активная ячейка.
История
Найди готовую курсовую работу выполненное домашнее задание решённую задачу готовую лабораторную работу написанный реферат подготовленный доклад готовую ВКР готовую диссертацию готовую НИР готовый отчёт по практике готовые ответы полные лекции полные семинары заполненную рабочую тетрадь подготовленную презентацию переведённый текст написанное изложение написанное сочинение готовую статью
Частица массой находится в одномерном потенциальном поле в стационарном состоянии, описываемом волновой функцией , где и — постоянные ( ). Найдите энергию частицы и вид функции , если .
Квантовый гармонический осциллятор находится в основном состоянии. Найдите вероятность обнаружения частицы в области , где — амплитуда классических колебаний.
Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками, имеющими ширину . В каких точках интервала плотность вероятности обнаружения частицы одинакова для основного и второго возбуждённого состояний?
Частица массой находится в кубической потенциальной яме с абсолютно непроницаемыми стенками. Найдите длину ребра куба, если разность энергий 6-ого и 5-ого уровней равна . Чему равна кратность вырождения 6-ого и 5-ого уровней?
Частица массой находится в основном состоянии в двумерной квадратной потенциальной яме с бесконечно высокими стенками. Найдите энергию частицы, если максимальное значение плотности вероятности местонахождения частицы равно .
Частица находится в двумерной квадратной потенциальной яме с бесконечно высокими стенками во втором возбуждённом состоянии. Сторона ямы равна а. Определите вероятность нахождения частицы в области: а) ; б) ; в) .
Частица находится в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками. Координаты x и y частицы лежат в пределах 0 50 руб.
Волновая функция основного состояния электрона в атоме водорода имеет вид , где — расстояние электрона до ядра, — первый радиус боровской орбиты. Определите наиболее вероятное расстояние электрона от ядра.
Пользуясь решением задачи о гармоническом осцилляторе, найдите энергетический спектр частицы массой в потенциальной яме вида Здесь , а — собственная частота гармонического осциллятора.
Оцените с помощью соотношения неопределённостей Гейзенберга неопределённость скорости электрона в атоме водорода, полагая размер атома . Сравните полученную величину со скоростью электрона на первой боровской орбите.
Оцените относительную ширину спектральной линии, если известны время жизни атома в возбуждённом состоянии и длина волны излучаемого фотона .
Найти плотность сепарированной нефти 1-го горизонта при температуре 64 оС, если плотность ее при 20 оС равна 854 кг/м3, и нефти 2-го горизонта при 82 оС, если плотность ее при 20 оС равна 886 кг/м3.
При прохождении нефтегазовой смеси через штуцер в сепараторе образуются капли нефти диаметром 65 мкм. Смесь находится под давлением 0,4 МПа при 305 К. Найти скорость осаждения капель нефти и определить пропускную способность вертикального гравитацион
На дожимной насосной станции (ДНС) в сепараторе первой ступени поддерживают давление 0,4 МПа. Длина сборного коллектора, идущего от АГЗУ до ДНС, 12 км и (внутренний) диаметр его 0,3 м, разность геодезических отметок 10 м. Сборный коллектор горизонтал
Рассчитать основные параметры процесса освоения скважины, методом замены жидкости, выбрать промывочную жидкость и необходимое оборудование. Составить схему размещения оборудования при освоении скважины. Скважина заполнена буровым раствором плотностью
14.1. ОСНОВНЫЕ ПОНЯТИЯ
ИСТОРИЯ ПОЯВЛЕНИЯ И РАЗВИТИЯ ЭЛЕКТРОННОЙ ТАБЛИЦЫ
Идея создания электронной таблицы возникла у студента Гарвардского университета (США) Дэна Бриклина (Dan Bricklin) в 1979 г. Выполняя скучные вычисления экономического характера с помощью бухгалтерской книги, он и его друг Боб Франкстон (Bob Frankston), который разбирался в программировании, разработали первую программу электронной таблицы, названную ими VisiCalc.
VisiCalc скоро стала одной из наиболее успешных программ. Первоначально она предназначалась для компьютеров типа Apple П, но потом была трансформирована для всех типов компьютеров. Многие считают, что резкое повышение продаж компьютеров типа Apple в то время и было связано с возможностью использования на них табличного процессора VisiCalc. В скоро появившихся электронных таблицах-аналогах (например, SuperCalc) основные идеи VisiCalc были многократно усовершенствованы.
Новый существенный шаг в развитии электронных таблиц — появление в 1982 г. на рынке программных средств Lotus 1-2-3. Lotus был первым табличным процессором, интегрировавшим в своем составе, помимо обычных инструментов, графику и возможность работы с системами управления базами данных. Поскольку Lotus был разработан для компьютеров типа IBM, он сделал для этой фирмы то же, что VisiCalc в свое время сделал для фирмы Apple. После разработки Lotus 1-2-3 компания Lotus в первый же год повышает свой объем продаж до 50 млн. дол. и становится самой большой независимой компанией — производителем программных средств. Успех компании Lotus привел к ужесточению конкуренции, вызванной появлением на рынке новых электронных таблиц, таких, как VP Planner компании Paperback Software и Quattro Pro компании Borland International, которые предложили пользователю практически тот же набор инструментария, но по значительно более низким ценам.
Следующий шаг — появление в 1987 г. табличного процессора Excel фирмы Microsoft, Эта программа предложила более простой графический интерфейс в комбинации с ниспадающими меню, значительно расширив при этом функциональные возможности пакета и повысив качество выходной информации. Расширение спектра функциональных возможностей электронной таблицы, как правило, ведет к усложнению работы с программой.
Разработчикам Excel удалось найти золотую середину, максимально облегчив пользователю освоение программы и работу с ней. Благодаря этому Excel быстро завоевала популярность среди широкого круга пользователей. В настоящее время, несмотря на выпуск компанией Lotus новой версии электронной таблицы, в которой использована трехмерная таблица с улучшенными возможностями, Excel занимает ведущее место на рынке табличных процессоров.
Имеющиеся сегодня на рынке табличные процессоры способны работать в широком круге экономических приложений и могут удовлетворить практически любого пользователя.
Читайте также:
- Почему в российских школах нет черлидинга
- Как можно заразиться дизентерией кратко
- Что такое плацебо в медицине при коронавирусе простыми словами определение кратко
- Кто такой часовой кратко
- Что такое рогатка кратко
14.1. ОСНОВНЫЕ ПОНЯТИЯ
ИСТОРИЯ ПОЯВЛЕНИЯ И РАЗВИТИЯ ЭЛЕКТРОННОЙ ТАБЛИЦЫ
Идея создания электронной таблицы возникла у студента Гарвардского университета (США) Дэна Бриклина (Dan Bricklin) в 1979 г. Выполняя скучные вычисления экономического характера с помощью бухгалтерской книги, он и его друг Боб Франкстон (Bob Frankston), который разбирался в программировании, разработали первую программу электронной таблицы, названную ими VisiCalc.
VisiCalc скоро стала одной из наиболее успешных программ. Первоначально она предназначалась для компьютеров типа Apple П, но потом была трансформирована для всех типов компьютеров. Многие считают, что резкое повышение продаж компьютеров типа Apple в то время и было связано с возможностью использования на них табличного процессора VisiCalc. В скоро появившихся электронных таблицах-аналогах (например, SuperCalc) основные идеи VisiCalc были многократно усовершенствованы.
Новый существенный шаг в развитии электронных таблиц — появление в 1982 г. на рынке программных средств Lotus 1-2-3. Lotus был первым табличным процессором, интегрировавшим в своем составе, помимо обычных инструментов, графику и возможность работы с системами управления базами данных. Поскольку Lotus был разработан для компьютеров типа IBM, он сделал для этой фирмы то же, что VisiCalc в свое время сделал для фирмы Apple. После разработки Lotus 1-2-3 компания Lotus в первый же год повышает свой объем продаж до 50 млн. дол. и становится самой большой независимой компанией — производителем программных средств. Успех компании Lotus привел к ужесточению конкуренции, вызванной появлением на рынке новых электронных таблиц, таких, как VP Planner компании Paperback Software и Quattro Pro компании Borland International, которые предложили пользователю практически тот же набор инструментария, но по значительно более низким ценам.
Следующий шаг — появление в 1987 г. табличного процессора Excel фирмы Microsoft, Эта программа предложила более простой графический интерфейс в комбинации с ниспадающими меню, значительно расширив при этом функциональные возможности пакета и повысив качество выходной информации. Расширение спектра функциональных возможностей электронной таблицы, как правило, ведет к усложнению работы с программой.
Разработчикам Excel удалось найти золотую середину, максимально облегчив пользователю освоение программы и работу с ней. Благодаря этому Excel быстро завоевала популярность среди широкого круга пользователей. В настоящее время, несмотря на выпуск компанией Lotus новой версии электронной таблицы, в которой использована трехмерная таблица с улучшенными возможностями, Excel занимает ведущее место на рынке табличных процессоров.
Имеющиеся сегодня на рынке табличные процессоры способны работать в широком круге экономических приложений и могут удовлетворить практически любого пользователя.
ИНТЕРФЕЙС ТАБЛИЧНОГО ПРОЦЕССОРА
Рекомендуемые материалы
Что такое электронная таблица
Электронная таблица — компьютерный эквивалент обычной таблицы, в клетках (ячейках) которой записаны данные различных типов: тексты, даты, формулы, числа.
Результат вычисления формулы в клетке является изображением этой клетки. Числовые данные и даты могут рассматриваться как частный случай формул. Для управления электронной таблицей используется специальный комплекс программ — табличный процессор.
Главное достоинство электронной таблицы — это возможность мгновенного пересчета всех данных, связанных формульными зависимостями при изменении значения любого операнда.
Строки, столбцы, ячейки и их адреса
Рабочая область электронной таблицы состоит из строк и столбцов, имеющих свой имена. Имена строк — это их номера. Нумерация строк начинается с 1 и заканчивается максимальным числом, установленным для данной программы. Имена столбцов — это буквы латинского алфавита сначала от А до Z , затем от АА до AZ , ВА до BZ и т. д.
Максимальное количество строк и столбцов определяется особенностями используемой программы и объемом памяти компьютера. Современные программы дают возможность создавать электронные таблицы, содержащие более 1 млн. ячеек, хотя для практических целей в большинстве случаев этого не требуется.
Пересечение строки и столбца образует ячейку таблицы, имеющую свой уникальный адрес. Для указания адресов ячеек в формулах используются ссылки (например, А2 или С4).
Ячейка — область, определяемая пересечением столбца и строки электронной таблицы.
Адрес ячейки определяется названием (номером) столбца и номером строки. Ссылка — способ (формат) указания адреса ячейки.
Указание блока ячеек
В электронной таблице существует понятие блока (диапазона) ячеек, также имеющего свой уникальный адрес. В качестве блока ячеек может рассматриваться строка или часть строки, столбец или часть столбца, а также прямоугольник, состоящий из нескольких строк и столбцов или их частей (рис. 14.1). Адрес блока ячеек задается указанием ссылок первой и последней его ячеек, между которыми, например, ставится разделительный символ — двоеточие <:> или две точки подряд <..>.
Пример 14.1.
• Адрес ячейки, образованной на пересечении столбца G и строки 3, будет выражаться ссылкой G3.
• Адрес блока, образованного в виде части строки 1, будет А1..Н1.
• Адрес блока, образованный в виде столбца В, будет В1..В10.
• Адрес блока, образованный в виде прямоугольника, будет D4..F5.
Каждая команда электронной таблицы требует указания блока (диапазона) ячеек, в отношении которых она должна быть выполнена.
Блок используемых ячеек может быть указан двумя путями: либо непосредственным набором с клавиатуры начального и конечного адресов ячеек, формирующих диапазон, либо выделением соответствующей части таблицы при помощи клавиш управления курсором. Удобнее задавать диапазон выделением ячеек.
Типичными установками, принимаемыми по умолчанию на уровне всех ячеек таблицы, являются: ширина ячейки в 9 разрядов, левое выравнивание для символьных данных и основной формат для цифровых данных с выравниванием вправо.
Блок ячеек — группа последовательных ячеек. Блок ячеек может состоять из одной ячейки, строки (или ее части), столбца (или его части), а также последовательности строк или столбцов (или их частей).
Типовая структура интерфейса
Как видно на рис. 14.1, при работе с электронной таблицей на экран выводятся рабочее поле таблицы и панель управления. Панель управления обычно включает: Главное меню, вспомогательную область управления, строку ввода и строку подсказки. Расположение этих областей на экране может быть произвольным и зависит от особенностей конкретного табличного процессора.
Рис. 14.1. Вид электронной таблицы на экране
Строка главного меню содержит имена меню основных режимов программы. Выбрав один из них, пользователь получает доступ к ниспадающему меню, содержащему перечень входящих в него команд. После выбора некоторых команд ниспадающего меню появляются дополнительные подменю.
Вспомогательная область управления включает:
• строку состояния;
• панели инструментов;
• вертикальную и горизонтальную линейки прокрутки.
В строке состояния (статусной строке) пользователь найдет сведения о текущем режиме работы программы, имени файла текущей электронной таблицы, номере текущего окна и т.п. Панель инструментов (пиктографическое меню) содержит определенное количество кнопок (пиктограмм), предназначенных для быстрой активизации выполнения определенных команд меню и функций программы. Чтобы вызвать на экран те области таблицы, которые на нем в настоящий момент не отображены, используются вертикальная и горизонтальная линейки прокрутки. Бегунки (движки) линеек прокрутки показывают относительную позицию активной ячейки в таблице и используются для быстрого перемещения по ней. В некоторых табличных процессорах на экране образуются специальные зоны быстрого вызова. При щелчке мыши в такой зоне вызывается соответствующая функция. Например, при щелчке мыши на координатной линейке вызывается диалог задания параметров страницы.
Строка ввода отображает вводимые в ячейку данные. В ней пользователь может просматривать или редактировать содержимое текущей ячейки. Особенность строки ввода — возможность видеть содержащуюся в текущей ячейке формулу или функцию, а не ее результат. Строку ввода удобно использовать для просмотра или редактирования текстовых данных.
Строка подсказки предназначена для выдачи сообщений пользователю относительно его возможных действий в данный момент.
Приведенная структура интерфейса является типичной для табличных процессоров, предназначенных для работы в среде Windows. Для табличных процессоров, работающих в DOS, чаще всего отсутствуют командные кнопки панелей инструментов и линейки прокрутки.
Рабочее поле — пространство электронной таблицы, состоящее из ячеек, названий столбцов и строк.
Панель управления — часть экрана, дающая пользователю информацию об активной ячейке и ее содержимом, меню и режиме работы.
Текущая ячейка и экран
Текущей (активной) называется ячейка электронной таблицы, в которой в данный момент находится курсор. Адрес и содержимое текущей ячейки выводятся в строке ввода электронной таблицы. Перемещение курсора как по строке ввода, так и по экрану осуществляется при помощи клавиш движения курсора.
Возможности экрана монитора не позволяют показать всю электронную таблицу. Мы можем рассматривать различные части электронной таблицы, перемещаясь по ней при помощи клавиш управления курсором. При таком перемещении по таблице новые строки (столбцы) автоматически появляются на экране взамен тех, от которых мы уходим. Часть электронной таблицы, которую мы видим на экране монитора, называется текущим (активным) экраном.
Окно, рабочая книга, лист
Основные объекты обработки информации — электронные таблицы — размещаются табличным процессором в самостоятельных окнах, и открытие или закрытие этих таблиц есть,
по сути, открытие или закрытие окон, в которых они размещены. Табличный процессор дает возможность открывать одновременно множество окон, организуя тем самым «многооконный режим» работы. Существуют специальные команды , позволяющие изменять взаимное расположение и размеры окон на экране. Окна, которые в настоящий момент мы видим на экране, называются текущими (активными).
Рабочая книга представляет собой документ, содержащий несколько листов, в которые могут входить таблицы, диаграммы или макросы. Вы можете создать книгу для совместного хранения в памяти интересующих вас листов и указать, какое количество листов она должна содержать. Все листы рабочей книги сохраняются в одном файле. Заметим, что термин «рабочая книга» не является стандартным. Так, например, табличный процессор Framework вместо него использует понятие Frame (рамка).
ДАННЫЕ, ХРАНИМЫЕ В ЯЧЕЙКАХ ЭЛЕКТРОННОЙ ТАБЛИЦЫ
Типы входных данных
В каждую ячейку пользователь может ввести данные одного из следующих возможных видов: символьные, числовые, формулы и функции, а также даты.
• Символьные (текстовые) данные имеют описательный характер. Они могут включать в себя алфавитные, числовые и специальные символы. В качестве их первого символа часто используется апостроф, а иногда — кавычки или пробел.
Пример 14.2. Символьные данные:
‘ Ведомость по начислению премии
‘ Группа №142
• Числовые данные не могут содержать алфавитных и специальных символов, поскольку с ними производятся математические операции. Единственными исключениями являются десятичная точка (запятая) и знак числа, стоящий перед ним.
Пример 14.3. Числовые данные:
100 -135
123.32 .435
• Формулы. Видимое на экране содержимое ячейки, возможно, — результат вычислений, произведенных по имеющейся, но не видимой в ней формуле. Формула может включать ряд арифметических, логических и прочих действий, производимых с данными из других ячеек.
Пример 14.4. Предположим, что в ячейке находится формула +В5 + ( С5 + 2 * Е5) / 4. В обычном режиме отображения таблицы на экране вы увидите не формулу, а результат вычислений по ней над числами, содержащимися в ячейках В5, С5 и Е5.
• Функции. Функция представляет собой программу с уникальным именем, для которой пользователь должен задать конкретные значения аргументов функции, стоящих в скобках после ее имени. Функцию (так же, как и число) можно считать частным случаем формулы. Различают статистические, логические, финансовые и другие функции.
Пример 14.5. Ячейка содержит функцию вычисления среднего арифметического значения множества чисел, находящихся в ячейках В4, В5, В6, В8, в следующем виде:
@AVG (В4 .. В6, В8).
• Даты. Особым типом входных данных являются даты. Этот тип данных обеспечивает выполнение таких функций, как добавление к дате числа (пересчет даты вперед и назад) или вычисление разности двух дат (длительности периода). Даты имеют внутренний (например, дата может выражаться количеством дней от начала 1900 года или порядковым номером дня по Юлианскому календарю) и внешний формат. Внешний формат используется для ввода и отображения дат. Наиболее употребительны следующие типы внешних форматов дат:
– ДЦ-МММ-ГГ (04-Янв-95);
– МММ-ДЦ-ГГ (Янв-04-95);
– ДЦ-МММ (04-Янв);
– МММ-ГГ (Янв-95).
Внимание! Тип входных данных, содержащихся в каждой ячейке, определяется первым символом, который должен трактоваться не как часть данных, а как команда переключения режима:
• если в ячейке содержатся числа, то первый их символ является либо цифрой, либо десятичной точкой, либо знаком числа (плюсом или минусом);
• если в ячейке содержится формула, то первый ее символ должен быть выбран определенным образом в соответствии со спецификой конкретного табличного процессора. Для этого часто используются левая круглая скобка, знак числа (плюс или минус), знак равенства и т. п.;
• ячейка, содержащая функцию, всегда использует в качестве первого специальный символ @ ;
• если ячейка содержит символьные данные, ее первым символом может быть одинарная (апостроф) или двойная кавычка, а также пробел.
Форматирование числовых данных в ячейках
Вы можете использовать различные форматы представления числовых данных в рамках одной и той же электронной таблицы. По умолчанию числа располагаются в клетке, выравниваясь по правому краю. В некоторых электронных таблицах предусмотрено изменение этого правила. Рассмотрим наиболее распространенные форматы представления числовых данных.
• Основной формат используется по умолчанию, обеспечивая запись числовых данных в ячейках в том же виде, как они вводятся или вычисляются.
• Формат с фиксированным количеством десятичных знаков обеспечивает представление чисел в ячейках с заданной точностью, определяемой установленным пользователем количеством десятичных знаков после запятой (десятичной точки). Например, если установлен режим форматирования, включающий два десятичных знака, то вводимое в ячейку число 12345 будет записано как 12345.00, а число 0.12345 — как.12.
• Процентный формат обеспечивает представление введенных данных в форме процентов со знаком % (в соответствии с установленным количеством десятичных знаков). Например, если установлена точность в один десятичный знак, то при вводе 0.123 на экране появится 12.3%, а при вводе 123 — 12300.0%.
• Денежный формат обеспечивает такое представление чисел, где каждые три разряда разделены запятой. При этом пользователем может быть установлена определенная точность представления (с округлением до целого числа или в два десятичных знака). Например, введенное число 12345 будет записано в ячейке как 12,345 (с округлением до целого числа) и 12,345.00 (с точностью до двух десятичных знаков).
• Научный формат, используемый для представления очень больших или очень маленьких чисел, обеспечивает представление вводимых чисел в виде двух компонентов:
– мантиссы, имеющей один десятичный разряд слева от десятичной точки, и некоторого (определяемого точностью, заданной пользователем) количества десятичных знаков справа от нее;
– порядка числа.
Пример 14.6. Введенное число 12345 будет записано в ячейке как 1.2345Е +04 (если установленная точность составляет 4 разряда) и как 1.23Е +04 (при точности в 2 разряда). Число .0000012 в научном формате будет иметь вид 1.2Е -06.
Форматирование символьных данных в ячейках
По умолчанию символьные данные выравниваются по левому краю ячейки. Вы можете изменить формат представления символьных данных в электронной таблице. Для этого существуют следующие возможности.
• Выравнивание к левому краю ячейки располагает первый символ вводимых вами данных в крайней левой позиции ячейки. Для многих программ этот режим используется по умолчанию как основной.
• Выравнивание к правому краю ячейки располагает последний символ вводимых в ячейку данных в ее крайней правой позиции.
• Выравнивание по центру ячейки располагает вводимые данные по центру ячейки.
Форматирование данных — выбор формы представления числовых или символьных данных в ячейке.’
Изменение ширины колонки
Отображение числовых данных зависит не только от выбранного формата, но также и от ширины колонки (ячейки), в которой эти данные располагаются. Ширина колонки при текстовом режиме экрана устанавливается в знаках, а при графическом режиме экрана — в независимых единицах. Количество знаков в ячейке зависит от ее ширины, кегля, гарнитуры, а также от конкретного текста. Так, например, не составляет проблемы расположить число 12345 в формате с запятой без дробной части в ячейке шириной в 9 знаков. Однако вы не сможете его расположить там в денежном формате с двумя десятичными знаками, поскольку число $12,345.00 занимает 10 разрядов, превышая тем самым ширину ячейки. В данном случае необходимо изменить используемый формат представления числа либо увеличить ширину колонки.
Внимание! Если ширина вводимого числа превышает ширину ячейки (колонки), ячейка заполняется звездочками, сигнализирующими о том, что ширина ячейки недостаточна для отображения данных.
Формулы
Вычисления в таблицах производятся с помощью формул. Результат вычисления помещается в ячейку, в которой находится формула.
Формула начинается со знака плюс или левой круглой скобки и представляет собой совокупность математических операторов, чисел, ссылок и функций.
При вычислениях с помощью формул соблюдается принятый в математике порядок выполнения арифметических операций.
Формулы состоят из операторов и операндов, расположенных в определенном порядке. В качестве операндов используются данные, а также ссылки отдельных ячеек или блоков ячеек. Операторы в формулах обозначают действия, производимые с операндами. В зависимости от используемых операторов различают арифметические (алгебраические) и логические формулы.
В арифметических формулах используются следующие операторы арифметических действий:
+ сложение,
— вычитание,
* умножение,
/ деление,
^ возведение в степень.
Каждая формула в электронной таблице содержит несколько арифметических действий с ее компонентами. Установлена последовательность выполнения арифметических операций. Сначала выполняется возведение в степень, затем — умножение и деление и только после этого — вычитание и сложение. Если вы выбираете между операциями одного уровня (например, между умножением и делением), то следует выполнять их слева направо. Нормальный .порядок выполнения операций изменяют введением скобок. Операции в скобках выполняются первыми.
Арифметические формулы могут также содержать операторы сравнения: равно (=), не равно (< >), больше (>), меньше (<), не более (<=), не менее (>=). Результатом вычисления арифметической формулы является число.
Логические формулы могут содержать указанные операторы сравнения, а также специальные логические операторы:
#NOT# — логическое отрицание «НЕ»,
#AND# — логическое «И»,
#OR# — логическое «ИЛИ».
Логические формулы определяют, выражение истинно или ложно. Истинным выражениям присваивается численная величина 1, а ложным — 0. Таким образом, вычисление логической формулы заканчивается получением оценки «Истинно» (1) или «Ложно» (0).
Пример 14.7. Приведем несколько примеров вычисления арифметических и логических формул по следующим данным:
|
А |
В |
С |
|
|
1 |
3 |
5 |
2 |
|
2 |
3 |
12 |
1 |
|
3 |
4 |
7 |
6 |
Формула Результат Объяснение
=А1+В1*3 18 Содержимое ячейки В1 умножается на 3, и результат складывается с содержимым
ячейки А1. (Умножение выполняется первым).
=А2-ВЗ+С2 -3 Содержимое ячейки ВЗ вычитается из содержимого ячейки А2, а затем к
результату добавляется содержимое ячейки С2. (Сложение и вычитание как
действия одного уровня выполняются слева направо).
=В2/(С1*А2) 2 Содержимое ячейки С1 умножается на содержимое А2, и затем содержимое
ячейки В2 делится на полученный результат. (Любые действия в скобках
выполняются первыми).
=В1^С1-В2/АЗ 22 Содержимое ячейки В1 возводится в степень, определяемую содержимым ячейки
С1, затем определяется частное от деления содержимого ячейки В2 на
содержимое ячейки A3 . Полученное частное вычитается из первого результата.
(Возведение в степень выполняется первым, затем выполняется деление и только
потом — вычитание).
=A1>0#OR#C3X) 1 Поскольку содержимое ячеек А! (3>0) и СЗ (6>0) представляет собой
положительные числа, всему выражению присваивается численная величина 1
(«Истинно»).
По умолчанию электронная таблица вычисляет формулы при их вводе, пересчитывает их повторно при каждом изменении входящих в них исходных данных. Формулы могут включать функции.
Функции
Под функцией понимают зависимость одной переменной (у) от одной (*) или нескольких переменных (х1, х2, …, хп). Причем каждому набору значений переменных х1, х2, …, хп будет соответствовать единственное значение определенного типа зависимой переменной у. Функции вводят в таблицу в составе формул либо отдельно. В электронных таблицах могут быть представлены следующие виды функций:
математические;
статистические;
текстовые;
логические;
финансовые;
функции даты и времени и др.
Математические функции выполняют различные математические операции, например, вычисление логарифмов, тригонометрических функций, преобразование радиан в градусы и т. п.
Статистические функции выполняют операции по вычислению параметров случайных величин или их распределений, представленных множеством чисел, например, стандартного отклонения, среднего значения, медианы и т. п.
Текстовые функции выполняют операции над текстовыми строками или последовательностью символов, вычисляя длину строки, преобразовывая заглавные буквы в строчные и т.п.
Логические функции используются для построения логических выражений, результат которых зависит от истинности проверяемого условия.
Финансовые функции используются в сложных финансовых расчетах, например определение нормы дисконта, размера ежемесячных выплат для погашения кредита, определение амортизационных отчислений и др.
Все функции имеют одинаковый формат записи и включают имя функции и находящийся в круглых скобках перечень аргументов, разделенных запятыми. Приведем примеры наиболее часто встречающихся функций.
Пример 14.8. SUM(Список) — статистическая функция определения суммы всех числовых значений в Списке. Список может состоять из адресов ячеек и блоков, а также числовых значений.
SUM(B5..E5)
SUM(A3..E3, 230)
АУЕКАОЕ(Список) — статистическая функция определения среднего арифметического значения всех перечисленных в Списке величин.
AVERAGE(5, 20,10, 5)
AVERAGE(B10..B13,B17)
МАХ(Список) — статистическая функция, результатом которой является максимальное значение в указанном Списке.
МАХ(ВЗ..В8,АЗ..А6)
IF(Условие, Истинно, Ложно) — логическая функция, проверяющая на истинность заданное логическое условие. Если условие выполняется, то результатом функции является значение аргумента «Истинно». Если условие не выполняется, то результатом функции становится значение аргумента «Ложно».
IF(B4<100, 100,200)
— если ячейка В4 содержит число меньше 100, то функции присваивается значение 100, если же это условие не выполняется (т.е. содержимое ячейки В4 больше или равно 100), функции присваивается значение 200.
АВТОМАТИЧЕСКОЕ ИЗМЕНЕНИЕ ОТНОСИТЕЛЬНЫХ ССЫЛОК ПРИ КОПИРОВАНИИ И ПЕРЕМЕЩЕНИИ ФОРМУЛ
Буфер промежуточного хранения
Важной особенностью многих электронных таблиц является буфер промежуточного хранения. Буфер используется при выполнении команд копирования и перемещения для временного хранения копируемых или перемещаемых данных, после которого они направляются по новому адресу. При удалении данных они также помещаются в буфер. Содержимое буфера сохраняется до тех пор, пока в него не будет записана новая порция данных.
Буфер промежуточного хранения — это область оперативной памяти, предоставляемая в распоряжение пользователя, при помощи которой он может перенести данные из одной части таблицы в другую, из одного окна (таблицы) в другое или из одного приложения Windows в другое.
Относительная и абсолютная адресация
При копировании или перемещении формулы в другое место таблицы необходимо организовать управление формированием адресов исходных данных. Поэтому в электронной таблице при написании формул наряду с введенным ранее понятием ссылки используются понятия относительной и абсолютной ссылок.
Абсолютная ссылка — это не изменяющийся при копировании и перемещении формулы адрес ячейки, содержащий исходное данное (операнд).
Для указания абсолютной адресации вводится символ $. Различают два типа абсолютной ссылки: полная и частичная.
• Полная абсолютная ссылка указывается, если при копировании или перемещении адрес клетки, содержащий исходное данное, не меняется. Для этого символ $ ставится перед наименованием столбца и номером строки.
Пример 14.9. $В$5; $D$12 — полные абсолютные ссылки.
• Частичная абсолютная ссылка указывается, если при копировании и перемещении не меняется номер строки или наименование столбца. При этом символ $ в первом случае ставится перед номером строки, а во втором — перед наименованием столбца.
Пример 14.10. В$5, D$12 — частичная абсолютная ссылка, не меняется номер строки; $В5, SD12 — частичная абсолютная ссылка, не меняется наименование столбца.
Относительная ссылка — это изменяющийся при копировании и перемещении формулы адрес ячейки, содержащий исходное данное (операнд). Изменение адреса происходит по правилу относительной ориентации клетки с исходной формулой и клеток с операндами.
Форма написания относительной ссылки совпадает с обычной записью.
Правило относительной ориентации клетки
Формула, где в качестве операндов используются ссылки ячеек, воспринимается системой как шаблон, а ссылки ячеек в таком шаблоне — как средство указания на местоположение ячеек с операндами относительно ячейки с формулой.
Рассмотрим правило относительной ориентации клетки на примере.
Пример 14.11. Клетка со ссылкой С2 содержит формулу-шаблон сложения двух чисел, находящихся в ячейках А1 и В4. Эти ссылки являются относительными и отражают ситуацию взаимного расположения исходных данных в ячейках А1 и В4 и результата вычисления по формуле в ячейке С2. По правилу относительной ориентации клеток ссылки исходных данных воспринимаются системой не сами по себе, а так, как они расположены относительно клетки С2: ссылка А1 указывает на клетку, которая смещена относительно клетки С2 на одну клетку вверх и на две клетки влево; ссылка В4 указывает на клетку, которая смещена относительно клетки С2 на две клетки вниз и одну клетку влево.
Копирование формул
Другой особенностью электронных таблиц является возможность автоматического изменения ссылок при копировании и перемещении формул.
Копирование содержимого одной ячейки (блока ячеек) в другую (блок ячеек) производится для упрощения ввода однотипных данных и формул. При этом осуществляется автоматическая настройка относительных ссылок операндов. Для запрета автоматической настройки адресов используют абсолютные ссылки ячеек.
Исходная формула, подлежащая копированию или перемещению, воспринимается как некий шаблон, где указывается местоположение входных данных относительно местоположения клетки с формулой.
Копируемую формулу назовем формулой-оригиналом. Скопированную формулу — формулой-копией. При копировании формул действует правило относительной ориентации клеток. Поэтому после окончания копирования относительное расположение клеток, содержащих формулу-копию и исходные данные (заданные относительными ссылками), остается таким же, как в формуле-оригинале. Поясним на примере.
Пример 14.12. На рис. 14.2 мы видим результат копирования формулы, содержащейся в ячейке A3, при использовании относительных, полностью абсолютных и частично абсолютных ссылок. При копировании формулы с использованием относительных ссылок происходит их автоматическая подстройка (рис.14.2о). Результаты копирования с использованием абсолютных ссылок со знаком $ приведены на рис. 14.26. Как нетрудно заметить, применение абсолютных ссылок запрещает автоматическую настройку адресов, и копируемая формула сохраняет свой первоначальный вид. В приведенном на рис. 14.2в примере для запрещения автоматической подстройки адресов используются смешанные ссылки.
Рис. 14.2. Копирование формул: а — с относительными ссылками; б — с абсолютными ссылками; в — с частично абсолютными ссылками
Автоматическое изменение ссылок происходит не только при копировании субъекта (т.е. формул, содержащих ссылки), но и при перемещении объекта (т.е. ячейки, на которую имеются ссылки в других местах).
Перемещение формул
В электронной таблице часто перемещают данные из одной ячейки (диапазона ячеек) в другую заданную ячейку (блок ячеек). После перемещения данных исходная ячейка окажется пустой. Это главное отличие перемещения от процесса копирования, в котором копируемая ячейка сохраняет свои данные. Перемещение формул также связано с автоматической подстройкой входящих в нее адресов операндов. При перемещении формул, так же как при их копировании, действует правило относительной ориентации клеток. Поэтому после перемещения относительное расположение клеток, содержащих перемещенную формулу и исходные данные (заданные относительными адресами), сохраняется таким же, как в формуле-оригинале.
Обратите внимание на лекцию «11 — Мочеполовая система».
Пример 14.13. На рис. 14.3а мы видим перемещение содержимого отдельной ячейки A3 в ячейку СЗ. В этом случае содержимое исходной ячейки, не изменяясь, перемещается в ячейку назначения, а исходная ячейка остается пустой. Рис. 14.36 иллюстрирует случай перемещения содержимого трех ячеек Al, A2 и A3. При этом ячейки взаимосвязаны — содержимое третьей ячейки включает в себя содержимое первых двух. После перемещения мы видим, что в результате автоматической подстройки ссылок содержащаяся в ячейке A3 формула изменилась, чтобы отразить произошедшие в электронной таблице изменения (теперь компоненты содержащейся в ячейке СЗ суммы находятся в других ячейках). Так же как и в предыдущем случае диапазон исходных ячеек после выполнения операции перемещения опустел.
На рис. Н.Зв мы видим перемещение содержимого ячейки A3 в ячейку СЗ, когда адрес переносимой ячейки входит в другую формулу. Это случай перемещения зависимых ячеек. Например, имеется дополнительная ячейка В1, содержимое которой зависит от содержимого перемещаемой ячейки A3. В данном случае содержимое перемещаемой ячейки не изменяется, но изменяется содержимое зависимой ячейки В1 (хотя она не перемещается). Автоматическая подстройка адресов и в данном случае отразит изменения в электронной таблице так, чтобы результат формулы, содержащейся в ячейке В1, не изменился.
Последний случай, не рассмотренный на рис. 14.3, связан с возможностью использования абсолютных адресов. Нетрудно заметить, что использование абсолютных адресов при выполнении команды перемещения не имеет смысла, поскольку над ними также выполняется автоматическая подстройка адресов для отражения изменений, происходящих в таблице.
Рис. 14.3. Перемещение содержимого ячеек: а — одной ячейки; б — колонки; в — зависимых ячеек
В целом команда перемещения является непростой командой, и вам следует хорошо подумать, прежде чем перемещать формулы и функции, содержащие ссылки. При перемещении символьных данных никаких трудностей не возникает.