Цель урока: продолжить формирование
навыков работы с электронными таблицами.
Задачи:
- обучающие: формировать умения создания,
редактирования, форматирования и выполнения
простейших вычислений в электронных таблицах. - развивающие: расширить представления
учащихся о возможных сферах применения
электронных таблиц; развивать навыки
аналитического мышления, речи и внимания. - воспитательные: формировать и воспитывать
познавательный интерес; прививать навыки
самостоятельности в работе.
План урока.
- Организационный момент.
- Актуализация знаний учащихся.
- Проверка домашнего задания.
- Решение задач.
- Самостоятельное решение задачи.
- Подведение итогов. Оценки.
- Домашнее задание.
Ход урока
1. Организационный момент.
Сообщить тему урока, сформулировать цели и
задачи урока.
Сегодня мы вновь окажемся в гостях у маленького
великана Васи в Сказочной стране. Ему, как всегда,
требуется ваша помощь, ребята.
Сможете ли вы помочь Васе? Сейчас проверим!
2. Актуализация знаний учащихся.
1) Устно ответить на вопросы.
| A | B | C | D | |
| 1 | 2 | 1 | =A1+3*B1 | =A1^2+B1 |
| 2 | 4 | 6 | =A2+3*B2 | =A2^2+B2 |
- Что такое электронная таблица?
- Какие основные элементы электронной таблицы
вам известны? - Как задается имя ячейки (строки, столбца) в
электронной таблице? - Что может быть содержимым ячейки?
- Число 1 находится в столбце …, в строке …, в
ячейке с адресом … - Число 4 находится в ячейке с адресом …
- Каковы правила записи формул в ячейках?
- Чему равно значение, вычисляемое по формуле, в
ячейке С1? - Чему равно значение, вычисляемое по формуле, в
ячейке D2?
2) Какой результат будет получен в ячейках с
формулами?
| А | В | |
| 1 | 25 | 4 |
| 2 | 2 | =A1*B1/2 |
| 3 |
Ответ: 25*4/2=50
| A | B | C | D | |
| 1 | 5 | 2 | 1 | |
| 2 | 6 | 8 | 3 | |
| 3 | 8 | 3 | 4 | |
| 4 | =СУММ(B1:D3) |
- Что означает запись =СУММ(В1:D3)?
- Сколько элементов содержит блок В1:D3? Ответ: 9.
- Содержимое ячейки D3? Ответ: 5+2+1+6+8+3+8+3+4= 40
3) Проверка домашнего задания
Результаты соревнований по плаванию
Один ученик рассказывает, как он выполнил
домашнее задание (через проектор).
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3.23 | 3.44 | 3.30 | |||
| 2 | Моржов | 3.21 | 3.22 | 3.24 | |||
| 3 | Акулов | 3.17 | 3.16 | 3.18 | |||
| 4 | Рыбин | 3.24 | 3.20 | 3.18 | |||
| 5 | Черепахин | 3.56 | 3.44 | 3.52 | |||
| Лучший результат соревнований |
|||||||
| Среднее время участников соревнований |
|||||||
| Максимальное отклонение |
- Среднее время для каждого спортсмена находится
как среднее арифметическое трех его заплывов. - В ячейку «Лучшее время» записывается
минимальный результат из 3 заплывов. - В ячейку «Лучший результат соревнований»
записывается минимальное время из столбца. - В столбец «Отклонение» записывается
разность между лучшим временем спортсмена и
лучшим результатом соревнований. - В ячейку «Максимальное отклонение»
записывается максимальное значение столбца.
| Результаты соревнований по плаванию |
|||||||
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3,23 | 3,44 | 3,30 | 3,23 | 3,32 | 0,07 |
| 2 | Моржов | 3,21 | 3,22 | 3,24 | 3,21 | 3,22 | 0,05 |
| 3 | Акулов | 3,17 | 3,16 | 3,18 | 3,16 | 3,17 | 0,00 |
| 4 | Рыбин | 3,24 | 3,20 | 3,18 | 3,18 | 3,21 | 0,02 |
| 5 | Черепахин | 3,56 | 3,44 | 3,52 | 3,44 | 3,51 | 0,28 |
| Лучший результат соревнований |
3,16 | ||||||
| Среднее время участников соревнований |
3,29 | ||||||
| Максимальное отклонение | 0,28 |
4) Решение простых задач.
Маленький великан Вася решил отремонтировать
забор вокруг своего огорода и вскопать его под
посадку овощей (наступила очередная весна),
разметить грядки прямоугольной формы. Для работы
ему потребовалось найти длину забора и площадь
участка. Но ведь в школе он никогда не учился.
Поможем Васе.
№ 1. Вычислить периметр и площадь
прямоугольника со сторонами:
а) 3 и 5; б) 6 и 8; в) 10 и 7.
Эту задачу обсуждаем совместно с детьми:
- Как оформить таблицу?
- Какие формулы использовать?
- Как использовать уже записанные формулы для
следующего прямоугольника?
Оформление таблицы – на доске и в тетрадях.
В то же время другой ученик самостоятельно
решает следующую задачу и представляет свое
решение учащимся (через проектор).
№ 2. Маленький великан Вася решил
подсчитать, через сколько дней в его копилке
будет 100 руб., если ежедневно он стал класть туда
на 5 руб. больше, чем в предыдущий день. Помогите
Васе. Сейчас в его копилке 2,02 руб.
Обсудив решение задачи № 2, переходим к решению
следующей.
Один ученик показывает, как работать с
формулами, другой – как использовать функцию
суммирования, числовой формат (общий, денежный) и
т.д. (Таблица уже готова, ученикам предстоит
ввести формулы, использовать суммирование и
получить ответ).
№ 3. Посчитайте, используя ЭТ, хватит ли
Васе 150 рублей, чтобы купить все продукты, которые
ему заказала мама, и хватит ли на чипсы за 10
рублей? Сдачу мама разрешила положить в копилку.
Сколько рублей попадет в копилку?
Предполагаемое решение:
| № | Наименование | Цена в рублях | Количество | Стоимость |
| 1 | Хлеб | 9,6 | 2 | =C2*D2 |
| 2 | Кофе | 2,5 | 5 | =C3*D3 |
| 3 | Молоко | 13,8 | 2 | =C4*D4 |
| 4 | Пельмени | 51,3 | 1 | =C5*D5 |
|
Итого: |
=СУММ(E2:E5) | |||
| После покупок останется | =150-E6 | |||
| После покупки чипсов останется |
=D7-10 |
5) Самостоятельное решение задачи.
Маленький великан Вася часто бывал в гостях у
жителей Цветочного города.
Собираясь на пляж, веселые человечки решили
запастись прохладительными напитками. Незнайка
взял с собой 2 литра кваса, 1 литр газировки и 1
литр малинового сиропа, Пончик – 3 литра
газировки и 2 литра малинового сиропа, Торопыжка
– 2 литра газировки, доктор Пилюлькин – 1 литр
кваса и 1 литр касторки.
- Сколько литров напитков каждого вида взяли все
человечки вместе? - Сколько всего литров напитков взял с собой
каждый из человечков? - Сколько всего литров напитков взяли все
человечки вместе?
Оформите таблицу произвольно и сохраните в
своей личной папке.
Результат работы.
| Веселые человечки. Напитки. |
|||||
| Напиток | Незнайка | Пончик | Торопыжка | Пилюлькин | Всего |
| Квас, л | 2 | 0 | 0 | 1 | 3 |
| Газировка, л | 1 | 3 | 2 | 0 | 6 |
| Сироп, л | 1 | 2 | 0 | 0 | 9 |
| Касторка, л | 0 | 0 | 0 | 1 | 1 |
| ИТОГО: | 4 | 5 | 2 | 2 | 13 |
7) Подведение итогов. Оценки.

Подумайте и решите эту задачу, если известны
еще следующие величины.
Как изменится таблица? Какие формулы появятся?
Известно, что 1 литр кваса в Цветочном городе
стоит 1 монету, 1 литр газировки – 3 монеты, 1 литр
малинового сиропа – 6 монет, 1 литр касторки – 2
монеты.
- Сколько монет истратил на покупку напитков
каждый человечек? - Сколько монет затрачено на покупку напитков
каждого вида? - Сколько потрачено денег всеми человечками
вместе?
Литература
- Информатика. Задачник-практикум в 2 т. /Под ред.
И.Г.Семакина, Е.К.Хеннера – М.: Лаборатория
Базовых Знаний, 2010. - Ефимова О. Курс компьютерной технологии с
основами информатики. – М.: ООО “издательство
АСТ”; АВF, 2005.
Презентация
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
- Информация о материале
- Задачи по Excel
-
03 января 2017
Задание 1.
- Ввести исходные данные, оформить таблицу с помощью обрамления, добавить заголовок, расположив его по центру таблицы, шапку таблицы оформить заливкой. Для форматирования текста используйте Формат Ячейки/ Выравнивание.
- Добавить в таблицу дополнительные ячейки для внесения формул и получения результата.
- Функции, используемые при выполнении работы:
Математические:
- СУММ — сумма аргументов;
- ПРОИЗВЕД — произведение аргументов;
- СУММПРОИЗВ — сумма произведений соответствующих массивов.
Статистические:
- СРЗНАЧ — среднее арифметическое аргументов;
- МАКС — максимальное значение из списка аргументов;
- МИН — минимальное значение из списка аргументов;
- СЧЕТЕСЛИ — подсчитывает количество непустых ячеек в диапазоне, удовлетворяющих заданному условию.
- Заполнить таблицу (5-7 строк). Имеющиеся в шапке таблицы данные (года, месяцы, дни недели) заносить с помощью автозаполнения.
- Оформить таблицу с помощью обрамления, добавить заголовок, расположив его по центру таблицы. Шапку таблицы выполнить в цвете (шрифт и фон), полужирным шрифтом.
- Переименовать лист книги по смыслу введенной информации.
- Добавить в начало таблицы столбец «№ пп» и заполнить его автоматически.
- Выполнить соответствующие вычисления.
Найти:
- Максимальный прирост населения за пятилетие по каждому городу.
- Средний прирост населения за пятилетие по каждому городу.
- Общий прирост населения по всем городам за каждый год.
- Построить гистограмму прироста населения за каждый год.
Задание 2.
В формуле для расчета премии используется абсолютная ссылка на адрес ячейки, в которую введено значение процента премии.
| Ведомость начисления заработной платы за ________ 200_ г. | |||
| Процент премии: | 35% | ||
| Фамилия, И.О. | Заработная плата, руб. | Премия, руб. | Всего начислено, руб. |
| Прокопович А.Н. | 265000 | 92750 | 357750 |
| Маслов Н.П. | 361000 | 126350 | 487350 |
| Герасимов А.А. | 215200 | 75320 | 290520 |
| Смежинский П.П. | 290000 | 101500 | 391500 |
| Игнатьева Н.В. | 453000 | 158550 | 611550 |
| Климашевич Т.В. | 323000 | 113050 | 436050 |
| Итого: | 1907200 | 667520 | 2574720 |
Задание 3.
Пусть в ячейках A1,A2,A3 записаны три числа, задающих длины сторон треугольника.
В ячейке С1 написать формулу определения типа треугольника (равносторонний, равнобедренный, разносторонний). Использовать вложенные функции ЕСЛИ, И,. ИЛИ.
Задание 4.
- Создайте предложенною таблицу.
- Заполните 1-6 поле (столбец) 20-тью записями (строками). Для полей 5, 6 создайте проверку данных при вводе: они должны быть положительными. Выполните это с помощью верхнего меню Данные – Проверка данных.
- Поля 7-8 заполните с помощью Списков: Данные – Проверка данных– Параметры – Список. В поле Источник введите имя диапазона, который задайте сами: Вставка – Имя – Присвоить. Списки создайте на отдельном листе.
- Поле 9 заполните «+» (счетчик есть) и «-» (счётчика нет).
- Поле 10 заполните значениями с проверкой при вводе (см. п. 2).
- Поле 11 заполните с помощью функции ЕСЛИ:
- Поле 12 заполните с помощью функции ЕСЛИ:
- Поле 13 рассчитайте по формуле: Начислено * % льгот.
- Поле 14 рассчитайте по формуле: Начислено – льготы.
- С помощью Условного форматирования выполните автоматическую заливку ячеек поля 2 в зависимости от вида льгот (цвет выбрать самим).
- Установить Автофильтр для удобного просмотра данных таблицы: Данные – Фильтр – Автофильтр.
тариф по счётчику 5 руб./м3, без счётчика – 10 руб/м2.
Начислено (по счётчику) = показания счётчика * тариф;
Начислено (без счётчика) = отапливаемая площадь * количество проживающих * тариф.
Задание 5.
| Динамика экспорта России по основным статьям (млрд дол.) | |||
| Статьи экспорта | 2008. | 2009. | 2009. в % к 2008 |
| Нефть сырая | 6 825,5 | 8 193,0 | 20,0% |
| Нефтепродукты | 2 534,6 | 3 447,0 | 36,0% |
| Природный газ | 6 695,4 | 7 298,0 | 9,0% |
| Каменный уголь | 594,3 | 630,0 | 6,0% |
| Железные руды и концентраты | 193,1 | 247,0 | 27,9% |
| Минеральные удобрения | 826,6 | 495,0 | -40,1% |
| Чугун | 194,6 | 218,0 | 12,0% |
| Алюминий | 878,4 | 1 423,0 | 62,0% |
| Машины и оборудование | 3 720,8 | 2 865,0 | -23,0% |
| Всего | 22 463,3 | 24 816,0 | 10,5% |
| Среднее | 2 495,9 | 2 757,3 | 10,5% |
| Максимальное | 6 825,5 | 8 193,0 | 20,0% |
| Минимальное | 193,1 | 218,0 | 12,9% |
Рассчитать:
- Уровень экспорта 2009 года по сравнению с 2008 годом (в %);
- По каждому году общее, среднее, максимальное и минимальное значения экспорта.
Скачать примеры решения задач по Excel
Всем удачи!
Содержание
- Excel задания с решениями. Скачать примеры
- Задание 1
- Решение задания
- Задание 2
- Задачи по Excel
- Решение задач по Excel. Выпуск 4
- Решение задач по Excel. Выпуск 3
- Решение задач по Excel. Выпуск 2
- Решение задач по Excel. Выпуск 1
- Решение простых задач с помощью Excel
Excel задания с решениями. Скачать примеры
В этом уроке мы постараемся закрепить то, что прошли на предыдущих. Рассмотрим несколько заданий с примерами решения.
Задание 1
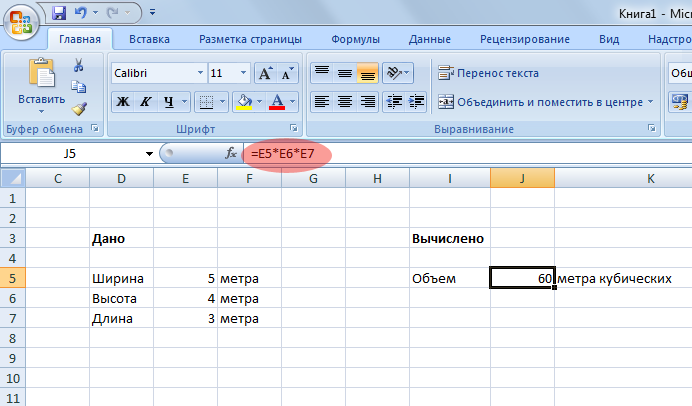
Ниже на рисунке изображена таблица автоматически вычисляющая объем прямоугольной канистры. Даны ее размеры. Это самое простое задание, с которого мы начнем. Для начала постарайтесь добиться решения самостоятельно.
Решение задания
Первое, что необходимо сделать это заполнить ячейки словами «дано», «ширина», «высота» и так далее. Обратите внимание на то, что слово «метра» я вписал один раз, а потом автозаполнением заполнил оставшиеся 2 ячейки. Для того, чтобы отформатировать текст (сделать жирным слова «дано» и «Вычислено» выберите ячейку и воспользуйтесь инструментом Ж (полужирный) на панели вверху в закладке Главная.
После того как вы создали внешний вид таблицы (т.е. вписали в ячейки все кроме цифр) переходим к решению самой задачи. У меня в примере ячейка J5 содержит формулу для вычисления объема. Сама по себе формула просто, чтобы вычислить объем прямоугольного параллелипипеда надо перемножить длины всех его 3 сторон.
В нашем примере значение ширины, высоты и длины содержится в ячейках E5, E6, E7. Как раз их нам надо и перемножить и результат записать в ячейку J5, для этого в ячейке J5 пишем формулу =E5*E6*E7. и жмем Enter.
Внимание! если вы не вписали значение ширины, высоты и длины, то там где будет ответ высветиться предупреждение об ошибки, чтобы оно исчезло просто введите значение сторон, чтобы компьютеру было, что ему перемножать.
Задание 2
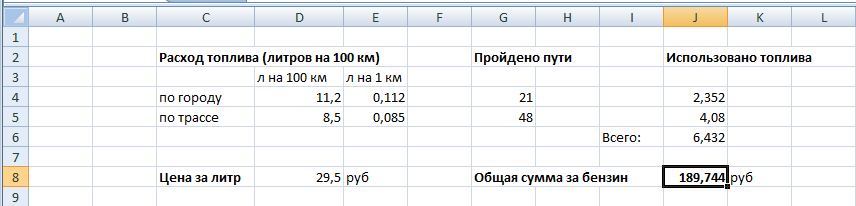
Это задание не чуть не сложнее, просто больше надо заполнять и больше ввести формул, если Вы все верно поняли в первом задании и разобрались, то решение этого задание в не составит особого труда
В этом задании все, что нам дано это количество расхода бензина на 100 км, пройденный путь и цена на топливо. Все остальное значения в ячейках программа Excel считает автоматически после того как будут введены формулы.
Скачать файл Еxcel с примером решения этой задачи.
Для тех кому понравился стиль объяснения и подробного описания рекомендую статью про выпадающие списки в экселе все так же подробно и понятно
Жми Привет! Если статья полезна, поддержи меня и сайт, поделись ей
Источник
Задачи по Excel
Решение задач по Excel. Выпуск 4
Задание 1.
- Ввести исходные данные, оформить таблицу с помощью обрамления, добавить заголовок, расположив его по центру таблицы, шапку таблицы оформить заливкой. Для форматирования текста используйте Формат Ячейки/ Выравнивание.
- Добавить в таблицу дополнительные ячейки для внесения формул и получения результата.
- Функции, используемые при выполнении работы:
Математические:
- СУММ — сумма аргументов;
- ПРОИЗВЕД — произведение аргументов;
- СУММПРОИЗВ — сумма произведений соответствующих массивов.
Статистические:
- СРЗНАЧ — среднее арифметическое аргументов;
- МАКС — максимальное значение из списка аргументов;
- МИН — минимальное значение из списка аргументов;
- СЧЕТЕСЛИ — подсчитывает количество непустых ячеек в диапазоне, удовлетворяющих заданному условию.
- Заполнить таблицу (5-7 строк). Имеющиеся в шапке таблицы данные (года, месяцы, дни недели) заносить с помощью автозаполнения.
- Оформить таблицу с помощью обрамления, добавить заголовок, расположив его по центру таблицы. Шапку таблицы выполнить в цвете (шрифт и фон), полужирным шрифтом.
- Переименовать лист книги по смыслу введенной информации.
- Добавить в начало таблицы столбец «№ пп» и заполнить его автоматически.
- Выполнить соответствующие вычисления.
Решение задач по Excel. Выпуск 3
1. Спланируйте расходы на бензин для ежедневных поездок из п. Половинка в г. Урай на автомобиле. Если известно:
- расстояние м/д населёнными пунктами в км. (30 км. в одну сторону)
- расход бензина (8 литров на 100 км.)
- количество поездок в месяц разное (т.к. разное количество рабочих дней.)
- цена 1 литра бензина ( n рублей за литр.)
- ежемесячный прогнозируемый рост цены на бензин — k% в месяц
Рассчитайте ежемесячный и годовой расход на бензин. Постройте график изменения цены бензина и график ежемесячных расходов.
2. Представьте, что вы директор ресторана. Общий месячный фонд заработной платы — 10000$. На совете акционеров было установлено, что:
- официант получает в 1,5 раза больше мойщика посуды;
- повар — в 3 раза больше мойщика посуды;
- шеф-повар — на 30$ больше.
Решение задач по Excel. Выпуск 2
1. Рассчитайте еженедельную выручку зоопарка, если известно:
- количество проданных билетов каждый день,
- цена взрослого билета — 15 руб,
- цена детского на 30% дешевле чем взрослого.
Постройте диаграмму (график) ежедневной выручки зоопарка.
2. Подготовьте бланк заказа для магазина, если известно:
- продукты (хлеб, мука, макаронные изделия и т.д., не менее 10 наименований)
- цена каждого продукта
- количество заказанного каждого продукта
Рассчитайте на какую сумму заказано продуктов. Усовершенствуйте бланк заказа, добавив скидку (например 10%), если стоимость купленных продуктов будет более 5000 руб. Постройте диаграмму (гистограмму) стоимости.
Решение задач по Excel. Выпуск 1
1. Найти решение уравнения вида kx + b = 0, где k, b — произвольные постоянные.
2. Сахарный тростник содержит 9% сахара. Сколько сахара будет получено из 20 тонн сахарного тростника?
3. Школьники должны были посадить 200 деревьев. Они перевыполнили план посадки на 23%. Сколько деревьев они посадили?
4. Из 50 кг. семян, собранных учениками, 17% составили семена клена, 15% — семена липы, 25% — семена акации, а стальное — семена дуба. Сколько килограмм.
Источник
Решение простых задач с помощью Excel
Классы: 6 , 7
Ключевые слова: Excel , функции в Excel , ячейка , адрес ячейки , таблица
Цель урока: продолжить формирование навыков работы с электронными таблицами.
Задачи:
- обучающие: формировать умения создания, редактирования, форматирования и выполнения простейших вычислений в электронных таблицах.
- развивающие: расширить представления учащихся о возможных сферах применения электронных таблиц; развивать навыки аналитического мышления, речи и внимания.
- воспитательные: формировать и воспитывать познавательный интерес; прививать навыки самостоятельности в работе.
План урока.
- Организационный момент.
- Актуализация знаний учащихся.
- Проверка домашнего задания.
- Решение задач.
- Самостоятельное решение задачи.
- Подведение итогов. Оценки.
- Домашнее задание.
1. Организационный момент.
Сообщить тему урока, сформулировать цели и задачи урока.
Сегодня мы вновь окажемся в гостях у маленького великана Васи в Сказочной стране. Ему, как всегда, требуется ваша помощь, ребята.
Сможете ли вы помочь Васе? Сейчас проверим!
2. Актуализация знаний учащихся.
1) Устно ответить на вопросы.
| A | B | C | D | |
| 1 | 2 | 1 | =A1+3*B1 | =A1^2+B1 |
| 2 | 4 | 6 | =A2+3*B2 | =A2^2+B2 |
- Что такое электронная таблица?
- Какие основные элементы электронной таблицы вам известны?
- Как задается имя ячейки (строки, столбца) в электронной таблице?
- Что может быть содержимым ячейки?
- Число 1 находится в столбце . в строке . в ячейке с адресом .
- Число 4 находится в ячейке с адресом .
- Каковы правила записи формул в ячейках?
- Чему равно значение, вычисляемое по формуле, в ячейке С1?
- Чему равно значение, вычисляемое по формуле, в ячейке D2?
2) Какой результат будет получен в ячейках с формулами?
| A | B | C | D |
| 1 | 5 | 2 | 1 |
| 2 | 6 | 8 | 3 |
| 3 | 8 | 3 | 4 |
| 4 | =СУММ(B1:D3) |
- Что означает запись =СУММ(В1:D3)?
- Сколько элементов содержит блок В1:D3? Ответ: 9.
- Содержимое ячейки D3? Ответ: 5+2+1+6+8+3+8+3+4= 40
3) Проверка домашнего задания
Результаты соревнований по плаванию
Один ученик рассказывает, как он выполнил домашнее задание (через проектор).
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3.23 | 3.44 | 3.30 | |||
| 2 | Моржов | 3.21 | 3.22 | 3.24 | |||
| 3 | Акулов | 3.17 | 3.16 | 3.18 | |||
| 4 | Рыбин | 3.24 | 3.20 | 3.18 | |||
| 5 | Черепахин | 3.56 | 3.44 | 3.52 | |||
| Лучший результат соревнований | |||||||
| Среднее время участников соревнований | |||||||
| Максимальное отклонение |
- Среднее время для каждого спортсмена находится как среднее арифметическое трех его заплывов.
- В ячейку «Лучшее время» записывается минимальный результат из 3 заплывов.
- В ячейку «Лучший результат соревнований» записывается минимальное время из столбца.
- В столбец «Отклонение» записывается разность между лучшим временем спортсмена и лучшим результатом соревнований.
- В ячейку «Максимальное отклонение» записывается максимальное значение столбца.
| Результаты соревнований по плаванию | |||||||
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3,23 | 3,44 | 3,30 | 3,23 | 3,32 | 0,07 |
| 2 | Моржов | 3,21 | 3,22 | 3,24 | 3,21 | 3,22 | 0,05 |
| 3 | Акулов | 3,17 | 3,16 | 3,18 | 3,16 | 3,17 | 0,00 |
| 4 | Рыбин | 3,24 | 3,20 | 3,18 | 3,18 | 3,21 | 0,02 |
| 5 | Черепахин | 3,56 | 3,44 | 3,52 | 3,44 | 3,51 | 0,28 |
| Лучший результат соревнований | 3,16 | ||||||
| Среднее время участников соревнований | 3,29 | ||||||
| Максимальное отклонение | 0,28 |
4) Решение простых задач.
Маленький великан Вася решил отремонтировать забор вокруг своего огорода и вскопать его под посадку овощей (наступила очередная весна), разметить грядки прямоугольной формы. Для работы ему потребовалось найти длину забора и площадь участка. Но ведь в школе он никогда не учился. Поможем Васе.
№ 1. Вычислить периметр и площадь прямоугольника со сторонами:
а) 3 и 5; б) 6 и 8; в) 10 и 7.
Эту задачу обсуждаем совместно с детьми:
- Как оформить таблицу?
- Какие формулы использовать?
- Как использовать уже записанные формулы для следующего прямоугольника?
Оформление таблицы – на доске и в тетрадях.
В то же время другой ученик самостоятельно решает следующую задачу и представляет свое решение учащимся (через проектор).
№ 2. Маленький великан Вася решил подсчитать, через сколько дней в его копилке будет 100 руб., если ежедневно он стал класть туда на 5 руб. больше, чем в предыдущий день. Помогите Васе. Сейчас в его копилке 2,02 руб.
Обсудив решение задачи № 2, переходим к решению следующей.
Один ученик показывает, как работать с формулами, другой – как использовать функцию суммирования, числовой формат (общий, денежный) и т.д. (Таблица уже готова, ученикам предстоит ввести формулы, использовать суммирование и получить ответ).
№ 3. Посчитайте, используя ЭТ, хватит ли Васе 150 рублей, чтобы купить все продукты, которые ему заказала мама, и хватит ли на чипсы за 10 рублей? Сдачу мама разрешила положить в копилку. Сколько рублей попадет в копилку?
Итого:
| № | Наименование | Цена в рублях | Количество | Стоимость |
| 1 | Хлеб | 9,6 | 2 | =C2*D2 |
| 2 | Кофе | 2,5 | 5 | =C3*D3 |
| 3 | Молоко | 13,8 | 2 | =C4*D4 |
| 4 | Пельмени | 51,3 | 1 | =C5*D5 |
| =СУММ(E2:E5) | ||||
| После покупок останется | =150-E6 | |||
| После покупки чипсов останется | =D7-10 |
5) Самостоятельное решение задачи.
Маленький великан Вася часто бывал в гостях у жителей Цветочного города.
Собираясь на пляж, веселые человечки решили запастись прохладительными напитками. Незнайка взял с собой 2 литра кваса, 1 литр газировки и 1 литр малинового сиропа, Пончик – 3 литра газировки и 2 литра малинового сиропа, Торопыжка – 2 литра газировки, доктор Пилюлькин – 1 литр кваса и 1 литр касторки.
- Сколько литров напитков каждого вида взяли все человечки вместе?
- Сколько всего литров напитков взял с собой каждый из человечков?
- Сколько всего литров напитков взяли все человечки вместе?
Оформите таблицу произвольно и сохраните в своей личной папке.
| Веселые человечки. Напитки. | |||||
| Напиток | Незнайка | Пончик | Торопыжка | Пилюлькин | Всего |
| Квас, л | 2 | 0 | 0 | 1 | 3 |
| Газировка, л | 1 | 3 | 2 | 0 | 6 |
| Сироп, л | 1 | 2 | 0 | 0 | 9 |
| Касторка, л | 0 | 0 | 0 | 1 | 1 |
| ИТОГО: | 4 | 5 | 2 | 2 | 13 |
7) Подведение итогов. Оценки.

Подумайте и решите эту задачу, если известны еще следующие величины.
Как изменится таблица? Какие формулы появятся?
Известно, что 1 литр кваса в Цветочном городе стоит 1 монету, 1 литр газировки – 3 монеты, 1 литр малинового сиропа – 6 монет, 1 литр касторки – 2 монеты.
- Сколько монет истратил на покупку напитков каждый человечек?
- Сколько монет затрачено на покупку напитков каждого вида?
- Сколько потрачено денег всеми человечками вместе?
Источник
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Содержание
- Транспортная задача: описание
- Подготовительный этап: включение функции “Поиск решения”
- Пример задачи и ее решение
- Условия
- Алгоритм решения
- Заключение
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
- Закрытая – совокупное предложение продавца равняется общему спросу.
- Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
- Открываем меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
- В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
- В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
- Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
- Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
- В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
- На экране отобразится окно, в котором нужно заполнить аргументы:
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
- по готовности жмем OK.
- Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
- На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
- Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
- В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
- Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
- Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
- В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
- С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
- Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
- Перед нами появится окно с параметрами функции:
- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
- Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.
- Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
- Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
- больше или равно нулю;
- целое число.
- В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
- В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
- Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.