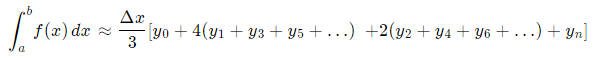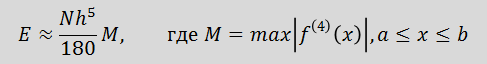30 сентября 2015
Давайте разберёмся, как вычислить определённый интеграл таблично заданной функции с помощью программы Excel из состава Microsoft Office.
Вам понадобится
- — компьютер с установленным приложением MS Excel;
- — таблично заданная функция.
Инструкция
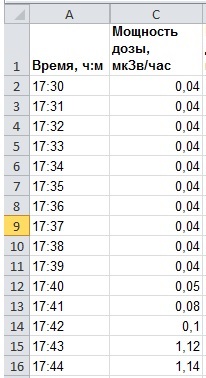
Допустим, у нас есть таблично заданная некоторая величина. Для примера пусть это будет накопленная доза радиации при авиаперелёте. Скажем, был такой эксперимент: человек с дозиметром летел на самолёте из пункта А в пункт Б и периодически измерял дозиметром мощность дозы (измеряется в микрозивертах в час). Вас, возможно, это удивит, но при обычном перелёте на самолёте человек получает дозу радиации в 10 раз больше, чем фоновый уровень. Но воздействие это кратковременное и поэтому не опасное. По результатам измерений у нас есть таблица вот такого формата: Время — Мощность дозы.
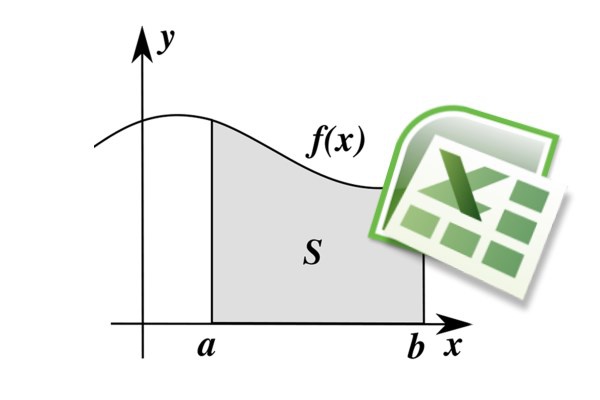
Суть метода в том, что определённый интеграл — это площадь под графиком нужной нам величины. В нашем примере, если полёт длился почти 2 часа, с 17:30 до 19:27 (см. рисунок), то чтобы найти накопленную дозу, нужно определить площадь фигуры под графиком мощности дозы — графиком таблично заданной величины.
Вычислять интеграл мы будем самым простым, но довольно точным методом — методом трапеций. Напомню, каждую кривую можно разделить на трапеции. Сумма площадей этих трапеций и будет искомым интегралом.
Площадь трапеции определяется просто: полусумма оснований, умноженная на высоту. Основания в нашем случае — это табличные измеренные значения мощности дозы за 2 последовательных промежутка времени, а высота — это разница времени между двумя измерениями.
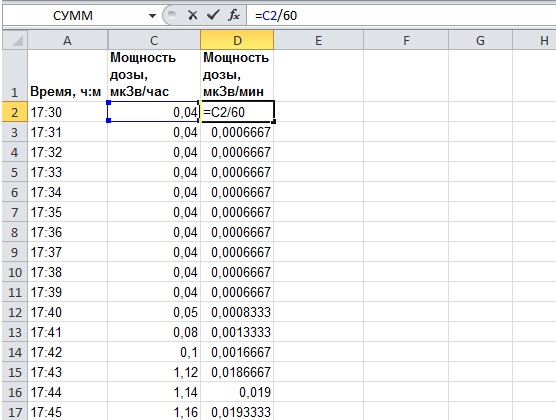
В нашем примере измерения мощности дозы радиации даётся в мкЗв/час. Переведём это в мкЗв/мин, т.к. данные даются с периодичностью 1 раз в минуту. Это нужно для согласования единиц измерения. Мы не можем брать интеграл по времени, измеряемому в минутах, от величины, измеряемой в часах.
Для перевода просто разделим мощность дозы в мкЗв/час построчно на 60. Добавим ещё один столбец в нашу таблицу. На иллюстрации в столбце «D» в строке 2 вписываем «=С2/60». А потом с помощью маркера заполнения (тянем мышью чёрный прямоугольник в правом нижнем углу ячейки) распространяем эту формулу на все остальные ячейки в столбце «D».
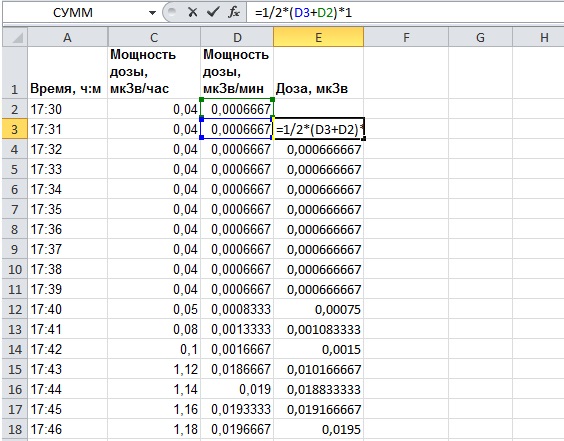
Теперь нужно найти площади трапеций за каждый промежуток времени. В столбце «E» будем вычислять по приведённой выше формуле площади трапеций.
Полусумма оснований — это половина суммы двух последовательных мощностей дозы из столбца «D». Так как данные идут с периодом 1 раз в минуту, а мы берём интеграл по времени, выраженному в минутах, то высота каждой трапеции будет равна единице (разница времени между каждыми двумя последовательными измерениями, например, 17ч31м — 17ч30м = 0ч1м).
Получаем формулу в ячейке «E3»: «=1/2*(D2+D3)*1». Понятно, что «*1» можно не писать, я сделал это просто для полноты картины. Рисунок поясняет всё более наглядно.
Аналогично, с помощью маркера заполнения, распространяем формулу на весь столбец. Теперь в каждой ячейке столбца «Е» посчитана накопленная доза за 1 минуту полёта.
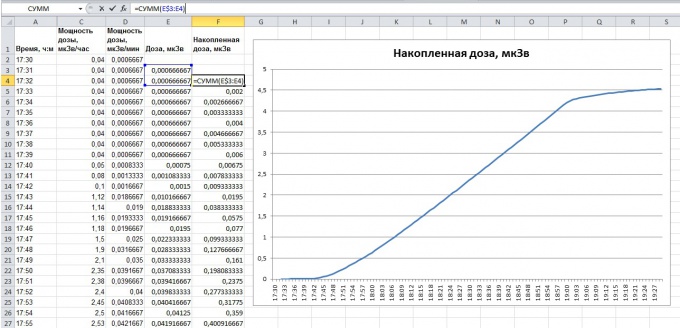
Осталось найти сумму вычисленных площадей трапеций. Можно в ячейке «F2» написать формулу «=СУММ(E:E)», это и будет искомым интегралом — сумма всех значений в столбце «E».
Можно сделать немного сложнее, чтобы определить накопленную дозу в разные моменты полёта. Для этого в ячейке «F4» впишем формулу: «=СУММ(E$3:E4)» и маркером заполнения распространим на весь столбец «F». Обозначение «E$3» говорит программе Excel, что менять индекс первой ячейки, от которой ведём счёт, не нужно.
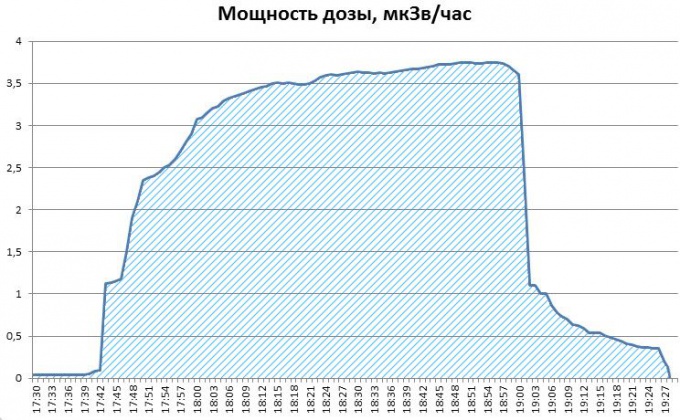
Построим график по столбцам «F» и «A», т.е. изменение накопленной дозы радиации во времени. Наглядно видно увеличение интеграла, как и должно быть, и окончательное значение накопленной за двухчасовой полёт дозы радиации равно примерно 4,5 микрозиверт.
Таким образом, мы только что нашли определённый интеграл таблично заданной функции в программе Excel на реальном физическом примере.
Давайте разберёмся, как вычислить определённый интеграл таблично заданной функции с помощью программы Excel из состава Microsoft Office.
1Постановка физической задачина расчёт определённого интеграла
Допустим, у нас есть таблично заданная некоторая величина. Для примера пусть это будет накопленная доза радиации при авиаперелёте. Скажем, был такой эксперимент: человек с дозиметром летел на самолёте из пункта А в пункт Б и периодически измерял дозиметром мощность дозы (единицы измерений – микрозиверт в час, мкЗв/ч). Возможно, Вас это удивит, но при обычном перелёте на самолёте человек попадает под радиоактивное излучение, превышающее фоновый уровень до 10 раз и даже больше. Но воздействие это кратковременное, и поэтому не столь опасное. По результатам измерений у нас есть таблица вот такого формата: Время – Мощность дозы.
Необходимо посчитать суммарную накопленную за время полёта дозу.
2Геометрический смыслопределённого интеграла
Как мы помним из курса школьной алгебры, определённый интеграл – это площадь под графиком измеряемой величины. Чтобы определить накопленную дозу радиации в рассматриваемом примере, нужно определить площадь фигуры под графиком таблично заданной мощности дозы. Накопленная доза радиации равна площади фигуры под графиком мощности дозы
3Методика вычисленияопределённого интеграла
Вычислять интеграл мы будем самым простым, но довольно точным методом – методом трапеций. Напомню, площадь фигуры под графиком любой кривой можно разделить на прямоугольные трапеции. Сумма площадей этих трапеций и будет искомым значением определённого интеграла.
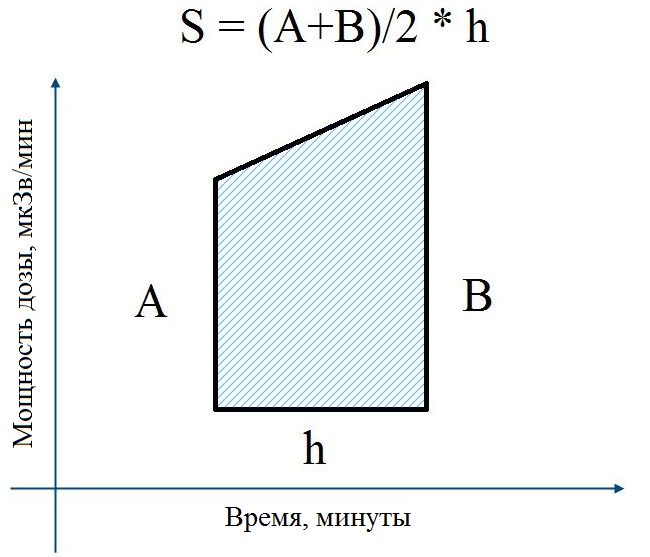
Площадь трапеции определяется как полусумма оснований, умноженная на высоту: Sтрап = (A + B) / 2 × h Основания в нашем случае – это табличные измеренные значения мощности дозы за 2 последовательных промежутка времени, а высота – это разница времени между двумя измерениями.
4Согласованиеединиц измерения
В нашем примере измерения мощности дозы радиации даётся в мкЗв/час, а шкала времени – с точностью до минут. Мы не можем брать интеграл по времени, измеряемому в минутах, для величины, измеряемой в часах. Поэтому необходимо перевести мкЗв/час в мкЗв/мин.
Для перевода просто разделим мощность дозы в мкЗв/час построчно на количество минут в часе, т.е. на 60. Добавим ещё один столбец в нашу таблицу. На иллюстрации это столбец «D». В столбце «D» в строке 2 вписываем =С2/60 А потом с помощью маркера заполнения распространяем эту формулу на все остальные ячейки в столбце «D», (т.е. тянем мышью чёрный прямоугольник в правом нижнем углу ячейки). Таким образом, в столбце «D» у нас появятся значения мощности дозы радиации, измеряемые в микрозивертах в минуту для каждой минуты перелёта.
5Вычисление площадей отдельных трапеций
Теперь нужно найти площади трапеций за каждый промежуток времени. В столбце «E» будем вычислять по приведённой выше формуле площади трапеций.
Полусумма оснований – это половина суммы двух последовательных мощностей дозы из столбца «D». Так как данные идут с периодом 1 раз в минуту, а мы берём интеграл по времени, выраженному в минутах, то высота каждой трапеции будет равна единице (разница времени между каждыми двумя последовательными измерениями, например, 17ч31мин — 17ч30мин = 0ч1мин = 1мин).
Получаем формулу в ячейке «E3»: =1/2*(D3+D2)*1. Понятно, что «×1» в этой формуле можно не писать. И аналогично, с помощью маркера заполнения, распространяем формулу на весь столбец. Теперь в каждой ячейке столбца «Е» посчитана накопленная доза за 1 минуту полёта.
Если бы данные шли не через 1 минуту, то нам нужно было бы написать формулу так:
=1/2*(D3+D2)*(МИНУТЫ(A3) – МИНУТЫ(A2)).
Правда при этом, если есть переход на следующий час, то получится отрицательное значение. Чтобы этого не произошло, впишем в формулу часы:
=1/2*(D3+D2)*(ЧАС(A3)*60+МИНУТЫ(A3)) – (ЧАС(A2)*60+МИНУТЫ(A2)).
Если переходим на следующие сутки, то нужно будет уже добавлять даты, и т.д.
5Определение площадипод графиком функции
Осталось найти сумму вычисленных площадей трапеций. Можно в ячейке «F2» написать формулу: =СУММ(E:E) Это и будет сумма всех значений в столбце «E», т.е. численное значение искомого определённого интеграла. Но давайте сделаем вот что: определим накопленную дозу в разные моменты полёта. Для этого в ячейку «F4» впишем формулу =СУММ(E$3:E4) и маркером заполнения распространим на весь столбец «F».
Обозначение E$3 говорит программе Excel, что увеличивать индекс ячейки «3» в столбце «E» при переносе формулы на следующие строки не нужно. Т.е. в строке 4 формула будет определять сумму в ячейках с «Е3» по «Е4», в строке 5 – сумму с «Е3» по «Е5», в строке 6 – с «Е3» по «Е6» и т.д.
Построим график по столбцам «F» и «A». Это график изменения накопленной дозы радиации во времени. Наглядно видно монотонное увеличение накопленной дозы радиации за время полёта. Это говорит о том, что мы правильно рассчитали интеграл. И окончательное значение накопленной за двухчасовой полёт дозы радиации, которое получается в последней ячейке этого столбца, равно примерно 4,5 микрозиверт.
Таким образом, мы только что нашли определённый интеграл таблично заданной функции в программе Excel на реальном физическом примере. В качестве приложения к статье – файл Excel с нашим примером.
history 27 ноября 2022 г.
- Группы статей
Вычислим в MS EXCEL определенный интеграл методом Симпсона (англ. Simpson’s rule). Покажем как оценить ошибку интегрирования, построим график функции.
Примечание: Основная статья про численное интегрирование — Интегрирование в MS EXCEL. Метод трапеций. В этой статье дана небольшая теория.
В данной статье используем тот же полином третьего порядка, что и в статье про Метод трапеций. Т.к. метод Симпсона использует параболу для аппроксимации подинтегральной функции, то при нахождении этим методом интеграла от полинома третьего порядка (и ниже) мы будем получать точное значение (это можно доказать строго математически). Т.е. ошибка интегрирования точно равна 0.
Построение модели
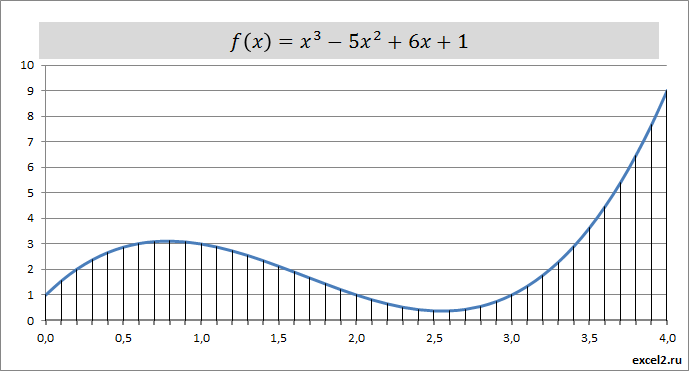
Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥3−5𝑥2+6𝑥+1. График этой функции в диапазоне от 0 до 4 выглядит следующим образом (см. файл примера).
Примечание: про тонкости построения графика функции можно прочитать в этой статье https://excel2.ru/articles/grafik-vs-tochechnaya-diagramma-v-ms-excel.
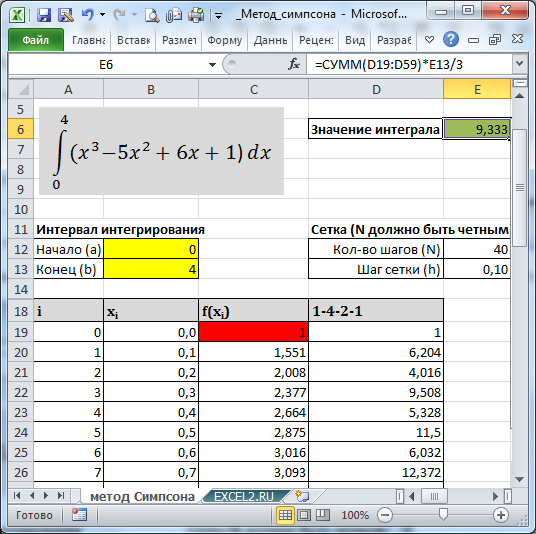
В файле примера построим таблицу значений функции для 41 точки (от 0 до 40), что составляет 40 интервалов (для метода Симпсона обязательно должно быть ЧЕТНОЕ количество интервалов).
Формула для вычисления интеграла Методом Симпсона следующая:
Примечание: В файле примера вместо Δх (шаг по х) будем использовать символ h, который используется в математических формулах численного интегрирования гораздо чаще, чем Δх. Хотя для первого знакомства, конечно, Δх является более знакомым обозначением шага изменения х.
Как видно из формулы, чтобы вычислить значение интеграла достаточно сложить значения y=f(x) в узлах сетки с определенным весом:
- Значения в узлах 0 и n, которые соответствуют пределам интегрирования а и b, берутся с весом 1;
- Значения в узлах с нечетным индексом берутся с весом 4;
- Значения в узлах с четным индексом берутся с весом 2.
В MS EXCEL вычислить веса по этому правилу можно с помощью простой формулы =ЕСЛИ(ИЛИ(A19=0;A19=$E$12);1; ЕСЛИ(ЕНЕЧЁТ(A19);4;2)). В файле примера это реализовано в столбце D (дополнительно вес домножен на соответствующее значение y).
В итоге, значение определенного интеграла, вычисленное по методу Симпсона, можно записать простой формулой =СУММ(D19:D59)*E13/3
Вычислив интеграл аналитически, можно убедиться, что полученное значение точно равно значению, вычисленного формулами (напомним, что это справедливо только для полиномов не выше третьего порядка).
Ошибка интегрирования
Формула для оценки ошибки интегрирования основана на вычислении 4-й (!) производной, что достаточно трудоемко и совсем не удобно для реализации в MS EXCEL.
После вычисления 4-й производной подинтегральной функции нужно найти ее максимум в интервале интегрирования, а затем подставить в вышеуказанную формулу. Понятно, что для полиномов не выше третьего порядка оценка будет равна 0, а значит точность метода Симпсона для таких функций выше чем Метод трапеций.
Для более сложных функций нахождение 4-й производной будет трудоемко, но к счастью есть много сайтов, которые помогут в этом вопросе, например https://www.derivative-calculator.net/
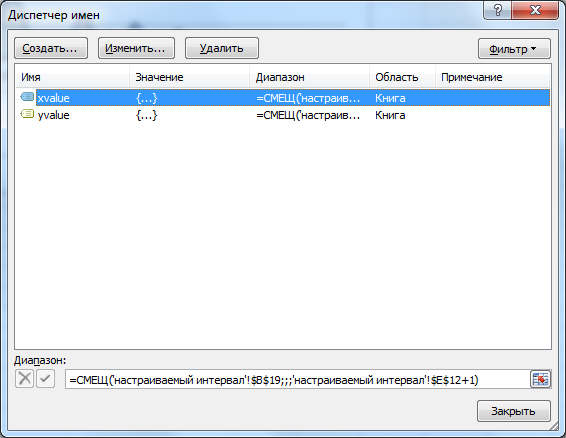
Настраиваемый интервал
На листе Настраиваемый интервал сделана удобная форма для вычисления интеграла при различных значениях шага интегрирования. График функции также перестраивается динамически благодаря использованию Имен и функции СМЕЩ().
Данная форма удобна когда необходимо ответить на вопрос «Какой шаг сетки нужно выбрать, чтобы точность интегрирования была не хуже заданному значению?». Правда, для этого потребуется вычислить 4-ю производную, найти максимум этой функции и, наконец, по формуле оценить ошибку.
Лирическое отступление
Зачем оценивать ошибку интегрирования? Можно ведь взять «маленький» шаг сетки и заведомо получить «точный» результат, и не важно что потребуется сделать 1000 или более шагов интегрирования, ведь вычислительные мощности так дешевы!
На этот счет есть 2 замечания: для больших интервалов интегрирования может потребоваться слишком много шагов и если вычисление интеграла лишь часть задачи, да еще и если оно находится в цикле, то это может замедлить работу программы. И второй момент: если мы не знаем ошибки, то как мы можем быть уверены, что вычисленное значение нам подходит? Например, мы вычисляем интеграл, чтобы получить значение, которое мы будем затем сравнивать с неким критерием. Если значение больше критерия, то мы принимаем одно решение, а если нет, то другое. Из-за недостаточной точности вычисления интеграла может случиться, что будет принято неверное решение, что соответственно приведет к некорректной работе программы (в определенной ситуации).
8 апреля 2022 г.
Интеграция является важным понятием в высшей математике и функцией, которую вы можете выполнять в программном обеспечении для работы с электронными таблицами Excel. Программное обеспечение для работы с электронными таблицами может помочь вам выполнять расширенные вычисления и свести к минимуму некоторые сложные шаги, которые вы могли бы предпринять при ручных вычислениях. Понимание того, как интегрировать в Excel, поможет вам быстрее и точнее вычислять числовое интегрирование. В этой статье мы дадим определение интеграции в Excel, рассмотрим семь простых шагов по интеграции и предложим несколько советов, как сделать процесс более эффективным и точным.
Интеграция в Excel — это математическая функция, которую можно использовать для расчета различных математических параметров, таких как площадь трапециевидного сечения под кривой в наборе данных. Excel предоставляет полезные математические инструменты, которые делают эти расчеты потенциально более точными и намного более быстрыми, чем расчеты вручную. Интеграция в исчислении — это концепция, которая помогает найти значение полной единицы, используя «срезы» или части целого. Это одно из двух основных понятий исчисления, второе — дифференцирование. В математике есть два типа интегралов, в том числе:
Определенные интегралы
Определенные интегралы представляют число только тогда, когда верхний и нижний пределы вычисления являются константами. Эти значения, представленные соответственно a и b, позволяют вычислить площадь интеграла с помощью функции f(x). Обычно формула выглядит так:
б
∫ f(x)dx
а
Неопределенные интегралы
Неопределенный интеграл не имеет указанных пределов, что вместо получения точной площади для интеграла возвращает функцию каждой независимой переменной и произвольной константы. Вы можете использовать неопределенные интегралы, чтобы найти первообразную функции. Например, если вы хотите узнать, от чего 2x является производной, вы можете использовать неопределенную интегральную функцию, чтобы найти ответ. Вот общая формула для неопределенных интегралов:
∫ f(x)dx=g(x)+c
Как интегрировать в Excel
Для интеграции в Excel вы можете импортировать большие наборы данных и создавать формулы, используя ячейки для определения ширины, высоты и площади ваших трапециевидных сечений под кривой данных. Это позволяет определить интеграл для каждого из них и рассчитать необходимую информацию. Вот семь шагов для интеграции в Excel:
1. Загрузите ваши данные в Excel
Загрузите все необходимые данные в электронную таблицу Excel. Вы можете перейти на вкладку «Главная» и нажать «Открыть», чтобы найти правильный путь к файлу. Кроме того, вы можете перейти к пути к файлу, щелкнуть правой кнопкой мыши файл, который хотите загрузить, нажать «открыть с помощью» и выбрать Excel в качестве своей программы. Импортируйте все свои данные в Excel одновременно и проверьте целостность, точность и полноту ваших наборов данных, прежде чем приступать к каким-либо математическим расчетам. Недостающая часть информации потенциально может изменить результат ваших расчетов.
2. При необходимости преобразуйте любые измерения
Некоторые наборы данных требуют преобразования в другие единицы измерения, чтобы Excel мог их соответствующим образом считывать. Например, вы можете использовать набор данных от транспортного средства, которое использует мили в час, что может потребовать преобразования в более простую функцию «скорости» в Excel. Рассмотрите каждую единицу измерения и убедитесь, что Excel может правильно считывать данные. Определите, нужны ли какие-либо преобразования, а затем примените эти преобразования.
3. Определите свои трапециевидные размеры
Когда вы измеряете трапеции под кривой данных, вы сначала устанавливаете параметры или размеры трапеции, которую хотите измерить. Это сообщает Excel, что именно вы измеряете, и ограничивает расчеты этими измерениями, позволяя вам быть более конкретными с данными, которые вы собираете. Вы можете выбрать все оси x и y вашего графика в качестве размеров или выбрать одну или несколько трапеций для конкретных измерений. Ось X обычно представляет столбец ширины, а ось Y представляет столбец высоты, который вы создаете на следующем шаге.
4. Создайте столбец ширины
В таблице данных, которую вы импортировали в Excel, перейдите в крайний правый угол таблицы, найдите пустой столбец и назовите этот столбец «шириной». Столбец ширины представляет данные по оси X.
Выберите ячейку непосредственно под ячейкой «Ширина» и введите «=ABS». Затем щелкните второе измерение в наборе данных, представляющее значения ширины, и нажмите клавишу тире. Щелкните первое измерение в наборе данных в том же столбце, затем введите закрывающую скобку. Ваша формула может выглядеть так: =ABS(A4-A3). Вы можете убедиться, что формула генерирует числовое значение, и снова щелкнуть первую ячейку в столбце ширины. Перетащите курсор вниз по столбцу, выделив все, кроме последней ячейки в столбце ширины. Убедитесь, что каждая ячейка заполнена числовыми значениями.
5. Создайте столбец высоты
Перейдите к следующему пустому столбцу в таблице данных рядом с созданным вами столбцом ширины. Здесь вы можете создать столбец высоты, который представляет любые измерения, назначенные вами в качестве значений высоты. В этом столбце вычисляются высоты ваших трапеций.
Выберите ячейку непосредственно под ячейкой высоты, которая пуста, и введите «= 0,5 *». Затем перейдите к первому измерению в таблице данных в любом столбце, который вы назначаете высоте, и щелкните первое измерение, чтобы выделить его. Затем нажмите клавишу «плюс» и щелкните второе измерение в том же столбце, нажмите клавишу ввода и закройте скобки. Убедитесь, что первая ячейка в столбце высоты генерирует числовое значение. Наконец, щелкните первую ячейку в столбце высоты и перетащите курсор вниз к ячейке непосредственно перед последней ячейкой.
6. Создайте столбец области
Определив ширину и высоту каждой трапеции, вы можете умножить их, чтобы вычислить площадь каждой из них. Создайте столбец площади рядом со столбцом высоты, чтобы создать числовые значения площади каждой трапеции.
Затем щелкните ячейку непосредственно под заголовком «область» и введите «=» в этой ячейке, затем щелкните первое значение в столбце ширины и нажмите клавишу «*». Это создаст формулу в вашей ячейке области, похожую на «=A1*». Щелкните первое значение в столбце высоты и нажмите клавишу ввода, чтобы сгенерировать числовое значение в ячейке площади. Щелкните первую ячейку в столбце области и перетащите курсор вниз по всему столбцу, остановившись перед последней ячейкой в столбце. Убедитесь, что каждая ячейка заполнена числовым значением площади.
7. Создайте интегральную колонку
Столбец интегралов позволяет вычислить интеграл каждой площади ваших трапеций. Создайте интегральный столбец непосредственно рядом со столбцом области и назовите его соответствующим образом. Затем создайте математическую функцию для измерения интеграции, щелкнув первую ячейку под заголовком интеграла и введя «=СУММ(». Затем щелкните первую ячейку в столбце области и перетащите курсор вниз по всему столбцу, пока не появится Вы выделили все значения площади. Нажмите клавишу ввода, чтобы сгенерировать числовое значение в столбце интегралов. Это и есть ваш интегральный ответ.
Советы по интеграции в Excel
Вот несколько советов по более плавной интеграции в Excel:
-
Проверьте целостность ваших данных. Для большей точности и ускорения вычислений проверьте целостность и точность набора данных перед началом вычислений. Вы можете просмотреть данные с коллегой или с аналогичным набором данных.
-
Проверьте свои функции. При использовании математических функций в Excel важно убедиться, что ваши функции точно соответствуют направлениям, чтобы они могли правильно вычислить ваши значения.
-
Исправьте ошибки перед дальнейшим расчетом. Если в ячейке появляются ошибки или отсутствующие числа, проверьте правильность функции и исправьте все ошибки, прежде чем вычислять дополнительные значения.
-
Используйте больше трапеций для более точных измерений. Для более точных измерений обычно требуется больше данных, что означает использование большего количества трапеций и получение большего количества значений площади, высоты и ширины для вычисления интеграла.
Обратите внимание, что ни одна из компаний, упомянутых в этой статье, не связана с компанией Indeed.
Нахождение интеграла и производной при помощи Excel
Раскрыть первое сообщение
Как вычислить интеграл в Excel?
Ниже приводится решение интегралов, а также нахождение производной в excel (численное интегрирование и дифференцирование)
Кому-то поможет на лабах
Нахождение производной
Нахождение интеграла
Скачать обе страницы в виде DJVU-файла (54 Кб): mat_task.djvu.zip
DySprozin (написано 12.11.2010 в 23:16)