Как возвести экспоненту в степень в excel

В этой статье описаны синтаксис формулы и использование функции EXP в Microsoft Excel.

Описание

Возвращает число e, возведенное в указанную степень. Число e равно 2,71828182845904 и является основанием натурального логарифма.

Синтаксис

EXP(число)

Аргументы функции EXP описаны ниже.

• Число    — обязательный аргумент. Показатель степени, в которую возводится основание e.

Замечания

• Чтобы вычислить степень с другим основанием, используйте оператор возведения в степень (^).

• Функция EXP является обратной по отношению к функции LN, т. е. к натуральному логарифму числа.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
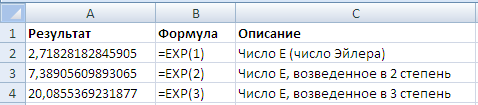
=EXP(1)	Приблизительное значение e	2,71828183
=EXP(2)	Основание натурального логарифма e, возведенное в квадрат	7,3890561

Рассмотрим возможности возведения экспоненты в степень и в частности использования числа Е в Excel, также известного как число Эйлера.

Число Е — основание натурального логарифма, математическая константа равная приблизительно 2,71828.
Также данное число называют как число Эйлера или число Непера.
Экспонента — показательная функция f(x) = exp (x) = e x , где е — число Эйлера.
Также в Excel есть возможность использовать другую известную математическую константу — число Пи.

Функция EXP в Excel

Чтобы возвести экспоненту в степень в Excel можно воспользоваться стандартной функцией:

EXP(число)
Возвращает экспоненту заданного числа.

• Число(обязательный аргумент) — степень, в которую возводится число Е (приблизительное значение 2,71828182845904).

Для получения числа Е в Excel достаточно в качестве аргумента функции EXP взять значение 1:

Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.

Вычисление экспоненты в Эксель

Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:

где e – это число Эйлера, а n – степень возведения.

Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.

Способ 1: вычисление экспоненты при помощи ручного ввода функции

Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:

То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.

Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:

Для выполнения расчета щелкаем по кнопке Enter. Итог выводится в заранее указанную ячейку.

Способ 2: использование Мастера функций

Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.

Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.

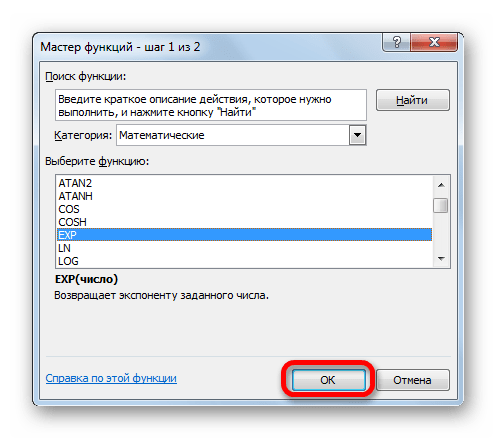
Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».

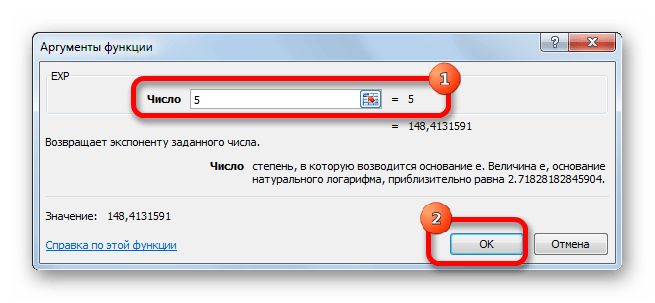
Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».

После вышеперечисленных действий результат расчета будет показан в той ячейке, которая была выделена в первом пункте данного способа.

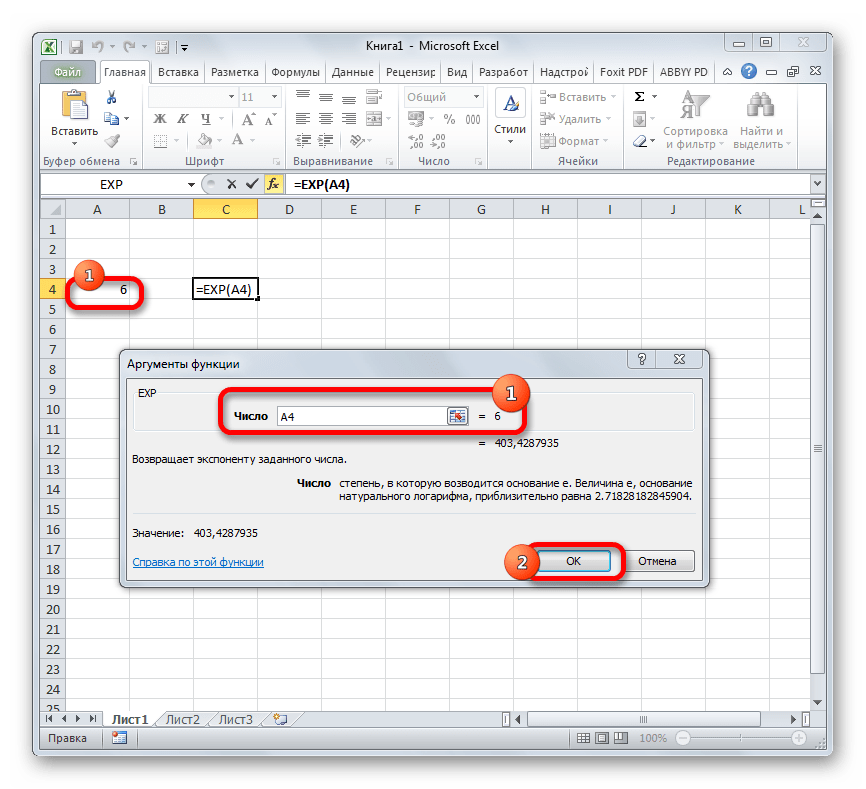
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».

Способ 3: построение графика

Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.

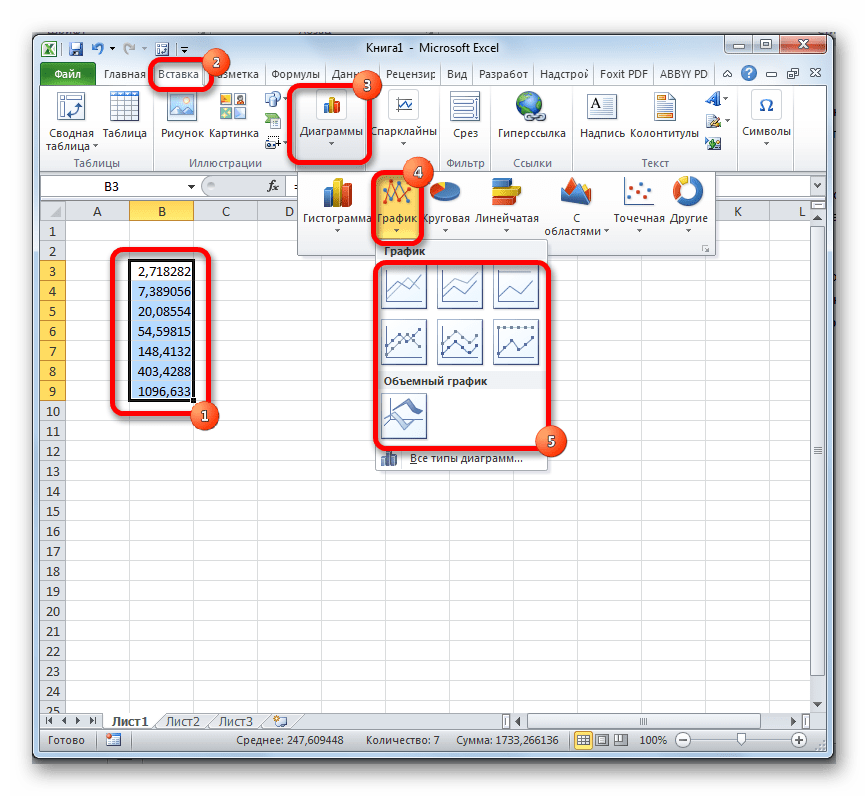
Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.

После того, как тип графика выбран, программа построит и отобразит его на том же листе, согласно указанным экспонентам. Далее его можно будет редактировать, как и любую другую диаграмму Экселя.

Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.

Отблагодарите автора, поделитесь статьей в социальных сетях.

В этой статье описаны синтаксис формулы и использование функции EXP в Microsoft Excel.

Описание

Возвращает число e, возведенное в указанную степень. Число e равно 2,71828182845904 и является основанием натурального логарифма.

Синтаксис

Аргументы функции EXP описаны ниже.

Число — обязательный аргумент. Показатель степени, в которую возводится основание e.

Замечания

Чтобы вычислить степень с другим основанием, используйте оператор возведения в степень (^).

Функция EXP является обратной по отношению к функции LN, т. е. к натуральному логарифму числа.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Приблизительное значение e

Основание натурального логарифма e, возведенное в квадрат

Содержание

• Вычисление экспоненты в Эксель
  • Способ 1: вычисление экспоненты при помощи ручного ввода функции
  • Способ 2: использование Мастера функций
  • Способ 3: построение графика
• Вопросы и ответы

Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.

Вычисление экспоненты в Эксель

Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:

f(x) = e^n,

где e – это число Эйлера, а n – степень возведения.

Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.

Способ 1: вычисление экспоненты при помощи ручного ввода функции

Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:

=EXP(число)

То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.

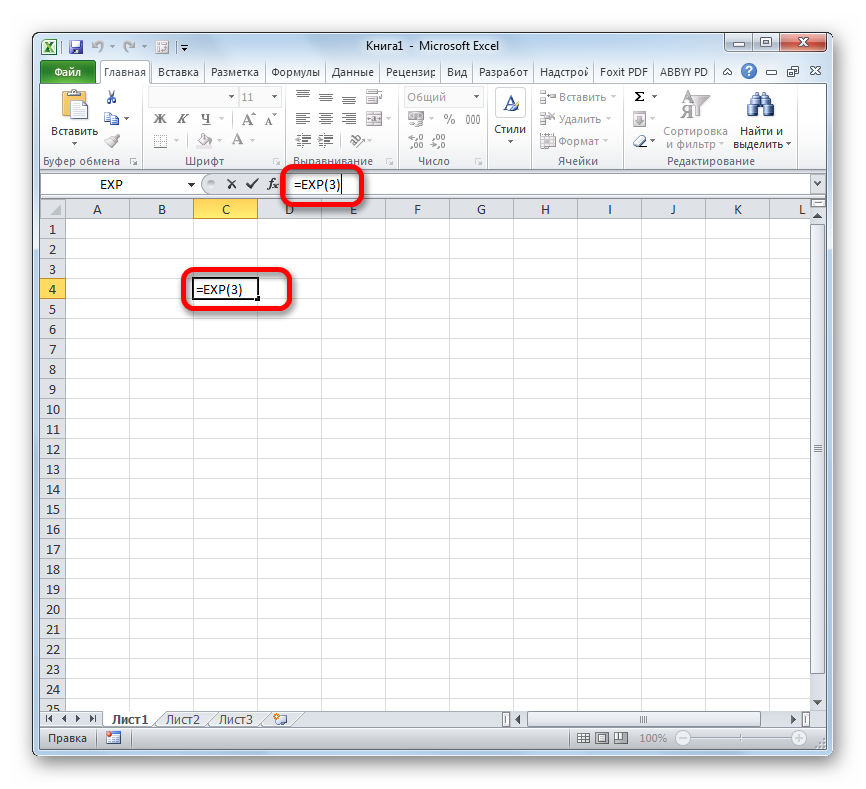
1. Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:

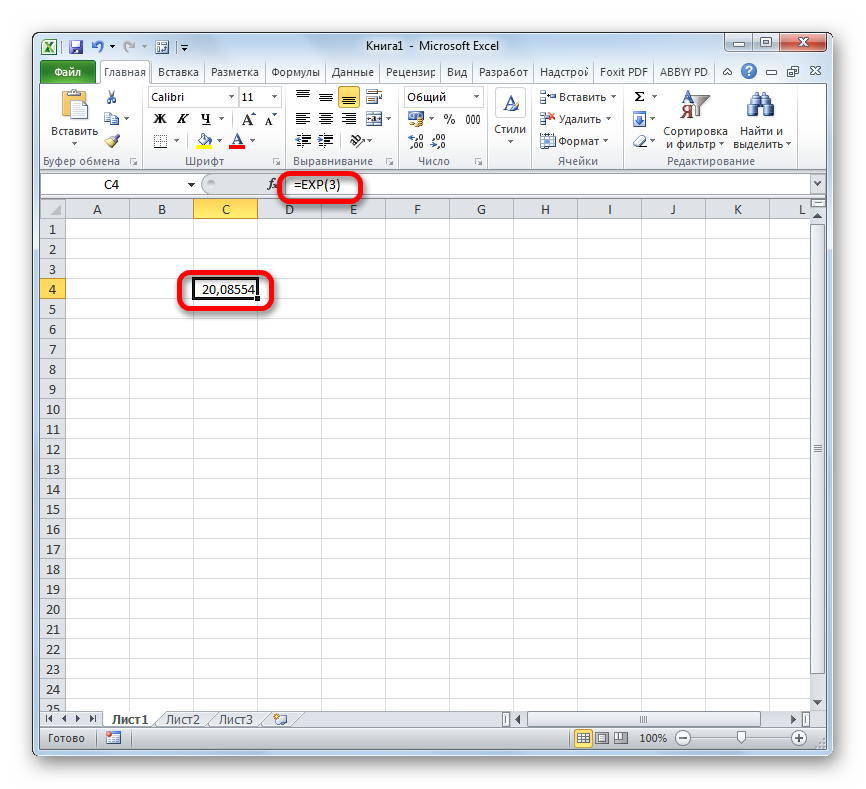
   =EXP(3)



2. Для выполнения расчета щелкаем по кнопке Enter. Итог выводится в заранее указанную ячейку.

Урок: Другие математические функции в Эксель

Способ 2: использование Мастера функций

Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.

1. Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.



2. Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».





3. Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».



4. После вышеперечисленных действий результат расчета будет показан в той ячейке, которая была выделена в первом пункте данного способа.

Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».

Урок: Мастер функций в Microsoft Excel

Способ 3: построение графика

Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.

1. Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.



2. После того, как тип графика выбран, программа построит и отобразит его на том же листе, согласно указанным экспонентам. Далее его можно будет редактировать, как и любую другую диаграмму Экселя.

Урок: Как сделать график в Excel

Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.

Еще статьи по данной теме:

Помогла ли Вам статья?

Мы немного затронули тему экспоненты в статье про округление больших чисел. В этой же статье мы обсудим, что же такое экспонента в Excel и, самое главное, для чего она может пригодиться в обычной жизни или в бизнесе.

В студенческие годы часто приходилось слышать фразы типа: «Зачем мы вообще учим ‘это’, в жизни нам ‘это’ никогда не пригодится». Одним из таких ‘это’ часто была экспонента или, например, факториал. У меня была слабая высшая математика при первом образовании, о чем я жалею. И вот сейчас приходиться догонять темы, что упустил раньше. Делюсь пересказом своих знаний.

Экспонента. Что это такое?

Мы знаем, что наш мир описан точными науками — т.е. набором правил и законов более-менее точно описывающих происходящее. Для этого в большинстве случаев помогают функции/формулы. В природе довольно часто встречаются экспоненциальные явления (описываем экспонентой) формулой с числом e, а у = e в степени x уже будет экспоненциальной функцией:

Число e — это т.н. число Эйлера, приблизительно равное 2,72. Примечательно оно тем, что производная от этой функции равна самой функции exp(x)` = exp(x).

Что это вообще такое, и что для нас означает?

Лучше всего действие экспоненты показывают графики ниже:

Две функции: y = 2 в степени x и y = e в степени x , где x = время, к примеру. Мы видим, что скорость роста экспоненциального графика увеличивается быстрее. А все почему? Потому что производная (скорость роста или уменьшения) функции равна самой функции, т.е. скорость увеличения функции равна значению функции.

Если грубо, то в природе, это действительно встречается часто — чем больше клеток делятся, тем быстрее их становиться больше. Чем больше у вас денег в банке, тем большую прибыль они приносят. Например:

Вы вложили 1 000 руб. в банк, через год они принесли свои 100 руб. процентами, еще через год на вас работают уже 2 работника 1 000 руб. и 100 руб. и так далее, пока вы не заберете деньги или не случится банковский кризис.

Кстати, население на планете Земля тоже растет по экспоненте;)

Принцип Парето и экспонента

Слышали о таком принципе? Думаю да. «20% усилий приносят 80% результата». Это он.  Лучшее определение для запоминания, мне кажется:

20% любителей пива употребляют 80% всего пива

На принципе Парето построен и ABC анализ запасов, например.

Этот принцип Парето — еще один пример экспоненты.

Кстати, очень справедливый закон в реальной жизни, подтверждаю своим опытом.Когда-то на первом своем проекте я заметил, что примерно за 20% времени ты создаешь 80% продукта (в количественном эквиваленте), далее работаешь на качество. Т.е. еще 80% времени допиливаешь, ищешь ошибки, настраиваешь. Я даже слышал, что говорят «разработка в стадии экспоненты» — т.е. в стадии приближения к идеалу.

При таком «допиливании» проекта важно вовремя остановиться, ведь продукт никогда не будет идеальным. Поэтому заранее определитесь, какое качество вы хотели бы получить в конце. Если делаете не себе, обязательно соберите требования с заказчика. Принцип выглядит примерно так:

Экспонента в Excel

По смыслу функции более-менее объяснил, теперь напишу как считать ее и есть ли функция экспонента в Excel. Само собой есть.

В Эксель все посчитать несложно:

=EXP(A1)

или можно число возвести в степень

=2.72^A1

Дополнение. Как запомнить 15 знаков числа е?

В качестве отвлечения привожу способ, как запомнить число e c точностью до 15 знаков

• запишите 2,7,
• затем дважды год рождения Льва Толстого – 1828,
• затем величины углов равнобедренного прямоугольного треугольника – 45°, 90°, 45°,
• в итоге получается: 2,718281828459045.

Как фанат Льва Николаевича, я не смог забыть этот способ Кстати, отличная книга о том как запоминать много информации и как работает память здесь.