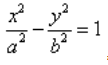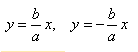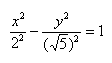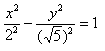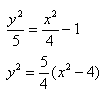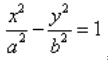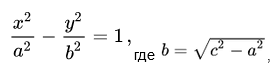Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
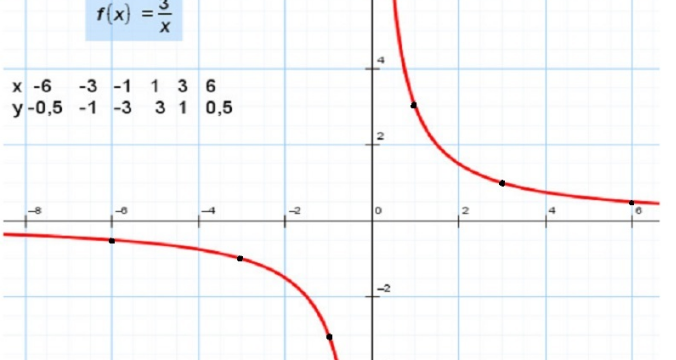
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
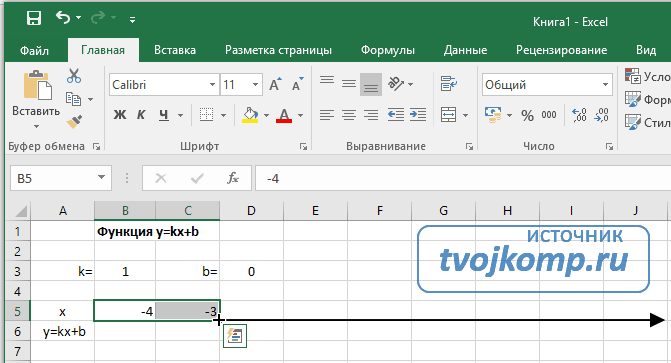
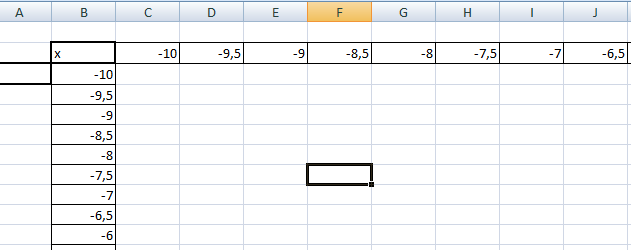
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
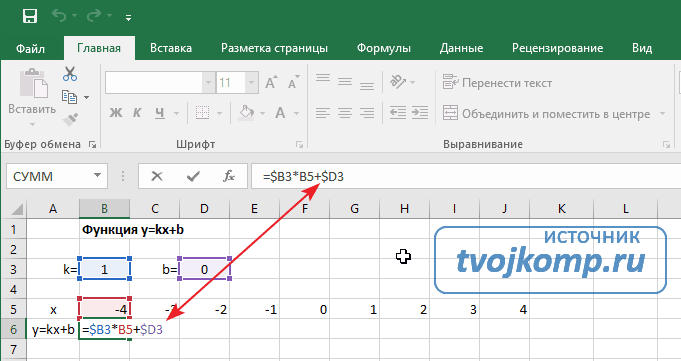
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
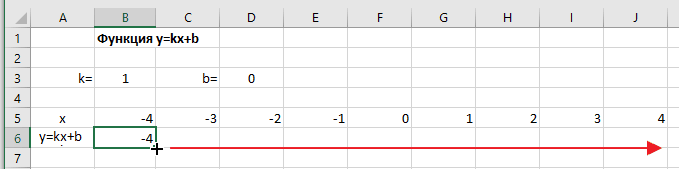
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
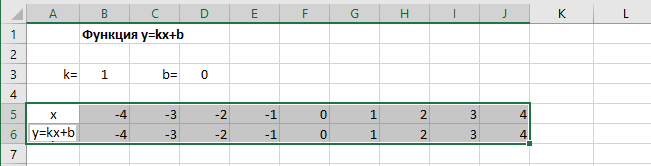
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
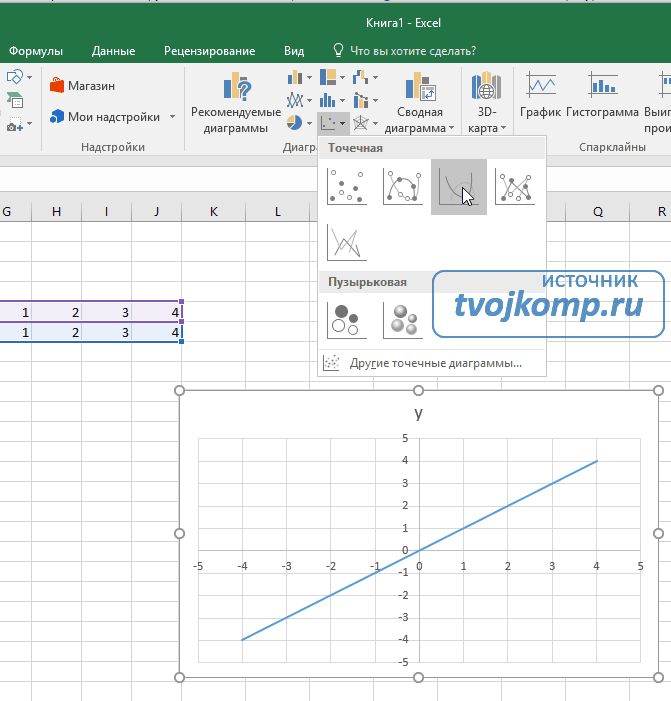
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
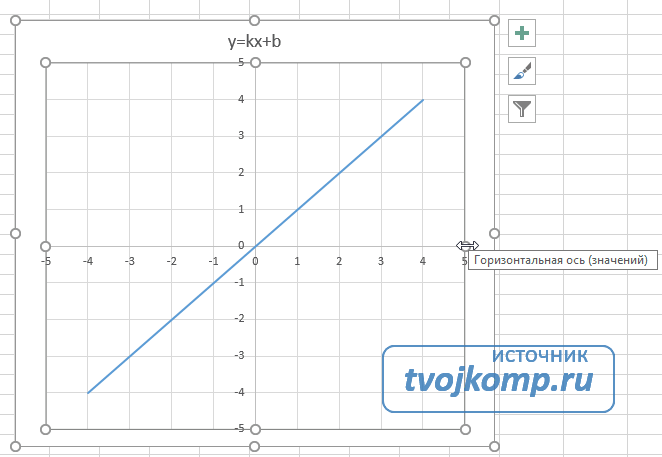
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
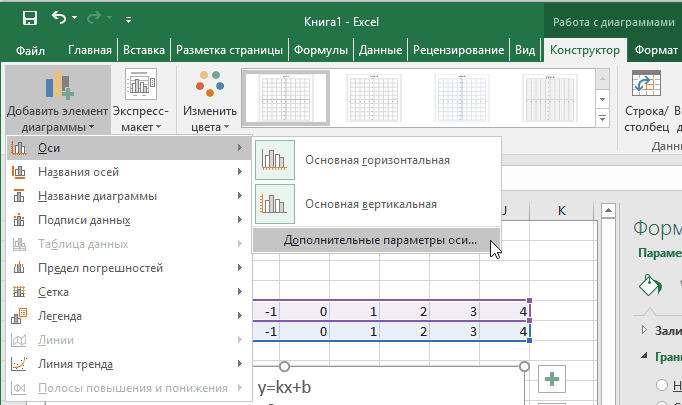
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
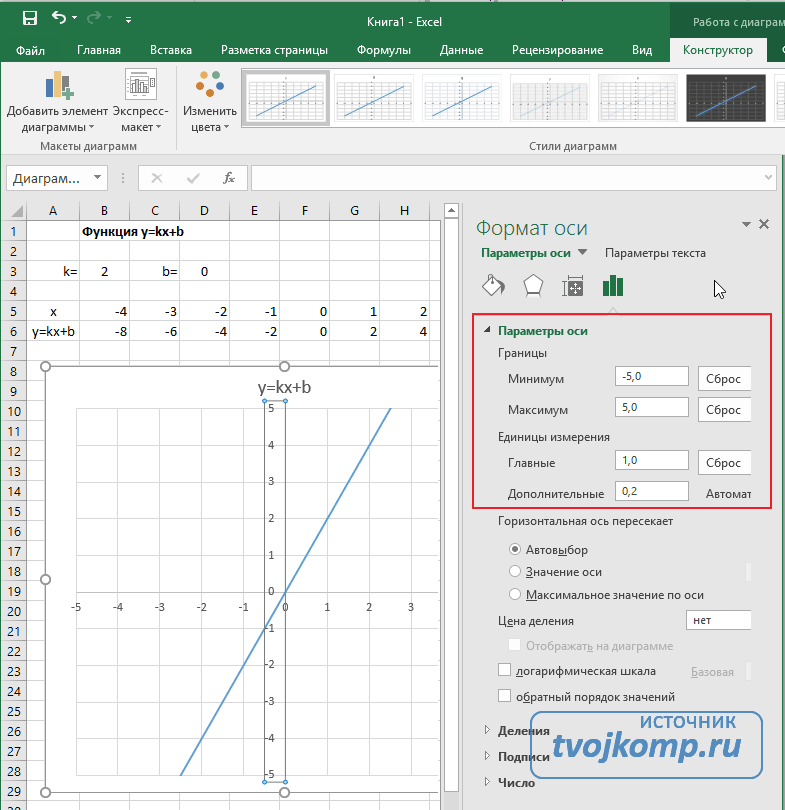
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
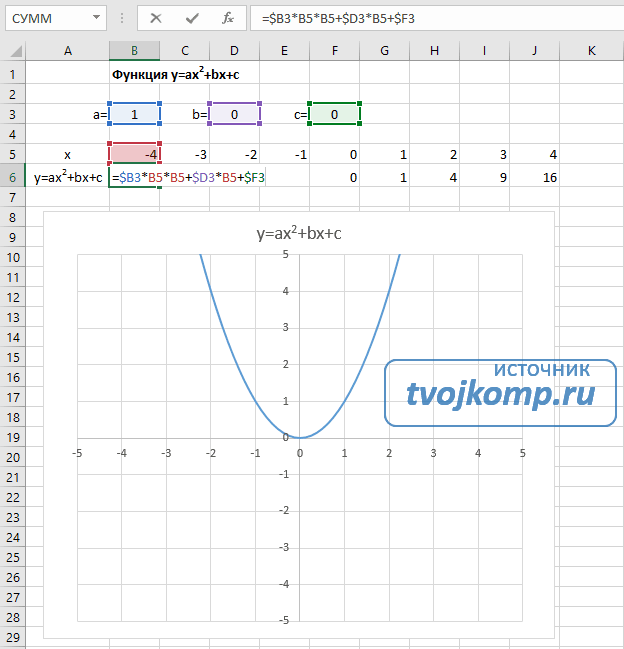
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
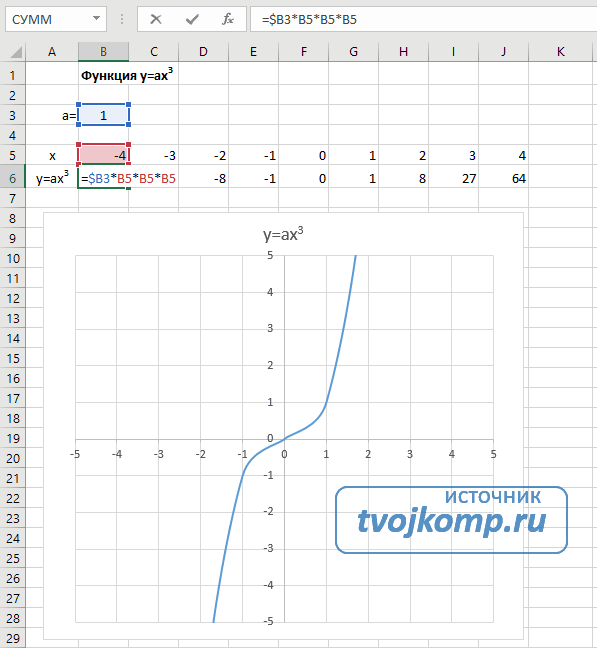
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
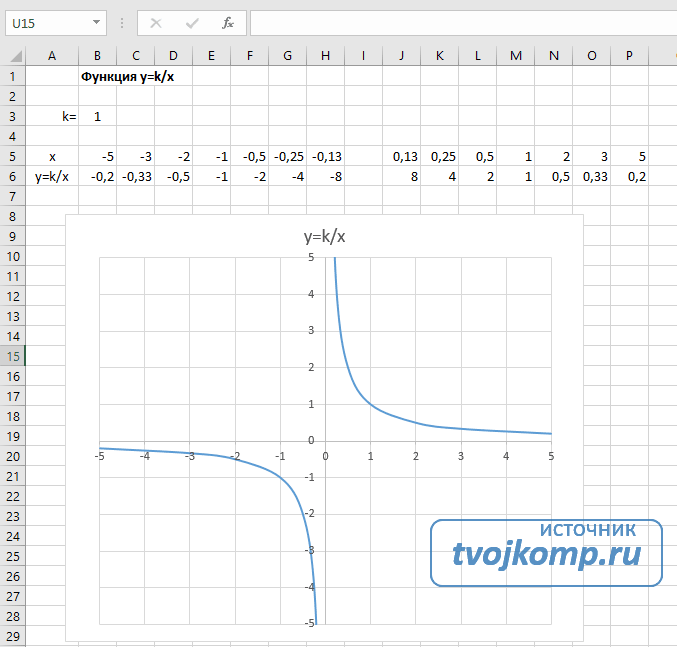
Гипербола y=k/x
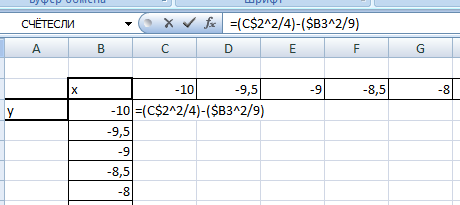
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
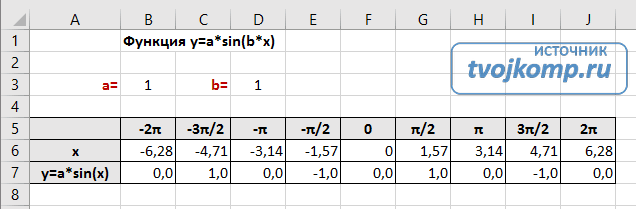
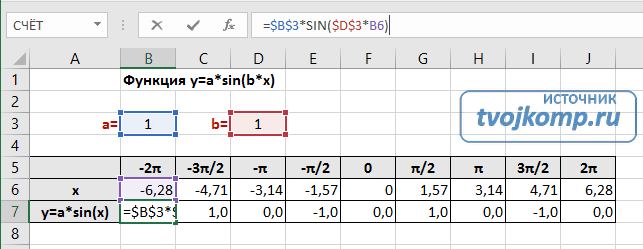
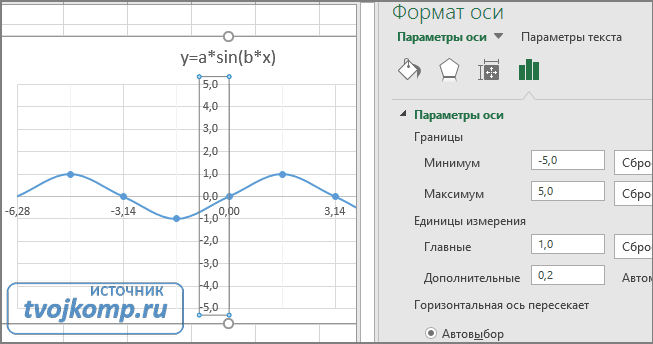
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
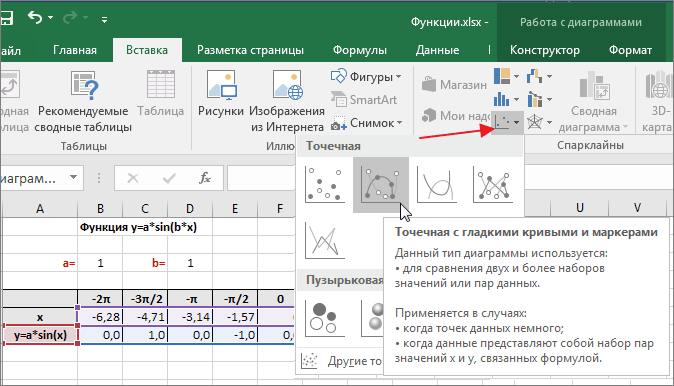
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
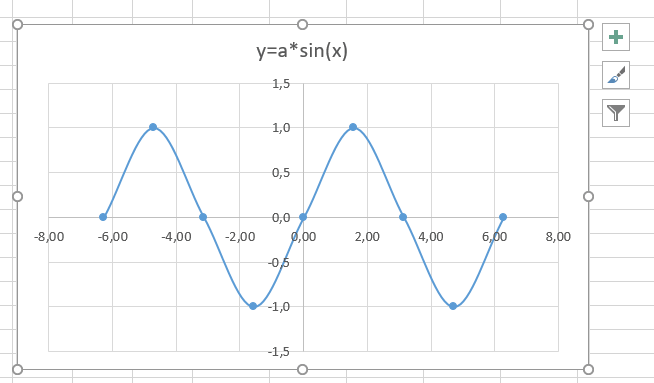
В итоге получим диаграмму.
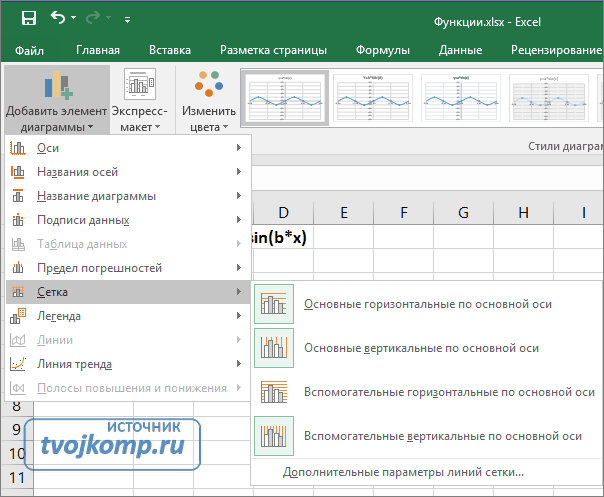
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
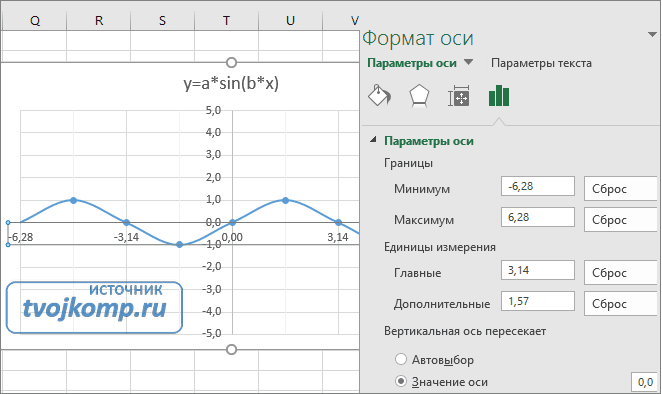
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
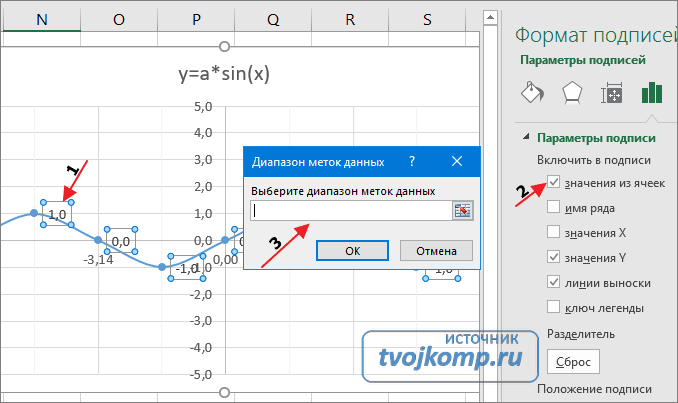
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
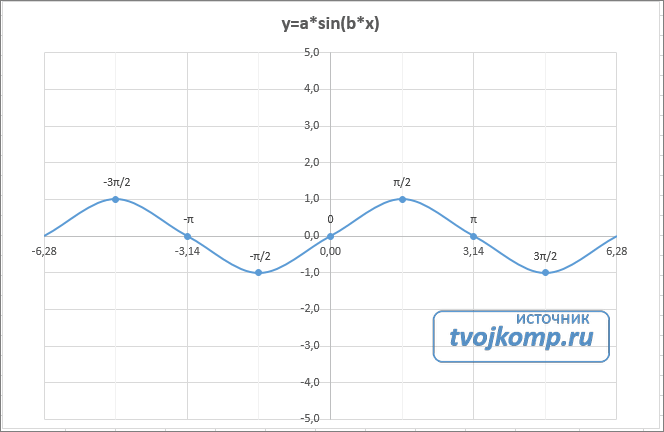
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!

Содержание
- Элементарный график изменения
- Создание графика с несколькими кривыми
- Создание второй оси
- Excel: методика создания графика функции
- Вычисление значений функции
- Создание таблицы и вычисление значений функций
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение точечной диаграммы
- Построение обычного графика
- Редактирование графика
- Как добавить название в график Эксель
- Как подписать оси в графике Excel
- Добавление второй оси
- Наложение и комбинирование графиков
- Особенности оформления графиков в Excel
- Добавление в график вспомогательной оси
- Как построить два графика в Excel
- Как построить график в Excel – Расширение таблицы исходных данных
- Как построить график в Excel – Выбрать данные
- Как построить график в Excel – Выбор источника данных
- Как построить график в Excel – Два графика на одной точечной диаграмме
- Заключение
Элементарный график изменения
График необходим, если от человека требуется продемонстрировать, насколько определенный показатель изменился за конкретный период времени. И обычного графика для выполнения этой задачи вполне достаточно, а вот различные вычурные диаграммы на деле могут только сделать информацию менее читаемой.
Предположим, у нас есть таблица, которая предоставляет информацию о чистой прибыли компании за последние пять лет.
Важно. Эти цифры не представляют фактические данные и могут быть нереалистичными. Они предоставляются только в образовательных целях.
Затем отправьтесь к вкладке «Вставка», где у вас есть возможность осуществить выбор типа графика, который будет подходящим в конкретной ситуации.
Нас интересует тип «График». После нажатия на соответствующую кнопку, появится окошко с настройками внешнего вида будущего графика. Чтобы понять, какой вариант подходит в конкретном случае, вы можете навести указатель мыши на определенный тип, и появится соответствующее приглашение.
После выбора нужного вида диаграммы вам необходимо скопировать таблицу данных связать ее с графиком. Результат будет следующим.
В нашем случае на диаграмме представлено две линии. Первая имеет красный цвет. Вторая – синий. Последняя нам не нужна, поэтому мы можем удалить ее, выбрав ее и нажав кнопку «Удалить». Поскольку мы имеем лишь одну линию, легенда (блок с названиями отдельных линий графика) также может быть удалена. Но маркеры лучше назвать. Найдите панель «Работа с диаграммами» и блок «Подписи данных» на вкладке «Макет». Здесь вы должны определить положение чисел.
Оси рекомендуется называть, чтобы обеспечить большую удобочитаемости графика. На вкладке «Макет» найдите меню «Названия осей» и задайте имя для вертикальной или горизонтальной осей соответственно.
Но вы можете смело обходиться без заголовка. Чтобы удалить его, вам нужно переместить его в область графика, которая невидима для постороннего глаза (над ним). Если вам все еще нужно название диаграммы, вы можете получить доступ ко всем необходимым настройкам через меню «Название диаграммы» на той же вкладке. Вы также можете найти его на вкладке «Макет».
Вместо порядкового номера отчетного года достаточно оставить только сам год. Выберите требуемые значения и щелкните по ним правой кнопкой мышки. Затем кликните по пункту «Выбор данных» – «Изменить подпись горизонтальной оси». Далее вам следует задать диапазон. В случае с нами, это первая колонка таблицы, являющейся источником информации. Результат такой.
Но вообще, можно все оставить, этот график вполне рабочий. Но если есть необходимость сделать привлекательный дизайн графика, то к вашим услугам – Вкладка “Конструктор”, которая позволяет указать фоновый цвет графика, его шрифт, а также разместить его на другом листе.
Создание графика с несколькими кривыми
Предположим, нам надо продемонстрировать инвесторам не одну лишь чистую прибыль предприятия, но и то, сколько в общей сумме будут стоить ее активы. Соответственно, выросло количество информации.
Невзирая на это, в методике создания графика принципиальных отличий нет по сравнению с описанным выше. Просто теперь легенду надо оставить, поскольку ее функция отлично выполняется.
Создание второй оси
Какие же действия необходимо предпринять, чтобы создать еще одну ось на графике? Если мы используем общие метрические единицы, то необходимо применить советы, описанные ранее. Если применяются данные различных типов, то придется добавлять еще одну ось.
Но перед этим нужно построить обычный график, как будто используются одни и те же метрические единицы.
После этого главная ось выделяется. Затем вызовите контекстное меню. В нем будет много пунктов, один из которых – «Формат ряда данных». Его нужно нажать. Затем появится окно, в котором необходимо найти пункт меню «Параметры ряда», а далее выставить опцию «По вспомогательной оси».
Далее закройте окно.
Но это всего лишь один из возможных методов. Никто не мешает, например, использовать для вторичной оси диаграмму другой разновидности. Надо определиться, какая линия требует того, чтобы мы добавили дополнительную ось, и потом кликнуть правой кнопкой мыши по ней и выбрать пункт «Изменить тип диаграммы для ряда».
Далее нужно настроить «внешность» второго ряда. Мы решили остановиться на линейчатой диаграмме.
Вот, как все просто. Достаточно сделать лишь пару кликов, и появляется еще одна ось, настроенная под иной параметр.
Это уже более нетривиальная задача, и для ее выполнения необходимо выполнить два основных действия:
- Сформировать таблицу, служащую источником информации. Сперва следует определиться с тем, какая будет конкретно в вашем случае использоваться функция. Например, y=x(√x – 2). При этом в качестве используемого шага мы выберем значение 0,3.
- Собственно, построить график.
Итак, нам необходимо сформировать таблицу, где есть два столбца. Первый – это горизонтальная ось (то есть, X), второй – вертикальная (Y). Вторая строка содержит первое значение, в нашем случае это единица. На третьей строке нужно написать значение, которое будет на 0,3 большим предыдущего. Это можно сделать как с помощью самостоятельных подсчетов, так и записав непосредственно формулу, которая в нашем случае будет следующей:
=A2+0,3.
После этого нужно применить автозаполнение к следующим ячейкам. Для этого нужно выделить ячейки A2 и A3 и перетащить квадратик на нужное количество строк вниз.
В вертикальной колонке мы указываем формулу, используемую, чтобы на основе готовой формулы построить график функции. В случае с нашим примером это будет =А2*(КОРЕНЬ(А2-2). После этого подтверждает свои действия с помощью клавиши Enter, и программа автоматически рассчитает результат.
Далее нужно создать новый лист или перейти на другой, но уже существующий. Правда, если есть острая необходимость, можно вставить диаграмму здесь же (не резервируя под эту задачу отдельный лист). Но лишь при условии, что есть много свободного пространства. Затем нажимаем следующие пункты: «Вставка» – «Диаграмма» – «Точечная».
После этого надо решить, какой тип диаграммы нужно использовать. Далее делается правый клик мышью по той части диаграммы, для которой будут определяться данные. То есть, после открытия контекстного меню следует нажать на кнопку «Выбрать данные».
Далее нужно выделить первый столбик, и нажать «Добавить». Появится диалоговое окно, где будут настройки названия ряда, а также значения горизонтальной и вертикальной осей.
Ура, результат есть, и выглядит очень даже мило.
Аналогично графику, построенному в начале, можно удалять легенду, поскольку мы имеем только одну линию, и нет необходимости ее дополнительно подписывать.
Но есть одна проблема – на оси X не нанесены значения, лишь номер точек. Чтобы скорректировать эту проблему, надо дать названия этой оси. Чтобы это сделать, нужно кликнуть правой кнопкой мыши по ней, а затем выбрать пункт «Выбрать данные» – «Изменить подписи горизонтальной оси». По окончании этих операций выделяется требуемый набор значений, и график станет выглядет так.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение точечной диаграммы
Как правило, точечная диаграмма используется для построения графиков функций. Например, возьмем функцию y=x^2.
- Построим таблицу данных из двух столбцов.
Таблица данных y=x^2
- Выделяем данные и вызываем уже упомянутую панель диаграм и выбираем на этот раз точечную.
Виды точечных диаграмм
- После этого получаем диаграмму, я выбрал с маркерами, на листе.
График, построенный при помощи точечной диаграммы
- Как уже было ранее показано, перемещаем диаграмму, меняем название, убираем легенду, заливаем фон.
График функции
- Теперь поработаем на вкладке “Конструктор”. Добавим еще пару рядов данных:
Вторая таблица данных
- Переходим на диаграмму и на вкладке “Конструктор” нажимаем кнопку “Выбрать данные”. Появится окно, где мы можем выбрать в качестве диапазона нашу новую таблицу данных.
Окно выбора данных
- В этом же окне мы можем изменить параметры каждого ряда
Корректировка данных рядов
Можно поставить свое произвольное название ряда. Если вдруг Excel неверно взял какой-то ряд в качестве независимой или зависимой переменной, можно произвольно определить нужные диапазоны.
- Добавляем легенду, меняем название диаграммы и получаем вот такую картинку
Итоговый график
Построение обычного графика
Рисовать график в Excel можно только после того, как готова таблица с данными, на основе которой он будет строиться.
- Находясь на вкладке «Вставка», выделяем табличную область, где расположены расчетные данные, которые мы желаем видеть в графике. Затем на ленте в блоке инструментов «Диаграммы» кликаем по кнопке «График».
- После этого открывается список, в котором представлено семь видов графиков:
- Обычный;
- С накоплением;
- Нормированный с накоплением;
- С маркерами;
- С маркерами и накоплением;
- Нормированный с маркерами и накоплением;
- Объемный.
Выбираем тот, который по вашему мнению больше всего подходит для конкретно поставленных целей его построения.
- Дальше Excel выполняет непосредственное построение графика.
Редактирование графика
После построения графика можно выполнить его редактирование для придания объекту более презентабельного вида и облегчения понимания материала, который он отображает.
- Чтобы подписать график, переходим на вкладку «Макет» мастера работы с диаграммами. Кликаем по кнопке на ленте с наименованием «Название диаграммы». В открывшемся списке указываем, где будет размещаться имя: по центру или над графиком. Второй вариант обычно более уместен, поэтому мы в качестве примера используем «Над диаграммой». В результате появляется название, которое можно заменить или отредактировать на свое усмотрение, просто нажав по нему и введя нужные символы с клавиатуры.
- Задать имя осям можно, кликнув по кнопке «Название осей». В выпадающем списке выберите пункт «Название основной горизонтальной оси», а далее переходите в позицию «Название под осью».
- Под осью появляется форма для наименования, в которую можно занести любое на свое усмотрение название.
- Аналогичным образом подписываем вертикальную ось. Жмем по кнопке «Название осей», но в появившемся меню выбираем «Название основной вертикальной оси». Откроется перечень из трех вариантов расположения подписи: повернутое, вертикальное, горизонтальное. Лучше всего использовать повернутое имя, так как в этом случае экономится место на листе.
- На листе около соответствующей оси появляется поле, в которое можно ввести наиболее подходящее по контексту расположенных данных название.
- Если вы считаете, что для понимания графика легенда не нужна и она только занимает место, то можно удалить ее. Щелкните по кнопке «Легенда», расположенной на ленте, а затем по варианту «Нет». Тут же можно выбрать любую позицию легенды, если надо ее не удалить, а только сменить расположение.
Как добавить название в график Эксель

На примерах выше мы строили графики курсов Доллара и Евро, без заголовка сложно понять про что он и к чему относится. Чтобы решить эту проблему нам нужно:
- Нажать на графике левой клавишей мыши;
- Нажать на “зеленый крестик” в правом верхнем углу графика;
- Во всплывающем окне поставить галочку напротив пункта “Название диаграммы”:
- Над графиком появится поле с названием графика. Кликните по нему левой клавишей мыши и внесите свое название:
Как подписать оси в графике Excel
Для лучше информативности нашего графика в Excel есть возможность подписать оси. Для этого:
- Щелкните левой клавишей мыши по графику. В правом верхнем углу графика появится “зеленый крестик”, нажав на который раскроются настройки элементов диаграммы:
- Щелкните левой клавишей мыши на пункте “Названия осей”. На графике под каждой осью появятся заголовки, в которые вы можете внести свой текст:
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
Сначала строим график так, будто у нас одинаковые единицы измерения.

Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» – «По вспомогательной оси».

Нажимаем «Закрыть» – на графике появилась вторая ось, которая «подстроилась» под данные кривой.

Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».

Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.

Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Наложение и комбинирование графиков
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:

Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.

Особенности оформления графиков в Excel
Несколько советов по оформлению графиков в Excel:
- Первое, что следует сделать пользователю, — ввести правильно название зависимости. Для этого нужно выделить щелчком мыши блок «Название диаграммы», щёлкнуть по нему ещё раз и ввести требуемое наименование. При необходимости этот блок можно удалить, выделив его и нажав клавишу Delete.
- Если требуется изменить не только название, но и стиль написания, следует, снова выделив блок, вызвать контекстное меню и выбрать в нём раздел «Шрифт». Подобрав подходящий вариант, юзер может нажимать на «ОК» и переходить к дальнейшим действиям.
- Вызвав меню «Формат названия диаграммы», можно определить, в какой части рисунка будет располагаться наименование: в центре, в левом верхнем, нижнем правом углу и так далее.
- Чтобы добавить на график названия осей, следует щёлкнуть мышью по «плюсику» справа от рисунка и в выплывающем списке установить галочку в соответствующем чекбоксе.
- Если изначальное расположение названий не устраивает пользователя, он может свободно перетаскивать их по полю графика, а также менять их наименования описанным ранее способом.
- Чтобы добавить на любую линию графика подписи (размещаются прямо на сетке) или выноски данных (в отдельных окошечках), нужно выделить её щелчком правой клавишей мыши и выбрать соответствующий параметр во вложенном меню «Добавить подписи данных».
- Юзер может свободно сочетать способы размещения подписей, выбирая любой из пунктов в расширенном меню окошка «Элементы диаграммы».
- Выбрав в том же меню «Дополнительные параметры», в боковом меню следует указать категорию представленных данных: простые числа, дроби, проценты, деньги и так далее.
- Чтобы добавить таблицу с данными непосредственно на график, нужно вызвать нажатием на «плюсик» всё те же «Дополнительные параметры» и установить галочку в одноимённом чекбоксе.
- Сетку, позволяющую найти значения графика в каждой точке, с помощью того же меню можно совсем убрать или добавить на неё основную и вспомогательную разметку.
- «Легенда» — не самый полезный, но привычный блок графиков Excel. Убрать или перенести его можно, сняв галочку в окне «Дополнительные параметры» или вызвав вложенное меню. Более простой вариант — выделить блок щелчком мыши и нажать клавишу Delete или перетащить по полю графика.
- Понять общее направление движения графика поможет линия тренда; добавить её для каждого ряда значений можно в том же окне.
- Перейдя на вкладку «Конструктор», пользователь может кардинально изменить вид графика, выбрав один из стандартных шаблонов в разделе «Стили диаграмм».
- А вызвав находящееся там же меню «Изменить цвета» — подобрать палитру для каждой линии в отдельности или для всего графика в целом.
- Меню «Стили» вкладки «Формат» позволяет найти оптимальное представление для текстовых элементов графика.
- Изменить фон, оставив нетронутым тип диаграммы, можно с помощью раздела «Стили фигур».
- На этом настройку графика можно считать оконченной. Пользователь может в любой момент изменить тип диаграммы, перейдя в одноимённое меню и выбрав понравившийся вариант.
Добавление в график вспомогательной оси
Нередко возникает необходимость на одной диаграмме разместить несколько графиков. В этом нет никакой сложности, если они имеют одинаковые меры исчисления. Но порой приходится совмещать несколько графиков с различными мерами исчисления, к примеру, чтобы показать зависимость одних данных от других. Делается это следующим образом.
- Первые шаги такие же, как и описанные выше. Выделяем таблицу, переходим во вкладку “Вставка” и выбираем наиболее подходящий вариант графика.
- В полученной диаграмме построено несколько графиков в соответствии с количеством столбцов выделенной таблицы. Теперь нужно нажать правой кнопкой мыши на тот, для которого необходима вспомогательная ось. Внизу появившегося списка выбираем «Формат ряда данных…».
- Откроются настройки формата данных, в котором выбираем “Построить ряд по вспомогательной оси”.
- После этого будет добавлена вспомогательная ось, и график перестроится. Далее можно скорректировать название, подписи данных, легенду, и выбрать для них подходящее место.
Примечание: в диаграмму можно добавить только одну дополнительную ось, что ограничивает возможность построения графиков для трёх и более различных мер исчисления.
Как построить два графика в Excel
Перейдем к вопросу, как построить два графика в Excel. Добавим еще один график кубической параболы. Создадим в таблице еще один столбец (столбец С), в котором введем формулу кубической параболы. Теперь наша таблица выглядит следующим образом:
Как построить график в Excel – Расширение таблицы исходных данных
Теперь во вкладке «Конструктор» выбираем пункт «Выбрать данные».
Как построить график в Excel – Выбрать данные
В появившемся окне, Excel предлагает выбрать источник данных.
Как построить график в Excel – Выбор источника данных
Мы можем либо изменить «Диапазон данных для диаграммы», выбрав нашу обновленную таблицу; либо добавить еще один ряд с помощью кнопки «Добавить». Мы воспользуемся вторым способом, и просто добавим еще один ряд.
В открывшемся окне в поле «Имя ряда» выбираем ячейку с заголовком столбца, в поле «Значения Х» – выбираем первый столбец таблицы, «Значения У» – третий. Нажимаем кнопку «ОК».
Как построить график в Excel – Два графика на одной точечной диаграмме
Для удобства добавим легенду и название диаграммы, и выберем желаемый стиль. Ну вот, график функции в Excel построен:
Заключение
Наряду с работой данных в табличном виде, в программе Microsoft Excel можно строить графики. Программа предлагает большое разнообразие видов и подвидов, которые прекрасно покрывают потребности пользователей в предоставлении информации в наиболее наглядном виде, значительно облегчающем ее восприятие.
Источники
- https://office-guru.ru/excel/diagrammy-grafika/grafik-v-excel-s-nulya.html
- https://pedsovet.su/excel/5883_grafik_funkcii
- https://tvojkomp.ru/kak-postroit-grafik-funktsii-v-microsoft-excel/
- http://excelpractic.ru/kak-postroit-grafik-v-excel.html
- https://lumpics.ru/how-to-make-a-graph-in-excel/
- https://excelhack.ru/kak-postroit-grafik-v-excel-po-dannym-tablicy/
- https://exceltable.com/grafiki/grafiki-i-diagrammi-v-excel
- https://konekto.ru/kak-postroit-grafik-v-excel.html
- https://MicroExcel.ru/postroenie-grafikov/
- https://naprimerax.org/kak-postroit-grafik-v-excel
- y = x (при k > 0)
- y = -x (при k < 0)
Смещение асимптот
Допустим у нас есть функция, заданная формулой:
- x = a – это вертикальная асимптота графика вместо оси Oy;
- y = b – горизонтальная асимптота вместо оси Ox.
Канонический вид уравнения гиперболы (координатные оси совпадают с осями графика):
Алгоритм построения гиперболы
Пример 1
Дана функция y = 4 /x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
См. ответ на вопрос про параболу в Эксель. Единственная разница — в функции, по которой определяется значение У. Для гиперболы формула имеет общий вид У = к / Х, и, соответственно, эта функция будет иметь разрыв при Х = 0, что нужно учитывать при задании диапазона для Х. Диапазонов может быть два — например, от -10 до -1 и от 1 до 10 с шагом 0,1 каждый. Формула, например, =3/A2.
График нужно будет построить сначала для одного из диапазонов, потом — щелкнуть правой кнопкой на линии графика, выбрать пункт «Выбрать данные» и нажать кнопку «Добавить», выбрав второй диапазон данных, после чего щелкнуть уже на второй линии, выбрав для нее тот же цвет и толщину, что и для первой линии, чтобы казалось, что график один.
Впрочем, можно поступить и проще — построить график сразу для всего диапазона, после чего удалить значения в ячейках из его середины (для Х = -1 и Х = 1). Внешне результат не изменится.
Построение гиперболы, на самом деле, очень простое занятие, если знать как, ведь для этого нужно построить массив значений гиперболы.
Для этого приходится брать произвольные значения Х, кроме того, когда знаменатель стремится к нулю, но не слишком близко к нулю. Затем, с помощью формулы установите значения У и растяните их, скопировав эту нужную формулу и получив, таким образом, значения У. Затем остаётся выделить получившийся диапазон значений Х и У, а затем выбрать во вкладке графика соответствующий вашим потребностям график. Мне лично нравится точечная диаграмма, но можно выбрать и график. Затем остаётся посмотреть на получившуюся диаграмму и добавить или убрать x-значения или заменить их другими.
Получите точки, согласно которым график будет построен. Обозначьте два столбца, у одного должно быть значение Х, у второго у. В первый столбец введите данные от -7 до 7, с шагом 1, но исключите ноль. Там где должен быть 0 следует оставить ячейку пустой.
После в ячейке В2 следует прописать формулу: «=1/A2». После, ее скопируйте на оставшиеся ячейке, пустую строку не трогайте. Получатся готовые данные для построения гиперболы.
После, следует выделить область со значением, также пустую строку. Зайдите на верхней панели во вкладку Вставка, выберите Точечная среди возможных графиков. Выберите второй график.
Получился график гиперболы, который можно оформить, прописав оси и функцию.
Для прописания осей, на панели Вставка найдите с правой стороны блок Текст. Нажмите на иконку с надписью — Надпись. При помощи курсора нажмите на любую область на графике и пропишите название оси, после перетащите в место, которое нужно для получение обоих оси.
Следует выделить надпись Ряд1 и нажать при помощи правой кнопки мыши для появления меню. В нем нужно выбрать Выбрать данные, а на экране будет новое меню. В левой части нужно выделить Ряд1, которое вы увидите и нажать на кнопку Изменить. В меню, которое появится вы сможете отредактировать название, а после можно закрыть таблицы, которые являются дополнительными.
Как в экселе построить гиперболу?
В программе эксель можно построить многие функции, которые проходят в школе на уроках математики. Давайте рассмотрим подробную инструкцию, как в программе эксель построить гиперболу.
Первый этап. Построим гиперболу следующей функции: Y=1/X. Сначала нужно получить точки, по которым можно построить данный график. Для этого обозначим два столбца: «Значение X» и «Значение Y». В первый столбец введем данный от -7 до 7 с шагом 1, но при этом исключим ноль. При этом в месте, где должен быть ноль, оставим просто пустые ячейки.
Второй этап. В ячейке «В2» пропишем следующую формулу: «=1/A2». После необходимо её скопировать на остальные ячейки, кроме пустой строки. В итоге данные для построения гиперболы готовы.
Третий этап. Выделим область со значением, в т.ч. пустую строку. После на верхней панели зайдем во вкладку «Вставка», где среди возможных графиков, выберем «Точечная». В появившемся меню выберем второй график.
Четвертый этап. График гиперболы готов, но его стоить оформить: подписать оси и функцию.
Пятый этап. Чтобы подписать оси, вам нужно на панели «Вставка», справа отыскать блок «Текст», в котором нажать на иконку с надписью «Надпись». Появившимся курсором, нажимаете на любую область графика, прописываете название оси и потом перетаскиваете в нужное место, чтобы получилось в итоге обе подписи:
Шестой этап. Выделите надпись «Ряд1», нажмите на правую клавишу, чтобы появилось меню, в котором выберете «Выбрать данные», на экране появиться новое меню, в его левой части вы увидите название «Ряд1», выделите его и нажмите на кнопку «Изменить», в появившемся меню можете отредактировать название, после закрывайте все дополнительные таблицы. Сверху может тоже появиться название функции, его можно удалить.
Содержание
- Как в экселе построить гиперболу?
- Видео как постоить гиперболу в excele
- Как построить гиперболу в excel по уравнению
- Как в экселе построить гиперболу?
- Видео как постоить гиперболу в excele
- Как построить гиперболу в excel по уравнению
- Как построить гиперболу в excel по уравнению
- Как построить график в Excel, если раньше с ними не работал
- Стандартный шаблон построения графика в Excel по данным таблицы с двумя осями X и Y
- Построение графика со вспомогательной осью в Excel
- Как построить график линейной функции в Excel
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение графика зависимости X от Y в Excel
- Несколько советов по оформлению графиков в Excel
Как в экселе построить гиперболу?
В программе эксель можно построить многие функции, которые проходят в школе на уроках математики. Давайте рассмотрим подробную инструкцию, как в программе эксель построить гиперболу.
Первый этап. Построим гиперболу следующей функции: Y=1/X. Сначала нужно получить точки, по которым можно построить данный график. Для этого обозначим два столбца: «Значение X» и «Значение Y». В первый столбец введем данный от -7 до 7 с шагом 1, но при этом исключим ноль. При этом в месте, где должен быть ноль, оставим просто пустые ячейки.
Второй этап. В ячейке «В2» пропишем следующую формулу: «=1/A2». После необходимо её скопировать на остальные ячейки, кроме пустой строки. В итоге данные для построения гиперболы готовы.
Третий этап. Выделим область со значением, в т.ч. пустую строку. После на верхней панели зайдем во вкладку «Вставка», где среди возможных графиков, выберем «Точечная». В появившемся меню выберем второй график.
Четвертый этап. График гиперболы готов, но его стоить оформить: подписать оси и функцию.
Пятый этап. Чтобы подписать оси, вам нужно на панели «Вставка», справа отыскать блок «Текст», в котором нажать на иконку с надписью «Надпись». Появившимся курсором, нажимаете на любую область графика, прописываете название оси и потом перетаскиваете в нужное место, чтобы получилось в итоге обе подписи:
Шестой этап. Выделите надпись «Ряд1», нажмите на правую клавишу, чтобы появилось меню, в котором выберете «Выбрать данные», на экране появиться новое меню, в его левой части вы увидите название «Ряд1», выделите его и нажмите на кнопку «Изменить», в появившемся меню можете отредактировать название, после закрывайте все дополнительные таблицы. Сверху может тоже появиться название функции, его можно удалить.
Видео как постоить гиперболу в excele
Источник
Как построить гиперболу в excel по уравнению
Как в экселе построить гиперболу?
В программе эксель можно построить многие функции, которые проходят в школе на уроках математики. Давайте рассмотрим подробную инструкцию, как в программе эксель построить гиперболу.
Первый этап. Построим гиперболу следующей функции: Y=1/X. Сначала нужно получить точки, по которым можно построить данный график. Для этого обозначим два столбца: «Значение X» и «Значение Y». В первый столбец введем данный от -7 до 7 с шагом 1, но при этом исключим ноль. При этом в месте, где должен быть ноль, оставим просто пустые ячейки.
Второй этап. В ячейке «В2» пропишем следующую формулу: «=1/A2». После необходимо её скопировать на остальные ячейки, кроме пустой строки. В итоге данные для построения гиперболы готовы.
Третий этап. Выделим область со значением, в т.ч. пустую строку. После на верхней панели зайдем во вкладку «Вставка», где среди возможных графиков, выберем «Точечная». В появившемся меню выберем второй график.
Четвертый этап. График гиперболы готов, но его стоить оформить: подписать оси и функцию.
Пятый этап. Чтобы подписать оси, вам нужно на панели «Вставка», справа отыскать блок «Текст», в котором нажать на иконку с надписью «Надпись». Появившимся курсором, нажимаете на любую область графика, прописываете название оси и потом перетаскиваете в нужное место, чтобы получилось в итоге обе подписи:
Шестой этап. Выделите надпись «Ряд1», нажмите на правую клавишу, чтобы появилось меню, в котором выберете «Выбрать данные», на экране появиться новое меню, в его левой части вы увидите название «Ряд1», выделите его и нажмите на кнопку «Изменить», в появившемся меню можете отредактировать название, после закрывайте все дополнительные таблицы. Сверху может тоже появиться название функции, его можно удалить.
Видео как постоить гиперболу в excele
Как построить гиперболу в excel по уравнению
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
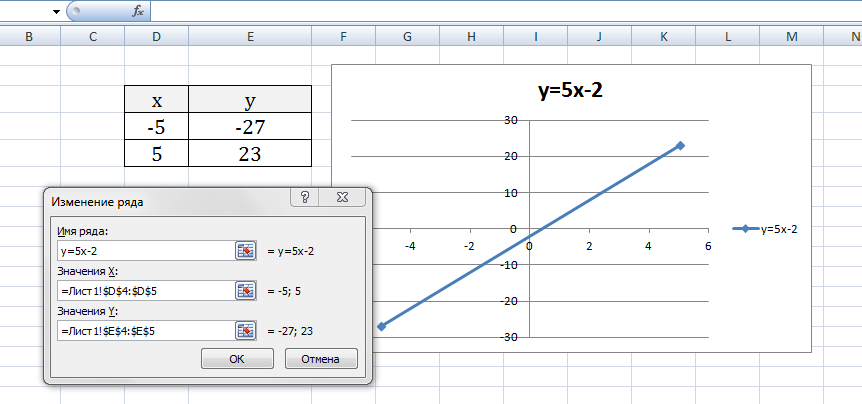
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
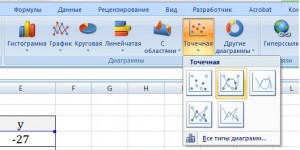
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
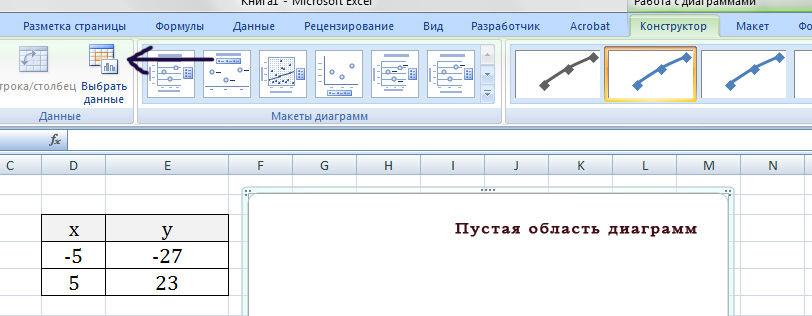
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
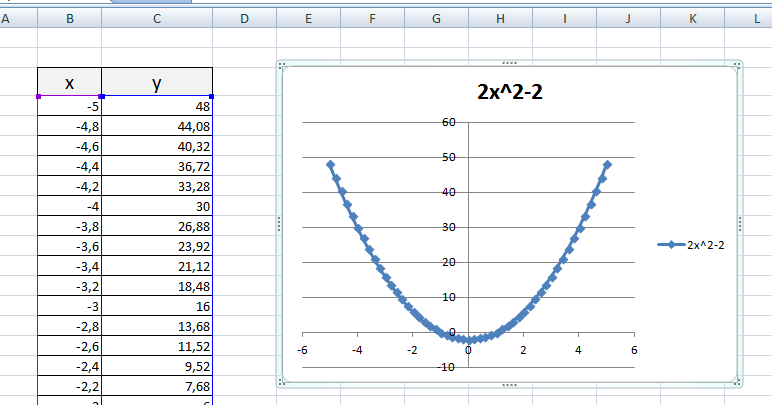
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x 2 -2
Параболу по двум точкам уже не построить, в отличии от прямой.
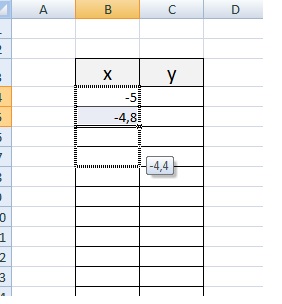
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
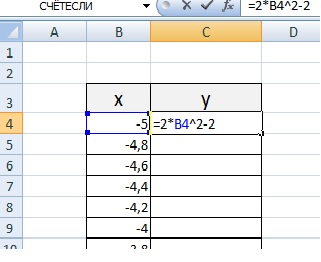
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
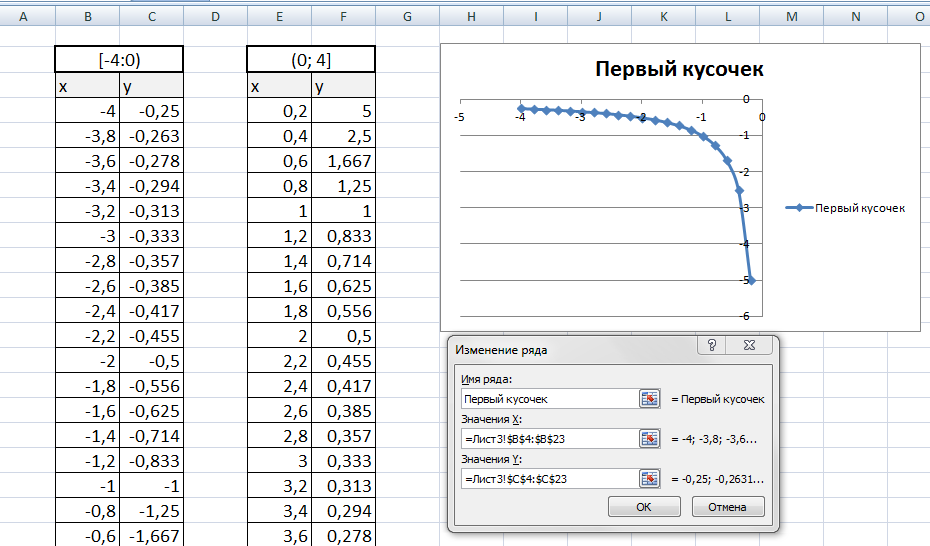
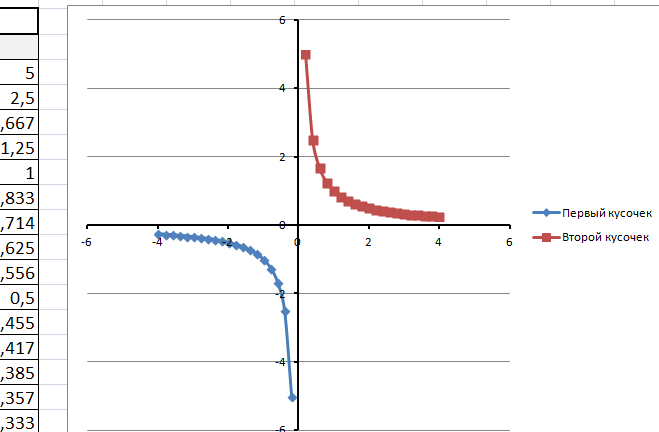
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
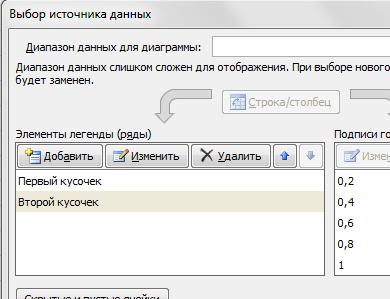
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Как построить гиперболу в excel по уравнению
На этом шаге мы рассмотрим несколько примеров построения кривых второго порядка на плоскости.
Задание 1. Построим параболу y = x 2 в диапазоне х [-3;3] с шагом = 0,5.
Решение этого задания можно посмотреть здесь.
Задание 2. Построить гиперболу в диапазоне х [0,1;10,1] с шагом = 0,5.
Решение этого задания можно увидеть здесь.
Задание 3. Построить верхнюю половину эллипса в диапазоне х [-3;3] с шагом = 0,5.
Решение этого задания можно посмотреть здесь.
Задание 4. Построить верхнюю часть параболы y 2 = x в диапазоне х [0;4] с шагом = 0,25.
Решение этого задания можно посмотреть здесь.
Задание 5. Построить верхнюю полуокружность эллипса в диапазоне х [-2;2] с шагом = 0,25.
Решение этого задания можно посмотреть здесь.
Задание 6. Построить гиперболы (диапазон и шаг выберите самостоятельно):
Решение этого задания можно посмотреть здесь.
На следующем шаге мы продолжим рассматривать задания на построение диаграмм.
Источник
Как построить график в Excel, если раньше с ними не работал
Как построить график в Excel? Далеко не все пользователи ПК знают обо всех возможностях этой программы. Для большинства работа в Excel заключается в построении и заполнении таблиц. Хотя, стоит отметить, даже обо всех его табличных возможностях знают буквально единицы.
График в Excel поможет отобразить зависимость данных и динамику их изменений. Представьте, насколько наглядной и информативной будет ваша таблица? Обо всех тонкостях построения графика в Excel расскажем прямо сейчас.
Стандартный шаблон построения графика в Excel по данным таблицы с двумя осями X и Y
Если вы хотите донести до человека какую-либо числовую информацию в виде динамики, то лучше всего использовать график. Чтобы создать такую диаграмму, не нужно иметь особых навыков. Понадобится лишь таблица, на которую будет опираться будущий чертеж. При этом вы можете произвольно менять его внешний вид.
Стандартный шаблон построения графика в Excel
Предположим, что у вас уже есть готовая таблица с данными. Вам нужно перейти на вкладку «Вставка» и выделить ту область таблицы, которую мы хотим отразить на графике. После этого в меню инструментов «Диаграммы» следует нажать на кнопку «График».
Затем вы увидите список, в котором имеется 7 разновидностей графиков:
- Обычный.
- С накоплением.
- Нормированный с накоплением.
- С маркерами.
- С маркерами и накоплением.
- Нормированный с маркерами и накоплением.
- Объемный.
Остается лишь подобрать оптимальный вариант с точки зрения ваших конкретных задач.
Построение графика со вспомогательной осью в Excel
В некоторых ситуациях вам может понадобиться расположить два и более графика на одной плоскости. В том случае, если все они имеют одинаковые единицы измерения, вам следует воспользоваться вышеуказанной инструкцией. Если же графики должны иметь разные меры исчисления, то дело обстоит немного иначе.
Перейдите на вкладку «Вставка», и выделите нужную область таблицы. Затем нажмите на «График» и подберите подходящую разновидность.
После этого будет создано два графика. Для того чтобы задать правильные меры исчисления для каждого чертежа, нужно нажать правой кнопкой мыши по тому из них, для которого необходимо добавить дополнительную ось. Вы увидите меню, в котором следует выбрать пункт «Формат ряда данных».
Построение графика со вспомогательной осью в Excel
В появившемся окне нужно перейти в раздел «Параметры ряда» и выбрать «По вспомогательной оси».
После того как вы закроете окно, сформируется новая ось, а график будет построен заново. Подпишите оси и название графика по тому же принципу, что мы описывали выше. Легенда будет очень полезна в том случае, если вы хотите продемонстрировать одновременно несколько диаграмм.
Как построить график линейной функции в Excel
Данная опция в Excel позволяет существенно сэкономить время выполнения определенных задач, к примеру, по алгебре. Разберемся с тем, как построить график в Excel по данным таблицы пошагово. В качестве примера возьмем линейную функцию y=x²+5.
- Сформируйте таблицу. Внесите в левый столбец значение х с требуемым шагом. При этом в правый столбце нужно записать формулу, которая будет рассчитывать значение у.
- После того как будет рассчитано значение для первой ячейки, вам необходимо «растянуть» формулу на другие строки. Потребуется навести курсор на правый нижний угол ячейки, после чего он поменяет свою форму на крестик. Далее следует зажать левую кнопку и потянуть выделение до нижней ячейки. Это позволит скопировать формулу и произвести расчёты значений в других строка.
- Выделите таблицу и нажмите на вкладку «Вставка». Теперь необходимо кликнуть на кнопку «Точечная». В появившемся окне нужно выбрать «Точечная с гладкими кривыми и маркерами».
- Осталось лишь отредактировать появившиеся график и убрать ненужные элементы.
Скачивайте и используйте уже сегодня:
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Объедините на одном поле два графика функций в Excel. При этом к прошлой функции нужно добавить следующую формулу: Z=X(√x – 3).
Выделите данные и вставьте их в область графика. Чтобы скорректировать те или иные детали диаграммы, воспользуйтесь вкладкой «Выбрать данные».
Построение графиков других функций
После построения таблицы и диаграммы можно приступить к созданию графиков других функций. Для этого потребуется слегка изменить исходную таблицу.
Квадратичная функция y=ax2+bx+c
Порядок действий будет таков:
- Измените заголовок в первой строке.
- Внесите коэффициенты и их значения в третью строку.
- Укажите обозначение функции в ячейку A6.
- Внесите формулу =$B3*B5*B5+$D3*B5+$F3 в ячейку B6.
- Протяните ее на весь диапазон значений аргумента вправо.
Кубическая парабола y=ax3
Вам необходимо внести следующие коррективы:
- Измените заголовок в первой строке.
- Внесите коэффициенты и их значения в третью строку.
- Укажите обозначение функции в ячейку A6.
- Внесите формулу =$B3*B5*B5*B5 в ячейку B6.
- Протяните её на весь диапазон значений аргумента вправо
Гипербола y=k/x
Чтобы сформировать гиперболу, вам нужно будет собственноручно заполнить таблицу. Следует оставить пустую ячейку в тех местах, где раньше стояло нулевое значение.
Построение графиков других функций
Затем придерживайтесь следующей последовательности действий:
- Измените заголовок в первой строке.
- Внесите коэффициенты и их значения в третью строку.
- Укажите обозначение функции в ячейку A6.
- Внесите формулу =$B3/B5 в ячейку B6.
- Протяните ее на весь диапазон значений аргумента вправо.
- Уберите формулу из ячейки I6.
- Измените диапазон исходных данных для графика. Это необходимо для того, чтобы правильно сформировать диаграмму (в данном примере диапазон больше, нежели в прошлых).
- Нажмите на диаграмму.
- Перейдите на вкладку «Работа с диаграммами», а затем в «Конструктор». Войдите в раздел «Данные» и кликните на «Выбрать данные».
- В появившемся окне мастера ввода данных нужно выделить прямоугольный диапазон ячеек A5:P6 с помощью мышки.
- Нажмите «ОК» в окне мастера.
Приглашаем вас на бесплатный онлайн-интенсив от Geek Brains.
За 3 часа эксперты подробно разберут каждый шаг новичка в IT, от составления резюме до выхода на зарплату в 200 000 ₽.
Также сразу после бесплатной регистрации на интенсив на вашу почту придут подарки от Geek Brains из закрытой базы:
Точный инструмент «Колесо компетенций»
Для детального самоанализа по выбору IT-профессии
Список грубых ошибок в IT, из-за которых сразу увольняют
Об этом мало кто рассказывает, но это должен знать каждый
Мини-тест из 11 вопросов от нашего личного психолога
Вы сразу поймете, что в данный момент тормозит ваш успех
Если вам необходим график функции cos(x), то потребуется вставить «cos(x)» вместо «sin(x)».
Данную последовательность действий можно применять и к графикам других функций. Правильно укажите вычислительные формулы и сформируете таблицу значений функции, ведь это основа любого чертежа в Excel.
Построение графика зависимости X от Y в Excel
Программа позволяет создавать графики зависимостей между двумя столбцами. Определитесь с разновидностью диаграммы: кликните мышью на «Точечная с гладкими кривыми и маркерами». Затем необходимо выполнить следующие действия:
- Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. Аналогичные действия нужно будет выполнять для всей таблицы.
Построение графика зависимости X от Y в Excel
Несколько советов по оформлению графиков в Excel
- Не ошибайтесь при вводе названия зависимости. Выделите блок «Название диаграммы» с помощью нажатия на кнопку мыши. После этого кликните по нему повторно и укажите наименование. Убрать данный блок можно посредством клавиши Delete.
- Хотите поменять стиль написания? В таком случае вам необходимо ещё раз выделить блок и открыть контекстное меню. Затем следует нажать на «Шрифт» и выбрать оптимальный для вас стиль. После этого останется лишь нажать на «ОК».
- Чтобы выбрать часть рисунка, в которой будет отображаться наименование (в центре, в левом верхнем, нижнем правом углу и т.д.), нужно открыть меню «Формат».
- Если вы хотите указать в графике названия осей, то нажмите на «плюсик» в правой части рисунка. После этого откроется список, в котором вам нужно будет выбрать соответствующий чекбокс.
- Не нравится расположение названий по умолчанию? Просто перетащите их по полю графика.
- Если вам нужно добавить на ту или иную линию графика подписи (создаются прямо на сетке) или выноски данных (в отдельных окнах), то потребуется выделить ее с помощью нажатия на правую кнопку мыши. Затем откройте меню «Добавить подписи данных» и подберите подходящий вариант.
- С помощью расширенного меню «Элементы диаграммы» вы можете в произвольной форме выбирать любые способы размещения подписей.
Советы по оформлению графиков в Excel
Источник
Большая доля людей легче и проще воспринимают информацию, когда она представлена наглядно. Сделать это самостоятельно можно с помощью презентаций и отчётов с использованием диаграмм и графиков. Это незаменимая составляющая практически любой аналитической деятельности.
При этом с построением диаграмм и графиков в программе Excel может справиться даже новичок. Это не так сложно, как изначально кажется.
Но потребуется освоить некоторые нюансы, разобраться с принципами построения, внимательнее изучить функционал программы.
Графики и диаграммы требуют отдельного рассмотрения.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Типов диаграмм очень много гистограмма, линейчатая, круговая, пузырьковая, сетчатая, биржевая В MS Excel 2003 34 типа и у каждого типа еще по нескольку вариантов. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Перейдя в контекстном меню к пункту «Выбрать данные», можно настроить, какая информация будет отображаться. Например, для указанного примера у пользователя есть возможность выделять данные только для конкретных месяцев. Для этого достаточно убирать галочки с ненужных дат или изменить формулу в графе «Диапазон данных для диаграммы».
Как построить график и диаграмму в Excel — подробная инструкция
Когда процентная диаграмма создаётся автоматически, зачастую она в полной мере не устраивает пользователя. Потому тут можно кликнуть по любому из секторов правой кнопкой, после чего появляются точки-границы. Через контекстное меню выберите «Формат ряда данных». Теперь для ряда задаются нужные параметры, и изменения сохраняются.
Немного теории
Вставить диаграмму в программе Microsoft Excel версий 2007, 2010,2013 и 2016 можно на вкладке Вид – группа Диаграммы.
График это один из типов диаграмм. Графики в Экселе бывают:
Краткий обзор диаграмм
В Экселе есть множество различных графиков, и чтобы их построить, необходимо составить таблицу данных. Что бы создать диаграмму нужно открыть вкладку «Вставка» и выбрать на панели «Диаграммы» подходящий вид.
Среди них самыми популярными являются следующие диаграммы:
Если нужно отобразить изменение ряда данных в течение времени, то выбирайте «График». Если данных немного, то можно выбрать «График с маркерами», если достаточно много, то выберите простой график.
Если есть функция зависимости, или необходимо изобразить сразу несколько графиков и сравнить пары значений, то лучше выбрать «Точечную диаграмму». Здесь маркеры также уместны при небольшом количестве данных.
Рассмотрим гистограммы. Они применяются для графического изображения значений по группам. Они также бывают плоскими и объемными. Вторые могут быть представлены в виде различных трехмерных фигур:
Если помимо разделения данных по категориям необходимо еще и отобразить вклад каждого значения в рамках одной категории, то следует выбрать «Гистограмму с накоплением».
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Они могут быть подписаны совершенно произвольно, но всегда смысл один каждой точке на горизонтальной оси соответствует значение по вертикали. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Видно неудобство: на одной вертикальной оси отражены и шкала температуры, и шкала влажности. Проблема решается вводом дополнительной вертикальной оси справа. Пусть справа будет шкала по влажности. Тогда наводим курсор на красную кривую влажности и кликаем по ней. Наверху страницы активировалось окно Работа с диаграммами:
Как построить график в Эксель — Microsoft Excel
В рассматриваемом примере y = 5x – 2. В ячейку для первой величины запишем формулу: = 5 • D4 — 2. В следующую ячейку следует также записать формулу, но нужно вместо D4 ввести D5. Или можно применить автоматическое заполнение при помощи маркера. В финале будет сформирована таблица:
Меняем тип графического объекта
Если после построения диаграммы Вы решили, что она недостаточно наглядна, можно изменить тип объекта всего в пару кликов. Рассмотрим этот процесс на примере построенной выше гистограммы движения финансовых средств. Предположим, что она должна стать графиком.
-
В меню «Конструктор» вкладки «Работа с диаграммами» выберите пункт «Изменить тип диаграммы».
Учтите, что не удастся заменить сложную диаграмму на более простую без потери части данных. Так, одной круговой диаграммы не хватит для отражения информации из гистограммы с двумя рядами.
Как построить диаграмму или график в Excel — инструкция по работе
Второй столбец Y. Тут прописывается расчётная формула, которая используется для формирования графика функции. Поэтому нужно кликнуть на Enter. Программа посчитает все заданные значения. Формулу можно размножить по столбцу, потянув вниз угол ячейки. Всё, таблица есть.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
С помощью данных инструментов можно вставить рисунок или сделать надпись, дать название диаграмме в целом или подписать отдельные ее части например, оси , добавить выборочные данные или таблицу данных целиком и многое другое. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
. вы поймете и запомните навсегда, как строить графики в Excel. Поняв, как и что нужно делать в Excel, вы легко затем по аналогии сможете при желании сделать график или диаграмму в программе Calc — процедуры разнятся незначительно.
Как построить график в Excel по данным таблицы: пошаговая инструкция |
С помощью контекстного меню на состоящем из нескольких рядов графике можно менять различные настройки, характеристики осей и линий, добавлять подписи и менять шрифты. А при изменении информации в таблице это автоматически отразится и на диаграмме. Данные, которые вводились вручную, (например, название оси или графика) придется менять тем же способом.
Добавление второй оси
Иногда информация может быть представлена в таблице так, что поместить ее на одной общей диаграмме, на первый взгляд, невозможно. Если представить, что накладные расходы указаны не в рублях, а в долларах, график получится некорректным.
Можно построить две разных диаграммы для каждого ряда данных. Или перед тем, как сделать график в Экселе, пересчитать сумму по действующем курсу — но это будет не слишком правильно, если затраты определялись именно в валюте. Решение проблемы — добавить вторую ось со своими единицами измерения.
Как построить график в Экселе — Блог Анатолия Бузова
График отображает изменения данных. Чаще всего изменения связаны со временем. К примеру, компания получила за определённый временной промежуток ту или иную прибыль. Вариантов много. Но суть везде одинаковая.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Чтобы за гистограммой были закреплены элементы управления, нужно преобразовать область данных в так называемую умную таблицу. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Тут будет использоваться только одна кривая. Потому смело удаляйте информацию справа от графика. Она называется «легенда». Для уточнений сделайте подписи к маркерам. Для этого нужно открыть вкладку «Макет», и выбрать «Подписи данных». Здесь выберите место, где будут располагаться цифры.
Как строить графики в Excel? | Блог Александра Воробьева
- Выделить таблицу с данными.
- Перейти на вкладку «Вставка», где можно выбирать вариант диаграммы: например, простой график функции, круговой или точечный.
- Убедиться в том, что данные в таблице были автоматически распределены так, как это было запланировано. В данном случае ошибки нет: значения указаны по оси X, даты — по OY.
К примеру, нужно показать не только число поступивших в вуз, но ещё и количество выпускников за тот же период. То есть появляется уже больше исходной информации в таблице. Хотя принцип создания графика не меняется. Зато есть смысл не удалять легенду.
Как построить график функции в Microsoft Excel
В MS Excel есть возможность не только проводить вычисления, используя разные формулы, но и также строить на их основе различные диаграммы: гистограммы, круговые диаграммы, точечные и т.д. В этом уроке мы разберем, для чего применяют графики. И так, графики – это разновидность диаграммы, схожая с гистограммой. Они бывают трех видов: простой, график с накоплением и нормированный график с накоплением. Каждый из этих графиков бывает двух видов: с маркером и без. Так эти два вида строятся одинаково, рассмотрим только маркированные графики. Коротко опишем применение каждого графика, и далее на примерах разберем более подробно, как их построить. a) Простой график нужен для того, чтобы изобразить, как изменяется некое значение во времени (прибыль по месяцам; рождаемость по годам и т.д.). b) График с накоплением показывает, как изменяется составляющая целого значения с течением времени. (Лучше использовать диаграмму с накоплением) c) Нормированный график с накоплением показывает изменение доли каждого значения с течением времени. Есть еще объемный график, который схож с простым графиком. Поэтому мы покажем только его конечный вид.






Принцип создания линейчатой диаграммы
Линейчатая диаграмма в Excel применяется для отображения совершенно разных информативных данных, касающихся выбранной таблицы. Из-за этого возникает потребность не только создать ее, но и настроить под свои задачи. Сперва следует разобраться с выбором линейной диаграммы, а уже потом перейти к изменению ее параметров.
-
Выделите необходимую часть таблицы или ее целиком, зажав левую кнопку мыши.
Простая диаграмма
Рассмотрим простой график на примере таком примере прибыли некоторой фирмы по 3 товарам за определенный период. Для этого выделим нужные нам ячейки, как на рисунке ниже.
Теперь строим простой маркированный график. Для этого выделяем диапазон В1:D6, на главное ленте выбираем Вставка–Диаграммы (нажимаем на стрелочку справа сверху). В появившемся окне выберем нужную нам диаграмму. В первом случае – простой график. Нажимаем ОК.
Выбираем график слева, т.к. он показывает изменение прибыли во времени. Если вы все сделали правильно, то должно получиться так, как на рисунке ниже:
Итак, диаграмма построена, но на ней не отображаются года. Изменить название диаграммы очень просто. Нужно нажать на заголовок и ввести подходящее название. Например, Прибыль по товарам в 2010-214 гг. Для того, чтобы года отображались на оси Х, необходимо нажать на ось правой кнопкой мыши для вызова контекстного меню и нажать Выбрать данные.
После этого появится такое окошко:
Изменяем подписи горизонтальной оси. Должно открыться такое окошко:
Нажимаем туда, где выделено красным и выбираем диапазон. В нашем случае это А2:А6. И нажимаем клавишу Enter и ОК. В результате этого должно открыться предыдущее окно, но выглядеть будет следующим образом:
Нажимаем ОК, меняем название диаграммы. Теперь она должна выглядеть так:
Осталось добавить подписи данных. В версии Excel 2013–2016 это делается очень просто. Нажимаем на плюсик справа, который вызывает различные команды и ставим галочку Название осей. Должно получиться так:
Как и в случае с названием, ставим курсор в область каждой из осей и подписываем их согласно условию. Например, ось Х – Год, ось Y – Прибыль. Должно получиться так, как на рисунке ниже:
В MS Excel версиях 2007-2010 форматировать оси, область диаграммы и т.д. с помощью дополнительной вкладки на ленте Работа с диаграммами.










Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо

График квадратичной функции
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо

График кубической параболы
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.

График гиперболы
График с накоплением
Строим по этим же данным график с накоплением. Повторяем все те же самые действия, как и в п.1. Поэтому мы покажем начало, на котором видно, какой график выбираем, и конец, на котором виден результат работы.
Объемный график
Объемный график похож на первый с той лишь разницей, что выполнен в объеме.
В этой работе были рассмотрены различные варианты построения такой разновидности диаграмм, как графики. А также случаи их применения. Для изучения построения диаграмм в программе Эксель заходите читать статьи на Справочнике!
Как сделать таблицу для гиперболы
В программе эксель можно построить многие функции, которые проходят в школе на уроках математики. Давайте рассмотрим подробную инструкцию, как в программе эксель построить гиперболу.
Второй этап. В ячейке «В2» пропишем следующую формулу: «=1/A2». После необходимо её скопировать на остальные ячейки, кроме пустой строки. В итоге данные для построения гиперболы готовы.
Третий этап. Выделим область со значением, в т.ч. пустую строку. После на верхней панели зайдем во вкладку «Вставка», где среди возможных графиков, выберем «Точечная». В появившемся меню выберем второй график.
Четвертый этап. График гиперболы готов, но его стоить оформить: подписать оси и функцию.
Пятый этап. Чтобы подписать оси, вам нужно на панели «Вставка», справа отыскать блок «Текст», в котором нажать на иконку с надписью «Надпись». Появившимся курсором, нажимаете на любую область графика, прописываете название оси и потом перетаскиваете в нужное место, чтобы получилось в итоге обе подписи:
Шестой этап. Выделите надпись «Ряд1», нажмите на правую клавишу, чтобы появилось меню, в котором выберете «Выбрать данные», на экране появиться новое меню, в его левой части вы увидите название «Ряд1», выделите его и нажмите на кнопку «Изменить», в появившемся меню можете отредактировать название, после закрывайте все дополнительные таблицы. Сверху может тоже появиться название функции, его можно удалить.
Видео как постоить гиперболу в excele
Гипербола. График функции и свойства.
теория по математике 📈 функции
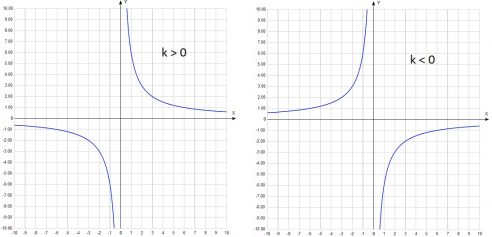
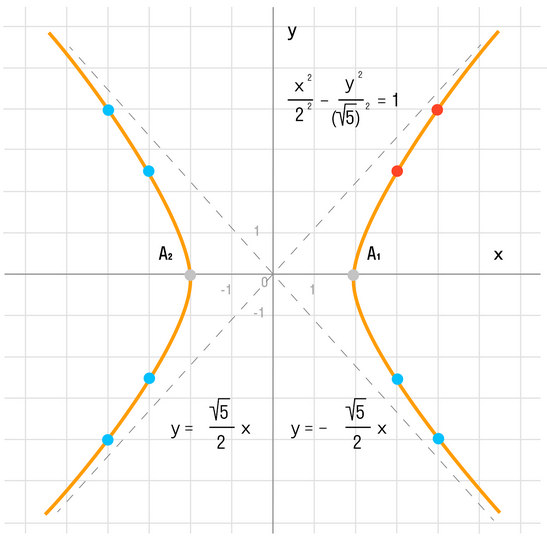
Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.
График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.
Построение графика функции
Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.
Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось
| х | 1 | 2 | 4 | 5 | 10 |
| у |
| х | –1 | –2 | –4 | –5 | –10 |
| у |
Теперь делим на эти числа 10, получим значения у:
| х | 1 | 2 | 4 | 5 | 10 |
| у | 10 | 5 | 2,5 | 2 | 1 |
| х | –1 | –2 | –4 | –5 | –10 |
| у | –10 | –5 | –2,5 | –2 | –1 |
Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.
Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.
| х | 1 | 2 | 5 | 10 |
| у | –5 | –2,5 | –1 | –0,5 |
| х | –1 | –2 | –5 | –10 |
| у | 5 | 2,5 | 1 | 0,5 |
Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.
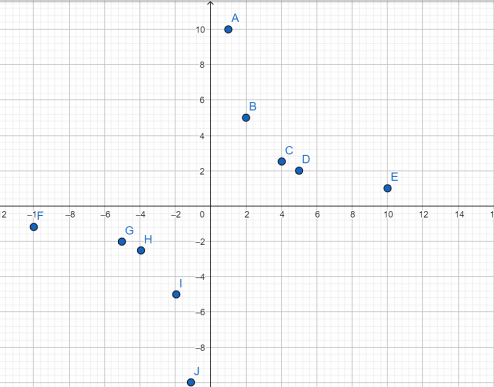
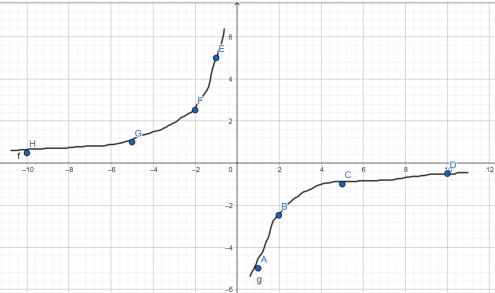
Установите соответствие между графиками функций и формулами, которые их задают.

Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Способы построения гиперболы самостоятельно
Гипербола в математике — что это такое
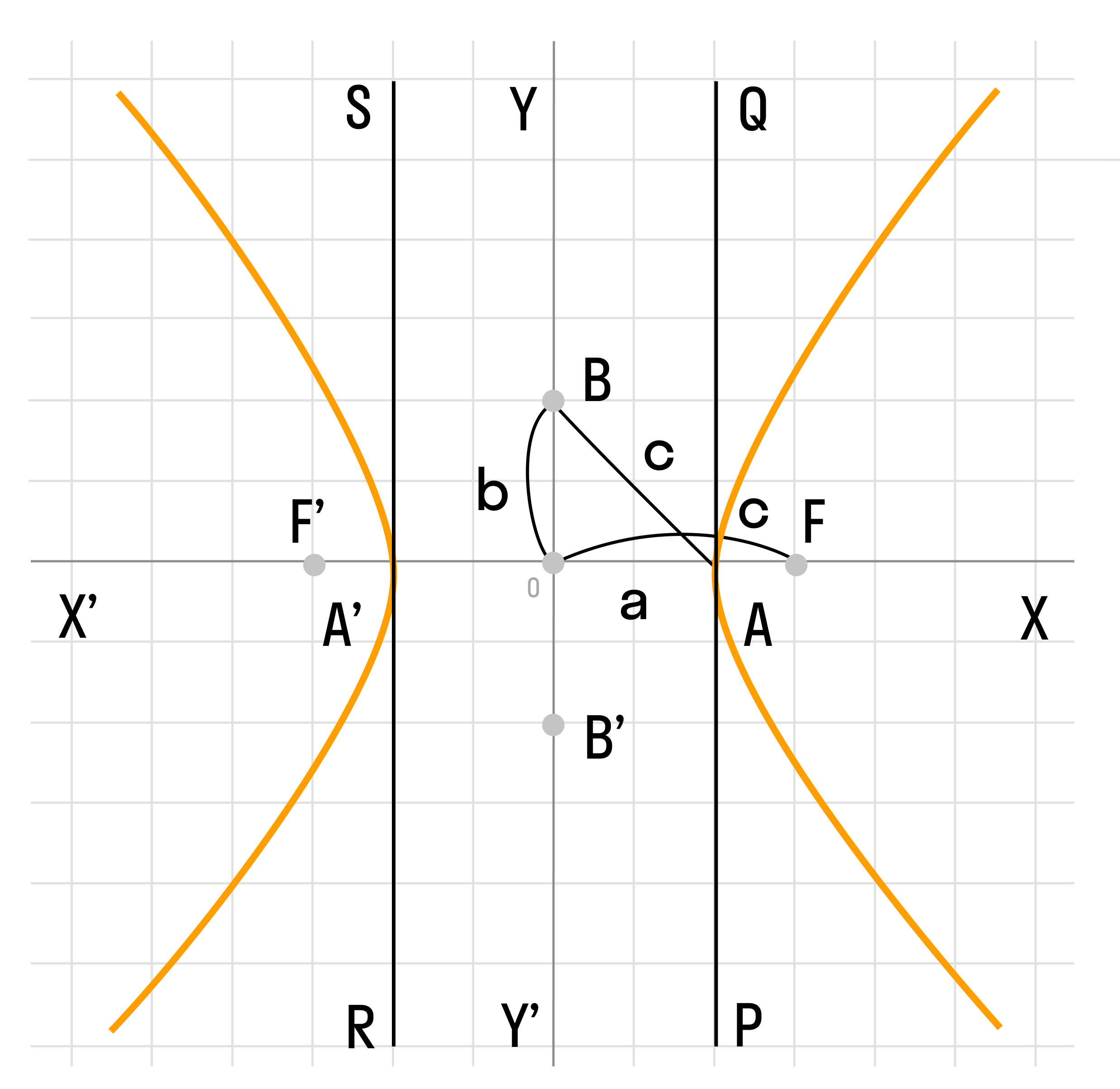
Гипербола представляет собой линию, определяемую в некой декартовой прямоугольной системе координат каноническим уравнением:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Ось ординат не имеет общих точек с гиперболой. В состав гиперболы входят две части, которые не связаны между собой. Они носят название ветвей гиперболы. Числа «a» и «b» являются соответственно вещественной и мнимой полуосями гиперболы.
Ветви гиперболы — это две отдельные кривые, из которых состоит гипербола.
Ближайшие друг к другу точки двух ветвей гиперболы являются вершинами гиперболы.
Большая ось гиперболы — наименьшее расстояние между двумя ее ветвями.
Центр гиперболы — это середина ее большой оси.
Большая полуось гиперболы — расстояние, на которое удалены центр и одна из вершин, обозначается «а».
Фокальное расстояние гиперболы — расстояние, на которое удалены друг от друга центр и один из фокусов, обозначается «с».
Оба фокуса гиперболы расположены на продолжении большой оси и равноудалены от центра гиперболы.
Прямая, включающая в себя большую ось гиперболы, носит название действительной, или поперечной, оси гиперболы.
Прямая в виде перпендикуляра к действительной оси, которая пересекает центр гиперболы — мнимая, или сопряженная ось гиперболы.
Отрезок между фокусом гиперболы и гиперболой, который перпендикулярен к действительной оси, — это фокальный параметр.
Прицельный параметр — расстояние от фокуса до асимптоты гиперболы, обозначается «b».
Перечисленные характеристики гиперболы взаимосвязаны. Справедливы следующие соотношения:
Оси симметрии гиперболы представляют собой оси канонической системы координат, а начало канонической системы является центром симметрии.
Когда требуется исследовать форму гиперболы, следует начать с поиска ее пересечения с произвольной прямой, пересекающей начало координат. Уравнение прямой можно задать в виде:
Такой выбор связан с тем, что прямая (x=0 ) не пересекает гиперболу. Абсциссы точек пересечения можно вычислить с помощью уравнения:
Таким образом, при (b^ -a^ k^ > 0) получим:
Полученное равенство позволит рассчитать координаты точек пересечения:
Руководствуясь свойством симметрии, можно проанализировать смещение первой из точек при изменении k, как показано на рисунке.
Прямая (y=bx/a) с угловым коэффициентом (b/a) не имеет точек пересечения с гиперболой, как и прямые с большими угловыми коэффициентами. Какая-либо прямая, обладающая меньшим положительным угловым коэффициентом, пересекает гиперболу.
К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a) : она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из вышесказанного следует вывод, что гипербола имеет вид, изображенный на рисунке.
Асимптоты гиперболы являются прямыми, описываемыми уравнениями (y=bx/a) и (y=-bx/a ) в канонической системе координат.
Предположим, что уравнения асимптот имеют вид:
Расстояния от точки (M(x, y)) до асимптот составят
В том случае, когда точка M расположена на гиперболе:
Из данного определения можно вывести ключевое свойство, которым обладают асимптоты гиперболы.
В том случае, когда точка совершает движение по гиперболе таким образом, что ее абсцисса по абсолютной величине неограниченно возрастает, расстояние от точки до одной из асимптот стремится к нулю.
В действительности получим, что хотя бы одно из расстояний (h_ ) или (h_ ) при этих условиях должно неограниченно увеличиваться. Если предположить, что утверждение не справедливо, то произведение не было бы постоянной величиной.
Введем такое число с, что:
Фокусы гиперболы — точки (F_ ) и (F_ ) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат.
Расстояния от произвольной точки (M(x, y)) на гиперболе до каждого из фокусов определяются абсциссой (x) :
Следует отметить, что равенства eqref можно представить в более подробной форме:
Директрисы расположены поблизости от центра в отличие от вершин. Из этого можно сделать вывод, что директрисы не имеют точек пересечения с гиперболой. Директриса и фокус, которые расположены по одну сторону от центра, считаются соответствующими друг другу.
Для того чтобы точка (M) была расположена на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы 2a.
С целью доказательства достаточности данного условия его следует записать в виде:
Следующие действия отличаются от доказательства соответствующего утверждения для эллипса только тем, что нужно воспользоваться равенством:
Можно доказать, к примеру, необходимость условия для фокуса (F_ (-c, 0).) Предположим, что (M'(x, y)) является точкой гиперболы. Расстояние от (M’) до директрисы с уравнением (x=-a/varepsilon) равно:
Касательная к гиперболе в точке (M_ (x_ , y_ )) представляет собой биссектрису угла между отрезками, которые соединяют рассматриваемую точку с фокусами.
Как построить гиперболу самостоятельно
Построение графика гиперболы следует начать с изображения прямоугольной системы координат Декарта. Алгоритм действий:
Гипербола представляет собой график функции, которая задана формулой:
где (k) — является каким-то коэффициентом, не равным нулю;
(x) — представляет собой независимую переменную.
Принцип построения гиперболы можно рассмотреть на примере, когда функция задана следующей формулой:
Полученные 6 точек с координатами необходимо отложить на системе координат. Далее точки соединяют с помощью кривых линий, как изображено на рисунке. В итоге получилась гипербола.
Построение гиперболы по фокусам
Что такое гипербола
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие гиперболы
Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы в алгебре выглядит так:
, где a и b — положительные действительные числа.
Кстати, канонический значит принятый за образец.
В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.
Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.
Вспомним особенности математической гиперболы:
Если гипербола задана каноническим уравнением, то асимптоты можно найти так:
Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:
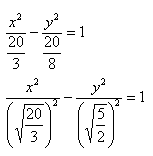
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).
В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.
Способ такой же, как при построении эллипса. Из полученного канонического уравнения
на черновике выражаем:
Уравнение распадается на две функции:
— определяет верхние дуги гиперболы (то, что ищем);
— определяет нижние дуги гиперболы.
Далее найдем точки с абсциссами x = 3, x = 4:
Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.
Действительная ось гиперболы — отрезок А1А2.
Расстояние между вершинами — длина |A1A2| = 2a.
Действительная полуось гиперболы — число a = |OA1| = |OA2|.
Мнимая полуось гиперболы — число b.
В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.
Форма гиперболы
Повторим основные термины и узнаем, какие у гиперболы бывают формы.
Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.
Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.
Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.
Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.
Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.
Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.
Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Фокальное свойство гиперболы
Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).
Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:
Рассмотрим, как это выглядит на прямоугольной системе координат:
Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:
Запишем это уравнение в координатной форме:
Избавимся от иррациональности и придем к каноническому уравнению гиперболы:
, т.е. выбранная система координат является канонической.
Директориальное свойство гиперболы
Директрисы гиперболы — это две прямые, которые проходят параллельно оси.
ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.
Директориальное свойство гиперболы звучит так:
Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.
Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
На самом деле для фокуса F2 и директрисы d2 условие
можно записать в координатной форме так:
Построение гиперболы
Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.
Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.
В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:
Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:
Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.
По определению эксцентриситет гиперболы равен
Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.
Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.


В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.
Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).
Построим график функции, называемый гиперболический параболоид, в Excel.
Уравнение гиперболического параболоида (общий вид):
где x, y, z — переменные; a, b — константы.
Рассмотрим конкретный случай:
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.
по горизонтали — значения х, по вертикали — значения у.
Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.
Для того, чтобы эта формула правильно копировалась с помощью маркера автозаполнения необходимо верно поставить знаки $ в формулу.
=(C$2^2/4)-($B3^2/9) , для ячейки со значением x фиксируем номер строки, для ячейки со значением y фиксируем букву столбца.
Используя маркер автозаполнения, копируем формулу для всех значений x и y.
Получим таблицу, в которой каждой паре (x, y) соответствует координата z.
Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Функция – это отображение элементов множества X на множество Y . При этом каждому элементу x множества X соответствует одно единственное значение y множества Y .
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
<img src=»/images-s1/3/kak-postroit-grafik-FA0D.png» alt=»График линейной функции, a
Если a = 0 , функция принимает вид y = b .
Парабола
Графиком функции y = a x 2 + b x + c является парабола .
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y .
- Коэффициент b помогает найти x в – координату вершины параболы.
Гипербола
Графиком функции y = k x является гипербола .
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .
Квадратный корень
Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале , если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Функция y = f ( x ) убывает на интервале , если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Для того, чтобы найти наибольшее значение функции , находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции , находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.
[expert_bq того, чтобы построить заданный орнамент мы его построим на определенном интервале, а затем перенесем все вычисления на заданный шаг и т. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq] Если рассмотреть любой геометрический орнамент, то с математической точки он представляет собой набор прямых или кривых на заданном интервале, иногда на одном интервале может быть задано несколько различных линий. Совокупность этих линий и кривых образует рисунок который и будем считать орнаментом.
Гипербола. График функции и свойства. ⋆ СПАДИЛО
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y .
- Коэффициент b помогает найти x в – координату вершины параболы.
В действительности получим, что хотя бы одно из расстояний (h_) или (h_) при этих условиях должно неограниченно увеличиваться. Если предположить, что утверждение не справедливо, то произведение не было бы постоянной величиной.
Гипербола
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Функция заданная формулой (y=frac), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:
1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k 0 ветви гиперболы находятся в 1 и 3 четверти.» width=»300″ height=»225″ /> гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти
Пример №2:
$y=frac-1$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Дробь (color >) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k
8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама
[expert_bq функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq] Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.
Построение и исследование графиков функций при помощи электронных Таблиц Excel. » | Образовательная социальная сеть
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2 . В другую ячейку формулу можно ввести аналогично (изменив D4 на D5 ) или использовать маркер автозаполнения.