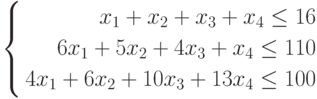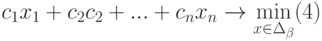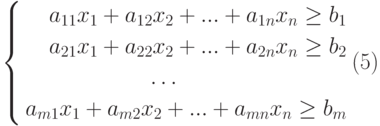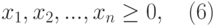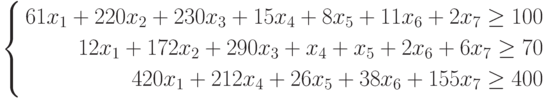Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике
Содержание
- Как включить функцию “Поиск решения”
- Подготовительный этап
- Применение функции и ее настройка
- Заключение
Как включить функцию “Поиск решения”
Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:
- Открываем меню “Файл”, кликнув по соответствующему названию.
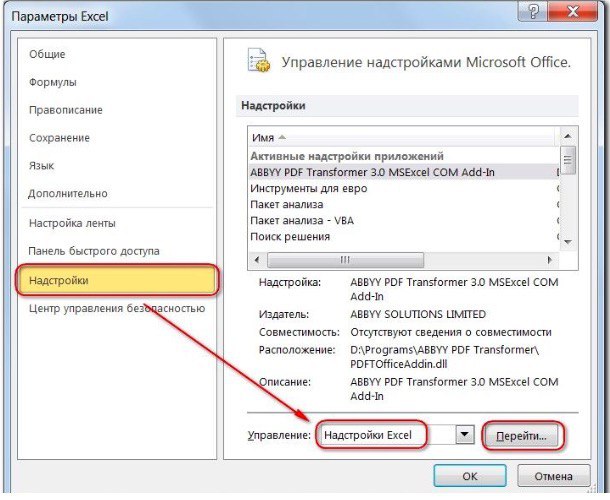
- Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
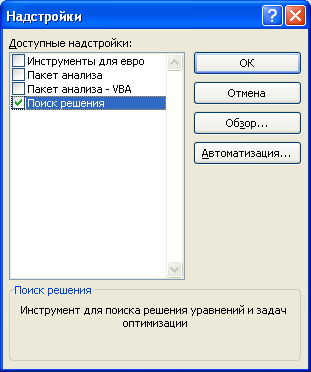
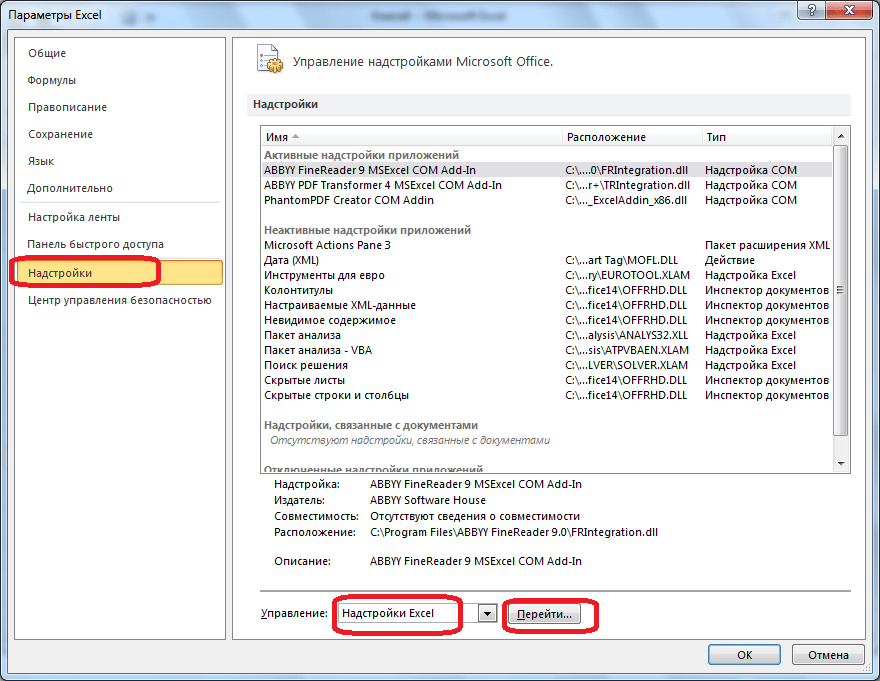
- Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
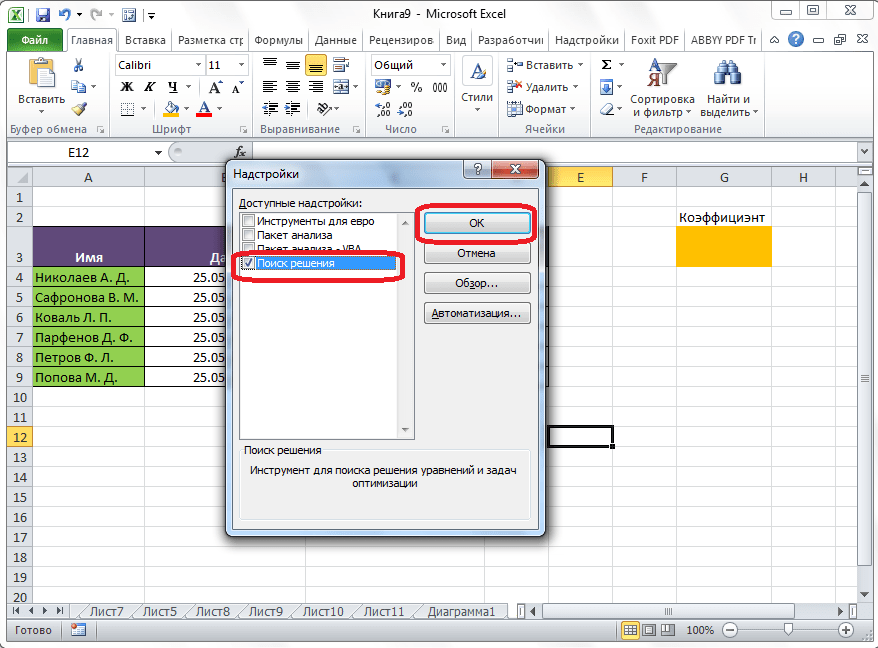
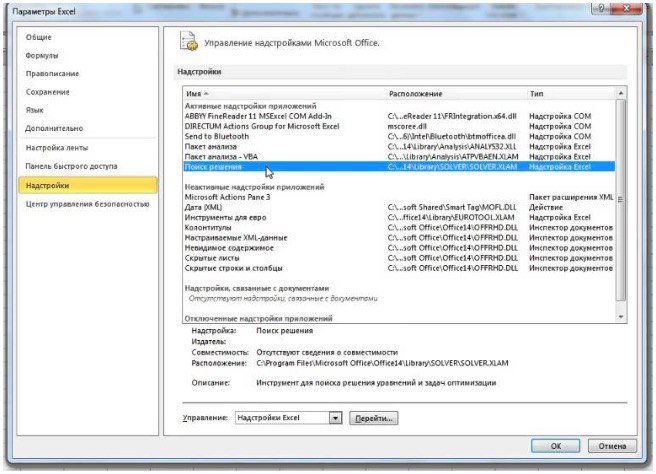
- На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
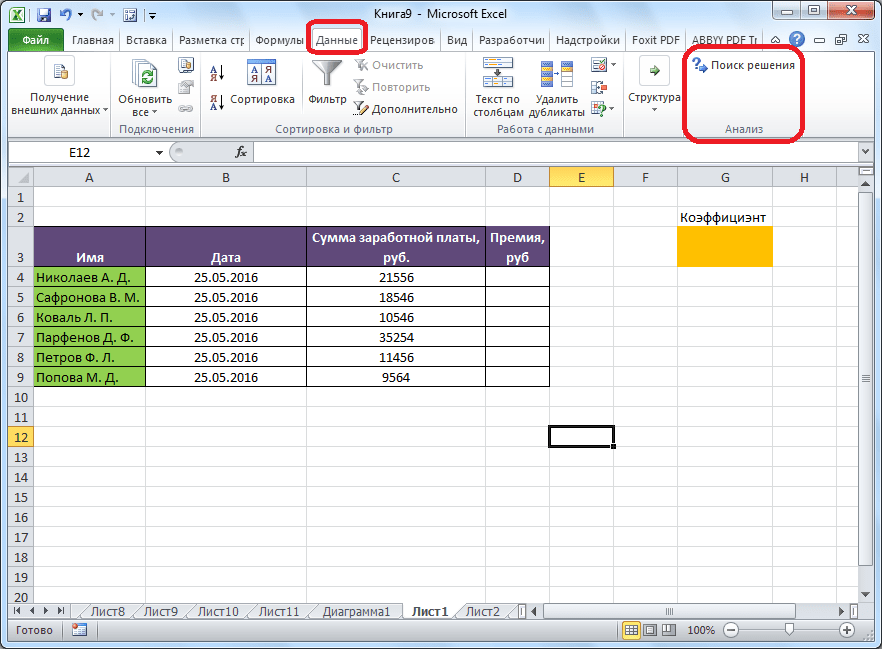
- Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.
Подготовительный этап
Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.
Итак, у нас есть данные про продаже товаров, представленные в табличном виде.
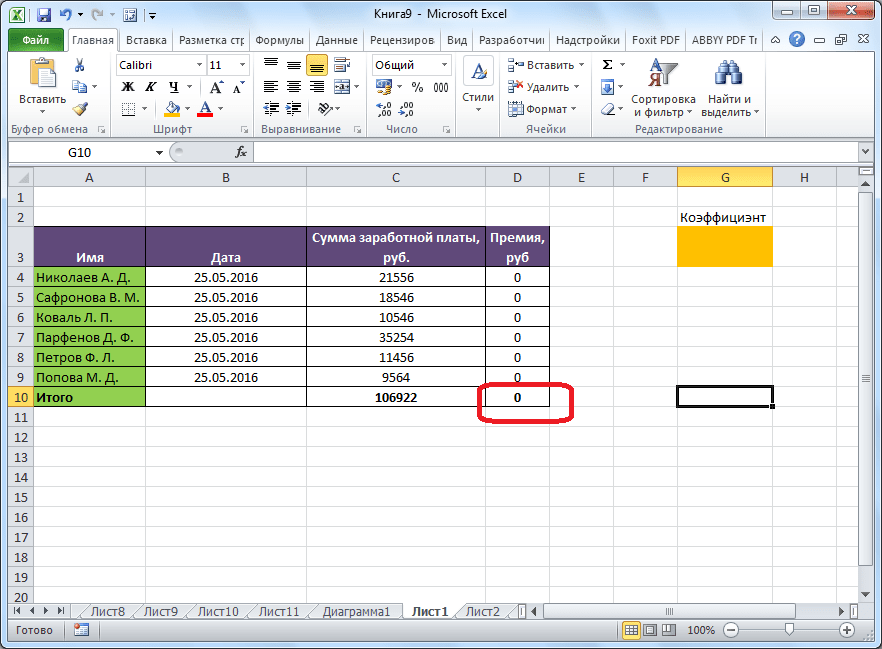
И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.
Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.
Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.
Применение функции и ее настройка
Формула готова. Теперь нужно применить саму функцию.
- Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
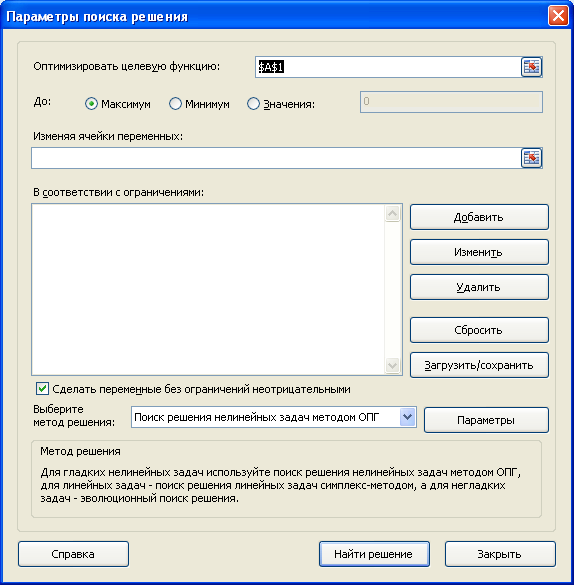
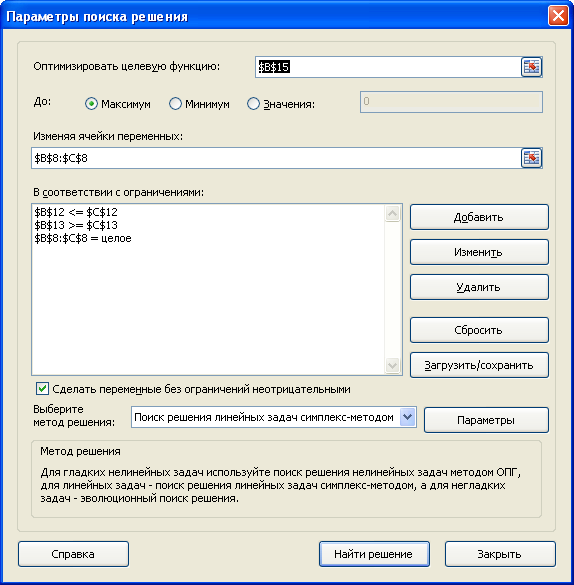
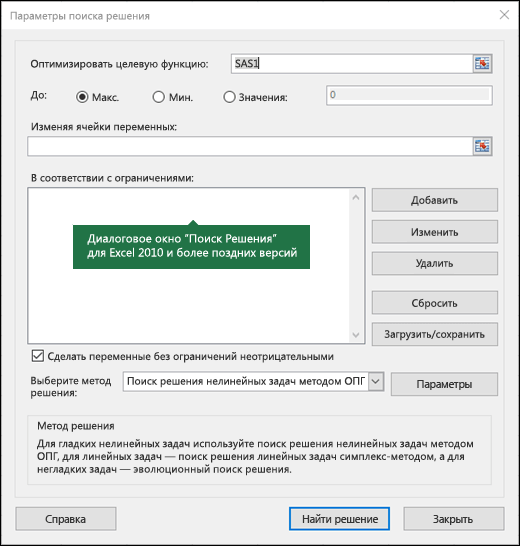
- Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
- Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
- Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
- Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
- Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
- После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
- Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
- В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
- Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
- После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
- Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
- Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
- Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
- Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
- Теперь наша таблица полностью готова в соответствии с поставленной задачей.
Заключение
Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.
«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.
Основные параметры поиска решений
Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.
Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:
Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).
Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон. При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.
Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.
Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.
Пример использования поиска решений
Теперь перейдем к самой функции.
1) Чтобы включить «Поиск решений», выполните следующие шаги:
- нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
- в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
- в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».
Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.
В нашем примере следующие ограничения:
- общее количество изделий 1000 штук ($D$13 = $D$3);
- число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
- количество дней меньше либо равно 30 ($F$9:$F$12 < = $D$6, либо как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).
5) В конце проверьте полученные данные на соответствие заданному целевому значению. Если что-то не сходится — нужно пересмотреть исходные данные, введенные формулы и ограничения.
Хотите научиться решать задачи в Excel, как это делают в компаниях-лидерах? Приходите на наш онлайн-курс, на котором вы освоите этот инструмент на уровне профи. Вашими преподавателями будут эксперты-практики, а после обучения вы сможете дополнить резюме весомой строчкой. Регистрируйтесь!
Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в
MS EXCEL 2010
(эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в
MS EXCEL 2007)
. В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
-
настройку
Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда
Поиск решения
находится в группе
Анализ
на вкладке
Данные
.
Если команда
Поиск решения
в группе
Анализ
недоступна, то необходимо включить одноименную надстройку. Для этого:
-
На вкладке
Файл
выберите команду
Параметры
, а затем — категорию
Надстройки
; -
В поле
Управление
выберите значение
Надстройки Excel
и нажмите кнопку
Перейти;
-
В поле
Доступные надстройки
установите флажок рядом с пунктом
Поиск решения
и нажмите кнопку ОК.
Примечание
. Окно
Надстройки
также доступно на вкладке
Разработчик
. Как включить эту вкладку
читайте здесь
.
После нажатия кнопки
Поиск решения
в группе
Анализ,
откроется его диалоговое окно
.
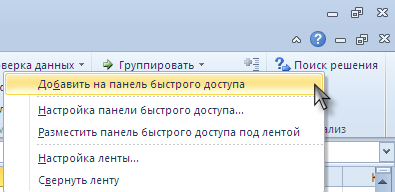
При частом использовании
Поиска решения
его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт
Добавить на панель быстрого доступа
.
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет
. Перед использованием
Поиска решения
настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка
Поиск решения
помогает определить
лучший способ
сделать
что-то
:
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
-
Определить
план производства
, при котором доход от реализации произведенной продукции максимальный;
-
Определить
схему перевозок
, при которой общие затраты на перевозку были бы минимальными;
-
Найти
распределение нескольких станков по разным видам работ
, чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется
Поиском решения
только по одному показателю
(этот оптимизируемый показатель называется
целевой функцией
). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.
Поиск решения
подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание
. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента
Подбор параметра
. Перед первым знакомством с
Поиском решения
имеет смысл сначала детально разобраться с родственным ему инструментом
Подбор параметра
. Основные отличия
Подбора параметра
от
Поиска решения
:
Подбор параметра
работает только с моделями с одной переменной;- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения
оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне
Поиска решения
возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет
. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки
Поиска решения
(см. ниже).
Приведем алгоритм работы с
Поиском решения
, который советуют сами разработчики (
]]>
www.solver.com
]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
-
С помощью диалогового окна
Поиск решения
введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений; -
Запустите
Поиск решения
для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования
Поиска решения
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см.
файл примера
).
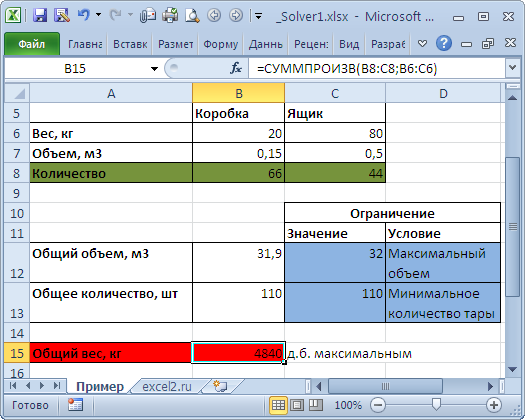
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему (<=32) – синим. Целевая функция рассчитывается по формуле
=СУММПРОИЗВ(B8:C8;B6:C6)
– это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем —
=СУММПРОИЗВ(B7:C7;B8:C8)
. Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков (<=32). Также для задания ограничения модели рассчитаем общее количество тары
=СУММ(B8:C8)
. Теперь с помощью диалогового окна
Поиск решения
введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки
Найти решение
будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Совет
: в статье »
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
» показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью
Поиска решения
является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью
Поиска решения
. Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью
Поиска решения
рассмотрено
в этом разделе
.
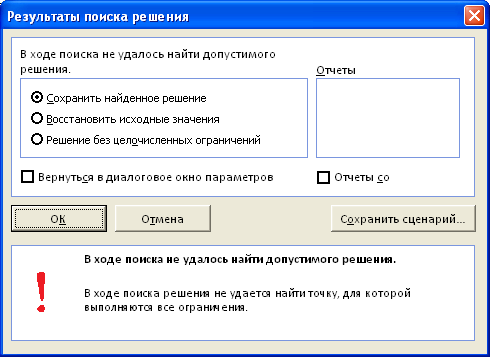
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда
Поиск решения
не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете
Симплекс метод решения линейных задач
, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите
Поиск решения
с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и
Поиск решения
не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае,
Поиск решения
может найти решение (если оно действительно существует).
Примечание
. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи
Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства
.
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3,
Поиск решения
не найдет решения.
При ограничении 17 м3
Поиск решения
найдет решение.
Некоторые настройки
Поиска решения
Метод решения
Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
Поиска решения
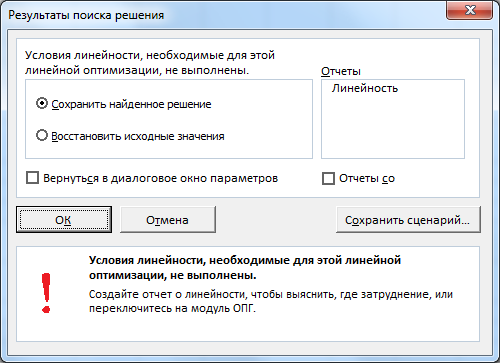
можно также проверить на линейность саму модель. В случае нелинейной модели Вы получите следующее сообщение:
В этом случае необходимо выбрать метод для решения нелинейной задачи. Примеры нелинейных зависимостей: V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2, где x – переменная, а V – целевая функция.
Кнопки Добавить, Изменить, Удалить
Эти кнопки позволяют добавлять, изменять и удалять ограничения модели.
Кнопка Сбросить
Чтобы удалить все настройки
Поиска решения
нажмите кнопку
Сбросить
– диалоговое окно очистится.
Сохранение и загрузка модели
Эта опция удобна при использовании разных вариантов ограничений. При сохранении параметров модели (кнопка
Загрузить/ Сохранить,
далее нажмите кнопку
Сохранить
) предлагается выбрать верхнюю ячейку диапазона (столбца), в который будут помещены: ссылка на целевую функцию, ссылки на ячейки с переменными, ограничения и параметры методов решения (доступные через кнопку
Параметры
). Перед сохранением убедитесь в том, что этот диапазон не содержит данных модели. Для загрузки сохраненных параметров нажмите сначала кнопку
Загрузить/ Сохранить
, затем, в появившемся диалоговом окне кнопку
Загрузить
, после чего задайте диапазон ячеек, содержащих сохраненные ранее настройки (нельзя указывать только одну верхнюю ячейку). Нажмите кнопку OK. Подтвердите сброс текущих значений параметров задачи и их замену на новые.
Точность
При создании модели исследователь изначально имеет некую оценку диапазонов варьирования целевой функции и переменных. Принимая во внимание
ограниченную точность
вычислений в MS EXCEL, рекомендуется, чтобы эти диапазоны варьирования были значительно выше точности вычисления (она обычно устанавливается от 0,001 до 0,000001). Как правило, данные в модели нормируют так, чтобы диапазоны варьирования целевой функции и переменных были в пределах 0,1 – 100 000. Конечно, все зависит от конкретной модели, но если ваши переменные изменяются более чем на 5-6 порядков, то возможно следует «загрубить» модель, например, с помощью операции логарифмирования.
Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.
Включение функции
Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».
Подготовка таблицы
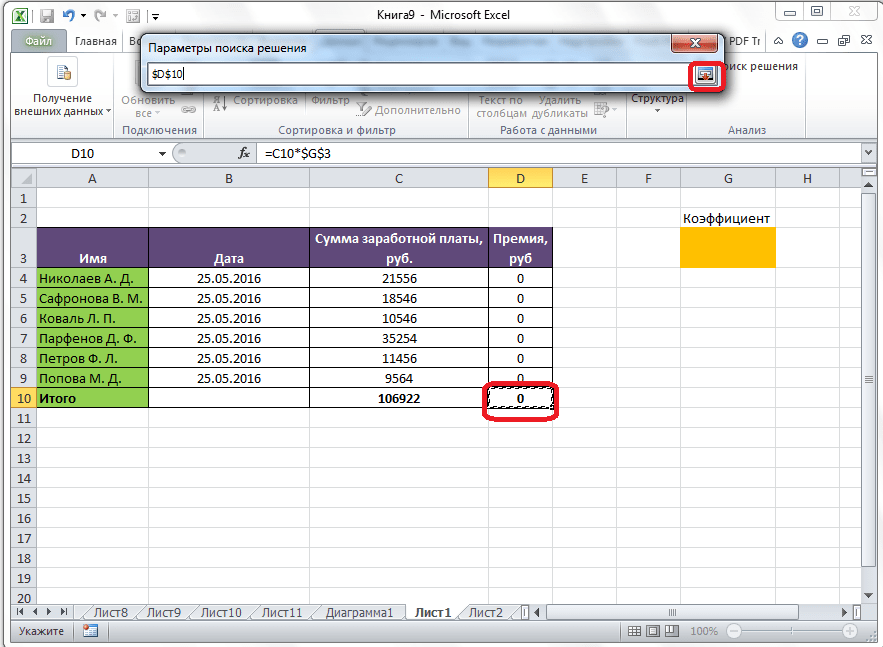
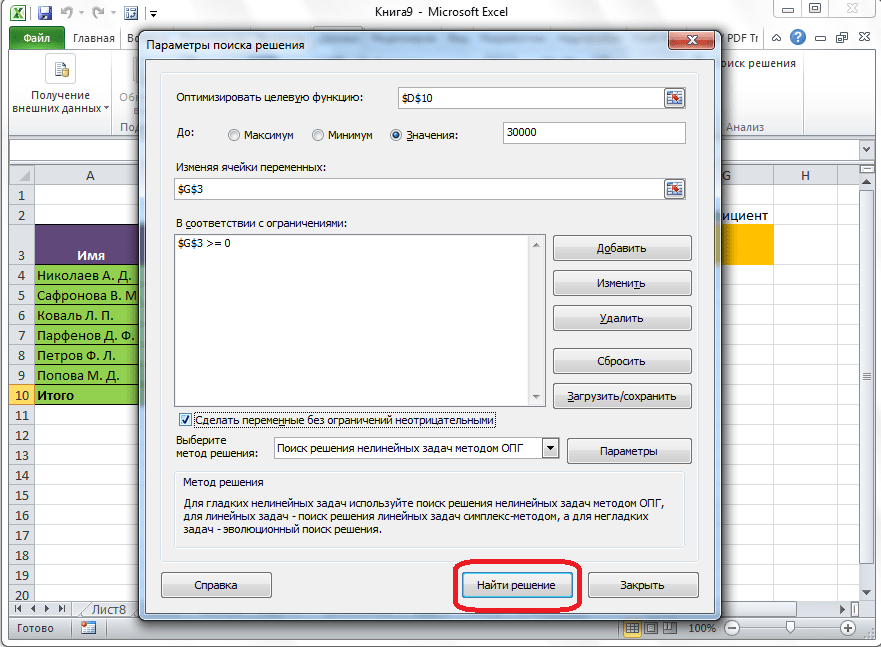
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.
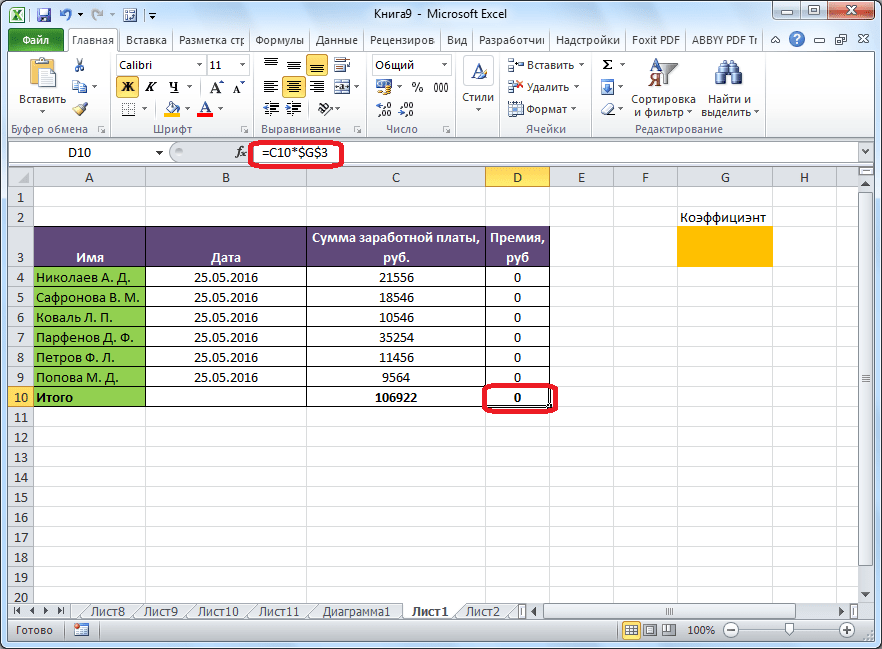
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.
Запуск инструмента Поиск решения
После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».
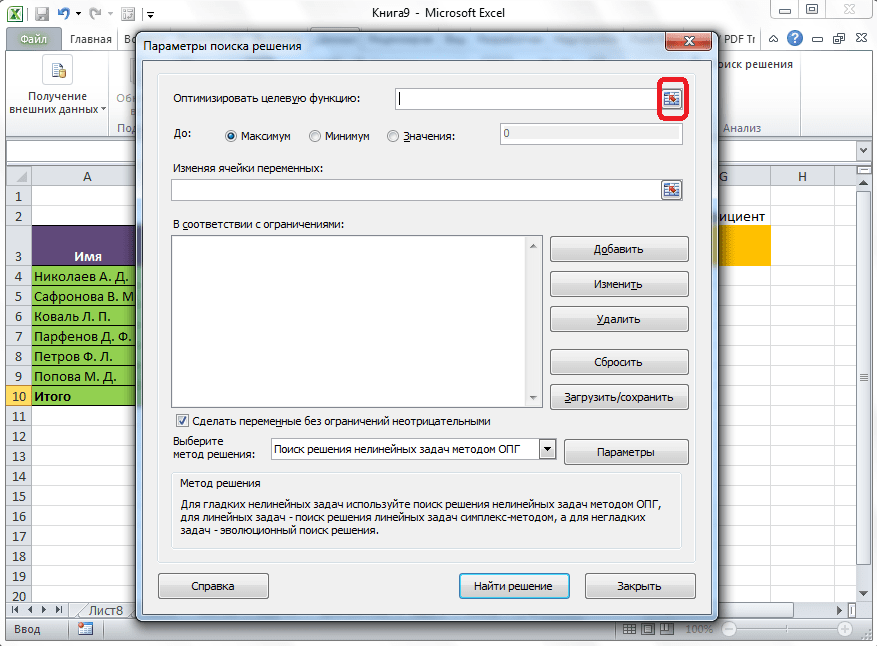
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.
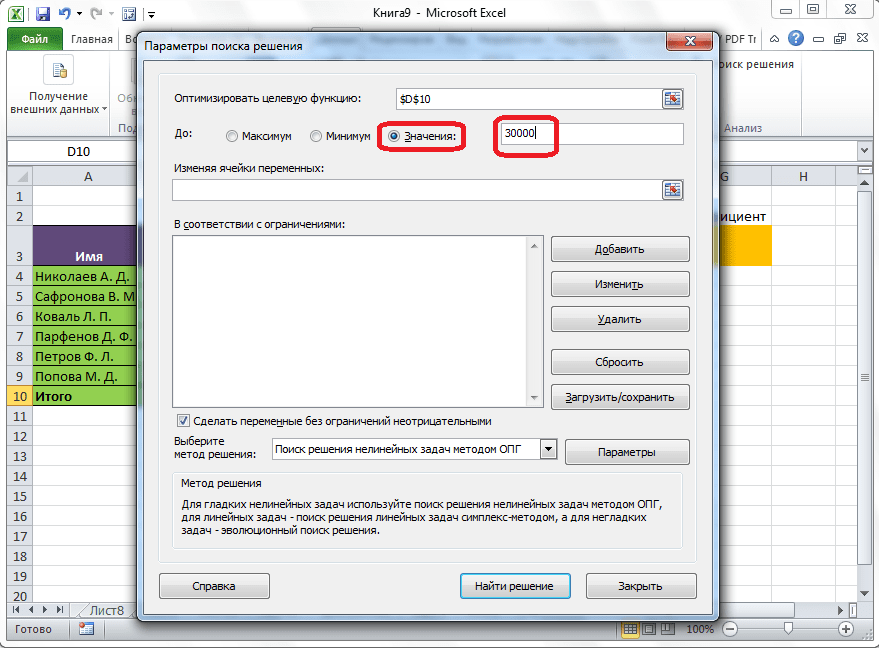
После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.
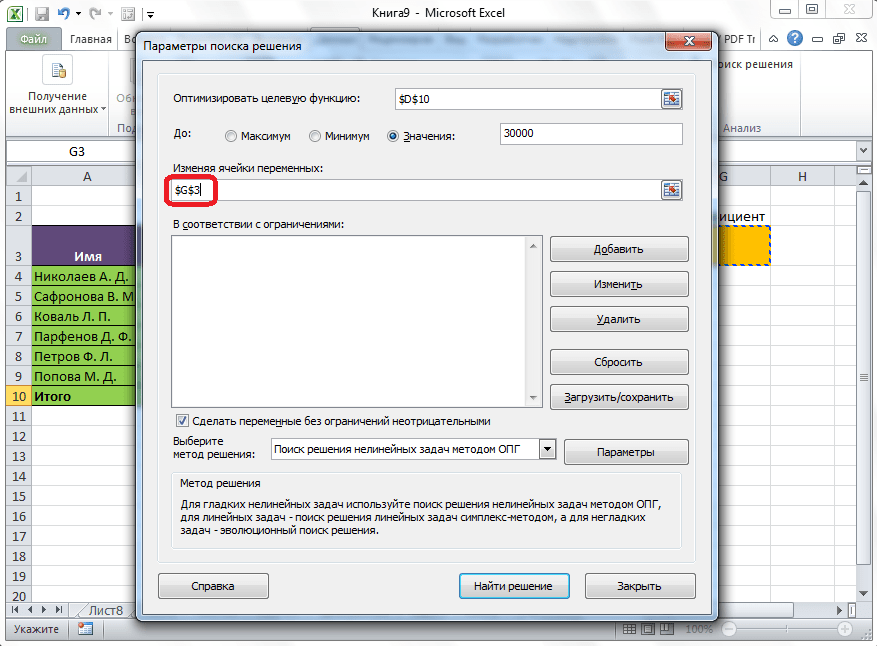
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.
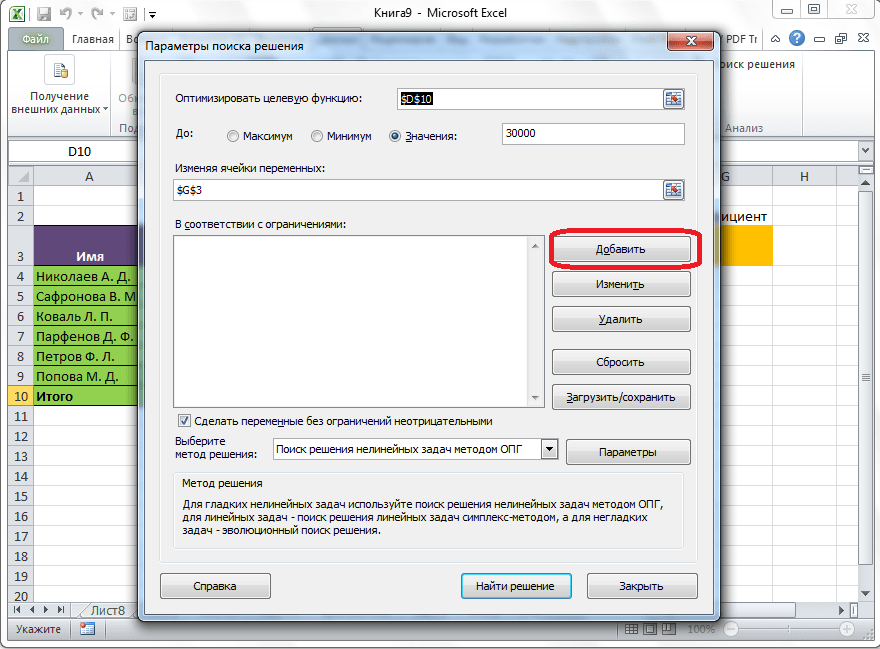
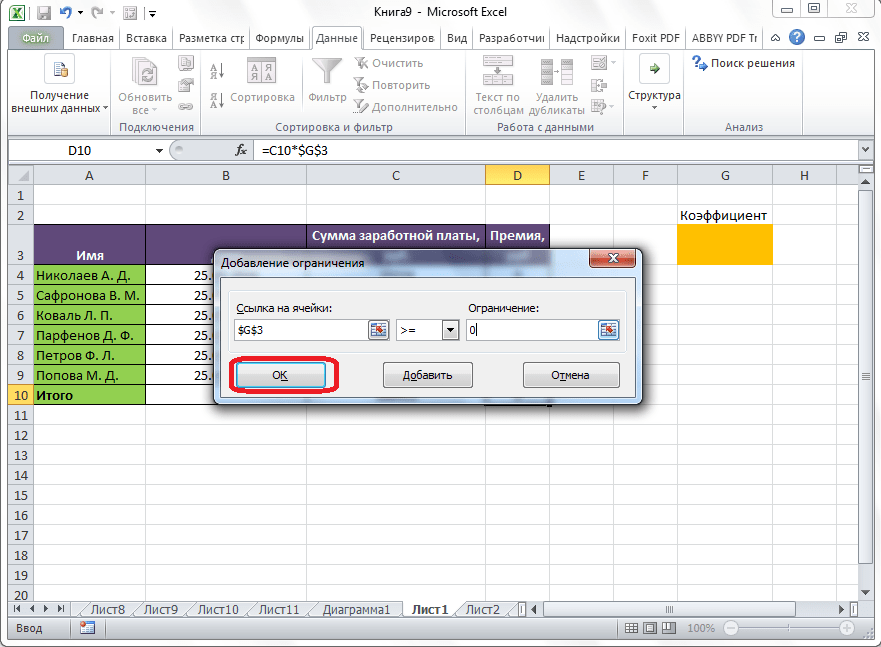
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.
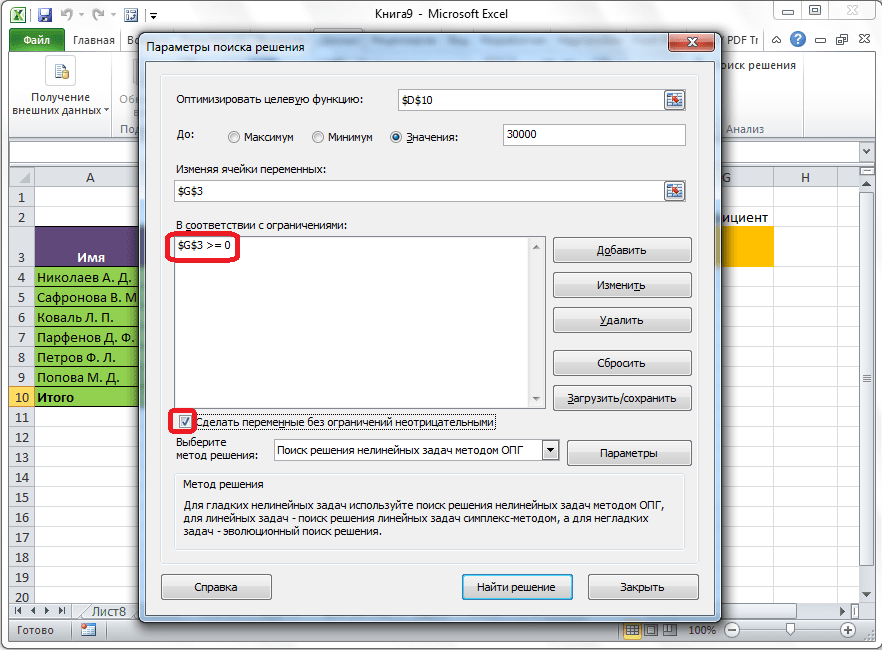
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».
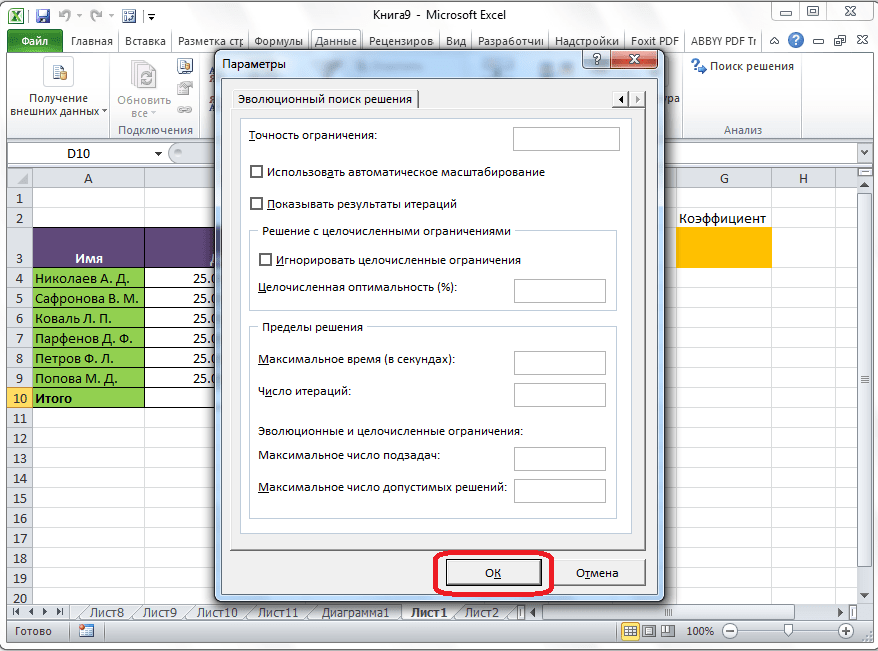
Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.
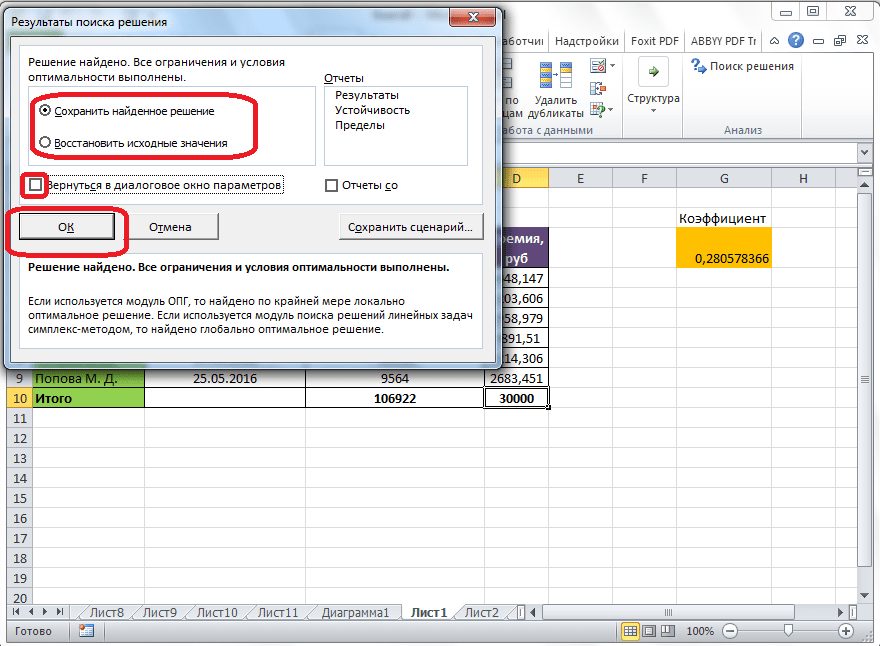
После того, как все настройки установлены, жмем на кнопку «Найти решение».
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».
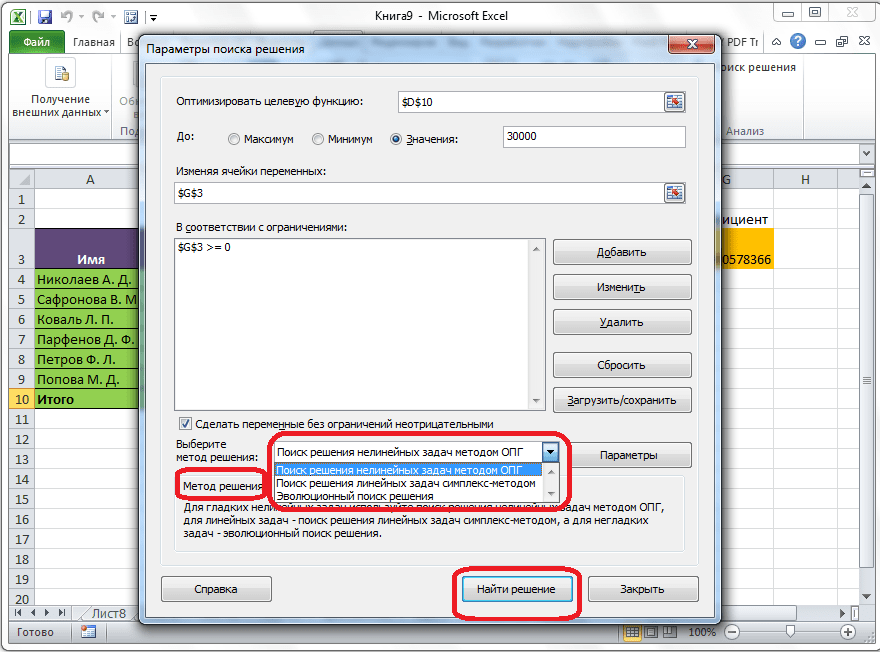
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.
Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.
Самое понятное объяснение, как это работает + коллекция новых задач
25.07.2017, Елена Позднякова
-
Оглавление
-
Как это работает
-
Какой ассортимент выпускать
-
Трансфертные цены
-
Задача инвестора
-
Настройка надстройки
Приходилось ли Вам когда-нибудь составлять план продаж, маркетинговый бюджет или схему доставки грузов? Если да, то наверняка какое-то решение зависело только от вашего профессионального суждения… Вы когда-нибудь сомневались в том, что Ваше решение наилучшее? Сожалели ли Вы о том, что не имеете возможности просчитать все варианты, ведь факторов так много, а время ограничено?
Умение легко и быстро найти правильный ответ, а еще и своевременно сформулировать вопрос, отличает профессионала высокого класса от начинающего специалиста.
Программа Excel умеет находить наилучшее решение там, где, казалось бы, лучше уже нельзя.
Чтобы это сработало, нужно уметь правильно сформулировать условия, это мы и будем учиться делать в настоящей статье.
Поиск решения — это надстройка программы Excel, по умолчанию она не установлена, поэтому, если Вы никогда ранее ее не использовали, ее нужно настроить.
На одном листе Excel будут расположены все исходные данные, формулы, взаимосвязи и ограничения: это называется математическая модель. В составе модели пять типов данных:
Константы — это исходная информация, которая имеется в модели: маржинальная прибыль по каждому продукту, стоимости перевозки от каждого поставщика к каждому покупателю, нормы расхода материалов и т.д. Эти данные могут быть как внесены и виде констант, так и рассчитываться с помощью формул.
Изменяемые ячейки — это переменные, которые мы в итоге ищем: количество продукта, которое нужно производить, чтобы прибыль была максимальной или объемы перевозок от каждого поставщика к конкретному покупателю, чтобы затраты были минимальными и т.д.
Изменяемая ячейка может быть одна или диапазон из нескольких ячеек.
Эти ячейки мы будем указывать, но оставлять пустыми, надстройка «Поиск решения» сама заполнит их наилучшими данными.
Целевая функция— для того, чтобы программа понимала, какие данные считать наилучшими, мы зададим целевую функцию. Это всегда только одна ячейка, в которую внесена формула. Формула связана с теми данными, которые мы ищем. Например, если мы ищем ассортимент, максимизирующий прибыль, формула целевой функции будет задана как сумма произведений количества каждого продукта (изменяемые данные) и маржинальной прибыли по каждому продукту (константы, внесенные в модель).
При запуске надстройки мы будем указывать, какие данные будут наилучшими для целевой ячейки: максимальное значение, минимальное значение или конкретное число.
Подбор данных в изменяемых ячейках будет осуществляться таким образом, чтобы в ячейке с целевой функцией появилось наилучшее значение.
Ограничения — являются главным элементом в Поиске решения. Все ресурсы, которые участвуют в модели и имеют максимально допустимые значения — это ограничения: объем инвестирования, объем покупательского спроса, срок реализации проекта.
Например, на складе всего 5 000 кг материала, который входит в состав всех продуктов, а мы ищем ассортимент, который даст максимальную прибыль. Чтобы правильно учесть ограничение, потребуется внести формулу, которая рассчитает объем материала, который потребуется для производства ассортимента Х — наших переменных. Далее уже непосредственно в самой надстройке будет задано ограничение:
Важно учитывать, что если переменные должны быть выражены неотрицательным или целым числом — это тоже ограничения, которые необходимо задать.
Дополнительные формулы — в модель может быть внесено любое количество дополнительных формул, которые не влияют на целевую функцию и ограничения, а несут справочную информацию по проекту.
Как это работает: пошаговая инструкция
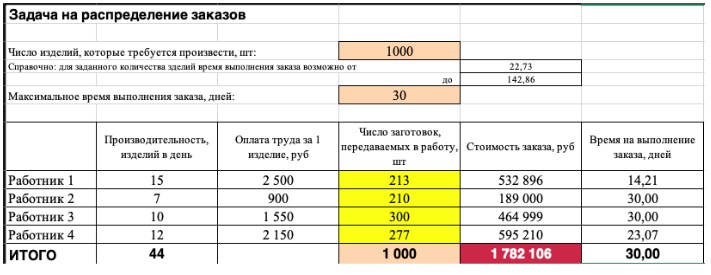
на примере задачи по распределению заказов
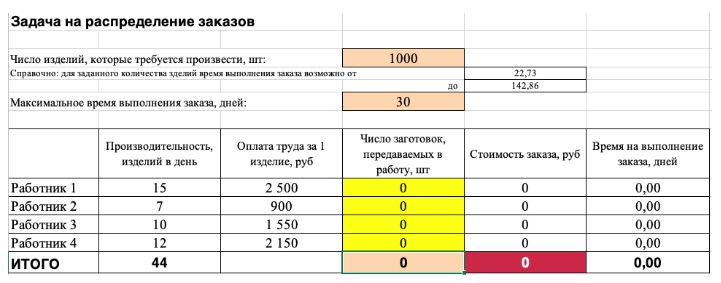
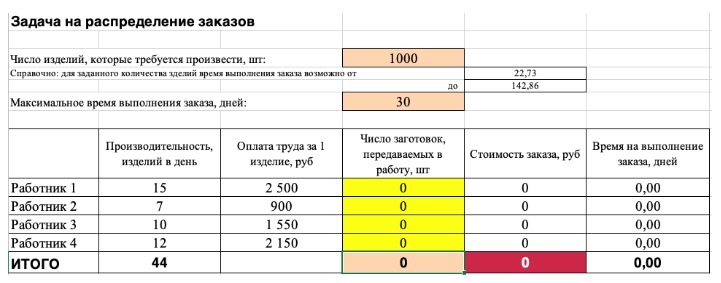
Попробуйте простыми расчетами решить такую задачу:
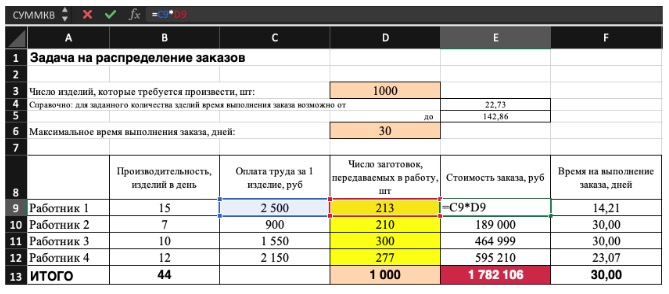
Компания занимается производством шкатулок ручной работы. В штате есть 4 мастера-надомника. Производительность мастеров в день представлена в таблице:
Мастер 1 — 3 шкатулки в день
Мастер 2 — 1,5 шкатулки в день
Мастер 3 — 2 шкатулки в день
Мастер 4 — 2,5 шкатулки в день
Поступил срочный заказ на 100 шкатулок и нужно раздать 100 заготовок, чтобы мастера успели справиться в самый короткий срок.
Сколько и кому раздать заготовок?
Эту задачу можно решить простыми расчетами, без использования поиска решений. Для начала так и поступим:
Рассчитаем, сколько шкатулок в день могут произвести все мастера:
3+1,5+2+2,5 = 9 шкатулок.
Теперь 100 шкатулок разделим на 9 шкатулок в день и получим 11,11 дней. Соответственно, сообщаем заказчику, что заказ будет готов за 12 дней
Распределим заготовки между мастерами с использованием округления:
Мастер 1: 3 х 11,11 = 33,33 Выдаем 34 заготовки
Мастер 2: 1,5 х 11,11 = 16,66 Выдаем 17 заготовок
Мастер 3: 2 х 11,11 = 22,22 Выдаем 21 заготовку
Мастер 4: 2,5 х 11,11 = 27,77 Выдаем 28 заготовок
А теперь дополним условие и введем индивидуальные тарифные ставки для мастеров за изготовление каждой шкатулки:
Мастер 1 — 1 500 руб
Мастер 2 — 950 руб
Мастер 3 — 1 100 руб
Мастер 4 — 1 150 руб
Рассчитаем для клиента, сколько стоит изготовить 100 шкатулок
34 х 1 500 = 51 000
17 х 950 = 16 150
21 х 1 100 = 23 100
28 х 1 150 = 32 200
Итого: 122 450
А теперь клиент задает нам вопрос, а если бы заказ был не срочный, во сколько минимально он мог бы обойтись? Как Вы думаете?
Посмотрим еще раз на таблицу с исходными данными:
Мы видим, что мастер 2, который работает медленнее всех — получает меньше всех. Значит, если мы не ограничены во времени и отдадим весь заказ ему, то вся работа будет стоить всего 95 000 (950 руб х 100 шкатулок). Но сколько это займет времени? 100/1,5 = 66,66 дней.
Таким образом, путем простых расчетов и логических рассуждений мы вывели основные отправные точки для диалога с клиентом:
Минимальный срок изготовления: 11,11 дней,
стоимость 122 450
Максимальный срок изготовления: 66,66 дней,
стоимость 95 000
Разница в сроке составляет 55,55 дней, а в сумме 27 450.
Вполне логично предположить, что клиент может задать вопрос:
А если я дам Вам срок 20 дней или месяц, как изменится стоимость?
Теоретически это задание можно решить простыми расчетами, но, надеюсь, Вы не затратили много времени на это, потому что нам пора применить опцию Поиск решения, чтобы мгновенно получать результат распределения заказов с учетом любых заданных ограничений!!!
Давайте вместе решим эту задачу с использованием надстройки «Поиск решения»
Создайте новый файл в программе Excel.
Проверьте, есть ли кнопка «Поиск решения» в закладке «Данные», если нет, то здесь инструкция, как ее установить.
Наша цель: как распределить заготовки, чтобы заказ был выполнен за 20 дней и стоимость была минимальной? Сколько будет стоить в этом случае выполнение заказа?Попытайтесь сами ответить на вопросы и записать ответы:
1. Какие у нас есть константы?
2. Что будет переменными?
3. Целевая функция
4. Ограничения
Константы: время выполнения заказа и ставка за одну шкатулку по каждому мастеру
Переменные: число заготовок, передаваемое каждому мастеру
Целевая функция: общая стоимость заказа (здесь формула: сумма произведений переменных на ставку за заказ), цель — минимум
Ограничения:
1. Число шкатулок в заказе = фиксированное значение 100 шт
2. Максимальное время для выполнения заказа <= фиксированное значение 20 дней
3. Переменные должны быть выражены неотрицательным и целым числом
А теперь найдите где какие данные расположены в этой таблице:
Заполните самостоятельно свою исходную таблицу в Excel в любой удобной для Вас форме.
Так выглядит окно Поиск решения
до того, как мы начали его заполнять,
После того, как Вы внесли все исходные данные, запускаем «Поиск решения» (вкладка «Данные»). Я покажу на примере Excel 2007 (Excel 2010 немножко отличается, но сам подход аналогичен).
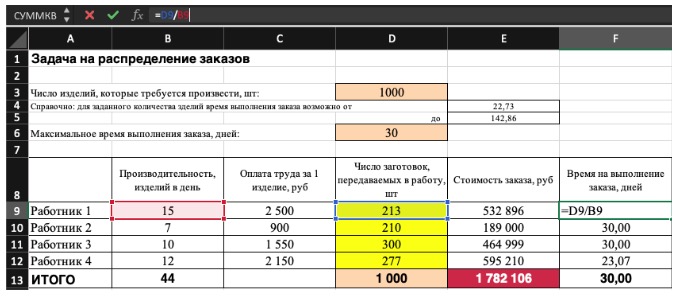
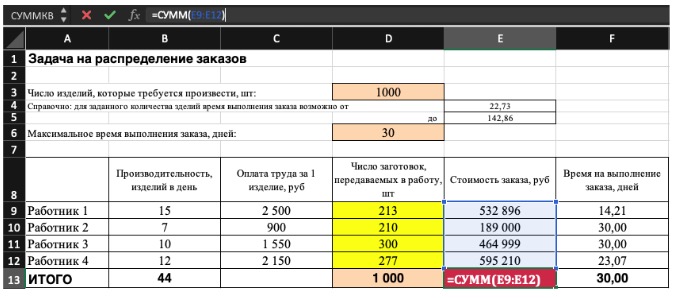
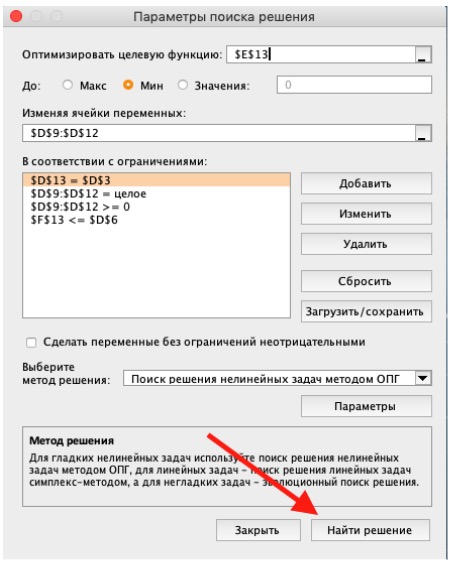
1. Устанавливаем целевую ячейку E13. Это целевая функция, которая равна общей стоимости заказа. Переключаем цель, чтобы она была равной минимальному значению.
2. Вносим диапазон переменных D9:D12 в поле «Изменяя ячейки».
3. Вносим ограничения:
D13 (общее число заготовок) = 100 (внесем не значение 100, а ячейку D3, чтобы в дальнейшем можно было изменить количество шкатулок в задаче)
Диапазон переменных D9:D12 = целые
Диапазон переменных D9:D12 >= 0 (неотрицательные)
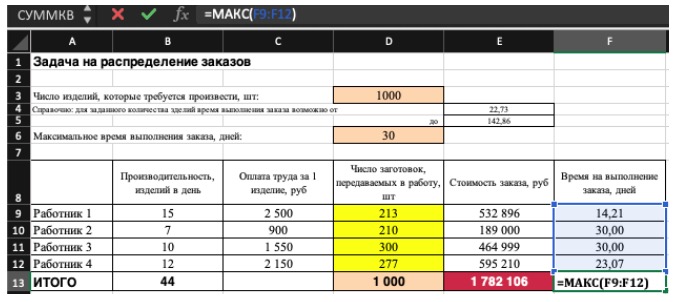
F13 (срок выполнения заказа: в эту ячейку внесена формула, которая выбирает максимальное значение из сроков по каждому мастеру, она выглядит так =МАКС(F9:F12)) <= 20 дней (внесем не значение 20, а ячейку D6, чтобы можно было изменять)
Осталось нажать кнопку «Выполнить»: переменные будут заполнены и появится окно с результатами. Обратите внимание на комментарий, что все ограничения и условия выполнены и решение найдено, если нет, возможно, исходные данные сформулированы неверно. Если все хорошо, нажимайте ОК, и ячейки с переменными останутся заполненными, если нажмете ОТМЕНА, заполненные данные не сохранятся.
Будьте внимательны! Всегда проверяйте, что написано в окне результаты, потому что результат бывает отрицательным: «Поиск не может найти подходящего решения».
В этом случае данные могут быть заполнены наилучшими по мнению надстройки, но эти данные могут быть неверными и не удовлетворять условию задачи!
Итоговый результат будет выглядеть так:
У Вас получилось? Если что-то непонятно или есть вопросы, скачайте мой файл с решением и проверьте в нем:
Теперь попробуйте самостоятельно рассчитать, сколько будет стоить заказ, если на него можно затратить 30 дней.
Молодцы, кто решил! 
Какой ассортимент выпускать, чтобы получить максимальную прибыль
классика жанра
Я решила не брать в качестве классического примера транспортную задачу, потому что она уже всем надоела, ее традиционно проходят в высших учебных заведениях и по ней написано множество инструкций в интернете.
В качестве классики приведу задачу из курса по управлению эффективностью бизнеса CIMA. Что интересно, сам поиск решения в рамках курса не проходят, а только учат формулировать целевую функцию и ограничения, а затем интерпретировать результаты. Что нужно сделать, чтобы этот результат получить, не знают даже выпускники CIMA!!!, но мы восполним этот пробел и раскроем тайну, как это делается. 
Приведенную здесь задачу я взяла из курса подготовки к CIMA Кузьмина Михаила Юрьевича, который проходила в 2016 году. Было очень интересно, рекомендую и вам!
THS производит два продукта из различных комбинаций одних и тех же ресурсов. Ниже приведена информация о продуктах:
THS готовит план производства на следующий месяц. Максимально доступные (за месяц) объемы ресурсов приведены в таблице:
Материал А — 5 000 кг
Материал В — 5 400 кг
Работа оборудования — 3 000 часов
Квалифицированный труд — 4 500 часов
Задание:
Определить оптимальный план производства, максимизирующий прибыль.
Подготовим расчеты для компьютерной обработки данных
Для решения задачи требуется рассчитать маржинальную прибыль по каждому продукту:
Переменные:
х — количество продукта Е
у — количество продукта R
Маржинальная прибыль от всего объема выпуска будет рассчитана по формуле:
35x + 66y
Наша цель: найти такой объем выпуска, который даст максимальное значение
Ограничения:
Материал А: 3х+2у<=5000
Материал В: 4x+3у<=5400
Работа оборудования: 2х+3у<=3000
Квалифицированный труд: 2х+5у<=4500
Объем спроса: y<=1500
Неотрицательность: х>=0, y>=0
Подготовим в Excel таблицу для ввода данных
Колонка «Значение»
По строкам 1 и 2 в будет внесено оптимальное количество продуктов. Сейчас их оставляем пустыми, функция сама их заполнит. На эти ячейки ссылаются все последующие формулы.
По строке 3 «Целевая функция» — вносим формулу со ссылкой на ячейки Х и У выше. Пока она равна нулю, ПОИСК РЕШЕНИЯ будет ее максимизировать и заполнит значение.
Далее по строкам 4-10 вносим ограничения в виде формул. Например, 3х+2у, также со ссылками на ячейки Х и У.
Колонка «Ограничение»
Ограничения можно внести как в ячейки на листе, так и непосредственно в окне «Поиск решения». В данном случае они внесены в таблицу, чтобы можно было заполнить формулу в следующей колонке (которая называется «Излишек»), т.к. она участвует в финальной матрице.
Колонка «Излишек»
Здесь вносим формулу: Ограничение — Значение. После того, как функция рассчитает все значения, мы сразу сможем видеть ограниченные ресурсы и излишки.
Итак, таблица готова и выглядит, как приведено выше.
Переходим к функции «Поиск решения»
Нажимаем кнопку «Поиск решения» в закладке «Данные» (если нет кнопки, настройка здесь)
Ограничения вносятся так:
Ограничения НЕ ОТРИЦАТЕЛЬНОСТИ можно вносить, выделяя целый диапазон ячеек:
В окне «Результаты поиска решения» проверьте, что решение найдено. И еще выберите тип дополнительного отчета: «Устойчивость», он появится на дополнительном листе, там будет полезная информация о теневой цене (что это, поясню далее).
Интерпретация полученных результатов
В итоге таблица выглядит так:
Максимальное значение прибыли 62 625 долл, достигается при выпуске оптимального ассортимента: Продукт Е — 375 ед, Продукт R — 750 ед. Смотрим колонку «Избыток»
Имеется избыток Материала А и материала В в размере 2 375 ед и 1 650 ед, соответственно.
На продукт У имеется нереализованный спрос 750 ед.
Оборудование и труд являются ограничивающими ресурсами. Это значит, что если бы у нас имелись дополнительные единицы этих ресурсов, мы могли бы произвести еще продукт и получить дополнительную прибыль.
Поиск решения позволяет проводить углубленный анализ модели и рассчитывает «теневую цену» — сложнейшее для понимания экономистов понятие.
Надбавка к номинальной цене за единицу ограниченного ресурса, которую имело бы смысл заплатить, чтобы получить еще одну дополнительную единицу ограниченного ресурса, называется теневая цена.
Теневая цена ограниченного ресурса -это дополнительная маржинальная прибыль, которая возникла бы, если бы имелась одна дополнительная единица ограниченного ресурса, либо потерянная маржинальная прибыль, которая возникла бы, если бы объем ограниченного ресурса был на единицу меньше.
Теневую цену смотрим из отчета по устойчивости:
Теперь объясню, что это значит на цифрах.
Еще одна дополнительная единица продукта, которую мы могли бы произвести, при наличии еще одной единицы ограниченного ресурса, представляет собой условную единицу. Это не одна единица E или R, а условная единица, в состав которой входят и Е, и R в той пропорции, в которой определен оптимальный план
Продукты E и R входят в оптимальный план в пропорции 375:750 или 1:2. Давайте рассмотрим минимальный набор оптимального плана, который включает 3 единицы: 1 единицу продукта Е и 2 единицы продукта R.
Вернемся к таблице с расчетом маржинальной прибыли:
Если мы приобретем все ресурсы, которые входят в состав по тем же ценам, что и прежде, то получим маржинальную прибыль 1 х 35 + 2 х 66 = 167$
Однако ресурс работы оборудования и рабочее время рабочих исчерпаны, а все остальные ресурсы есть. Значит, если мы можем арендовать дополнительную единицу оборудования и нанять еще рабочих, можно было бы доплатить. Сейчас оборудование стоит 7$ в час, труд – 10$ в час и мы и имеем маржинальную прибыль. Теневая цена показывает, что можно доплатить за 1 час работы оборудования — 10,75 (тогда он будет стоить 17,75), а за 1 час труда — 6,75 (будет стоить 16,75) — это максимальные суммы, при которых маржинальная прибыль будет равна нулю:
Итак, мы можем вести переговоры о приобретении дополнительных ресурсов с надбавкой к текущей стоимости в пределах теневой цены и нам это будет выгодно.
Если остались вопросы, скачайте мой файл с решением:
Трансфертные цены
Как установить цену продажи внутри группы, чтобы минимизировать налоги
Когда я писала эту статью, мне очень хотелось придумать задачу на Поиск решения, которая была бы полезна в реальной практике. Я опросила множество экономистов, никто из моих знакомых Поиск решения в своей работе не применял.
А у Вас есть идея,
как применить Поиск решения на практике?
Пишите мне на почту или в комментариях.
Если идея будет рабочая, я составлю задачу и опубликую ее здесь!
За идею задачи про трансфертные цены, которую я привожу в этом разделе, благодарю очень талантливого экономиста Алексея Д.!
Есть группа из 3 компаний. ООО «Крона» закупает телефоны в Китае, ООО «Стрим» продает телефоны мелкооптовыми партиями по России, ООО «Маркет» торгует телефонами через розничные точки.
Стрим и Маркет закупают телефоны у Кроны. Учитывая, что все 3 юридических лица входят в группу и имеют одного собственника, их можно рассматривать как подразделения одной компании. Перед финансовым директором стоит задача запланировать оптимальные трансфертные цены.
Трансфертная цена – это цена, по которой товары или услуги передаются между подразделениями одной и той же компании.
Имеется следующая информация о показателях деятельности на квартал:
Маркет несет дополнительные расходы в виде 30% процентов от маржинальной прибыли по сделкам, это премия управляющему директору. Сумма премии при выполнении плана реализации в 1000 штук в квартал, не может быть меньше 150 000 руб.
Ограничения:
В целях минимизации налоговых рисков в задаче установлены следующие ограничения:
Цена
Минимальная трансфертная цена не может быть ниже себестоимости, увеличенной на 5%.
Максимальная трансфертная цена для компании не может быть больше чем средняя продажная цена покупателям уменьшенная на 5%.
Цены не должны отличаться между собой не более, чем на 20%.
Прибыль
Прибыль после уплаты налогов по каждой компании должна составить не менее 1% от выручки.
Задание. Найти оптимальные трансфертные цены для реализации с Крона на Стрим и Маркет, при которых прибыль после уплаты налогов будет максимальной.
Оптимальные трансфертные цены должны удовлетворять следующим условиям:
1) распределять налоговую нагрузку внутри компании с целью минимизации налога на прибыль
2) находиться в рамках допустимого диапазона, чтобы дать возможность обосновать для контролирующих органов, что аналогичные цены использовали бы компании, действующие независимо друг от друга
3) обеспечить справедливую оценку деятельности подразделений
Для решения перенесем данные в Excel.
Сначала заполним исходные данные, которые будут участвовать в расчетах:
Теперь подготовим поля для переменных. Это 2 ячейки: цена с Кроны на Стрим и цена с Кроны на Маркет. Пока они остаются пустыми, Поиск решений сам их заполнит.
Заполним таблицу с финансовыми результатами
Это нужно, чтобы рассчитать результат целевой функции. В формулах уже участвуют ячейки с трансфертными ценами, но пока они не заполнены, итоговые значения в формулах будут нулевыми.
Выручка по Кроне рассчитывается по формуле:
количество единиц, проданных со Стрима, умноженное на трансфертную цену + количество единиц проданных с Маркета, умноженное на трансфертную цену
Выручка по Стриму и Маркету нам известна: умножаем продажи на цену
Себестоимость по Кроне нам известна: умножаем общую сумму продаж со Стрима и Маркета на покупную цену.
По Стриму и Маркету в расчете себестоимости участвуют трансфертные цены, поэтому заполним формулы, но значения пока равны нулю.
Маржинальная прибыль рассчитывается по формуле: выручка минус себестоимость
Налог. Для Кроны и Стрима используется формула маржинальная прибыль на ставку налога, у Маркета другая формула: выручка на 6%.
Премия управляющему: вносим только для Маркета: маржинальная прибыль, умноженная на 30%
Прибыль после уплаты налога по формуле: маржинальная прибыль минус премия минус налог
Целевая функция. Сумма прибыли после уплаты налога по всем компаниям
Рядом с премией управляющему сразу установим ограничение >= 150 000
Минимальное ограничение цены: 4 400 х 1,05 = 4 620
Максимальная возможная цена на Стрим: 15 200 х 0,95 = 14 440
Максимальная возможная цена на Маркет: 17 860 х 0,95 = 17 860
Для того, чтобы задать ограничение по диапазону удобно использовать формулу отношение одной цены к другой. Предварительно требуется прикинуть, какая из цен будет стремиться в большую сторону. В данном случае я сделала оценку, что цена на Маркет чем больше, тем лучше, потому что ставка премии управляющему директору выше, чем ставка налога в Кроне, а цена на Стрим, наоборот, чем меньше, чем лучше, потому что ставка налога в Стриме ниже. Можно не делать предварительную оценку, а запустить поиск решения без учета этого ограничения: выяснить максимальную цену, а затем задать ограничение. Ограничение диапазона в пределах 20% будет выглядеть так:
Значение цена на Маркет/цена на Стрим <= 1,2
И последнее ограничение: минимальная сумма прибыли после уплаты налогов. Здесь значение будем задавать через формулу: выручка, умноженная на 1%, потому что на Кроне в зависимости от изменения трансфертных цен выручка будет изменяться.
Прибыль будет максимальной — 23 246 500 руб, если мы установим цену с Кроны на Стрим — 14 100 руб и цену на Маркет — 16 920.
Задача инвестора.
Что построить на участке?
Сможете сами решить?
Инвестор приобрел 400 соток земли под застройку. На участке можно построить 3 типа объектов: коттеджи, дуплексы и пятиэтажные дома на 30 квартир.
Имеется следующая информация об объектах:
По условиям договора с покупателями управляющая компания не может быть заменена в течение 5 лет с момента начала реализации проекта, а значит, управляющая компания инвестора будет получать в дальнейшем прибыль от эксплуатации объекта
Размер инвестиций ограничен суммой 330 млн.
Вопрос: что построить на участке, чтобы в течение 5 лет с начала проекта получить максимальную прибыль и сколько это будет?
Когда я составляла эту задачу, я подгоняла условия, чтобы получить наилучший ответ, который уже был мне известен. Каково же было мое удивление, когда я запустила Поиск решения – и получила совершенно другой результат! Специально пока его не публикую, чтобы было интереснее решать.
А Вы сможете решить эту задачу? Напишите свой ответ в комментариях, и нравятся ли Вам такие задачи? И идеи, идеи!
Как настроить функцию «Поиск решения»
если у вас нет кнопки «Поиск решения» во вкладке «Данные»
Поиск решения в Excel расположен на вкладке «Данные»
Если вы у себя в Excel не видите такой кнопки, значит нужно ее настроить. Делается это так. Шаг 1: Открыть «Параметры Excel»
Шаг 2: В открывшемся окне переключиться в закладку «Надстройки», выделить приложение «Поиск решения» и нажать на кнопку «Перейти».
Шаг 3: Появится окно «Надстройки», здесь отметить галочкой надстройку «Поиск решения», нажать «ОК» и все готово.
Понравилась статья?
Поделитесь в соцсетях:
Подпишитесь на обновления, чтобы первыми узнавать о публикации новых статей
Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:
- В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
- В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.
С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.
Каждый отчет создается на отдельном листе текущей рабочей книги.
Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).
- Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
- Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
- Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.
Рассмотрим применение процессора Excel для решения ЗЛП на примерах.
Задача 1. Планирование производства
Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.
МП выпускает товары х1,х2,х3,х4, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.
| Затраты | х1 | х2 | x3 | х4 | Всего |
|---|---|---|---|---|---|
| Трудовые | 1 | 1 | 1 | 1 | 16 |
| Сырьевые | 6 | 5 | 4 | 1 | 110 |
| Финансы | 4 | 6 | 10 | 13 | 100 |
- Максимум прибыли в зависимости от оптимального распределения затрат.
- Минимум ресурсов, необходимых для получения максимальной прибыли.
Решение задачи средствами Excel состоит из 4 этапов:
- Создание математической модели задачи ЛП.
- Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
- Ввод данных из формы в окно Excel Поиск решения из меню Данные.
- Задание параметров поиска и решение задачи.
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:
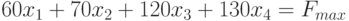
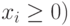
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.
Создание формы
- Составление формы в виде:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | х7 | х2 | x3 | х4 | Формула | Знак | Св.член |
| 2 | Значение | |||||||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | =СУММПРОИЗВ(В$2:Е$2;В3:Е3) | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | =СУММПРОИЗВ(В$2:Е$2;В4:Е4) |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | =СУММПРОИЗВ(В$2:Е$2;В5:Е5) |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | =СУММПРОИЗВ(В$2:Е$2;В6:Е6) |  |
100 |
- Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
- Ввод формул с помощью fx – Мастера функций.
Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций fx на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х1..х4), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).
Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.
Нажать клавишу ОК, в ячейку F3 запишется формула 60х1+70х2+120х3+ 130х4 в виде СУММПРОИЗВ(В2:Е2;В3:Е3).
Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:
После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.
В результате копирования мы увидим следующие формулы:
- в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
- в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
- в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).
Заполнение окна Поиск решения
Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).
Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак «
Аналогично через «Добавить» ввести 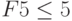
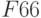
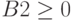
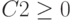
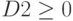
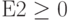
Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.
После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».
Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.
Параметры поиска
В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).
Результаты поиска решения с таблицей результатов:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | X1 | X2 | X3 | X4 | Формула | Знак | Св.член |
| 2 | Значение | 10 | 0 | 6 | 0 | |||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | 1320 | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | 16 |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | 84 |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | 100 |  |
100 |
Таким образом оптимальный план Х(Х1,Х2,Х3,Х4)=(10,0,6,0) при минимальном использовании ресурсов
- Трудовые – 16 (У1)
- Сырьевые – 84 (У2)
- Финансы – 100 (У3)
даёт максимум прибыли F в 1320 руб.
Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х1 и Х3 в количестве 10 и 6 штук соответственно, товары Х3 и Х4 выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У1) и финансовые (У3) ресурсы используются полностью, по сырьевым ресурсам (У2) есть запас в 110-84=26 ед.
Кроме того, это означает, что изменение трудовых ( y1 ) и финансовых ( y3 ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y2 ) – нет.
Разности между плановыми ресурсами и использованными являются двойственными переменными y1, y2 и y3 сопряжённой задачи линейного программирования. В данном случае y1=y3=0 , а y2=26 ед. Таким образом, ресурс y2 можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.
Задача 2. Задача об оптимальной диете
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа 

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.
Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:
где множество допустимых альтернатив 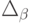
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.
Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).
Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2= 70, в углеводах b3 = 400.
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.
Таблица 1. Содержание питательных веществ в продуктах питания
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр «Российский» | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 61 | 220 | 230 | 15 | 8 | 11 | 6 |
| Жиры | 12 | 172 | 290 | 1 | 1 | 2 | 2 |
| Углеводы | 420 | 0 | 0 | 212 | 26 | 38 | 155 |
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:

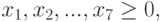
Создание формы
Для решения поставленной задачи выполним следующие подготовительные действия:
- Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
- В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с1 = 2060, с2 = 2430, с3 = 3600, с4 = 890, с5 = 140, с6 = 230, с7 = 650.
- В ячейку I2 введем формулу: =СУММПРОИЗВ( b 2:Н2;B3:H3), которая представляет целевую функцию (4).
- В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.
- В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b 1=100 , жирах b 2= 70 и углеводах b3 = 400.
- В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
- Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
- Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).
Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.
Заполнение окна Поиск решения
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.
После появления диалогового окна Поиск решения следует выполнить следующие действия:
- В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
- Для группы Равной: выбрать вариант поиска решения – минимальному значению.
- В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
- Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
- для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
- в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
- в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
- в качестве значения правой части ограничения выбрать ячейку $J$5 ;
- для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
- аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).
Параметры
В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.
Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х1 = 0, х2 = 0,211, 3 = 0,109, х4= 1,887, х5 = 0, х6 = 0, х7 = 0, которым соответствует значение целевой функции: fопт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.
Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.
ЗАДАНИЕ
- Составить математическую модель задачи линейного программирования.
- Решить задачу линейного программирования в Excel с помощью Поиска решения.
- Сохранить в виде модели установочные параметры.
Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:
Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.
Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:
Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.
Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа 

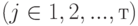
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).
Таблица 1. Содержание питательных веществ в продуктах питания
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр «Российский» | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 66 | 225 | 235 | 20 | 13 | 16 | 11 |
| Жиры | 17 | 177 | 295 | 1 | 1 | 7 | 7 |
| Углеводы | 425 | 0 | 0 | 217 | 31 | 43 | 200 |
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 105, в жирах b 2 = 75, в углеводах b 3 = 405.
Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.
Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:
Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.
Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:
Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.
Таблица 1. Расход химических веществ на изготовления клея, их запас на складе
| Вид клея /Химические вещества | Клей № 1 | Клей № 2 | Клей № 3 | Запас на складе |
|---|---|---|---|---|
| Крахмал | 0,4 | 0,3 | 0,2 | 20 |
| Желатин | 0,2 | 0,3 | 0,4 | 35 |
| Квасцы | 0,05 | 0,07 | 0,1 | 7 |
| Мел | 0,01 | 0,05 | 0,15 | 10 |
Стоимость каждого вида клея для оптовых покупателей следующая:с1 = 380 руб/кг,с2 =430 руб/кг,с3 = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.
Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с1 = 470,с2= 380,с3 = 350,с4 = 1460,с5 = 2150,с6 = 2070, с7 = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2 = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).
Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Поиск решения задач в Excel с примерами
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
источники:
http://intuit.ru/studies/courses/3659/901/lecture/32717
http://exceltable.com/vozmojnosti-excel/poisk-resheniya-v-excel
«Поиск решения» — это надстройка для Microsoft Excel, которую можно использовать для анализ «что если». С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка «Поиск решения» работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка «Поиск решения» изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.
Проще говоря, с помощью надстройки «Поиск решения» можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.
Примечание: В версиях надстройки «Поиск решения», выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка «Поиск решения» была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).
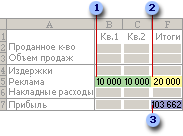
1. Ячейки переменных
2. Ячейка с ограничениями
3. Целевая ячейка
После выполнения процедуры получены следующие значения.

-
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
-
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
-
Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
-
Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
-
Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Щелкните связь (<=, =, >=, int,binили dif), которая требуется между ячейкой, на которую ссылается ссылка, и ограничением. Если щелкнуть int, в поле Ограничение появится integer. Если щелкнуть бин,в поле Ограничение появится двоичное поле. Если нажать кнопку dif,в поле Ограничение появится ссылкаalldifferent.
-
Если в поле Ограничение было выбрано отношение <=, = или >=, введите число, ссылку на ячейку (или имя ячейки) или формулу.
-
Выполните одно из указанных ниже действий.
-
Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
-
Чтобы принять ограничение и вернуться в диалоговое окно Параметрырешения, нажмите кнопку ОК.
Примечание Отношения int,binи dif можно применять только в ограничениях для ячеек переменных решения.Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
-
-
В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
-
Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
-
-
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
-
Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
-
Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
-
Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
-
Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
-
Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.
-
-
В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
-
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
-
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.
В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.
-
Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
-
Симплекс-метод. Используется для линейных задач.
-
Эволюционный метод Используется для негладких задач.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).
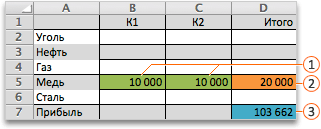
В результате выполнения получены следующие значения:

-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.
Примечание: Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
Задача
Необходимые действия
Сделать так, чтобы значение целевой ячейки было максимальным из возможных
Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных
Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение
Щелкните Значение, а затем введите нужное значение в поле.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.
Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.
Для этого выполните следующие действия:
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Во всплывающем меню <= задайте требуемое отношение между целевой ячейкой и ограничением. Если вы выбрали <=, =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.
Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
-
Выполните одно из указанных ниже действий.
Задача
Необходимые действия
Принять ограничение и добавить другое
Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения
Нажмите кнопку ОК.
-
-
Нажмите кнопку Найти решение и выполните одно из следующих действий:
Задача
Необходимые действия
Сохранить значения решения на листе
В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения
Щелкните Восстановить исходные значения.
Примечания:
-
Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из следующих действий:
Задача
Необходимые действия
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения
Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение
Нажмите кнопку Продолжить.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:
Задача
Необходимые действия
Настроить время решения и число итераций
На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.
Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.
Задать точность
На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости
На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.
-
Нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:
|
Метод решения |
Описание |
|---|---|
|
Нелинейный метод обобщенного понижающего градиента (ОПГ) |
Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции. |
|
Поиск решения линейных задач симплекс-методом |
Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, — и *. |
|
Эволюционный поиск решения |
Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных. |
Примечание: Авторские права на части программного кода надстройки «Поиск решения» версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку «Поиск решения» для анализа данных «что если», чтобы найти оптимальные решения.
Если у вас есть Excel, вы можете нажать кнопку Открыть в Excel, чтобы открыть книгу для использования надстройки «Поиск решения».
Дополнительная справка по надстройке «Поиск решения»
За дополнительной справкой по надстройке «Поиск решения» обращайтесь по этим адресам:
Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Веб-сайт: http://www.solver.com
Электронная почта: info@solver.com
«Решение» на www.solver.com.
Авторские права на части программного кода надстройки «Поиск решения» версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Использование «Решения» для бюджетов с использованием средств на счете вех
Использование «Решение» для определения оптимального сочетания продуктов
Введение в анализ гипотетических вариантов
Полные сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Обнаружение ошибок в формулах
Сочетания клавиш в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)














 Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK. Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.