Часть 10. Подбор формул по графику. Линия тренда
Для рассмотренных выше задач удавалось построить уравнение или систему уравнений. Но во многих случаях при решении практических задач имеются лишь экспериментальные (результаты измерений, статистические, справочные, опытные) данные. По ним с определенной мерой близости пытаются восстановить эмпирическую формулу (уравнение), которая может быть использована для поиска решения, моделирования, оценки решений, прогнозов.
Процесс подбора эмпирической формулы P(x) для опытной зависимости F(x) называется аппроксимацией (сглаживанием). Для зависимостей с одним неизвестным в Excel используются графики, а для зависимостей со многими неизвестными – пары функций из группы Статистические ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ .
В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.
Степень близости подбираемой функции оценивается коэффициентом детерминации R 2 . Если нет других теоретических соображений, то выбирают функцию с коэффициентом R 2 , стремящимся к 1. Отметим, что подбор формул с использованием линии тренда позволяет установить как вид эмпирической формулы, так и определить численные значения неизвестных параметров.
Excel предоставляет 5 видов аппроксимирующих функций:
1. Линейная – y=cx+b. Это простейшая функция, отражающая рост и убывание данных с постоянной скоростью.
2. Полиномиальная – y=c0+c1x+c2x 2 +…+c6x 6 . Функция описывает попеременно возрастающие и убывающие данные. Полином 2-ой степени может иметь один экстремум (min или max), 3-ей степени – до 2-х экстремумов, 4-ой степени – до 3-х и т.д.
3. Логарифмическая – y=clnx+b. Эта функция описывает быстро возрастающие (убывающие) данные, которые затем стабилизируются.
4. Степенная – y=cx b , (х>0и y>0). Функция отражает данные с постоянно увеличивающейся (убывающей) скоростью роста.
5. Экспоненциальная – y=ce bx , (e – основание натурального логарифма). Функция описывает быстро растущие (убывающие) данные, которые затем стабилизируются.
Для всех 5-ти видов функций используется аппроксимация данных по методу наименьших квадратов (см. справку по F1 «линия тренда»).
В качестве примера рассмотрим зависимость продаж от рекламы, заданную следующими статистическими данными по некоторой фирме:
| Реклама (тыс. руб.) | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| Продажи (тыс. руб.) |
Необходимо построить функцию, наилучшим образом отражающую эту зависимость. Кроме того, необходимо оценить продажи для рекламных вложений в 6 тыс. руб.
Приступим к решению. В первую очередь введите эти данные в Excel и постройте график, как на рис. 38. Как видно, график построен на основании диапазона B2:J2. Далее, щелкнув правой кнопкой мыши по графику, добавьте линию тренда, как показано на рис. 38.
Чтобы подписать ось Х соответствующими значениями рекламы (как на рис. 38), следует в ниспадающем меню (рис. 38) выбрать пункт Исходные данные. В открывшемся одноименном окне, в закладке Ряд, в поле Подписи оси Х, укажите диапазон ячеек, где записаны значения Х (здесь $B$1:$K$1):
В открывшемся окне настройки (рис. 39), на закладке Тип выберите для аппроксимации логарифмическую линию тренда (по виду графика). На закладке Параметры установите флажки, отображающие на графике уравнение и коэффициент детерминации.
После нажатия ОК Вы получите результат, как на рис. 40. Коэффициент детерминации R 2 =0.9846, что является неплохой степенью близости. Для подтверждения правильности выбранной функции (поскольку других теоретических соображений нет) спрогнозируйте развитие продаж на 10 периодов вперед. Для этого щелкните правой кнопкой по линии тренда – измените формат – после этого в поле Прогноз: вперед на: установите 10 (рис. 41).
После установки прогноза Вы увидите изменение кривой графика на 10 периодов наблюдения вперед, как на рис. 42. Он с большой долей вероятности отражает дальнейшее увеличение продаж с увеличением рекламных вложений.
Вычисление по полученной формуле =237,96*LN(6)+5,9606 в Excel дает значение 432 тыс. руб.
В Excel имеется функция ПРЕДСКАЗ(), которая вычисляет будущее значение Y по существующим парам значений X и Y значениям с использованием линейной регрессии. Функция Y по возможности должна быть линейной, т.е. описываться уравнением типа c+bx. Функция предсказания для нашего примера запишется так: =ПРЕДСКАЗ(K1;B2:J2;B1:J1). Запишите – должно получится значение 643,6 тыс. руб.
Часть11. Контрольные задания
Найти функцию по ее графику (аппроксимация)
Дано:
Два параметра, зависящих друг от друга (X; Y). На их основании построен график.
Задача: найти функцию, отражающую (приблизительно) зависимость между параметрами.
Я эту задачу пытаюсь решить с помощью инструмента в экселе (построение тренда; полиноминальная линия тренда 6й степени).
Эксель подсказывает мне формулу функции, но по факту эта формула выдает не верные параметры (т.е. «Y» по данному формуле рассчитывается не правильно).
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Вложения
| расчет.xlsx (15.9 Кб, 22 просмотров) |
Аппроксимация к графику
Здравствуйте! Проблема такая, приходится работать с данными с осциллографа и с помощью программы.
Найти функцию по графику(парабола)
Нужно найти функцию по графику(только параболу), пробовал по формулам с википедии, но что то не.
Нужно найти функцию по графику
Вот собственно график и из него надо получить функцию для того чтобы написать программу на паскале.
найти функцию сигнала по графику
Доброго времени суток, как по графику сигнала найти его изображение (ну или сначала оригинал.
Вложения
| расчет (1).xlsx (16.1 Кб, 55 просмотров) |
Сообщение было отмечено p1111 как решение
Решение
Как, оказывается, было просто.
Спасибо огромное, очень выручили.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Нужно найти функцию по графику
Здравствуйте, у меня есть данные для построения кусочка ВАХ-электрической дуги. Мне нужно найти.
Вывести функцию по графику
Процесс предполагается обратный от привычного, имея график, построить функцию. Как это сделать.
Написать функцию по графику
Помогите пожалуйста! По данному графику нужна функция (формула), чтобы я потом через if смог.
Составить функцию по графику.
Привет всем, помогите составить функцию, по графику, график приложен снизу функция в каком-то.
5 способов расчета значений линейного тренда в MS Excel
Добавление трендовой линии на график
Данный элемент технического анализа позволяет визуально увидеть изменение цены за указанный период времени . Это может быть месяц, год или несколько лет. Информация будет отображать значение средних показателей в виде геометрических фигур . Добавить линию тренда в Excel 2010 можно с помощью встроенных стандартных инструментов.
Построение графика


- Первым действием нужно выделить диапазон данных , например это А1:В9, затем активировать инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с гладкими кривыми и маркерами».
- После открытия графика пользователю станет доступна еще одна панель управления данными , на которой нужно выбрать следующее: «Работа с диаграммами»-«Макет»-«Линия тренда»-«Линейное приближение».
- Следующим шагом требуется выполнить двойной клик по образовавшейся линии тенденции в Excel . Когда появиться вспомогательное окно, отметить птичкой опцию «показывать уравнение на диаграмме».
Важно помнить, что если на графике имеется 2 или более линий , отображающих анализ данных, то перед выполнением 3 пункта нужно будет выбрать одну из них и включить в тенденцию. Эта короткая инструкция поможет начинающим специалистам разобраться, как строится линия тренда в Экселе.
Создание линии
Дальнейшая работа будет происходить непосредственно с трендовой линией.
Добавление тренда на диаграмму происходит следующим образом:
- Перейти во вкладку «Работа с диаграммами» , затем выбрать раздел «Макет»-«Анализ» и после подпункт «Линия тенденции» . Появится выпадающий список, в котором необходимо активировать строку «Линейное приближение».
- Если все выполнено правильно, в области построения диаграмм появится кривая линия черного цвета . По желанию цветовую гамму можно будет изменить на любую другую.
Этот способ поможет создать и построить тренд в Excel 2016 или более ранних версиях.

- лепесткового;
- кругового;
- поверхностного;
- кольцевого;
- объемного;
- с накоплением.
Настройка линии
Построение линий тренда имеет ряд вспомогательных настроек , которые помогут придать графику законченный и презентабельный вид.
Необходимо запомнить следующее:
- Чтобы добавить название диаграмме , нужно дважды кликнуть по ней и в появившемся окне ввести заголовок. Для выбора расположения имени графика необходимо перейти во вкладку «Работа с диаграммами», затем выбрать «Макет» и «Название диаграммы». После этого появится список с возможным расположением заглавия.
- Дополнительно в этом же разделе можно найти пункт, отвечающий за названия осей и их расположение относительно графика. Интересно, что для вертикальной оси разработчики программы продумали возможность повернутого расположения наименования, чтобы диаграмма читалась удобно и выглядела гармонично.
Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).
- Еще есть функция определения достоверности построенной модели . Для этого в дополнительных настройках требуется активировать пункт «Разместить на график величину достоверности аппроксимации» и после этого закрыть окно. Наилучшим значением является 1. Чем сильнее полученный показатель отличается от нее, тем ниже достоверность модели.
Прогнозирование
Для получения наиболее точного прогноза необходимо сменить построенный график на гистограмму . Это поможет сравнить уравнения.

- Вызвать для графика контекстное меню и выбрать «Изменить тип диаграммы» .
- Появится новое окно с настройками , в котором требуется найти опцию «Гистограмма» и после выбрать подвид с группировкой.
Теперь пользователю должны быть видны оба графика . Они визуализируют одни и те же данные, но имеют разные уравнения для образования тенденции.
Следующим шагом необходимо сравнить уравнения точки пересечения с осями на разных диаграммах .
Для визуального отображения нужно сделать следующее:
- Перевести гистограмму в простой точечный график с гладкими кривыми и маркерами . Процесс выполняется через пункт контекстного меню «Изменить тип диаграммы…».
- Выполнить двойной клик по прямой образовавшейся тенденции , задать ей параметр прогноза назад на 12,0 и сохранить изменения.
Такая настройка поможет увидеть, что угол наклона тенденции меняется в зависимости от вида графика , но общее направление движения остается неизменным. Это свидетельствует о том, что построить линию тренда в Эксель можно лишь в качестве дополнительного инструмента анализа и брать его в расчет следует только как приближающий параметр. Строить аналитические прогнозы, основываясь лишь на этой прямой, не рекомендуется.
Базовые понятия
Думаю, еще со школы все знакомы с линейной функцией, она как раз и лежит в основе тренда:
Y — это объем продаж, та переменная, которую мы будем объяснять временем и от которого она зависит, то есть Y(t);
t — номер периода (порядковый номер месяца), который объясняет план продаж Y;
a0 — это нулевой коэффициент регрессии, который показывает значение Y(t), при отсутствии влияния объясняющего фактора (t=0);
a1 — коэффициент регрессии, который показывает, на сколько исследуемый показатель продаж Y зависит от влияющего фактора t;
E — случайные возмущения, которые отражают влияния других неучтенных в модели факторов, кроме времени t.
Определение коэффициентов модели
Строим график. По горизонтали видим отложенные месяцы, по вертикали объем продаж:
В Google Sheets выбираем Редактор диаграмм -> Дополнительные и ставим галочку возле Линии тренда. В настройках выбираем Ярлык — Уравнение и Показать R^2.
Если вы делаете все в MS Excel, то правой кнопкой мыши кликаем на график и в выпадающем меню выбираем «Добавить линию тренда».
По умолчанию строится линейная функция. Справа выбираем «Показывать уравнение на диаграмме» и «Величину достоверности аппроксимации R^2».
Вот, что получилось:
На графике мы видим уравнение функции:
y = 4856*x + 105104
Она описывает объем продаж в зависимости от номера месяца, на который мы хотим эти продажи спрогнозировать. Рядом видим коэффициент детерминации R^2, который говорит о качестве модели и на сколько хорошо она описывает наши продажи (Y). Чем ближе к 1, тем лучше.
У меня R^2 = 0,75. Это средний показатель, он говорит о том, что в модели не учтены какие-то другие значимые факторы помимо времени t, например, это может быть сезонность.
Способ расчета значений линейного тренда в Excel с помощью графика

Для прогнозирования нам необходимо рассчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений линейного тренде нам будут известны:
- Время – значение по оси Х;
- Значение “a” и “b” уравнения линейного тренда y(x)=a+bx;
Рассчитываем значения тренда для каждого периода времени от 1 до 25, а также для будущих периодов с 26 месяца до 36.
Например, для 26 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551
27-го y=135134*27+4594044=8242686
Способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новые значения x; конста)
Подставляем в формулу
- известные значения y – это объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
- известные значения x – это номера периодов x для известных значений объёмов продаж y;
- новые значения x – это номера периодов, для которых мы хотим рассчитать значения линейного тренда;
- константа – ставим 1, необходимо для того, чтобы значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;
Для того чтобы рассчитать значения тренда для всего временного диапазона, в “новые значения x” вводим диапазон значений X, выделяем диапазон ячеек равный диапазону со значениями X с формулой в первой ячейке и нажимаем клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Общая информация
Линия тренда – это инструмент статистического анализа, который позволяет спрогнозировать дальнейшее развитие событий. Чтобы построить кривую, необходимо иметь массив данных, который отображает изменение величины во времени. На основании этой информации строится график, а затем применятся специализированная функция. Рассмотрим изменение цены золота за грамм в долларах с 2015 по 2019 год.
- Составляете небольшую таблицу.
- На основании этих данных строите линейный график. Для этого переходите во вкладку Вставка на Панели инструментов и выбираете нужный тип диаграммы.
- Получается некоторая кривая.
- Необходимо отредактировать график при помощи стандартных инструментов, которые находятся во вкладках Конструктор, Макет и Формат. Переименовываете диаграмму, выставляете пределы по вертикальной оси, чтобы изменения величины были более явными, подписываете оси, добавляете контрольные точки, а также подпись данных. После этого проводите окончательное форматирование.
- Чтобы добавить линию тренда, необходимо во вкладке Макет нажать одноименную кнопку и выбрать нужный тип приближения.
На заметку! Если линия тренда не активна, то используется не тот тип диаграммы. Данная функция работает только с диаграммами типа гистограмма, график, линейчатая и точечная.
6. Так выглядит линия тренда на графике.
На заметку! Построение линии приближения идентично для редакторов 2007, 2010 и 2016 годов выпуска.
Возможности инструмента
Рассмотрим подробнее настройки функции. Для перехода в окно параметров из выпадающего списка нужно выбрать последнюю строчку.
Окно содержит четыре настройки, в которые входят цвет, объем и тип линии, а также параметры самого инструмента.
Параметры линии тренда можно условно поделить на четыре блока:
- Тип приближения.
- Название полученной кривой, которое формируется автоматически или может быть задано пользователем.
- Блок прогнозирования, который позволяет продлить линию тренда на заданное количество периодов вперед или назад, на основании имеющихся данных. Что позволяет оценить дальнейшее изменение исследуемой величины.
- Дополнительные опции, которые отражают математическую составляющую кривой. Самой интересной и полезной строчкой здесь является величина достоверности. Если значение коэффициента близко к единице, то ошибка минимальна и дальнейший прогноз будет достаточно точным.
Выведем на исходный график уравнение линии и коэффициент достоверности.
Как видите, значение близко к 0,5, это говорит о низкой достоверности полученной линии тренда, и дальнейший прогноз будет ошибочным.
Разновидности
1 Линейная аппроксимация отлично подойдет для исследования величины, которая стабильно растет или убывает. Тогда кривая будет иметь вид прямой. Формула будет содержать одну переменную. Коэффициент достоверности близок к единице, что говорит о высокой точности совпадения прямой и массива данных. На основании такой линии тренда прогноз будет достаточно точным.
2. Экспоненциальная кривая используется только для массивов с положительными значениями, которые изменяются непрерывно.
3. Логарифмическую линию тренда целесообразнее использовать, если на первоначальном этапе наблюдается резкое увеличение или снижение показателя, а потом наступает период стабильности. Здесь формула содержит логарифм натуральный.
4. Полиномиальная аппроксимация применяется при большом количестве неоднородных данных. В основе лежит степенное уравнение, при этом количество степеней зависит от числа максимумов. Применим этот тип для первоначального примера с золотом.
Уравнение показывает переменные до третьей степени, поскольку график имеет два пика. Также видим, что коэффициент достоверности близок к единице (вместо 0,5 при линейной аппроксимации), значит линия тренда выбрана правильно и дальнейший прогноз будет точным.
Как видите, для статистического анализа данных необходимо правильно выбрать тип математического уравнения, которое максимально точно будет соответствовать характеру изменения величины. На основании полученных кривых можно осуществлять прогноз, подставляя в уравнение необходимое число.
Разбираемся с трендами в MS Excel
Большой ошибкой со стороны владельца сайта будет воспринимать диаграмму как есть. Да, невооруженным взглядом видно, что синий и оранжевый столбики «осени» выросли по сравнению с «весной» и тем более «летом». Однако важны не только цифры и величина столбиков, но и зависимость между ними. То есть в идеале, при общем росте, «оранжевые» столбики просмотров должны расти намного сильнее «синих», что означало бы то, что сайт не только привлекает больше читателей, но и становится больше и интереснее.
Что же мы видим на графике? Оранжевые столбики «осени» как минимум ни чем не больше «весенних», а то и меньше. Это свидетельствует не об успехе, а скорее наоборот — посетители прибывают, но читают в среднем меньше и на сайте не задерживаются!
Самое время бить тревогу и… знакомится с такой штукой как линия тренда .
Зачем нужна линия тренда
Линия тренда «по-простому», это непрерывная линия составленная на основе усредненных на основе специальных алгоритмов значений из которых строится наша диаграмма. Иными словами, если наши данные «прыгают» за три отчетных точки с «-5» на «0», а следом на «+5», в итоге мы получим почти ровную линию: «плюсы» ситуации очевидно уравновешивают «минусы».
Исходя из направления линии тренда гораздо проще увидеть реальное положение дел и видеть те самые тенденции, а следовательно — строить прогнозы на будущее. Ну а теперь, за дело!
Как построить линию тренда в MS Excel
Щелкните правой кнопкой мыши по одному из «синих» столбцов, и в контекстном меню выберите пункт «Добавить линию тренда» .
На листе диаграммы теперь отображается пунктирная линия тренда. Как видите, она не совпадает на 100% со значениями диаграммы — построенная по средневзвешенным значениям, она лишь в общих чертах повторяет её направление. Однако это не мешает нам видеть устойчивый рост числа посещений сайта — на общем результате не сказывается даже «летняя» просадка.
Линия тренда для столбца «Посетители»
Теперь повторим тот же фокус с «оранжевыми» столбцами и построим вторую линию тренда. Как я и говорил раньше: здесь ситуация не так хороша. Тренд явно показывает, что за расчетный период число просмотров не только не увеличилось, но даже начало падать — медленно, но неуклонно.
Ещё одна линия тренда позволяет прояснить ситуацию
Мысленно продолжив линию тренда на будущие месяцы, мы придем к неутешительному выводу — число заинтересованных посетителей продолжит снижаться. Так как пользователи здесь не задерживаются, падение интереса сайта в ближайшем будущем неизбежно вызовет и падение посещаемости.
Следовательно, владельцу проекта нужно срочно вспоминать чего он такого натворил летом («весной» все было вполне нормально, судя по графику), и срочно принимать меры по исправлению ситуации.
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://urok.1sept.ru/articles/564361
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
|
0 / 0 / 0 Регистрация: 04.05.2018 Сообщений: 3 |
|
|
1 |
|
Найти функцию по ее графику (аппроксимация)05.05.2018, 14:35. Показов 7822. Ответов 3
Добрый день. Дано: Задача: найти функцию, отражающую (приблизительно) зависимость между параметрами. Я эту задачу пытаюсь решить с помощью инструмента в экселе (построение тренда; полиноминальная линия тренда 6й степени). Файл приложен. В чем косяк?
0 |
|
0 / 0 / 0 Регистрация: 04.05.2018 Сообщений: 3 |
|
|
05.05.2018, 14:53 [ТС] |
2 |
|
правильный файл-вложение
0 |
|
1062 / 506 / 137 Регистрация: 27.02.2013 Сообщений: 1,451 |
|
|
05.05.2018, 17:16 |
3 |
|
Решениеp1111, замените график на точечную диаграмму.
1 |
|
0 / 0 / 0 Регистрация: 04.05.2018 Сообщений: 3 |
|
|
05.05.2018, 18:04 [ТС] |
4 |
|
Как, оказывается, было просто. Спасибо огромное, очень выручили.
0 |
Вариант 1: График функции X^2
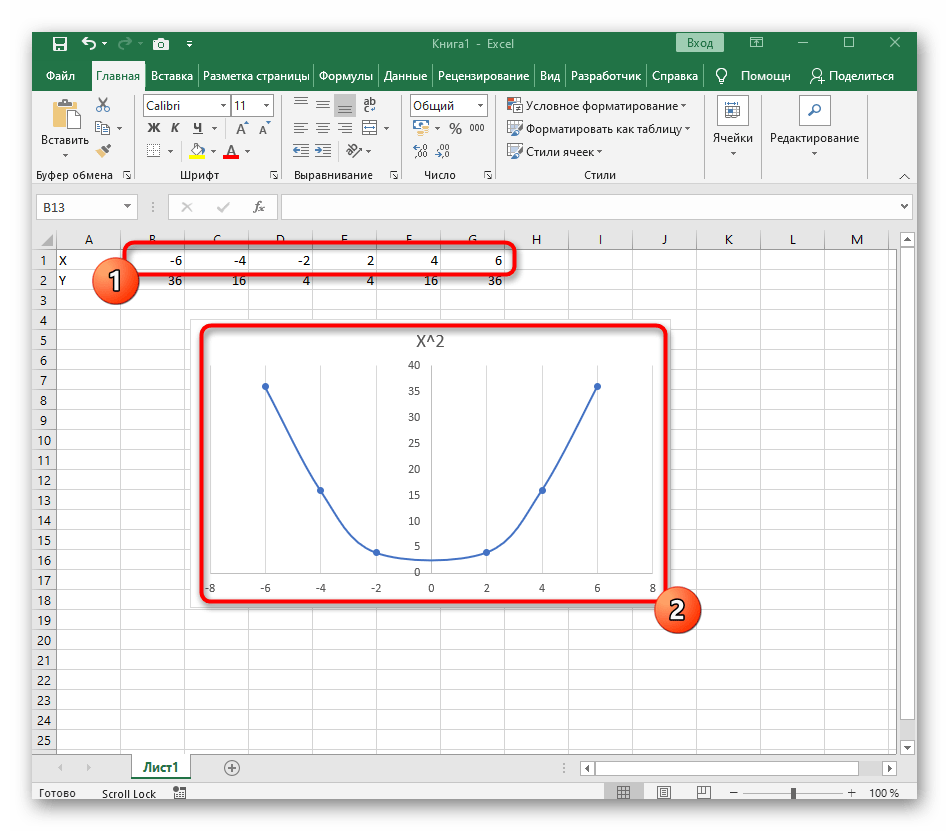
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
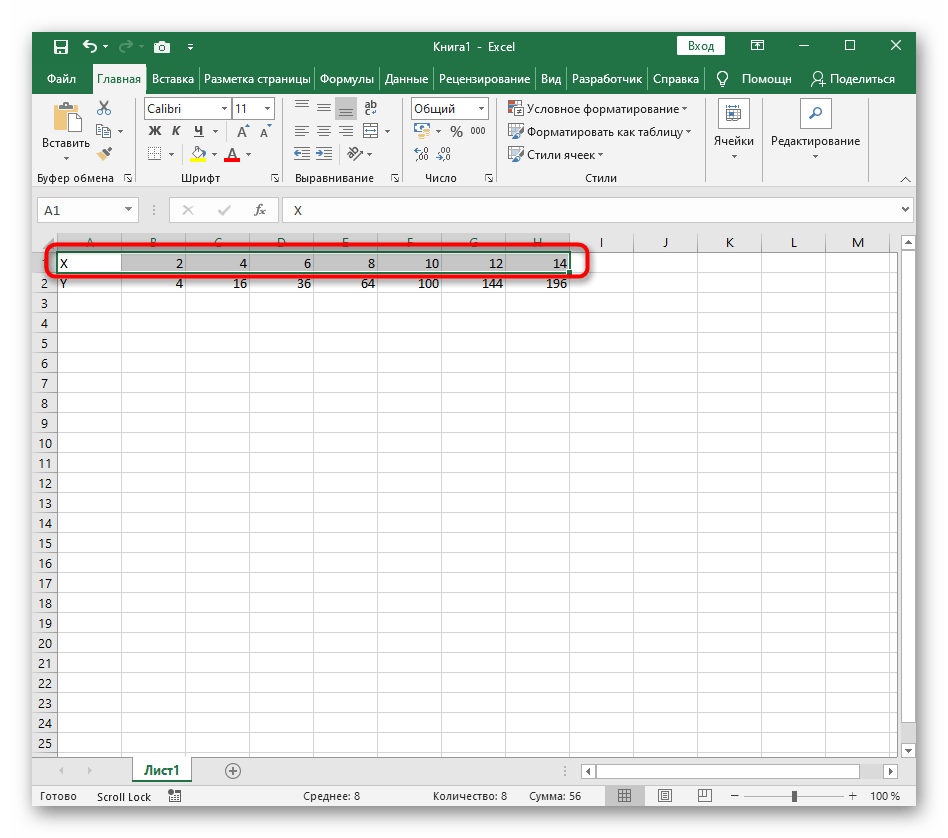
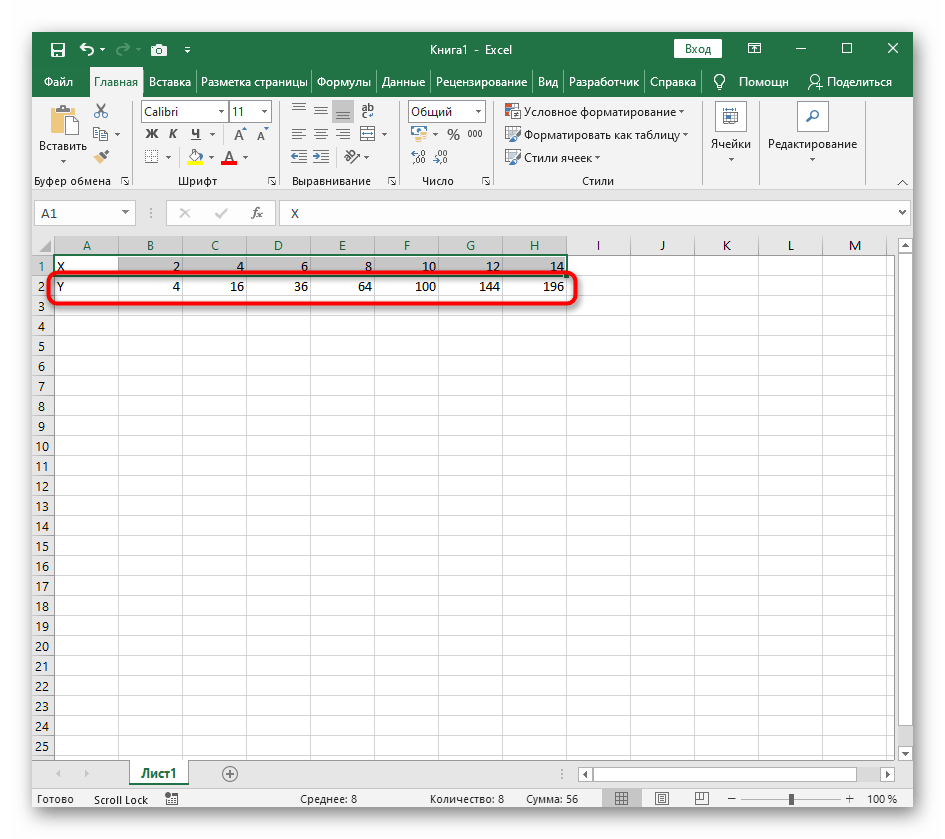
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
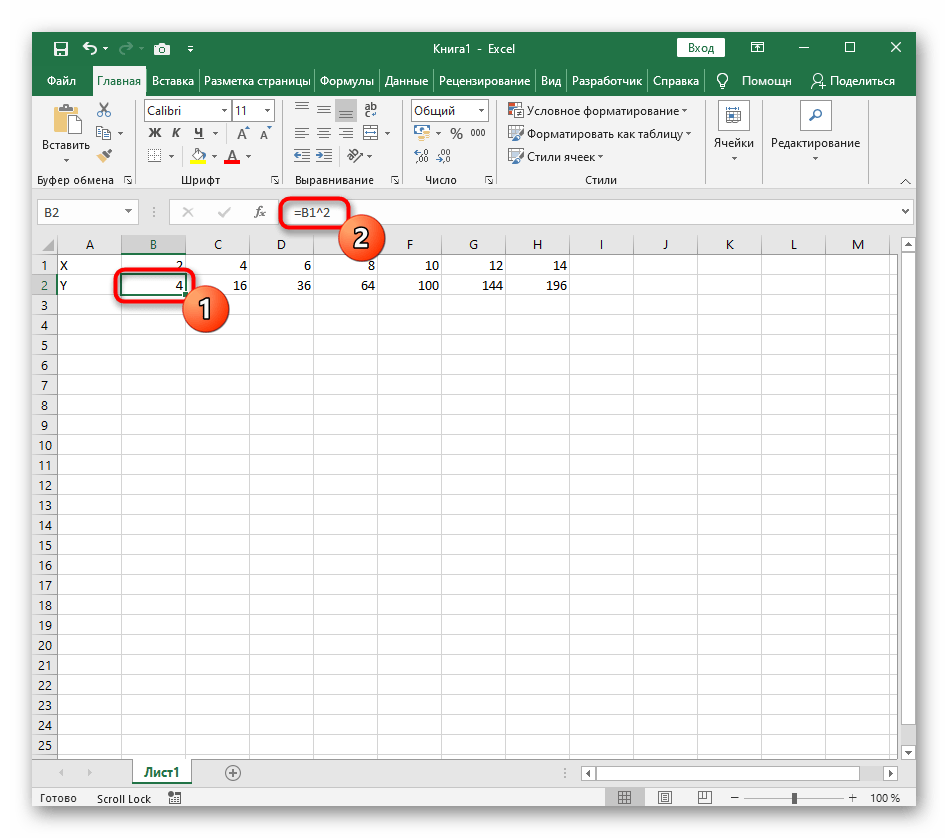
- Нажмите по первой ячейке и впишите
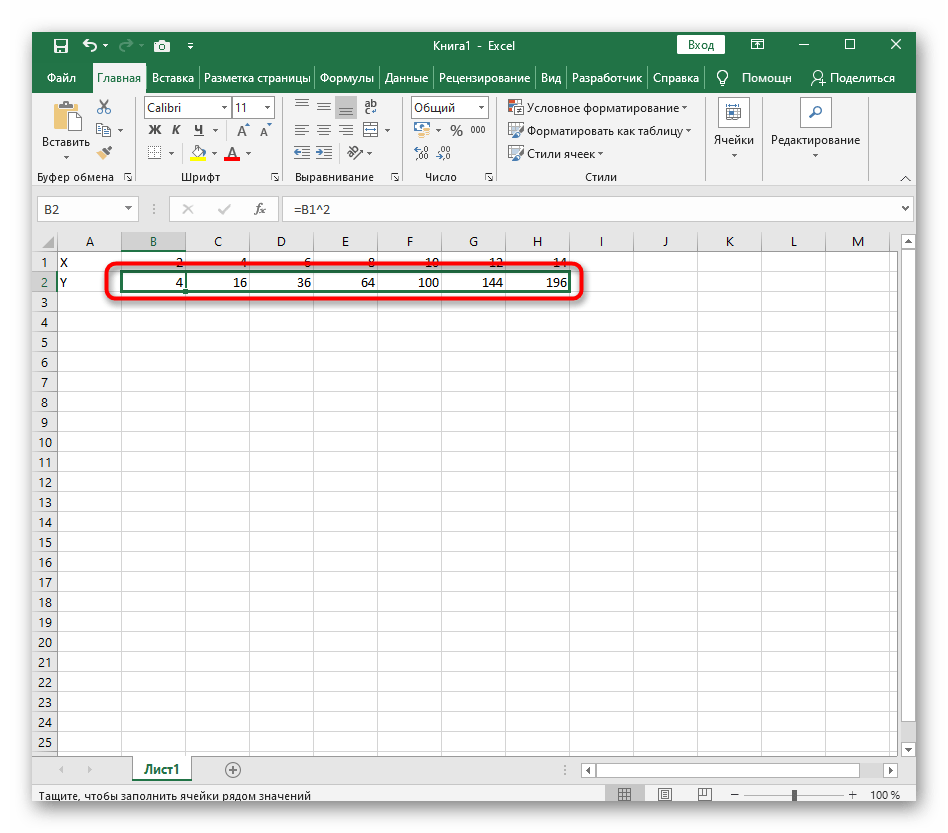
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
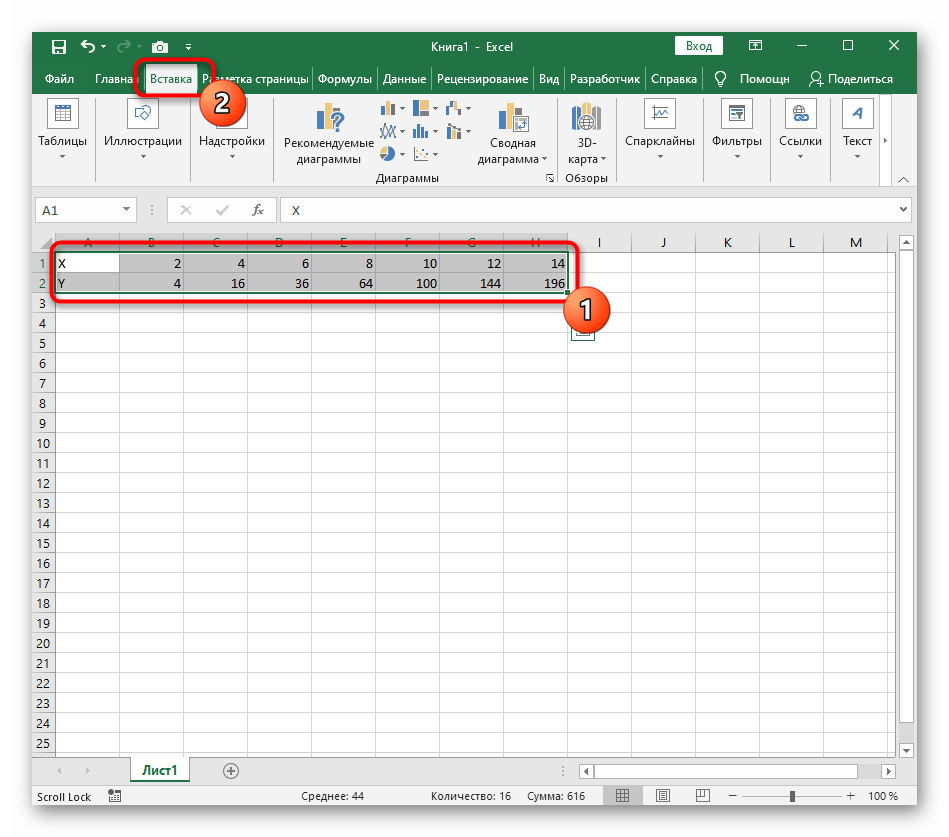
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
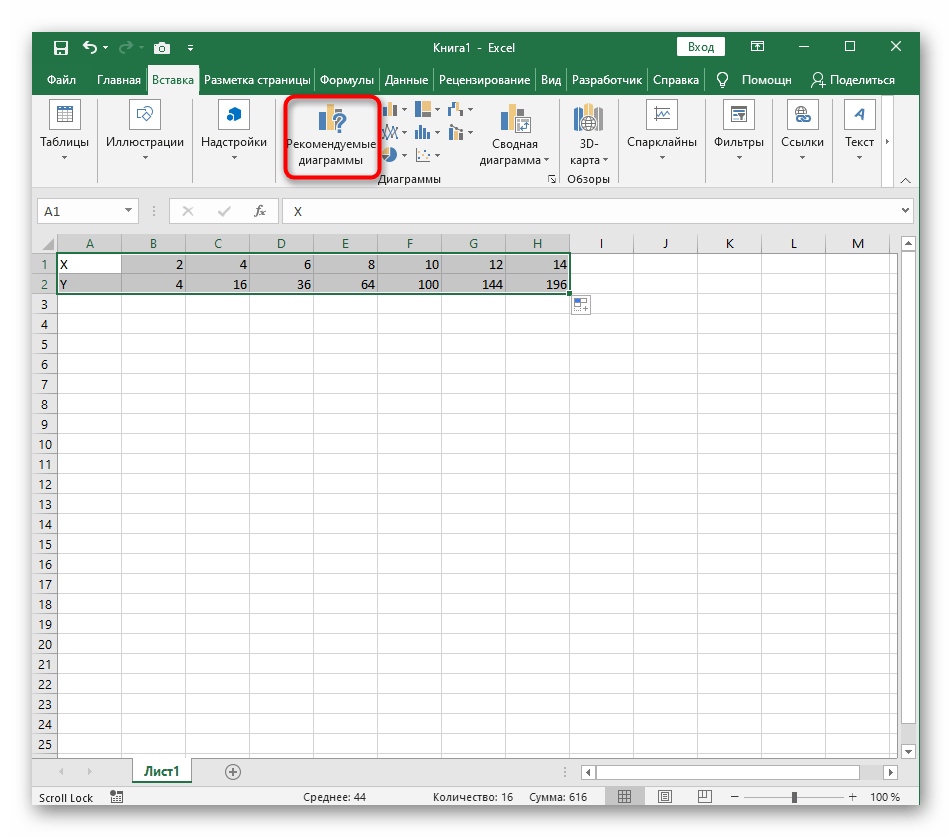
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
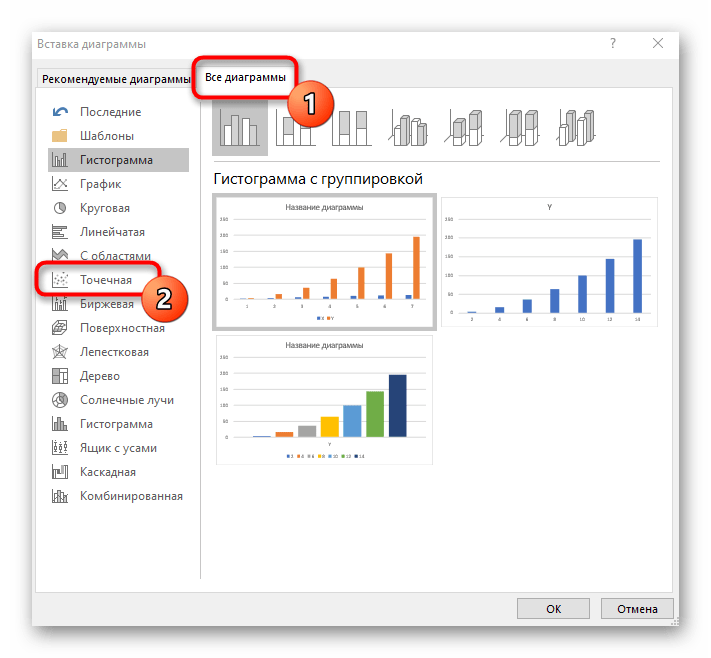
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
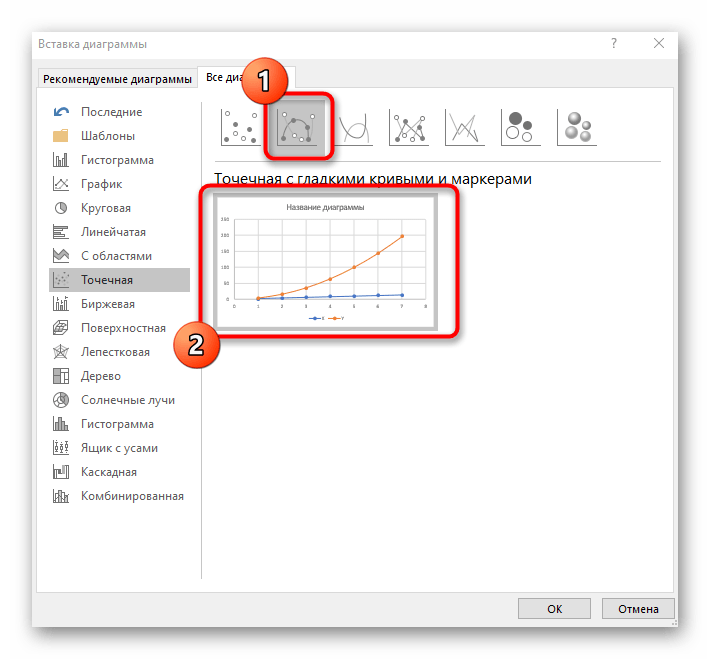
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
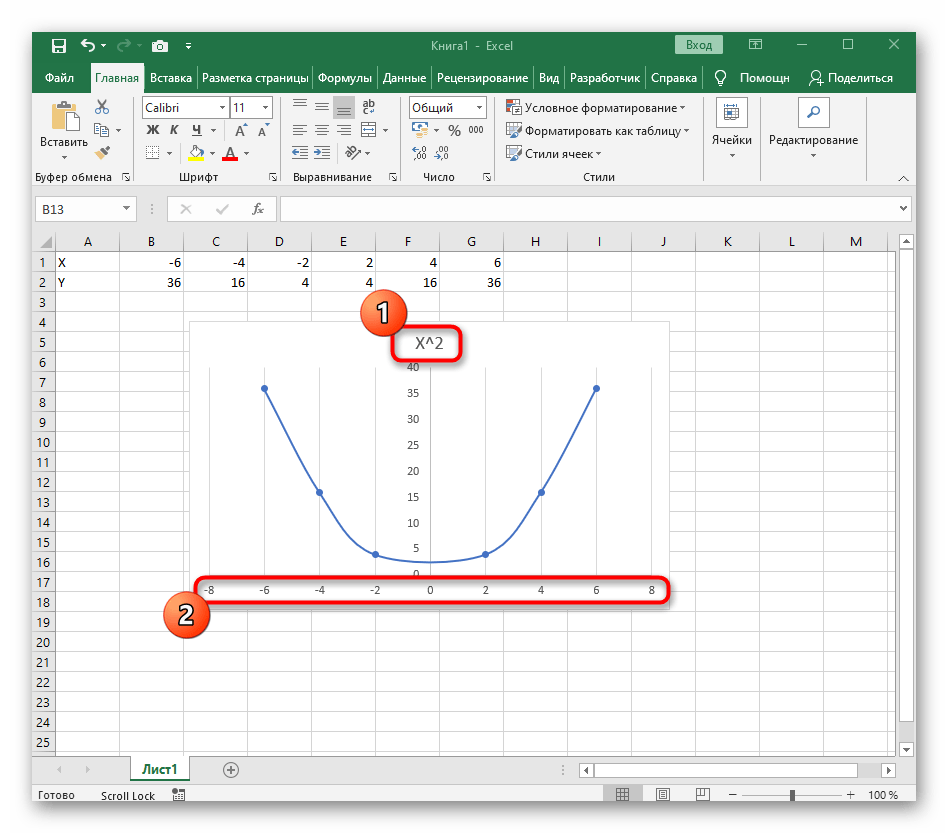
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
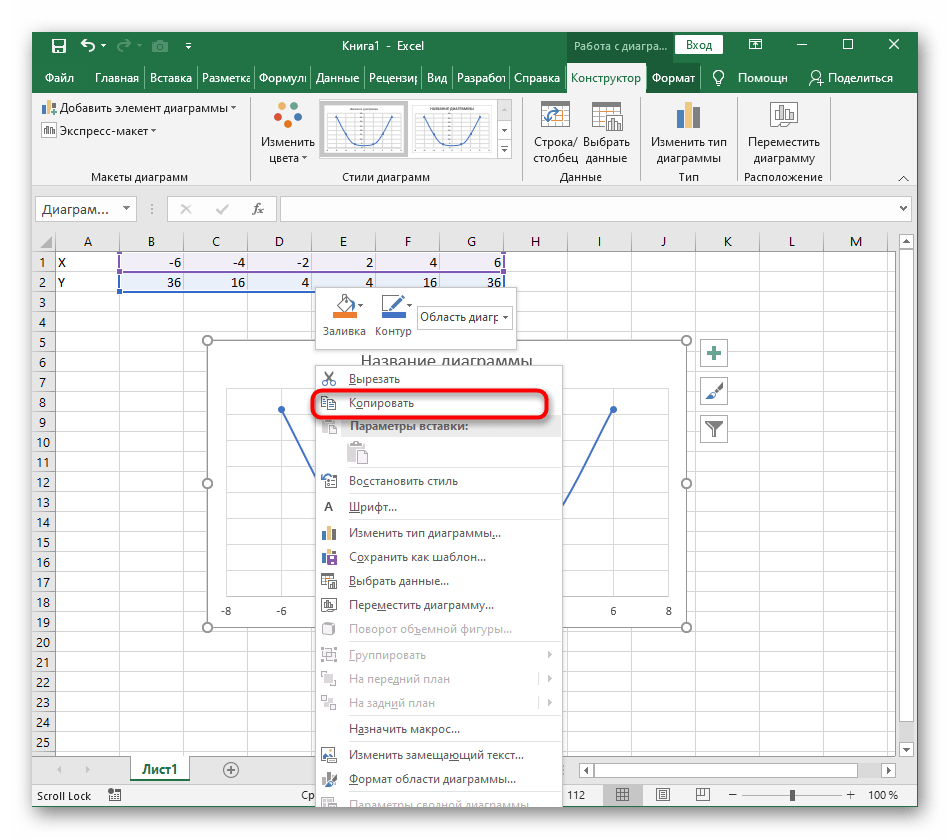
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
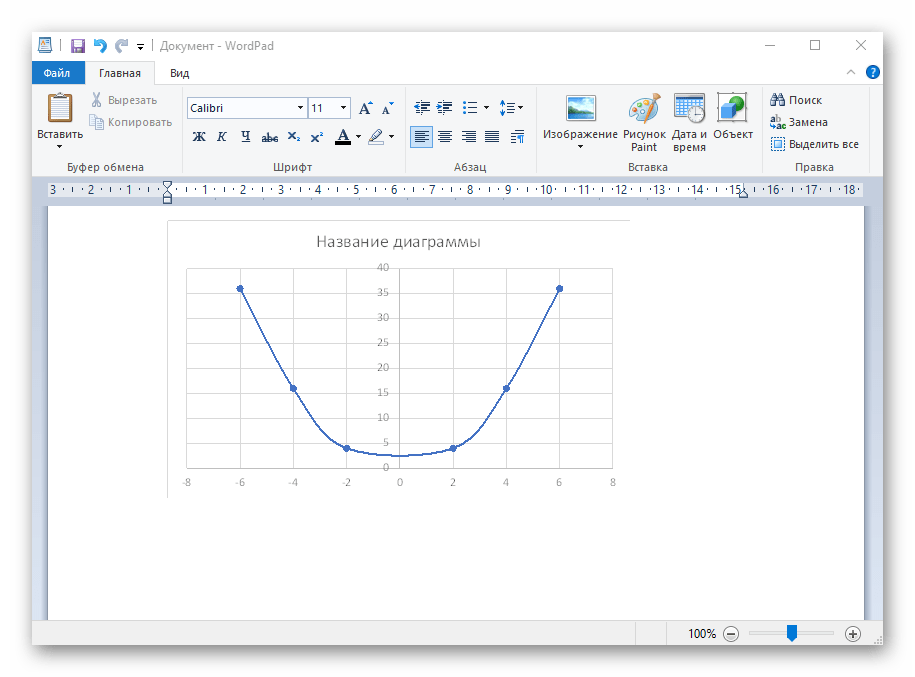
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме:
Помогла ли Вам статья?

Danz, Вы нашли ответ на Ваш вопрос о составлении формулы?
Помогите если уже знаете как вывести формулу, имея слудующие значения:
ось X Ось Y
100000 12.00
200000 6.00
300000 4.00
400000 3.00
500000 2.40
600000 2.00
700000 1.71
800000 1.50
900000 1.33
1000000 1.20
1100000 1.09
1200000 1.00
1300000 0.92
1400000 0.86
1500000 0.80
1600000 0.75
1700000 0.71
1800000 0.67
1900000 0.63
Цитата: oliver7 от 20.05.2008, 16:05
Danz, Вы нашли ответ на Ваш вопрос о составлении формулы?
Помогите если уже знаете как вывести формулу, имея слудующие значения:
ЧТО значит ВЫВЕСТИ ФОРМУЛУ?
таблично заданная функция МОЖЕТ быть ИНТЕРПОЛИРОВАНА кусочно-линейным или кусочно-квадратичным методом (как минимум … а то и еще КАК-ТО …)
и ЭТО , вроде, чистая математика … 
oliver7
Y=12000000/X
с округлением до 2 знаков после запятой
Вопрос не понятен.
Может имеется ввиду программно получить формулу для дальнейшего испрользования? Или вывестикоэффициенты зависимости на лист?
Скоорее всего подойдет такое решение:
Строим по имеющимся данным точечную диаграмму и добавляем линию тренда. В настройках линии тренда можно можно установить вывод на диаграмму уравнения регрессии Y на X.
Где-то в архиве, кстати, был пост с пользовательской функцией для извлечения уравнения регресси с диаграммы в ячейку листа.
Цитата: Алексей Шмуйлович от 21.05.2008, 11:29
Скоорее всего подойдет такое решение:
Строим по имеющимся данным точечную диаграмму и добавляем линию тренда. В настройках линии тренда можно можно установить вывод на диаграмму уравнения регрессии Y на X.
Где-то в архиве, кстати, был пост с пользовательской функцией для извлечения уравнения регресси с диаграммы в ячейку листа.
А по-точнее где ее поискать?
Знания недостаточно, необходимо применение. Желания недостаточно, необходимо действие. (с) Брюс Ли
- Профессиональные приемы работы в Microsoft Excel
-
►
Обмен опытом -
►
Microsoft Excel -
►
Как вывести формулу вида y=f(x) по графику построенному по числовым данным?










 Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).
Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).









































 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):





 Сообщение было отмечено p1111 как решение
Сообщение было отмечено p1111 как решение