Пользователи Excel часто озадачены очевидной неспособностью Excel выполнять простые математические операции. Это не ошибка программы: компьютеры по своей природе не обладают бесконечной точностью. Excel хранит числа в двоичном формате, используя 8 байт, которых хватает для обработки числа с 15 цифрами.
Некоторые числа не могут быть выражены именно с помощью 8 байт, поэтому хранятся в виде приближений. Чтобы продемонстрировать, как это ограничение может вызывать проблемы, введите следующую формулу в ячейку А1: =(5,1-5,2)+1.
Результат должен быть равен 0,9. Однако если вы отформатируете ячейку так, чтобы она отображала 15 знаков после запятой, то обнаружите, что программа вычисляет формулу с результатом 0,899999999999999 — значением, очень близким к 0,9, но никак не 0,9. Такой результат получается, поскольку операция в круглых скобках выполняется первой, и этот промежуточный результат сохраняется в двоичном формате с использованием приближения. Затем формула добавляет 1 к этому значению, а погрешность приближения распространяется на конечный результат.
Во многих случаях ошибки такого рода не представляют проблемы. Однако если вам необходимо проверить результат формулы с помощью логического оператора, это может стать головной болью. Например, следующая формула (которая предполагает, что предыдущая формула находится в ячейке А1) возвращает ЛОЖЬ: =A1-0,9.
Одно из решений этого типа ошибки заключается в использовании функции ОКРУГЛ. Следующая формула, например, возвращает ИСТИНА, поскольку сравнение выполняется с использованием значения в А1, округленного до одного знака после запятой: =ОКРУГЛ(А1;1)=0.9. Вот еще один пример проблемы точности. Попробуйте ввести следующую формулу: =(1,333-1,233)-(1,334-1,234). Эта формула должна возвращать 0, по вместо этого возвращает -2,22045Е-16 (число, очень близкое к нулю).
Если бы эта формула была в ячейке А1, то формула вернула бы Not Zero: =ЕСЛИ(А1=0;"Zero";"Not Zero"). Один способ справиться с такой ошибкой округления состоит в использовании формулы вроде этой: =ЕСЛИ(ABS(А1)<0.000001;"Zero";"Not Zero"). В данной формуле используется оператор «меньше чем» для сравнения абсолютного значения числа с очень малым числом. Эта формула будет возвращать Zero.
Другой вариант — указать Excel изменить значения листа в соответствии с их отображаемым форматом. Для этого откройте окно Параметры Excel (выберите Файл ► Параметры) и перейдите в раздел Дополнительно. Установите флажок Задать точность как на экране (который находится в области При пересчете этой книги).
Флажок Задать точность как на экране позволяет изменять числа в ваших листах так, что они постоянно будут соответствовать появлению на экране. Этот флажок применяется для всех листов активной книги. Такой вариант не всегда будет вам подходить. Убедитесь, что вы понимаете последствия установки флажка Задать точность как на экране.
As one of the most versatile calculators ever created, Excel is utilized to power innumerable business operations daily; however, can it ever fail to give you the correct results?
In the case of floating numbers, it can. The term floating point refers to the fact that there are no constant number of digits before or after the decimal point of a number. In other words, the decimal point itself can “float”.
Calculations may not show the correct results when dealing with high precision values. This is not a bug, but rather a design choice that affects every computing system to some degree.
Binary System
The main reason behind this behavior can be broken down to a fundamental design component of computer-based systems. Computer hardware and software communicate with one another using a binary system, consisting of values 1 and 0, as input and output data.
Therefore, the base-10 numerical system is also stored in binary format, which can cause issues with fractions. For example, the fraction of 2/10 is represented as 0.2 in the decimal number system, but identified by an infinitely repeating number 0.00110011001100110011 in the binary system. Data loss becomes inevitable when storing this number in a finite space. The data loss occurs after the 1E-15 point: more commonly known as the 15-digit limit in Excel.
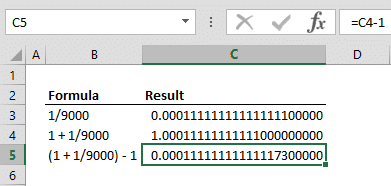
For instance, looking at the example below, you would agree that cells C3 and C5 are equal. However, adding a value of 1 to the value of C3 changes the precision level (i.e. there are eleven 1’s in cell C4, while there are fifteen in cell C3). Ultimately, we get a completely different result in C5, which supposedly contains the inverse function.
Standard
Excel uses a modified version of the IEEE 754-1985 standards. This is a technical standard for floating-point computation, established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The 754 revision became very popular and is the most widely used format for floating-point computation by both software libraries and hardware components (i.e. CPUs). According to Microsoft, it is used in all of today’s PC-based microprocessors, including the Intel, Motorola, Sun, and MIPS processors.
Limitations
Maximum / Minimum
Excel only has a finite space to store data. This limitation affects the maximum and minimum numbers allowed by the software. Here are some examples[2]:
| Smallest allowed negative number | -2.2251E-308 |
| Smallest allowed positive number | 2.2251E-308 |
| Largest allowed positive number | 9.99999999999999E+307 |
| Largest allowed negative number | -9.99999999999999E+307 |
| Largest allowed positive number via formula | 1.7976931348623158e+308 |
| Largest allowed negative number via formula | -1.7976931348623158e+308 |
Source: https://support.office.com/en-us/article/excel-specifications-and-limits-1672b34d-7043-467e-8e27-269d656771c3
Excel returns the #NUM! error if a larger number is calculated. This behavior is called an overflow. Excel evaluates very small numbers as 0s, and this behavior is called as underflow. Both will result in data loss.
Excel does not support infinite numbers and provides a #DIV/0! error when a calculation results in an infinite number.
Precision
Although Excel can display more than 15 digits, displayed values are not the actual values that are used in calculations. The IEEE standard upholds storage to only 15 significant digits, which can cause inconsistent results when working with very large or very small numbers.
Very large numbers
In the example below, Excel finds the sum of B8 and B9 to be equal to the value of B8. The 15-digit limit causes Excel to evaluate the calculation with the 15 largest digits. This example would have required Excel to work with 100-digit precision to evaluate accurately.
Very small numbers
If we add the value 1 to 0.000123456789012345 (which has 18 significant digits but contains numeric values in its smallest 15 digits), the result should be 1.000123456789012345. However, Excel gives 1.00012345678901 because it ignores the digits following the 15th significant digit.
Repeating Binary Numbers
Storing repeating binary numbers as non-repeating decimal number can affect the final values in Excel. For example, the formula ‘=(73.1-73.2)+1’ evaluates to 0.899999999999991 when you format the decimal places to 15 digits.
Accuracy within VBA
Unlike Excel calculations, VBA can work with more than a single type of data. Excel uses 8-byte numbers, while VBA offers different data types that vary from 1 byte (Byte) to 16 bytes (Decimal), which can provide precision at the 28-digit level. You can choose a variable type based on your data storage, accuracy, and speed requirements.
Floating point calculations can be relatively challenging due to technical limitations. However, VBA and other mathematical methods offer workarounds to ensure that you don’t miss a decimal if you’re aware of the existing limitations.
Ошибка округления точки с плавающей запятой вступает в игру, как только вы конвертируете число, которое невозможно точно представить. Он имеет тенденцию увеличиваться по мере выполнения расчетов.
Ближайшее представимое значение до 1.0554 составляет 1.0553999999999998937738610038650222122669219970703125. Ближайшим представляемым значением до 1.0554000000000001 является 1.055400000000000115818465928896330296993255615234375 — это, вероятно, то, что вышло из расчета макросов. Плохая новость заключается в том, что вы не получаете точно того значения, которое вы имели в виду. Хорошей новостью является то, что различие часто, как и в этом случае, слишком мало, чтобы иметь значение или даже быть измерено в реальной жизни.
Как правило, вы не хотите, чтобы точное значение печаталось. По умолчанию поведение toString в Java заключается в создании кратчайшего десятичного расширения, которое преобразуется во внутреннее значение. Это также обычно не то, что вы хотите для дисплеев конечных пользователей.
Правильная вещь, в большинстве случаев, именно то, что вы делаете в Excel — отображать только те цифры, которые, по вашему мнению, имеют значение для того, что вы делаете. В Java вы можете использовать DecimalFormat для преобразования double в String с контролем над отображаемыми цифрами.
На чтение 1 мин Опубликовано 31.07.2015
Excel хранит и вычисляет числа с плавающей запятой, но иногда результаты формул получаются приблизительными.
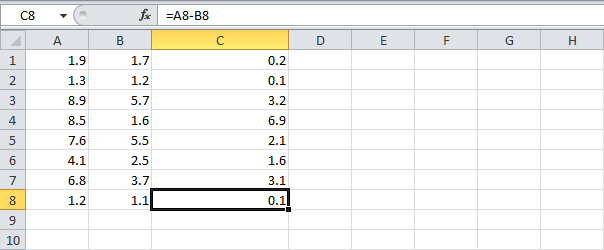
- К примеру, взгляните на формулы, приведенные на рисунке ниже. На первый взгляд все выглядит хорошо.
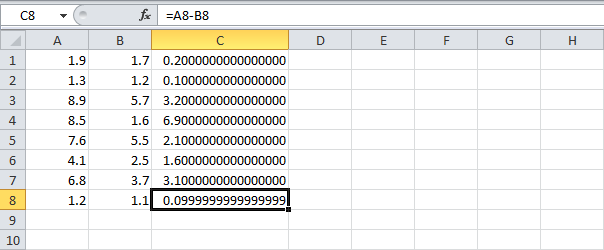
- Однако, если мы отобразим 16 десятичных знаков, то увидим, что один из результатов – это очень приближенное значение.
Вы не должны беспокоиться о проблеме плавающей запятой. Она встречается довольно редко. Даже если ваш лист содержит ошибку с плавающей запятой, в большинстве случаев это не вызывает проблем.
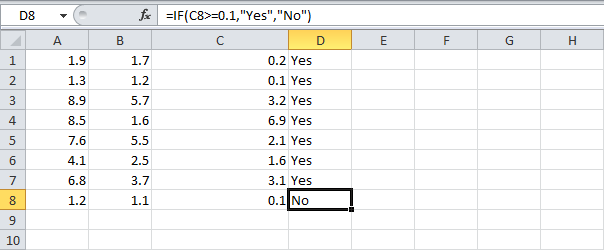
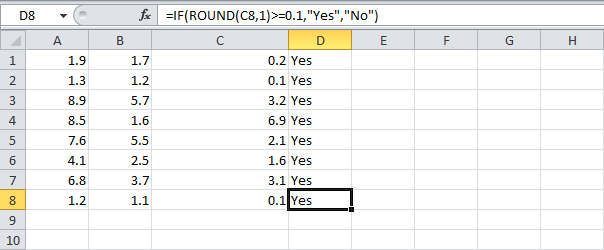
- Тем не менее, если сравнивать значение в ячейке С8 с другим значением, проблемы могут появиться.
=IF(C8>=0.1,"Yes","No")
=ЕСЛИ(C8>=0,1;"Yes";"No") - Используйте функцию ROUND (ОКРУГЛ), чтобы исправить это.
=IF(ROUND(C8,1)>=0.1,"Yes","No")
=ЕСЛИ(ОКРУГЛ(C8;1)>=0,1;"Yes";"No")
Оцените качество статьи. Нам важно ваше мнение:
Например, этот блог говорит, что 0,005 не точно 0,005, но округление этого числа дает правильный результат.
Я пробовал все виды округления в C++, и он терпит неудачу при округлении чисел до определенных десятичных знаков. Например, Round (x, y) округляет x до кратного y. So Round (37.785,0.01) должен дать вам 37.79, а не 37.78.
Я вновь открываю этот вопрос, чтобы обратиться за помощью к сообществу. Проблема заключается в неточности чисел с плавающей запятой (37,785 представлена как 37,78499999999).
Вопрос в том, как Excel справляется с этой проблемой?
Решение в этом раунде() для float в C++ неверно для указанной проблемы.
Ответ 1
«Круглый (37.785,0.01) должен дать вам 37.79, а не 37.78».
Во-первых, нет единого мнения, что 37.79 вместо 37.78 является «правильным» ответом здесь? Автоматические выключатели всегда немного жесткие. Хотя всегда округление в случае галстука является широко используемым подходом, это, безусловно, не единственный подход.
Во-вторых, это не обстановка. Численное значение в бинарном формате IEEE с плавающей запятой составляет 37.784999999999997 (приблизительно). Существует множество способов получить значение 37.784999999999997, кроме человека, набрав значение 37.785 и, как оказалось, преобразуется в это представление с плавающей запятой. В большинстве случаев правильный ответ составляет 37,78, а не 37,79.
добавление
Рассмотрим следующие формулы Excel:
=ROUND(37785/1000,2)
=ROUND(19810222/2^19+21474836/2^47,2)
Обе ячейки будут отображать одинаковое значение, 37.79. Существует законный аргумент в отношении того, должен ли 37785/1000 округлить до 37,78 или 37,79 с точностью до двух мест. Как справиться с этими краевыми случаями является немного произвольным, и консенсусного ответа нет. В Microsoft даже нет единого ответа: «Функция Round() несовместима с различными продуктами Microsoft по историческим причинам». (http://support.microsoft.com/kb/196652). При использовании машины с бесконечной точностью Microsoft VBA будет составлять 37,785 до 37,78 (раунд банкира), а Excel — 37,79 (симметричный арифметический раунд).
Нет никакого аргумента в отношении округления последней формулы. Это строго меньше 37.785, поэтому он должен округлить до 37.78, а не 37.79. Однако Excel округляет его. Зачем?
Причина связана с тем, как реальные числа представлены на компьютере. Microsoft, как и многие другие, использует формат с плавающей запятой в 64-битном формате IEEE. Число 37785/1000 страдает от потери точности, выраженного в этом формате. Эта точность не возникает с 19810222/2 ^ 19 + 21474836/2 ^ 47; это «точное число».
Я намеренно построил это точное число, чтобы иметь такое же представление с плавающей запятой, как и неточное 37785/1000. Этот Excel округляет это точное значение, а не вниз, является ключом к определению того, как работает функция Excel ROUND(): это вариант симметричного арифметического округления. Он округляется на основе сравнения с представлением с плавающей запятой для углового случая.
Алгоритм в C++:
#include <cmath> // std::floor
// Compute 10 to some positive integral power.
// Dealing with overflow (exponent > 308) is an exercise left to the reader.
double pow10 (unsigned int exponent) {
double result = 1.0;
double base = 10.0;
while (exponent > 0) {
if ((exponent & 1) != 0) result *= base;
exponent >>= 1;
base *= base;
}
return result;
}
// Round the same way Excel does.
// Dealing with nonsense such as nplaces=400 is an exercise left to the reader.
double excel_round (double x, int nplaces) {
bool is_neg = false;
// Excel uses symmetric arithmetic round: Round away from zero.
// The algorithm will be easier if we only deal with positive numbers.
if (x < 0.0) {
is_neg = true;
x = -x;
}
// Construct the nearest rounded values and the nasty corner case.
// Note: We really do not want an optimizing compiler to put the corner
// case in an extended double precision register. Hence the volatile.
double round_down, round_up;
volatile double corner_case;
if (nplaces < 0) {
double scale = pow10 (-nplaces);
round_down = std::floor (x * scale);
corner_case = (round_down + 0.5) / scale;
round_up = (round_down + 1.0) / scale;
round_down /= scale;
}
else {
double scale = pow10 (nplaces);
round_down = std::floor (x / scale);
corner_case = (round_down + 0.5) * scale;
round_up = (round_down + 1.0) * scale;
round_down *= scale;
}
// Round by comparing to the corner case.
x = (x < corner_case) ? round_down : round_up;
// Correct the sign if needed.
if (is_neg) x = -x;
return x;
}
Ответ 2
Для очень точной произвольной точности и округления чисел с плавающей запятой к фиксированному множеству десятичных знаков вы должны взглянуть на математическую библиотеку такую как GNU MPFR. В то время как это C-библиотека, веб-страница, которую я опубликовал, также связывает с несколькими различными связями на С++, если вы хотите избежать использования C.
Вы также можете прочитать статью под названием «Что каждый компьютерный ученый должен знать о арифметике с плавающей запятой» Дэвида Голдберга в Xerox Palo Исследовательский центр Альто. Это отличная статья, демонстрирующая базовый процесс, который позволяет аппроксимировать числа с плавающей запятой на компьютере, который представляет все в двоичных данных, и о том, как ошибки округления и другие проблемы могут появиться в математике с плавающей запятой на основе FPU.
Ответ 3
Я не знаю, как это делает Excel, но хорошо печатать числа с плавающей запятой — это тяжелая проблема: http://www.serpentine.com/blog/2011/06/29/here-be-dragons-advances-in-problems-you-didnt-even-know-you-had/
Ответ 4
Итак, ваш фактический вопрос, похоже, как правильно округлить конверсии с плавающей точкой → строка. Путем поиска по этим терминам вы получите кучу статей, но если вам интересно что-то использовать, большинство платформ предоставляют достаточно компетентные реализации sprintf()/snprintf(). Поэтому просто используйте их, и если вы найдете ошибки, отправьте отчет поставщику.
Ответ 5
Функция, которая принимает число с плавающей запятой в качестве аргумента и возвращает другое число с плавающей запятой, округленное точно до заданного числа десятичных цифр, не может быть записано, потому что существует множество чисел с конечным десятичным представлением, которые имеют бесконечное двоичное представление; один из самых простых примеров — 0,1.
Чтобы добиться того, что вы хотите, вы должны принять использование другого типа в результате функции округления. Если вам нужна срочная печать номера, вы можете использовать строку и функцию форматирования: проблема в том, как получить именно то форматирование, которое вы ожидаете. В противном случае, если вам нужно сохранить это число, чтобы выполнить точные вычисления на нем, например, если вы ведете учет, вам нужна библиотека, способная точно представлять десятичные числа. В этом случае наиболее распространенным подходом является использование масштабированного представления: целое число для значения вместе с числом десятичных цифр. Разделение значения на десять, поднятое до шкалы, дает вам исходный номер.
Если какой-либо из этих подходов подходит, я попытаюсь расширить свой ответ с практическими предложениями.
Ответ 6
Циклы Excel округляются так, как «правильно», делая WORK. Они начались в 1985 году с довольно «нормального» набора подпрограмм с плавающей запятой и добавили некоторую фальшивую плавающую точку с масштабированным целым, и с тех пор они настраивали эти вещи и добавляли специальные случаи. В приложении DID использовались большинство тех же «очевидных» ошибок, что и у всех остальных, это просто, что они в основном имели их давным-давно. Я подал пару себя, когда я занимался технической поддержкой для них в начале 90-х.
Ответ 7
Как говорит mjfgates, Excel делает тяжелую работу, чтобы получить это «право». Первое, что нужно сделать, когда вы пытаетесь переопределить это, — это определить, что вы подразумеваете под «правильным». Очевидные решения:
— реализовать рациональную арифметику
Медленный, но надежный.
— реализовать кучу эвристик
Быстро, но сложно получить право (подумайте «годы отчетов об ошибках» ).
Это действительно зависит от вашего приложения.
Ответ 8
Так же, как номера базы-10 должны округляться по мере их преобразования в base-2, можно округлить число, поскольку оно преобразуется из base-2 в base-10. Как только число будет иметь представление base-10, оно может быть округлено снова простым способом, взглянув на цифру справа от той, которую вы хотите округлить.
Пока нет ничего плохого в вышеупомянутом утверждении, существует гораздо более прагматичное решение. Проблема в том, что двоичное представление пытается как можно ближе подойти к десятичному числу, даже если этот двоичный код меньше десятичного. Сумма ошибки находится в пределах [-0,5,0,5] младших значащих бит (LSB) истинного значения. Для округления целей вы предпочтете, чтобы он находился в пределах [0,1] LSB, чтобы ошибка всегда была положительной, но это невозможно без изменения всех правил математики с плавающей запятой.
Единственное, что вы можете сделать, это добавить 1 LSB к значению, поэтому ошибка находится в пределах [0.5.1.5] LSB истинного значения. Это менее точный итог, но только очень крошечная сумма; когда значение округляется для представления в виде десятичного числа, его гораздо более вероятно округлить до правильного десятичного числа, потому что ошибка всегда положительна.
Чтобы добавить 1 LSB к значению перед округлением, см. ответы на этот вопрос. Например, в Visual Studio С++ 2010 процедура будет выглядеть так:
Round(_nextafter(37.785,37.785*1.1),0.01);
Ответ 9
Что вам нужно:
double f = 22.0/7.0;
cout.setf(ios::fixed, ios::floatfield);
cout.precision(6);
cout<<f<<endl;
Как это можно реализовать (просто обзор округления последней цифры)
long getRoundedPrec(double d, double precision = 9)
{
precision = (int)precision;
stringstream s;
long l = (d - ((double)((int)d)))* pow(10.0,precision+1);
int lastDigit = (l-((l/10)*10));
if( lastDigit >= 5){
l = l/10 +1;
}
return l;
}
Ответ 10
Есть много способов оптимизировать результат с плавающей запятой, используя статистические, численные… алгоритмы
Самым простым, вероятно, является поиск повторяющихся 9 или 0 в диапазоне точности. Если они есть, возможно, эти 9 лишние, просто округлите их. Но это может не сработать во многих случаях. Вот пример для числа с float с 6 цифрами точности:
2.67899999 → 2.679
12.3499999 → 12.35
1.20000001 → 1.2
Excel всегда ограничивает диапазон ввода до 15 цифр и округляет вывод до максимум 15 цифр, так что это может быть одним из способов использования Excel
Или вы можете включить точность вместе с числом. После каждого шага регулировка точности зависит от точности операндов. Например
1.113 → 3 decimal digits
6.15634 → 5 decimal digits
Поскольку оба числа находятся в диапазоне точности 16-17 цифр, их сумма будет точной для большего из них, то есть 5 цифр. Аналогично, 3 + 5 <16, поэтому их произведение будет с точностью до 8 десятичных чисел
1.113 + 6.15634 = 7.26934 → 5 decimal digits
1.113 * 6.15634 = 6.85200642 → 8 decimal digits
Но 4.1341677841 * 2.251457145 потребует только двойной точности, потому что реальный результат превышает двойную точность
Другой эффективный алгоритм — Грису, но у меня не было возможности попробовать.
В 2010 году Флориан Лойч опубликовал замечательную статью в PLDI » Быстрая и точная печать чисел с плавающей точкой с целыми числами», которая представляет собой самый большой шаг в этой области за последние 20 лет: он в основном выяснил, как использовать целые числа машин для точного рендеринга. ! Почему я говорю «в основном»? Поскольку алгоритм Loitsch «Grisu3» очень быстрый, он отказывается от примерно 0,5% чисел, и в этом случае вам придется прибегнуть к Dragon4 или производной
Здесь будут драконы: достижения в проблемах, о которых вы даже не знали
На самом деле, я думаю, что Excel должен сочетать в себе множество различных методов для достижения наилучшего результата из всех
Пример, когда значение достигает нуля
В Excel 95 или более ранней версии введите в новую книгу следующее:
A1: =1.333+1.225-1.333-1.225Щелкните правой кнопкой мыши ячейку A1 и выберите «Формат ячеек». На вкладке «Число» выберите «Научный» в категории Установите десятичные разряды на 15.
Вместо отображения 0 в Excel 95 отображается
-2.22044604925031E-16.Excel 97, однако, представил оптимизацию, которая пытается исправить эту проблему. Если операция сложения или вычитания приводит к значению, равному нулю или очень близкому к нему, Excel 97 и более поздние версии компенсируют любую ошибку, возникшую в результате преобразования операнда в двоичный код и обратно. Приведенный выше пример при выполнении в Excel 97 и более поздних версиях правильно отображает 0 или 0,000000000000000E + 00 в научной нотации.
Арифметика с плавающей точкой может давать неточные результаты в Excel
Ответ 11
Я считаю, что следующие номера раундов кода С#, поскольку они округлены в Excel. Чтобы точно воспроизвести поведение на С++, вам может понадобиться специальный десятичный тип.
На простом английском языке число с двойной точностью преобразуется в десятичное число, а затем округляется до пятнадцати значащих цифр (не путать с пятнадцати знаками после запятой). Результат округляется во второй раз до указанного количества знаков после запятой.
Это может показаться странным, но вы должны понимать, что Excel всегда отображает числа, округленные до 15 значащих цифр. Если функция ROUND() не использовала это отображаемое значение в качестве начальной точки и вместо этого использовала внутреннее двойное представление, тогда были бы случаи, когда ROUND (A1, N), похоже, не соответствовали фактическому значению в A1. Это будет очень запутанным для нетехнического пользователя.
Двойник, который ближе всего к 37.785, имеет точное десятичное значение 37.784999999999996589394868351519107818603515625. (Любой двойник может быть представлен точно конечной базой десяти десятичной, поскольку одна четверть, одна восьмая, одна шестнадцатая и т.д. Все имеют конечные десятичные разложения.) Если бы это число было округлено непосредственно до двух знаков после запятой, не было бы привязки к и результат будет равен 37,78. Если вы округлите до 15 значащих цифр, вы получите 37.7850000000000. Если это будет округлено до двух знаков после запятой, тогда вы получите 37.79, поэтому в действительности нет никакой тайны.
// Convert to a floating decimal point number, round to fifteen
// significant digits, and then round to the number of places
// indicated.
static decimal SmartRoundDouble(double input, int places)
{
int numLeadingDigits = (int)Math.Log10(Math.Abs(input)) + 1;
decimal inputDec = GetAccurateDecimal(input);
inputDec = MoveDecimalPointRight(inputDec, -numLeadingDigits);
decimal round1 = Math.Round(inputDec, 15);
round1 = MoveDecimalPointRight(round1, numLeadingDigits);
decimal round2 = Math.Round(round1, places, MidpointRounding.AwayFromZero);
return round2;
}
static decimal MoveDecimalPointRight(decimal d, int n)
{
if (n > 0)
for (int i = 0; i < n; i++)
d *= 10.0m;
else
for (int i = 0; i > n; i--)
d /= 10.0m;
return d;
}
// The constructor for decimal that accepts a double does
// some rounding by default. This gets a more exact number.
static decimal GetAccurateDecimal(double r)
{
string accurateStr = r.ToString("G17", CultureInfo.InvariantCulture);
return Decimal.Parse(accurateStr, CultureInfo.InvariantCulture);
}
Ответ 12
Большинство десятичных дробей не могут быть точно представлены в двоичном формате.
double x = 0.0;
for (int i = 1; i <= 10; i++)
{
x += 0.1;
}
// x should now be 1.0, right?
//
// it isn't. Test it and see.
Одним из решений является использование BCD. Я говорил. Но, это также попыталось и правда. У нас есть много других старых идей, которые мы используем каждый день (например, используя 0 для представления ничего…).
Другая технология использует масштабирование при вводе/выводе. Это имеет то преимущество, что почти вся математика является целочисленной математикой.