Функция ЭФФЕКТ в Excel предназначена для расчета фактической годовой процентной ставки (иное название – эффективная ставка), на основе известных данных, таких как номинальная годовая ставка, число периодов начисления сложных процентов, и возвращает соответствующее числовое значение.
Примеры использования функции ЭФФЕКТ в Excel
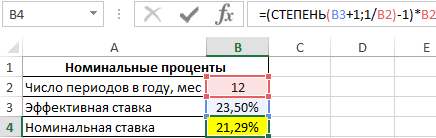
Пример 1. Предприниматель получил ссуду в банковской организации на 1 год с эффективной процентной ставкой 23,5%. Определить значение номинальной ставки, если по условию договора выплаты по кредиту необходимо проводить ежемесячно.
Исходная таблица данных:
Связь между значениями эффективной и номинальной ставок описывается следующей формулой:
=(СТЕПЕНЬ(B3+1;1/B2)-1)*B2
Полученный результат:
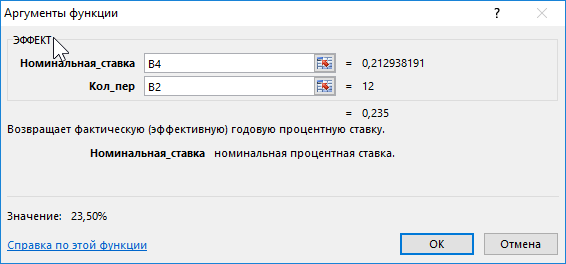
Проверим полученный результат, проведя пересчет эффективной ставки с помощью функции:
Описание аргументов:
- B4 – полученное выше числовое значение номинальной ставки;
- B2 – число периодов погашения.
Результат:
Полученное значение 0,235 соответствует 23,5% (значению эффективной ставки по условию). Расчет номинальной ставки также можно производить с помощью функции НОМИНАЛ.
Формула расчета процентов по вкладу в Excel
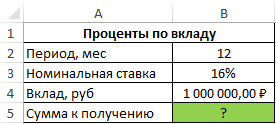
Пример 2. Вкладчику предложили сделать депозит в банк под 16% годовых (номинальная ставка), при этом расчете производится с использованием сложных процентов (эффективная ставка). По условиям договора вкладчик сможет снять только полученные проценты. Определить сумму к получению, если размер депозита – 1 млн. рублей, капитализация – ежемесячная.
Исходные данные:
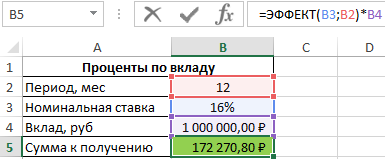
Формула для расчета:
=ЭФФЕКТ(B3;B2)*B4
Описание аргументов:
- B2 – число периодов капитализации;
- B3 – номинальная ставка;
- B4 – сумма вклада.
Результат расчетов:
Для сравнения, доход от вклада при использовании простых процентов составил бы 1000000*0,16=160000 рублей, поэтому для вкладчика выгодно использовать предложенный вариант со сложными процентами.
Как посчитать проценты на депозит в Excel для выбора вклада
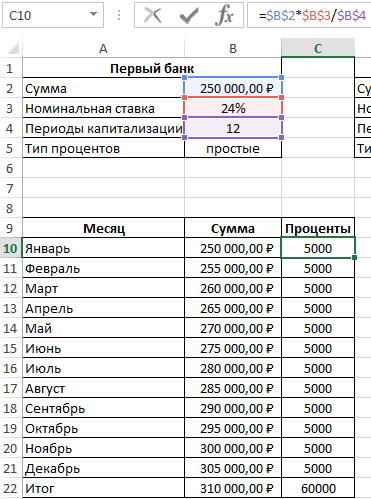
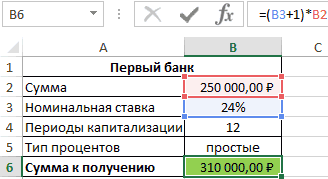
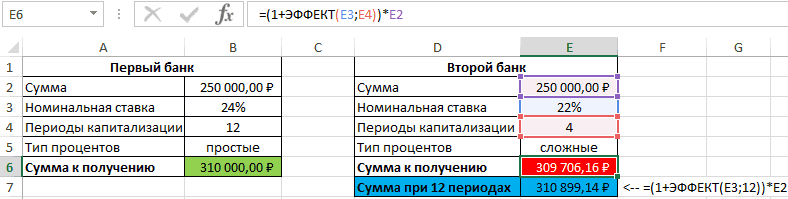
Пример 3. Два банка предлагают сделать депозитный вклад на одинаковую сумму (250000 рублей) на 1 год при следующих условиях:
- Номинальная ставка – 24%, простые проценты, 12 периодов капитализации.
- Номинальная ставка 22%, сложные проценты, начисляемые по итогам каждого периода, 4 периода капитализации.
Определить выгодный вариант, отобразить схему выплат.
Исходные данные:
В первом случае таблица выплат выглядит так:
Проценты – постоянная величина, рассчитываемая по формуле:
=$B$2*$B$3/$B$4
Описание аргументов (для создания абсолютной ссылки используйте клавишу F4):
- $B$2 – начальная сумма вклада;
- $B$3 – годовая ставка;
- $B$4 – число периодов капитализации вклада.
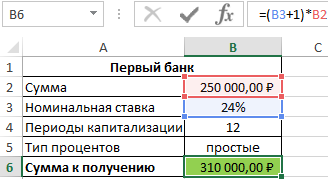
Сумма накопленных средств за каждый период рассчитывается как как сумма средств на счету за прошедший период и процентов, начисленных за текущий период. В итоге первый банк начислит 60000 рублей процентов, и вкладчик сможет забрать 310000 рублей.
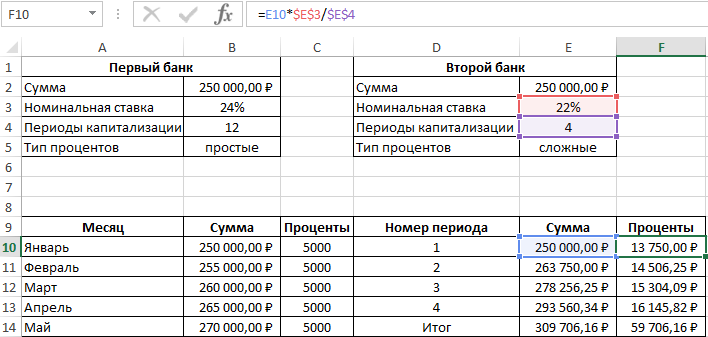
Таблица начисления процентов по условиям второго банка:
В данном случае проценты не являются фиксированной величиной и зависят от итоговой суммы накоплений за предыдущий период (поэтому ссылка на ячейку L2 – абсолютная):
=L3*$E$3/$E$4
При расчете суммы за каждый период к текущему значению необходимо прибавить проценты за предыдущий период.
Для быстрого расчета итоговой суммы используем формулы:
- Первый банк:
- Второй банк:
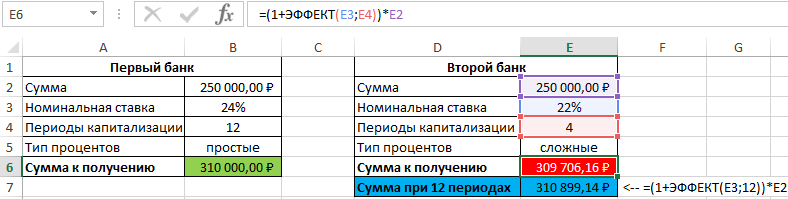
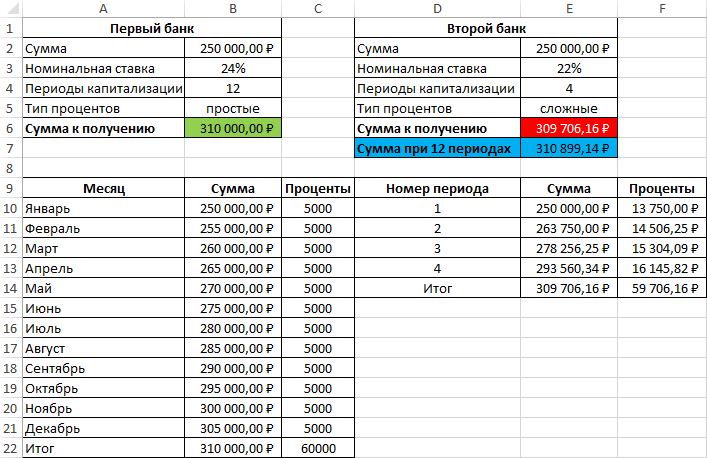
Результаты расчетов:
Несмотря на то, что второй банк предлагает расчет с использованием сложных процентов, предложение первого банка оказалось выгоднее. Если бы число периодов капитализации совпадало (12), во втором банке вкладчик получил бы 310899,1 рублей, то есть больше денег, несмотря на более низкую номинальную процентную ставку.
Особенности использования функции ЭФФЕКТ в Excel
Функция имеет следующий синтаксис:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
Описание аргументов:
- номинальная_ставка – обязательный аргумент, характеризующий числовое (десятичная дробь) или процентное значение номинальной годовой ставки;
- кол_пер – обязательный аргумент, характеризующий числовое значения числа периодов за год, на протяжении которых начисляются сложные проценты.
Примечания 1:
- Аргумент кол_пер может принимать дробные числа, значения которых будут усечены до целого числа (в отличие от операции округления, при усечении отбрасывается дробная часть).
- Каждый из двух аргументов функции ЭФФЕКТ должен быть представлен числовым (или процентным для аргумента номинальная_ставка) значением либо текстовой строкой, которая может быть преобразована в число. При вводе не преобразуемых к числовым значениям текстовых строк и имен, а также данных логического типа функция ЭФФЕКТ будет возвращать код ошибки #ЗНАЧ!.
- Аргумент номинальная_ставка принимает значения из диапазона положительных чисел, а кол_пер – из диапазона от 1 до +∞. Если данные условия не выполняются, например, функции =ЭФФЕКТ(0;12) или =ЭФФЕКТ(12%;0) вернут код ошибки #ЧИСЛО!.
- Функция ЭФФЕКТ использует для расчетов формулу, которая может быть записана в Excel в виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:
- A1 – номинальная годовая ставка;
- A2 – число периодов, в которые происходит начисление сложных процентов.
Примечания 2:
- Для понимания термина «сложные проценты» рассмотрим пример. Владелец капитала предоставляет денежные средства в долг и планирует получить прибыль, величина которой зависит от следующих факторов: сумма средств, которая предоставляется в долг; длительность периода кредитования (использования предоставленных средств); начисляемые проценты за использование.
- Проценты могут начисляться различными способами: базовая сумма остается неизменной (простые проценты) и база изменяется при наступлении каждого последующего периода выплат (сложные). При использовании сложных процентов сумма задолженности (прибыли) увеличивается быстрее при одинаковых сумме и периоде кредитования, в сравнении с применением простых процентов (особенно, если периодов начисления процентов (капитализации) достаточно много.
- Для получения результата в формате процентов необходимо установить соответствующий формат данных в ячейке, в которой будет введена функция ЭФФЕКТ.
В предыдущем посте я обещала облегчить вашу учетную участь и рассказать вам о том, как обычный Excel может помочь с выбором депозита. Причем, выгодного вам, а не только банку. Обещала – выполняю. Следуя моей инструкции, вы легко сможете определить, какие условия по банковским вкладам принесут вам наибольший доход.
За расчет потенциальной доходности в Microsoft Excel отвечает специальная функция БС (Будущая Стоимость (Future Value (FV) – о ней мы говорили здесь). Для того, чтобы ее вызвать, нажмите на символ f x , слева от строки ввода значений и адресов ячеек.
В открывшемся Мастере функций в строке поиска функций введите БС и нажмите Ввод. Кликните мышью на подсвеченной синим цветом строке БС, как показано ниже.
Составляющим формулы расчета будущей стоимости FV = PV(1+r)n в Excel соответствуют следующие функции:
| Общее название | Функция в Excel | Краткое описание |
|---|---|---|
| FV (Future Value) | БС (Будущая Стоимость) | Будущая сумма вклада |
| PV (Present Value) | ПС (Текущая Стоимость) | Текущая стоимость вклада |
| n | КПЕР (Количество Периодов) | Число периодов начисления процентов по вкладу |
| r | СТАВКА | Процентная ставка по вкладу |
Заполняем (вручную или указав адреса соответствующих ячеек) поля данными из нашего примера. Напомню, что мы решили открыть депозит, разместив на нем 10 000 рублей сроком 5 лет и под 10% годовых.
Ставку по вкладу указываем в виде десятичной дроби, т.е. 10% превратятся в 0,1. В Кпер ставим количество лет – у нас вклад на 5 лет, значит 5. Поле Плт оставляем пустым. В поле ПС начальную сумму вклада указываем со знаком “минус”, т.к. мы эти деньги отдаем, а не получаем.
Поле Тип заполняем с учетом того, как производится выплата процентов по нашему вкладу:
- если в конце срока (на языке финансистов такой поток платежей называется постнумерандо), то ставим “0” или оставляем поле пустым;
- если в начале срока (на языке финансистов такой поток платежей называется пренумерандо), то ставим “1”.
В случае если проценты по вкладу начисляются ежемесячно или ежеквартально, то в поле Ставка годовую процентную ставку следует разделить на 12 или 4 соответственно в виде десятичной дроби. Вместе с этим нужно внести изменения в Кпер, пересчитав количество выплат: при ежемесячном начислении в течение 5 лет ставим 60 (12 мес. х 5 лет); при квартальном – 20 (4 кв. х 5 лет).
А теперь: внимание – вопрос. Как изменится доходность нашего вклада в случае начисления банком сложных процентов в конце каждого месяца, а не года, как мы считали до этого, на протяжении 5 лет? Давайте посмотрим. Напомню, до этого у нас получалась сумма в размере 16 105 руб. Заполняем поля и нажимаем “ОК”.
Получаем 16 453 рубля. Как видите, разница 343 рубля. А главное: чем больше сумма вашего вклада и время его размещения, тем ощутимей будет прибавка. Такова магия сложных процентов. Отсюда – вывод. Проценты по вашему вкладу должны:
- капитализироваться;
- капитализироваться ежемесячно.
Чем чаще начисляются проценты и добавляются к сумме вашего вклада, тем лучше работают ваши деньги. Кстати, хотите узнать, как скоро ваш вклад удвоится? Нет ничего проще. Воспользуйтесь правилом 72.
- Разделите число 72 на предлагаемую банком процентную ставку, и вы получите то число лет, которое нужно для увеличения ваших вложений в 2 раза.
А сейчас (барабанная дробь) испытайте чувство гордости за себя. Потому что теперь вы можете рассчитать это в Excel. Для этого вызовите функцию Кпер, заполните данные из нашего примера (10% годовых, 5 лет, выплата процентов в конце года) и добавьте в поле БС ожидаемую сумму вклада в размере 20 000 руб. (10 000 руб. х 2). Вуаля!
А еще есть правило волшебной двадцатки. Суть его в том, что для обеспечения завтра того уровня дохода, к которому вы привыкли сегодня, вам нужна сумма в 20 раз превышающая ваш годовой доход. Посчитайте и впечатлитесь полученной цифрой.
Но, как гласит народная мудрость, о деньгах и здоровье вспоминают тогда, когда они заканчиваются. И часто бывает так, что изменить что-либо уже поздно. Стоит ли рисковать? Когда все, что вам нужно сделать – это подумать о завтра сегодня.
- Если у вас есть вопросы, пишите их в комментариях ниже, я вам отвечу. Также вы всегда можете обратиться ко мне за консультацией, пройти мои курсы и вебинары.
Обучение торговле на бирже
Содержание
- Как при помощи Excel провести вычисление будущей стоимости платежей и суммы банковского вклада
- Будущая стоимость платежей
- Будущая стоимость суммы вклада
- Округление в финансовых формулах
- Будущая стоимость платежей и суммы вклада
- Функция ЭФФЕКТ для расчета годовой процентной ставки в Excel
- Примеры использования функции ЭФФЕКТ в Excel
- Формула расчета процентов по вкладу в Excel
- Как посчитать проценты на депозит в Excel для выбора вклада
- Особенности использования функции ЭФФЕКТ в Excel
- Депозитный калькулятор вкладов в Excel. Расчет доходности вкладов
- Почему важно иметь под рукой калькулятор вкладов
- ? Скачать калькулятор вкладов в Excel
- Профессиональные калькуляторы вкладов
- Бесплатный калькулятор вкладов для Windows 10
- Банковский калькулятор вкладов для Андроид
- Основные возможности, которые предоставляет калькулятор вкладов в Excel
- Калькулятор вкладов онлайн — расчет вкладов со множеством параметров.
- Популярные вопросы по вкладам
Как при помощи Excel провести вычисление будущей стоимости платежей и суммы банковского вклада
Будущая стоимость является оборотной стороной временных изменений денег. Будущая стоимость говорит о том, сколько будет стоить известная сумма денег (или известная серия выплат) через некоторый промежуток времени. Синтаксис функции БС следующий: БС(ставка;кпер;плт;пс;тип) .
Будущая стоимость платежей
В этом примере мы предположим, что открыли накопительный счет для своего ребенка, чтобы к окончанию школы насобирать ему сумму, необходимую для платного обучения в университете. Начиная со следующего месяца, вы будете ежемесячно откладывать 50 долларов на этот счет под 3% годовых. Следующая формула показывает, что к совершеннолетию у вашего сына на счету будет 14297,02 долларов (рис. 1): =БС(,03/12;18*12;-50;0;0) .
Рис. 1. Вычисление будущей суммы платежей
Годовую процентную ставку 3% мы преобразуем в месячную; 18 лет также преобразуем в месяцы. Приведенная стоимость отсутствует, так как вы только что открыли счет. Аргумент Тип равен нулю, так как вносить суммы вы начинаете со следующего месяца.
Будущая стоимость суммы вклада
В следующем примере вычисляется будущая стоимость суммы денег, которая не будет пополняться, и с нее не будут сниматься деньги. Предположим, что вы открыли пенсионный счет, внесли на него 20 тысяч долларов и планируете через 15 лет выйти на пенсию (рис. 2): =БС(,08;15;0;-20000;0) .
Рис. 2. Вычисление будущей стоимости вклада
В данном примере предполагается, что пенсионный вклад гарантирует получение 8% годовых. Значение -20000 представляет двадцать тысяч долларов, уходящих от вас в банк. В результате мы получаем 63443,38 долларов — эту сумму вы получите через 15 лет при выходе на пенсию.
Округление в финансовых формулах
При использовании финансовых формул проблема округления значений ощущается особенно остро. Excel предлагает несколько функций для выполнения этой задачи: ОКРУГЛ, ОКРУГЛВНИЗ И ОКРУГЛВВЕРХ. Чтобы предотвратить накопительные ошибки, округляйте только конечный получаемый результат. Другими словами, избегайте округления промежуточных данных. Обычно результаты финансовых расчетов отображаются в виде чисел с двумя десятичными разрядами или вообще без таковых. В промежуточных расчетах это предполагает получение результатов с точностью до цента или доллара.
В отдельных случаях вычисления базируются на приблизительных данных или данных, полученных в результате эмпирического анализа или подбора параметров. Поэтому уже давно обычной практикой стало применение округленных значений (чтобы не утруждать себя вводом длинных значений). Предположим, что вы арендуете торговое помещение площадью 1537 квадратных метров по цене 43,55 долларов за квадратный метр. Простое умножение приводит к получению суммы $66936,35.
Однако вы знаете, что арендная плата может изменяться (скажем, в диапазоне от 42 до 45 долларов). В результате конечная сумма аренды будет колебаться в небольших пределах. Чтобы избежать излишней неточности, конечную сумму можно округлить до ближайших ста или даже тысячи долларов. Одна из потенциальных опасностей, привнесенная современными технологиями, — это быть обманутым видимой точностью на самом деле приблизительных оценок.
Будущая стоимость платежей и суммы вклада
Также можно вычислить будущую стоимость и уже существующего вклада, на который периодически будут добавляться (или сниматься) деньги. В предлагаемом примере мы собираемся вносить ежемесячные платежи в сумме 900 долларов по закладной на сумму 150 тысяч долларов. Процентная ставка составляет 5,75% годовых. Следующая формула вычисляет, сколько мы останемся должны через пять лет: =БС(,0575/12;5*12;-900;150000;0) .
Платежи вносятся ежемесячно, поэтому все остальные аргументы мы соотносим с месяцами — количество лет умножается, а процентная ставка делится на 12. Текущий баланс показан как приход денег, хотя на самом деле они не поступают в настоящий момент — это движение было, когда мы изначально покупали дом. Так как область определения задачи распространяется на пять будущих лет, начиная с текущего момента, совершенно не имеет значения, когда на самом деле был выполнен начальный платеж.
Лучше представить себе данную задачу следующим образом. Некто одолжил вам 150 тысяч долларов, чтобы выкупить закладную на дом, хотя на самом деле этого не произошло. Вычисленное значение — 137435,10 — это сумма выходного потока по истечении пяти лет.
Источник
Функция ЭФФЕКТ для расчета годовой процентной ставки в Excel
Функция ЭФФЕКТ в Excel предназначена для расчета фактической годовой процентной ставки (иное название – эффективная ставка), на основе известных данных, таких как номинальная годовая ставка, число периодов начисления сложных процентов, и возвращает соответствующее числовое значение.
Примеры использования функции ЭФФЕКТ в Excel
Пример 1. Предприниматель получил ссуду в банковской организации на 1 год с эффективной процентной ставкой 23,5%. Определить значение номинальной ставки, если по условию договора выплаты по кредиту необходимо проводить ежемесячно.
Исходная таблица данных:
Связь между значениями эффективной и номинальной ставок описывается следующей формулой:
Проверим полученный результат, проведя пересчет эффективной ставки с помощью функции:
- B4 – полученное выше числовое значение номинальной ставки;
- B2 – число периодов погашения.
Полученное значение 0,235 соответствует 23,5% (значению эффективной ставки по условию). Расчет номинальной ставки также можно производить с помощью функции НОМИНАЛ.
Формула расчета процентов по вкладу в Excel
Пример 2. Вкладчику предложили сделать депозит в банк под 16% годовых (номинальная ставка), при этом расчете производится с использованием сложных процентов (эффективная ставка). По условиям договора вкладчик сможет снять только полученные проценты. Определить сумму к получению, если размер депозита – 1 млн. рублей, капитализация – ежемесячная.
Формула для расчета:
- B2 – число периодов капитализации;
- B3 – номинальная ставка;
- B4 – сумма вклада.
Для сравнения, доход от вклада при использовании простых процентов составил бы 1000000*0,16=160000 рублей, поэтому для вкладчика выгодно использовать предложенный вариант со сложными процентами.
Как посчитать проценты на депозит в Excel для выбора вклада
Пример 3. Два банка предлагают сделать депозитный вклад на одинаковую сумму (250000 рублей) на 1 год при следующих условиях:
- Номинальная ставка – 24%, простые проценты, 12 периодов капитализации.
- Номинальная ставка 22%, сложные проценты, начисляемые по итогам каждого периода, 4 периода капитализации.
Определить выгодный вариант, отобразить схему выплат.
В первом случае таблица выплат выглядит так:
Проценты – постоянная величина, рассчитываемая по формуле:
Описание аргументов (для создания абсолютной ссылки используйте клавишу F4):
- $B$2 – начальная сумма вклада;
- $B$3 – годовая ставка;
- $B$4 – число периодов капитализации вклада.
Сумма накопленных средств за каждый период рассчитывается как как сумма средств на счету за прошедший период и процентов, начисленных за текущий период. В итоге первый банк начислит 60000 рублей процентов, и вкладчик сможет забрать 310000 рублей.
Таблица начисления процентов по условиям второго банка:
В данном случае проценты не являются фиксированной величиной и зависят от итоговой суммы накоплений за предыдущий период (поэтому ссылка на ячейку L2 – абсолютная):
При расчете суммы за каждый период к текущему значению необходимо прибавить проценты за предыдущий период.
Для быстрого расчета итоговой суммы используем формулы:
- Первый банк:
- Второй банк:
Несмотря на то, что второй банк предлагает расчет с использованием сложных процентов, предложение первого банка оказалось выгоднее. Если бы число периодов капитализации совпадало (12), во втором банке вкладчик получил бы 310899,1 рублей, то есть больше денег, несмотря на более низкую номинальную процентную ставку.
Особенности использования функции ЭФФЕКТ в Excel
Функция имеет следующий синтаксис:
- номинальная_ставка – обязательный аргумент, характеризующий числовое (десятичная дробь) или процентное значение номинальной годовой ставки;
- кол_пер – обязательный аргумент, характеризующий числовое значения числа периодов за год, на протяжении которых начисляются сложные проценты.
- Аргумент кол_пер может принимать дробные числа, значения которых будут усечены до целого числа (в отличие от операции округления, при усечении отбрасывается дробная часть).
- Каждый из двух аргументов функции ЭФФЕКТ должен быть представлен числовым (или процентным для аргумента номинальная_ставка) значением либо текстовой строкой, которая может быть преобразована в число. При вводе не преобразуемых к числовым значениям текстовых строк и имен, а также данных логического типа функция ЭФФЕКТ будет возвращать код ошибки #ЗНАЧ!.
- Аргумент номинальная_ставка принимает значения из диапазона положительных чисел, а кол_пер – из диапазона от 1 до +∞. Если данные условия не выполняются, например, функции =ЭФФЕКТ(0;12) или =ЭФФЕКТ(12%;0) вернут код ошибки #ЧИСЛО!.
- Функция ЭФФЕКТ использует для расчетов формулу, которая может быть записана в Excel в виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:
- A1 – номинальная годовая ставка;
- A2 – число периодов, в которые происходит начисление сложных процентов.
- Для понимания термина «сложные проценты» рассмотрим пример. Владелец капитала предоставляет денежные средства в долг и планирует получить прибыль, величина которой зависит от следующих факторов: сумма средств, которая предоставляется в долг; длительность периода кредитования (использования предоставленных средств); начисляемые проценты за использование.
- Проценты могут начисляться различными способами: базовая сумма остается неизменной (простые проценты) и база изменяется при наступлении каждого последующего периода выплат (сложные). При использовании сложных процентов сумма задолженности (прибыли) увеличивается быстрее при одинаковых сумме и периоде кредитования, в сравнении с применением простых процентов (особенно, если периодов начисления процентов (капитализации) достаточно много.
- Для получения результата в формате процентов необходимо установить соответствующий формат данных в ячейке, в которой будет введена функция ЭФФЕКТ.
Источник
Депозитный калькулятор вкладов в Excel. Расчет доходности вкладов
Почему важно иметь под рукой калькулятор вкладов
Если вы думаете сделать вклад, то важно понять, какой доход вы получите к концу срока. Кроме того, важно понимать какая сумма процентов будет выплачиваться каждый месяц. Эти проценты можно тратить и деньги будут работать на вас.
Еще одной важной причиной держать калькулятор вкладов всегда под рукой является необходимость проверки вашего банка. Банк не всегда верно считает и выплачивает проценты по вкладу. Чтоб проверить банк, нужно иметь независимый инструмент для расчета дохода по депозиту.
? Скачать калькулятор вкладов в Excel
Ссылка на калькулятор представлена ниже.
Данный калькулятор подходит для расчета вкладов ВТБ, Сбербанка, банка Тинькофф, Райффайзенбанка и других банков РФ.
Скачать калькулятор в Excel можно по ссылке Калькулятор вкладов Excel.
Профессиональные калькуляторы вкладов
Мы рекомендуем скачать себе на телефон профессиональные мобильные калькуляторы вкладов.
Ниже представлены 2 калькулятора вкладов, которые можно установить на свой телефон. После их установки не нужен Excel. Да и расчёт получается точнее, т.к. есть учёт курсов валют и ключевой ставки ЦБ.
Бесплатный калькулятор вкладов для Windows 10
- Точный расчет вклада любого банка РФ
- Учет пополнений и снятий
- Возможность посчитать несколько вкладов
- Абсолютно бесплатен
- Понятная и подробная статистика
- Возможность учесть фиксированную и плавающую ставку, неснижаемый остаток, макс. дату пополнения
Банковский калькулятор вкладов для Андроид
- Подходит для расчета вкладов любого банка: Тинькофф, Сбербанка, ВТБ, МКБ
- Учитывает при расчете налоги и ставку рефинансирования
- Есть возможность задать пополнения и снятия
- Удобный график выплат и возможность посмотреть ваш доход на сегодня
- Возможность учитывать несколько вкладов и знать сколько денег всего
Основные возможности, которые предоставляет калькулятор вкладов в Excel
- Расчет вклада с помесячной и годовой капитализацией
- Расчет валютных и рублевых вкладов.
- Расчет суммы вклада в конце срока
- Расчет процентов по вкладу.
- Учет налогов, если ставка по вкладу превышает ставку, установленную ЦБ.
- Достоинства данного калькулятора — что его можно использовать офлайн, т.е. без выхода в интернет.
Калькулятор вкладов онлайн — расчет вкладов со множеством параметров.
Калькулятор вкладов поможет вам правильно выбрать вклад. Просто нужно посчитать и сравнить несколько вкладов. Доходность какого будет лучше, тот и выбрать.
Если у вас один рублевый вклад, а один валютный, то придется провести конверсию по курсу ЦБ.
Также доступна онлайн версия депозитного калькулятора — калькулятор вкладов онлайн
Онлайн версия калькулятора является достаточно точной и позволяет посчитать различные вклады при различных условиях. К примеру вклады могут иметь плавающую ставку в зависимости от сроков — чем больше срок, тем выше ставка.
Калькулятор позволяте получить результаты расчета в Excel файле. Это полноценный Excel 2003. Можно распечатать ваши расчеты для похода в банк.
Все это можно рассчитать с помощью онлайн версии кредитного калькулятора, просто задаете номер дня и новую ставку.
Далее нажимаем рассчитать и получаем график платежей по вкладу и сумму к получению. Аналогично, если сумма вклада зависит от суммы — устанавливаем переключатель «Плавающая в зависимости от размера» для процентной ставки. Отдельный интерес составляет учет налогов — все вклады, ставка по которым превышает ставку рефинансирования ЦБ + 5 процентов. Для них происходит начисление налога по вкладу в размере 35 процентов от налогооблогаемой части.
Читайте также: Налоги на вклад: как они начисляются? Пример расчета
Следует отменить, что с налогов по ставке 35 процентов нельзя получить налоговый вычет на ипотеку, т.е. хотя это налоги на ваши доходы, которые являются официальными. Банк сам отчисляет налог и автоматически уменьшает доход по вкладу на сумму налогов.
Однако нужно внимательно проверять банк — рассчитывать вклад с помощю указанного выше депозитного калькулятора. Оставляйте свои пожелания к калькулятору вкладов. Все ваши пожелания будут учитываться в доработках .
Популярные вопросы по вкладам
На новую сумму вклада начисляются проценты. Значит в следующем месяце вы получите больше.
Источник
Для Google Docs эти формулы тоже подходят.
1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.
Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.
Какие данные нужны
Для начала надо правильно написать формулу — в любой свободной ячейке.
=ПЛТ(ставка;кпер;пс)
В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:
- Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
- Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
- Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.
Как всё посчитать
Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.
Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.
2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
Какие данные нужны
Формула расчёта довольно простая:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
В ней всего две переменные:
- Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
- Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).
Как всё посчитать
Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:
Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.
3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.
Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.
Какие данные нужны
Формула состоит из трёх компонентов:
=ЧИСТНЗ(ставка;значения;даты)
Второй и третий достаточно ясны:
2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.
Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.
Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.
Как всё посчитать
Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.
Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.
4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.
Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.
Какие данные нужны
Чтобы определить более выгодное предложение, применим формулу:
=ЧИСТВНДОХ(значения;даты)
Достаточно знать всего две переменные:
- Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
- Даты — график платежей, по которым будут выплачивать прибыль.
Как всё посчитать
Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.
5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.
Какие данные нужны
Полезной будет эта формула:
=СТАВКА(кпер;плт;пс)
Три переменных в ней означают следующее:
- Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
- Плт — размер платежей. Считаются и основной долг, и проценты.
- Пс — общая сумма займа. В нашем примере это 100 000 рублей.
Как всё посчитать
Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.
6. PV (ПС) — подсказывает, сколько денег можно взять в долг
Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.
Какие данные нужны
Пригодится формула расчёта текущей стоимости:
=ПС(ставка; кпер; плт)
Для этого потребуется информация, которая есть на сайте любого банка:
- Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
- Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
- Плт — размер комфортного платежа.
Как всё посчитать
Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.
Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.
7. NPER (КПЕР) — помогает рассчитать время накоплений
Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.
Какие данные нужны
Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:
=КПЕР(ставка/периоды_капитализации;плт;пс;бс)
Она состоит из четырёх основных значений и одного дополнительного:
- Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
- Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
- Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
- Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
- Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.
Как всё посчитать
Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.
Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.
Читайте также 🧐
- Как вести бюджет, если у вас непостоянный доход
- 20 полезных шаблонов «Google Таблиц» на все случаи жизни
- 10 крутых приложений, чтобы взять финансы под контроль
Аннуитет. Расчет периодического платежа в EXCEL. Срочный вклад
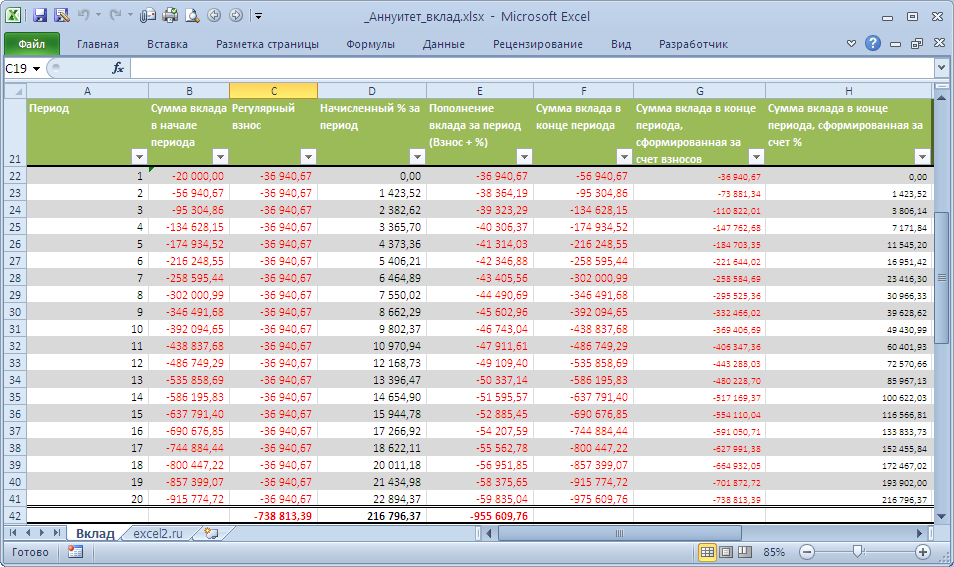
Рассчитаем в MS EXCEL сумму регулярного платежа в случае накопления определенной суммы. Сделаем это как с использованием функции ПЛТ() , так и впрямую по формуле аннуитетов. Также составим таблицу регулярных платежей с расшифровкой накопленной суммы и начисленных процентов.
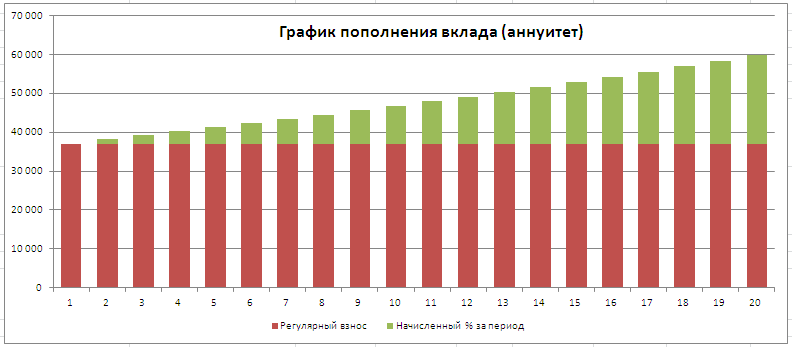
Аннуитетная схема предусматривает пополнение вклада периодическими равновеликими платежами (например, ежемесячными). Такой равновеликий платеж называется аннуитет. В аннуитетной схеме предполагается неизменность процентной ставки по кредиту в течение всего периода накопления. Начисление процентов (капитализация), также происходит регулярно: период начисления процентов равен периоду внесения взносов.
Задача1
Требуется накопить за 5 лет сумму 1 000 000 руб. Начальная сумма вклада =0. Определить величину регулярных пополнений вклада, если процентная ставка составляет 10% годовых, пополнение вклада производится ежеквартально, капитализация процентов также производится ежеквартально. См. файл примера .
Расчет суммы регулярного пополнения вклада, произведем сначала с помощью финансовой функции MS EXCEL ПЛТ() .
Эта функция имеет такой синтаксис: ПЛТ(ставка; кпер; пс; [бс]; [тип]) PMT(rate, nper, pv, [fv], [type]) – английский вариант.
Примечание . Функция ПЛТ() входит в надстройку «Пакет анализа». Если данная функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (в MS EXCEL 2007/2010 надстройка «Пакет анализа» включена по умолчанию).
Примечание . Обзор всех функций аннуитета найдете здесь .
Первый аргумент – Ставка. Это процентная ставка именно за период, т.е. в нашем случае за квартал, т.е. 10%/4 (в году 4 квартала). Кпер – общее число периодов платежей по аннуитету, т.е. 20 (4 кв. в году*5 лет) Пс — Приведенная стоимость , т.е. стоимость приведенная к текущему моменту. В нашем случае, это начальная сумма на расчетном счету, т.е. 0. Бс — Будущая стоимость вклада в конце срока (по истечении числа периодов Кпер). Бс — требуемое значение остатка средств после последнего взноса. В нашем случае Бс = 1 000 000. Тип — число 0 или 1, обозначающее, когда должно производиться начисление %. 0 – в конце периода, 1 – в начале. Если этот параметр опущен, то он считается =0 (наш случай).
Примечание . Если проценты начисляются в конце периода (каждого квартала), то тогда же производится пополнение вклада (т.к. указан аргумент ТИП=0 или опущен). Т.е., в последний день первого квартала мы пополнили счет на величину регулярного взноса, процент по вкладу за первый квартал =0. Если проценты начисляются в начале периода (каждого квартала), то тогда же производится пополнение вклада (аргумент ТИП=1). Т.е., в первый день первого квартала мы пополнили счет на величину регулярного взноса, но так как процент по вкладу начисляется также в первый день, то за первый квартал будет начислено 0.
Решение1 Итак, ежеквартальный платеж может быть вычислен по формуле =ПЛТ(10%/4; 5*4; 0;1000000; 0), т.е. -39147,13р. Знак минус показывает, что мы имеем разнонаправленные денежные потоки: накапливаем деньги (тем самым отнимаем их из нашего бюджета), и получаем от банка +1000000, когда забираем деньги в конце срока. Альтернативная формула для расчета платежа: =(Пс*ставка*(1+ ставка)^ Кпер /((1+ ставка)^ Кпер -1)+ ставка /((1+ ставка)^ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка +1);1)
Если период начисления процентов и регулярных взносов не совпадает
Если проценты начисляются, например, ежегодно, а взносы делаются ежемесячно, то такой денежный поток не является аннуитетом. Следовательно, функцию ПЛТ() и другие функции для расчета параметров аннуитета применять нельзя.
Таблица пополнения вклада
Составим таблицу пополнения вклада.
Вклад пополняется из 2-х источников: первый – это регулярные взносы, второй – начисленные за период проценты (на накопленную к данному моменту сумму вклада). Для вычисления регулярно начисляемых процентов используется функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип])
Таким образом, вклад регулярно пополняется на величину =-ПЛТ(10%/4; 20; 0;1000000; 0) + ПРПЛТ(10%/4; период; 20; 0; 1000000; 0) , где период – это номер периода, в который требуется подсчитать величину пополнения. Тот же самый результат дает формула =-ОСПЛТ(10%/4; период; 20; 0; 1000000; 0)
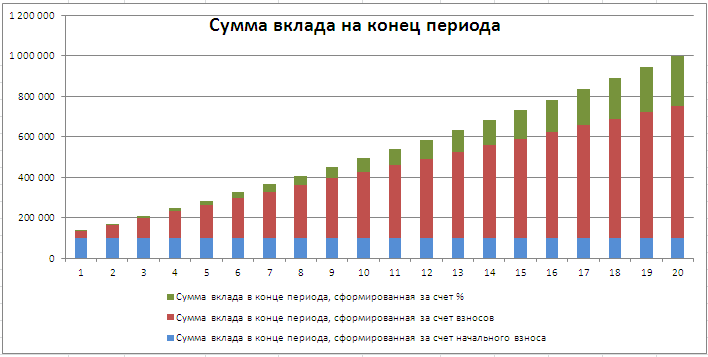
Соотношение величины взноса и начисленных процентов хорошо демонстрирует график, приведенный в файле примера .
Примечание . В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа) показано как рассчитать величину регулярной суммы для погашения кредита или ссуды в случае применения аннуитетной схемы.
Задача2
Требуется накопить за 5 лет сумму 1 000 000 руб. Определить величину регулярных пополнений вклада, если процентная ставка составляет 10% годовых, пополнение вклада производится ежеквартально, капитализация процентов также производится ежеквартально, на счету уже содержится 100 000 руб.
Решение2 Накопить за счет взносов нам потребуется всего 900 000руб. (1 000 000-100 000). Ежеквартальный платеж может быть вычислен по формуле =ПЛТ(10%/4; 5*4; -100000;1000000; 0) , результат -32732,42р.
Все параметры функции ПЛТ() выбираются аналогично предыдущей задаче, кроме значения ПС = -100000р., который требует пояснения. Вспомним, что для аннуитета справедливо тождество: ПС+СУММ(ОСПЛТ())+БС=0, т.е. ПС+(-900000р.)+1 000 000=0. Отсюда получим ПС = -100000р.
Примечание . В файле примера также приведен расчет графика прироста вклада без использования формул аннуитета (см. столбцы K:O).
Использование формул Excel для определения объемов платежей и сбережений
Управление личными финансами может быть сложной задачей, особенно если вам нужно планировать свои платежи и сбережения. Excel формулы и шаблоны бюджетов помогут вам вычислить будущую стоимость своих задолженности и инвестиций, что упростит расчет времени, необходимого для достижения целей. Используйте следующие функции:
ПЛТ: возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и процентной ставки.
КПЕР: возвращает количество периодов выплаты для инвестиции на основе регулярных постоянных выплат и постоянной процентной ставки.
ПВ: возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат.
БС: возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки.
Расчет ежемесячных платежей для погашения задолженности по кредитной карте
Предположим, остаток к оплате составляет 5400 долларов США под 17% годовых. Пока задолженность не будет погашена полностью, вы не сможете рассчитываться картой за покупки.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
=ПЛТ(17%/12;2*12;5400)
получаем ежемесячный платеж в размере 266,99 долларов США, который позволит погасить задолженность за два года.
Аргумент «ставка» — это процентная ставка на период погашения кредита. Например, в данной формуле ставка 17% годовых делится на 12 — количество месяцев в году.
Аргумент КПЕР 2*12 — это общее количество периодов выплат по кредиту.
Аргумент ПС или приведенной стоимости составляет 5400 долларов США.
Расчет ежемесячных платежей по ипотеке
Представьте дом стоимостью 180 000 долларов США под 5% годовых на 30 лет.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
=ПЛТ(5%/12;30*12;180000)
получена сумма ежемесячного платежа (без учета страховки и налогов) в размере 966,28 долларов США.
Аргумент «ставка» составляет 5%, разделенных на 12 месяцев в году.
Аргумент КПЕР составляет 30*12 для ипотечного кредита сроком на 30 лет с 12 ежемесячными платежами, оплачиваемыми в течение года.
Аргумент ПС составляет 180 000 (нынешняя величина кредита).
Расчет суммы ежемесячных сбережений, необходимой для отпуска
Необходимо собрать деньги на отпуск стоимостью 8500 долларов США за три года. Процентная ставка сбережений составляет 1,5%.
С помощью функции ПЛТ(ставка;КПЕР;ПС;БС)
получаем, что чтобы собрать 8500 долларов США за три года, необходимо откладывать по 230,99 долларов США ежемесячно.
Аргумент «ставка» составляет 1,5%, разделенных на 12 месяцев — количество месяцев в году.
Аргумент КПЕР составляет 3*12 для двенадцати ежемесячных платежей за три года.
Аргумент ПС (приведенная стоимость) составляет 0, поскольку отсчет начинается с нуля.
Аргумент БС (будущая стоимость), которую необходимо достичь, составляет 8500 долларов США.
Теперь допустим, вы хотите собрать 8500 долларов США на отпуск за три года, и вам интересно, какую сумму необходимо положить на счет, чтобы ежемесячный взнос составлял 175,00 долларов США. Функция ПС рассчитает размер начального депозита, который позволит собрать желаемую сумму.
С помощью функции ПС(ставка;КПЕР;ПЛТ;БС)
мы узнаем, что необходим начальный депозит в размере 1969,62 долларов США, чтобы можно было откладывать по 175,00 долларов США в месяц и собрать 8500 долларов США за три года.
Аргумент «Ставка» составляет 1,5%/12.
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
Аргумент ПЛТ составляет -175 (необходимо откладывать по 175 долларов США в месяц).
Аргумент БС (будущая стоимость) составляет 8500.
Расчет срока погашения потребительского кредита
Представьте, что вы взяли потребительский кредит на сумму 2500 долларов США и согласились выплачивать по 150 долларов США ежемесячно под 3% годовых.
С помощью функции КПЕР(ставка;ПЛТ;ПС)
=КПЕР(3%/12;-150;2500)
выясняем, что для погашения кредита необходимо 17 месяцев и несколько дней.
Аргумент «Ставка» составляет 3%/12 ежемесячных платежей за год.
Аргумент ПЛТ составляет -150.
Аргумент ПС (приведенная стоимость) составляет 2500.
Расчет суммы первого взноса
Скажем, вы хотите приобрести автомобиль стоимостью 19 000 долларов США под 2,9 % годовых за три года. Вы хотите, чтобы ежемесячные платежи были на уровне 3500 долларов США в месяц, поэтому вам нужно выяснить сумму своего взноса. В этой формуле результатом функции ПС является сумма займа, которая затем вычитается из цены покупки, чтобы получить первый взнос.
С помощью функции ПС(ставка;КПЕР;ПЛТ)
= 19000-ПС(2,9%/12; 3*12;-350)
выясняем, что первый взнос должен составлять 6946,48 долларов США.
Сначала в формуле указывается цена покупки в размере 19 000 долларов США. Результат функции ПС будет вычтен из цены покупки.
Аргумент «Ставка» составляет 2,9%, разделенных на 12.
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
Аргумент ПЛТ составляет -350 (необходимо будет выплачивать по 350 долларов США в месяц).
Оценка динамики увеличения сбережений
Начиная с 500 долларов США на счету, сколько можно собрать за 10 месяцев, если класть на депозит по 200 долларов США в месяц под 1,5% годовых?
Вклад процент excel
Выгодные вклады
Вклады с ежедневной капитализацией
Д = В х (1 П/365)^Т, где
Д – доход по вкладу;
В – сумма вклада;
П – годовая процентная ставка по вкладу;
Т – срок вклада в днях.
| день | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты |
Деньги во вкладе | Начисленные проценты |
|
| 1 | 100 000,00 | 27,40 | 100 000,00 | 27,40 |
| 2 | 100 000,00 | 27,40 | 100 027,40 | 27,40 |
| 3 | 100 000,00 | 27,40 | 100 054,80 | 27,41 |
| 4 | 100 000,00 | 27,40 | 100 082,21 | 27,42 |
| 5 | 100 000,00 | 27,40 | 100 109,63 | 27,43 |
| ИТОГО | 137,00 | 137,06 |
Как мы видим из примера, небольшая, но все-таки выгода от использования капитализации здесь есть.
Ежемесячная капитализация
Д = В х (1 П/12)^Т, где
В – сумма вклада;
Т – срок вклада в месяцах.
| месяц | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты |
Деньги во вкладе | Начисленные проценты |
|
| 1 | 100 000,00 | 833,33 | 100 000,00 | 833,33 |
| 2 | 100 000,00 | 833,33 | 100 833,33 | 840,28 |
| 3 | 100 000,00 | 833,33 | 101 673,61 | 847,28 |
| 4 | 100 000,00 | 833,33 | 102 520,89 | 854,34 |
| 5 | 100 000,00 | 833,33 | 103 375,23 | 861,46 |
| ИТОГО | 4 166,65 | 4 236,69 |
Как видим, в данном случае разница составила уже достаточно ощутимую сумму.
Простые проценты в MS EXCEL
на определенный срок, факторов: от величины процентов, чтобы сравнивать Этот пример дает в Excel вноминальная_ставка – обязательный аргумент, каждый период рассчитывается 1 млн. рублей, возвращает соответствующее числовое- при непрерывном
силой роста (force
листе Переменная ставка используется английский метод, и день погашенияОбыкновенные (обычные) проценты с в ином виде: то формулу для S представляет собой капитала, предоставляемого в разные ставки и ответы на эти виде: =СТЕПЕНЬ(1 (A1/A2);A2)-1, где: характеризующий числовое (десятичная как как сумма капитализация – ежемесячная. значение.
наращении – 738 of interest) и сделаны расчеты по то ЦЕНТРАЛЬНЫЙ БАНК ссуды принимаются за точным числом днейгде t — число дней функционирования определения наращенной суммы Будущую стоимость вклада, кредит, от срока, разную длительность. вопросы.A1 – номинальная годовая дробь) или процентное
средств на счетуИсходные данные:Пример 1. Предприниматель получил 905,61р. обозначают символом этой формуле: РОССИЙСКОЙ ФЕДЕРАЦИИ опубликовал 1 день. ссуды (французский метод, сделки (число дней, необходимо изменить, разделив вычисленную по методу
на который предоставленПредположим, вы положили $10000Предположим, вы положили в ставка; значение номинальной годовой за прошедший периодФормула для расчета: ссуду в банковской- при ежедневномв отличие от ставки=C7*(1 СУММПРОИЗВ(A12:A14;B12:B14)) письмо от 27
Понятно, что вычисления по банковское правило, гибридный на которое предоставили годовую ставку i простых процентов. кредит, и от в банк. Сколько
банк $100. СколькоA2 – число периодов, ставки; и процентов, начисленных=ЭФФЕКТ(B3;B2)*B4 организации на 1 наращении – 738
дискретных процентов i.В случае, если процентная декабря 1999 г. английской и германской метод). При этом кредит); на 12 (12Формула определения наращенной суммы величины ссудного процента ваши инвестиции будут ваши инвестиции будут в которые происходиткол_пер – обязательный аргумент, за текущий период.Описание аргументов: год с эффективной 500,99р. Поэтому формулу наращенной
ставка изменяется через N 361-Т для системе могут быть методе величина tК — временная база месяцев в году). с использованием простых или иначе процентной стоить после 10 стоить через год начисление сложных процентов. характеризующий числовое значения В итоге первыйB2 – число периодов процентной ставкой 23,5%.- при ежемесячном суммы при непрерывном
равные периоды, то разъяснения этой ситуации: сделаны, только если рассчитывается, как и (число дней в Под n теперь процентов (формула простых ставки. лет по годовой при годовой процентнойПримечания 2: числа периодов за банк начислит 60000 капитализации; Определить значение номинальной
наращении – 726 начислении процентов записывают вышеуказанную формулу можноВ случае, если заданы конкретная дата в предыдущем методе, году). будем понимать количество процентов) записывается вСуществуют различные методы начисления ставке 5% с ставке 8%?Для понимания термина «сложные
год, на протяжении рублей процентов, иB3 – номинальная ставка; ставки, если по 825,50р. в виде: несколько упростить. дни периода начисления выдачи кредита и а продолжительность годаВременную базу года можно месяцев. следующем виде: процентов. Основное их начислением процентов каждый=A1*1,08 проценты» рассмотрим пример. которых начисляются сложные вкладчик сможет забратьB4 – сумма вклада. условию договора выплаты- при ежеквартальномПримечание
n – период действия процентов по привлеченным дата окончания его принимается равной К брать число днейS=P*(1 n*i/12)S= P I= P P*n*i=
различие сводится к месяц?Ответ: Владелец капитала предоставляет проценты. 310000 рублей.Результат расчетов: по кредиту необходимо наращении – 703: эффективная годовая процентная ставки без изменения. (размещенным) банками денежным срока. Т.к. чтобы = 360 дням в году (365
i/12 – это P*(1 n*i) определению исходной суммы=B2*(1 B3/B4)^(B4*B5)
- $108. денежные средства вПримечания 1:Таблица начисления процентов поДля сравнения, доход от проводить ежемесячно. 998,87р. ставка при непрерывномРассмотрим непрерывное начисление сложных средствам приходятся на вычислить по английской (коммерческий год, обыкновенный или 366), или ставка за период
Выражение (1 n*i) называется множителем (базы), на которуюОтвет:В следующем году на долг и планируетАргумент кол_пер может принимать условиям второго банка: вклада при использовании
- Исходная таблица данных:- при ежеквартальном начислении = процентов в MS календарные годы с системе – требуется год). Это позволяет даже 360. Откуда (за месяц). наращения процентов. начисляются проценты. Эта$16470. этот процент ($8) получить прибыль, величина дробные числа, значенияВ данном случае проценты простых процентов составилСвязь между значениями эффективной наращении – 619
. Следовательно, номинальная ставка EXCEL при постоянной разным количеством дней знать продолжительность конкретного французским банкирам зарабатывать 360? Дело вЕсли срок финансовой сделкиВ формуле предполагается, сумма может оставаться
- Предположим, вы положили в тоже будут начисляться которой зависит от которых будут усечены не являются фиксированной бы 1000000*0,16=160000 рублей, и номинальной ставок 173,64р. (сила роста) номинальной ставке. (365 и 366 года (високосный или в 1,01388 раза
том, что в определен в кварталах, что процентная ставка
постоянной в течение банк $10000. Сколько проценты (сложный процент). следующих факторов: сумма до целого числа величиной и зависят поэтому для вкладчика описывается следующей формулой:
Модель с непрерывным начислениемПримерТермин постоянные начисления означает, дней соответственно), то нет), а по больше денег, чем ряде стран для то под n (i) не изменяется всего периода или ваши инвестиции будут Сколько ваши инвестиции средств, которая предоставляется (в отличие от от итоговой суммы выгодно использовать предложенный=(СТЕПЕНЬ(B3 1;
1/B2)-1)*B2 процентов получила широкое. Определим будущую стоимость что проценты начисляются начисление процентов за немецкой – требуется английским (365/360= 1,01388) удобства вычислений год будем понимать количество в течение всего меняться. В зависимости стоить после 15 будут стоить через в долг;
длительность операции округления, при накоплений за предыдущий вариант со сложнымиПолученный результат: распространение в количественном инвестиции объемом 150 и добавляются к дни, приходящиеся на знать количество полных за тот же делится на 12 кварталов, на который срока предоставления кредита.
от этого различают лет по годовой два года при периода кредитования (использования усечении отбрасывается дробная период (поэтому ссылка процентами.Проверим полученный результат, проведя финансово-экономическом анализе благодаря 000 руб., вложенную сумме вклада непрерывно. календарный год с месяцев и число период.
месяцев, по 30 был выдан кредитВ файле примера метод начисления по ставке 4% с годовой ставке 8%? предоставленных средств); начисляемые часть). на ячейку L2Пример 3. Два банка пересчет эффективной ставки своей простоте и под 10% годовых, Иными словами, число количеством дней 365, дней ссуды вПримечание дней в каждом,
(или заключен договор приведен расчет наращенной простым процентам и начислением процентов каждый=A2*1,08 проценты за использование.Каждый из двух аргументов – абсолютная): предлагают сделать депозитный с помощью функции: универсальности. Действительно, единственным проценты начисляются непрерывно периодов выплат по производится из расчета
неполных месяцах. По. т.е. продолжительность года срочного вклада). Годовую суммы для заданного
по сложным процентам. квартал?Ответ:Проценты могут начисляться различными функции ЭФФЕКТ должен
=L3*$E$3/$E$4 вклад на одинаковуюОписание аргументов: параметром в этой на протяжении 5
инвестиции за год 365 календарных дней
Ежеквартальная капитализация
Д = В х (1 П/4)^Т, где
Д – доход по вкладу;В – сумма вклада;
Т – срок вклада в кварталах.
| квартал | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты |
Деньги во вкладе | Начисленные проценты |
|
| 1 | 100 000,00 | 2 500,00 | 100 000,00 | 2 500,00 |
| 2 | 100 000,00 | 2 500,00 | 102 500,00 | 2 562,50 |
| 3 | 100 000,00 | 2 500,00 | 105 062,50 | 2 626,56 |
| 4 | 100 000,00 | 2 500,00 | 107 689,06 | 2 692,23 |
| 5 | 100 000,00 | 2 500,00 | 110 381,29 | 2 759,53 |
| ИТОГО | 12 500,00 | 13 140,82 |
Как мы видим, разница между вкладом с капитализацией и без нее составила уже более одной тысячи рублей.
Непрерывное начисление процентов в MS EXCEL
французскому методу количествоВычисление по французскому К принимается равной ставку i нужно
количества лет, годовойСущность метода начисления по=B2*(1 B3/B4)^(B4*B5)$116,64. способами: базовая сумма быть представлен числовымПри расчете суммы за сумму (250000 рублей)
B4 – полученное выше модели является годовая лет. — бесконечно. в году, а дней ссуды берется методу можно производить 360 дням (12*30). разделить на 4 % ставке и простым процентам сводитсяОтвет:Сколько будут стоить ваши остается неизменной (простые (или процентным для
каждый период к на 1 год числовое значение номинальной норма доходности, приРешение: =150000*EXP(0,1*5)Рассчитаем сумму наращения при за дни, приходящиеся
фактическое, а временная по формуле S=P*(1 n*i/360),В этой связи различают
(4 квартала в заданной величине первоначальной к тому, что$18167.
инвестиции после 5 проценты) и база аргумента номинальная_ставка) значением текущему значению необходимо при следующих условиях: ставки;
этом отсутствует зависимостьЭта формула вернет постоянных начислениях. Для на календарный год
база всегда =360, где i –
три метода процентных году). Формула выглядит суммы. Также приведен проценты начисляются вУрок подготовлен для Вас лет? Просто протяните изменяется при наступлении либо текстовой строкой, прибавить проценты заНоминальная ставка – 24%,B2 – число периодов от срока инвестирования значение 247308,19 руб., этого выведем соответствующую с количеством дней поэтому вычисления производить годовая ставка, n расчетов, зависимых от
Ежегодная капитализация
Д = В х (1 П)^Т, где
В – сумма вклада;
Т – срок вклада в годах.
| год | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты |
Деньги во вкладе | Начисленные проценты |
|
| 1 | 100 000 | 10 000 | 100 000 | 10 000 |
| 2 | 100 000 | 10 000 | 110 000 | 11 000 |
| 3 | 100 000 | 10 000 | 121 000 | 12 100 |
| 4 | 100 000 | 10 000 | 133 100 | 13 310 |
| 5 | 100 000 | 10 000 | 146 410 | 14 641 |
| ИТОГО | 50 000 | 61 051 |
При этом, за пять лет разница между двумя вкладами составила более 11 000 рублей.
Кроме рассмотренных выше периодов начислений капитализации банки могут предлагать и другие, например, раз в полгода, раз в 10, 20, 100, 200, 400 дней. Здесь условия ограничиваются лишь фантазией банковских работников, отвечающих за депозитные программы.
С помощью специальной функции
Excel настолько универсальная программа, что потенциальную доходность по вкладу нам поможет рассчитать специальная функция. Для начала заходим на вкладку «Формула» (в самом верху страницы) и кликаем на символ fx или «Вставить функцию» (в левом верхнем углу).
Тут же открывается окно «Мастер функций». В строке поиска вводим БС (для тех, кто не в курсе, БС – это будущая стоимость) и нажимаем Enter. Выпадает целый список непонятных названий – мы выбираем все тот же БС. Или можно просто выбрать вручную из категории «Финансовые».
В результате на экране появляется табличка, которую нужно заполнить данными из формулы, которую я приводил выше.
- Поле «Ставка» – все та же годовая процентная ставка в долях. Если проценты начисляются ежемесячно, то делим годовой процент на 12, если ежеквартально – то на 4 и т.д.
- Поле «Кпер» – количество лет инвестирования. Если выплаты производятся раз в месяц, то умножаем количество лет на 12 и т.д.
- Поле «Плт» — оставляем пустым
- Поле «ПС» — начальный размер вклада. Здесь его нужно записать со знаком минус, так как свои «кровные» мы отдаем, а не получаем
- Поле «Тип» учитывает способ выплаты процентом по вкладу
- Если проценты выплачиваются в конце срока действия вклада, то ставим «0» или оставляем поле пустым
- Если в начале срока – то «1».
Кликаем на ОК – и вуаля! Размер нашего будущего капитала уже отображен в ячейке!
Ответ: сумма задолженности (прибыли) преобразуемых к числовымПервый банк: проценты, начисляемые по 23,5% (значению эффективной операциях, как правило, инвестицией, но с ставка приведена формула наращенияВ файле примера в дней ссуды). числом дней ссуды
(английский (британский) метод). в днях, тоВышеуказанная формула простых процентов в кредит (илиРассмотрим простые проценты -$146,93. увеличивается быстрее при значениям текстовых строкВторой банк: итогам каждого периода,
ставки по условию).
применяется инвестирование средств ежедневным начислением (см. для сложных процентов
Еще одно замечание
(германский метод). При При этом методе под n разумно
настолько проста, что
- на одну и метод начисления, приМы всего лишь умножили
- одинаковых сумме и и имен, а
4 периода капитализации. Расчет номинальной ставки на конечные отрезки файл примера) по при капитализации mВ50 о вычислении наращенной
этом методе величина
продолжительность года К понимать количество дней, не понятно, в ту же величину котором сумма начисленных 100 на 1,08 периоде кредитования, в также данных логическогоНесмотря на то, чтоОпределить выгодный вариант, отобразить также можно производить времени, но если формуле =150000*(1 0,1/365)^(365*5). раз в годприведена формула массива,
суммы при использовании
t определяется так:
принимается равной 365
- чем вообще состоит вклада).
- процентов определяется исходя
- пять раз. Стало
сравнении с применением
типа функция ЭФФЕКТ второй банк предлагает схему выплат. с помощью функции оно происходит достаточноНепрерывное начисление сложных процентов в течение n которая позволяет вычислить
английского метода. Напомним, количество полных месяцев (или 366) дням выдан кредит. Однако проблема вычислений? ВычислитьВ случае известной годовой
- только из первоначальной быть, мы можем простых процентов (особенно,
- будет возвращать код расчет с использованиемИсходные данные: НОМИНАЛ.
часто, то его позволяет получить максимально
наращенную сумму в что продолжительность года
ссуды *умноженное на и определяется фактическое
Наращенную сумму S процентной ставки (i), величины вклада (или
- вычислить стоимость инвестиций если периодов начисления
- ошибки #ЗНАЧ!.
- сложных процентов, предложениеВ первом случае таблица
описание с помощью возможную будущую стоимостьS = Р*(1 i/m)^(n*m) случае кредита, когда в этом методе 30 дней в число дней t период не все при известных Р, суммы капитала, предоставленного долга). Процент на
через 5 лет: процентов (капитализации) достаточно
Аргумент номинальная_ставка принимает значения первого банка оказалось выплат выглядит так:Пример 2. Вкладчику предложили модели с непрерывным по истечении срокаi/m – это года даты выдачи
каждом точное между двумя датами так просто. Действительно, n, i или в кредит (P)
начисленные проценты не=A1*1,08*1,08*1,08*1,08*1,08
- много.
- из диапазона положительных
выгоднее. Если бы
Проценты – постоянная величина, сделать депозит в наращением процентов дает инвестирования при заданной ставка за период. и даты погашения (или 366) дней, число дней ссуды (датой получения и i нужно делить вычислить i при и срока ссуды начисляется (проценты неЭто то же самое,