Как в excel неизвестное число

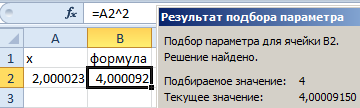
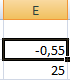«Подбор параметра» — ограниченный по функционалу вариант надстройки «Поиск решения». Это часть блока задач инструмента «Анализ «Что-Если»».

В упрощенном виде его назначение можно сформулировать так: найти значения, которые нужно ввести в одиночную формулу, чтобы получить желаемый (известный) результат.

Где находится «Подбор параметра» в Excel

Известен результат некой формулы. Имеются также входные данные. Кроме одного. Неизвестное входное значение мы и будем искать. Рассмотрим функцию «Подбора параметров» в Excel на примере.

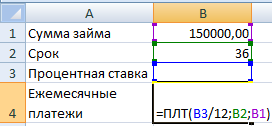
Необходимо подобрать процентную ставку по займу, если известна сумма и срок. Заполняем таблицу входными данными.

Процентная ставка неизвестна, поэтому ячейка пустая. Для расчета ежемесячных платежей используем функцию ПЛТ.

Когда условия задачи записаны, переходим на вкладку «Данные». «Работа с данными» — «Анализ «Что-Если»» — «Подбор параметра».

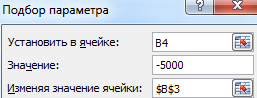
В поле «Установить в ячейке» задаем ссылку на ячейку с расчетной формулой (B4). Поле «Значение» предназначено для введения желаемого результата формулы. В нашем примере это сумма ежемесячных платежей. Допустим, -5 000 (чтобы формула работала правильно, ставим знак «минус», ведь эти деньги будут отдаваться). В поле «Изменяя значение ячейки» — абсолютная ссылка на ячейку с искомым параметром ($B$3).

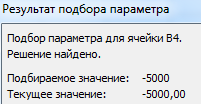
После нажатия ОК на экране появится окно результата.

Чтобы сохранить, нажимаем ОК или ВВОД.

Функция «Подбор параметра» изменяет значение в ячейке В3 до тех пор, пока не получит заданный пользователем результат формулы, записанной в ячейке В4. Команда выдает только одно решение задачи.



Решение уравнений методом «Подбора параметров» в Excel

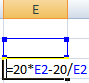
Функция «Подбор параметра» идеально подходит для решения уравнений с одним неизвестным. Возьмем для примера выражение: 20 * х – 20 / х = 25. Аргумент х – искомый параметр. Пусть функция поможет решить уравнение подбором параметра и отобразит найденное значение в ячейке Е2.

В ячейку Е3 введем формулу: = 20 * Е2 – 20 / Е2.

А в ячейку Е2 поставим любое число, которое находится в области определения функции. Пусть это будет 2.

Запускам инструмент и заполняем поля:

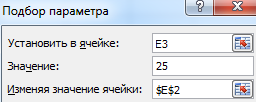
«Установить в ячейке» — Е3 (ячейка с формулой);

«Значение» — 25 (результат уравнения);

«Изменяя значение ячейки» — $Е$2 (ячейка, назначенная для аргумента х).

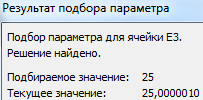
Результат функции:

Найденный аргумент отобразится в зарезервированной для него ячейке.

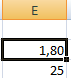
Решение уравнения: х = 1,80.

Функция «Подбор параметра» возвращает в качестве результата поиска первое найденное значение. Вне зависимости от того, сколько уравнение имеет решений.

Если, например, в ячейку Е2 мы поставим начальное число -2, то решение будет иным.

Примеры подбора параметра в Excel

Функция «Подбор параметра» в Excel применяется тогда, когда известен результат формулы, но начальный параметр для получения результата неизвестен. Чтобы не подбирать входные значения, используется встроенная команда.

Пример 1. Метод подбора начальной суммы инвестиций (вклада).

Известные параметры:

• срок – 10 лет;
• доходность – 10%;
• коэффициент наращения – расчетная величина;
• сумма выплат в конце срока – желаемая цифра (500 000 рублей).

Внесем входные данные в таблицу:

Начальные инвестиции – искомая величина. В ячейке В4 (коэффициент наращения) – формула =(1+B3)^B2.

Вызываем окно команды «Подбор параметра». Заполняем поля:

После выполнения команды Excel выдает результат:

Чтобы через 10 лет получить 500 000 рублей при 10% годовых, требуется внести 192 772 рубля.

Пример 2. Рассчитаем возможную прибавку к пенсии по старости за счет участия в государственной программе софинансирования.

Входные данные:

• ежемесячные отчисления – 1000 руб.;
• период уплаты дополнительных страховых взносов – расчетная величина (пенсионный возраст (в примере – для мужчины) минус возраст участника программы на момент вступления);
• пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза);
• ожидаемый период выплаты трудовой пенсии – 228 мес.;
• желаемая прибавка к пенсии – 2000 руб.

С какого возраста необходимо уплачивать по 1000 рублей в качестве дополнительных страховых взносов, чтобы получить прибавку к пенсии в 2000 рублей:

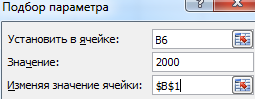
1. Ячейка с формулой расчета прибавки к пенсии активна – вызываем команду «Подбор параметра». Заполняем поля в открывшемся меню.



2. Нажимаем ОК – получаем результат подбора.

Чтобы получить прибавку в 2000 руб., необходимо ежемесячно переводить на накопительную часть пенсии по 1000 рублей с 41 года.

Функция «Подбор параметра» работает правильно, если:

• значение желаемого результата выражено формулой;
• все формулы написаны полностью и без ошибок.

Решение уравнений с одной неизвестной в эксель

Если в ячейку Excel введена формула, содержащая ссылку на эту же самую ячейку (может быть и не напрямую, а опосредованно — через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). На практике к циклическим ссылкам прибегают, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя ее устранения. Excel не может провести вычисления, так как циклические ссылки порождают бесконечное количество вычислений. Есть два выхода из этой ситуации: устранить циклические ссылки или допустить вычисления по формулам с циклическими ссылками (в последнем случае число повторений цикла должно быть конечным).

Рассмотрим задачу нахождения корня уравнения методом Ньютона с использованием циклических ссылок. Возьмем для примера квадратное уравнение: х 2 — 5х + 6=0, графическое представление которого приведено на рис. 8. Найти корень этого (и любого другого) уравнения можно, используя всего одну ячейку Excel.

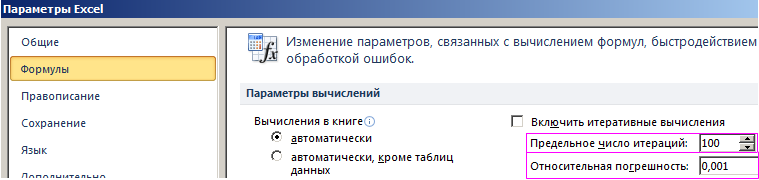
Для включения режима циклических вычислений в меню Сервис/Параметры/вкладка Вычисления включаем флажок Итерации, при необходимости изменяем число повторений цикла в поле Предельное число итераций и точность вычислений в поле Относительная погрешность (по умолчанию их значения равны 100 и 0,0001 соответственно). Кроме этих установок выбираем вариант ведения вычислений: автоматически или вручную. При автоматическом вычислении Excel выдает сразу конечный результат, при вычислениях, производимых вручную, можно наблюдать результат каждой итерации.

Рис. 8. График функции

Выберем произвольную ячейку, присвоим ей новое имя, скажем — Х, и введем в нее рекуррентную формулу, задающую вычисления по методу Ньютона:

где F и F1 задают соответственно выражения для вычисления значений функции и ее производной. Для нашего квадратного уравнения после ввода формулы в ячейке появится значение 2, соответствующее одному из корней уравнения (рис. 8). В нашем случае начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке Х и равного нулю. А как получить второй корень? Обычно это можно сделать изменением начального приближения. Решать проблему задания начальных установок в каждом случае можно по-разному. Мы продемонстрируем один прием, основанный на использовании функции ЕСЛИ. С целью повышения наглядности вычислений ячейкам были присвоены содержательные имена (рис. 9).

• В ячейку Хнач (В4) заносим начальное приближение — 5.
• В ячейку Хтекущ (С4) записываем формулу:
  =ЕСЛИ(Хтекущ=0;Хнач; Хтекущ-(Хтекущ^2-5*Хтекущ+6)/(2*Хтекущ-5)).
• В ячейку D4 помещаем формулу, задающую вычисление значения функции в точке Хтекущ, что позволит следить за процессом решения.
• Заметьте, что на первом шаге вычислений в ячейку Хтекущ будет помещено начальное значение, а затем уже начнется счет по формуле на последующих шагах.
• Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Хнач и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного
  

  Рис. 9. Определение начальных установок

  значения. Чтобы обнулить значение, хранящееся в ячейке Хтекущ, нужно заново записать туда формулу. Для этого достаточно для редактирования выбрать ячейку, содержащую формулу, дважды щелкнув мышью на ней (при этом содержимое ячейки отобразится в строке формул). Щелчок по кнопке (нажатие клавиши) Enter запустит вычисления с новым начальным приближением.

2.2. Подбор параметра

Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

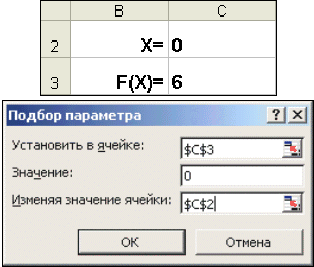
Возьмем в качестве примера все то же квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:

• В ячейку С3 (рис. 10) введем формулу для вычисления значения функции,
  

  Рис. 10. Окно диалога Подбор параметра

  стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.

• В окне диалога Подбор параметра (рис. 10) в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
• После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.

Вернемся к примеру. Опять возникает вопрос: как получить второй корень? Как и в предыдущем случае необходимо задать начальное приближение. Это можно сделать следующим образом (рис. 11,а):

• В ячейку Х (С2) вводим начальное приближение.
• В ячейку Х_i (С3) вводим формулу для вычисления очередного приближения к корню, т.е.
  =X-(X^2-5*X+6)/(2*X-5).
• В ячейку С4 поместим формулу, задающую вычисление значения функции, стоящей в левой части исходного уравнения, в точке Х_i.
• После этого выбираем команду Подбор параметра, где в качестве изменяемой ячейки принимаем ячейку С2. Результат вычислений изображен на рис. 11,б (в ячейке С2 — конечное значение, а в ячейке С3 — предыдущее).

Однако все это можно сделать и несколько проще. Для того чтобы найти второй корень, достаточно в качестве начального приближения (рис. 10) в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.

2.3. Поиск решения

Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.

Задачи, которые можно решать с помощью Поиска решения, в общей постановке формулируются так:

Искомые переменные — ячейки рабочего листа Excel — называются регулируемыми ячейками. Целевая функция F(х₁, х₂, … , х_n), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:

• найти максимум целевой функции F(х₁, х₂, … , х_n);
• найти минимум целевой функции F(х₁, х₂, … , х_n);
• добиться того, чтобы целевая функция F(х₁, х₂, … , х_n) имела фиксированное значение: F(х₁, х₂, … , х_n) = a.

Функции G(х₁, х₂, … , х_n) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.

Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решать. И тогда для решения конкретной оптимизационной задачи требуется специально для нее сконструированный метод. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ.

Выше для нахождения корней квадратного уравнения был применен метод Ньютона (п. 1.4) с использованием циклических ссылок (п. 2.1) и средство Подбор параметра (п. 2.2). Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.

Рис. 12. Окно диалога Поиск решения

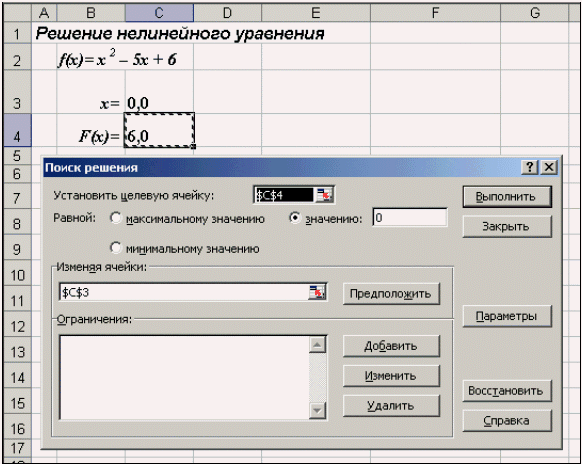
После открытия диалога Поиск решения (рис. 12) необходимо выполнить следующие действия:

1. в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
2. для максимизации значения целевой ячейки, установить переключатель максимальному значению в положение 8 , для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
3. в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
4. в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
5. для запуска процесса поиска решения нажать кнопку Выполнить.

Рис. 13. Результаты поиска

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.

Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения), следующие (рис. 14):

Рис. 14. Настройка параметров Решателя

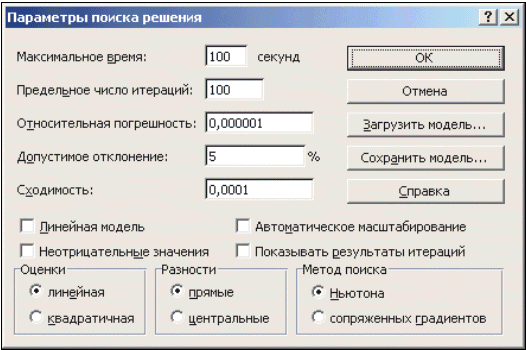
• Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).
• Предельное число итераций — еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, и, чаще всего, если решение не получено за 100 итераций, то при увеличении их количества (в поле можно ввести время, не превышающее 32767 секунд) вероятность получить результат мала. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.
• Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).
• Допустимое отклонение — задается в % только для задач с целочисленными ограничениями. Поиск решения в таких задачах сначала находит оптимальное нецелочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более, чем на указанное данным параметром количество процентов.
• Сходимость — когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа (дробь из интервала от 0 до 1), указанного в данном параметре, поиск прекращается.
• Линейная модель — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Это ускоряет процесс поиска решения.
• Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.
• Автоматическое масштабирование — этот флажок следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, определяющая максимальную прибыль, измеряется в миллиардах рублей.
• Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.
• Оценки — эта группа служит для указания метода экстраполяции — линейная или квадратичная, — используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Линейная служит для использования линейной экстраполяции вдоль касательного вектора. Квадратичная служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.
• Разности (производные) — эта группа служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций. Параметр Прямые используется в большинстве задач, где скорость изменения ограничений относительно невысока. Параметр Центральные используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается.
• Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.

Сохранить модель поиска решения можно следующими способами:

1. при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;
2. если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например найти максимум и минимум одной функции, или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Параметры/Сохранить модель окна Поиск решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Параметры/Загрузить модель диалога Поиск решения;
3. еще один способ сохранения параметров поиска — сохранение их в виде именованных сценариев. Для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений.

Кроме вставки оптимальных значений в изменяемые ячейки Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения. Рассмотрим более подробно каждый из них.

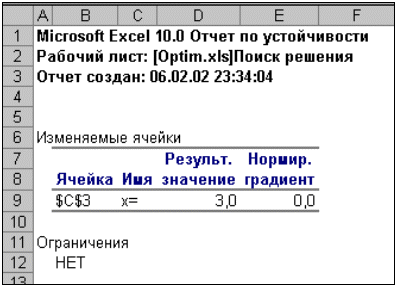
Рис. 15. Отчет по устойчивости

Отчет по устойчивости (рис.15) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. Раздел для изменяемых ячеек содержит значение нормированного градиента, которое показывает, как целая ячейка реагирует на увеличение значения в соответствующей изменяемой ячейке на одну единицу. Подобным образом, множитель Лагранжа в разделе для ограничений показывает, как целевая ячейка реагирует на увеличение соответствующего значения ограничения на одну единицу. При использовании целочисленных ограничений Excel выводит сообщение Отчеты устойчивость и Пределы не применимы для задач с целочисленными ограничениями. Если в окне диалога Параметры поиска решения установлен флажок Линейная модель, то отчет по устойчивости содержит несколько дополнительных столбцов информации.

Рис. 16. Отчет по результатам

Отчет по результатам (рис.16) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй — значения искомых переменных, полученные в результате решения задачи, в третьей — результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы — это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение — это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение — это ограничение, которое было выполнено с ненулевым значением разницы.

Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Уравнения и задачи на подбор параметра в Excel

Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?

При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.

Подбор параметра и решение уравнений в Excel

Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:

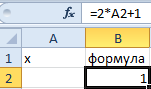
• y =7 является функцией x ;
• нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

1. Заполните ячейки листа, так как показано на рисунке:
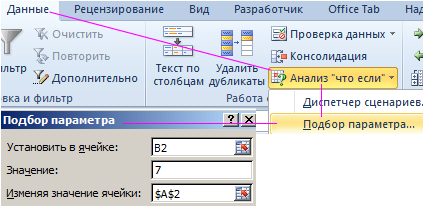
2. Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
3. В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

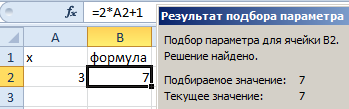
В результате мы получили правильное значение 3.

Получили максимально точный результат: 2*3+1=7

Второй пример использования подбора параметра для уравнений

Немного усложним задачу. На этот раз формула выглядит следующим образом:

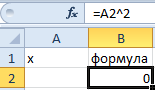
1. Заполните ячейку B2 формулой как показано на рисунке:
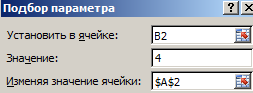
2. Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
3. Сравните 2 результата вычисления:

Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.

Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:

Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.

По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:

Таким образом, если нас не устраивает результат вычислений, можно:

1. Увеличить в настройках параметр предельного числа итераций.
2. Изменить относительную погрешность.
3. В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).

Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.

О подборе нескольких параметров в Excel узнаем из примеров следующего урока.

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

2. Переходите к инструменту и заполняете все необходимые поля

3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

Вычисление неизвестного от исходного числа и процентов

Edgar_rouz Дата: Четверг, 06.10.2016, 13:52 | Сообщение № 1 Группа: Пользователи Ранг: Прохожий Сообщений: 9 Репутация: 0 ± Замечаний: 0% ± Excel 2003 Здравствуйте. Не могу сделать так, чтобы при введении в окошко № 1 числа (например 12345) в окошке № 2 выводилась сумма, отняв от которой 10% получится 12345, т.е. должна автоматом выводиться 13716,67. и так для любого числа, введённого в Окошко № 1. Пока что я всё подбираю вручную почти. Задачу максимально упростил, поэтому такие исходные данные, но на самом деле формула очень нужна в бухгалтерии ЖКХ. Прошу ознакомиться с данными и моим «ручным способом» в прикреплённом файле. К сообщению приложен файл: 3116590.xlsx (11.6 Kb)   Ответить

китин Дата: Четверг, 06.10.2016, 14:00 | Сообщение № 2 Группа: Модераторы Ранг: Экселист Сообщений: 6973 Репутация: 1063 ± Замечаний: 0% ± Excel 2007;2010;2016 К сообщению приложен файл: 444111.xlsx (11.8 Kb) Не судите очень строго:я пытаюсь научиться ЯД 41001877306852 Сообщение отредактировал китин — Четверг, 06.10.2016, 14:01   Ответить

_Boroda_ Дата: Четверг, 06.10.2016, 14:01 | Сообщение № 3 Группа: Модераторы Ранг: Местный житель Сообщений: 16618 Репутация: 6465 ± Замечаний: 0% ± 2003; 2007; 2010; 2013 RUS Так нужно? Файл не смотрел Добавлено Игорь Объяснялка Есть какое=то число, если от него отнять 10%, то получим число А. Все это можно записать так Х — Х * 10% = А Х * (1-0,1) = А 0,9 * Х = А Х = А / 0,9 Скажи мне, кудесник, любимец ба’гов… Платная помощь: Boroda_Excel@mail.ru Яндекс-деньги: 41001632713405 | Webmoney: R289877159277; Z102172301748; E177867141995   Ответить

Edgar_rouz Дата: Четверг, 06.10.2016, 14:28 | Сообщение № 4 Группа: Пользователи Ранг: Прохожий Сообщений: 9 Репутация: 0 ± Замечаний: 0% ± Excel 2003 Извиняюсь, забыл уточнить. Процент тоже переменная. Например 13% Собственно, мне для 13% и нужно было.   Ответить

_Boroda_ Дата: Четверг, 06.10.2016, 14:36 | Сообщение № 5 Группа: Модераторы Ранг: Местный житель Сообщений: 16618 Репутация: 6465 ± Замечаний: 0% ± 2003; 2007; 2010; 2013 RUS Так? Переменный процент в С4 Скажи мне, кудесник, любимец ба’гов… Платная помощь: Boroda_Excel@mail.ru Яндекс-деньги: 41001632713405 | Webmoney: R289877159277; Z102172301748; E177867141995   Ответить

Edgar_rouz Дата: Четверг, 06.10.2016, 14:37 | Сообщение № 6 Группа: Пользователи Ранг: Прохожий Сообщений: 9 Репутация: 0 ± Замечаний: 0% ± Excel 2003 Всё догнал, там вместо 0,9 тогда будет 0,87=))) Всем спасибо!!! Особенно Бороде за ОБЬЯСНЯЛКУ. Так и понял про 0,87. Кармы всем=) Для тех, кто будет читать: для 13% в итоге применил =G3/0,87 Ещё не смог поменять название темы. Думаю, полезнее для других было бы изменить название и переместить тему в подходящее место: «13% НДФЛ» — что-то типа этого. Сообщение отредактировал Edgar_rouz — Четверг, 06.10.2016, 15:02   Ответить

И это работает в рамках ограничений, поэтому, если одна переменная не может быть изменена или может изменяться только в пределах указанного диапазона, Солвер примет это во внимание.

Это отличный способ найти несколько неизвестных переменных в Excel. Но найти и использовать это не просто.

Давайте взглянем на загрузку надстройки Solver, а затем рассмотрим, как использовать Solver в Excel 2016.

Как загрузить надстройку Solver

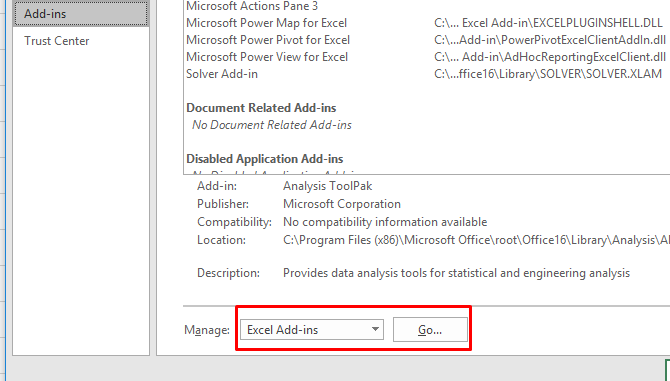
В Excel нет Солвера по умолчанию. Это надстройка, поэтому, как и другие мощные функции Excel, , вы должны загрузить его в первую очередь. К счастью, это уже на вашем компьютере.

Перейдите в Файл> Параметры> Надстройки . Затем нажмите « Перейти» рядом с « Управление: надстройки Excel» .

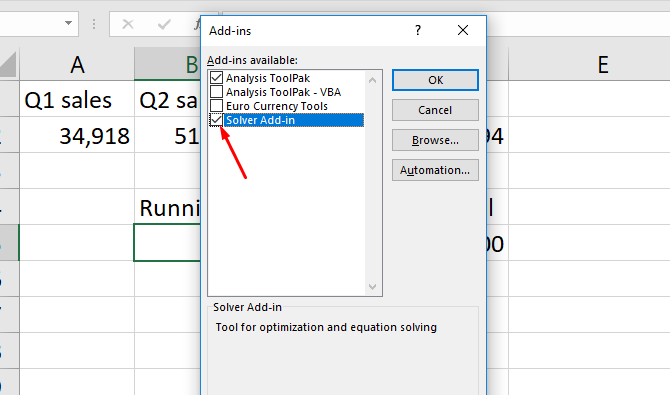
Если в этом раскрывающемся списке указано что-то отличное от «Надстройки Excel», вам необходимо изменить его:

В появившемся окне вы увидите несколько вариантов. Убедитесь, что установлен флажок рядом с надстройкой Solver , и нажмите ОК .

Теперь вы увидите кнопку Солвер в группе Анализ на вкладке Данные :

Если вы уже использовали пакет инструментов анализа данных , вы увидите кнопку анализа данных. Если нет, Солвер появится сам.

Теперь, когда вы загрузили надстройку, давайте посмотрим, как ее использовать.

Как использовать Солвер в Excel

У любого действия Солвера есть три части: цель, переменные ячейки и ограничения. Мы пройдем через каждый из шагов.

1. Нажмите Данные> Решатель . Вы увидите окно Solver Parameters ниже. (Если вы не видите кнопку Solver, см. Предыдущий раздел о том, как загрузить надстройку Solver.)
   
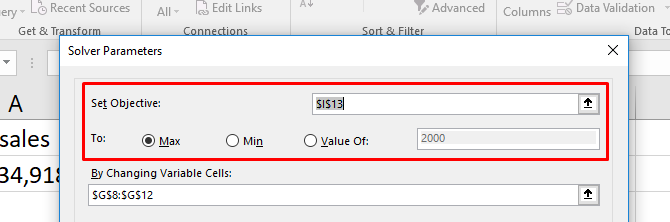
2. Установите цель своей ячейки и сообщите Excel свою цель. Цель находится в верхней части окна Солвера и состоит из двух частей: ячейка цели и выбор максимизации, минимизации или определенного значения.
   
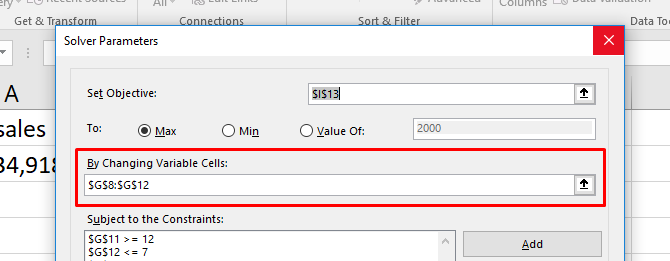
   Если вы выберете Max , Excel отрегулирует ваши переменные, чтобы получить максимально возможное число в вашей целевой ячейке. Мин — наоборот: Солвер минимизирует количество целей. Значение Of позволяет вам указать конкретное число для поиска Солвера.
3. Выберите ячейки переменных, которые Excel может изменить. Ячейки переменных задаются с помощью поля « Изменение ячеек переменной» . Нажмите стрелку рядом с полем, затем нажмите и перетащите, чтобы выбрать ячейки, с которыми Солвер должен работать. Обратите внимание, что это все клетки, которые могут варьироваться. Если вы не хотите менять ячейку, не выбирайте ее.
   
4. Установите ограничения для нескольких или отдельных переменных. Наконец, мы подошли к ограничениям. Это где Solver действительно мощный. Вместо того, чтобы менять любую ячейку переменной на любое желаемое число, вы можете указать ограничения, которые должны быть выполнены. Подробнее см. Раздел о том, как установить ограничения ниже.
5. Как только вся эта информация собрана, нажмите « Решить», чтобы получить ответ. Excel обновит ваши данные, чтобы включить новые переменные (поэтому мы рекомендуем сначала создать копию ваших данных).

Вы также можете создавать отчеты, которые мы кратко рассмотрим в нашем примере Solver ниже.

Как установить ограничения в Солвере

Вы могли бы сказать Excel, что одна переменная должна быть больше 200. При попытке использовать другие значения переменной Excel не будет идти ниже 201 с этой конкретной переменной.

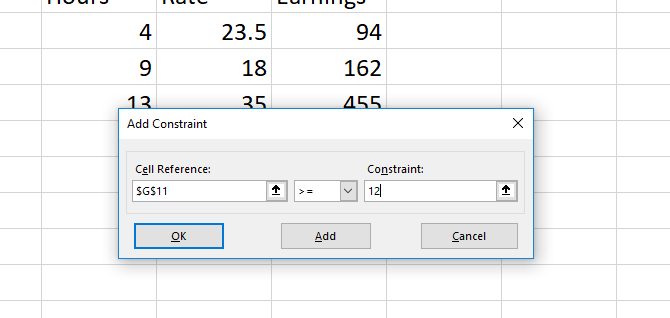
Чтобы добавить ограничение, нажмите кнопку « Добавить» рядом со списком ограничений. Вы получите новое окно. Выберите ячейку (или ячейки) для ограничения в поле « Ссылка на ячейку» , затем выберите оператора.

Вот доступные операторы:

• <= (меньше или равно)
• = (равно)
• => (больше или равно)
• int (должно быть целым числом)
• bin (должно быть 1 или 0)
• AllDifferent

AllDifferent немного сбивает с толку. Он указывает, что каждая ячейка в диапазоне, который вы выбираете для ссылки на ячейку, должна иметь разные номера. Но это также указывает, что они должны быть между 1 и количеством ячеек. Таким образом, если у вас есть три ячейки, вы получите цифры 1, 2 и 3 (но не обязательно в этом порядке)

Наконец, добавьте значение для ограничения.

Важно помнить, что вы можете выбрать несколько ячеек для ссылки на ячейку. Например, если вы хотите, чтобы шесть переменных имели значения больше 10, вы можете выбрать их все и сообщить Solver, что они должны быть больше или равны 11. Вам не нужно добавлять ограничение для каждой ячейки.

Вы также можете использовать флажок в главном окне Солвера, чтобы убедиться, что все значения, для которых вы не указали ограничения, являются неотрицательными. Если вы хотите, чтобы ваши переменные становились отрицательными, снимите этот флажок.

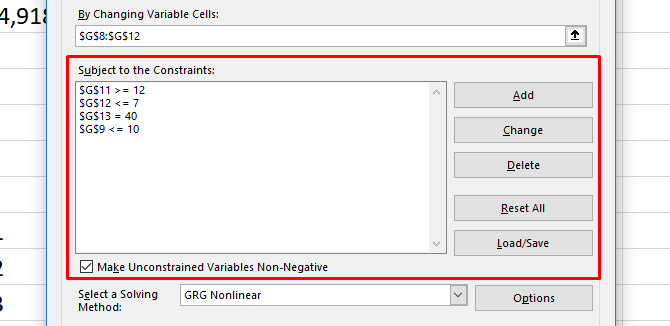
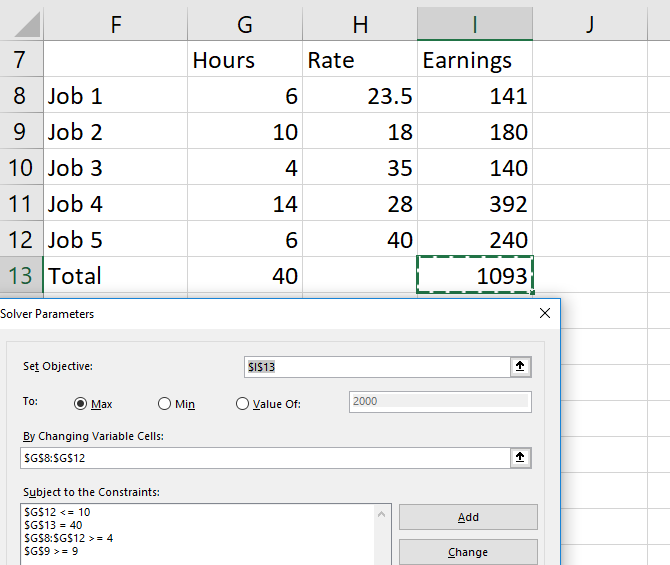
Пример решателя

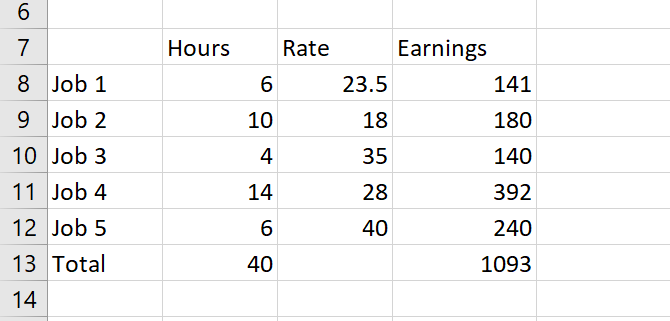
Чтобы увидеть, как все это работает, мы будем использовать надстройку Solver для быстрого расчета. Вот данные, с которых мы начинаем:

В нем у нас есть пять разных работ, каждая из которых платит разные ставки. У нас также есть количество часов, которое теоретический работник проработал на каждой из этих работ в течение данной недели. Мы можем использовать надстройку Solver, чтобы узнать, как максимизировать общую заработную плату, сохраняя определенные переменные в рамках некоторых ограничений.

Вот ограничения, которые мы будем использовать:

• Никакая работа не может упасть ниже четырех часов.
• Задание 2 должно быть больше восьми часов .
• Работа 5 должна быть менее одиннадцати часов .
• Общее количество отработанных часов должно быть равно 40 .

Это может быть полезно, чтобы написать ваши ограничения, как это, прежде чем использовать Solver.

Вот как мы настроили это в Солвере:

Во-первых, обратите внимание, что я создал копию таблицы, поэтому мы не перезаписываем исходную, которая содержит наше текущее рабочее время.

И во-вторых, обратите внимание, что значения в ограничениях «больше» и «меньше» на одно выше или ниже того, что я упоминал выше. Это потому, что нет вариантов больше или меньше. Есть только больше или равно или меньше или равно.

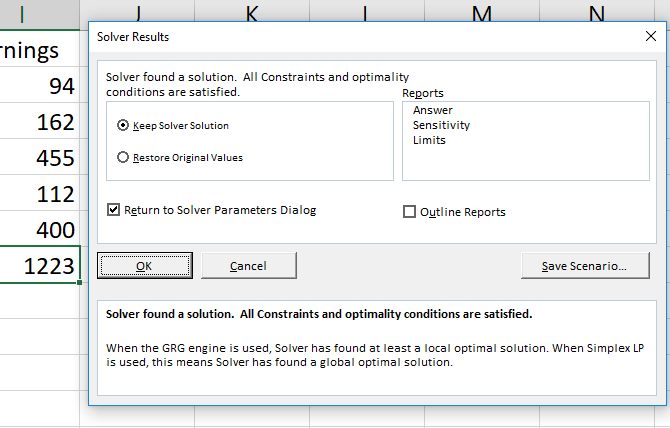
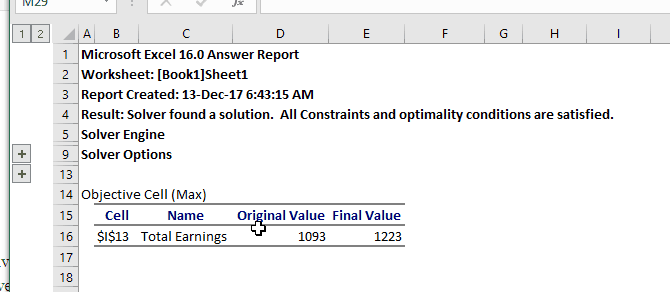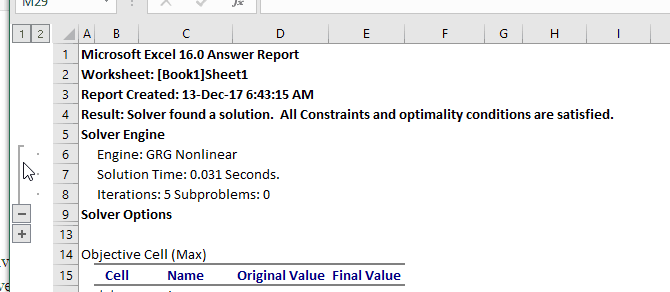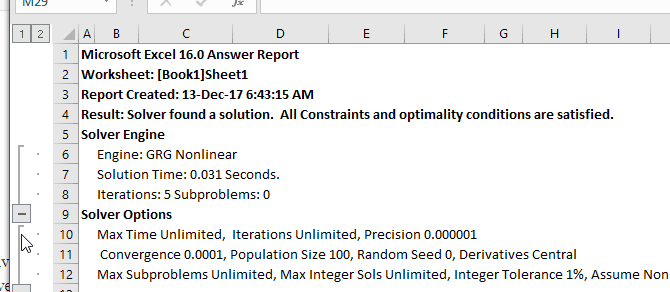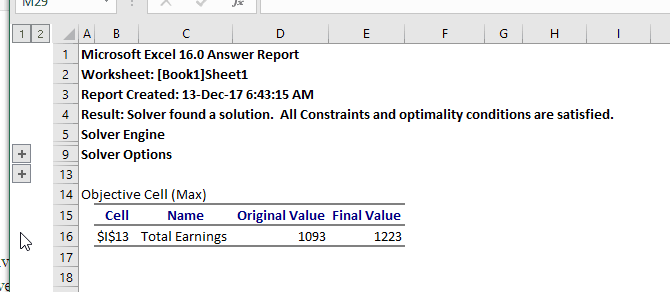
Давайте нажмем « Решить» и посмотрим, что произойдет.

Солвер нашел решение! Как видно из приведенного выше окна, наши доходы увеличились на 130 долларов. И все ограничения были выполнены.

Чтобы сохранить новые значения, убедитесь, что установлен флажок Keep Solver Solution и нажмите OK .

Если вам нужна дополнительная информация, вы можете выбрать отчет в правой части окна. Выберите все отчеты, которые вы хотите, скажите Excel, хотите ли вы, чтобы они были изложены (я рекомендую это), и нажмите ОК .

Отчеты создаются на новых листах в вашей рабочей тетради и дают вам информацию о процессе, который надстройка Solver прошла, чтобы получить ваш ответ.

В нашем случае отчеты не очень захватывающие, и там не так много интересной информации. Но если вы запустите более сложное уравнение Солвера, вы можете найти некоторую полезную отчетную информацию в этих новых рабочих листах. Просто нажмите кнопку + на стороне любого отчета, чтобы получить больше информации:

Solver Advanced Options

Если вы не очень разбираетесь в статистике, вы можете игнорировать расширенные опции Солвера и просто запустить ее как есть. Но если вы выполняете большие и сложные вычисления, вы можете посмотреть на них.

Наиболее очевидным является метод решения:

Вы можете выбрать между GRG Nonlinear, Simplex LP и Evolutionary. Excel предоставляет простое объяснение того, когда вы должны использовать каждый из них. Для лучшего объяснения требуются некоторые знания статистики. и регресс.

Чтобы настроить дополнительные параметры, просто нажмите кнопку « Параметры» . Вы можете сообщить Excel о целочисленной оптимальности, установить временные ограничения вычислений (полезно для массивных наборов данных) и настроить методы расчета GRG и Evolutionary при выполнении своих вычислений.

Опять же, если вы не знаете, что это значит, не беспокойтесь об этом. Если вы хотите узнать больше о том, какой метод решения использовать, Engineer Excel предлагает вам хорошую статью . Если вам нужна максимальная точность, возможно, Evolutionary — хороший путь. Просто знайте, что это займет много времени.

Поиск цели и решатель: вывод Excel на новый уровень

Теперь, когда вы знакомы с основами решения неизвестных переменных в Excel, для вас открыт совершенно новый мир расчета электронных таблиц.

Goal Seek может помочь вам сэкономить время, ускорив некоторые вычисления, а Solver значительно расширит вычислительные возможности Excel.

Это просто вопрос освоения с ними. Чем больше вы их используете, тем полезнее они станут.

Используете ли вы Goal Seek или Solver в своих таблицах? Какие еще советы вы можете дать, чтобы получить из них лучшие ответы? Поделитесь своими мыслями в комментариях ниже!

Функции программы Microsoft Excel: подбор параметра

Очень полезной функцией в программе Microsoft Excel является Подбор параметра. Но, далеко не каждый пользователь знает о возможностях данного инструмента. С его помощью, можно подобрать исходное значение, отталкиваясь от конечного результата, которого нужно достичь. Давайте выясним, как можно использовать функцию подбора параметра в Microsoft Excel.

Суть функции

Если упрощенно говорить о сути функции Подбор параметра, то она заключается в том, что пользователь, может вычислить необходимые исходные данные для достижения конкретного результата. Эта функция похожа на инструмент Поиск решения, но является более упрощенным вариантом. Её можно использовать только в одиночных формулах, то есть для вычисления в каждой отдельной ячейке нужно запускать всякий раз данный инструмент заново. Кроме того, функция подбора параметра может оперировать только одним вводным, и одним искомым значением, что говорит о ней, как об инструменте с ограниченным функционалом.

Применение функции на практике

Для того, чтобы понять, как работает данная функция, лучше всего объяснить её суть на практическом примере. Мы будем объяснять работу инструмента на примере программы Microsoft Excel 2010, но алгоритм действий практически идентичен и в более поздних версиях этой программы, и в версии 2007 года.

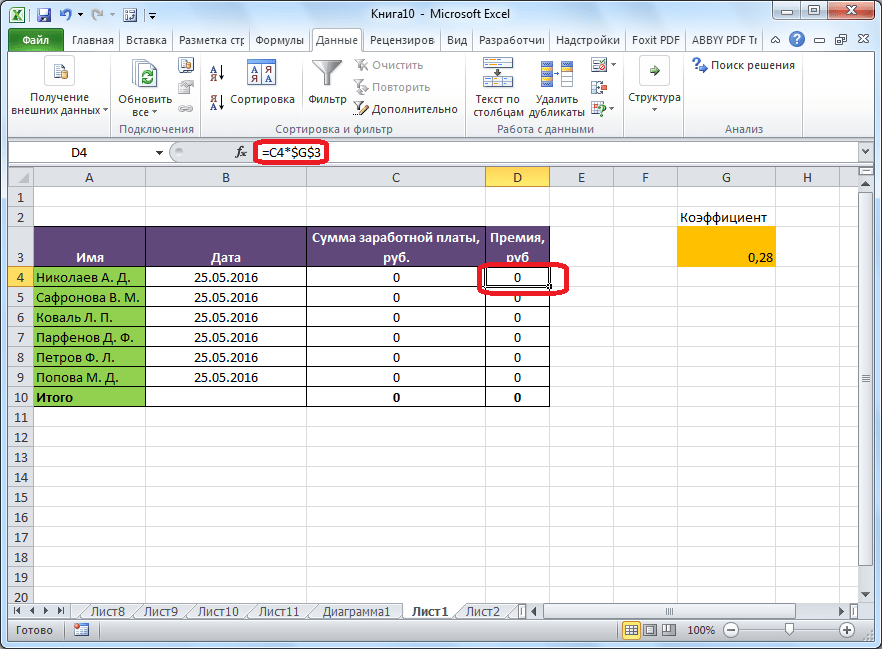
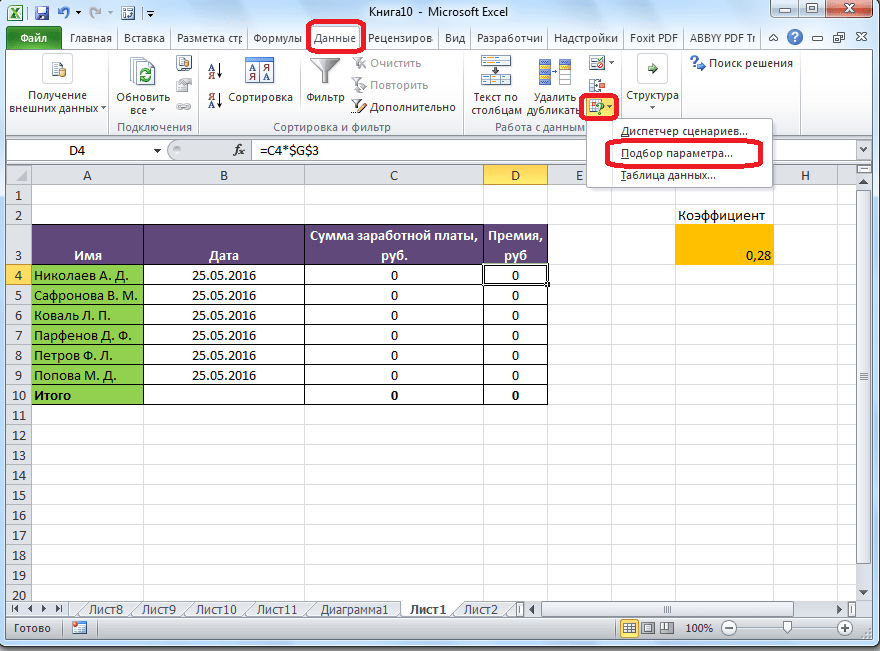
Имеем таблицу выплат заработной платы и премии работникам предприятия. Известны только премии работников. Например, премия одного из них — Николаева А. Д, составляет 6035,68 рублей. Также, известно, что премия рассчитывается путем умножения заработной платы на коэффициент 0,28. Нам предстоит найти заработную плату работников.

Для того, чтобы запустить функцию, находясь во вкладке «Данные», жмем на кнопку «Анализ «что если»», которая расположена в блоке инструментов «Работа с данными» на ленте. Появляется меню, в котором нужно выбрать пункт «Подбор параметра…».

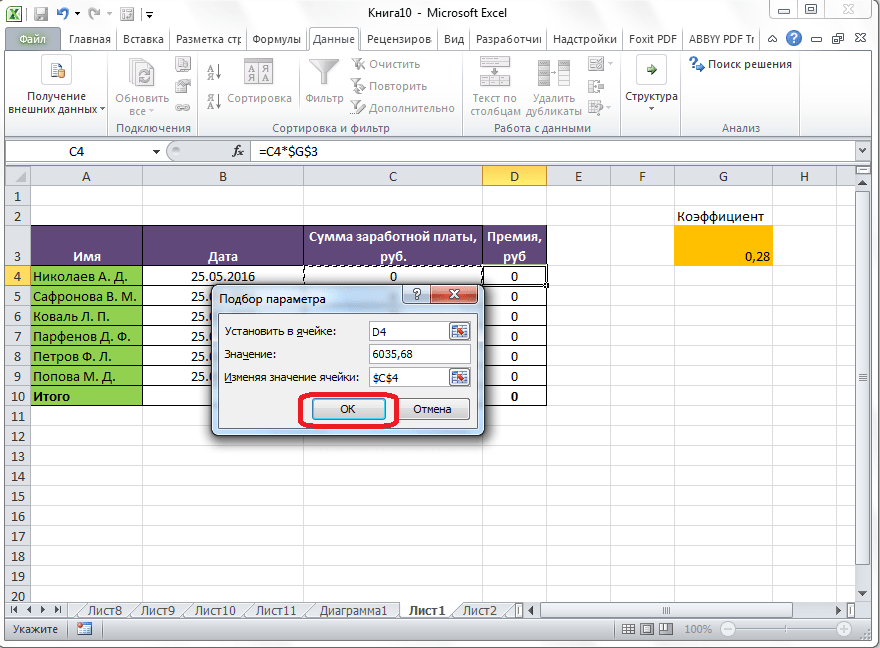
После этого, открывается окно подбора параметра. В поле «Установить в ячейке» нужно указать ее адрес, содержащей известные нам конечные данные, под которые мы будем подгонять расчет. В данном случае, это ячейка, где установлена премия работника Николаева. Адрес можно указать вручную, вбив его координаты в соответствующее поле. Если вы затрудняетесь, это сделать, или считаете неудобным, то просто кликните по нужной ячейке, и адрес будет вписан в поле.

В поле «Значение» требуется указать конкретное значение премии. В нашем случае, это будет 6035,68. В поле «Изменяя значения ячейки» вписываем ее адрес, содержащей исходные данные, которые нам нужно рассчитать, то есть сумму зарплаты работника. Это можно сделать теми же способами, о которых мы говорили выше: вбить координаты вручную, или кликнуть по соответствующей ячейке.

Когда все данные окна параметров заполнены, жмем на кнопку «OK».

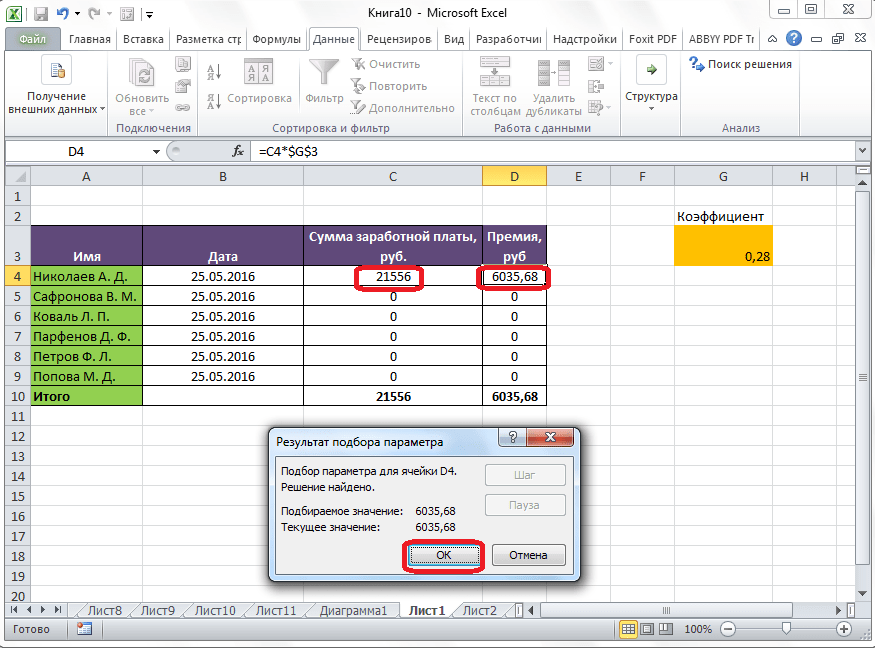
После этого, совершается расчет, и в ячейки вписываются подобранные значения, о чем сообщает специальное информационное окно.

Подобную операцию можно проделать и для других строк таблицы, если известна величина премии остальных сотрудников предприятия.

Решение уравнений

Кроме того, хотя это и не является профильной возможностью данной функции, её можно использовать для решения уравнений. Правда, инструмент подбора параметра можно с успехом использовать только относительно уравнений с одним неизвестным.

Допустим, имеем уравнение: 15x+18x=46. Записываем его левую часть, как формулу, в одну из ячеек. Как и для любой формулы в Экселе, перед уравнением ставим знак «=». Но, при этом, вместо знака x устанавливаем адрес ячейки, куда будет выводиться результат искомого значения.

В нашем случае, формулу мы запишем в C2, а искомое значение будет выводиться в B2. Таким образом, запись в ячейке C2 будет иметь следующий вид: «=15*B2+18*B2».

Запускаем функцию тем же способом, как было описано выше, то есть, нажав на кнопку «Анализ «что если»» на ленте», и перейдя по пункту «Подбор параметра…».

В открывшемся окне подбора параметра, в поле «Установить в ячейке» указываем адрес, по которому мы записали уравнение (C2). В поле «Значение» вписываем число 45, так как мы помним, что уравнение выглядит следующим образом: 15x+18x=46. В поле «Изменяя значения ячейки» мы указываем адрес, куда будет выводиться значение x, то есть, собственно, решение уравнения (B2). После того, как мы ввели эти данные, жмем на кнопку «OK».

Как видим, программа Microsoft Excel успешно решила уравнение. Значение x будет равно 1,39 в периоде.

Изучив инструмент Подбор параметра, мы выяснили, что это довольно простая, но вместе с тем полезная и удобная функция для поиска неизвестного числа. Её можно использовать как для табличных вычислений, так и для решения уравнений с одним неизвестным. Вместе с тем, по функционалу она уступает более мощному инструменту Поиск решения.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Подбор параметра в MS EXCEL

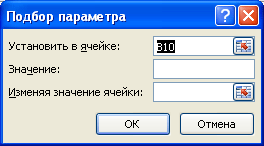
Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра.

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным.

Простейший пример

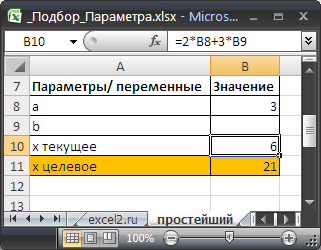
Найдем значение параметра b в уравнении 2*а+3*b=x, при котором x=21, параметр а=3.

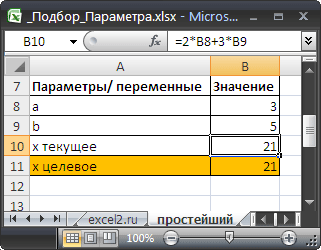
Подготовим исходные данные.

Значения параметров а и b введены в ячейках B8 и B9. В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x). Целевое значение x в ячейке B11 введено для информации.

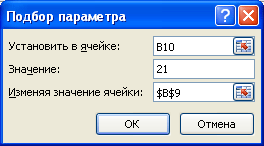
Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…).

В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b).

Инструмент Подбор параметра подобрал значение параметра b равное 5.

Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно.

Примечание: Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b, которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший.

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

Калькуляция, подбираем значение прибыли

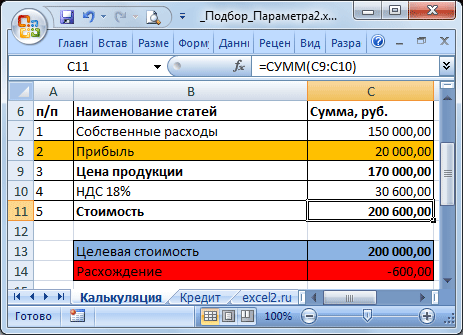
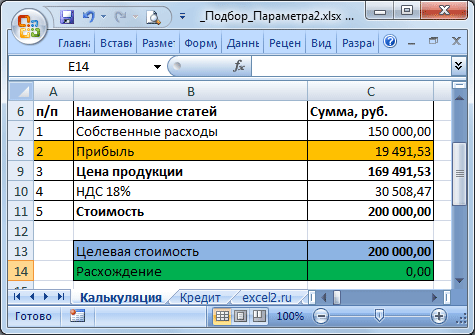
Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (С8), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (С14) равно 0.

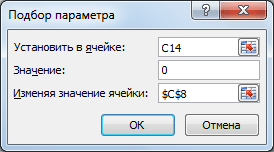
В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).

Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра.

Выделите ячейку С14, вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).

Теперь, о том когда этот инструмент работает.
1. Изменяемая ячейка не должна содержать формулу, только значение.
2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.
3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.

Подбор суммы кредита

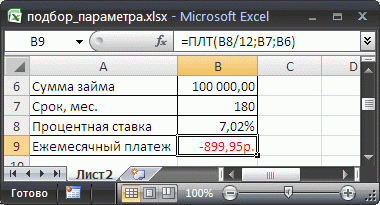
Предположим, что нам необходимо определить максимальную сумму кредита, которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).

В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.

Введем в ячейку B6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B7, % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).

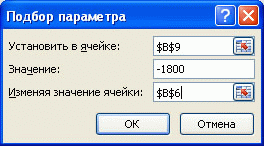
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:

• на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…;
• в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9;
• введите искомый результат в поле Значение. В данном примере он равен -1800;
• В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6;
• Нажмите ОК

Что же сделал Подбор параметра? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.

Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения. Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.

Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.

Подбор параметра в Excel и примеры его использования

«Подбор параметра» — ограниченный по функционалу вариант надстройки «Поиск решения». Это часть блока задач инструмента «Анализ «Что-Если»».

В упрощенном виде его назначение можно сформулировать так: найти значения, которые нужно ввести в одиночную формулу, чтобы получить желаемый (известный) результат.

Где находится «Подбор параметра» в Excel

Известен результат некой формулы. Имеются также входные данные. Кроме одного. Неизвестное входное значение мы и будем искать. Рассмотрим функцию «Подбора параметров» в Excel на примере.

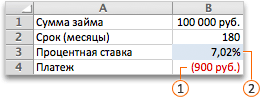
Необходимо подобрать процентную ставку по займу, если известна сумма и срок. Заполняем таблицу входными данными.

Процентная ставка неизвестна, поэтому ячейка пустая. Для расчета ежемесячных платежей используем функцию ПЛТ.

Когда условия задачи записаны, переходим на вкладку «Данные». «Работа с данными» — «Анализ «Что-Если»» — «Подбор параметра».

В поле «Установить в ячейке» задаем ссылку на ячейку с расчетной формулой (B4). Поле «Значение» предназначено для введения желаемого результата формулы. В нашем примере это сумма ежемесячных платежей. Допустим, -5 000 (чтобы формула работала правильно, ставим знак «минус», ведь эти деньги будут отдаваться). В поле «Изменяя значение ячейки» — абсолютная ссылка на ячейку с искомым параметром ($B$3).

После нажатия ОК на экране появится окно результата.

Чтобы сохранить, нажимаем ОК или ВВОД.

Функция «Подбор параметра» изменяет значение в ячейке В3 до тех пор, пока не получит заданный пользователем результат формулы, записанной в ячейке В4. Команда выдает только одно решение задачи.

Решение уравнений методом «Подбора параметров» в Excel

Функция «Подбор параметра» идеально подходит для решения уравнений с одним неизвестным. Возьмем для примера выражение: 20 * х – 20 / х = 25. Аргумент х – искомый параметр. Пусть функция поможет решить уравнение подбором параметра и отобразит найденное значение в ячейке Е2.

В ячейку Е3 введем формулу: = 20 * Е2 – 20 / Е2.

А в ячейку Е2 поставим любое число, которое находится в области определения функции. Пусть это будет 2.

Запускам инструмент и заполняем поля:

«Установить в ячейке» — Е3 (ячейка с формулой);

«Значение» — 25 (результат уравнения);

«Изменяя значение ячейки» — $Е$2 (ячейка, назначенная для аргумента х).

Найденный аргумент отобразится в зарезервированной для него ячейке.

Решение уравнения: х = 1,80.

Функция «Подбор параметра» возвращает в качестве результата поиска первое найденное значение. Вне зависимости от того, сколько уравнение имеет решений.

Если, например, в ячейку Е2 мы поставим начальное число -2, то решение будет иным.

Примеры подбора параметра в Excel

Функция «Подбор параметра» в Excel применяется тогда, когда известен результат формулы, но начальный параметр для получения результата неизвестен. Чтобы не подбирать входные значения, используется встроенная команда.

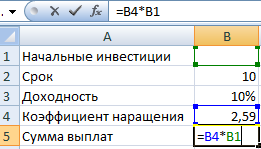
Пример 1. Метод подбора начальной суммы инвестиций (вклада).

• срок – 10 лет;
• доходность – 10%;
• коэффициент наращения – расчетная величина;
• сумма выплат в конце срока – желаемая цифра (500 000 рублей).

Внесем входные данные в таблицу:

Начальные инвестиции – искомая величина. В ячейке В4 (коэффициент наращения) – формула =(1+B3)^B2.

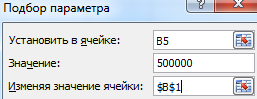
Вызываем окно команды «Подбор параметра». Заполняем поля:

После выполнения команды Excel выдает результат:

Чтобы через 10 лет получить 500 000 рублей при 10% годовых, требуется внести 192 772 рубля.

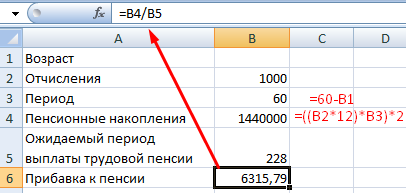
Пример 2. Рассчитаем возможную прибавку к пенсии по старости за счет участия в государственной программе софинансирования.

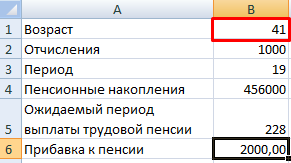
• ежемесячные отчисления – 1000 руб.;
• период уплаты дополнительных страховых взносов – расчетная величина (пенсионный возраст (в примере – для мужчины) минус возраст участника программы на момент вступления);
• пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза);
• ожидаемый период выплаты трудовой пенсии – 228 мес.;
• желаемая прибавка к пенсии – 2000 руб.

С какого возраста необходимо уплачивать по 1000 рублей в качестве дополнительных страховых взносов, чтобы получить прибавку к пенсии в 2000 рублей:

1. Ячейка с формулой расчета прибавки к пенсии активна – вызываем команду «Подбор параметра». Заполняем поля в открывшемся меню.
2. Нажимаем ОК – получаем результат подбора.

Чтобы получить прибавку в 2000 руб., необходимо ежемесячно переводить на накопительную часть пенсии по 1000 рублей с 41 года.

Функция «Подбор параметра» работает правильно, если:

• значение желаемого результата выражено формулой;
• все формулы написаны полностью и без ошибок.

Использование средства подбора параметров для получения требуемого результата путем изменения входного значения

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).

Если вы знаете, какой результат вычисления формулы вам нужен, но не можете определить входные значения, позволяющие его получить, используйте средство подбора параметров. Предположим, что вам нужно занять денег. Вы знаете, сколько вам нужно, на какой срок и сколько вы сможете платить каждый месяц. С помощью средства подбора параметров вы можете определить, какая процентная ставка обеспечит ваш долг.

Если вы знаете, какой результат вычисления формулы вам нужен, но не можете определить входные значения, позволяющие его получить, используйте средство подбора параметров. Предположим, что вам нужно занять денег. Вы знаете, сколько вам нужно, на какой срок и сколько вы сможете платить каждый месяц. С помощью средства подбора параметров вы можете определить, какая процентная ставка обеспечит ваш долг.

Примечание: Подбор параметров поддерживает только одно входное значение переменной. Если вы хотите оставить более одного входного значения; Например, сумма ссуды и сумма ежемесячного платежа для ссуды можно использовать в надстройке «Поиск решения». Дополнительные сведения можно найти в статье определение и устранение проблем с помощью надстройки «Поиск решения».

Пошаговый анализ примера

Рассмотрим предыдущий пример шаг за шагом.

Так как вы хотите вычислить ставку процентных ценностей, необходимую для достижения цели, вы можете использовать функцию ПЛТ. Функция ПЛТ вычисляет сумму ежемесячного платежа. В данном примере эту сумму и требуется определить.

Подготовка листа

Откройте новый пустой лист.

Прежде всего добавьте в первый столбец эти подписи, чтобы сделать данные на листе понятнее.

В ячейку A1 введите текст Сумма займа.

В ячейку A2 введите текст Срок в месяцах.

В ячейку A3 введите текст Процентная ставка.

В ячейку A4 введите текст Платеж.

Затем добавьте известные вам значения.

В ячейку B1 введите значение 100 000. Это сумма займа.

В ячейку B2 введите значение 180. Это число месяцев, за которое требуется выплатить ссуду.

Примечание: Хотя вам известна необходимая сумма платежа, не вводите ее как значение, поскольку она получается в результате вычисления формулы. Вместо этого добавьте формулу на лист и укажите значение платежа на более позднем этапе при использовании средства подбора параметров.

Теперь добавьте формулу, результат которой вас интересует. Например, используйте функцию ПЛТ.

В ячейке B4 введите =ПЛТ(B3/12;B2;B1). Эта формула вычисляет сумму платежа. В данном примере вы хотите ежемесячно выплачивать 900 ₽. Это значение здесь не вводится, поскольку вам нужно определить процентную ставку с помощью средства подбора параметров, а для этого требуется формула.

Формула ссылается на ячейки B1 и B2, значения которых вы указали на предыдущих этапах. Она также ссылается на ячейку B3, в которую средство подбора параметров поместит процентную ставку. Формула делит значение из ячейки B3 на 12, поскольку был указан ежемесячный платеж, а функция ПЛТ предусматривает использование годовой процентной ставки.

Поскольку в ячейке B3 нет значения, Excel полагает процентную ставку равной 0 % и в соответствии со значениями из данного примера возвращает сумму платежа 555,56 ₽. Пока вы можете игнорировать это значение.

Использование средства подбора параметров для определения процентной ставки

На вкладке Данные в группе Работа с данными нажмите кнопку Анализ «что если» и выберите команду Подбор параметра.

В поле Установить в ячейке введите ссылку на ячейку, в которой находится нужная формула. В данном примере это ячейка B4.

В поле Значение введите нужный результат формулы. В данном примере это -900. Обратите внимание, что число отрицательное, так как представляет собой платеж.

В поле Изменяя значение ячейки введите ссылку на ячейку, в которой находится корректируемое значение. В данном примере это ячейка B3.

Примечание: Формула в ячейке, указанной в поле Установить в ячейке, должна ссылаться на ячейку, которую изменяет средство подбора параметров.

Нажмите кнопку ОК.

Выполняется подбор параметров, результат которого показан на рисунке ниже.

Напоследок отформатируйте целевую ячейку (B3) так, чтобы результат в ней отображался в процентах.

На вкладке Главная в группе Число нажмите кнопку Процент.

Чтобы задать количество десятичных разрядов, нажмите кнопку Увеличить разрядность или Уменьшить разрядность.

Если вы знаете, какой результат вычисления формулы вам нужен, но не можете определить входные значения, позволяющие его получить, используйте средство подбора параметров. Предположим, что вам нужно занять денег. Вы знаете, сколько вам нужно, на какой срок и сколько вы сможете платить каждый месяц. С помощью средства подбора параметров вы можете определить, какая процентная ставка обеспечит ваш долг.

Примечание: Подбор параметров поддерживает только одно входное значение переменной. Если вы хотите присвоить несколько входных значений, например сумма займа и сумма ежемесячного платежа для займа, используйте надстройку «Поиск решения». Дополнительные сведения можно найти в статье определение и устранение проблем с помощью надстройки «Поиск решения».

Пошаговый анализ примера

Рассмотрим предыдущий пример шаг за шагом.

Так как вы хотите вычислить ставку процентных ценностей, необходимую для достижения цели, вы можете использовать функцию ПЛТ. Функция ПЛТ вычисляет сумму ежемесячного платежа. В данном примере эту сумму и требуется определить.

Подготовка листа

Откройте новый пустой лист.

Прежде всего добавьте в первый столбец эти подписи, чтобы сделать данные на листе понятнее.

В ячейку A1 введите текст Сумма займа.

В ячейку A2 введите текст Срок в месяцах.

В ячейку A3 введите текст Процентная ставка.

В ячейку A4 введите текст Платеж.

Затем добавьте известные вам значения.

В ячейку B1 введите значение 100 000. Это сумма займа.

В ячейку B2 введите значение 180. Это число месяцев, за которое требуется выплатить ссуду.

Примечание: Хотя вам известна необходимая сумма платежа, не вводите ее как значение, поскольку она получается в результате вычисления формулы. Вместо этого добавьте формулу на лист и укажите значение платежа на более позднем этапе при использовании средства подбора параметров.

Теперь добавьте формулу, результат которой вас интересует. Например, используйте функцию ПЛТ.

В ячейке B4 введите =ПЛТ(B3/12;B2;B1). Эта формула вычисляет сумму платежа. В данном примере вы хотите ежемесячно выплачивать 900 ₽. Это значение здесь не вводится, поскольку вам нужно определить процентную ставку с помощью средства подбора параметров, а для этого требуется формула.

Формула ссылается на ячейки B1 и B2, значения которых вы указали на предыдущих этапах. Она также ссылается на ячейку B3, в которую средство подбора параметров поместит процентную ставку. Формула делит значение из ячейки B3 на 12, поскольку был указан ежемесячный платеж, а функция ПЛТ предусматривает использование годовой процентной ставки.

Поскольку в ячейке B3 нет значения, Excel полагает процентную ставку равной 0 % и в соответствии со значениями из данного примера возвращает сумму платежа 555,56 ₽. Пока вы можете игнорировать это значение.

Использование средства подбора параметров для определения процентной ставки

Выполните одно из следующих действий:

В Excel 2016 для Mac: на вкладке данные щелкните анализ » что если«, а затем — Подборпараметров.

В Excel для Mac 2011: на вкладке данные в группе Работа с данными нажмите кнопку анализ » что если«, а затем выберите вариант Подборпараметров.

В поле Установить в ячейке введите ссылку на ячейку, в которой находится нужная формула. В данном примере это ячейка B4.

В поле Значение введите нужный результат формулы. В данном примере это -900. Обратите внимание, что число отрицательное, так как представляет собой платеж.

В поле Изменяя значение ячейки введите ссылку на ячейку, в которой находится корректируемое значение. В данном примере это ячейка B3.

Примечание: Формула в ячейке, указанной в поле Установить в ячейке, должна ссылаться на ячейку, которую изменяет средство подбора параметров.

Нажмите кнопку ОК.

Выполняется подбор параметров, результат которого показан на рисунке ниже.

Напоследок отформатируйте целевую ячейку (B3) так, чтобы результат в ней отображался в процентах. Выполните одно из указанных ниже действий.

В Excel 2016 для Mac: на вкладке Главная нажмите кнопку Увеличить разрядность или Уменьшить разрядность .

В Excel для Mac 2011: на вкладке Главная в группе число нажмите кнопку Увеличить разрядность или Уменьшить разрядность , чтобы установить число десятичных разрядов.

Функция Excel: подбор параметра

Программа Excel радует своих пользователей множеством полезных инструментов и функций. К одной из таких, несомненно, можно отнести Подбор параметра. Этот инструмент позволяет найти начальное значение исходя из конечного, которое планируется получить. Давайте разберемся, как работать с данной функцией в Эксель.

Зачем нужна функция

Как было уже выше упомянуто, задача функции Подбор параметра состоит в нахождении начального значения, из которого можно получить заданный конечный результат. В целом, эта функция похожа на Поиск решения (подробно вы можете с ней ознакомиться в нашей статье – “Поиск решения в Excel: пример использования функции”), однако, при этом является более простой.

Применять функцию можно исключительно в одиночных формулах, и если потребуется выполнить вычисления в других ячейках, в них придется все действия выполнить заново. Также функционал ограничен количеством обрабатываемых данных – только одно начальное и конечное значения.

Использование функции

Давайте перейдем к практическому примеру, который позволит наилучшим образом понять, как работает функция.

Итак, у нас есть таблица с перечнем спортивных товаров. Мы знаем только сумму скидки (560 руб. для первой позиции) и ее размер, который для всех наименований одинаковый. Предстоит выяснить полную стоимость товара. При этом важно, чтобы в ячейке, в которой в дальнейшем отразится сумма скидки, была записана формула ее расчета (в нашем случае – умножение полной суммы на размер скидки).

Итак, алгоритм действий следующий:

1. Переходим во вкладку “Данные”, в которой нажимаем на кнопку “Анализ “что если” в группе инструментов “Прогноз”. В раскрывшемся списке выбираем “Подбор параметра” (в ранних версиях кнопка может находиться в группе “Работа с данными”).
2. На экране появится окно для подбора параметра, которе нужно заполнить:
   • в значении поля “Установить в ячейке” пишем адрес с финальными данными, которые нам известны, т.е. это ячейка с суммой скидки. Вместо ручного ввода координат можно просто щелкнуть по нужной ячейке в самой таблице. При этом курсор должен быть в соответствующем поле для ввода информации.
   • В качестве значения указываем сумму скидки, которая нам известна – 560 руб.
   • В поле “Изменяя значение ячейки” вручную или посредством клика мышью указываем координаты ячейки (должна участвовать в формуле расчета суммы скидки), в которой планируем вывести начальное значение.
   • по готовности нажимаем OK.
3. Программа выполнит расчеты и выдаст результат в небольшом окошке, которое можно закрыть, нажав кнопку OK. Также найденные значения автоматически появятся в заданных ячейках таблицы.
4. Аналогичным образом можно посчитать цену без скидки для других товаров, если нам известна точная сумма скидки по каждому из них.

Решение уравнений с помощью подбора параметра

Несмотря на то, что это не основное направление использования функции, в некоторых случаях, когда речь идет про одну неизвестную, она может помочь в решении уравнений.

Например, нам нужно решить уравнение: 7x+17x-9x=75 .

1. Пишем выражение в свободной ячейке, заменив символ x на адрес ячейки, значение которой нужно найти. В итоге формула выглядит так: =7*D2+17*D2-9*D2 .
2. Щелкаем Enter и получаем результат в виде числа , что вполне логично, так как нам только предстоит вычислить значение ячейки D2, которе и является “иксом” в нашем уравнении.
3. Как было описано в первом разделе статьи, во вкладке “Данные” нажимаем кнопку “Анализ “что если” и выбираем “Подбор параметра”.
4. В появившемся окошке заполняем параметры:
   • В значении поля “Установить в ячейке” указываем координаты ячейки, в которой мы написали уравнение (т.е. B4).
   • В значении, согласно уравнению, пишем число 75.
   • В поле “Изменяя значения ячейки” указываем координаты ячейки, значение которой нужно найти. В нашем случае – это D2.
   • Когда все готово, нажимаем OK.
5. Как и в примере, рассмотренном выше, будут произведены вычисления и получен результат, о чем будет свидетельствовать небольшой окошко.
6. Таким образом, нам удалось решить уравнение и найти значение x, которое оказалось равным числу 5.

Заключение

Подбор параметра – функция, которая может помочь в поиске неизвестного числа в таблице или, даже решении уравнения с одной неизвестной. Главное – овладеть навыками использования данного инструмента, и тогда он станет незаменимым помощников во время выполнения различных задач.

Операторы определяют операции, которые необходимо выполнить над элементами формулы. В Excel используются общие математические правила для вычислений, в том есть круглые скобки, экспоненты, умножение и деление, сложение и вычитание, а также сокращенное пемдас (заставьте Уважаемый родственницей Салли). С помощью скобок вы можете изменить порядок вычислений.

Типы операторов. Существуют четыре разных типа операторов вычислений: арифметическое, Сравнение, Объединение текстаи ссылка.

• Арифметические операторы

  Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.

  Арифметический оператор	Значение	Пример
  + (знак «плюс»)	Сложение	= 3 + 3
  – (знак «минус»)	Вычитание Отрицание	= 3 – 3 =-3
  * (звездочка)	Умножение	= 3 * 3
  / (косая черта)	Деление	= 3/3
  % (знак процента)	Доля	30
  ^ (крышка)	Возведение в степень	= 3 ^ 3

• Операторы сравнения

  Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.

  Оператор сравнения	Значение	Пример
  = (знак равенства)	Равно	= A1 = B1
  > (знак «больше»)	Больше	= A1>B1
  < (знак «меньше»)	Меньше	= A1<B1
  >= (знак «больше или равно»)	Больше или равно	= A1>= B1
  <= (знак «меньше или равно»)	Меньше или равно	= A1<= B1
  <> (знак «не равно»)	Не равно	= A1<>B1

• Текстовый оператор конкатенации

  Амперсанд (&) используется для объединения (соединения) одной или нескольких текстовых строк в одну.

  Текстовый оператор	Значение	Пример
  & (амперсанд)	Соединение или объединение последовательностей знаков в одну последовательность	= «Север» & «обмотка» — это результат «Борей». Если ячейка a1 содержит «Last Name», а B1 — «First Name», = a1& «,» &B1 — «фамилия, имя».

• Операторы ссылок

  Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.

  Оператор ссылки	Значение	Пример
  : (двоеточие)	Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки.	B5:B15
  ; (точка с запятой)	Оператор объединения. Объединяет несколько ссылок в одну ссылку.	= СУММ (B5: B15, D5: D15)
  (пробел)	Оператор пересечения множеств, используется для ссылки на общие ячейки двух диапазонов.	B7:D7 C6:C8

Если в ячейку Excel введена формула, содержащая ссылку на эту же самую ячейку (может быть и не напрямую, а опосредованно — через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). На практике к циклическим ссылкам прибегают, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя ее устранения. Excel не может провести вычисления, так как циклические ссылки порождают бесконечное количество вычислений. Есть два выхода из этой ситуации: устранить циклические ссылки или допустить вычисления по формулам с циклическими ссылками (в последнем случае число повторений цикла должно быть конечным).

Рассмотрим задачу нахождения корня уравнения методом Ньютона с использованием циклических ссылок. Возьмем для примера квадратное уравнение: х 2 — 5х + 6=0, графическое представление которого приведено на рис. 8. Найти корень этого (и любого другого) уравнения можно, используя всего одну ячейку Excel.

Выберем произвольную ячейку, присвоим ей новое имя, скажем — Х, и введем в нее рекуррентную формулу, задающую вычисления по методу Ньютона:

2.2. Подбор параметра

Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.

Однако все это можно сделать и несколько проще. Для того чтобы найти второй корень, достаточно в качестве начального приближения (рис. 10) в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.

2.3. Поиск решения

Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.

Задачи, которые можно решать с помощью Поиска решения, в общей постановке формулируются так:

Искомые переменные — ячейки рабочего листа Excel — называются регулируемыми ячейками. Целевая функция F(х₁, х₂, … , х_n), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:

• найти максимум целевой функции F(х₁, х₂, … , х_n);
• найти минимум целевой функции F(х₁, х₂, … , х_n);
• добиться того, чтобы целевая функция F(х₁, х₂, … , х_n) имела фиксированное значение: F(х₁, х₂, … , х_n) = a.

Функции G(х₁, х₂, … , х_n) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.

Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решать. И тогда для решения конкретной оптимизационной задачи требуется специально для нее сконструированный метод. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ.

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.

Сохранить модель поиска решения можно следующими способами:

1. при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;
2. если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например найти максимум и минимум одной функции, или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Параметры/Сохранить модель окна Поиск решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Параметры/Загрузить модель диалога Поиск решения;
3. еще один способ сохранения параметров поиска — сохранение их в виде именованных сценариев. Для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений.

Отчет по результатам (рис.16) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй — значения искомых переменных, полученные в результате решения задачи, в третьей — результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы — это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение — это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение — это ограничение, которое было выполнено с ненулевым значением разницы.

Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Решение систем уравнений в среде Microsoft Excel

обучающие:

• повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
• повторение алгоритма решения систем уравнений;
• формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;

развивающие:

• формирование умений анализировать, выделять главное, сравнивать, строить аналогии;

воспитывающие:

• осуществление эстетического воспитания;
• воспитание аккуратности, добросовестности.

Тип урока: урок закрепления изученного материала и объяснения нового.

ХОД УРОКА

I. Организационная часть.

Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!

Ответ: “Знание – сила!”

Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)

Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).

II. Повторение пройденного материала.

Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)

Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.

III. Объяснение нового.

А. Решим систему графическим способом. Преобразуем данную систему . Для решения воспользуемся диаграммой, на которой отобразим графики обеих функций. Заполняем столбец А: заполняем ячейки А2:А22 числами от -5 до 5 с шагом 0,5. (в ячейку А2 заносим число -5, в ячейку А3 – число -4,5, выделяем ячейки А2 и А3, установим курсор мыши на правый нижний угол рамки (указатель примет форму черного крестика) и растягиваем рамку вниз, пока последнее значение не станет равным 5). При заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22. (протянем формулу за правый нижний угол). При заполнении столбца С в ячейку С2 заносим формулу =1-2*А2, копируем ее до ячейки С22. Выделим блок с данными, с помощью Мастера диаграмм выберем тип диаграммы Точечная и построим графики функций. Координаты точек пересечения графиков – решения системы.

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.

Запишем алгоритм решения систем уравнений графическим способом:

1. Преобразовать систему уравнений, если это необходимо.

2. Задать начальные значения для Х.

3. Найти значение первой функции при заданных Х.

4. Найти значение второй функции при тех же Х.

5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.

6. Решение системы — точка пересечения графиков функций.

7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.

Б. Решить систему уравнений . Занесем в электронную таблицу исходные данные и расчетные формулы следующим образом:.

Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:

При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.

Запишем примерный алгоритм решения системы уравнений, используя Поиск решения

1. Преобразовать систему уравнений, если это необходимо

2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.

3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.

4. Выбрать команду Сервис – Поиск решения.

5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения

6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)

7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК

8. Решить систему уравнений, щелкнув кнопкой Выполнить

IV. Практическая работа на компьютере.

А. Решите систему уравнений графическим способом

Б. Решите систему уравнения, воспользовавшись командой Поиск решения:

А. Решите систему уравнений графическим способом

Б. Решите систему уравнения, воспользовавшись командой Поиск решения:

V. Подведение итогов.

Повторить алгоритмы решения систем уравнений

Выставить оценки за тестирование в журнал

VI. Домашнее задание.

Решить рациональным способом системы уравнений: