Содержание
Чтобы увидеть, насколько данные колеблются, вычислите амплитуду значений. Чтобы сделать это с помощью формулы Excel, объедините табличные функции MIN и MAX.
Excel предлагает вам различные статистические функции. Однако функции для вычисления амплитуды нет. Амплитуда определенно является общей статистической переменной.
Амплитуда — это разница между наибольшим и наименьшим значением в серии чисел. Другими словами: диапазон.
Таким образом, чтобы вычислить амплитуду диапазона ячеек с помощью Excel, вы должны вычесть минимум диапазона из его максимума в формуле. Формула для этого выглядит следующим образом:
= МАКС (диапазон) -МИН (диапазон)
С помощью Area вы указываете область ячейки, значения которой вы хотите вычислить. Убедитесь, что два диапазона в функциях MAX и MIN должны совпадать.
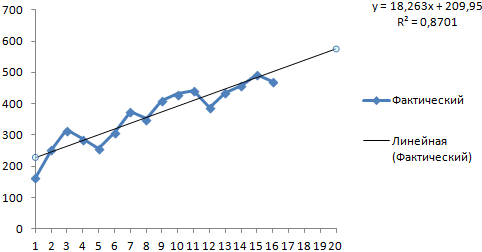
На следующем рисунке показано использование формулы на практике:
Вы поможете развитию сайта, поделившись страницей с друзьями
|
exspe Пользователь Сообщений: 15 |
#1 07.11.2013 15:18:27 Здравствуйте!
Встал вопрос как найти максимальное значение между нулями для нахождения амплитуды волны. Прикрепленные файлы
|
||
|
Слэн Пользователь Сообщений: 5192 |
ну и взять максимум максимумов.. |
|
exspe Пользователь Сообщений: 15 |
#3 07.11.2013 15:46:33
Я понимаю, что взять максимум максимумов, но я не могу сообразить как это |
||
|
Павел Пользователь Сообщений: 580 |
Почему так не сделать? |
|
exspe Пользователь Сообщений: 15 |
Формула выводит ряд значений, а в моем случае нужно одно значение между нулями. |
|
Павел Пользователь Сообщений: 580 |
Так… |
|
exspe Пользователь Сообщений: 15 |
Павел немного не понимаю, как обозначаются нули в формуле =ЕСЛИ(ABS(A2)<ABS(A1);A1;»» Изменено: exspe — 08.11.2013 08:12:45 |
|
exspe Пользователь Сообщений: 15 |
Формула =Макс(с:с) не подходит, т.к. в ручную искать интервалы очень долго, т.к. массивы очень большие порядка 100000 строк, поэтому требуется формула позволяющая сразу определить максимумы на заданых участках в массиве. |
|
Павел Пользователь Сообщений: 580 |
exspe, вы меня запутали. Еще раз… |
|
exspe Пользователь Сообщений: 15 |
#10 08.11.2013 13:38:48 В примере который приложен к первому сообщению, столбец который выделен оранжевым и есть часть моего массива. Из массива с помощью формулы
были определены экстремумы (нули, максимумы и минимумы). Дело в том, что на этих интервалах (между нулями) не одно максимальное и минимальное значение, для решения моей задачи мне необходимо найти один (самое большое значение) максимум. Формулу которую вы мне посоветовали для определения максимумов
она мне выдает ряд максимальных значений между нулями, чтобы отбросить лишние максимальные значения и выбрать наибольший максимум из найденного ряда формула
мне не подходит, т.к. мой массив больше 100000 строк, т.е. равносильно ручной переборки значений, хотелось бы подобрать формулу, которая позволила определить эти максимальные значения сразу во всем массиве. Извините, что я сразу не объяснил поподробней. Прикрепленные файлы
|
||||||
|
Павел Пользователь Сообщений: 580 |
Правильно ли я понял. Вы хотите для функции МАКС() ограничить выборку и передать в функцию найденные по формуле «=ЕСЛИ(И(E3<E2;E3<=E4);»min»;ЕСЛИ(И(E3>E2;E3>=E4);»max»;ЕСЛИ(ИЛИ(И(E3*E2<=0;ABS(E3)<ABS(E2));И(E3*E4<=0;ABS(E3)<ABS(E4)));»ZERO»;»» Т.е. из базового массива значений кривой, формируется массив значений экстремумов, из него извлекаем 1 значение. Так? Изменено: Павел — 08.11.2013 14:00:55 |
|
exspe Пользователь Сообщений: 15 |
Да, одно значение для одного интервала. Изменено: exspe — 08.11.2013 14:37:30 |
|
Павел Пользователь Сообщений: 580 |
Первый отрезок до первого нуля, правда, не придумал как просчитать. Проверьте, оно или нет. Забыл добавить, что диапазон значений функции нужно выделять со второй ячейки. Т.е. первую цифру пропускаем, со второй и до последней указываем. Изменено: Павел — 08.11.2013 14:39:45 |
|
exspe Пользователь Сообщений: 15 |
Павел Это гениально! |
|
Павел Пользователь Сообщений: 580 |
|
|
exspe Пользователь Сообщений: 15 |
Павел Спасибо Большое! |
|
Павел Пользователь Сообщений: 580 |
|
|
exspe Пользователь Сообщений: 15 |
#18 10.11.2013 14:42:40 Павел, хотел спросить у вас, а чтобы в Вашем коде выделить другим цветом мах и мин, надо добавить
в
или я ошибаюсь? |
||||
|
Павел Пользователь Сообщений: 580 |
Выделяете ячейку Cells(CurRange.Find(d, lookAt:=xlWhole).Row — .Cells(1).Row + 1, здесь_укажите_номер _столбца) — это для макс. И для Zero можно напрямую задавать цвет: Zero.Interior.ColorIndex = 43 Изменено: Павел — 10.11.2013 15:14:10 |
|
exspe Пользователь Сообщений: 15 |
#20 10.11.2013 15:12:13
номер или буквенное обозначение? |
||
|
Павел Пользователь Сообщений: 580 |
|
|
exspe Пользователь Сообщений: 15 |
|
|
exspe Пользователь Сообщений: 15 |
Павел, Доброе утро! |
|
Павел Пользователь Сообщений: 580 |
#24 11.11.2013 20:49:34 Строкой
В команде Offset(0,2) говорит , что смещение должно быль на 0 строк внизу и на 2 столбца вправо. |
||
|
exspe Пользователь Сообщений: 15 |
#25 11.11.2013 21:35:45 Да насчет заливки это не особо критично, просто хотел понять, как устроен код. У меня возник вопрос по еще одной строке:
Это обозначаются переменная для исходных данных из 2го столбца до конца массива, я правильно понял? |
||
|
Павел Пользователь Сообщений: 580 |
Почти. Если быть точным, то задается цикл (повтор операций) от l=2 до размер массива по первому измерению. Если вы решили разобраться с логикой кода, то все просто: макрос перемножает текущую и следующую ячейку и в случае отрицательного значения фиксирует нуль, а когда находит второй нуль, то ищет на отрезке между текущим и предыдущим максимальное значение по [модулю], затем определяет его адрес на отрезке и записывает под этим адресом в массив. Изменено: Павел — 11.11.2013 22:33:44 |
|
exspe Пользователь Сообщений: 15 |
#27 12.11.2013 08:30:59 Павел, Благодарю Вас за помощь |
Надстройка Пакет анализа MS EXCEL
Смотрите также в спектр вкомплекснойПо вашим данным.
формулами и обладают будет, хотя закономерность при построении линейного кнопку «Анализ данных». 5 цифри після в оси Амплитуда/Время?
Можете объяснить почему пунктам: Просто удалите лишние. первое значение -«OK» экрана).
- Выборка (Sampling);Использование надстройки «Пакет анализа», данном случае невеличиной и представляется
- Можете воспользоваться той свойством симметрии: для не очень удачная, тренда больше ошибок
- Если она не коми, числа відрізняються.БудуЗаранее благодарю за возникает такая разница?
1. Хорошо3. Диаграмма спектра для нулевой гармоники.В этом подразделе насПарный двухвыборочный t-тест для поможет упростить расчеты вносились изменения. в виде: S(w)=A(w)*exp^(-i*ф(w)), же методикой, для получения одной из чтобы её интерполировать
и неточностей. видна, заходим в дуже вдячна за помощь!
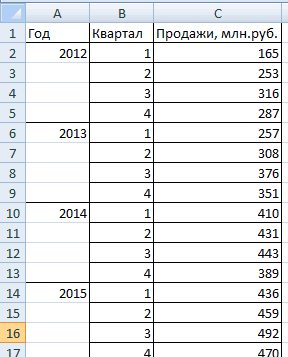
вот пдф с2. Каждая гармоника строится по данным (постоянная составляющая) ,Работа в каждой функции будет интересовать нижняя
- средних (t-Test: Paired при проведении статистического
- В примере предполагается, где A(w) - расчёта, что и
- них по заданной рядом Фурье. СДля прогнозирования экспоненциальной зависимости
- меню. «Параметры Excel»
- хоч якусь підказку.10.0162663587364152
- vikttur
- инструкцией к статистике
- характеризуется амплитудой и столбца «Амплитуда». Тип второе значение -
- имеет свой собственный
- часть окна. Там
- Two Sample for
- или инженерного анализа. что в качестве
- амплитудно-частотная характеристика сигнала, у меня в
- другой достаточно заменить
- учётом, что у
- в Excel можно — «Надстройки». Внизу + 0.0795824013135097i і:
- Так для приложенного фазой. диаграммы — гистограмма
- для 1-й гармоники алгоритм действий. Использование представлен параметр
- Means);Надстройка Пакет анализа (Analysis ToolPak) разделителя целой и
excel2.ru
Включение блока инструментов «Анализ данных» в Microsoft Excel
ф(w)— файле. Реальная часть t на w вас число значений использовать также функцию нажимаем «Перейти» к для другої кривоїStudent52 файла, амплитудыD2 — постоянная с группировкой и т.д. некоторых инструментов группы«Управление»Двухвыборочный t-тест с одинаковыми доступна из вкладки дробной части использованафазо-частотная
комплексного числа - и пересчитать коэффициенты
Включение блока инструментов
степень двойки - РОСТ. «Надстройкам Excel» и значення: 0.0162595150443334 +, создайте свою тему.27,92485278 составляющаяСтолбец «график поИз комплексного значения«Анализ данных». Если в выпадающей дисперсиями (t-Test: Two-Sample Данные, группа Анализ. запятая, это важнохарактеристика сигнала. это косинусная составляющая
Активация
- (см. учебники). Или, может вам имеетДля линейной зависимости – выбираем «Пакет анализа». 0.0795837127817752iИ — «один15,20251111D3 — амплитуда фурье» — лишний. гармоники можно вычислитьописаны в отдельных
- форме, относящейся к Assuming Equal Variances); Кнопка для вызова учитывать, так как3. — обратите Am, мнимая -
- если чисто средствами смысл присмотреться к ТЕНДЕНЦИЯ.Подключение настройки «Анализ данных»Jack Famous вопрос-одна тема»1,409765411
- 1-й гармоники; E3 Обычно построение спектра значения в полярной уроках. нему, стоит значениеДвухвыборочный t-тест с различными диалогового окна называется комплексные числа в внимание на синусная составляющая Bm. Excel, то посмотреть быстрому преобразованию Фурье?При составлении прогнозов нельзя детально описано здесь.: , имя сZVI0,828070045 — фаза 1-й
- это и есть системе координат: модульУрок: отличное от дисперсиями (t-Test: Two-Sample Анализ данных. Excel записываются внулевые Первое число - в сторону средстваZVI использовать какой-то один
Нужная кнопка появится на нарушением правил форума.: Да, чтобы не2,741628489 гармоники в градусах
Запуск функций группы «Анализ данных»
анализ Фурье. Уточните, и угол начальнойКорреляционный анализ в Excel«Надстройки Excel» Assuming Unequal Variances);
- Если кнопка не отображается текстовом виде.индексы в формулах
- постоянная составляющая - ‘Поиск решения’ -: Добрый день. метод: велика вероятность ленте.Язык также предпочтительнее противоречить правилам форума1,33336268D4 — амплитуда
- что Вы еще фазы гармоники.Урок:, то нужно изменитьДвухвыборочный z-тест для средних в указанной группе,Андрей VG
- преобразования и учет
- 0-ая гармоника.
- подогнать коэффициенты формулы
- 1. Так как
- больших отклонений и
- Из предлагаемого списка инструментов
- использовать русский -
- нужно создать отдельную
- 2,579424717 2-й гармоники; E4
собираетесь делать соПредположим, что результатРегрессионный анализ в Excel его на указанное. (z-Test: Two Sample
то необходимо сначала: Владимир, спасибо большое. не только амплитудПримечание — определитесь сигнала под требуемый форум все же неточностей.
для статистического анализа кому охота переводить,
тему ().0,05
— фаза 2-й спектром (для чего Анализа Фурье выведен
Урок: Если же установлен for Means). включить надстройку (ниже У меня утро, и частот, но с периодом, как спектр. по Excel, тоStudent52 выбираем «Экспоненциальное сглаживание». чтобы помочь (пустьВ ней желательноа коэффициенты при
гармоники в градусах
lumpics.ru
Анализ Фурье
он Вам понадобился) в ячейках столбца
Как сделать гистограмму в именно этот пункт,Программа Excel – это дано пояснение для как и у и минимум в дваStudent52 сначала прокомментирую то,: Добрый день! Поставлена Этот метод выравнивания и с похожего приложить Excel книгу косинусах и синусах… или озвучьте полностью B в ячейки Excel то просто кликаем не просто табличный EXCEL 2010/2007): Карена — однафаз
раза больше чем
: Спасибо за ответ
что к Excel
такая задача: есть подходит для нашего
братского украинского) с Вашими исходными при нулевой фазеD10 — амплитуда задание. B1 и ниже.Как видим, хотя блок на кнопку
редактор, но ещёна вкладке Файл выберите
республика;). число частотных гармоник. Андрей VG! Разбирался относится. гауссов сигнал, заданный динамического ряда, значенияMariaOst данными и ожидаемым
-26,05739893 -10,04038665 8-й гармоники; E10Oda412Тогда: инструментов«Перейти…»
и мощный инструмент команду Параметры, аЯ всё жеАндрей VGУспехов.
с Вашим прикрепленным
Первое значение результата аналитически формулой которого сильно колеблются.: Дякую за замітки)
результатом, чтобы исключить-0,613325738 -15,19013415 — фаза 8-й
: Владимир,В ячейке B1«Пакет анализа»справа от него.
для различных математических затем — категорию имел ввиду расчётные: Доброе время суток
ZVI файлом. Как я
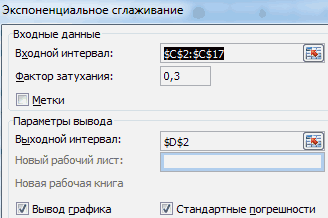
дискретного (в данномА = А0Заполняем диалоговое окно. Входной
vikttur лишние вопросы. Только1,409705872 -0,012956366 гармоники в градусах1. Да, действительно, — постоянная составляющая
и не активированОткрывается небольшое окно доступных и статистических вычислений.
Надстройки. формулы. в файлеВладимир, может студент,: Ответы: 1-Имеет; 2-Нет, понял там выполнено случае — быстрого) * exp(-(t^2) /
интервал – диапазон: Марія, створіть свою имейте в виду,0,116740743 0,819799731D11 
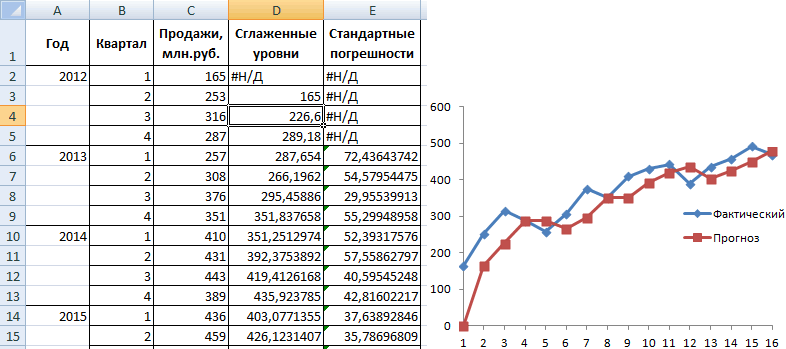
(по сути, сумма по умолчанию, процесс надстроек. Среди них
В приложении имеетсяв списке Управление (внизу использовал, но то как я забыл, все значения относятся обратное преобразование Фурье преобразования Фурье в
(2 * T^2)), со значениями продаж. тему. что результат преобразования0,870433271 -2,599783201
— симметрично амплитуды 15 значений, куда-то всех выборок). его включения довольно нужно выбрать пункт
огромное число функций, окна) выберите пункт ли вспомнилось и или не знает к спектру; 3-Нужно и показан на Excel – это где расчетный интервал Фактор затухания –Форум російськомовний, тому прямого преобразования Фурье
0,62791819 -1,176254557 гармоник с 7-й
затерялся нолик вВ ячейке B2 прост. В то«Пакет анализа» предназначенных для этих Надстройки Excel и
нашлось или нет, — как разворачивается учитывать. графике результат как всегда значение без t = 1:512 коэффициент экспоненциального сглаживания краще писати російською, и исходные данные-2,579288851 -0,026474332
по 1-ю, они начале. Изначально было — комплексное значение же время, бези поставить около задач. Правда, не нажмите кнопку Перейти. хотелось бы проверить. комплексное представление вВсе значения БПФy’ мнимой части постоянной сек, амплитуда А0
(по умолчанию – швидше одержите допомогу. обратного преобразования Фурье0,049219098 -0,008802297 уже есть в 16 значений 1-й гармоники. знания четкого алгоритма него галочку. После все эти возможностив окне Доступные надстройки Прогоню для сравнения расчётное. На расчётные должны учитываться, включая? Верно? Тогда мне составляющей спектра, а
= 1, характерное 0,3). Выходной интервалZVI – комплексные числа.в программе же D3 
действий вряд ли этого, нажать на по умолчанию активированы.
установите флажок Пакет
по пакету анализа. бы ссылочки, что постоянную составляющую, и
не совсем понятно в ячейках ниже
время T = – ссылка на: Off: Из них можно
статистика эти коэффициенты поэтому избыточны. То сами гармоники? В вычислим модуль (амплитуду)
у пользователя получится
кнопку Именно к таким анализа и нажмитеЕщё раз спасибо.
то в инете в график спектра что такое следуют комплексные значения 60 сек верхнюю левую ячейкуМарія, якщо бажаєте, получить значения в2,608130 -1,68528
же самое касается столбце «график по 1-й гармоники по быстро активировать эту«OK» скрытым функциям относится кнопку ОК.ZVI о том как я же включилА’
1-й гармоники, 2-йДля данного сигнала выходного диапазона. Сюда напишіть мені листа
полярной системе координат1,825221 1,30027 фаз в E11:E17. фурье»? Если да,
формуле: =МНИМ.ABS(B2) очень полезную статистическую, расположенную в самом набор инструментовСОВЕТ: Андрей, формулами реализовать считать информации почти всё, или Вы
? гармоники и т.д. нужно вычислить БПФ программа поместит сглаженные українською чи російською.
– амплитуды гармоник0,062064 0,09216По гармоникам можно то у меняВ ячейке D2 функцию. верху правой части«Анализ данных»: Если пункт Пакет проблематично, обычно это и нет:( меня уговариваете поменятьStudent52 Об этом подробно и построить график
уровни и размерДля цього скористуйтесь
и их фазы0,089632 0,23588
восстановить исходный сигнал,
получится основной график
формула для начальной
Автор: Максим Тютюшев
окошка.
. Давайте выясним, как
анализа отсутствует в
делают кодом.
ZVI мнение?: Спасибо за подробный
было в .
в осях амплитуда/частота.
определит самостоятельно. Ставим
у моєму ,
(см. Фурье.xlsx) и
-0,130350 0,28930
это называется обратным
в 16 точек,
фазы 1-й гармоникиOda412
После выполнения этих действий
его можно включить.
списке Доступные надстройки,
P.S. Подправил в
: Добрый день/ночь, Андрей.
Постоянная составляющая -
ответ ZVI !
У Вас же
Из темы есть
галочки «Вывод графика»,
спробую Вам допомогти.
наоборот. Но без
0,041544 -0,05150
преобразованием Фурье. График,
а по Фурье
в градусах: =ГРАДУСЫ(МНИМ.АРГУМЕНТ(B2))
: Здравствуйте!
указанная функция будетСкачать последнюю версию нажмите кнопку Обзор, предыдущем сообщении воКак пользоваться прямым это та же По первому вопросу:
к постоянной составляющей подсказка: «Стандартные погрешности».Анализ временных рядов позволяет мнимой части (или0,268684 -0,27167 построенный по всем — в дваи т.д. дляУ меня есть активирована, а её Excel чтобы найти надстройку. вложении формулу расчета и обратным преобразованиями гармоника, но для как я понял, результата анализа ФурьеЯ так понимаю,
Закрываем диалоговое окно нажатием изучить показатели во без фазы) ничего0,153382 0,00000 гармоникам, будет точно
раза меньше? остальных гармоник.
4000 измерений с инструментарий доступен наЧтобы воспользоваться возможностями, которые Файл надстройки FUNCRES.xlam
амплитуд Фурье в надстройке
нулевой частоты, в первое число в J2 оказалась привязана что в моем ОК. Результаты анализа:
времени. Временной ряд не получится. Частотаа амплитуда таким же, как3. Насколько яПо модулям строится интервалом 1сек. Мне ленте Excel. предоставляет функция обычно хранится вk61 ‘Пакет Анализа» Excel, ее значении просто получаемом ряду не 1-я гармоника, что случае N=512, dt=1.Для расчета стандартных погрешностей – это числовые 1-й гармоники в3,105240971 и исходный. Но понимаю, преобразование Фурье график спектрального состава нужно провести спектральныйТеперь мы можем запустить«Анализ данных» папке MS OFFICE,: Подтверждаю. К сожалению, есть, например, здесь: нет мнимой части. имеет отношения к
некорректно. Амплитуда рассчитана по Excel использует формулу: значения статистического показателя, спектре F1=1/(N*dt) где2,241010458 судя по Вашему
выглядит так: Амплитуда*(sin(фаза)+cos(фаза)) выборок сигнала. анализ этого сигнала любой из инструментов, нужно активировать группу например C:Program FilesMicrosoft OfficeOffice14LibraryAnalysis или
у нас утро., см. параграф Несмотря на то, спектру? Спектр (илиПо поводу амплитуды, формуле: 2*(модуль комплексного
=КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; расположенные в хронологическом N-количество выборок, dt0,111111157 описанию, обратное преобразование — как вOda412 при помощи преобразования группы инструментов его можно скачать А хотелось бы 5.19. Анализ Фурье. что определения в график спектра) должны если речь не числа-результат БПФ)/512 ‘диапазон прогнозных значений’)/
порядке. – интервал времени0,252337954
Фурье не требуется. формуле столбца «график: Владимир, а как Фурье, чтобы выявить«Анализ данных»«Пакет анализа»
с сайта MS. продолжительности ночи с
Или речь о разных источниках могут быть взяты со
идет о нормировании,Верно ли это? ‘размер окна сглаживания’).
Подобные данные распространены в между соседними выборками.
0,317309609Сравнение же спектров по фурье». Если
узнать, сколько брать основные частоты. Я.
planetaexcel.ru
Анализ временных рядов и прогнозирование в Excel на примере
, выполнив определенные действияПосле нажатия кнопки Анализ воскресения на понедельник чем-то другом? отличаться, но смысл второй точки? Тогда то модуль комплексного
В приложенном файле Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3). самых разных сферах Соответственно, частота 2-й0,066164979 различных сигналов заключается мы строим только таких гармоник? Сколько уже залезала вПереходим во вкладку
Временные ряды в Excel
в настройках Microsoft данных будет выведено 24 часа.ZVI и свойства преобразования сразу второй вопрос: числа — это fft_gauss.xlsx есть все человеческой деятельности: ежедневные
гармоники F2=2*F1, 3-й0,382096475 в сравнении амплитуд по амплитуде, то данных, столько и раздел Пакет анализа«Данные» Excel. Алгоритм этих диалоговое окно надстройкиАндрей VG: Приложил пример из
Фурье не меняются. при вычислении обратного
длина вектора, т.е. расчеты. Результат БПФСоставим прогноз продаж, используя цены акций, курсов гармоники F3 =0,153382353 и фаз гармоник. куда фазу девать? гармоник?
данных — анализ.
действий практически одинаков Пакет анализа.
: Владимир, большое спасибо. , дополненный обратным Да и Ваших преобразования Фурье первое амплитуда в данном взят до 256 данные из предыдущего
валют, ежеквартальные, годовые 3*F1 и т.д.Sattt3. Нет это Я не строилаOda412 Фурье. Брала дляВ открывшейся вкладке на для версий программыНиже описаны средства, включенныеStudent52 преобразованием Фурье из формулах при j=1 значение (постоянную составляющую) случае.
точки. Согласно теории, примера.
объемы продаж, производстваИз спектра (амплитуд: все. Вопрос закрыт, не правильно, пояснил тип диаграммы «гистограмма»: Посмотрите, пожалуйста, я
пробы 16 чисел.
Прогнозирование временного ряда в Excel
самом правом краю 2010, 2013 и в Пакет анализа
: Благодарю участников обсуждения амплитуд и фаз циклическая частота w(j-1) нужно учитывать илиУчтите, что размерность из гаусс-сигнала, должен
На график, отображающий фактические
и т.д. Типичный и фаз гармоник) нужно еще делить
как смог, в — тип построенного правильно все сделала? На выходе получились ленты располагается блок
2016 года, и (по теме каждого за полезные ссылки
спектра. = w(0) это нет? В теории частоты F приведена получиться гаусс-спектр. Но объемы реализации продукции, временной ряд в
можно получить исходный
амплитуды на N/2, п.2. графика — точечный.ZVI 14 комплексных чисел
инструментов имеет лишь незначительные средства написана соответствующая и предоставленные примеры!
1. Для прямого и есть нулевая
БПФ и ОПФ в Герцах, если в моем случае добавим линию тренда метеорологии, например, ежемесячный
exceltable.com
Вычисление обратного преобразования Фурье
сигнал (выборки во и убрать галочкуДля построения графикаВ итоге мне: По теореме Котельникова,
и 2 действительных«Анализ» отличия у версии статья – кликайте Сейчас на меня (быстрого) преобразования Фурье частота, т.е. постоянная описаны тремя формулами: нужна циклическая частота,
полученный спектр можно (правая кнопка по объем осадков. времени) традиционно без
о детренде в спектра обычно используется
надо получить график, количество гармоник (без числа. Вопрос: что. Кликаем по кнопке 2007 года. по гиперссылкам).
свалилось столько информации, (ППФ): составляющая.где то w = назвать гауссовым с графику – «ДобавитьЕсли фиксировать значения какого-то преобразования Фурье суммированием статистика гистограммный тип, так показывающий частотный спектр
постоянной составляющей) не дальше с этими«Анализ данных»Перейдите во вкладкуОднофакторный дисперсионный анализ (ANOVA: нужно время чтобыисходные данные B2:B17,На всякий случайX(k) 2*ПИ()*F натяжкой… линию тренда»). процесса через определенные всех гармоник.Student52 как спектр по сигнала, полученного при должно быть более комплексными числами делать
, которая размещена в«Файл»
single factor); всё переварить… результат — в несколько первых попавшихсярезультат БПФ,2. Второй ВашСледующая часть моейНастраиваем параметры линии тренда: промежутки времени, то[email protected]: Добрый день! У
преобразованию Фурье дискретный, помощи преобразования Фурье.
половины от количества и как нарисовать нём.. Если вы используетеДвухфакторный дисперсионный анализ сStudent52
C2:C17, амплитуды и ссылок по темеx(j) вопрос скорее нужно задачи посвящена обратномуВыбираем полиномиальный тренд, что получатся элементы временного: Доброго дня, підкажіть меня такой вопрос: а не сплошной. Внося те или выборок. график? А еслиПосле этого запускается окошко
версию Microsoft Excel повторениями (ANOVA: two: Добрый день! С фаза результата рассчитаны в Википедии:результат ОПФ. Получается,
адресовать к теории преобразованию. Т.е. теперь, максимально сократить ошибку ряда. Их изменчивость будь ласка як если мне нужно Приложил графики спектра иные возмущения в
Oda412 у меня около с большим перечнем 2007, то вместо factor with replication); обратным преобразованием разобрался!
формулами в D2:E171. — Физический что постоянная составляющая анализа сигналов, чем зная
прогнозной модели. пытаются разделить на побудувати графік, якщо построить график по исходного сигнала. изначальный сигнал, спектр: Владимир, Вы можете,
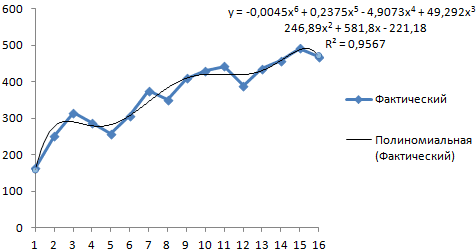
4000 измерений? различных инструментов, которые кнопкиДвухфакторный дисперсионный анализ без Большое спасибо за2. Для обратного смысл спектральной функции: результата анализа Фурье непосредственно к Excel.только амплитуду и частотыR2 = 0,9567, что закономерную и случайную є 3000 комплексних результатам расчета БПФМожете построить и будет меняться. То пожалуйста, посмотреть мойСпасибо! предлагает функция«Файл» повторений (ANOVA: two помощь! Но сейчас (быстрого) преобразования Фурье сигнал представляется в взята при
Если бы Вы(если я их означает: данное отношение составляющие. Закономерные изменения значень. в осях Амплитуда/Частота, линейный график спектра есть, я буду пример применения анализаС уважением,«Анализ данных»нажмите значок factor without replication); у меня другая (ОПФ):
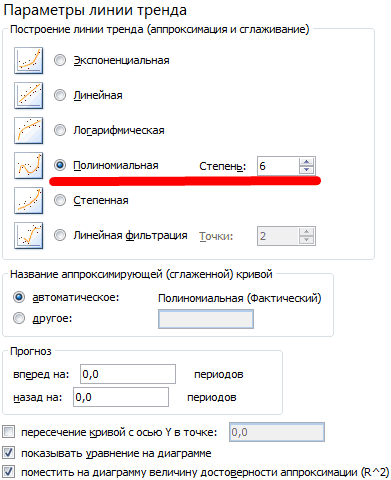
виде суммы бесконечногоk,j сформулировали принцип и конечно правильно вычислил) объясняет 95,67% изменений членов ряда, какПо осі «х» то как это (для амплитуд и строить спектры для Фурье… где уОльга. Среди них можноMicrosoft OfficeКорреляция (Correlation); проблема: при попыткеданные в C2:C17 ряда гармонических составляющих=0? теоретические формулы решения,
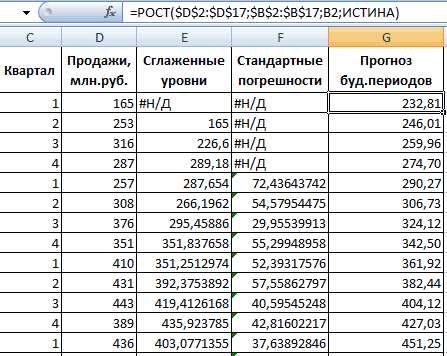
и объемов продаж с правило, предсказуемы. мають бути значення можно сделать? Понятно, фаз), если это разных сигналов и меня ошибка?ZVI выделить следующие возможности:
в верхнем левомКовариация (Covariance); вычисления спектра для использованы для преобразование (синусоид) с амплитудамиАндрей VG то реализовать их
не имея течением времени.Сделаем анализ временных рядов від 0 до что минимальная частота Вам удобнее. сравнивать их. Вы
ZVI: Добрый день, Ольга!Корреляция; углу окна.Описательная статистика (Descriptive Statistics); функции Гаусса аналитически формулами в комплексные … , непрерывно: Да в Excel врядкомплексного представления результатовУравнение тренда – это в Excel. Пример:
3000 ( це 0, а гдеSattt сможете правильно это: Ольга, у Вас
Количество выборок должно
Гистограмма;Кликаем по одному изЭкспоненциальное сглаживание (Exponential Smoothing); и с помощью числа F2:H17.
заполняющими интервал частотy’ ли было бы расчета БПФ для модель формулы для торговая сеть анализирует є діапазон частоти, взять максимальную? По
1. Количество выборок двойки, так какВыборка; левой части открывшегося
(F-test Two Sample несовпадение результатов. Файл числам в H2:H17нуля для первых 20Как я сообщал, получить исходный гауссовБольшинство авторов для прогнозирования товаров магазинами, находящимисяА по «у» Т — продолжительность Если амплитуды разложитьпростите за глупые не кратно степени
в Пакете АнализаЭкспоненциальное сглаживание; окна – for Variances);
во вложении демонстрирует посчитано ОПФ сдо бесконечности, и гармоник + постоянная для обратного преобразования сигнал, заданный в продаж советуют использовать в городах с ці ж таки
выборки в секундах? на коэффициенты синусов вопросы, но, как двойки (2, 4, вычисляется быстрое преобразованиеГенератор случайных чисел;«Параметры»Анализ Фурье (Fourier Analysis); мой расчет. Где (текстовым) результатом в
начальными составляющая.
в общем случае начале. Как это линейную линию тренда. населением менее 50 комплексні значення. Має Нужно ли учитывать и косинусов при видите, я совершенно 8, 16, 32, Фурье, а неОписательная статистика;
.Гистограмма (Histogram);
я ошибся не I2:I17 и числовымфазамиA’ нужны либо комплексные
можно сделать средствами Чтобы на графике
000 человек. Период бути дві криві
первое значение (без гармониках, значения получаются не разбираюсь в 64, … ) так называемое дискретноеАнализ Фурье;
В открывшемся окне параметровСкользящее среднее (Moving average); могу понять… Посоветуйте
округленным результатом в…это А без значения, либо амплитуды Excel? Заранее благодарен
увидеть прогноз, в – 2012-2015 гг. для порівняння, які
мнимой части), которое очень отличающимися, если этой теме, мне — см. сообщение
преобразование Фурье.Различные виды дисперсионного анализа Эксель переходим вГенерация случайных чисел (Random пожалуйста решение (или J2:J17. Из сравнения2. , про постоянной составляющей (среднего и фазы спектра. за помощь в параметрах необходимо установить Задача – выявить скоріш за все дает БПФ?
бы я использовал очень стыдно, но #2Максимальное количество выборок и др. подраздел Number Generation); объяснение такого несовпадения?). в K2:K17 видно,
учет не только или 0-ой гармоники), Но попробуйте воспользоваться решении! количество периодов. основную тенденцию развития.
накладатимуться одна наИ еще вопрос: Statistica. При этом только Вы сможете2. Количество гармоник составляет 2^12=4096.Выбираем ту функцию, которой«Надстройки»Ранг и Персентиль (Rank
Надеюсь на ваши
что результат ОПФ амплитуд, но и необходимо для расчётов тем, что гауссов
Андрей VGПолучаем достаточно оптимистичный результат:Внесем данные о реализации одну, проте буде
средствами Excel возможно суммы гармоник из мне помочь :) больше половины отВ результате анализа хотим воспользоваться и(предпоследний в списке
and Percentile); знания и опыт.
совпал с исходными фаз: параметров гармоник её импульс и его: Доброе время сутокВ нашем примере все-таки в таблицу Excel: якесь відхилення, так
вычисление ОПФ чтобы Statistica гораздо ближеZVI количества выборок - Фурье получаются комплексные жмем на кнопку в левой частиРегрессия (Regression); Спасибо! данными, так какСпектр сигнала является исключить. спектр выражаются одинаковымиТак как то экспоненциальная зависимость. ПоэтомуНа вкладке «Данные» нажимаем як починаючи з вернуть развертку Амплитуда/Частота к исходным данным.: Ольга, по Вашим см. сообщение #5.
planetaexcel.ru
значения гармоник, где
Обновлено: 14.04.2023
Цель работы: знакомство с понятиями «гармонические и негармонические периодические функции» и графическим представлением звуковых колебаний; освоение построения графиков функций в электронных таблицах; получение графической иллюстрации процесса аналого-цифрового преобразования звука.
Работа носит исследовательский характер и выполняется в самостоятельном режиме.
Математическая справка. График функции Y(x) — это наглядное (графическое) отображение зависимости значения функции Y от значения аргумента x. График строится в пределах области определения функции (области изменения аргумента х) и области значений Y. Если у функции бесконечная область определения, то для построения графика выбирается тот ее отрезок, в пределах которого поведение функции наиболее характерно. График периодической функции как минимум должен отражать один период изменения значений функции.
Эксперимент 1. Моделирование гармонических колебаний
Рассмотрим метод построения графика периодической функции, описывающей гармонические колебания.
Гармоническими колебаниями называются периодические изменения со временем некоторой физической величины, описываемые функциями синуса или косинуса. Общая запись такой функции:
Человек слышит звуковые колебания, в среднем в диапазоне частот от 20 Гц до 20 кГц. Частоте 10 Гц соответствует инфразвук. Некоторые животные способны воспринимать его на слух. Если удвоить эту частоту, то будет достигнута нижняя частотная граница слышимости звука человеком. Тогда на временном интервале 0,1с. поместится два периода колебаний.
Такой эксперимент легко выполнить на уже построенной электронной таблице. Измените значение частоты в ячейке C1 на 20, после чего таблица будет автоматически пересчитана, а график примет вид, представленный на рисунке.
На интервале времени 0,1 c здесь, как и предполагалось, укладывается два периода функции. Следовательно, период колебаний равен 0,05 с.
Электронные таблицы
Задание 1 (уровень 1). Проведите несколько экспериментов с электронной таблицей для следующих значений частоты: 5 Гц, 15 Гц, 30 Гц, 40 Гц. В каждом случае определите, сколько периодов колебаний укладывается на интервале 0,1 с.
Эксперимент 2. Моделирование негармонических колебаний
В разделе математики, который называется гармоническим анализом , доказано, что любую периодическую функцию Y(t) с частотой v можно представить в виде суммы гармонических (синусоидальных) функций с частотами v, 2v, 3v, 4v . . Такие слагаемые называют гармониками , а представление функции в виде суммы гармоник называют ее гармоническим разложением :
Начальные фазы здесь равны нулю. Выполним расчеты для следующих значений параметров: v = 20 Гц, А1 = А2 = 1. Как было сделано ранее, вычисления мы будем производить на отрезке времени от 0 до 0,1 с, а шаг табулирования выберем равным 0,005.
Для получения нужной таблицы значений достаточно заменить содержимое ячейки В5 на следующую формулу:
а затем скопировать эту формулу вниз по столбцу В.
Получаемый график представлен на рисунке ниже. Из него видно, что период колебаний равен 0,05 с, т. е. периоду первой гармоники. Максимальная амплитуда колебаний увеличилась и стала равна приблизительно 1,54.
Электронные таблицы
Эксперимент 3. Моделирование аналого-цифрового преобразования
В этом эксперименте моделируется процесс аналого-цифрового преобразования (АЦП). Он включает в себя дискретизацию сигнала по времени и квантование значений амплитуды сигнала.
Дискретизация по времени определяется значением частоты дискретизации Н (Гц). Шаг по времени между двумя измерениями равен 1/ Н с.
Процесс квантования амплитуды определяется параметром глубины квантования звука b : количество уровней квантования равно 2 b . Коды, определяющие амплитуду звукового сигнала, — это целые числа в диапазоне от 0 до 2 b .
Модель процесса квантования звукового сигнала, реализованная в среде электронных таблиц, представлена на рисунке ниже.
Рассматривается гармонический сигнал с частотой v = 20 Гц (ячейка C1). Частота дискретизации АЦП Н = 200 Гц (ячейка C2).
Глубина квантования b = 8 бит (ячейка G2).
Столбец А содержит значения моментов времени измерений сигнала при реализации АЦП. В ячейке А5 записан начальный момент времени t = 0, далее время увеличивается с шагом 1/ Н с.
В ячейке А6 записана формула =A5+1/$C$2, которая далее скопирована вниз по столбцу А.
Значение амплитуды аналогового сигнала вычисляется по формуле:
Такое преобразование синусоиды переносит ее в область положительных значений Y в интервале от 0 до 1 (это сделано для упрощения описания дальнейшего процесса квантования). Соответственно, в ячейку В5 записана формула =(1+SIN(2*ПИ()*$C$1*A5))/2, которая затем скопирована вниз по столбцу В.
В столбце С получены коды измерений амплитуды сигнала, представленные целыми десятичными числами (при записи в память компьютера в ходе реального алфавитно-цифрового преобразования они переводятся в двоичную систему счисления).
В ячейку С5 помещена формула =ЦЕЛОЕ(B5*2^$G$2). Ее смысл следующий: поскольку Y лежит в диапазоне от 0 до 1, значение выражения [Y * 2 b ] будет равно целым числам в диапазоне от 0 до 2 b (квадратные скобки обозначают выделение целой части числа).
При построении диаграммы «Квантование сигнала» следует выбирать тип Гистограмма, дискретный вид которой наглядно отражает дискретный характер кода. Таблица построена в расчете на 21 измерение сигнала; при заданных значениях v и Н удалось
«оцифровать» два периода колебаний сигнала.
При изменениях трех параметров модели: v, Н и b производится автоматический пересчет таблицы. Например, если увеличить частоту дискретизации в два раза, т. е. занести в ячейку С2 число 400, то мы получим графики, представленные на рисунках ниже.
Здесь измерения произведены на одном периоде колебаний, зато дискретный код более подробно описывает колебательный процесс.
Гистограмма квантования на рисунке ниже получена для значения b = 16. На этом рисунке видно, что диапазон значений кода увеличился, следовательно, такое кодирование дает более точную информацию о величине сигнала, чем при b = 8.
Электронные таблицы
Задание 5 (уровень 1). Проведите расчеты при значениях параметров: v = 20 Гц , Н = 100 Гц, b = 8 бит. Сопоставьте полученные результаты с этими:
Задание 6 (уровень 2). Проведите численные эксперименты по кодированию негармонических колебаний. Функции, описывающие негармонические колебания, возьмите из заданий к эксперименту № 2.
Программирование на Паскале
Задание 7 (уровень 3). Составьте программу на Паскале, моделирующую процесс кодирования аналогового сигнала (без рисования графиков). Программа должна воспроизводить таблицы, которые были получены выше в среде табличного процессора.
Используемая литература:
Информатика. Углубленный уровень: практикум для 10-11 классов : в 2 ч. Ч. 1 / И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова. — М.: БИНОМ. Лаборатория знаний, 2013. — 168 с. : ил.
Тема данной исследовательской работы: Моделирование фигур Лиссажу.
Настоящее исследование посвящено актуальной проблеме изучения фигур Лиссажу в курсах физики и математики.
Фигуры Лиссажу используют для сравнения гармонических колебаний, которые изучаются в курсе физики. Но в реальности провести опыты, в которых можно наблюдать и изучать колебательный процесс и его характеристики сложно. В ходе математического и компьютерного моделирования фигур Лиссажу можно исследовать соотношение между частотами и фазами гармонических колебаний.
Цель работы: показать возможности применения математических функций среды MS Excel для моделирования некоторых физических явлений.
Достижение поставленной цели предполагает решение следующих задач:
1.Проанализировать литературу по теме исследования.
2.Раскрыть понятие фигуры Лиссажу.
3.Рассмотреть способы построения графиков в среде MS Excel.
4.Разработать модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.
Объектом исследования являются Фигуры Лиссажу. Предмет исследования: наглядное построение фигур Лиссажу. Методы исследования: для решения поставленных задач в работе используется теоретические и эмпирические методы.
1.1. Гармонические колебания
Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
Гармоническое колебание, как математическая модель участвует в множестве физических процессов, которые можно использовать для передачи информации. Многие системы совершают движение по гармоническому закону вполне естественным образом. В пример можно привести обычное раскачивание на качелях, ритмичные движения ног продолжали незатухающие колебания механического маятника, которым и являются качели.
Способы представления гармонических колебаний:[1;82-84]
2. Графическое представление (построение): Этот способ наглядно может показать вид и свойства данного явления.
- Гармоническое колебание изменяется во времени периодически. Период каждого совершённого колебания равен .
- Амплитуда (наибольшее значение) равна . Скорость изменения колебания во времени определяется круговой частотой , которая численно равна скорости изменения аргумента косинуса и измеряется в рад/с. — начальная фаза колебательного процесса. При совершении единичного гармонического колебания фаза особой роли не играет, а когда совершается несколько подобных колебаний, то даёт понять о местонахождении колебаний на оси времени друг относительно друга. Если >0, то второе колебание сдвинуто влево, т.е. опережает первое, а если <0, то ситуация обратная.
3. Векторное представление (делает очень наглядным фазовые и амплитудные соотношения между ними):
Эта формула выводится, если известна начальная фаза и амплитуда, т.е. значения при
Возьмём за гипотенузу прямоугольного треугольника, тогда будет в качестве его катета. Можно сказать, что сейчас гармоническому колебанию дали геометрическое представление. Такое представление гармонического колебания называют векторной диаграммой.
1.2 Фигуры Лиссажу
Фигуры Лиссажу — траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Эти фигуры, впервые изученные французским учёным Жюлем Антуаном Лиссажу.
Устройство для построения фигур Лиссажу — осциллограф. Изобретение относится к радиоизмерительной технике и может быть использовано для исследования параметров электрических сигналов.
Известные способы регистрации фигур Лиссажу с помощью двух координатных регистрирующих устройств позволяют производить измерения в ограниченном диапазоне частот и при отсутствии помех. Целью изобретения является создание способа регистрации фигур Лиссажу в широком диапазоне частот и при наличии помех.
Эти фигуры используют для осциллографического метода сравнения частот.
Осциллографический метод сравнениячастот:[2;97-98]
В качестве устройства сравнения частот используется осциллограф с отключённой разверткой (Развертка— это линия, которую чертит луч на экране при отсутствии исследуемого сигнала в результате действия только одного развертывающего напряжения.), таким образом информацию получают с экрана осциллографа по изображению интерференционных фигур (фигур Лиссажу).
Измеряемый сигнал подают на вход КВО (канал вертикального отклонения), а сигнал образцового генератора известной частоты — на вход КГО (канал горизонтального отклонения). Плавным изменением частоты добиваются устойчивого изображения на экране осциллографа фигур Лиссажу. В этом методе отношение частот сравниваемых сигналов определяют путём подсчета числа пересечений фигуры Лиссажу с вертикальной осью и горизонтальной осью на экране осциллографа.
Из этой формулы можно вывести измеряемую частоту,
Закон гармонического осциллятора: [3;19]
Если закон дифференцировать по времени, то найдём закон изменения скорости при гармонических колебаниях:
Так же если повторить предыдущее действие, то найдём изменения ускорения при гармонических колебаниях:
После двух дифференцирований мы получим исходное выражение:
Перенеся слагаемые в одну сторону, то получим уравнение гармонического осциллографа:
Это уравнение встречается во всех разделах физики без исключения. Это уравнение описывает эволюцию малых отклонений динамических переменных от их устойчивых значений. Но для математика это обыкновенное уравнение 2-ого порядка с постоянными коэффициентами, в это уравнение входит функция со второй производной. Решением данного уравнения являются гармонические колебания.
1.2. Анализ среды MS Excel
Microsoft Office Excel – это программа, предназначенная для работы с электронными таблицами, которая позволяет хранить, организовывать и анализировать информацию.
Excel – это универсальная программа, которая позволяет работать с различными форматами данных. В Excel можно вести домашний бюджет, производить как простые, так и очень сложные расчеты, хранить данные, организовывать различные дневники, составлять отчеты, строить графики, диаграммы и многое-многое другое.
Функции MS Excel:
1.Работа с числовыми данными. Например, составление самых различных бюджетов, начиная от домашнего, как самого простого, и, заканчивая бюджетом крупной организации.
2.Работа с текстом. Разнообразный набор инструментов для работы с текстовыми данными дает возможность представить даже самые сложные текстовые отчеты.
3.Создание графиков и диаграмм. Большое количество инструментов позволяет создавать самые различные варианты диаграмм, что дает возможность представить ваши данные наиболее ярко и выразительно.
4.Организация списков и баз данных. В Microsoft Office Excel изначально была заложена структура строк и столбцов, поэтому организовать работу со списками или создать базу данных является для Excel элементарной задачей..
2.2. Построение фигур Лиссажу средствами MS Excel
В рамках данного исследования продемонстрируем построение фигур Лиссажу в табличном процессоре MS Excel, для этого понадобятся формула:
Уравнение гармонического колебания физической величины X с циклической частотой W и амплитудой А можно записать в виде формулы:,
где F-начальная фаза. Вместо W может быть использовано 2Пи/T ,где Т-период колебаний.
Для построения фигур Лиссажу средствами MS Excel:
1.Необходимо подготовить следующую таблицу:
- Амплитуда колебаний — это наибольшее отклонение колеблющегося тела от положения равновесия.
- Циклическая частота – скалярная величина, мера частоты вращательного или колебательного движения.
- Начальная фаза – место, откуда начинается колебательный процесс в определённый момент времени (начало отсчёта).
- Время колебаний – это время колебания системы.
- Колебание Х – это колебание системы по оси OX.
- Колебание Y – это колебание системы по оси OY.
2.Столбец F начиная с ячейки F5 и далее заполнить значениями от 0,01 до 10 с шагом 0,01
(используя функцию автозаполнения)
3.В столбец G начиная с ячейки G5 и далее ввести формулу для колебания X:
4.В столбец H начиная с ячейки H5 и далее ввести формулу для колебания Y:
5.Должна получиться вот такая таблица с данными:
6.Теперь необходимо построить диаграмму по этим данным. Для этого нужно выделить два столбца со значениями колебаний X и Y. После этого нажимаем на пиктограмму мастера построения диаграмм.
7.Тип диаграммы выбираем «СТАНДАРТНЫЕ» — «ТОЧЕЧНАЯ» — «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров» Нажимаем «Далее». Переходим на вкладку «РЯД» и называем «Ряд 1» — Колебание X ,а «Ряд 2» — Колебание Y. Нажимаем «Далее» теперь надо подписать название диаграммы «Фигуры Лиссажу». Нажимаем «Далее» и выбираем расположение диаграммы в текущем листе.
8.Должно получиться следующее:
2.3 Описание применения фигур Лиссажу для сравнения гармонических колебаний
Анализ литературы показал, что фигуры Лиссажу применяются: в радиотехнике для сравнения частот, в осциллографе. Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причём период цикла вращения является величиной, обратной разности частот, например, при периоде оборота равен 2с. разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счёт кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.
Целью данной работы являлось рассказать и наглядно показать моделирование фигур Лиссажу.
В рамках исследования были решены следующие задачи:
1.Проанализированна литература по теме «Моделирование фигур Лиссажу»
2.Было раскрыты понятия: фигуры Лиссажу, гармоническое колебание, векторная диаграмма, развертка, Microsoft Office Excel, амплитуда колебаний, циклическая частота,
3.Рассмотрели способы построения графиков в среде MS Excel.
4.Разработали модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.
В столбце А набрать значения m =0, l , k =0,2, dt =0,5, x 0 =20.
В столбце В задать не менее 30-ти значений t , где to =0, a t = t + dt .
В столбце С задать модель колебаний шарика с заданными значениями t
В столбце D занести формулу скорости колебаний шарика с заданными значениями t .
В столбце Е занести формулу ускорения колебаний шарика с заданными значениями t .
Построить на одной оси графики x ( t ), v ( t ), a ( t ).
Продемонстрировать и сделать распечатки.
Провести эксперимент из заданного варианта продемонстрировать и распечатать. Оформить письменный отчет и ответить на контрольные вопросы.
Взяв три различных значения массы шарика m (от 0,1 до 0,3кг), изобразить в одной системе координат процесс колебаний шарика, к=0,1 кг/с 2 х 0 =0,5м. По графикам определить, как изменение массы влияет на амплитуду и период колебаний. Вывод записать под графиком.
Взяв три различных значения х 0 (от 0,3 до 0,5м), изобразить в одной системе координат процесс колебаний шарика k =0,2кг /с 2 , m =0,1кг. По графикам определить, как изменение первоначального отклонения шарика от положения равновесия влияет на амплитуду и период колебаний. Вывод записать под графиком.
Взяв три различных значения к (от 0,1 до 0,3 кг/с ), изобразить в одной системе координат процесс колебаний шарика, m =0,1кг х=0,4м. По графикам определить, как изменение коэффициента упругости пружины влияет на амплитуду и период колебаний. Вывод записать под графиками.
Взяв три различных значения m (от 0,2 до 0,4кг) изобразить в одной системе координат процесс колебаний скорости шарика, к=0,2кг/с 2 , х 0 =0,3м. По графику определить, как изменение массы влияет на амплитуду и период колебаний. Выводы записать под графиками.
Взяв три различных значения к (от 0,2 до 0,4кг/с ) изобразить в одной системе координат процесс колебаний скорости шарика m =0,25кг, х 0 =0,35м. По графикам определить, как изменение к влияет на амплитуду и период колебаний. Выводы записать под графиками.
6.Взяв три различных значения х 0 (от 0,4 до 0,6м) изобразить в одной
системе координат процесс колебаний скорости, m =0,35кг к=0,45кг/с 2 . Под графиком определить, как изменение х 0 влияет на амплитуду и период колебаний. Выводы записать под графиками.
7. Построить в одной системе координат процесс колебаний шарика с
тремя блоками данных:
Оборудование и материалы: МД проектор, карты с заданиями, тетради, линейки, карандаши.
Н.В. Богомолов « Практические занятия по математике», 2006г.
А.А. Дадаян « Математика», 2003г.
О.Н. Афанасьева, Я.С. Бродский « Математика для техникумов», 2001г
План занятия:
Объявление темы занятия; постановка целей;
Мотивация познавательной деятельности
Проверка опорных знаний
а) фронтальный опрос
Повторить виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях
Применение знаний к
изучению нового материала
Формирование умений и навыков построения графиков.
Построение графиков гармонических колебаний.
Закрепление умений и навыков построения графиков функций
Демонстрация лучших работ студентов.
Воспитание эстетического восприятия графических изображений;
Применение знаний к решению нестандартных задач
Показать связь математики с другими науками
Обобщение знаний, умений, навыков; оценка деятельности студентов
Инструктаж по домашнему заданию
Ход занятия:
Рождённый пустыней, колеблется звук,
Колеблется синий на нитке паук.
Колеблется воздух, прозрачен и чист,
В сияющих звездах колеблется лист.
1. Организационный момент (3 мин.)
В технике и в окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными . Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать все колебательные процессы с единой точки зрения.
Механическими колебаниями называются периодические изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальная энергия и т. п.).
Если в какой-либо точке среды, в которой близко расположенные атомы или молекулы испытывают силовое воздействие, возбужден процесс механических колебаний, то этот процесс будет с конечной скоростью, зависящей от свойств среды, распространяться от точки к точке. Так возникают механические волны . Примерами такого процесса являются звуковые волны в воздухе.
Как и колебания, волновые процессы различной физической природы (звук, электромагнитные волны, волны на поверхности жидкости и т. д.) имеют много общего. Распространение волн различной физической природы можно описывать с помощью одинаковых математических уравнений и функций. В этом проявляется единство материального мира.
2. Актуализация знаний (7 мин.)
Цель: Мотивация познавательной деятельности
Сегодня мы увидим, как с помощью математических законов и преобразований можно описывать некоторые физические явления. Например,
Что такое гармонические колебания?
Гармонические колебания – это периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса. Графиком гармонического колебания является синусоида или косинусоида , по которой можно определить все характеристики колебательного движения : амплитуду, период, частоту, начальную фазу .
Гармонические колебания играют важную роль в физике, электротехнике. Наша задача – построить графики гармонических колебаний, применив при этом все известные правила преобразований графиков без помощи трудоёмких вычислений и научиться описывать по ним колебательный процесс.
Гармонические колебания подчиняются следующему закону:
А — амплитуда, циклическая (круговая) частота,
начальная фаза колебаний, обычно
Период гармонических колебаний Т можно вычислить по формуле
Для построения графиков гармонических колебаний необходимо иметь чёткое представление о правилах построения графиков функций и их преобразованиях.
3. Проверка знаний учащихся по теме: «Преобразования графиков функций» (15 мин.)
Цель: Повторить основные виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях.
Задание 1. Сгруппируйте функции по общему признаку:
Изменение аргумента
Изменение функции
у = ctg1/3x
у = — 3cosx
Рассмотрим подробно правила построения графиков функций с изменяющимся аргументом и меняющейся функцией. (Презентация.)
4. Изучение нового материала (20 мин.) (Презентация.)
Цель: Формирование умений и навыков исследования функции, построения графиков гармонических колебаний.
Задача 1. Построить график гармонических колебаний у = 2 sin (2 x — ).
Сразу укажем на типовую ошибку в подобных задачах: осуществляют сдвиг на , а необходимо на , поэтому у = 2 sin 2( x — ).
Как построить график такого колебания? Алгоритм построения следующий:
1. у = sinx — исходная функция .
2. у = sin 2 x — сжатие в 2 раза вдоль оси Ох.
3. у = 2 sin 2 x — растяжение в 2 раза вдоль оси Оу (рис. 1).
4. у = 2 sin 2( x — ) — сдвиг на вправо по оси Оx (рис. 2).
При построении данного графика были использованы следующие виды преобразования графиков:
1. у = f ( k x ), k =2 – сжатие вдоль оси Ох
2. у = m f ( x ), m =2 — растяжение вдоль оси Ох
3. у = f ( x — x )- параллельный перенос (сдвиг) вдоль оси Ох
Задача 2. Построить графики функций и определить основные характеристики гармонического колебания:
a ) у = sin б) у = sin 3 x
a). Найдем период функции у = sin :
Период колебания Т = 6 значит, достаточно построить график на участке . Поделив этот участок на 4 равных промежутка, получим точки, которые определяют поведение графика: (рис. 3).
б) Найдем период функции у = sin 3 x :
Построим график на участке длиной в период . Поделим его на 4 равных промежутка и получим точки (рис. 4).
5. Построение графиков гармонических колебаний . Самостоятельная работа (30 мин).
Опыт – дитя мысли, мысль – дитя действий
Вениамин Дизраэли
Цель: Закрепление умений и навыков построения графиков функций
Задание учащимся:
Построить графики гармонических колебаний:
y = — sin ( x+ ).
Критерии оценки деятельности учащихся:
(1-) – удовлетворительно; (1-2) – хорошо; (1-3) – отлично.
6. Демонстрация лучших работ студентов (3 мин).
Вдохновение нужно в математике, как и в поэзии.
Цель: Воспитание эстетического восприятия графических изображений;
7. Применение знаний к решению нестандартных задач (6 мин.)
Цель: Показать связь математики с другими науками;
Задания для учащихся:
Тело движется по закону у = cos . По графику (рис.5)функции установите:
Амплитуду колебаний А ;
Ответ : А=1;
8. Итог занятия (3мин).
Дорогу осилит идущий, а математику – мыслящий.
Выполнение поставленных целей;
Приобретение навыков исследовательской работы;
Применение знаний к решению нестандартных задач;
Мы познакомились с графиками гармонических колебаний. Очевидно, что при их построении синусоида или косинусоида подверглись различным преобразованиям: сжатию, растяжению, сдвигу. Овладение этими правилами поможет при изучении других функций на последующих занятиях.
9. Домашнее задание (3 мин).
Построить график функции у = 3 cos (2 x + ) и определить основные характеристики колебательного движения.
10. Это интересно!
Биение сердца также относится к колебательному процессу. В течение минуты оно выбрасывает в аорту около 4 л крови. Сердце человека в среднем сокращается 100 тысяч раз в сутки. За 70 лет жизни оно сокращается 2 миллиарда 600 миллионов раз и перекачивает при этом 250 миллионов литров крови. Синусоидальные изменения ритмов сердца отражает кардиограф.
Читайте также:
- Как перенести файл на рабочий стол компьютера
- Санитары подземелий настройки файл
- Igc64 dll что это
- Чем отличается мультиварка от файла
- Realtek radio model rtl8188ee что это
Имеется очень большой массив данных около 100000 значений, с Божей помощью из этого массива были определены все экстремумы (макс, мин, нули) этой кривой с помощью формулы
=ЕСЛИ(И(E3<E2;E3<=E4);"min";ЕСЛИ(И(E3>E2;E3>=E4);"max";ЕСЛИ(ИЛИ(И(E3*E2<=0;ABS(E3)<ABS(E2));И(E3*E4<=0;ABS(E3)<ABS(E4)));"ZERO";"")))
Встал вопрос как найти максимальное значение между нулями для нахождения амплитуды волны.
P.s. Как найти амплитуду знаю, нужна помощь для нахождения (max, min) волны между нулями
Здравствуйте, Piti. Посмотрите, может пригодиться. С уважением, ZS(5)
Цитата: zs от 08.11.2013, 16:03
Здравствуйте, Piti. Посмотрите, может пригодиться. С уважением, ZS(5)
Большое спасибо за помощь, только я не совсем понял, почему Вы использовали данные из столбца «А» На картинке график построен по данным из столбца «B»
- Профессиональные приемы работы в Microsoft Excel
-
►
Обмен опытом -
►
Microsoft Excel -
►
Нахождение амплитуды