Функция поиск решения в Excel по умолчанию отключена. Для того, что начать пользоваться данным инструментом, вам необходимо его сначала подключить.
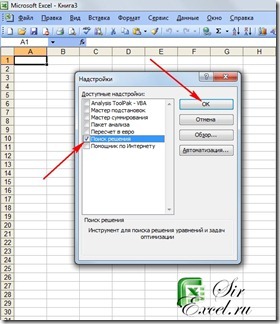
Как включить поиск решения в Excel 2003? Ответ очень прост. Для этого необходимо подключить надстройку Поиск решения. Для ее подключения перейдите в Сервис | Надстройки
Обратите внимание, что функция Поиск решения подключается в меню Надстройки, а не Настройки. Далее откроется окно доступных надстроек и вам необходимо поставить галочку напротив надстройки Поиск решения.
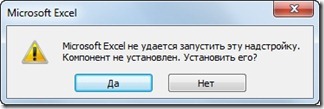
Если компонент Поиск решения не установлен, то Microsoft Excel предложит вам установить его.
После установки функции Поиск решения в Excel 2003, она станет доступной для использования.
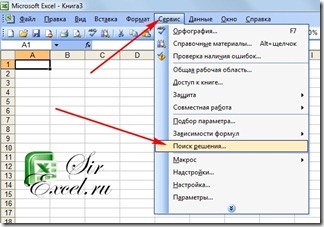
Где находится Поиск решения в Excel 2003? Ответ так же очень прост — в меню Сервис | Поиск решения
Содержание
- Надстройка Microsoft Excel «Поиск решения»
- Краткое описание надстройки
- Как установить надстройку?
- Как подключить надстройку?
- Где найти надстройку «Поиск решения» в Excel 2003/2007/2010?
- 2003 эксель поиск решения
Надстройка Microsoft Excel «Поиск решения»
Надстройка Microsoft Excel «Поиск решения» является мощным средством поиска решений и применяется при решении задач оптимизации. Процедура поиска решения позволяет находить оптимальное значение формулы содержащейся в ячейке, которую называют целевой. Процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке.
Краткое описание надстройки
Для получения заданного результата по формуле, процедура изменяет значения во влияющих ячейках. Для уменьшения интервала значений, используемых в модели, используются ограничения значений. Надстройка поиск решений является стандартной надстройкой Microsoft Office Excel и доступна сразу при установке Microsoft Office в целом или Microsoft Excel в частности.
Как установить надстройку?
Надстройку «Поиск решения» можно установить двумя способами. Стандартные надстройки, такие как «Поиск решения» и «Пакет анализа» устанавливаются вместе с MS Office или MS Excel. Если при первоначальной установке стандартная надстройка не была установлена, то следует запустить процесс установки повторно. Рассмотрим установку надстройки «Поиск решения» на примере Microsoft Office 2010. В версиях 2003 и 2007 все делается аналогично.
Итак, запускаем установочный диск с пакетом приложений MS Office 2010 и выбираем опцию «Добавить или удалить компоненты».


Как подключить надстройку?
Перед использованием необходимо предварительно включить надстройку, поставив галочку перед ее названием в списке доступных надстроек диалогового окна «Надстройки».
Вызов этого окна несколько различается в зависимости от версии приложения. Подробно об этом написано в отдельной статье «Как установить надстройку для Excel 2003/2007/2010/2013/2016?» со скриншотами для каждой версии приложения Excel, поэтому не буду повторяться. Да, добавлю лишь несколько слов о втором способе установки этой надстройки. Можно отыскать на просторах Интернета файл с названием Solver.xla (это и есть надстройка «Поиск решения») и произвести установку в соответствии с описанием по ссылке выше.
Где найти надстройку «Поиск решения» в Excel 2003/2007/2010?
После установки и подключения надстройки в Excel 2007/2010 на вкладке «Данные» появляется группа «Анализ» с новой командой «Поиск Решения». В Excel 2003 — появляется новый пункт меню «Сервис» с одноименным названием. Поиск решения — стандартная надстройка, существуют также и другие надстройки для Excel, служащие для добавления в MS Excel различных специальных возможностей.
Источник
2003 эксель поиск решения
Ограничения для выпуска продукции
Создание модели в Excel
1. Открыть табличный процессор Excel.
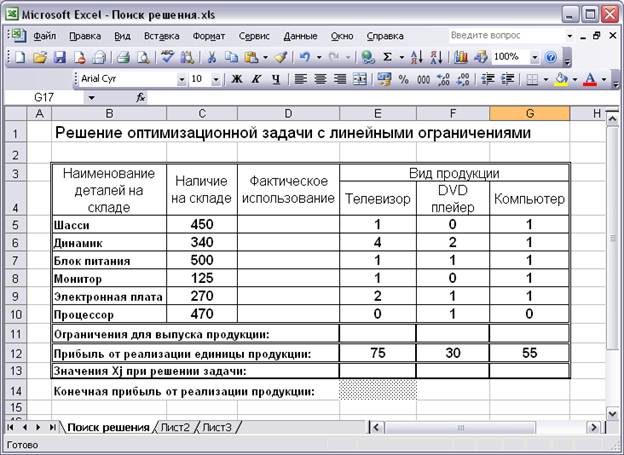
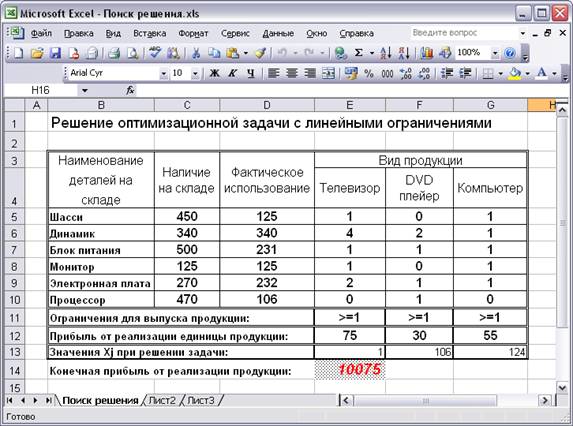
Подготовить начальную таблицу для размещения описаний задачи, исходных данных, ограничений, коэффициентов целевой функции, место для проведения вычислений и сохранения результатов. Начальная таблица, как она будет выглядеть в Excel , представлена на рис. 1. Столбец D введен для занесения результатов в ячейки D 5: D 10 . В этих ячейках будут отображаться результаты вычислений, т.е. сколько на самом деле будет задействовано единиц каждого вида ресурса для выпуска всей номенклатуры продукции. Добавить в таблицу новые обозначения, которые понадобятся для ввода начальных значений и вывода результатов. Для этой цели:
· в строке 11 (ячейки E 11: G 11 ) ввести коэффициенты для целевой функции, ее название — «Прибыль от реализации единицы продукции»;
· в строке 12 создать заголовок – «Значения Xj при решении задачи», ячейки E 12: G 12 понадобятся для ввода формул;
· ячейку E 13 можно выделить, в которой будет формироваться результат, поэтому в строке 13 сделана запись – «Конечная прибыль от реализации продукции», это и есть значение целевой функции.
2. Ввести формулы в таблицу с начальными данными. Для решения оптимизационной задачи методом линейного программирования необходимо математическую модель записать в терминах Excel , т.е. в определенные ячейки предварительно необходимо ввести формулы. В таблице 2 указаны координаты ячеек для рассматриваемого примера, математическая запись уравнений и формулы, которые введены в соответствующие ячейки в табличном процессоре Excel .
Таблица 2. Перечень формул для установки в ячейках таблицы Excel
=$E$13*E 6 +$F$13*F 6 +$G$13*G 6
=$E$13*E 7 +$F$13*F 7 +$G$13*G 7
=$E$13*E 8 +$F$13*F 8 +$G$13*G 8
=$E$13*E 9 +$F$13*F 9 +$G$13*G 9
=$E$13*E 10 +$F$13*F 10 +$G$13*G 10
3. Работа с надстройкой Excel – Поиск решения
· Вызвать окно: Поиск решения (рис. 1), нажать на кнопку 
· Ввести начальные значения Xj в ячейки E 13: G 13 . Например, по двадцать единиц каждого вида изделия.
· Выделить курсором ячейку E 14 с целевой функцией.
· Выбрать команду в меню Сервис-Поиск решения.
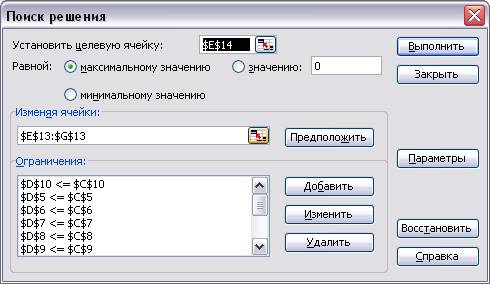
· В открывшемся диалоговом окне – Поиск решения, заполнить окна: Изменяя ячейки и Ограничения (можно проверить в диалоговом окне факт установки курсора на целевой ячейке, если требуется, то ее положение можно изменить). На рис. 3 показано всплывающее диалоговое окно Поиск решения, в котором проведены все перечисленные подготовительные действия.
· Установить диапазон ячеек в строке всплывающего окна: Изменяя ячейки, в которых будет отображаться результат с количеством номенклатуры Xj изделий. В рассматриваемом примере, это будут ячейки E 13: G 13 , которые должны быть фиксированными (перед координатами ячее ставится знак $).
· Отметить селекторную кнопку: Равной максимальному значению, т.к. определяется максимальное использование ресурсов.
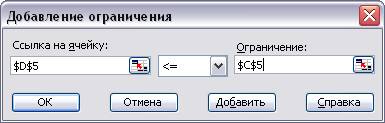
· В окно с наименованием Ограничения последовательно ввести все ограничения для уравнений модели. В данном примере ячейки C 5: C 10 содержат количество деталей на складе, которые потребуются для выпуска всей номенклатуры продукции, а в ячейки D 5: D 10 были внесены формулы модели по каждому виду комплектующей, следовательно, суммарное количество используемых деталей не должно превышать величину, указанную в правой части уравнения. Для ввода ограничений, необходимо нажать на кнопку 
· Если требуется ввести еще ограничения, то нажать на кнопку 
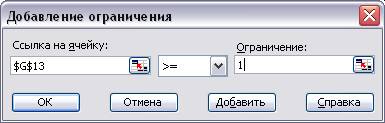
· Ввести ограничения на выпуск номенклатуры продукции в ячейки E 13: G 13 (в примере всего три вида продукции). Так, в качестве примера, на рис. 5 показано диалоговое окно для добавления ограничений, в котором указано, что вычисляемое значение в ячейке G 13 должно быть более 1 единицы (это условие записано в исходной таблице для изделия – Компьютеры).
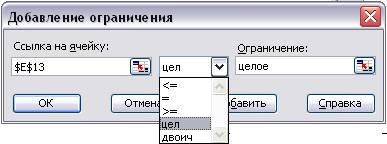
· Ввести ограничения на форму представление результатов. В данной постановке задачи подразумевается, что количество изделий не может быть дробной величиной, а должны отображаться только целыми числами, следовательно, при выполнении расчетов, это обстоятельство необходимо учитывать. На рис. 6 показано диалоговое окно для добавления ограничений, в котором для ячейки E 13 (в ней отображается количество единиц изделия), установлено условие ‘ цел’, что означает целочисленное решение. В раскрывающемся списке выбирается необходимое условие.
- Установить параметры для оптимизационной задачи, для чего в диалоговом окне: Поиск решения, нажать на кнопку
. После того, как откроется диалоговое окно с наименованием Параметры поиска решения, представленное на рис. 7.
- В окне установить пометку: Линейная модель, и закрыть кнопкой ОК.
· Провести вычисления, для чего в диалоговом окне Поиск решения, нажать на кнопку 
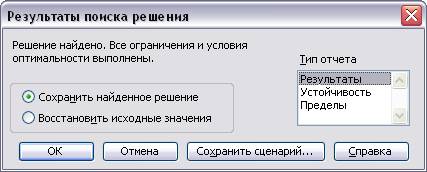
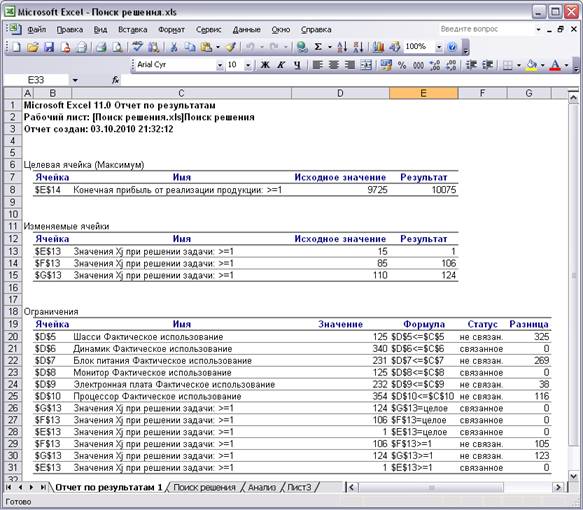
Программа формирует три типа отчетов: Результаты, Устойчивость и Пределы. Если отметить любой из них или все вместе, а затем вызвать, то можно провести анализ исходных данных и конечных результатов, об этом будет сказано ниже. В том случае, если в окне Результаты поиска решения появится сообщение: « Ошибка в модели. Проверьте правильность значений в ячейках и ограничениях», то отчеты получить невозможно, а следует открыть окно Поиск решения (рис. 4), и проверить правильность установки знаков ограничений, наименования ячеек, в которых должна быть вычислена целевая функция и установлены начальные значения изменяемых ячеек. На рис. 9 показан лист Excel , который содержит исходные данные и результаты решения оптимизационной задачи методом линейного программирования по заданным начальным значениям и тем условиям, которые были установлены, в соответствии с постановкой задачи.
Анализ результатов: После того, как будет получено решение, требуется проанализировать результаты. Анализ помогает выработать управленческое решение, направленное на дальнейшую стратегию деятельности предприятия.
· Принятие решения о производственной программе может быть направлено на то, что следует изменить некоторые условия, например, предприятие производитель имеет обязательства перед потребителем о поставке в текущем периоде 15 телевизоров. Следовательно, условие в ячейке E 13 должно быть изменено (вместо 1 следует установить 15).
· Принятие решения о закупках комплектующих проводится в соответствии с полученным результатом, из которого видно, что при принятии программы выпуска номенклатуры изделий в соответствии с оптимальным планом потребуется определенное количество комплектующих.
· Принятие решения о цене, на выпускаемую продукцию, обосновывается при изменении прибыли (снижении цены на продукцию), для чего можно провести новые расчеты, изменив только величину прибыли от реализации единицы продукции.
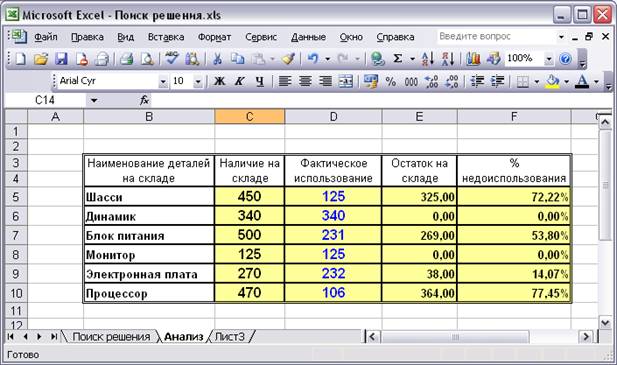
На рис. 10 представлена таблица с результатами проведенных вычислений по заданным параметрам с добавлением дополнительных граф, в которых отражается информация о тех потерях, которые получит предприятие производитель.
Кроме того, для анализа можно использовать стандартные средства, а именно при заполнении окна Результаты поиска решения (рис. 8), достаточно отметить тип отчета (напомним, что при решении целочисленных задач отчет по устойчивости и отчет по пределам, не составляется). Когда будет отмечен тип отчета и нажата кнопка ОК, тогда в текущей книге добавится новый лист (появится ярлык) с наименованием: Отчет по результатам. Внешний вид отчета показан на рис. 11. Отчет с наименованием Результаты, который формируется системой, состоит из трех таблиц. Первые две таблицы понятны и не требуют комментариев.
Последняя таблица похожа на ту, которая была построена самостоятельно (рис. 11). При анализе результатов достаточно взглянуть на столбец Статус таблицы на рис. 11. В том случае, если ресурс был использован полностью, тогда система записывает в соответствующую ячейку текстовое сообщение «Связанное», в противном случае появляется текст «Не связан». Следовательно, получен ответ о недоиспользованных ресурсах, что позволяет внести новые ограничения и решить задачу заново.
Задание: Провести изменения в условиях задачи, заменив количества видов продукции и наличия деталей на складе. Попробуйте применить надстройку Подбор параметров для изменяемой ячейки с количеством деталей на складе для условия, что конечная прибыль должна составлять 15000 руб.
Вопросы для самопроверки
1. Каким образом представляют условия постановки задачи с многими неизвестными?
- Почему в условия решения задачи вводят дополнительные переменные вида Xi > 0?
- Как вызвать инструментальное средство для решения оптимизационных задач Поиск решения?
- Какие шаги следует предпринять, чтобы ввести параметры уравнений и ограничений в окне Поиск решения?
Источник
Начало работы
В данном разделе мы рассмотрим, как можно решить производственную задачу в
программе Microsoft Excel версии 2003 или более низкой. Если у вас более новая
версия программы Microsoft Excel, то посмотрите сюда.
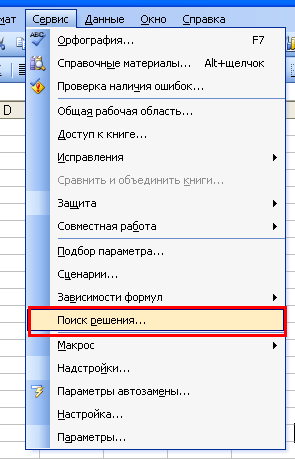
Итак, запустим Microsoft Excel, и перейдем в меню «Сервис». Там должен быть
пункт «Поиск решения», как на картинке:
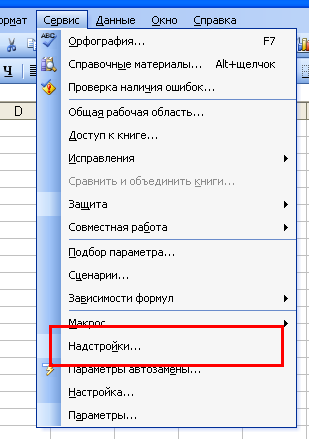
Если же этого пункта нет, то необходимо включить соответствующую надстройку.
Для этого откроем меню «Сервис», и выберем пункт «Надстройки»:
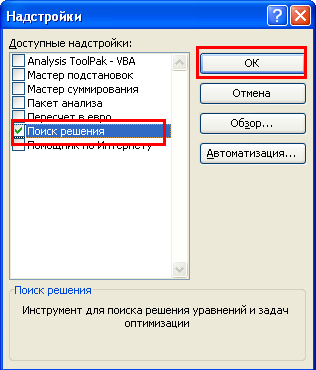
Появится следующее окно, в котором необходимо отметить галочкой необходимую надстройку
(Поиск решения), и нажать кнопку «ОК».
После этого может сразу произойти установка надстройки, а может быть
показано следующее сообщение:
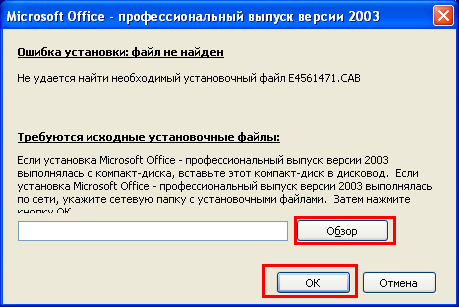
Нужно нажать на кнопку OK. Начнется установка, и, возможно она попросит у вас
указать, где находятся установочные файлы Microsoft Office:
Нажмите на кнопку «Обзор», укажите папку, в которой находится дистрибутив программы
Microsoft Office, и нажмите на кнопку OK. Надстройка будет установлена. Соответствующий
пункт меню появится в меню «Сервис»
Полезная страница? Сохрани или расскажи друзьям
Пример решения ЗЛП в Эксель 2003
Возьмем ту же задачу, которую мы решали в предыдущем разделе, и попытаемся
решить с помощью компьютера:
| Ресурс | Изделие A | Изделие B | Изделие C | Сколько ресурса на складах |
| R1 | 1 | 2 | 3 | 35 |
| R2 | 2 | 3 | 2 | 45 |
| R3 | 3 | 1 | 1 | 40 |
| Прибыль | 4 | 5 | 6 |
Как мы помним, ограничения и целевая функция выглядят следующим образом:
$$begin{array}{l}
left{ {begin{array}{*{20}{c}}
{{x_A} + 2{x_B} + 3{x_C} le 35}\
{2{x_A} + 3{x_B} + 2{x_C} le 45}\
{3{x_A} + {x_B} + {x_C} le 40}
end{array}} right.\
{x_A},{x_B},{x_C} ge 0\
F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C} to max
end{array}$$
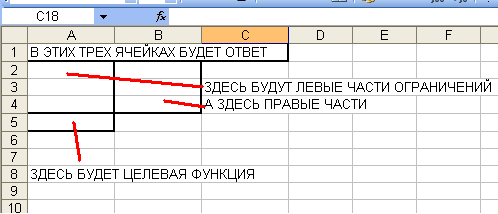
Мы будем заносить данные в следующие ячейки листа Excel:
Итак, начнем заполнение. В верхние три ячейки нужно занести ответ, то есть,
количество производимых изделий A, B и C. Так как ответ мы не знаем (а иначе
зачем бы мы задачу решали), то пока занесем туда три нуля:
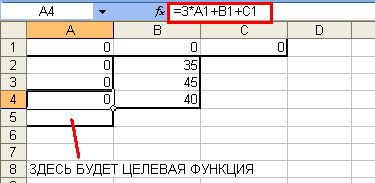
Занесем левые и правые части ограничений в соответствующие ячейки. Например,
для первого ограничения ${x_A} + 2{x_B} + 3{x_C} le 35$ нам нужно занести в ячейку
A2 формулу «=A1+2*B1+3*C1», а в ячейку B2 — правую часть ограничения — 35. Точно
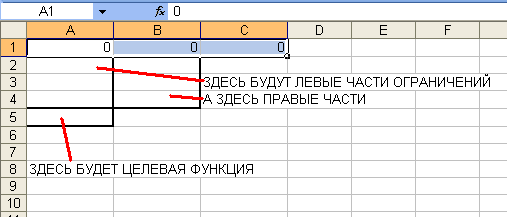
так же занесем и два других ограничения. Не стоит пугаться, что в ячейках A2-A4
пока будут нули — это естественно, так как пока наше «решение» состоит в том,
чтобы не производить ни одного изделия. Должно получиться следующее (красным
цветом выделено значение ячейки A4, то есть, третье ограничение $3{x_A} + {x_B} + {x_C} le 40$):
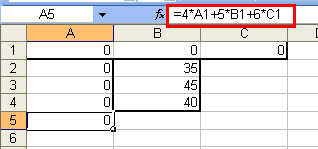
Точно так же, в ячейку A5 занесем формулу для целевой функции $F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C}$ —
в Excel это будет формула «=4*A1+5*B1+6*C1». Точно так же, не обращаем внимания,
что результатом будет 0 — это естественно, ведь целевая функция представляет из
себя прибыль предприятия, а раз мы ничего не производим, то естественно, получаем
нулевую прибыль:
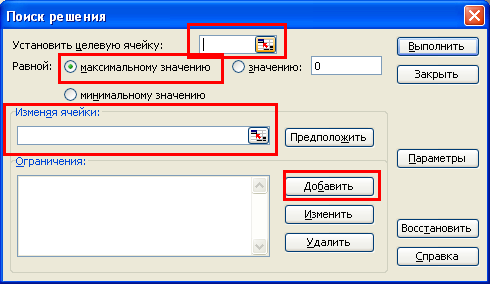
Мы занесли все необходимые данные, теперь необходимо выполнить поиск решения. Для
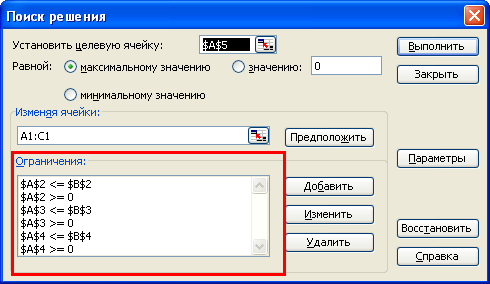
этого на вкладке «Данные» нажимаем кнопку «Поиск решения». Видим следующее окно:
В поле «Установить целевую ячейку» записываем A5, так как именно в ячейке A5
у нас записана целевая функция. В следующей строке выбираем «Максимальное значение»,
так как нам необходимо максимизировать целевую функцию, то есть, прибыль. В поле
«Изменяя ячейки» записываем A1:C1, так как в ячейках A1, B1 и C1 у нас количество
производимых товаров, которые необходимо подобрать. Теперь необходимо задать
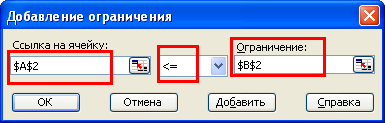
ограничения. Для этого нажимаем на кнопку «Добавить», и пишем (для первого ограничения)
следующее:
То есть, говорим, что значение ячейки A2 (первое ограничение) должно быть «меньше
или равно» значению ячейки B2 (правой части первого ограничения). Нажимаем OK, и
ограничение добавится в список. Таким же образом добавляем два других ограничения,
а также еще три ограничения — что наши переменные должны быть больше или равны
нулю. Должно получиться следующее:
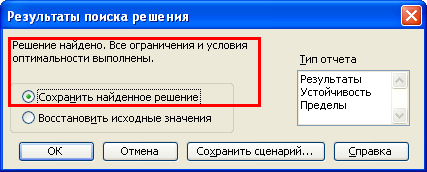
Задача почти решена. Просто нажимаем кнопку «Выполнить», и появляется окно,
в котором нам сообщают, что задача решена (решение найдено), а также спрашивают,
хотим ли мы его сохранить:
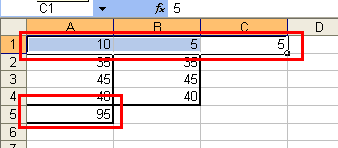
Нажимаем OK, и видим решение в ячейках A1, B1, C1:
В ячейке A1 мы видим число 10 — число изделий A, которые необходимо произвести,
в ячейке A2 — число 5 — число изделий B, которые необходимо произвести, а в ячейке
A3 — число 5 — число изделий C, которые необходимо произвести. То есть, мы получили
решение (10;5;5) — такое же, как и в предыдущем разделе. Кроме того, в ячейке A5
мы видим максимальное значение целевой функции — тоже, такое же, как и в предыдущем
разделе. Задача решена верно.
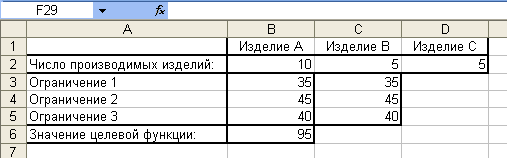
Конечно, мы решили задачу совсем без оформления. Если вам нужно решить такую
задачу для сдачи в университет, то вы можете оформить ее, например, так:
Итоги
Мы научились решать производственную задачу с помощью надстройки Excel под
названием «Поиск решения». В следующем разделе мы рассмотрим решение целочисленной
производственной задачи, то есть задачи ЛП с дополнительным ограничением —
все значения переменных должны быть целыми.
Далее: 2.1.5. Целочисленное решение ЗЛП
Полезное по теме
- Готовые решений задач ЛП в Excel
- Решенные контрольные по линейному программированию
- Заказать контрольную по ЛП
Функция поиска решения пригодится при необходимости определить неизвестную величину
Табличный процессор Microsoft Excel может выполнять не только простые операции с числами (сложение, умножение), расчет суммы или среднего значения. У этой программы имеется очень мощный функционал, который позволяет решать задачи разной сложности. Например, Эксель может оптимизировать значения в таблице, подставляя их таким образом, чтобы они удовлетворяли определенным критериям. Для этого программа оснащена специальными средствами для анализа данных: первый — это подбор параметра, а второй — поиск решения.
Видео пример поиска решения в Excel
Функция «Подбор параметра»
Подбор параметра в Excel позволяет подобрать какой-то определенный параметр, значение которого неизвестно. Чтобы было понятней, можно привести такой пример. Допустим, есть прямоугольник со сторонами A и B. Известно, что общая площадь этой фигуры составляет 400 квадратных метров, а сторона B — 40 метров. Сторона A неизвестна и, соответственно, нужно ее найти. Для решения такой задачи необходимо заполнить рабочий лист программы теми данными, которые уже известны. Для этого нужно создать таблицу с 2 колонками и 3 строками (диапазон ячеек A1:B3).
Первый столбец будет содержать название сторон прямоугольника и букву, обозначающую его площадь (т.е. A, B и S). А во втором столбце необходимо указать известные значения:
- в соседней ячейке для стороны B (ячейка B2) написать — 40 (значение для стороны А остается пустым);
- а в соседнем поле для площади прямоугольника (поле B3) написать следующую формулу: = B1*B2 (т.е. формула для расчета площади).
Если все было сделано правильно, то в поле B3 должно быть значение 0. Затем надо выделить эту ячейку и выбрать в панели меню пункты: «Сервис — Подбор параметра». В появившемся окне нужно указать то значение, которое должно быть получено в результате, т.е. 400. В строке «Установить в ячейке» будет указано поле «B3»: менять его не нужно, так и должно быть (сюда будет выведен результат). А в строке «Изменяя значение» необходимо выбрать неизвестный параметр, т.е. поле B1. После нажатия кнопки «ОК» программа выдаст результат: сторона А — 10 метров, а в поле общей площади прямоугольника будет указано число 400.
Это была очень простая задача на уровне 3 класса, но с помощью такой функции можно решать и более сложные задачи. Например, вы решили приобрести себе автомобиль в кредит. Вы точно знаете, что сможете выплачивать ежемесячную выплату в размере 1000 $ (но не больше), а также, что банк выдает автокредит с процентной ставкой 6,5%. Суть задачи заключается в следующем: «Какова максимальная сумма машины, которую можно взять в кредит на таких условиях?». То есть теперь программа будет искать стоимость автомобиля, отталкиваясь от того, что ежемесячный платеж не должен превышать 1000 $. Такой пример является уже более сложным, а также более практичным, нежели расчет площади прямоугольника.
Надстройка «Поиск решения»
Параметры инструмента поиск решения
Еще одним средством анализа данных в Экселе, с помощью которого решают похожие задачи, является надстройка«Поиск решения». Если в первом случае Excel мог подбирать значение только в одной ячейке, то с помощью этой надстройки можно оптимизировать одновременно несколько значений. Эта функция имеется во всех версиях Excel, но по умолчанию она отключена. Чтобы включить эту надстройку в Excel 2003 версии, необходимо в панели меню выбрать пункты «Сервис — Надстройки» и поставить галочку напротив пункта «Поиск решения». После этого эту надстройку можно вызвать через этот же пункт «Сервис». В новых версиях существует другой способ: надо щелкнуть пункты «Файл — Параметры — Надстройки», затем выбрать «Надстройки Excel — Перейти» и поставить галочку напротив нужной строки.
Поиск оптимального решения в Excel
Решение задач оптимизации в Excel чаще всего осуществляется именно с помощью надстройки «Поиск решения».Например, с помощью этой функции можно решить транспортную задачу. Как известно, главной целью транспортной задачи является расчет оптимального маршрута, чтобы затраты на перевозки груза при этом были минимальными. В таких задачах имеется уже не один, а одновременно несколько значений, которые нужно рассчитывать. Как правило, обычно известно лишь количество фирм, количество поставщиков, общие запасы товара и потребность каждой фирмы в этом товаре (кому сколько нужно). И нужно рассчитать, как весь этот груз развести, чтобы стоимость перевозок была минимальной.
Процедура поиска оптимального значения в Excel осуществляется не так уж и просто, но принцип примерно тот же, что и в первом случае: пользователь указывает диапазон изменяемых ячеек и поле, куда выводить итоговый результат, а все остальное программа сделает сама. Вот такими способами осуществляется решение задач оптимизации в табличном процессоре Microsoft Excel.
Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике
Содержание
- Как включить функцию “Поиск решения”
- Подготовительный этап
- Применение функции и ее настройка
- Заключение
Как включить функцию “Поиск решения”
Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:
- Открываем меню “Файл”, кликнув по соответствующему названию.
- Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
- Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
- На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
- Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.
Подготовительный этап
Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.
Итак, у нас есть данные про продаже товаров, представленные в табличном виде.
И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.
Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.
Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.
Применение функции и ее настройка
Формула готова. Теперь нужно применить саму функцию.
- Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
- Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
- Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
- Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
- Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
- Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
- После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
- Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
- В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
- Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
- После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
- Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
- Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
- Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
- Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
- Теперь наша таблица полностью готова в соответствии с поставленной задачей.
Заключение
Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.


 . После того, как откроется диалоговое окно с наименованием Параметры поиска решения, представленное на рис. 7.
. После того, как откроется диалоговое окно с наименованием Параметры поиска решения, представленное на рис. 7.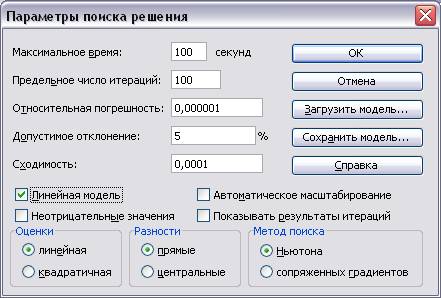















 Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK. Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.






