Содержание
- Процедура перемножения матриц
- Способ 1: функция МУМНОЖ
- Способ 2: использование составной формулы
- Вопросы и ответы
Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
=МУМНОЖ(массив1;массив2)
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
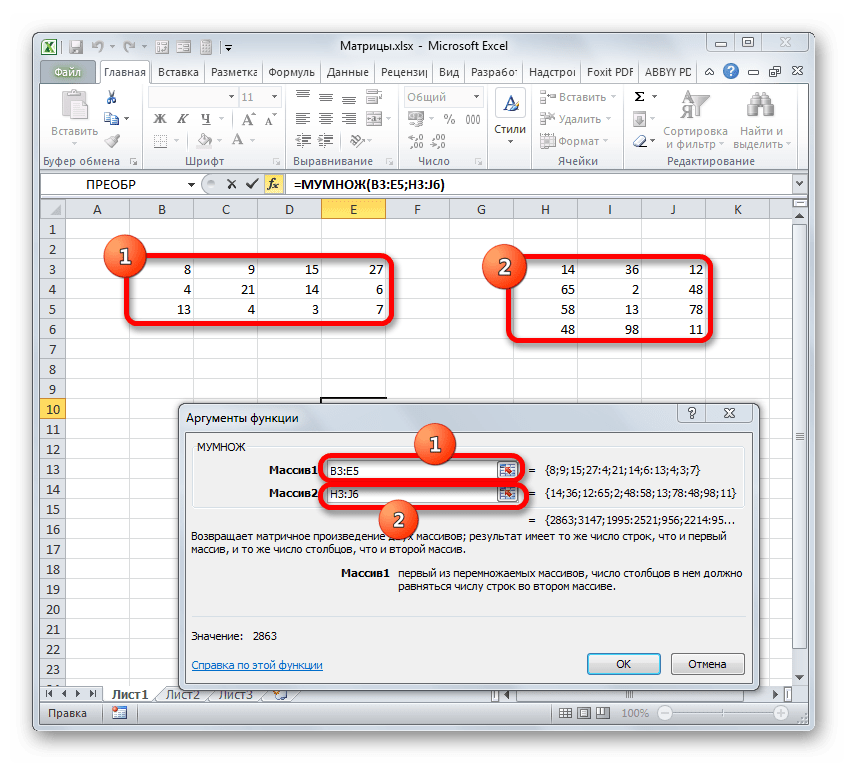
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
- Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.
- Будет выполнен запуск окна аргументов требуемой функции. В этом окне имеется два поля для ввода адресов матричных массивов. Ставим курсор в поле «Массив1» и, зажав левую кнопку мыши, выделяем на листе всю область первой матрицы. После этого её координаты отобразятся в поле. Ставим курсор в поле «Массив2» и аналогичным образом выделяем диапазон второй матрицы.
После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки «OK» жмем комбинацию кнопок Ctrl+Shift+Enter.
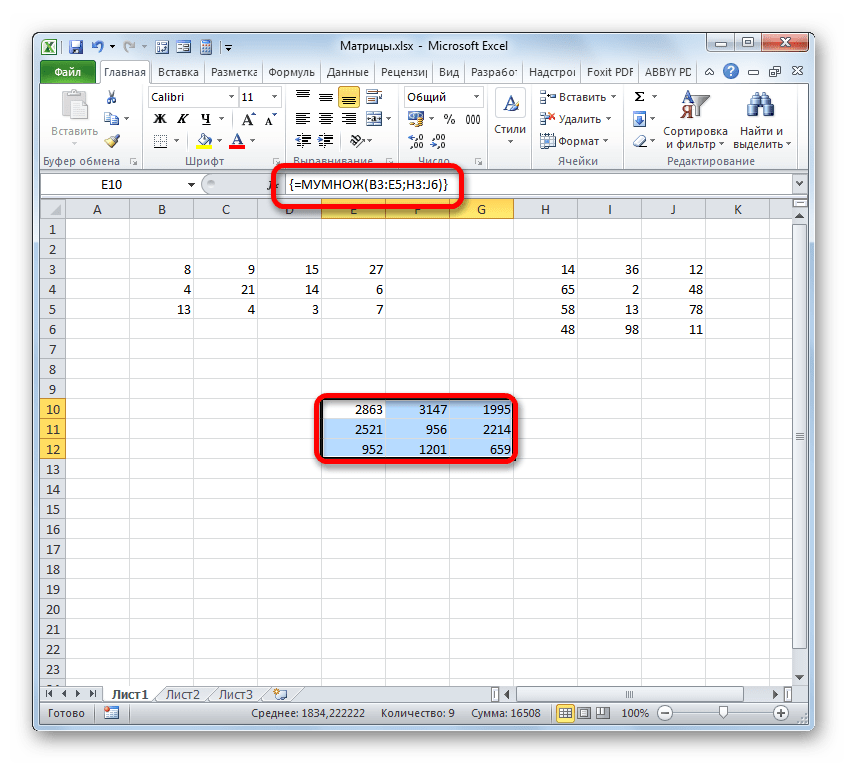
- Как видим, после этого предварительно выделенный диапазон был заполнен данными. Это и есть результат умножения матричных массивов. Если взглянуть на строку формул, после выделения любого из элементов данного диапазона, то мы увидим, что сама формула обернута в фигурные скобки. Это и есть признак функции массива, который добавляется после нажатия сочетания клавиш Ctrl+Shift+Enter перед выводом результат на лист.
Урок: Функция МУМНОЖ в Экселе
Способ 2: использование составной формулы
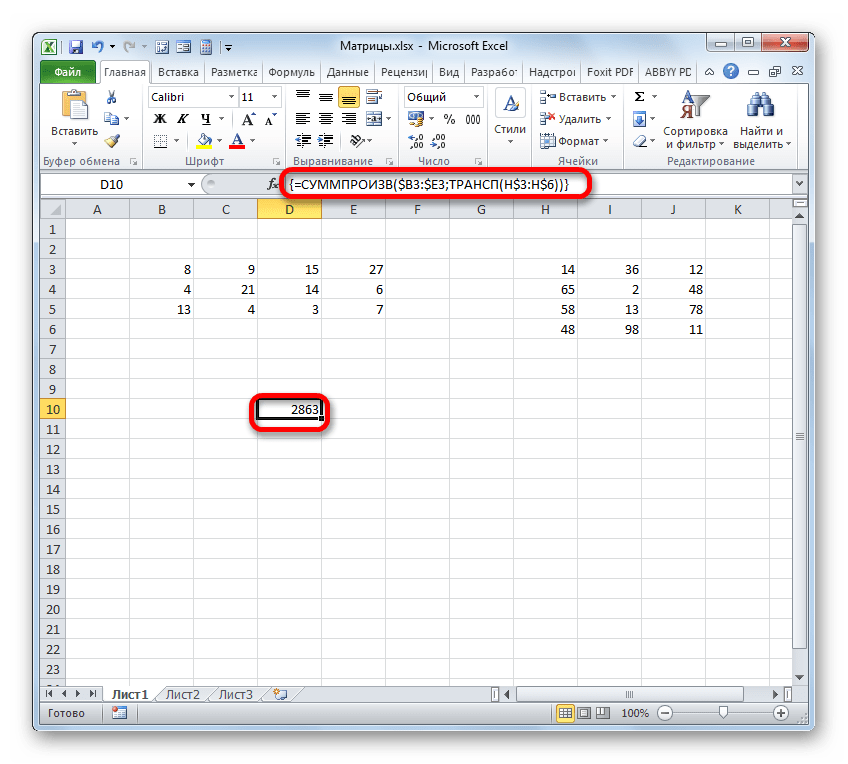
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
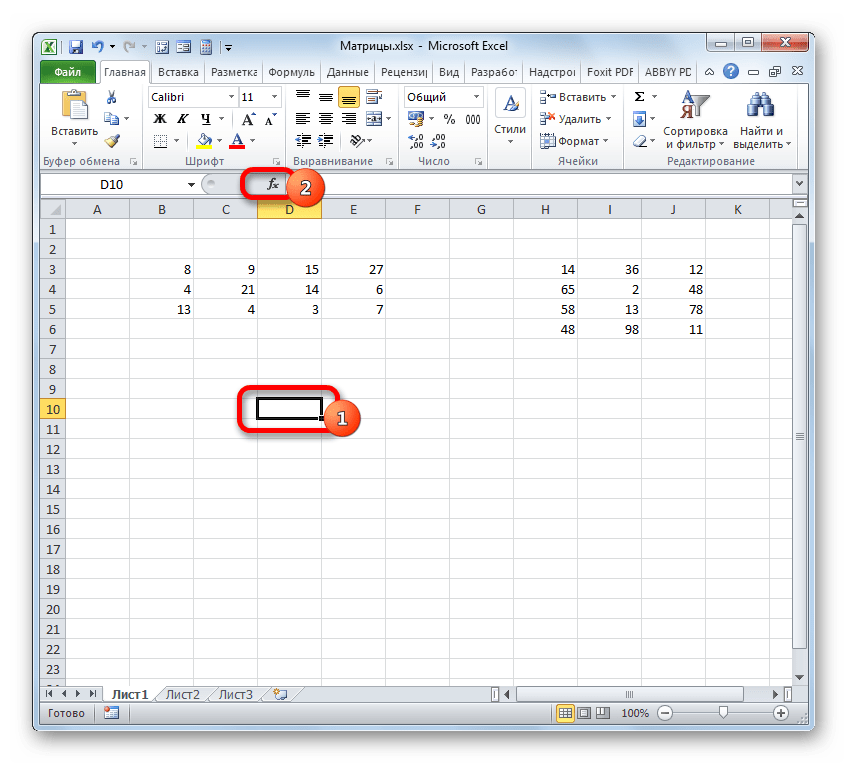
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».
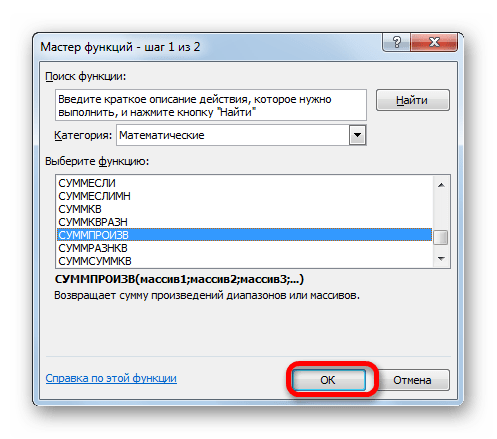
- Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».
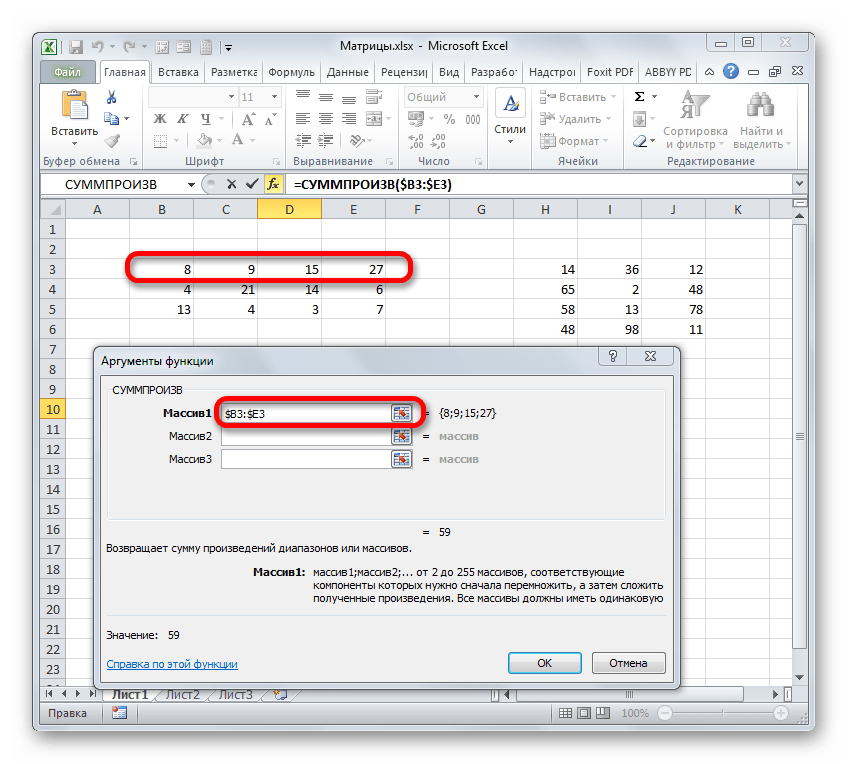
- Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:
=СУММПРОИЗВ(массив1;массив2;…)В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.
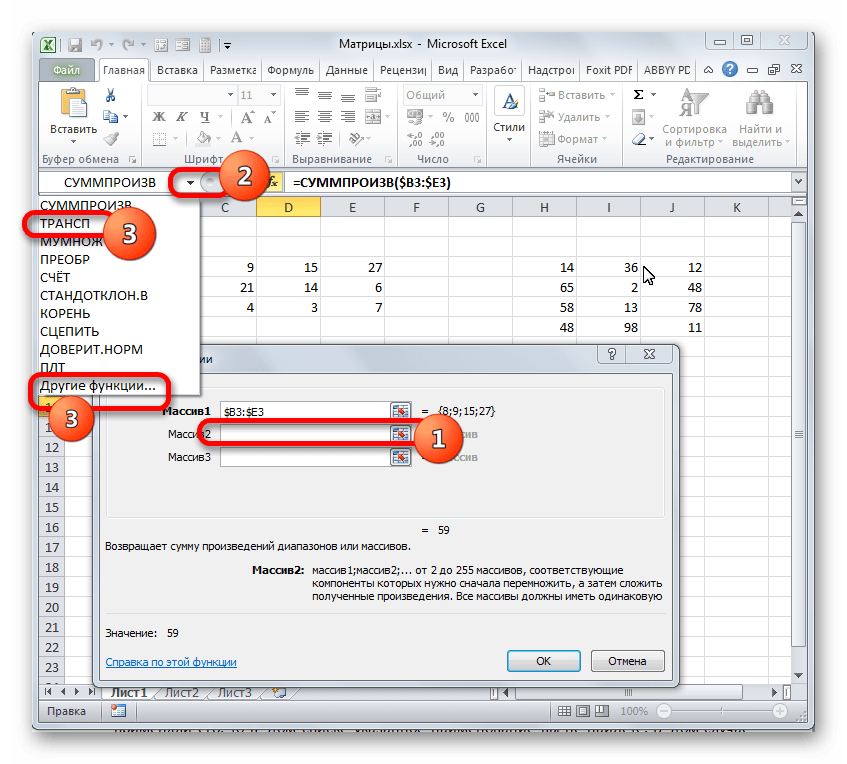
- После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.
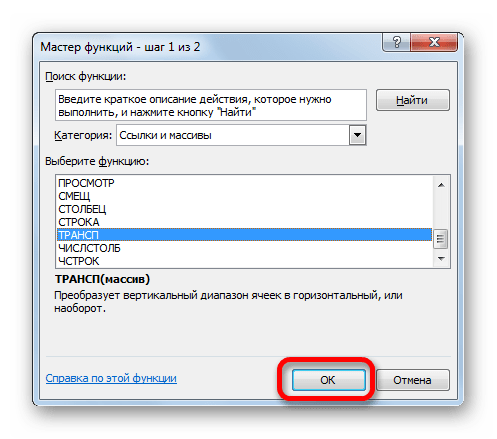
Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту «Другие функции…».
- Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».
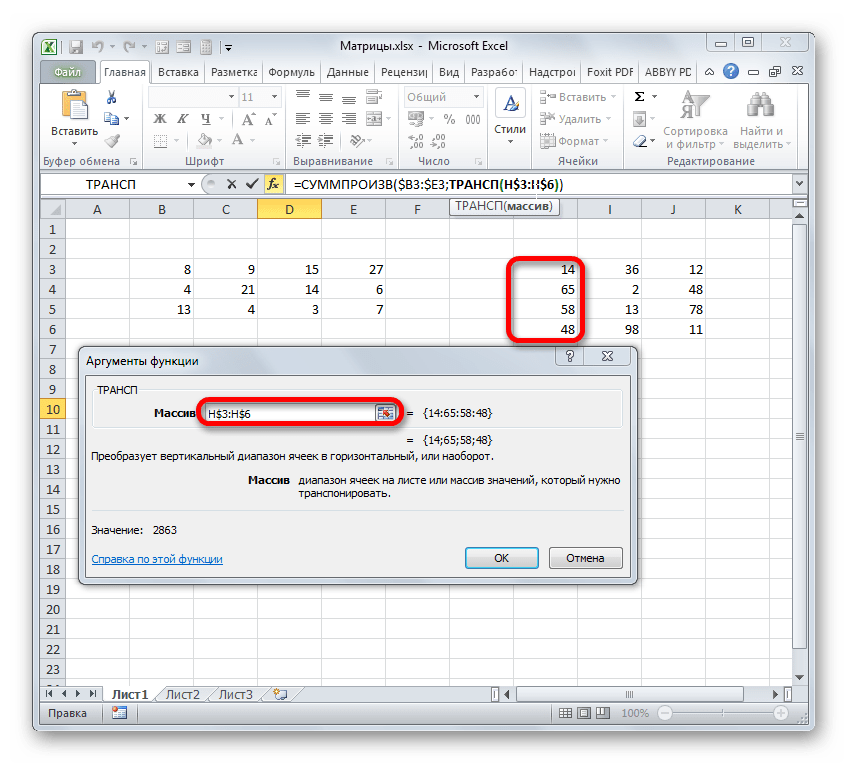
- Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:
=ТРАНСП(массив)То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.
- Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.
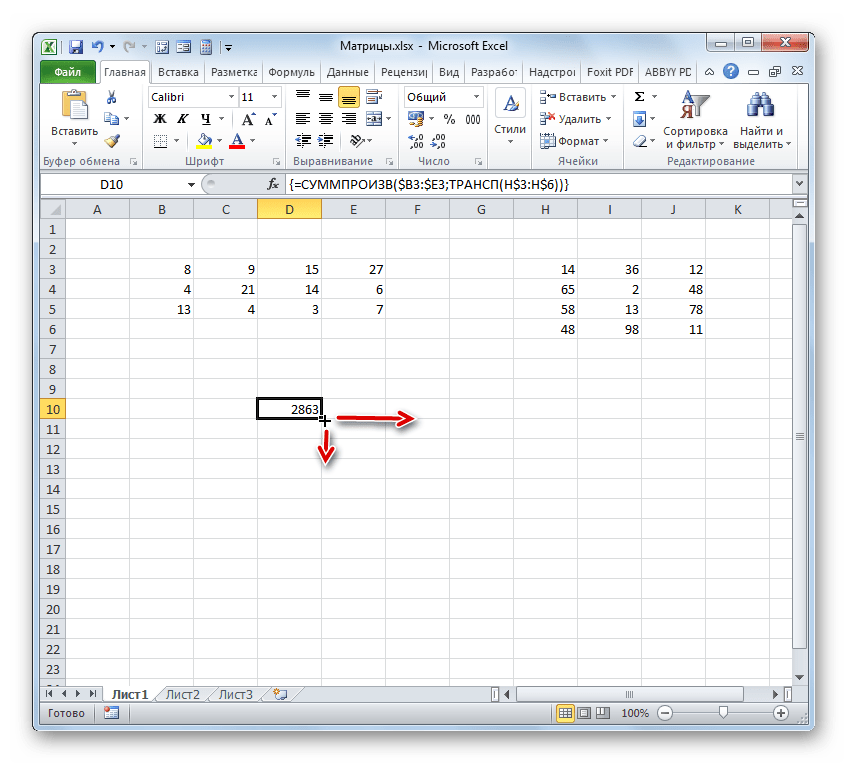
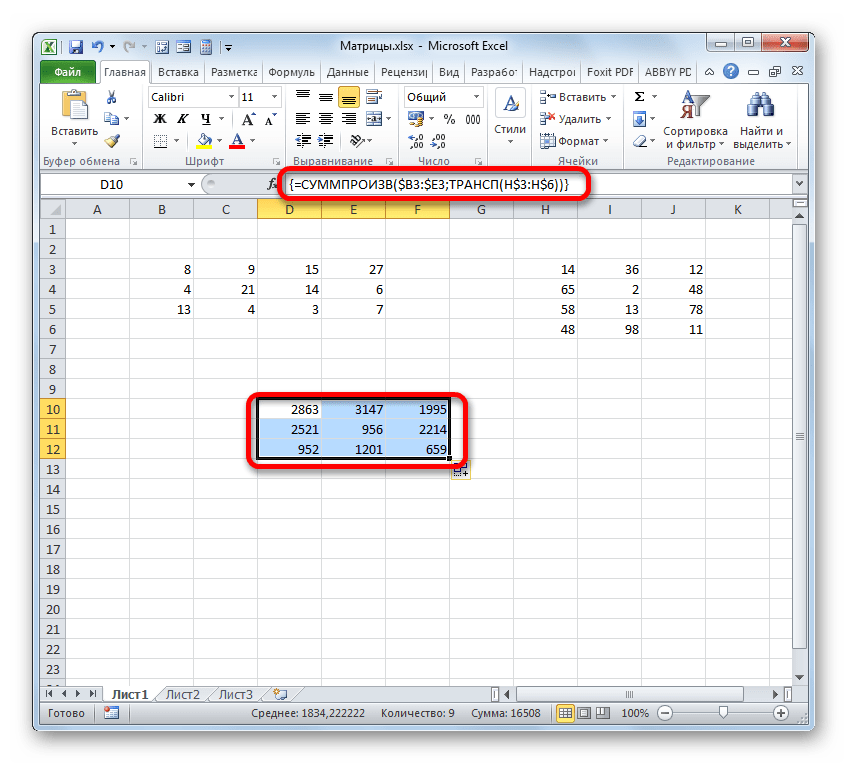
- Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.
Для копирования прибегнем к использованию маркера заполнения. Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.
- Как видим, выделенный диапазон заполнен данными. Если их сравнить с тем результатом, который мы получили благодаря применению оператора МУМНОЖ, то увидим, что значения полностью идентичны. Это означает, что умножение двух матриц выполнено верно.
Урок: Работа с массивами в Экселе
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Еще статьи по данной теме:
Помогла ли Вам статья?
В этой статье рассмотрены операции умножения матриц с помощью функции
МУМНОЖ()
или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Операция умножения двух матриц
А
и
В
определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.
Произведение матрицы
А
порядка P x
N
и матрицы
В
порядка
N
x Q — это такая матрица
С
порядка P x Q, у которой каждый элемент равен сумме произведений элементов
i-ой
строки матрицы
А
на соответствующие элементы
j-ого
столбца матрицы
В
, то есть:
Для умножения матриц в MS EXCEL существует специальная функция
МУМНОЖ()
, которую нужно вводить как
формулу массива
.
Рассмотрим сначала умножение квадратных матриц 2 х 2.
Разместим матрицы в диапазонах
А8:В9
и
D8:E9
(см.
файл примера
).
Результат, также матрицу 2 х 2, будем вводить в диапазон
H8:I9
.
Для этого:
-
выделите указанный диапазон
H8:I9
-
поставьте курсор в
Строку формул
(или нажмите клавишу
F2
) -
введите формулу
=МУМНОЖ(A8:B9;D8:E9)
-
нажмите
CTRL+SHIFT+ENTER
Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо б
о
льший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу
DEL
).
Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите
F2
, исправьте формулу и нажмите
CTRL+SHIFT+ENTER
.
Альтернативной формулой для перемножения матриц является
формула массива
=СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9))
. Введите формулу в верхнюю левую ячейку диапазона и нажмите
CTRL+SHIFT+ENTER
. Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция
МУМНОЖ()
вернет ошибку #ЗНАЧ!
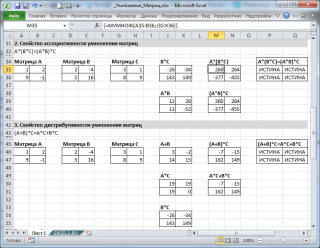
В
файле примера
также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.
Три способа умножения матриц в Excel — fastai part-2, lesson-8
Перевод
Ссылка на автора
Часть-2 изФастай «Из фондов»наконец-то вышел. Я не помню, когда в последний раз я был так взволнован по поводу MOOC. Как только курс был обнародован, я начал копаться в нем, чтобы углубить свое понимание глубокого обучения и основополагающих концепций.
На этот раз я решил последовать совету Джереми и Рэйчел и написать блоги. Эта конкретная статья объясняетразличные методы умножения матриц,что Джереми реализует в Уроке-8. Я буду использоватьМайкрософт Эксельдля иллюстрации.
Итак, начнем!
Умножение матриц
Отличное и интерактивное место для понимания умножения матриц, на которое ссылается Джереми, доступно по адресу:
По сути, как видно из изображения, мы берем транспонирование второй матрицы, умножаем и складываем элементы вместе, чтобы получить результат. Как пример, самый первый пункт15в результирующей матрице происходит от1*2 + 6*2 + 1*1 = 2 + 12 + 1 = 15,
Хотя это объяснение визуально приятно, по моему скромному мнению, его трудно преобразовать в код. Так что давайте использовать Excel и понимать матричное умножение по-другому!
Рассмотрим две матрицыа такжеВразмера4x3а также3x4,
Примечание: я буду использовать жирный шрифта такжеВсослаться на матрицы в этой статье. Обычная практика — ссылаться на векторы и матрицы, используя жирный шрифт.
Из изображения, которое мы видели раньше, если вы помните, мы взяли транспонированиеВи умноженные строкис колоннамиВчтобы получить результирующую матрицу. Скорее, давайте пропустим этот шаг, сделав транспонирование на этот раз, и сразу умножим строки и столбцы.
Поэтому строка 0 изумножается на столбец 0Впоэлементные и результирующие поэлементные продукты добавляются для получения первого элемента в результирующей матрицеСв положении[0][0],
Вот как это выглядит в Excel:
Точно так же мы получаемC[0][3]поэлементно умножая строку 0 изи кол 3 изB.В Excel это выглядит так:
И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой ящик вСчтобы получить окончательный результат.
Вот и мы! Вот так мы делаем матричное умножение! Это было легко, не так ли? Мы теперь не только поняли умножение матриц, но и внедрили его в Excel! Как это круто?
Я лично считаю, что теперь вы готовы работать с некоторыми правилами, связанными с умножением матрицMatMul):
- Позволять
ar,acбыть количеством строк и столбцов вA.Точно так же, пустьbr, bcбыть количеством строк и столбцов вB.Тогда для выполнения умножения матриц необходимо, чтобыac == br, Зачем? Итак, как вы видели в Excel, мы умножили строки и столбцы поэлементно, а затем добавили промежуточные продукты, чтобы получить конечный результат. Если есть несоответствие в размерах, и один вектор длиннее другого, мы больше не можем выполнять поэлементное умножение! - Размеры результирующей матрицы всегда будут
ar,bc, То есть количество строк исходит оти количество столбцов исходит отB.
Способ 1: использование 3-х циклов FOR
Вот еще один отказ от ответственности, при реализации умножения матриц в Excel, мы не только поняли это, но и повторили первый метод Джереми, который использовал 3 цикла FOR. Вот как это выглядит в коде:
def matmul1(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar, bc)
for i in range(ar):
for j in range(bc):
for k in range(ac): #or br
c[i,j] += a[i,k]*b[k,j]
return c
Надеюсь, теперь вы сможете лучше понять это. Если нет, то сейчас самое время сделать паузу, поэкспериментировать с кодом и посмотреть, что на самом деле происходит. Я обещаю вам, это так же, как наша версия Excel!
Хорошо, я предполагаю, что вы потратили некоторое время на размышления о коде, поэтому давайте обсудим это!
- Почему первые две петли в
range(ar)а такжеrange(bc)? Ну, как вы помните изПравило-2наша результирующая матрица будет иметь размерыar,bc, И из Excel мы увидели, что мы пересекаем каждый элементСследовательно, один за другим, чтобы пройтиarстроки иbcстолбцы нам нужно 2 цикла вrange(ar)а такжеrange(bc), - Итак, почему третий цикл FOR в
range(ac) #or br? Ну изПравило-1, мы знаем этоac==brтак что на самом деле не имеет значения, ставим ли мыrange(ac)илиrange(br)в третьем цикле. По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, дляC[0][0]это где шагC[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951произойдет, и, наконец, мы перейдем к следующей коробке. Количество предметов, которые умножаются и складываются вместе, равноac or br,
Это действительно так! Это метод-1 для вас! Вот песня, чтобы помнить Матричное Умножение. (Я узнал об этом первым из fast.ai, оригинальный автор неизвестен)
Надеюсь, теперь вы понимаете, как две матрицы умножаются друг на друга. Если не, Вот это еще один учебник Хан Академии
Метод 2: Использование поэлементного умножения
Так что до сих пор мы разбираем каждую позицию в результирующей матрицеC,найти отдельные элементы, а затем суммировать их вместе. Если вы помните, что-то вродеC[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951, Конечно, должен быть другой путь? Что если вместо того, чтобы делать отдельные продукты, а затем суммировать их, мы умножаем векторы за один раз, чтобы получить результирующий вектор, и суммируем полученный вектор, чтобы получить конечный элемент?
m = tensor([1, 2, 3])
n = tensor([10, 10, 10])
m*n>>tensor([10, 20, 30])
До сих пор мы находили отдельные продукты10, 20, 30и сложить их вместе10 + 20 + 30 = 60, Но, действительно, все это можно заменить на:
m = tensor([1, 2, 3])
n = tensor([10, 10, 10])
(m*n).sum()>>tensor(60)
Если вы помните, самый внутренний цикл вrange(ac) #or brнаходил отдельные продукты и добавлял их. Ну, мы можем заменить этот цикл, чтобы выполнить векторное поэлементное произведение и положить.sum()в конце концов, и PyTorch / NumPy имеют возможность выполнять поэлементные операции для нас!
Вот как это выглядит в Excel:
Точно так же мы получаемC[0][3]путем умножения вектора в строке 0с вектором на цв 3Ви суммируя полученный вектор.
И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой ящик вСчтобы получить окончательный результат.
Обратите внимание, как это отличается отМетод-1? На этот раз мы просто говорим Excel или PyTorch: умножьте строку 0с col 0 изВи суммируем полученный вектор, чтобы дать нам ответ. Вместо того чтобы делать1*1 + 10*5 + 100*9, Например, дляC[0][0]этот метод умножает Vector на строку 0tensor([1,10,100])с вектором в столбце 0 изВtensor{[1,5,9])чтобы получить промежуточный продукт Векторtensor([1,50,900])и суммирует это, чтобы дать результат в положенииC[0][0]какtensor(951),
В коде это выглядит так:
def matmul2(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar,bc)
for i in range(ar):
for j in range(bc):
c[i,j] = (a[i,:]*b[:,j]).sum()
return c
Таким образом, мы просто анализируем каждую позициюC,используя две петли FOR и введите соответствующий результат в этой позиции. Еслиi,jпредставляют строки и столбцы вСэто выглядит примерно так …
i:0,j:0
a:tensor([ 1, 10, 100]),b:tensor([1, 5, 9])
tensor([[951., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:1
a:tensor([ 1, 10, 100]),b:tensor([ 2, 6, 10])
tensor([[ 951., 1062., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:2
a:tensor([ 1, 10, 100]),b:tensor([ 3, 7, 11])
tensor([[ 951., 1062., 1173., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:0,j:3
a:tensor([ 1, 10, 100]),b:tensor([ 4, 8, 12])
tensor([[ 951., 1062., 1173., 1284.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
---
i:1,j:0
a:tensor([ 2, 20, 200]),b:tensor([1, 5, 9])
tensor([[ 951., 1062., 1173., 1284.],
[1902., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
И так далее .. пока мы не получим полную матрицуС,
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[3804., 4248., 4692., 5136.]])
Метод 3: вещание
Заметили общую тему здесь? Каждый раз мы должны умножить каждый рядс каждым столбцомВполучитьС, Вы замечаете повторение? Мы умножаем один и тот же вектор строки вbcраз! И мы повторяем этот процессarраз!
Есть ли способ умножить вектор строкисо всеми столбцамиВполучить соответствующий ряд вC?Да, есть! Войдите в трансляцию …
Примечание: я не буду объяснять вещание, Джереми делает это очень хорошо Вот,
Вместо этого давайте посмотрим, что это за волшебный кусок кода
for i in range(ar):
c[i] = (a[i,:].unsqueeze(-1).expand_as(b)*b).sum(dim=0)
Как обычно, давайте повторим в Excel! Это сделает вещи действительно легкими. Давайте сделаем это поэтапно.
Шаг 1)Выберите i-й рядa[i,:], Мы выбираем строку 0 в качестве примера.
Шаг 2)Возьмите егоТранспонированиеa[i,:].unsqueeze(-1)
Шаг 3)Развернуть матрицу столбца какВa[i,:].unsqueeze(-1).expand_as(b)
Шаг-4)Элемент мудрый умножить наВa[i,:].unsqueeze(-1).expand_as(b)*b
Шаг-5)Суммируйте по строкам, чтобы получить строку 0 C
Полный процесс вещания для каждого рядавыглядит примерно так:
Я надеюсь, что теперь вы получитевещания!Итак, давайте посмотрим, как это выглядит в коде ..
def matmul3(a,b):
ar,ac = a.shape
br,bc = b.shape
assert ac==br
c = torch.zeros(ar,bc)
for i in range(ar):
c[i] = (a[i,:].unsqueeze(-1).expand_as(b)*b).sum(dim=0)
print(f"i:{i}")
print(c)
return c
Вывод выглядит так:
i:0
tensor([[ 951., 1062., 1173., 1284.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
i:1
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
i:2
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[ 0., 0., 0., 0.]])
i:3
tensor([[ 951., 1062., 1173., 1284.],
[1902., 2124., 2346., 2568.],
[2853., 3186., 3519., 3852.],
[3804., 4248., 4692., 5136.]])
Это именно то, как мы ожидаем, что это будет так же, как нашиВерсия Excel!
Вот и все! Мы успешно рассмотрели три метода умножения матриц, включая вещание.
Google лист для вышеупомянутой иллюстрации можно найти Вот, Спасибо за чтение! Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь обращаться ко мне по адресу https://linkedin.com/in/aroraaman/,
В
— это наборы чисел, расположенные
горизонтально (вектор-строка) или
вертикально (вектор-столбец).
-
сложение
—
два векторааиbс
одинаковым числом компонент образуют
новый векторс:сi
= ai
+ bi; -
умножение
на число — каждая компонента вектора
умножается на число, т.е. b
= λа
означает bi
= λаi
здесь
i— номер компоненты вектора.
Упражнение
6.1.1.
Сложить два вектора:
-
Ввести
в первую строку вектор Х
— (А1:Е1) -
Ввести
во вторую строку вектор Y
— (А2:Е2) -
Найти
сумму векторов –
-
выделить
блок ячеек для результата в третьей
строке (А3:Е3); -
ввести
в строке формул =А1:Е1+А2:Е2 -
нажать
Ctrl+Shift+Enter.
Иллюстрация
к примеру — рис. 14.
А
В С D
E

2
3
Рис.
14.
Иллюстрация к упражнению 6.1.1.
Задача
6.1.1.
Умножить
вектор на число.
Упражнение
6.1.2.
Умножение
вектор-столбца на вектор-строку.

блоке (вектор-столбце) А2:А5 записаны
числа: 1,2,3,4. Требуется получить в блоке
B2:D5 три вектор-столбца, каждый из которых
представляет собой результат умножения
исходного вектор-столбца на вектор-строку:
2, -3, 4 (B1:D1).
Рис.15.
К упр. 6.1.2.
Решение.
1-й
способ: записать в ячейку В2 формулу
=$А2*В$1
и скопировать ее в остальные ячейки
диапазона B2:D5.
2
-й способ (более экономный): выделить
блок B2:D5. Запишем в него формулу
массива {=А2:А5*B1:D1}.
А
решения.
Табличный массив {2;-3;4} — вектор-строка,
а блок А2:А5 — вектор-столбец. Значит,
матрица B2:D5 размерностью 4Х3
является
результатом умножения вектор-столбца
А2:А5 (4Х1)
на
вектор-строку B1:D1
(1Х3).
Примечание.
Если ввести формулу {=B1:D1*
А2:А5}, то получится тот же результат,
хотя с позиций матричной алгебры
вектор-строку (1х3)
нельзя умножать на вектор-столбец (4х1)
из-за несогласованности размеров (число
столбцов в первом сомножителе должно
равняться числу строк во втором
сомножителе).
У
6.1.3.
Вычислить скалярное произведение двух
векторов.
-
У
становить
курсор в ячейку, где нужен результат. -
Щёлкнуть
кнопку автосуммы — . -
Выделить
массив Х
(А5:А12). -
Нажать
знак умножить —*. -
Выделить
массив Y
(B5:B12). -
Нажать
Ctrl
+ Shift + Enter.
Примечание.
Тот
же результат можно получить с помощью
обычной функции:
=СУММПРОИЗВ
(А5:А12,
В5:В12).
6.2. Матричные операции
Простейшие
операции, которые можно проделывать с
матрицами: сложение (вычитание),
умножение на число, перемножение,
транспонирование, вычисление обратной
матрицы.
Упражнение
6.2.1.
Сложение
матриц.
Задание.
Сложить
матрицы М и N, где
Решение.
M=
и N=
1-й
способ:
-
Ввести
матрицу М в блок А1:С2, а матрицу N в блок
Е1:G2. -
В
блок А4:С5 ввести табличную формулу {=
А1:С2 + E1:G2}.
Примечание.
Выделен
блок, имеющий те же размеры, что и
исходные матрицы.
2-й
способ:
Использование
имен
делает процедуру ввода табличной
формулы намного проще:
-
Задать
диапазонам А1:С2 и E1:G2 имена М и N. -
В
блок E4:G5 ввести табличную формулу {
= М + N }.
Результат,
естественно, тот же: M+N
=
Упражнение
6.2.2.
Вычислить линейную
комбинацию
матриц 2*М — N (матрицы М.и N из упражнения
6.2.1.).
Решение.
В
блок А7:С8 ввести табличную формулу
{= 2*М — N
}.
Результат:
2*M
— N
=
Задача
6.2.1.
Осмысленные
результаты (не имеющие ничего общего
с матричной алгеброй) получаются при
сложении матриц разных размеров.
Придумать примеры и попытаться выявить
правила, по которым Excel выполняет такое
сложение.
Д
операций
в Excel предусмотрены функции, входящие
в категорию «Математические»:
МОПРЕД
— вычисление определителя матрицы;
МОБР
— вычисление обратной матрицы;
МУМНОЖ
— перемножение матриц;
ТРАНСП
— транспонирование.
Примечание.
Первая из этих функций возвращает
число, поэтому вводится как обычная
формула. Остальные функции возвращают
блок ячеек, поэтому они должны вводиться
как табличные
формулы.
У
6.2.3.
Вычислить определитель
и обратную
матрицу
для матрицы:
А
=
Решение.
Разместить
исходную матрицу в блоке А1 :СЗ.
-
В
ячейке Е2 поместить формулу для
вычисления определителя =
МОПРЕД (А1:СЗ). -
В
блок А5:С7 ввести формулу для вычисления
обратной матрицы:
-
выделить
блок
А5:С7 (он имеет три строки и три столбца,
как и исходная матрица). -
Ввести
формулу {=МОБР
(А1:СЗ)}.
Примечания:
-
При
использовании Мастера функций нужно
завершать ввод нажатием комбинации
клавиш Ctrl+Shift+Enter
(вместо щелчка по кнопке «ОК»). -
Для
удобства работы рекомендуется задавать
имена
исходной матрице и обратной матрице.
-
Проверить
правильность вычисления обратной
матрицы умножением ее на исходную:
-
задать
имена исходной матрице — А и обратной
матрице — АО; -
в
блок D5:F7 ввести формулу {=МУМНОЖ
(А,АО)}. -
к
ак
и следовало ожидать, получилась матрица,
близкая к единичной.
Рис.
16. Иллюстрация к упражнению 6.2.3.
У
Решение:
пражнение 6.2.4.
Вычислить абсолютные отклонения
величин в матрицах.
В
блок А9:С11 ввести табличную формулу {=
abs
(A-AО)}.
Примервычисления определителя матрицы
А, введенной в
формулу как массив констант:
=МОПРЕД({-73;
78; 24:
92;
66; 25:
-80; 37; 10}).
Задача
6.2.2.
При каком значении элемента а33
определитель
матрицы А обратится в нуль.
Задача
6.2.3.
Дана матрица S
=
.
Вычислить матрицу2SSТ
— Е,
где
Т — операция транспонирования,
Е
— единичная матрица.
Задача
6.2.4.
Вычислить обратную матрицу для
и
применить форматирование, чтобы элементы
матрицы представляли собой правильные
дроби. Выбрать формат на основе величины
определителя матрицы.
Набор
матричных операций в Excel беден.
Если
нужно серьезно работать с матрицами,
лучше прибегнуть к помощи таких
математических пакетов, как MatLAB
(Matrix LABoratory), Mathematica, Derive.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Умножение и деление матрицы на число в Excel
Способ 1
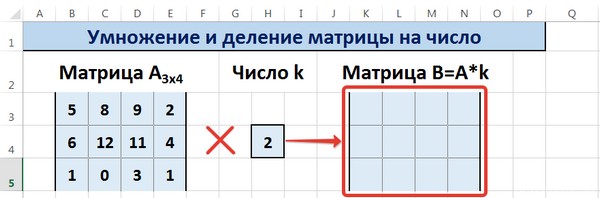
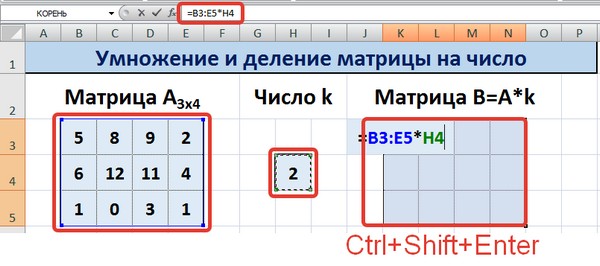
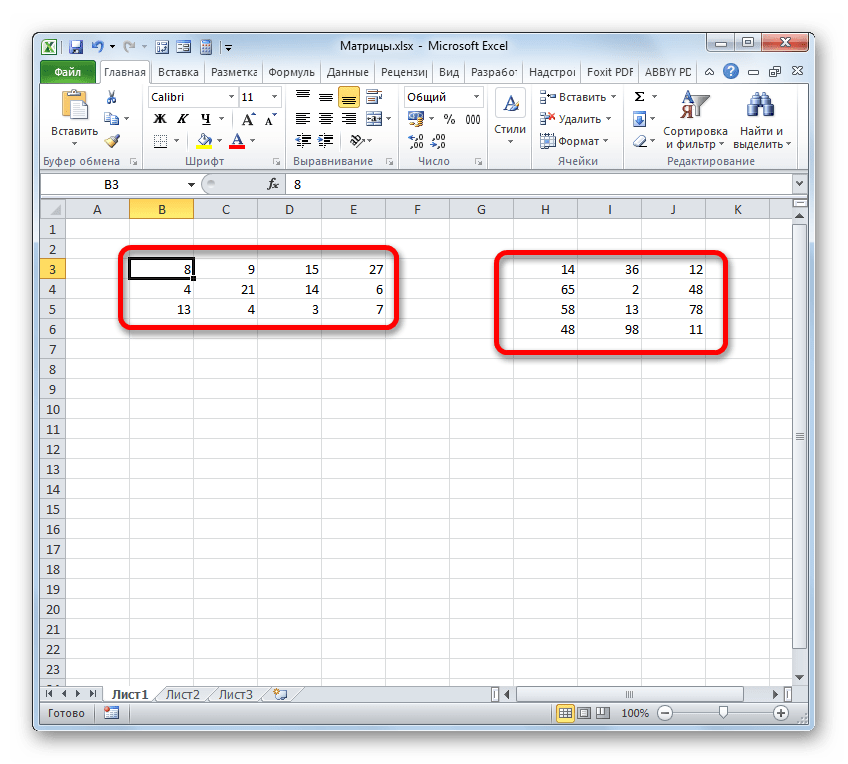
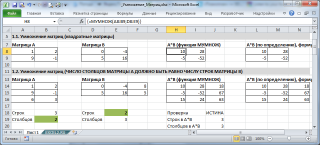
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
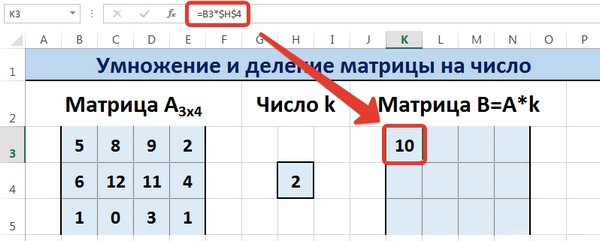
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
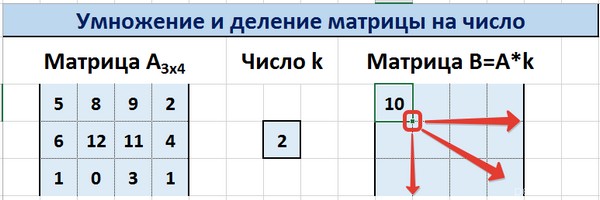
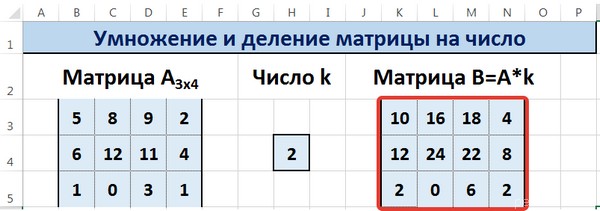
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
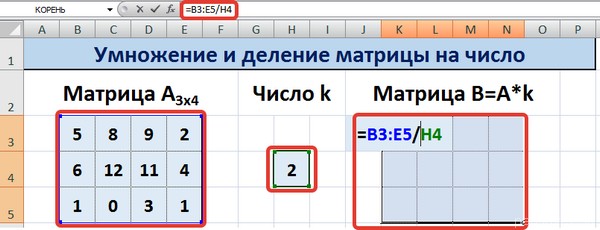
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
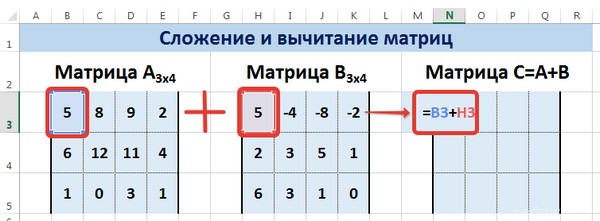
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
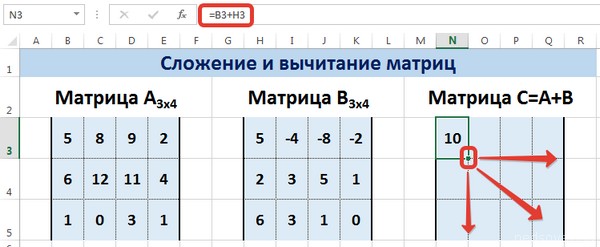
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
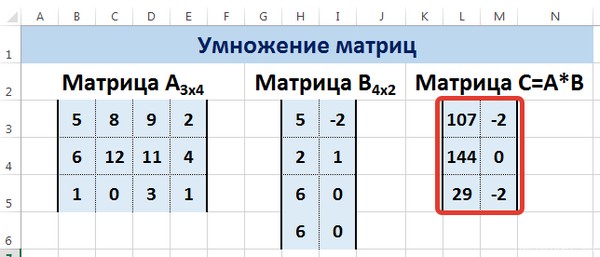
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
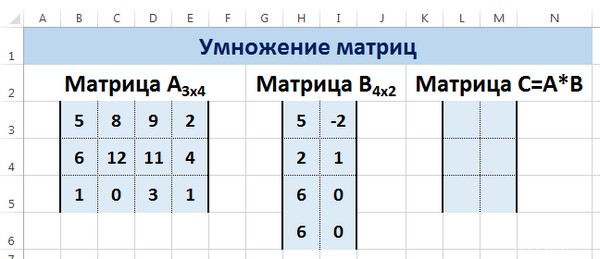
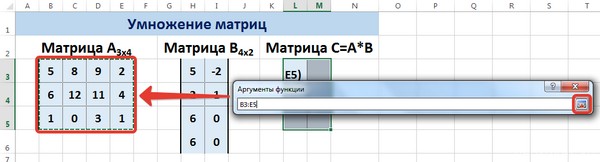
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
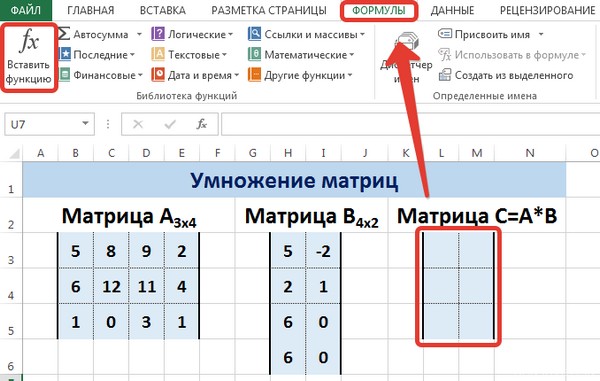
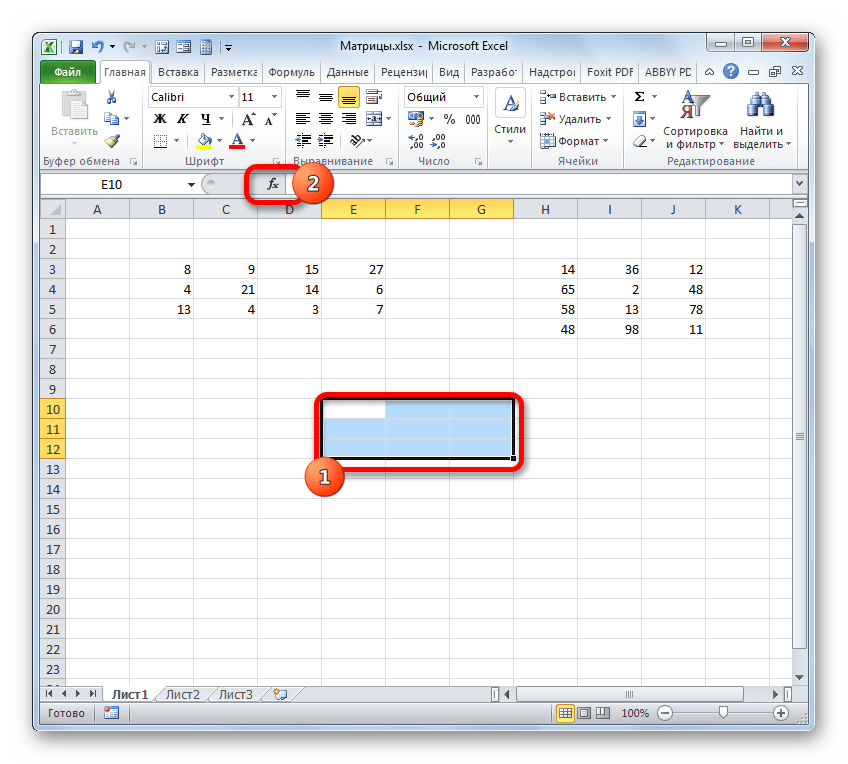
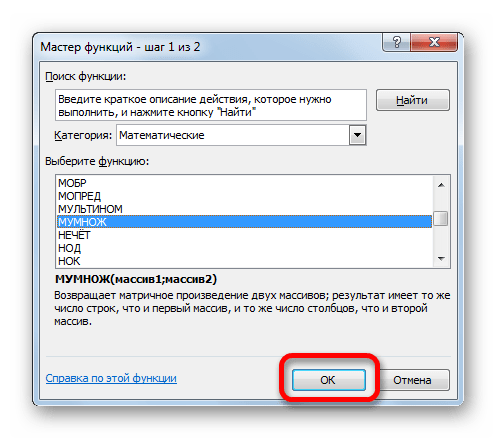
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
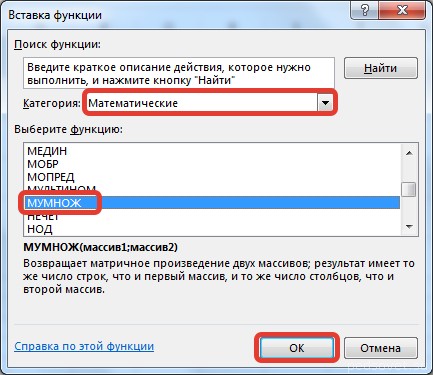
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
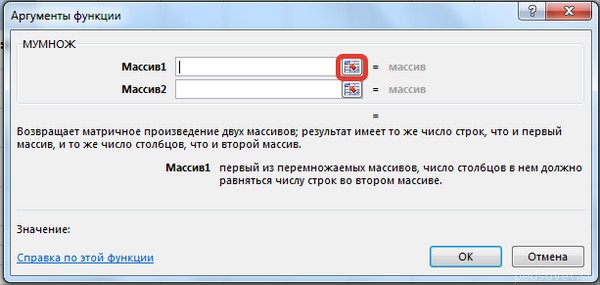
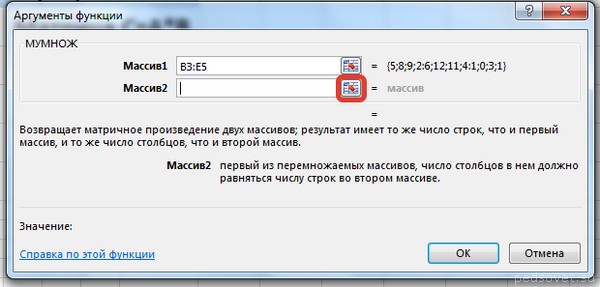
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
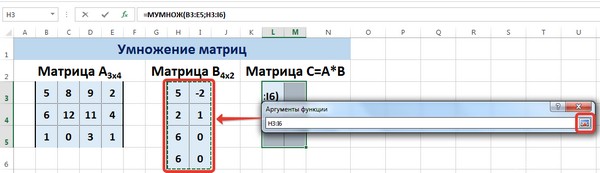
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
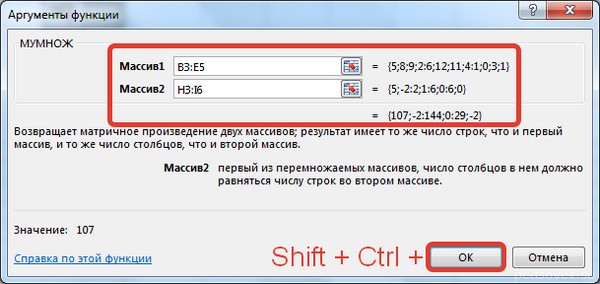
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
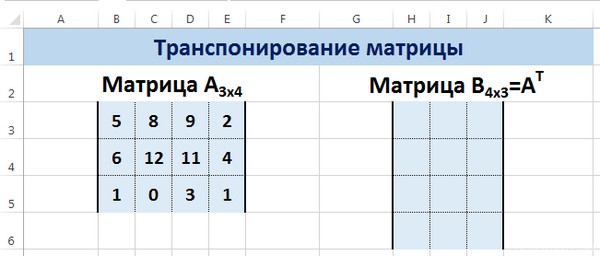
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу АТ.
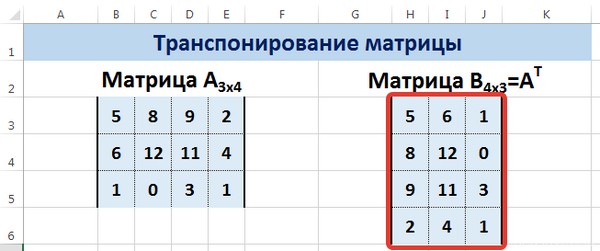
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу АТ, причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
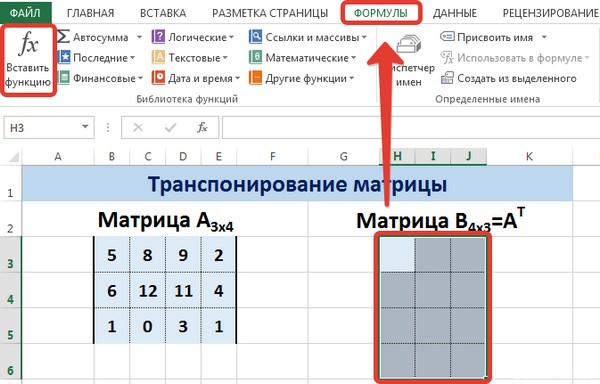
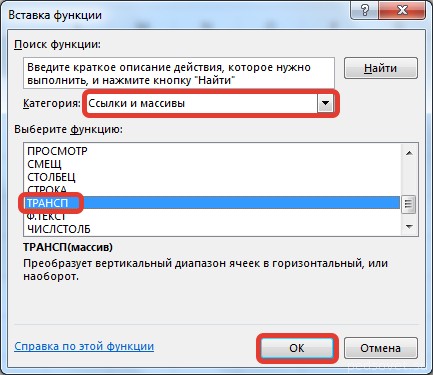
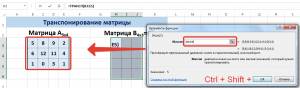
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы АТ.
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А-1 называется обратной для матрицы А, если АА-1=А-1А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
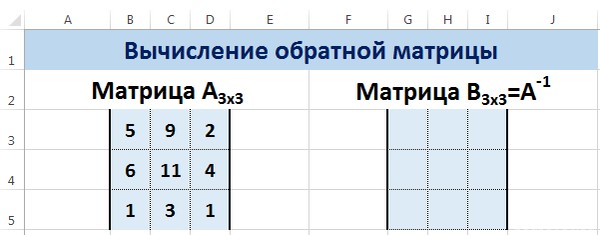
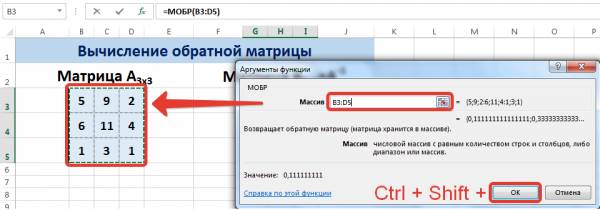
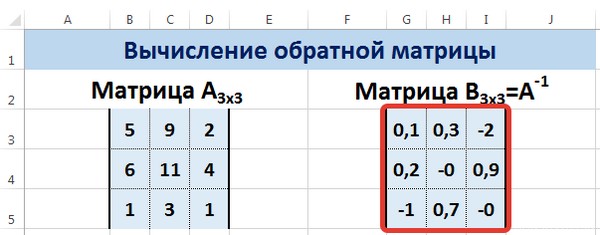
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
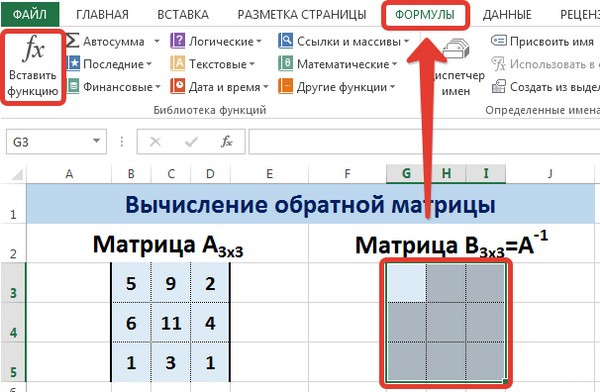
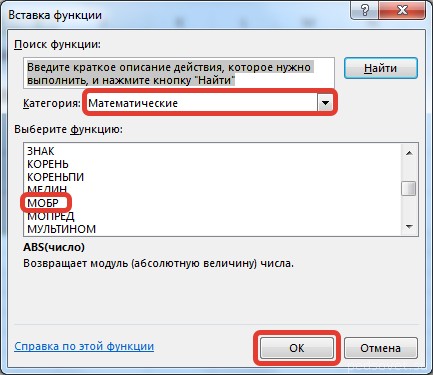
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А-1.
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
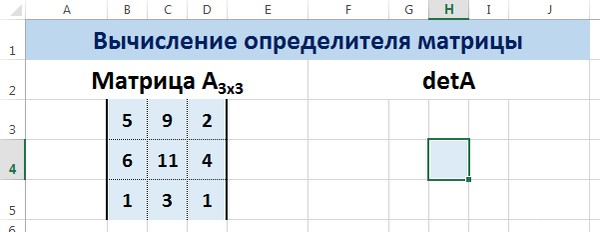
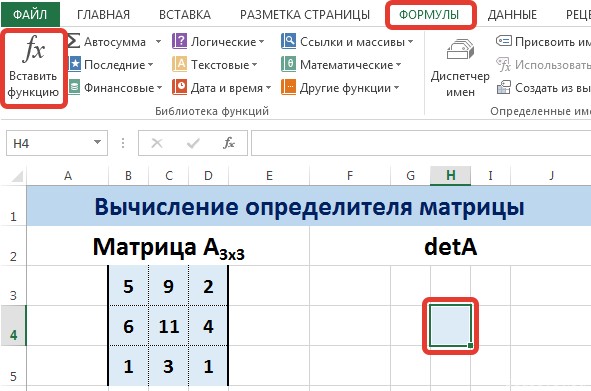
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
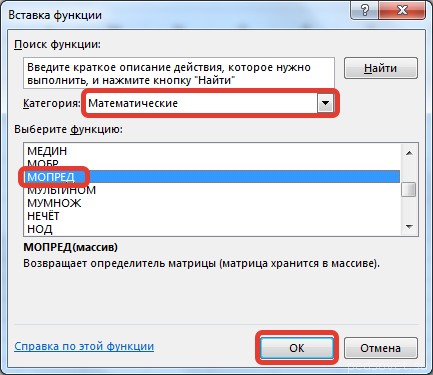
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
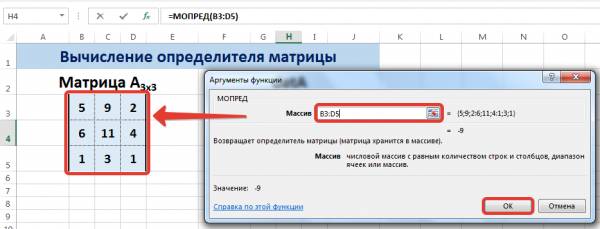
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
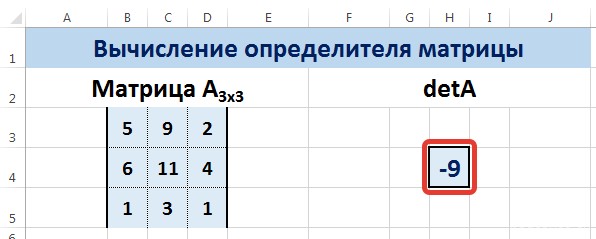
Нажмите для увеличения
Мы вычислили определитель матрицы А.
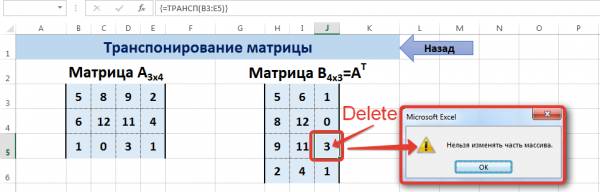
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.



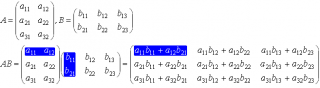

















 становить
становить
 ак
ак